Gating of Single N-type Calcium Channels Recorded from Bullfrog Sympathetic Neurons

Abstract

For many neurons, N-type calcium channels provide the primary pathway for calcium influx during an action potential. We investigated the gating properties of single N-type calcium channels using the cell-attached patch technique. With 100 mM Ba²⁺ in the pipet, mean N-channel open probability (P _o, measured over 100 ms) increased with depolarization, but the range at a single voltage was large (e.g., P _o at +40 mV ranged from 0.1 to 0.8). The open dwell time histograms were generally well fit by a single exponential with mean open time (τ_o) increasing from 0.7 ms at +10 mV to 3.1 ms at +40 mV. Shut time histograms were well fit by two exponentials. The brief shut time component (τ_sh1 = 0.3 ms) did not vary with the test potential, while the longer shut time component (τ_sh2) decreased with voltage from 18.9 ms at +10 mV to 2.3 ms at +40 mV. Although N-channel P _o during individual sweeps at +40 mV was often high (∼0.8), mean P _o was reduced by null sweeps, low P _o gating, inactivation, and slow activation. The variability in mean P _o across patches resulted from differences in the frequency these different gating processes were expressed by the channels. Runs analysis showed that null sweeps tended to be clustered in most patches, but that inactivating and slowly activating sweeps were generally distributed randomly. Low P _o gating (P _o = 0.2, τ_o = 1 ms at +40 mV) could be sustained for ∼1 min in some patches. The clustering of null sweeps and sweeps with low P _o gating is consistent with the idea that they result from different modes of N-channel gating. While P _o of the main N-channel gating state is high, the net P _o is reduced to a maximum value of close to 0.5 by other gating processes.

introduction

N-type calcium channels are important for neurotransmitter release at synapses of the peripheral and central nervous system. Although there has been much progress on characterizing the kinetics and modulation of whole-cell N-current (Hess, 1991; Bertolino and Llinás, 1992; Jones and Elmslie, 1992, 1997; Hille, 1994; Dolphin, 1996), relatively few studies have examined the gating of single N-channels. One problem has been the identification of the N-channel. Single calcium channels identified as N-type in some early publications (Delcour et al., 1993; Delcour and Tsien, 1993; Lipscombe et al., 1989) now appear to have been misidentified (Elmslie et al., 1994; Elmslie, 1997). These misidentified channels activate at voltages greater than −30 mV, inactivate strongly at a −40 mV holding potential, and the single channel current at 0 mV is 0.5–0.8 pA (Delcour et al., 1993; Delcour and Tsien, 1993; Lipscombe et al., 1989), which closely matches the properties of a ω-conotoxin GVIA-insensitive calcium channel, which we now call E_f channel (Elmslie, 1997).

Our laboratory recently identified the N-type calcium channel in bullfrog sympathetic neurons by comparing the single channel properties to those of the whole-cell N-current in isotonic Ba²⁺ (Elmslie et al., 1994; Elmslie, 1997). In 100 mM Ba²⁺, N-channels activate at voltages >0 mV, have a slope conductance of ∼20 pS, a single channel current at 0 mV of 1.4 pA, and are active from a holding potential of −40 mV. In addition, we showed that single N-channels were blocked by ω-conotoxin GVIA, but L- and E_f-type channels were insensitive to this specific N-channel blocker (Elmslie, 1997).

Several studies have examined gating from identified N-channels (Plummer and Hess, 1991; Rittenhouse and Hess, 1994; Carabelli et al., 1996). Studies on neonatal rat sympathetic neurons found that N-channels, like L-type calcium channels, could gate in different modes. Three activation modes and two inactivation modes were characterized (Plummer and Hess, 1991; Rittenhouse and Hess, 1994). However, a recent study of N-channels in a human neuroblastoma cell line (IMR32 cells) failed to detect different gating modes (Carabelli et al., 1996).

To better understand the relationship between calcium influx and neurotransmitter release, kinetic models have been generated based on whole-cell recordings from large nerve terminals (Borst and Sakmann, 1998; Llinás et al., 1981). Information on P _o, mean open and shut times, and different gating modes is important for the development of such models. Here, we examine the gating kinetics of single N-channels. Similar to Carabelli et al. (1996), we find that active N-channels usually gate with a single, characteristic P _o at a given voltage, which we call high P _o gating. However, several gating processes are important in establishing mean P _o (measured over many sweeps). One of these is a low P _o gating state in which the channel can dwell for an extended period. Unlike the rat N-channel (Rittenhouse and Hess, 1994), sustained low P _o gating was observed infrequently. Other processes that alter P _o include null gating, inactivation, and slow activation. Null sweeps and sweeps exhibiting low P _o tend to be clustered, which is consistent with the idea that N-channels can alter their gating properties by changing gating modes.

methods

Cells

Neurons were dissociated from caudal paravertebral sympathetic ganglia of adult bullfrogs (Rana catesbeiana) by a collagenase/dispase digestion and trituration. Cells were maintained in L-15 culture medium, supplemented with 10% fetal bovine serum and penicillin/streptomycin, at 4°C until use (usually 1–10 d) (Kuffler and Sejnowski, 1983; Jones, 1987; Elmslie, 1992).

Cell-attached Patch Recording

Recording conditions were similar to those previously published from our laboratory (Elmslie, 1997). In brief, the pipet solution consisted of (mM) 100 BaCl₂, 10 tetraethylammonium chloride, 5 4-aminopyridine, and 10 N-methyl-d-glucamine (NMG)–HEPES. The extracellular solution was designed to zero the cell's membrane potential and contained (mM) 100 KCl, 10 K-HEPES, and 5 NMG-EGTA, pH 7.2. The zeroing solution contained 1 μM (±) Bay K 8644 (Research Biochemicals Inc.) to reveal the presence of L-channels in the patch (Plummer et al., 1989). Patches containing L-type calcium channels were excluded from analysis.

Electrodes for single channel experiments were fabricated from either Corning 7740, Kimble EN-1 (both o.d. 2.0 mm, i.d. 0.7 mm; Garner Glass Co.) or Corning 7052 (o.d. 1.5 mm, i.d. 0.86 mm; A-M Systems) glass. These electrodes had resistances ranging from 15 to 40 MΩ. Recordings were done using fiber-filled glass to facilitate the filling of the electrode. The glass fiber did not appear to alter either the quality or frequency of seal formation when using Corning 7740 or 7052. However, we had problems getting seals with the EN-1 glass and we do not yet know if this problem was due to the glass fiber. The electrodes were coated with the General Electric equivalent of Sylgard (GE Silicones RTV615; General Electric Co.).

An Axopatch 200A amplifier (Axon Instruments) was used to amplify and filter (2 kHz) the currents. Currents were amplified an additional 10× by a Bessel filter (900; Frequency Devices Inc.) and digitized with a MacAdios II analogue-digital converter (GW Instruments) at 10 kHz (five times the filter cut off frequency). The experiment was controlled by a Macintosh II computer running S3 data acquisition software written by Dr. Stephen Ikeda (Guthrie Research Institute, Sayre, PA), and the data were analyzed using IgorPro (WaveMetrics).

Data were obtained in sets of 100 voltage steps of 100-ms duration delivered at a 2-s interval. This interval is long with respect to the recovery from inactivation at our holding potential of −40 mV (τ = ∼300 ms; Jones and Marks, 1989b), which is equivalent to −80 mV in 2 mM Ba²⁺ (Elmslie et al., 1994). Therefore, it is unlikely that the stimulation frequency will influence our results. The test voltage was varied randomly across data sets to compensate for drifts in open probability (P _o) during the recording.

Analysis of Single-Channel Records

Uncorrected capacitative current and voltage-independent leakage current were removed from the records by averaging null sweeps and subtracting them from the active sweeps. If null sweeps were rare, a null record was made by averaging sweeps after the active regions had been blanked. Single channel current amplitudes were determined using low variance analysis (Patlak, 1988, 1993; Elmslie et al., 1994; Elmslie, 1997).

Single channel events were detected using the 50% threshold detection method after being Gaussian filtered at 1 kHz. These events were log binned into open and shut dwell time histograms (10 bins/decade; Sigworth and Sine, 1987). The first closed time and the last event in the step (whether closed or open) were excluded from these dwell time histograms. The dwell time distributions were fit to exponential functions using the Marquardt-Levenberg algorithm (IgorPro routine). The first closed time was used to generate the cumulative first latency histogram.

We have used two methods to calculate P _o during voltage steps. (a) To facilitate comparisons with whole-cell activation vs. voltage plots, P _o was calculated by dividing the sum of all open times during the step by the step duration. The mean P _o was calculated by averaging the P _o measured from all sweeps at a particular voltage. The plot of P _o vs. voltage was fit using the Boltzmann equation to obtain the half activation voltage (V_1/2), the e-fold change in P _o with voltage, and the maximum P _o. (b) When we examined the stationarity of N-channel gating, P _o was calculated on a sweep by sweep basis by excluding the first and last shut times. P _o calculated in this manner is referred to as P _o-ex to distinguish it from the other method.

results

The criteria for identification of N-channels in cell-attached patch recordings was established in a previous paper (Elmslie, 1997). In brief, N-channels recorded in 100 mM Ba²⁺ activate at voltages ≥+10 mV, are active from a holding potential of −40 mV, have a slope conductance of ∼20 pS, and a single channel current at 0 mV of ∼1.4 pA. The data for this paper was compiled from 18 cell-attached patch recordings that contained one (n = 11), two (n = 5), or three (n = 2) N-channels. 8 of 11 patches that contained a single N-channel also had at least one E_f-channel. As shown previously, N- and E_f-channel activities are easily distinguished since the single channel current amplitude of E_f-channels is approximately one third that of the N-channel, and E_f-channel activity is strongly inactivated at the −40-mV holding potential used for most of these recordings (Elmslie et al., 1994; Elmslie, 1997). All patches containing L-channels were excluded from analysis because of the difficulty of distinguishing single N- from L-channel currents (Plummer et al., 1989; Elmslie, 1997). The slope conductance for the channels used in this study ranged from 20–25 pS (mean 22.2 ± 1.5 pS [SD], n = 18).

Voltage-dependent Properties

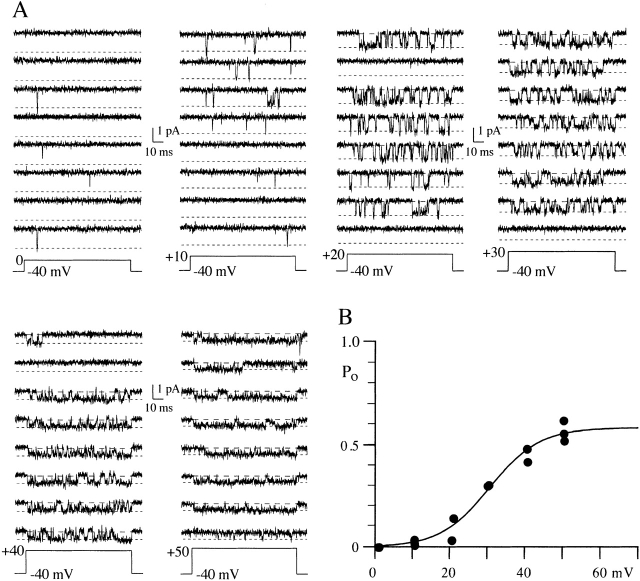
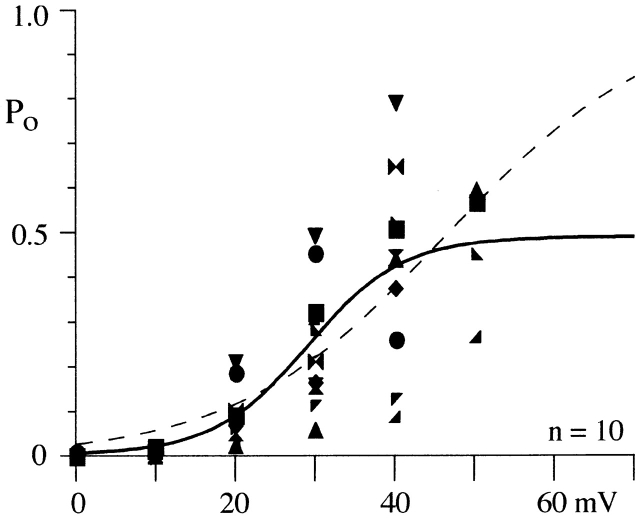
Activation of whole-cell N-current has been shown to be steeply voltage dependent with the activation vs. voltage relation rising e-fold for 7–9 mV (Jones and Marks, 1989a). We measured P _o from 100-ms voltage steps ranging from 0 to +50 mV in single N-channel patches (Figs. 1 and 2). Data were obtained from 10 patches for the voltage range +10 to +40 mV; however, we have data for 0 mV in only two patches and +50 mV in five. The noise level of the patch must be very low for us to resolve N-channel activity at +50 mV since the single channel current amplitude is generally ≤0.4 pA. The mean P _o (including null sweeps) increased from 0.01 at +10 mV to ∼0.5 at +40 mV. Fig. 1 B shows this for a single patch, while the data from all patches are shown in Fig. 2. The data from individual patches were well fit by a single Boltzmann equation (Fig. 1 B). However, fitting parameters vary when compared across cells because of differences in mean P _o (Table I). Since whole-cell data is generated from the activity of many channels, we fit a single Boltzmann equation to the data from all patches, which yielded a V_1/2 of +29 mV, a slope of 6 mV, and a max P _o of 0.49 (Fig. 2). This slope is consistent with that measured from whole-cell recordings from frog sympathetic neurons (7–9 mV, Jones and Marks, 1989a; 4.5 mV, Boland and Bean, 1993). In addition, the V_1/2 is ∼50 mV depolarized to that measured in 2 mM Ba²⁺ (approximately −20 mV; Jones and Marks, 1989a; Elmslie et al., 1992; Boland and Bean, 1993). This is consistent with the 40-mV rightward shift observed in the whole-cell current–voltage relation when switching from 2 to 90 mM Ba²⁺ (Elmslie et al., 1994). However, the variability in P _o across patches was large (Fig. 2). Therefore, we also fit the data by constraining P _o = 1 to allow comparisons to the unconstrained fit. This fit yielded a V_1/2 of 47 mV and a slope of 13.4 mV (dashed line on P _o vs. voltage plot, Fig. 2), which are not consistent with the whole-cell data discussed above. The large variability in P _o measured from different patches makes it difficult to identify maximum N-channel P _o. However, this variability results from several gating processes that decrease P _o from that of the main gating mode. These processes are physiologically important and are considered in detail below.

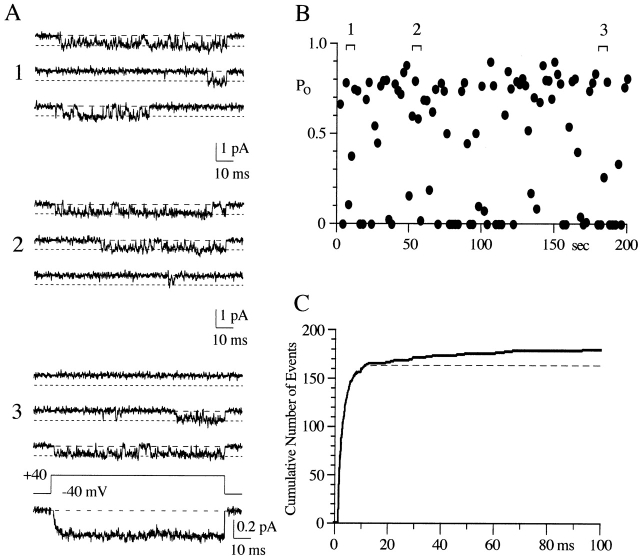
Figure 1.

Effect of voltage on N-channel gating. (A) Eight consecutive sweeps are shown for each voltage. This patch contained one N-channel and at least one E_f-channel. The illustrated records were Gaussian filtered at 1 kHz. The two dashed lines indicate the channel open level (short dashes) and the baseline (long dashes). (B) P _o vs. voltage relation for the patch illustrated in A. P _o was measured from 100-ms voltage steps ranging from 0 to +50 mV, and each symbol is the mean P _o (included nulls) calculated from a 100-sweep data set. Multiple data sets were obtained at each voltage. The solid line is from a single Boltzmann fit to all points. The parameters for the line are V_1/2 = 31 mV, slope = e-fold for 7 mV, and maximum P _o = 0.58.

Figure 2.

N-channel P _o varies across patches. The mean P _o (including null sweeps) for each patch is plotted for all voltages examined. Data from each of the 10 single N-channel patches is shown as a different symbol, and the same symbol code is used again in Fig. 4. The solid line is from a single Boltzmann fit to all points. The parameters for the line are V_1/2 = 29 mV, slope = e-fold for 6 mV, and maximum P _o = 0.49. The dashed line is single Boltzmann fit constrained to P _o = 1. For this fit, V_1/2 = 47 mV and slope = e-fold for 13 mV.

Table I.

Boltzmann Parameters from Fits to P_O vs. Voltage Data from Individual Patches

Patch		V1/2		Slope		Maximum P O
		mV
960325a		30.8		6.6		0.58
960520c		36.9		3.2		0.61
960521b		29.1		6.6		0.94
960907b		41.8		8.6		0.83
980122a		19.8		3.0		0.13
980122e		28.1		4.2		0.49

The parameters are given for six patches in which P _O was measured over a range of at least 40 mV (usually +10 to +40 mV).  

The increase in N-channel P _o with voltage is driven by an increase in the mean open time and a decrease in the mean shut time. Qualitatively, this can be observed in the single channel records illustrated in Fig. 1. Fig. 3 shows this quantitatively in open- and shut-time histograms. For 7 of 10 patches, the open time histogram was well fit by a single exponential function at each voltage tested. On average, the mean open time increased from 0.7 ms at +10 mV to 2.6 ms at +40 mV (n = 7; Fig. 4 A). In the additional three patches, two exponentials were required to fit the open time histogram at +40 mV. The time constant from one of the two components (τ = 4.3 ± 1.3 ms, n = 3) matched that of the single exponential fits described above. The time constant of the other component was smaller (τ = 1.0 ± 0.3 ms, n = 3) and resulted from N-channels gating with low P _o at +40 mV (see Fig. 6).

Figure 3.

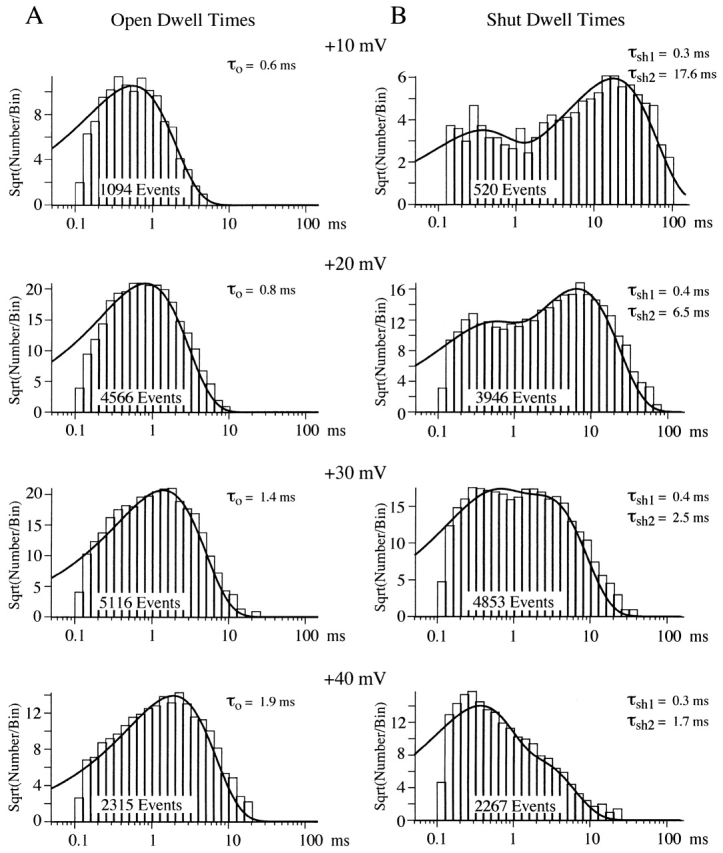
Mean open and shut times change with voltage. These open and shut times were measured from a patch with a single N-channel and at least one E_f-channel. (A) Open times were log-binned at 10 bins/decade. The ordinate was square-root transformed and the histogram was fit to a single exponential (smooth line). The number of events in the histogram and the mean open time is shown for each voltage. (B) Shut times from the same patch are displayed as in A. The smooth line is a double exponential fit to the histogram. The number of events in the histogram and the mean shut time for each exponential component are shown for each voltage. Note that the time constant of brief shut time component appears to be invariant over this voltage range.

Figure 4.

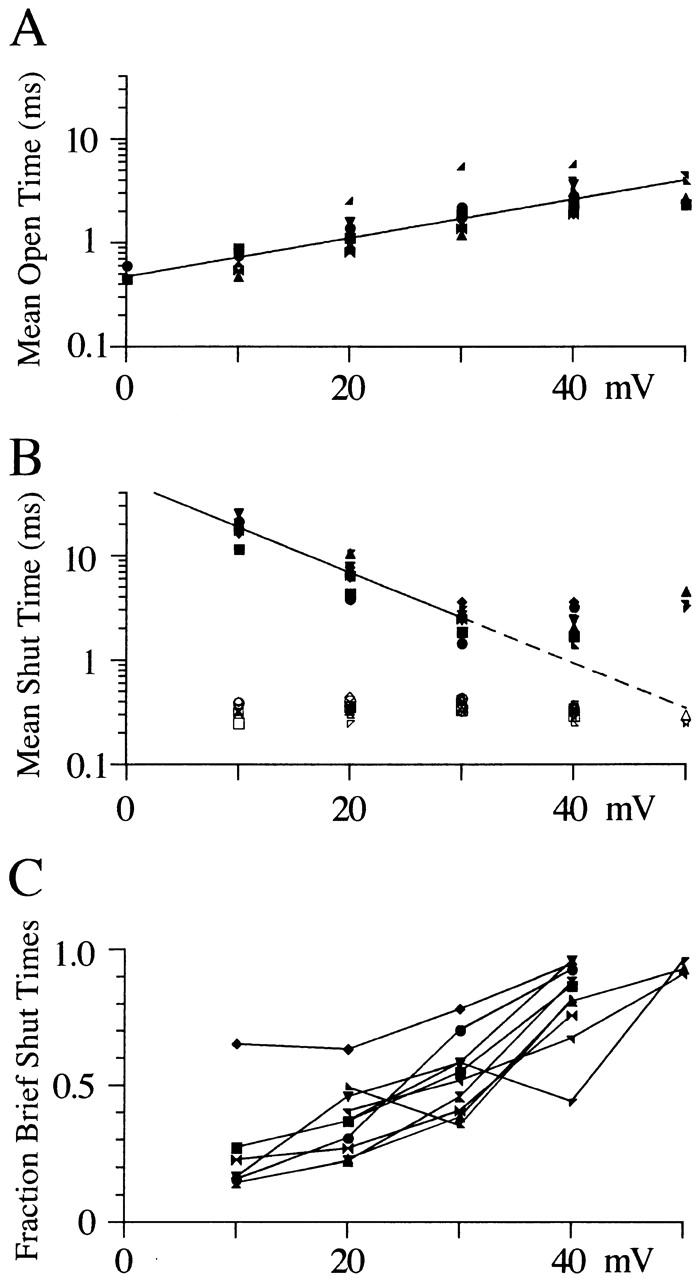
The effect of voltage on open and shut times is similar for all N-channel patches studied. (A) Mean open times from single-exponential fits to log-binned histograms are plotted against voltage for each of the 10 single N-channels studied. The same symbol code adopted for Fig. 1 is used here. The line shows an e-fold change in open time for 23 mV. Note that the number of observations is only 2 for 0 mV and 5 for +50 mV. (B) Mean shut times are plotted against voltage for each of the two exponential components. The line shows an e-fold change in shut time for 10 mV. (C) The fraction of brief shut times was calculated by dividing the amplitude of the brief exponential component by the sum of both exponential component amplitudes. The fractional shut times are plotted against step potential. The lines connect points from the same patch.

Figure 6.

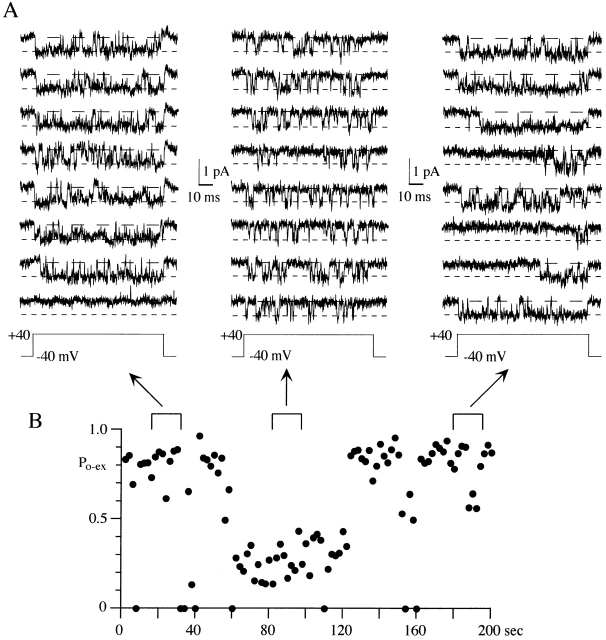
A single N-channel can show continuous periods of low P _o gating. (A) Eight consecutive sweeps are shown from three regions of 100-ms voltage steps to +40 mV. Early and late in the data set, the N-channel exhibited high P _o gating (P _o > 0.5). However, after sweep 30, the channel switched to low P _o gating for the next 33 sweeps (∼66 s). Note the shorter open times and longer shut times during low P _o gating. Slow activation (long first latency) is also seen in three of the last eight sweeps shown. This patch contained a single N-channel. (B) P _o-ex is shown in this diary plot for each of the 100 sweeps in the +40-mV data set. The brackets above the plot illustrate the areas shown in A.

Shut-time histograms illustrated in Fig. 3 were well fit by two exponentials. Interestingly, the mean shut time for the brief component was independent of the step potential, while the longer shut events showed a decrease in mean shut time with voltage (Figs. 3 B and 4 B). We were able to identify these two components in all the patches examined (Fig. 4). However, in a few patches, the histograms showed longer events (especially at +40 mV), which were not well described by the two-exponential fit. We attempted to obtain better fits with three or four exponentials, but the number of events was too small to obtain consistent convergence. Although we were unable to fit these longer events, their existence supports the presence of additional component(s). One limitation in this study is that our data were generated using 100-ms voltage steps (some 40-ms steps were also used). Therefore, components with mean shut times longer than ∼25 ms would be poorly resolved in our study.

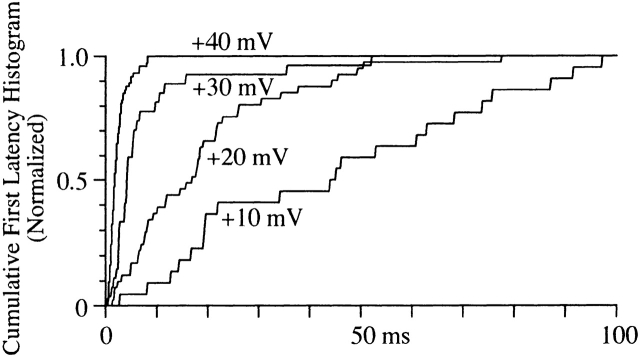
Measurement of the first latency to first channel opening can provide information about the pathway to channel opening. As expected, both the mean first latency and the time at which the cumulative distribution saturated decreased as voltage increased (Fig. 5). In the patch shown in Fig. 5, the maximum latency decreased from 78 ms at +20 mV to 9 ms at +40 mV (but see below and Fig. 10). In many patches, the first latency distribution rose monotonically after a brief delay. However, in other patches, a slow rising phase was observed in the distribution, which we have attributed to a slow activation process detailed below.

Figure 5.

First latency distribution. The times to first channel opening at each voltage were binned (0.2-ms bin width) into a cumulative histogram. Each histogram has been normalized to the value of the last bin to facilitate comparison. The number of events in each histogram is 22 for +10 mV, 41 for +20 mV, 27 for +30 mV, and 74 for +40 mV. The holding potential for this patch was −80 mV.

Figure 10.

A few sweeps showed long delays to first channel opening at +40 mV. (A) Three sets of three consecutive sweeps are shown for voltage steps to +40 mV. This patch contained a single N-channel and at least one E_f-channel. The pseudomacroscopic current at the bottom of the single channel records was averaged from 87 sweeps. The smooth line through the pseudomacroscopic current is a single exponential fit to the current after a delay (1.2 ms, see below) with a τ of 1.9 ms. (B) The diary plot of P _o measured over the 100-ms sweep duration shows the activity regions from which the example records (A) were taken. The numbered brackets correspond to the numbers in A. (C) The cumulative first latency histogram for voltage steps to +40 mV. The total number of sweeps is 178. To illustrate the fraction of short latency sweeps, the first 20 ms of the distribution was fit to a single exponential after a delay of 1.2 ms (dashed line). The 1.2-ms delay resulted from amplifier saturation by the uncorrected capacitative currents (see methods). The τ was 2.1 ms and maximum number of events is 165. The percentage of sweeps showing a long first latency at +40 mV was 7.3% in this patch.

Stability of N-Channel Gating

The variability in P _o measured from different patches was large. We were interested in identifying N-channel gating processes that were the source of this variability. Several processes can contribute to nonstationary gating of voltage-dependent ion channels. Some of these include (a) high P _o gating vs. low P _o gating (Hess et al., 1984), (b) null vs. active sweeps (Hess et al., 1984; Horn et al., 1984), (c) inactivating vs. noninactivating sweeps (Plummer and Hess, 1991), and (d) slow- vs. fast-activating sweeps (Carabelli et al., 1996; Patil et al., 1996). Many of these gating processes have been interpreted as the channel switching between different gating modes (Hess et al., 1984; Horn et al., 1984; Plummer and Hess, 1991). We examined possible nonstationary N-channel gating by focusing on sweeps recorded during voltage steps to +40 mV. The rationale was that the P _o at +40 mV is typically high (∼0.8), which would make null sweeps and low P _o sweeps stand out. In addition, the peak of the current–voltage (I–V) relation occurs near +40 mV in 100 mM Ba²⁺ (Elmslie, 1997), and inactivation is maximal near the peak of the I–V (Jones and Marks, 1989b). Observed nonstationary gating processes were analyzed using runs analysis (Horn et al., 1984) for evidence of clustering that would support a modal hypothesis.

High Versus Low P_o Gating

During voltage steps to +40 mV, the P _o of active sweeps was generally ∼0.8 with mean open times greater than ∼2 ms, but occasionally we noticed sweeps where the channel gated with low P _o and brief openings (Fig. 6). To examine these gating changes, we calculated P _o by excluding first and last shut times (P _o-ex; see methods), which ensures that the measurement will not be influenced by changes in activation or inactivation. Histograms of P _o-ex at different voltages show a general increase in P _o with voltage. A single peak in the histogram was noted for each voltage except +40 and +50 mV, where a second, smaller peak could be detected (Fig. 7). At +40 mV, the peaks of the histogram occur at 0.8 for the high and 0.2 for the low P _o gating.

Figure 7.

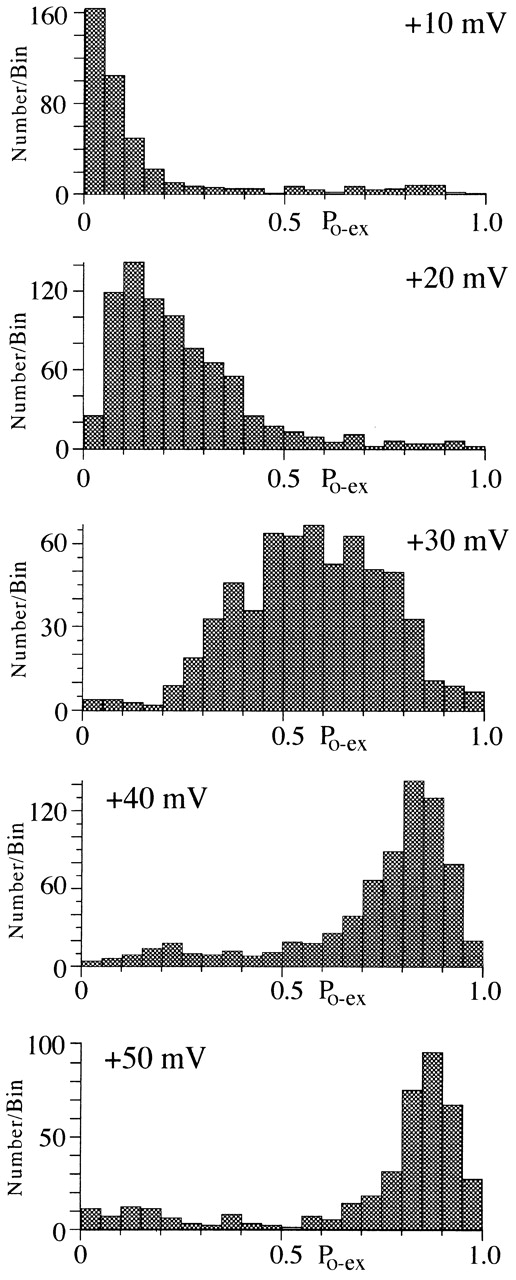
N-channel activity appears to gate with a characteristic P _o at each voltage. The stability of P _o at each test voltage was examined by constructing a histogram of P _o excluding first and last shut times (P _o-ex). The bin width was 0.05 P _o units. Data for 10 single N-channel patches are included in the histogram. The total number of sweeps measured was 385 for +10 mV, 810 for +20 mV, 632 for +30 mV, and 715 for +40 mV.

A different method of examining active sweeps for gating changes is to plot the mean open time for each sweep vs. the mean shut time for the same sweep (Delcour et al., 1993). This is shown in Fig. 8 for same data as Fig. 7. As expected from the P _o histogram, a main cluster of points is observed for each voltage. However, a second cluster of points is observed at +40 mV. As with the two peaks of the P _o histogram, these two clusters of points are nicely separated at P _o = 0.5 (Fig. 8, dashed line). Thus, these two methods of displaying P _o support the existence of high (mean ∼0.8) and low (mean ∼0.2) P _o gating at +40 mV. At the other voltages, some variability in P _o was evident, but too few of these sweeps were recorded to allow further analysis.

Figure 8.

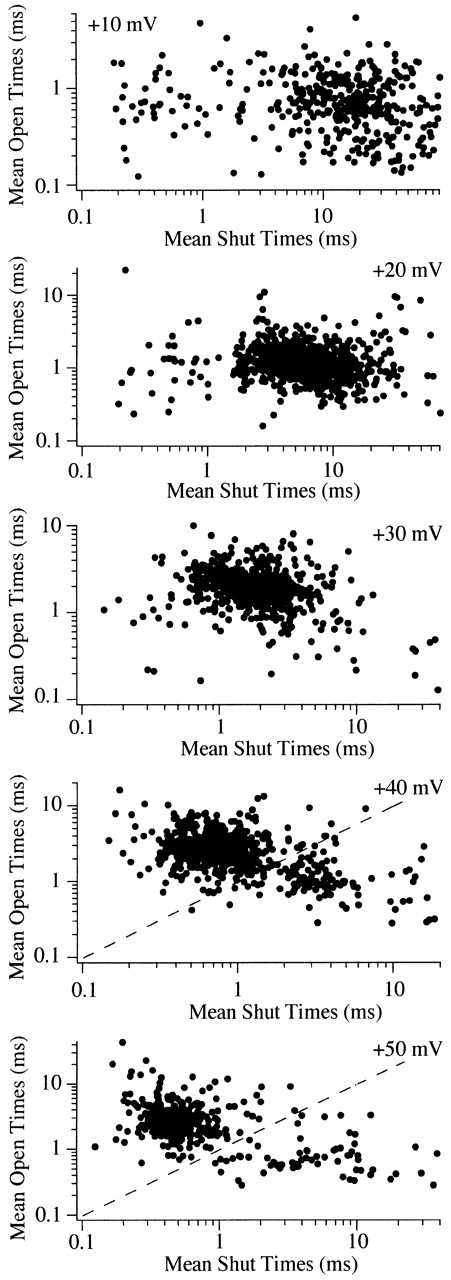
A plot of mean open vs. mean shut time supports a second gating state at +40 mV. Mean open and mean shut times were calculated for each sweep used to generate Fig. 7 and plotted on a log–log scale. The plot for each voltage shows a main cluster of points that corresponds to the peak of the P _o-ex histogram in Fig. 7. However, a second cluster is observed in the plot of the data at +40 mV. The dashed line represents P _o = 0.5 and is presented to show the cutoff P _o used to calculate the fraction of sweep with high vs. low P _o gating.

At +40 mV, active N-channels mainly gate with high P _o, with occasional sojourns into low P _o gating. A P _o of 0.5 appears to separate the high and low P _o sweeps fairly well, so it was used to calculate the percentage of sweeps in the two groups. Examination of all 715 active sweeps at +40 mV revealed that 86% had P _o > 0.5. In individual patches, the percentage of sweeps with P _o > 0.5 ranged from 40 to 96%. This large range is misleading since high P _o was observed in >90% of the active sweeps in six of eight patches. Although comprising only a small fraction of sweeps in most patches, we were interested if the sweeps showing low P _o gating were clustered as expected from the modal hypothesis. Fig. 6 shows an example from a single N-channel patch where the channel remained in a low P _o gating state for ∼1 min before returning to high P _o gating. This type of gating is consistent with the modal hypothesis, and runs analysis of this data set revealed significant clustering of sweeps with P _o < 0.5 (Z = 12.6; Z > 1.65 is significant). A second patch (not shown) also showed sustained (∼1 min) low P _o gating (Z = 7.6). However, in the majority of patches (five of eight), no clustering of low P _o sweeps was detected. Thus, the mean Z for all eight single N-channel patches examined was −0.2. An example where low P _o sweeps were randomly distributed is the patch shown in Fig. 10 (Z = 0.1). The sustained low P _o gating observed in 2 of 8 patches suggests that N-channels can undergo a modal gating change. However, the dominance of high P _o gating in the majority of patches demonstrates that these mode shifts are rare.

Null Versus Active Sweeps

Null sweeps were found in every data set recorded at +40 mV (359/1,100 sweeps, 33%) and, in some of these data sets, null records appeared to be clustered (see diary plots of Figs. 9 and 10). Clustering of null records has been shown in several voltage-dependent channels (Hess et al., 1984; Horn et al., 1984). We used runs analysis to test whether the clustering of null sweeps was significant. The results reached significance in six of nine single N-channels patches with Z values ranging from 2.2 to 6.1 (mean 3.7 ± 1.5). For example, runs analysis applied to the 100-sweep data set illustrated in Fig. 10 indicated that null sweeps were significantly clustered (26 nulls, 30 runs, 38 expected runs), since the Z value was 2.2. In two additional data sets (+40 mV) from the same patch, the calculated Z values were 1.9 and 1.6. The average Z for the three data sets in that patch was 1.9, which is significant. Runs analysis of the 100-sweep data set illustrated in Fig. 9 gave the Z value of 6.1 (26 nulls, 15 runs, 38 expected runs). However, in three patches, runs analysis indicated that null sweeps and active sweeps were randomly mixed since Z values were 0.33, 0.53, and 0.78. One of these patches, shown in Fig. 6, had a Z value of 0.78 (7 nulls, 12 runs, 13 expected runs) for the 100-sweep data set. The variability of runs analysis may indicate that longer recording periods are required to show significant clustering in some patches. Alternatively, the variability may result from different gating processes creating null sweeps, only some of which yield clustered null records.

Figure 9.

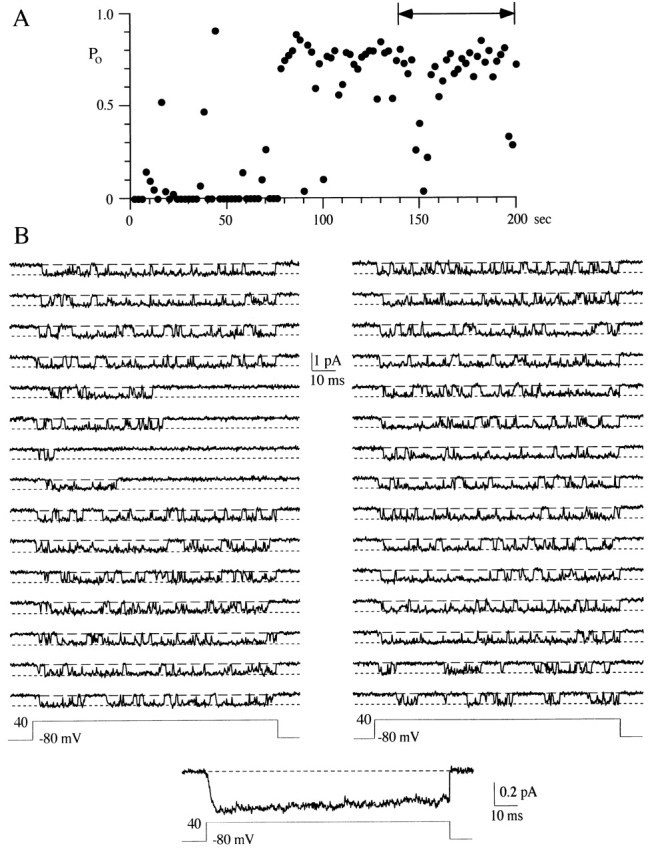
Inactivation can reduce the P _o measured over the duration of the voltage step. (A) A diary plot of P _o measured over the 100-ms sweep duration is shown for 100 consecutive voltage steps to +40 mV. This patch contained a single N-channel. The holding potential was −80 mV and the interval between sweeps was 2 s. The two-headed arrow shows the area illustrated in B. (B) 30 consecutive sweeps are shown for voltage steps to +40 mV. The pseudomacroscopic current at the bottom of the single channel records was averaged from 100 sweeps.

Inactivating Versus Noninactivating Sweeps

Inactivation is another gating process that can lower P _o during a voltage step. Fig. 9 B illustrates an example of inactivation in single N-channel patch. It is interesting that, of the 30 sweeps shown, inactivation is observed in four consecutive sweeps. In addition, the first 40 sweeps in this data set were dominated by nulls and inactivating sweeps (Fig. 9 A). The clustering of inactivating sweeps suggests that inactivation of the frog N-channel is modal, as has been reported for the rat N-channel (Plummer and Hess, 1991). Before applying runs analysis, sweeps were classified as inactivating or noninactivating. A sweep was defined as inactivating if the last event in the sweep was a closing longer than 20 ms (five times the largest mean shut time). Runs analysis determined that inactivating sweeps were significantly clustered for the data shown in Fig. 9 (Z = 3.3) and in one other patch (Z = 3.4). However, the clustering of inactivating sweeps was not significant in six of eight patches examined (range −2.2–0.9). On average, inactivation was observed in 18% of all 715 sweeps examined (range 3–35%). Although two patches showed significant clustering of inactivating sweeps, the majority of our data did not. One problem is that the duration of our voltage steps was 100 ms, while the inactivation time constant is ∼150 ms (Werz et al., 1993). It is likely that our “short” voltage steps caused us to underestimate inactivating sweeps, which could result in missed clustering.

Slow Versus Fast Activation

An additional property that can reduce P _o measured over the entire voltage step is a long latency to first channel opening. As shown in Fig. 5, N-channel first latencies at +40 mV were generally <20 ms. However, a few long latency sweeps were observed in some patches (Fig. 10). To gauge the abundance of these long latency sweeps, we quantified the number of sweeps with latencies >20 ms. For the example patch in Fig. 10, 13 of 178 (7%) active sweeps at +40 mV had a first latency >20 ms. This fraction of long-latency sweeps was typical of our single N-channel patches where the fraction of long-latency sweeps at +40 mV ranged from 0 to 11% (mean 6.2%, n = 8). These few long-latency sweeps did not affect the pseudomacroscopic current, which was well fit by a single exponential function (Fig. 10 A). The long-latency sweeps appeared to be distributed throughout the 100-sweep data sets (Fig. 10). This observation was confirmed by runs analysis, which determined that long latency sweeps were randomly distributed in all eight patches examined. A delay in the latency to first opening has been shown for neurotransmitter modulation of N-channels gating (Carabelli et al., 1996; Patil et al., 1996). Thus, it is possible that these long-latency sweeps result from modulation of N-channel activity under control conditions, as has been demonstrated for N-current (Ikeda, 1991; Kasai, 1991).

discussion

We have examined the gating of single N-type calcium channels over a range of voltages. The increase in P _o with voltage was driven by an increase in the mean open time and a decrease in the mean shut time. A decrease in the fraction of long shut events with depolarization also contributed to the increase in P _o. N-channel activity was dominated by a gating process we called high P _o gating (P _o ∼ 0.8 at +40 mV). However, mean P _o calculated from all recorded sweeps rarely reached that expected from high P _o gating, and it was highly variable across patches. This arose from the influence of other gating processes on our calculation of mean P _o. The most common of these processes was null gating, which was followed by inactivation, low P _o gating, and slow activation. All of these gating processes reduced mean P _o. The magnitude of that reduction was correlated with the frequency N-channels gated in the different “modes.”

Voltage Dependence

P_o.

N-channels typically gate with a characteristic P _o that ranges from 0.05 at +10 mV to 0.8 at +40 mV (Fig. 7). This change in P _o with voltage appears to reflect the voltage dependence of the main gating mode, which we call high P _o. This conclusion is supported by the single component to the open time distribution generally observed at each voltage and by the monotonic increase in P _o with voltage. We currently lack evidence of low P _o gating at voltages less than +40 mV. One possibility is that the low P _o events are too brief for us to resolve below +40 mV. Alternatively, +40 mV may be the threshold voltage for N-channels gating in the low P _o mode.

Maximum P _o obtained from fitting the Boltzmann equation to the P _o–voltage (P _o–V) data from all patches was 0.48. This value must be considered an approximation because of the large variability and the lack of data at +60 or +70 mV, where the Boltzmann curve reaches maximum P _o. However, we believe our calculated maximum to be a good estimate since the V_1/2 and slope from the Boltzmann fit match those values obtained from whole-cell data (after adjustments for differences in recording conditions). In addition, our maximum P _o is similar to that obtained from single N-channels recorded from human IMR32 cells (0.6; Carabelli et al., 1996). One difference between our work and that of Carabelli et al. (1996) is that the slope of their P _o–V curve was e-fold for 12 mV, which is shallow compared with our e-fold for 6 mV. A shallow slope for the P _o–V relation was also obtained from N-channels recorded in rat sympathetic neurons (e-fold for 12 mV; Plummer et al., 1989). However, both Carabelli et al. (1996) and Plummer et al. (1989) excluded the first and last shut times from the calculation of P _o. This method overestimates P _o at low relative to high voltages, which results in an underestimation of the steepness of the activation curve. Since we used the step duration and included null sweeps to calculate P _o, the steepness of our activation curve is comparable with that from whole-cell data.

τ_o.

The mean open time of the bullfrog N-channel at +30 mV (τ_o = 1.5 ms) was longer than that measured from N-channels in IMR32 cells (τ_o = 0.7 ms; Carabelli et al., 1996) or α_1B mRNA expressed in HEK 293 cells (along with β_2a and α₂; τ_o = 0.3 ms; Patil et al., 1996), but was similar to the open time of N-channels in rat sympathetic neurons (τ_o = 1.2–3.6 ms; Rittenhouse and Hess, 1994). One possibility is that mean open time depends on which β subunit complexes with the N-channel. N-channels isolated from rabbit brain were found to be associated with several different β subunits (Scott et al., 1996) and these subunits can have differential effects on calcium channel kinetics (Olcese et al., 1994; Stea et al., 1994). Alternatively, different N-channel isoforms have been isolated, and these isoforms show different kinetics when expressed in Xenopus oocytes (Lin et al., 1997).

The increase in τ_o with depolarization corresponded to an e-fold change every 23 mV. This voltage dependence is similar to that observed in sodium channels (e-fold for 16–20 mV; Huang et al., 1984; Horn et al., 1984) and for the Shaker A-type potassium channel (Hoshi et al., 1994). Carabelli et al. (1996) also showed that N-channel open times are voltage dependent. On the other hand, data from L-type calcium channels (Marks and Jones, 1992) and T-type calcium channels (Chen and Hess, 1990) are consistent with voltage-independent open times. N-channel open times are less sensitive to voltage than the voltage-dependent shut time component, approximately e-fold for 23 mV vs. e-fold for 10 mV, respectively (Fig. 4). Therefore, the voltage dependence of activation mainly reflects a decrease in shut times, as suggested by van Lunteren et al. (1993).

The voltage dependence of the N-channel open time may be important in limiting the calcium influx through N-channels during the action potential. Several calcium-activated potassium channels (maxi K_Ca and small K_Ca) hyperpolarize the membrane after one or more action potentials (Pennefather et al., 1985). The membrane potential can reach −80 mV during these after-hyperpolarizations (AHPs), which would create a large Ca²⁺ influx through open calcium channels. However, we estimated mean open time at −80 mV to be <0.1 ms under physiological conditions (2 mM Ca²⁺). This estimate is based on extrapolation of the e-fold change in open time for 23 to −40 mV, which would be equivalent to approximately −80 mV after adjusting for the differences in divalent cation concentration. Our data supports the brief open times at −40 mV, since we rarely observed tail openings. Thus, calcium influx through N-type calcium channels during the AHP is predicted to be very small.

One well known model for neurotransmitter release predicts that the majority of calcium enters the nerve terminal on repolarization of the action potential as a tail current (Llinás et al., 1981, 1982). At synapses where N-channels mediate release, we predict that the channels would rapidly shut during repolarization so that, unlike the squid giant synapse (Llinás et al., 1981, 1982), there would be no calcium influx during the after-hyperpolarization. In agreement with our prediction, recent recordings from cerebellar synapses (Sabatini and Regehr, 1996) and the calyx of Held (Borst and Sakmann, 1998) show little or no calcium influx after the action potential repolarization.

τ_sh.

We were able to fit exponential functions to two components of the shut time distribution. One component was voltage independent with a τ of 0.3 ms over the voltage range +10 to +40 mV. In the other component, τ decreased with voltage from 18.9 ms at +10 mV to 2.3 ms at +40 mV. N-channel shut times were also fitted with two exponentials in IMR32 cells (Carabelli et al., 1996). However, both components were voltage dependent, with the longer shut times matching our voltage-dependent shut time component. In some patches, we noticed longer events in the shut time distributions that were not well described by a two-exponential function. Although the number of events was too small to obtain a consistent fit to three or four exponentials, we believe that at least one more shut time component exists in the frog N-channel.

Voltage-independent shut times have also been observed in other channel types (e.g., L-type calcium channel [Marks and Jones, 1992] and Shaker A-type potassium channel [Zagotta and Aldrich, 1990]). In models of these channels, the voltage-independent time constants were accounted for in either (a) the final closed-to-open transition in the activation pathway (Marks and Jones, 1992; Zagotta and Aldrich, 1990), or (b) closed-open transitions out of the activation pathway (Zagotta et al., 1994). We have not formulated a model that describes our observations, but analysis supports the idea that the gating state described by the voltage-independent shut time is close to the open state. We calculated from double-exponential fits the fraction of brief vs. total shut events (Fig. 4 C). The fraction of rapid closings increases with depolarization, paralleling P _o, suggesting that the rapid closings reflect occupancy of a closed state near the open state. This closed state could be in the activation pathway, where it might be rate limiting at strongly depolarized voltages (...C–O), or it could be out of the main activation pathway, “to the right of” the open state (...O–C).

Nonstationary Gating

We identified four properties that reduced N-channel P _o at depolarized voltages. These properties were null sweeps, low P _o gating, inactivation, and slow activation. Several of these gating processes behaved in a manner consistent with the modal hypothesis. In particular, null sweeps were significantly clustered in the majority of our single N-channel patches. Clustering of null records has been reported for L-type calcium channels (Hess et al., 1984), skeletal muscle sodium channels (Horn et al., 1994), and N-type calcium channels (Rittenhouse and Hess, 1994). These clustered null sweeps were interpreted to result from a gating mode from which the channel will not open. Such a mode could be represented by a long-lived inactivated state that had a mean dwell time lasting several sweep intervals (4–6 s in our recordings). Whole-cell recordings have demonstrated an inactivation process from which N-current is slow to recover (Jones and Marks, 1989b).

In three single N-channel patches, we observed long periods (∼1 min) with few or no active sweeps (see Fig. 9 A for one example). Since we included null records in our calculation of mean P _o, these null periods contributed to the low values at +40 mV in the mean P _o vs. voltage plot (Fig. 2). In skeletal muscle sodium channels, long periods of null sweeps were termed “hibernation” since the channel would appear to “sleep” for extended periods (Horn et al., 1984). We do not know what induces long null (hibernating) periods of N-channel gating, nor do we have good information on their frequency or duration. However, we do know that the channel can recover from such periods to gate with typical P _o.

One process that may contribute to null sweeps is closed-state inactivation. Recently, it has been recognized that inactivation from closed states on the pathway to open can generate a U-shaped inactivation vs. voltage relationship (Klemic et al., 1998; Patil et al., 1998), which is the voltage profile shown for N-channel inactivation (Jones and Marks, 1989b). This mechanism has been proposed for N-channel inactivation based on whole-cell experiments on HEK 293 cells expressing recombinant N-channels (α_1b, α₂, β₃; Patil et al., 1998). Inactivation from “intermediate” closed states could be one mechanism generating null sweeps as the channel inactivates during the activation process. This mechanism is associated with fast inactivation (τ = 150 ms) and may account for some randomly distributed null sweeps, since current models of this inactivation process do not appear to predict modal inactivation.

Inactivation of active N-channels was examined at +40 mV. While inactivating sweeps were observed in every patch, the number was generally small (average 18%). The minor effect of inactivation over our 100-ms voltage steps can be seen in the pseudomacroscopic currents (Fig. 9 B and 10 A). The majority of our patches showed a random distribution of inactivating sweeps, which superficially would support a nonmodal inactivation process. However, the duration of our voltage steps was short compared with the time constant of inactivation (τ = 150 ms; Werz et al., 1993), which would have caused us to miss inactivating sweeps. Plummer and Hess (1991) using 1,400-ms voltage steps observed a nonrandom distribution of inactivating sweeps and suggested that N-channels inactivated in a modal fashion. The significant clustering of inactivating sweeps that we observed in 2 of 10 patches provides the impetus to examine single N-channel inactivation using longer voltage steps.

The P _o of actively gating N-channels is typically within a small range (Fig. 7). However, sweeps with P _o outside the “typical” range were found for each voltage tested. For the majority of voltages, the sweeps were few in number with the P _o scattered over a wide range. However, at +40 mV, these sweeps formed a minor peak (P _o ∼ 0.2) in the P _o histogram. Since P _o = 0.5 appeared to separate the major and minor peaks in the P _o histogram at +40 mV, it was used as the criteria for separating high and low P _o sweeps. In patches with prominent low P _o gating, two exponentials were required to fit the open time distribution at +40 mV. From these fits, we estimate the mean open time to be ∼1 ms during low P _o gating and ∼3 ms during high P _o gating (at +40 mV). Although sweeps with P _o outside the typical range were observed at other voltages, the numbers were too few to allow further analysis. For this reason, we have focused our examination of low P _o gating on sweeps at +40 mV.

Sweeps showing low P _o gating were randomly distributed in the majority of single N-channel patches examined. However, two patches were noteworthy since sustained low P _o gating was observed (duration = 66 [Fig. 6] and 52 s). These sustained periods are consistent with the existence of a low P _o gating mode for the N-channel. Since low P _o gating was observed in only a small fraction of the sweeps at +40 mV (∼14%), occupancy of this hypothesized gating mode appears to be low.

Several single N-channel studies have been previously published. Carabelli et al. (1996) showed that N-channels in human IMR32 typically gate within a small P _o range, as we have shown for the frog N-channel. However, other publications have proposed several modes of N-channel gating. Delcour et al. (1993) could distinguish three gating modes in a calcium channel recorded from frog sympathetic neurons that they believed to be the N-type calcium channel. However, that channel is now known to be a non–ω-conotoxin GVIA-sensitive calcium channel that we have called novel or E_f-channel (Elmslie et al., 1994; Elmslie, 1997).

Recording from neonatal rat sympathetic neurons, Rittenhouse and Hess (1994) characterized three gating modes for the N-type calcium channel, which were distinguished by P _o and single channel current amplitude. We have no data to explain the apparent differences between frog and rat N-channels. However, the similarity between the N-channel from frog (our data) and human IMR32 cells (Carabelli et al., 1996) suggests that we need to look beyond species differences. It is possible that differences in subunit composition of the channel underlie the kinetic differences between frog and rat N-channels.

A somewhat surprising finding was delayed channel opening, which resembles the effect of neurotransmitters on N-channel gating (Carabelli et al., 1996; Patil et al., 1996). It has been well documented in mammalian preparations that N-channels are exposed to a low level of G protein modulation under control conditions (Ikeda, 1991; Kasai, 1991; Swartz, 1993). This type of modulation is small in frog sympathetic neurons, accounting for ∼10% reduction in peak current (Elmslie, 1992; Yang and Tsien, 1993). We find delayed channel opening in an average of 6% of sweeps at +40 mV and these few sweeps have little effect on the pseudomacroscopic current (Figs. 9 B and 10 A). The close correspondence between whole-cell and single channel data supports the idea that a low concentration of G proteins is active under our control conditions, which occasionally produces delayed N-channel opening.

Summary and Conclusions

The most commonly observed N-channel gating at +40 mV is characterized by a high P _o (∼0.8) and long open time (∼2.6 ms). If this were the only gating process, maximum N-channel P _o would be expected to be close to 1. However, other gating processes reduce P _o to a maximum value closer to 0.5. The most common of these processes was null gating, which was followed by inactivation, low P _o gating, and slow activation. These processes are potential targets for physiological regulation. We know that inactivation can be modulated by phosphorylation and that activation can be slowed during neurotransmitter-induced inhibition. Null and low P _o gating are additional processes that could be modulated by the neuron to control the amount of calcium entering the cell during the action potential.