Cation-π interactions in structural biology

Abstract

Cation-π interactions in protein structures are identified and evaluated by using an energy-based criterion for selecting significant sidechain pairs. Cation-π interactions are found to be common among structures in the Protein Data Bank, and it is clearly demonstrated that, when a cationic sidechain (Lys or Arg) is near an aromatic sidechain (Phe, Tyr, or Trp), the geometry is biased toward one that would experience a favorable cation-π interaction. The sidechain of Arg is more likely than that of Lys to be in a cation-π interaction. Among the aromatics, a strong bias toward Trp is clear, such that over one-fourth of all tryptophans in the data bank experience an energetically significant cation-π interaction.

The three-dimensional structure of a protein is determined by a delicate balance of weak interactions. Hydrogen bonds, salt bridges, and the hydrophobic effect all play roles in folding a protein and establishing its final structure. In addition, the cation-π interaction (1–3) is increasingly recognized as an important noncovalent binding interaction relevant to structural biology. Theoretical and experimental studies have shown that cation-π interactions can be quite strong, both in the gas phase and in aqueous media. A number of studies have established a role for cation-π interactions in biological recognition, especially in the binding of acetylcholine (4, 5). Here we present a detailed analysis of the extent and nature of cation-π interactions that are intrinsic to a protein’s structure and likely contribute to protein stability. We find that energetically significant cation-π interactions are common in proteins—a “typical” protein will contain several. We also have documented some significant preferences for certain amino acid pairs as partners in a cation-π interaction.

Important early work indicated a role for cation-π interactions in protein structures. Following work by Levitt and Perutz (6–8) suggesting a hydrogen bond between aromatic and amino groups, Burley and Petsko identified the “amino aromatic” interaction (9), in which NH-containing groups tend to be positioned near aromatic rings within proteins. It is now appreciated that the interaction of a cationic group with an aromatic—a cation-π interaction—is much more favorable than an analogous interaction involving a neutral amine (10, 11). Important subsequent studies by Thornton (12–17) modified the Burley and Petsko analysis, especially with regard to the amino-aromatic “hydrogen bond.” In addition, explicit studies of Arg interacting with aromatic residues have been reported by Flocco and Mowbray (18) and by Thornton (14), and other efforts to search the Protein Data Bank (PDB) for cation-π interactions between ligands and proteins have been reported (19, 20).

Previous protein database searches relied on geometric definitions of sidechain interactions, focusing on when a cationic sidechain displayed a certain distance/angle relationship to an aromatic sidechain. The different geometries of Lys vs. Arg and Trp vs. Phe/Tyr can make such comparisons problematical. In addition, not all cation-aromatic contacts represent energetically favorable cation-π interactions. Unlike ion pairs, for which any close contact will be energetically favorable, a cation interaction with an aromatic can be attractive or repulsive. The electrostatic potential surfaces of the aromatics, which control such distinctions (1), can be complex, and it is difficult to clearly distinguish attractive from repulsive cation-aromatic contacts using geometric criteria alone. To circumvent this problem, and to put the diverse array of potential cation-π interactions on a more nearly equal footing, we have chosen to use energy-based, rather than geometry-based, criteria in this study. Our goals in this study are twofold. First, we wish to develop meaningful statistics for cation-π interactions for structures within the PDB (21). Second, we wish to develop a simple, unambiguous protocol for identifying cation-π interactions that can be easily applied by other workers.

Within a protein, cation-π interactions can occur between the cationic sidechains of either lysine (Lys, K) or arginine (Arg, R) and the aromatic sidechains of phenylalanine (Phe, F), tyrosine (Tyr, Y) or tryptophan (Trp, W). Because histidine can participate in cation-π interactions as either a cation or as a π-system, depending on its protonation state, we do not consider histidine in this study. We assume Lys and Arg are always protonated.

METHODS

In this section, we detail our strategy for identifying and ranking cation-π interactions in proteins. In brief, we use a variant of the optimized potentials for liquid simulations (OPLS) force field (22, 23) to provide an energetic evaluation of all potential cation-π interactions in a protein. Only cation-π interactions with binding energies that rise above a certain threshold are retained. Readers concerned only with the results of this analysis may proceed to the next section.

Our development of a simple, general protocol to identify cation-π interactions within the PDB proceeded as follows: (i) Potential cation-π interactions from a test dataset of 68 proteins were identified by using only geometric criteria. (ii) The binding energy of each interaction was evaluated by using ab initio calculations. (iii) A force field-based method was developed to reproduce the trends in the ab initio data. (iv) The force field-based method was used to select energetically significant cation-π interactions from a larger dataset of 593 proteins.

To search the PDB, a computer program [capture (Cation-π Trends Using Realistic Electrostatics)]‡ was developed to calculate the distance between the cationic group [the ammonium nitrogen (NZ) in Lys or the guanidinium carbon (CZ) in Arg] and the centers of all aromatic rings. By using a 6.0-Å distance cutoff and no other geometrical constraints, 359 potential cation-π pairs were selected from a dataset of 68 nonhomologous, high-resolution protein structures (16). Each pair then was reduced to a system that could be studied computationally. Lys and Arg were represented as ammonium and guanidinium ions, and Phe, Tyr, and Trp were represented as benzene, phenol, and indole, respectively. Using HF/6–31G** minimum energy structures for these fragments, we established the relative orientations of the partners from the PDB and determined the binding energy of each using HF/6–31G** calculations corrected for basis set superposition error (24, 25). We appreciate that a higher level of theory (such as MP2) might provide a better estimate of the gas phase interaction energy for any pair, but that is not our goal (26, 27). We seek a simple criterion that will put all cation-aromatic contacts on a consistent scale. In addition, because high resolution macromolecular structures have some structural ambiguity, we feel that attempting very high level calculations on relatively “low level” geometries is not sensible.

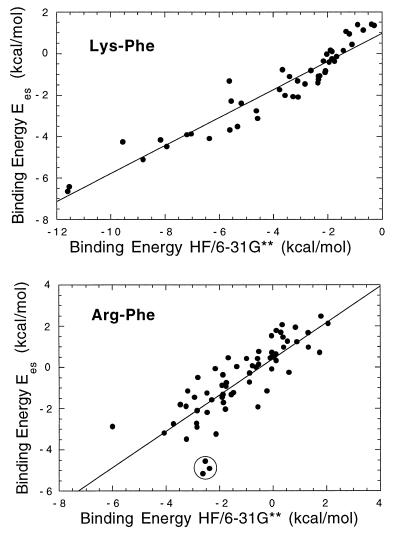
Although standard force field methods are challenged to quantitatively model the cation-π interaction (28–30), it is clear that force field methods can correctly reproduce trends in the binding energies. We therefore implemented within capture a subset of the OPLS force field (22, 23) in which only electrostatic (E_es) and van der Waals (E_vdW) interactions are considered. When the OPLS binding energies (E_tot = E_es + E_vdW) for each of the 359 interactions described above were compared with the HF binding energies, a poor correlation was obtained. Previous studies have shown that trends in the electrostatic component determine trends in cation-π binding ability (31). Thus, we attempted to correlate the electrostatic component of the OPLS binding energy (E_es) with the total ab initio binding energy. These measurements correlate well (Fig. 1) and represent an enormous computational savings. The correlations are better when Lys is the cation, possibly because the more complex Arg sidechain has several different binding modes available. This may lead to variations in the van der Waals interactions, which are included in the ab initio calculations but are excluded from our force field calculation.

Figure 1.

Plots of E_es vs. CP-corrected, HF/6–31G** binding energies for selected cation-π interactions. Correlation coefficients are 0.93 for Lys-Phe and 0.81 for Arg-Phe. Comparable plots are seen for Lys-Trp and Arg-Trp interactions. Three outliers are circled in the Arg-Phe plot. Inspection of these pairs reveals spurious close contacts, which lead to erroneously high energies in the HF calculations but not in the OPLS calculations (see text). Removing these points improves the correlation coefficient to 0.85.

An advantage of excluding E_vdW from our calculation is that many of the most favorable cation-π interactions produce spurious, repulsive E_vdW terms. This results from the inherently low resolution of macromolecular crystal structures, which occasionally have unrealistic atom–atom contacts. Such pairs would be rejected as cation-π interactions if E_tot were the evaluation criterion. Because electrostatics are much less sensitive to close contacts (1/r) than van der Waals repulsions (1/r¹²), the effects of small geometry errors are minimized when only E_es is considered.

We note another advantage of this energy-based selection criterion over geometry-based methods. Like other workers, our initial geometric screen involved a distance (r) from the center of positive charge to the aromatic, but there is a danger in rejecting structures solely on the basis of r. For example, there are many structures in which the NZ of Lys will be >5 Å (a common cutoff) from the aromatic, but the CE will be within 5Å. Because the CE of Lys has a substantial positive charge, such a structure should be considered as a possible cation-π interaction, and our calculations reflect this. Although we considered all pairs with r ≤ 10 Å, in 99% of our accepted cation-π structures, r ≤ 6 Å when both NZ and CE of Lys or CZ and CD of Arg are considered and 88% have r ≤ 5Å.

With a basic strategy in place, we refined the model for application to the full dataset. Because a significant fraction of positive charge resides on CD of Arg and CE of Lys, we included these “methyl-groups” as united atoms. Thus, Lys was now represented as methylammonium and Arg as methylguanidinium. The inclusion of methyl groups on the aromatics does not significantly alter their cation-π binding ability (32), and they were not added. Aromatic hydrogens were placed in idealized geometries and were treated explicitly by using the standard parameters in the OPLS force field.

Tyrosine presents a special problem for this analysis. The position of the proton of the phenolic OH is typically not well determined in protein crystal structures, and its location can significantly affect cation binding ability through an interaction of the ion with the OH bond dipole. Because phenylalanine and tyrosine are nearly equivalent in their idealized cation-π binding ability (31, 32), we have chosen to treat them with identical charge parameters. The phenolic oxygen of tyrosine retains its steric parameters but has zero charge. To make the ring electrostatically equivalent to Phe, a dummy charge is placed in an equivalent location to that of the para-hydrogen of phenylalanine, and all other atomic charges are set equal to those of phenylalanine. Thus, in interactions of a cation with Tyr, we are considering only the cation-π interaction. In the actual protein, the cation–tyrosine interaction may be larger because of interactions with the oxygen (see below).

With a computationally efficient selection method established, we could now examine a larger number of proteins and extend the interaction distance cutoff to 10 Å. Within this expanded search, some cation-π pairs involving tryptophan gave a favorable value of E_es but had the cation quite far from the aromatic rings. Although these interactions are attractive in the gas phase, they are likely attenuated in the protein. Thus, we added a simple, geometry-based criterion to eliminate long range structures. To do this, we asked whether a water-sized probe (a 2.8-Å diameter sphere) could fit between the van der Waals surfaces of the cation and the aromatic at their point of closest approach. If the water molecule fits, the structure is rejected, regardless of its electrostatic energy. In practice, this criterion eliminates a small number of distant interactions.

It remains to choose a threshold value for E_es, below which a pair is considered to experience a cation-π interaction. The simplest model suggests that, if E_es is less than zero, i.e., if the electrostatic interaction is favorable, then the pair should be counted as a cation-π interaction. However, inspection of structures with E_es only slightly below zero shows that, although these interactions may be significant in the gas phase, they are unlikely to contribute to protein stability. Conversely, it is clear that, if E_es ≤ −2.0 kcal/mol, then the pair is experiencing a significant cation-π interaction. Also, if E_es > −1.0 kcal/mol, no cation-π interaction should be considered. For −2.0 < E_es ≤ −1.0 kcal/mol, the choice is not so clear. Some structures are desirable whereas, in other cases, the interacting partners are too far apart, even though there is no 2.8-Å gap. To distinguish these, we consider the van der Waals term of the OPLS interaction energy as an indicator of whether the pair is interacting significantly. It is safe to include E_vdW for these relatively weaker interactions because they are generally not the closest contacts and therefore not susceptible to spurious van der Waals interactions. We conclude that, if E_vdW ≤ −1.0 kcal/mol, the interaction is significant. We emphasize that these refinements to the protocol are meant to produce the best possible selection criterion, but they do not have a major impact on the final list. No global conclusions presented would be substantially altered if they were not included.

To summarize, then, our protocol for selecting cation-π interactions is as follows. All cation-π pairs (K or R with F, Y, or W) within 10 Å of each other are considered. If there is a gap large enough to insert a water molecule at closest contact, the structure is rejected, and the residues are considered “noninteracting.” For the remaining “interacting pairs,” the OPLS electrostatic energy, E_es, is evaluated. If E_es ≤ −2.0 kcal/mol, the pair is counted as a cation-π interaction. If E_es > −1.0 kcal/mol, the structure is rejected. If −2.0 < E_es ≤ −1.0 kcal/mol, the structure is retained only if E_vdW ≤ −1.0 kcal/mol. It is worth remembering that the interaction energies we will discuss below are only the OPLS electrostatic energies. The actual interaction energy—the true magnitude of the cation-π interaction—is larger by an amount equal to the van der Waals interaction energy. For most pairs considered, E_vdW is comparable to E_es, and so the true cation-π interaction energy is roughly twice as large as E_es. Although these are gas phase numbers, a recently completed computational study (J.P.G. and D.A.D., unpublished work) shows that, unlike salt bridges, cation-π interactions are not severely attenuated in aqueous media.

RESULTS AND DISCUSSION

Using the above criteria, we scanned a larger dataset of representative protein crystal structures, taken from the “PDB Select” list of Hobohm and Sander (refs. 33 and 34; ftp://ftp.embl-heidelberg.de/pub/databases/pdb_select). We initially considered single and mulitsubunit proteins separately. However, in most analyses, no significant differences between these two sets were found, and thus the combined set of 593 proteins is considered unless otherwise noted. All proteins had resolutions better than 2.5 Å, and residues with fractional occupancies <0.95 were rejected. For the combined sets, 230,504 residues were considered, producing 14,030 interacting pairs and 2,994 significant cation-π interactions (Table 1). The energies of many of the cation-π interactions are quite substantial, with roughly one quarter of the total having E_es ≤ −4.0 kcal/mol.

Table 1.

Frequency of cation-π interactions within proteins

Amino acid	Total number*	Interacting pairs†	Cation-π interactions‡	Amino acid pair	Cation-π interactions‡	Percent§
K	13,446	5,881	1,006	KF	285	14.5
R	10,919	8,149	1,988	KY	438	14.7
F	9,162	4,969	915	KW	283	30.2
Y	8,309	6,615	1,187	RF	630	21.0
W	3,412	2,446	892	RY	749	20.6
				RW	609	40.4

^*The total number of times a particular amino acid appears in the dataset of 593 proteins. 

^†The number of times a particular amino acid occurs in an interacting pair. 

^‡The number of times a particular amino acid or pair of amino acids occurs in a cation-π interaction. 

^§Percent of interacting pairs that are energetically significant cation-π interactions. 

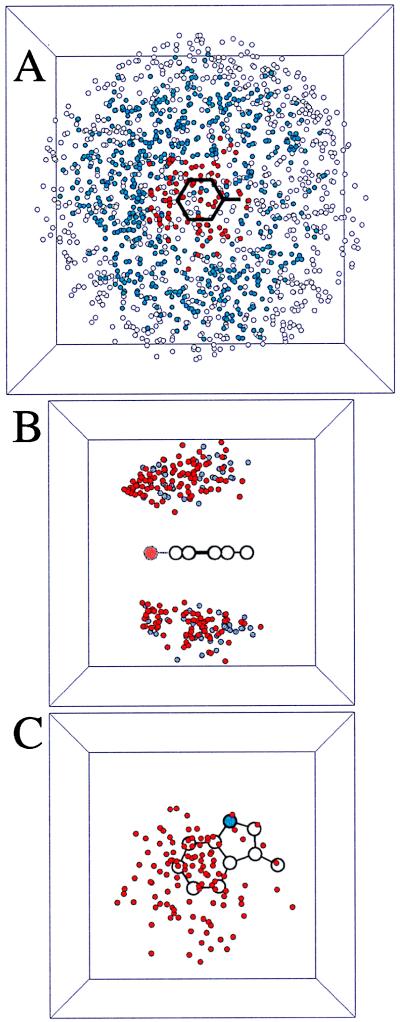
Fig. 2A gives a visual representation of our selection procedure. Lys/Phe pairs are divided into three categories: rejected based on the gap criterion (open circles); interacting (no gap) but with E_es > −1.0 kcal/mol (blue circles); and cation-π interactions (red circles). Clearly our selection is “sensible”—the three classes form concentric rings around the aromatic ring.

Figure 2.

Scatter plots from the analysis of all 323 single subunit proteins. In each case, the cation is Lys, and a circle denotes the location of the sidechain N in one particular pair. Pictures are projections of a 10- × 10- × 10-Å cube in A and a 7- × 7- × 7-Å cube in B and C. (A) All Lys-Phe interactions. The phenyl ring plus the β carbon are denoted by black lines. A red circle denotes an interaction that is an accepted cation-π interaction; a blue circle denotes an interacting pair; a white circle denotes a structure rejected by the gap criterion. In this projection view, a few open/blue circles are seen to lie over the ring, but they are too far “above” the ring to have a favorable cation-π interaction. (B) Cation-π interactions involving Lys and Phe (gray circles) or Tyr (red circles). Note clustering of Tyr interactions near the phenolic oxygen (larger, light red circle). (C) Top down projection of all Lys-Trp cation-π interactions. The indole N is a blue circle. Note the cluster of structures above the six-membered ring.

With 2,994 cation-π interactions in 230,504 residues, there is an average of 1 energetically significant cation-π interaction for every 77 residues in a protein. This number does not vary systematically with the length of the protein, although there is some scatter. For example, the 126 amino acid mutant human fibroblast growth factor (PDB ID code: 1BFG) contains five significant cation-π interactions whereas penicillopepsin (PDB ID code: 2WEA, 323 amino acids) is the largest single chain protein studied that contains no energetically significant cation-π interactions. The number of cation-π interactions per residue is the same whether single chain or multisubunit proteins are considered.

For comparison, one might ask how common salt bridges are in proteins. Although the energetic significance of salt bridges is debated, to get a sense of the relative frequency of the two types of interactions, we considered all ion pairs (Lys/Asp, Lys/Glu, Arg/Asp, Arg/Glu) that meet the interacting pair criterion. We find that salt bridges are common, with almost 27,000 occurring in our collection of proteins (compared with 14,030 cation-aromatic interacting pairs). There is no significant preference for one pair over another.

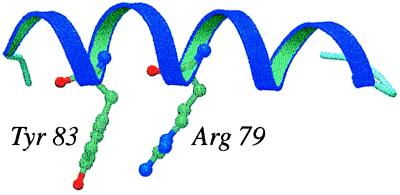
The most common cation-π interaction is between neighboring residues in the sequence, with 7.3% of the interactions occurring between adjacent residues. Interactions between residues at the i and (i + 4) positions are the second most common. This suggests that cation-π interactions may commonly occur within α-helices, as in the structure of the vaccinia virus protein VP39 (PDB ID code: 1V39) (Fig. 3).

Figure 3.

An example of a strong cation-π interaction in an α-helix (E_es = −4.2 kcal/mol). The plot was created by using molscript and raster3d (36, 37).

Cationic Amino Acids.

Table 1 indicates a striking preference for the sidechain of arginine to be located near aromatic sidechains in proteins. Over 70% of all Arg sidechains are near an aromatic sidechain, consistent with earlier studies (12), and this bias for Arg vs. Lys persists when considering energetically significant cation-π interactions.

It is perhaps surprising that arginine is more likely to be found in a cation-π interaction than lysine. Ab initio calculations indicate that, in the gas phase, ammonium ion (“Lys”) interacts more strongly with aromatics than guanidinium ion (“Arg”) (35). At the HF/6–31G** level, the binding energy for ammonium to benzene is −15.3 kcal/mol whereas that for guanidinium binding to benzene is −4.1 kcal/mol (parallel) and −10.6 kcal/mol (T-shaped). To determine whether our statistics reflect an artifact of our electrostatic models for either Lys or Arg, we modeled each sidechain as a point charge by placing a unit charge at the location of either NZ of lysine or CZ of arginine. Because these positions essentially overlap in space, we eliminate any potential bias in the charge model for the cation. Using this simplified model, we still find that Arg is substantially more likely than Lys to be found in a cation-π interaction, suggesting that nonelectrostatic effects are responsible. Because the sidechain of arginine is larger and less well water-solvated than that of lysine, it likely benefits from better van der Waals interactions with the aromatic ring. In addition, as suggested by Thornton and colleagues (14), the sidechain of Arg may still donate several hydrogen bonds while simultaneously binding to an aromatic ring (if it is stacked) whereas lysine would typically have to relinquish hydrogen bonds to bind to an aromatic.

Thus, although arginine is more prevalent than lysine in cation-π interactions, we suggest that this does not reflect the intrinsic cation-π binding ability of Arg but, rather, other factors, as discussed above. Consistent with this view, the average strengths of cation-π interactions involving either Lys (−3.3 ± 1.5 kcal/mol) or Arg (−2.9 ± 1.4 kcal/mol) are similar. In addition, the 12 strongest interactions involve lysine, consistent with the ab initio calculations discussed above.

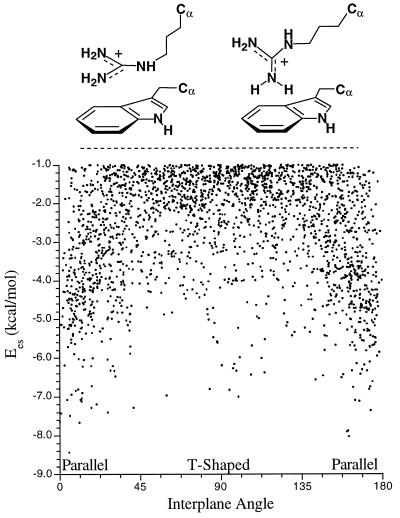
Arginine can participate in cation-π interactions in two limiting geometries, as shown in Fig. 4. Computationally, the T-shaped geometry is favored in the gas phase, but, in solution, the parallel geometry is preferred (35). In agreement with previous studies (12, 14, 18), we find that the parallel geometry is preferred in protein structures (Fig. 4), although some of the strongest cation-π interactions involve T-shaped geometries.

Figure 4.

Cation-π interactions involving arginine. (Upper) Parallel and T-shaped geometries. (Lower) Variation in interplane angle.

Concerning the orientation of the lysine sidechain in cation-π interactions, the ɛ-carbon (CE) of lysine is 2.4× more likely to be closer to the ring centroid than the nitrogen (NZ). This preference is contrary to expectations based only on electrostatics, although it disappears when only the strongest binding structures (E_es ≤ −5.0 kcal/mol) are considered. Note that positioning the carbon closest to the ring may contribute favorable van der Waals binding, and exposing the ammonium group may lead to better interactions with solvent or hydrogen bonding groups.

Aromatic Amino Acids.

Table 1 shows a marked preference for tyrosine and tryptophan to interact with cationic sidechains when the data are adjusted for the overall occurrence of the sidechain in the database. Theory indicates that tyrosine and phenylalanine are equivalent in their cation-π binding ability (31). This suggests that the increased number of cation-π interactions involving tyrosine must be attributable to other effects, such as the ability of the OH group of the tyrosine to act as a hydrogen bond donor. If the tyrosine OH donates a hydrogen bond, it substantially potentiates the cation-π binding ability of the phenolic ring (32). Also, the negative electrostatic potential on the oxygen could directly contribute to cation binding, as discussed above. Supporting this view, the scatter plot of Fig. 2B shows a clear bias for the cation to be closer to the OH.

Perhaps the most surprising result is that 26% of all tryptophans in the dataset are involved in at least one energetically significant cation-π interaction. We had postulated that tryptophan would be overrepresented at cation-π sites because, in the gas phase, indole binds cations more tightly than either benzene or phenol (1, 31, 32). Because this bias has a strong electrostatic component, it could be argued that it is was inevitable that tryptophan would appear to be a better cation-π binder when using an electrostatic criterion. To address this concern, two limiting reasons why tryptophan might be more prevalent at cation-π sites were considered. The first is that the larger volume of tryptophan allows it to contact a greater number of cations relative to phenylalanine or tyrosine. Were this true, it should be evident in the number of interacting pairs, and it is not (Table 1). To determine whether the bias for Trp reflects a bias in our energy model, we reduced tryptophan’s cation-π binding ability 50% by halving the electrostatic energy of each interaction involving Trp. This reduction substantially penalizes tryptophan, making it a less potent cation binder than phenylalanine. Nevertheless, using this model for Trp, we still find that it is favored over phenylalanine by a factor of 2. We thus conclude that the substantial overrepresentation of Trp in our collection of cation-π interactions directly reflects the enhanced cation-π binding ability of the indole ring.

A view of the Lys-Trp interaction is shown in Fig. 2C. A clear bias for the six ring of Trp to be involved in cation-π interactions is evident, as anticipated from inspection of the electrostatic potential surface of indole (1). Also contributing to this bias is a steric effect; the protein backbone is nearer the five ring and may interfere with cation binding. Such an effect is evident in Fig. 2B, but it is much less pronounced than the bias seen with Trp.

An interesting question concerns the location of cation-π interactions within protein structures. Cationic residues generally prefer to be on the surface of proteins whereas aromatic amino acids prefer to remain in the hydrophobic core. Because a cation-π interaction contains both a cation and an aromatic, it is not clear whether the interacting pairs should prefer to be located on the surfaces of proteins or in the cores. Traditional methods for determining residue surface accessibility rely on calculating the water-exposed surface area for a given amino acid. Because cation-π partners are necessarily in contact with one another, their water-accessible surface is diminished, even though the interacting pair as a unit may be well solvated. Thus, it is difficult to determine whether a cation-π interaction is on the surface of a protein using only surface accessibility. We have not visually inspected all 2,994 cation-π interactions, but examination of many structures suggests that cation-π interactions tend to be on the surfaces of proteins, consistent with an earlier conclusion by Flocco and Mowbray (18) and recent computational work establishing the strength of cation-π interactions in water (J.P.G. and D.A.D., unpublished work).

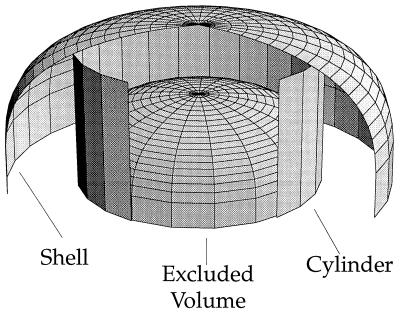
Although arginine and lysine often experience favorable electrostatic interactions with aromatic amino acids via the cation-π interaction, the question remains whether nature uses this advantage to orient these sidechains in folded proteins. To answer this question, we consider the simplest system—lysine/phenylalanine—and ask whether the sidechains of these residues are placed in an electrostatically favorable orientation more frequently than expected based on a random distribution. Using a geometric approach outlined in Fig. 5, we ask whether the number of lysines located in a cylinder above the phenylalanine ring is greater than what would be expected by chance. The cylindrical region above the ring occupies 32% of the total volume, suggesting that 32% of the Lys should be in this region. However, 48% of the 1716 Lys lie in this cylinder, indicating a nonrandom distribution at a confidence level >99.999%. Similar trends are observed for the other cation-π pairs. Thus, proteins do position cations at nonrandom positions relative to aromatics, to optimize cation-π interactions. Although the methodology differs, our results agree with the findings of Singh and Thornton (17), who observe nonrandom angle preferences for cationic sidechains interacting with aromatic sidechains.

Figure 5.

Schematic view of model used to calculate the preferred location for lysine phenylalanine pairs. The excluded volume region represents the volume of benzene plus the volume unavailable to atoms of radius 1.7 Å. The cylinder is tangent to the benzene (radius = 4.8 Å), obtained by adding the radius of benzene (1.4 + 1.7 Å) and the radius of a neighboring carbon atom (1.7 Å). The shell is obtained by adding a constant radius of 2.8 Å—the diameter of a water molecule—to the excluded volume region. This view shows the only the top half of the excluded volume and has portions of the shell and cylinder removed for clarity.

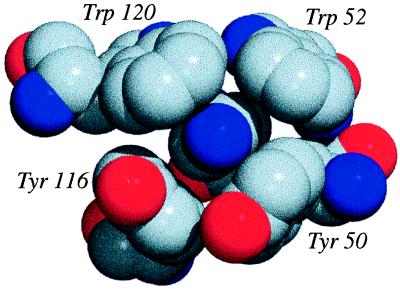
Finally, in Fig. 6, we present a spectacular example of a single lysine that experiences four strong cation-π interactions with four different aromatics. The total value of E_es around this Lys exceeds −22 kcal/mol (A gallery of other cation-π interactions from proteins is available at http://www.cco.caltech.edu/∼dadgrp/gallery.html).

Figure 6.

A cluster of cation-π interactions from the protein glucoamylase (PDB ID code: 1GAI). The NH₃⁺ of the lysine (central blue sphere; Hs not shown) is surrounded by two tryptophans and two tyrosines that contribute −22 kcal/mol E_es. The figure was generated by using povchem (http://grserv.med.jhmi.edu/∼paul/PovChem.html) and povray (http://www.povray.org/). Gray, carbon; red, oxygen; blue, nitrogen.

CONCLUSIONS

By developing an energy-based criterion that puts all cation-π interactions on an equal footing, we have been able to develop meaningful statistics for the frequency of occurrence of cation-π interactions in proteins and to evaluate whether specific cation-π pairs are preferred. We find that cation-π interactions are common—one favorable interaction can be expected for every 77 residues of protein length. Although the weakest interactions considered here (E_es ≈ −1.0 kcal/mol) may make only a small contribution to the overall stability, it is clear that some of the more favorable pairs contribute at least as much to protein stability as more conventional interactions, such as hydrogen bonds and salt bridges.

We find that Trp is the most likely of the aromatics to be involved in a cation-π interaction, with a remarkable 26% of all Trps involved in energetically significant cation-π interactions. This is consistent with theoretical arguments (1, 32) that predicted the Trp sidechain would be especially well suited to cation-π interactions. We also find that Arg is more likely than Lys to be involved in an energetically significant cation-π interaction. This is likely not attributable to an intrinsic aspect of the Arg cation-π interaction but more likely reflects the differing geometric features of the Arg and Lys sidechains. These results make a compelling case that cation-π interactions should be considered alongside the more conventional hydrogen bonds, salt bridges, and hydrophobic effects in any analysis of protein structure.

ABBREVIATIONS

PDB

Protein Data Bank

OPLS

optimized potentials for liquid simulations