Reliability of trunk shape measurements based on 3-D surface reconstructions

Abstract

This study aimed to estimate the reliability of 3-D trunk surface measurements for the characterization of external asymmetry associated with scoliosis. Repeated trunk surface acquisitions using the Inspeck system (Inspeck Inc., Montreal, Canada), with two different postures A (anatomical position) and B (‘‘clavicle’’ position), were obtained from patients attending a scoliosis clinic. For each acquisition, a 3-D model of the patient’s trunk was built and a series of measurements was computed. For each measure and posture, intraclass correlation coefficients (ICC) were obtained using a bivariate analysis of variance, and the smallest detectable difference was calculated. For posture A, reliability was fair to excellent with ICC from 0.91 to 0.99 (0.85 to 0.99 for the lower bound of the 95% confidence interval). For posture B, the ICC was 0.85 to 0.98 (0.74 to 0.99 for the lower bound of the 95% confidence interval). The smallest statistically significant differences for the maximal back surface rotation was 2.5 and 1.5° for the maximal trunk rotation. Apparent global asymmetry and axial trunk rotation indices were relatively robust to changes in arm posture, both in terms of mean values and within-subject variations, and also showed a good reliability. Computing measurements from cross-sectional analysis enabled a reduction in errors compared to the measurements based on markers’ position. Although not yet sensitive enough to detect small changes for monitoring of curve natural progression, trunk surface analysis can help to document the external asymmetry associated with different types of spinal curves as well as the cosmetic improvement obtained after surgical interventions. The anatomical posture is slightly more reliable as it allows a better coverage of the trunk surface by the digitizing system.

Introduction

Over the past few years, a number of contactless 3-D body scanner / measurement devices and techniques have been developed (Inspeck, Cyberware, TC², Minolta Vivid, Vitus 3D). The range of application areas is rapidly expanding for 3-D body modeling and measurements, including animation, anthropometry, computer games, ergonomy, made-to-measure clothing, medical, movies, and virtual reality. Current and potential medical applications include brace design, cosmetic surgery, posture evaluation, body weight control, and scoliosis monitoring.

Scoliosis is clinically apparent by observing the asymmetry of spinous processes, ribs, and scapulae, as well as the lateral imbalance and the left–right asymmetry [22] of the trunk. Beyond the clinician’s eyes and simple tools such as the measuring tape, numerous techniques help physicians in scoliosis diagnosis and monitoring. Historically, the surface deformity has been analyzed with inclinometers and plaster casts of the back [25].

Clinicians routinely assess spinal posture and back shape by simple visual analysis, and rely on radiographic evaluation for quantitative measurements. Considering the risks associated with radiation exposure from repeated radiographs, there is an increasing need for an objective and less invasive assessment to monitor treatment effectiveness. As cosmetic appearance is a serious concern for the patients [5, 6, 21], it is important to develop more reliable tools to assess spinal posture and back shape, since current tools for measurement are either unreliable or too complex.

Several methods to quantify the scoliotic deformity from back or trunk surface asymmetry have been introduced since the 1970s: Moiré contour topography [17, 32], raster systems such as the ISIS [26, 28–31] or the Quantec scanner [5, 16, 27]. The value of quantifying not only the back surface but also the 360° deformity of the entire scoliotic trunk has also been investigated [2, 7, 10, 11, 20, 23]. Each new technology introduces a different approach to understanding scoliosis via a different set of data describing the spine or the trunk. Out of this ever-increasing mass of information, researchers must pick accurate measurements to diagnose, detect, and follow progression of scoliosis and also to define new ways of quantifying and analyzing the deformity that can be helpful for the clinician to understand and assess treatment.

Contrary to the assessment of scoliotic deformities from X-ray images where the Cobb angle is the gold standard, there is no consensus on a set of indices that can be used to assess these deformities from the trunk surface.

When standardizing the posture for the data acquisition, decisive factors are: reproducibility, surface coverage, and similarity with postures currently adopted for the clinical or radiological assessment of the scoliosis deformity. From the viewpoint of correlating the bone structure deformity and the surface asymmetry, an obvious choice is to adopt the same posture as the one used for X-rays, with the arms roll up to the clavicles (“clavicle” position) [9]. To combine technical constraints, such as minimizing the occlusion of camera fields, another choice is a natural positioning of patients, using the traditional standing anatomical posture adopted by clinicians and by many other researchers [1, 5, 27].

The challenge for the evaluation of surface asymmetry associated with scoliosis comes from the precision and accuracy needed, considering that the goal is to be able to detect and quantify small but significant changes of the trunk surface. The present study aimed to estimate the reliability of 3-D trunk surface measurements for the characterization of external asymmetry associated with scoliosis based on two different arm postures.

Materials and methods

Subjects

All subjects were enrolled on a voluntary basis, and an informed consent was obtained for each subject as approved by the Ethical Committee of our institution. The inclusion criteria were: (1) a diagnosis of idiopathic scoliosis and (2) an age between 10 and 20 years. The exclusion criteria were: (1) any neurological disorder or (2) inability to stand upright.

Surface topography of the entire trunk was obtained on 49 patients (42 girls and 7 boys) attending the scoliosis clinic over a period of 15 months. Among them, 35 were evaluated as part of their routine pre-operative visit, 7 were evaluated post-surgery and 7 before a brace prescription (Table 1).

Table 1.

Information about the cohort

n = 49	Mean	Standard deviation	Range
Age (year)	14.2	1.1	11.0–19.7
Height (cm)	160	9	146–184
Weight (kg)	50	11	28–81
Body mass index (kg m−2)	19.8	4.3	11.7–36.1

Instrumentation

Trunk surface was digitized using a multihead INSPECK system (INSPECK Inc., Montreal, QC, Canada), consisting of four optical 3-D digitizers, a frame grabber for video signal acquisition and conversion, and a computer for data processing. The computer communicates with the digitizers for operation control and timing purposes. Each optical 3-D digitizer consists of a 1,024 × 768 pixels color CCD camera and a structured light projector (halogen light source and grating slide). The deformed patterns, due to the relief of a person’s body, are captured by the camera for four different pattern positions obtained by shifting the fringes by displacement of the grating slide. A fifth image without fringes is also acquired for the texture mapping procedure. For every recording sequence, the video images are processed to retrieve shape and texture information with a hybrid algorithm based on interferometric techniques and active optical triangulation [24].

Each of the four digitizers provides a partial surface, as seen from a selection of angles, to cover the entire trunk. Those partial models are brought into a common coordinate system, registered, and merged to reproduce the overall shape of the trunk. The texture of each partial model is also merged and mapped, based on a ray-tracing scheme, to provide a final textured 3-D model [24].

The main strengths of the system are a short acquisition time of 4–5 s for the whole trunk combined with a high sampling density. The multihead INSPECK system was previously assessed [19] for a three-digitizer configuration with a lateral resolution of 1.8 mm. The accuracy, estimated from repeated acquisitions of a manikin, was of 1.4 mm for a set of markers fixed all over the surface. For back surface data only, the accuracy was estimated as 0.56 mm. To improve these results, a different configuration was adopted in this study, which consisted of four serial color optical 3-D digitizers with standard color CCD cameras that allow images of 1,024 × 768 pixels to be grabbed with a lateral resolution of 1.2 mm.

Acquisition protocol

Before acquisition, erasable small crosses were drawn on the subjects’ skin over the anterior-superior iliac spines (ASIS) and vertebra prominence (VP) of C7 or T1 to define an axis system associated to the trunk model. Other markers were drawn around the trunk to get corresponding points on the overlapping parts of the partial surfaces to improve the surface assembly procedure [19].

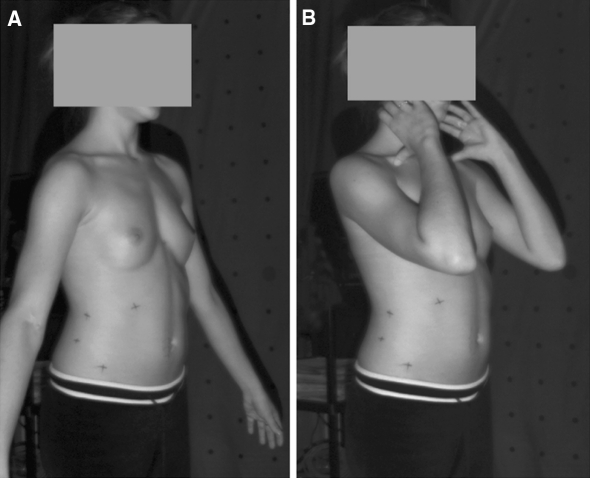
Subjects stood in the center of the system, marked on the floor, with their shoes removed, and with any long hair tied up over the neck. They were asked to stand still during acquisition, focusing on a point above the front digitizer. Each patient had her or his trunk digitized four times: two acquisitions in two different arm postures. Between each acquisition, the subject relaxed at least half a minute before the second arm posture or repositioning. Two postures for surface acquisition were tested:

1. The posture similar to the anatomical posture adopted by clinicians and by many other researchers [5, 25, 27] with the arms in slight abduction by the side (Fig. 1a). This posture minimizes the occlusion of camera fields.

2. The ‘‘clavicle’’ position with the elbows up forward, hands on the side of the neck (Fig. 1b). This posture is similar to the posture adopted for X-ray acquisition at Sainte Justine hospital, and recommended by Horton et al. [9] as the most accurate for radiographic exposure.

Each posture was explained and demonstrated to the subjects before the acquisition series. Skin-markers were not redrawn between acquisitions.

Fig. 1.

Postures A and B

Data processing

Trunk surface generation and features extraction

From each acquisition, a 3-D model of the trunk surface was reconstructed from the partial surfaces acquired from each of the four digitizers [19]. The result was a textured polygonal surface counting, depending of the patient’s height, about 40,000–70,000 points that were locally not uniformly spaced. The operator identified the skin markers and the acromia interactively through a graphical interface.

The axis system was defined by: the Y-axis that was vertical up, the X-axis was the horizontal parallel to the ASIS line towards the right of the patient, the origin (O) was the normal projection of ASIS line middle-point on the back surface, and the Z-axis was directed out of the back surface. The dimples of the posterior-superior iliac spines (PSIS) have been generally used to define the axis system for back surface topography [4, 5, 29] but with the entire trunk, the ASIS landmarks are accessible and easier to locate. They have the advantage of being more distant so that the error on axis direction is lower than for the PSIS.

For computation purposes, 250 horizontal cross-sections were generated between the PSIS level and the T1 level, which represented a vertical step of about 2.5 to 3 mm according to the trunk length. The cross-sections were approximated with cubic splines [18].

For each cross-section, four characteristic points and two axes were defined:

• The geometric centre of the section;

• The right and left “humps” were defined as local maxima on the back profile (zeros of the first derivative);

• The tangent to the back profile passed by the right and left humps of the section.

• The principal axis of the section was defined by least-squares approximation of the depth coordinate.

Right and left mid-lateral and central curves were created by smoothing from the series of right and left humps and section centers, respectively.

Measurements

The trunk inclination was defined as the shift of the vertebra prominence (VP) relative to the vertical line passing through origin. The inclination was measured in the frontal plane (lateral inclination) and in the sagittal plane (forward–backward inclination). The origin–VP distance measured the trunk height.

The pelvic tilt was the angle between the horizontal plane and the ASIS line.

The shoulder imbalance was the angle between the shoulder line and the horizontal axis in the frontal plane.

The back surface rotation was the angle between the tangent line to the back profile and the X-axis.

The axial trunk rotation was the angle between the principal axis of the section and the X-axis.

The deviation of the central curve was computed from the line passing through the centers of the first and last sections.

The area between the right (left) mid-lateral curve and the Y-axis was computed in the frontal plane. The global apparent asymmetry in the frontal view was calculated both as the ratio and as the difference between right and left areas. The upper limit for the area computation was the lower acromion. The lower limit was the section such as the vertical coordinate Y = 0. In the lateral view, the global asymmetry was the root-mean-square difference between the right and left mid-lateral curves.

Statistical analysis

For each of the 49 subjects and each of the four acquisitions per subject, the 3-D trunk surface was reconstructed and measurements of the trunk asymmetry were computed. Reliability of the measurements was evaluated for both postures using Intraclass Correlation Coefficients (ICC) obtained using a bivariate analysis of variance, with subject and trial as factors. Reliability was reported using ICC and typical error of measurement (TEM). A 95% confidence interval (CI) of the typical error of measurement was calculated.

The equation for intraclass correlation coefficient [8] is

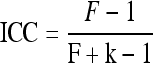1

where F is the ratio of the mean squares due to the subject factor versus the mean associated to the error, and k was the number of tests.

The ICC assesses the proportion of the total variability that is explained by the between-subjects variation [8, 12]. The smallest detectable differences (SDD) were calculated for each measurement using the equation

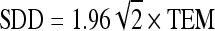2

The smallest detectable difference is the threshold required to detect a statistically significant change in an individual when taking into account the variability associated with both the measurement technique and experimental sample. Multivariate analysis of variance was also performed with subject, trial, and posture as factors to estimate the effect of posture on the measurements. The P value for posture addresses the issue of overall differences between the means of the postures.

Pre–post-surgery comparison: case examples

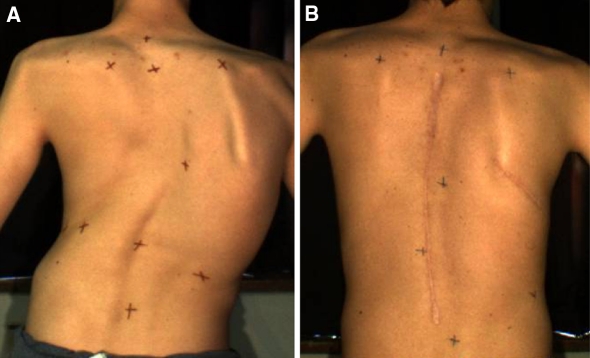
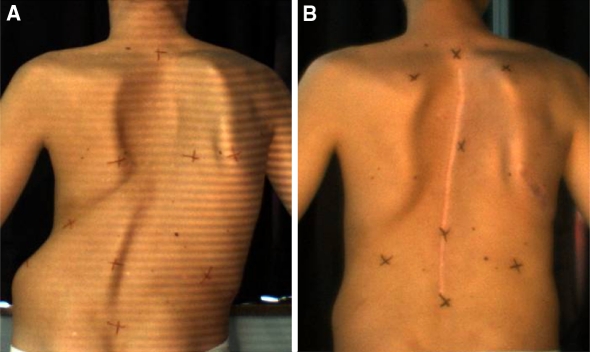
To illustrate the external surface measurements applied to the quantification of the effect of spinal instrumentation on the cosmetic appearance, we selected the cases of two adolescents with right thoracic scoliosis. For both, the Cobb angle was 74° before the surgery and 16° after. Figures 2 and 3 are pictures of their backs before and after the surgery. External surface measurements were computed and compared.

Fig. 2.

Patient 1 a before and b after surgery

Fig. 3.

Patient 2 a before and b after surgery

Results

Differences between the two postures

The results of the reliability study, for postures A and B, are presented in Table 2. The last column presents the P value for difference between the measurement values obtained for the two postures. When considering posture as a factor, the P value from the analysis of variance gave an indication of what would be the reliability of the external asymmetry if no standard position of the arms were defined in the acquisition protocol. The results suggest that not all indices were affected in the same way by a change of positioning. Indices measured on the lateral and frontal views were more sensitive to changes of trunk posture than indices computed from transversal sections, such as the axial trunk rotation and the global apparent asymmetry.

Table 2.

Results for postures A and B

	Posture A						Posture B						P value Posture
	Mean ± SD	TEM	TEM UL	SDD	ICC	ICC 95% CI	Mean ± SD	TEM	TEM UL	SDD	ICC	ICC 95% CI
Back surface rotation max. (°)	11.6 ± 4.5	1.41	1.75	2.48	0.93	0.88–0.96	12.0 ± 4.8	1.36	1.69	2.39	0.92	0.86–0.95	0.01
Axial trunk rotation max. (°)	6.8 ± 3.5	0.84	1.04	1.48	0.97	0.95–0.98	6.8 ± 3.5	0.81	1.01	1.43	0.97	0.95–0.98	0.61
Frontal asymmetry ratio	1.8 ± 1.6	0.28	0.35	0.49	0.99	0.98–0.99	1.7 ± 1.5	0.52	0.65	0.92	0.90	0.84–0.94	0.26
Frontal asymmetry (mm)	13.2 ± 36.7	4.74	5.91	8.35	0.99	0.98–0.99	12.9 ± 35.7	4.89	6.10	8.62	0.98	0.97–0.99	0.67
Lateral asymmetry (mm)	5.4 ± 10.2	2.66	3.32	4.69	0.95	0.91–0.97	5.0 ± 10.3	2.48	3.09	4.37	0.94	0.90–0.97	0.35
Maximum centre deviation (mm)	17.6 ± 9.8	3.19	3.98	5.62	0.91	0.85–0.95	19.7 ± 9.9	3.90	4.86	6.87	0.85	0.74–0.91	<0.01
Trunk height (mm)	394 ± 30	3.0	3.8	5.3	0.99	0.98–0.99	382 ± 31	5.17	6.44	9.11	0.97	0.95–0.98	<0.01
Lateral trunk inclination (°)	0.4 ± 3.4	0.88	1.10	1.55	0.97	0.94–0.98	0.9 ± 3.4	1.17	1.46	2.06	0.92	0.86–0.96	<0.01
Forward-backward trunk inclination (°)	−5.6 ± 3.3	0.75	0.94	1.32	0.95	0.92–0.97	0.2 ± 3.1	1.54	1.92	2.71	0.88	0.79–0.93	<0.01
Frontal pelvic tilt (°)	0.2 ± 3.4	0.69	0.86	1.22	0.97	0.94–0.98	0.0 ± 3.4	1.05	1.31	1.85	0.95	0.91–0.97	0.207

SD standard deviation, TEM typical error of measurement, UL upper limit, SDD smallest detectable difference, ICC intraclass correlation coefficient, CI confidence interval

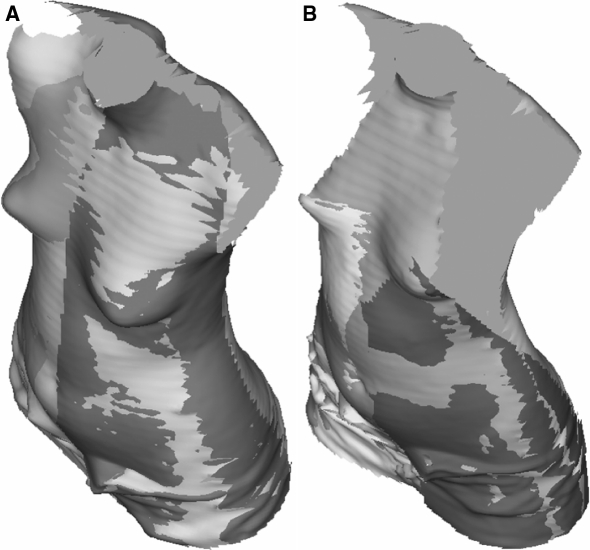
Despite the instructions, for two of the patients, in “clavicle position”, the arms occluded too much surface to allow measurements on the anterior thoracic area of the torso. However, for the largest subjects, this posture allowed a better coverage on the sides of the trunk under the arms (Fig. 4). The results for lateral and forward–backward trunk inclination show that posture A was more reproducible (ICC of 0.97 and 0.95, respectively), compared to posture B (0.92 and 0.88). When viewing the back surface only, the main visible differences between the two postures, in terms of back shape, were the tips of the scapulae and the lumbar curvature. When viewing the front side of the trunk, posture A was obviously better because the arms did not hide the torso surface, the shoulders were better covered, and the acromia more easily identifiable. The forward–backward inclination was significantly different (P < 0.01) with an average difference about 5.8° between the postures. The trunk tended to be inclined more backward when the elbows were up (posture B). The shape of the trunk was different, particularly in the sagittal plane with posture B tending to increase the apparent lordosis by around 5°.

Fig. 4.

Surface coverage for posture A and B. The figure shows the partial surfaces from the four digitizers, brought into a common coordinate system [19]

Reliability of measurements

For each posture, the first two columns in Table 2, present the typical errors of measurements (TEM) and the corresponding upper limits of the 95% confidence intervals (UL). The third column presents the smallest detectable difference (SDD) calculated with formula 2. The fourth and fifth columns present the ICC, calculated with formula 1, and the corresponding 95% confidence interval. For ICC, within the interval 0.90–0.95 we considered that reliability was fair, within 0.95–0.98 it was good, and above 0.98 it was very good. When considering the entire set of indices, posture A (anatomical posture) provided a better reliability with ICC ≥ 0.91 for most indices and was the one recommended for clinical use.

The apparent global asymmetry was relatively robust to changes in arm posture, as well as the axial trunk rotation index, both in terms of mean values and within-subject variations. These measurements also showed a good reliability.

Labelle et al. [13] reported reliability of 1.1° for rib hump measured on rib cage 3-D reconstructions, based on repeated measures but not on repeated acquisitions. The reliability of the apparent rib hump index, based on back surface rotation, was comparable, with a typical error of measurement of 1.4°, considering that our results included the repositioning error. A visual examination of the mid-lateral curves indicated that most of the outliers were produced by large local deviations, at scapula level, by a prominent tip and/or a pronounced fold under the scapula. The direct consequence was a greater variability of back surface rotation in the upper thoracic region. The axial trunk rotation tended to minimize the amplitude of the apparent deformity and had a better reliability (ICC = 0.97 for axial trunk rotation vs. 0.93 for back surface rotation) partly because it was less sensitive to the noise from the scapula borders.

Sample size for further studies

Assuming we want to measure the efficiency of the treatment on the external trunk surface, the back surface rotation or axial trunk rotation would be the main variable to study. Actually, this measurement is the closest to the thoracic gibbosity measured on the 3-D skeletal rib cage structure, and it was reliable. Furthermore, the gibbosity measurement is the most representative of an adequate 3-D correction of the thorax according to previous studies on AIS treatment evaluation [3, 14, 15]. An average improvement up to 3° would be clinically significant. Considering that the smallest statistically significant difference is 2.5°, a sample of 44 subjects would be sufficient to detect a difference between two groups with a 0.05 type I error and 80% power [8].

Pre/post-surgery comparison: exemplar cases

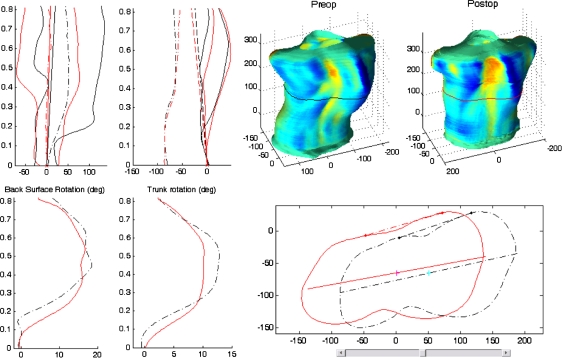
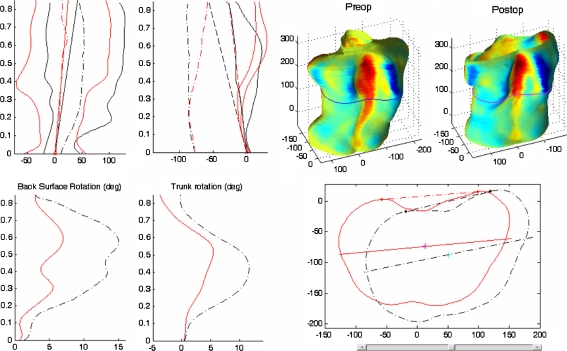
Figures 5 and 6 display the comparative measurements before and after the surgery for two patients (Table 3). Asterisks (*) indicate statistically significant differences (superior to the smallest detectable differences presented in the Table 2). The last column is the difference between the two patients before their surgery. Statistically, the pre-operative external asymmetries were significantly different for most of the measurements. Whereas both showed good correction in the frontal plane, the ranges of corrections in other planes were not comparable. The change in the shape of the cross-sectional sections was particularly representative of the overall correction.

Fig. 5.

Comparative measurements for patient 1. In the top left corner, the right and left mid-lateral and central curves, in frontal and lateral plane. In the bottom left corner, the back surface and axial trunk rotation angle along the normalized trunk height (=1 at the vertebra prominence). In the top right corner, the preoperative and postoperative trunk surface with color corresponding to the depth Laplacian, 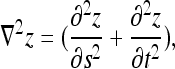where s and t are the parameters of the surface. In the bottom right corner, corresponding cross-sections, with tangents to the back profiles (used to compute the back surface rotation) and principal section axes (used to compute the axial trunk rotation)

Fig. 6.

Comparative measurements for patient 2. In the top left corner, the right and left mid-lateral and central curves, in frontal and lateral plane. In the bottom left corner, the back surface and axial trunk rotation angle along the normalized trunk height (=1 at the vertebra prominence). In the top right corner, the preoperative and postoperative trunk surface with color corresponding to the depth Laplacian, 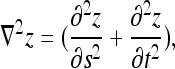where s and t are the parameters of the surface. In the bottom right corner, corresponding cross-sections, with tangents to the back profiles (used to compute the back surface rotation) and principal section axes (used to compute the axial trunk rotation)

Table 3.

Comparative measurements, in posture A, for two exemplar cases

	Patient 1				Patient 2				|2−1|
	Preop	Postop	Correction		Preop	Postop	Correction		Preop
Back surface rotation max. (°)	18.5	16.7	1.8	10.0%	15.1	7.0	8.1*	53.6%	3.4*
Axial trunk rotation max. (°)	12.8	10.2	2.6*	20.3%	11.6	5.5	6.2*	52.9%	1.2
Frontal asymmetry ratio	5.3	1.2	4.1*	76.5%	8.6	1.8	6.8*	78.7%	3.3*
Frontal asymmetry (mm)	83.5	13.0	70.5*	84.5%	93.8	35.9	57.9*	61.7%	10.3*
Lateral asymmetry (mm)	27.1	24	3.1	11.5%	22.3	9.1	13.2*	59.2%	4.8*
Maximum centre deviation (mm)	30.6	3.0	27.6*	90.1%	24.7	4.9	19.8*	80.0%	5.9*
Lateral trunk inclination (°)	4.1	1.5	2.6	62.6%	8.7	4.7	4.0	46.2%	4.6*

The last column is the difference between the two patients before their surgery. Asterisks indicate statistically significant differences (superior to the smallest detectable differences presented in the Table 2). Preop preoperative evaluation, Postop postoperative evaluation

Discussion and conclusion

The surface reconstruction system used for this study allowed rapid acquisition of the entire trunk digital data, with a high density of points, thus allowing as many acquisitions as deemed necessary. The reconstruction process requires about 30 min for a trained operator, and the indices computation a few minutes. With further refinements of the technology currently underway and allowing full automation of the procedure, the entire processing time could be reduced to a few minutes and the intra- and inter-operator variability could be eliminated.

Within-subject variations

One goal of trunk surface analysis is to characterize and quantify the apparent asymmetry associated with the spinal deformity and to detect and quantify its progression. To characterize the apparent asymmetry, indices must ideally have a very small within-subject variation relative to between-subject variation and a relative robustness to small changes in positioning. To detect a progression between two evaluations, indices must have a small typical-error relative to the smallest change that the clinician would like to detect. The results of the present study were very satisfying with ICC ≥ 0.91 for most indices in the anatomical posture. The within-subject standard deviation for the maximal back surface rotation was 1.4° (1.8° upper limit of the 95% confidence interval) and 0.8° (1.0° upper limit of the 95% confidence interval) for the maximal trunk rotation. The respective smallest statistically significant differences were 2.5° and 1.5°. Some measurements, as the axial trunk rotation and the global apparent asymmetry, seem to be little sensitive to change in arms positioning, while having a good reliability.

Description of trunk deformity

With spinal deformities, the trunk deformity needs more than a single value index to be described adequately. We believe surface asymmetry analysis should be seen as a dashboard to monitor the status and evolution of a scoliotic deformity. Main indices were the back surface rotation and the axial trunk rotation, as they seemed similar in their definition, but they did not measure exactly the same characteristic. Axial trunk rotation measurement includes also the anterior profile that contributes to the perception of cosmetic deformation. With a combined interpretation of both measures, it would be possible to differentiate the axial rotation of transversal sections and their deformations. Together, they would provide a more adequate characterization of the rib cage deformity. To detect a progression it would be more appropriate to compare curves, representing measurements along the trunk length, rather than just considering single maximal values, because they would provide indications on the extent of the rib cage deformity.

It is interesting to note that for two right thoracic scoliotic deformities with equal Cobb angle, their external asymmetries were significantly different, at least statistically. This observation strongly suggests that simple correlation between Cobb angle and one external asymmetry measure is not the best method to predict the internal deformity from the external asymmetry.

In the current study, subjects had moderate-to-severe spinal deformities. Consequently, their results cannot be taken as reference for screening purposes. Further evaluations will be necessary to describe the variability and reliability of these indices in smaller deformities. Nevertheless, external measurements can provide non-invasive complementary evaluation of changes in external asymmetry. If not sensitive enough to detect smaller changes for natural progression monitoring, trunk surface analysis can still document the external asymmetry associated with different types of spinal curves and could provide a 3-D classification of scoliotic deformities. The measurements presented in this study can also be used for posture analysis as well as for the evaluation of the cosmetic improvement obtained with surgical interventions.

Arms positioning

Finally, both the anatomical posture and the “clavicle” position are reliable, although the postures are different in the sagittal plane, the “clavicle” position inducing a more backward inclination of the trunk and an increase in lumbar lordosis. Although the anatomical posture would be slightly preferable when analyzing the external asymmetry alone as it allows a better coverage of the trunk surface by the digitizing system, the “clavicle position” can also be chosen to allow better correlation between the external trunk asymmetry and deformities of the underlying bone structures obtained from multiple X-rays acquired with the “clavicle position”.