Kinematics of the lumbar spine in trunk rotation: in vivo three-dimensional analysis using magnetic resonance imaging

Abstract

In vivo three-dimensional (3D) kinematics of the lumbar spine has not been well evaluated by the conventional methods because of their methodological limitations, while 3D intervertebral motions have been quantitatively determined by cadaver studies. We thus developed a novel 3D analyzing system for the relative motions of individual vertebrae using 3D magnetic resonance imaging (MRI) and analyzed in vivo 3D intervertebral motions of the lumbar spine during trunk rotation. Ten healthy volunteers underwent 3D MRI of the lumbar spine in nine positions with 15° increments during trunk rotation (0°, 15°, 30°, 45°, and maximum). Relative motions of the lumbar spine were calculated by automatically superimposing a segmented 3D MRI of the vertebra in the neutral position over images of each position using the voxel-based registration method. These 3D motions were represented with 6 degrees of freedom by Euler angles and translations on the coordinate system. The mean axial rotation of ten healthy volunteers of each lumbar spinal segment in 45° trunk rotation to each side ranged from 1.2° to 1.7°. Coupled flexion with axial rotation was observed at the segments from L1/2 to L5/S1. Coupled lateral bending of the segments from L1/2 to L4/5 was in the opposite direction of the trunk rotation, while that of T12/L1 and L5/S1 was in the same direction. The direction of the coupled lateral bending in the present study was different from that in the previous cadaver study only at L4/5. This difference might result from the non-load state of the supine position in the current study and/or the non-physiological state in the cadaver study. Our system has two limitations: (1) the study was conducted with each volunteer in the supine position, and (2) because the rotation device regulated trunk rotation, trunk rotation might not have been physiological. In vivo 3D intervertebral motions of the lumbar spine during trunk rotation were evaluated using our novel motion analysis system. These data may be useful for the optimal orthopaedic management of lumbar spinal disorders.

Electronic supplementary material

The online version of this article (doi:10.1007/s00586-007-0373-3) contains supplementary material, which is available to authorized users.

Introduction

Biomechanical consideration is essential in elucidating the pathophysiologies of various musculoskeletal disorders and orthopaedic management should be based on such understanding. The pathological kinematics cannot be detected without normal kinematics data. Regarding normal lumbar spinal motions, Lovett confirmed concomitant spinal motions other than the primary motion using cadaver spines and documented so-called coupled motions for the first time in 1905 [7]. Panjabi et al. [11] reported in vitro three-dimensional (3D) intervertebral motions of the lumbar spine quantitatively. However, in vivo 3D kinematics of the normal lumbar spine has not been well analyzed because of the limitations of each method [5, 12, 14]. To analyze in vivo 3D kinematics more accurately, we developed a novel 3D motion analysis system using 3D magnetic resonance imaging (MRI). Our colleagues have already reported in vivo 3D kinematics of the cervical spine and wrist joint using this original method [1–4]. In addition to these studies, in vivo 3D intervertebral motions of the normal lumbar spine in various trunk motions have also been under investigation. In this initial report, the in vivo 3D kinematics of the normal lumbar spine during trunk rotation is described.

Materials and methods

Ten healthy volunteers (six men and four women) were examined using our novel system. Their mean age was 26.4 years (range 23–31 years). None had low back pain or a medical history of lumbar disorders. All participants provided written informed consent before participation in this study.

Acquisition of 3D-MRI

Magnetic resonance images of the lumbar spine were acquired using a 1.0-T commercial magnetic resonance system (Signa LX, General Electric, Milwaukee, WI, USA) in conjunction with a torso-phased array coil. A 3D-fast gradient recalled acquisition in the steady state (GRASS) pulse sequence was employed with repetition time/echo time of 8.0/3.3 ms, 1.5 mm slice thickness, and no interslice gap. Flip angle was 10° with a 30-cm field-of-view and a 256 × 224 in plane acquisition matrix. First, MRIs in the neutral position were acquired. In all subjects, the absence of degenerative changes or abnormalities was confirmed in the lumbar spine. Our original device was used to rotate the trunk of the subjects as reproducibly as possible (Fig. 1). The pelvis of the volunteer was tightly fixed to the rotation device using a belt. Then, they were placed supine on the MRI table and their shoulders were tightly strapped to the table. As their trunks were rotated passively without fixing the legs, each volunteer was instructed to keep their knees straight and rotate their legs in a fashion comparable to the trunk rotation, in order to minimize the effects of leg rotation on trunk rotation. 3D MRIs were obtained in nine positions with 15° increments of trunk rotation (0°, 15°, 30°, 45°, and maximum). Maximum trunk rotation was defined as the position in which their trunks were rotated as much as possible without their bilateral shoulders pulled away from the MRI table. The degree of trunk rotation was measured by axial scout-view images as the angle between a line perpendicular to the MRI table and a line from the sacral spinal process through to the center of the sacral body. Imaging time was approximately 5 min for each position. MRI data were saved in Digital Imaging and Communications in Medicine (DICOM) format and transmitted to a computer workstation, where image processing such as segmentation and volume registration were performed using a software program developed in our laboratory (Virtual Place M series; Medical Imaging Laboratory Inc., Tokyo, Japan).

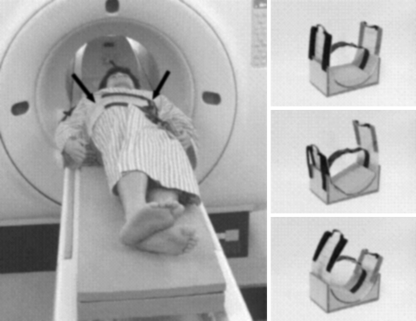
Fig. 1.

Acquisition of 3D-MRI. Our original device (arrow) was used to rotate the trunk of the subjects as reproducibly as possible. 3D MRIs were obtained in nine positions with 15° increments of trunk rotation (0°, 15°, 30°, 45°, and maximum). Maximum trunk rotation was defined as the position in which the trunks were rotated as much as possible without the bilateral shoulders pulled away from the MRI table

Segmentation of the vertebrae

Segmentation was defined as extracting vertebrae required for processing [1–4]. Contours of individual vertebrae in the neutral position were semi-automatically segmented from 3D MRI using intensity thresholding techniques.

Volume registration

Volume registration is an image processing method for matching volume images based on voxel values. Kinematic variables were measured by automatically superimposing segmented 3D MRI of the vertebrae in the neutral position over images for each position using this method of registration [1–4]. The correlation coefficient was used as a method of measuring similarity of voxel values for registration. With this method of measuring, a matrix that allowed for the maximal correlation of the two images was calculated.

Motion analysis

The anatomical orthogonal coordinate systems of vertebrae were defined as described by Panjabi et al. [11] (Fig. 2). 3D motions of relative upper vertebra to subjacent vertebrae were calculated by converting the matrix obtained from volume registration into a matrix representing relative motion and described with 6 degrees of freedom by rigid body Euler angles and translations using the coordinate systems. We presented Euler angles with coordinates of yaw (X), pitch (Y), and roll (Z). Translation was calculated based on the origin of the coordinate system. In addition, the degree of trunk rotation was measured on the absolute spatial coordinate system using volume registration of the sacrum.

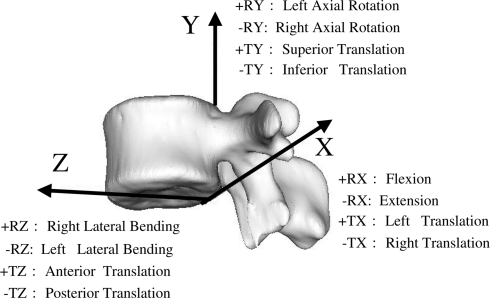
Fig. 2.

Anatomical orthogonal coordinate system. The origin was located at the most inferior point on the posterior wall of the vertebral body in the mid-sagittal plane. The Z-axis was defined as the line connecting the anterior and posterior points in the inferior plane of the vertebral body (anterior considered to be positive). The Y-axis was defined as perpendicular to the Z-axis, with superior being positive. The positive X-axis was directed to the left. Translation was calculated based on the origin of the coordinate system

Visualization of motion

Animations of spinal motions during trunk rotation were created from the calculated motions and surface bone models that were reconstructed from 3D-MRI data using the marching cubes algorithm in the Visualization Toolkit (VTK) [6].

Accuracy

The accuracy of this analysis system was reported previously: 0.24° for flexion–extension, 0.31° for lateral bending, 0.43° for axial rotation, 0.52 mm for superoinferior translation, 0.51 mm for anteroposterior translation, and 0.41 mm for lateral translation, as described in detail previously [2].

Statistical analysis

Means and standard deviations (SD) for range of motion to one side were computed. Intervertebral motions of different levels under axial rotation were compared using a factorial analysis of variance. Fisher’s least significant difference post hoc test was used at a confidence level of 95% to determine which levels differed significantly from one another for axial rotation.

Results

The mean (±SD) angle of axial rotation of the trunk from neutral to maximum positions was 56.1 ± 7.5°. The 3D intervertebral motions of the lumbar spine during trunk rotation are shown in Figures 3 and 4 (Fig. 4; video can be viewed at the Journal’s web site).

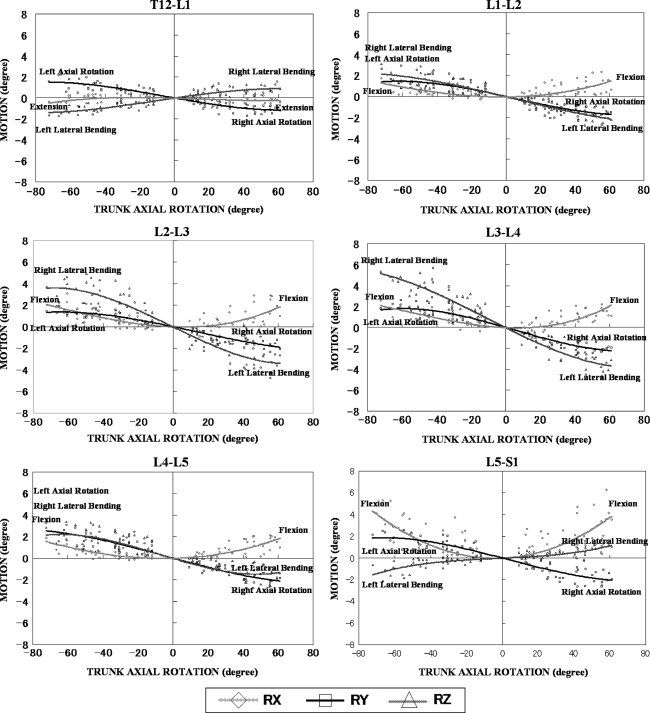
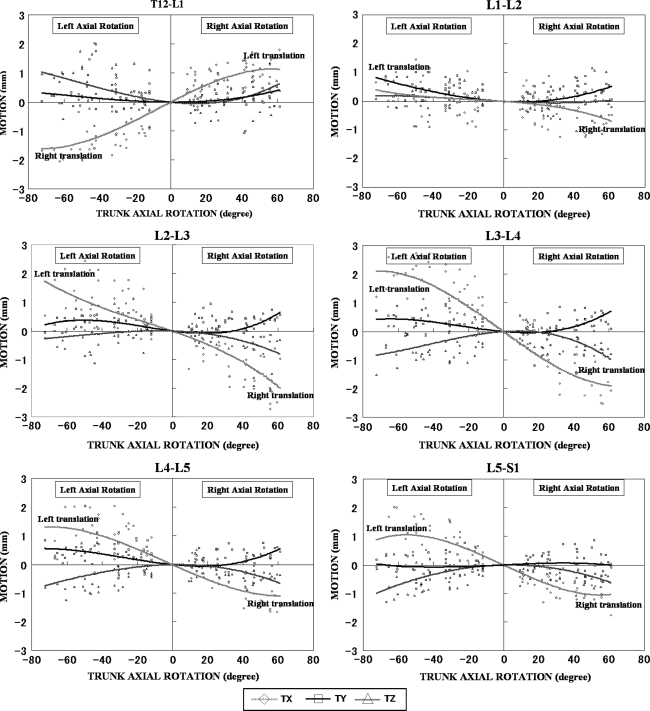
Fig. 3.

Intervertebral motions of the lumbar spine during trunk axial rotation. The degree of trunk axial rotation was plotted on the X-axis. The degree of rotational motion along each axis on the anatomical orthogonal coordinate system and the length of translational motion at each level were plotted on the Y-axis. Approximate curves, which were prepared as tertiary approximate curves based on multiple function approximation were drawn. Statistical analysis of right and left rotation data showed no significant difference, thus ruling out asymmetric kinematics

Fig. 4.

Three-dimensional motions of the lumbar spine during trunk axial rotation. (To access the video illustration, visit the online issue of European Spine Journal)

Axial rotation

The mean axial rotation at each level of the lumbar spine to one side when volunteer’s trunks were rotated 45° was 1.2 ± 0.4° at T12/L1, 1.3 ± 0.5° at L1/2, 1.4 ± 0.3° at L2/3, 1.7 ± 0.6° at L3/4, 1.7 ± 0.6° at L4/5, and 1.6 ± 0.7° at L5/S1. Axial rotation was thus greater in lower lumbar than upper lumbar, although no statistical significances were found among all levels.

Coupled flexion–extension

Coupled flexion with axial rotation when volunteer’s trunks were rotated 45 degrees was observed in L1/2 (0.8 ± 0.6°), L2/3 (1.0 ± 0.8°), L3/4 (1.3 ± 0.5°), L4/5 (0.9 ± 0.6°), and L5/S1 (1.9 ± 1.6°). While in the thoracolumbar junction (T12/L1), coupled flexion and extension with axial rotation were within the range of error (−0.1 ± 0.4°) (Table 1).

Table 1.

Ranges of motion in axial rotation (AR) in Normal subject or cadaveric specimens from literature

		Level	Flex–ext	Left AR	LB	Flex–ext	RightAR	LB
Peacy (1984)	In vivo	L1–2	0	1	3	0	−1	−3
		L2–3	0	1	3	0	−1	−4
		L3–4	0	2	3	0	−1	−3
		L4–5	0	2	2	0	−1	−1
		L5-S1	0	0	−1	0	−1	2
Panjabi (1994)	In vitoro	L1–2	1.3 ± 0.9	2.3 ± 1.2	1.9 ± 0.8	0.6 ± 1.7	−1.2 ± 0.9	−1.9 ± 0.8
		L2–3	1.0 ± 0.4	1.7 ± 0.9	2.2 ± 1.8	1,2 ± 0.5	−2.7 ± 0.9	−3.1 ± 1.4
		L3–4	1.9 ± 1.4	2.3 ± 0.7	0.2 ± 1.6	0.1 ± 0.3	−2.1 ± 0.9	−1.7 ± 0.7
		L4–5	0.9 ± 1.4	1.2 ± 1.0	−2.2 ± 0.5	1.6 ± 1.0	−2.0 ± 0.9	1.4 ± 0.4
		L5-S1	0.7 ± 1.8	10. ± 1.0	−2.5 ± 1.8	1.3 ± 1.3	−1.1 ± 0.8	2.9 ± 1.1
Authors (2006)	In vivo	Th12-L1	−0.2 ± 0.5	1.2 ± 0.5	−1.2 ± 0.2	−0.1 ± 0.4	−1.1 ± 0.4	0.6 ± 0.3
		L1–L2	0.7 ± 0.5	1.2 ± 0.6	1.6 ± 0.7	0.8 ± 0.7	−1.3 ± 0.5	−1.7 ± 0.7
		L2–L3	1.2 ± 0.6	1.2 ± 0.6	3.0 ± 1.0	0.9 ± 1.0	−1.5 ± 0.4	−2.9 ± 0.9
		L3–L4	1.3 ± 0.6	1.5 ± 0.6	3.8 ± 1.0	1.2 ± 0.5	−1.9 ± 0.6	−2.9 ± 0.8
		L4–L5	0.5 ± 0.4	1.9 ± 0.6	2.0 ± 1.1	1.2 ± 0.7	−1.6 ± 0.5	−1.3 ± 0.8
		L5–S1	1.7 ± 1.6	1.6 ± 0.6	−0.7 ± 0.6	2.1 ± 1.5	−1.7 ± 0.9	0.5 ± 0.7

Coupled lateral bending

Coupled lateral bending according to axial rotation when volunteer’s trunks were rotated 45 degrees was −1.6 ± 0.7° in L1/2, −3.0 ± 1.0° in L2/3, −3.4 ± 0.9° in L3/4, and −1.6 ± 0.9° in L4/5 in the opposite direction of axial rotation, while that was 0.9° ± 0.3 in T12/L1 and 0.6° ± 0.6 in L5/S1 in the same direction.

Coupled translations

Slight lateral translation coupled with axial rotation when volunteer’s trunks were rotated 45° was observed in the same direction as axial rotation in L1/2 (0.3 ± 0.7 mm), L2/3 (1.2 ± 0.7 mm), L3/4 (1.6 ± 0.8 mm), L4/5 (1.1 ± 0.7 mm), and L5/S1 (1.0 ± 0.7 mm), while that was in the opposite direction in T12/L1 (−0.9 ± 0.8 mm). Coupled anteroposterior and superoinferior translation with axial rotation were hardly found.

Discussion

In 1905, Lovett confirmed concomitant spinal motions other than the primary motion using cadaver spines and documented so-called coupled motions for the first time [7]. Quantitative data on 3D intervertebral motions of the lumbar spine have been provided by in vitro studies using cadaver specimens. In those cadaver studies, however, the osteoligamentous spine without muscle tone might not accurately reflect physiological lumbar motions [10, 11, 16]. Conversely, in vivo 3D normal kinematics of the lumbar spine has not been well analyzed. So far, in vivo lumbar spinal motions have been largely analyzed by the two-dimensional (2D) methods using X-rays, fluoroscopy, and 2D-MRI [7–9, 13]. However, previously reported 2D methods are not able to analyze 3D coupled motions of the lumbar spine. To investigate in vivo 3D kinematics of the lumbar spine, some researchers employed biplanar radiography [12]. Their study revealed coupled motions of the lumbar spine with axial rotation. However, their method has major difficulties in identifying the same reference points on four separate views of the same vertebra precisely. Although other investigators used the 3-Space Isotrak System, discrepancies between motions of the vertebrae and those of skin markers were problematic [5, 14]. We thus developed a novel 3D motion analysis system using 3D MRI to analyze in vivo 3D kinematics more accurately than previously reported methods. In vivo 3D intervertebral motions of the normal lumbar spine in various trunk motions have also been under investigation using this unique system. In the present report, the kinematics of the normal lumbar spine during trunk rotation is presented.

The current study reported that each lumbar spine had a small degree of axial rotation, approximately 1–2°, during trunk rotation. This result was consistent with the results of most previous reports [10, 12]. The small degree of axial rotation seemed to be attributed to sagittalization of the facet joint articulations of the lumbar spine. Morphological studies of facet orientation in the thoracolumbar spine [15] have reported that facet orientation dramatically changes in the thoracolumbar junction and that thoracic facets are generally frontally oriented. Additionally, a previous cadaver study reported that the degree of axial rotation is larger in the thoracic region than in the lumbar region. The total of degree of axial rotation was approximately 45° in the thoracic region and approximately 10° in the lumbar region, which suggests that trunk rotations occur in the thoracic region rather than in the lumbar region.

In the current study, coupled flexion with axial rotation was observed in the lumbar spine from L1/2 to L5/S1. The direction of coupled flexion–extension was consistent with the result of the cadaver study by Panjabi et al. [11]. On the other hand, coupled lateral bending with axial rotation in the lumbar spine was observed in the opposite direction as axial rotation at L1/2, L2/3, L3/4, and L4/5, and in the same direction at T12/L1 and L5/S1. The direction of the coupled lateral bending was consistent with the result of a previous in vivo study using bi-planar radiography by Pearcy et al. [12]. Conversely, in a cadaver study, Panjabi et al. [11] reported that coupled lateral bending with axial rotation was observed in the opposite direction as axial rotation at L1/2, L2/3, and L3/4, and in the same direction at L4/5 and L5/S1. The direction of the coupled lateral bending in this in vivo study was different from that in the in vitro study only at L4/5. This difference might result from the non-load state of the supine position in the current study and/or the non-physiological state in the in vitro study.

In addition to the 3D kinematics of the normal lumbar spine during trunk rotation, normal 3D kinematics of various lumbar spine motions can be analyzed using this useful system. Subsequently, based on these data of the normal lumbar spine, the pathological kinematics due to various lumbar spinal disorders can be elucidated. These data may be useful for the optimal orthopaedic management of lumbar spinal disorders. However, the present study has two limitations. First of all, because trunk rotation was analyzed in the supine position, gravitational force was not involved. During trunk rotation in the standing position, gravitational force causes axial compression, which increases intervertebral pressure and elevates stiffness. Also, in order to maintain the standing position, paraspinal muscles are contracted [15]. It is difficult to predict the effects of such conditions on kinematics, and this will need to be resolved in the future. Secondly, since an original device was used to rotate the trunk, trunk rotation might not have been physiological. In the present study, in order to make trunk rotation as uniform as possible, we created our own rotation device. As the rotation axis varied depending on the body shape of the volunteer, it was difficult to predict what type of motion will have how much affect on rotation. This is another shortcoming of the study.