Material properties in unconfined compression of human nucleus pulposus, injectable hyaluronic acid-based hydrogels and tissue engineering scaffolds

Abstract

Surgical treatment for lower back pain related to degenerative disc disease commonly includes discectomy and spinal fusion. While surgical intervention may provide short-term pain relief, it results in altered biomechanics of the spine and may lead to further degenerative changes in adjacent segments. One non-fusion technique currently being investigated is nucleus pulposus (NP) support via either an injectable hydrogel or tissue engineered construct. A major challenge for either approach is to mimic the mechanical properties of native NP. Here we adopt an unconfined compression testing configuration to assess toe-region and linear-region modulus and Poisson’s ratio, key functional parameters for NP replacement. Human NP, experimental biocompatible hydrogel formulations composed of hyaluronic acid (HA), PEG-g-chitosan, and gelatin, and conventional alginate and agarose gels were investigated as injectable NP replacements or tissue engineering scaffolds. Testing consisted of a stress-relaxation experiment of 5% strain increments followed by 5-min relaxation periods to a total of 25% strain. Human NP had an average linear-region modulus of 5.39 ± 2.56 kPa and a Poisson’s ratio of 0.62 ± 0.15. The modulus and Poisson’s ratio are important parameters for evaluating the design of implant materials and scaffolds. The synthetic HA-based hydrogels approximated NP well and may serve as suitable NP implant materials.

Introduction

Nucleus pulposus (NP) replacement is a non-fusion technique currently being investigated to treat painful disc degeneration. Replacement of NP with an injectable implant or tissue engineered construct, in patients with healthy annulus fibrosus (AF), may reduce pain while simultaneously restoring spinal mobility and delaying disc degeneration [8, 11, 20, 26, 29, 31]. The challenge for any synthetic nucleus replacement material is to mimic the function of native NP. However, NP mechanical behavior has been described as either incompressible [16, 34, 41, 44] or as biphasic/poroelastic [1, 24, 33, 37] with a wide range of assumed material properties with little experimental basis. The task of finding a mechanically comparable replacement material is a difficult one, but should focus on characteristics critical to NP function as it relates to motion segment mechanics.

The NP is restricted axially by the superior and inferior cartilaginous end plates and circumferentially by the AF. Compressive load on the NP is transferred to the annulus when it distends radially. Thus, the NP behaves physiologically in an environment that is neither completely confined nor completely unconfined. The mechanical properties of human NP in confined compression have been previously reported [24]. The current study utilizes unconfined compression to measure equilibrium toe-region and linear-region modulus and Poisson’s ratio. Poisson’s ratio, a material property describing lateral expansion under axial compression, is a key functional parameter for NP, as it may provide for AF fiber tension. NP lateral expansion, through Poisson’s ratio mechanisms and/or swelling pressurization, provides for effective compressive load transfer in the disc. We utilize a modified photogrammetric method for determining Poisson’s ratio using an unconfined compression stress-relaxation experiment with optical imaging.

Injectable hydrogels have been evaluated as to their potential for NP implant support based on their ability to swell and maintain hydrostatic pressure. The aim of hydrogel implantation is to restore native, non-degenerate NP mechanics to support overall disc function [7, 8, 25, 26]. In this study, we specifically investigate three experimental synthetic hyaluronic acid (HA)-based prototypes and compare their performance to native NP.

An alternative to injectable hydrogels is tissue-engineered NP constructs. The goal of a tissue engineering approach is to regenerate living tissue capable of self-maintenance and remodeling while contributing near-natural mechanical and biological properties. Alginate and agarose commonly serve as scaffolds for NP cell-seeding [17, 19, 40] due to their high-incorporation rate and ability to maintain cell phenotype [18, 38, 39, 43, 46]. Previous reports on the properties of alginate and agarose in compression, tension and/or shear vary greatly with gel concentration, cross-linking agent, material source, and storage environment [12, 34, 42]. Importantly, Poisson’s ratio has not been reported for these gels. The mechanical characterization of both alginate and agarose hydrogels is therefore critical for selecting proper scaffolds for tissue-engineering applications.

The objectives of this study were to (1) quantify human NP mechanical properties in unconfined compression including the equilibrium toe-region and linear-region modulus and Poisson’s ratio, and (2) compare several synthetic HA-based hydrogels currently being investigated as potential NP replacements and natural alginate and agarose gels of varying concentrations to human NP properties.

Materials and methods

Materials

Five human lumbar spines (three males, two females; age range 19–76 years, median 25 years) were obtained from IRB approved tissue sources (National Disease Research Interchange, Philadelphia, PA and International Institute for the Advancement of Medicine, Jessup, PA). Non-degenerate lumbar intervertebral discs, assessed via morphological grading, were removed from each spine via sharp dissection along the superior and inferior end plates. A 12.7 mm plug was removed using a Miltex dermal biopsy punch (Fischer Scientific, Malvern, PA) from the nuclear region and sectioned to a uniform thickness of 5 mm using a Leica microtome (Model S42400, Leica Microsystems, Wetzlar, Germany). A 7.1 mm sample was subsequently removed using a Miltrex dermal biopsy punch (Fischer Scientific), wrapped in plastic wrap, and stored at −20°C until the time of mechanical testing.

Three experimental synthetic HA-based hydrogels were recently developed by the coauthors Drs. Chen and Malhotra as potential NP replacements [36]. The procedures for preparation of hydrogels A and B were modified from comparable hydrogels previously explored for other applications [9, 10]. Formulation A was prepared by first blending 0.9 ml of 1% HA solution with an equal volume of 7% polyethylene glycol-g-chitosan solution (extent of polyethylene glycol grafting: 48%); gelation was initiated by swiftly mixing in 70 μl of a 17% ethyl-3-[3-dimethyl amino] propyl carbodiimide solution with an equal volume of a 6.5% N-hydroxysuccinimide solution. Formulation B was prepared according to the same method, except the concentration of HA solution was 2.6%. Samples of hydrogels A and B were prepared for mechanical testing by using a 7.1 mm cylindrical punch. Formulation C was prepared by blending two precursors: partially oxidized hyaluronan and gelatin [50]. Briefly, partially oxidized-HA and gelatin solutions of 20% (w/v) concentration (both dissolved in 0.1 M borax) were prepared, separately at 37°C. Partially oxidized-HA/Gelatin hydrogels were formulated by rapidly mixing equal volumes of both solutions and it was injected directly into a mold designed to generate 7.1 mm diameter hydrogel samples for mechanical testing.

Either low or medium viscosity sodium salt alginic acid (Sigma Chemical Co., St. Louis, MO) was used in all alginate gels. Alginate is a natural material derived from brown sea algae which is polymerized into hydrogel form when monomers are cross-linked with divalent cations such as calcium or barium. Alginate solutions, in concentrations between 1 and 4% by weight, were solubilized in deionized water. Molds were placed in a six-well plate, filled with the alginate solution, and immersed in 100 mM CaCl₂ solution for 18 h. Cylindrical punches 7.1 mm in diameter were removed from the alginate gels and microtomed to a uniform thickness. Agarose comes from marine red algae and gels into a three-dimensional network of helical agarose fibers when cooled. About 2% medium-viscosity agarose (Sigma Chemical Co.) by weight was cast in molds and allowed to cool overnight. All gels used in the study (n = 5 for each type) were microtomed to a uniform thickness and then wrapped in plastic wrap and stored at 4°C until mechanical testing.

Mechanical testing

A testing configuration was designed to directly measure Poisson’s ratio optically [51]. A custom-built clear acrylate tank on a 15 cm tall platform was constructed and a 432 mm equivalent digital camera (Canon Powershot S2IS) with flat-field lens was mounted directly underneath the testing surface (Fig. 1). All samples were tested in a phosphate buffered solution. A flat, non-porous plunger was attached to an Instron mechanical testing system (Instron 5542, Canton, MA) fitted with a 5 N load cell. The plunger was lowered to make contact with the platform base to zero the instrument displacement. Specimens, stained with blue dye (Toluidine Blue Dye, Fischer Scientific) to improve delineation of sample boundaries, were then placed on the platform and a 0.05 N preload was applied for 10 min. The load was removed and the sample was allowed to equilibrate for 5 min. An incremental stress-relaxation test was then performed consisting of 5% strain increments at a rate of 5%/s, followed by 5 min of relaxation which in pilot studies was sufficient to allow complete relaxation (<0.001 kPa/s change in stress). Strain increments were repeated to 25% strain (Fig. 2a). Load and displacement data were recorded at 100 Hz. At the end of each relaxation period a digital image of the sample and calibration grid was manually acquired from below for lateral strain analysis. Images were acquired at 0.083 mm/pixel. Potential optical distortions were minimized by using a flat-field lens, using the central region of the image field, and including a calibration grid adjacent to the sample and in the same plane. In preliminary studies, the system was validated by testing commercial rubber, demonstrating ν = 0.5 [48].

Fig. 1.

Unconfined compression testing configuration consisting of optically translucent testing surface with space for mounting of digital camera

Fig. 2.

a Schematic of stress-relaxation experiment, consisting of incremental steps of 5% strain followed by a 5-min relaxation period to a total of 25% strain. b Average equilibrium stress–strain curves produced using mean A and B values curve fit according to the equation 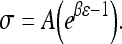c Representative linear regression for calculation of Poisson’s ratio

Data analysis

The non-linear stress–strain data at the end of each relaxation period were curve fit according to the equation 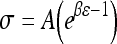(Graphpad Prism 4.0). Toe-region modulus was calculated as the slope of this curve at 0% strain. Linear-region modulus was calculated as the slope of the stress–strain curve at 20% strain. Percent relaxation was calculated as 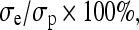where σ_e is the equilibrated stress and σ_p is the peak stress. Image software (Uthscsa Image Tool 3.0) was used to calculate the sample diameter at each time point. Each image was measured three times and the results were averaged. Lateral strain (ε_l) was then calculated as the change in diameter over the initial diameter of the cylindrical sample. Axial strain (ε) was calculated by the change in cross-head displacement over initial height. Poisson’s ratio 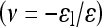was calculated as previously described using a linear regression of the data [13]. Students t-tests were used to compare each material to human NP properties, with significance set at P < 0.05. For alginate and agarose, an analysis of variance with a post hoc Bonferoni test was used to compare each formulation of the gels.

Results

Curve fit of the equilibrium stress–strain data for human NP produced a good fit (Fig. 2b, r² > 0.99, n = 5). Toe-region modulus at equilibrium was 3.25 ± 1.56 kPa while linear-region modulus was 5.39 ± 2.56 kPa (Table 1). Linear regression of the data to calculate Poisson’s ratio for all materials was well fit (Fig. 2c, r² > 0.95, n = 55). Poisson’s ratio for NP was 0.62 ± 0.15. Human NP percent relaxation was 65.8 ± 11.3%.

Table 1.

Unconfined compression equilibrium properties and relaxation for NP and potential replacement materials

Material	Toe modulus (kPa)	Linear modulus (kPa)	Poisson’s ratio	Relaxation (%)
Human NP	3.25 (1.56)	5.39 (2.56)	0.62 (0.15)	65.77 (11.30)
Hydrogel A	2.82 (1.19)	6.97 (2.10)	0.48 (0.24)	19.86 (6.38)*
Hydrogel B	7.91 (4.21)*	21.90 (4.82)*	0.59 (0.16)	13.89 (4.71)*
Hydrogel C	8.37 (1.61)*	14.47 (0.63)*	0.56 (0.13)	30.67 (5.90)*
1.2% lv alginate	n/a	3.11 (1.73)	0.43 (0.10)*	98.23 (0.95)*
1.0% mv alginate	1.49 (0.64)	5.45 (0.70)	0.35 (0.07)*	83.95 (1.72)*
1.2% mv alginate	6.72 (0.44)	8.60 (2.29)	0.33 (0.07)*	86.58 (9.96)*
2.0% mv alginate	3.42 (1.89)	7.46 (2.31)	0.22 (0.04)*	83.39 (4.72)*
3.0% mv alginate	5.02 (4.82)	7.88 (5.15)	0.15 (0.07)*	78.14 (3.11)*
4.0% mv alginate	4.41 (1.05)	13.02 (4.31)*	0.17 (0.04)*	82.95 (0.93)*
2.0% mv agarose	n/a	13.45 (1.53)*	0.12 (0.03)*	79.88 (2.12)*

All values reported mean (SD)

lv low viscosity, mv medium viscosity

*Significantly different than human NP (P < 0.05)

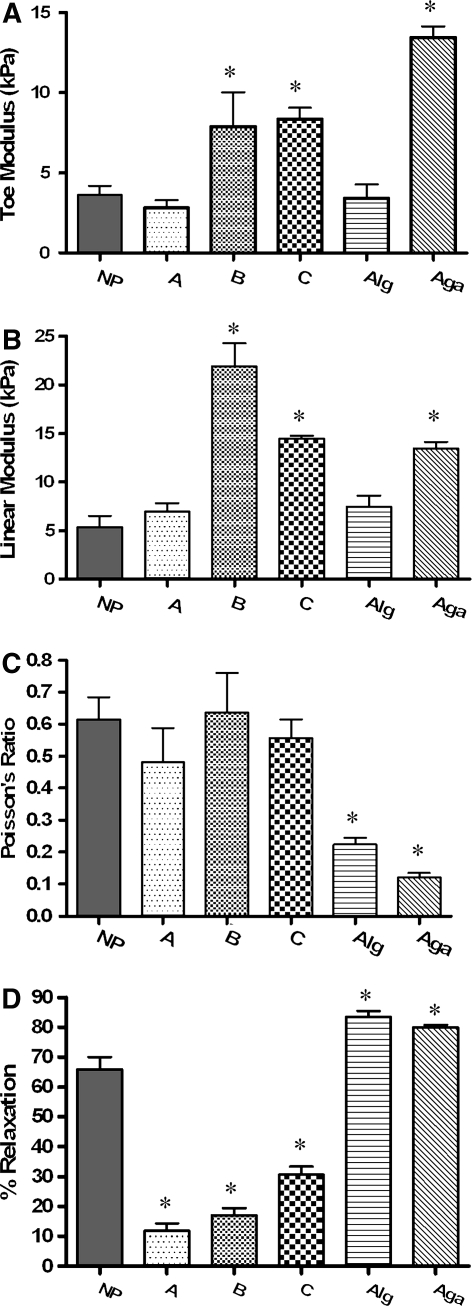
All hydrogels were also well fit to the non-linear equation (r² > 0.99, n = 45). The low-viscosity alginate and agarose (Fig. 2b) were linear, so were fit using a linear regression through the stress–strain data. Mean toe-region modulus values (Fig. 3a and Table 1) ranged from 2.82 to 8.37 kPa for the synthetic HA-based hydrogels while linear-region modulus values (Fig. 3b) ranged from 6.97 to 21.90 kPa. Formulation B and C and agarose were significantly greater than human NP (P < 0.05). Toe-region modulus values for the medium viscosity alginate ranged from 1.49 ± 0.64 to 6.72 ± 0.44 kPa (Table 1), and only the 1 and 1.2% were significantly different from each other (ANOVA, post hoc analysis, P < 0.05). The linear-region modulus of alginate ranged from 5.45 ± 0.70 kPa for 1.0% alginate to 13.02 ± 4.31 kPa for 4.0% alginate (Table 1). Only the 1 and 4% were significantly different from each other (ANOVA, post hoc analysis, P < 0.05). Medium viscosity alginate had a higher linear-region modulus than low-viscosity alginate. The linear-region modulus for 2% agarose was not different than 4% alginate.

Fig. 3.

Comparison of material properties in unconfined compression. NP nucleus pulposus, A–C three experimental hyaluronic acid-based hydrogels, alg 2.0% medium viscosity alginate, aga 2.0% med viscosity agarose. a Toe modulus calculated at 0% strain, b linear region modulus calculated at 20% strain, c Poisson’s ratio, d relaxation (%) *significantly different than human NP (P < 0.05)

Poisson’s ratio for HA-based hydrogels (Fig. 3c and Table 1) ranged from 0.48 ± 0.23 to 0.59 ± 0.16, and was not significantly different than human NP. Since the materials exhibited no bulging, friction was not considered to be a significant factor in these tests. Poisson’s ratio values for alginate and agarose were significantly lower than human NP. The Poisson’s ratio for medium viscosity alginate gels ranged from 0.35 ± 0.07 for 1.0% down to 0.17 ± 0.04 for 4.0% alginate (Table 1); 1.0% alginate was significantly different than 2.0, 3.0, and 4.0%, while 1.2% alginate was significantly different than 3.0 and 4.0% (ANOVA, post hoc analysis, P < 0.05).

The HA-based hydrogels relaxed significantly less than human NP, while the alginate and agarose gels had significantly higher percent relaxation values (Fig. 3d). Medium viscosity alginate (86.58 ± 9.96%) relaxed less than low-viscosity alginate (98.23 ± 0.95) and for the medium viscosity alginate, percent relaxation values ranged from 78.14 (3.0%) to 86.58 (1.2%) and none were significantly different from each other.

Discussion

A complete description of human NP mechanics is critical for evaluating potential NP replacement materials and tissue engineering scaffolds as well as developing finite element models of the disc. Implanted materials should function mechanically similar to NP in order to mimic its role in motion segment mechanics. Here we report an unconfined compressive toe-region modulus of 3.25 ± 1.56 kPa and a linear-region modulus for non-degenerate human NP of 5.39 ± 2.56 kPa, which is in agreement with that previously reported by our lab and elsewhere [23, 47]. As expected, this equilibrium modulus is much lower than the confined compressive effective aggregate modulus (H^eff_A), which is the sum of the confined compressive modulus and the osmotic pressure term Π, of 1.01 ± 0.43 MPa [2, 24]. As physical loading of NP is between the case of unconfined and confined compression, both the unconfined and confined properties are important for understanding NP function and how it behaves in conjunction with the AF in vivo. The advantage of unconfined compression testing is that it permits assessment of Poisson’s ratio, which is important for interactions between the NP and AF. Other studies have also measured NP mechanics in shear, indentation, and cyclic compression [22, 32, 47]

We report a Poisson’s ratio of 0.62 ± 0.15 which is slightly larger than the maximum value of 0.5 for an isotropic incompressible material, suggesting that the NP is anisotropic due to fiber reinforcement and/or is compressible due to fluid loss under load. It is notable, however, that the NP values for Poisson’s ratio are much closer to 0.5 than that of either AF or articular cartilage which have Poisson’s ratio values between 0.60–1.80 and 0.62–1.87, respectively [14, 15]. Optical determination of Poisson’s ratio has previously been utilized both in articular cartilage [27, 30, 49] and chondrocytes seeded in agarose [28], although Poisson’s ratio has not previously been measured directly for NP. Previous finite element models have described the NP as an incompressible fluid or have selected values of Poisson’s ratio ranging from 0.35 to 0.49 [1, 16, 21, 33, 35, 36, 41, 44]. Finite element model implementation of the NP using an isotropic constitutive formation would not be thermodynamically permissible using the mean measured value of 0.62. Since the allowable 0.5 value is within one standard deviation of the measured value, it would be reasonable to use that limit for model purposes; alternatively either a compressible or anisotropic formulation would be required.

In order to mimic in vivo functioning of the NP, selection of NP implants should be based on matching material mechanics to that of native tissue. The ideal parameters for a NP replacement have been previously outlined [5]. Bao and Yuan [6] suggest selecting a material with stiffness greater than or equal to NP. An implant that is less stiff may lead to an underconstrained motion segment, resulting in hypermobility and increased stresses on adjacent discs. However, an implanted material that is too stiff may lead to subsidence through the endplate and subsequent motion segment failure [4, 45]. An implant that is similar to native NP in confined compression, unconfined compression and motion segment mechanics is critical to ensuring normal disc function.

Proper function of the NP involves lateral expansion under axial compressive loads, thereby putting the AF into circumferential tension. This interaction between the nucleus and annulus, maintained by a high-Poisson’s ratio and/or swelling pressure, remains a major challenge in formulating a functional NP replacement and in constructing tissue engineered NPs. We contend that, together with the modulus, the most important parameter for selecting a nuclear implant material is the Poisson’s ratio. Designing an NP implant with focus on replicating native NP Poisson’s ratio provides the greatest potential for an implant to radially transfer loads to the AF in a manner similar to non-degenerate NP. An implant that effectively transfers loads to the AF will have the greatest potential to permit normal motion segment mechanics. Hydrogels A–C had values between 0.48 and 0.59, approximating NP well. The polymers studied here showed less stress relaxation compared to human tissue. Although the viscoelasticity of normal intervertebral disc is critical to normal disc function, further investigation is needed in order to relate the viscoelastic properties of isolated tissue and synthetic material with that of in situ function.

The data presented here confirm that the mechanical properties of alginate depend on both gel type and concentration. Linear-region modulus and relaxation values support the notion that alginate and agarose make suitable substrates for NP seeding. Poisson’s ratios for these gels are lower than that of NP although this may be overcome by the gels’ ability to generate pressure if fluid is contained and thereby transfer loads radially to the AF. Furthermore, the data shown here are for unseeded gels. These scaffolds may achieve NP mechanical function following glycosaminoglycan production in culture.

While this study introduces new data for both human NP and potential implant materials in unconfined compression, the authors acknowledge a few limitations. The optical analysis for calculation of Poisson’s ratio requires user definition of diameters. Edge detection was improved by dying all hydrogels prior to testing to optimize sample contrast. Furthermore, we were able to assume uniform lateral expansion in calculating Poisson’s ratio because all testing equipment and materials were selected for minimal friction. Finally, although these results are limited to unconfined compression, future studies should investigate these materials in confined compression as well as conduct biocompatibility, cell interaction and in vitro motion segment studies. Preliminary motion segment studies in our lab, as well as published work elsewhere, have already shown potential in restoring compressive stiffness, viscoelasticity, disc height, and range of motion after nucleotomy [3, 26, 29, 52].

Conclusions

In conclusion, we define an appropriate method for measuring the equilibrium mechanical properties, including Poisson’s ratio, in an unconfined compression experiment. We report, for the first time, unconfined compression data on native NP and potential nuclear replacement materials. These data are important for selecting NP implant materials and finite element modeling of the disc. Future work should include investigating biocompatibility, cellular interaction, and conducting in vitro motion segment studies.