Abstract
Forward dynamic models suggest that muscle-induced joint motions depend on dynamic coupling between body segments. As a result, biarticular muscles may exhibit non-intuitive behavior in which the induced joint motion is opposite to that assumed based on anatomy. Empirical validation of such predictions is important for models to be relied upon to characterize muscle function. In this study, we measured, in vivo, the hip and knee accelerations induced by electrical stimulation of the rectus femoris (RF) and the vastus medialis (VM) at postures representatives of the toe-off and early swing phases of the gait cycle. Seven healthy young subjects were positioned side-lying with their lower limb supported on air bearings while a 90 ms pulse train stimulated each muscle separately or simultaneously. Lower limb kinematics were measured and compared to predictions from a similarly configured dynamic model of the lower limb. We found that both RF and VM, when stimulated independently, accelerated the hip and knee into extension at these postures, consistent with model predictions. Predicted ratios of hip acceleration to knee acceleration were generally within 1 s.d. of average values. In addition, measured responses to simultaneous RF and VM stimulation were within 13% of predictions based on the assumption that joint accelerations induced by activating two muscles simultaneously can be found by adding the joint accelerations induced by activating the same muscles independently. These results provide empirical evidence of the importance of considering dynamic effects when interpreting the role of muscles in generating movement.
1. Introduction
Forward dynamic simulations provide a powerful framework to characterize muscle function during movement. For example, simulations of walking have been used to determine the contributions of muscles to joint velocities (Goldberg et al., 2004; Piazza and Delp, 1996), joint accelerations (Kimmel and Schwartz, 2006; Riley and Kerrigan, 1999) and vertical support and forward progression of the body (Anderson and Pandy, 2002; Neptune et al., 2001). Other investigators have used forward dynamic simulations to evaluate the influence of muscles in walking disorders, such as stiff knee (Riley and Kerrigan, 1998), crouch (Arnold et al., 2005), and post stroke hemiparetic (Higginson, 2006) gaits. Some of the predictions made using dynamic models challenge commonly held anatomical interpretations of muscle function. For example, a simulation study suggested that the rectus femoris (RF) induces extension about the hip during the early swing phase of walking. This non-intuitive prediction arises from dynamic coupling between body segments, such that biarticular muscles can induce accelerations in direction opposite to the joint moment they generate (Zajac and Gordon, 1989). In the case of the rectus femoris, which generates hip flexor and knee extensor moments, the knee extensor moment induces an extension acceleration about the hip. When this hip extension acceleration exceeds the hip flexion acceleration generated by the hip flexor moment, the net result is hip extension.
There is a need to assess the accuracy of dynamic models (Piazza, 2006) given the discrepancy between anatomical classifications of muscles and model-based predictions of muscle function. Inherent assumptions regarding the geometry (Delp et al., 1990) and independent action of muscles (Maas et al., 2004), the representation of joints as kinematic constraints (Yamaguchi and Zajac, 1989) and the consideration of segments as rigid bodies (Liu and Nigg, 2000) could make model-based functional predictions differ from reality. In this study, we used electrical stimulation to empirically test whether the RF could induce hip extension, as previously predicted (Piazza and Delp 1996). Stimulations were introduced at two lower limb postures that represent phases of the gait cycle when RF activity would be expected during normal walking. For comparison, we also stimulated the vastus medialis (VM), a uniarticular muscle crossing the knee, at the same postures. We hypothesized that both RF and VM would extend the hip and knee, but that the relative magnitude of induced hip and knee accelerations would differ between postures and between muscles, according to the predictions of a dynamic model. Theoretically, postural effects arise from the dependence of the system inertia matrix (Zajac and Gordon, 1989) and muscle moment arms (Delp et al., 1990) on the joint angles. In addition, muscle effects are expected due to the difference in spanned joints. We also tested the hypothesis that superposition, an assumption of most dynamic models, would hold for this two-muscle system, such that the sum of the joint accelerations induced by the muscles’ independent actions would be a good approximation of the joint accelerations induced during simultaneous muscle stimulation.
2. Methods
2.1. Experimental procedure
Seven young, healthy adults (5 males, 2 females; age 26 ± 2.5 years, height 1.77 ± 0.11 m, mass 71.0 ± 7.8 kg) with no history of musculoskeletal problems or neurological dysfunction provided their informed consent prior to participating in our University of Wisconsin IRB-approved protocol.
Subjects were positioned side-lying with their right limb supported against gravity via air bearings (Fig. 1), allowing nearly frictionless sagittal plane motion. Muscle stimulating and electromyographic (EMG) recording locations were identified based on muscle maps (Perotto, 1994). A dual-channel, current-controlled stimulator (Grass S88, Astro-Med, Inc., West Warwick, RI) was used to induce muscle contractions. Stimulating locations were verified by passing single 300 μs pulses to each muscle of interest (RF, VM) using surface electrodes on alcohol cleaned, gel-primed skin, while slowly increasing the current level until the muscle twitched. The skin was cleaned again and the surface electrodes replaced with two indwelling stainless steel fine-wires (0.003” bare diameter, A-M Systems, Inc., Carlsborg, WA) for use during testing sessions. EMG signals were recorded at 2000 Hz throughout the trials from RF, VM, vastus lateralis (VL) and the hip adductors (AD) using pre-amplified single differential surface electrodes (DE-2.1, DelSys, Inc, Boston, MA) to assess whether or not the stimulus spilled over to adjacent, non-stimulated muscles.
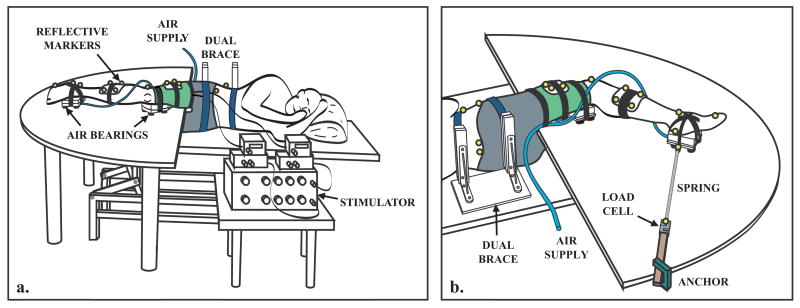
Fig. 1.
Experimental Setup. (a) The lower extremity was supported on air bearings that allowed near frictionless motion in the sagittal plane. Pelvis motion was restricted by a dual brace, padded restraint. An electrical stimulator delivered a pulse train to the rectus femoris, the vastus medialis or both muscles simultaneously. Reflective markers were used to measure the induced lower extremity kinematics via an 8-camera motion capture system. (b) Compliant springs, attached to fixed load cells, were used to hold the limb in a desired posture prior to stimulation.
Testing sessions involved three stimulating paradigms (VM, RF or both muscles simultaneously) and two postures (toe-off and early swing) for a total of 6 experimental conditions. The toe-off and early swing postures were approximately 60% and 70% of the normal gait cycle (Perry, 1992). Three trials were performed at each condition, with a single representative trial used in the analysis. Posture order was randomized across subjects, and stimulating paradigms were randomized within subjects. A 90 ms pulse train (four 300 μs pulses at 33 Hz) was used to stimulate muscles. At each posture, the stimulation current for each muscle was adjusted within the range of 1–50 mA to generate visible angular motion at the hip and knee, then kept constant throughout the trials. Compliant springs were connected from one or both of the frictionless carts to fixed load cells (Omega Engineering Ltd., Stamford, CN) to maintain the limb in the desired posture when the muscles were at rest. Due to across-subject variability in passive resistance about the joints, the stiffness of the springs varied from 7 to 63 N/m. Load cell data was used to evaluate the contribution of spring forces to the net joint moments (Fig. 1b). An 8-camera motion capture system (Motion Analysis, Santa Rosa, CA) tracked 15 reflective markers (100 Hz) on the pelvis, thigh, shank and foot. Test trials were also recorded with a video camera.
2.2. Dynamic musculoskeletal model
A three segment, two degree of freedom (d.o.f.) musculoskeletal model of the pelvis and lower extremity (based on Delp et al., 1990) was used to predict the instantaneous sagittal hip and knee accelerations induced by the RF and VM at the postures of interest (Fig. 2a, 2b). The hip was represented by a hinge and the knee was modeled as a one d.o.f. joint in which tibiofemoral translations were a constrained function of knee flexion angle (Yamaguchi and Zajac, 1989). The air bearings were assumed frictionless and their masses (0.57 kg each) were added to the inertial properties of the corresponding segments (de Leva, 1996). The muscle paths of the RF and VM were represented by line segments from origin to insertion, with via points used to model wrapping about joints (Delp et al., 1990).
Fig. 2.
Two degree of freedom lower limb model at (a) toe-off and (b) early swing phase postures. Rectangular shapes represent the frictionless carts. (c) Our model predicted that both RF and VM induce hip and knee extension at both postures, resulting in positive hip/knee acceleration ratios (circles indicate the model predictions). Higher acceleration ratios are predicted at toe-off (TO curve) than early swing (ES curve) due to postural effects on the inertia matrix (section 2.2, equation 1). The slopes along the curves illustrate the sensitivity of the hip/knee acceleration ratio on the assumed relative moment arms of the muscles about the hip and knee. Flexion is defined as positive in the model.
SIMM Pipeline (Musculographics Inc., Motion Analysis Corp., Santa Rosa, CA) was used in conjunction with SD/FAST (Parametric Technology Corporation, Waltham, MA) to obtain the model’s equations of motion, which took the form:
| (1) |
where q are joint angles, q¨ are joint angular accelerations, r are muscle moment arms, F are muscle forces, and I is a posture-dependent inertia matrix. Subscripts h and k refer to the hip and knee, respectively, while superscripts rf and vm refer to the muscles included in the model. Gravity-dependent forces are not included in equation (1) since the experiment was conducted in a non-gravitational plane. Velocity- and position-dependent forces are also excluded because the stimulation was introduced while the limb was at rest. The predicted accelerations obtained via equation (1) were then converted into a ratio of hip/knee accelerations which, for an individual muscle, was independent of the muscle force produced. This acceleration ratio was plotted against the hip/knee moment arm ratio to illustrate the dependence of the former ratio on both the inertia matrix (producing a shift in the curves) and the moment arms of the muscles about the joints (causing changes in sensitivity along the curves) (Fig. 2c).
The three segment model of the lower limb was also used to characterize the measured joint kinematics and kinetics. For this purpose, the model was scaled to represent the segment lengths and inertia properties of individual subjects. Body segment coordinate systems, tracking marker locations and segment lengths were first established using the marker positions collected during an upright static calibration trial. Hip joint location was determined via a functional spherical joint center identification algorithm (Piazza et al., 2004). Hip and knee angles were computed using an inverse kinematics routine that minimized the sum of squared differences between measured marker positions and corresponding positions on the model. Joint angles were low-pass filtered at 6 Hz (99.5% of the signal power) and numerically differentiated twice to obtain the angular accelerations induced by the stimulated muscle contractions.
2.3. Data analysis
Muscle-induced joint accelerations were defined as the peak accelerations observed within 110 ms following the end of the stimulation train. This time period was chosen to be long enough to accommodate electromechanical delays between stimulation and induced forces, while being short enough to avoid the influence of induced velocities and potential reflex arcs. Acceleration ratios were calculated by dividing the hip acceleration by the knee acceleration at each point in the trials, then averaging the resulting values over a 40 ms period about the point where the product of hip and knee accelerations peaked. The measured hip/knee acceleration ratio for each condition was then determined as the average of the individual ratios across subjects.
The superposition assumption was tested for each joint/posture combination separately. We added the joint accelerations that resulted from stimulating RF and VM independently (calculated accelerations) and compared them to the measured accelerations in conditions where the two muscles were stimulated simultaneously. We then generated a zero-intercept linear regression through each set of data and inquired whether or not the best-fit line was close to the theoretical relationship (calculated acceleration = measured acceleration) and explained most of the variability in the plot. The first criterion was gauged by comparing the slopes of the theoretical and best-fit lines, since the intercepts in both cases were zero. The second criterion was judged by the coefficient of determination (R2).
Rectified EMG signals were used to assess which muscles were activated by each stimulation paradigm (Fig. 3a). The first peak in the EMG signal following a stimulating pulse corresponded primarily to stimulus artifact while the second peak was predominantly muscular activation (Riewald and Delp, 1997). We empirically determined a time window within the second peak (16 to 23 ms following stimulus onset) where the EMG levels of activated muscles were elevated and always included the maximum. The magnitudes of the individual muscle traces were averaged over this period. Then, the averages of the stimulated muscles were divided by those of the non-stimulated muscles to determine a ratio of EMG activity. Load cell forces were used to compute the joint moments that the springs induced during each trial. These spring-induced joint moments were compared with the net joint moments to confirm that the former did not substantially contribute to the induced joint accelerations (Fig. 3b).
Fig. 3.

Methods of verification. (a) Confirmation of proper muscle stimulation. The electrical stimulation pulse train consisted of four 300 μs pulses spaced at 30 ms intervals. The rectified EMG traces of four muscles were monitored over a 200 ms window following stimulus onset. The sharp peaks that occur in the EMG traces with each stimulating pulse correspond to stimulus artifact. The second peaks, seen only in the traces of stimulated muscles (RF and VM in the example above), reflect muscle activation. We compared the average value of the EMG traces in the time window between 13 and 26 ms following the first pulse (dashed lines) to assess whether or not the stimulus spilled over from stimulated to non-stimulated muscles. We also inspected each trace for possible reflex activity. (b) Confirmation of negligible spring-induced joint moments. Spring-induced joint moments and net joint moments were compared to determine the contribution that the springs made to the induced joint accelerations. In both (a) and (b), experimental worst-case results are shown.
3. Results
The average EMG activity of the stimulated muscles ranged from 22 to 67 times greater than the activity of the non-stimulated muscles during the inter-pulse intervals, suggesting that stimulus spill-over to neighboring muscles was small (Fig. 3a). The net joint moments induced by electrical stimulation of muscles ranged from 1.3 to 10.0 Nm at the hip and from 1.8 to 12.4 Nm at the knee. The spring-induced joint moments were less than 0.2 Nm at the hip and less than 0.1 Nm at the knee. Thus, on average, the spring contribution to the net joint moments was less than 1%, and reached a maximum 4.4% in the worst-case trial among all subjects and conditions (Fig. 3b).
We found that RF and VM, when stimulated independently, accelerated the hip and knee into extension at both limb postures studied (Fig. 4). Video footage of all 7 subjects confirmed this observation (Fig. 5). At the toe-off posture, the superposition assumption overestimated the theoretical relationship between calculated and measured accelerations at the hip by 6% and underestimated this same relationship at the knee by 10% (Fig. 6a). At the early swing phase posture, superposition underestimated the relationship at the hip by 13% and overestimated the relationship at the knee by 4% (Fig. 6b). The coefficients of determination between calculated and measured accelerations were high in the toe-off (hip R2 = 0.82, knee R2 = 0.80) and early swing phase (hip R2 = 0.95, knee R2 = 0.91) postures.
Fig. 4.
Hip and knee accelerations after stimulation of RF, VM or both muscles simultaneously at (a) toe off and (b) early swing phase posture. Each curve represents a different subject. Peak induced accelerations over a 110 ms window following the end of the stimulation (i.e. from 90 to 200 ms after the stimulus onset) are highlighted by small circles. Induced hip and knee accelerations were extensor (negative direction) in all cases, and largest for simultaneous muscle stimulation.
Fig. 5.
Video sequence of one subject during an RF stimulation trial. Frames shown are at −40, 40 and 120 ms from the first evidence of movement. A comparison of the limb position against its original configuration (shown by overlaid lines) confirms that both the hip and knee extended. All 7 subjects exhibited similar behavior.
Fig. 6.
Superposition tests for (a) toe off (TO) and (b) early swing phase (ES) postures. Each graph is a scatter plot of calculated accelerations (by addition of RF and VM induced acceleration responses) versus measured accelerations (the response to simultaneous stimulation of RF and VM). The theoretical relationship between these two variables, assuming superposition, is calculated acceleration = 1*measured acceleration. Best-fit lines with 0 intercept (solid lines) are compared to the theoretical relationship (dashed lines). Best-fit lines are close to the theoretical relationship (coefficients ≈1) and coefficients of determination are high (R2 ≥ 80%) in all cases.
The average (±1 s.d.) hip/knee acceleration ratios for RF stimulation were 0.29±0.02 in the toe-off posture and 0.24±0.05 in the early swing phase posture. The corresponding values for VM stimulation were 0.34±0.02 and 0.31±0.02. The hip/knee acceleration ratios predicted by the model were within one standard deviation of the measured ratios in all test conditions except VM at early swing phase posture, where the deviation was 1.6 standard deviations (Fig. 7). Hence, the acceleration ratios became significantly smaller in going from the toe-off to the early swing phase posture (average change = −0.043, p < 0.05).
Fig. 7.
Predicted (light gray) vs. measured (dark gray) hip/knee acceleration ratios. Measured ratios represent averages across subjects and are shown with ±1 s.d. bars. Experimental differences in the ratio due to changing the posture from toe off (TO) to early swing (ES) were significant (p < 0.05, t-tests) for both RF and VM stimulation and reflect the trends predicted by the model.
4. Discussion
Our results provide experimental evidence of the potential for muscles to exhibit nonintuitive dynamic functions. Specifically, we showed that RF could accelerate the hip into extension, not flexion, at limb postures representative of toe-off and the early swing phase of gait. This behavior had been predicted based on dynamic simulations (Piazza and Delp, 1996) but, to our knowledge, had never been measured in vivo. We also showed that VM could extend the hip at these postures, even if this muscle only spans the knee. Furthermore, we demonstrated that a two d.o.f., rigid-link dynamic model of the lower extremity correctly predicted experimentally observed posture-dependent changes in the muscle-induced hip/knee acceleration ratio. Two factors contribute to these changes. The first factor is inter-segmental dynamic coupling, which refers to the joint accelerations that arise from joint reaction forces (Zajac and Gordon, 1989). This coupling is modeled mathematically by the system inertia matrix I, which depends explicitly on the hip and knee joint angles (eq. 1). The second factor is the posture-dependent changes in muscle moment arms that arise from musculoskeletal geometry (Delp et al. 1990). For example, the model predicts a large decrease in the hip/knee acceleration ratio for RF stimulation when moving from toe-off to the early swing phase posture, attributable almost equally to changes in dynamic coupling and the muscle’s hip/knee moment arm ratio (Fig. 2c). In contrast, the model predicts a smaller decrease in the acceleration ratio for VM stimulation, due only to changes in dynamic coupling (because VM’s hip/knee moment arm ratio is always zero). These model based estimates of the distinct contributions to the acceleration ratio were supported by the magnitudes of the measured acceleration ratios (Fig. 7).
It is important to note that there was also substantial across-subject variability in the measured ratios (standard deviations, Fig. 7), particularly in the behavior of RF at the early swing phase posture. This subject-dependence of the measured ratios may have been due to anthropomorphic differences in the hip-to-knee moment arm ratio across subjects. Consistent with this logic, our sensitivity study showed that the acceleration ratio was more sensitive to variations in moment arm ratios at the early swing phase posture than at the toe-off posture (Fig. 2c). These results reinforce the importance of performing sensitivity studies to fully understand the ramifications of musculoskeletal model assumptions.
The test of superposition revealed how the dynamic functions of muscles combined. When the induced accelerations of simultaneous RF and VM stimulation were calculated by superposition and compared to the corresponding measured accelerations, a zero-intercept linear regression yielded coefficients near 1 under all conditions. In addition, the best-fit line explained a large percentage of the variability regardless of the posture tested (toe off or early swing phase) or the joint observed (hip or knee). Thus, our results showed that linear superposition, which has been often assumed in dynamic musculoskeletal models (e.g., Neptune et al., 2001; Delp and Loan, 2000; Anderson and Pandy, 1999) and experimental studies (e.g., Zhang and Nuber, 2000), was a reasonable approximation of how muscle functions combined in the sagittal plane. Further studies are needed to determine if superposition assumptions hold for other muscles and in non-sagittal directions.
The results of our study cannot be directly used to infer RF muscle function during walking due to the kinematic restrictions imposed. In particular, we restrained the pelvis from moving in this study, whereas muscles have the potential to induce pelvis motion during normal walking. Thus, we cannot assume that the hip joint acceleration will be the same under conditions where the pelvis is free to move. Additionally, we restricted limb motion to the sagittal plane, but walking involves motion in all three directions. Investigations are needed to determine whether the RF and VM, which have greatest moment-generating capability in the sagittal plane, can induce substantial three-dimensional motion of the limb in the unrestricted case. Nevertheless, our study has identified conditions under which the RF can extend the hip. This is an important finding because it demonstrates in vivo that biarticular muscles can accelerate one of their spanned joints in a direction opposite to what would be inferred anatomically.
There are also limitations in our ability to measure joint accelerations that should be noted. First, while pelvic motion was restricted passively, a small amount of pelvic motion could potentially occur due to compliance in the restraint system. Secondly, soft-tissue motion, due primarily to induced muscle contractions, could introduce errors when inferring skeletal motion from measured marker kinematics. Finally, the use of numerical differentiation to estimate accelerations can amplify any noise in the kinematic data. Despite these potential shortcomings, visual analyses of video data confirmed the directions of the measured hip and knee accelerations (Fig. 5). Furthermore, these directions (Fig. 4) and the measured changes in the hip/knee acceleration ratio were consistent across all seven subjects and with model predictions (Fig. 7). These results suggest that we achieved reasonably accurate estimates of the muscle-induced joint accelerations.
In conclusion, we have measured non-intuitive dynamic muscle function and postural effects on joint accelerations that are consistent with the predictions of a dynamic musculoskeletal model. These results demonstrate the utility of dynamic models and emphasize the importance of considering dynamic coupling when inferring muscle function during human movement (Zajac et al., 2002, 2003).
Acknowledgments
Antonio Hernández was supported by NIH Training Grant T32 AG20013 (Institute on Aging, Sanjay Asthana, PI) and the Graduate Engineering Research Scholars at the University of Wisconsin-Madison. Funding was also received from NIH AG24276 and the Midwest Rehabilitation Research Network. The authors gratefully acknowledge the contributions of Dr. Deborah McLeish, Dr. James Leonard, Betsy Hunter, Amy Silder, Yomary Muñoz and Andrew Sterling.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson FC, Pandy MG. Individual muscle contributions to support in normal walking. Gait & Posture. 2002;17(2):159–169. doi: 10.1016/s0966-6362(02)00073-5. [DOI] [PubMed] [Google Scholar]
- Anderson FC, Pandy MG. A dynamic optimization solution for vertical jumping in three dimensions. Computer Methods in Biomechanics and Biomedical Engineering. 1999;2:201–231. doi: 10.1080/10255849908907988. [DOI] [PubMed] [Google Scholar]
- Arnold A, Anderson FC, Pandy MG, Delp SL. Muscular contributions to hip and knee extension during the single limb stance phase of normal gait: a framework for investigating the causes of crouch gait. Journal of Biomechanics. 2005;38:2181–2189. doi: 10.1016/j.jbiomech.2004.09.036. [DOI] [PubMed] [Google Scholar]
- de Leva P. Adjustments to Zatsiorsky-Seluyanov's Segment Inertia Parameters. Journal of Biomechanics. 1996;29(9):1223–1230. doi: 10.1016/0021-9290(95)00178-6. [DOI] [PubMed] [Google Scholar]
- Delp SL, Loan JP. A computational framework for simulation and analysis of human and animal movement. IEEE Computing in Science and Engineering. 2000;2(5):46–55. [Google Scholar]
- Delp SL, Loan JP, Hoy MG, Zajac FE, Topp EL, Rosen JM. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Transactions in Biomedical Engineering. 1990;37(8):757–67. doi: 10.1109/10.102791. [DOI] [PubMed] [Google Scholar]
- Goldberg SR, Anderson FC, Pandy MG, Delp SL. Muscles that influence knee flexion velocity in double support: implications for stiff-knee gait. Journal of Biomechanics. 2004;37(8):1189–96. doi: 10.1016/j.jbiomech.2003.12.005. [DOI] [PubMed] [Google Scholar]
- Kimmel SA, Schwartz MH. A baseline of dynamic muscle function during gait. Gait & Posture. 2006;23(2):211–21. doi: 10.1016/j.gaitpost.2005.02.004. [DOI] [PubMed] [Google Scholar]
- Liu W, Nigg BM. A mechanical model to determine the influence of masses and mass distribution on the impact force during running. Journal of Biomechanics. 2000;33(2):219–24. doi: 10.1016/s0021-9290(99)00151-7. [DOI] [PubMed] [Google Scholar]
- Maas H, Baan GC, Huijing PA. Muscle force is determined also by muscle relative position: isolated effects. Journal of Biomechanics. 2004;37(1):99–110. doi: 10.1016/s0021-9290(03)00235-5. [DOI] [PubMed] [Google Scholar]
- Neptune RR, Kautz SA, Zajac FE. Contributions of the individual ankle plantar flexors to support, forward progression and swing initiation during walking. Journal of Biomechanics. 2001;34:1387–1398. doi: 10.1016/s0021-9290(01)00105-1. [DOI] [PubMed] [Google Scholar]
- Perotto AO. Anatomical Guide for the Electromyographer: The limbs and Trunk. 3. Charles C. Thomas; Springfield, IL: 1994. [Google Scholar]
- Perry J. Gait Analysis: Normal and Pathological Function. Slack Incorporated; Thorofare, NJ: 1992. [Google Scholar]
- Piazza SJ. Muscle-driven forward dynamic simulations for the study of normal and pathological gait. Journal of NeuroEngineering and Rehabilitation. 2006;3:5. doi: 10.1186/1743-0003-3-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piazza SJ, Delp SL. The influence of muscles on knee flexion during the swing phase of gait. Journal of Biomechanics. 1996;29(6):723–733. doi: 10.1016/0021-9290(95)00144-1. [DOI] [PubMed] [Google Scholar]
- Riewald SA, Delp SL. The action of the rectus femoris muscle following distal tendon transfer: does it generate knee flexion moment? Developmental Medicine and Child Neurology. 1997;39(2):99–105. doi: 10.1111/j.1469-8749.1997.tb07391.x. [DOI] [PubMed] [Google Scholar]
- Riley PO, Kerrigan DC. Kinetics of stiff-legged gait: induced acceleration analysis. IEEE Transactions on Rehabilitation Engineering. 1999;7(4):420–426. doi: 10.1109/86.808945. [DOI] [PubMed] [Google Scholar]
- Riley PO, Kerrigan DC. Torque action of two-joint muscles in the swing period of stiff-legged gait: a forward dynamic model analysis. Journal of Biomechanics. 1998;31(9):835–40. doi: 10.1016/s0021-9290(98)00107-9. [DOI] [PubMed] [Google Scholar]
- Yamaguchi GT, Zajac FE. A planar model of the knee joint to characterize the knee extensor mechanism. Journal of Biomechanics. 1989;22:1–10. doi: 10.1016/0021-9290(89)90179-6. [DOI] [PubMed] [Google Scholar]
- Zajac FE, Gordon ME. Determining muscle’s force and action in multi-articular movement. Exercise and Sport Sciences Review. 1989;17:187–230. [PubMed] [Google Scholar]
- Zajac FE, Neptune RR, Kautz SA. Biomechanics and muscle coordination of human walking Part I: Introduction to concepts, power transfer, dynamics and simulations. Gait & Posture. 2002;16:215–232. doi: 10.1016/s0966-6362(02)00068-1. [DOI] [PubMed] [Google Scholar]
- Zajac FE, Neptune RR, Kautz SA. Biomechanics and muscle coordination of human walking Part II: lessons from dynamical simulations and clinical implications. Gait & Posture. 2003;17(1):1–17. doi: 10.1016/s0966-6362(02)00069-3. [DOI] [PubMed] [Google Scholar]
- Zhang LQ, Nuber GW. Moment distribution among human elbow extensor muscles during isometric and submaximal extension. Journal of Biomechanics. 2000;33:145–154. doi: 10.1016/s0021-9290(99)00157-8. [DOI] [PubMed] [Google Scholar]