Heterogeneity in EGF-binding affinities arises from negative cooperativity in an aggregating system

Abstract

Scatchard analysis of the binding of EGF to its receptor yields concave up plots that indicate the presence of two classes of binding sites. However, how two independent classes of sites arise from the expression of a single EGF receptor protein has never been adequately explained. Using a new analytical approach involving the simultaneous fitting of binding isotherms from cells expressing increasing levels of EGF receptors, we show that ¹²⁵I-EGF-binding data can be completely explained by a model involving negative cooperativity in an aggregating system. This approach provides an experimentally determined value for the monomer–dimer equilibrium constant, which, for wild-type EGF receptors, corresponds to ≈50,000 receptors per cell. Therefore, changes in receptor expression within the physiological range can modulate the outcome of a signaling stimulus. Analysis of the L680N-EGF receptor mutant, in which the formation of asymmetric kinase domain dimers is blocked, indicates that the kinase dimers make a substantial energetic contribution to the ligand-independent association of EGF receptor monomers, but are not necessary for negative cooperativity. The model accurately predicts the behavior of receptor mutants, such as the dimerization-defective Y246D-EGF receptor, which exhibit a single class of binding sites and provides a framework for understanding secondary dimer formation and lateral signaling in the EGF receptor family.

The EGF receptor is a classic receptor tyrosine kinase with an extracellular ligand-binding domain, a single-pass transmembrane domain, and an intracellular domain that has tyrosine kinase activity (1). The EGF receptor is thought to exist in cells as a monomer that dimerizes upon EGF binding (2). Structural analysis of the receptor has elucidated the mechanism of dimer formation.

The extracellular domain of the EGF receptor is comprised of four subdomains (I–IV). The unliganded receptor monomer is held in a closed conformation by an intramolecular tether formed by loops in subdomains II and IV (3). In the ligand-occupied EGF receptor dimer, this intramolecular tether is broken, and the receptor is opened into an extended conformation. This open form of the receptor interacts with another monomer, forming a back-to-back dimer (4, 5).

A characteristic feature of the EGF receptor is that EGF binding exhibits a concave up Scatchard plot (6–11). The data have most often been interpreted as indicating the presence of high- and low-affinity binding sites (6–11). However, they also are consistent with the existence of negative cooperativity (12). After the discovery of EGF receptor dimers, it was hypothesized that the low-affinity sites represent receptor monomers, whereas the high-affinity sites correspond to receptor dimers (2). However, because this model predicts that EGF binding would be positively cooperative and should show a concave down Scatchard plot (12), the hypothesis is not consistent with experimental evidence. Heterogeneity in the spatial distribution of receptors also has been proposed as a cause of the EGF receptor's concave up Scatchard plots (13). However, experimental support for this hypothesis is lacking.

The identification of the tethered and extended forms of the EGF receptor led to the suggestion that they represented the low- and high-affinity states of the receptor, respectively (3–5, 14). However, mathematical modeling of this system fails to produce the observed concave up Scatchard plots (15), and the binding properties of mutant receptors in which the tether was weakened are not consistent with the assignment of the high-affinity state to the extended form of the receptor (10). Therefore, Klein et al. (15) proposed a model in which the EGF receptor binds to an external binding protein to generate the observed concave up Scatchard plots.

In this work, the applicability to the EGF receptor of a generalized model of ligand binding in a dimerizing system has been examined. In this model, unoccupied EGF receptor monomers are in a preexisting equilibrium with unoccupied EGF receptor dimers. EGF can bind to free monomer, unligated dimer, or singly ligated dimer. A diagnostic feature of this system is that ligand-binding properties vary with the concentration of receptor if the ligand shows differential affinity for the different receptor forms.

Using an analytical approach that involves global modeling of EGF binding to cells with increasing numbers of receptors, we show that EGF binding can be readily explained by a model invoking negative cooperativity in an aggregating system. We experimentally determine the monomer–dimer association constant for the full-length EGF receptor in intact cells and demonstrate the utility of the approach for defining structure–function relationships within the EGF receptor. The model provides a framework for understanding the behavior of receptor mutants that exhibit a single class of binding sites, as well as the phenomena of secondary dimer formation and lateral signaling in the EGF receptor family (16–18).

Results

Model and Analytical Approach.

A Scatchard analysis plots the ratio of bound/free ligand versus bound ligand concentration. However, a more direct and less error-sensitive method for analyzing saturation-binding data is to plot fractional saturation of the receptor (Ȳ) versus the log of the ligand activity, which equates with free ligand concentration in these experiments (19). Because this presentation also facilitates the comparison of ligand binding at different concentrations of receptors, this approach was employed for the analysis of ¹²⁵I-EGF binding.

The ¹²⁵I-EGF used in these experiments was made by using the ICl reaction (20). As previously reported (21), but not widely appreciated, radioiodination of EGF by using the chloramine T method results in oxidative damage of the EGF and yields radioligand that is not equivalent to native EGF with respect to receptor binding. This damage leads to multiple artifacts, including changes in the early portion of the binding isotherm and an underestimation of the number of EGF receptors if unlabeled ligand is added to radioligand-binding assays to generate saturation plots. The equivalence in ligand–receptor interaction between native EGF and ¹²⁵I-EGF produced by the ICl method (21) permits an accurate assessment of binding isotherms when mixtures of labeled and unlabeled EGF are used.

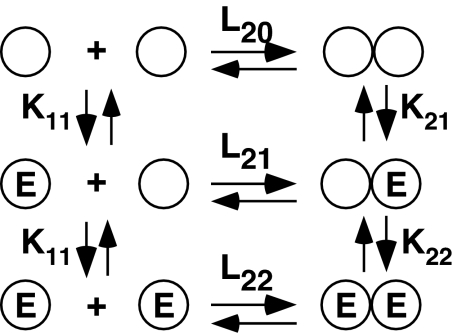
Fig. 1 shows the model used to analyze EGF binding in these studies. In this model, EGF receptor monomers and dimers are in a preexisting equilibrium described by the association constant, L₂₀. The initial binding of EGF to a receptor monomer is described by the equilibrium association constant, K₁₁, whereas binding to the unoccupied dimer is described by the equilibrium association constant, K₂₁. A third binding reaction, that of EGF binding to the second site on a dimer, is described by K₂₂. Positive cooperativity is said to exist if K₂₂ > K₂₁, whereas negative cooperativity exists if K₂₂ < K₂₁.

Fig. 1.

Model of EGF binding in an aggregating system. Circles indicate receptor subunits. The equilibrium association constants are written above or beside the reaction to which they apply. E, EGF molecule.

In this system, the fractional saturation, Ȳ, of the EGF receptor as a function of ligand concentration can be described as

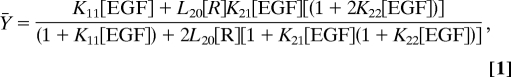where [R] = concentration of unoccupied EGF receptor monomers (22). Fitting to Eq. 1 requires the use of four parameters: L₂₀, K₁₁, K₂₁, and K₂₂. The remaining parameters, L₂₁ and L₂₂, are fully determined and calculated from the others based on the principle of microscopic equilibrium.

The concentration of receptor monomers depends on the total concentration of receptor R₀, as well as the four fitted parameters. R₀ is obtained experimentally from the plateau of the binding hyperbola and is entered as a constant during fitting. The concentration of unoccupied receptor monomers is calculated during the fitting by using the following equation:

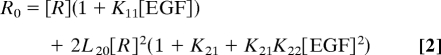as derived by Wyman and Gill (19).

As can be determined from Eq. 1, the aggregation model shown in Fig. 1 predicts that the binding behavior of EGF depends on the concentration of EGF receptors if different forms of the receptor have different affinities for EGF. This finding follows directly from the law of mass action because total receptor concentration sets the position of the monomer–dimer equilibrium and help determines the concentration of the different species at a given concentration of EGF. Information on the dependence of binding on receptor concentration allows the experimental determination of the equilibrium constant for dimer formation (L₂₀).

Because EGF receptors are restricted to the cell surface, rather than being dispersed throughout the entire assay volume, receptor concentration was expressed as a density (mol receptor per dm²) in these analyses. This approach yields a monomer–dimer equilibrium constant that is related to the number of receptors per cell, rather than receptors per 3D assay volume. We derived the values for receptor density from fluorescence correlation spectroscopy measurements of the number of GFP-EGF receptors in a beam of known radius in CHO cells expressing a known level of GFP-EGF receptors per cell (23). This experimentally determined density was scaled up to dm² because this unit is the 2D correlate of a liter, which is a dm³. Therefore, the units for L₂₀ are (mol/dm²)⁻¹, which is referred to as D⁻¹. This formalism has no effect on the magnitude of the ligand-binding constants because the L₂₀ units cancel out in all of the mass action law equations. The units for the association constants for ligand-binding events remain in M⁻¹.

Binding to Wild-Type EGF Receptors Is Negatively Cooperative.

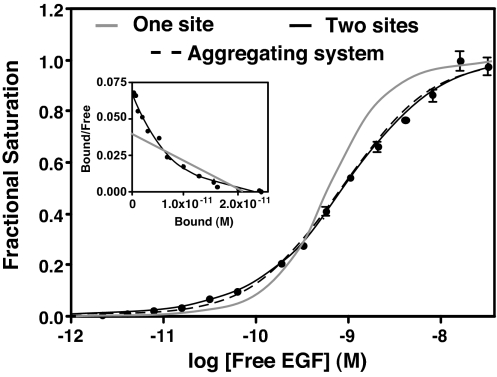
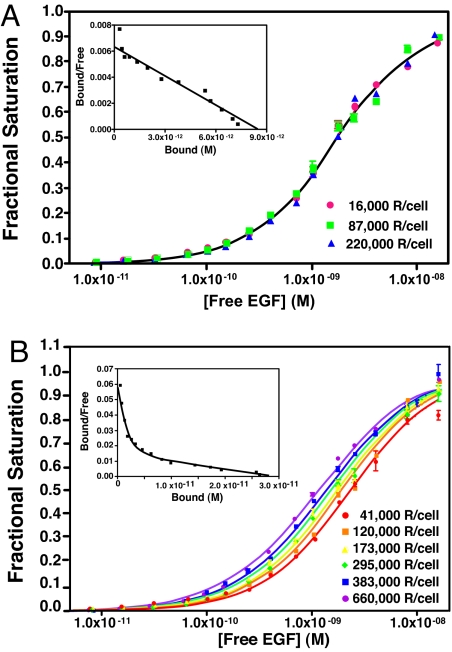
Fig. 2 shows a titration-binding isotherm for the binding of ¹²⁵I-EGF to CHO cells induced to express ≈300,000 receptors per cell. All binding was done at 4°C to block internalization and trafficking of EGF. A Scatchard plot of the same data is shown in Fig. 2 Inset. The gray line shows the fit to a single class of sites. The solid black line shows the fit to the equation for binding to two independent classes of sites. This analysis yields values of 50 pM and 1.1 nM for the high- and low-affinity sites, respectively, and indicates that 14% of the sites are of high affinity. Thus, the EGF receptor in these cells shows binding properties that are typical for this receptor.

Fig. 2.

¹²⁵I-EGF-binding isotherms generated from two different models. ¹²⁵I-EGF saturation-binding data were fit to a binding isotherm equation invoking two independent classes of sites (solid black line) or to the aggregating system shown in Fig. 1 (dashed line). The solid gray line shows the shape of a binding isotherm corresponding to a single class of sites. (Inset) Scatchard plots corresponding to the one-site (gray line) and two-site (black line) fits.

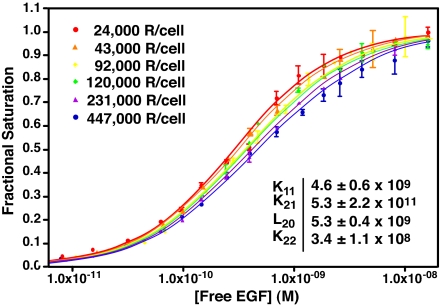
These same data are well fit by Eq. 1, which describes ligand binding in an aggregating system (dashed line). Unlike the two-site model, the aggregation model predicts that ligand-binding properties should show a dependence on receptor levels if the ligand has different affinities for different forms of the receptor. To determine whether EGF binding can be explained by this model, CHO cells were stably transfected with a vector-encoding wild-type EGF receptor expressed from a tet-inducible promoter. These tet-on EGFR-CHO cells were induced to express EGF receptors by using six different concentrations of doxycycline, and the equilibrium binding of ¹²⁵I-EGF was assessed. Consistent with the predictions of Eq. 1, the data in Fig. 3 show that the position of the EGF binding isotherms varied as a function of receptor concentration. Specifically, the binding isotherms moved from left to right as the number of receptors per cell increased 20-fold from 24,000 to 450,000 receptors per cell.

Fig. 3.

Binding of EGF to cells expressing increasing levels of wild-type EGF receptors. CHO-K1 tet-on EGFR cells were induced to express EGF receptors by using increasing doses of doxycycline. ¹²⁵I-EGF-binding isotherms were generated from each set of cells, and all six isotherms were globally fit to Eq. 1, with only the value of R₀ varying among curves. Data points represent the mean ± SD of triplicate determinations. Solid lines represent the fitted curve through the data points of the same color.

Global modeling of all binding isotherms yielded a single set of parameters (see Fig. 3 Inset) that accurately fit (r² = 0.99) all six binding curves. The fitted equilibrium constants for K₁₁, K₂₁, and K₂₂ are association constants. Their inverses were taken to obtain the affinity constants for subsequent discussion. The data yield an EGF affinity of ≈220 pM for the monomer and ≈190 pM for the unligated dimer, indicating that the affinity of EGF for these two receptor species is essentially equivalent. By contrast, the affinity of EGF for binding to the second site on the dimer is 15-fold lower (2.9 nM) than that for the binding of EGF to the first site on the dimer (190 pM). This finding indicates that binding of the second EGF is negatively cooperative.

The fitted value of L₂₀, the equilibrium constant for the monomer–dimer association reaction, is 5.3 × 10¹¹ D⁻¹, which corresponds to a receptor density of ≈50,000 EGF receptors per cell. A similar value, 6.0 × 10¹¹ D⁻¹, is obtained for L₂₁, the equilibrium constant for the association of one unoccupied and one ligated EGF receptor monomer. By contrast, the value of L₂₂, the association constant for two occupied EGF receptor monomers, is 4.5 × 10¹⁰ D⁻¹. This finding indicates that the affinity of two occupied monomers for each other is lower by an order of magnitude than the affinity of an occupied monomer for an unoccupied monomer.

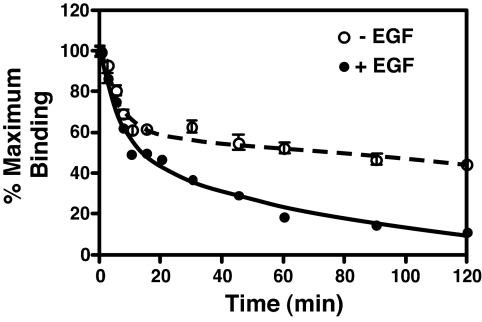
To provide independent evidence for negative cooperativity, the effect of unlabeled EGF on the dissociation of ¹²⁵I-EGF was examined (24). For this experiment, cells were allowed to come to equilibrium with 10 nM ¹²⁵I-EGF at 4°C. The binding medium was then replaced with fresh medium with or without 10 nM unlabeled EGF, and the release of ¹²⁵I-EGF was followed (Fig. 4). In the absence of added unlabeled EGF, the dissociation of ¹²⁵I-EGF was best fit by a double exponential decay model. The t_1/2 of the rapid phase was 3.6 ± 1.1 min, whereas the t_1/2 for the slow phase was 234 ± 77 min. When EGF was present in the dissociation medium, ¹²⁵I-EGF also exhibited two phases of dissociation. The t_1/2 of the rapid phase was essentially identical to that seen in the absence of added unlabeled EGF (t_1/2 = 4.1 ± 1 min). However, for the slower phase, the t_1/2 was reduced from 234 to 46 ± 9.6 min. These data are consistent with the interpretation that the rapid phase represents dissociation of EGF from the low affinity, doubly occupied dimer, whereas the slower phase represents dissociation from the higher affinity, singly ligated dimers and monomers. The presence of EGF in the dissociation medium does not change dissociation from the doubly occupied dimer because both sites are occupied. However, because of negative cooperativity, unlabeled EGF binding to the unoccupied site in a singly ligated dimer decreases the affinity and enhances the rate of dissociation of ¹²⁵I-EGF from the other site. Both the complex dissociation kinetics and the effect of EGF on ligand dissociation are entirely in accord with negative cooperativity in the binding of EGF to its receptor.

Fig. 4.

Dissociation of ¹²⁵I-EGF from CHO cells expressing EGF receptors. CHO cells were incubated overnight with 10 nM ¹²⁵I-EGF. Binding medium was removed, cells were washed, and the medium was replaced with Hams' F12 containing 25 mM Hepes (pH 7.0) and 2 mg/ml BSA in the absence (open circles) or presence (filled circles) of 10 nM unlabeled EGF. Cultures were incubated for the indicated times at 4°C, and residual EGF binding was determined as described in Materials and Methods. Data points represent the mean ± SD of triplicate determinations. Solid lines show the fit to a double exponential model by using GraphPad Prism 4.0.

Analysis of Binding to EGF Receptor Mutants.

The observed receptor concentration-dependent shift of EGF binding isotherms (Fig. 3) depends on the ability of the receptor to dimerize and generate receptor species with different affinities for ligand. Mutation of Tyr-246, a key residue in the dimerization of the EGF receptor extracellular domain (4, 5), prevents dimerization of the receptor and blocks downstream signaling (11). Therefore, the Y246D-EGF receptor should not exhibit negative cooperativity, and the position of the binding isotherms should be independent of receptor concentration.

To test this prediction, CHO cells were stably transfected with the Y246D-EGF receptor expressed from a tet-inducible promoter. The cells were induced to express EGF receptors with three different concentrations of doxycycline, and ¹²⁵I-EGF-binding isotherms were generated. The data in Fig. 5A demonstrate that, despite expressing up to 15-fold different levels of EGF receptor, the cells yielded indistinguishable binding isotherms. The data were best fit by a model invoking only a single class of binding sites with an affinity of 1.7 nM. As shown in Fig. 5A Inset, these data generated linear Scatchard plots. These findings confirm the requirement for dimer formation to observe the shift in binding isotherm positions and the heterogeneity in binding affinities associated with negative cooperativity.

Fig. 5.

Binding of ¹²⁵I-EGF to EGF receptor mutants. (A) ¹²⁵I-EGF-binding isotherms for cells expressing three different levels of Y246D-EGF receptors. All curves fit to a single-site model with a shared K₁ of 5.8 ± 0.1 × 10⁸ with r² = 0.99. (B) ¹²⁵I-EGF-binding isotherms for cells expressing six different levels of L680N-EGF receptors. K₁₁, 3.6 ± 0.2 × 10⁸; K₂₁, 4.8 ± 2.3 × 10¹⁰; K₂₂, 7.9 ± 1.1 × 10⁸; L₂₀, 6.1 ± 3.3 × 10⁸. The r² value for the global fit was 0.99. Points represent the mean ± SD of triplicate determinations.

Recently, Zhang et al. (25) identified an asymmetric crystallographic dimer of the EGF receptor kinase domain. Mutations in the asymmetric dimer interface, such as L680N, ablate EGF-stimulated kinase activation in full-length EGF receptors (25). To assess the contribution of the asymmetric kinase dimers to the behavior of the aggregating receptor system, CHO cells were stably transfected with a tet-inducible plasmid encoding the L680N-EGF receptor. The binding isotherms at six different expression levels of the L680N-EGF receptors are shown in Fig. 5B. Fig. 5B Inset shows a representative Scatchard plot from one of the curves.

Like wild-type EGF receptors, the L680N-EGF receptor exhibited a curvilinear Scatchard plot, suggesting that little had changed. However, major differences are apparent when one examines the dependence on receptor levels. In contrast to the wild-type receptor, which shifted from left to right with increasing receptor numbers, the L680N-EGF receptor binding isotherms shifted from right to left with increasing receptor levels.

Global fitting of all of the binding isotherms yielded a set of parameters for the L680N-EGF receptor that identified the basis for this difference. Most notably, the association constant for the monomer–dimer equilibrium is reduced by nearly three orders of magnitude from 5.3 × 10¹¹ D⁻¹ in wild type to 6.1 ± 3.3 × 10⁸ D⁻¹ in the L680N-EGF receptor. In addition, the affinity of EGF for free monomer is decreased ≈10-fold to 2.8 nM compared with wild-type receptor, whereas the affinity of the unoccupied L680N dimer for EGF is increased ≈10-fold to ≈20 pM. This change produces significant positive linkage between ligand binding and dimer assembly and is the basis of the leftward shift of the curves with increasing receptor concentration. The binding of EGF to the second site on the L680N-EGF receptor dimer exhibited a K_d of 1.3 nM and thus remains negatively cooperative, compared with binding to the first site on the dimer.

Discussion

In this report, we show that the binding of EGF to its receptor can be understood within the rubric of a simple model of ligand binding in an aggregating system (Fig. 1). The critical feature of our approach is the global analysis of binding isotherms from cells expressing different concentrations of EGF receptors. This feature yields experimentally determined values for the EGF receptor monomer–dimer equilibrium constant in intact cells and demonstrates the presence of negative cooperativity in EGF binding.

Klein et al. (15) previously considered this model, but applied two constraints on their parameters that effectively disallowed any type of cooperativity. Under these conditions, the binding equations could not fit the observed binding data. The discrepancy was resolved by proposing an external binding site to account for the concave up Scatchard plots. By contrast, Wofsy et al. (12) made no such assumptions and reported that, in theory, EGF binding data could be fit by this model if negative cooperativity were allowed. These latter workers could not fully parameterize the model because ligand binding as a function of receptor concentration was not investigated. Instead, fixed values for K₁₁ and L₂₀ were assumed before the analysis of binding isotherms at a single receptor concentration.

We have overcome this limitation by examining the binding of EGF to cells with increasing numbers of EGF receptors. The parameters derived from a global fit of all binding isotherms for wild-type EGF receptors indicate that unoccupied EGF receptor dimers have essentially the same high affinity for EGF (190 pM) as do EGF receptor monomers (220 pM). Under these circumstances, EGF binding would not promote receptor dimer formation. However, the model envisages a monomeric form of the EGF receptor that is capable of dimer formation (i.e., it is in the extended conformation), whereas, in reality, the receptor must undergo a significant conformational change to reach this configuration (3). Therefore, the data are consistent with the view that EGF promotes dimer formation by stabilizing the open conformation of the receptor.

The results indicate that the affinity of EGF for binding to the second site on a dimer (2.9 nM) is 15-fold lower than the affinity of EGF for binding to the first site on a dimer (190 pM). This finding is a classic case of negative cooperativity and explains why Scatchard plots of EGF binding are concave up. The interpretation of negative cooperativity is supported by the observation that dissociation of EGF from its receptor follows a double exponential decay model and that the rate of dissociation can be enhanced by adding EGF to the dissociation medium.

An important result of these experiments is the estimate for the equilibrium constant between unoccupied EGF receptor monomers and dimers. The value of 5.3 × 10¹¹ D⁻¹ for L₂₀ equates with a level of ≈50,000 EGF receptors per cell. Because this is roughly the number of EGF receptors expressed in a typical cell, physiologically relevant variations in the receptor level will lead to changes in the position of the monomer–dimer equilibrium and could alter the output signal. L₂₁ is essentially the same as L₂₀, indicating that the affinity of an unoccupied monomer is the same for occupied and unoccupied monomers. However, L₂₂ is ≈10-fold lower than either L₂₀ or L₂₁, meaning that dimerization becomes less favorable as occupancy levels of the receptor increase. This leads to the unexpected prediction that, at high concentrations, EGF should induce disassembly of receptor dimers.

A central role for dimer dissociation in EGF-stimulated signaling is supported by several experimental observations. Verveer et al. (16) showed that focal stimulation of cells with immobilized EGF led to the lateral propagation of the signal over the entire cell. They suggested that this lateral signaling was due to the dissociation of activated dimers and the subsequent activation of unliganded receptors by those activated monomers through a process known as secondary dimer formation. Using a biochemical approach, Gamett et al. (17) and Graus Porta et al. (18) obtained data that support this interpretation and suggested that EGF receptor family members signal by a mechanism in which ligand-induced dimers dissociate and subsequently activate unoccupied monomers through secondary dimer formation.

Our findings provide a theoretical underpinning for these observations. The existence of negative cooperativity in EGF-binding promotes the dissociation of doubly occupied receptor dimers, enabling their dimerization with and activation of additional unoccupied EGF receptor monomers. Thus, rather than impairing signal transduction, negative cooperativity would promote dimer dissociation and secondary dimer formation, leading to the rapid local propagation of the signaling stimulus.

The model predicts that at subsaturating concentrations of ligand, the most abundant form of the receptor is the singly occupied dimer. The fact that some signaling responses, such as activation of MAP kinase, can be maximally induced at pM concentrations of ligand suggests that singly occupied dimers are signaling-competent. At pM doses of EGF, only one of the monomers in the dimer would likely be phosphorylated. Thus, responses that occur through the high-affinity EGF receptor may be those that require activation or phosphorylation of only one kinase in a dimer. Responses that occur through the low-affinity EGF receptor may be those that require both monomers to be occupied and/or phosphorylated.

The value of the proposed model of EGF binding is demonstrated by its ability to predict, identify, and explain differences in binding that occur upon mutation of the EGF receptor. Because negative cooperativity depends on the presence of dimers, the model predicts that the nondimerizing Y246D-EGFR (11) should exhibit only a single type of EGF-binding site (the monomer). Further, the EGF-binding isotherms should not shift with increasing receptor concentrations because there is no monomer–dimer equilibrium to affect. Both of these predicted behaviors were observed, which supports the applicability of the proposed model to the EGF receptor system.

The case of the L680N-EGFR mutant, in which kinase domain dimerization is blocked, provides an example of the power of this approach to identify and molecularly explain changes in binding behavior that are not apparent using traditional methods. Scatchard analysis of the binding of EGF to the L680N-EGFR yielded typical curvilinear plots, suggesting that no change had occurred in EGF binding. However, global analysis of six binding isotherms indicates that the equilibrium constant for the association of two unoccupied L680N-EGFR monomers (L₂₀) is ≈1,000-fold less than what is observed for the wild-type receptor. This indicates that the kinase dimers make a substantial energetic contribution to the ligand-independent association of wild-type EGF receptor monomers. The L₂₁ value for L680N-EGFR is 10-fold lower than the corresponding value for wild-type receptors, indicating that kinase domain interactions also exert a positive effect on the association of an unoccupied monomer with an occupied monomer. However, the L₂₂ for L680N-EGFR is 4-fold higher than that in the wild-type EGF receptor. This suggests that conformational changes associated with dual ligation of the receptor may contribute to the destabilization of such dimers.

In the L680N-EGFR, the affinity for EGF binding to the first and second sites on the receptor dimer are 21 pM and 1.3 nM, respectively. Thus, negative cooperativity is still present in this mutant, suggesting that the asymmetric kinase dimers are not structurally involved in this process. Kinase-dead EGF receptors yield curvilinear Scatchard plots (12, 26), demonstrating that kinase activity is not required for binding-site heterogeneity. However, removal of the entire intracellular domain of the EGF receptor leads to a single class of EGF-binding sites (27, 28), suggesting that the intracellular domain is nonetheless required for negative cooperativity. It is possible that sequences in the EGF receptor cytosolic domain, other than those at the asymmetric dimer interface, play a role in generating negative cooperativity. Alternatively, in the absence of the intracellular domain, the association constant for the dimerization of monomers may be so low that few dimers are formed and, hence, no cooperativity can be established.

The L680N mutation leads to a 10-fold decrease in the affinity of the receptor monomer for EGF (220 pM in wild type vs. 2.8 nM in L680N). It is counterintuitive that a mutation that affects an intracellular dimerization interface should cause changes in the affinity of the receptor monomer for EGF. However, this observation can be understood from a kinetic perspective. The binding of EGF to monomers can be visualized as a two-step process, in which the ligand binds to a closed form of the receptor, which then opens into the extended form. Rapid dimerization of the extended monomers would pull the earlier binding equilibrium forward, making the affinity of the monomer appear higher than it actually is. Any mutation that affected the rate of dimer formation, which could be the case for the L680N mutation, would therefore affect the apparent binding affinity of the monomer. Consistent with this view, the affinity of the dimerization-defective Y246D-EGF receptor also is lower than that of the wild-type receptor monomer.

For these studies, the data analysis was done by assuming that the concentration of EGF receptors is uniform among the cells in an induced population. However, it is clear from an examination of doxycycline-induced CHO cells expressing GFP-EGF receptors that there is, in fact, a narrow, but distinct, distribution of receptor levels within a given population. This fact is unavoidable when working in a cell-based system. Wofsy et al. (12) demonstrated that the presence of a small population of vesicles containing 100-fold higher EGF receptor densities than the bulk vesicle population can alter the shape of the resulting Scatchard plot. Thus, variation in receptor density could theoretically affect our results. However, our variation in receptor expression levels is much less than 100-fold and, assuming a relatively Gaussian distribution of receptor densities, the average binding behavior should reflect the population average receptor level. Nonetheless, caution should be exercised when interpreting small differences between fitted equilibrium constants.

These studies were performed at 4°C to inhibit receptor internalization. Published data suggest that the binding K_ds for EGF are similar at 0°C, 25°C, and 37°C (29), and our unpublished data indicate that the rightward shift of the binding isotherms also occurs at higher temperatures. Thus, although our results likely reflect the general behavior of the system at all temperatures, it is possible that there are quantitative differences in the various equilibrium constants at different temperatures.

In summary, the heterogeneity of binding affinities for EGF can be explained by a model incorporating negative cooperativity in an aggregating system. The analysis allows the experimental determination of the monomer–dimer equilibrium constant for the full-length receptor in intact cells and can identify and explain changes in ligand-binding properties that are invisible to other methods of analysis. Use of this analysis on other EGF receptor mutants or other receptor tyrosine kinases will permit a better understanding of structure–function relationships within this important class of proteins.

Materials and Methods

Construction of EGF Receptor Mutants and Plasmids.

Wild-type EGF receptor was ligated into the pBI Tet Vector (Clontech) between the NheI and EcoRV sites in multiple cloning region 1. The Y246D and L680N EGF receptor mutants were constructed by using the Quik Change Mutagenesis Kit (Stratagene) with wild-type EGF receptor in the pcDNA5/FRT vector (Invitrogen) as a template. Mutant receptors were sequenced in entirety, cut with NheI and EcoRV, and ligated into the pBI-Tet Vector.

Cells and Tissue Culture.

CHO-K1 tet-on cells were purchased from Clontech. Cells were cotransfected with pTK-Hyg and the pBI Tet vector engineered to express wild-type or mutant EGF receptors from a single side by using Lipofectamine 2000 (Invitrogen) according to the manufacturer's instructions. Stable clones were isolated by selection in 400 μg/ml hygromycin (Invitrogen). Clonal lines were grown in DMEM containing 10% FBS, 100 μg/ml hygromycin, and 100 μg/ml G418. EGF receptor expression was induced by the addition of 20–1,000 ng/ml doxycycline for 24 h.

¹²⁵I-EGF Synthesis and Binding.

Murine EGF was purified according to the method of Savage and Cohen (30) and was radioidodinated to a specific activity of 250–300 μCi/μg EGF by using the ICl method (20). The ¹²⁵I-EGF was tested for equivalence to native EGF in ligand binding as described by Kienhuis et al. (21).

Radioligand-binding assays were performed in triplicate in 6- or 12-well dishes depending on the level of EGF receptor induction. Cells were incubated on ice for 24 h in 3 ml of Hams' F12 medium containing 25 mM Hepes (pH 7.0), 2 mg/ml BSA, and 10–30 pM ¹²⁵I-EGF with increasing concentrations of unlabeled EGF up to 64 nM. At the end of the incubation, the binding medium was aspirated, and the plates were washed three times in 2 ml of HBSS. Monolayers were dissolved in 1 ml of 1N NaOH and counted for ¹²⁵I. Nonspecific binding was determined by fitting the raw binding data to a competition binding model and by using the fitted bottom value as nonspecific.

Receptor number was calculated by fitting the data to a standard saturation-binding curve. This number was then used to convert each curve to a binding isotherm. The data from multiple binding isotherms were then globally fit to Eq. 1 by using GraphPad Prism 4.0. For the curve in Fig. 1, in which the data were fit to the equation for two independent classes, the following equation was used:

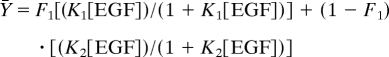where K₁ is the association constant of the first site, K₂ is the association constant of the second site, and F₁ equals the fraction of the total sites that have the affinity, K₁. No restrictions were placed on the possible values of any parameters other than that they be >0. Cell numbers were determined by direct counting of duplicate wells incubated in the absence of radioligand.