Amplified temperature dependence in ecosystems developing on the lava flows of Mauna Loa, Hawai'i

Abstract

Through its effect on individual metabolism, temperature drives biologically controlled fluxes and transformations of energy and materials in ecological systems. Because primary succession involves feedbacks among multiple biological and abiotic processes, we expected it to exhibit complex dynamics and unusual temperature dependence. We present a model based on first principles of chemical kinetics to explain how biologically mediated temperature dependence of “reactant” concentrations can inflate the effective temperature dependence of such processes. We then apply this model to test the hypothesis that the temperature dependence of early primary succession is amplified due to more rapid accumulation of reactants at higher temperatures. Using previously published data from the lava flows of Mauna Loa, HI, we show that rates of vegetation and soil accumulation as well as rates of community compositional change all display amplified temperature dependence (Q₁₀ values of ≈7–50, compared with typical Q₁₀ values of 1.5–3 for the constituent biological processes). Additionally, in young ecosystems, resource concentrations increase with temperature, resulting in inflated temperature responses of biogeochemical fluxes. Mauna Loa's developing ecosystems exemplify how temperature-driven, biologically mediated gradients in resource availability can alter the effective temperature dependence of ecological processes. This mechanistic theory should contribute to understanding the complex effects of temperature on the structure and dynamics of ecological systems in a world where regional and global temperatures are changing rapidly.

Biological metabolism—the uptake, transformation, and allocation of energy and materials by living things—shapes ecological phenomena (1). The metabolic theory of ecology has identified body size and temperature as critical variables driving metabolic rates and, thereby, ecological processes such as photosynthesis, respiration, population growth, and secondary succession (1–3). Through such processes, biological metabolism largely controls global cycles of carbon and nitrogen.

Primary succession—the development of ecosystems on new substrates such as lava flows, sand dunes, or land exposed by receding glaciers—is a complex process involving the accumulation of carbon and nutrients in biomass and soil and the concurrent assembly of a diverse biotic community (4, 5). It is driven by multiple interacting processes, including substrate weathering, primary production, soil formation, and colonization and subsequent turnover of plant, animal, fungal, and microbial species. Most of these processes are mediated by organisms whose biological function exhibits clear temperature dependence (1). It is known that temperature affects the rate of primary succession (4, 6–9). Not well understood, however, is how the multiple ecological processes interact to affect the overall rate of ecosystem development and to determine its temperature dependence.

Rates of ecological processes are ultimately consequences of chemical kinetics (1). It is standard to characterize the rate of a chemical reaction as the product of a temperature-dependent rate constant and the concentrations of reactants (10). For a simple case, where two reactants combine to produce a product, this gives

where V is the reaction rate; v₀ is a normalization constant; and e^−E_a/kT is the Arrhenius expression, where T is temperature (Kelvin), k is Boltzmann's constant (8.62 × 10⁻⁵ eV·K⁻¹), and E_a (eV) is an activation energy characterizing the magnitude of the temperature dependence. The last two terms, [R₁]^m₁ and [R₂]^m₂, are the concentrations of the reactants, R₁ and R₂, raised to powers m₁ and m₂ (assumed >0), which quantify the effects of their concentrations on V. When reactants are not limiting or where their concentrations do not vary systematically with T, Eq. 1 reduces to V ∝ e^−E_a/kT, the familiar exponential increase in rate with temperature characteristic of both abiotic and metabolic processes (1). This Arrhenius formulation from physical chemistry theory differs from the Q₁₀ commonly used in biology in that its somewhat shallower form more accurately characterizes fundamental reaction kinetics (10–13). Our focus is on the strength of the temperature response, here characterized by E_a (higher E_a signifies stronger temperature response).

The inherent kinetics of the constituent processes of primary succession have been described using data from a variety of systems. Rates of abiotic substrate weathering exhibit modest temperature dependence in both field (E_a ≈ 0.4–0.5 eV for basalt) (14, 15) and laboratory (E_a ≈ 0.4–0.9 eV for a variety of silicate minerals) (16). Most of the other processes involved in ecosystem development are consequences of biological metabolism, and their temperature dependence reflects the kinetics of the underlying reactions (1, 11). Photosynthesis-fueled rates, such as net primary production (2) and biomass accumulation during secondary succession (3), typically have E_a values of ≈0.3 eV (equivalent to Q₁₀ ≈ 1.5) over the temperature range 0–30°C, reflecting the temperature dependence of Rubisco-limited C₃ photosynthesis (2). In contrast, respiration-fueled rates, including heterotrophic respiration and growth (11, 17), typically exhibit E_a values of ≈0.65 eV (equivalent to Q₁₀ ≈ 2.5), reflecting the average activation energy for enzyme-catalyzed aerobic metabolism (11). Biological nitrogen fixation also is temperature-dependent. In vitro, the temperature dependence of the nitrogenase reaction is biphasic (E_a = 2.18 eV below 22°C and 0.65 eV above 22°C) (18), but empirical in vivo estimates of E_a appear to be intermediate (e.g., E_a ≈ 0.95 eV for Mauna Loa's lichen Stereocaulon vulcani) (19).

The kinetics of primary succession could be vastly different from those of its constituent processes (as described above) if the rates of contributing reactions depend on concentrations of limiting “reactants” produced by other processes. Specifically, if the concentrations of reactants in Eq. 1 increase with temperature (e.g., [R₁] ∝ e^{−E[R₁]/kT}, where E_[R1] is a parameter characterizing the temperature dependence of [R₁]) and we assume m ≈ 1,^¶ then the temperature terms (e.g., e^−E_a/kT and e^{−E[R₁]/kT}) will combine multiplicatively such that the exponents sum to characterize the overall temperature dependence of the process. For notation, we refer to the new effective “activation energy” as ε:

Thus, whenever a limiting reactant concentration increases with temperature (i.e., E_[R] > 0), the overall temperature dependence will be increased (i.e., ε > E_a). In systems dominated by positive feedbacks, these effects will be compounded through time as the products from each time step move on to serve as reactants in the next.

Consideration of the pertinent reactants shows why primary succession is a prime candidate for the sort of dynamics described above. To apply Eq. 1 to an ecosystem context, we define three categories of reactants. First, the densities (g·m⁻²) of the structures that are sites of reactions (e.g., leaves, roots, and soil; g·m⁻²) contribute to the [R] values. Second, concentrations (g·g⁻¹) of key enzymes, organelles (e.g., chloroplasts and mitochondria), or microbes, which are often correlated with leaf or soil N and P (20, 21), represent key reactants. Finally, pools of biologically available limiting resources (e.g., nitrate, phosphate, organic C, and water; g·m⁻²) represent the most ephemeral category of reactants. The last category may not display a predictable relationship with temperature (although throughput rates generally do increase with temperature), but the two former categories, which represent products of temperature-dependent biotic growth, should increase more rapidly in warmer climates and, in so doing, feed back to affect the overall kinetics of early primary succession.

Here, we evaluate the hypothesis that the temperature dependence of early primary succession is amplified by more rapid accumulation of reactants at higher temperatures. During the initial rapidly accelerating phase of ecosystem development (i.e., before biomass accumulation plateaus), this mechanism should produce three observable patterns. First, long-term rates of net ecosystem development—measured in terms of accumulation rates of biomass or soil (g·m⁻²·yr⁻¹) or rates of community compositional change (species per year)—should display a temperature dependence much stronger than that of any of the constituent processes (i.e., ε > E_a) as described above because ε should be an aggregate of the activation energies of the constituent processes (Eq. 2) and should be inflated through time as feedback effects accrue. Second, at any point in time, concentrations of critical reactants should increase with temperature (i.e., E_[R] values > 0; see Eq. 2) as a result of their more rapid accumulation at higher temperatures. Third, because of these gradients in resource concentration, biogeochemical fluxes (g·m⁻²·yr⁻¹) should also exhibit inflated apparent temperature dependence (i.e., ε > E_a; see Eq. 2).

We test these predictions by using data from the active volcano of Mauna Loa, HI, which is an ideal system in which to study the temperature dependence of ecosystem development. Lava flows of various ages span a broad elevational gradient, creating a matrix of sites with different combinations of age, climate, and lava type that lends itself to the study of climatic effects on succession (6, 7). The first ≈3,000–4,000 yr of ecosystem development are well characterized. Carbon pools in live vegetation, detritus, and soil all increase (5–7, 9, 22, 23). Nitrogen, which enters the ecosystem through atmospheric deposition and biological fixation, and phosphorus, which is released from weathering lava, accumulate in the soil and vegetation (5, 9, 22–24). We use the wealth of data from this system to quantify the temperature dependence of aboveground biomass, soil, and soil nutrient accumulation rates (g·m⁻²·yr⁻¹) and of rates of species colonization, loss, and turnover (species per year) during the initial rapidly accelerating phase of primary succession. Additionally, using data from relatively young ecosystems (109–138 yr), we test for a temperature gradient in reactant concentrations (leaf biomass, N, and P; g·m⁻²) and consider the temperature dependence of biogeochemical fluxes [e.g., aboveground net primary production (ANPP) and decomposition; g·m⁻²·yr⁻¹].

Results

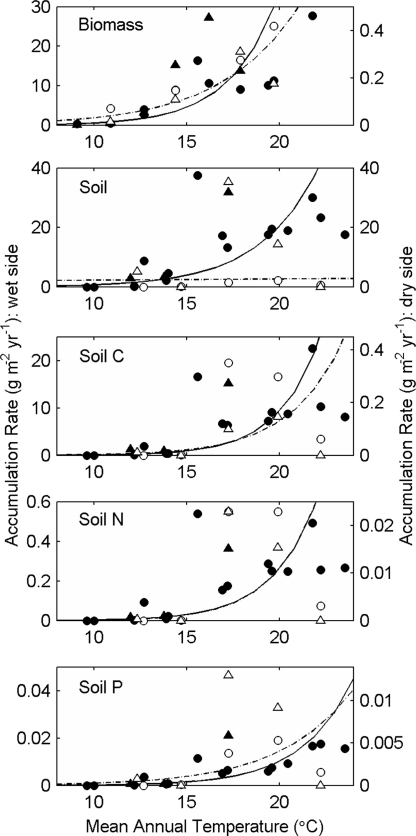
Rates of ecosystem development (g·m⁻²·yr⁻¹) increase rapidly with temperature along the elevational gradient (Fig. 1) and are generally well fit by an Arrhenius model of temperature dependence (Table 1). Plots of raw accumulation rates as a function of mean annual temperature (Fig. 1) correctly suggest that there is considerable variation, but much of this can be attributed to the covariates precipitation and lava type (Table 1). After accounting for these variables, estimates of ε for different processes range from 1.3 to 2.6 when precipitation is analyzed quantitatively as a continuous variable, and these estimates tend to be even higher when precipitation is treated as a categorical variable (i.e., “wet” or “dry”) (Table 1). We focus our discussion on the former, more conservative, estimates. Development is faster in wet climates, regardless of whether the effects of precipitation are characterized categorically or quantitatively, and the effects of precipitation are nonlinear (Table 1). Finally, rates tend to be higher on chunky ‘a’a than on ropey pāhoehoe lava flows, although lava type is often not a significant contributor when precipitation is characterized categorically (Table 1).

Fig. 1.

Accumulation rates of aboveground biomass and soil mass, C, N, and P over the first century of primary succession on ‘a’a (triangles) and pāhoehoe (circles) flows along the elevation/temperature gradient on the wet (filled symbols; left axes) and dry (open symbols; right axes) sides of Mauna Loa. Note that the y axes differ. Solid and dashed lines indicate separate fits to wet- and dry-side data, respectively [supporting information (SI) Table 3].

Table 1.

Multipredictor models for various rates of primary succession on the slopes of Mauna Loa as a function of average annual temperature, precipitation, and lava flow type

Models	n*	Temperature		Precipitation		Flow Type	R2
		ε (SE)†	t	Response or α;β (SE)‡	t	'a'a > pāhoehoe, t
Aboveground biomass accumulation
Model 1	25	2.6 (0.2)	6.8	wet > dry	8.7	n.s.	84.8
Model 2	25	≥1.4 (0.35)§	4.0	4.05 (0.56); −0.0011 (0.0003)	7.3; −3.6	n.s.	92.2
Soil accumulation
Model 1	24 (29)	>2.1 (0.5)	4.1	wet > dry	2.8	−2.6	56.2
Model 2	24 (29)	>1.3 (0.5)	2.3	β = 0.0001 (0.0002)	4.3	−3.5	64.8
Soil C accumulation
Model 1	24 (29)	>3.2 (0.7)	4.5	wet > dry	5.2	n.s.	66.5
Model 2	24 (29)	>2.3 (0.8)	3.0	2.8 (1.1); −0.0003 (0.0006)	2.6; −0.4	−2.2	80.0
Soil N accumulation
Model 1	24 (29)	>3.1 (0.7)	4.6	wet > dry	4.3	n.s.	62.3
Model 2	24 (29)	>2.6 (0.7)	3.5	2.7 (1.1); −0.0004 (0.0006)	2.5; 0.6	−2.0	77.6
Soil P accumulation
Model 1	24 (29)	>2.6 (0.5)	5.0	wet > dry	1.1	n.s.	54.9
Model 2	24 (29)	2.6 (0.4)	5.8	α = 0.7 (0.2)	3.0	−2.8	71.0
Community compositional change
Colonization	5	1.6 (0.2)	6.7	—	—	—	93.7
Loss	5	2.8 (0.7)	4.2	—	—	—	85.5
Turnover	5	1.8 (0.3)	6.1	—	—	—	92.6
All processes¶
Model 1	136	2.8 (0.3)	10.7	wet > dry	9.4	−3.2	85.2
Model 2	136	1.8 (0.3)	6.0	1.8 (0.5); −0.0001 (0.0003)	3.9; −0.4	−3.9	87.8

Precipitation is analyzed either categorically (wet or dry; Model 1) or quantitatively (mm·yr⁻¹; Model 2) (see Eq. 3). All accumulation rates are in g·m⁻²·yr⁻¹. Community compositional change is measured as species per year. n.s., nonsignificant effects (P > 0.05); —, nonapplicable cofactors. Nonsignificant parameters characterizing the effects of temperature and precipitation are reported, along with their t values.

*Numbers in parentheses include zero-values that were excluded from the reported analyses.

^†″>″ indicates that replacing zero-values with any reasonable value (e.g., lowest measured value, 1/10 lowest measured value) results in a steeper slope (higher ε).

^‡See Eq. 3.

^§Exclusion of one to three highly influential points gives higher ε.

^¶Process type (i.e., biomass accumulation, soil accumulation, etc.) is included as covariate and is highly significant (P < 0.0001).

Community compositional change is also strongly temperature dependent; rates of plant species colonization, loss, and turnover (species per year) all increase with temperature (ε = 1.6–2.6; R² = 85.5–93.7). Because peak rates of community change occur later in time in the colder environments at high elevations (25), this analysis underestimates the true degree of temperature dependence. We note, however, that the temperature dependence of rates of community change during succession is highly complex, influenced by factors such as species richness, dispersal, and temporal patterns in succession rate; therefore, this temperature dependence should be viewed not as a mechanistic explanation but as an empirical response variable.

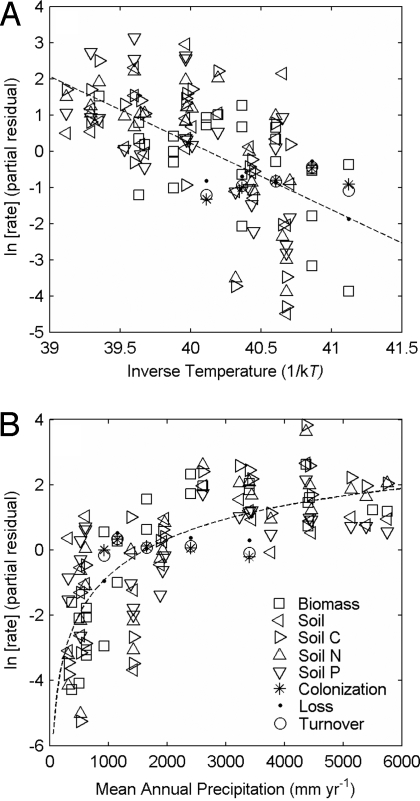
When all of the aforementioned rates are combined into a single statistical model characterizing the overall rate of primary succession (Fig. 2), the integrated model gives ε = 1.8, with precipitation analyzed as a continuous variable, and shows that temperature, precipitation, and lava type all have significant effects on the overall rate of primary succession (Table 1).

Fig. 2.

Effects of mean annual temperature (plotted as inverse temperature, 1/kT, so that the slope is −ε) (A) and mean annual precipitation (Eq. 3) (B) on rates of primary succession on the lava flows of Mauna Loa. Plotted are partial residuals or the rate corrected for all variables but the one of interest. The full model (Table 1) accounts for process type, temperature, precipitation (Eq. 3) and lava type (‘a’a versus pāhoehoe).

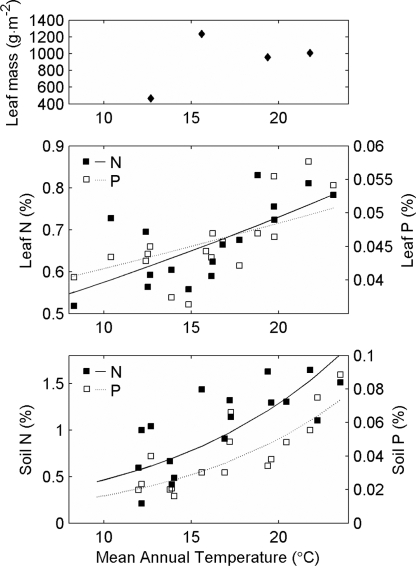
Resource concentrations increase over the course of ecosystem development, resulting in a gradient in resource availability along the temperature gradient. As has been previously documented (5, 23, 24), soil N and P (%) are lower in young (<140 yr) than in old (>2,800 yr) ecosystems (both t > 4.9; P ≥ 0.0001) and leaf N (%) is higher in old ecosystems (t = 6.3; P < 0.0001); however, there is no significant age-related variation in leaf P (%) on this centennial timescale (P = 0.68). Correspondingly, when ecosystems of similar ages (109–140 yr) at different elevations are compared, the concentrations of the reactants increase with temperature (Fig. 3). Specifically, leaf biomass (g·m⁻²; E_[R] = 0.47 ± 0.43; P not significant) (Fig. 3A), leaf N and P (both P < 0.03) (Fig. 3B), and soil N and P (both P < 0.003) (Fig. 3C) all increase with temperature, meaning that the E_[R] values characterizing their temperature dependence are greater than zero. In the case of leaf and soil nutrients, after significant effects of precipitation are accounted for, E_[R] values are ≥0.17 ± 0.04 for leaf N, ≥0.11 ± 0.04 for leaf P, 1.31 ± 0.49 for soil N, and 1.12 ± 0.34 for soil P (all P ≤ 0.02) (see SI Table 4).

Fig. 3.

Concentrations of key reactants (leaf biomass, leaf nutrients, and soil nutrients) in young sites (109–138 yr) spanning a temperature gradient.

Biogeochemical fluxes in Mauna Loa's young ecosystems (110–136 yr) also respond strongly to temperature (Table 2); comparisons of four young wet-side ecosystems reveal high values of ε for rates of aboveground net primary production, litterfall, N and P uptake by plants (g·m⁻²·yr⁻¹; ε = 1.10–1.53), and decomposition (k; ε = 0.90).

Table 2.

Estimated temperature dependence of various fluxes on young (i.e. 110–136 yr) flows on Mauna Loa

Fluxes	Temperature response
	ε ± SE	t	p	R2
ANPP	1.53 ± 0.42	−3.6	0.07	86.9
Litterfall	1.24 ± 0.24	−5.1	0.04	92.9
N uptake	1.27 ± 0.19	−6.7	0.02	95.7
P uptake	1.10 ± 0.12	−8.9	0.01	97.6
Decomposition	0.90 ± 0.14	−6.3	0.02	95.2

All fluxes are measured in g·m⁻²·yr⁻¹, except decomposition, which is measured as k. Small sample sizes (all n = 4) precluded consideration of the effects of precipitation.

Discussion

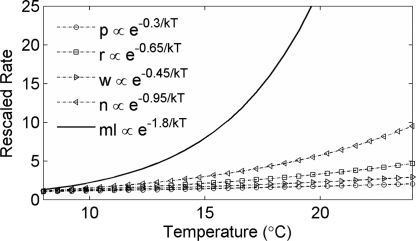
The strong temperature dependence of the rate of early primary succession, together with observed gradients in resource concentrations and the kinetics of biogeochemical fluxes in young ecosystems, supports the hypothesis that the temperature dependence of early primary succession is amplified through more rapid accumulation of reactants at higher temperatures. First, the overall temperature dependence of ecosystem development is greater than that inherent to any of its constituent processes (ε > E_a). Accumulation rates of aboveground biomass and soil (Fig. 1) and rates of species compositional changes have effective activation energies, ε, ranging from 1.4 to 2.8 (Q₁₀ ≈ 7–50) (Table 1), and the overall temperature dependence (estimated from a combination of all rates) is similarly strong (ε = 1.8; Q₁₀ ≈ 12) (Fig. 2). The magnitude of this temperature dependence is much greater than that of the constituent processes of substrate weathering, photosynthesis, and aerobic respiration measured in isolation (E_a ≈ 0.3–0.7 eV; Q₁₀ ≈ 1.5–3.0) (Fig. 4) and is much greater than that of biomass accumulation during secondary succession (E_a ≈ 0.3 eV; Q₁₀ ≈ 1.5), whose kinetics appear to be driven by photosynthesis (3). Consequently, it is unlikely that the dynamics of primary succession are due to domination of a single temperature-dependent process. The only single process that might account for such high values of ε is nitrogen fixation; it has a very high activation energy (E_a = 2.18 eV below 22°C) (18) when measured in isolation in the laboratory. However, observed rates of biological N fixation by Mauna Loa's lichen S. vulcani have a smaller (although still substantial) temperature dependence (E_a ≈ 0.95 eV) (19). In any case, soil N accumulation rates on Mauna Loa are controlled primarily by atmospheric deposition rather than nitrogen fixation (5, 22). Rates of atmospheric deposition of N probably scale with precipitation, which does not vary monotonically with elevation on Mauna Loa. This exceptional temperature response of ecosystem development remains after the removal of a precipitation response (Fig. 2B) that is much stronger than the precipitation effect on global productivity (26), suggesting that effects of precipitation may also be amplified.

Fig. 4.

Comparison of the average temperature dependence of primary succession on Mauna Loa (ml; ε = 1.8) (Table 1) with the rates typically observed for some of the constituent processes: nitrogen fixation by S. vulcani (n; E_a ≈ 0.95 eV), basalt weathering (w; E_a ≈ 0.4–0.5 eV), aerobic respiration rates (r; E_a ≈ 0.65 eV), and photosynthesis (p; E_a ≈ 0.3 eV). For display purposes, values are rescaled to normalize the rates to 1 at 7°C.

Second, age- and temperature-related variation in reactant concentrations supports our prediction that gradients in [R] values should develop in relation to temperature (E_[R] > 0). Indeed, leaf biomass, N, and P as well as soil N and P all are present at higher concentrations or densities in warmer sites (i.e., E_[R] > 0) (Fig. 3). The low E_[R] values (<0.2) of leaf N and P are not surprising given that plants tend to allocate available nutrients more toward new leaf growth than to increased leaf N (27); however, they do represent a meaningful difference for physiological function (21, 28) and, when multiplied by leaf biomass, for total ecosystem leaf nitrogen (g·m⁻²). Although our analysis focuses on leaf and soil N and P, we note that other resources also accumulate fastest at high temperatures (e.g., other soil nutrients, soil organic matter, and the nitrogen-fixing lichen S. vulcani) (9, 23, 29), thereby contributing to the temperature dependence in reactant concentration.

Finally, biogeochemical fluxes in young sites—ANPP, litterfall, N and P uptake by plants, and decomposition—have unusually strong temperature responses, which are presumably driven by the temperature dependence of reactant concentrations, such as those described above. The four vegetative processes have ε values ranging from 1.1–1.5 (Q₁₀ ≈ 4.8–8.3) (Table 2), much stronger than photosynthesis-fueled metabolism (E_a ≈ 0.3 eV; Q₁₀ ≈ 1.5) (2). Likewise, the rate of litter decomposition increases more steeply with temperature on these young Mauna Loa flows (ε = 0.9; Q₁₀ ≈ 3.4) (Table 2) than in environments where it is controlled straightforwardly by the kinetics of respiration (E_a ≈ 0.65 eV; Q₁₀ ≈ 2.5) (2). An even stronger temperature dependence of decomposition was previously observed for additional substrates on both young and old lava flows (Q₁₀ values of 4–11) and was interpreted as reflecting greater nutrient supply in warmer ecosystems (30), an interpretation that is entirely consistent with our feedback hypothesis. Thus, three lines of mutually consistent evidence support the hypothesis that the temperature dependence of early primary succession on the lava flows of Mauna Loa is amplified through more rapid accumulation of reactants at higher temperatures.

The amplified temperature dependence, together with existing evidence of several major feedbacks, suggests that positive feedbacks govern the dynamics of early ecosystem development on Mauna Loa. As yet, we cannot assess the relative importance of several potentially important feedbacks that could contribute to the observed high ε. First, biotic growth feeds back on itself; for example, growth of leaves allows more photosynthesis and thereby more growth. Second, biological activities (e.g., enhanced acidity at weathering surface and plant rooting) accelerate weathering (31) such that the weathering rate of Hawaiian basalts is at least an order of magnitude greater underneath plants than on nonvegetated surfaces (32, 33). In turn, substrate weathering enhances plant growth through the release of phosphorus and other elements that can limit plant production (34) and biological nitrogen fixation (22, 35–37). Third, plant productivity and nitrogen accumulation are mutually dependent. Nitrogen is the most strongly limiting nutrient in Hawaii's young ecosystems (5, 34, 38), and biota increase the rate of nitrogen accumulation by retaining atmospheric inputs and through limited nitrogen fixation (22). Lastly, accumulation of biota and soil organic matter, both of which are driven by temperature-dependent growth and metabolism, are mutually dependent. Soil organic matter is derived from biomass that decomposes through the action of microorganisms and invertebrates. In turn, organic matter enhances soil water-holding capacity and nutrient content (4, 39), which are especially critical in young ecosystems, where runoff can remove water and nutrients before they can be taken up by plants. The highly interdependent nature of these and other processes makes it unsurprising that rates of biomass accumulation, soil formation, and even community compositional change respond steeply and similarly to temperature (Table 1 and Fig. 2).

Because of these feedbacks, primary succession on Mauna Loa exhibits a temperature dependence (ε = 1.8; Q₁₀ ≈ 12) that dwarfs those of most metabolically mediated biological rate processes (Fig. 4). The overall rate of primary succession increases >50-fold over the 16°C temperature gradient between the highest (2,480 m) and lowest (60 m) elevations for which data are available. Lava flows only about a century old in the wet lowlands have already accumulated a relatively productive (ANPP ≈ 400–600 g·m⁻²·yr⁻¹) developing forest with substantial aboveground biomass (1–3 kg·m⁻²) and numerous species (6, 9), whereas flows the same age above a 2,000-m elevation support little or no vegetation and soil (6, 7, 23).

Amplification of temperature dependence, such as that observed here, should be general to systems whose dynamics are strongly shaped by positive feedbacks. An obvious application is to other cases of primary succession, whose rates do exhibit temperature dependence. For example, primary succession rate after the eruption of Mount St. Helens exhibits temperature dependence along an elevational gradient (8), and substantial differences in succession rate may be seen on recently formed volcanic islands, where the difference in temperature is due to latitude rather than elevation (40, 41). Subarctic Surtsey (33 km from Iceland; T̄ ≈ 5°C) has remained relatively depauperate of vegetation for four decades after eruption (42), whereas tropical Anak Krakatau (40 km from Sumatra; T̄ ≈ 26°C) supported forest vegetation exceeding 10 m in height only two decades after eruption (43). Although it remains to be seen whether these and other developing ecosystems will exhibit approximately the same magnitude of temperature dependence observed here, the underlying mechanisms should hold. Such amplified temperature dependence also is likely to be seen on land exposed by receding ice sheets and where ecosystem restoration involves multiple processes of soil and vegetation development.

More broadly, ecosystem development on Mauna Loa provides an example of how temperature-driven, biologically mediated gradients in resource availability can alter the effective temperature dependence of ecological processes. Such phenomena are not uncommon in ecology; for example, ε values of ecosystem respiration may be inflated by temperature-driven gradients in photosynthate supply to root growth or litterfall (44–46). Our model goes beyond the straightforward effect of temperature on constituent metabolic processes (1, 11) to describe cases where interactions among multiple processes affect the kinetics by altering resource concentrations. In an era of global warming, a mechanistic theory based on first principles of chemical kinetics could contribute to understanding the complex effects of temperature on the structure and dynamics of ecological systems.

Methods

All data were collected previously on the slopes of Mauna Loa, HI (19°29′ N, 155°36′ W). Mauna Loa is an active shield volcano whose broad, gentle slopes are covered by lava flows of various ages. Lava flows differ in form, including chunky ‘a’a and smooth, ropy pāhoehoe flows, but vary little in chemistry. Average annual temperature (T̄) decreases at a lapse rate of 6.4°C per kilometer (47), resulting in a decrease of ≈17°C between sea level and the upper range of vegetation around 2,400 m. Precipitation varies dramatically between the wet windward NE flank of Mauna Loa and its dry NW flank (48, 49). On the wet side, precipitation increases from ≈3,600 mm·yr⁻¹ at sea level to a peak of ≈5,700 mm·yr⁻¹ near 700 m and then declines as a roughly exponential function (7, 48). On the dry side, precipitation averages <750 mm·yr⁻¹ over the entire altitudinal gradient, with a peak between 900 and 1,600 m (49).

The data sources and analytical methods that we used are given below and in the SI Tables 5 and 6 and SI Methods). The data provided challenges in sorting out the separate and interactive effects age, temperature, precipitation, and lava type. Although there is no single “right” way to analyze these data, we tried to use the most statistically rigorous and ecologically realistic methods. We also tried alternative analytical procedures, which gave similar results. In general, we report analyses that give conservative estimates of ε.

Rates of aboveground biomass and soil accumulation were calculated as the slopes of linear regressions as a function of age (3), which were forced through the origin to enforce the assumption that initial values were zero. Data for these processes were available for both ‘a’a and pāhoehoe sites between 80 and 2,480 m on both the wet and dry sides of Mauna Loa (SI Table 5). For biomass, ages ranged from 5 to 4,000 years, but many old sites, particularly at low elevations, were excluded because accumulation of biomass had already decelerated. Calculations of the biomass accumulation rate are detailed in SI Methods and SI Table 6. For soil and its components, all data were from young ecosystems (109–140 yr), so rate was simply mass divided by age. Data for soil accumulation contained zero-values (primarily at high elevations), which we were forced to exclude from our analyses. Replacing these zeros with any value less than or equal to the lowest measured value resulted in a higher ε value.

Changes in species composition were determined by using presence–absence data for wet side ‘a’a flows of five ages (5–3,400 yr) and five elevations (1,219–2,438 m) (SI Table 5) (6, 25). Average colonization and loss rates were defined as the total number of species gained or lost along the entire chronosequence divided by chronosequence age (3,400 yr), and turnover rate is the average of colonization and loss (25). Temporary absences of species along the chronosequence (<16% of all absences) were attributed to sampling error or stochasticity and counted as presences. Data were insufficient to test for effects of precipitation.

Leaf and soil nutrient data from Vitousek et al. (23) were reanalyzed. Age-related variation was determined by using a paired t test for soil nutrients and an ANOVA for leaf nutrients. Temperature-related variation was analyzed for young (109–138 yr) sites (SI Tables 4 and 5).

Data on biogeochemical fluxes (ANPP, litterfall, N and P uptake, and decomposition) from four relatively young (110–136 yr) pāhoehoe flows on the wet side (SI Table 5) (9, 30) were used to estimate temperature dependence of these processes. Again, data were insufficient to test for effects of precipitation.

We used multiple linear regression (Type III SS) to characterize the response of the above rates to three environmental variables: temperature, precipitation, and lava type. Average annual temperature (T̄; Kelvin) was expressed as 1/kT̄ (see Eq. 1), so −ε is the slope of the Arrhenius plot of ln [rate] as a function 1/kT̄ (Fig. 2A). Precipitation covaries nonlinearly with temperature along the altitudinal gradient, so there is no straightforward method to isolate its effects from those of temperature. We assessed the effect of precipitation in two ways: (i) We categorized precipitation regimes as wet (>900 mm·yr⁻¹) or dry (<750 mm·yr⁻¹), corresponding to the windward NE and the leeward NW slopes of Mauna Loa, respectively; (ii) we analyzed precipitation (w; mm·yr⁻¹) as a continuous quantitative variable using a model that can capture complex curvilinear and peaked functions (SI Methods):

Here, α and β can be either positive or negative exponents and c is a normalization constant containing any differences between lava flow types.