Abstract
Mammalian central pattern generators (CPGs) producing rhythmic movements exhibit extremely robust and flexible behavior. Network architectures that enable these features are not well understood. Here we studied organization of the brain stem respiratory CPG. By sequential rostral to caudal transections through the pontine-medullary respiratory network within an in situ perfused rat brain stem–spinal cord preparation, we showed that network dynamics reorganized and new rhythmogenic mechanisms emerged. The normal three-phase respiratory rhythm transformed to a two-phase and then to a one-phase rhythm as the network was reduced. Expression of the three-phase rhythm required the presence of the pons, generation of the two-phase rhythm depended on the integrity of Bötzinger and pre-Bötzinger complexes and interactions between them, and the one-phase rhythm was generated within the pre-Bötzinger complex. Transformation from the three-phase to a two-phase pattern also occurred in intact preparations when chloride-mediated synaptic inhibition was reduced. In contrast to the three-phase and two-phase rhythms, the one-phase rhythm was abolished by blockade of persistent sodium current (INaP). A model of the respiratory network was developed to reproduce and explain these observations. The model incorporated interacting populations of respiratory neurons within spatially organized brain stem compartments. Our simulations reproduced the respiratory patterns recorded from intact and sequentially reduced preparations. Our results suggest that the three-phase and two-phase rhythms involve inhibitory network interactions, whereas the one-phase rhythm depends on INaP. We conclude that the respiratory network has rhythmogenic capabilities at multiple levels of network organization, allowing expression of motor patterns specific for various physiological and pathophysiological respiratory behaviors.
INTRODUCTION
The structural and functional organizations of various central pattern generators (CPGs) producing rhythmic movements have been studied for decades in an attempt to understand the neural basis of motor behavior. In contrast to CPGs in several invertebrates and lower vertebrates (Grillner 2006; Marder and Calabrese 1996; Selverston and Ayers 2006), the spatial and functional architectures of CPG circuits in the mammalian CNS, such as those generating breathing movements, have not been well defined. Breathing in mammals is a dynamically mutable motor behavior that not only performs a vital homeostatic function but is also integrated with many other physiological functions including suckling, swallowing, sniffing, chewing, and vocalization. With such functional diversity, respiratory CPG circuits must have a robust, yet highly flexible organization, permitting multiple state-dependent modes of operation. Here, we have attempted to uncover structural and functional properties of respiratory circuits that enable multiple modes of rhythmic motor pattern generation.
Breathing movements are produced by a pontine-medullary respiratory network that generates rhythmic patterns of alternating inspiratory and expiratory activities to coordinate activity of spinal and cranial motoneurons (Bianchi et al. 1995; Cohen 1979; Feldman and Smith 1995; Richter 1996). The motor pattern during normal breathing was considered to consist of three phases: inspiration, postinspiration, and late expiration (Richter 1996; Richter and Spyer 2001), which can be recognized in the integrated activities of the phrenic and cranial (e.g., laryngeal) nerves. This pattern originates within a bilateral column of medullary neurons—the ventral respiratory column (VRC)—and is controlled by the pons. The VRC includes three rostro-caudally arranged compartments (Figs. 1 and 2): Bötzinger complex (BötC), pre-Bötzinger complex (pre-BötC), and rostral ventral respiratory group (rVRG). Respiratory neurons in these compartments are usually classified based on their firing pattern (e.g., decrementing, augmenting) and the phase of activity relative to the breathing cycle, such as early-inspiratory (early-I) with a decrementing inspiratory pattern; ramp-inspiratory (ramp-I) with a augmenting inspiratory pattern; postinspiratory (post-I) or decrementing expiratory (dec-E); augmenting or stage II expiratory (aug-E or E-2); and preinspiratory (pre-I) (see Richter 1996 for review).
FIG. 1.
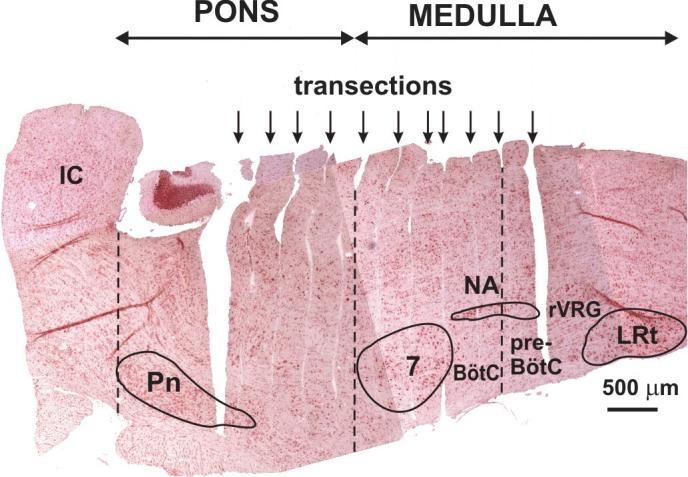
Example of a parasagittal section (neutral red stain) of the brain stem after rostral to caudal serial transections (250- to 350-μm-thick slices indicated by arrows) made with a piezo-driven microvibratome (custom built) from an arterially perfused brain stem–spinal cord preparation of a 4-wk-old rat. Transection levels containing respiratory network structures including BötC, pre-BötC, rVRG, and lateral pons are labeled. The brain stem–spinal cord was fixed in situ and embedded in gelatin before microtome sectioning and staining. Dashed lines delimit rostro-caudal extent of pons and separate BötC and pre-BötC. See Fig. 2 for more detailed reconstruction of brain stem structures associated with the different rhythms analyzed in this study. 7, facial nucleus; BötC, Bötzinger complex; IC, inferior colliculus; LRt, lateral reticular nucleus; NA, nucleus ambiguus (compact and semicompact divisions outlined); Pn, pontine nucleus; pre-BötC, pre-Bötzinger complex; rVRG, rostral ventral respiratory group.
FIG. 2.
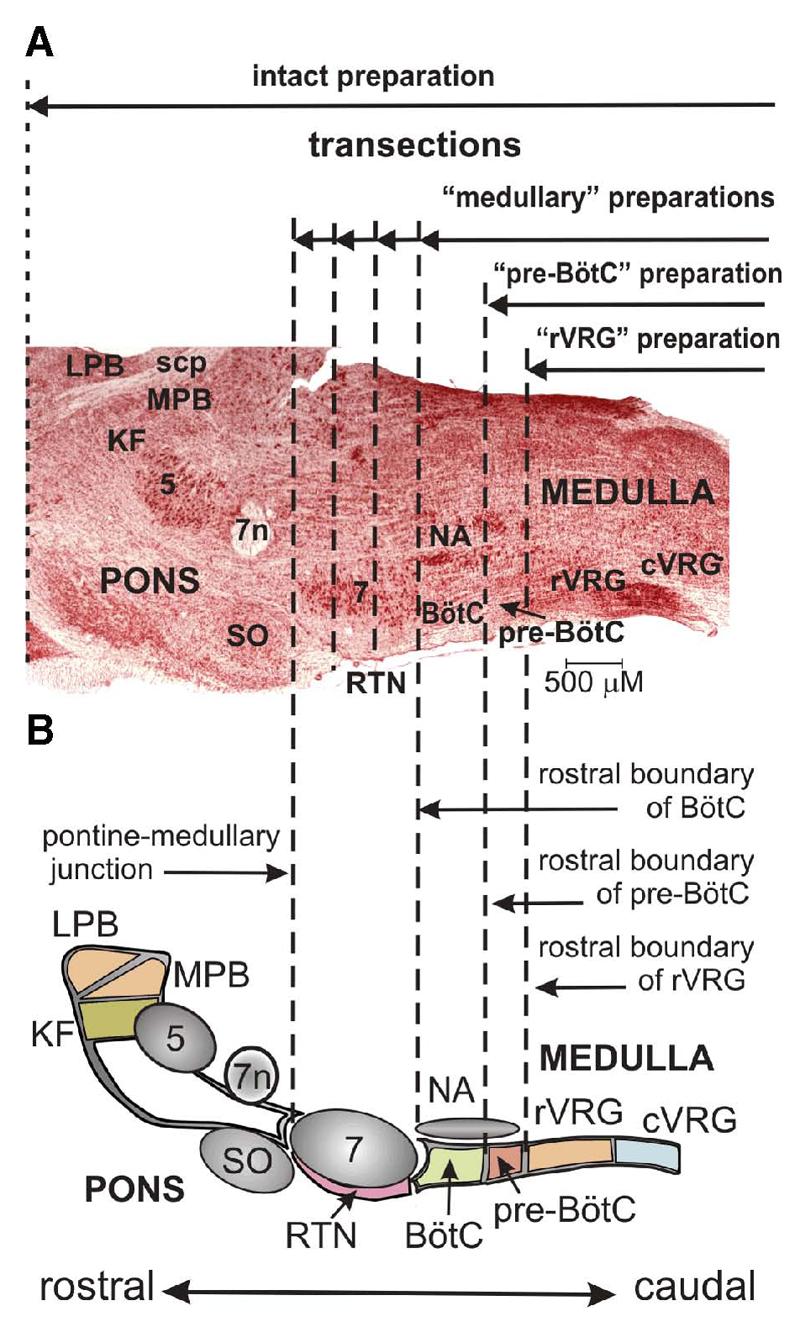
A: parasagittal section (neutral red stain) of the brain stem at the level of NA, VRG, 7, and lateral pons. B: schematic diagram depicting spatial arrangement of respiratory-related structures. Vertical dashed lines indicate several experimental transections and levels, which delineate rostral extent of reduced preparations (solid horizontal lines with arrows): medullary preparations, obtained after transections through various rostral-caudal levels of the facial nucleus or rostral boundary of BötC; pre-BötC preparation, after transection at rostral boundary of pre-BötC; rVRG preparation, after transection at rostral boundary of rVRG. 5, trigeminal nucleus; 7n, facial nerve; cVRG, caudal VRG; KF, Kölliker-Fuse nucleus; LPB, lateral parabrachial nucleus; MPB, medial parabrachial nucleus; RTN, retrotrapezoid nucleus; scp, superior cerebellar peduncle; SO, superior olive.
The pontine respiratory regions include the Kölliker-Fuse (KF) nucleus and parabrachial (PB) complex [lateral (LPB) and medial (MPB) nuclei] in the dorsolateral pons and several areas in the ventrolateral pons. Although the pons has been shown to interact with multiple medullary compartments and provide strong modulation of the medullary respiratory network (Alheid et al. 2004; Cohen 1979; Cohen and Shaw 2004; Ezure 2004; Ezure and Tanaka 2006; Okazaki et al. 2002; Song and Poon 2004; St.-John 1998), its functional role in the generation and control of respiratory rhythm and pattern has not been fully established. In addition, several medullary structures, specifically the retrotrapezoid nucleus (RTN; located below the facial nucleus rostral to BötC) and the medullary raphé nucleus, both involved in central chemoreception, modulate medullary respiratory network performance via various drives that adapt the CPG activity to the metabolic state of the system such as the level of carbon dioxide in blood (Guyenet et al. 2005; Richerson 2004).
The BötC, with predominately expiratory neurons (post-I and aug-E), is considered a major source of expiratory activity (Ezure 1990; Ezure et al. 2003; Jiang and Lipski 1990; Tian et al. 1999). The adjacent, more caudal pre-BötC contains circuitry essential for generating inspiratory activity (Feldman and Del Negro 2006; Smith et al. 1991, 2000). The activity of bulbospinal inspiratory (ramp-I) neurons of the rVRG, projecting to phrenic motoneurons and shaping the phrenic output motor pattern, is driven by the pre-BötC and inhibited (during expiration) by the BötC. Although the function of the BötC and its interactions with other VRC compartments were well studied (Ezure 1990; Ezure and Manabe 1988; Ezure et al. 2003; Fedorko and Merrill 1984; Jiang and Lipski 1990; Long and Duffin 1986; Shen et al. 2003; Tian et al. 1999), an exclusive role of BötC neurons in the expression of expiration and coordination of inspiratory and expiratory activities has been recently debated. Specifically, it has been proposed that a separate expiratory oscillator, located outside of the BötC in the parafacial respiratory group (pFRG), interacts with the pre-BötC to generate coordinated patterns of inspiratory and expiratory activity (Feldman and Del Negro 2006; Janczewski and Feldman 2006).
The medullary pre-BötC has been of intense interest because it is thought to function as a kernel structure that can be experimentally isolated in vitro and expresses autorhythmic or pacemaker-like activity (Johnson et al. 2001; Koshiya and Smith 1999). This activity is proposed to be based on intrinsic persistent sodium current (INaP)-dependent mechanisms (Butera et al. 1999a,b; Rybak et al. 2003b, 2004b; Smith et al. 2000). The isolated pre-BötC generates a rudimentary pattern of inspiratory activity (Smith et al. 1991, 2000). However, the mechanisms underlying inspiratory pattern generation in the pre-BötC under more physiological conditions when the pre-BötC is embedded in the intact brain stem have not been established.
Here, we tested our hypotheses that there is a spatial and functional compartmentalization of the respiratory network and that the pre-BötC, as one of the key compartments, is functionally embedded in the spatially distributed brain stem network and, depending on interactions with other compartments, can operate in multiple modes of rhythm generation, such as intrinsic bursting, which does not require phasic inhibition, or a tonic activity mode that needs phasic inhibition for rhythmic bursting activity (Butera et al. 1999a,b; Rybak et al. 2003b, 2004b; Smith et al. 2000). We proposed that inputs from the BötC (providing phasic inhibition) and from more rostral structures including the pons (controlling the state of the pre-BötC) define the mode of pre-BötC operation and hence the rhythmogenic mechanism expressed in the entire brain stem respiratory network.
To uncover this potential hierarchy of network interactions, we used an in situ arterially perfused rat brain stem–spinal cord preparation and performed sequential rostral to caudal transections through the pontine-medullary respiratory column. We analyzed resulting transformations of respiratory motor patterns and studied the dependence of these patterns on chloride-mediated inhibition and intrinsic INaP-dependent mechanisms. A computational model of the brain stem respiratory network with a hierarchy of pontine-medullary circuit components was used to suggest how the inhibitory and excitatory network interactions and the intrinsic INaP-dependent mechanisms contribute to rhythm generation in the different network states. We conclude that there are at least three rhythmogenic mechanisms embedded within hierarchically interacting pontine-medullary circuits that define the expression of different motor patterns underpinning distinct physiological and pathophysiological respiratory behaviors.
METHODS
In situ brain stem–spinal cord preparation
The experimental studies were performed using the in situ perfused brain stem–spinal cord preparation of the juvenile rat (Paton 1996). This preparation allows precise control of arterial perfusion of the in situ brain stem–spinal cord with independent control of perfusate O2/CO2 concentrations, as well as administration of pharmacological agents through the perfusate that would be incompatible with viability of in vivo preparations.
All procedures conformed to the UK Animals (Home Office Scientific Procedures) Act 1986 and were approved by the University of Bristol ethical review committee. In brief, preheparinzed (1,000 units, given intraperitoneally) male Wistar rats (60–110 g) were anesthetized deeply with halothane until loss of paw withdrawal reflex. Rats were bisected subdiaphragmatically, the head and thorax was immersed in ice-chilled carbogenated Ringer solution, and the brain was decerebrated precollicularly. The cerebellum was removed to gain direct visual access to the dorsal brain stem surface. Thoracic phrenic (PN), cervical vagus (cVN), and hypoglossal (HN) nerves (all left) were cut distally. Preparations were transferred to a recording chamber and positioned prone, and the head was fixed using ear bars and a snout clamp that ensured the brain stem was orientated similarly in all preparations. A double lumen cannula (DLR-4, Braintree Scientific) was inserted into the descending aorta for retrograde perfusion. Perfusion was supplied through a peristaltic roller pump (Watson Marlow 505D) and consisted of carbogenated Ringer solution at 32°C. The second lumen of the cannula was used to monitor aortic perfusion pressure. The baseline perfusate flow was preset between 20 and 24 ml/min and adjusted until the inspiratory motor pattern consisted of an augmenting burst discharge. In addition, vasopressin (200–400 pM as required) was added to the perfusate to raise perfusion pressure to between 80 and 90 mmHg (Pickering and Paton 2006).
Solutions and pharmacological agents
The composition of the Ringer solution was (in mM) 125 NaCl, 24 NaHCO3, 3 KCl, 2.5 CaCl2, 1.25 MgSO4, 1.25 KH2PO4, and 10 dextrose, pH 7.35–7.4 after carbogenation. Osmolality was 290 ± 5 mosm·kg H2O−1. Ficoll 70 (1.25%) was added as an oncotic agent. For experiments in which the chloride concentration was reduced, KCl was replaced by KGluconate, NaCl was replaced by NaGluconate, and CaCl2 was replaced by CaSO4 in appropriate concentrations so that the final concentration of Cl− used was 60, 40, or 20% of normal. In all cases, the osmolarity of these low chloride perfusates were matched with the normal solution. Unless stated, all chemicals were from Sigma. Vecuronium bromide (4 μg/ml; Organon Teknica, Cambridge, UK) was added to the perfusion solution to block neuromuscular transmission. Riluzole hydrochloride (Tocris), a persistent sodium current blocker, was prepared fresh daily by dissolving in distilled water (1 mM) and added to the perfusate to give final concentrations of 1–20 μM.
Precision transverse sectioning of the brain stem in situ
A custom-made microvibratome consisting of a piezoelectric bending element (Piezo Systems, Waltham, MA) mounted on a X-Y translational stage and motor driven z-axis (SD Instruments, Grants Pass, OR) was designed to make sequential transverse cuts through the brain stem of the in situ preparation while recording motor activity. Razor blades were cut to size (5.2–5.4 mm) and secured in a miniature clamp at the end of the bending element, which was driven by custom electronics controlling frequency and amplitude of the vibration. This allowed cuts to extend the entire width of the brain stem. We adjusted the flow rate of the perfusion pump or applied vasopressin to the perfusate to correct for any changes in perfusion pressure.
Stimulation of respiratory network activity
To provide a powerful excitatory drive into the respiratory network, the following were performed: 1) stimulation of the peripheral chemoreceptors by injection of low doses of sodium cyanide (NaCN; 0.03% solution; 50- to 100-μl bolus) into the aorta; and 2) brain stem ischemia produced by a transient arrest of brain stem perfusion (40–60 s). These procedures were applied before and after application of riluzole, or under conditions where transections transiently eliminated network activity, allowing us to test whether the respiratory network could be reactivated.
Histological reconstruction
For all experiments, the level of each transverse cut made with the vibratome was documented post hoc by histological reconstruction and related to the changes in motor pattern and response to riluzole. The head of the preparation with the transected brain stem in situ was fixed in 10% buffered formaldehyde–30% sucrose solution for ≥2 days, and subsequently, the brain stem was removed and embedded in 10% gelatin (300 bloom, Sigma). The gelatin blocks were postfixed in 10% formaldehyde–30% sucrose solution for 3 h. Sagittal sections were cut (50 μm thick), mounted onto subbed slides, and stained with neutral red (1%; Fig. 1). This allowed reconstruction of the precise boundaries separating the different respiratory patterns and mechanisms underpinning the distinct rhythms generated.
Electrophysiological recording and data analysis
Simultaneous recordings of PN, cVN, and HN activity were obtained with three bipolar suction electrodes mounted on separate three-dimensional (3D) micromanipulators. Population recordings were made from the BötC, pre-BötC, and rVRG with tungsten microelectrodes (1–2 MΩ), or in some experiments, single units were recorded with glass microelectrodes filled with 4 N NaCl (10–15 MΩ), positioned with a 3D micromanipulator and nanostepper (custom made). We determined recording sites in these compartments by extensively mapping population activity profiles along the rVRG–pre-BötC–BötC column by electrolytic lesions performed at recording sites with subsequent histological reconstruction in some experiments and by histological reconstruction of electrode penetration tracts in fixed counterstained tissue. In reduced preparations, we also positioned electrode penetrations in stereotaxic relationship to vibratome-cut surfaces that were subsequently shown from histological reconstruction to delineate compartment boundaries. All recordings were AC amplified and band-pass filtered (80 Hz to 3 kHz). Nerve and population activity signals were rectified and integrated (50-ms time constant) on-line (Spike 2 software, Cambridge Electronic Design). All electrophysiological data were digitized (5–10 kHz, Cambridge Electronic Design A-D converter) with Spike 2 software and analyzed off-line. Parameters of nerve or population activity (cycle period/frequency, inspiratory duration, expiratory duration, activity amplitude) were measured, and cycle-triggered averages for waveform analysis were made using a custom script for Igor Pro (5.0, Wave-metrics). Significance of data were assessed with either a two-tailed Student's t-test or ANOVA followed by either Dunnett's or Student-Newman-Keul's posttest or Wilcoxon signed-rank test as appropriate (Prism 4, Graphpad Software). All values indicated are the mean ± SD, and n is the number of preparations unless otherwise specified. Differences were considered significant at the 95% confidence limit.
Modeling methods
The model has been developed based on previous models (Rybak et al. 2004a; Smith et al. 2000). All neurons were modeled in the Hodgkin-Huxley style (single-compartment models) and incorporated known biophysical properties and channel kinetics characterized in respiratory neurons in vitro. Specifically, the kinetics of the fast sodium (INa) and the persistent (slowly inactivating, INaP) sodium channels was described using the experimental data obtained in studies of neurons from the rat rostral ventrolateral medulla (Rybak et al. 2003a); the kinetics of high-voltage activated calcium current (ICaL) was described based on the study of calcium currents in rat VRG neurons (Elsen and Ramirez 1998); the intracellular calcium dynamics was described using data by Frermann et al. (1999); the descriptions of other ion channels, e.g., the potassium rectifier (IK) and calcium-dependent potassium (IK,Ca), synaptic conductances, and all other cellular parameters, were as described in previous models (Rybak et al. 1997a,b, 2003b, 2004a,b). Each neuronal type was represented by a population of 50 neurons. The heterogeneity of neurons within each population was set by a random distribution of some parameters and the initial conditions for values of membrane potential, calcium concentrations, and channel conductances. The full description of the model and model parameters can be found in the APPENDIX.
Modeling was performed using a simulation package NSM 2.0, developed at Drexel University by S. N. Markin, I. A. Rybak, and N. A. Shevtsova. Differential equations were solved using the exponential Euler integration method (MacGregor 1987) with a step of 0.1 ms (for details see Rybak et al. 2003b).
RESULTS
Respiratory pattern in the intact pontine-medullary respiratory network in situ
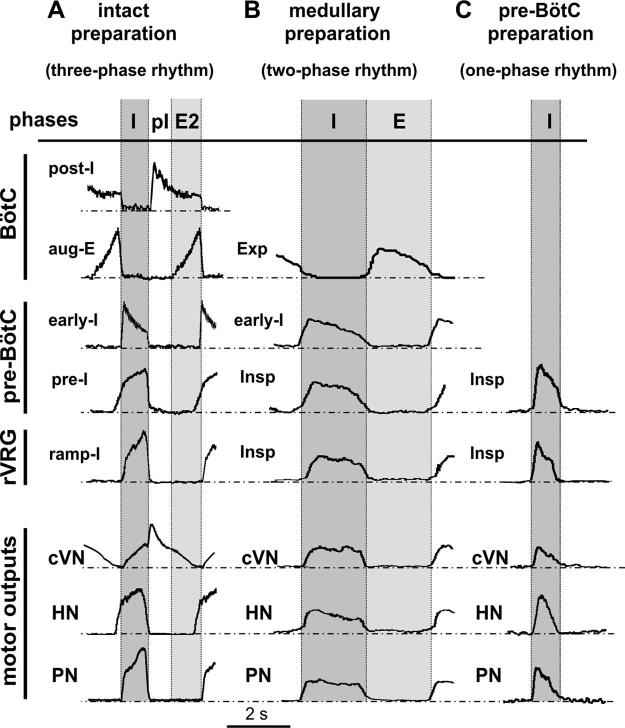
The stereotypical patterns of PN, HN, and cVN activities generated by the intact preparation are shown in Fig. 3A. PN burst frequency in these preparations was in the range 0.24–0.47 bursts/s with a relatively constant PN burst duration (1.00 ± 0.14 s, n = 20 preparations). The activity profiles of different VRC neuron populations and integrated nerve activities are shown in Fig. 4A. These patterns resembled those recorded in vivo during generation of a normal three-phase respiratory rhythm (St.-John and Paton 2003) and exhibited the following characteristics (Fig. 3A): 1) an augmenting shape of PN bursts; 2) preinspiratory onset of HN bursts (50–100 ms before the onset of PN bursts); and 3) a prominent epoch of decrementing postinspiratory (post-I) discharge in cVN.
FIG. 3.
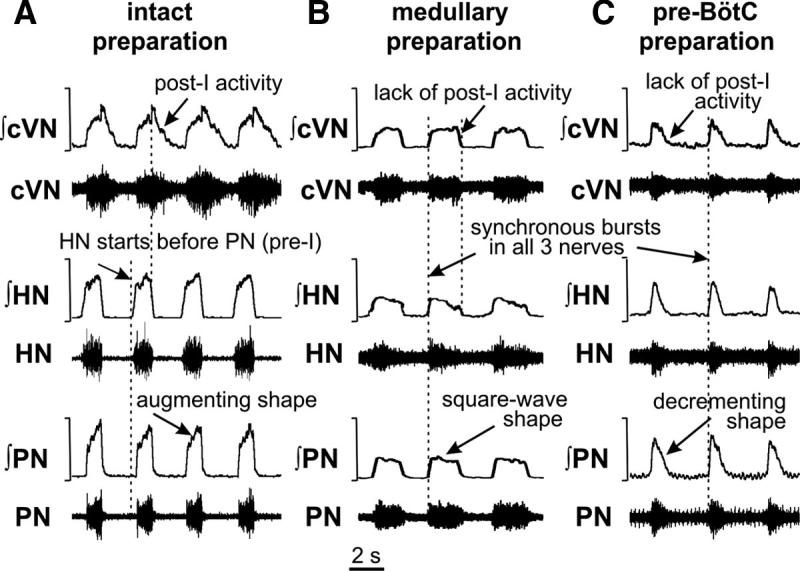
Representative activity patterns of phrenic (PN), hypoglossal (HN), and central vagus (cVN) nerves recorded from intact (A), medullary (B), and pre-BötC (C) preparations. Each panel shows raw (bottom traces) and integrated (top traces) motor nerve discharge. Vertical dashed lines in A indicate onsets of HN inspiratory burst and the postinspiratory component of cVN activity; dashed lines in B and C indicate synchronous onset of inspiratory bursts in all nerves.
FIG. 4.
Neuronal activity patterns within several respiratory compartments recorded in both intact and reduced in situ preparations. Activity patterns shown (top set of traces) within BötC, pre-BötC, and rVRG (indicated at left) are composite recordings obtained from intact (A), medullary (B), and pre-BötC (C) preparations after sequential transections. Traces are averaged cycle-triggered waveforms showing activity patterns of different types of respiratory neurons that are representative for the groups of cells/population activities analyzed [post-I (n = 7), aug-E (n = 7), early-I (n = 3), pre-I (n = 7), and ramp-I (n = 6) in A; inspiratory, Insp (n = 5) and expiratory, Exp (n = 5) in B; Insp (n = 6) in C] in relation to motor output patterns (bottom traces: cVN, HN, PN). Activity waveforms were computed from integrated signals with onset of PN activity as trigger, averaged over multiple cycles (≥20) for a representative cell/population activity recording in each example; phase durations from different experiments were normalized. Inspiratory (I), postinspiratory (pI), and stage-2 expiratory (E2) phases are indicated for the intact 3-phase rhythm-generating state in A. Inspiratory (I) and expiratory (E) phases are indicated in B for 2-phase rhythm of medullary preparations lacking the post-I phase. Period of I (inspiratory) activity in the pre-BötC and rVRG in the one-phase rhythm is indicated in C.
Neural activities recorded within the VRC could be clearly subdivided into three phases (Fig. 4A): inspiratory (I) that corresponded to PN activity, postinspiratory (pI), and active expiratory (E2), whose timing corresponded to the onset of augmenting expiratory (aug-E) activity recorded in the BötC (below). Extracellular recordings from intact preparations (Fig. 4A) revealed typical neuronal types with the following characteristic activity patterns: 1) neurons with decrementing post-I, and with augmenting expiratory (aug-E) discharges within BötC; 2) neurons with a preinspiratory onset of activity (pre-I), and with an early-inspiratory (early-I) decrementing discharge within pre-BötC; and 3) neurons with augmenting activity patterns (ramp-I) within rVRG.
Transformations of respiratory pattern with sequential brain stem transections in situ
The spatial organization of pontine-medullary respiratory networks was studied by sequentially reducing the network with a series of rostral to caudal brain stem microtransections starting at the level of the pons or near the pontine-medullary junction. Figure 1 shows an example of the histological appearance of the postfixed brain stem in sagittal view after a series of such transections. These transections allowed us to remove specific circuit components along the brain stem “respiratory column” bilaterally, which included severance of connections across the midline, and to analyze corresponding transformations of neuronal activity and motor output patterns. Vertical dashed lines in Fig. 2 indicate several experimental transections and levels, which delineate the rostral extent of the reduced preparations used in this study. The medullary preparations were obtained after transections through the facial nucleus from the pontine-medullary junction at the rostral end to the rostral boundary of BötC at the caudal end. The pre-BötC preparation was obtained after transection at the rostral boundary of pre-BötC, whereas the rVRG preparation was made after transection at the rostral boundary of rVRG (Fig. 2).
On production of a medullary preparation, by transecting at the rostral end of facial nucleus (i.e., pontine-medullary junction; Fig. 2), the three-phase rhythm was converted into a two-phase inspiratory-expiratory pattern (Figs. 3B and 4B), which was characterized by a nonramping “square-wave” inspiratory motor profile with the onset of activity synchronized in all nerves and by a lack of post-I discharge in cVN. Burst frequency in medullary preparations was in the range 0.14–0.32 burst/s (n = 20); the inspiratory phase duration was 1.73 ± 0.45 s. The amplitude of inspiratory bursts was reduced by >50% relative to bursts generated by the intact brain stem. Neuronal activities within the BötC, pre-BötC, and rVRG during the two-phase rhythm included decrementing expiratory (in BötC) and inspiratory (in pre-BötC and rVRG) discharges (Fig. 4B).
The cycle-to-cycle variability of inspiratory burst frequency in the two-phase rhythm generated by medullary preparations was greater compared with the three-phase rhythm. This variability increased with more caudal transections (reducing the remaining part of FN/RTN; Fig. 2) because of the emergence of shorter duration “ectopic” bursts interposed between longer duration square-wave bursts (Fig. 5). Interestingly, administration of riluzole (≤10 μM) eliminated the ectopic bursting and stabilized the two-phase rhythm (Fig. 5).
FIG. 5.

The 2-phase rhythmic motor pattern generated by medullary preparations. Transection of the brain stem through the rostral facial nucleus (FN) transformed the normal 3-phase pattern with incrementing PN discharges (top trace) into a 2-phase pattern with square-wave-like PN discharges (2nd trace). Subsequent caudal transections (3rd trace) resulted in “ectopic” bursts—shorter duration bursts with irregular frequency and amplitude (indicated by *) interposed between longer duration square-wave bursts. Application of INaP blocker riluzole (≤10 μM concentration) eliminated ectopic bursts and stabilized the 2-phase rhythm.
Transection at the rostral border of pre-BötC (pre-BötC preparation indicated in Fig. 2; n = 8) to remove the BötC compartment disrupted rhythmic activity, or resulted in low frequency spontaneous decrementing PN discharges (0.5–1.5 s in duration, 0.04–0.07 bursts/s frequency range). This spontaneous activity could be stabilized at a higher burst frequency (0.13– 0.37 bursts/s range) by elevating the perfusate CO2 concentration (≤10%) and/or extracellular K+ (≤9 mM). In preparations where activity was eliminated by transection, the rhythm could be reactivated by either peripheral chemoreceptor stimulation or stopping the perfusion for ≤1 min. The rhythmic motor pattern was stabilized and maintained by a combination of elevating CO2 and extracellular K+. The resultant rhythmic activity pattern consisted of decrementing inspiratory bursts synchronized in all motor outputs as shown in Fig. 3C. Integrated population activity of pre-BötC and rVRG exhibited similar decrementing inspiratory discharge patterns (Fig. 4C). This inspiratory rhythm and its activation/reactivation properties (e.g., with elevation of extracellular K+) were analogous to those described previously for in vitro slices from the neonatal rat medulla containing the pre-BötC (Del Negro et al. 2001; Koshiya and Smith 1999). We called this activity a one-phase inspiratory rhythm because it occurred in the absence of expiratory activity and involved an endogenous bursting mechanism presumably operating within the pre-BötC.
Transection at the rostral boundary of rVRG, which removed the pre-BötC (rVRG preparation in Fig. 2), eliminated all rhythmic motor activity from the PN, HN, and cVN. After this transection, we failed to find rhythmically active neurons in the rVRG (n = 8 preparations). Activity could not be restored by chemosensory stimulation with NaCN injections and/or elevated CO2, and/or elevated extracellular K+ concentrations. This confirmed that pre-BötC circuits are required for the one-phase inspiratory rhythm, as originally shown for the neonatal systems under in vitro conditions (Smith et al. 1991).
Probing for persistent sodium (INaP)-dependent rhythmogenic mechanisms
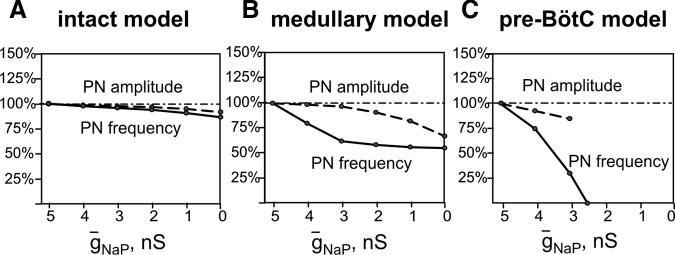
To study a possible contribution of INaP-dependent mechanisms to the generation of the three-, two-, and one-phase rhythms, we used riluzole (1–20 μM), a pharmacological blocker of INaP (Urbani and Belluzzi 2000). Riluzole was added to the perfusate in the intact and reduced preparations at concentrations (1–20 μM) that were previously shown to attenuate and finally block INaP at the cellular level and abolish intrinsic bursting activity of the pre-BötC in vitro and in situ (Koizumi and Smith 2002; Paton et al. 2006; Rybak et al. 2003b). Figure 6, A and A1, shows effects of riluzole on the frequency and amplitude of PN bursts in the intact pontinemedullary network (n = 8). The INaP blocker reduced the PN burst amplitude but did not significantly affect burst frequency (Fig. 6A).
FIG. 6.
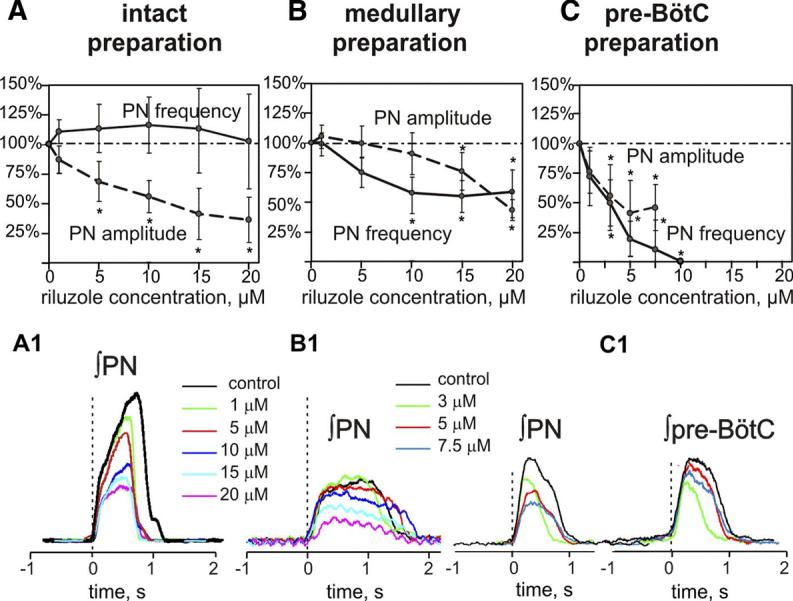
A–C: steady-state dose-dependent effects of riluzole on burst frequency (solid lines) and amplitude (dashed lines) of integrated phrenic (PN) activity recorded in the intact (A), medullary (B), and pre-BötC (C) preparations. PN amplitudes and frequency are normalized (% control). Burst frequency does not change significantly in the intact preparation (n = 8, A) but is reduced to a constant value in medullary preparations (n = 7, B). In pre-BötC preparations (n = 7, C), PN burst frequency is reduced monotonically with increasing riluzole concentration, and rhythmogenesis is abolished at drug concentration ≤10 μM. All values represent means ± SD (error bars). *Statistical significance (P < 0.05). A1–C1: riluzole concentration-dependent attenuation of PN burst amplitude from representative preparations; pre-BötC population activity (C1, right) is also shown for pre-BötC preparation. Traces are averaged cycle-triggered waveforms (≥10 cycles) computed from integrated signals with onset of PN burst as trigger signal (vertical dashed lines).
In all medullary preparations generating a two-phase rhythm, low concentrations of riluzole (≤7.5 μM) eliminated ectopic bursting (Fig. 5) and stabilized the rhythm at a reduced (∼60% of control) burst frequency (n = 7; Fig. 6B); discharge amplitude and frequency were reduced further to ∼50% of control with progressive elevation of riluzole concentrations to the maximum tested (20 μM; Fig. 6, B and B1).
In contrast, in pre-BötC preparations (n = 7) generating a one-phase rhythm, there was a dose-dependent reduction in discharge frequency, and finally rhythmic activity was terminated at relatively low riluzole concentrations (≤10 μM; Fig. 6C). The discharge amplitude was less sensitive to riluzole but also was attenuated (∼50%) before loss of the rhythm (Fig. 6, C and C1). Recordings of pre-BötC population activity mirrored alterations of motor rhythm and amplitude with INaP blockade and verified complete loss of rhythmic activity in the pre-BötC coincident with the loss of motor output (Fig. 6C1). Without exception, rhythmic activity in the PN or pre-BötC could not be restored with hypoxic stimulation, elevations of CO2 and/or extracellular K+, or any combination of these stimuli.
Computational modeling of the brain stem respiratory network: model description
A computational model of the spatially distributed brain stem respiratory network was developed to reproduce the above experimental findings and suggest explanations for transformations of the rhythm-generating mechanism with sequential reduction of the network. The schematic of the model is shown in Fig. 7. The model includes the pons and three major medullary compartments: BötC, pre-BötC, and rVRG. Although some respiratory neuron types (e.g., post-I, aug-E) are not localized in particular compartments but rather distributed throughout the VRC, in our model, we assumed for simplicity that each medullary compartment contains only populations of respiratory neuron types that are known to be dominantly present in this compartment. The BötC compartment contains two populations of inhibitory expiratory neurons, the augmenting expiratory (aug-E) and the postinspiratory (post-I), which are both known to provide widely distributed inhibition within the medullary respiratory network during expiration (Ezure 1990; Ezure and Manabe 1988; Ezure et al. 2003; Fedorko and Merrill 1984; Jiang and Lipski 1990; Shen et al. 2003; Tian et al. 1999). In the model, these populations inhibit neural populations within the pre-BötC and rVRG and each other (Fig. 7). In addition, the BötC compartment contains an excitatory population [conditionally called post-I(e)] that contributes to the post-I component of cVN motor output. We assumed that all BötC neurons [comprising the post-I, post-I(e), and aug-E populations] have intrinsic adapting properties defined by the high-voltage activated calcium (ICaL) and calcium-dependent potassium (IK,Ca) currents in these neurons (see APPENDIX).
FIG. 7.
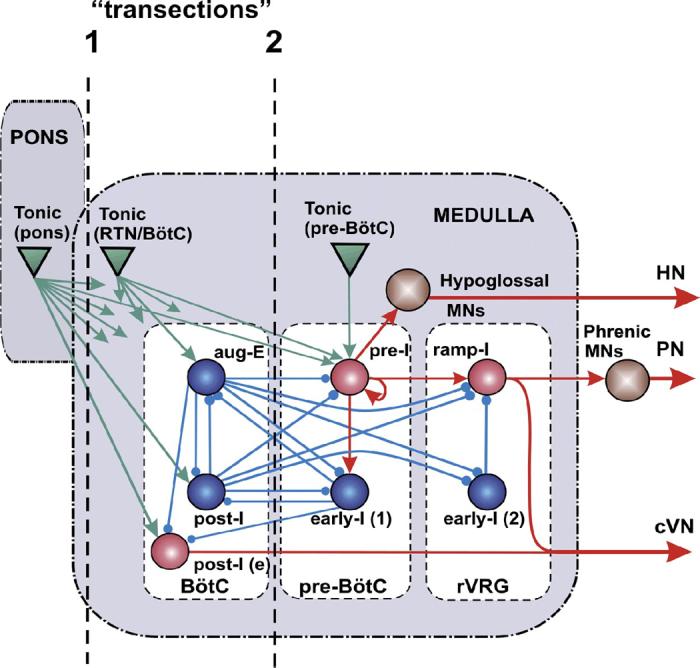
Schematic of the computational model of the brain stem respiratory network. Model includes interacting neuronal populations within major brain stem respiratory compartments (Pons, BötC, pre-BötC, and rVRG). Spheres represent neuronal populations (excitatory, red; inhibitory, blue; motoneuronal, brown); green triangles represent sources of tonic excitatory drives (in pons, RTN/BötC, and pre-BötC compartments) to different neural populations (only several drives are shown connected; for the full drive connections, see Table 3 in APPENDIX). Excitatory and inhibitory synaptic connections are indicated by arrows and small circles, respectively. Simulated “transections” (dashed lines) mimic those performed in situ.
The pre-BötC compartment includes two neural populations: pre-I and early-I(1) (Fig. 7). The pre-I population is the key excitatory population of pre-BötC that serves as a major source of inspiratory activity in the network. This population projects to the ramp-I population of premotor inspiratory neurons of rVRG and (through a hypoglossal premotor neural population not present in the model) to the hypoglossal motor output (HN). The pre-I population comprises excitatory neurons with INaP-dependent endogenous bursting properties (see APPENDIX) and mutual excitatory synaptic connections within the population. At a relatively low level of neuronal excitability or tonic excitatory drive, this population can operate in a bursting mode and intrinsically generate rhythmic bursting activity (Butera et al. 1999a,b; Rybak et al. 2003b, 2004b; Smith et al. 2000) that closely reproduces the population rhythmic bursting activity recorded from the pre-BötC in vitro (Johnson et al. 2001; Koshiya and Smith 1999). Previous modeling studies have shown that an increase in the average neuronal excitability or in external excitatory drive produces an increase in the burst frequency and, finally, switches population activity to the mode of tonic (asynchronous) spiking in the population. This was confirmed experimentally by an increase of extracellular potassium concentration in medullary slices containing the pre-BötC (Del Negro et al. 2001; Koshiya and Smith 1999; Rybak et al. 2003b). In this model under normal conditions, most neurons of this population operate in a tonic-spiking mode because of high tonic excitatory input and are inhibited by expiratory neurons (post-I, aug-E) during expiration.
The early-I(1) population of pre-BötC is a population of inhibitory interneurons with adapting properties (defined by ICaL and IK,Ca, see APPENDIX). This population receives excitation from the pre-I population and serves as a major source of inspiratory inhibition (Bianchi et al. 1995; Ezure 1990; Segers et al. 1987). In this model, this population inhibits all expiratory neurons during inspiration (Fig. 7).
The rVRG compartment contains the ramp-I, and early-I(2) populations (Fig. 7). Ramp-I is a population of excitatory premotor inspiratory neurons that project to phrenic motoneurons. Activity of this population defines phrenic motor output (PN) and the inspiratory component of cVN discharge. The major role of the inhibitory early-I(2) population (with adapting neurons containing ICaL and IK,Ca, see APPENDIX) in the model is in shaping the augmenting patterns of ramp-I neurons (Bianchi et al. 1995; Richter 1996; Segers et al. 1987).
The pons also contains specific compartments with multiple populations of neurons exhibiting various types of tonic and phasic respiratory modulated activities (Bianchi et al. 1995; Cohen 1979; Ezure and Tanaka 2006; Song and Poon 2004; St.-John 1998). These populations seem to have multiple specific uni- and bidirectional connections with particular VRC compartments (Bianchi et al. 1995; Ezure 2004; Ezure and Tanaka 2006; Song and Poon 2004), which allow the pons to control the timing of respiratory phase transitions and phase durations and contribute to respiratory reflexes (Alheid et al. 2004; Cohen and Shaw 2004; Okazaki et al. 2002; Song and Poon 2004; St.-John and Paton 2003). Our previous model (see Rybak et al. 2004a) included different populations of respiratory neurons in the rostral and caudal pons and considered uniand bidirectional interactions between pontine and VRC compartments and their role in control of respiratory phase durations, phase switching, and respiratory reflexes. However, for simplicity, and also to fit the current experimental studies described here (that did not include recording of pontine neurons and investigations of the effects of transections within the pons), only tonic excitatory drives from the pons to the VRC have been considered.
The behavior of the respiratory CPG depends on a variety of afferent inputs to different respiratory neurons that allow breathing to maintain the appropriate homeostatic levels of O2 and CO2 and adaptively respond to various metabolic demands. These inputs are modeled as “excitatory drives” that carry state-characterizing information provided by multiple sources distributed within the brain stem (pons, RTN, raphé, NTS), including those considered to be major chemoreceptor sites (sensing CO2/pH), and/or receiving input from peripheral chemoreceptors (sensing CO2/pH and low O2) (i.e., RTN, raphé, see Guyenet et al. 2005; Nattie 1999; Richerson 2004). Although currently undefined, these drives seem to have a certain spatial organization that maps specifically on the spatial organization of the brain stem respiratory network. These drives are conditionally represented in the model by three separate sources located in pons, RTN/BötC, and pre-BötC compartments (Fig. 7).
Modeling reorganization of rhythm generating mechanisms after brain stem transections
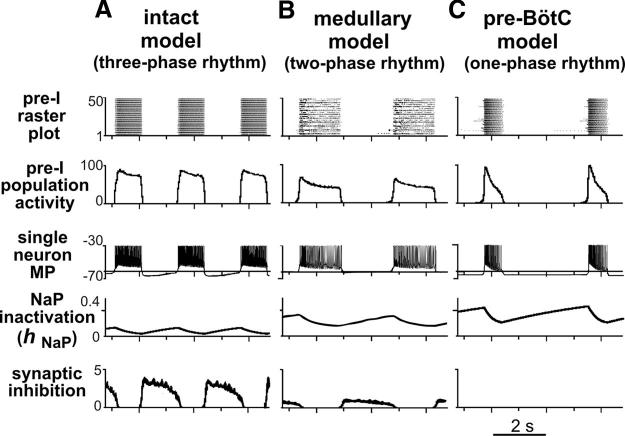
Figure 8, A, A1, and A2, shows the performance of the intact model. The activity of each population in Fig. 8A1 is represented by an average spike-frequency histogram of population activity. The post-I population of BötC shows decrementing activity during expiration. This population inhibits all other neuron populations in the model [except post-I(e)] during the first half of expiration (postinspiratory phase). With the progressive reduction of post-I inhibition from the adapting post-I neurons, the aug-E population starts firing later in expiration and forms a late expiratory (E2) phase. At the end of expiration, the pre-I population of pre-BötC is released from inhibition and activates the early-I(1) population that in turn inhibits all expiratory populations within the BötC. As a result, the ramp-I [and early-I(2); Fig. 7] population of rVRG is released from inhibition (with some delay relative to pre-I) and initiates the next inspiratory phase. During the inspiratory phase, the activity of the early-I(1) population of pre-BötC decreases providing a slow disinhibition of the post-I population of BötC. Once the post-I population starts firing, it inhibits all inspiratory activity completing the inspiratory off-switch. Then the process repeats. In summary, the three-phase respiratory rhythm in the intact model emerges from the mutual inhibitory interactions between early-I(1), post-I, and aug-E populations comprising a three-population ring structure (marked by gray shading in Fig. 8A), with the pre-I excitatory population participating in the onset of inspiration (Fig. 8A).
FIG. 8.
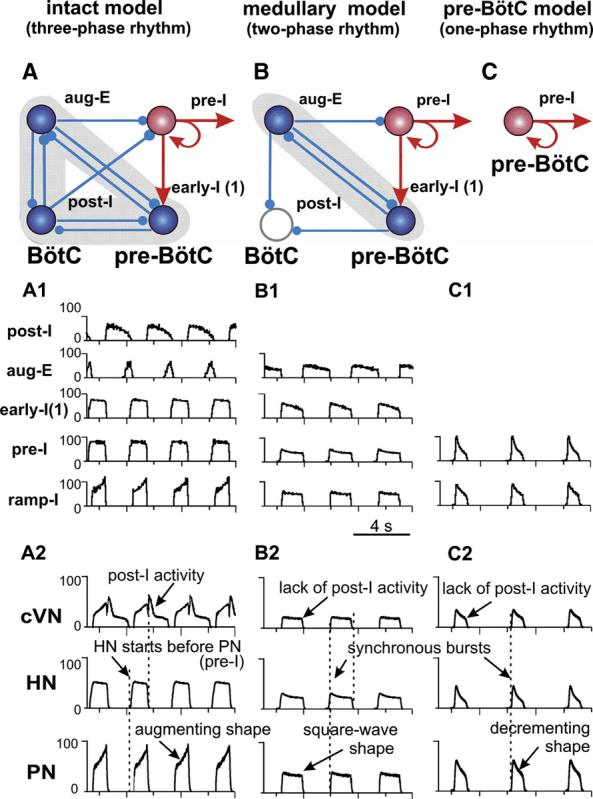
A–C: key elements and circuits within the intact (A), medullary (B), and pre-BötC (C) models involved in rhythmogenesis (excitatory drives are not shown; excitatory populations, red; inhibitory, blue). A1–C1: activity of selected neuronal populations in the model. Activity of each population is represented by a histogram of average neuronal spiking frequency within population (spikes/s/neuron, bin size = 30 ms). A2–C2: Motor outputs (cVN, HN, PN) in each model.
Motor output patterns (Fig. 8A2) and population activities (Fig. 8A1) in the intact model reproduce all major characteristics of the experimentally recorded three-phase respiratory pattern (for comparison, see Figs. 3A and 4A), including 1) an augmenting profile of ramp-I and PN inspiratory bursts; 2) a preinspiratory onset of bursts in the pre-I population of pre-BötC and HN (relative to PN); 3) a decrementing activity of post-I neurons in BötC and prominent post-I component in cVN bursts; and 4) an augmenting expiratory activity of BötC aug-E neurons.
To model perturbations caused by transections removing the pons, we removed the pontine excitatory drive (Fig. 7, transection 1), reducing the intact model to a medullary model. The performance of the medullary model is shown in Fig. 8, B, B1, and B2. Based on experimental evidence that stimulation of the dorsolateral pons (PB/KF region) provides strong activation of post-I neurons (Dutschmann and Herbert 2006; Rybak et al. 2004a), we suggested that a major portion of excitatory tonic drive to post-I neurons of BötC comes from the pons. In contrast, the aug-E population in the model is less dependent on pontine drive but receives a major excitatory drive from the RTN and other medullary sources. Thus in our model, removal of the pons reduces the excitability of post-I neurons relative to aug-E neurons so that the post-I population becomes fully inhibited by the aug-E population, which now exhibits a decrementing pattern (defined by ICaL and IK,Ca). Therefore the two-phase rhythm generated in the medullary model is based on an inhibitory half-center circuit of reciprocally interacting populations of adapting aug-E and early-I(1) neurons (see gray shading in Fig. 8B and neuronal activities in Fig. 8B1). In addition, elimination of pontine drive reduces the excitability and firing frequency of the pre-I and ramp-I populations, reducing the amplitude of all motor outputs (Fig. 8B2). The medullary model reproduces all major characteristics of the respiratory pattern recorded in the corresponding reduced preparations (Figs. 3B and 4B): 1) the loss of post-I activity in the network and cVN; 2) a reduced amplitude, square-wave-like/slightly decrementing profile of all inspiratory populations and motor bursts; and 3) synchronized onset of bursts in all motor outputs (Fig. 8B2).
The pre-BötC model (Fig. 7, transection 2) is characterized by a further reduction in tonic excitatory drive to the pre-I population of pre-BötC and loss of expiratory-related phasic inhibition (Fig. 7). These alterations switch the operating state of the pre-I population, which now generates endogenous bursting activity based on the expression of INaP and mutual excitatory interactions within the population (Butera et al. 1999b; Rybak et al. 2003b, 2004b; Smith et al. 2000) (Fig. 8C, C1). This pre-BötC activity with a decrementing burst shape now drives the activity of the rVRG and all motor outputs exhibit one-phase (inspiratory) oscillations with a decrementing burst shape (Fig. 8, C1 and C2), similar to that recorded from the pre-BötC preparation (Figs. 3C and 4C).
Testing the dependency of model performance on INaP
To study the role of INaP and compare model behaviors to experimental data obtained with the INaP blocker riluzole (Fig. 6, A-C), the mean maximal conductance of NaP channels (ḡNaP) was progressively reduced (to zero) in all pre-BötC (pre-I) neurons. As shown in Fig. 9A, a progressive reduction of ḡNaP in the intact network model causes only a small reduction in the amplitude and frequency of PN bursts. In the medullary model generating the two-phase rhythm, the oscillatory frequency and PN amplitude become more sensitive to INaP block because after removing pontine excitatory drive the mean level of INaP inactivation is reduced, enabling some participation of the pre-I population in the expiratory-inspiratory cycle dynamics. The two-phase rhythm, however, persists even at ḡNaP = 0 (Fig. 9B). In the pre-BötC model, the one-phase rhythm is generated solely by endogenous INaP-dependent bursting activity within the pre-I population of the pre-BötC (Fig. 8C). Therefore reducing ḡNaP progressively decreases PN burst frequency and finally abolishes the rhythm when ḡNaP becomes less than a critical value (Fig. 9C, 2.5 nS). These modeling results are fully consistent with our experimental data (Fig. 6, A-C).
FIG. 9.
Effects of reducing INaP on frequency and amplitude of motor output (PN) in the intact (A), medullary (B), and pre-BötC (C) models. Attenuation of INaP by riluzole in experiments is modeled by uniformly reducing the maximum conductance for the persistent sodium channels (ḡNaP) in all neurons of the pre-I population of pre-BötC. Effects of reducing ḡNaP on frequency (solid lines) and amplitude (dashed lines) of PN bursts (% control) closely reproduce experimental data shown in Fig. 5, A-C, including the initial decrease in frequency in the medullary preparation (B, cf. with Fig. 5B), and the decrease in burst frequency with decreasing ḡNaP and termination of rhythm generation (at ḡNaP = 2.5 nS) in the case of 1-phase rhythm (C, cf. with Fig. 5C). Reduction of burst amplitudes (dashed lines) is also consistent with experimental data, although perturbations in model are smaller than those observed experimentally.
Figure 10 presents a more detailed explanation for the differences in the dependence of rhythmogenesis on the pre-BötC INaP-dependent intrinsic mechanism in the intact and reduced models. In the intact model (Fig. 10A), strong pontine and RTN excitatory drives depolarize all neurons in the pre-I population and almost completely inactivate the voltage-dependent INaP in these neurons (see trace 4). In addition, these neurons receive strong phasic inhibition from BötC post-I (and aug-E) neurons (see bottom trace in Fig. 10A). Therefore the three-phase rhythm is generated primarily by inhibitory network interactions without critical involvement of the intrinsic INaP-based mechanism (Fig. 9A). In the medullary model (Fig. 10B), the total drive to the pre-I population is reduced (because of the removal of the pontine portion of total drive), and NaP channels become more active (see elevated hNaP values). Simultaneously, the elimination of pontine drive to post-I neurons reduces phasic inhibition to pre-I neurons (bottom trace). Therefore the INaP-dependent intrinsic mechanism starts contributing to excitability of the pre-I population and to the control of frequency and amplitude of motor outputs. However, network mechanisms (phasic inhibition from aug-E neurons) are still strong enough to maintain rhythm generation even when INaP is completely blocked (Fig. 9B). In the pre-BötC model (Fig. 10C), excitatory drive is further reduced, which allows full activation of INaP-dependent bursting properties (4th trace) and eliminates phasic inhibition (bottom trace). The intrinsic INaP-dependent bursting properties and mutual excitatory interactions within the pre-I population now completely define rhythmic activity (1-phase rhythm). This rhythm can be abolished by suppression of NaP currents (Fig. 9C).
FIG. 10.
Dynamics of pre-I population in the intact (A), medullary (B), and pre-BötC (C) models. Top traces are activity raster plots for all 50 neurons in the modeled pre-I population (each lines represents single neuron spiking, dots indicate spikes). The 2nd traces show average population activity histograms (number of spikes per second per neuron, bin = 30 ms); 3rd trace represents changes of membrane potential (MP, mV) in a representative single neuron (spikes are truncated at −30 mV); 4th trace shows changes of the NaP channel inactivation variable (hNaP) in the same representative neuron; 5th trace represents integrated synaptic inhibition that a single neuron receives (total postsynaptic inhibitory conductance in nS is plotted). In the intact model (A), strong pontine and RTN excitatory drive depolarizes all neurons in the pre-I population and almost completely inactivates the voltage-dependent INaP in these neurons (4th trace shows low values of hNaP, which makes NaP conductance ḡNaP to be very small). In addition, pre-I neurons receive strong phasic inhibition (bottom trace) from BötC post-I (and aug-E) neurons. Therefore the 3-phase rhythm is generated primarily by inhibitory network interactions without critical involvement of the intrinsic INaP-based mechanisms. In the medullary model (B), total drive to the pre-I population is reduced (because pontine drive is removed), and NaP channels become more active (see elevated hNaP values in 4th trace). Simultaneously, elimination of pontine drive to post-I neurons reduces phasic inhibition to pre-I neurons (bottom trace). INaP-dependent intrinsic mechanisms therefore start contributing to the excitability of the pre-I population and control the frequency and amplitude of motor outputs. However, network mechanisms (phasic inhibition from aug-E neurons) are strong enough to maintain rhythm generation even when INaP is completely blocked. In the pre-BötC model (C), excitatory drive is further reduced, which allows full activation of INaP-dependent bursting properties (4th trace) and eliminates phasic inhibition (bottom trace). Intrinsic INaP-dependent bursting properties and mutual excitatory interactions within pre-I population completely define rhythmic activity (1-phase rhythm).
Figure 11A represents our simulation of the changes of rhythm and pattern generated in the medullary preparation after transections through the caudal half of FN/RTN (Fig. 5). The medullary model was used, but the RTN drive in the medullary model was reduced by 50%. The reduction of this drive caused ectopic bursts similar to those recorded experimentally (Fig. 5). The raster plot of the pre-BötC pre-I population (top trace) shows that ectopic bursts seen in motor outputs originate from a subpopulation of neurons within the heterogeneous pre-I population. Figure 11B shows that attenuation of INaP, by reducing the average maximal conductance of NaP channels (ḡNaP) in the pre-I population, eliminates ectopic bursts and stabilizes the two-phase rhythm. These simulation results are fully consistent with our experimental findings (Fig. 5).
FIG. 11.
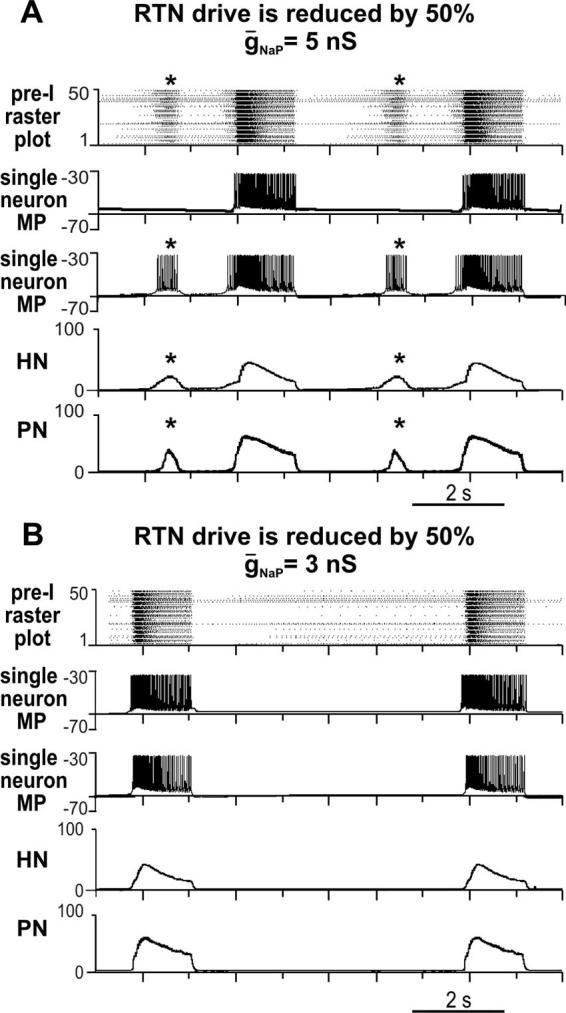
To simulate changes of rhythm and pattern generated in the medullary preparation after transections through caudal FN/RTN, the RTN drive in the medullary model (see Fig. 6) was reduced by 50%. A: reduction of RTN drive caused ectopic bursts (indicated by *) similar to those recorded experimentally (see Fig. 4). Raster plot of the pre-BötC pre-I population (top) shows that ectopic bursts seen in motor outputs (HN and PN activity histograms at bottom) originate from a subpopulation of neurons within heterogeneous pre-I population. Second trace shows membrane potential (MP, mV) of a single pre-I neuron that generates bursting only in synchrony with the main population. Third trace shows MP of another pre-I neuron that bursts with the ectopic subpopulation. B: similar to our experimental results (Fig. 4), attenuation of INaP, by reducing average maximal conductance of NaP channels (ḡNaP) in the pre-I population (from 5 to 3 nS), eliminates ectopic bursts and stabilizes 2-phase rhythm.
Pattern transformations with progressive reduction of Cl−-mediated synaptic inhibition
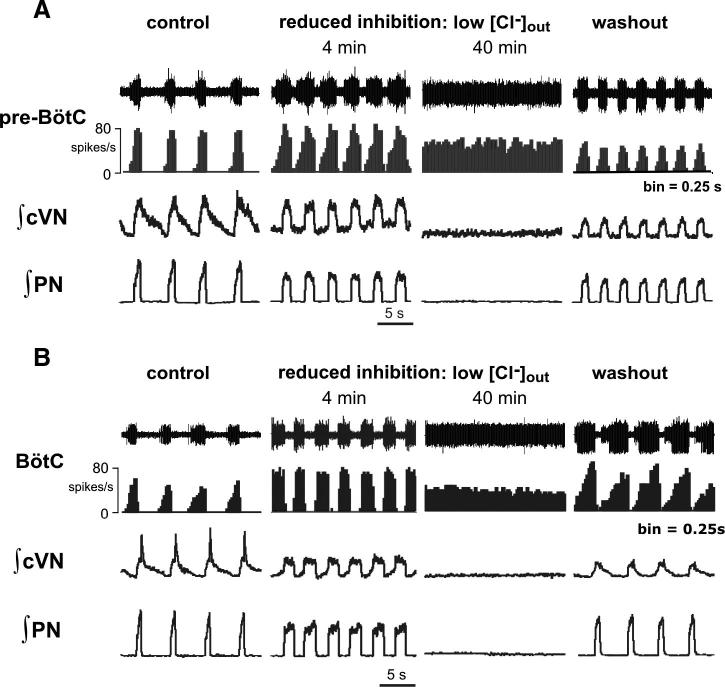
Our model predicted that the generation of the three- and two-phase rhythmic patterns is based on inhibitory synaptic interactions. Both glycine and GABA, known to be the major inhibitory neurotransmitters in the brain stem respiratory network (Büsselberg et al. 2001; Ezure et al. 2003; Haji et al. 2000; Paton and Richter 1995; Schreihofer et al. 1999), involve Cl−-mediated inhibition. Therefore to test the role of Cl−-mediated inhibition, we switched the normal perfusate in intact preparations to a solution containing reduced Cl− concentration (60, 40, or 20% of control concentrations in separate experiments: n = 6, n = 7, and n = 10, respectively; see methods). In all cases, after switching to the reduced Cl− perfusate, the three-phase motor output pattern transformed to a two-phase pattern. This transformation developed progressively with time reflecting a slow process of equilibration of the brain extracellular fluid to the reduced Cl− conditions. This transformation was accompanied by a loss of the post-I component in the cVN activity, a reduction of amplitudes of all motor outputs, and an alteration of the shapes of motor bursts similar to those occurring after brain stem transections (synchronous, square-wave-like inspiratory bursts of PN and cVN; Figs. 12, A and B, 2nd columns, and 13B). Further in time, rhythmic motor output terminated under the low Cl− conditions (Figs. 12, A and B, 3rd columns, and 13C).
FIG. 12.
Transition from 3- to 2-phase rhythmic pattern and subsequent termination of rhythm generation during progressive reduction of Cl−-mediated inhibition in situ. A: simultaneous recordings of raw and continuous histograms (0.25-s bins) of pre-BötC (pre-I) population (A) or BötC population aug-E (B) activity, integrated cVN, and PN activities before (left, control) and during perfusion (after 4 and 40 min; middle) with solution containing low Cl− concentration (20% of control solution) from 2 representative in situ preparations. Recordings show progressive transformation of activity patterns from a 3- to a 2- phase and subsequently to tonic activity patterns (pre-BötC and BötC) with progressive attenuation of Cl−-mediated inhibition. Transition to a 2-phase pattern after 4 min is associated with loss of post-I activity on cVN, transformation of PN and cVN inspiratory motor pattern (PN, cVN) to a square-wave-like profile, reduced cycle period, and augmentation of pre-I and aug-E population activities. This is comparable to that observed in medullary preparations. Partial recovery of the activity patterns is obtained after restoring perfusate to solution containing control Cl− concentration (right).
FIG. 13.
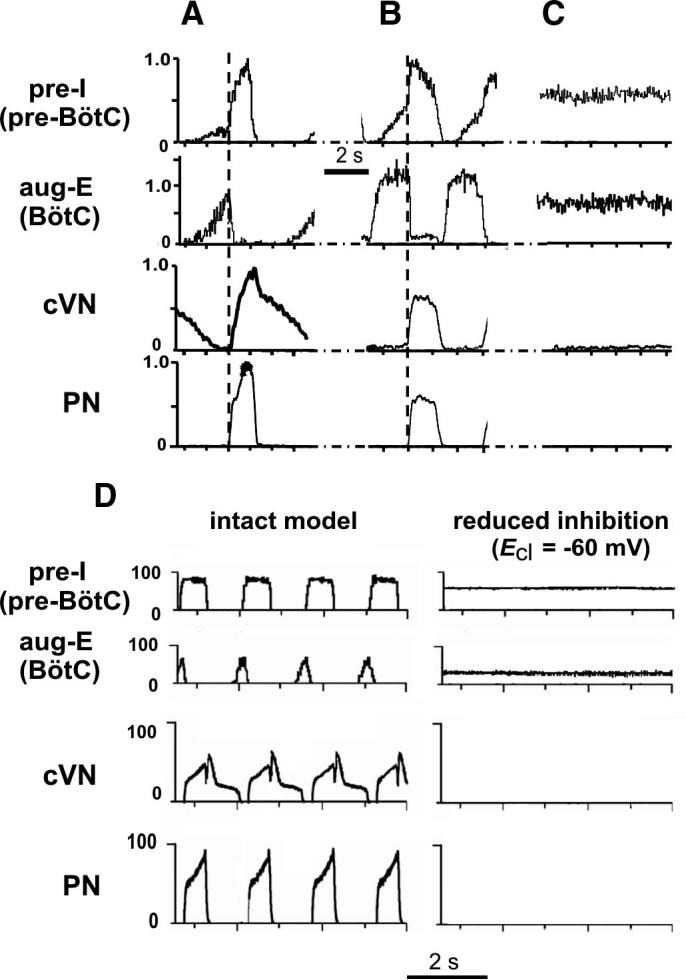
Composite cycle-triggered histograms of integrated PN, cVN, pre-BötC (pre-I), and BötC (aug-E) population activities showing temporal relationships and profiles of population activities under control conditions (A) and 8 min after switching perfusate to a solution containing 20% of control Cl− concentration (B). Square-wave-like profile and synchronous discharge of PN and cVN inspiratory activities, alternating with BötC E discharge is characteristic of the 2-phase rhythm. C: tonic activity state of pre-BötC pre-I and BötC aug-E population activity after 30 min of low Cl− conditions. Traces were obtained by averaging over 15 cycles from representative preparations and normalized to amplitudes under control conditions. Vertical dashed line, onset of PN activity was used as a trigger signal for histogram computation (bin = 30 ms). D: simulated activities of pre-I population of pre-BötC and aug-E population of BötC, cVN, and PN motor outputs obtained from intact model (left) and after reduction of inhibition in the network by changing ECl (ESynI) from −75 to −60 mV (right). Similar to our experimental results (A and C), reduction of inhibition abolished rhythmic activity in PN and cVN motor outputs and produced sustained activity in pre-I and aug-E populations.
Recordings of aug-E activity in the BötC (n = 6) and pre-I activity in the pre-BötC (n = 8) during perfusion with low Cl− showed a progressive expansion of pre-I activity into the E phase and aug-E activity into the post-I phase. As a result, the post-I discharge was fully abolished indicating the transition to a two-phase rhythm generating state (Fig. 12, A and B, 2nd columns). In this state, E-discharge occurred throughout the E phase, alternating with square-wave-like inspiratory activity (see Figs. 12, A and B, and 13B for quantitative analysis of population spiking profiles) similar to that observed in a two-phase rhythm obtained by brain stem transections. With time, this E activity progressively encroached on the inspiratory phase, until both BötC E and pre-BötC population activities became tonic, indicating severe reduction of Cl−-mediated inhibition that fully terminated rhythm generation (Figs. 12, A and B, 3rd columns, and 13C).
Figure 12, A and B, shows the results of separate experiments in which rhythm and pattern transformations were obtained with a perfusate solution containing 20% of control Cl− concentration. With this perfusate, the transition to a two-phase rhythm occurred on average within 4 min, and the termination of rhythmic activities was observed within 30–40 min. In experiments with perfusate solutions containing 60 or 40% of control Cl− concentrations, the sequential pattern transformation described above was consistently observed as well, but the times to the three- to two-phase rhythm transition and to the subsequent termination of rhythmic activity were progressively longer (∼1.5 and 2 times longer at 60 and 40% Cl− solutions, respectively). In all cases, rhythmic activity was restored when the perfusate was replaced with the control solution, although, after the 20% Cl− perfusate, we could typically achieve only partial recovery of the normal pattern and discharge amplitudes (Fig. 12, A and B, right columns).
To simulate the effect of reduction of chloride-based inhibition by lowering extracellular Cl− concentration ([Cl−]out), the chloride reversal potential in the model (ECl = ESynI) was changed from −75 to −60 mV (to be equal to the average neuronal resting potential), which, according to the Nernst equation and with the temperature T = 305 K (used in the experimental preparation), approximately corresponds to a 50% decrease of [Cl−]out. The results of simulation are shown in Fig. 13D. Similar to our experimental results (Figs. 12, A and B, 3rd columns, and 13C), changing ECl to −60 mV abolished rhythmic activity in PN and cVN motor outputs and produced sustained activity in the aug-E population of BötC and the pre-I population of pre-BötC (Fig. 13D, right). However, the model did not reproduce the transition from the three-phase to a two-phase rhythm after a smaller reduction of inhibition if the latter was applied uniformly to all neuronal populations in the model. The direct simulation of this transition, as observed in our experiments, is difficult because the reduced inhibition during perfusion of low Cl− solutions may provide different effects on different populations of respiratory neurons and/or has different time courses, which are currently unknown.
DISCUSSION
Previous theories postulated different models for the functional organization of brain stem respiratory networks. These include three-phase models involving predominantly inhibitory network interactions (Richter 1996; Richter and Spyer 2001; Rybak et al. 1997b), hybrid pacemaker-network models (Rybak et al. 2004a; Smith et al. 2000) in which the pre-BötC with autorhythmic properties is dynamically controlled by inhibitory networks, a dual pacemaker model (Ramirez et al. 2004), and more recently, an alternating inspiratory-expiratory two oscillator model (Feldman and Del Negro 2006; Janczewski and Feldman 2006). However, the actual spatial and dynamical organization of the brain stem respiratory network has not been unequivocally defined.
Our experimental approach was based on precision transverse sectioning of the perfused brain stem in situ. Although such transections may be considered crude interventions with potential disadvantages (e.g., they may disrupt connections across the midline, see Long and Duffin 1986), starting with Lumsden's (1923) classical experiments, this technique has yielded important results and insights into respiratory network spatial organization, including, but not limited to, the discovery of the pre-Bötzinger complex (Smith et al. 1991). In contrast to earlier in vivo studies, the use of perfused in situ preparations allowed us to maintain perfusion pressure and avoid the detrimental consequences of hemorrhage and hypotension that would have caused alterations in blood gases and pH within the brain stem. In addition, we were able to avoid the direct deleterious effects that hemorrhaged blood could have on brain tissues. Because of the relatively high spatial resolution of our cutting system, we were able to systematically perform serial sections and very accurately reconstruct the spatial boundaries associated with generation of the distinct motor patterns found. Furthermore, we were able to readily obtain recordings of neuron population activities for analysis of activity patterns before and after transections.
At the same time, our approach of sequentially reducing the pontine-medullary network, coupled with analysis of network activity patterns and probing for pre-BötC autorhythmic mechanisms, has provided a new unified view that integrates several of the earlier models (Richter and Spyer 2001; Rybak et al. 2004a; Smith et al. 2000). We found a spatial and dynamical hierarchy of interacting pontine, BötC, and pre-BötC circuits, each of which controls different aspects of rhythm generation and pattern formation, which are revealed as the system is progressively reduced. We propose that the expression of each rhythmogenic mechanism is state-dependent and produces specific motor patterns appropriate for a distinct behavior. Our results suggest the existence of a special rostral-caudal spatial architecture and three distinct rhythmogenic mechanisms that can be expressed in different states of a mammalian CPG. Such detailed structure-function relationships have previously been determined only for selected invertebrate and lower vertebrate central pattern generation circuits (Grillner 2006; Marder and Calabrese 1996; Selverston and Ayers 2006). Our computational model realistically reproduces the experimental results presented here and suggests mechanistic explanations for the proposed concepts. We note, however, that because of the lack of some specific data, the model is based on a series of assumptions and remains hypothetical. Further experiments are necessary to test model predictions and elaborate the model.
Three-phase rhythm: role of the pons and network inhibitory interactions
The in situ perfused mature rat brain stem–spinal cord preparation generates a three-phase respiratory pattern similar to that recorded in vivo (Paton et al. 2006; St.-John and Paton 2003). According to our model, this rhythm involves reciprocal inhibitory interactions between post-I, aug-E, and early-I(1) neurons operating in a ring-like network architecture, with the pre-BötC excitatory network participating dynamically in E-I phase transitions and inspiratory phase generation. Removal of pontine circuits transforms this pattern to the two-phase rhythm without postinspiratory activity and postinspiratory phase. Thus we conclude that pontine input to medullary circuits contributes significantly to postinspiratory activity. Moreover, our model suggests that this contribution occurs through pontine activation of inhibitory BötC post-I neurons, which is consistent with previous findings (Dutschmann and Herbert 2006; Rybak et al. 2004a).
Our results with progressive attenuation of Cl−-mediated inhibition confirm that the three-phase rhythm critically depends on inhibitory interactions (see also Hayashi and Lipski 1992). Our results are also consistent with the previous findings that blockade of glycinergic inhibition in situ eliminates post-I activity and transforms the three-phase to a two-phase pattern (Büsselberg et al. 2001; Dutschmann and Paton 2002). Lowering the extracellular chloride concentration ([Cl−]out) depolarizes (shifts to more positive values) the chloride reversal potential (ECl), which reduces the driving force for inhibitory synaptic currents and hence reduces inhibitory postsynaptic potentials (IPSPs) in all neurons. The results of our experiments suggest that this suppression of IPSPs affects the aug-E neurons more strongly and/or earlier than the post-I neurons. As a result, the balance of the mutual inhibition between post-I and aug-E neurons shifts to a domination of aug-E neurons, which inhibit post-I activity and finally produce the switch to a two-phase rhythm. One possible explanation for this imbalance may be that input resistance of aug-E neurons is generally higher than that of post-I neurons. However, the above change in the inhibitory balance may result from many, currently unknown, intrinsic and/or extrinsic factors (e.g., differences in kinetics or sensitivity of glycine vs. GABAA receptors, different resting membrane potentials, effects of different membrane currents, different neuron morphology, and different inputs from other neurons, e.g., from early-I); it is therefore currently difficult to propose a definitive mechanistic explanation for this phenomenon.
Based on our studies, we propose that the state and operating conditions of the pre-BötC excitatory network are controlled by multiple excitatory drives from the pons, RTN, and raphé. Our model suggests that an INaP-dependent mechanism operating in pre-BötC is not critically involved in three-phase respiratory rhythm generation. Because of the specific voltage-dependent inactivation of INaP, this current is significantly inactivated by excitatory drives during inspiration and is dynamically reset by phasic inhibition during expiration.
Our results agree with previous experimental results that input from pontine circuits shape the respiratory pattern and specifically controls the durations of expiration (through activation of the post-I neurons; Dutschmann and Herbert 2006) and inspiration (through control of inspiratory off-switch mechanisms; Alheid et al. 2004; Cohen and Shaw 2004; Okazaki et al. 2002; Rybak et al. 2004a; Song and Poon 2004; St.-John and Paton 2003).
Two-phase rhythm and rhythmogenic mechanisms
Our results showed that, in the absence of pontine input (after removal of the pons by brain stem transections), medullary circuits generate two-phase oscillations involving BötC expiratory activity alternating with pre-BötC inspiratory activity. These results are consistent with the critical role of the BötC as a major source of expiratory activity in the respiratory network (Ezure 1990; Ezure and Manabe 1988; Jiang and Lipski 1990; Shen et al. 2003; Tian et al. 1999). Our model proposes that the two-phase rhythm results mechanistically from inhibitory interactions between the expiratory BötC (aug-E) and early-I(1) pre-BötC populations, which together form the active reciprocal inhibitory half-center structure remaining after removing post-I neuronal activity. The proposed mechanism for two-phase rhythm generation is therefore similar to that proposed earlier by Duffin (1991).
We acknowledge, however, that because it was not possible to maintain continuous recordings of aug-E neurons during transection of the pons, we cannot be certain that aug-E neurons of the BötC, rather than post-I neurons, form the expiratory discharge in the two-phase rhythm. However, this suggestion is consistent with the observations that post-I activity in the medulla and in cVN motor output is enhanced by pontine input and reduced or eliminated by the pharmacological suppression or removal of the rostral pons (Dutschmann and Herbert 2006; Rybak et al. 2004a). Therefore because of the mutual inhibition between the post-I and aug-E populations, a reasonable expectation is that the reduction of post-I activity with the removal of the pons enhances the activity of the aug-E population, which further suppresses post-I activity in the network.
In contrast to the transection experiments, the recordings could be maintained when the transitions from a three-phase to a two-phase rhythm were induced by low Cl− perfusion. In such cases (see example in Fig. 12B), the loss of post-I activity in the cVN motor output (3rd trace in Fig. 12B) was accompanied by a change of expiratory activity recorded from the BötC from an augmenting to a constant/decrementing activity pattern (see the 2nd trace). This provides support for the mechanism suggested above. Finally, we showed that the two-phase rhythm is disrupted by further attenuation of Cl−-mediated inhibition, which provides additional support for a critical role of inhibition in the two-phase rhythm generation.
A two-oscillator hypothesis has been proposed (Feldman and Del Negro 2006; Janczewski and Feldman 2006; Onimaru and Homma 2003; Onimaru et al. 1988) that suggests the existence of a separate rhythm generator located in the parafacial respiratory group (pFRG). Moreover, it has been hypothesized that this separate generator in pFRG may operate as an independent generator of expiratory activity. This hypothesis remains controversial. However in any case, this hypothesis cannot explain the two-phase oscillations that we found, because the latter persist after removal of pFRG and hence do not require involvement of neural circuits from this region. Moreover, in our experiments, we never observed rhythmic expiratory oscillations occurring independently of rhythmic inspiratory activity. The pFRG may provide yet another (4th) oscillatory mechanism that can be expressed under specific conditions (Janczewski and Feldman 2006). The possible role of the pFRG (which is partially coextensive with RTN), in respiratory oscillations generated under different conditions is not yet clear. Generally, RTN neurons have chemosensory properties and project to most medullary compartments including BötC, pre-BötC, and rVRG, providing excitatory drive to multiple medullary respiratory neuron types (Guyenet et al. 2005; Mulkey et al. 2004; Nattie 1999). This role of RTN neurons seems to be opposed to the concept of an expiratory oscillator in the pFRG (Feldman and Del Negro 2006; Janczewski and Feldman 2006), unless the pFRG and the chemosensory RTN neurons represent functionally separate populations of cells. This issue, however, requires further study and will be considered in more detail in a future publication.
We note that the two-phase rhythm usually became unstable when transections were made through the caudal half of facial nucleus, which may reflect the loss of RTN chemosensory excitatory drive. We have incorporated this excitatory drive in our models, and accordingly, we viewed the RTN as a separate functional compartment providing a critical source of drive.
One-phase rhythmogenic mechanisms in the pre-BötC
The pre-BötC was proposed to be a “kernel” structure (Rekling and Feldman 1998; Smith et al. 1991, 2000) with INaP-dependent autorhythmic properties and to play a central role in generating neonatal inspiratory activity in vitro (Butera et al. 1999a,b; Smith et al. 2000). We have now confirmed these properties for the mature rodent nervous system. When isolated from more rostral structures in situ, the pre-BötC generated a one-phase inspiratory rhythm, similar to that generated by the isolated neonatal pre-BötC in vitro (Del Negro et al. 2001; Johnson et al. 2001; Koshiya and Smith 1999). This rhythm was highly sensitive to blockade of INaP by riluzole, which progressively reduced the oscillation frequency and finally eliminated the rhythm at drug concentrations shown to block INaP in pre-BötC neurons (Del Negro et al. 2005; Paton et al. 2006) and terminate inspiratory oscillations in vitro (Koizumi and Smith 2002; Rybak et al. 2003b).
Our previous study showed that INaP-dependent neuronal oscillations can be found in the pre-BötC of intact in situ preparations under normal conditions, and they become critically involved in rhythm generation under extreme hypoxic conditions (Paton et al. 2006). Here we present data indicating involvement of INaP in rhythmogenesis in reduced preparations under normoxic conditions. Furthermore, after blocking INaP in the reduced pre-BötC preparations, we could not reactivate the one-phase inspiratory activity by stimulation of peripheral or central chemosensory mechanisms—the most potent physiological activators of pre-BötC activity in situ. These results are not consistent with recent suggestions that INaP-dependent mechanisms do not play a role in rhythm generation in the pre-BötC (Del Negro et al. 2002b, 2005; Pace et al. 2007). However, our data do not allow us to exclude the possibility that, after more rostral brain stem regions have been sectioned off, the rhythmogenic neurons receive an essential excitatory drive from remaining tonically active neurons (such as those located in raphé nuclei), whose activity may be also reduced by riluzole (Pace et al. 2007). This mechanism, if it really operates in the in situ system, may play a role in the riluzole concentration-dependent reduction of inspiratory burst frequency in the pre-BötC preparation. However, this does not exclude the essential role of INaP-dependent intrinsic mechanisms operating within the pre-BötC as suggested by our study. INaP is a ubiquitous property of pre-BötC neurons (Del Negro et al. 2002a; Rybak et al. 2003a), and the presence of INaP-dependent neuronal bursting in the pre-BötC has been shown in our in situ preparations (Paton et al. 2006). This issue requires further study and will be considered in another publication. In any case, our results suggested that the role of INaP-dependent mechanisms becomes increasingly important when the reduced levels of drive from other structures alter the dynamic state of the pre-BötC and its interactions with expiratory inhibitory populations.
Insights into the organization of the brain stem respiratory network
Based on our experimental and modeling studies, we propose that the pontine-medullary respiratory network has a specific hierarchical spatial organization extending from rostral pons to the rVRG. Although some respiratory neuron types (e.g., post-I, aug-E, early-I) are not strictly localized within particular medullary compartments, but rather distributed throughout the VRC, each compartment contains dominant populations that may define the specific functional role of this compartment. Each compartment in this structure operates under control of more rostral compartments. Specifically, inspiratory activity of rVRG bulbospinal premotor neurons, located at the caudal end of this structure, is formed by excitatory inspiratory synaptic drive from the pre-BötC excitatory neurons and phasic inhibition from BötC expiratory neurons. The pre-BötC is controlled in turn by more rostral compartments—the BötC that inhibits the pre-BötC during expiration, and the RTN and pontine nuclei, which provide excitatory drives to BötC, pre-BötC, and rVRG. The pontine activation of expiratory BötC populations (especially post-I neurons) provides a widely distributed inhibition within the network during expiration, which seems critical for rhythm and pattern generation under normal conditions. In addition, the pons and RTN control the excitability and hence the level of expression of intrinsic INaP-dependent mechanisms within the pre-BötC. With a reduction of these drives, the system can be switched to the state in which endogenous INaP-dependent mechanisms emerge.
Functional significance of multiple oscillatory modes
Our results indicate that the brain stem respiratory CPG incorporates at least three oscillatory mechanisms. We used extreme experimental manipulations to uncover these rhythm-generating states. We suggest, however, that similar states can occur under different physiological and pathophysiological conditions. Changes in metabolic conditions (levels of carbon dioxide/pH, or oxygen) that alter the balance of excitatory/inhibitory drives and excitability of pontine, BötC, and pre-BötC populations, may change network interactions and produce transformations from a three- to the two- or one-phase rhythms. Specifically, severe hypoxia switches the respiratory system to generation of a one-phase, INaP-dependent gasping rhythm (Paton et al. 2006) that represents a functional un-embedding of INaP-dependent intrinsic oscillations of the pre-BötC. Other studies have shown that hypocapnia can convert the respiratory network to generation of two-phase oscillations (Sun et al. 2001), which we have confirmed (Abdala, Smith, Rybak, and Paton, unpublished observations). Furthermore, the pre-BötC alone may have several modes of inspiratory rhythm generation (Lieske et al. 2000; Purvis et al. 2007).
We conclude that the respiratory network has rhythmogenic capabilities at multiple levels of cellular and network organization. It remains to be established how the brain alters cellular properties and network interactions within the respiratory CPG to transform the respiratory rhythm and pattern to adapt to different physiological states and metabolic conditions.
Acknowledgments
GRANTS
This study was supported by National Institute of Neurological Disorders and Stroke Grant R01 NS-057815 (and partly by Grant RO1 NS-048844) and in part by the Intramural Research Program of the National Institute of Neurological Disorders and Stroke. J.F.R. Paton is the recipient of a Royal Society Wolfson Research Merit Award.
APPENDIX
Single neuron descriptions
All neurons were modeled in the Hodgkin-Huxley style as single-compartment models
| (1) |
where V is the membrane potential, C is the membrane capacitance, and t is time. The terms in the right part of this equation represent ionic currents: INa, fast sodium (with maximal conductance ḡNa); INaP, persistent (slow inactivating) sodium (with maximal conductance ḡNaP); IK, delayed-rectifier potassium (with maximal conductance ḡK); ICaL, high-voltage activated calcium-L (with maximal conductance ḡCaL); IK,Ca, calcium-dependent potassium (with maximal conductance ḡK,Ca); IL, leakage (with constant conductance gL); ISynE (with conductance gSynE) and ISynI (with conductance gSynI), excitatory and inhibitory synaptic currents, respectively.
Currents are described as follows
| (2) |
where ENa, EK, ECa, EL, ESynE, and ESynI are the reversal potentials for the corresponding channels.
Variables mi and hi with indexes indicating ionic currents represent, respectively, the activation and inactivation variables of the corresponding ionic channels. Kinetics of activation and inactivation variables is described as follows
| (3) |
The expressions for steady-state activation and inactivation variables and time constants are shown in Table 1. The value of maximal conductances for all neuron types are shown in Table 2.
TABLE 1.
Steady-state activation and inactivation variables and time constants for voltage-dependent ionic channels
| Ionic channels |
m∞(V), V, in mV; τm(V), ms; h∞(V), V, in mV; τh(V), ms |
|---|---|
| Fast sodium (Na) |
m∞Na = 1/{1 + exp[−(V + 43.8)/6]}; τmNa = τmNamax/cosh[(V + 43.8)/14], τmNamax = 0.252. h∞Na = 1/{1 + exp[(V + 67.5)/10.8]}; τhNa = τhNamax/cosh[(V + 67.5)/12.8], τhNamax = 8.456. |
| Persistent sodium (NaP) |
m∞NaP = 1/{1 + exp[−(V + 47.1)/3.1]}; τmNaP = τmNaPmax/cosh[(V + 47.1)/6.2], τmNaPmax = 1. h∞NaP = 1/{1 + exp[(V + 60)/9]}; τhNaP = τhNaPmax/[cosh(V + 60)/9], τhNaPmax = 5,000. |
| Delayed rectifier potassium (K) |
α∞K = 0.01·(V + 44)/{1 − exp[−(V + 44)/5]}; β∞K = 0.17·{exp[ − (V + 49)/40]}; m∞K = α∞K/(α∞K + β∞K); τmK = τmK max/(α∞K + β∞K), τmK max = 1. |
| High-voltage–activated calcium (CaL) |
m∞CaL = 1/(1 + exp[−(V + 27.4)/5.7)]; τmCaL = 0.5. h∞CaL = 1/{1 + exp[(V + 52.4)/5.2]}; τhCaL = 18. |
| Calcium-dependent potassium [K(Ca2+)] |
α∞K,Ca = 1.25 · 108 · [Ca]i2, β∞K,Ca = 2.5; m∞K,Ca = α∞K,Ca/(α∞K,Ca + β∞K,Ca); τ∞K,Ca = τmK,Camax · 1000/(α∞K,Ca + β∞K,Ca), τmK max = 1–8. |
TABLE 2.
Maximal conductances of ionic channels in different neuron types
| Neuron Type | ḡNa, nS | ḡNaP, nS | ḡK, nS | ḡCaL, nS | ḡK,Ca, nS | ḡL, nS |
|---|---|---|---|---|---|---|
| Pre-I | 170 | 5.0 | 180 | 2.5 | ||
| Post-I | 400 | 250 | 6.0 | |||
| All others | 400 | 250 | 0.05 | 3.0–6.0 | 6.0 |
The kinetics of intracellular calcium concentration Ca is described as follows (Rybak et al. 1997a)
| (4) |
where the first term constitutes influx (with the coefficient kCa) and buffering (with the probability PB), and the second term describes pump kinetics with resting level of calcium concentration Ca0 and time constant τCa
| (5) |
where B is the total buffer concentration and K is the rate parameter.
The calcium reversal potential is a function of Ca
| (6) |
The excitatory (gSynE) and inhibitory synaptic (gSynI) conductances are equal to zero at rest and may be activated (opened) by the excitatory or inhibitory inputs, respectively
| (7) |
where the function S{x} = x, if x ≥ 0, and 0, if x < 0. In Eq. 7, each of the excitatory and inhibitory synaptic conductances has two terms. The first term describes the integrated effect of inputs from other neurons in the network (excitatory and inhibitory, respectively). The second term describes the integrated effect of inputs from external drives dmi. Each spike arriving to neuron i from neuron j at time tkj increases the excitatory synaptic conductance by ḡE · wji if the synaptic weight wji > 0 or increases the inhibitory synaptic conductance by − ḡI · wji if the synaptic weight wji < 0. ḡE and ḡI are the parameters defining an increase in the excitatory or inhibitory synaptic conductance, respectively, produced by one arriving spike at |wji| = 1. τSynE and τSynE are the decay time constants for the excitatory and inhibitory conductances, respectively. In the second terms of Eq. 7, ḡEd and ḡEd are the parameters defining the increase in the excitatory or inhibitory synaptic conductance, respectively, produced by external input drive dmi = 1 with a synaptic weight of |wdmi| = 1. All drives were set equal to 1. The relative weights of synaptic connections (wji and wdmi) are shown in Table 3.
TABLE 3.
Weights of synaptic connections in the network
| Target population (location) | Excitatory drive {weight of synaptic input} or source population {weight of synaptic input from single neuron} |
|---|---|
| Ramp-I (rVRG) | drive(pons) {2.0}; early-I(2) {−0.275}; pre-I {0.06}; aug-E{−2.0}; post-I {−1.0}. |
| Early-I(2) (rVRG) | drive(pons) {1.7}; aug-E {−0.25}; post-I {−1.0}. |
| Pre-I (pre-BötC) | drive(pre-BötC) {0.3}; drive(RTN/BötC) {0.13}; drive(pons) {0.55}; pre-I {0.03}; aug-E {−0.025}; post-I {−0.225}. |
| Early-I(1) (pre-BötC) | drive(RTN/BötC) {0.7}; drive(pons) {1.1}; pre-I {0.034}; aug-E {−0.145}; post-I {−0.4}. |
| Aug-E (BötC) | drive(RTN/BötC) {1.0}; drive(pons) {0.4}; early-I(1) {−0.115}; post-I {−0.32}. |
| Post-I (BötC) | drive(RTN/BötC) {0.1}; drive(pons) {1.5}; early-I(1) {−0.04}; aug-E {−0.01}. |
| Post-I (e) (BötC) | drive(RTN/BötC) {0.1}; drive(pons) {1.0}; early-I(1) {−0.2}; aug-E {−0.15}. |
Values in figure brackets represent relative weights of synaptic inputs from the corresponding source populations (wji) or drives (wdmi); see Eq. 7. Abbreviations: ramp-I, ramp-inspiratory; rVRG, rostral ventral respiratory group; early-I, early-inspiratory; pre-I, preinspiratory; pre-BötC, pre-Bötzinger Complex; aug-E, augmenting expiratory; post-I, postinspiratory.
Neuronal parameters
Capacitance: C = 36 pF. Reversal potentials: ENa = 55 mV; EK = −94 mV; ESynE = 0 mV; ESynI = ECl = −75 mV. To provide heterogeneity of neurons within neural populations, the value of EL was randomly assigned from normal distributions using average value ± SD. Leakage reversal potential for all neurons (except for pre-I) EL = −60 ± 1.2 mV; for pre-I neurons, EL = −68 ± 1.36 mV. Synaptic parameters: ḡE = ḡI = ḡEd = ḡId = 1.0 nS; τSynE = 5 ms; τSynI = 15 ms. Parameters of calcium kinetics: Ca0 = 5 × 10−5 mM; kCa = 5.18 × 10−8 mM/C; τCa = 500 ms, B = 0.030 mM; K = 0.001 mM. The motoneuron populations have not been modeled. Integrated activities of the ramp-I and pre-I population were considered as PN and XII motor outputs, respectively. The weighted sum of integrated activities of the ramp-I (1/3) and the post-I(e) (2/3) populations was considered as cVN motor output.
Modeling neural populations
In this model, each functional type of neuron is represented by a population of 50 neurons. Connections between the populations were established so that, if a population A was assigned to receive an excitatory or inhibitory input from a population B or external drive D, each neuron of population A received the corresponding excitatory or inhibitory synaptic input from each neuron of population B or from drive D, respectively. The heterogeneity of neurons within each population was set by a random distribution of EL (mean values ± SD) and initial conditions for values of membrane potential, calcium concentrations, and channel conductances. In all simulations, initial conditions were chosen randomly from a uniform distribution for each variable, and a settling period of 20 s was allowed in each simulation before data were collected. Each simulation was repeated 20–30 times and showed qualitatively similar behavior for particular values of the SD of EL and initial conditions.
REFERENCES
- Alheid GF, Milsom WK, McCrimmon DR. Pontine influences on breathing: an overview. Respir Physiol Neurobiol. 2004;143:105–114. doi: 10.1016/j.resp.2004.06.016. [DOI] [PubMed] [Google Scholar]
- Bianchi AL, Denavit-Saubie M, Champagnat J. Central control of breathing in mammals: neuronal circuitry, membrane properties, and neurotransmitters. Physiol Rev. 1995;75:1–45. doi: 10.1152/physrev.1995.75.1.1. [DOI] [PubMed] [Google Scholar]
- Büsselberg AM, Bischoff AM, Paton JFR, Richter DW. Reorganization of respiratory network activity after loss of glycinergic inhibition. Eur J Physiol. 2001;441:444–449. doi: 10.1007/s004240000453. [DOI] [PubMed] [Google Scholar]
- Butera RJ, Rinzel JR, Smith JC. Models of respiratory rhythm generation in the pre-Bötzinger complex: I. Bursting pacemaker neurons. J Neurophysiol. 1999a;82:382–397. doi: 10.1152/jn.1999.82.1.382. [DOI] [PubMed] [Google Scholar]
- Butera RJ, Rinzel JR, Smith JC. Models of respiratory rhythm generation in the pre-Bötzinger complex: II. Populations of coupled pacemaker neurons. J Neurophysiol. 1999b;82:398–415. doi: 10.1152/jn.1999.82.1.398. [DOI] [PubMed] [Google Scholar]
- Cohen MI. Neurogenesis of respiratory rhythm in the mammal. Physiol Rev. 1979;59:1105–1173. doi: 10.1152/physrev.1979.59.4.1105. [DOI] [PubMed] [Google Scholar]
- Cohen MI, Shaw C-F. Role in the inspiratory off-switch of vagal inputs to rostral pontine inspiratory-modulated neurons. Respir Physiol Neurobiol. 2004;143:127–140. doi: 10.1016/j.resp.2004.07.017. [DOI] [PubMed] [Google Scholar]
- Del Negro CA, Johnson SM, Butera RJ, Smith JC. Models of respiratory rhythm in the pre-Bötzinger complex: III. Experimental tests of model predictions. J Neurophysiol. 2001;86:59–74. doi: 10.1152/jn.2001.86.1.59. [DOI] [PubMed] [Google Scholar]
- Del Negro CA, Koshiya N, Butera RJ, Smith JC. Persistent sodium current, membrane properties and bursting behavior of pre-Bötzinger complex inspiratory neurons in vitro. J Neurophysiol. 2002a;88:2242–2250. doi: 10.1152/jn.00081.2002. [DOI] [PubMed] [Google Scholar]
- Del Negro CA, Morgado-Valle C, Feldman JL. Respiratory rhythm: an emergent network property? Neuron. 2002b;34:821–830. doi: 10.1016/s0896-6273(02)00712-2. [DOI] [PubMed] [Google Scholar]
- Del Negro CA, Morgado-Valle C, Hayes JA, Mackay DD, Pace RW, Crowder EA, Feldman JL. Sodium and calcium current-mediated pacemaker neurons and respiratory rhythm generation. J Neurosci. 2005;25:446–453. doi: 10.1523/JNEUROSCI.2237-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duffin J. A model of respiratory rhythm generation. Neuroreport. 1991;2:623–626. doi: 10.1097/00001756-199110000-00018. [DOI] [PubMed] [Google Scholar]
- Dutschmann M, Herbert H. The Kölliker-Fuse nucleus gates the postinspiratory phase of the respiratory cycle to control inspiratory off-switch and upper airway resistance in rat. Eur J Neurosci. 2006;24:1071–1084. doi: 10.1111/j.1460-9568.2006.04981.x. [DOI] [PubMed] [Google Scholar]
- Dutschmann M, Paton JFR. Glycinergic inhibition is essential for coordinating cranial and spinal respiratory motor outputs in the neonatal rat. J Physiol. 2002;543:643–653. doi: 10.1113/jphysiol.2001.013466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elsen FP, Ramirez JM. Calcium currents of rhythmic neurons recorded in the isolated respiratory network of neonatal mice. J Neurosci. 1998;18:10652–10662. doi: 10.1523/JNEUROSCI.18-24-10652.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ezure K. Synaptic connections between medullary respiratory neurons and consideration on the genesis of respiratory rhythm. Prog Neurobiol. 1990;35:429–450. doi: 10.1016/0301-0082(90)90030-k. [DOI] [PubMed] [Google Scholar]
- Ezure K. Respiration-related afferents to parabrachial pontine regions. Respir Physiol Neurobiol. 2004;143:167–175. doi: 10.1016/j.resp.2004.03.017. [DOI] [PubMed] [Google Scholar]
- Ezure K, Manabe M. Decrementing expiratory neurons of the Bötzinger complex. Exp Brain Res. 1988;72:159–166. doi: 10.1007/BF00248511. [DOI] [PubMed] [Google Scholar]
- Ezure K, Tanaka I. Distribution and medullary projection of respiratory neurons in the dorsolateral pons of the rat. Neuroscience. 2006;141:1011–1023. doi: 10.1016/j.neuroscience.2006.04.020. [DOI] [PubMed] [Google Scholar]
- Ezure K, Tanaka I, Kondo M. Glycine is used as a transmitter by decrementing expiratory neurons of the ventrolateral medulla in the rat. J Neurosci. 2003;23:8941–8948. doi: 10.1523/JNEUROSCI.23-26-08941.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fedorko L, Merrill EG. Axonal projections from the rostral expiratory neurones of the Bötzinger complex to medulla and spinal cord in the cat. J Physiol. 1984;350:487–496. doi: 10.1113/jphysiol.1984.sp015214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman JL, Del Negro CA. Looking for inspiration: new perspectives on respiratory rhythm. Nat Rev Neurosci. 2006;7:232–241. doi: 10.1038/nrn1871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman JL, Smith JC. Neural control of respiratory pattern in mammals: an overview. In: Dempsey JA, Pack AI, editors. Regulation of Breathing. Decker; New York: 1995. pp. 39–69. [Google Scholar]
- Frermann D, Keller BU, Richter DW. Calcium oscillations in rhythmically active respiratory neurones in the brainstem of the mouse. J Physiol. 1999;515:119–131. doi: 10.1111/j.1469-7793.1999.119ad.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grillner S. Biological pattern generation: the cellular and computational logic of networks in motion. Review. Neuron. 2006;52:751–766. doi: 10.1016/j.neuron.2006.11.008. [DOI] [PubMed] [Google Scholar]
- Guyenet PG, Mulkey DK, Stornetta RL, Bayliss DA. Regulation of ventral surface chemoreceptors by the central respiratory pattern generator. J Neurosci. 2005;25:8938–8947. doi: 10.1523/JNEUROSCI.2415-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haji A, Takeda R, Okazaki M. Neuropharmacology of control of respiratory rhythm and pattern in mature mammals. Pharmacol Ther. 2000;86:277–304. doi: 10.1016/s0163-7258(00)00059-0. [DOI] [PubMed] [Google Scholar]
- Hayashi F, Lipski J. The role of inhibitory amino acids in control of respiratory motor output in an arterially perfused rat. Respir Physiol. 1992;89:47–63. doi: 10.1016/0034-5687(92)90070-d. [DOI] [PubMed] [Google Scholar]
- Janczewski WA, Feldman JL. Distinct rhythm generators for inspiration and expiration in the juvenile rat. J Physiol. 2006;570:407–420. doi: 10.1113/jphysiol.2005.098848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang C, Lipski J. Extensive monosynaptic inhibition of ventral respiratory group neurons by augmenting neurons in the Bötzinger complex in the cat. Exp Brain Res. 1990;81:639–648. doi: 10.1007/BF02423514. [DOI] [PubMed] [Google Scholar]
- Johnson SM, Koshiya N, Smith JC. Isolation of the kernel for respiratory rhythm generation in a novel preparation: the pre-Bötzinger complex “island”. J Neurophysiol. 2001;85:1772–1776. doi: 10.1152/jn.2001.85.4.1772. [DOI] [PubMed] [Google Scholar]
- Koizumi H, Smith JC. Perturbation of respiratory pattern and rhythm in vitro by block of persistent sodium current (INaP) Soc Neurosci Abstr. 2002;173.6 [Google Scholar]
- Koshiya N, Smith JC. Neuronal pacemaker for breathing visualized in vitro. Nature. 1999;400:360–363. doi: 10.1038/22540. [DOI] [PubMed] [Google Scholar]
- Lieske SP, Thoby-Brisson M, Telgkamp P, Ramirez JM. Reconfiguration of the neural network controlling multiple breathing patterns: eupnea, sighs and gasps. Nat Neurosci. 2000;3:600–607. doi: 10.1038/75776. [DOI] [PubMed] [Google Scholar]
- Long SE, Duffin J. The neuronal determinants of respiratory rhythm. Prog Neurobiol. 1986;27:101–182. doi: 10.1016/0301-0082(86)90007-9. [DOI] [PubMed] [Google Scholar]
- Lumsden T. Observations on the respiratory centres in the cat. J Physiol. 1923;57:153–158. doi: 10.1113/jphysiol.1923.sp002052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacGregor RI. Neural and Brain Modelling. Academic Press; New York: 1987. [Google Scholar]
- Marder E, Calabrese RL. Principles of rhythmic motor pattern generation. Physiol Rev. 1996;76:687–717. doi: 10.1152/physrev.1996.76.3.687. [DOI] [PubMed] [Google Scholar]
- Mellen NM, Janczewski WA, Bocchiaro CM, Feldman JL. Opioid-induced quantal slowing reveals dual networks for respiratory rhythm generation. Neuron. 2003;37:821–826. doi: 10.1016/s0896-6273(03)00092-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulkey DK, Stornetta RL, Weston MC, Simmons JR, Parker A, Bayliss DA, Guyenet PG. Respiratory control by ventral surface chemoreceptor neurons in rats. Nat Neurosci. 2004;7:1360–1369. doi: 10.1038/nn1357. [DOI] [PubMed] [Google Scholar]
- Nattie E. CO2, brainstem chemoreceptors and breathing. Prog Neurobiol. 1999;59:299–331. doi: 10.1016/s0301-0082(99)00008-8. [DOI] [PubMed] [Google Scholar]
- Okazaki M, Takeda R, Yamazaki H, Haji A. Synaptic mechanisms of inspiratory off-switching evoked by pontine pneumotaxic stimulation in cats. Neurosci Res. 2002;44:101–110. doi: 10.1016/s0168-0102(02)00091-3. [DOI] [PubMed] [Google Scholar]
- Onimaru H, Arata A, Homma I. Primary respiratory rhythm generator in the medulla of brainstem-spinal cord preparation from newborn rat. Brain Res. 1988;445:314–324. doi: 10.1016/0006-8993(88)91194-8. [DOI] [PubMed] [Google Scholar]
- Onimaru H, Homma I. A novel functional neuron group for respiratory rhythm generation in the ventral medulla. J Neurosci. 2003;23:1478–1486. doi: 10.1523/JNEUROSCI.23-04-01478.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pace RW, Mackay DD, Feldman JL, Del Negro CA. Role of persistent sodium current in mouse pre-Botzinger neurons and respiratory rhythm generation. J Physiol. 2007;2:485–496. doi: 10.1113/jphysiol.2006.124602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paton JFR. A working heart-brainstem preparation of the mouse. J Neurosci Methods. 1996;65:63–68. doi: 10.1016/0165-0270(95)00147-6. [DOI] [PubMed] [Google Scholar]
- Paton JFR, Abdala APL, Koizumi H, Smith JC, St-John WM. Respiratory rhythm generation during gasping depends on persistent sodium current. Nat Neurosci. 2006;9:311–313. doi: 10.1038/nn1650. [DOI] [PubMed] [Google Scholar]
- Paton JFR, Richter DW. Role of fast inhibitory synaptic mechanisms in respiratory rhythm generation in the maturing mouse. J Physiol. 1995;484:505–521. doi: 10.1113/jphysiol.1995.sp020682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickering AE, Paton JFR. A decerebrate, artificially-perfused in situ preparation of rat: utility for the study of autonomic and nociceptive processing. J Neurosci Methods. 2006;155:260–271. doi: 10.1016/j.jneumeth.2006.01.011. [DOI] [PubMed] [Google Scholar]
- Purvis L, Smith JC, Koizumi H, Butera RJ. Intrinsic bursters increase the robustness of rhythm generation in an excitatory network. J Neurophysiol. 2007;97:1515–1526. doi: 10.1152/jn.00908.2006. [DOI] [PubMed] [Google Scholar]
- Ramirez JM, Tryba AK, Pena F. Pacemaker neurons and neuronal networks: an integrative view. Curr Opin Neurobiol. 2004;14:665–674. doi: 10.1016/j.conb.2004.10.011. [DOI] [PubMed] [Google Scholar]
- Rekling JC, Feldman JL. Pre-Bötzinger complex and pacemaker neurons: hypothesized site and kernel for respiratory rhythm generation. Annu Rev Physiol. 1998;60:385–405. doi: 10.1146/annurev.physiol.60.1.385. [DOI] [PubMed] [Google Scholar]
- Richerson GB. Serotonergic neurons as carbon dioxide sensors that maintain pH homeostasis. Nat Rev Neurosci. 2004;5:449–461. doi: 10.1038/nrn1409. [DOI] [PubMed] [Google Scholar]
- Richter DW. Neural regulation of respiration: rhythmogenesis and afferent control. In: Gregor R, Windhorst U, editors. Comprehensive Human Physiology. Vol. 2. Springer-Verlag; Berlin: 1996. pp. 2079–2095. [Google Scholar]
- Richter DW, Spyer KM. Studying rhythmogenesis of breathing: comparison of in vitro and in vivo models. Trends Neurosci. 2001;24:464–472. doi: 10.1016/s0166-2236(00)01867-1. [DOI] [PubMed] [Google Scholar]
- Rybak IA, Paton JFR, Schwaber JS. Modeling neural mechanisms for genesis of respiratory rhythm and pattern: I. Models of respiratory neurons. J Neurophysiol. 1997a;77:1994–2006. doi: 10.1152/jn.1997.77.4.1994. [DOI] [PubMed] [Google Scholar]
- Rybak IA, Paton JFR, Schwaber JS. Modeling neural mechanisms for genesis of respiratory rhythm and pattern: II. Network models of the central respiratory pattern generator. J Neurophysiol. 1997b;77:2007–2026. doi: 10.1152/jn.1997.77.4.2007. [DOI] [PubMed] [Google Scholar]
- Rybak IA, Ptak K, Shevtsova NA, McCrimmon DR. Sodium currents in neurons from the rostroventrolateral medulla of the rat. J Neurophysiol. 2003a;90:1635–1642. doi: 10.1152/jn.00150.2003. [DOI] [PubMed] [Google Scholar]
- Rybak IA, Shevtsova NA, Paton JFR, Dick TE, St-John WM, Mörschel M, Dutschmann M. Modeling the ponto-medullary respiratory network. Respir Physiol Neurobiol. 2004a;143:307–319. doi: 10.1016/j.resp.2004.03.020. [DOI] [PubMed] [Google Scholar]
- Rybak IA, Shevtsova NA, Ptak K, McCrimmon DR. Intrinsic bursting activity in the pre-Bötzinger Complex: role of persistent sodium and potassium currents. Biol Cybern. 2004b;90:59–74. doi: 10.1007/s00422-003-0447-1. [DOI] [PubMed] [Google Scholar]
- Rybak IA, Shevtsova NA, St.-John WM, Paton JFR, Pierrefiche O. Endogenous rhythm generation in the pre-Bötzinger complex and ionic currents: modelling and in vitro studies. Eur J Neurosci. 2003b;18:239–257. doi: 10.1046/j.1460-9568.2003.02739.x. [DOI] [PubMed] [Google Scholar]
- Schreihofer AM, Stornetta RL, Guyenet PG. Evidence for glycinergic respiratory neurons: Bötzinger neurons express mRNA for glycinergic transporter 2. J Comp Neurol. 1999;407:583–597. doi: 10.1002/(sici)1096-9861(19990517)407:4<583::aid-cne8>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- Segers LS, Shannon R, Saporta S, Lindsey BG. Functional associations among simultaneously monitored lateral medullary respiratory neurons in the cat: I. Evidence for excitatory and inhibitory connections of inspiratory neurons. J Neurophysiol. 1987;57:1078–1100. doi: 10.1152/jn.1987.57.4.1078. [DOI] [PubMed] [Google Scholar]
- Selverston AI, Ayers J. Oscillations and oscillatory behavior in small neural circuits. Biol Cybern. 2006;95:537–554. doi: 10.1007/s00422-006-0125-1. [DOI] [PubMed] [Google Scholar]
- Shen LL, Li YM, Duffin J. Inhibitory connections among rostral medullary expiratory neurones detected with cross-correlation in the decerebrate rat. Pfluegers Arch. 2003;446:365–372. doi: 10.1007/s00424-003-1024-0. [DOI] [PubMed] [Google Scholar]
- Smith JC, Butera RJ, Koshiya N, Del Negro C, Wilson CG, Johnson SM. Respiratory rhythm generation in neonatal and adult mammals: the hybrid pacemaker-network model. Respir Physiol Neurobiol. 2000;122:131–147. doi: 10.1016/s0034-5687(00)00155-9. [DOI] [PubMed] [Google Scholar]
- Smith JC, Ellenberger H, Ballanyi K, Richter DW, Feldman JL. Pre-Bötzinger complex: a brain stem region that may generate respiratory rhythm in mammals. Science. 1991;254:726–729. doi: 10.1126/science.1683005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song G, Poon C-S. Functional and structural models of pontine modulation of mechanoreceptor and chemoreceptor reflexes. Respir Physiol Neurobiol. 2004;143:281–292. doi: 10.1016/j.resp.2004.05.009. [DOI] [PubMed] [Google Scholar]
- St.-John WM. Neurogenesis of patterns of automatic ventilatory activity. Prog Neurobiol. 1998;56:97–117. doi: 10.1016/s0301-0082(98)00031-8. [DOI] [PubMed] [Google Scholar]
- St.-John WM, Paton JFR. Defining eupnea. Respir Physiol Neurobiol. 2003;139:97–103. doi: 10.1016/s1569-9048(03)00193-9. [DOI] [PubMed] [Google Scholar]
- Sun Q-J, Goodchild AK, Pilowsky PM. Firing patterns of pre-Bötzinger and Bötzinger neurons during hypocapnia in the adult rat. Brain Res. 2001;903:198–206. doi: 10.1016/s0006-8993(01)02447-7. [DOI] [PubMed] [Google Scholar]
- Tian GF, Peever JH, Duffin J. Bötzinger-complex, bulbospinal expiratory neurones monosynaptically inhibit ventral-group respiratory neurones in the decerebrate rat. Exp Brain Res. 1999;124:173–180. doi: 10.1007/s002210050612. [DOI] [PubMed] [Google Scholar]
- Urbani A, Belluzzi O. Riluzole inhibits the persistent sodium current in mammalian CNS neurons. Eur J Neurosci. 2000;12:3567–3574. doi: 10.1046/j.1460-9568.2000.00242.x. [DOI] [PubMed] [Google Scholar]