The speed limit for protein folding measured by triplet–triplet energy transfer

Abstract

A direct measure of intramolecular chain diffusion is obtained by the determination of triplet–triplet energy-transfer rates between a donor and an acceptor chromophore attached at defined points on a polypeptide chain. Single exponential kinetics of contact formation are observed on the nanosecond time scale for polypeptides in which donor and acceptor are linked by repeating units of glycine and serine residues. The rates depend on the number of peptide bonds (N) separating donor and acceptor and show a maximum for the shortest peptides (N = 3) with a time constant (τ = 1/k) of 20 ns. This sets an upper limit for the speed of formation of the first side-chain contacts during protein folding.

Protein folding starts from an ensemble of random coil conformations to finally reach the native state with well defined side-chain contacts. For many proteins, rapid chain collapse precedes formation of the native structure (1–3). In a number of small proteins, in contrast, collapse and formation of the native interactions occur simultaneously (4–8). In both scenarios, the search for energetically favorable conformations requires formation of interactions between parts of the polypeptide chain, which is limited by chain dynamics. Intrachain diffusion can thus be regarded as the elementary process that determines the maximum rate at which a protein can fold. Models for the rate-limiting steps and for the distance dependence of intrachain diffusion have been proposed in a number of theoretical studies (9–13), but to date no direct experimental data are available for the rates of contact formation between two defined points on a polypeptide chain.

Triplet–triplet energy transfer provides an excellent tool to measure such rates of contact formation. Energy transfer between an electronically excited triplet donor (sensitizer) and an acceptor proceeds by an electron-exchange mechanism (Dexter mechanism), which requires van der Waals contact between the donor and acceptor. Rates of intermolecular exothermic triplet energy transfer approach, but do not exceed, the diffusion-controlled limit (14). The process is readily monitored by triplet–triplet absorption by using laser-flash photolysis. The fast formation and the long lifetimes of many triplet states allow measurements of processes in the range from nanoseconds to microseconds.

MATERIALS AND METHODS

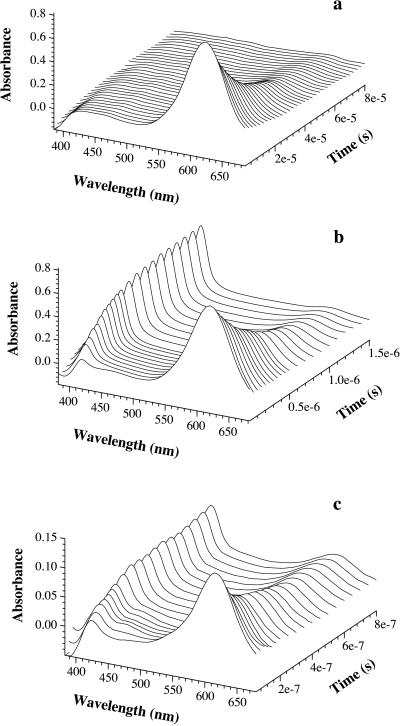
Thioxanthone (E_T = 265 kJ⋅mol⁻¹) was used as a triplet donor, which can be excited selectively with an excimer laser pulse at 351 nm in the presence of naphthalene (E_T = 253 kJ⋅mol⁻¹) as the acceptor (15). The amount of thioxanthone triplets was monitored by their strong triplet–triplet absorbance at λ_max = 620 nm. Fig. 1a shows the transient absorbance of triplet thioxanthone after excitation by a 351-nm laser flash of 20-ns duration. In the absence of acceptor, the thioxanthone triplets decay with a half-life of 30 μs. The decay rate of the thioxanthone triplets increases on addition of naphthalene, because of the formation of triplet naphthalene (Fig. 1b). The second-order rate coefficient for triplet-energy transfer (k_et) from thioxanthone to naphthalene was obtained from the slope of the linear increase of the pseudo first-order rate constants with increasing naphthalene concentration (data not shown). The resulting value of k_et = 4 × 10⁹ M⁻¹⋅s⁻¹ corresponds to that expected for the diffusion-controlled encounter of small molecules in ethanol solutions (16).

Figure 1.

Transient absorbance spectra of thioxanthone (a) and a mixture of thioxanthone and naphthyl-acetic acid (b) after selective excitation of thioxanthone by a 20-ns laser pulse at 351 nm. The concentration of thioxanthone was 86 μM in both cases. The populations of donor (thioxanthone) and acceptor (1-naphthylalanine) triplets can be easily measured by their strong absorbance bands at 620 nm and 420 nm, respectively. The half-life of triplet thioxanthone in the absence of acceptor (a) was 30 μs with the experimental conditions used. The decay was of mixed order because of triplet–triplet annihilation. In the presence of 0.5 mM 1-naphthylalanine (b), the lifetime of thioxanthone triplets decreases to 500 ns. This effect is due to triplet–triplet energy transfer to the acceptor chromophore as indicated by the concomitant growth of triplet absorbance by 1-naphthylalanine at 420 nm. c displays the same experiments as b, but with donor and acceptor chromophores attached to a polypeptide chain [peptide A(n = 4)]. The experiments were carried out in ethanol. For intramolecular transfer (c), the solution contained 40% glycerol. This slows contact formation (compare Fig. 4) and thus enables the recording of time resolved spectra. The peptide concentration was 15 μM.

Laser-Flash Photolysis.

Thioxanthone was selectively excited by a 20-ns, 351-nm light pulse from a XeF excimer laser with a pulse energy of 150 mJ. The amounts of thioxanthone and naphthalene triplets were quantified by measuring transient absorbance at 620 and at 420 nm, respectively. All solutions were degassed before the measurements to minimize triplet quenching by oxygen.

Peptide Synthesis.

Peptides were synthesized by using fluorenylmethoxycarbonyl-protected amino acids on Rink-amide resin. All couplings were performed with 2-(1H-benzotriazole-1-yl)-1,1,3,3-tetramethyluronium tetrafluoroborate/N-hydroxybenzotriazole/Hünig’s base chemistry in dimethylformamide by using 4-fold excess. A 20% solution of piperidine in dimethylformamide was used for deprotection of resin-bound fluorenylmethoxycarbonyl-conjugated peptides. First attempts of simultaneous detachment from the resin and side-chain deprotection with 50% trifluoroacetic acid in methylene chloride gave the desired peptides after HPLC (RP-8) purification in poor yields. Because of the acid sensitivity of the thioxanthone, a number of side products were detected. Therefore, we used Sieber-amide resin and the Lewis acid ZnCl₂/diethylether complex in methylene chloride as deprotection reagens. This gives much higher yields of the desired product (unpublished results). The purity of all peptides was checked by HPLC and capillary electrophoresis. In all cases, purity exceeded 95%. The structure was confirmed by matrix-assisted laser desorption ionization–time-of-flight mass spectrometry.

Viscosity Dependence.

The viscosity was varied by adding up to 70% glycerol to the solutions. For all solutions, the viscosity was measured by using a falling-ball viscometer. The data were normalized to the viscosity dependence of the rates of triplet–triplet transfer between free donor and acceptor, which was supposed to follow a perfect linear dependence of lnk with lnη exhibiting a slope of −1. This procedure corrected for small effects of solvent polarity on the rates of triplet–triplet energy transfer, leading to a vanishing energy gap between donor and acceptor at high concentrations of glycerol. This results in a doubling of the apparent rate constant of transfer because of equal contributions of both the forward and the backward reaction to the observed rate constants.

RESULTS AND DISCUSSION

Intrachain Contact Formation.

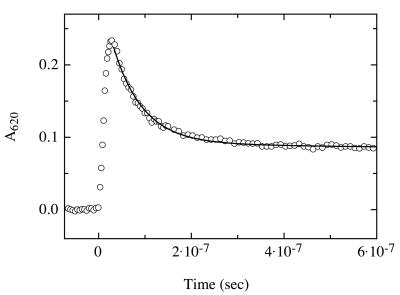
Because triplet–triplet energy transfer between thioxanthone and naphthalene is diffusion controlled, this pair is well suited to measure the rate of intramolecular contact formation, restricted by the dynamics of a polypeptide backbone. The time range for the measurements is given on the one end by the duration of the laser flash (20 ns) and on the other end by the lifetime of the thioxanthone triplets in the absence of acceptor (30 μs; Fig. 1a). To measure intrachain diffusion, a carboxyl derivative of thioxanthone was attached to the N terminus of model peptides via an amide bond. Naphthalene was incorporated into the peptides by using the unnatural amino acid 1-naphthyl alanine. To obtain information on the upper limit of the rates of contact formation, we synthesized a series of short and flexible peptides A, in which the distance between donor and acceptor was varied by placing n = 1–4 glycine/serine pairs between thioxanthone and naphthylalanine, resulting in N = 3–9 peptide bonds between donor and acceptor. Fig. 1c shows intramolecular triplet–triplet energy-transfer measurements for the peptide A(n = 4). In ethanol, the transfer process can be described by a first-order rate law with a rate constant (k) of 1.4 ± 0.2 × 10⁷ s⁻¹ (Fig. 2). The experiments were carried out with ethanol solutions, because the triplet energy of the donor drops below that of the acceptor in water, and energy transfer becomes inefficient. However, we measured the rates of contact formation in ethanol/water mixtures containing between 25 and 95% ethanol and obtained the same rate constants as in pure ethanol, which indicates that the nature of the solvent has little influence on the rate of contact formation.

Figure 2.

Transient triplet absorbance of thioxanthone after 351-nm laser flash photolysis of peptide A(n = 4) in ethanol. The laserflash was applied at t = 0. The decrease in thioxanthone triplet absorbance at 620 nm (○) can be described by a single-exponential process with a rate constant of 1.4 ± 0.2 × 10⁷ s⁻¹ (solid line). Because intermolecular triplet-energy transfer was shown to be diffusion-controlled, this rate corresponds to the rate of intrachain diffusion between donor and acceptor. The peptide concentration was 40 μM. Under these conditions, the half-life of thioxanthone triplets in peptides containing no acceptor was 30 μs (data not shown). The experiments were carried out in ethanol at 22°C. About 30% of the thioxanthone molecules remain in the triplet state after the equilibrium is reached, because of the small difference in triplet energy between donor and acceptor in polar solvents. These equilibrated triplet states decay on a much slower time scale and with the same rate as decay of the acceptor triplets occurs (1/k ≈30 μs; data not shown).

NMR and CD measurements of the peptides did not detect any preferred structure and confirmed a random coil distribution of conformations (data not shown). To test for possible contributions of intermolecular transfer processes, we used a mixture of two peptides, one containing only thioxanthone and the other one only naphthalene. The peptides were used in the same molar concentrations as in the measurements of intramolecular chain diffusion. In this mixture, no energy transfer to naphthalene was observed, and the half-life of thioxanthone triplets was 30 μs (data not shown).

Distance Dependence.

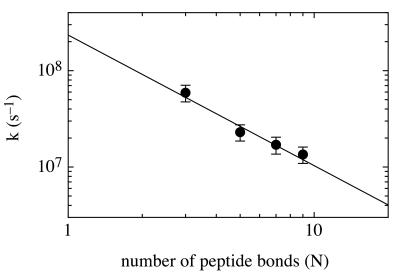
Changing the number (n) of glycine/serine pairs between donor and acceptor, n = 1–4, allowed us to determine the distance dependence of contact formation (Fig. 3). Single-exponential kinetics were observed for all peptides A. The rate of contact formation increased with decreasing number of peptide bonds (N) separating donor and acceptor. The rate constants for the different peptides are proportional to N^{−1.36 ± 0.26} and reach a maximum value of 5 × 10⁷ s⁻¹ for the shortest peptide A(n = 1) with donor and acceptor separated by N = 3 peptide bonds. However, the number of amino acids changes only by a factor of three in our series of peptides, leaving an uncertainty for scaling to longer distances. A possible influence of through-bond triplet energy transfer can be ruled out even for the shortest peptide A(n = 1) with a donor–acceptor separation of 11 chemical bonds. Through-bond intramolecular transfer depends strongly on the number of bonds between donor and acceptor and on their conformation. Intramolecular triplet energy-transfer rates in model systems in which the donor and acceptor are covalently linked by a rigid tether with an optimal geometry for coupling through seven saturated bonds gave transfer rates that were about two orders of magnitude lower than in our shortest peptides A(n = 1) (17).

Figure 3.

Distance dependence of the rate of intramolecular chain diffusion. The rates of contact formation in the different peptides A(n = 1–4) are plotted against the number of peptide bonds (N) separating donor and acceptor. Experimental conditions were as in Fig. 2. The peptide concentration was 15 μM. A linear fit of the double exponential plot gives a slope of −1.36 ± 0.26.

The observation of single-exponential kinetics for contact formation in all peptides A may seem surprising in view of theoretical models for peptide dynamics, which postulate a large number of discrete eigenvalues (18, 19) or a continuum of eigenvalues (20). Our measurements are, however, not sensitive for the complete spectrum of dynamical processes in the polypeptide backbone. They selectively monitor the formation of a subset of peptide conformations that allow contact between donor and acceptor. At the time of the laser flash, the peptides populate a large number of different conformations exhibiting a close to Gaussian distribution of end-to-end distances (21). The expected behavior of such an ensemble is an initial fast energy transfer in those conformations that allow immediate contact between donor and acceptor at the time of excitation (static quenching). The amplitudes of the transfer process measured at 620 nm and at 420 nm (Figs. 1c and 2) suggests that the fraction of instantaneous transfer is small (<5%) in all peptides. After this fast reaction, a redistribution of the conformations will occur, which leads to contact formation in the remaining molecules. Single-exponential behavior for intrachain contact formation has been predicted by using a first passage time approach. Szabo et al. (10) showed that end-to-end diffusion in random polymers can be approximated by single-exponential kinetics when the interconversion between individual conformations is fast and when the equilibrium population of conformations allowing end-to-end contact is small. The latter prerequisite is fulfilled even for our shortest peptide A(n = 1), as judged by the minor fraction of instantaneous energy transfer. The observation of single-exponential kinetics implies rapid conformational transitions between the accessible local minima in the Ramachandran plot by rotation around the two single bonds involving the Cα atoms of the peptide. Interestingly, Jacobsen and Stockmeyer (9) and Szabo et al. (10) predicted that the rate of contact formation scales with N^−1.5 for intrachain diffusion processes in polymers, which is in good agreement with the value observed for the distance dependence of the rate of contact formation in the model peptides A(n = 1–4). However, both theories describe the behavior of Gaussian chains and might thus not be directly applicable to short polypeptides, even if they are very flexible.

The present experiments provide direct measurements of intramolecular diffusion processes in unfolded polypeptide chains. Haas et al. (22) studied resonance energy transfer (singlet energy transfer) between donor and acceptor groups attached at the ends of short peptides to get information on chain dynamics. Converting the reported average diffusion constants into time constants (τ = 1/k) of contact formation at van der Waals distance gives values between 9 and 3 ns for a donor–acceptor separation of between four and eight peptide bonds, respectively. This is significantly faster than the rates of contact formation determined in our glycine/serine-based peptides of comparable length (Fig. 3). However, resonance transfer does not measure contact formation directly. Rather, it gives the average diffusion constant at a distance around the characteristic transfer distance (R₀), which is 22 Å for the donor–acceptor pair used by Haas et al. Thus, the method should be sensitive for a large number of normal modes of polypeptide chain dynamics, and the results cannot be directly compared with ours. Rates of intrachain diffusion have also been estimated from the rate of intramolecular bond formation in guanidinium chloride-unfolded cytochrome c (23). The reaction of a methionine with a heme group at a distance of 50–60 aa was measured and extrapolated to shorter distances. This gave an estimate of 1 μs for the time constant of contact formation at a distance of nine peptide bonds, which is about 15 times slower than the rate determined in our measurements (Fig. 3). In contrast to triplet–triplet energy transfer, the cytochrome c system does not provide a direct measure for the maximum rate of contact formation, because extrapolation over a rather long distance had to be carried out by using scaling laws derived for Gaussian chains (10). In addition, the effect of guanidinium chloride binding to the polypeptide backbone might influence the chain dynamics.

Viscosity Dependence.

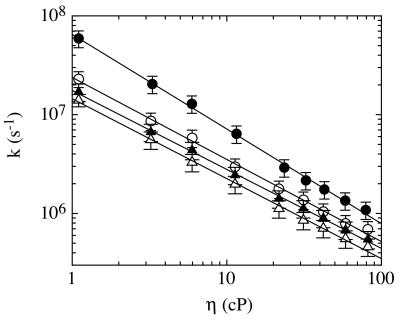
To determine whether contact formation is limited by intrinsic barriers for polypeptide chain dynamics or by solvent friction, we measured the viscosity dependence of the transfer rates in solvent mixtures of glycerol and ethanol. The logarithm of the rate constants decreases linearly with the logarithm of solvent viscosity for all peptides A(n = 1–4) (Fig. 4). For the shortest peptide A(n = 1), the slope is −0.96, which is close to the value of −1 expected for processes limited exclusively by solvent friction (24). For all other peptides A(n = 2–4), the slopes are between −0.80 and −0.83, indicating that solvent friction is not the only process contributing to the barriers of contact formation at longer distances. Theoretical models on peptide motion predict a larger stiffness for short chain segments, which should result in a less pronounced viscosity dependence in rates of contact formation for movements involving <8–10 peptide bonds (25, 26). This is in accord with experimental studies on the stiffness of unfolded polypeptide chains that showed persistence lengths between five and nine amino acids for different unfolded proteins (27–29). Consequently, the maximum rate for contact formation would be expected between residues separated by about five to nine peptide bonds. This is in contrast to results from our model peptides, which show an increase in the rate of contact formation even below the expected persistence length of polypeptide chains (Fig. 3). This effect is most likely caused by the special properties of glycine residues. Flory and coworkers (30) calculated the effect of an increasing fraction of glycine residues on the properties of random copolymers of glycine and alanine. They showed that the expected end-to-end distance and the chain stiffness decrease as the fraction of glycines increases. For polyalanine, a persistence length of nine amino acids is observed. This value reduces to three amino acids for a 50% alanine/glycine mixture, which should be a good approximation for our model peptides A. This effect leads to shorter donor–acceptor distances in our glycine/serine based series and to an increased flexibility of the chains compared with glycine-free peptides.

Figure 4.

Viscosity dependence of the rate of contact formation for peptides A containing n = 1 (●), 2 (○), 3 (▴) and 4 (▵) glycine/serine pairs between thioxanthone and 1-naphthylalanine. Linear fits of the double logarithmic plot of the data give slopes of −0.96 ± 0.05, −0.83 ± 0.05, −0.80 ± 0.05, and −0.81 ± 0.05, respectively.

Maximum Rate of Protein Folding.

Our results show that the maximum time constant of contact formation is about 20 ns and that the process is well described by single-exponential kinetics. The measurements were carried out in ethanol/water mixtures between 25 and 100%, and the rates might be slightly different in pure water. However, the kinetics were independent of the water content in the measured range of ethanol concentrations, indicating that the values in pure water will be similar.

We do not know whether the rates for comparable processes in non-glycine peptides are slower. The decreased end-to-end distance and the smaller persistence length introduced by glycine residues facilitates contact formation. This is, however, opposed by a larger conformational freedom for glycine, which results in an extended search in conformational space. Even if the contact rates in glycine-based peptides are faster than comparable processes in less flexible sequences, our data still put an upper limit on the rate of protein folding. During protein folding, the process of contact formation is especially important at the ends of loop regions and in hairpin structures. Statistical analysis of protein loops showed that their average size is 6–10 residues and that they are especially glycine- or proline-rich (31). Our results suggest that such structures can form on a time scale of 50–100 ns. Very tight glycine-containing turns of three to four amino acids, which are often found at the ends of β-hairpins (32), will be able to form faster, with a maximum time constant around 20 ns.

The fastest processes measured in protein folding are much slower than the rates of contact formation observed here. A time constant of 50 μs was measured for molecular collapse as the initial step in refolding of cytochrome c, which should also involve local intrachain diffusion processes. Comparison of this value with the maximum rates for formation of side-chain contacts implies major additional free-energy barriers for molecular collapse. The fastest experimentally measured folding reactions leading to native protein are in the range of 100 μs–1 ms at 20°C (7), orders of magnitude slower than the rate of intrachain diffusion. The slower, but diffusion-controlled (33, 34) folding of proteins suggests that folding occurs via the diffusive motions of ordered structural elements with large diffusion constants or that the rate-limiting steps additionally involve significant energy barrier.