The 3D NOESY-[¹H,¹⁵N,¹H]-ZQ-TROSY NMR experiment with diagonal peak suppression

Abstract

In our 3D NOESY-[¹H,¹⁵N,¹H]-ZQ-TROSY experiment, the TROSY principle (transverse relaxation-optimized spectroscopy) is used in three-dimensional (3D) ¹⁵N-resolved nuclear Overhauser enhancement spectroscopy (NOESY), which enables resonance assignments by sequential nuclear Overhauser effects and the collection of structural constraints in large ¹⁵N- or ²H,¹⁵N-labeled proteins. Our experiment affords optimization of the transverse relaxation in all three frequency dimensions, provides suppression of the strong diagonal autorelaxation peaks, which otherwise tend to interfere with the analysis of nearby informative crosspeaks, and yields improved resolution for the entire spectrum when compared with conventional 3D ¹⁵N-resolved-[¹H,¹H]-NOESY, because of the narrower lineshapes along both proton dimensions. The key element of this experiment is an approach for correlating the ¹⁵N and ¹H chemical shifts with two-dimensional ZQ-[¹⁵N,¹H]-TROSY, where zero-quantum (ZQ) coherence is generated and the remote cross-correlation between the ¹H and ¹⁵N chemical shift anisotropy interactions is used to reduce transverse relaxation during ¹⁵N evolution. Practical applications are illustrated with spectra of a protein with a molecular mass of 110,000 Da.

The introduction of transverse relaxation-optimized spectroscopy (TROSY) (1) has greatly expanded the molecular size range accessible for solution NMR experiments that correlate the chemical shifts of either ¹⁵N and ¹H in N–H groups (2, 3) or ¹³C and ¹H in aromatic C–H fragments (4) and for triple-resonance experiments used for sequential assignments of [²H, ¹³C, ¹⁵N]- or [¹³C,¹⁵N]-labeled proteins (5). With regard to extending NMR structure determination to larger molecular sizes, it is further of keen interest to improve sensitivity and resolution of nuclear Overhauser effect (NOE) experiments with the use of TROSY, which is the subject of this paper. NOE spectroscopy (NOESY) yields ¹H–¹H distance constraints that enable de novo determination of three-dimensional (3D) structures of biological macromolecules by NMR in solution (6).

In initial implementations of the TROSY principle in NOE experiments, [¹³C,¹H]-TROSY and [¹⁵N,¹H]-TROSY have been used in 3D ¹³C-resolved and ¹⁵N-resolved [¹H,¹H]-NOESY to resolve homonuclear ¹H–¹H NOEs along the heteronuclear dimension (7, 8). In these NOE experiments, the conventional [¹³C,¹H]- or [¹⁵N,¹H]-heteronuclear single-quantum coherence or heteronuclear multiple-quantum coherence schemes (9) were substituted by the corresponding single-quantum TROSY-type chemical shift correlation schemes (2, 4), whereby the desired transverse relaxation optimization was achieved along the ¹³C frequency axis (7) or in the ¹⁵N and ¹H^N dimensions (8), respectively. Because in 3D heteronuclear-resolved NOESY experiments the most interesting information resides in the [¹H,¹H]-spectral planes and high spectral resolution should therefore primarily be achieved along the two ¹H dimensions, this approach is of only limited use. Here, we introduce a 3D ¹⁵N-resolved NOE experiment, 3D NOESY-[¹H,¹⁵N,¹H]-ZQ-TROSY, which affords optimization of the transverse relaxation in all three spectral dimensions. An additional important feature of this experiment is artifact-free suppression of the diagonal peaks, which are typically much stronger than the crosspeaks and tend to interfere with crosspeak identification and integration in NOESY spectra. A key element of 3D NOESY-[¹H,¹⁵N,¹H]-ZQ-TROSY is that the ¹⁵N and ¹H chemical shifts are correlated by sensitivity-enhanced two-dimensional (2D) ZQ-[¹⁵N,¹H]-TROSY steps, which use the remote cross-correlation between ¹H chemical shift anisotropy (CSA) and ¹⁵N CSA interactions (10) to reduce the transverse relaxation rate of the [¹⁵N,¹H]-ZQ coherence.

METHODS

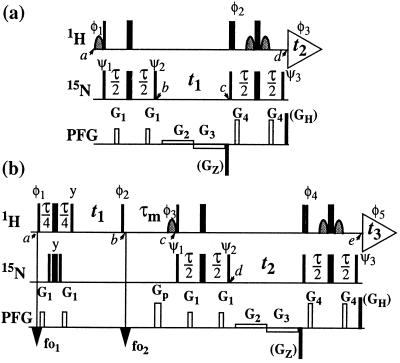
The experimental schemes that are introduced in this paper (Fig. 1) are described by the product operator formalism (11) by using the single-transition basis operators I_i¹³ = 1/2 I_i + I_iS_i and I_i²⁴ = 1/2 I_i − I_iS_i, where I and S represent the ¹H and ¹⁵N spins, and i stands for “z,” “+,” or “−.” The abbreviations DQ_± = I_±S_± and ZQ_± = I_∓S_± are used for the double-quantum (DQ) and ZQ operators, respectively. For the 2D ZQ-[¹⁵N,¹H]-TROSY element, two equivalent magnetization transfer pathways are given by Eqs. 1 and 2:

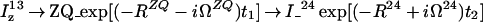1

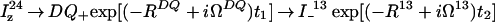2

The initial steady-state ¹H polarization at time point a (Fig. 1a), I_z is the sum of the single-transition polarization operators, I_z = I_z¹³ + I_z²⁴, which can be considered separately. Ω_I and Ω_S are the chemical shifts relative to the carrier frequency of the spins I and S, J is the scalar coupling constant between I and S, Ω^ZQ = Ω_I − Ω_S, Ω^DQ = Ω_I + Ω_S, Ω²⁴ = Ω_I − πJ, and Ω¹³ = Ω_I + πJ. R²⁴ and R¹³ are the previously described relaxation rates of the individual single-quantum transitions 2 → 4 and 1 → 3 (1, 4). R^ZQ and R^DQ are the relaxation rates of the ZQ and DQ coherences given by Eqs. 3 and 4.

3

4

For rigid spheres, the spectral densities, J(ω), can be written as

5

In Eqs. 3–5, ω_S and ω_I are the Larmor frequencies of the spins S and I, the dipole–dipole (DD) interaction is p² = 1/8(γ_Iγ_Sћ/r_IS³)², the CSA interactions are δ_S² = 1/18(ω_SΔσ_S)² and δ_I² = 1/18(ω_IΔσ_I)², γ_I and γ_S are the gyromagnetic ratios of I and S, ћ is the Planck constant divided by 2π, r_IS the distance between the nuclei S and I, Δσ = σ_zz − 0.5 (σ_xx + σ_yy), P₂(φ) = (3 cos² φ − 1)/2, where φ is the angle between the principal directions of the chemical shift tensors of the spins S and I, and 1/T_2I and 1/T_2S are the contributions to the transverse relaxation rates of the spins I and S because of DD coupling with remote protons (1).

Figure 1.

Schemes for the experiments discussed in this paper. (a) 2D ZQ-[¹⁵N,¹H]-TROSY. (b) 3D NOESY-ZQ-[¹H,¹⁵N,¹H]-TROSY with transverse relaxation optimization in all three dimensions and suppression of the diagonal peaks. On the lines marked ¹H and ¹⁵N, narrow and wide bars stand for nonselective 90° and 180° rf pulses, respectively, and curved shapes represent water-selective 90° rf pulses. Water saturation is minimized by returning the water magnetization to the +z axis before data acquisition (15, 18). The time period τ is set to 5.4 ms. The line marked PFG indicates pulsed magnetic field gradients applied along the z axis. (a) The gradients are: G₁ amplitude 30 G/cm, duration 1 ms; G₂, 5 G/cm, 0.5⋅t₁; G₃, −5 G/cm, 0.5⋅t₁; G₄, 40 G/cm, 1 ms. The phases for the rf pulses are: φ₁ = {−x}; φ₂ = {x}; φ₃ = {x, −x, −y, y}; ψ₁ = {−x, x, −y, y}; ψ₂ = {y, −y, x, −x}; ψ₃ = {y}; x on all other pulses. To obtain a complex interferogram, a second free induction decay (FID) is recorded for each t₁ delay, with the following different phases: φ₁ = {x}, φ₂ = {−x}, φ₃ = {x, −x, y, −y}, ψ₃ = {−y}. After Fourier transformation in the ω₂ dimension, the complex interferogram is multiplied by exp[−iΩ_Ht₁], where Ω_H is the offset in the ω₂ dimension relative to the ¹H carrier frequency in rad s⁻¹. Further data processing following ref. 2. (b) The gradients are: G₁, 30 G/cm, 1 ms; G_p, 40 G/cm, 2 ms; G₂, 5 G/cm, 0.5⋅t₂; G₃, −5 G/cm, 0.5⋅t₂; G₄, 40 G/cm, 1 ms. The phases of the rf pulses are: φ₁ = {4(45°), 4(225°)}; φ₂ = {x}; φ₃ = {−x}; φ₄ = {x}; φ₅ = {x, −x, −y, y, −x, x, y, −y}; ψ₁ = {−x, x, −y, y}; ψ₂ = {y, −y, x, −x}; ψ₃ = {y}; x on all other pulses. The ¹H carrier frequency offsets are set to 8.7 ppm at time point fo₁ and to 4.8 ppm at fo₂. Quadrature detection in ω₁ is achieved by the States time-proportional phase incrementation method (9) applied with the phase φ₂. For each t₂ increment, a second FID is recorded with the following different phases: φ₃ = {x}, φ₄ = {−x}, φ₅ = {x, −x, y, −y, −x, x, −y, y}, ψ₃ = {−y}. Further data processing as described for a. As an alternative, in both schemes the coherence selection can be supported by addition of the PFGs G_Z (−50 G/cm, 1.59 ms) and G_H (50 G/cm, 0.177 ms). G_Z is then inverted in concert with the phase shifts used to obtain a complex interferogram, and the nonzero initial values for the evolution times need to be taken into account.

In the slow tumbling limit, only terms in J(0), 1/T_2I and 1/T_2S need to be retained in Eqs. 3 and 4. For backbone ¹⁵N–¹H amide moieties in proteins, where δ_S ≈ δ_I and the unique axes of the ¹H and ¹⁵N CSA tensors are nearly parallel (12, 13), P₂(φ) ≈ 1 and the transverse relaxation caused by ¹H CSA and ¹⁵N CSA interactions is largely suppressed for ZQ coherence (Eq. 3). Because ¹⁵N–¹H DD relaxation is negligible for ZQ coherence (11) and the acquired signal comes from the relaxation-optimized single-transition 2 → 4 (2), Eq. 1 represents a way for obtaining TROSY-type 2D [¹⁵N,¹H]-correlation spectra with the transverse relaxation optimized in both dimensions. The unfavorable pathway of Eq. 2 is suppressed by phase cycling, pulsed field gradient (PFGs), or a combination of both (Fig. 1a).

The ZQ-[¹⁵N,¹H]-TROSY experiment contains a sensitivity-enhanced quadrature detection scheme that requires only a single insensitive nuclei enhanced by polarization transfer (INEPT) element for the transfer of both precessing orthogonal components of the ZQ coherence to the observable signal. When compared with the serial arrangement of two INEPT elements in the standard single transition-to-single transition polarization transfer enhancement scheme (2), a single INEPT element results in a smaller number of ¹H and ¹⁵N pulses and an overall shorter pulse sequence, with concomitant improvement in sensitivity. With the use of the PFGs for coherence pathway selection according to Eq. 1, only a one-step phase cycle is required for the collection of a phase-sensitive sensitivity-enhanced 2D spectrum. These features make 2D ZQ-[¹⁵N,¹H]-TROSY an attractive building block in more complex NMR experiments (see below).

Relaxation caused by remote DD coupling is not affected by TROSY, either in the ZQ variant or in the standard version with single-quantum coherence optimized by cross-correlation of DD coupling and CSA interactions (1, 2). The best results with the experiments of Fig. 1 will therefore be obtained in uniformly ²H,¹⁵N-labeled proteins, where 1/T_2I and 1/T_2S are affected only by interactions between closely spaced ¹⁵N–¹H groups.

In the two independent polarization transfer pathways of the experiment of Fig. 1a (Eqs. 1 and 2), the initial spin-polarizations associated with the individual transitions 1 → 3 and 2 → 4 are not mixed during the experiment, so that they can be separately detected as single transitions. Because the signal detected through the 2 → 4 transition (Eq. 1) is also independent of the initial spin-polarization of the 2 → 4 transition, the scheme of Fig. 1a can be used as a building block in the 3D NOESY-ZQ-[¹H,¹⁵N,¹H]-TROSY experiment (Fig. 1b), where the diagonal autorelaxation peaks are suppressed, and the transverse relaxation is optimized in all three spectral dimensions. In the following, the experiment of Fig. 1b is analyzed for a combination of two 2-spin systems representing two ¹⁵N–¹H groups interacting by ¹H–¹H DD coupling. The two spin systems are distinguished by additional superscripts, (1) and (2). Only the relevant magnetization transfer pathways are considered, and relaxation during the polarization transfer steps is neglected. Between the timepoints a and b (Fig. 1b), the equilibrium density matrix, δ_a = I_z⁽¹⁾ + I_z⁽²⁾, is transformed into a density matrix that contains the relevant terms given by Eq. 6.

6

Because of the S³E element (14) at the beginning of the pulse sequence (Fig. 1b), the steady-state magnetizations associated with the 1 → 3 proton transitions of both amide moieties are not ¹H frequency labeled during t₁; they are kept transverse during the NOE mixing time τ_m and eventually dephased by the gradient G_p (Fig. 1b). During τ_m, the 1 → 3 transitions can be repolarized by DD cross relaxation, with rates σ, and by longitudinal autorelaxation, with rates ρ^ijkl, resulting in exchange of magnetization between the i → j and k → l transitions as given by Eq. 7.

7

with

8

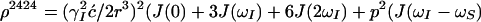9

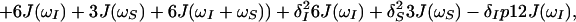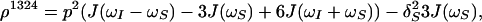10

and

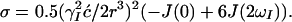11

The time evolution of I¹³⁽¹⁾ is obtained by integration of Eq. 7 with the initial conditions I_z¹³⁽¹⁾(0) = 0, I_z¹³⁽²⁾(0) = 0, I_z²⁴⁽¹⁾(0) = I₀/2 cos(ω_I²⁴⁽¹⁾t_I) and I_z²⁴⁽²⁾(0) = I₀/2 cos(ω_I²⁴⁽²⁾t₁), where the steady-state proton magnetization I₀ was arbitrarily set to 2 when the following equations were written. The resulting expression for I_z¹³⁽¹⁾(τ_m) can be simplified, for the limit of slow tumbling (ω_Iτ_c ≫ 1), with the initial buildup rate approximation (στ_m ≪ 1) (11), which results in a density submatrix describing the magnetization of the spin I⁽¹⁾ at time c:

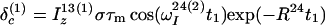12

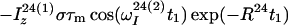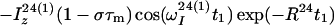δ_c⁽²⁾ can be obtained by permuting the labels (1) and (2) in Eq. 12. The condition στ_m ≪ 1 can readily be fulfilled. For example, with τ_c = 70 ns, r = 0.29 nm and τ_m = 50 ms, στ_m has the value 0.13.

After the time point c in Fig. 1b, the ¹H longitudinal polarizations, I_z¹³ and I_z²⁴, are converted to heteronuclear ZQ and DQ coherences, respectively, of which only the ZQ component is retained:

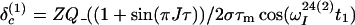13

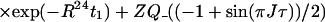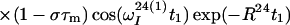The first and second terms in Eq. 13 represent the crosspeaks and the diagonal peaks, respectively, as detected through the spin I⁽¹⁾. From the second term, it is seen that for the INEPT condition of τ = 1/(2J), the diagonal peak vanishes if J ≡ ¹J(¹⁵N,¹H).

Finally, the transfer function for the experimental scheme of Fig. 1b within the chosen approximations is

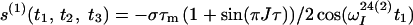14

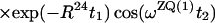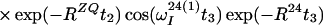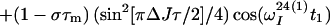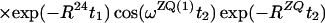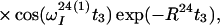where ΔJ is the difference between the actual coupling constant, ¹J(¹⁵N, ¹H), and J. The first term in Eq. 14 represents the NOESY crosspeak connecting the chemical shifts of the 2 → 4 transitions of ¹H⁽¹⁾ and ¹H⁽²⁾. Considering the small variation of ¹J(¹⁵N,¹H) observed along polypeptide chains in proteins, the residual intensity of the diagonal peaks should, on average for all residues, be less than 3% of the full intensity for any reasonably chosen set of experimental conditions. To facilitate practical applications, the experiment was designed so that residual diagonal peaks will always have opposite sign to the crosspeaks (Eq. 14). Loss in signal amplitude for kinetically labile ¹⁵N–¹H groups by transfer of saturation from the solvent is minimized by aligning a large part of the water magnetization along +z before data acquisition (15). During τ_m radiation damping is used to accelerate the return of the phase-coherent water magnetization to thermal equilibrium (16, 17). For the remainder of the pulse sequence, the water magnetization is aligned along +z by using standard procedures (18, 19).

RESULTS

The experiments introduced in this paper are of interest primarily for studies of large proteins. All the illustrations shown in this section have therefore been recorded with a protein of molecular mass 110,000, the 7,8-dihydroneopterin aldolase (DHNA) from Staphylococcus aureus (20). For the present NMR experiments, this protein was labeled in the extent of 70% with ²H and uniformly with ¹⁵N, and it was dissolved in a mixed solvent of 95% ¹H₂O/5% ²H₂O at 25°C and pH 6.0. DHNA is a homooctamer protein containing 8 subunits of 121 aa residues each. Because of the high symmetry, the complexity of the NMR spectra is manageable in spite of the large size.

The ZQ coherence-based 2D ZQ-[¹⁵N,¹H]-TROSY experiment of Fig. 1a is evaluated in Fig. 2 by comparison with the single-quantum coherence-based [¹⁵N,¹H]-TROSY experiment of ref. 2 and a water-flip-back version of the conventional single-quantum coherence-based [¹⁵N,¹H]-COSY experiment (9), which both also correlate the ¹H and ¹⁵N resonances of ¹⁵N–¹H moieties. The figure shows cross-sections along both the ¹⁵N and ¹H chemical shift axes of a well-separated cross peak. In a and b, only the upfield component of the ¹H doublet is observed, so that the peak positions along ω₂ (¹H) differ from that observed for the same ¹⁵N–¹H fragment in the conventional [¹⁵N,¹H]-COSY experiment by about 45 Hz (1). A similar shift is seen for the peak position of b along ω₁ (¹⁵N) when compared with c. The ω₁ (¹⁵N) positions in a and c are identical, because in a the ¹H frequency was subtracted from the ZQ precession frequency (see Fig. 1 legend). As expected from the experimental procedures used (Fig. 1a and ref. 2; the spectra of Fig. 2a and 2b both show transverse relaxation-optimized narrow line shapes along ω₂ (¹H). Only the single-quantum coherence-based [¹⁵N,¹H]-TROSY experiment (Fig. 2b) provides an appreciably narrower line width along the ¹⁵N dimension, so that this scheme also yields the highest signal amplitude. Overall, the presently introduced 2D ZQ-[¹⁵N,¹H]-TROSY scheme (Fig. 1a) provides better sensitivity and resolution than the conventional [¹⁵N,¹H]-COSY experiment (Fig. 2c), but the [¹⁵N,¹H]-TROSY experiment of ref. 2 clearly gives the best result (Fig. 2b). As we will see in the following, the ZQ-based scheme is nonetheless a preferred element in 3D heteronuclear-resolved NOESY experiments.

Figure 2.

Comparison of three [¹⁵N,¹H]-correlation experiments. (a) 2D ZQ-[¹⁵N,¹H]-TROSY recorded with the scheme of Fig. 1a. (b) 2D single-quantum-[¹⁵N,¹H]-TROSY recorded according to ref. 2. (c) Water-flip-back version of the conventional [¹⁵N,¹H]-HSQC experiment (9). The experiments were performed at a ¹H frequency of 750 MHz with a solution of [70% ²H,u¹⁵N] DHNA from S. aureus (20) in 95% ¹H₂O/5% ²H₂O at 25°C and pH = 6.0. DHNA is a homooctamer protein of molecular mass 110,000; the concentration in the NMR sample was 0.4 mM as calculated per subunit. The measuring time and the experimental setup were identical for all three spectra. For a well-separated cross peak, cross sections along the ¹H and ¹⁵N dimensions are shown.

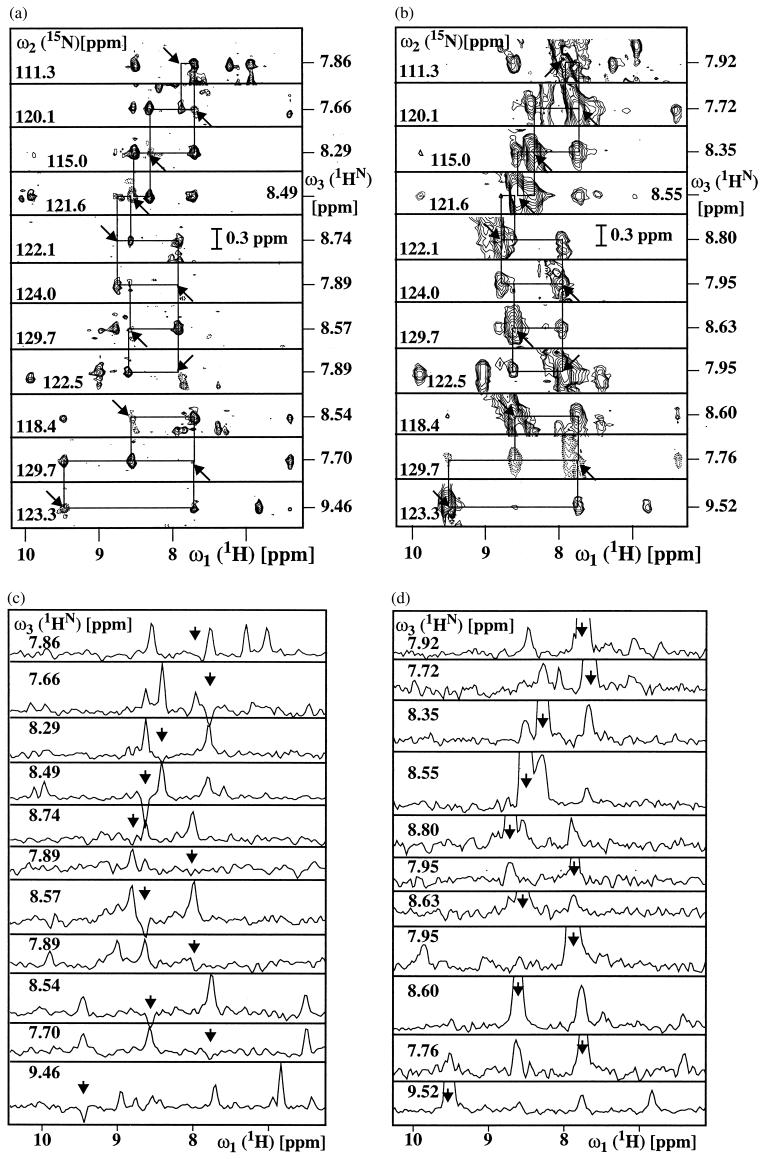
In 3D ¹⁵N-resolved experiments, the line width in the ¹⁵N dimension is usually, for practical reasons, determined by the relatively short maximal ¹⁵N chemical shift evolution time rather than by the effective transverse relaxation time. The narrow ¹⁵N line width obtained with single-quantum coherence-based [¹⁵N,¹H]-TROSY (Fig. 2b) would therefore usually be masked by the experimental conditions used. As a consequence, the comparatively small number of polarization transfer delays, the absence of loss of magnetization during the ¹⁵N quadrature detection, and the individual single-transition-to-individual multiple-quantum coherence transfer scheme used (see Methods) make 2D ZQ-[¹⁵N,¹H]-TROSY attractive as a building block in 3D ¹⁵N-resolved experiments such as 3D NOESY-[¹H,¹⁵N,¹H]-ZQ-TROSY (Fig. 1b). Fig. 3 a and c present a spectrum of the protein DHNA recorded with the experiment of Fig. 1b by a set of strips, i.e., 2D ω₁ (¹H)/ω₃(¹H^N) contour plots approximately centered about the ω₃(¹H^N) shift corresponding to the diagonal peak position of interest and taken at the chemical shift of the directly bound ¹⁵N nucleus in the ω₂-dimension, and the corresponding one-dimensional cross sections taken along the ω₁ dimension at the ω₃(¹H^N) positions of the diagonal peaks identified by the arrows. As a reference for evaluation of the new experiment, a similar presentation of the same regions of a conventional 3D ¹⁵N-resolved [¹H,¹H]-NOESY spectrum (16) of DHNA is displayed in Fig. 3b and d. Along both ¹H frequency axes, corresponding peak positions in the two spectra differ by approximately 45 Hz (1). Comparison of the two spectra shows that an important advantage of the 3D NOESY-[¹H,¹⁵N,¹H]-ZQ-TROSY experiment results from the fact that the diagonal peaks are either completely suppressed or have very small residual negative intensity (arrows in Fig. 3). The traces in Fig. 3c show that the scheme of Fig. 1b yields artifact-free suppression of the diagonal peaks, so that the crosspeaks near the diagonal become amenable for detailed analysis. The two spectra further demonstrate that significantly narrower crosspeak line widths were achieved when using TROSY, which in turn also yielded higher signal amplitudes.

Figure 3.

Comparison of corresponding spectral regions in a 3D NOESY-ZQ-[¹H,¹⁵N,¹H]-TROSY spectrum recorded with the scheme of Fig. 1b (a, c) and a conventional 3D ¹⁵N-resolved [¹H,¹H]-NOESY spectrum recorded according to ref. 16 (b, d). Both experiments were recorded with the sample of DHNA described in Fig. 2, using a Bruker DRX-750 spectrometer. Data size 128(t₁)*30(t₂)*1024(t₃) complex points, t_1max = 24 ms, t_2max = 15 ms and t_3max = 105 ms. Eight scans per increment were acquired, resulting in a measuring time of 34 h per spectrum. The spectra were processed with the program prosa (22). (a and b): Contour plots of [ω₁(¹H),ω₃(¹H)] strips. NOE connectivities are shown with thin horizontal and vertical lines. (c and d): Cross-sections taken along ω₁(¹H) at the ω₃(¹H) positions of the diagonal peaks in the strips a and b, respectively. In a–d, the positions of the diagonal peaks are indicated by arrows.

DISCUSSION

This paper describes an extension of the principle of transverse relaxation-optimization (1) in three ways. Firstly, crosscorrelation between ¹⁵N CSA and ¹H^N CSA is used to reduce transverse relaxation during the ¹⁵N evolution time. So far, cross-correlated relaxation was used in TROSY schemes only between ¹⁵N–¹H^N DD coupling and ¹⁵N CSA for optimization during the ¹⁵N evolution, between aromatic ¹³C–¹H DD coupling and ¹³C CSA for optimization during the ¹³C evolution (4, 7) and between ¹⁵N–¹H^N DD coupling and ¹H^N CSA for optimization during ¹H^N acquisition (1), and in cross-correlated relaxation-enhanced polarization transfer (CRINEPT) between ¹⁵N–¹H DD coupling and ¹⁵N CSA for optimization during magnetization transfers (21). Secondly, compared to previous TROSY implementations in 3D heteronuclear-resolved NOE experiments (7, 8), where transverse relaxation was optimized during the evolution of the heteronuclear spin and the directly observed ¹H dimension, the experiment of Fig. 1b affords optimization in all three dimensions and thus yields narrower lines and concomitantly increased peak heights in both dimensions of the all-important [¹H,¹H]-NOESY planes. Thirdly, the scheme of Fig. 1b results in high-quality suppression of the diagonal peaks, which enables a quantitative analysis of NOESY crosspeaks in spectral regions that would otherwise be only hardly accessible.

The newly introduced 3D NOESY-[¹H,¹⁵N,¹H]-ZQ-TROSY experiment (Fig. 1b) uses two different types of the aforementioned cross-correlation effects. The cross-correlation between ¹⁵N–¹H^N DD coupling and ¹H^N CSA interactions is used to compensate transverse relaxation during the ¹H chemical shift evolution period t₁ and the ¹H^N signal acquisition period, t₃ (1, 2). Thereby the magnitude of the DD/CSA cross-correlation effect depends strongly on the strength of the polarizing magnetic field, B₀ (1, 3). Although very good results were obtained at the presently used field strength corresponding to a ¹H resonance frequency of 750 MHz (Fig. 3), further improvement is anticipated at higher fields, with an optimum between 1.0 and 1.1 GHz (1, 3). The remote cross-correlation between ¹⁵N CSA and ¹H^N CSA within the ¹⁵N–¹H^N moieties is used to compensate transverse relaxation during the ¹⁵N chemical shift evolution period t₂. The CSA/CSA cross-correlation effect is determined exclusively by the magnitudes and mutual orientations of the ¹H and ¹⁵N CSA tensors and is therefore independent of the field strength B₀, which is in contrast with DD/CSA cross-correlation. Because in proteins the principal axes of the axially symmetric CSA tensors for ¹⁵N and ¹H are both nearly parallel to the ¹⁵N–¹H^N bond (12, 13), and the contributions of ¹H CSA and ¹⁵N CSA to transverse relaxation are comparable in magnitude, the presently described use of CSA/CSA cross-correlation for TROSY-type relaxation compensation becomes possible. The use of CSA/CSA cross-correlation requires the generation of ¹⁵N–¹H^N ZQ coherence. Although the original single-quantum coherence-based scheme using DD/CSA cross-correlation (2) provides intrinsically better compensation than the ZQ-coherence-based scheme (Fig. 2), this potential advantage can hardly be exploited in 3D heteronuclear-resolved experiments (see Results), and we obtained good quality artifact-free data only with the use of the ZQ-coherence-based scheme. Further, the desired transfer function (Eq. 14) can be obtained with a lesser number of INEPT-type transfer steps than would be required with alternative single-quantum coherence-based schemes, and in this way signal loss during the magnetization transfer periods can be minimized. In addition, the resonances of the ¹⁵N–¹H₂ groups of Gln and Asn residues are not suppressed by the ZQ-TROSY correlation scheme, so that NOE crosspeaks with these groups are also observed in 3D NOESY-[¹H,¹⁵N,¹H]-ZQ-TROSY spectra.

In the experiment of Fig. 1b, the suppression of the strong diagonal peaks that are typically obtained with conventional NOESY schemes (6, 11, 16) may turn out to be of considerable interest in practice. A comparison of the two top slices in Fig. 3c with the corresponding slices in Fig. 3d shows that some ¹H^N–¹H^N cross-peaks can be resolved in the 3D NOESY-[¹H,¹⁵N,¹H]-ZQ-TROSY spectrum that are totally obscured by strong diagonal peaks in the corresponding conventional NOESY experiment. Diagonal peak suppression is achieved through selective saturation of the 1 → 3 transitions in all amide groups at the beginning of the experimental scheme of Fig. 1b and repolarization via NOE cross-relaxation with the magnetization of the 2 → 4 transitions. If both polarization transfer pathways of Eqs. 1 and 2 were recovered, two 3D ¹⁵N-resolved NOESY spectra could be obtained, with and without diagonal peaks, respectively.

ABBREVIATIONS

2D

two-dimensional

3D

three-dimensional

DQ

double-quantum

ZQ

zero-quantum

DD

dipole–dipole

CSA

chemical shift anisotropy

TROSY

transverse relaxation-optimized spectroscopy

NOE

nuclear Overhauser effect

NOESY

NOE spectroscopy

INEPT

insensitive nuclei enhanced by polarization transfer

DHNA

7,8-dihydroneopterin aldolase