Divalent Cation Selectivity Is a Function of Gating in Native and Recombinant Cyclic Nucleotide–gated Ion Channels from Retinal Photoreceptors

Abstract

The selectivity of Ca²⁺ over Na⁺ is ∼3.3-fold larger in cGMP-gated channels of cone photoreceptors than in those of rods when measured under saturating cGMP concentrations, where the probability of channel opening is 85–90%. Under physiological conditions, however, the probability of opening of the cGMP-gated channels ranges from its largest value in darkness of 1–5% to essentially zero under continuous, bright illumination. We investigated the ion selectivity of cGMP-gated channels as a function of cyclic nucleotide concentration in membrane patches detached from the outer segments of rod and cone photoreceptors and have found that ion selectivity is linked to gating. We determined ion selectivity relative to Na⁺ (PX/PNa) from the value of reversal potentials measured under ion concentration gradients. The selectivity for Ca²⁺ over Na⁺ increases continuously as the probability of channel opening rises. The dependence of PCa/PNa on cGMP concentration, in both rods and cones, is well described by the same Hill function that describes the cGMP dependence of current amplitude. At the cytoplasmic cGMP concentrations expected in dark-adapted intact photoreceptors, PCa/PNa in cone channels is ∼7.4-fold greater than that in rods. The linkage between selectivity and gating is specific for divalent cations. The selectivity of Ca²⁺ and Sr²⁺ changes with cGMP concentration, but the selectivity of inorganic monovalent cations, Cs⁺ and NH₄ ⁺, and organic cations, methylammonium⁺ and dimethylammonium⁺, is invariant with cGMP. Cyclic nucleotide–gated channels in rod photoreceptors are heteromeric assemblies of α and β subunits. The maximal PCa/PNa of channels formed from α subunits of bovine rod channels is less than that of heteromeric channels formed from α and β subunits. In addition, Ca²⁺ is a more effective blocker of channels formed by α subunits than of channels formed by α and β subunits. The cGMP-dependent shift in divalent cation selectivity is a property of αβ channels and not of channels formed from α subunits alone.

introduction

The essential functions of ion-conducting channels, selectivity and gating, have historically been described as independent processes, each determined by different features of the molecular structure of the channels (thoroughly reviewed by Andersen and Koeppe, 1992). Direct investigation of cloned channels, however, has demonstrated that these functions may be linked. In voltage-gated K⁺ channels, for example, the mutation of a single amino acid can change both the ion selectivity and the voltage dependence of activation (Yool and Schwarz, 1991; Heginbotham and MacKinnon, 1992). In N-methyl-d-aspartate channels, ion selectivity changes with the state of channel activity (Schneggenburger and Ascher, 1997); this is also the case in some voltage-gated K⁺ channels (Zheng and Sigworth, 1997). Because of structural similarities, cGMP-gated ion channels are recognized as members of the superfamily of voltage-gated ion channels (reviewed in Zagotta and Siegelbaum, 1996). In cGMP-gated channels, there is no direct evidence that ion selectivity is linked to the state of channel activity. However, Cervetto et al. (1988) have reported that the relative ability of various divalent cations to carry current through these channels in intact rod photoreceptors appears to change as a function of cGMP concentration.

The activity of cGMP-gated channels underlies the light-dependent conductance of rod and cone photoreceptors in the vertebrate retina. These channels select divalent over monovalent cations (rods: Colamartino et al., 1991; Zimmerman and Baylor, 1992; Wells and Tanaka, 1997; cones: Picones and Korenbrot, 1995; Haynes, 1995), although they select poorly among monovalent cations (rods: Furman and Tanaka, 1990; Menini, 1990; cones: Picones and Korenbrot, 1992; Haynes, 1995). The relative selectivity of Ca²⁺ over Na⁺ (PCa/ PNa) is higher in cone than in rod channels, both in native membranes (Haynes, 1995; Picones and Korenbrot, 1995) and in recombinant channels formed from α subunits alone (Frings et al., 1995). This difference may be important in understanding the difference in phototransduction signals between the two receptor types, because the Ca²⁺ influx through these channels, and its balance with efflux via a Na⁺/Ca²⁺,K⁺ exchanger, helps maintain the cytoplasmic free Ca²⁺ concentration in these cells (Yau and Nakatani, 1985; Miller and Korenbrot, 1987). The differences in PCa/ PNa between cones and rods make it likely that light-dependent changes in cytoplasmic Ca²⁺ caused by the same light intensity will be larger and faster in cones than in rods (Miller and Korenbrot, 1994; Korenbrot, 1995). Studies of ion selectivity in cGMP-gated channels of photoreceptor membranes, however, have only been conducted at ligand concentrations that fully activate the channels. Yet, in intact photoreceptors and under physiological conditions, at most 1–5% of the cGMP-gated channels are open (Cobbs et al., 1985; Hestrin and Korenbrot, 1987; Cameron and Pugh, 1990), which indicates that the highest cytoplasmic concentration of cGMP in the cells is about four- to five-fold smaller than K _1/2, the nucleotide concentration that half-saturates current amplitude. If ion selectivity were linked to gating, then the channel attributes in the intact photoreceptor might differ from those known from studies under saturating agonist concentrations.

We investigated the ion selectivity of cGMP-gated channels from both rods and cones as a function of cGMP concentration in membrane patches detached from intact outer segments. Contrary to the traditional view, we have found that the selectivity is indeed linked to gating: the selectivity for Ca²⁺ over Na⁺ increases continuously as the probability of channel opening rises. This proportionality is steeper in channels of rods than in those of cones. Under physiological cGMP concentrations, PCa/PNa in cone channels is ∼7.5-fold larger than that in rod channels, significantly larger than had been previously measured at saturating concentrations of cGMP (Picones and Korenbrot, 1995).

Cyclic nucleotide–gated channels in rod photoreceptors are heteromeric assemblies composed of at least two structural subunits, α and β (Chen et al., 1993; Korschen et al., 1995). By homology, it is likely that channels in cones also comprise α and β subunits, but such subunits have not been identified to date. α subunits of bovine rod and cone channels expressed in Xenopus oocytes preserve the differences in Ca²⁺ selectivity characteristic of native channels, but the ability of Ca²⁺ to block the channel and the absolute values of PCa/PNa differ from those of native channels (Frings et al., 1995; Picones and Korenbrot, 1995). This suggests that the selectivity and interaction of Ca²⁺ with cGMP-gated channels may depend on the interaction of α and β subunits. Using Xenopus oocytes as an expression system, we determined that the cGMP-dependent shift in divalent cation selectivity is a property of heteromeric αβ channels and not of homomeric channels formed from α subunits alone.

materials and methods

Materials

Striped bass (Morone saxitilis) were obtained from Professional Aquaculture Services and maintained in the laboratory for up to 6 wk under 10:14-h dark:light cycles. Tiger salamanders (Ambystoma tigrinum) were received from Charles Sullivan and maintained in the laboratory in an aquarium at 6°C under 12:12-h dark:light cycles. The UCSF Committee on Animal Research approved protocols for the upkeep and killing of the animals. l-cis-diltiazem was the kind gift of Tanabe Seiyako Co. Ltd.

Photoreceptor Isolation

Under infrared illumination and with the aid of a TV camera and monitor, retinas were isolated from dark-adapted animals and photoreceptors were dissociated as described in detail elsewhere (Miller and Korenbrot, 1993, 1994). Single cones were isolated by mechanical dissociation of fish retinas briefly treated with collagenase and hyaluronidase. Solitary cones were maintained in a Ringer's solution consisting of (mM): 143 NaCl, 2.5 KCl, 5 NaHCO₃, 1 Na₂HPO₄, 1 CaCl₂, 1 MgCl₂, 10 glucose, 10 HEPES, pH 7.5, osmotic pressure 309 mOsM. Rod outer segments were isolated by mechanical dissociation of tiger salamander retinas and were maintained in a Ringer's solution composed of (mM): 100 NaCl, 2 KCl, 5 NaHCO₃, 1 Na₂HPO₄, 1 CaCl₂, 1 MgCl₂, 10 glucose, 10 HEPES, pH 7.5, osmotic pressure 227 mOsM.

Solitary photoreceptors were firmly attached to a glass coverslip derivatized with wheat germ agglutinin (Picones and Korenbrot, 1992). The coverslip formed the bottom of a recording chamber held on the fixed stage of an upright microscope equipped with DIC optics and operated under visible light. A suspension of photoreceptors in Ringer's in which glucose was replaced with 5 mM pyruvate was added to the recording chamber and cells were allowed to settle and attach to the coverslip. After 5 min, the bath solution was exchanged with the normal, glucose-containing Ringer's.

The recording chamber consisted of two side-by-side compartments. Cells were held in one compartment that was continuously perfused with glucose containing Ringer's. The second, smaller compartment was continuous with the first one, but a movable barrier could be used to separate them (Picones and Korenbrot, 1992). We used tight-seal electrodes to obtain inside-out membrane fragments detached from the side of the outer segments of either cones or rods. Electrodes were produced from aluminosilicate glass (1.5 × 1.0 mm o.d. × i.d., 1724; Corning Glass Works). After forming a giga-seal and detaching the membrane fragment, the electrode was moved under the solution surface from the compartment containing the cells to the smaller compartment. The barrier was moved to isolate the two compartments and the electrode tip was placed within 100 μm from the opening of a 300-μm diameter glass capillary that delivered test solutions onto the cytoplasmic (outside) surface of the membrane patch. In a significant fraction of patches, we initially failed to observe cGMP-activated currents. We assumed these were closed vesicles since we frequently succeeded in eliciting currents after rapidly crossing the air–water interface.

Expression of Channels in Xenopus Oocytes

Plasmids containing either the α or β subunits of the bovine rod cGMP-gated channel flanked by 5′ and 3′ untranslated regions of the Xenopus β-globin gene (Liman et al., 1992) were kindly provided by the laboratories of W. Zagotta (University of Washington, Seattle, WA) and R. Molday (University of British Columbia, Vancouver, British Columbia, Canada), respectively. Capped RNA was transcribed from the linearized plasmid with T7 RNA polymerase (Swanson and Folander, 1992). RNA was purified by extractions with phenol/chloroform, recovered by ethanol precipitation and dissolved in RNAase-free water at a concentration of 2 μg/μl. Xenopus laevis oocytes, generously provided by the lab of L.Y. Jan (University of California at San Francisco) were each injected with ∼45 nl of RNA (90 ng). When α and β subunits were coinjected, RNA was mixed at a weight ratio of 4:1 (β:α). Injected oocytes were gently rocked at 18°C in ND96 media supplemented with 2.5 mM sodium pyruvate, 100 U/ml penicillin, and 100 μg/ml streptomycin. Oocytes were suitable for electrical studies 3–5 d after injection. Immediately before patch clamping, each oocyte was incubated for 5 min in a hypertonic solution composed of (mM): 200 NaCl, 10 HEPES, 1 CaCl2, 1 MgCl2, pH 7.5, and its vitelline membrane removed. Denuded oocytes were attached to clean glass coverslips in the recording chamber described above and bathed in ND96. We used tight-seal electrodes to obtain inside-out detached membrane patches. The electrodes were produced from aluminosilicate glass (1.5 × 1.0 mm o.d. × i.d.) with large tip openings (∼2 μm).

Ionic Solutions

In studies of both rod and cone photoreceptor membranes, we filled the tight-seal electrodes with the same, standard solution (mM): 150 NaCl, 5 BAPTA, 10 HEPES, adjusted with tetramethylammonium hydroxide (TMA-OH) to pH 7.5, osmotic pressure 300 mOsM. TMA-OH was used to titrate pH in all solutions because TMA does not permeate the channels of rods or cones (Picones and Korenbrot, 1992; Picco and Menini, 1993). Free Ca²⁺ concentration in this solution was <10⁻¹⁰ M. After detachment, all membrane patches were first exposed for at least 2 min to a standard solution composed of (mM): 150 NaCl, 1 EDTA, 1 EGTA, and 10 HEPES, adjusted with TMA-OH to pH 7.5. This solution thoroughly removed any endogenous modulator that might remain associated with the channels (Hackos and Korenbrot, 1997). Ionic concentrations were calibrated by measuring the osmotic pressure of the solutions and comparing it with published standards (Weast, 1987).

The solution bathing the cytoplasmic membrane surface was selected among four possible test conditions, depending on the objective of the experiment: (a) the standard solution defined above; (b) the standard solution containing varying concentrations of cGMP; (c) the standard solution containing varying concentrations of Ca²⁺ or other divalent cations, with or without cGMP; and (d) solutions containing 150 mM of various monovalent cations replacing Na⁺ in the standard solution, with or without cGMP. We began every experiment by measuring current– voltage (I–V)¹ curves under symmetric NaCl solutions first in the absence, and then in the presence, of 1 mM cGMP. The point at which these two curves intersect defined the origin (0,0) in the I–V plane for all measurements in that membrane patch. At the end of experimental manipulations, these curves were again measured. We only analyzed data from membrane patches in which the origin did not shift and in which the maximum cGMP-dependent conductance changed by ≤10%.

Internal and external solutions used to study membrane patches detached from Xenopus oocytes were similar to those used in studies of photoreceptor membranes, except that Cl⁻ was replaced with methanesulfonate to eliminate the Ca²⁺-activated Cl⁻ current characteristic of the oocyte membranes (Miledi and Parker, 1984). To use a Ag/AgCl electrode in the absence of Cl⁻ ions, we modified the tight-seal electrode holder to incorporate a 1-M KCl/agar bridge between the electrode-filling solution and the Ag/AgCl half-cell.

Electrical Recordings

We measured membrane currents under voltage clamp at room temperature with a patch clamp amplifier (8900; Dagan Corp.). Analogue signals were low-pass filtered below 1 kHz with an eight-pole Bessel filter (Frequency Devices Inc.) and were digitized on line at 3 kHz (FastLab; Indec). Membrane voltage was normally held at 0 mV and membrane currents were activated with continuous voltage ramps from −70 to +70 mV (over 1 s) or from −30 to +30 mV (over 0.5 s). In experiments with biionic solutions of monovalent cations, the holding voltage was set at the reversal potential corresponding to the ionic condition under investigation. We did so to avoid current flow at the holding voltage in order to minimize errors due to ion accumulation (or depletion) within the electrode's tip. Before initiating the voltage ramp, the voltage was held for 200 ms at either −70 or −30 mV (depending on the ramp range). This interval was sufficient to attain a steady current at −70 or −30 mV, following the time- dependent changes due to the relief by voltage of divalent cation channel block (rods: Colamartino et al., 1991; Zimmerman and Baylor, 1992; cones: Picones and Korenbrot, 1995). A Ag/AgCl reference electrode was connected to the bath through a 1-M KCl agar bridge to avoid shifts in electrode potential as solutions changed. As is conventional, outward currents are positive and the extracellular membrane surface was defined as ground.

Permeability Calculations

We calculated permeability ratios from reversal potentials using the Goldman-Hodgkin-Katz constant field equation. To determine reversal potentials of cGMP-activated currents, a straight line was fit to their I–V curve between −15 and +10 mV. Reversal was that potential at which this straight line intercepted the I–V curve measured in the same patch and under the same ionic gradient, but in the absence of cGMP (the leak current). Under biionic monovalent cation solutions, ion selectivity was expressed as a permeability ratio defined by the equation:

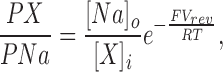1

where PX/PNa is the permeability ratio of the cation X relative to Na⁺, V_rev is the measured reversal potential, [Na]_o is the extracellular Na⁺ activity, and [X]_i is the intracellular activity of cation X. F, R, and T have their usual thermodynamic meanings. Activity coefficients were taken from Robinson and Stokes (1959).

Under conditions of symmetric Na⁺ with Ca²⁺ (or other divalent cation) added only to the intracellular side of the membrane, we used the following equation derived from a more general equation given by Lewis (1979):

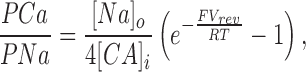2

where [Na] is the Na⁺ activity on both sides of the membrane, and [Ca]_i is the intracellular Ca²⁺ activity. Activity coefficients for Ca²⁺ in the presence of monovalent cations were taken from Butler (1968), and then squared in accordance with the Guggenheim convention (Robinson and Stokes, 1959). Activity coefficients for Sr²⁺ were assumed to be the same as for Ca²⁺.

Mathematical functions were fit to experimental data using nonlinear, least square minimization algorithms (Origin; Microcal Software, Inc.). Statistical errors are presented throughout as mean ± SD.

results

The Ca²⁺ to Na⁺ Selectivity Ratio in Channels of cGMP-gated Channels of Rod Photoreceptors Depends on Ligand Concentration

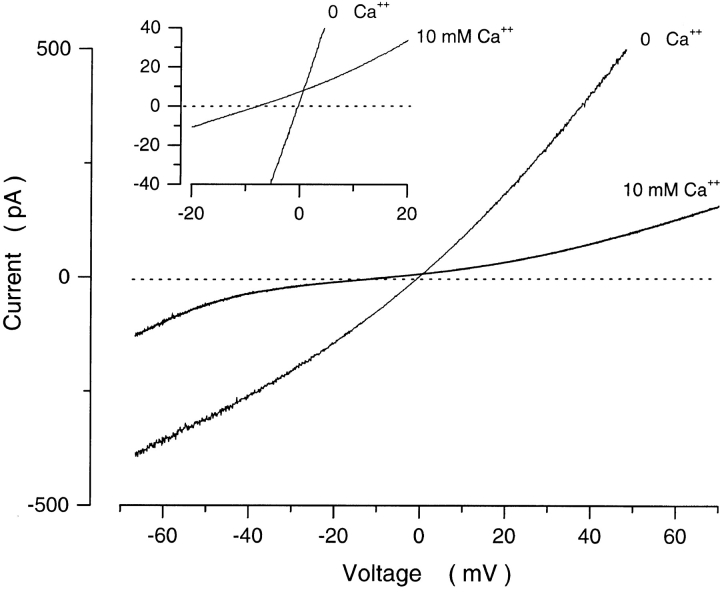
We examined cGMP-dependent currents in inside-out membrane patches detached from the outer segment of rods isolated from the tiger salamander retina. In the presence of 300 μM cGMP, a concentration at which the probability of channel opening is at its maximum value, the currents under symmetric Na⁺ solutions reversed direction at ∼0 mV and their I–V curves were nearly linear (Fig. 1). Addition of Ca²⁺ to the cytoplasmic membrane surface shifted the reversal potential to a more negative value and changed the shape of the I–V curve (Fig. 1), as has been previously reported (Colamartino et al., 1991; Zimmerman and Baylor, 1992; Tanaka and Furman, 1993; Picones and Korenbrot, 1995). The shift in reversal potential reveals that the channels are more permeable to Ca²⁺ than to Na⁺ and the change in the I–V curve reflects a voltage-dependent block of the channels by Ca²⁺. The average shift in reversal potential with 10 mM Ca²⁺ was −6.3 ± 0.27 mV (range −8.5 to −5.1, n = 7). This indicates (Eq. 2, using ion activities and assuming the Guggenheim convention, see materials and methods) that the average value of PCa/PNa is 6.48 ± 0.35.

Figure 1.

Effect of cytoplasmic Ca²⁺ on the I–V curve of cGMP-dependent currents measured in an inside out membrane patch detached from a tiger salamander rod outer segments. Currents were activated with a voltage ramp from −70 to +70 mV in the presence of 300 μM cGMP. Shown are currents measured in the same patch under symmetric Na⁺ solutions (150 mM) before (0 Ca²⁺) and after addition of 10 mM Ca²⁺. The inset illustrates the same data at higher resolution. Addition of Ca²⁺ blocked the current in a voltage-dependent manner and shifted the zero current potential to a more negative value (−7.3 mV), indicating that Ca²⁺ is more permeable than Na⁺ and PCa/PNa = 7.8. The currents shown are corrected for the leak current measured under the same ionic conditions, but in the absence of cGMP.

We investigated whether the value of PCa/PNa changed with cGMP concentration. Under symmetric Na⁺ solutions with 10 mM Ca²⁺ added to the cytoplasmic membrane surface, we measured membrane currents generated by voltage ramps in the presence of various cGMP concentrations (Fig. 2). As has been repeatedly shown before (reviewed in Yau and Chen, 1995; Zagotta and Siegelbaum, 1996), the amplitude of the current, at a fixed voltage, increased with cGMP in a manner well described by the Hill equation (Fig. 2 B).

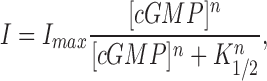3

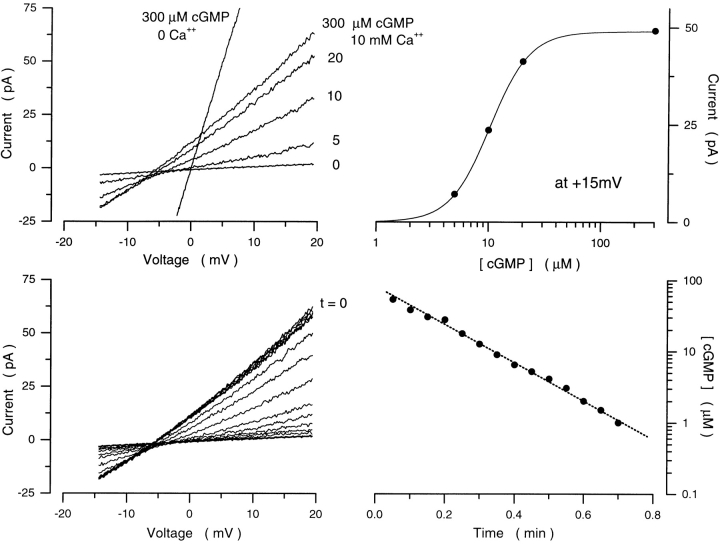
Figure 2.

The cGMP concentration ramp. (Top left) The rod membrane patch was first exposed to symmetric NaCl solutions free of divalent cations, and I–V curves recorded with a voltage ramp both before and after adding 300 μM cGMP. The I–V curve measured at 300 μM indicates the maximum possible current, and its intersection with the I–V curve measured at 0 cGMP defines the origin (0,0) of the I–V plane for this patch. Currents were then measured with 10 mM Ca²⁺ added to the cytoplasmic surface in the steady presence of 5, 10, 20, and 300 μM. (Top right) The current amplitude measured at a fixed voltage (+15 mV) in the I–V curves is a function of [cGMP] well described by the Hill equation (Eq. 3). For the data shown, K _1/2 = 10.3 μM and n = 2.48 define the “calibration” of the patch. (Bottom left) A step of 300 μM cGMP was next presented to the patch until a maximum, time-invariant current was observed. At t = 0, the superfusate was switched to the same solution, but free of cGMP. Rapid (500 ms) I–V curves were repeatedly measured at 2-s intervals as cGMP concentration declined. The concentration present at the moment any given I–V was recorded was determined by measuring the current amplitude at +15 mV and using the calibration curve in the top right. (Bottom right) Time course of cGMP washout from the patch determined from the I–V curves at bottom left. cGMP concentration in front of the membrane patch declined along a single exponential time course with time constant 12.6 s.

where I is the amplitude of the cGMP-dependent membrane current, I _max is its maximum value, [cGMP] is the concentration of cGMP, K _1/2 is that concentration necessary to reach one half the I _max value, and n is a parameter that reflects the cooperative interaction of cGMP molecules in activating the membrane current. Remarkably, the reversal potential of the I–V curves shifted as the cGMP concentration changed (Fig. 2), suggesting that PCa/PNa is not constant, but changes as a function of channel gating.

For experimental convenience and to reduce uncertainties due to potential changes in the leakage of the tight electrode seal, we used an alternative method to rapidly change cGMP concentration, which we will refer to as a cGMP concentration ramp. In this protocol, the patch was continuously superfused. In the presence of symmetric Na⁺ with 10 mM Ca²⁺ on the cytoplasmic membrane surface, we first measured I–V curves activated by fixed concentrations of cGMP up to 300 μM (Fig. 2). We used these data to generate a current amplitude–concentration function at a fixed voltage, +15 mV, for that patch (Fig. 2 B). Next, we imposed a step change in cGMP concentration to 300 μM and waited until currents reached a maximum, stationary value (typically 30 s). We then switched to a solution free of cGMP and continued superfusing, while repeatedly measuring I–V curves with rapid voltage ramps (−30 to +30 mV/0.5 s) delivered at 2-s intervals. As the cGMP diffused away from the patch, currents decreased in amplitude (Fig. 2). As expected from simple diffusion between two compartments, the time course of cGMP loss was well described by a single exponential (Fig. 2). We limited our analysis to patches in which the time constant of this exponential was ≥12 s. Under these conditions, we assume that individual I–V curves (each measured in 500 ms) are measured at constant cGMP. We measured current amplitude at +15 mV in each ramp I–V curve and, using the calibration data first generated in the same patch, we established the cGMP concentration at which each ramp I–V curve was measured.

Using cGMP concentration ramps, we confirmed that the reversal potential measured under a Ca²⁺ concentration gradient changes with cGMP concentration. The reversal potential shifted progressively towards less negative values as cGMP concentration decreased, revealing that the channels become less selective for Ca²⁺ over Na⁺ as their probability of opening decreases (Fig. 3). The dependence of reversal potential, and therefore PCa/PNa (Eq. 2), on [cGMP] was well described by a Hill function modified in the following form (Fig. 3):

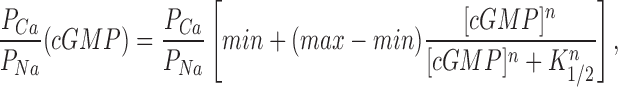4

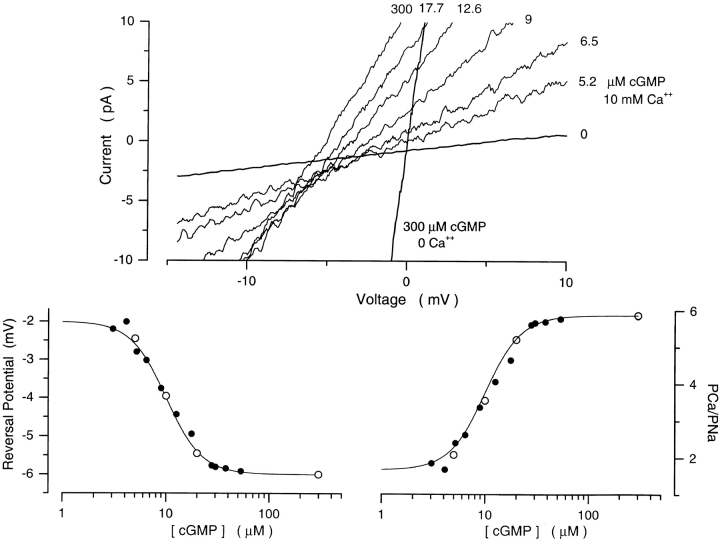
Figure 3.

Ca²⁺ selectivity of cGMP-gated channels in rods is a function of cGMP concentration. (Top) I–V curves measured with a cGMP concentration ramp in the presence of symmetric Na⁺ (150 mM) with Ca²⁺ (10 mM) added to the cytoplasmic surface of the membrane. The data is from the same patch illustrated in Fig. 2. The cGMP concentration at the moment each I–V curve was measured is given next to the curve. Also shown are currents measured in the same patch under symmetric Na⁺ solutions without added Ca²⁺ before (0) and after adding 300 μM cGMP. The reversal potential was measured by fitting a straight line to the I–V curves between −15 and +10 mV, and determining the voltage at which this straight line crossed the 0 cGMP I–V curve (the leak current). (Bottom left) Reversal potential and membrane conductance as a function of [cGMP]. (•) Reversal potentials measured in the data on top, (○) normalized current amplitude (plotted as 1 − I/I_max and scaled) measured in the same patch at +15 mV with steps of cGMP concentration (5, 10, 20, 300 μM). The continuous line depicts the modified Hill equation (Eq. 4) optimally fit to the data points. The values of the adjustable parameters were K _1/2 = 10.3 μM, n = 2.48, min = −2.0 mV, and max = −6.1 mV. (Bottom right) PCa/PNa calculated from the reversal potentials on the left as a function of [cGMP]. The continuous line is the same Hill equation as on the left, with PCa/PNa_min = 1.7 and PCa/PNa_max = 5.93.

where

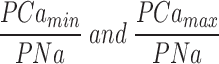are the asymptotic minimum and maximum values attained by PCa/PNa, K _1/2 is the concentration at which PCa/PNa has a value midway between its maximum and minimum values, and n is an adjustable parameter that reflects ligand cooperativity. The average value of the parameters that best fit our data were K _1/2 = 17.2 ± 8.6 μM, n = 2.43 ± 0.37, PCa/PNa_max = 6.48 ± 0.35, and PCa/PNa_min = 1.89 ± 0.52 (n = 14). In every patch tested (n = 14), the values of K _1/2 and n that best described the cGMP dependence of PCa/PNa were exactly the same as those that best described the dependence of membrane conductance on nucleotide concentration (Eq. 3). This is illustrated in Fig. 3, where the change in conductance is plotted as the value of (1 − I/I_max) at +15 mV, where I is the current at a given cGMP concentration and I_max is its maximum value. The plot is scaled to have its minimum and maximum values, 0 and 1, respectively, match the minimum and maximum values of PCa/PNa. While plotting conductance this way is unconventional, since the function decreases as cGMP concentration increases, it allows us to compare directly the cGMP dependence of conductance and PCa/PNa. Membrane conductance is a direct measure of the average probability of channel opening (Picones and Korenbrot, 1994). In rods, therefore, PCa/PNa changes 3.42 ± 0.95-fold (n = 14) between its minimum and maximum values in a manner that is directly proportional to the probability of channel activation.

cGMP-dependent Shifts in Reversal Potential Do Not Occur under Symmetric Na⁺ Solutions

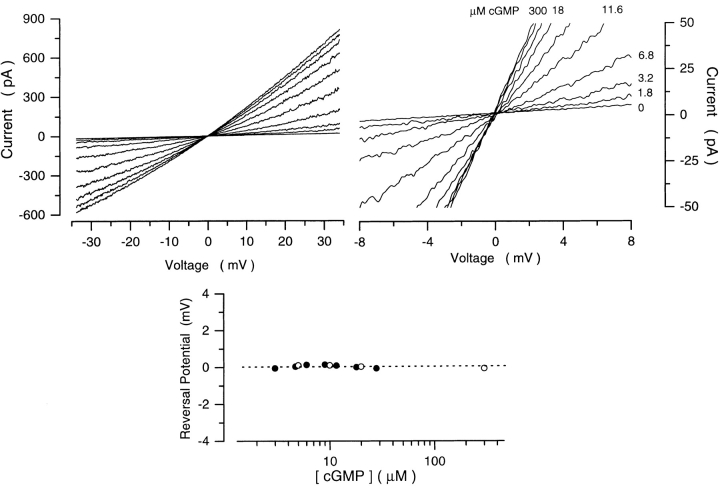
Patches excised from tiger salamander rod outer segments often exhibit cGMP-activated currents as large as 1–2 nA at −70 mV under symmetric Na⁺ solutions. These large currents, when sustained over a long time period, display a slow exponential decline in amplitude caused by the accumulation of Na⁺ ions at the electrode tip and a consequent, slow shift in reversal potential (Zimmerman et al., 1988). It was important, therefore, to ascertain that the rapid changes in reversal potential we observed in the presence of symmetric Na⁺ and a Ca²⁺ gradient did not arise from Na⁺ accumulation at the electrode tip. Using cGMP concentration ramps, we measured the reversal potential under symmetric Na⁺ solutions as a function of cGMP (Fig. 4). If Na⁺ accumulation occurred to a significant extent under our experimental protocol, then the reversal potential should shift in time. In fact, we found that the reversal potential was time invariant and independent of [cGMP]. The same results were obtained in every patch we studied with this protocol (n = 21). In solutions containing 10 mM Ca²⁺, Na⁺ accumulation should occur to an even lesser extent since ionic currents are much smaller due to Ca²⁺-dependent block of the pore. Furthermore, accumulation of Ca²⁺ ions on the extracellular side of the patch cannot occur due to the presence of 5 mM BAPTA in the patch pipette solution. Thus, the cGMP-dependent shift in reversal potential under Ca²⁺ concentration gradients reflects changes in PCa/PNa, and not the generation of an asymmetry in Na⁺ or Ca²⁺ concentrations.

Figure 4.

In rod channels, reversal potential under symmetric Na⁺ solutions (150 mM) is independent of cGMP. (Top left) I–V curves measured between −30 and +30 mV with a cGMP concentration ramp. (Top right) High resolution presentation of the data on the left. The cGMP concentration at the moment each I–V curve was measured is given next to the curve. (Bottom) Reversal potential as a function of [cGMP]. The mean value is 0 mV and is independent of cGMP concentration.

Effectiveness of Ca²⁺ Block Is also a Function of cGMP Concentration

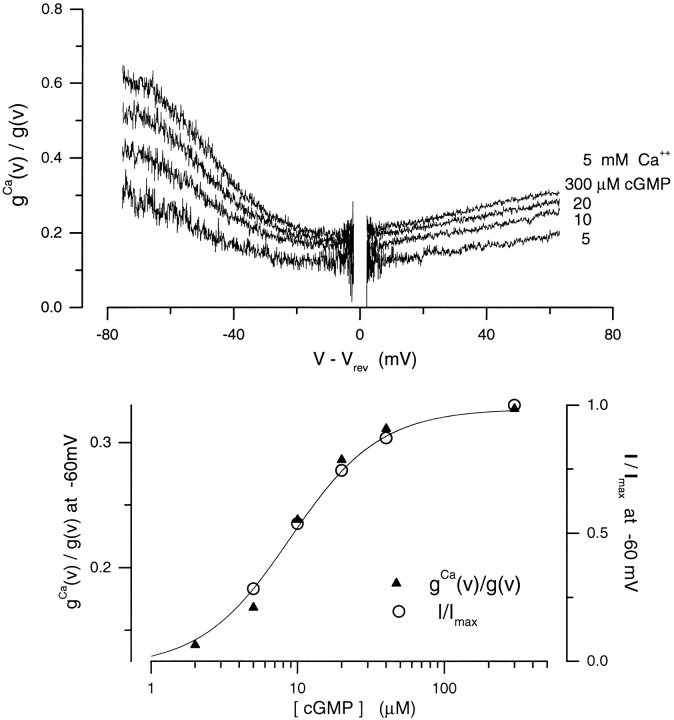
Our results reveal the complex interactions between gating and ion selectivity for Ca²⁺ ions. Previous reports have documented that the blocking effect of Ca²⁺ on the channels is also a function of cGMP (Colamartino et al., 1991; Karpen et al., 1993; Tanaka and Furman, 1993). Fig. 5 illustrates this phenomenon in our experiments. The extent of conductance block by 5 mM Ca²⁺ in the voltage range between −80 and +80 mV was measured in the same patch at various cGMP concentrations (5, 10, 20, 40, 300 μM). The I–V curves under symmetric Na⁺ solutions (150 mM) were first measured in the presence of the various cGMP concentrations using a voltage ramp. The same curves were then measured again at each of the cGMP concentrations, but now with 5 mM Ca²⁺ added to the cytoplasmic surface. The extent of Ca²⁺-dependent conductance block, g ^Ca(v)/g(v) was determined by dividing, for each cGMP concentration tested, the current ramp measured in the presence of 5 mM cytoplasmic Ca²⁺ by the current ramp measured in its absence (Fig. 5). At all cGMP concentrations, the conductance block was maximal near the reversal potential, and it was relieved by either depolarization or hyperpolarization. At any given voltage, the extent of block was a function of cGMP, and this dependence was well described by the same Hill function that describes the cGMP dependence of current amplitude (Fig. 5). We obtained the same results in every patch we tested (n = 4). Thus, changing the probability of channel opening affects not only the ion selectivity of the channel for Ca²⁺, but also the interaction between Ca²⁺ and the pore.

Figure 5.

Extent of voltage- dependent Ca²⁺ block is a function of cGMP concentration in rod photoreceptors. (Top) The extent of conductance block by 5 mM Ca²⁺ in the voltage range between −80 and +80 mV was measured in the same patch at various cGMP concentrations (5, 10, 20, and 300 μM, as labeled). The I–V curves under symmetric Na⁺ solutions (150 mM) were first measured in the presence of the various cGMP concentrations using a voltage ramp. The same curves were then measured again at each of the cGMP concentrations, but now with 5 mM Ca²⁺ added to the cytoplasmic surface. The extent of Ca²⁺-dependent conductance block, g ^Ca(v)/g(v) was determined by dividing, for each cGMP concentration tested, the current ramp measured in the presence of 5 mM cytoplasmic Ca²⁺ by the ramp measured in its absence. (Bottom) The extent of Ca²⁺ block measured at −60 mV (▴), measured from the data on top, is a function of cGMP well described by a modified Hill equation (Eq. 4). The continuous line is a Hill function optimally fit to the data. The values of the adjustable parameters are: K _1/2 = 9.43, n = 1.4, max = 0.33, min = 0.095. The same function describes the dependence of current amplitude on cGMP concentration (○) in the same patch in the presence of Ca²⁺.

The Selectivity for Other Divalent Cations over Na⁺ Is a Function of cGMP Concentration

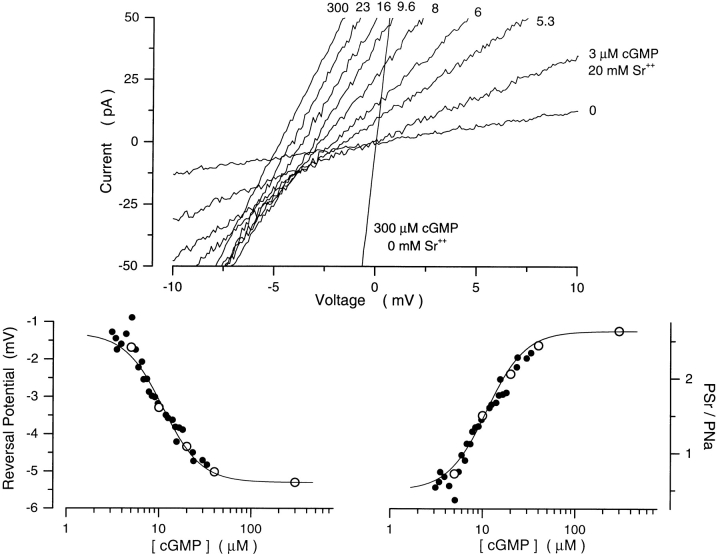
We explored whether the effect of cGMP on Ca²⁺ selectivity was specific for this ion or was a feature common to other divalent cations. We elected to study the selectivity properties of Sr²⁺, rather than Mg²⁺, because this cation permeates the channels, but is a less effective channel blocker than Ca²⁺ or Mg²⁺. Using cGMP concentration ramps, we measured the reversal potential under symmetric Na⁺ solutions with 20 mM Sr²⁺ added to the cytoplasmic membrane surface of the patch (Fig. 6). In the presence of saturating cGMP (300 μM), the reversal potential was −5.3 ± 0.21 mV (n = 8), which indicates that PSr/PNa = 2.71 ± 0.13. As with Ca²⁺, the reversal potential shifted to less negative values as cGMP decreased (Fig. 6). We calculated PSr/PNa from the reversal voltage (Eq. 2) and found that the dependence on cGMP of this selectivity ratio was well described by the modified Hill equation (Eq. 4; Fig. 6). On average, the values of the parameters that best fit our data were: K _1/2 = 14.8 ± 6.2 μM, n = 2.6 ± 0.32, PSr/PNa_min = 0.64 ± 0.27, and PSr/PNa_max = 2.71 ± 0.13 (n = 8). Again, in each instance, the values of K _1/2 and n were the same as those that best described the dependence of current amplitude on cGMP in the same patch (Eq. 3). Thus, the effects of channel gating on selectivity are not specific for Ca²⁺.

Figure 6.

Sr²⁺ selectivity of the cGMP-gated channels in rods is a function of cGMP concentration. (Top) I–V curves measured with a cGMP concentration ramp in the presence of symmetric Na⁺ (150 mM) with 20 mM Sr²⁺ added to the cytoplasmic surface of the membrane. The cGMP concentration at the moment each I–V curve was measured is given next to the curve. (Bottom left) Reversal potential and membrane conductance as a function of [cGMP]. (•) Reversal potentials measured in data in top, (○) normalized current amplitude (plotted as scaled, 1 − I/I_max) measured in the same patch at +15 mV with steps of cGMP concentration (5, 10, 20, 40, 300 μM). The continuous line is the modified Hill equation (Eq. 4) optimally fit to the data. The values of the adjustable parameters are K _1/2 = 11.0 μM, n = 2.1, min = −1.38 mV, and max = −5.33 mV. (Bottom right) PSr/ PNa calculated from the reversal potentials on left as a function of [cGMP]. The continuous line is the same Hill function as on the left, but with PSr/PNa_min = 0.47 and PSr/PNa_max = 2.71.

Inorganic Monovalent Cation Selectivity Does Not Change as a Function of cGMP Concentration

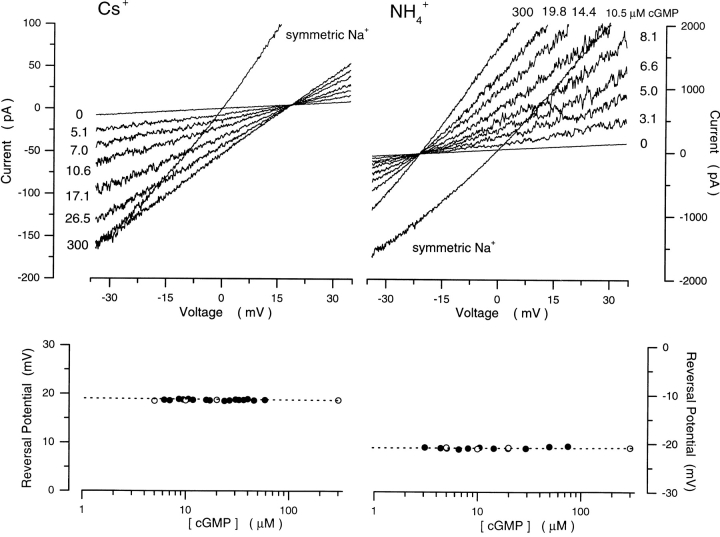
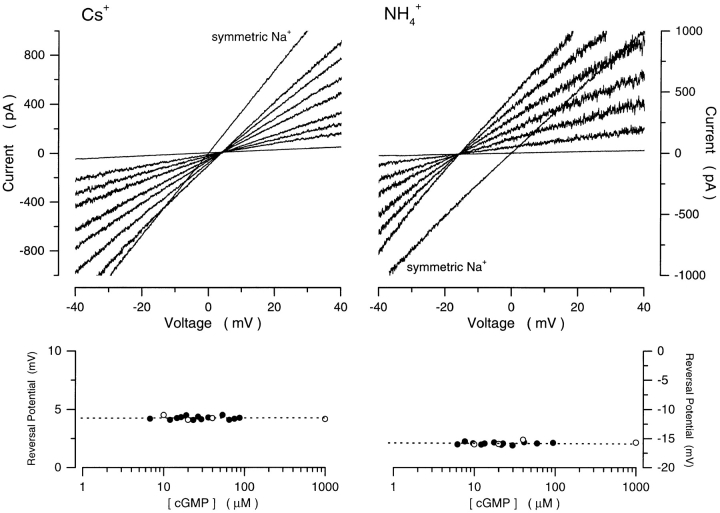
While the selectivity among monovalent cations is poor in the rod channel, there are, nonetheless systematic differences in selectivity among these ions (Furman and Tanaka, 1990; Menini, 1990). We explored whether channel gating affected the selectivity among inorganic monovalent cations. We elected to test the effects of cGMP on the selectivity between Cs⁺ and Na⁺ or NH₄ ⁺ and Na⁺. Cs⁺ is less permeable than Na⁺, while NH₄ ⁺ is more permeable (Furman and Tanaka, 1990; Menini, 1990). Using cGMP concentration ramps, we measured the reversal potential under biionic conditions of either 150 mM Cs⁺/150 mM Na⁺ or 150 mM NH₄ ⁺/150 mM Na⁺ (Fig. 7). At 300 μM cGMP, the reversal potential was 18.1 ± 1.6 mV (n = 8) for Cs⁺ and −22.2 ± 2.2 mV for NH₄ ⁺ (n = 6). These results reproduce those previously reported by others (Furman and Tanaka, 1990; Menini, 1990). From Eq. 1, we find that PCs/PNa = 0.50 ± 0.03 and PNH₄/PNa = 2.44 ± 0.21. Unlike our findings with divalent cations, the reversal potential under monovalent biionic conditions was constant and independent of cGMP (Fig. 7). Thus, the effect of gating on ion selectivity is exclusive for divalent cations.

Figure 7.

Cs⁺ and NH₄ ⁺ selectivity of cGMP-gated channels in rod photoreceptors is independent of cGMP concentration. (Top left) I–V curves activated with a cGMP concentration ramp in the presence of biionic solutions: Cs⁺ (150)/Na⁺ (150). The cGMP concentration at the moment each I–V curve was measured is given next to the curve. Also shown is the I–V curve activated by 300 μM cGMP in the same patch in the presence of symmetric Na⁺ solutions. (Top right) I–V curves measured with a cGMP concentration ramp in the presence of biionic NH₄ ⁺ (150)/Na⁺ (150) solutions. The cGMP concentration at the moment each I–V curve was measured is given next to the curve. Also shown is the I–V curve activated by 300 μM cGMP in the same patch in the presence of symmetric Na⁺ solutions. (Bottom left) Reversal potential as a function of [cGMP] measured in the biionic Cs⁺/Na⁺ solutions shown on top. The dashed line is the mean of these values, 18.6 mV, which yields PCs/PNa = 0.49. (Bottom right) Reversal potential as a function of [cGMP] measured in the biionic NH₄ ⁺/Na⁺ solutions shown on top. The dashed line is the mean of these values, −20.8 mV, which yields PNH₄/PNa = 2.31.

The Organic Monovalent Cation Selectivity Does Not Change as a Function of cGMP Concentration

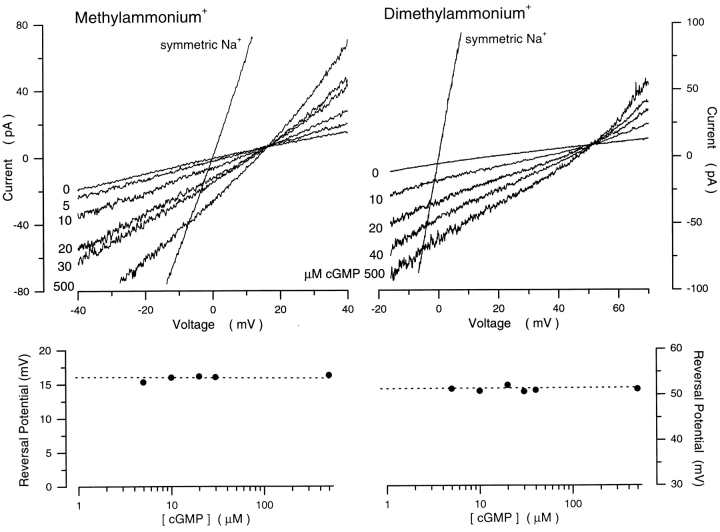
The relative selectivity of organic cations through the cGMP-gated channels has been used to asses the steric hindrance imposed on ion flux by the selectivity filter in the channel (rods: Picco and Menini, 1993; cones: Stotz and Haynes, 1996). To determine whether gating affects steric hindrance, we investigated the effects of cGMP on the selectivity between methylammonium (MA⁺) and Na⁺ or dimethylammonium (DMA⁺) and Na⁺. Using cGMP concentration ramps, we measured the reversal potential under biionic conditions of either 150 mM MA⁺/150 mM Na⁺ or 150 mM DMA⁺/ 150 mM Na⁺ (Fig. 8). At 500 μM cGMP, the reversal potential was 16.5 ± 1.5 mV (n = 4) for MA⁺ and 52.0 ± 2.2 mV (n = 5) for DMA⁺ (Fig. 8). Eq. 1 yields relative selectivities of PMA/PNa = 0.53 ± 0.03 and PDMA/ PNa = 0.13 ± 0.011, in agreement with previous measurements (Picco and Menini, 1993). As in the case of inorganic cations, we found no changes in the channel selectivity for organic monovalent cations as a function of cGMP (Fig. 8). Thus the apparent pore radius of the selectivity filter does not appear to change as a function of channel gating.

Figure 8.

Methylammonium⁺ and dimethylammonium⁺ selectivity of cGMP-gated channels in rod photoreceptors is independent of cGMP concentration. (Top left) I–V curves activated with steps of cGMP, as labeled next to each curve, in the presence of biionic solutions: MA (150)/Na⁺ (150). Also shown is the I–V curve activated by 500 μM cGMP in the same patch in the presence of symmetric Na⁺ solutions. (Top right) I–V curves activated with steps of cGMP, as labeled next to each curve, in the presence of biionic solutions: DMA (150)/ Na⁺ (150). Also shown is the I–V curve activated by 500 μM cGMP in the same patch in the presence of symmetric Na⁺ solutions. (Bottom left) Reversal potential as a function of [cGMP] measured in the biionic MA/Na⁺ solutions shown on top. The dashed line is the mean of these values, 16.0 mV, which yields PMA/PNa = 1.90. (Bottom right) Reversal potential as a function of [cGMP] measured in the biionic DMA/Na⁺ solutions shown on top. The dashed line is the mean of these values, 51.5 mV, which yields PDMA/PNa = 7.94.

The Effects of Gating on the Ion Selectivity of Recombinant Channels from Rods

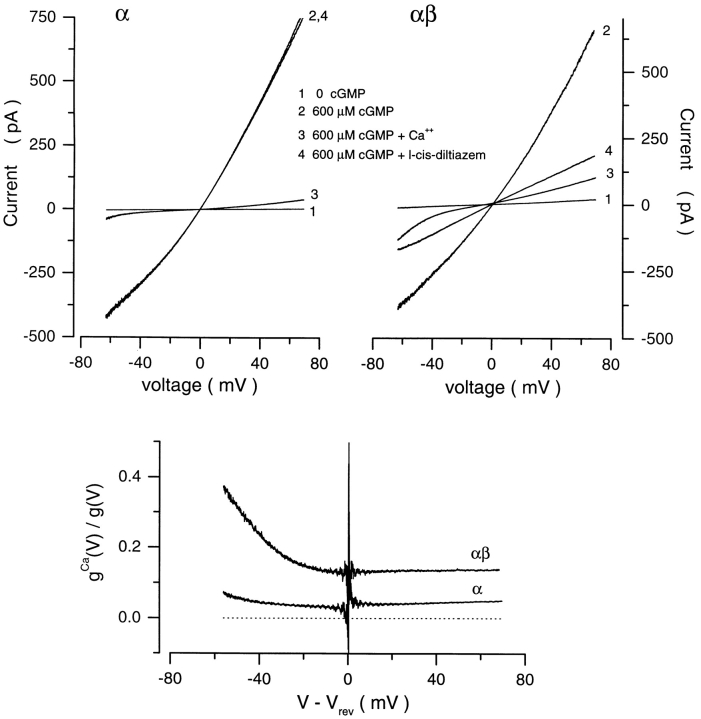
Cyclic nucleotide–gated channels in rod photoreceptors and olfactory neurons are heteromeric assemblies of at least two structural subunits, α and β (Chen et al., 1993; Bradley et al., 1994; Liman and Buck, 1994; Korschen et al., 1995). We investigated whether the cGMP dependence of ion selectivity of the native channel is a feature of the α subunits or requires the coexpression of α and β subunits. We expressed bovine rod α or αβ channels in Xenopus oocytes and measured cGMP- dependent currents in inside-out, detached membrane patches. As discussed in materials and methods, we took precautions to eliminate contamination of the recorded currents by Ca²⁺-dependent Cl⁻ currents native to the oocyte. In experiments with αβ channels, we verified that the channels were indeed formed from both α and β subunits by testing the action of l-cis-diltiazem (10 μM), which effectively blocks only αβ heteromeric channels, and not α homomeric channels (Chen et al., 1993; Korschen et al., 1995) (Fig. 9). Also, our data confirms that homomeric α channels are more sensitive to block by Ca²⁺ than αβ channels (Fig. 9) (Korschen et al., 1995).

Figure 9.

Homomeric α channels are functionally distinguishable from heteromeric αβ channels expressed in Xenopus oocytes. I–V curves were measured in the presence (curve 2) or absence (curve 1) of saturating cGMP concentration (600 μM) in inside out membrane patches expressing bovine α (top left) or αβ (top right) channels. In each of the same membrane patches, cGMP-activated currents were measured under symmetric Na⁺ (150 mM) solutions (curve 2), and also after adding to the cytoplasmic surface either Ca²⁺ (10 mM) (curve 3) or l-cis-diltiazem (10 μM) (curve 4). l-cis-diltiazem is an effective blocker of αβ, but not α channels. (Bottom) Voltage-dependent current block by Ca²⁺ calculated from the data on top by dividing the cGMP-dependent current measured after adding Ca²⁺ by that measured before.

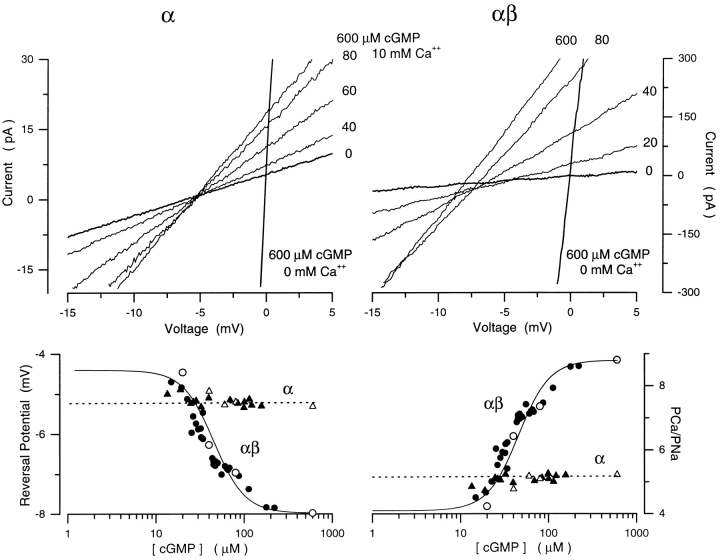
We measured I–V curves of cGMP-dependent currents in the presence of symmetric Na⁺ with 10 mM Ca²⁺ added to the cytoplasmic surface of the membrane containing either α or αβ channels (Fig. 10). At saturating cGMP, the reversal potential for α channels was −4.8 ± 1.2 mV (n = 7), which implies that PCa/ PNa = 4.6 ± 0.79, but for αβ channels the reversal potential was −8.4 ± 1.1 mV (n = 12), which implies that PCa/PNa = 9.4 ± 1.1. Thus the heteromeric αβ channel is about twice more selective for Ca²⁺ over Na⁺ than the α homomeric channel.

Figure 10.

Ca²⁺ selectivity as a function of cGMP in recombinant bovine rod α or αβ cGMP-gated channels. I–V curves measured in Xenopus oocyte membranes expressing either homomeric α (top left) or heteromeric αβ (top right) channels. Currents were activated with step concentrations of cGMP in the presence of symmetric Na⁺ (150 mM) solutions with Ca²⁺ (10 mM) added to the cytoplasmic side of membrane. cGMP concentrations are given next to each curve. Each trace is the signal average of 10 individual curves measured at each cGMP concentration. Also shown are I–V curves measured under symmetric Na⁺ in the absence of cGMP or after addition of saturating cGMP (600 μM) in order to define the origin (0,0) of the I–V plane. (Bottom left) Reversal potentials as a function of [cGMP] measured in α (▴) or αβ (•)channels. Open symbols are data measured in the same patch with steps of cGMP, while filled symbols are data measured with a cGMP concentration ramp. The mean value of the reversal potential measured at all cGMP concentrations in α channels (dashed line) is −5.2 mV. The continuous line is the modified Hill equation (Eq. 4) that best fits the data collected on αβ channels. The adjustable parameters are: K _1/2 = 45.4 μM, n = 2.45, min = −4.38 mV, and max = −8.0 mV. The same parameters define the Hill equation that best describes the dependence on cGMP of current amplitude measured at +15 mV in the same patch, under the same ionic conditions. (Bottom right) PCa/PNa as a function of [cGMP] measured in α (▴) and αβ (•) channels from the data on the left. The mean PCa/PNa for the α channel (dashed line) is 5.1. For the αβ channels, the same Hill function as on the left fits the data optimally with PCa/PNa_min = 4.1 and PCa/PNa_max = 8.8.

More remarkable, however, is the difference between the channels on the effect of gating on ion selectivity. In α channels, PCa/PNa was invariant with cGMP concentration in every patch we tested (n = 8) (Fig. 10). In αβ channels, as in native channels, the divalent cation selectivity decreased as cGMP concentration was lowered (Fig. 10). The dependence of PCa/PNa on cGMP was well described by the modified Hill equation, (Eq. 4). The average value of the parameters in the equation that best fit our data were: K _1/2 = 45.2 ± 15.6 μM, n = 2.6 ± 0.24, PCa/PNa_max = 9.4 ± 1.1, PCa/PNa_min = 4.4 ± 1.4 (n = 12).

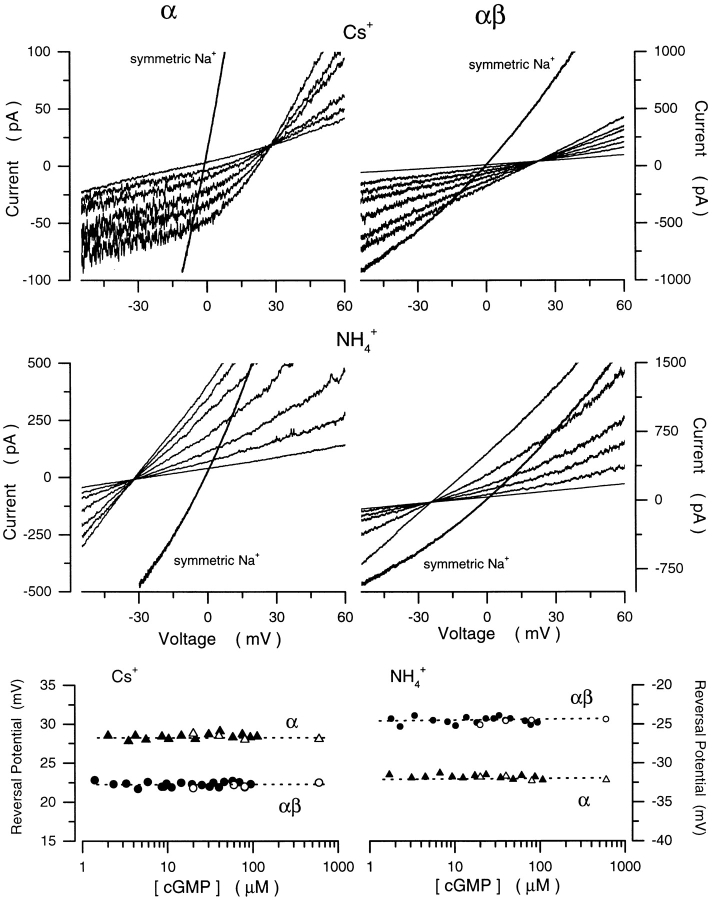
To determine whether the shifts in selectivity for the αβ channel were specific for divalent cations, we tested the selectivity for Cs⁺ and NH₄ ⁺ in both α and αβ channels. In Fig. 11, we illustrate I–V curves of cGMP-dependent currents measured in the presence of biionic solutions of Cs⁺/Na⁺ or NH₄ ⁺/Na⁺. The I–V curves were generally similar to those recorded from native rod channels under comparable conditions (see Fig. 7), except that α channels in the presence of biionic solutions of Cs⁺/Na⁺ display an unusual nonlinearity at potentials more negative than the reversal potential. In the presence of saturating cGMP, the selectivity sequence of αβ was the same as α, although the absolute values of PX/ PNa differed between the two channels. Mean values of V_rev for the α channel were Cs⁺, 28.6 ± 2.5 mV (n = 8); NH₄ ⁺, −31.2 ± 1.8 mV (n = 8), which yields PCs/PNa = 0.33 ± 0.03 and PNH₄/PNa = 3.49 ± 0.25. Mean values of V_rev for the αβ channel were Cs⁺, 21.9 ± 1.9 mV (n = 6); NH₄ ⁺, −24.5 ± 2.2 mV (n = 6), which indicate that PCs/PNa = 0.43 ± 0.32 and PNH₄/PNa = 2.67 ± 0.23. The reversal potentials were the same at all cGMP concentrations tested (Fig. 11). Thus, recombinant α or αβ channels, just like native channels, select poorly among monovalent cations, and this selectivity is unaffected by gating. However, the absolute value of the selectivity among monovalent cations, just as among divalents, differs in homomeric and heteromeric channels.

Figure 11.

Cs⁺ and NH₄ ⁺ selectivity is not a function of cGMP in recombinant bovine rod α or αβ cGMP-gated channels. Panels illustrate I–V curves measured using cGMP concentration ramps in the presence of biionic solutions of either Cs⁺ (150 mM)/Na⁺ (150 mM) (top) or NH₄ ⁺ (150 mM)/Na⁺ (150 mM) (middle). (Left, top and middle) Currents measured in α channels. (Right, top and middle) Currents measured in αβ channels. Reversal potentials as a function of [cGMP] for Cs⁺ (bottom left) or NH₄ ⁺ (bottom right) measured in α (▴) and αβ (•) channels. Open symbols are data measured with steps of cGMP, while filled symbols are data measured with a cGMP concentration ramp in the same membrane. The average reversal potentials are, for α channels: Cs⁺ = 28.3 mV; NH₄ ⁺ = −31.8 mV, which correspond to PCs/PNa = 0.32 and PNH₄/ PNa = 3.59. For αβ channels: Cs⁺ = 22.5 mV and NH₄ ⁺ = −24.5 mV, which correspond to PCs/PNa = 0.40 and PNH₄/ PNa = 2.68.

Relative Ca²⁺ Permeability also Depends on cGMP in Channels of Cone Photoreceptors

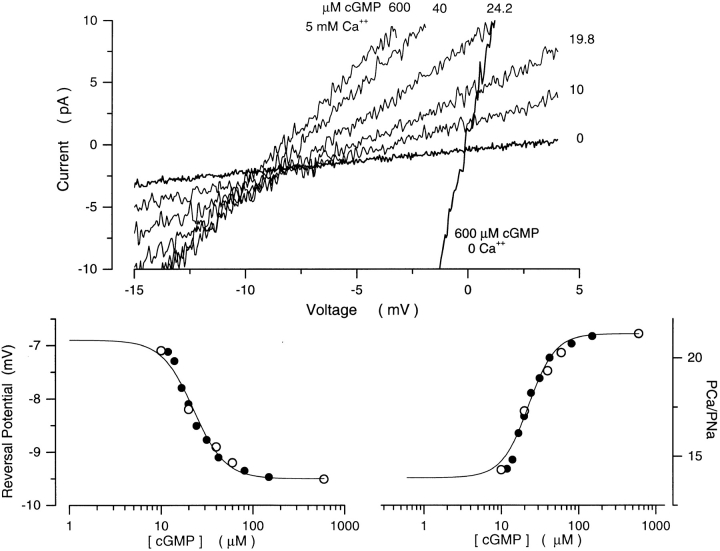
cGMP-gated channels of cone photoreceptors are significantly more permeable to Ca²⁺ than those of rods (Frings et al., 1995; Haynes, 1995; Picones and Korenbrot, 1995). However, past measurements were conducted under saturating cGMP concentrations. If channels in cones, like those of rods, change divalent cation selectivity as a function of cGMP, then differences observed under high cGMP concentrations might not occur under lower concentrations, such as those expected in the photoreceptor cells under physiological conditions. We investigated the effects of cGMP on the value of PCa/PNa in cGMP-gated channels from the striped bass single cone. Using cGMP concentration ramps, we measured the reversal potential under symmetric Na⁺ solutions with 5 mM Ca²⁺ added to the cytoplasmic membrane surface (Fig. 12). At saturating cGMP, the reversal potential was −9.4 ± 0.5 mV (n = 12), which implies that, in cones, PCa/PNa = 21.7 ± 1.65 (n = 12), consistent with earlier measurements (Picones and Korenbrot, 1995). As in rods, the reversal potential shifted to less negative values as cGMP concentration declined (Fig. 3). Again, the dependence on cGMP of PCa/PNa was well described by the modified Hill equation, (Eq. 4; Fig. 12). On average, we found that K _1/2 = 43 ± 14 μM, n = 2.8 ± 0.4, PCa/PNa_min = 14.0 ± 1.6 and PCa/PNa_max = 21.7 ± 1.7 (n = 12). The extent of shift in divalent cation selectivity with cGMP, however, was less in cones than in rods. The decrease in Ca²⁺ permeability between saturating and zero cGMP (PCa/ PNa_max and PCa/PNa_min) was 1.55 ± 0.21 (n = 12). Thus, in intact, dark-adapted photoreceptor cells, where only ∼3% of the channels are open, PCa/PNa in cones can be expected to be 7.41 ± 0.85-fold larger than in rods.

Figure 12.

Ca²⁺ selectivity in cGMP-gated channels of cone photoreceptors is a function of cGMP. (Top) I–V curves measured with a cGMP concentration ramp in the presence of symmetric Na⁺ (150 mM) with Ca²⁺ (5 mM) added to the cytoplasmic surface of the membrane. The cGMP concentration at the moment each I–V curve was measured is given next to the curve. Also shown are currents measured in the same patch under symmetric Na⁺ solutions without added Ca²⁺ before (0), and after adding 600 μM cGMP. (bottom left) Reversal potential as a function of cGMP. For the same patch illustrated on top: •, data measured with a cGMP concentration ramp; ○, data measured with steps of cGMP concentrations (10, 20, 40, 60, 600 μM). The continuous line is a modified Hill equation (Eq. 4) optimally fit to the data. The values of the adjustable parameters are: K _1/2 = 22.5 μM, n = 2.5, min = −6.91 mV, and max = −9.5 mV. The same parameters describe the dependence of current amplitude on cGMP concentration in the same patch and under the same ionic conditions at +15 mV. (Bottom right) PCa/PNa as a function of [cGMP] calculated from the reversal potentials on the left. The continuous line is the same Hill function as in the left, but with PCa/PNa_min = 13.9 and PCa/PNa_max = 21.2.

Monovalent Cation Selectivity Is Independent of cGMP in Channels of Cones

We tested whether in channels of cones, like those of rods, the selectivity among monovalent inorganic cations was independent of cGMP. We studied Cs⁺ and NH₄ ⁺ selectivities relative to Na⁺ using cGMP concentration ramps under biionic solutions of 150 mM Cs⁺/ Na⁺ or 150 mM NH₄ ⁺/Na⁺ (Fig. 13). At saturating cGMP concentrations, the reversal potentials were 4.2 ± 0.53 (n = 5) for Cs⁺ and −16.4 ± 1.4 mV (n = 6) for NH₄ ⁺. Eq. 1 yields PCs/PNa = 0.87 ± 0.02 and PNH₄/ PNa = 1.94 ± 0.11, similar values to those previously reported by others (Picones and Korenbrot, 1992; Haynes, 1995). We found no changes in the reversal potentials at different cGMP concentrations. Thus, in cone channels, gating modifies the selectivity for divalent but not monovalent cations.

Figure 13.

Cs⁺ and NH₄ ⁺ selectivity of cGMP-gated channels in cone photoreceptors is independent of cGMP concentration. (Top left) I–V curves activated with a cGMP concentration ramp in the presence of biionic solutions: Cs⁺ (150)/Na⁺ (150). The cGMP concentration at the moment each I–V curve was measured were 0, 16.4, 23.2, 35.6, 40, 58, 87, and 1,000 μM. Also shown is the I–V curve activated by 1 mM cGMP in the same patch in the presence of symmetric Na⁺ solutions. (Bottom left) Reversal potential as a function of [cGMP]. (•) Reversal potentials measured from the data shown on top, (○) data measured in the same patch with steps of cGMP concentrations (10, 20, 40, and 1,000 μM). The dashed line is the mean of these values, 4.3 mV, which yields PCs/ PNa = 0.84. (Top right) I–V curves measured with a cGMP concentration ramp in the presence of biionic NH₄ ⁺ (150)/Na⁺ (150) solutions. The cGMP concentrations at the moment of each I–V curve were 0, 17.6, 22.7, 40, 47, 93.9, and 1,000. Also shown is the I–V curve activated by 1,000 μM cGMP in the same patch in the presence of symmetric Na⁺ solutions. (Bottom right) Reversal potential as a function of [cGMP]. (•) Reversal potentials measured from the data on top, (○) data measured in the same patch with steps of cGMP concentrations (10, 20, 40, and 1,000 μM). The dashed line is the mean of these values, −15.8 mV, which yields PNH₄/PNa = 1.89.

discussion

We report that cyclic nucleotide–gated (CNG) channels in both rod and cone retinal photoreceptors change their relative Ca²⁺ to Na⁺ selectivity as a function of cGMP concentration. The linkage between selectivity and channel activity is specific for divalent cations and is not observed when the selectivity among inorganic or organic monovalent cations is explored. The dependence on cGMP concentration of the changes in relative ion selectivity is well described by a Hill equation, the same one that describes the dependence of probability of channel opening on the nucleotide concentration. The coupling of ion selectivity and gating is a feature of heteromeric recombinant rod channels formed by α and β subunits, but is absent in homomeric channels formed by α subunits alone.

Two alternative molecular mechanisms could explain our macroscopic findings of the effect of cGMP on ion selectivity: (a) two or more types of CNG channels exist that differ in their ion selectivity or (b) only one type of channel exists that exhibits two or more conductance states, each of different ion selectivity. If two distinct channels exist, then one must have a high sensitivity to cGMP and low PCa/PNa, while the other must have a lower sensitivity to cGMP and higher PCa/PNa. Thus, at saturating cGMP concentrations, both channel types would be open and the selectivity would be the weighted sum of the selectivities of each type. As cGMP concentration declines, the low sensitivity channel would close, and the selectivity of the high sensitivity channel would define the selectivity observed experimentally. If a single molecular type of channel exists with multiple conductance states, than the probability of occupying different conductance states must be cGMP dependent, and the conductance states that exist primarily at low cGMP concentrations should have a much lower Ca²⁺ permeability than states that exist at high cGMP concentrations.

In intact rod photoreceptors, there exist two molecularly distinct types of cGMP-gated channels that differ in their kinetic properties (Torre et al., 1992). In the inner segment membrane, ∼1 of 20 CNG channels exhibit slow kinetics that are similar to those of recombinant channels composed of α subunits alone (Torre et al., 1992). The remaining channels, in contrast, exhibit rapid flickering similar to that observed in recombinant αβ channels (Torre et al., 1992; Chen et al., 1993) and in channels of the outer segment (Taylor and Baylor, 1995). We do not think that the existence of these two kinetically distinct types of channels underlie the macroscopic behavior we report here since: (a) the channels are located in the inner segment of the cell and their copy number is variable, yet we observe cGMP-dependent permeability changes on every patch isolated from the outer segment alone; and (b) the two known channel types have identical sensitivity to cGMP, yet our observations demand that the channel types differ in their sensitivity to cGMP.

Biochemical experiments have previously suggested that two types of cGMP-gated channels might exist in rod outer segments. Experiments on purified bovine rod outer segment membrane vesicles revealed two cGMP-dependent components with different Ca²⁺ efflux kinetics (Koch et al., 1987). In these findings, however, the high Ca²⁺ permeability component has a high affinity for cGMP. This behavior is contrary to our electrophysiological findings. Moreover, additional evidence suggests that the two kinetic components observed in the biochemical studies likely reflect the existence of two types of membrane vesicles, those with and those without Na⁺-Ca²⁺,K⁺ exchangers, rather than two different types of cGMP-gated channels (Schnetkamp, 1987).

Modulation might give rise to the presence of populations of functionally distinct channels in the same patch. Recordings of cGMP-dependent currents in both photoreceptor and oocyte membranes show a high variability in the absolute value of K _1/2 from patch to patch and over time in the same patch, a fact that may reflect modulation, perhaps due to channel phosphorylation (Gordon et al., 1992; Ruiz et al., 1999). Also, an endogenous modulator, partially mimicked by calmodulin, is known to modify K _1/2 in both rods (Hsu and Molday, 1994; Gordon et al., 1995) and cones (Hackos and Korenbrot, 1997; Rebrik and Korenbrot, 1998). To explain the data presented here, known modulation of the CNG channels would have to affect both the affinity for cGMP and the divalent cation selectivity. In the case of calmodulin or the calmodulin-like endogenous modulator, PCa/PNa of the channels in the presence and absence of the modulator is the same (Hackos and Korenbrot, 1997), and thus such modulation cannot explain the cGMP- dependent changes in selectivity.

Any form of modulation that changes both the cGMP affinity and divalent cation selectivity should give rise to two observable features in our data. (a) The extent of modulation should be measurable by observing either the maximal PCa/PNa or K _1/2. Thus, maximal PCa/ PNa (that measured at saturating cGMP) should vary from patch to patch, and over time in the same patch, just as K _1/2 varies. (b) Patches with low K _1/2 would be expected to have low maximal PCa/PNa values and vice versa. While K _1/2, and to a lesser extent maximal PCa/ PNa, vary from patch to patch, we did not find any correlation between K _1/2 and maximal PCa/PNa, making it unlikely that modulation or in fact any multiple channel mechanism could explain our findings.

If multiple populations of channels with different cGMP sensitivity and ionic selectivity do not coexist in patches of CNG channels, than there must be a more direct mechanism involved. A direct functional linkage between ion selectivity and gating has been previously observed in both voltage- and ligand-gated channels. In the presence of biionic solutions of monovalent cations, N-methyl-d-aspartate–gated currents do not exhibit a single reversal potential, and current fluctuations do not disappear at the reversal voltage (Schneggenburger and Ascher, 1997). Single channel recordings demonstrate that this macroscopic behavior reflects the existence of at least two subconductance states that differ in their ion selectivity (Schneggenburger and Ascher, 1997). Shaker K⁺ channels exhibit at least two subconductance states that differ in their monovalent cation selectivity (Zheng and Sigworth, 1997). Our observations could be explained if the open pore of a single channel had several possible structural states that differ in divalent cation permeability. Each of these open states might also correspond to the well documented subconductance states of the CNG channels.

The presence of multiple conductance states in CNG channels was recognized in the first published single channel recordings (Haynes et al., 1986; Zimmerman and Baylor, 1986), but only later analysis focused on these features. In studies of bovine rod membrane vesicles incorporated into lipid bilayers, Ildefonse and Bennett (1991) observed several single channel conductance states and proposed that sequential binding of four cGMP molecules correspond to the opening of four discrete conductance levels. Taylor and Baylor (1995) observed subconductance levels in single channel recordings from tiger salamander rods and reported that the fraction of time spent in the subconductance level decreased with increasing cGMP concentration, suggesting that the sublevel may be due to opening of partially liganded channels. Since cGMP-gated channels are tetrameric with four cyclic nucleotide binding sites (Liu et al., 1996), the subconductance levels have generally been interpreted as representing distinct states of one, two, or three bound cGMP molecules. Ruiz and Karpen (1997), however, have suggested that this interpretation is incorrect. Using a photocross-linkable cGMP analogue, they locked single channels formed from α subunits in a specific ligand-bound state. Their results indicate that these channels do not have significant probability of opening until at least three ligands are bound and that the number of bound cGMP molecules alters the probability of occupying a particular open state, but does not define which state is occupied. Triply liganded channels display two strong subconductance states in addition to the fully open state, while the fully liganded channel mainly occupies only the fully open conductance state. Consistent with these findings, we suggest that the macroscopic effect of cGMP on ion selectivity may reflect the existence of at least two conductance states each of distinct ion selectivity. At low cGMP, the prevalent state is predicted to be of lower PCa/PNa than the state prevalent at high cGMP concentration.

What types of pore structural changes might give rise to the subconductance states and the cGMP-dependent permeability changes observed here? Sun et al. (1996) have shown in a series of cysteine accessibility studies that the CNG channel pore may undergo large structural changes during gating and may in fact be the gate itself. Particularly intriguing is the finding that tetracaine binds to the pore, depending on whether it is open or closed, by forming a salt bridge with the E363 residue within the pore (Fodor et al., 1997). The fact that tetracaine does not bind to the open channel may indicate that a conformational change within the pore alters either the position of E363 or its accessibility to tetracaine. Since E363 is critical in determining the divalent cation block and permeation in the cGMP-gated channel (Root and MacKinnon, 1993; Eismann et al., 1994), and since this residue may change its position or accessibility in the course of gating (Fodor et al., 1997), it is then possible that this structural change may also contribute to linking changes in gating with changes in divalent cation selectivity. If changes in open pore structure occur, these are not reflected in the steric dimensions of the pore since the selectivity for monovalent organic cations, a simple test of steric hindrance in these channels (Picco and Menini, 1993), is unaffected by cGMP. Changes not within, but around the mouth of the pore might also affect selectivity (Seifert et al., 1999).

The proposition that cGMP controls the prevalence of conducting state of different ion selectivity might be tested experimentally in single channel studies, but not with channels formed from recombinant alpha subunits alone since these channels do not exhibit cGMP-dependent changes in selectivity. On theoretical grounds, however, a simple model of two conducting states (triply liganded and fully saturated), each with different divalent cation selectivities, cannot fully explain our results. This is because a model of two conducting states with four cGMP binding sites can be shown to predict that changes in divalent cation selectivity as a function of cGMP should show little, if any, cooperativity when compared with the cooperativity of the current–cGMP relationship. Contrary to this expectation, we have found that the dependence of changes of PCa/PNa on cGMP is the same as the dependence of current on cGMP. Thus, a more complex mechanism must be at play. Resolving whether cGMP changes ion selectivity by affecting the structure of the pore or by changing the probability of opening of subconductance states of differing ion selectivity must await further experimental work.

The stoichiometry of α and β subunits in the cyclic nucleotide–gated channels appears to be 2:2 in channels of olfactory neurons (Shapiro and Zagotta, 1998). The photoreceptor β subunit, while itself unable to form functional channels (Chen et al., 1993), confers several functional properties to the channel that are absent in channels formed from α subunits alone. These properties include: (a) the ability to flicker rapidly (Torre et al., 1992), (b) the Ca²⁺-dependent modulation of sensitivity to cGMP mediated by calmodulin (Chen et al., 1994), (c) increased sensitivity to diltiazem (Chen et al., 1993), and (d) reduced sensitivity to Ca²⁺ block (Korschen et al., 1995). We now add the dependence on cGMP of divalent cation selectivity and channel block.

Physiological Implications of the Results

Under physiological conditions, in both rods (Hestrin and Korenbrot, 1987; Cameron and Pugh, 1990) and cones (Cobbs et al., 1985; Miller and Korenbrot, 1993), the probability of opening of the cGMP-gated channels ranges from its largest value in darkness of 1–5% to essentially zero under continuous, bright illumination. That is, in the intact photoreceptor, channels spend nearly all their time exposed to very low concentrations of cGMP. Since the Ca²⁺ permeability reaches its minimum value at low cGMP concentrations, we would not expect the Ca²⁺ permeability to change significantly in the course of the normal photoresponse. However, if the channel's Ca²⁺ selectivity changes with cGMP in other cells, where the operating range of changes in cytoplasmic is larger than in photoreceptors, then modulation of Ca²⁺ fluxes by cGMP (or cAMP) should be considered as a potentially important physiological modulation.

Cone cGMP-gated channels are more permeable to Ca²⁺ than those in rods (Frings et al., 1995; Haynes, 1995; Picones and Korenbrot, 1995). At saturating cGMP concentrations, we find that channels from striped bass cones are ∼3.3-fold more permeable to Ca²⁺ than those of tiger salamander rods, a result consistent with previous measurements (Picones and Korenbrot, 1995). This difference is even larger at physiologically relevant cGMP concentrations. At the cytoplasmic cGMP concentrations expected in dark adapted cells, PCa/PNa in cone channels is ∼7.4-fold greater than that in rods. The physiologically significant parameter, however, is not the difference in the values of PCa/PNa, but in the fraction of the ionic current carried by Ca²⁺ in rods and cones.