A Bayesian Approach to Copy-Number–Polymorphism Analysis in Nuclear Pedigrees

Abstract

Segmental copy-number polymorphisms (CNPs) represent a significant component of human genetic variation and are likely to contribute to disease susceptibility. These potentially multiallelic and highly polymorphic systems present new challenges to family-based genetic-analysis tools that commonly assume codominant markers and allow for no genotyping error. The copy-number quantitation (CNP phenotype) represents the total number of segmental copies present in an individual and provides a means to infer, rather than to observe, the underlying allele segregation. We present an integrated approach to meet these challenges, in the form of a graphical model in which we infer the underlying CNP phenotype from the (single or replicate) quantitative measure within the analysis while assuming an allele-based system segregating through the pedigree. This approach can be readily applied to the study of any form of genetic measure, and the construction permits extension to a wide variety of hypothesis tests. We have implemented the basic model for use with nuclear families, and we illustrate its application through an analysis of the CNP located in gene CCL3L1 in 201 families with asthma.

Evidence that segmental copy-number variants (CNVs) represent a significant portion of human genetic variation is accumulating.¹ A CNV is generally defined as a segment of DNA >1 kb and present at variable copy number when compared with a reference genome.^1,2 More than 6,000 such CNVs have been reported (Database of Genomic Variants), and recent genomewide studies estimate that thousands of CNVs exist in the human genome.^1,3 It is likely that these variants lead to phenotypic variation and modification of disease risk through gene-dose or position effects.^2,4,5

Redon et al.² showed that the presence of CNVs is associated with low call rates in SNPs; hence, CNVs tend to occur in regions with low densities of validated SNPs. This is likely to be due in part to the diploid-genome assumption being effectively violated in these CNV regions. The accurate assignment of the copy number (integer count) in an individual will present new challenges to assays,⁶ and proposals to use quantitative SNP genotypes to infer CNVs will require more-refined calling algorithms.² Accurate quantification of counts of CNV repeats, which can be thought of as allele sizes, is not yet routinely possible; most technologies are able to quantify only the total phenotype or the sum of all alleles detected. CNVs seen in at least 1% of the population are termed copy-number polymorphisms (CNPs) and are good candidates for disease-risk modifiers. Consideration of these polymorphisms in case-control association studies requires no specialized methods, and, when sufficient evidence has accumulated, candidate loci can be further studied and characterized in population-based family studies.⁷ In the family-based context, however, the underlying allelic segregation must be inferred from the CNP phenotypes. Although some traditional segregation and linkage analysis tools, such as PAP and LINKAGE, allow genotypes to be inferred from observed phenotype classes, more-recently developed methods aimed at genetic linkage or candidate-gene analysis cannot handle this type of data, since they assume codominant markers. Many CNPs behave as multiallelic systems,² and this may lead to nonnegligible error when integers are assigned from quantitative CNP assays. This makes it desirable to develop a method that models the relationship between CNP phenotype and genotype and allows for the CNP phenotype assignment to occur within the statistical segregation analysis itself.

We present a Bayesian graphical model that enables the statistical evaluation of a candidate CNP. Whatever property or aspect of the candidate CNP that is assumed to be associated with disease can then be specifically observed through stochastic elements of the graphical model or the construction of a logical node. A logical node, in this context, means one whose value or state is determined by the states of its parental variables. We have implemented this model in WinBUGS, to analyze nuclear families. The distinctive feature of our implemented method is that the multiple (or repeated) raw assessments of individual CNP phenotype are used directly, rather than use of a single summary measure or an integer value assigned by an algorithm. We assume that the CNP phenotype results from the sum of two independently inherited alleles and that each allele consists of a discrete number of repeats (which may include a null allele). This, of course, may not be true for all CNPs, since the repeated homologous sequence may be located at multiple sites throughout the genome.

The presented implementation has been constructed to evaluate the candidate CNP CCL3L1 isoform (MIM 601395), which contains a segment that is present in multiple copies. The variation in copy number in this gene segment has been well studied. Within populations, lower copy number is associated with both risk of HIV-1 infection and more rapid progression to AIDS⁸ and with reduced risk of Kawasaki disease.⁹ Variation in copy number within this gene may affect susceptibility to or progression of other diseases of the autoimmune and inflammatory response systems, such as asthma. This polymorphism has therefore been investigated as a candidate CNP in a series of 201 nuclear families ascertained because of the presence of at least two affected offspring with asthma.

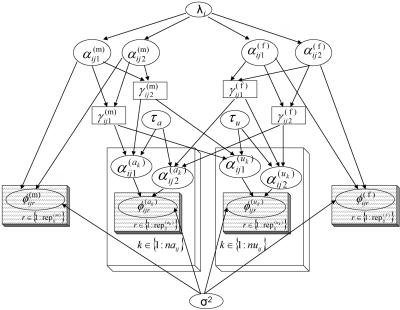
The graphical model is presented in figure 1. In founders, copy-number alleles are assumed to be sampled from a Poisson distribution, where the rate, λ, may be different in each population (as observed by Gonzalez et al.⁸ for this same polymorphism). Therefore, the distribution of copy-number phenotype (the sum of the two allele lengths) in the population will follow a Poisson distribution with rate 2λ. In this specific implementation, of interest is whether there is a Mendelian-transmission distortion, in which the lighter allele is transmitted to affected offspring.

Figure 1. .

Model represented as a directed acyclic graph. Ovals represent stochastic nodes, rectangles represent logical nodes, and shaded rectangles summarize repeated structures.

The various nodes in figure 1 represent the following.

λ_i: 

Poisson rate, used in prior population-allele frequency distribution in subpopulation i.

α^(m)_ijl (and α^(f)_ijl): 

Allele l for the mother (and father) in nuclear family j in population i.

γ^(m)_ij1 (and γ^(f)_ij1): 

The “lighter” of the two alleles in the mother (and father).

γ^(m)_ij2 (and γ^(f)_ij2): 

The “heavier” of the same two alleles.

τ_a (and τ_u): 

The probability that a parent transmits the heavier allele to affected (and unaffected) offspring.

α^(a_k)_ij1 (and α^(a_k)_ij2): 

The allele inherited by affected offspring a_k from the mother (and father) of family j in population i.

α^(u_k)_ij1 (and α^(u_k)_ij2): 

The allele inherited by unaffected offspring u_k from the mother (and father) of family j in population i.

φ^(m)_ijr (and φ^(f)_ijr): 

CNP-phenotype assay replicate r for the mother (and father) of family j in population i.

φ^(a_k)_ijr (and φ^(u_k)_ijr): 

CNP-phenotype assay replicate r for affected (and unaffected) offspring k in family j in population i.

σ²: 

Copy-number–phenotype assay variance.

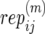(and ): 

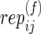Number of replicate copy-number–phenotype assays for mother (and father) in family j in population i.

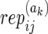(and ): 

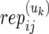Number of replicate copy-number–phenotype assays for affected (and unaffected) offspring.

na_ij (and nu_ij): 

Number of affected (and unaffected) offspring in family j in population i.

This formulation declares the basic model. It is straightforward to extend it to include slight variations or to examine other hypotheses, such as copy-number–threshold effects. Adding further logical nodes enables the estimation of identity-by-descent (IBD) sharing probabilities.

The true copy-number phenotype for a single individual is determined by the sum of their two inherited discrete allele lengths. Therefore, the observed CNP phenotype φ_ijr is assumed to be a normally distributed variable with mean α_ij1+α_ij2 and variance σ². In practice, the phenotype must be treated as a censored variable, since this assay is truncated at zero. When null alleles exist, some individuals will be effectively homozygous for the null allele, and the assay may yield small positive values. Any copy-number assay replicate returning a zero is treated as a censored observation with true value <0.

Founder alleles are sampled from the Poisson distribution, and the genotype is then configured so the first allele is the lighter (if heterozygous). An inheritance vector then identifies which of the two configured parental alleles has been transmitted to offspring. If the gene polymorphism is not associated with disease, you would expect to see equally likely transmission of light or heavy alleles, consistent with Mendelian segregation. This configuration enables the transmission parameter to be estimated and, hence, the alternative hypothesis to be tested. The graphical model distinguishes between affected and unaffected offspring, so unaffected offspring are used only to assist in the inference of parental genotypes.

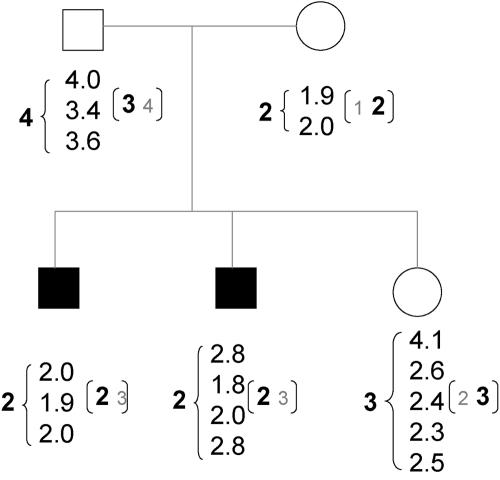
Nuclear families from two European populations, representing a subset of a larger multicenter study,¹⁰ were collected from centers in Sheffield, United Kingdom, and in Thessaloniki, Greece. The U.K. families include a small number of unaffected offspring (table 1). The estimation of copy-number phenotype was determined by quantitative real-time PCR, by use of a previously validated technique.¹¹ The copy number was quantified at least twice; if a clear, discrete copy-number count was not achieved, further replicates were generated until the mean value approached an integer value. A similar protocol was followed by Gonzalez et al.⁸ This procedure was employed for every member of the nuclear family. Figure 2 shows a selected U.K. pedigree illustrating the variable number of copy-number assays performed within one family. This selected pedigree also provides an example of how assigning the integer closest to the mean, as outlined above, can lead to Mendelian inconsistencies. In this case, the inconsistency was able to be resolved if, for example, the father's phenotype was 3 or the unaffected offspring's phenotype was 0, 2, 4, or 6. Assigning phenotype by the integer closest to the mean resulted in Mendelian inconsistencies detected in 20 of the 201 families. Obviously, some inconsistencies might be expected to be due to nonpaternity, but that cause can be excluded in this series, since all families were screened for nonpaternity before their use in genomewide linkage studies.¹⁰

Table 1. .

Details of Nuclear Family Size and Distribution of Affected Siblings in the Two Samples

	No. of Families with
	No. of Affected Siblings			No. of Unaffected Siblings
Family Origin	2	3	4	0	1	2
United Kingdom	84	14	1	81	15	3
Greece	96	6	0	98	4	0

Figure 2. .

One selected U.K. family. Blackened symbols represent individuals affected with asthma. The column of numbers below each individual lists the replicate CNP assay measure for each. The number to the left of the column represents the integer (closest to the mean) assignment. The numbers to the right in parentheses reflect the most likely (in larger, bold type) and the next most likely underlying phenotype taken from the marginal posterior probability for each individual.

The graphical model was implemented as a WinBUGS procedure (CNPrep) allowing for up to six replicate assays per individual. The censoring function was applied only to the first two assay results, since, for this assay at least, a null-copy phenotype was easy to classify. Because of this declared experimental design, missing replicate assays were assumed to be ”missing at random.”

The combined use of inheritance vectors, which point to the alleles transmitted, and the quantitative estimate of the true copy-number phenotype means that the Markov-chain iterations do not suffer from the problem of reducibility often experienced in Markov-chain pedigree analysis.¹² The assumption that the phenotype is measured with error allows the founder alleles to be sampled from the full prior distribution. Although some founder genotypes are extremely unlikely, they are not impossible.

The implemented procedure needed a long burn-in but did not appear to be sensitive to starting values, and convergence was assessed using standard diagnostics.¹³ Multiple runs with three simultaneous sampling chains showed no evidence of reducibility or convergence to local maxima. There is strong evidence that the allele distributions in the Greek and U.K. populations are different (table 2), but there is only suggestive evidence of a transmission distortion favoring transmission of the lighter allele to affected offspring (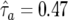 [95% CI 0.43–0.53]). A weak tendency for affected sibs to share two alleles IBD was also observed.

Table 2. .

Parameter Estimates Generated by WinBUGS Analysis

Parametera	Mean	2.5% CI	97.5% CI
Greek Poisson rate	1.08	.98	1.18
U.K. Poisson rate	1.32	1.21	1.44
Transmission probabilityb	.47	.43	.53
z0	.22	.17	.27
z1	.50	.44	.57
z2	.27	.22	.32

^aThe terms z₀, z₁, and z₂ represent the probabilities that a pair of affected siblings share 0, 1, or 2 alleles IBD.

^bProbability of transmission of the heavy allele to affected offspring by heterozygote.

Figure 2 shows the most likely distribution of copy-number phenotype for each person in the selected pedigree, based on the results of the WinBUGS procedure (this is shown by the bold number in parentheses on the right of the column of repeated values). These values represent the most (and next most) likely underlying integer phenotype for each individual taken from the posterior distribution for each person, not the joint distribution for the whole family.

The graphical model outlined in figure 1 constrains the genotype distribution within the pedigree to be consistent with Mendelian segregation. It does not allow for mutation at the CNP, nor does it allow a CNP phenotype to be the “sum” of allele lengths at several unlinked loci. Modifications to incorporate these facets are straightforward, but more prior knowledge or additional data sets allowing characterization through hierarchical modeling would be needed. Currently, available data suggest that CNPs are generally stably inherited (i.e., consistent with a high heritability),¹⁴ but more work is needed to distinguish between technical artifacts, high error rates, and high mutability.

Further refinement of the model would include exploration of appropriate prior distributions for allele frequencies and models allowing assay variance to be a function of the underlying true copy-number phenotype. Our use of the Poisson as the prior for allele frequencies has the benefit that a single parameter defines the distribution; however, for the investigated CNP CCL3L1, this was not entirely justified, since the range of allele lengths observed was wider than a Poisson would predict. One effect of the Poisson assumption is illustrated in figure 2. Since the Poisson rate for the U.K. set finds shorter alleles more likely, the father is therefore more likely to have phenotype 3 than phenotype 4, and this resolves the potential Mendelian inconsistency highlighted before between the father and unaffected offspring.

When studying related individuals for segregation analysis of candidate loci, it is not only possible but also beneficial to include raw, possibly replicate, genotype or phenotype measurements. It is beneficial for two reasons: (1) it is more efficient to incorporate the error model into the analysis and to use the raw data directly than to take summary assignments and compose an error function that relates to the summary assignment and the underlying true value, and, (2) although the true Mendelian system is assumed to be discrete, if the quantitative measures can be assumed to be drawn from continuous distributions, then this facilitates the use of a Markov chain–Monte Carlo (MCMC) approach,¹² which allows a general graphical model to form the basis for any genetic hypothesis to be tested. Our approach is illustrated through a simple example implemented in WinBUGS. WinBUGS was chosen because of its favorable environment for flexible model development, but many alternative Bayesian techniques could be used equally well. It should be possible to incorporate this integrated genetic-marker model into existing genetic-analysis tools that use MCMC or hidden Markov models, such as MORGAN or MERLIN, thereby taking advantage of their many other algorithmic and computational features.

This approach and the realization that presence of CNVs can be detected through SNP-driven technology suggest that the model can be extended to SNP analysis. In genetic association studies, SNPs have become the marker of choice¹⁵ because of their high genomic density and technical advantages over the more polymorphic but less frequent and technically more difficult microsatellites. In spite of their technical advantages, not all discovered SNPs meet required quality-control (QC) standards, and some genomic regions are relatively sparsely covered by SNPs.¹⁶ It is now clear that some of the QC failures may be due to the presence of copy-number–variable regions.^2,17 This makes it desirable to work toward models able to simultaneously analyze SNP and CNP observations together, to more precisely identify the segregation of genetic material through pedigrees, and hence to formally assess the disease risk. A recent genetic linkage analysis that mapped autism risk loci¹⁸ took advantage of the information on individual CNV status contained in the SNP arrays. Because of the current lack of both integrated statistical methods and firm knowledge of suitable and reliable inheritance models for CNVs, the patterns of CNV clustering were used to subclassify families rather than to inform the genetic linkage process. The analysis of further detailed experimental data such as those reported in the linkage analysis¹⁸ is required to ensure appropriate models integrating the effect of CNP on neighboring SNPs.

Genomewide case-control association studies are an efficient way to screen large numbers of genetic loci for association with multifactorial disease. Candidate regions suggested by the genomewide studies may be followed up in population-based family resources, since they provide a powerful framework to quantify gene-gene and gene-environment interactions. CNPs present a promising class of candidate loci, but the error associated with measuring the population-based variation may be large when assigning phenotype to individuals, requiring consideration of the error or the assignment within the statistical analysis. We have outlined an efficient approach to do this, using a Bayesian graphical model for candidate-gene segregation analysis that jointly models the relationship between (single or replicate) quantification assays and true underlying genotype and/or phenotype. As we have demonstrated, this basic model is easily adapted to suit the nature of the data studied and the hypothesis in question.