Intracellular pH Regulation in Cultured Astrocytes from Rat Hippocampus

Abstract

In the preceding paper (Bevensee, M.O., R.A. Weed, and W.F. Boron. 1997. J. Gen. Physiol. 110: 453–465.), we showed that a Na⁺-driven influx of HCO₃ ⁻ causes the increase in intracellular pH (pH_i) observed when astrocytes cultured from rat hippocampus are exposed to 5% CO₂/17 mM HCO₃ ⁻. In the present study, we used the pH-sensitive fluorescent indicator 2′,7′-biscarboxyethyl-5,6-carboxyfluorescein (BCECF) and the perforated patch-clamp technique to determine whether this transporter is a Na⁺-driven Cl-HCO₃ exchanger, an electrogenic Na/HCO₃ cotransporter, or an electroneutral Na/HCO₃ cotransporter. To determine if the transporter is a Na⁺-driven Cl-HCO₃ exchanger, we depleted the cells of intracellular Cl⁻ by incubating them in a Cl⁻-free solution for an average of ∼11 min. We verified the depletion with the Cl⁻-sensitive dye N-(6-methoxyquinolyl)acetoethyl ester (MQAE). In Cl⁻-depleted cells, the pH_i still increases after one or more exposures to CO₂/HCO₃ ⁻. Furthermore, the pH_i decrease elicited by external Na⁺ removal does not require external Cl⁻. Therefore, the transporter cannot be a Na⁺-driven Cl-HCO₃ exchanger. To determine if the transporter is an electrogenic Na/ HCO₃ cotransporter, we measured pH_i and plasma membrane voltage (V_m) while removing external Na⁺, in the presence/absence of CO₂/HCO₃ ⁻ and in the presence/absence of 400 μM 4,4′-diisothiocyanatostilbene-2,2′-disulphonic acid (DIDS). The CO₂/HCO₃ ⁻ solutions contained 20% CO₂ and 68 mM HCO₃ ⁻, pH 7.3, to maximize the HCO₃ ⁻ flux. In pH_i experiments, removing external Na⁺ in the presence of CO₂/HCO₃ ⁻ elicited an equivalent HCO₃ ⁻ efflux of 281 μM s⁻¹. The HCO₃ ⁻ influx elicited by returning external Na⁺ was inhibited 63% by DIDS, so that the predicted DIDS-sensitive V_m change was 3.3 mV. Indeed, we found that removing external Na⁺ elicited a DIDS-sensitive depolarization that was 2.6 mV larger in the presence than in the absence of CO₂/ HCO₃ ⁻. Thus, the Na/HCO₃ cotransporter is electrogenic. Because a cotransporter with a Na⁺:HCO₃ ⁻ stoichiometry of 1:3 or higher would predict a net HCO₃ ⁻ efflux, rather than the required influx, we conclude that rat hippocampal astrocytes have an electrogenic Na/HCO₃ cotransporter with a stoichiometry of 1:2.

INTRODUCTION

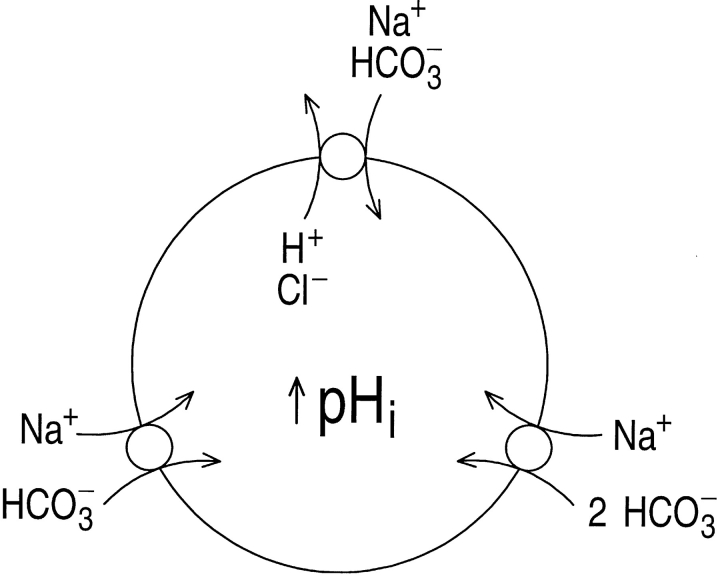
As described in the accompanying paper (Bevensee et al., 1997), exposing rat hippocampal astrocytes to CO₂/ HCO₃ ⁻ causes pH_i to decrease initially, due to the influx of CO₂, and then generally to increase to a value higher than the initial one prevailing in the nominal absence of CO₂/HCO₃ ⁻. Because this pH_i increase is blocked by the HCO₃ ⁻-transport inhibitors 4,4′-diisothiocyanatostilbene-2,2′-disulphonic acid (DIDS)¹ and 4-acetamido-4′-isothiocyanatostilbene-2,2′-disulfonic acid (SITS), and requires external Na⁺, we concluded that the astrocytes have a Na⁺-driven HCO₃ ⁻ transporter. The data are consistent with the presence of one or more of three HCO₃ ⁻ transporters known to exist in other cells (Fig. 1): (a) a Na⁺-driven Cl-HCO₃ exchanger, (b) an electroneutral Na/HCO₃ cotransporter with a Na⁺:HCO₃ ⁻ stoichiometry of 1:1, and (c) an electrogenic Na/HCO₃ cotransporter with a Na⁺:HCO₃ ⁻ stoichiometry of 1:2. Theoretically, a fourth possibility is the electrogenic NaHCO₃ cotransporter with a 1:3 stoichiometry, as exists in renal proximal tubules (Boron and Boulpaep, 1983; Soleimani et al., 1987). However, given the ion and voltage gradients likely to prevail in an astrocyte, this 1:3 cotransporter would almost certainly mediate net HCO₃ ⁻ efflux, and not the influx necessary to account for the observed CO₂/HCO₃ ⁻-induced alkalinization.

Figure 1.

Hippocampal astrocytes could have any of three known Na⁺-driven HCO₃ ⁻ transport mechanisms.

Compared with the 1:1 and 1:2 Na/HCO₃ cotransporters, the Na⁺-driven Cl-HCO₃ exchanger is unique in requiring internal Cl⁻. Because the Na⁺-driven Cl-HCO₃ exchanger normally moves Na⁺ and HCO₃ ⁻ into a cell and Cl⁻ out, transport in its normal (“forward”) direction should be inhibited by depleting cells of internal Cl⁻. However, because the K_1/2 of Cl⁻ for the Na⁺-driven Cl-HCO₃ exchanger in mammalian cells is not known, even low levels of intracellular Cl⁻ ([Cl⁻]_i) might still support the exchanger in cells preincubated in a Cl⁻-free solution. Indeed, depleting [Cl⁻]_i has proven difficult in some cells. For example, renal mesangial cells had to be incubated in a Cl⁻-free solution for 1–2 h to achieve substantial inhibition of their Na⁺-driven Cl-HCO₃ exchanger (Boyarsky et al., 1988b ). In pyramidal neurons from rat hippocampus, the Na⁺-driven Cl-HCO₃ exchanger was active even after the cells were preincubated in a Cl⁻-free solution for up to 4 h (Schwiening and Boron, 1994). Therefore, one must be cautious when interpreting results from experiments designed to assess the effect of acute extracellular Cl⁻ removal on transporters requiring intracellular Cl⁻. In the present study, we use the Cl⁻-sensitive dye N -(6-methoxyquinolyl) acetoethyl ester (MQAE) to study the time course of depletion of [Cl⁻]_i, finding that [Cl⁻]_i falls to very low levels when astrocytes are incubated in a Cl⁻-free solution for as few as ∼11 min. Under these conditions, the Na⁺-driven HCO₃ ⁻ transporter still operates in the forward direction, and moves HCO₃ ⁻ into cells exposed to CO₂/ HCO₃ ⁻. Furthermore, in the absence of external Cl⁻, the transporter still operates in the reverse direction, and moves HCO₃ ⁻ out of cells exposed to a Na⁺-free solution.

The other possibilities shown in Fig. 1 are two Na/ HCO₃ cotransporters, one that is electroneutral and has a Na⁺:HCO₃ ⁻ stoichiometry of 1:1, and one that is electrogenic and has a stoichiometry of 1:2. In the present study, we distinguish between these two by using the perforated patch-clamp technique to record plasma membrane voltage (V_m) in astrocytes, and determine whether the movement of net negative charge accompanies the movement of HCO₃ ⁻. We found that removing Na⁺ elicits a DIDS-sensitive depolarization that is larger in the presence than in the absence of CO₂/HCO₃ ⁻. Comparing the size of the DIDS-sensitive, HCO₃ ⁻-dependent depolarizations with the magnitude of the DIDS-sensitive HCO₃ ⁻ effluxes measured under similar conditions, we conclude that the Na⁺-driven HCO₃ ⁻ transporter in hippocampal astrocytes is an electrogenic Na/HCO₃ transporter, presumably with a Na⁺:HCO₃ ⁻ stoichiometry of 1:2.

METHODS

Solutions

The solutions used in the present study, with the exception of the ones buffered with 20% CO₂/68 mM HCO₃ ⁻, are described in the accompanying paper (Bevensee et al., 1997). These 20% CO₂ solutions were made by isotonically substituting 68 mM HCO₃ salt for HEPES and a Cl salt. The patch-pipette filling solution contained (mM): 105 KCl, 45 NaCl, 1.0 MgCl₂, 0.2 CaCl₂, 10 EGTA, and 1.0 HEPES. The pH of the patch-pipette solution (pH_pip) was adjusted to 7.4 with Tris. pH_pip was buffered with only 1 mM HEPES to minimize the effect of pH_pip on the pH_i of a patched cell. In some early experiments, we used 120 KCl and 30 NaCl in the pipette solution. Pipette solutions contained either nystatin or amphotericin B (80–300 μM). MQAE was obtained from Molecular Probes, Inc. (Eugene, OR). Bumetanide, nystatin, and amphotericin B were obtained from Sigma Chemical Co. (St. Louis, MO). All other reagents were obtained as described in the accompanying paper (Bevensee et al., 1997).

Measurement of [Cl⁻]_i in Astrocytes

Handling of cells.

We measured [Cl⁻]_i in astrocytes using the Cl-sensitive indicator MQAE, developed by Verkman et al. (1989). Astrocytes were grown to confluence, as described in the accompanying paper (Bevensee et al., 1997), and passaged onto 8.5 × 8.5–mm glass coverslips. 2–8.25 h (average 4.7 ± 0.3 h, n = 23) before each experiment, a coverslip with confluent astrocytes was transferred to a HEPES-buffered solution containing 5 mM MQAE.

Optics.

After cells were exposed to dye, the coverslip was placed into a quartz cuvette designed to fit into a SPEX Fluorolog-2 spectrofluorometer (CM1T10E; Spex Industries, Inc., Edison, NJ). The coverslip was mounted at a 30° angle to the excitation light. Solutions flowed through the cuvette from bottom to top through Tygon^® or stainless-steel tubing. Both the tubing and the cuvette were maintained at 37°C by a water jacket. The temperature of the cuvette was monitored continually during an experiment with a thermistor placed at the base of the cuvette. During an experiment, we used only one of the excitation monochromators of the dual-beam spectrofluorometer, continuously exciting with light at 320 nm (1.89-nm bandwidth). A photomultiplier tube mounted on an emission monochromator monitored the emitted fluorescence intensity (I₃₂₀) at 460 nm (4.71-nm bandwidth). During each 3.0-s data collection cycle, the spectrofluorometer integrated the emitted intensity for 1.0 s, and corrected for fluctuations in the arc-lamp intensity (continuously monitored). The background fluorescence of cells containing no dye was measured daily, and subtracted from the total emitted fluorescence. The background fluorescence averaged 10.4 ± 1.5% (n = 23) of total I₃₂₀ at the beginning of an experiment.

Spectral properties of MQAE.

The fluorescence of the quinolinium dye MQAE is quenched at progressively higher concentrations of halides such as Cl⁻. Fig. 2 A shows the fluorescence excitation and emission spectra of 5 μM MQAE in HEPES-buffered solutions of different Cl⁻ concentrations. The spectra were obtained at 37°C; all solutions were maintained at a constant ionic strength of ∼305 mosmol by replacing Cl⁻ with cyclamate. The excitation spectra (Fig. 2 A, left) were obtained by measuring the emitted fluorescence at 460 nm while exciting the dye with light from 270 to 420 nm in intervals of 1 nm. For each of the seven excitation spectra, there was a major peak at ∼320 nm and a minor peak at ∼350 nm. The emission spectra (Fig. 2 A, right) were obtained by exciting the dye at 350 nm and measuring the emitted fluorescence from 375 to 600 nm in intervals of 1 nm. For each of the seven emission spectra, the peak was at ∼460 nm. These spectral data are similar to those previously reported (Verkman et al., 1989), except that our 320-nm peaks in the excitation spectra were more prominent.

Figure 2.

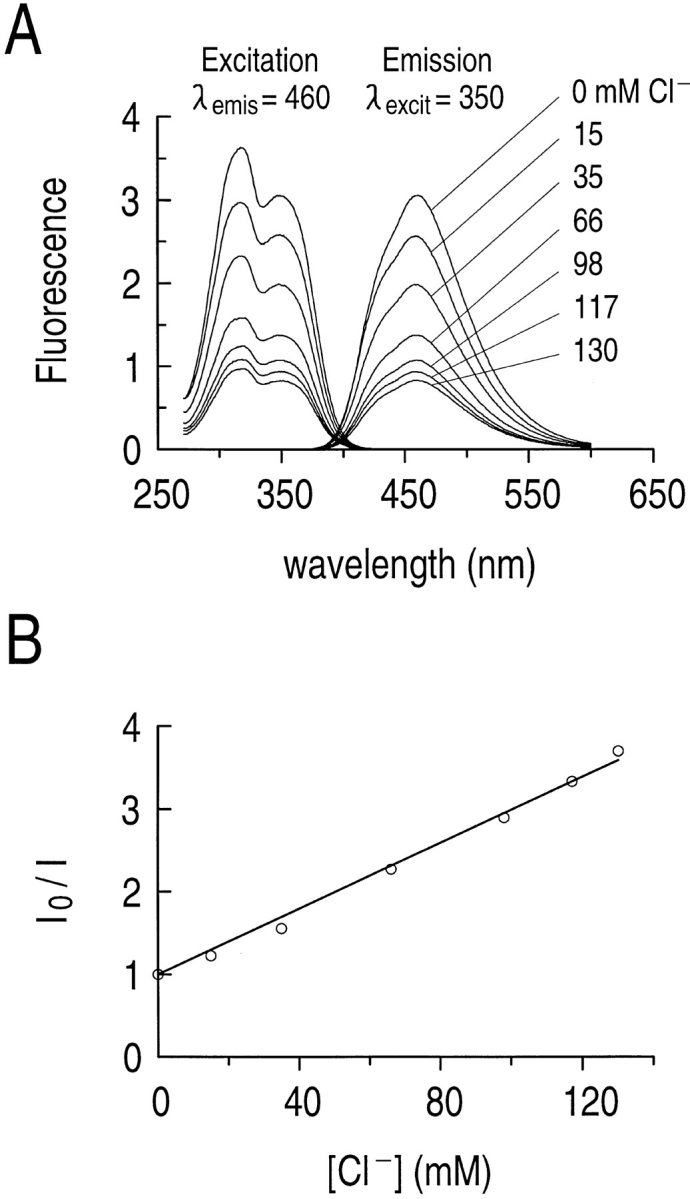
Cl⁻ quenches MQAE fluorescence. (A) The fluorescence excitation and emission spectra of 5 μM MQAE in a cuvette containing solutions of different Cl⁻ concentrations. Both the excitation curves (left) and emission curves (right) were obtained in solutions containing 0, 15, 35, 66, 98, 117, and 130 mM Cl⁻ (top to bottom). (B) The Stern-Volmer relationship for Cl⁻ quenching of MQAE from the emission spectra in A. For the least-square fit to the data points, r   ² = 0.996.

From the emission spectra shown in Fig. 2 A, we plotted the emitted fluorescence as a function of [Cl⁻] (Fig. 2 B), using the Stern-Volmer equation: I ₀/I = 1 + K _Cl × ([Cl⁻]), where I ₀/I is the ratio of emitted fluorescence in the absence and presence of Cl⁻. K _Cl is the Stern–Volmer quenching constant for Cl⁻ (in M⁻¹). From the best-fit line to the data (Fig. 2 B), we conclude that K _Cl is 21 M⁻¹ for MQAE in a cuvette. Although Verkman et al. (1989) reported a K _Cl of 200 M⁻¹ for MQAE, their fluorescence spectra were in solutions containing only 5 mM Na phosphate and variable amounts of NaCl (rather than our standard HEPES buffer at fixed osmolality). Indeed, Koncz and Daugirdas (1994) found that raising osmolality from 5 to 150 mosmol kg⁻¹ caused the K _Cl of MQAE to fall by ∼53%. Also, Lau et al. (1994) found that switching from an unbuffered to a HEPES-buffered solution caused the K _Cl of intracellular MQAE to fall by ∼57%.

Intracellular calibration of MQAE.

In experiments on astrocytes loaded with MQAE, we calibrated the dye using the high K⁺/nigericin/tributyltin chloride technique (Chao et al., 1989). At the end of an experiment, astrocytes were exposed to a solution containing (a) 105 mM K⁺ and 10 μM nigericin to force pH_i to approach pH_o (Thomas et al., 1979), and (b) 5 μM tributyltin chloride, an ionophore that exchanges Cl⁻ and OH⁻, and thus forces [Cl⁻]_i to approach [Cl⁻]_o. By exposing astrocytes to a high K⁺/nigericin/tributyltin chloride solution and changing external Cl⁻, we determined the Stern–Volmer relationship (see above) for intracellular MQAE in each experiment. The average K _Cl of MQAE in hippocampal astrocytes was 8.7 ± 0.8 M⁻¹ (n = 16). Intracellular values in the range of 5.3 to 25 M⁻¹ have been reported for the K _Cl of MQAE in other cell types (Lancer et al., 1990; Engblom and Akerman, 1993; Lau et al., 1994; Koncz and Daugirdas, 1994; Martínez-Zaguilán et al., 1994).

In nine experiments on hippocampal astrocytes loaded with MQAE, applying 0.01% saponin caused the fluorescent signal to decrease to 10.7 ± 1.7% of the signal at the start of the experiment. Because 0.01% saponin is thought to permeabilize only the plasma membrane (Lin et al., 1990), we conclude that 89% of intracellular MQAE is located in the cytoplasm.

Measurement of pH_i in Single Astrocytes

We measured pH_i using the pH-sensitive dye 2′,7′-biscarboxyethyl-5,6-carboxyfluorescein (BCECF) in astrocytes cultured from the hippocampus of the rat, as described in the accompanying paper (Bevensee et al., 1997).

Electrophysiology

V_m was recorded with a patch-clamp amplifier (PC-501A; Warner Instruments Corp., Hamden, CT), using the perforated whole-cell recording technique in current-clamp mode (Horn and Marty, 1988). Recordings were made on the stage of a microscope equipped for epi-fluorescence (IM-35; Carl Zeiss, Inc., Thornwood, NY), as described in the accompanying paper (Bevensee et al., 1997). Signals were filtered at 1 kHz with a 4-pole Bessel filter. V_m was digitized on-line at 50 Hz using an analog-to-digital converter board (Labmaster TL-1; Scientific Solutions Inc., Solon, OH) interfaced with a personal computer (Dell Computers, Austin, TX) based on an Intel-80486 microprocessor. The control of data acquisition and the analysis of data were performed with either a custom-modified version of WinClamp (Indec System, Inc., Capitola, CA) or pClamp (Axon Instruments, Inc., Foster City, CA). LG16 borosilicate glass capillaries (Dagan Corp., Minneapolis, MN) were pulled (PP-83; Narishige Scientific Instruments, Tokyo, Japan) and fire polished (MF-83; Narishige Scientific Instruments, Toyko, Japan) to make patch pipettes with resistances of 2–6 MΩ. In some experiments, the patch pipettes were coated with Sylgard^® (Dow Corning Corp., Midland, MI) before being fire polished to minimize noise. V_m recordings were usually made at 37°C, and in no case <34°C.

Statistics

Data are reported as mean ± SEM. Means were compared using the paired and unpaired forms of the Student's t test (one-tail). P < 0.05 is considered significant. The best-fit line to the I ₀/I vs. [Cl⁻] data plotted in Fig. 2 B was determined using a least-squares method. Rates of MQAE loss from cells was determined by fitting a line to the fluorescence vs. time data using a least-squares method. Rates of change in pH_i (dpH_i/dt) were determined by fitting a line to pH_i vs. time data using a least-squares method.

RESULTS

Using MQAE to Measure Intracellular Cl⁻ in Hippocampal Astrocytes

Na/K/Cl cotransport contributes to the high resting [Cl⁻]_i in astrocytes.

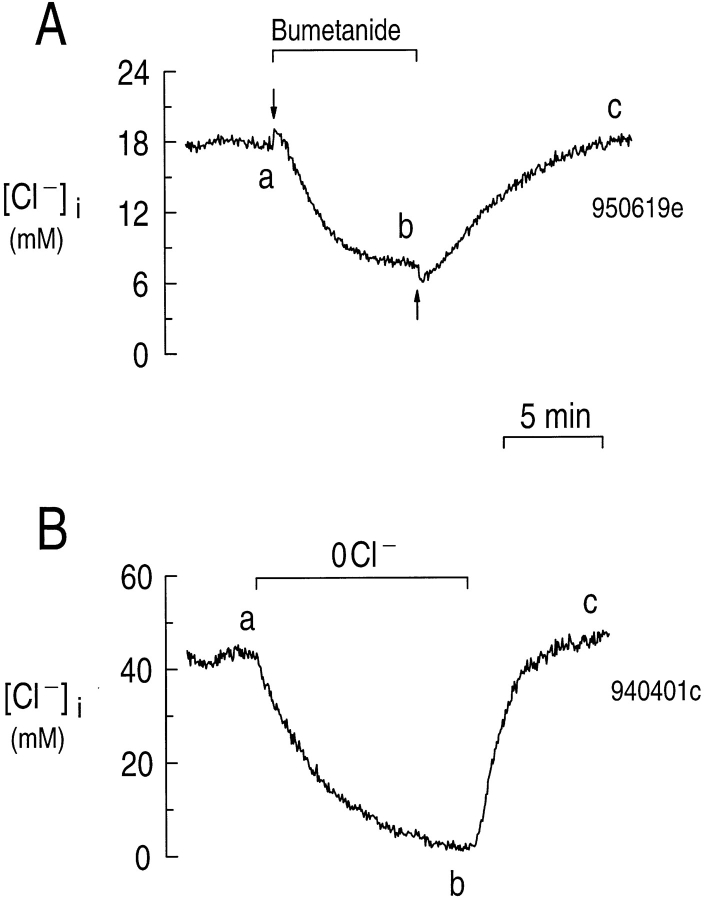
In 16 experiments in which we measured [Cl⁻]_i using the Cl⁻-sensitive dye MQAE, astrocytes had a resting [Cl⁻]_i of 36 ± 4 mM. This is similar to values in the range 25–30 mM, reported by Walz and Hertz (1983) for mouse astrocytes cultured from the cortex. The average resting [Cl⁻]_i of 36 mM is well above the equilibrium value of 4.0 mM that is predicted from the mean V_m of ∼−88 mV that we observed (see below) for astrocytes in a HEPES-buffered solution containing 130 mM Cl⁻. Therefore, Cl⁻ must be actively transported into the cells. In mouse astrocytes, a furosemide-sensitive Na/K/Cl cotransporter is responsible for maintaining intracellular Cl⁻ well above the value predicted if Cl⁻ were passively distributed (Walz and Hertz, 1983). In the experiment shown in Fig. 3 A, we determined whether a similar bumetanide-sensitive Na/K/Cl cotransporter contributes to the high resting [Cl⁻]_i in rat hippocampal astrocytes. The [Cl⁻]_i time course shown in Fig. 3 A is the result of a series of steps, outlined in Appendix, for converting MQAE fluorescence into [Cl⁻]_i values. The astrocytes in this experiment had an initial [Cl⁻]_i of ∼18 mM before point a (Fig. 3 A, a). When we exposed the cells to a solution containing 1 μM bumetanide, [Cl⁻]_i decreased to ∼8 mM (Fig. 3 A, ab). Returning the cells to a bumetanide-free solution elicited an increase in [Cl⁻]_i to a value similar to that at the start of the experiment (Fig 3 A, bc). Because 1 μM bumetanide fluoresces when excited at 320 nm, we subtracted the signal due to bumetanide from the total I₃₂₀. This correction resulted in offsets in the [Cl⁻]_i vs. time trace at the points where bumetanide was applied and removed (Fig. 3 A, arrows). In four experiments, bumetanide caused [Cl⁻]_i to decrease from 23 ± 3 to 15 ± 3 mM (P < 0.005). A bumetanide-insensitive Cl⁻ uptake mechanism could also contribute to the elevated [Cl⁻]_i in the presence of bumetanide. We conclude that a bumetanide-sensitive Na/K/Cl cotransporter contributes to the high resting [Cl⁻]_i in hippocampal astrocytes. Others have found that applying furosemide or bumetanide to cultured hippocampal astrocytes causes a decrease in intracellular Na⁺ ([Na⁺]_i), suggesting that the Na/K/Cl cotransporter also helps maintain a high resting [Na⁺]_i (Rose and Ransom, 1996).

Figure 3.

Adding bumetanide or removing external Cl⁻ elicits a reversible decrease in [Cl⁻]_i of hippocampal astrocytes. (A) Between a and b, we exposed the cells to 1 μM bumetanide. (B) Between a and b, we replaced the extracellular Cl⁻ with cyclamate.

Removing extracellular Cl⁻ elicits a rapid decrease in [Cl⁻]_i.

In Fig. 3 B, we show the record of [Cl⁻]_i in an experiment in which astrocytes were exposed to a solution in which Cl⁻ was replaced with cyclamate. The cells in this experiment had an initial [Cl⁻]_i of ∼43 mM before point a (Fig. 3 B, a). Removing external Cl⁻ elicited a sharp decrease in [Cl⁻]_i to ∼2 mM (Fig. 3 B, ab). Returning external Cl⁻ caused [Cl⁻]_i to increase to its initial value (Fig. 3 B, bc). In 11 experiments similar to that shown in Fig. 3 B, removing external Cl⁻ caused [Cl⁻]_i to decrease from an average resting value of 40 ± 5 to 2.8 ± 1.5 mM in 10.7 ± 1.9 min. [Cl⁻]_i decreased at an initial rate of 277 ± 71 μM s⁻¹ (n = 11).

Na⁺-driven HCO₃ ⁻ Influx: Testing the Intracellular Cl⁻ Dependence

Intracellular Cl⁻ is not required for the forward transport of HCO₃ ⁻ into astrocytes after an acid load imposed by an NH₄ ⁺ prepulse.

If the CO₂/HCO₃ ⁻-induced alkalinization were mediated by a Na⁺-driven Cl-HCO₃ exchanger, then the alkalinization should require the efflux of substantial amounts of Cl⁻. In the following experiments, we monitored pH_i in single astrocytes, using the pH-sensitive dye BCECF. Our first approach was to acid load the astrocytes repeatedly, using the NH₄ ⁺ prepulse technique (Boron and De Weer, 1976), with 0.9 mM amiloride present to inhibit Na-H exchange. Because the amiloride was added as the Cl⁻ salt, [Cl⁻]_o was ∼  0.9 mM. After each acid load, we added CO₂/HCO₃ ⁻to activate the Na⁺-driven Cl-HCO₃ ⁻uptake mechanism. From the magnitude of the pH_i recovery and from the known β_T, we can compute how much internal Cl⁻ would have to be transported out of the cell to achieve each pH_i recovery.

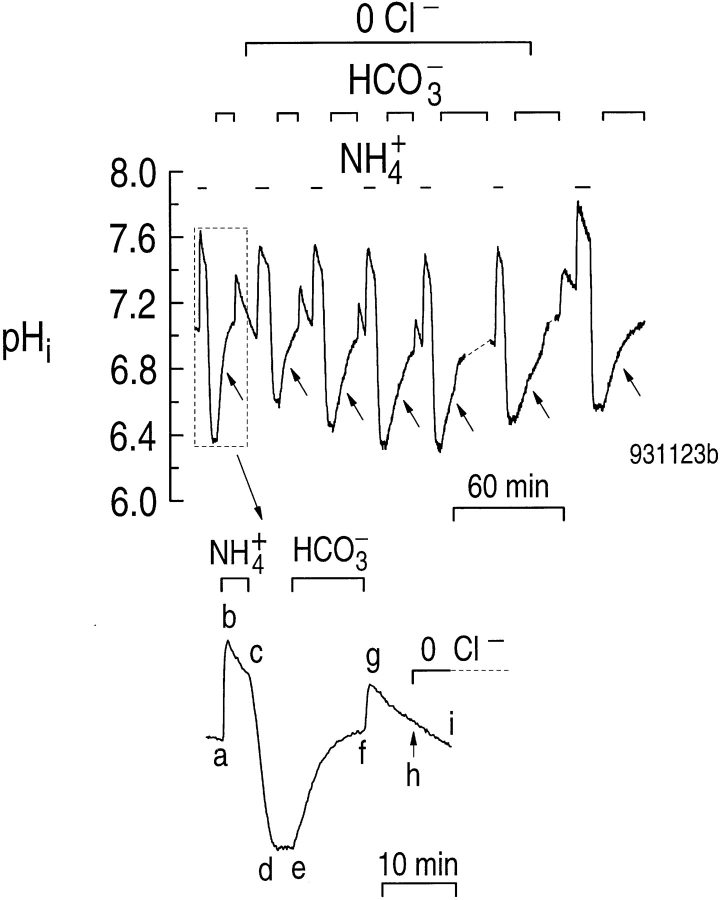
In the experiment of Fig. 4, we acid loaded the astrocytes seven times, the first time in the presence of 130 mM Cl⁻. As shown in the inset, applying and removing 20 mM NH₃/NH₄ ⁺ caused the usual series of pH_i changes (Fig. 4, abcd), as noted in the accompanying study (Bevensee et al., 1997). In the absence of CO₂/ HCO₃ ⁻, the pH_i recovery was blocked by amiloride (Fig. 4, de). However, adding CO₂/HCO₃ ⁻ caused pH_i to increase rapidly (Fig. 4, ef ). Removing the CO₂/ HCO₃ ⁻ caused a transient pH_i increase (Fig. 4, fg), due to CO₂ efflux, followed by a slower decline (Fig. 4, ghi). At point h, we reduced [Cl⁻]_o to ∼0.9 mM and did not return [Cl⁻]_o to 130 mM until the recovery from the sixth NH₄ ⁺ pulse. Each of the seven CO₂/HCO₃ ⁻-induced pH_i recoveries is indicated by an arrow in Fig. 4. Two technical points are noteworthy. First, after the recovery from the fifth NH₄ ⁺ pulse, we continued the experiment on a nearby cell on the same cover slip, because of evidence of dye loss from the original astrocyte. Similarly, we switched to a third cell after the sixth NH₄ ⁺ pulse. We used this third cell, as well as two neighbors, for the calibration of intracellular BCECF. Second, there was a general tendency for the rates of pH_i recovery in the presence of CO₂/HCO₃ ⁻ to decrease somewhat over the course of this very long experiment (>4 h). Indeed, the rate of the seventh and final pH_i recovery (Cl⁻ present) was ∼1/3 less than that of the first pH_i recovery (Cl⁻ present).

Figure 4.

Astrocytes that are acid loaded in HEPES display pH_i recoveries when exposed to CO₂/HCO₃ ⁻ in the absence of external Cl⁻. As shown in the inset, astrocytes were acid loaded by a brief exposure to a solution containing 20 mM NH₄Cl (a–d ). At c, the astrocytes were exposed to 0.9 mM amiloride for the duration of the experiment. During the indicated period, the cells were then exposed to 5% CO₂/17 mM HCO₃ ⁻ (ef  ). Subsequently, the astrocytes were acid loaded in amiloride and exposed to CO₂/ HCO₃ ⁻ five more times in the absence of Cl⁻ (top). The cells were then returned to the Cl⁻-containing solution and acid loaded one last time.

The CO₂/HCO₃ ⁻-induced alkalinization after the second NH₄ ⁺ pulse in Fig. 4 (i.e., the first in the absence of Cl⁻) would require the efflux of 4.5 mM Cl⁻, if it were mediated by Na⁺-driven Cl-HCO₃ exchange. Similarly, the third through sixth CO₂/HCO₃ ⁻-induced alkalinizations would require effluxes of 4.9, 4.9, 5.5, and 2.5 mM Cl⁻. However, based on the results from experiments similar to Fig. 3 B, the [Cl⁻]_i just before the addition of CO₂/HCO₃ ⁻ in Fig. 4 was probably only ∼3 mM. Therefore, it appears unlikely that the pH_i recoveries in 0 Cl⁻ could be mediated by a Na⁺-driven Cl-HCO₃ exchanger unless substantial amounts of Cl⁻ could recycle back into the cell from the 0.9 mM Cl⁻ in the external solution. However, for the first pH_i recovery in the absence of extracellular Cl⁻, the maximal rate of HCO₃ ⁻ influx would have required a Cl⁻ efflux of 2.7 mM min⁻¹. Because the Na/K/Cl cotransporter in primary cultures of rat astrocytes has a K _m for external Cl⁻ of 40 mM (Tas et al., 1987), it is unlikely that recycling could keep up with the Cl⁻ depletion caused by HCO₃ ⁻ transport. Thus, [Cl⁻]_i during the CO₂/HCO₃ ⁻-induced pH_i recovery (i.e., Cl⁻ efflux) was probably substantially less than the initial ∼3 mM mentioned above. Even if Cl⁻ recycling were substantial, the five pH_i recoveries under low [Cl⁻]_o conditions could have been mediated by a Na⁺-driven Cl-HCO₃ exchanger only if the hypothetical Na⁺-driven Cl-HCO₃ exchanger had an extremely high affinity for intracellular Cl⁻. In squid axons, the only preparation in which the K _m for intracellular Cl⁻ has been determined for the Na⁺-driven Cl-HCO₃ exchanger, K _m (Cl⁻) is about the same as the resting [Cl⁻]_i (Boron and Russell, 1983). Even if the K _m (Cl⁻) for a hypothetical Na⁺-driven Cl-HCO₃ exchanger in astrocytes were substantially less than the resting [Cl⁻]_i of 36 mM, this K _m (Cl⁻) would still be several times higher than the likely [Cl⁻]_i during the CO₂/ HCO₃ ⁻-induced pH_i increase.

Intracellular Cl⁻ does not appear to be necessary for the forward transport of HCO₃ ⁻ into astrocytes when they are first exposed to CO₂/HCO₃ ⁻.

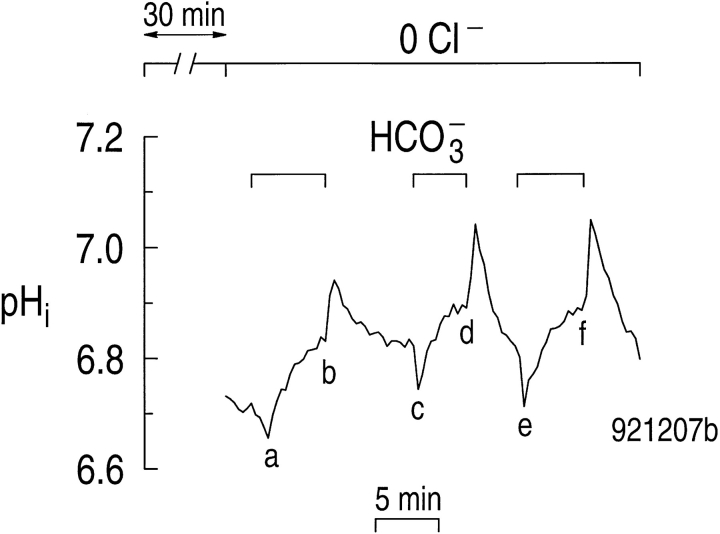
Our second approach for assessing the Cl⁻ dependence of the CO₂/HCO₃ ⁻-induced alkalinization was to determine if depleting astrocytes of Cl⁻ slows this alkalinization. Before the start of the experiment in Fig. 5, the coverslip containing astrocytes was incubated in a Cl⁻-free solution for 30 min, enough time to reduce [Cl⁻]_i to an average of ∼3 mM (Fig. 3 B). The Cl⁻-free solution also contained 1 mM isoguvacine, which stimulates the GABA_A-activated Cl⁻ channels known to be present in astrocytes in rat hippocampal slices (MacVicar et al., 1989). Thus, with isoguvacine accelerating the Cl⁻ loss, [Cl⁻]_i should have been extremely low by the outset of the experiment.

Figure 5.

Astrocytes preincubated in a Cl⁻-free solution still alkalinize when exposed to CO₂/HCO₃ ⁻. Before the start of the experiment, the astrocyte was incubated for 30 min in a Cl⁻-free, HEPES-buffered solution containing 1 mM of the GABA_A-agonist isoguvacine. During the experiment, 5% CO₂/17 mM HCO₃ ⁻ was applied and removed three times in the continued absence of external Cl⁻.

In Fig. 5, the astrocyte remained in Cl⁻-free solutions throughout the experiment. The initial pH_i was ∼6.7 in the standard HEPES solution. We then exposed the astrocyte to a CO₂/HCO₃ ⁻-buffered solution three times. With each exposure, pH_i decreased transiently, due to CO₂ influx (Fig. 5, a, c, and e), and then increased rapidly to a value higher than in the HEPES solution, due to Na⁺-driven HCO₃ ⁻ influx (Fig. 5, b, d, and f  ). The three pH_i increases were of similar speed, and had a magnitude close to that observed in the accompanying paper (Bevensee et al., 1997) under control conditions (i.e., presence of extracellular Cl⁻). If the alkalinizations ab, cd, and ef were due to a Na⁺-driven Cl-HCO₃ exchanger, then each alkalinization would further deplete the cell of intracellular Cl⁻. From the sum of the pH_i increases in Fig. 5, ab, cd, and ef, and the average buffering power (β_T), we calculate that, at a minimum, 9.5 mM HCO₃ ⁻ was transported into the cell. If this HCO₃ ⁻ transport were mediated by a Na⁺-driven Cl-HCO₃ exchanger moving two HCO₃ ⁻ ions for each Na⁺ and Cl⁻ ion, then 4.7 mM Cl⁻ would be required.² As summarized in Table I, the computed Cl⁻ loss was 8.8 and 12.3 in two other experiments. Because it is unlikely that these cells could have had >∼3 mM intracellular Cl⁻ at the outset, it would appear that there was insufficient Cl⁻ to support the CO₂/HCO₃ ⁻-induced pH_i increases, if the alkalinizations were mediated by a Na⁺-driven Cl-HCO₃ exchanger.

Table I.

Intracellular Cl⁻ Dependence of the Alkalinizations When Astrocytes Are Exposed to Multiple CO₂/HCO₃ ⁻ Pulses in the Absence of External Cl⁻

Experiment		0 Cl−-incubation		Exposures to CO2/HCO3 −		ΣΔpHi		Σ[Cl−]i required
		min						mM
921207b		30*		3		0.51		4.7
930729c		12.5		8		0.91		12.3
940111a		16		3‡		0.74		8.8

^*0 Cl⁻-incubation solution contained 1 mM isoguvacine.  

^‡ Solutions contained 10 μM ethylisopropylamiloride (EIPA).  

Na⁺-driven HCO₃ ⁻ Efflux: Testing the Extracellular Cl⁻ Dependence

The transporter moves HCO₃ ⁻ out of astrocytes exposed to a Na⁺-free, CO₂/HCO₃ ⁻-buffered solution.

The data in Figs. 4 and 5 suggest that the Na⁺-driven HCO₃ ⁻ transporter in astrocytes does not require intracellular Cl⁻ to operate in the forward direction (i.e., HCO₃ ⁻ influx). We also tested the hypothesis that the transporter does not require extracellular Cl⁻ to operate in the reverse direction (i.e., HCO₃ ⁻ efflux). This assay has the advantage that one can be reasonably confident that the Cl⁻ has been rapidly and completely removed.

Our first step was to determine if the Na⁺-driven HCO₃ ⁻ transporter in astrocytes can be forced to operate in the reverse direction by removing external Na⁺, thereby causing the net movement of Na⁺ and HCO₃ ⁻ out of the cells, and decreasing pH_i. Fig. 6 illustrates an experiment on a single astrocyte with a steady state pH_i of ∼7.0 in a HEPES solution. Exposing the cell to a solution in which Li⁺ replaced Na⁺ as the major cation caused the pH_i to decrease by ∼0.1 (Fig. 6, ab), presumably due to reversal of Na-H exchange. The pH_i decrease with Li⁺ as the replacement cation was substantially less than that observed with NMDG⁺, because Li⁺, in contrast to NMDG⁺, can partially substitute for Na⁺ on the Na-H exchanger (Bevensee et al., 1997). Returning the cell to the Na⁺-containing solution caused pH_i to increase (Fig. 6, bc) and actually overshoot the initial value (Fig. 6, c vs. a). This overshoot could be due to stimulation of Na-H exchange, inasmuch as the exchanger is stimulated by intracellular Li⁺ in barnacle muscle fibers (Davis et al., 1992). When the astrocyte in Fig. 6 was then switched to a solution buffered with 5% CO₂/17 mM HCO₃ ⁻, the pH_i decreased initially (Fig. 6, cd), and then increased slowly due, in part, to the Na⁺-driven HCO₃ ⁻ transporter (Fig. 6, de). Removing external Na⁺ (replaced with Li⁺) in the presence of CO₂/HCO₃ ⁻ elicited a decrease in pH_i (Fig. 6, ef) that was faster and larger than in HEPES (Fig. 6, ab), presumably because the Na⁺-driven HCO₃ ⁻ transporter was operating in the reverse direction and moving HCO₃ ⁻ out of the cell. As shown in the previous manuscript, Li⁺ is a poor substitute for Na⁺ on the Na⁺-driven HCO₃ ⁻ transporter in hippocampal astrocytes (Bevensee et al., 1997). After its initial decrease, pH_i began to increase slowly (Fig. 6, fg), presumably because external Li⁺ exchanged with internal H⁺ via the Na-H exchanger. Returning the astrocyte to the Na⁺-containing solution caused the pH_i to increase (Fig. 6, gh) and overshoot the initial value (Fig. 6, h vs. e). In 14 experiments on astrocytes with an average pH_i of 6.98 ± 0.04 in a HEPES solution, removing external Na⁺ elicited an average initial acid influx (ϕ_L) of 26.0 ± 3.7 μM s⁻¹. However, in 27 experiments on astrocytes with a similar average pH_i of 6.95 ± 0.02 in a CO₂/HCO₃ ⁻-buffered solution, removing external Na⁺ elicited a mean ϕ_L of 102 ± 6 μM s⁻¹. Therefore, ϕ_L is approximately fourfold greater when Na⁺ is removed in the presence than in the absence of CO₂/HCO₃ ⁻, consistent with Na/ HCO₃ efflux.

Figure 6.

Removing external Na⁺ elicits a larger and faster pH_i decrease when astrocytes are exposed to CO₂/HCO₃ ⁻ rather than to HEPES. We replaced external Na⁺ with Li⁺ when the cell was exposed to a HEPES-buffered solution (ab) and a 5% CO₂/17 mM HCO₃ ⁻-buffered solution (e–g).

DIDS inhibits the increase in pH_i when astrocytes are switched from Li⁺ to Na⁺ in the presence of CO₂/HCO₃ ⁻.

Initially, we attempted to determine if DIDS could block the HCO₃ ⁻-dependent pH_i decrease observed when astrocytes are exposed to a Na⁺-free solution. However, we found that exposing cells to DIDS in the presence of CO₂/HCO₃ ⁻ causes a decrease in steady state pH_i (not shown), presumably, in part, because DIDS inhibits the Na-dependent HCO₃ ⁻ transporter that is active in the steady state. Because pH_i was lower in the presence of DIDS, it was not possible to compare rates of acidification at similar pH_i values in the presence and absence of DIDS. Therefore, we compared rates of alkalinization when astrocytes were reexposed to external Na⁺ in the presence and absence of DIDS.

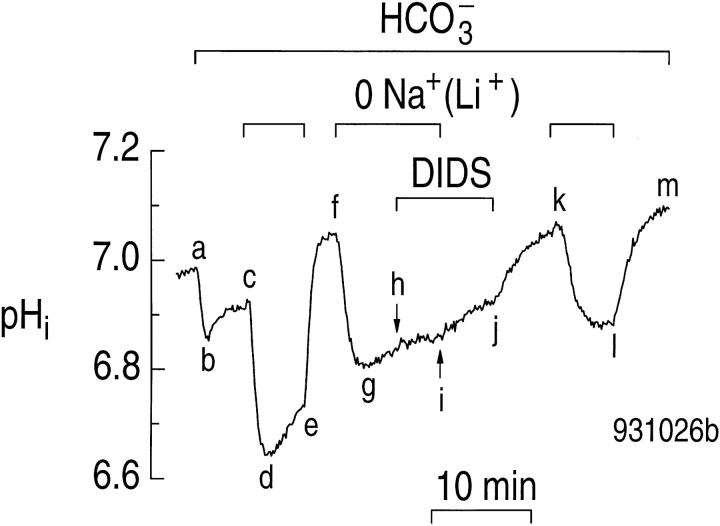
At the start of the experiment in Fig. 7, the astrocyte had a steady state pH_i of ∼7.0 in a HEPES-buffered solution (before point a). Exposing the cell to CO₂/ HCO₃ ⁻ caused the usual changes in pH_i (Fig. 7, abc). Replacing the Na⁺ with Li⁺ in the presence of CO₂/ HCO₃ ⁻ elicited a rapid decrease in pH_i (Fig. 7, cd), followed by a slow increase (Fig. 7, de), as seen in Fig. 6. Returning Na⁺ to the external solution caused pH_i to increase (Fig. 7, ef  ) to a value higher than that prevailing in the presence of CO₂/HCO₃ ⁻ (Fig. 7, f vs. c). After we replaced Na⁺ with Li⁺ a second time, and observed the fall and partial recovery of pH_i (Fig. 7, fgh), we added 400 μM DIDS. This addition had little effect on pH_i (Fig. 7, hi). When we now returned external Na⁺ in the presence of DIDS, the acceleration of the pH_i recovery (Fig. 7, ij vs. hi) was much smaller than in the absence of DIDS (Fig. 7, ef vs. de). Removing DIDS from the external solution allowed pH_i to increase even faster (Fig. 7, jk), indicating that DIDS was partially reversible. Removing external Na⁺ a third time in the absence of DIDS elicited the expected decrease in pH_i (Fig. 7, kl). However, DIDS may not have been entirely reversible, inasmuch as the rate of the pH_i decrease (Fig. 7, k) was slower than at Fig. 7, c and f. Similarly, the pH_i recovery elicited by returning Na⁺ the third time (Fig. 7, lm) was slower than for the first time (Fig. 7, ef  ).

Figure 7.

DIDS inhibits the pH_i increase caused by returning external Na⁺ to astrocytes bathed in 5% CO₂/17 mM HCO₃ ⁻. Between a and m, the cell was exposed to 5% CO₂/17 mM HCO₃ ⁻. We replaced external Na⁺ with Li⁺ three times (c–e, f–i, and kl ). 400 μM DIDS was present between points h and j.

Summarizing data from four such experiments, we found that returning Na⁺ in the presence of DIDS was associated with an acid extrusion rate (ϕ_E) of 13 ± 9 μM s⁻¹ at a pH_i of 6.83 ± 0.03. In paired experiments in the absence of DIDS, ϕ_E was 127 ± 15 μM s⁻¹ at a slightly lower pH_i of 6.75 ± 0.03. Therefore, DIDS inhibits ∼90% of the acid extrusion when astrocytes in CO₂/HCO₃ ⁻ are returned to a solution containing Na⁺ (P < 0.0003). The effect of DIDS is also CO₂/HCO₃ ⁻ dependent: returning external Na⁺ to astrocytes bathed in a HEPES solution containing 400 μM DIDS elicited a ϕ_E of 23 ± 9 μM s⁻¹ at a pH_i of 6.82 ± 0.07 (n = 6). In paired experiments at a similar pH_i, ϕ_E in a HEPES solution in the absence of DIDS was nearly the same (25 ± 8 μM s⁻¹, P = 0.26).

Na⁺-driven HCO₃ ⁻ transporter can move HCO₃ ⁻ out of astrocytes even in the absence of external Cl⁻.

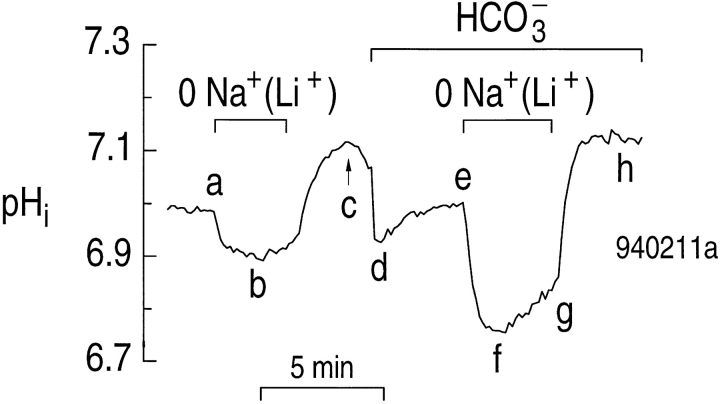
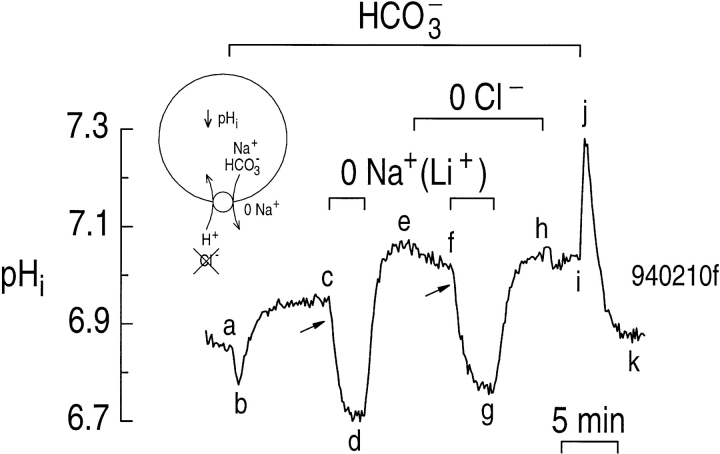
If a Na⁺-driven Cl-HCO₃ exchanger were responsible for the CO₂/ HCO₃ ⁻-dependent decrease in pH_i when astrocytes are exposed to a Na⁺-free solution, then the pH_i decrease should require external Cl⁻ (Fig. 8, inset). In the experiment shown in Fig. 8, the astrocyte at the start of the experiment had a pH_i of ∼6.85 in a HEPES solution. Switching to CO₂/HCO₃ ⁻ caused pH_i to decrease (Fig. 8, ab), and then to increase promptly (Fig. 8, bc) to a value ∼0.1 higher than in the HEPES solution (Fig. 8, c vs. a). Removing external Na⁺ elicited a rapid and reversible pH_i decrease (Fig. 8, cde), similar to that seen in Figs. 6 and 7. When the astrocyte was exposed to a Cl⁻-free solution, the pH_i decreased slowly (Fig. 8, ef  ). If the cells had either a Na⁺-driven Cl-HCO₃ exchanger or a Cl-HCO₃ exchanger, one might have expected pH_i to increase in the absence of external Cl⁻, due to exchange of internal Cl⁻ for external HCO₃ ⁻. In the continued absence of external Cl⁻, removing external Na⁺ elicited a rapid decrease in pH_i (Fig. 8, fg) that was of the same rate as observed in the presence of external Cl⁻ (Fig. 8, arrows). Returning the astrocyte to a solution containing Na⁺, but not Cl⁻ caused pH_i to increase to its initial value (Fig. 8, gh). Reintroducing Cl⁻ had little effect on pH_i (Fig. 8, hi). Finally, switching back to the HEPES solution elicited a sharp increase in pH_i (Fig. 8, ij), followed by a rapid decrease (Fig. 8, jk) to the pH_i prevailing at the start of the experiment (Fig. 8, k vs. a). In a total of eight experiments similar to that in Fig. 8, the ϕ_L caused by Na⁺ removal in the presence of external Cl⁻ (Fig. 8, cd) was 101 ± 5 μM s⁻¹ at a pH_i 6.91 ± 0.03. ϕ_L in the absence of external Cl⁻ (Fig. 8, fg) was 96 ± 10 μM s⁻¹ (P = 0.32, paired t test) at the same pH_i of 6.91 ± 0.03. As noted above, 75% of the acid influx (ϕ_L) observed during removal of extracellular Na⁺ in the presence of CO₂/HCO₃ ⁻ is due to reversal of the Na⁺-driven HCO₃ ⁻ transporter. Because ϕ_L was unaffected by removing external Cl⁻, the Na⁺-driven HCO₃ ⁻ transporter could not have been a Na⁺-driven Cl-HCO₃ exchanger.

Figure 8.

The pH_i decrease elicited by removing external Na⁺ in CO₂/HCO₃ ⁻ does not require external Cl⁻. In the presence of 5% CO₂/17 mM HCO₃ ⁻ (a–i), the cell was exposed twice to a solution in which Li⁺ replaced external Na⁺ (cd and fg). During the indicated period, cyclamate replaced external Cl⁻ (e–h). As shown in the inset, a hypothetical cell possessing a Na⁺-driven Cl-HCO₃ exchanger should have exhibited a pH_i decrease upon removing external Na⁺, and this pH_i decrease should have required external Cl⁻. The arrows point to the initial pH_i decrease elicited by removing external Cl⁻.

Na/HCO₃ Cotransport in 20% CO₂ /68 mM HCO₃ ⁻

Because the Na⁺-driven HCO₃ ⁻ transporter in hippocampal astrocytes does not require intracellular Cl⁻ to operate in the normal forward direction, nor extracellular Cl⁻ to operate in the reverse direction, we conclude that the transporter cannot be a Na⁺-driven Cl-HCO₃ exchanger. By default (see introduction), the Na⁺-driven HCO₃ ⁻ transporter must be a Na/HCO₃ cotransporter with a Na⁺:HCO₃ ⁻ stoichiometry of either 1:1 (electroneutral) or 1:2 (electrogenic). If the transporter were electrogenic, then the acid influx mediated by the transporter operating in reverse (Fig. 8, cd) should be associated with an inward current that depolarizes the astrocyte. From the initial rate of pH_i decrease during Fig. 8, cd, we calculate³ that a 1:2 Na/ HCO₃ cotransporter would produce a DIDS-sensitive depolarization of 1.7 mV. Because such a small depolarization could be difficult to detect, we attempted first to enhance the HCO₃ ⁻ efflux, and thus the predicted depolarization.

DIDS inhibits the Na/HCO₃ cotransporter in astrocytes exposed to 20% CO₂ /68 mM HCO₃ ⁻.

We performed experiments (not shown) identical to that in Fig. 7, except that the CO₂/HCO₃ ⁻ solutions contained 20% CO₂ and 68 mM HCO₃ ⁻, pH 7.3. The HCO₃ ⁻ efflux from astrocytes should be greater when the cells, at the same pH_i, are incubated in this “high CO₂/HCO₃ ⁻” solution because the fourfold increase in [HCO₃ ⁻]_i would increase the efflux (if the cotransporter were not already saturated). In the continued presence of high CO₂/HCO₃ ⁻, removing external Na⁺ elicited a rapid decrease in pH_i that was reversed upon returning Na⁺. In paired experiments, returning external Na⁺ in the presence of DIDS elicited a pH_i increase that was substantially slower than in the absence of DIDS. Summarizing the HCO₃ ⁻-influx data for astrocytes bathed in 20% CO₂/68 mM HCO₃ ⁻, DIDS caused ϕ_E (measured when we returned Na⁺) to decrease from 239 ± 48 to 87 ± 15 μM s⁻¹ at a pH_i of ∼6.7 (n = 6; P < 0.008). Thus, DIDS inhibited acid extrusion less in 20% CO₂ (63%) than in 5% CO₂ (90%), suggesting that HCO₃ ⁻ may compete with DIDS.

Summarizing HCO₃ ⁻-efflux data in 20% CO₂, we found that removing Na⁺ was associated with a ϕ_L of 281 ± 31 μM s⁻¹, at a pH_i of 6.96 ± 0.03 (n = 14). This efflux is 2.8-fold greater than the ϕ_L of 101 μM s⁻¹ observed in 5% CO₂. Assuming that 63% of the HCO₃ ⁻ efflux in 20% CO₂ is DIDS sensitive, the predicted DIDS-sensitive depolarization would be ∼3.3 mV, approximately twice as large as in 5% CO₂. In the next section, we describe experiments in which we attempted to detect this predicted ∼3.3-mV depolarization.

Electrogenic Na/HCO₃ Cotransport

Astrocytes exposed to 20% CO₂/68 mM HCO₃ ⁻ had a resting V_m of −92 mV and an input resistance of 236 MΩ in the perforated patch-clamp configuration.

The average resting V_m of astrocytes in a HEPES solution was −87.5 ± 0.8 mV (range: −72.0 to −97.7, n = 52), whereas the average resting V_m of astrocytes in a 20% CO₂/68 mM HCO₃ ⁻-buffered solution was −92.0 ± 0.7 mV (range: −80.8 to −99.1, n = 40). In 28 experiments in which we switched from HEPES to CO₂/HCO₃ ⁻, V_m became more negative by an average of 4.3 ± 0.5 mV (P < 0.0001; paired t test). At least qualitatively, this hyperpolarization is consistent with the movement of net negative charge into the cell via electrogenic Na/HCO₃ cotransport.

The input resistance of astrocytes was computed at the beginning of some experiments from the current step (ΔI) in response to a 5-ms, 5-mV depolarizing pulse (ΔV) from a holding potential of ∼−80 mV. The average input resistance (ΔV/ΔI) was 236 ± 32 MΩ (n = 18). In other experiments, we computed total resistance at each sample point from the change in V_m in response to current injections. Total resistance did not appear to change when astrocytes were switched from a HEPES- to a CO₂/HCO₃ ⁻-buffered solution or vice versa.

In the perforated patch-clamp configuration, the pipette contents have little effect on pH_i.

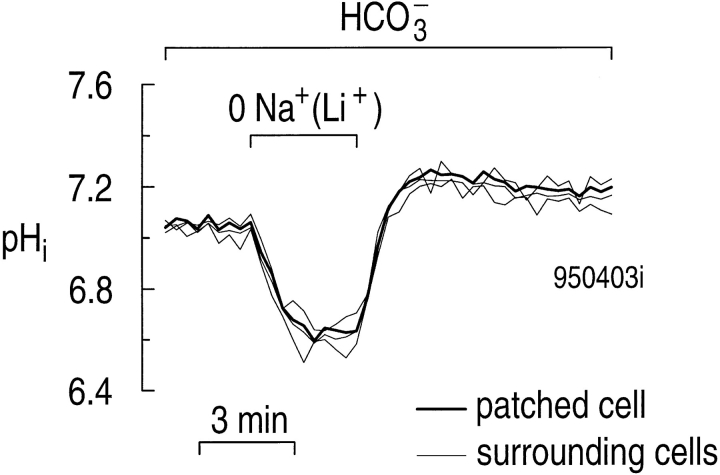
Because the pH of the patch-pipette solution was only weakly buffered (1 mM HEPES), and because a perforated patch limits the diffusion of solutes between cell and pipette, we hoped that patched astrocytes subjected to manipulations of the extracellular solution would display the same pH_i changes as unpatched cells. In the experiment shown in Fig. 9, we used a digital-imaging system to monitor pH_i in four astrocytes, one of which was attached to the patch pipette (thick trace). In the presence of 5% CO₂/17 mM HCO₃ ⁻, all cells underwent similar (and expected) pH_i changes in response to replacing extracellular Na⁺ with Li⁺.

Figure 9.

The patch pipette in the cell-attached configuration has little effect on the pH_i changes in astrocytes exposed to a Na⁺-free (Li⁺) solution in 5% CO₂/17 mM HCO₃ ⁻. The patched cell (thick trace), as well as three surrounding cells (thin traces), were exposed to a HCO₃ ⁻-containing solution in which we replaced external Na⁺ with Li⁺. Similar results were obtained in three other experiments.

Removing external Na⁺ elicits an HCO₃ ⁻-dependent depolarization that is blocked by DIDS.

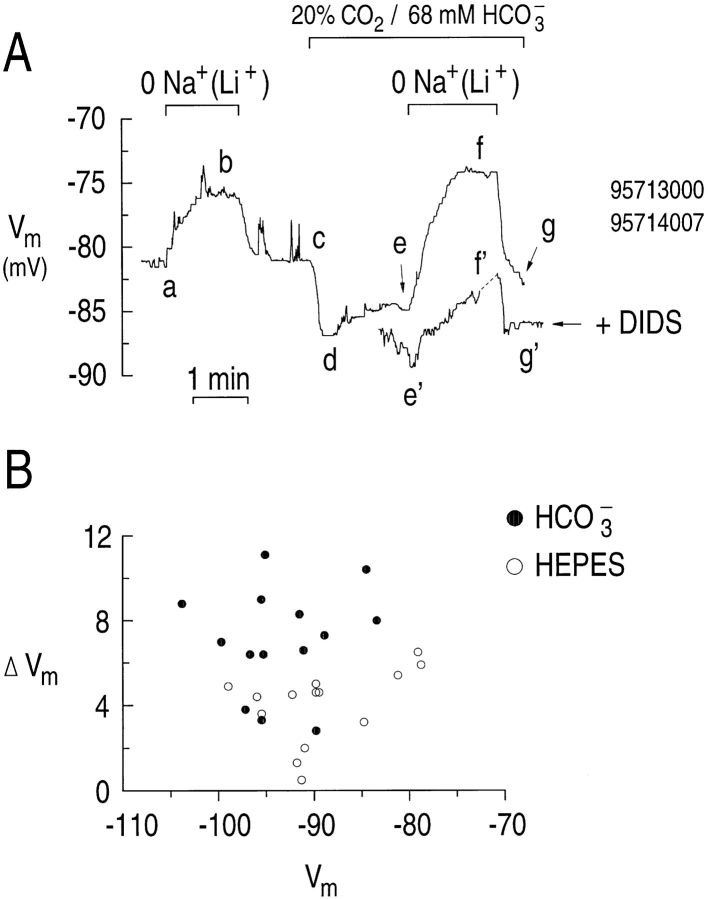
In the experiment shown in Fig. 10 A, the astrocyte had a resting V_m of ∼−82 mV in the nominal absence of CO₂/HCO₃ ⁻ (Fig. 10 A, a). Replacing external Na⁺ with Li⁺ elicited a depolarization to ∼−76 mV (Fig. 10 A, ab) that was completely reversed when we returned the Na⁺ (Fig. 10 A, bc). Some of this depolarization may be due to the inhibition of a Na-dependent K⁺ conductance (Martin and Dryer, 1989). Subsequently, exposing the cell to 20% CO₂/68 mM HCO₃ ⁻ elicited an initial hyperpolarization to ∼−87 mV (Fig. 10 A, cd), followed by a slower depolarization to ∼−84 mV (Fig. 10 A, de). As noted above, the initial hyperpolarization is qualitatively consistent with the hypothesis that a Na/HCO₃ cotransporter moves net negative charge into the cell. When the astrocyte was exposed to a Na⁺-free solution in the presence of CO₂/HCO₃ ⁻, the cell depolarized to ∼−73 mV (Fig. 10 A, ef  ). The depolarization in the presence of CO₂/ HCO₃ ⁻ was ∼6 mV greater than in the absence of CO₂/HCO₃ ⁻. Moreover, compared with the depolarization in the nominal absence of CO₂/HCO₃ ⁻, the one in the presence of CO₂/HCO₃ ⁻ started at a more negative V_m and finished at a more positive V_m, ruling out the possibility that the difference in depolarizations was due to the voltage dependence of the conductances. When Na⁺ was returned to the external solution, the astrocyte hyperpolarized towards the initial resting V_m in the presence of CO₂/HCO₃ ⁻ (Fig. 10 A, fg). In a separate experiment, the changes in V_m produced by removing and returning external Na⁺ in the presence of 20% CO₂/68 mM HCO₃ ⁻ were greatly reduced in the presence of DIDS (Fig. 10 A, e ' f ' g ' ).

Figure 10.

Removing external Na⁺ elicits a depolarization that is inhibited by DIDS or by removing 20% CO₂/68 mM HCO₃ ⁻. (A) Effect of removing Na⁺ on the V_m of astrocytes exposed to a “high” CO₂/HCO₃ ⁻ solution. We replaced external Na⁺ with Li⁺ when the cell was exposed to a HEPES-buffered solution (ab) and a 20% CO₂/68 mM HCO₃ ⁻-buffered solution (ef  ). In a separate experiment on an astrocyte exposed to 400 μM DIDS, we replaced external Na⁺ with Li⁺ in the presence of 20% CO₂/68 mM HCO₃ ⁻ (e ' f '  ). (B) The magnitude of the depolarization plotted as a function of V_m for 14 astrocytes in which external Na⁺ was removed in either HEPES (○) or 20% CO₂/68 mM HCO₃ ⁻ (•). Some data points represent the average depolarization elicited by removing external Na⁺ more than once in a single experiment.

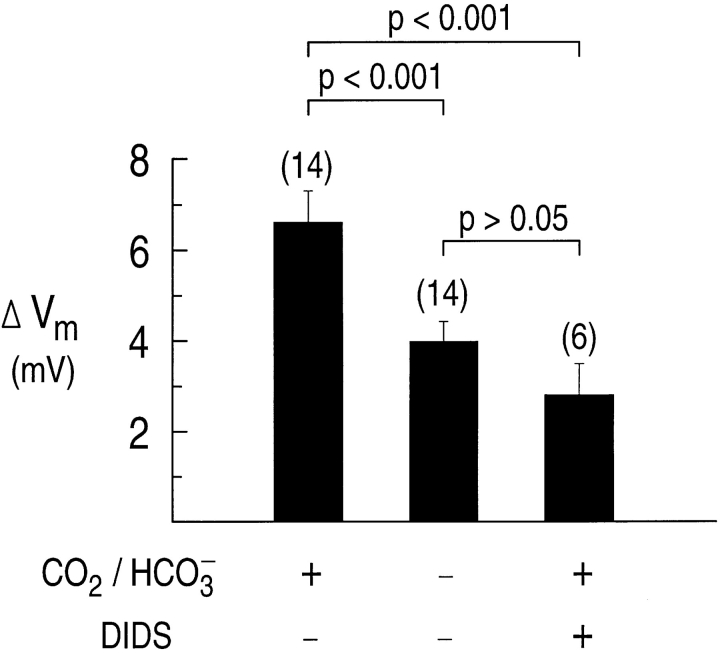
Fig. 10 B summarizes the results from 14 experiments similar to that shown in Fig. 10 A. In each case, the astrocyte was exposed to a Na⁺-free solution in the presence and absence of 20% CO₂/68 mM HCO₃ ⁻. The magnitude of the depolarizations in either the presence or absence of CO₂/HCO₃ ⁻ are plotted as a function of the resting V_m before the Na⁺ removal. In general, the ΔV_m in the presence of CO₂/HCO₃ ⁻ (•) is larger than in HEPES (○). In the presence of CO₂/ HCO₃ ⁻ (average resting V_m = −93.4 ± 1.5 mV), removing external Na⁺ elicited a mean depolarization of 6.6 ± 0.7 mV (Fig. 11). In the absence of CO₂/HCO₃ ⁻ (average resting V_m = −89.0 ± 1.7 mV), removing external Na⁺ caused a statistically smaller mean depolarization of 4.0 ± 0.5 mV. In the presence of DIDS, removing external Na⁺ in CO₂/HCO₃ ⁻ elicited a depolarization of only 2.8 ± 0.7 from a resting V_m of −93.3 ± 2.6. Thus, the depolarization in CO₂/HCO₃ ⁻ is larger than in either HEPES or CO₂/HCO₃ ⁻ plus DIDS, and the depolarization in HEPES is similar to that in CO₂/ HCO₃ ⁻ plus DIDS.

Figure 11.

Removing external Na⁺ from hippocampal astrocytes exposed to a 20% CO₂/68 mM HCO₃ ⁻-buffered solution elicits a mean depolarization that is larger than that observed for cells exposed to (a) a HEPES-buffered solution, or (b) a 20% CO₂/68 mM HCO₃ ⁻-buffered solution containing 400 μM DIDS.

Na/HCO₃ cotransport elicited simultaneously recorded changes in pH_i and V_m in single astrocytes.

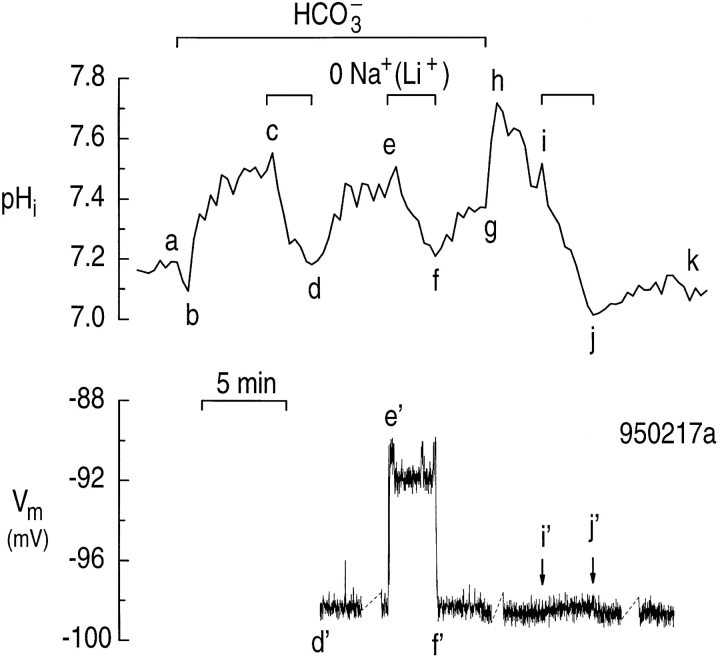
Fig. 12 illustrates an experiment in which we recorded pH_i and V_m simultaneously in a single astrocyte. The cell had an initial pH_i of ∼7.2 in a HEPES solution. When the astrocyte was exposed to a solution buffered with 5% CO₂/17 mM HCO₃ ⁻, the pH_i decreased (Fig. 12, ab), and then increased rapidly to a value well above the initial pH_i (Fig. 12, bc). Replacing bath Na⁺ with Li⁺ elicited a rapid pH_i decrease (Fig. 12, cd) that was reversible (Fig. 12, de). The resting V_m was ∼−98 mV when the astrocyte was returned to the Na⁺-containing solution at Fig. 12, d'. The V_m recording before Fig. 12, d' was unstable and is therefore not shown. When Na⁺ was removed from the bath a second time, pH_i again decreased (Fig. 12, ef  ). From the speed of the pH_i decrease, we predict a ΔV_m of 8.1 mV for an electrogenic Na/HCO₃ cotransporter with a 1:2 stoichiometry. The onset of the pH_i decrease (Fig. 12, e) coincided with an abrupt depolarization⁴ of ∼7 mV (Fig. 12, e'). When Na⁺ was returned to the bath, the pH_i increased as expected (Fig. 12, fg). The onset of the pH_i increase (Fig. 12, f  ) coincided with the return of V_m to the initial resting value (Fig. 12, f  '). When the astrocyte was switched to a HEPES-buffered solution, the pH_i increased rapidly (Fig. 12, gh), and then decreased (Fig. 12, hi). Switching to a Na⁺-free solution, now in the nominal absence of CO₂/HCO₃ ⁻, caused a further decrease in pH_i (Fig. 12, ij), but only a small depolarization (Fig. 12, i '). When Na⁺ was returned to the bath before the pH_i stabilized, pH_i began to increase (Fig. 12, jk), but the cell hyperpolarized only slightly (Fig. 12, j '). The simultaneous recording of pH_i and V_m in hippocampal astrocytes demonstrates that removing/returning external Na⁺ in the presence of CO₂/HCO₃ ⁻ elicits pH_i changes that coincide with V_m changes.

Figure 12.

Removing external Na⁺ elicits a simultaneous depolarization and pH_i decrease in a single hippocampal astrocyte. The astrocyte was exposed to 5% CO₂/17 mM HCO₃ ⁻ between points a and g. During the indicated periods, we replaced external Na⁺ with Li⁺ (cd, ef, and ij).

DISCUSSION

Evidence Against Na⁺-driven Cl-HCO₃ Exchange in Hippocampal Astrocytes

The transporter can move HCO₃ ⁻ into astrocytes when internal Cl⁻ is largely depleted.

In the accompanying paper (Bevensee et al., 1997), we demonstrate that cultured hippocampal astrocytes exposed to CO₂/HCO₃ ⁻ display, on average, an increase in their steady state pH_i. The pH_i increase is mediated, in part, by a HCO₃ ⁻ transporter that requires Na⁺ and is blocked by the stilbene derivatives DIDS and 4-acetamido-4′-isothiocyanatostilbene-2,2′-disulfonic acid (SITS). In the present study, we show that this transporter does not require intracellular Cl⁻ to operate in the normal, forward direction. Our approach was to deplete cells of intracellular Cl⁻, and then monitor the pH_i increase in the cells exposed multiple times to CO₂/HCO₃ ⁻. Using the Cl⁻-sensitive indicator MQAE, we found that hippocampal astrocytes could be nearly depleted of intracellular Cl⁻ by incubating the cells in a Cl⁻-free solution for an average of ∼11 min. This Cl⁻ depletion was probably mediated, at least in part, by a bumetanide-sensitive Na/K/Cl cotransporter. In the absence of external Cl⁻, cells exposed to CO₂/ HCO₃ ⁻ still displayed an increase in pH_i similar to that observed in the presence of Cl⁻. In fact, astrocytes exposed multiple times to CO₂/HCO₃ ⁻ in the absence of external Cl⁻ displayed multiple increases in pH_i. It is unlikely that these pH_i increases could have been mediated by a Na⁺-driven Cl-HCO₃ exchanger, inasmuch as such an exchanger would have required substantial amounts of intracellular Cl⁻.

The transporter can move HCO₃ ⁻ out of astrocytes in the absence of external Cl⁻.

We also tested the Cl⁻ dependence of the transporter using a simpler and briefer protocol in which we drove the transporter in the reverse (i.e., HCO₃ ⁻ outward) direction by removing external Na⁺ in the presence of CO₂/HCO₃ ⁻. Under such conditions, we found the rate of pH_i decrease to be the same in both the presence and absence of external Cl⁻. If the transporter were a Na⁺-driven Cl-HCO₃ exchanger, which would require external Cl⁻ to operate in the reverse direction, the pH_i decrease should have been substantially reduced in the absence of external Cl⁻.

Evidence for Electrogenic Na/HCO₃ Cotransport in Hippocampal Astrocytes

Switching from HEPES to CO₂/HCO₃ ⁻ causes a hyperpolarization.

Because the Na⁺-driven HCO₃ ⁻ transporter is not coupled to Cl⁻, it presumably is either a 1:1 (electroneutral) or a 1:2 (electrogenic) Na/HCO₃ cotransporter. If this astrocyte cotransporter were electrogenic, then it should simultaneously move net negative charge and HCO₃ ⁻ in the same direction. In the accompanying study (Bevensee et al., 1997), we show that hippocampal astrocytes exposed to 5% CO₂/HCO₃ ⁻ at 37°C first acidify due to CO₂ influx, and then display a maximum net acid extrusion (i.e., HCO₃ ⁻ uptake) rate of 47.7 μM s⁻¹, of which 75% is inhibited by DIDS. Therefore, the DIDS-sensitive HCO₃ ⁻ influx is 35.8 μM s⁻¹. From the average cell volume and input resistance of astrocytes, we predict⁵ that such a HCO₃ ⁻ influx would generate a current of only 2.9 pA and a hyperpolarization of only 0.7 mV. Such small CO₂/HCO₃ ⁻-induced currents and V_m changes would be difficult to measure.

Our measured net acid extrusion, after the addition of CO₂/HCO₃ ⁻, could have underestimated the unidirectional DIDS-sensitive HCO₃ ⁻ influx if the actual HCO₃ ⁻ influx were partially masked by an acid-loading process (e.g., Cl-HCO₃ exchange). Imagine that the DIDS-sensitive HCO₃ ⁻ influx was in fact 360 μM s⁻¹, 10-fold higher than we suspect, but that this was opposed by a Cl-HCO₃ exchange of 324 μM s⁻¹. In this case, the net flux would be only 36 μM s⁻¹, as observed. Whereas masking of a substantial HCO₃ ⁻ influx is theoretically possible, we think that it is unlikely inasmuch as astrocytes seem to lack significant Cl-HCO₃ exchange (see Fig. 8). The potential complexity of the pH_i changes associated with exposing a cell to CO₂/HCO₃ ⁻ underscores the difficulty of using the application of CO₂/HCO₃ ⁻ as an assay for electrogenic Na/HCO₃ cotransport.

Brune et al. (1994), working on cultured rat cerebellar astrocytes, observed a mean hyperpolarization threefold larger than our prediction, 2.3 mV. O'Connor et al. (1994), working on cultured rat hippocampal astrocytes, observed hyperpolarizations ranging from ∼0 mV (V_m ≅ −75 mV) to ∼25 mV (V_m ≅ −40 mV). Because our calculations show that a depolarization of 0.7 mV would be coupled to a DIDS-sensitive acid-extrusion rate of 35.8 μM s⁻¹, we can conclude that a depolarization of ∼25 mV would be coupled to a DIDS-sensitive acid-extrusion rate of 35.8 × (25/0.7) ≅ 1,280 μM s⁻¹. This figure is substantially greater than any transporter-mediated acid–base flux of which we are aware. For example, it is about eightfold greater than the flux of 160 μM s⁻¹ mediated jointly by Na-H and Na-dependent Cl-HCO₃ exchangers in acid-loaded renal mesangial cells (Boyarsky et al., 1988a ), or the flux of 170 μM s⁻¹ mediated by two similar transporters in acid-loaded pyramidal neurons from rat hippocampus (Bevensee et al., 1996), or the flux of 170 μM s⁻¹ induced by basolateral CO₂/HCO₃ ⁻ addition in rabbit S3 proximal tubules (Nakhoul et al., 1993). One could argue that, under the depolarized conditions (∼40 mV) at which the data from O'Connor et al. (1994) were obtained, the electrogenic Na/HCO₃ cotransporter influx may have been substantially higher than in our cells (mean V_m ≅ −88 mV). Therefore, we measured the net HCO₃ ⁻ influx after addition of CO₂/HCO₃ ⁻ in astrocytes depolarized with 2 or 5 mM Ba²⁺ (V_m ≅ −56 mV). We found no significant difference (not shown) between the net HCO₃ ⁻ influx under normally polarized and depolarized conditions. The large hyperpolarization observed upon first exposing astrocytes to CO₂/HCO₃ ⁻ may primarily reflect processes other than electrogenic Na/ HCO₃ cotransport, such as the influx of HCO₃ ⁻ through channels (see Bevensee et al., 1997, introduction). This large hyperpolarization may, in fact, inhibit the electrogenic influx of Na/HCO₃ after cells are exposed to CO₂/HCO₃ ⁻.

In addition to the large magnitudes of some of the previously observed CO₂/HCO₃ ⁻-induced hyperpolarizations, one could argue that the very assay (i.e., an exposure to CO₂/HCO₃ ⁻) is not sufficiently specific for identifying an electrogenic Na/HCO₃ cotransporter. As discussed in the accompanying paper (Bevensee et al., 1997, introduction), CO₂ not only lowers pH_i rapidly in the unstirred layer on the inner surface of the cell membrane, but also reacts with susceptible amino groups on proteins to form carbamino compounds (Morrow et al., 1974), thereby shifting their net charge in a negative direction. Moreover, adding HCO₃ ⁻ could induce HCO₃ ⁻ currents, such as those observed through GABA_A-receptor channels in cultured rat astrocytes (Kaila et al., 1991). The sensitivity of CO₂/ HCO₃ ⁻-induced electrical changes to DIDS, which is not specific for Na-coupled HCO₃ ⁻ transporters, or their sensitivity to Na⁺ removal, which changes a wide range of cellular parameters, could be due to the nonspecific effects of these treatments.

Removing external Na⁺ causes a DIDS-sensitive, CO₂/ HCO₃ ⁻-dependent depolarization.

Our approach for assaying for the electrogenicity of the cotransporter in hippocampal astrocytes was to expose cells to a Na⁺-free solution in the presence vs. the absence of CO₂/ HCO₃ ⁻, and in the presence vs. the absence of DIDS. This was the assay used for the initial identification of the electrogenic Na/HCO₃ cotransporter in proximal-tubule cells (Boron and Boulpaep, 1983), and for expression cloning the transporter in Xenopus oocytes (Romero et al., 1997). The advantages of this assay, over the less specific addition of CO₂/HCO₃ ⁻, are discussed in the accompanying paper (Bevensee et al., 1997). In our initial experiments, we removed Na⁺ in the continued presence of 5% CO₂ and 17 mM HCO₃ ⁻, pH 7.3. Under such conditions, however, removing external Na⁺ elicited an acid influx that predicts only small currents and V_m changes. To enhance the predicted responses to Na⁺ removal/readdition, we performed experiments in solutions buffered with 20% CO₂ and 68 mM HCO₃ ⁻, pH 7.3. Under these conditions, DIDS inhibited 63% of the acid extrusion caused by Na⁺ readdition. Assuming that DIDS inhibits, to the same extent, the acid loading elicited by Na⁺ removal, then the DIDS-sensitive flux elicited by Na⁺ removal was 281 μM s⁻¹ × 0.63 = 177 μM s⁻¹. This flux predicts a ΔV_m of 3.3 mV, assuming a Na⁺:HCO₃ ⁻ stoichiometry of 1:2. Indeed, we found that the depolarization elicited by removing external Na⁺ was 2.6 mV larger in the presence vs. the absence of CO₂/HCO₃ ⁻. In the presence of 20% CO₂/68 mM HCO₃ ⁻, the DIDS-sensitive ΔV_m was 4.8 mV (paired experiments). Thus, because the predicted and observed V_m changes were similar quantitatively, our Na⁺-removal data are consistent with the idea that the Na/HCO₃ cotransporter in hippocampal astrocytes is electrogenic.

One would expect that removing Na⁺ may also alter V_m by influencing the activity of the Na-K pump. Initially, removing external Na⁺ should drive the pump in its normal forward direction, thereby leading to a hyperpolarization, not a depolarization. In our experiments, we replaced Na⁺ with Li⁺, a cation known to promote active efflux of Na⁺ via the Na-K pump in human red blood cells (McConaghey and Maizels, 1962; Maizels, 1968; Beaugé and Del Campillo, 1976), presumably by substituting for extracellular K⁺. Therefore, replacing external Na⁺ with Li⁺ may actually stimulate the Na-K pump in astrocytes, and elicit a hyperpolarization (J.F. Hoffman, personal communication). In the continual absence of external Na⁺, however, the cells would eventually become depleted of internal Na⁺, thereby leading to inhibition of the Na-K pump and a gradual, but continual depolarization. To avoid this inhibition, we added Na⁺ to the patch pipette solution in experiments in which we measured V_m using the perforated patch-clamp technique.

Electrogenic Na/HCO₃ cotransport contributes to depolarization-induced alkalinizations in many preparations.

Because the Na/HCO₃ cotransporter we have identified in hippocampal astrocytes is electrogenic, it is reasonable to expect it to be modulated by V_m. When leech glial cells are depolarized by an increase in [K⁺]_o, the electrogenic Na/HCO₃ cotransporter drives HCO₃ ⁻ into the cells and elicits an increase in pH_i (Deitmer and Szatkowski, 1990). Such a depolarization-induced alkalinization (DIA) was first described in the proximal tubule of the salamander kidney, where ∼50% of the DIA is believed to be mediated by the electrogenic Na/HCO₃ cotransporter, and the remainder is due to stimulation of one of two apparently electroneutral lactate transporters (Siebens and Boron, 1989).

As in leech glial cells and salamander proximal-tubule cells, the pH_i of rat forebrain astrocytes (Boyarsky et al., 1993) and several other mammalian astrocyte preparations also increases when the cells are depolarized. An exception is C6 glioma cells (Shrode and Putnam, 1994). The DIA generally is larger in the presence than in the absence of CO₂/HCO₃ ⁻. In cultured astrocytes from the cerebral cortex of the mouse (Brookes and Turner, 1994), astrocytes in gliotic hippocampal slices from the rat (Grichtchenko and Chesler, 1994) and cultured astrocytes from the hippocampus of the rat (Pappas and Ransom, 1994), the DIA was partially or completely inhibited by removing external Na⁺, and unaffected by acutely removing external Cl⁻. Stilbene derivatives partially inhibited the DIA in astrocytes from the mouse cortex and the rat hippocampus, but not the DIA in astrocytes from the gliotic hippocampal slices. Thus, the electrogenic Na/HCO₃ cotransporter described in the present studies could be responsible for at least a part of the DIAs in these mammalian astrocytes.

APPENDIX

Ratiometric Correction for a Nonratiometric Indicator: Application to the Cl⁻-sensitive Dye MQAE

Theory and application.

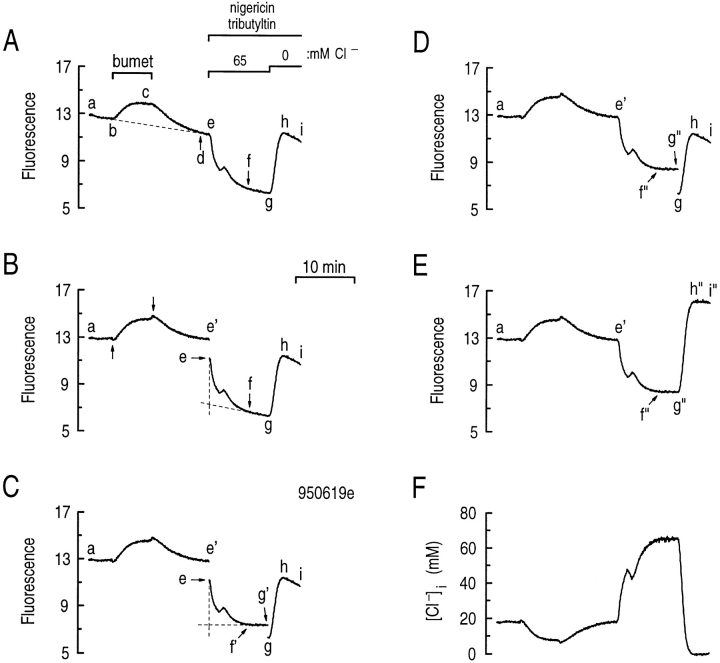
Fig. 13 A is the time course of the raw MQAE fluorescence used to generate the [Cl⁻]_i vs. time trace shown in Fig. 3 A. At the outset of the experiment, I₃₂₀ decreased slowly (Fig. 13 A, ab) in the astrocytes, which were bathed in the standard HEPES-buffered solution. This slow decrease probably represents both dye loss from cells, as well as loss of cells that become dislodged from the coverslip. When we exposed the cells to 1 μM of bumetanide, an inhibitor of the Na/K/Cl cotransporter, I₃₂₀ increased (Fig. 13 A, bc), presumably because intracellular Cl⁻ decreased and relieved the quenching of intracellular MQAE. Removing bumetanide caused I₃₂₀ to decrease (Fig. 13 A, cd) to a level below that before removing external Cl⁻ (Fig. 13 A, d vs. b). Subsequently, I₃₂₀ continued to decline (Fig. 13 A, de) at about the same rate as in Fig. 13 A, ab. Exposing the cells to a high K⁺/nigericin/tributyltin calibration solution containing 65 mM Cl⁻ caused I₃₂₀ to decrease rapidly at first (Fig. 13 A, ef  ), and then more slowly (Fig. 13 A, fg). Conversely, exposing the cells to a calibration solution without Cl⁻ caused I₃₂₀ first to increase rapidly (Fig. 13 A, gh), and then to decline more slowly (Fig. 13 A, hi).

Figure 13.

A corrected MQAE fluorescence loss from hippocampal astrocytes. (A) Raw fluorescence vs. time record for the experiment shown in Fig. 3 A. During the indicated period, the astrocytes were exposed to 1 μM bumetanide (bc). At the end of the experiment, the cells were exposed to a high K⁺/nigericin/ tributyltin chloride calibration solution containing 65 and 0 mM Cl⁻ (e–g and g–i, respectively). (B) Partially corrected fluorescence vs. time record. Segment ae' was obtained by using the time-dependent, ratiometric correction technique (Eq. A2) to correct for dye loss during segment a–e in A. (C) Partially corrected fluorescence vs. time record. Similarly, ef  'g' was obtained by using Eq. A2 to correct for the dye loss when the astrocytes were exposed to the 65 mM Cl⁻ calibration solution (B, e–g). (D) Partially corrected fluorescence vs. time record. ef  'g' in C was scaled (using Eq. A3) such that ae' was continuous with e'f  ”g”. (E) Fully corrected fluorescence vs. time record. Using the ratiometric correction (Eq. A2) and the scaling technique (Eq. A3) as described for segment e–g in B, g–i in D was converted into g”h”i”. (F) [Cl⁻]_i vs. time record. The fully corrected I₃₂₀ vs. time record in E was converted into the [Cl⁻]_i vs. time record using the Stern-Volmer relationship as described in methods.

In the experiment shown in Fig. 13 A, the cells were probably losing dye at different rates in each of three different time periods. (a) During the main part of the experiment (Fig. 13 A, a–e), dye was lost at a relatively low rate. Notice that a single line (Fig. 13 A) fits the data before and after the application of bumetanide. (b) During the first part of the calibration (Fig. 13 A, e–g), the rate of dye loss was somewhat higher. (c) During the second part of the calibration (Fig. 13 A, g–i), when [Cl⁻]_o was zero, the rate of dye loss was greatest.

We corrected for dye loss separately in each of these three segments using a novel approach that compensates not only for dye loss per se at a particular [Cl⁻]_i, but also for the change in quenching that occurs as [Cl⁻]_i changes. For example, during Fig. 13 A, ab and de, when [Cl⁻]_i is presumably at some fixed initial value, the time-dependent decrease in I₃₂₀ represents only a linear loss of dye. To correct for this simple dye loss, it would be reasonable to determine the rate of I₃₂₀ decrease by fitting a line simultaneously to the data in Fig. 13 A, ab and de (broken line). Starting from the original or “raw” I₃₂₀ values (I  ^t _raw) at each time t in Fig. 13 A, one could thus obtain corrected I₃₂₀ values (I^t _corr) by adding a fraction of the final difference between the intensities at Fig. 13 A, a and e (I  ^a _raw  –  I  ^e _raw), assuming that this difference increased linearly with time:

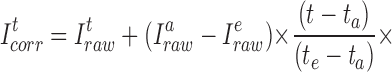A1

However, a problem with this simplistic approach is that, at any given time, the computed increment in I₃₂₀ is independent of [Cl⁻]_i. For example, to compensate for the dye loss during the bumetanide exposure in Fig. 13 A, bc in which [Cl⁻]_i is decreasing, there must be two components to the total increment I₃₂₀. First, we must increment I₃₂₀ to compensate for dye loss per se, as in Eq. A1. Second, we must increment I₃₂₀ by an additional amount because the dye that was lost would have been sensing a lower than normal [Cl⁻]_i, and thus would have been quenched to a lesser extent. Therefore, we did not use Eq. A1. Rather, we introduced an approach in which we simultaneously compensate for both components by multiplying I^t _raw by a time-dependent correction as follows.

Imagine that there had been no dye loss in Fig. 13 A. We will assume that at Fig. 13 A, e, where [Cl⁻]_i has the value x, I₃₂₀ is 50 arbitrary fluorescence units. We also will assume that when [Cl⁻]_i is zero, I₃₂₀ will be 100. Thus, at Fig. 13 A, e, the [Cl⁻]_i of x would have produced a Stern-Volmer ratio of I₀/I = 100/50 = 2. Now imagine that, in fact, half the dye had been lost between Fig. 13 A, a and e. The Stern-Volmer ratio at e would thus be I₀/I = 50/25 = 2. If we were to compensate for dye loss by simply adding 25 to both I₀ and I (as in Eq. A1), then I₀/I would be 75/50 = 1.5, and we would underestimate [Cl⁻]_i. Thus, to compensate for having lost half the dye by the end of the time interval, we must multiply both I₀ and I by 2 at Fig. 13 A, e. At the beginning of the interval, we would have to multiply both I₀ and I by 1; between Fig. 13 A, a and e, we would have to multiply by a factor between 1 and 2. The general, time-dependent ratiometric correction is given by the following equation:

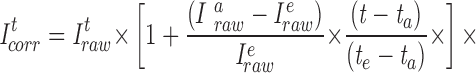A2

Applying this formula to Fig. 13 A, a–e yields the corrected curve ae' in Fig. 13 B. Notice that the uncorrected segment e–i in Fig. 13 B is now discontinuous with the corrected segment ae'.

To correct for the dye loss in Fig. 13 A, e–g, we applied the same formula (Eq. A2) that we used to correct for the dye loss in Fig. 13 A, a–e. This yielded the partially corrected curve ef'g' shown in Fig. 13 C. Notice that this curve is discontinuous with both Fig. 13 C, ae' and g–i. To reestablish continuity, one might imagine adding the same correction to all points in Fig. 13 C, ef'g'. Although such an addition would yield the correct [Cl⁻]_i for the transformed point e, the computed [Cl⁻]_i values at all other points would be incorrect. The reason is that Stern-Volmer relationship deals with ratios of intensities. All [Cl⁻]_i values in the transformed segment can be correct only if the transformation maintains its relative ratios. Therefore, we reestablished the continuity of Fig. 13 C, ae' and ef'g' by scaling all the points in segment ef'g' by a factor that made I₃₂₀ identical at Fig. 13 C, e and e' :

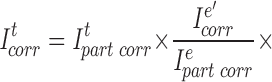A3

The result, shown in Fig. 13 D, is that the ratio e'/g” is the same as the ratio e/g' in Fig. 13 C. Thus, the [Cl⁻]_i computed at point g” is the same as that computed at g'.

To compensate for dye loss in Fig. 13 D, g–i, we applied the same two-step correction that we did in Fig. 13 B, e–g. The result is shown as segment g”h”i” in Fig. 13 E. Finally, we used the Stern-Volmer relationship to convert the fully corrected fluorescence data in Fig. 13 E to the [Cl⁻]_i time course shown in Fig. 13 F.

Potential sources of error.

The greatest potential source of error in the time-dependent ratiometric correction described above is in assuming a constant rate of dye loss, especially when a solution change is made during the period of the correction. This assumption of constant dye loss can sometimes be verified directly. For example, in Fig. 13 A, a single best-fit line passes through a and b (before addition of bumetanide) as well as through d and e (after recovery from bumetanide withdrawal). Thus, it is reasonable to conclude that MQAE disappeared at a constant rate throughout the entire segment Fig. 13 A, a–e. On the other hand, we cannot directly verify that the rate of dye loss during Fig. 13 B, ef is the same as during fg, nor that the rate during Fig. 13 B, gh is the same as during hi.

Our ratiometric-correction technique is not well suited to compensate for changes in the dye signal arising from factors other than dye loss or changes in [Cl⁻]_i. For example, our approach would not properly compensate for changes in the dye signal due to cell shrinkage or swelling.

Broader applicability.

The time-dependent ratiometric correction described above for MQAE could be applied to other nonratiometric dyes, such as the Ca²⁺ indicator Fluo-3. In fact, our ratiometric correction could, in principle, be applied to any indicator whose fluorescence (a) is proportional to dye concentration, and (b) changes with substrate binding. For example, in experiments in which pH_i is measured with BCECF, one could apply our ratiometric-correction technique to the I₄₉₀ (i.e., pH sensitive) signal to arrive at a corrected I₄₉₀ vs. time record that compensates for dye loss. Thus, without any knowledge of I₄₄₀, one could use this corrected I₄₉₀ to arrive at a pH_i vs. time record, similar to that obtained using the standard I₄₉₀/I₄₄₀ ratiometric approach.