Sodium and Calcium Inward Currents in Freshly Dissociated Smooth Myocytes of Rat Uterus

Abstract

Freshly dissociated myocytes from nonpregnant, pregnant, and postpartum rat uteri have been studied with the tight-seal patch-clamp method. The inward current contains both I_Na and I_Ca that are vastly different from those in tissue-cultured material. I_Na is abolished by Na⁺-free medium and by 1 μM tetrodotoxin. It first appears at ∼−40 mV, reaches maximum at 0 mV, and reverses at 84 mV. It activates with a voltage-dependent τ of 0.2 ms at 20 mV, and inactivates as a single exponential with a τ of 0.4 ms. Na⁺ conductance is half activated at −21.5 mV, and half inactivated at −59 mV. I_Na reactivates with a τ of 20 ms. I_Ca is abolished by Ca²⁺-free medium, Co²⁺ (5 mM), or nisoldipine (2 μM), and enhanced in 30 mM Ca²⁺, Ba²⁺, or BAY-K 8644. It first appears at ∼−30 mV and reaches maximum at +10 mV. It activates with a voltage-dependent τ of 1.5 ms at 20 mV, and inactivates in two exponential phases, with τ's of 33 and 133 ms. Ca²⁺ conductance is half activated at −7.4 mV, and half inactivated at −34 mV. I_Ca reactivates with τ's of 27 and 374 ms. I_Na and I_Ca are seen in myocytes from nonpregnant estrus uteri and throughout pregnancy, exhibiting complex changes. The ratio of densities of peak I_Na/I_Ca changes from 0.5 in the nonpregnant state to 1.6 at term. The enhanced role of I_Na, with faster kinetics, allows more frequent repetitive spike discharges to facilitate simultaneous excitation of the parturient uterus. In postpartum, both currents decrease markedly, with I_Na vanishing from most myocytes. Estrogen-enhanced genomic influences may account for the emergence of I_Na, and increased densities of I_Na and I_Ca as pregnancy progresses. Other influences may regulate varied channel expression at different stages of pregnancy.

introduction

Smooth muscles comprise a diverse group of involuntary excitable tissues, which are dispersed widely throughout the body, subserving important physiological functions. Because individual smooth myocytes are small, their ionic channel functions have not been studied in earnest until the introduction of the tight-seal patch-clamp method (Hamill et al., 1981), and successful regimens of dissociating individual myocytes from tissue assemblies (Bagby et al., 1971; Fay and Delise, 1973; Momose and Gomi, 1980). However, the usefulness of enzyme-dissociated smooth myocytes as physiological models has not been tested. The uterine smooth muscle is singularly suitable for addressing this issue because it has been studied as multicellular preparations (Anderson, 1969; Mironneau, 1974; Kao and McCullough, 1975), as dissociated cells (references below), and in tissue culture (e.g., Mollard et al., 1986; Amedee et al., 1987; Toro et al., 1990; Rendt et al., 1992).

Because the structure and function of uterine smooth muscle change markedly under the influence of ovarian hormones and during pregnancy (see Kao, 1989), it is also suitable for studying hormonal regulation of ionic channels. Although several papers on freshly dissociated uterine myocytes have appeared (Ohya and Sperelakis, 1989; Inoue et al., 1990; Inoue and Sperelakis 1991; Miyoshi et al., 1991; Piedras-Renteria et al., 1991), each dealt with a limited aspect of myometrial function. In this and another paper (Wang, S.Y., M. Yoshino, and C.Y. Kao, manuscript submitted for publication), we will provide a wider coverage of ionic channel functions of uterine myocytes in the nonpregnant state and throughout pregnancy. There are significant changes in these functions during pregnancy that not only profoundly influence the ultimate physiological functions, but also illustrate some hormonal influence on ionic channels. In this paper, we address the inward currents and changes in them during pregnancy; in the other paper, we will deal with the outward currents. Preliminary accounts have been given (Suput et al., 1989; Kao et al., 1989; Yoshino et al., 1989, 1990; Wang and Kao, 1993; Wang et al., 1996).

methods

Female rats (Sprague-Dawley; Harlan Sprague Dawley Inc., Indianapolis, IN) were mated individually, and pregnancy was dated from the morning when cervical plugs were found. Dating was confirmed at the experiment from fetal size (Witschi, 1956). Uteri from days 2–22 (term) of pregnancy and postpartum were used. For nonpregnant rats, the estrus status was ascertained by cytological examinations of vaginal washing.

Isolation of Uterine Myocytes

The procedures for cell isolation are similar to those used for taenia coli myocytes (Yamamoto, et al., 1989). Briefly, strips (∼2 × 15 mm) of endometrium-free longitudinal myometrium were incubated in 0.1% collagenase (Wako Bioproducts, Richmond, VA) in a Ca²⁺-free modified Krebs solution for 30 min. They were then washed free of collagenase before being triturated. Use of higher concentrations of collagenase or other additional proteolytic enzymes were associated with more cells with large leakage conductance and poor ionic currents, whereas longer incubations were associated with higher incidences of myocytes coated with a layer of optically transparent material that interfered with cell settling and seal formation with electrodes. In practice, concentrations of 200–300 cells/μl (by hemocytometer counting) have been obtained (see also Fig. 1 A). The myocytes, kept in a high K⁺, Ca²⁺-free medium (“KB” medium, Isenberg and Klöckner, 1982) at 5–8°C, retained good electrophysiological properties for 3 d. Most data were obtained within 6 h after isolation. All myocytes used for this work were relaxed and adhered to the bottom of the plastic or glass chamber with no additional substrate. More than 90% remained relaxed when exposed to Ca²⁺; after visual screening, 70–80% of the cells selected for study would have good ionic currents.

Figure 1.

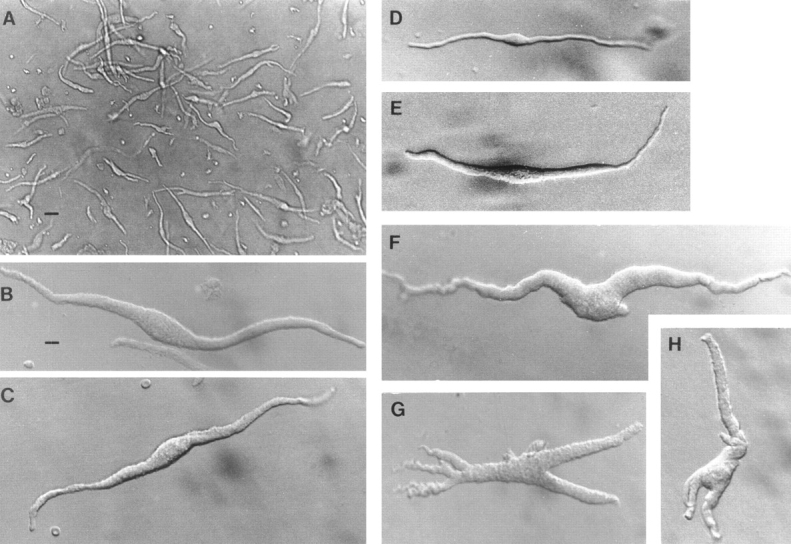
Freshly dissociated myocytes from rat uterus. Cells in C–E are in bath solution containing 3 mM Ca²⁺; cells in other panels are in “KB” solution (Ca²⁺ free). Scale bar in A represents 40 μm; that in B represents 10 μm, and applies also to all other frames. (A) Low magnification to show usual density of cells obtained from late-pregnant uteri; nonpregnant uteri will yield fewer cells. Under Hoffman modulation optics, most cells present a slight 3-dimensional appearance. Only such cells are used for this work. (B and C) Two individual myocytes from the late (18–21-d)-pregnant uterus. (D) Myocyte from a nonpregnant estrus uterus. (E) Myocyte from a mid (14-d)-pregnant uterus. Morphometric data are shown in Table I. (F–H) Myocytes showing marked pleomorphism, from swelling around midportion to arms and branches, are most frequently encountered in late pregnancy, where they may comprise ∼10% of the population (see also A). Because their complex geometry may pose problems for uniform voltage control, such cells were not used in this work.

Electrophysiological Methods

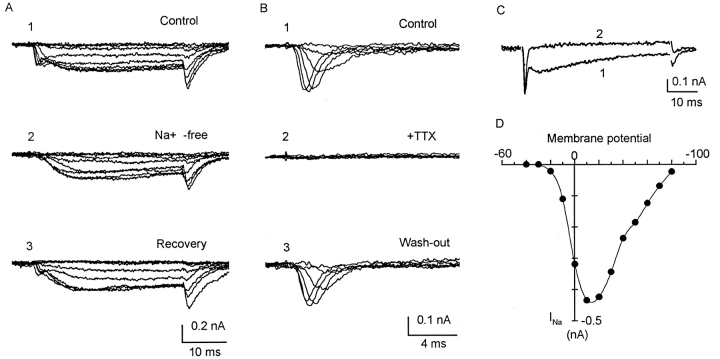
The methods are similar to those used for the work on taenia myocytes (Yamamoto et al., 1989), in which the quality of the voltage clamp and the isopotentiality of the whole cell were demonstrated experimentally. Adequacy of control of the uterine myocytes can be surmised from the gradual current–voltage (I-V)¹ relations in the negative resistance region. For this work, the range of capacitance cancellation in the amplifier (EPC-7; List Electronic, Darmstadt, Germany) was extended to cover 200 pF to accommodate the larger pregnant uterine myocytes. Because of the presence of fast I_Na, series-resistance compensation and capacitance cancellation were essential, as these procedures introduced some positive feedback, accelerating the charging of the membrane capacity (Sigworth, 1986). For the usual recording, the settling time was <800 μs. For small myocytes under optimal compensation, the transient artifact could be reduced to <150 μs. In selecting results for inclusion, we looked for a state of zero current between the end of the transient and the beginning of I_Na (e.g., Fig. 3 B). Leakage currents and residual transient artifacts after hardware correction were corrected with a p/4 protocol.

Figure 3.

I_Na of uterine myocytes, all recorded with Cs⁺ electrodes. (A) Myocyte from 18-day pregnant uterus, 187.6 pF. Holding potential −80 mV; step depolarized to −40, and then to 30 mV in 10-mV increments. A, 1 shows myocyte response in solution containing (mM): 120 Na⁺, 1 Ca²⁺, 10 TEA, 5 4-aminopyridine, and 5 Cs⁺. The inward current is complex, with fast and slow components and tail current, similar to currents shown in Fig. 2. A, 2 was taken after 5 min in a similar solution in which 120 mM choline chloride replaced NaCl. The fast component disappeared, but the slow component as well as the tail current was unaffected. A, 3 was taken 4 min after returning to Na⁺ bath. (B) Myocyte from 13-day pregnant uterus, 71.2 pF. Holding potential, −80 mV; step depolarized to −40, and then to 30 mV in 10-mV increments. Bath solution as in A. First currents (not shown) were complex, similar to that in A, 1. Traces in B, 1–3 were taken with myocytes in similar bath solution, but containing an additional 2 μm nisoldipine. Slow component has been blocked. These currents are similar to those shown in C. B, 1 shows only the fast component, which could be fully blocked by 1 μM TTX (B, 2), in a reversible manner (B, 3). (C) Myocytes from 18-day pregnant uterus; 112 pF. Holding potential −80 mV; command to −40 mV, and then to 80 mV in 10-mV increments (similar to those in I-V plot in D). (C) Superimposed current traces at 10 mV. Trace 1 was taken in solution containing 105 mM Na⁺ and 3 mM Ca²⁺, with inward current showing both fast and slow components. Trace 2 was taken after 5 min in solution containing 105 mM Na⁺ and 0 Ca²⁺. Slow component has disappeared. The responses to ion substitutions (A and C) and to TTX and nisoldipine (B) indicate that the fast component is I_Na and the slow component is I_Ca. (D) I-V relation of I_Na of a different myocyte from 17-d pregnant uterus; 134 pF, in solution containing 120 mM Na⁺. Pipette solution contains 4 mM Na⁺. Actual currents are similar to those of myocytes shown in C. I_Na is first detected at ∼−30 mV; reaches a maximum at +10 mV. Reversal potential is 85 mV, in good agreement with expected Nernst potential of 85.7 mV.

All experiments were conducted at room temperature (∼22°C).

Solutions

The bath contained (mM): 135 NaCl, 5.4 KCl, 3 CaCl₂, 1 MgCl₂, 5 glucose, 10 HEPES, pH adjusted to 7.25 with NaOH. Ca²⁺ was sometimes increased (as specified), with an equimolar reduction in Na⁺. The pipette solution contained (mM): 140 KCl, 1 EGTA, 2 Na₂ATP, 10 HEPES, pH adjusted to 7.25 with KOH. Osmolarity of all solutions was routinely maintained at 275–290 mosM. For studying the inward current, the K⁺ in the pipette solution was replaced with Cs⁺, and the bath contained 30 mM tetraethylammonium chloride (TEA) and 5.4 mM CsCl with equimolar reduction of Na⁺. Run-down of I_Ca, which was a problem only in small myocytes of nonpregnant or early pregnant uteri, could be obviated by incorporating 5 mM each of potassium salts of pyruvate, oxaloacetate, and succinate in the pipette solution (Klöckner and Isenberg, 1985).

results

Cell Morphology

Because the uterine myocyte hypertrophies during pregnancy, cellular morphometric data at different stages of pregnancy are needed to correlate with physiological observations. Although freshly dissociated uterine myocytes were usually long, slender, and fusiform, pleomorphism was common, especially in late pregnancy when cells with irregularly swollen central regions or terminal arms (Fig. 1) constituted ∼10% of the population. In the present study, to avoid possible inadequate space clamp in cells with such complex geometry, we used only long and relaxed myocytes, assuming that the pleomorphic cells shared similar basic electrophysiological properties.

Morphometric data at three stages were collected: nonpregnant (also representing early pregnancy from days 1–8), midpregnancy (14 d, also representing days 9–16), and late pregnancy (days 17–21). Table I shows that during pregnancy, the maximum diameter of the individual myocyte increased 2.8-fold from 8 to 22 μm, and the length increased 1.7-fold from 130 to 225 μm. Such changes led to a fourfold increase of surface area to 7,600 μm², and an eightfold increase of cell volume to 21 pl in the term myocyte.

Table I.

Some Morphometric Parameters of Rat Uterine Smooth Myocytes

		Nonpregnant		Midpregnancy		Late pregnancy
Number of myocytes		14		22		13
Maximum diameter (μm)		7.9 ± 0.4		15.2 ± 0.4		21.0 ± 1.7
		(6.3 − 10.4)		(10.8 − 18.8)		(14.1 − 28.4)
Average diameter* (μm)		4.5 ± 0.2		7.5 ± 0.2		10.6 ± 0.5
		(3.2 − 4.9)		(5.7 − 9.3)		(7.0 − 14.1)
Length‡ (μm)		129.7 ± 11.4		238.2 ± 8.3		225.1 ± 12.6
		(68.3 − 191.1)		(171.5 − 298.6)		(168.0 − 304.7)
Surface (μm2)		1,928.4 ± 235.1		5,193 ± 188.4		7,599.4 ± 639.7
		(686 − 3,422)		(3,071 − 6,299)		(4,198 − 12,220)
Volume (pl)		2.6 ± 0.4		11.0 ± 0.5		21.0 ± 2.5
		(0.6 − 5.5)		(5.1 − 14.3)		(7.3 − 28.2)

All values are means ± SEM, with range in parentheses underneath.  

^*Average diameter over the entire length of the cell.  

^‡End-to-end length. Except for cell-lengths for mid- and late pregnancy, all comparable parameters at different stages are significantly different (P < 0.05).  

Membrane Properties

In the present experiments, the seal resistance ranged from 5 to 40 GΩ. When studied with Cs⁺-filled pipettes, the input resistance of the whole myocyte ranged from 0.5 to 3 GΩ. Resting and action potentials were not routinely measured because the Cs⁺-pipette solution caused a significant depolarization. However, myocytes for this work were selected for their low leakage conductance. If the average input resistance were taken as 1 GΩ, then the specific membrane resistance for the averaged size late-pregnant myocyte would be 76 kΩ-cm².

Consistent with hypertrophy, the cell capacitance increased as pregnancy progressed (Table II). In early pregnancy, the average cell capacitance remained ∼30 pF, slightly higher than that of the nonpregnant myocyte (25 pF). In midpregnancy, capacitance increased markedly, possibly stimulated by fetal growth and stretch of the uterus. In late pregnancy, capacitance stabilized at ∼110 pF, because there were no statistically significant differences among the values listed for days 18–21. Within 18-h postpartum, there were no significant changes in the cell capacitance.

Table II.

Stage of Pregnancy and Total Myocyte Capacitance

Days pregnant		Cell capacitance		Number of samples
		pF
0*		25.0 ± 1.6		39
2		27.7 ± 2.1		14
5		29.1 ± 2.2		20
9		33.1 ± 2.7		18
14		80.9 ± 7.9		17
17		92.3 ± 8.4		22
18		103.5 ± 8.8		50
19		101.7 ± 4.8		48
20		104.8 ± 8.7		14
21		120.6 ± 8.6		16
postpartum‡		134.1 ± 8.5		12

All values are means ± SEM.  

^*Nonpregnant.  

^‡14–18 h postpartum. Because of wide variability, differences within the span of a few days in each stage of pregnancy are insignificant (P > 0.05), but differences between stages (day 5 vs. day 14; day 14 vs. day 20) are significant (P < 0.05).  

As the amount of caveolae in myocytes at different stages of pregnancy is not known, estimation of specific membrane conductance is based on the morphometric surface. Taking the average of 108 pF as the cell capacitance for the late-pregnant myocyte with an average surface area of 7,600 μm² (Table I), the specific membrane capacitance works out to be 1.42 μF/cm². For the nonpregnant myocyte, based on a surface area of 1,928 μm², the specific capacitance works out to be 1.30 μF/cm².

inward currents

Coexistence of I_Na and I_Ca

The inward current consists of two distinct components: a fast activating and inactivating component, followed by a more slowly activating and more sustained component (Fig. 2). Although the peak magnitudes of the two components and the degree of overlap vary considerably from cell to cell, the slow component is seen in all myocytes, and the fast component in half of the myocytes from nonpregnant estrus uterus or early pregnancy, and >90% of myocytes from late pregnancy.

Figure 2.

Coexistence of I_Na and I_Ca in single rat uterine myocytes from different stages of pregnancy. Top trace shows voltage protocol applied to all cells shown. Holding potential −80 mV; step depolarized to 10 mV for 36 ms. All myocytes were bathed in solution containing (mM): 105 Na⁺, 3 Ca²⁺, 30 TEA⁺, 5 4-aminopyridine, and 5 Cs⁺. Pipette solution contained 120 Cs⁺, which, along with external TEA, 4-aminopyridine, and Cs⁺, was used to block outward K⁺ currents. Cell capacitances (pFs) are: 29.6 for nonpregnant (day 0) myocytes; 47.2 for day-5 myocytes; 90.8 for day-17 myocytes; 148.4 for day-21 myocytes, and 200 for postpartum myocytes. In all cells, fast and slower components are seen, which are identified as I_Na and I_Ca, respectively. Such currents were recorded in about half of nonpregnant and day-2–pregnant myocytes, and in >90% of late-pregnant myocytes. Note the variability of the currents in relative peak amplitudes and degree of overlap. At end of the depolarizing step, tail current is entirely I_Ca, because I_Na is fully inactivated by this time. Other details in text and Table III.

The nature of each component is readily identifiable by ion substitution and by selective blocking agents. In a Na⁺-free medium, the fast component was abolished, whereas the slow component and its associated tail current were unchanged (Fig. 3 A). The fast component was fully blocked by tetrodotoxin (TTX) at 1 μM concentration (Fig. 3 B, also Ohya and Sperelakis, 1989). In a Ca²⁺-free medium, the slow component was abolished, leaving the fast component (Fig. 3 C). It was also abolished when nisoldipine (2 μm) was added to the bath (Fig. 4 C). Thus, the fast component can be identified as I_Na and the slow component as I_Ca.

Figure 4.

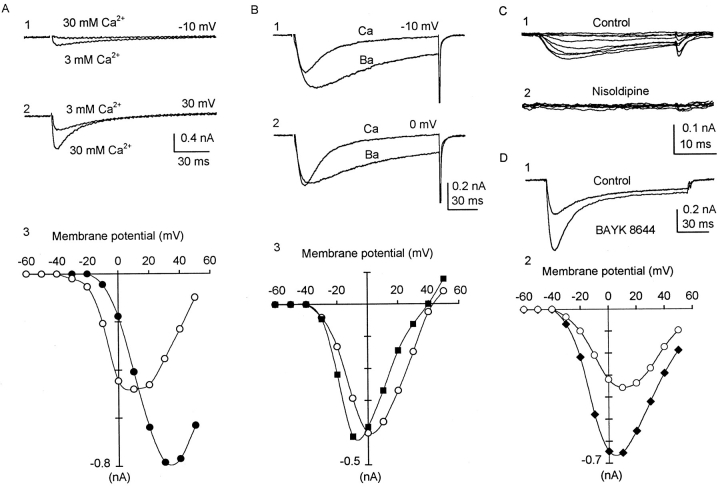
I_Ca in uterine myocytes. (A) Effects of increasing [Ca²⁺]_o on inward current. Myocytes from 20-d pregnant uterus, 90 pF. Holding potential −60 mV (which inactivated much of I_Na); command to 60 mV in 10-mV increments. A, 1 and 2 shows superimposed current traces in 3 and 30 mM Ca²⁺. A, 3 shows full I-V relations. In 3 mM Ca²⁺ (○), first current detected at −30 to −20 mV; maximum current at +10 mV. In 30 mM Ca²⁺ (•), first current detected at 0 to −10 mV; maximum current at +30 mV. Activation is shifted towards positive (screening effect). Reversal potential (if extrapolated) would be shifted by 30 mV towards positive (increased driving force). (B) Effects of replacing 3 mM Ca²⁺ with 3 mM Ba²⁺ on slow component of inward current. Myocyte from 17-d pregnant uterus, 61 pF. Holding potential −60 mV, step depolarized to 50 mV in 10-mV increments. Myocytes were first bathed in solution containing 3 mM Ca²⁺. After currents were elicited, bath solution was changed to one in which 3 mM Ba²⁺ replaced the Ca²⁺. B, 1 and 2 shows overlaid currents at same voltages. B, 3 shows full I-V relations. I_Ca (○), I_Ba (▪). Note that Ba²⁺ shifted activation slightly to negative voltages, resulting in appearance of seemingly larger currents at small depolarizations. Maximum current in Ba²⁺ was approximately the same as in Ca²⁺. Reversal potentials were similar. The most prominent difference is that Ba²⁺ current inactivated much slower than I_Ca. Ba²⁺ current was eliminated after addition of 5 mM Co²⁺ (not shown). (C) Effect of nisoldipine (2 μM) on nonpregnant myocytes from a diestrus uterus, 17.4 pF, in solution containing 1 mM Ca²⁺. Holding potential −80 mV. Currents are produced by step depolarizations in 10-mV increments from −40 to 30 mV. This myocyte had no recordable I_Na. (C, 1) I_Ca and its tail current. (C, 2) 5 min after addition of nisoldipine to the bath, I_Ca and tail currents were completely blocked. Similar effects of nisoldipine have been seen in other nonpregnant myocytes, as well as pregnant myocytes. (D) Effects of BAY K 8644 on I_Ca. Myocytes from 18-d pregnant uterus. 40 pF, in 3 mM Ca²⁺. Holding potential −80 mV; step depolarized to 50 mV in 10-mV increments. (D, 1) Overlaid current traces at +10 mV. Note that the larger I_Ca in BAY K also inactivated much faster. (D, 2) I-V relations. Maximum I_Ca at +10 mV is 357 pA in 3 mM Ca²⁺ (○), 652 pA in BAY K (♦). Time constant of inactivation of I_Ca (in ms), at −20, −10, 0, 10, 20, 30, 40, and 50 mV are (in Ca²⁺, followed by τ in BAY K in parentheses): 52 (20), 34 (15), 31 (20), 33 (28), 40 (39), and 53 (51).

I_Na first appeared at ∼−40 mV, reached a maximum at 0–10 mV, and reversed at 80–84 mV (Fig. 3 D), in good agreement with the expected E_Na. The magnitude of I_Na varied widely, in part because of differences in cell size, and in part with the stage of pregnancy (see below). When normalized to cell capacitance, and adjusted for the morphometric surface areas, peak I_Na works out to be 2.77 μA/cm² for nonpregnant myocytes, and 5.10 μA/cm² for late-pregnant myocytes.

In 3 mM [Ca²⁺]_o, I_Ca was first seen at ∼−30 mV, and reached a maximum at +10 mV (Fig. 4 A). The magnitude of I_Ca varied because of cell size and stage of pregnancy. When normalized to cell capacitance and the morphometric surface, peak I_Ca (in 3 mM Ca²⁺) works out to be 5.67 μA/cm² for the nonpregnant myocyte and 3.43 μA/cm² for the late-pregnant myocyte. In 30 mM Ca²⁺, the activation of I_Ca shifted positive by ∼15 mV. The maximum current increased, and the voltage at which it was attained also shifted positive by ∼20 mV (Fig. 4 A), as expected from a screening effect on surface negative charges (Frankenhauser and Hodgkin, 1957).

When 3 mM Ba²⁺ replaced Ca²⁺ in the bath solution, the inward current activated as rapidly, reached approximately the same maximum but slightly later, and the I-V relation was shifted ∼10 mV to the negative. The inactivation was markedly slower (Fig. 4 B), probably because of interference with Ca²⁺-mediated Ca²⁺ inactivation (see below). The Ba²⁺ current, as well as I_Ca, could be fully blocked by 5 mM Co²⁺ (not illustrated).

BAY K 8644, a dihydropyridine compound, increased the magnitude of the I_Ca without shifting the I-V relations (Fig. 4 D). In contrast to Ba²⁺, it did not slow the inactivation, and the larger current was inactivated at an appreciably faster rate. Nisoldipine (2 μM) readily blocked the I_Ca of pregnant (Fig. 3 B, legend) and nonpregnant myocytes (Fig. 4 C), similar to those reported for 10 μM nifedipine (Miyoshi et al., 1991) and on Ba²⁺ current (Ohya and Sperelakis, 1989).

I_Na and I_Ca in Relation to Stages of Pregnancy

I_Ca was recordable in all uterine myocytes. I_Na was additionally seen in 19 of 38 myocytes taken from nonpregnant estrus, metestrus, or diestrus, but not from proestrus, animals. I_Na was seen in 11 of 22 myocytes from 2-d pregnant uterus, and almost all myocytes from day 5 of pregnancy to term.

Table III summarizes the I_Na and I_Ca at different stages of pregnancy. The data are based on currents that were stable for at least 15–20 min. For comparing cellular properties, only myocytes with both I_Na and I_Ca were included. Several features are apparent in the data, (a) from baseline values at the beginning of pregnancy, the densities of both I_Na and I_Ca increased during the first trimester; (b) they then declined during the second trimester; (c) whereas I_Na reached its lowest density on the 17th d and began to recover by the 18th d, I_Ca continued to decline and reached its lowest value on the 18th d; (d) from days 2 to 17, peak I_Na density was less than peak I_Ca density, but in late-pregnant myocytes, this relation was reversed; and (e) the net changes over the course of pregnancy are that the density of peak I_Na increased by 1.8-fold, while that of I_Ca decreased by 1.7-fold.

Table III.

Stage of Pregnancy and I_Na and I_Ca of Uterine Myocyte

Days pregnant		Number of cells		INa				ICa				INa/ICa
				pA/pF		μA/cm2		pA/pF		μA/cm2
0		12		1.83 ± 0.53		2.77		3.74 ± 1.08		5.67		0.53 ± 0.15
2		5		2.03 ± 0.20		3.08		4.38 ± 1.18		6.64		0.66 ± 0.12
5		12		2.84 ± 0.17		4.30		7.06 ± 0.70		10.70		0.45 ± 0.07
9		6		2.25 ± 0.46		3.41		5.22 ± 0.30		7.91		0.54 ± 0.11
14		8		1.99 ± 0.17		3.32		3.12 ± 0.28		5.20		0.86 ± 0.16
17		13		1.24 ± 0.41*		2.07		3.70 ± 0.72*		6.17		0.65 ± 0.24
18		15		2.47 ± 0.51*		3.43		1.87 ± 0.42*		2.60		2.00 ± 0.41
21		8		3.67 ± 0.72		5.10		2.47 ± 0.51		3.43		1.62 ± 0.32
PP‡		12		0.42‡				0.83 ± 0.12				0.57

Direct experimental values in pA/pF are means ± SEM.  

^*Values for I_Na and for I_Ca on days 17 and 18 were significantly different from each other (P = 0.03). I_Na/I_Ca was determined for each myocyte before averaging. For current densities per unit surface, average morphometric areas from Table I are used. Weighted average cell capacitance (from Table II) used are 29 pF (0–9 d pregnant), 87 pF (14- and 17-d pregnant), and 108 pF (18- and 21-d pregnant).  

^‡14–18 h postpartum; only 1 of 12 myocytes had I_Na.  

In 12 myocytes from uteri that were 14–18 h postpartum, I_Ca was observed in every myocyte, but I_Na was observed in only one. This myocyte was large, with a cell capacitance of 200 pF. Both the average peak I_Ca density and the peak I_Na density of the single myocyte were lower than the least values recorded during pregnancy. The decline in the current densities occurred even as the cell capacitance remained the same (Table II). Also, peak I_Na/I_Ca in this single myocyte was 0.57, similar to that in nonpregnant myocytes.

activation and inactivation Kinetics of Activation and Inactivation

Activation.

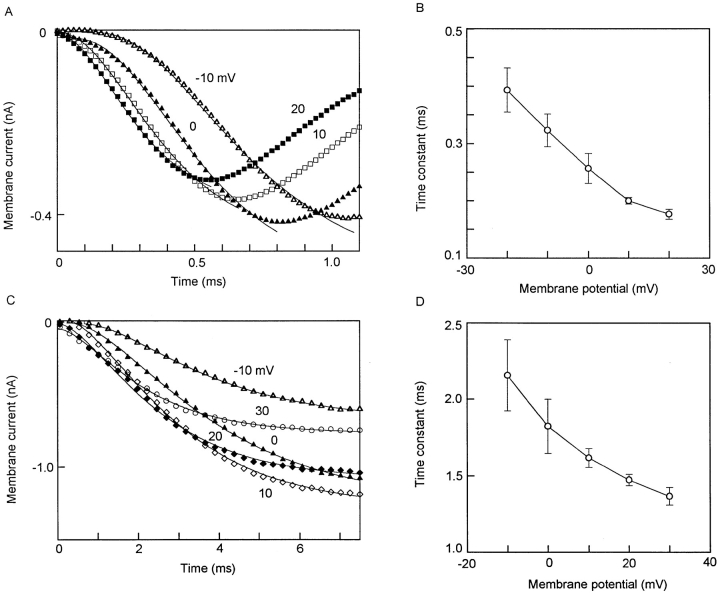
To avoid possible errors in time-to-peak measurements caused by current inactivation, kinetics of activation was examined by curve fitting the early part of the ionic currents. With optimum compensation, I_Na can be distinctly separated from the capacitive current transient (e.g., Figs. 2 and 3). At ∼22°C, I_Na reached a peak in ∼1 ms. The best fit was obtained with a fourth-power function (Fig. 5 A), with voltage-dependent τ's varying between 0.39 ms at −20 mV and 0.18 ms at 20 mV (Fig. 5 B).

Figure 5.

Kinetics of activation of I_Na and I_Ca. (A and B) I_Na. Myocyte in (A) was from 18-d pregnant uterus. 63 pF. HP −80 mV. Symbols denote currents observed when depolarized to voltages attached to each curve. Smooth curves fitted to: I = I_∞•[1 − exp(−t/τ)]⁴. (B) Voltage dependence of rate of activation of I_Na. Data are average from three cells (mean ± SEM). Actual values (ms): 0.39 ± 0.03 (at −20 mV), 0.32 ± 0.02 (−10 mV), 0.26 ± 0.03 (0 mV), 0.20 ± 0.05 (+10 mV), 0.18 ± 0.01 (+20 mV). (C and D) I_Ca. Myocyte in C was from 17-d pregnant uterus, 101 pF. HP −80 mV. Conventions similar to those in A and B. Smooth curves are fitted to: I = I_∞•[1 − exp(−t/τ)]². (D) Voltage dependence of rate of activation of I_Ca. Data are average from three cells. Actual values (ms): 2.16 ± 0.23 (−10 mV), 1.82 ± 0.17 (0 mV), 1.62 ± 0.06 (+10 mV), 1.47 ± 0.03 (+20 mV), 1.37 ± 0.06 (+30 mV).

In contrast, the activation of I_Ca was best fitted with a square function (Fig. 5 C), with τ's varying between 2.2 ms at −10 mV to 1.4 ms at 30 mV (Fig. 5 D).

Inactivation.

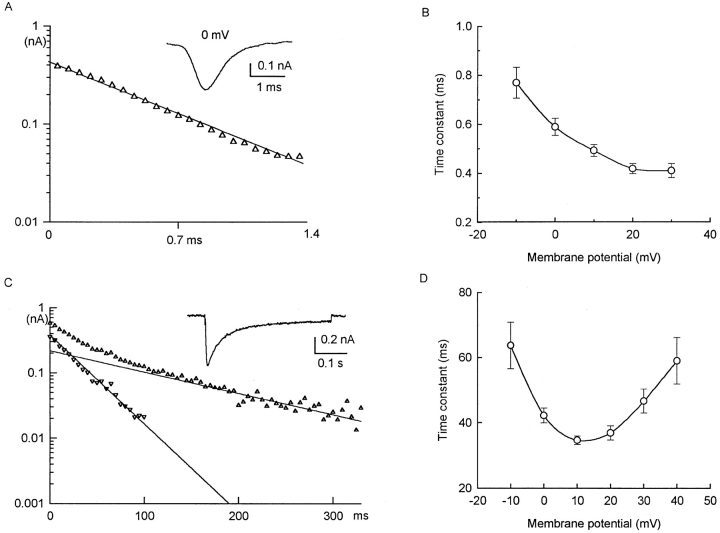
I_Na inactivated as a single exponential (Fig. 6 A), with a voltage-dependent τ that varied from 0.77 ms at −10 mV to 0.41 ms at 30 mV (Fig. 6 B).

Figure 6.

Kinetics of inactivation of I_Na and I_Ca. (A and B) I_Na. Myocytes in (A). Inactivation of I_Na in a myocyte from 18-d pregnant uterus, 112 pF, in solution containing no Ca²⁺. HP −80 mV. Depolarized to 0 mV. Symbols are from observed currents; smooth curves are fitted to −y = 0.417 exp (−t/0.58). (B) Voltage dependence of rate of inactivation of I_Na. Average data from five cells (means ± SEM). Actual data (ms): 0.77 ± 0.06 (−10 mV), 0.59 ± 0.03 (0 mV), 0.49 ± 0.02 (+10 mV), 0.42 ± 0.02 (+20 mV), 0.41 ± 0.02 (+30 mV). (C and D) I_Ca. (C) Inactivation of I_Ca in a myocyte from 20-d pregnant uterus, 104 pF, in solution containing 3 mM Ca²⁺. HP −60 mV, depolarized to +10 mV. Decay can be fitted by two exponential terms, with τ's of 32 and 133 ms. Thus, −y = 0.38 exp(−t/0.32) + 0.22 exp(−t/ 133) + 0.06 suggest two classes of inactivating Ca²⁺ currents and a small noninactivating or very slowly inactivating component. (B) Voltage dependence of fast inactivating component (τ_f) of I_Ca. Data are average of five cells. Note U-shape of curve, with fastest inactivation at +10 mV, and inactivation slowing at more positive voltages. These features suggest a role of Ca²⁺ in Ca²⁺ inactivation. Slow inactivating component may have some voltage dependence, but data are too scattered to be significant.

For I_Ca, inactivation was more complex. In a small number of myocytes, a small fraction (<5%) of I_Ca remained even at the end of a 400-ms step (Fig. 6 C, inset). The inactivation time course can be fitted with two exponential phases, with τ's of ∼32 ms (τ_f) and 133 ms (τ_s) (Fig. 6 C). τ_f was strongly voltage dependent, showing a U-shaped relation with the fastest rate at 10 mV (usually <40 ms) and significantly slower rates at either more negative or more positive voltages (Fig. 6 D). τ_s may also be voltage dependent (175 ms at −10 mV, 81 ms at +20 mV, 289 ms at +40 mV), but there was too much variability in the small sampling to support any statistically significant differences.

Deactivation.

Deactivation of both I_Na and I_Ca follow single exponential time constants. In five myocytes, in the presence of a high concentration of nisoldipine (20 μM), I_Na, when repolarized from 0 to −80 mV, decreased with a τ of 0.87 ± 0.10 ms. In another group of five myocytes in which I_Na had been abolished by depolarizing steps of >10 ms, I_Ca (repolarizing from +10 to −80 mV) deactivated with a τ of 2.71 ± 0.23 ms.

Steady State Activation and Inactivation

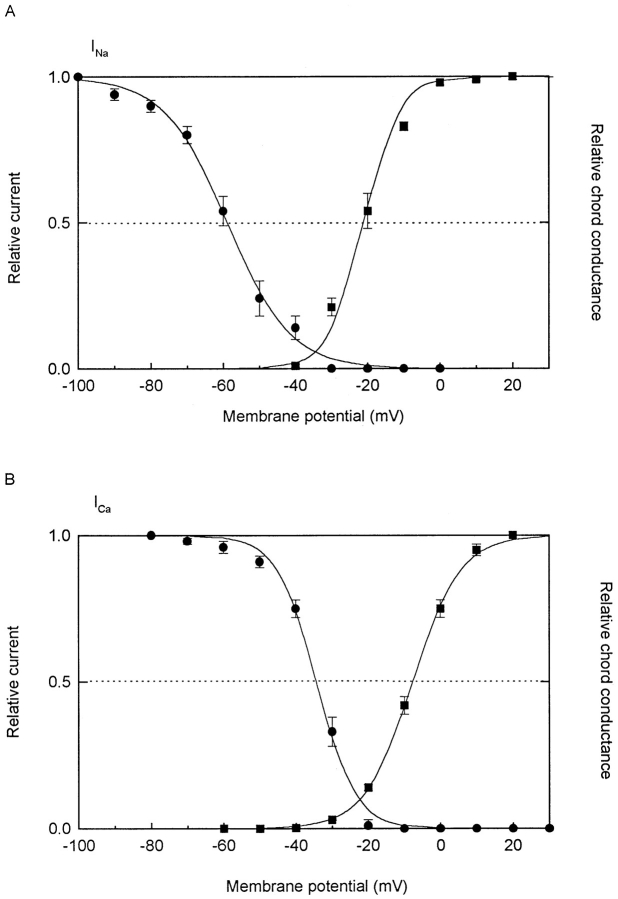
Fig. 7 shows the steady state activation and inactivation of I_Na and I_Ca. These observations were made on four to five different cells from 17-, 18-, and 20-d pregnant uteri that show both I_Na and I_Ca. To facilitate the experiments, one current was blocked so that the other could be studied.

Figure 7.

Steady state voltage-activation and -inactivation relations for I_Na (A) and I_Ca (B). Each point represents averaged data of four to five individual myocytes, with vertical bars representing ± 1 SEM if larger than the symbol. (A) For I_Na, all myocytes were in solution containing 3 mM Ca²⁺ and 2 μM nisoldipine to block I_Ca. For activation (right ordinate, ▪), chord conductance: I/E − E_rev. Reversal potential is 85 mV; relative conductances are normalized to conductance at +20 mV. Smooth curve is fitted to Boltzmann distribution: 1/[1 + exp(V + 21.1)/−5.0], where half activation is at −21.1 mV. For inactivation curve (left ordinate, •), the usual 2-pulse method was used, with abscissa representing conditioning (V₁) voltage, and ordinate representing ratio of test (V₂) currents in the presence and absence of V₁. For studying I_Na, both V₁ and V₂ are 100-ms long. Smooth curve is fitted to Boltzmann function: 1/[1 + exp (V + 58.9)/8.7], with half inactivation at −59 mV. (B) For I_Ca, all myocytes were in solution containing 3 mM Ca²⁺ and 1 μM TTX to block I_Na. Conventions similar to those for I_Na in A. Reversal potential was determined for each cell, except in two cells where it was extrapolated. Relative conductances are normalized to conductance at +30 mV. Smooth curve is fitted to Boltzmann function: 1/[1 + exp(V + 7.4)/−6.6], where half activation is at −7 mV. For inactivation curve, V₁ was 3 s, long enough to inactivate almost all I_Ca. V₂ was 100 ms. Smooth curve is Boltzmann distribution: 1/[1 + exp(V + 34.3)/5.4], with half inactivation at −34 mV.

For both I_Na and I_Ca, the activation relations followed Boltzmann distributions. For I_Na (Fig. 7 A), significant conductance was first seen at ∼−40 mV. Half activation occurred at −21 mV, full activation at ∼+20 mV. The slope factor was 5 mV. For I_Ca (Fig. 7 B), the first detectable conductance appeared at ∼−30 mV; half activation at −8 mV, full activation at ∼+30 mV. The slope factor was 6.6 mV.

For the steady state inactivation curves, the relations also followed Boltzmann distributions well. For I_Na (Fig. 7 A), half inactivation occurred at −59 mV, and the slope was 8.7 mV. For I_Ca (Fig. 7 B), half inactivation occurred at −34 mV, and the slope was 5.4 mV. Therefore, at the usual resting potential of ∼−50 mV, 24% of I_Na and 95% of I_Ca are available.

For both I_Na and I_Ca, there was a small overlap of the activation and inactivation relations (window current), with that for I_Na peaking to ∼5% of the maximum current at −35 mV, and that for I_Ca peaking to 10% of the maximum at −25 mV.

Recovery from Inactivation

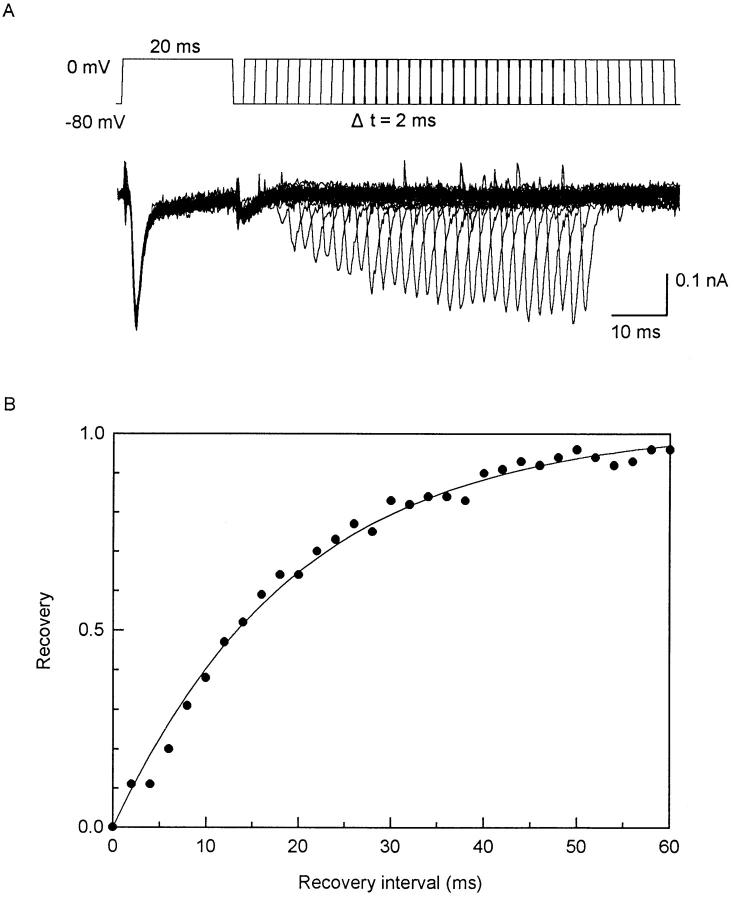
Because the spontaneous electrical activity of the myometrium consists typically of bursts of action potentials that lead to contractions (see Kao, 1989), the influence of an action potential on those following it can be important. Fig. 8 shows the recovery of I_Na from inactivation. The data are closely clustered even though the myocytes came from different stages of pregnancy. They are also well fitted by a single exponential curve with a time constant of 20 ms.

Figure 8.

Recovery from inactivation of I_Na. (A) Voltage protocol and representative currents from myocyte from 13-d pregnant uterus. 72 pF. In solution containing 1 mM Ca²⁺. V₁ and V₂ are both 20 ms, with an interval between two steps varying on 2-ms increments. Large initial current produced by V₁ is I_Na, but small I_Ca is still present, which is especially clear as a tail current. Contribution of I_Ca to V₂ current is negligible because of its much slower reactivation kinetics (see Fig. 9). (B) Averaged reactivation time course of I_Na. Abscissa is interval between voltage steps; ordinate is V₂ current as a fraction of V₁ current. Data are from eight myocytes, three from 20-d pregnant uteri, two from 19-d, and one each from 7-, 13-, and 21-d uteri (means; all SEM are smaller than symbol). Although not all myocytes contributed to the entire range of the curve, data points are well fitted by y = 1 − exp(−t/19.8) (solid line). Single exponential with time constant of 19.8 ms for myocytes from different stages of pregnancy suggests participation of one class of sodium channels throughout entire course of pregnancy.

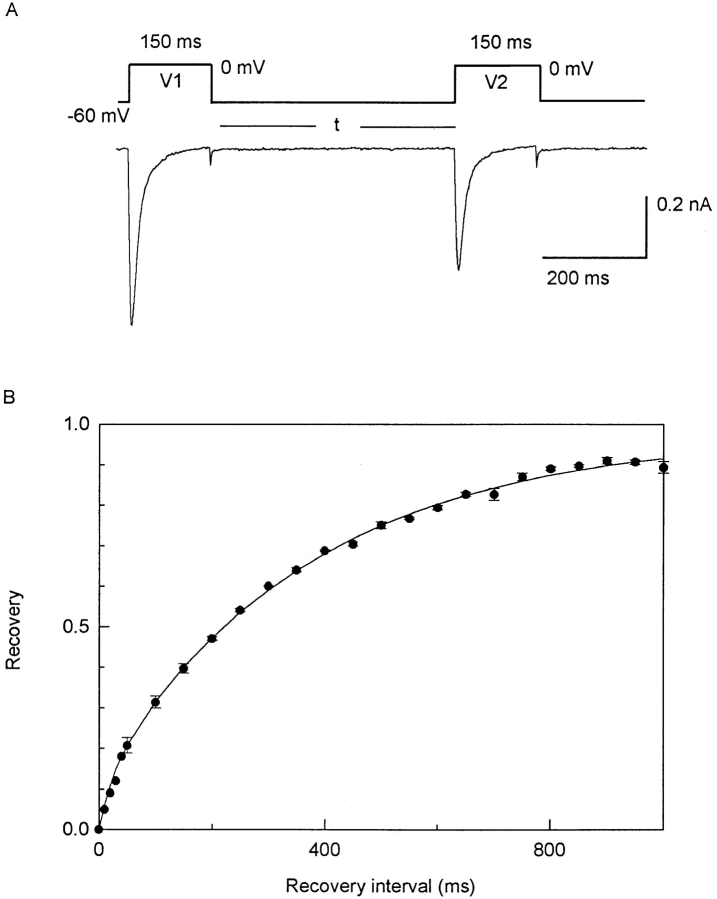
Fig. 9 shows the recovery of I_Ca from inactivation. The recovery is best fitted by two exponential components; the smaller component (12%) has a τ of 27 ms, and the larger component (86%) has a τ of 374 ms.

Figure 9.

Recovery from inactivation of I_Ca. (A) Voltage protocol and representative currents from myocyte from 18-d pregnant uterus. 82 pF. In solution containing 3 mM Ca²⁺ and 1 μM TTX. V₁ and V₂ are both 150 ms, long enough to have inactivated all of the fast component (τ_f = 33 ms) and most of the slow component (τ_s = 133 ms; Fig. 6). Interval (t) between V₁ and V₂ is varied, and is plotted as abscissa in B. At intervals of 10, 20, 30, and 40 ms, the residual tail current of the first I_Ca was substantial and the test I_Ca was measured as currents additional to such tail currents. (B) Time course of recovery, where ordinate represents V₂ current as a fraction of V₁ current. Each point represents averaged data from three myocytes from 18-d pregnant uterus (mean ± SEM, if larger than symbol), and from one myocyte from a 19-d pregnant uterus (for intervals <50 ms). Smooth curve is fitted by y = 0.12[1 − exp(−t/ 27)] + 0.86[1 − exp(−t/374)]. Two exponential terms suggest role of two classes of calcium channels, with 12% of recovery occurring with τ of 27 ms, and 86% of recovery occurring with τ of 374 ms.

Viewed differently, for I_Na, 50% recovery is attained in <15 ms and 80% recovery (possibly needed to generate propagated action potentials) is attained in ∼30 ms. For I_Ca, 50% recovery is attained in ∼200 ms, and 80% recovery in ∼600 ms. Since the rates of recovery from inactivation are important determinants of the rates of repetitive action potentials, the widely different reactivation of the two types of channels must affect their respective contributions to myometrial excitability.

discussion

Dissociated Smooth Myocytes as Physiological Models

The tight-seal patch-clamp method and improved cell-isolation procedures have fostered a surge of recent studies on dissociated single smooth muscle cells, which are unencumbered by complex intercellular connections, ion accumulation in extracellular clefts, and insurmountable cleft resistance encountered in multicellular preparations. Although the procedures of enzyme-aided dissociation are conceded as potentially injurious (Bolton et al., 1985; Sanders, 1989), the suitability of such myocytes as models has rarely been tested. The pregnant rat myometrium provides an opportunity for a critical scrutiny of this issue, because it possesses some unique tissue-specific properties that can serve as markers, and because it has been studied in a wide spectrum of organization levels and in tissue culture. The small multicellular preparations, against which dissociated myocytes can be compared, were subjected only to being dissected free from the uterus but not to any enzymes or artificial intracellular milieu. Hence, their ionic channel functions are likely to be as nearly physiological as any isolated tissue or cells can be.

Using new information obtained on dissociated uterine myocytes (specific capacitance, 1.42 μF/cm²; surface:volume ratio, 0.36 μm⁻¹; average cell capacitance, 108 pF; see results), the active region of a previous study (with a total capacitance of 0.13 μF; Kao and McCullough, 1975) can be estimated to contain ∼1,000 (867–1,204) cells. In such preparations, the presence of a Na⁺ and a Ca²⁺ component in the inward current had already been shown (also Anderson et al., 1971; Kao, 1978), as had an increasing relative contribution of the Na⁺ component in late pregnancy as term approached (Nakai and Kao, 1983). Phenotypic expression of a Na⁺ channel is rare among visceral smooth muscles. Confirmation in dissociated uterine myocytes not only of that rare phenotype but also of its participation in highly tissue-specific functional changes demonstrate that such cells, if properly prepared, do not deviate substantially from physiological norms.

Because of such similarities, the freshly dissociated uterine myocytes can also serve as a basis for assessing some tissue-cultured preparations as physiological models (e.g., Mollard et al., 1986; Amedee et al., 1987; Toro et al., 1990; Rendt et al., 1992). Such a comparison reveals so many differences as to suggest that the observed channel functions pertain to different cells.

Some of the key differences are: (a) most fresh myocytes used in this work had a readily recordable I_Na, which could be elicited from holding potentials of −90 to −60 mV (also Ohya and Sperelakis, 1989). It was fully blocked by 1 μM TTX (Fig. 3 B), which had a K _d of 27 nM (Ohya and Sperelakis, 1989), characterizing the TTX receptor as a high affinity type (references in Kao and Levinson, 1986). In cultured cells, with the exception of the human uterine myocyte (Young and Herndon-Smith, 1991), none showed any Na⁺ action potentials (Mollard et al., 1986) or any I_Na, all the inward current being attributed to I_Ca (Amedee et al., 1987; Rendt et al., 1992). Some cultured cells had no inward currents at all (Toro et al., 1990). In cultured cells, I_Na could be elicited only after interference with Na⁺ inactivation; when elicited, the K _d of TTX blockade was 2 μM (Amedee et al., 1986), characterizing the receptor as a low affinity type. The different TTX sensitivities could reflect different amino acid compositions of the channel molecules. (b) In fresh (Fig. 4 C), but not cultured (Rendt et al., 1992) nonpregnant myocyte, I_Ca was susceptible to blockade by dihydropyridines. (c) In fresh myocytes, half activation of the Ca²⁺ conductance in 3 mM of Ca²⁺ was at −8 mV (Fig. 7 B). In cultured cells, half activation in 10 mM Ca²⁺ was at −14 mV (Amedee et al., 1987), or at −7 mV (Rendt et al., 1992), in spite of a known screening effect of 10 mM Ca²⁺ on surface negative charges (Frankenhauser and Hodgkin, 1957; Yamamoto et al., 1989; Sui and Kao, 1997; and Fig. 4 A), which should have caused a significant positive displacement. (d) In fresh myocytes, the steady state I_Ca inactivation was almost all voltage dependent, with half inactivation at −34 mV. In cultured cells, 10–12% of the I_Ca did not inactivate, and the remainder had a half inactivation voltage of −17 (Amedee et al., 1987) or −55 (Rendt et al., 1992) mV.

Hence, the cultured myometrial cells described so far possess none of the unique cell-specific functional properties of the freshly dissociated uterine myocytes, and therefore are less likely to provide physiologically relevant information on ionic channel functions of uterine myocytes.

Charge Carriers and Channels for Inward Currents

The density of Na⁺ channels in uterine myocytes (3–5 μA/cm²) is two to three orders of magnitude lower than those in peripheral nerves, skeletal, or cardiac muscles. Kinetic data suggest the presence of a single class of Na⁺ channels in uterine myocytes.

The Ca²⁺ channels in rat uterine myocytes are mostly of the L-type (also Ohya and Sperelakis, 1989; Miyoshi et al., 1991), resembling the case in other visceral smooth myocytes (urinary bladder, Klöckner and Isenberg, 1985; ureter, Sui and Kao, 1997; taenia coli, Yamamoto et al., 1989). However, in human uterine myocytes, T-type Ca²⁺ channels have been described (Inoue et al., 1990; Young et al., 1993). Inactivation of I_Ca involves both voltage-dependent and Ca²⁺-mediated mechanisms. A voltage-dependent mechanism is demonstrated in the steady state voltage-inactivation relation, whereas a Ca²⁺-mediated mechanism is seen in the U-shaped relation between τ_f of inactivation and I_Ca (Fig. 6 D), in a slowing of the rate when Ba²⁺ replaced Ca²⁺ (Fig. 4 B), and in an increased rate when I_Ca was enhanced by BAY-K 8644 (Fig. 4 D).

The density of I_Ca in uterine myocytes (3–11 μA/cm²) is approximately midway in a spectrum among different visceral smooth myocytes (urinary bladder, 20 μA/cm², Klöckner and Isenberg, 1985; taenia coli, 20 μA/cm², Yamamoto et al., 1989; ureter, 3 μA/cm², Sui and Kao, 1997). In taenia coli myocytes (Yamamoto et al., 1989) and urinary bladder myocytes (Sui et al., 1993), Ca²⁺ influx during an action potential is capable of discharging the membrane capacity and raising [Ca²⁺]_i to 8–13 μM. Thus, the influx is potentially adequate for initiating various physiological functions. In the non- and early-pregnant uterine myocytes, the situation is similar and the same conclusion may apply. In the late-pregnant myocyte, the situation is more complex. Although the cell capacitance is larger, the combined influx of Na⁺ and Ca²⁺ may still discharge it to initiate the action potential. However, the cell volume is much larger while the density of I_Ca is lower (Tables II and III). Under such circumstances, whether influx of Ca²⁺ alone is adequate to supply the needed Ca²⁺ or whether internal sources become more important are problems that require further study.

Changing Densities of I_Na and I_Ca in Pregnancy and Their Implications

Using small multicellular preparations from 16–21-d pregnant rat uterus, Nakai and Kao (1983) described a changing ratio of the Na⁺ and Ca²⁺ components of the inward current, such that the ratio of peak I_Na/peak I_Ca increased as term approached. Those observations are now confirmed on single uterine myocytes, and extend to cover the entire pregnancy.

Although Inoue and Sperelakis (1991) have made a similar confirmation, they found no I_Na in any day-5 myocyte, and constant densities of I_Na and I_Ca in individual myocytes from day 9 to term (their Fig. 5 A). They also found that the fraction of myocytes expressing I_Na increased with the progression of pregnancy (their Fig. 5 B). By interpreting the frequency of their observing I_Na as a probability of I_Na occurrence, and by averaging data from all cells, including all day-5 cells with no I_Na, they concluded that the density of I_Na increased towards term (their Fig. 5 C).

Our observations are quite different. We found I_Na in myocytes from all stages of pregnancy, from day 2 to term, and also in those from nonpregnant uteri under estrogen stimulation. Although only half of the day-2 myocytes had recordable I_Na, the finding of any I_Na indicates that conditions for the phenotypic expression of Na⁺ channels were already in place. Whereas a specific ionic current indicates both the presence and the expression of that channel, its absence only indicates the nonexpression of the channel and not its nonexistence. Because of this consideration, and because of our belief that population phenomena should be supported by more inclusive random sampling than can be provided by the usual limited sampling of whole-cell patch-clamp studies, we focused our interest on the properties of individual myocytes and compared only those myocytes in which both I_Na and I_Ca were recorded. Our data show that, in individual myocytes, densities of both I_Na and I_Ca change during the course of pregnancy.

Two broad categories of regulation by ovarian hormones can account for the observed changes: genomic and nongenomic influences. Considering the fourfold increase of the surface area in the hypertrophied uterine myocyte during pregnancy, new channel proteins must be synthesized at a rate exceeding that needed for replacement, because the densities of I_Na and I_Ca are always more than a quarter of the original level in the nonpregnant myocyte. In the simplest sense, these increased current densities might be attributed to estrogen-enhanced transcription, leading to more copies of Na⁺ and Ca²⁺ channels (genomic influence). However, the regulation may be more complex, and may include significant contributions from nongenomic influences. For Na⁺ channels, it involves bringing forth a previously unexpressed phenotype (as in the estrus–diestrus phase of nonpregnant uteri), and then rapidly extinguishing it (as in postpartum uteri). The decline in the densities of I_Na and I_Ca in midpregnancy may involve progesterone, which is known to rise at that time and has an antiestrogen effect on the expression of a K⁺ channel (Yang et al., 1994). Whatever the regulatory mechanism might be, the observed changes are probably physiological, because the envelope of their effects has already been observed in multicellular preparations (Nakai and Kao, 1983) that contained enough individual myocytes to provide a reasonably inclusive random sampling.

The increased role of I_Na in late pregnancy subserves well the physiological functions of the parturient uterus. The more intense sodium currents could contribute to a faster spread of the electrical impulse throughout the parturient uterus. More importantly, the faster inactivation and reactivation of I_Na would permit more frequent repetitive spike discharges than would be possible with the slower I_Ca. Furthermore, because of a concomitant “de-expression” of some large-conductance Ca²⁺-activated K⁺ channels (Kao et al., 1989; and Wang, S.Y., M. Yoshino, and C.Y. Yao, manuscript submitted for publication), the membrane conductance is lowered, and the membrane potential less negative than otherwise. Perhaps, through a combination of these processes, the excitability of the parturient uterus is enhanced and coordinated across large areas of the whole organ to facilitate contraction throughout.