Molecular Analysis of ATP-sensitive K Channel Gating and Implications for Channel Inhibition by ATP

Abstract

The β cell K_ATP channel is an octameric complex of four pore-forming subunits (Kir6.2) and four regulatory subunits (SUR1). A truncated isoform of Kir6.2 (Kir6.2ΔC26), which expresses independently of SUR1, shows intrinsic ATP sensitivity, suggesting that this subunit is primarily responsible for mediating ATP inhibition. We show here that mutation of C166, which lies at the cytosolic end of the second transmembrane domain, to serine (C166S) increases the open probability of Kir6.2ΔC26 approximately sevenfold by reducing the time the channel spends in a long closed state. Rundown of channel activity is also decreased. Kir6.2ΔC26 containing the C166S mutation shows a markedly reduced ATP sensitivity: the K _i is reduced from 175 μM to 2.8 mM. Substitution of threonine, alanine, methionine, or phenylalanine at position C166 also reduced the channel sensitivity to ATP and simultaneously increased the open probability. Thus, ATP does not act as an open channel blocker. The inhibitory effects of tolbutamide are reduced in channels composed of SUR1 and Kir6.2 carrying the C166S mutation. Our results are consistent with the idea that C166 plays a role in the intrinsic gating of the channel, possibly by influencing a gate located at the intracellular end of the pore. Kinetic analysis suggests that the apparent decrease in ATP sensitivity, and the changes in other properties, observed when C166 is mutated is largely a consequence of the impaired transition from the open to the long closed state.

introduction

The β cell K_ATP channel is an octameric complex of two structurally unrelated subunits that assemble with 4:4 stoichiometry (Inagaki et al., 1995, 1997; Sakura et al., 1995; Clement et al., 1997; Shyng and Nichols, 1997). Kir6.2 acts as an ATP-sensitive pore while SUR1 is a regulatory subunit that endows Kir6.2 with sensitivity to sulfonylureas, K-channel openers, and the potentiatory effects of MgADP and MgGDP (Nichols et al., 1996; Gribble et al., 1997a ; Shyng et al., 1997a ; Trapp et al., 1997; Tucker et al., 1997). Although both subunits are normally required for functional expression of the K_ATP channel, a truncated form of Kir6.2, which lacks the last 26 amino acids (Kir6.2ΔC26), is able to express independently of SUR1 (Tucker et al., 1997). This truncated isoform of Kir6.2 is inhibited by ATP, suggesting that ATP mediates channel inhibition by interacting with the Kir6.2 rather than the SUR1 subunit of the K_ATP channel. In support of this idea, mutations in Kir6.2 render the channel less sensitive to ATP (Tucker et al., 1997, 1998; Shyng et al., 1997b ). While exploring the effect of sulfhydryl reagents on K_ATP channel activity, we observed that mutation of the cysteine residue at position 166 to serine dramatically decreases the sensitivity of Kir6.2ΔC26 currents to ATP (see accompanying paper, Trapp et al., 1998). In this paper, we have characterized the properties of this mutant channel in detail. We show that the C166S mutation markedly increases the channel open probability by reducing the percentage of time the channel spends in a long closed state. By substituting different amino acids for C166, we show that a more hydrophilic or bulkier residue at this position simultaneously modifies the intrinsic gating properties of the channel and reduces its sensitivity to ATP. A correlation between ATP sensitivity and channel open probability has also been reported for mutations at N160, within the second transmembrane domain of Kir6.2, although the shift in ATP sensitivity was much less dramatic (Shyng et al., 1997b ). We discuss our results in terms of a model in which C166 influences entry of the channel into the long closed state, and the reduced ATP sensitivity produced by mutation of this residue is largely a consequence of the change in the channel gating kinetics, rather than in the affinity of ATP for its binding site.

materials and methods

Molecular Biology

Mouse Kir6.2 (Genbank D50581; Inagaki et al., 1995; Sakura et al., 1995) and rat SUR1 (Genbank L40624, kindly supplied by Dr. G. Bell, University of Chicago, Chicago, IL; Aguilar-Bryan et al., 1995) were used in this study. A 26 amino acid COOH-terminal deletion of mouse Kir6.2 (Kir6.2ΔC26) was made by introduction of a stop codon at the appropriate residue using site-directed mutagenesis (Tucker et al., 1997). Site-directed mutagenesis of Kir6.2ΔC26 was carried out by subcloning the appropriate fragments into the pALTER vector (Promega Corp., Madison, WI). Mutations are indicated by the single amino acid letter code. For oocyte expression studies, constructs were subcloned into the pBF expression vector, which provides the 5′ and 3′ untranslated regions of the Xenopus β globin gene. Synthesis of capped mRNA was carried out using the mMessage mMachine large scale in vitro transcription kit (Ambion Inc., Austin, TX).

Oocyte Handling

Female Xenopus laevis were anaesthetized with MS222 (2 g/liter added to the water). One ovary was removed via a mini-laparotomy, the incision was sutured, and the animal was allowed to recover. Once the wound had completely healed, the second ovary was removed in a similar operation and the animal was then killed by decapitation while under anaesthesia. Immature stage V–VI Xenopus oocytes were incubated for 75 min with 1.0 mg/ml collagenase (type A; Boehringer Mannheim, Mannheim, Germany) and manually defolliculated. In most experiments, oocytes were injected with ∼2 ng of mRNA encoding Kir6.2ΔC26. For coexpression experiments, ∼0.04 ng Kir6.2 or Kir6.2ΔC26 was coinjected with ∼2 ng SUR1 (giving a 1:50 ratio). The final injection volume was ∼50 nl/oocyte. Control oocytes were injected with water. Isolated oocytes were maintained in tissue culture and studied 1–4 d after injection (Gribble et al., 1997b ).

Electrophysiology

Macroscopic currents were recorded from giant excised inside-out patches at a holding potential of 0 mV and at 20–24°C (Gribble et al., 1997b ). Patch electrodes were pulled from thick-walled borosilicate glass (GC150; Clark Electromedical Instruments, Reading, UK) and had resistances of 250–500 kΩ when filled with pipette solution. Currents were evoked by repetitive 3-s voltage ramps from −110 to +100 mV and recorded using an EPC7 patch-clamp amplifier (List Electronik, Darmstadt, Germany). They were filtered at 0.2 kHz, digitized at 0.5 kHz using a Digidata 1200 Interface, and analyzed using pClamp software (Axon Instruments, Burlingame, CA). Single-channel currents were recorded from small inside-out membrane patches. They were filtered at 5 kHz using an eight-pole Bessel filter and sampled at 10 kHz.

The pipette solution contained (mM): 140 KCl, 1.2 MgCl₂, 2.6 CaCl₂, 10 HEPES, pH 7.4 with KOH, and the internal (bath) solution contained (mM): 110 KCl, 2 MgCl₂, 1 CaCl₂, 30 KOH, 10 EGTA, 10 HEPES, pH 7.2 with KOH, and nucleotides as indicated. Tolbutamide was made up as a 0.05 M stock solution, and diazoxide as a 0.02 M stock solution, in 0.1 M KOH. Solutions containing ATP were made up fresh each day and the pH was readjusted after addition of the nucleotide. Rapid exchange of solutions was achieved by positioning the patch in the mouth of one of a series of adjacent inflow pipes placed in the bath.

Data Analysis

All data are given as mean ± SEM. The symbols in the figures indicate the mean and the vertical bars indicate 1 SEM (where this is larger than the symbol). Statistical significance was tested using an unpaired Student's t test, a paired t test, or by analysis of variance, as appropriate.

Macroscopic currents.

The slope conductance was measured by fitting a straight line to the current–voltage relation between −20 and −100 mV; an average of five consecutive ramps was calculated in each solution. ATP dose–response relationships were measured by alternating the control solution with a test ATP solution of decreasing concentration. The extent of inhibition by ATP was then expressed as a fraction of the mean of the value obtained in the control solution before and after ATP application. ATP dose–response curves were fit to the Hill equation:

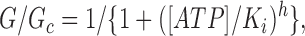1

where [ATP] is the ATP concentration, K _i is the ATP concentration at which inhibition is half maximal, and h is the slope factor (Hill coefficient). In some cases (indicated in the text), we have also fit the dose–response curves with a modified form of the Hill equation (Eq. 2) that does not assume that a saturating ATP concentration causes complete current block:

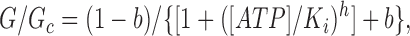2

where b is the fractional conductance remaining in the presence of a saturating ATP concentration.

Single-channel currents.

Single channel currents were analyzed using a combination of pClamp and in-house software written by Dr. P.A. Smith (Oxford University, Oxford, UK). Single-channel current amplitudes were calculated from an all-points amplitude histogram. Channel activity (nP _o) was measured as the mean patch current (I) divided by the single channel current amplitude (i), for segments of the current records of ∼1 min duration. Open probability (P _o) was calculated from nP _o/n, where n is the number of channels in the patch and was estimated from the maximum number of superimposed events. In the case of the C166S mutation, we analyzed patches that showed no superimposed events, and we can be confident that only a single channel was present because of the high channel open probability. For analysis of channel kinetics, events were detected using a 50% threshold level method. Burst analysis was carried out as described by Jackson et al. (1983).

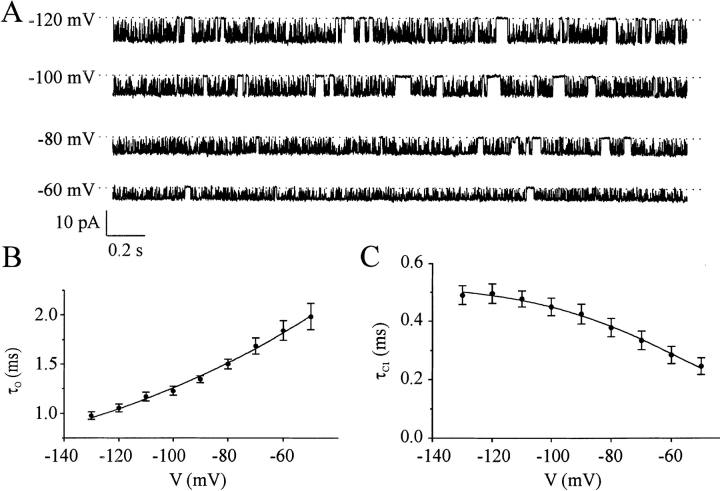
For measurement of the voltage dependence of the kinetics of Kir6.2ΔC26-C166S (see Fig. 4, E and D), test potentials were alternated with a control potential of −60 mV, to correct for time-dependent changes in channel kinetics (such as those produced by rundown). In contrast to Kir6.2ΔC26/SUR1 currents, Kir6.2ΔC26 currents showed fast rundown. To control for this rundown, we expressed the channel open probability at a given voltage as a fraction of the mean of that measured at −60 mV before and after the test voltage was applied. All data was normalized to the open probability measured at −60 mV immediately after patch excision.

Figure 4.

Effect of voltage on Kir6.2ΔC26-C166S single-channel kinetics. (A) Single Kir6.2ΔC26-C166S channel currents recorded from an inside-out patch at the potentials indicated. (C and D) Voltage dependence of the mean open time, τ_o (C), and short closed time, τ_C1 (D), measured for three patches.

Kinetic Model

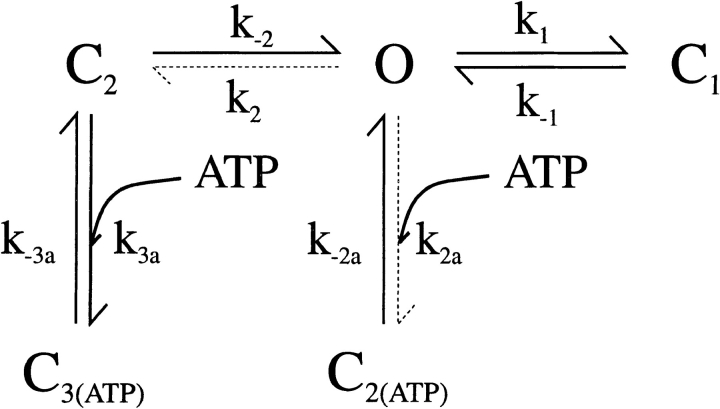
We fitted our data to the kinetic scheme given in Fig. 9, where O is the open state, C₁ represents the short closed state observed within a burst of openings, and C₂ represents the long closed state observed in the absence of ATP, which governs the interburst duration. In the presence of ATP, two additional closed states were observed: C_2(ATP) and C_3(ATP). The rate constants for this kinetic scheme were calculated directly from the data, using the following equations:

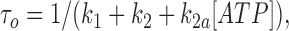3

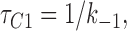4

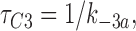5

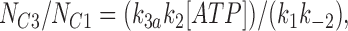6

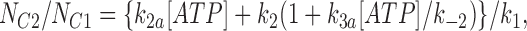7

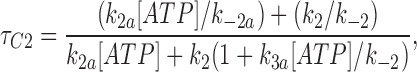8

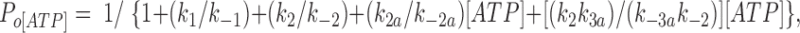9

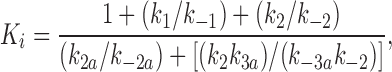10

Figure 9.

A simple kinetic scheme for Kir6.2ΔC26 channel gating in the presence of ATP. C_2(ATP) and C_3(ATP) indicate additional closed states observed in the presence of ATP. The dotted lines represent the rate constants affected by the C166S mutation.

where τ_o is the mean open time, τ_C1 is the mean short closed time, τ_C2 is the mean long closed time, τ_C3 is an additional long closed state observed only in the presence of ATP, N_C1, N_C2, and N_C3 are the number of C₁, C₂, and C₃ events, respectively, P _o[ATP] is the open probability in the presence of ATP, and K _i is the ATP concentration that produces half-maximal inhibition.

results

The C166S Mutation Alters the Macroscopic Current Properties

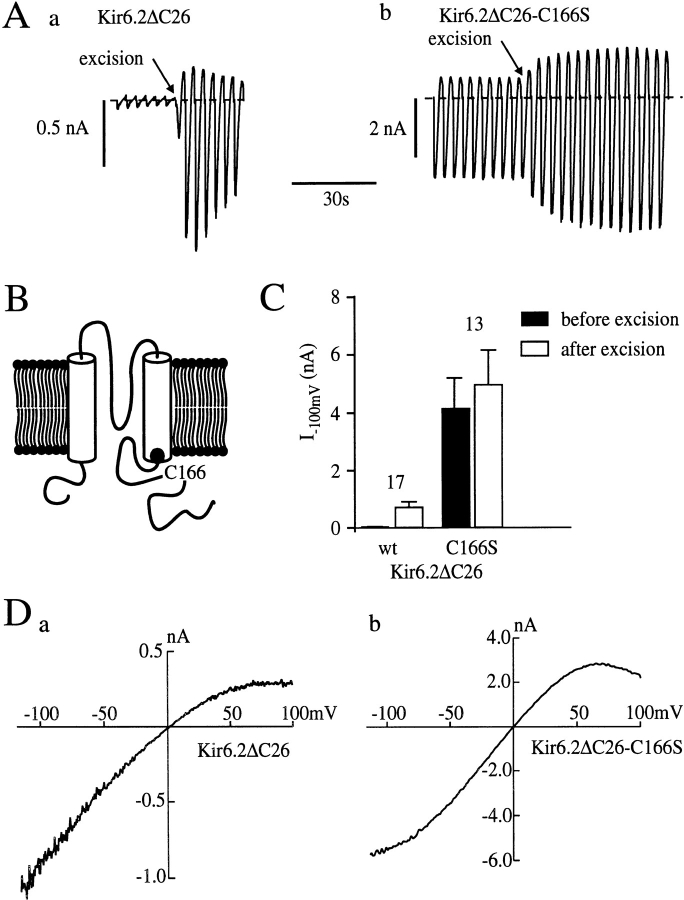
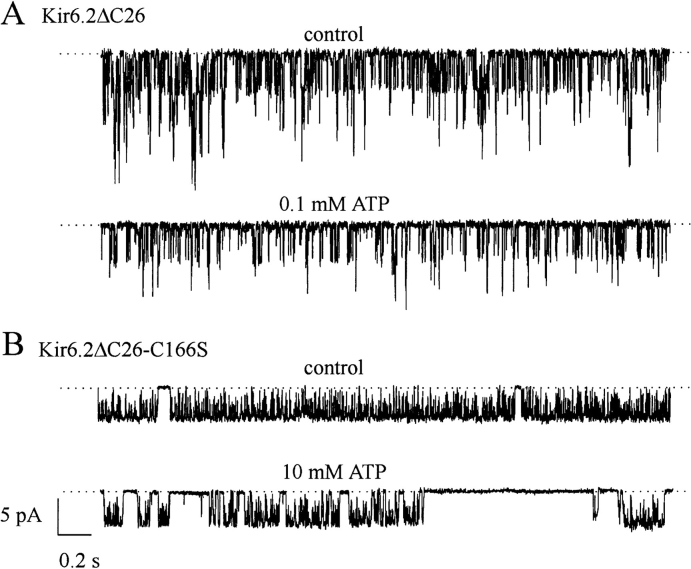
Currents recorded from cell-attached patches on oocytes expressing wild-type (wt)¹ Kir6.2ΔC26 were very small, but increased ∼20-fold when patches were excised into nucleotide-free solution (Fig. 1 A, a), reflecting the relief of the blocking action of ATP present in the oocyte cytoplasm. In contrast, when the cysteine at position 166 was mutated to serine (C166S; Fig. 1 B), much larger currents were recorded in the cell-attached configuration, and a smaller increase in conductance was observed on patch excision (Fig. 1 A, b). After patch excision, the current at −100 mV increased by 19 ± 2-fold (n = 17) for wtKir6.2ΔC26 currents and by 1.5 ± 0.2-fold (n = 13) for Kir6.2ΔC26-C166S currents (Fig. 1 C). This is consistent with our previous observation that the C166S mutation renders the channel less sensitive to ATP (Trapp et al., 1998; Tucker et al., 1998).

Figure 1.

Properties of wtKir6.2ΔC26 and Kir6.2ΔC26-C166S macroscopic currents. (A) Macroscopic currents recorded from cell-attached patches on oocytes injected with mRNA encoding wtKir6.2ΔC26 (a) or Kir6.2ΔC26-C166S (b). The patch was excised at the point indicated by the arrow. Currents were elicited in response to a series of voltage ramps from −110 to +100 mV. The dashed line indicates the zero current level. (B) Putative membrane topology of Kir6.2 with the position of C166 marked. (C) Mean current amplitude recorded before and after excision of membrane patches from oocytes expressing wtKir6.2ΔC26 (wt) or Kir6.2ΔC26-C166S (C166S). The number of oocytes is given above the bars. (D) Macroscopic current–voltage relations recorded in response to a voltage ramp from −110 to +100 mV from inside-out patches on oocytes injected with mRNA encoding wtKir6.2ΔC26 (a) or Kir6.2ΔC26-C166S (b).

Kir6.2ΔC26-C166S currents were also approximately sevenfold larger than wtKir6.2ΔC26 currents in excised patches. The mean current amplitudes at −100 mV after patch excision were −0.73 ± 0.18 nA (n = 17) for wtKir6.2ΔC26 and −4.99 ± 1.17 nA (n = 13) for Kir6.2ΔC26-C166S (P < 0.001, t test). Thus, the C166S mutation may enhance the functional expression of the channel, and/or augment the open probability, and/ or increase the single-channel conductance. Both native K_ATP currents and wtKir6.2ΔC26 currents exhibit a time-dependent decline in amplitude in excised patches (Fig. 1 A, a). By contrast, little or no rundown of Kir6.2ΔC26-C166S currents was observed (Fig. 1 A, b), even over a 15-min period. Likewise, while the amplitude of wtKir6.2ΔC26 currents is often increased above control levels after removal of MgATP (Tucker et al., 1997), a similar “refreshment” was not observed for Kir6.2ΔC26-C166S currents (Fig. 2 A). These differences suggest that the C166S mutation impairs channel rundown: the inability of MgATP to refresh the current may be a consequence of the fact that channel activity is already maximal, or reflect an additional defect in the reactivation process itself.

Figure 2.

Effects of ATP on wtKir6.2ΔC26 and Kir6.2ΔC26-C166S macroscopic currents. (A) Macroscopic currents recorded from an inside-out patch on an oocyte injected with mRNA encoding Kir6.2ΔC26-C166S. ATP was added to the internal solution as indicated by the bar. Currents were elicited in response to a series of voltage ramps from −110 to +100 mV. The patch was excised at the point indicated by the arrow. The dashed line indicates the zero current level. (B) Macroscopic wtKir6.2ΔC26 (i) or Kir6.2ΔC26-C166S (ii) currents. ATP was added to the internal solution as indicated by the bar. Currents were elicited in response to a series of voltage ramps from −110 to +100 mV. The dashed line indicates the zero current level. (C) Mean ATP dose–response relationships for wtKir6.2ΔC26 currents (○, n = 7) and Kir6.2ΔC26-C166S currents (•, n = 10). Test solutions were alternated with control solutions and the slope conductance (G) is expressed as a fraction of the mean (G_c) of that obtained in control solution before and after exposure to ATP. Conductance was measured between −20 and −100 mV and is the mean of five voltage ramps. The dotted and solid lines are the best fit of the data to the Hill equation (Eq. 1) using the mean values for K _i and h given in the text. The dashed line has been fit to the Kir6.2ΔC26-C166S data using a modified form of the Hill equation (Eq. 2) in which it is not assumed that ATP block at saturating concentrations is complete. Mean values for K _i and h are given in the text.

Fig. 1 D illustrates representative macroscopic current– voltage relations for wtKir6.2ΔC26 and Kir6.2ΔC26-C166S currents. The rectification at positive potentials is not much altered by the C166S mutation, but at hyperpolarized potentials the current–voltage relation deviates from linearity.

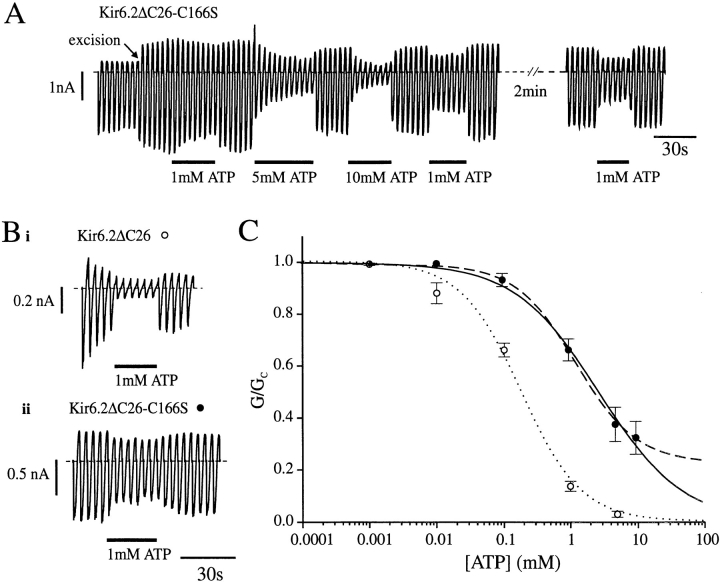
ATP Sensitivity

The ATP sensitivity of wtKir6.2ΔC26 and Kir6.2ΔC26-C166S currents is compared in Fig. 2. Kir6.2ΔC26-C166S currents were always significantly less ATP sensitive, as previously reported (see Trapp et al., 1998). Although we observed considerable variability in ATP sensitivity between patches initially, we subsequently discovered that this arises, in part, because the first application of a high concentration of ATP renders the mutant channel more sensitive to subsequent ATP applications (Fig. 2 A, compare responses to 1 mM ATP). For this reason, we applied 10 mM ATP for ∼30 s to “sensitize” Kir6.2ΔC26-C166S channels before measuring the ATP dose–response relationship.

Fig. 2 B shows that wtKir6.2ΔC26 currents were half-maximally blocked (K _i) by 175 ± 27 μM ATP (n = 7): the Hill coefficient was 0.96 ± 0.12 (n = 7). In contrast, even as much as 10 mM ATP was not sufficient to inhibit Kir6.2ΔC26-C166S currents completely. Consequently, it was not clear whether ATP is able to block the mutant channel fully, or if inhibition plateaus out at some saturating level. If it is assumed that the current is completely blocked by ATP, and the data are fit to the Hill equation, we obtain a K _i of 2.82 ± 0.34 mM and a Hill coefficient of 0.69 ± 0.07 (n = 10) for the Kir6.2ΔC26-C166S data. If, instead, we do not assume that the current is completely blocked at saturating ATP concentrations, the data are best fit with a modified form of the Hill equation with a K _i of 1.26 ± 0.23 mM, a Hill coefficient of 0.97 ± 0.13, and a residual conductance of 23 ± 5% (n = 10) at saturating ATP concentrations. With both methods of analysis, however, it is clear that the ATP sensitivity of Kir6.2ΔC26-C166S channels is significantly less than that of wtKir6.2ΔC26 channels.

A mutation may reduce the ATP sensitivity of Kir6.2ΔC26 in one or more of the following ways: it may (a) impair the ability of the channel to close, (b) interfere with the transduction mechanism by which ATP binding induces channel closure, or (c) reduce the affinity of the ATP binding site. To distinguish between these possibilities, we examined the single-channel kinetics of wild-type and mutant channels.

Single-Channel Current Analysis

Fig. 3, A and B, shows single-channel currents and mean single-channel current–voltage relations recorded from inside-out patches excised from oocytes expressing wtKir6.2ΔC26 and Kir6.2ΔC26-C166S. The single-channel conductance, measured between −20 and −80 mV, was 71.7 ± 1.9 pS (n = 3) for wtKir6.2ΔC26 and 67.2 ± 1.9 pS (n = 3) for Kir6.2ΔC26-C166S, respectively. These values are not significantly different, which indicates that the cysteine mutation does not alter the single-channel conductance. The larger macroscopic currents observed for the C166S mutation (Fig. 1) must therefore reflect an enhanced channel density and/or open probability.

Figure 3.

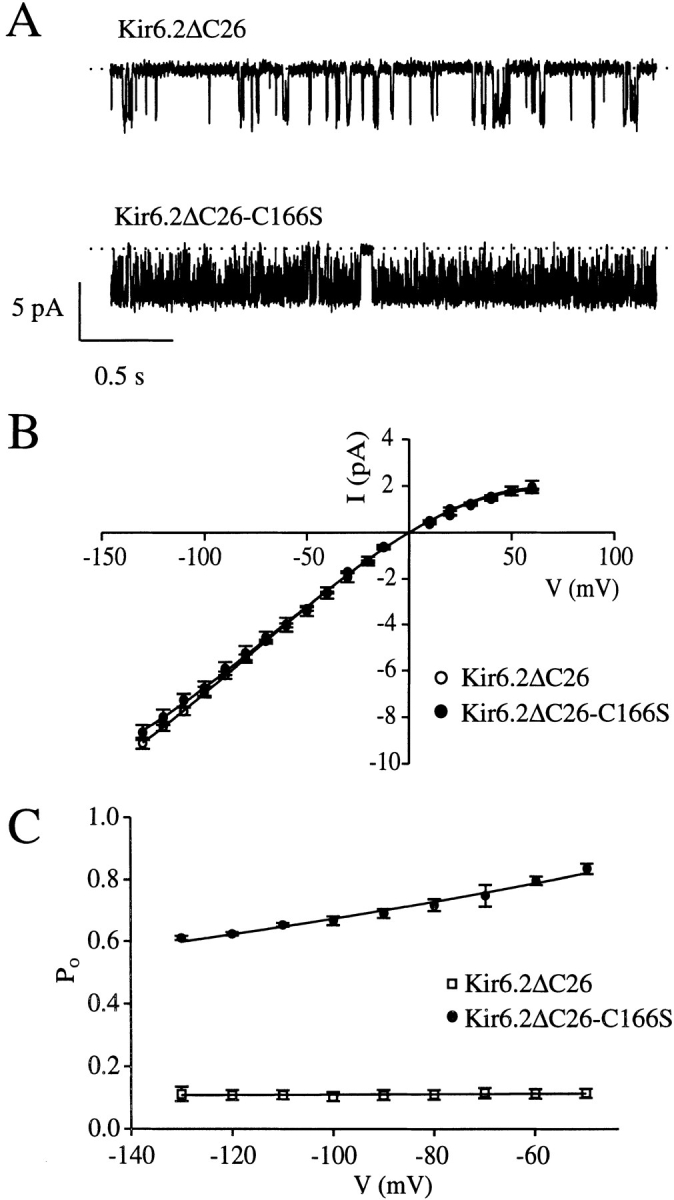
Properties of wtKir6.2ΔC26 and Kir6.2ΔC26-C166S single-channel currents. Single-channel currents at −60 mV (A) and mean single-channel current–voltage relations (B) recorded for wtKir6.2ΔC26 (○, n = 3) or Kir6.2ΔC26-C166S (•, n = 3) currents in inside-out patches. (C) Voltage dependence of the mean open probability of wtKir6.2ΔC26 (○, n = 3) and Kir6.2ΔC26-C166S (•, n = 3) channels.

In contrast to the single-channel conductance, the kinetics of Kir6.2ΔC26-C166S channels were markedly different from those of wtKir6.2ΔC26 channels (Fig. 3 A). At negative membrane potentials, both native K_ATP channel openings and those of wtKir6.2ΔC26 occur in bursts that are separated by relatively long closed intervals (Ashcroft et al., 1988; Sakura et al., 1995; Tucker et al., 1997; Proks and Ashcroft, 1997). The duration of these bursts is prolonged, and the frequency of the interburst intervals is reduced when C166 is mutated to serine. As a consequence, the open probability at −60 mV was increased approximately sevenfold, from 0.11 ± 0.03 for wtKir6.2ΔC26 currents (n = 3) to 0.79 ± 0.02 for Kir6.2ΔC26-C166S currents (n = 6; Table I). This effect can entirely account for the larger macroscopic currents observed for Kir6.2ΔC26-C166S, which were also approximately sevenfold larger than wtKir6.2ΔC26 currents.

Table I.

Open Probability and ATP Sensitivity of C166 Mutants Are Correlated

		Mean P o		K i ATP		Hill coefficient		n		Hydropathy
Kir6.2ΔC26		0.11 ± 0.03		175 ± 27 μM		0.96 ± 0.12		7		2.5
Kir6.2ΔC26-C166S		0.79 ± 0.02		2.82 ± 0.34 mM		0.69 ± 0.07		10		−0.8
Kir6.2ΔC26-C166T		0.73 ± 0.04		3.8 ± 0.1 mM		0.91 ± 0.04		7		−0.7
Kir6.2ΔC266-C166A		0.82 ± 0.03		6.1 ± 0.3 mM		0.76 ± 0.04		8		1.8
Kir6.2ΔC26-C166M		0.76 ± 0.04		4.2 ± 0.3 mM		1.11 ± 0.08		7		1.9
Kir6.2ΔC26-C166F		0.77 ± 0.03		5.3 ± 0.3 mM		0.82 ± 0.04		6		2.5
Kir6.2ΔC26-C166L		0.38 ± 0.05		584 ± 109 μM		1.03 ± 0.16		6		3.8
Kir6.2ΔC26-C166V		0.10 ± 0.04		136 ± 24 μM		0.95 ± 0.14		8		4.2
Coexpressed with SUR1
Kir6.2 + SUR1		0.22 ± 0.09		27 ± 5 μM		1.01 ± 0.14		7		2.5
Kir6.2ΔC26-C166S + SUR1		0.84 ± 0.01		3.9 ± 0.4 mM		0.98 ± 0.12		10		−0.8

n values refer to the number of macropatches used to measure the ATP sensitivity (K  _i, Hill coefficient). The number of single channel patches used for measurement of the channel open probability (P _o) was three in each case (except for Kir6.2ΔC26/C166S, where n = 6). Hydropathy values are given for the residue at position 166 and are taken from Kyte and Dolittle (1982). One mutation (C166D) did not express functional channels (six oocytes from two different batches).  

Table II compares the kinetic parameters of wtKir6.2ΔC26 and Kir6.2ΔC26-C166S currents measured at −60 mV in the absence of ATP. The open time distribution of wtKir6.2ΔC26 currents was best fit by a single exponential, with a mean open time (τ_o) of 0.79 ± 0.06 ms (n = 3), while the closed time distribution was fit by the sum of two exponentials, with mean time constants of 0.31 ± 0.03 and 12.6 ± 2.9 ms (n = 3), respectively. The short closed time (τ_C1) represents the closures that occur within a burst of openings, while the long closed time (τ_C2) represents those that occur between bursts. The value of τ_C1 is similar to that previously reported for wtKir6.2ΔC26 currents (Proks and Ashcroft, 1997) and for both native and wild-type K_ATP channels (Table II; Ashcroft et al., 1988; Proks and Ashcroft, 1997). The mean open time of wtKir6.2ΔC26 currents is significantly shorter than that of wtK_ATP currents (Kir6.2/SUR1; Table II), consistent with earlier observations that the sulfonylurea receptor influences channel gating (Proks and Ashcroft, 1997).

Table II.

Kinetics of C166 Mutants

		Open time τo		Short closed time, τC1		Long closed time, τC2		Percent C2		Burst duration		Openings per burst		τC3		Percent C3
		ms		ms		ms				ms				ms
Kir6.2ΔC26		0.79 ± 0.06		0.31 ± 0.03		12.6 ± 2.9		41.3 ± 8.0		2.4 ± 0.6		2.4 ± 0.3
Kir6.2ΔC26-C166S		1.66 ± 0.10		0.28 ± 0.02		11.8 ± 1.5		0.64 ± 0.03		260 ± 48		129 ± 20
Kir6.2ΔC26-C166T		1.36 ± 0.09		0.32 ± 0.07		10.5 ± 3.6		0.59 ± 0.05		222 ± 63		121 ± 41
Kir6.2ΔC26-C166A		2.06 ± 0.30		0.32 ± 0.04		18.1 ± 2.3		0.37 ± 0.05		363 ± 26		163 ± 22
Kir6.2ΔC26-C166M		1.27 ± 0.06		0.29 ± 0.03		16.0 ± 5.5		0.53 ± 0.12		258 ± 51		161 ± 25
Kir6.2ΔC26-C166L		1.31 ± 0.20		0.30 ± 0.02		2.6 ± 0.74		4.6 ± 0.33		44 ± 21		30 ± 19		17.1 ± 61.3		1.3 ± 0.6
Kir6.2ΔC26-C166V		0.93 ± 0.06		0.30 ± 0.02		15.6 ± 11.7		44.5 ± 3.6		2.6 ± 0.6		2.3 ± 0.4
Coexpressed with SUR1
Kir6.2 + SUR1		1.69 ± 0.11		0.33 ± 0.01		16.1 ± 6.6		18.0 ± 5.4		13.5 ± 4.4		7.1 ± 4.6
Kir6.2ΔC26-C166 + SUR1		2.13 ± 0.05		0.30 ± 0.06		13.1 ± 6.1		0.09 ± 0.01		385 ± 23		154 ± 19

Kinetic parameters were measured at −60 mV. Three patches were analyzed in each case except for Kir6.2ΔC26/C166S, where n = 6.  

One effect of mutating C166 to serine on the kinetics of Kir6.2ΔC26 was a dramatic reduction in the frequency with which the channel entered the long closed state (C₂). As Table II shows, the percentage of closed times accounted for by this state decreased ∼80-fold. In addition, the mean open time and the number of openings per burst were markedly increased, resulting in prolongation of the mean burst duration by >100-fold (Table II). These effects account for the increase in open probability. Both τ_C1 and τ_C2 were unaffected.

Fig. 3   C    illustrates the effect of membrane potential on the open probability of wild-type and mutant Kir6.2ΔC26 channels. While the open probability of wtKir6.2ΔC26 showed no significant voltage dependence, that of Kir6.2ΔC26-C166S decreased slightly with hyperpolarization. The latter effect accounts for the small rectification of the macroscopic Kir6.2ΔC26-C166S currents observed over the same voltage range (Fig. 1 D, b).

Since Kir6.2ΔC26-C166S currents do not run down, it was possible to analyze their kinetics accurately at a number of voltages in the same patch. We found that τ_o slightly decreased, and τ_C1 slightly increased, on hyperpolarization (Fig. 4). A similar behavior was observed for the intraburst kinetics of wild-type K_ATP channels in ventricular myocytes (Zilberter et al., 1988). The observed changes in τ_o and τ_C1 are not sufficient to account for the decrease in the channel open probability, suggesting that an increase in τ_C2 or in the frequency of the C₂ state must also occur. Because of the rarity of the long closed state in Kir6.2ΔC26-C166S channels, it was not possible to measure with sufficient accuracy whether these parameters were changed, but as discussed later this may be estimated from a kinetic model.

Finally, we explored the effect of ATP on wtKir6.2ΔC26 and Kir6.2ΔC26-C166S single-channel kinetics (Fig. 5). Application of ATP to the intracellular solution reduced the open probability of both types of channels, ∼40% inhibition being produced by 100 μM and 10 mM ATP in the case of wtKir6.2ΔC26 and Kir6.2ΔC26-C166S channels, respectively. As observed for the macroscopic currents, the ATP sensitivity of Kir6.2ΔC26-C166S single-channel currents was quite variable. It was not possible to sensitize the channels in the same way as described for the macroscopic patches because many single-channel patches did not recover full activity upon washout of ATP.

Figure 5.

Effect of ATP on the kinetics of wtKir6.2ΔC26 and Kir6.2ΔC26-C166S single-channel currents. Single-channel currents recorded from an inside-out patch at −60 mV in the presence and absence of ATP, as indicated, from oocytes expressing Kir6.2ΔC26 (B) or Kir6.2ΔC26-C166S (A).

Kinetic analysis of wtKir6.2ΔC26 currents (Table III) revealed that ATP reduced τ_o, but was without effect on τ_C1. Similar results have previously been described for native K_ATP channels (Nichols et al., 1991; Kakei et al., 1985). Because of the presence of multiple channels in the patch, the low open probability, and rundown of channel activity, it is not possible to give an accurate estimate of the effect of ATP on the long closed state for wtKir6.2ΔC26 currents. The high open probability and lack of rundown of Kir6.2ΔC26-C166S channels, however, enables a more detailed kinetic analysis. This shows (Table III) that, in addition to decreasing the open time, ATP reduces the burst duration, increases the percentage of the long closed state (C₂), and causes the appearance of a further long closed state (C₃).

Table III.

Effect of Patch Excison and ATP on Single-Channel Kinetics

		c/a		Control (i/o)		ATP (i/o)		Wash (i/o)
Kir6.2ΔC26 (n = 3)
P o				0.088 ± 0.01		0.050 ± 0.01		0.063 ± 0.01
τo (ms)				0.82 ± 0.07		0.72 ± 0.06		0.78 ± 0.07
τC1 (ms)				0.30 ± 0.03		0.31 ± 0.03		0.31 ± 0.03
Kir6.2ΔC26-C166S (n = 3)
P o		0.63 ± 0.05		0.78 ± 0.05		0.49 ± 0.13		0.68 ± 0.02
τo (ms)		1.43 ± 0.1		1.47 ± 0.08		1.36 ± 0.07		1.34 ± 0.02
τC1 (ms)		0.34 ± 0.04*		0.28 ± 0.01		0.28 ± 0.01		0.28 ± 0.01
τC2 (ms)		21.4 ± 5.5		14.2 ± 2.3		9.9 ± 2.0		18.1 ± 1.4
Percent C2		1.06 ± 0.31		0.46 ± 0.2		4.8 ± 3.7		0.90 ± 0.35
τC3 (ms)						159 ± 39
Percent C3						0.35 ± 0.11
Burst duration (ms)		47 ± 9		247 ± 56		38 ± 9		152 ± 63
No. openings/burst		27 ± 5		129 ± 25		22 ± 6		81 ± 29

All parameters were measured at −60 mV. c/a, cell attached; i/o, inside out; Percent C₂ and C₃, percentage of closed time occupied by C₂ and C₃. The ATP concentration was 100 μM in the case of wtKir6.2ΔC26 currents and 10 mM for Kir6.2ΔC26-C166S currents.  

^* P < 0.05 against the excised patch data (paired t test).  

We also analyzed Kir6.2ΔC26-C166S single-channel currents recorded in the cell-attached configuration (Table III). In cell-attached patches, the open probability was higher than that observed for inside-out patches exposed to 10 mM ATP, and the mean open time was slightly smaller. Surprisingly, although it is unaffected by ATP in excised patches, τ_C1 was somewhat longer in cell-attached patches. Furthermore, we only observed a single long closed state in the cell-attached configuration, in contrast to the two long closed states found when inside-out patches were exposed to 10 mM ATP. These differences in gating between the cell-attached patch and the inside-out patch exposed to ATP argue that in the intact cell channel activity may be regulated by cytosolic substances other than ATP, and/or that disruption of the cytoskeleton on patch excision alters channel gating.

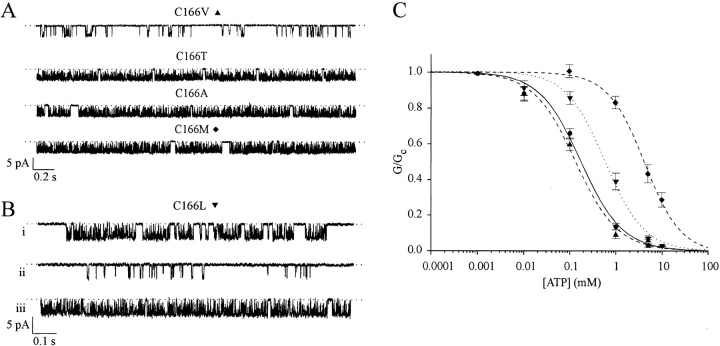
Effects of Mutating C166 to Other Residues

To further explore how mutation of cysteine 166 affects the channel gating and ATP sensitivity, we engineered a range of mutations at this site. The effect of these mutations on the single-channel kinetics, open probability, and ATP sensitivity is shown in Fig. 6 and Tables I and II. Replacement of cysteine 166 with valine had little effect on any of these parameters, indicating that a cysteine at position 166 is not critical for channel function and arguing that C166 is probably not involved in disulfide bond formation. Threonine, alanine, methionine, and phenylalanine at position 166 caused a marked increase in channel open probability and a parallel reduction in ATP sensitivity, similar to that observed with the serine mutation. As is the case for the C166S mutation, the increase in open probability reflects a marked reduction in the frequency of the long closed times. Indeed, there was a strong correlation between the effect of the mutation on the single-channel kinetics and on the ATP sensitivity (Tables I and II). Currents recorded for Kir6.2ΔC26-C166L channels were unusual in that they exhibited three different modes of gating (Fig. 6 B). On rare occasions, the channel kinetics were similar to those observed for wtKir6.2ΔC26, while on other, more frequent, occasions the channel entered a highly active state resembling that found for Kir6.2ΔC26-C166S currents. Most of the time, however, the channel exhibited an intermediate form of kinetic behavior and the data given in Table II was calculated for this mode of gating. As expected from its intermediate effect on the single-channel kinetics, leucine produced a smaller shift in both ATP sensitivity and open probability than the C166S mutation (Fig. 6 C, Table I).

Figure 6.

Effects of different amino acid substitutions at position 166 of Kir6.2ΔC26 on single-channel currents and ATP sensitivity. (A) Single-channel currents recorded at −60 mV from inside-out patches excised from oocytes injected with the different mutant mRNAs indicated. (B) Three different types of single-channel kinetics observed for Kir6.2ΔC26-C166L, recorded from an inside-out patch at −60 mV. (C) Mean ATP dose–response relationships for wtKir6.2ΔC26 (•, n = 7) and for Kir6.2ΔC26 containing the mutations C166V (▴, n = 8), C166L (▾, n = 6), and C166M (♦, n = 7), measured for macroscopic currents recorded from giant inside-out membrane patches. Test solutions were alternated with control solutions and the slope conductance (G) is expressed as a fraction of the mean (G_c) of that obtained in control solution before and after exposure to ATP. Conductance was measured between −20 and −100 mV and is the mean of five voltage ramps. The lines are the best fit of the data to the Hill equation (Eq. 1) using the mean values for K _i and h given in Table I.

Coupling to SUR

We next examined the effect of SUR1 on the open probability and single-channel kinetics of wild-type and mutant channels. When SUR1 and wtKir6.2 were coexpressed, the channel open probability was approximately double that of wtKir6.2ΔC26 (Table I). This effect reflects an increase in the mean open time and a marked reduction in the percentage of long closed times (Table II). The number of openings per burst was also increased so that the burst duration of wtK_ATP currents was longer than that of Kir6.2ΔC26 currents. These effects account for the higher open probability of Kir6.2 currents when coexpressed with SUR1. Similar results have previously been reported for coexpression of Kir6.2ΔC26 and SUR1 (Proks and Ashcroft, 1997). In contrast, SUR1 produced only a slight increase in the mean open time of Kir6.2ΔC26-C166S channels and did not affect the burst duration (Table II). Although there is a marked reduction in the percentage of long closed times, this does not produce a significant increase in the open probability, largely because the long closed state occurs so rarely in the mutant channel. The ability of SUR1 to enhance the ATP sensitivity of Kir6.2 was also absent when C166 was mutated to serine; indeed, SUR1 appeared to decrease the ATP sensitivity (Table I). A possible explanation for the apparent reduction in ATP sensitivity produced by SUR1 is that, like MgADP, MgATP interacts with the NBDs of SUR1 to promote K_ATP channel activity (Gribble et al., 1998). This effect would be more apparent for Kir6.2 mutants that show reduced ATP sensitivity.

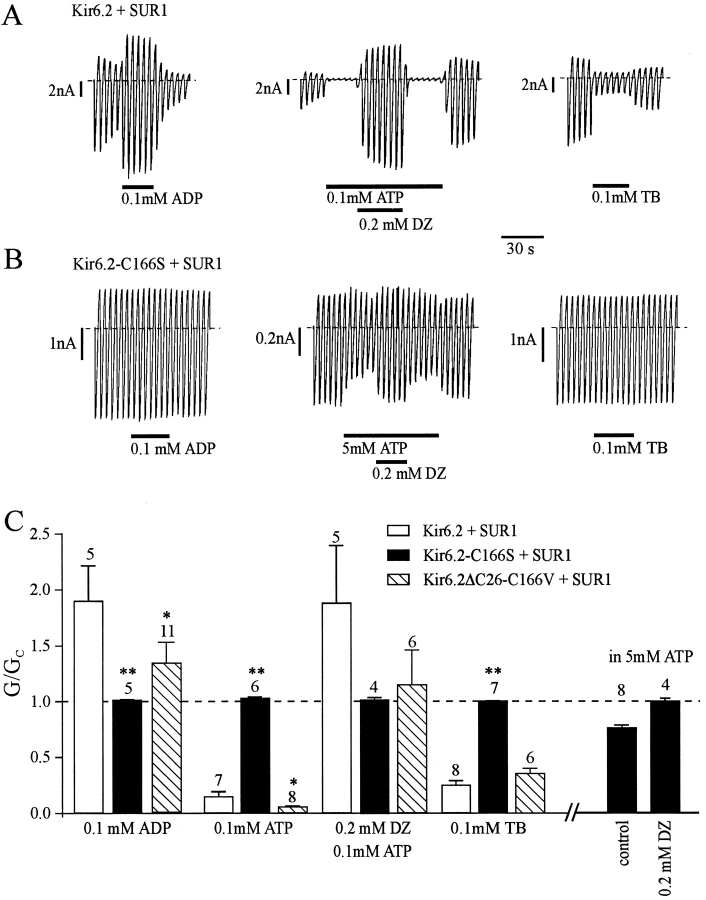
We also explored whether the C166S mutation influences the ability of SUR1 to endow Kir6.2 with sensitivity to MgADP, diazoxide, and tolbutamide. To ensure that the K_ATP current we record only reflects current flow through channels comprising both Kir6.2 and SUR1 subunits, we used full length Kir6.2 containing the C166S mutation and coexpressed it with SUR1. Like Kir6.2 (Inagaki et al., 1995; Sakura et al., 1995), Kir6.2-C166S does not express functional channels independently of SUR1, as only background currents (similar to those recorded in uninjected oocytes) were observed in patches excised from oocytes expressing Kir6.2-C166S (not shown). Thus, all channels recorded from oocytes coinjected with Kir6.2-C166S and SUR1 must be composed of both types of subunit. Fig. 7 A confirms that SUR1 endows Kir6.2 with sensitivity to the blocking effect of tolbutamide and the potentiatory actions of MgADP and diazoxide. Diazoxide was tested in the presence of MgATP because its stimulatory action is dependent upon the presence of intracellular hydrolyzable nucleotides (Dunne, 1989; Kozlowski et al., 1989). In contrast to wild-type K_ATP currents, 100 μM MgADP, 200 μM diazoxide (tested in the presence of 100 μM ATP), and 100 μM tolbutamide did not influence Kir6.2-C166S/SUR1 currents (Fig. 7, B and C). One possible explanation for the lack of effect of agents that potentiate channel activity, such as MgADP and diazoxide, is that Kir6.2-C166S/SUR1 channels are already fully activated in control solution. This idea is supported by the fact that diazoxide was able to enhance Kir6.2-C166S/SUR1 currents if the current amplitude was first reduced by 5 mM ATP (Fig. 7, B and C). Taken together, these results suggest that the coupling of Kir6.2 to SUR1 is partially, but not completely, impaired by the C166S mutation.

Figure 7.

Effect of mutations at residue C166 on the coupling of Kir6.2 to SUR1. (A and B) Macroscopic currents recorded from inside-out patches in response to a series of voltage ramps from −110 to +100 mV. Oocytes were injected with mRNAs encoding Kir6.2 + SUR1 (A) or Kir6.2-C166S + SUR1 (B). MgADP, MgATP, diazoxide (DZ), or tolbutamide (TB) were added to the internal solution as indicated by the bars. (C) Mean macroscopic slope conductance recorded in the presence of the agents indicated (G), expressed as a fraction of the mean (G_c) of that obtained in control solution (no additions) before and after exposure to the test compound(s). The dashed line indicates the current level in the absence of the test compound. Oocytes were injected with mRNAs encoding Kir6.2 + SUR1 (white bars), Kir6.2-C166S + SUR1 (black bars), or Kir6.2ΔC26-C166V + SUR1 (hatched bars). The number of oocytes is given above the bars. *P < 0.05, **P < 0.01 against Kir6.2 + SUR1.

Fig. 7 C also shows that mutation of C166 to valine (rather than serine) partially restored the effects of agents that mediate their effects through SUR1. There was no significant difference in tolbutamide block of Kir6.2ΔC26-C166V/SUR1 and wild-type K_ATP currents (t test), while the difference in the stimulatory effect of MgADP was barely significant (P = 0.05). The ability of diazoxide to stimulate channels inhibited by ATP was also largely restored (compare data in the presence of 100 μM ATP with those in the presence of 100 μM ATP plus diazoxide; P < 0.001). The inhibitory effect of 100 μM ATP was also enhanced by SUR1 when C166 was mutated to valine: 100 μM ATP blocked Kir6.2ΔC26-C166V currents by 40 ± 3% (n = 11), compared with 94 ± 1% (n = 8) when the mutant channel was coexpressed with SUR1 (compare also Figs. 6 C and 7 C). These results indicate that the coupling of Kir6.2 to SUR1 is not markedly impaired, if at all, by the C166V mutation. A disulfide bond between the cysteine residue at position 166 of Kir6.2 and SUR1 is therefore not essential for subunit interaction.

discussion

C166 Is Involved in Channel Gating

Our results suggest that the cysteine residue at position 166 plays an important role in the gating of the K_ATP channel pore. Mutation of this residue to serine, threonine, alanine, methionine, or phenylalanine causes a marked increase in the channel open probability, principally by causing a dramatic decrease in the frequency of the long closed state. Thus, C166 may lie within, or close to, a gate that is involved in closing the K_ATP channel. Its location at the cytoplasmic end of the putative second transmembrane domain (TM2) is consistent with this idea. Further support is provided by the observation that mutation of the adjacent residue (I167M) also had a profound effect on channel gating (Tucker et al., 1998). The fact that the C166S mutation does not affect the short closed time indicates that the conformational change associated with this state is distinct from that of the long closed state and suggests that there may be two distinct gating mechanisms.

Mutation of N160 in TM2 of Kir6.2 to aspartate alters the rectification properties of the Kir6.2/SUR1 channel (Shyng et al., 1997b ), as is expected by analogy with other Kir channels (Lopatin et al., 1994), and indicates that this residue lies within the channel pore. Surprisingly, this mutation also enhanced the channel open probability, leading Shyng et al. (1997b) to propose that N160 may be involved in channel gating. However, while mutations in C166 can increase P _o up to sevenfold, those in N160 produced rather moderate increases in open probability (up to 1.2-fold; Shyng et al., 1997b ). An alternative hypothesis, therefore, is that mutation of N160 has an allosteric effect on a gate located at the end of TM2. However, since we observed that the presence of SUR1 affects gating, the possibility that the N160 mutations affect the link between SUR1 and Kir6.2, and thereby the channel open probability, cannot be excluded.

A gate located at the intracellular mouth of the pore has also been postulated for both voltage-gated K⁺ channels and cyclic nucleotide-gated (CNG) channels on the basis of mutagenesis studies within, or close to, the cytosolic end of the sixth transmembrane domain (S6), which is equivalent to the region of Kir6.2 in which C166 is located (Liu et al., 1997; Loukin et al., 1997; Zong et al., 1998). Mutations in the S6 domain of the yeast voltage-gated K⁺ channel have a similar effect on the gating kinetics to that of mutating C166 to serine in Kir6.2: they markedly decrease a long closed state, and thereby prolong the burst duration and increase the channel open probability (Loukin et al., 1997). Likewise, in CNG channels, three amino acids within the cytosolic domain connecting S6 to the cyclic nucleotide-binding domain in the COOH terminus profoundly affect the gating kinetics (Zong et al., 1998). Further support for the idea that the cytosolic end of S6 is involved in channel gating comes from experiments in which cysteines were introduced into this region of the Shaker K⁺ channel. Thiol-reactive reagents were able to block the modified channel in the open state but not in the closed state, arguing that access to the pore is regulated by an intracellular gate (Liu et al., 1997). This gate may operate as an intracellular lid to the pore, which leaves an internal cavity between the gate and the selectivity filter when it closes, because large molecules, such as quaternary ammonium ions, can be trapped inside the pore of the Shaker K⁺ channel when the gate is closed (Holmgren et al., 1997). Whether a similar mechanism operates for the pore of Kir6.2 remains a matter for speculation.

Kinetic Model of the K_ATP Channel

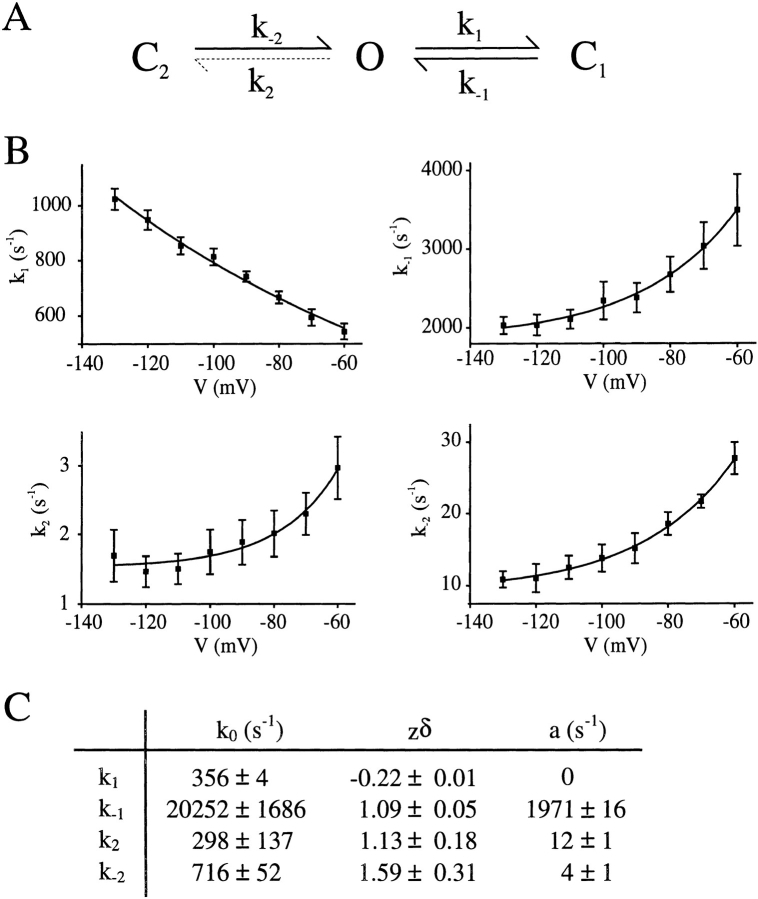
To understand the effect of the C166S mutation on the channel open probability, it is helpful to consider a model of channel gating. Fig. 8 A shows the simplest kinetic scheme capable of explaining our data: O is the open state, C₁ represents the short closed state observed within a burst of openings, and C₂ represents the long closed state observed in the absence of ATP, which governs the interburst duration. The values of the rate constants at −60 mV calculated for wtKir6.2ΔC26, Kir6.2ΔC26-C166S, wtKir6.2/SUR1, and Kir6.2ΔC26-C166S/SUR1 currents are given in Table IV. The major effect of the C166S mutation was a profound decrease in the rate constant k₂, which was reduced to <1% of that of the wild-type channel. This indicates that, although the mutation decreases the rate of entry into the long closed state (C₂), it does not influence the exit rate. Thus the higher open probability of Kir6.2ΔC26-C166S is explained by the fact that this channel rarely enters the long closed state. The presence of the sulfonylurea receptor also affected the rate constants, markedly decreasing k₂ and slightly reducing k₁, for both wild-type and mutant channels.

Figure 8.

(A) A simple kinetic scheme for Kir6.2ΔC26 channel gating in ATP-free solution, where O is the open state, C₁ represents the short closed state observed within a burst of openings, and C₂ represents the long closed state that governs the interburst duration. The dotted line represents the rate constant affected by the C166S mutation. (B) Voltage dependence of the rate constants k₁, k₋₁, k₂, and k₋₂ in the absence of ATP, calculated for Kir6.2ΔC26-C166S currents (n = 3). The rate constants were calculated from measured values of τ_o, τ_C1, P _o, and percent C₂. The lines are fitted to the equation k = a + k _o exp (zδVF/RT), where k _o is the rate constant at a membrane potential of 0 mV, V is the membrane potential, zδ is a term describing the electrical distance through the membrane, and a is a voltage-independent component. (C) Values of the parameters used to fit the voltage dependence of the rate constants shown in B.

Table IV.

Effects of the C166S Mutation, and of SUR1, on the Intrinsic Rate Constants

		k1		k−1		k2		k−2
		s−1		s−1		s−1		s−1
Kir6.2ΔC26		743 ± 62		3329 ± 344		523 ± 73		86 ± 16
Kir6.2ΔC26/C166S		719 ± 65		3536 ± 212		4.5 ± 1.3*		91 ± 10
Coexpressed with SUR1
Kir6.2 + SUR1		494 ± 34		3035 ± 195		103 ± 45*		89 ± 34
Kir6.2ΔC26/166S + SUR1		470 ± 10		3411 ± 392		0.44 ± 0.08*		83 ± 8

Rate constants were calculated for −60 mV. n = 3 in each case.  

^* P < 0.05 against Kir6.2ΔC26.  

It was not possible to examine the voltage dependence of the rate constants for wtKir6.2ΔC26 currents because of the presence of channel rundown. We were able to do so, however, for channels containing the C166S mutation, which does not run down. The voltage dependence of the rate constants k₁, k₋₁, k₂, and k₋₂ in the absence of ATP, calculated for Kir6.2ΔC26-C166S currents, is given in Fig. 8 B. These values were calculated directly from the measured data and provide a unique solution to the kinetic scheme. Whereas k₁ decreases with depolarization, the three other rate constants increase as the membrane potential is made more positive. The fact that k₋₂ decreases with hyperpolarization means that τ_C2 must increase with hyperpolarization and will therefore contribute to the observed decrease in open probability (Fig. 3 C) and rectification of the current–voltage relation (Fig. 1 D, b) at negative potentials. The values for zδ, which reflect the voltage dependence of gating, were greater than unity for k₂ and k₋₂, suggesting that more than one charge must move to gate the channel. Interestingly, there appears to be a small voltage-independent component to k₋₁, k₂, and k₋₂, which suggests that part of the gating mechanism is located outside the membrane voltage field. Although we cannot measure whether the rate constants for Kir6.2ΔC26 channels show a similar voltage dependence, it seems likely that this is the case for k₁, k₋₁, and k₂ since the voltage dependence of the open and closed times of the native K_ATP channel (Kir6.2/ SUR1) resembles that of Kir6.2ΔC26-C166S (Zilberter et al., 1988).

Mechanism of Action of C166 Mutations

The residue at C166 is critical for the gating of Kir6.2ΔC26, since most mutations at this position substantially affected the single-channel kinetics. Two main modes of gating were observed: the wild-type mode and a high P _o mode found when C166 was mutated to S, T, A, or M. An intermediate mode of gating was observed with the C166L mutation, but this appeared to be thermodynamically less favorable as it was less stable and at times the channel switched to either the wild-type or the high P _o mode. The data therefore suggest that the channel prefers to adopt either the wild-type or high P _o mode of gating.

Analysis of a range of mutations at residue 166 of Kir6.2ΔC26 suggests that for the channel to enter the long closed state (C₂) this residue must be both small and hydrophobic. Replacement of cysteine by serine is a relatively conservative substitution, yet it had a dramatic effect on channel gating. The major difference in these two amino acids is their hydrophobicity (2.5 and −0.8, respectively, Table I), which suggests that hydrophobicity may be an important factor. This may also explain why alanine (which is smaller, but less hydrophobic [1.8], than cysteine) markedly alters the channel kinetics. Size also appears to be a critical factor since phenylalanine, which has a similar hydrophobicity to cysteine but is much larger, also caused a dramatic increase in the channel open probability.

Effect of Mutations on Channel ATP Sensitivity

The results obtained for channels carrying mutations at position 166 shed some light on the mechanisms by which ATP closes the K_ATP channel. In particular, they clearly show that ATP does not inhibit the K_ATP channel by acting as an open channel blocker; if this were the case, an increase in channel open probability should result in an enhanced ATP sensitivity, whereas a reduction in the inhibitory potency of ATP is actually observed. The conclusion that ATP does not block the channel pore is also consistent with the fact that the block by ATP is not voltage dependent.

Our results demonstrate a striking correlation between the effect of mutations at C166 on the channel open probability and ATP sensitivity. A similar correlation has been observed for mutations at N160, although the absolute changes in both parameters were much less dramatic: K _i shifted to 46 μM and P _o increased 1.2-fold with the N160D mutation (Shyng et al., 1997b ). Shyng et al. (1997b) hypothesized that the apparent decrease in ATP sensitivity resulted from changes in the channel gating, rather than alteration of ATP binding, although they did not examine the single-channel kinetics.

To explain how mutation of C166 may alter the ATP sensitivity, we once again turn to a kinetic model of the channel (Fig. 9, see Appendix). In wtKir6.2ΔC26 channels, ATP was without effect on the short closed time (C₁), but reduced the mean open time (Table III). A reduction in the mean open time with ATP (Nichols et al., 1991; Kakei et al., 1985), and no measurable effect of ATP on the short closed time (Qin et al., 1989), has also been reported for native K_ATP channels. Thus, ATP either does not bind to the short closed state or, if it does, this binding does not cause a transition to the long closed state. By contrast, ATP must interact with the open state (by interaction we mean that the effect of bound ATP is manifest when the channel is in a given state, but do not imply that ATP binding is state dependent). We introduce a new closed state C_2(ATP) to describe the closed state in which ATP is bound (Fig. 9). As discussed in more detail in the Appendix, it seems very likely that C₂ and C_2(ATP) represent equivalent conformational states that differ only in that in one case ATP is bound to the channel and in the other case it is not. The effects of ATP on the long closed times could not be accurately quantified for wtKir6.2ΔC26 currents because of the presence of channel rundown and the difficulty of determining whether the patch contained more than one channel. But it is clear from simple observation of the current records that ATP enhances the frequency of the long closed state (C₂), as previously suggested for native K_ATP channels (Nichols et al., 1991; Kakei et al., 1985).

We now consider the effect of mutating C166 to serine. As is the case for wtKir6.2ΔC26 channels, ATP was without effect on the short closed time, but reduced the mean open time, of Kir6.2ΔC26-C166S channels. Because of their high open probability and reduced rundown, we were able to analyze the effect of ATP on the long closed times of Kir6.2ΔC26-C166S channels. We observed that ATP increased the percentage of long closed times and reduced their lifetime (Table III). It also introduced an additional closed state, C₃. These data suggest that in addition to interacting with the open state, ATP interacts with the long closed state, C₂. In our model, this additional closed state is designated C_3(ATP) (Fig. 9; see Appendix). Further support for the idea that C₂ and C_2(ATP) represent similar conformational states is provided by the fact that their mean lifetimes must be very similar, as we observe only three exponentials in the closed time distribution. As is clear from Fig. 9, we have assumed that only a single ATP molecule binds to the channel at a time; thus, when ATP is bound, the channel will be either in state C_2(ATP) or C_3(ATP). Consequently, our model gives a Hill coefficient of 1 for ATP binding, as is observed experimentally.

As described in detail in the Appendix, kinetic analysis of our results favors the idea that the rate constant k_2a, like k₂, is affected by the C166S mutation. As a consequence, the transition from the open state to the long closed state C_2(ATP) is impaired. The reduction in k_2a is sufficient to fully account for the observed effect of the C166S mutation on the apparent ATP sensitivity and it is not necessary to assume changes in other rate constants. However, access to the C_3(ATP) state is reduced indirectly, due to the diminished occupancy of the state C₂, which results from the decrease in k₂.

The rate constant k_2a contains both ATP-dependent and ATP-independent components as it includes gating of the pore, ATP-binding, and the transduction mechanism by which ATP binding results in channel closure. Our kinetic analysis suggests that the C166S mutation affects only the ATP-independent part of the rate constant k_2a (see Appendix). Thus, it is not necessary to invoke a change in either the affinity ATP binding or the transduction process to explain our results.

Shyng et al. (1997b) proposed that the modest shifts in ATP sensitivity produced by mutation of N160 are secondary to changes in the intrinsic gating of the channel. While we also favor this idea, the shift in ATP sensitivity they observed was not large enough to exclude the possibility that it results from a partial functional uncoupling of Kir6.2 from SUR1, since SUR1 enhances the ATP sensitivity of Kir6.2. When SUR1 is absent, the K _i for ATP inhibition increases from 10 to 100 μM (Tucker et al., 1997), a shift that is greater than that observed for the N160 mutations. This explanation cannot account for our results, however, since we observed marked shifts in the ATP sensitivity of Kir6.2ΔC26 in the absence of SUR1.

Why Do Mutant Channels Not Show Rundown and Reactivation?

Wild-type K_ATP currents and Kir6.2ΔC26 currents run down with time after patch excision, but are reactivated after exposure to MgATP (Tucker et al., 1997). A similar phenomenon is observed for native K_ATP channels (Findlay and Dunne, 1986; Ohno-Shosaku et al., 1987). The mechanism of rundown remains unknown, but since Kir6.2ΔC26 currents run down when expressed in the absence of SUR1, the rundown state cannot represent a dissociation from the sulfonylurea receptor. Both rundown and reactivation are almost completely abolished when cysteine 166 is mutated to serine. The simplest explanation for the lack of reactivation is that the open probability of the mutant channel is already maximal and thus cannot be further increased. The reason why rundown does not occur is less clear. One possibility is that the rate constant for entering the rundown state is dramatically reduced by the cysteine mutation. Another possibility is that the rundown state is accessed from the long closed state, which is only rarely entered by the mutant channel. We favor the latter explanation because, in wild-type channels, rundown is associated with a gradual increase in the frequency and duration of the long closed state. Furthermore, when C166 is mutated to valine, which does not affect the channel kinetics, the currents also run down.

Effect of Mutation of C166 on Coupling to SUR1

When C166 was mutated to serine in the full-length form of Kir6.2, and the mutant channel was coexpressed with SUR1, the resulting currents were no longer sensitive to tolbutamide. The simplest explanation of this finding is that SUR1 is unable to couple to Kir6.2-C166S. We do not think this is the case, however, for two reasons. First, Kir6.2-C166S did not express by itself, but only when coexpressed with SUR1. This argues that Kir6.2-C166S requires the presence of SUR1 for functional expression, as is the case for wild-type Kir6.2, and that the mechanism by which SUR1 enables the functional expression of Kir6.2 remains intact in this mutant. Secondly, diazoxide was able to increase Kir6.2-C166S/SUR1 currents, providing they were first partially blocked by high ATP concentrations. It is now well established that the potentiatory effect of diazoxide is endowed by SUR1 (Inagaki et al., 1996; Gribble et al., 1997a ; Shyng et al., 1997a ). Thus, this result implies that SUR1 is able to confer diazoxide sensitivity on Kir6.2-C166S as well as on wild-type Kir6.2. Given that SUR1 is able to couple to Kir6.2, why is an inhibitory effect of tolbutamide not observed? One possibility is that it may be a consequence of the change in the gating kinetics since tolbutamide, like ATP, stabilizes the long closed state (C₂) (Gillis et al. 1989), which is only rarely accessed in Kir6.2-C166S channels. The fact that tolbutamide inhibition is not compromised when C166 is mutated to valine, which also does not affect the single-channel kinetics, is consistent with this idea.

Conclusions

In conclusion, our results suggest that the cytosolic end of the second transmembrane domain of Kir6.2 may contribute to an intracellular gate that regulates access to the channel pore and governs the long closed state of the channel. Mutation of C166 to a more hydrophilic or bulkier residue modifies the intrinsic gating properties, such that the channel enters the long closed state more rarely. Because ATP acts by enhancing entry into this state, mutation of C166 to serine (or to threonine, alanine, methionine, or phenylalanine) reduces the ability of ATP to cause channel inhibition. This effect appears to be primarily a consequence of the altered intrinsic gating kinetics rather than any change in the affinity of the ATP-binding site, or in the mechanism by which ATP-binding is linked to gating. The inability of tolbutamide, which also enhances the long closed state, to block Kir6.2-C166S/SUR1 channels is also consistent with this idea. Mutations that alter the apparent ATP sensitivity of the channel cannot therefore be taken to suggest a change in the ATP-binding site unless it can be shown that the intrinsic gating of the channel is unaffected.

Abbreviation used in this paper

wt

wild type

appendix

The simplest kinetic scheme capable of explaining our data is given in Fig. 9. Here we discuss the major implications of the kinetic analysis of this model.

Effects of the Mutation C166S on the Transition between the Open State and Long Closed States C₂, C_2(ATP)

Our results favor the idea that the rate constant k_2a, like k₂, is affected by the C166S mutation. We have estimated whether this is the case in the following way. We can calculate k_2a for both wtKir6.2ΔC26 and Kir6.2ΔC26-C166S from the reduction in the mean open time in the presence of ATP (using Eq. 3), which gives a value of 1.4 × 10⁶ and 2.9 × 10³ s⁻¹ M⁻¹, respectively. It is also possible to derive k_2a independently for the C166S mutation by simultaneously solving Eqs. 4–9 in the presence and absence of ATP: this gives a value of 4.1 ± 1.7 × 10³ s⁻¹ M⁻¹. In our experiments, the mean inhibitory effect of 10 mM ATP on single Kir6.2ΔC26-C166S channel currents was less than that measured for the macroscopic currents, and the K _i for the single-channel currents derived from the kinetic model shown in Fig. 9 was 18 mM, compared with a value of 2.8 mM measured for the macroscopic currents. In contrast, the inhibitory effect of 100 μM ATP on the single-channel Kir6.2ΔC26 currents was comparable to that measured for the macroscopic currents (196 and 175 μM, respectively). To calculate k_2a for the C166S mutation, we therefore used data obtained from the single-channel patch in which the block by 10 mM ATP was comparable to that observed for the macroscopic currents (62 vs. 68%, respectively). This yields a value for k_2a of 9.7 × 10³ s⁻¹ M⁻¹. Thus, regardless of how k_2a is calculated, its value is at least two orders of magnitude smaller than that obtained for the wild-type channel. This indicates that the C166S mutation impairs the ability of the channel to enter the long closed state C_2(ATP).

The rate constant k_2a is influenced not only by the intrinsic closing rate of the channel, but also by the affinity of ATP for its binding site and by the mechanism that transduces ATP binding into changes in channel gating. A key question, therefore, is whether the C166S mutation produces a change in the affinity with which ATP binds to the channel, or if it influences the transduction mechanism. The ratio of the rate constants k_2a for wild-type Kir6.2ΔC26 (wt) and Kir6.2ΔC26-C166S (C/S) currents is similar to that obtained for the ratio of the rate constants k₂:

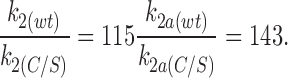11

This suggests that the effect of the C166S mutation on the rate constant k_2a, which governs channel closing in the presence of ATP, is similar to that found for the intrinsic closing rate constant k₂ (Fig. 9).

We may express the rate constants in terms of Eyring rate theory as follows

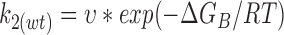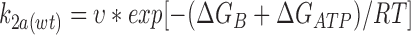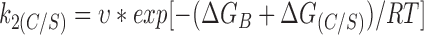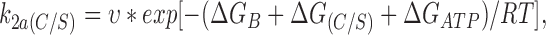where υ is the vibration frequency (6.2 × 10¹² s⁻¹ at T = 298°K), and the energy barriers correspond to that for wild-type Kir6.2ΔC26 (ΔG_B), an additional barrier introduced by the C166S mutation (ΔG_(C/S)), and a reduction in the energy barrier produced by ATP, which is ΔG_ATP for wild-type Kir6.2Δ26 and ΔG_ATP(C/S) for Kir6.2Δ26-C166S. Eq. 11 implies that the reduction of the energy barrier in the presence of ATP is identical for Kir6.2ΔC26 and Kir6.2ΔC26-C166S channels (i.e., ΔG_ATP = ΔG_ATP(C/S)). Therefore, it is unlikely that the C166S mutation has an effect on the affinity of the ATP-binding site or the transduction mechanism by which ATP binding influences gating. This suggests that the mutation principally affects the transition rate between the open state and the second closed state C_2(ATP). Further,

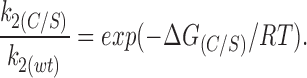12

Using values calculated for k_2(C/S) and k_2(wt) in the absence of ATP, ΔG_(C/S) = 11.8 kJ/mol. We can also estimate ΔG_ATP and ΔG_B, which are −19.4 and 79.4 kJ/ mol, respectively, for wild-type Kir6.2ΔC26.

Effects of the Mutation C166S on Other Rate Constants

We now consider the effect of the C166S mutation on the other ATP-dependent rate constants (k_−2a, k_3a, k_−3a). From the model shown in Fig. 9, the ratio of the K _i's for wild-type Kir6.2ΔC26 and for Kir6.2ΔC26 carrying the C166S mutation can be expressed (from Eq. 10) as:

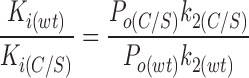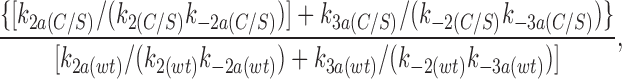where P _o is the open probability in the absence of ATP. Using the values measured for P _o, k₂, and K _i (obtained from the macroscopic currents) it can be shown that

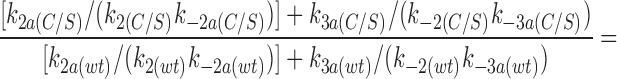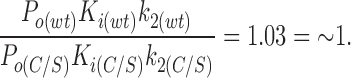The ratio k_2a/k₂ is the same for wtKir6.2ΔC26 and for Kir6.2ΔC26-C166S (see above). Thus, the apparent shift in the ATP sensitivity caused by the C166S mutation can be explained by a change in the rate constants determining the transition from the open state to the second closed state (k₂, k_2a), and it is not necessary to postulate additional effects on other ATP-dependent rate constants. We cannot completely exclude the possibility that effects on other rate constants do, in fact, occur, but in this case they must be balanced by a compensating change in another rate constant. It is worth noting that the above condition for the ratio of ATP-dependent terms also holds for the alternative model in which the C_3(ATP) state is accessed from C_2(ATP) rather than from C₂.

Consideration of Other Kinetic Schemes

A variation on the model given in Fig. 9 would be to assume that C_3(ATP) is accessed from C_2(ATP), rather than from C₂, via an ATP-independent transition. Although the rate constant k₃ will be somewhat smaller in this case, the model is qualitatively the same as that shown in Fig. 9. We also considered models in which more than one ATP molecule interacts with the channel. It is known from previous studies of the effect of ATP on the macroscopic current kinetics that K_ATP channel closure by ATP is a first order process (Qin et al., 1989; Nichols et al., 1991); that is, the closed state is produced by binding of a single molecule of ATP. However, it remains possible that additional ATP molecules may bind to the closed state(s). The Hill coefficient of ATP inhibition will be 1, provided that all states with more than one ATP molecule bound make a negligible contribution to the channel open probability. If this is not the case, and states with two or more ATP molecules bound contribute significantly to the channel open probability, then the Hill coefficient will be >1 (for a discussion of models with more than one ATP molecule bound and Hill coefficients >1, see Nichols et al., 1991). If we assume that an additional ATP molecule can bind to the C_2(ATP) state of our kinetic scheme to produce C_3(ATP)2 rather than binding to C₂ (Fig. 9), then

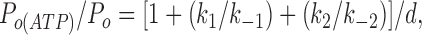where

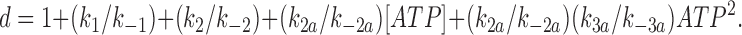Channel activity at different ATP concentrations was calculated from this equation, using the rate constants calculated from measured values determined from the single channel recordings. The relationship between channel activity and [ATP] was the fit with the Hill equation to determine the Hill coefficient of the model; a Hill coefficient close to 2 was obtained. This is greater than that observed experimentally (h = ∼1 in all cases) and leads us to favor the scheme shown in Fig. 9. We cannot exclude the possibility that further ATP molecules do, in fact, bind (for example, to C_2(ATP) or C_3(ATP)), but if this is the case, the closed state(s) they produce must occur very rarely as they are not observed experimentally for the C166S mutation.