Temperature Dependence of Voltage-gated H⁺ Currents in Human Neutrophils, Rat Alveolar Epithelial Cells, and Mammalian Phagocytes

Abstract

H⁺ currents in human neutrophils, rat alveolar epithelial cells, and several mammalian phagocyte cell lines were studied using whole-cell and excised-patch tight-seal voltage clamp techniques at temperatures between 6 and 42°C. Effects of temperature on gating kinetics were distinguished from effects on the H⁺ current amplitude. The activation and deactivation of H⁺ currents were both highly temperature sensitive, with a Q ₁₀ of 6–9 (activation energy, E _a, ≈ 30–38 kcal/mol), greater than for most other ion channels. The similarity of E _a for channel opening and closing suggests that the same step may be rate determining. In addition, when the turn-on of H⁺ currents with depolarization was fitted by a delay and single exponential, both the delay and the time constant (τ_act) had similarly high Q ₁₀. These results could be explained if H⁺ channels were composed of several subunits, each of which undergoes a single rate-determining gating transition. H⁺ current gating in all mammalian cells studied had similarly strong temperature dependences. The H⁺ conductance increased markedly with temperature, with Q ₁₀ ≥ 2 in whole-cell experiments. In excised patches where depletion would affect the measurement less, the Q ₁₀ was 2.8 at >20°C and 5.3 at <20°C. This temperature sensitivity is much greater than for most other ion channels and for H⁺ conduction in aqueous solution, but is in the range reported for H⁺ transport mechanisms other than channels; e.g., carriers and pumps. Evidently, under the conditions employed, the rate-determining step in H⁺ permeation occurs not in the diffusional approach but during permeation through the channel itself. The large E _a of permeation intrinsically limits the conductance of this channel, and appears inconsistent with the channel being a water-filled pore. At physiological temperature, H⁺ channels provide mammalian cells with an enormous capacity for proton extrusion.

introduction

Voltage-gated H⁺ channels were described first in snail neurons (Thomas and Meech, 1982; Byerly et al., 1984), and more recently have been found in mammalian cells (DeCoursey, 1991). A recent burst of interest in this channel has resulted from its proposed role in extruding protons from neutrophils and other phagocytes. During the “respiratory burst,” NADPH oxidase secretes superoxide anion to kill bacteria and simultaneously releases protons into the cytoplasm. Henderson and colleagues (1987, 1988a, 1988b) deduced that electrogenic H⁺ efflux provided the necessary charge compensation, on the basis of pH and membrane potential changes in human neutrophils. The presence of voltage- and pH-activated H⁺-selective channels in human neutrophils was subsequently confirmed by voltage clamp (DeCoursey and Cherny, 1993). Despite increasing interest in this channel, its molecular identity has not been established and numerous questions about the properties and physiological regulation of this channel remain unanswered.

Here we explore the effects of temperature on two fundamental properties of voltage-activated H⁺ channels: pH-dependent gating and H⁺ permeation. Interpreting the results requires distinguishing the effects of temperature on the voltage- and pH-dependent gating mechanism from those on the conductance of the open channel. A recent suggestion that H⁺ currents in murine mast cells have a greater temperature sensitivity than other H⁺ channels (Kuno et al., 1997) led us to examine the temperature dependence in several mammalian cells and cell lines. In addition, it is now clear that the properties of H⁺ channels differ in different cells. We studied H⁺ currents in rat alveolar epithelial cells, rat macrophages, human neutrophils, human monocyte THP-1 cells, human promyelocyte HL-60 cells, and mouse microglial BV-2 cells. These cells include both type e (epithelial) and p (phagocyte) H⁺ channel varieties (DeCoursey, 1998) and 6 of the 17 mammalian cells or cell lines and 3 of 5 mammalian species in which H⁺ currents have been reported. We find similarly high temperature sensitivity in all mammalian cells.

Voltage-gated H⁺ channels are extremely selective for H⁺ (and deuterium), with no detectable permeability to other cations (Barish and Baud, 1984; Byerly et al., 1984; DeCoursey, 1991; Bernheim et al., 1993; Kapus et al., 1993; Demaurex et al., 1993; DeCoursey and Cherny, 1994a, 1994b, 1997; Gu and Sackin, 1995; Gordienko et al., 1996; Kuno et al., 1997). Although the macroscopic conductance increases at lower pH_i, the increase is only 1.7-fold/U decrease in pH_i when measured in inside-out patches (DeCoursey and Cherny, 1995, 1996a ), far less than the 10-fold increase expected if the conductance were proportional to the permeant ion concentration, [H⁺]_i. In contrast, the H⁺ conductance of gramicidin (Akeson and Deamer, 1991; Cukierman et al., 1997) and several other H⁺ permeable channels (reviewed by DeCoursey and Cherny, 1994b ) increases in direct proportion to [H⁺] up to pH ∼0, and then saturates. Thus, the conductance of the voltage-gated H⁺ channel appears to be nearly saturated at pH 7. Because relatively small changes in g _H are seen when either intracellular or extracellular buffer concentrations were varied 100-fold (DeCoursey and Cherny, 1996b ), neither buffer diffusion nor direct proton transfer from buffer to channel can be rate determining steps in conduction. The ratio of H⁺ to D⁺ current was 1.9 at 20°C (DeCoursey and Cherny, 1997), much larger than 1.41–1.52 for the ratio of H⁺ to D⁺ conductivities in bulk solution at 20°C (Lewis and Doody, 1933; Roberts and Northey, 1974). Taken together, these studies suggest that the rate-determining step in H⁺ permeation occurs in the pore rather than in the diffusional approach of either protonated buffer or H₃O⁺. The activation energy (E _a)¹ reported here for H⁺ permeation is large enough to rule out conclusively the possibility that diffusion to the channel is rate determining. That the E _a is as high as for hydrolysis leads to renewed consideration of this mechanism (Kasianowicz et al., 1987) as a possible source for a fraction of the protons that carry current through these channels.

A quintessential feature of all voltage-gated H⁺ channels is the striking dependence of their voltage-gating mechanism on pH_o and pH_i. This interaction was examined systematically in alveolar epithelial cells, where the voltage–activation curve was found to shift −40 mV/U increase in the pH gradient, ΔpH = pH_o − pH_i (Cherny et al., 1995). The threshold voltage at which the g _H is first detectably activated can be predicted from:

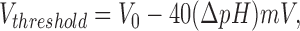1

where V₀ was typically 20 mV (Cherny et al., 1995), or:

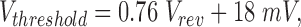2

where V_rev is the observed reversal potential (DeCoursey and Cherny, 1997). The importance of the regulation of gating by pH is that the g _H is activated only when there is an outward ΔpH, thus the channel evidently functions to extrude H⁺ from the cell. We have proposed that the regulation of gating by ΔpH is mediated by internal and external protonation sites, which are accessible only to one side of the membrane at a time, and whose accessibility is governed by a conformational change in the channel molecule that can occur only when the sites are deprotonated (Cherny et al., 1995). The effects of temperature on gating kinetics further elucidate the gating mechanism. The surprising similarity of the Q ₁₀ for activation and deactivation suggests that the same process is rate determining for both opening and closing of H⁺ channels.

materials and methods

Cells

Human neutrophils.

Neutrophils were isolated from normal human blood by density gradient centrifugation (Schmeichel and Thomas, 1987), and kept on ice in nominally divalent-free buffer. Immediately before recording, neutrophils were transferred to the glass recording chamber and superfused with Ringer's solution (see Solutions, below). In some experiments, fresh blood from the authors was studied without purification, and neutrophils were identified visually by their size (∼8 μm diameter) and spherical, granular appearance, as described previously (DeCoursey and Cherny, 1993).

THP-1 cells.

THP-1 cells were obtained from American Type Culture Collection (Rockville, MD). Cells were cultured in suspension in RPMI medium supplemented with 0.29 mg/ml glutamine, 10% fetal bovine serum (Gibco Laboratories, Grand Island, NY), 100 U/ml of penicillin, 100 μg/ml streptomycin, and 0.25 μg/ml Fungizone (Amphotericin B; Gibco Laboratories). Cells were incubated at 37°C in a humidified atmosphere of 5% CO₂ in air. Every 2–3 d, about half of the media was replaced with fresh media, and once per week the cells were removed, centrifuged at 1,800 rpm for 10 min at 4°C in an RT6000 refrigerated centrifuge with an H1000B rotor (both from Sorvall, Newtown, CT). The cell pellet was resuspended in fresh media at 1–2 × 10⁶ cells/ml. THP-1 cells are nonadherent. With maintained weak positive pressure, the pipette was placed on or near a cell, and then suction was initiated.

BV-2 cells.

BV-2 cells were a gift from Claudia Eder (University of California at Irvine, Irvine, CA). The cells were maintained in DMEM with 10% FCS and 1% l-glutamine.

HL-60 cells.

HL-60 cells were obtained from American Type Culture Collection. They were grown in RPMI 1640 media containing 20% FCS. Some cells were studied after treatment with 1% DMSO for 7 d to induce differentiation into granulocytes.

Rat alveolar epithelial cells.

Type II alveolar epithelial cells were isolated from adult male Sprague-Dawley rats using enzyme digestion, lectin agglutination, and differential adherence, as described in detail elsewhere (DeCoursey et al., 1988; DeCoursey, 1990), with the exception that we now use elastase without trypsin to dissociate the cells. Some earlier experiments on cells isolated with trypsin and elastase are included here. Before invasive procedures were initiated, the rats were anesthetized deeply using sodium pentobarbital. In brief, the lungs were lavaged to remove macrophages, elastase was instilled, and then the tissue was minced and forced through fine gauze. Lectin agglutination and differential adherence further removed contaminating cell types. The preparation at first includes mainly type II alveolar epithelial cells, but after several days in culture the properties of the cells are more like type I cells. No changes in the properties of H⁺ currents have been observed during this differentiation process. H⁺ currents were studied in approximately spherical cells up to several weeks after isolation.

Rat macrophages.

Rat macrophages were obtained by lavage during the isolation of type II alveolar epithelial cells. They were studied <1 d after removal from the rat.

Solutions

Most solutions (both external and internal) contained 1 mM EGTA, 2 mM MgCl₂, and 100 mM buffer, with tetramethylammonium methanesulfonate (TMAMeSO₃) added to bring the osmolarity to ∼300 mosM, and titrated to the desired pH with tetramethylammonium hydroxide (TMAOH) or methanesulfonic acid (solutions using bis-Tris as a buffer). The pH 7 and 8 solutions contained 3 mM CaCl₂ instead of MgCl₂. A stock solution of TMAMeSO₃ was made by neutralizing TMAOH with methanesulfonic acid. Buffers (Sigma Chemical Co., St. Louis, MO), which were used near their pK in the following solutions, were: pH 5.5–6.0 Mes; pH 6.5 bis-Tris (bis[2-hydroxyethyl]amino-tris[hydroxymethyl]methane); pH 7.0 Bes (N,N-bis[2-hydroxyethyl]-2-aminoethanesulfonic acid); pH 7.5 HEPES; pH 8.0 Tricine (N-tris[hydroxymethyl]methylglycine). In a few experiments (done 5–6 yr ago), TEA⁺ replaced TMA⁺, and 20 mM buffer was used. Whether TEA⁺ is inert with respect to H⁺ channels is uncertain, but the temperature dependence of the currents appeared consistent with other data using TMA⁺. In a few other experiments, N-methyl-d-glucamine was used as an impermeant cation instead of TMA⁺. The initial bath solution was usually Ringer's solution containing (mM): 160 NaCl, 4.5 KCl, 2 CaCl₂, 1 MgCl₂, 5 HEPES, pH 7.4.

Electrophysiology

Conventional whole-cell, cell-attached, or excised inside-out patch configurations were used. Inside-out patches were generally formed by lifting the pipette into the air briefly. Micropipettes were pulled in several stages using a Flaming Brown automatic pipette puller (Sutter Instruments, Co., San Rafael, CA) from EG-6 glass (Garner Glass Co., Claremont, CA), coated with Sylgard 184 (Dow Corning Corp., Midland, MI), and heat polished to a tip resistance ranging typically from 3 to 10 MΩ. Electrical contact with the pipette solution was achieved by a thin sintered Ag-AgCl pellet (In Vivo Metric Systems, Healdsburg, CA) attached to a silver wire covered by a Teflon tube. A reference electrode made from a Ag-AgCl pellet was connected to the bath through an agar bridge made with Ringer's solution. The current signal from the patch clamp (List Electronic, Darmstadt, Germany) was recorded and analyzed using an Indec Laboratory Data Acquisition and Display System (Indec Corp., Sunnyvale, CA). Data acquisition and analysis programs were written in BASIC23 or FORTRAN. Seals were formed with Ringer's solution in the bath, and the zero current potential established after the pipette was in contact with the cell. Inside-out patches were formed by lifting the pipette into the air briefly.

Pulse duration.

Pulse duration was adjusted at different temperatures with the intent of balancing two opposing factors. Longer pulses tend to provide a better estimate of both gating kinetics and steady state current amplitudes. However, the longer the pulse, the greater the increase in pH_i caused by H⁺ efflux- mediated depletion of protonated buffer from the cell. Depletion directly distorts the H⁺ current waveform and also necessitates long interpulse intervals to allow pH_i to recover. Most whole-cell measurements above 30–35°C were plagued by signs of changes in bulk pH_i due to the massive H⁺ extrusion during voltage pulses, even though we tried to use relatively small and brief depolarizations to avoid this complication. We generally stopped increasing the temperature when pronounced droop of the H⁺ current occurred.

Temperature Control

Bath temperature was controlled by Peltier devices in a feedback arrangement, and was monitored by a resistance temperature detector (RTD) element (Omega Scientific, Stamford, CT) placed in the bath near the cell. Bath temperature was recorded at the end of the pulse just before writing to disk, and was stored with each current record. The maximum rate of change of bath temperature was ∼0.1°C/s. During temperature changes, the temperature often changed during long pulses. We usually stayed for several minutes at temperatures in intervals of 5–10°C to fix the behavior more accurately. Before lowering the bath temperature, we lifted the cell (via the pipette) because otherwise thermal contraction of the copper housing supporting the bath lifted the chamber enough to smash the pipette tip.

Temperature effects on buffer pK_a.

The pK _a of most buffers decreases with increased temperature by 0.01–0.02 U/°C. When we change the temperature, the pK _a of the buffers used to establish the pH of internal and external solutions will change, and consequently H⁺ will be released or bound by buffer. When the same buffer, or buffers with similar temperature dependence, are used in the bath and pipette solutions, temperature will not affect the pH gradient, ΔpH, but will change the absolute pH. However, when buffers with different temperature dependences are used in the bath and pipette solutions, ΔpH (as well as the absolute pH) will change. Most experiments were done with Mes or bis-Tris in the pipette solution, both of which have weaker temperature dependence than the most frequently used extracellular buffers (Bes, less often HEPES, Tricine, or others). Consequently, ΔpH will decrease at higher temperatures, and E _H will generally change less at higher temperatures and in some situations actually decrease (because changes in ΔpH and T in the Nernst equation tend to cancel each other). Over a temperature range spanning 30°C for the buffers used, the largest change in absolute pH is 0.42 U (for Tricine), and the largest net change in ΔpH is ∼0.26 U for pH 8.0//6.5 (Tricine//bis-Tris). Most measurements were done at pH 7.0//5.5 (Bes//Mes), where ΔpH changes 0.04 U/10°C. All solutions are described according to their nominal pH when titrated at room temperature (20–24°C).

Conventions

We refer to pH in the format pH_o//pH_i. In the inside-out patch configuration, the solution in the pipette sets pH_o, defined as the pH of the solution bathing the original extracellular surface of the membrane, and the bath solution sets pH_i. Currents and voltages are presented in the normal sense; that is, upward currents represent current flowing outward through the membrane from the original intracellular surface, and potentials are expressed by defining as 0 mV the original bath solution. Current records are presented without correction for leak current or liquid junction potentials.

Data Analysis

The time constant of H⁺ current activation, τ_act, was obtained by fitting the current record by eye with a single exponential after a delay (as described in DeCoursey and Cherny, 1995):

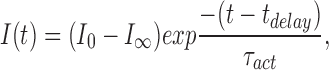where I ₀ is the initial amplitude of the current after the voltage step, I _∞ is the steady state current amplitude, t is the time after the voltage step, and t _delay is the delay. The H⁺ current amplitude (I _H) is defined as (I ₀ − I _∞). No other time-dependent conductances were observed consistently under the ionic conditions employed. The tail current time constant, τ_tail, was obtained by fitting the current with a single exponential:

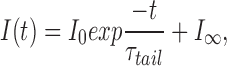where I ₀ is the amplitude of the decaying part of the tail current.

Calculation of Q₁₀ or Arrhenius activation energies.

The relative change in a parameter for a 10°C change in temperature, the Q ₁₀, was calculated by:

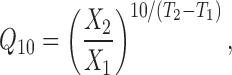3

where X ₂ is the parameter value at the higher temperature T ₂, X ₁ is the parameter value at the lower temperature T ₁. Operationally, we usually extracted Q ₁₀ values by plotting the data on semilog axes, drawing a straight line through the points (by eye or by linear regression), and determining its slope. Data considered less reliable were given lower weight in this process. Arrhenius activation energies were calculated from:

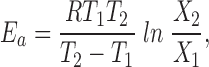4

where R is the gas constant (8.314 J or 1.9872 cal °K⁻¹ mol⁻¹), and T ₁ and T ₂ are in °K (Kimura and Meves, 1979).

results

The amplitude and kinetics of voltage-gated H⁺ currents are strongly temperature dependent. For example, evaporative heat loss from the solution in the recording chamber lowers the temperature by ∼1°C, producing a noticeable change in the H⁺ currents. Fig. 1 illustrates families of H⁺ currents recorded in a human neutrophil at 11, 20, and 36°C (note the different time bases). Increasing the temperature by 25°C increased the H⁺ current amplitude >7-fold and the rate of activation (turn on) of the current with depolarization >20-fold. At all temperatures, H⁺ currents activated during depolarizing pulses with a sigmoidal time course, suggesting that the channel passes through more than one closed state before opening (DeCoursey and Cherny, 1994b ; Cherny et al., 1995). In general, the behavior of H⁺ currents appeared to be fairly consistent at all temperatures; that is, after scaling the amplitude and time scales, there were no obvious changes in the characteristic properties or appearance of the current waveforms.

Figure 1.

Families of H⁺ currents in a human neutrophil at 11, 20, and 36°C. From V_hold = −60 mV, pulses were applied in 20-mV increments from −40 to +40 mV. Bath solution was TMAMeSO₃ at pH_o 7.0; the pipette contained NMGMeSO₃ at pH_i 5.5. The current calibration bar applies to all panels; note the change in time calibration.

Fig. 2 illustrates tail currents and V_rev measurements in the same neutrophil as in Fig. 1. A depolarizing prepulse opened many H⁺ channels, and then the membrane was repolarized to various potentials. The time course of current decay reflects the progressive closing of channels at each potential. The tail current decay was well fitted by a single exponential, giving τ_tail, the time constant. The rate of channel closing (1/τ_tail) is evidently highly temperature sensitive (note the change in time base), as was the rate of channel opening in Fig. 1. When τ_tail was measured over a wide voltage range at different temperatures (Fig. 2 C), the τ_tail–V relationship appeared to scale uniformly at all potentials. Our model (Cherny et al., 1995) predicts a 5% steeper slope of the τ_tail–V relationship at higher temperatures (V.S. Markin, personal communication). However, the measurement is not sufficiently accurate to detect this subtle a change. To a first approximation, the Q ₁₀ of τ_tail is independent of voltage.

Figure 2.

Tail currents at 20.5 (A) and 36.5°C (B) in the same human neutrophil as in Fig. 1 (also at pH 7.0//5.5). The temperature varied several tenths of a degree from pulse to pulse and we have rounded to the nearest half degree. From V _hold = −60 mV, a prepulse to +30 (A) or +20 (B) mV was followed by test pulses to the indicated voltages, shown in 20-mV increments. (C) Voltage dependence of τ_tail at 20.5 and 36.5°C in the same experiment as A and B. The slopes are similar, 39 and 44 mV/e-fold change in τ_tail, respectively, giving an average Q ₁₀ of 8.5 in this cell.

The reversal potential V_rev was determined from tail current measurements like those in Fig. 2, A and B. In the illustrated neutrophil, V_rev was close to −80 mV at both 20.5 and at 36.5°C. The Nernst potential for H⁺, E _H, at nominally pH_o 7.0//5.5, is −87 mV at 20.5°C and −88 mV at 36.5°C after correction for shifts in the true pH due to the temperature dependence of the pK _a of the buffers used (see materials and methods). In other cells, V_rev generally was unchanged or somewhat more positive at lower temperatures. The actual value obtained for V _rev is sensitive to depletion of protonated buffer from the cell by previous pulses, including the prepulse used in standard tail current measurements. Within the reliability of the measurement, temperature does not appear to alter V _rev beyond the small change in E _H predicted by the Nernst equation.

The steady state voltage dependence of the g _H (the activation curve) was generally similar at all temperatures. This result is important partially for technical reasons. The comparison of H⁺ current kinetics at a fixed test potential at different temperatures would become less valid if the P _open were different. A hyperpolarizing shift in P _open at high temperature would tend to artificially enhance the temperature dependence of the activation time constant, τ_act, and perhaps reduce the temperature dependence of τ_tail. The voltage dependence of channel opening is not easy to evaluate quantitatively because the chord conductance (g _H) often does not saturate, the g _H–V relationship is poorly described by a Boltzmann function, whole-cell currents are susceptible to depletion effects, and for other reasons discussed at more length elsewhere (DeCoursey, 1991; DeCoursey and Cherny, 1994a , 1994b ; Cherny et al., 1995). Therefore, several approaches were taken (not all are illustrated). In Fig. 3 A, g _H was determined in an inside-out patch from an alveolar epithelial cell, from the amplitude of an exponential fit to the rising phase of H⁺ currents. Using the fitted amplitude corrects data in which activation did not achieve steady state during the pulse. In this experiment, activation appeared to occur at more negative potentials (by ∼10–15 mV) at higher temperatures. However, both the tremendous increase in gating kinetics, as well as the increase in H⁺ current amplitude, will tend to give this impression, even if there were no true shift. Small changes in ΔpH and E _H due to temperature effects on buffers predict net shifts of a few millivolts in the depolarizing direction at higher temperatures (see Fig. 3, legend). We also looked for changes in V_threshold, the threshold potential at which time-dependent outward current was first detectable. In some experiments, careful examination revealed little or no shift, whereas in other experiments shifts of 5–10 mV occurred, with activation usually occurring at more negative voltages at higher temperatures. The impression gained from these attempts was that any shift in the voltage–activation curve was smaller than could be demonstrated convincingly. We cannot distinguish whether increasing the temperature produced a small (∼10 mV) hyperpolarizing shift or no effect. Likewise, we cannot resolve whether high temperature might have steepened the g _H–V relationship somewhat as predicted by our model (Cherny et al., 1995).

Figure 3.

The voltage dependence of H⁺ current activation does not change much with temperature. (A) Chord conductance–voltage relationship in an inside-out patch from a rat alveolar epithelial cell, at the indicated temperatures, at pH_o 7.5 (pipette)//pH_i 6.5 (bath). The order of measurement was 20, 10, 21, 30, and 40°C. At 40°C, g _H at +20 mV was 1.24 nS (not plotted). Because of the difference in temperature dependence of the buffers used (the pK _a of bis-Tris decreases 0.008/°C and HEPES 0.014/°C), the pH gradient across the cell membrane, ΔpH (pH_o − pH_i), will decrease by 0.06 U every 10°C. Assuming that the g _H–V relationship shifts −40 mV/U increase in ΔpH (Eq. 1), this effect would give rise to a depolarizing shift of 4.8 mV (or 2.3 mV if the g _H–V relation is set by V _rev according to Eq. 2) as the temperature is increased from 10 to 30°C. (B) Voltage dependence of τ_act at various temperatures in the same patch. The lines show the slopes by linear regression, which range from 46 to 64 mV/e-fold change in act and did not change consistently with temperature.

The time course of H⁺ currents, at least for moderate depolarizing pulses, was reasonably well described by a single exponential rise after a delay. Fig. 3 B illustrates the voltage dependence of the activation time constant, τ_act, measured at several temperatures in the inside-out patch shown in Fig. 3 A. As was found for τ_tail, the Q ₁₀ appeared to be independent of the voltage at which the measurement was made. Our model (Cherny et al., 1995) predicts some temperature dependence of the slope of the τ_act–V relationship. However, within the accuracy of the measurement, both kinetic parameters appeared simply to scale uniformly with temperature at all voltages. Similar results were obtained in whole-cell experiments.

To evaluate H⁺ channel gating and conductance over a wide range of temperature, we used a moderate depolarizing test pulse, followed by repolarization either to V_hold or to another voltage at which the tail current decay was resolvable. This pulse protocol permitted obtaining all four parameters nearly simultaneously: τ_act, the delay time, τ_tail, and I _H. As the temperature was varied, the pulse durations were adjusted to resolve the kinetic parameters. Low temperatures required very long pulses (up to 80 s), with the result that the temperature sometimes changed significantly during the pulse. Some hysteresis in the data is to be expected in this situation. Fig. 4 illustrates the temperature dependence of the parameters studied in a rat alveolar epithelial cell. All four parameters have roughly linear temperature dependence (in a semi-log plot), and thus each can be described by a single Q ₁₀. The same data are plotted in Fig. 4 B in a conventional Arrhenius plot in which the slope gives the E _a.

Figure 4.

( A) Temperature dependence of the amplitude and gating kinetics of H⁺ currents in an alveolar epithelial cell at pH 7.0//6.5. Pulses were applied from V_hold = −20 to +50 mV, and then to 0 mV. The durations of these pulses were varied from 0.5–25 s according to the temperature range. The rising currents at +50 mV were fitted by a delay (○) followed by a single exponential to obtain τ_act (•) and the extrapolated H⁺ current amplitude, I _H (♦). Upon repolarization to 0 mV, the tail current was fitted by a single exponential to obtain τ_tail (▴). The delay was the least well defined parameter. The slopes, determined by linear regression, correspond with Q ₁₀ values of 11.9 for τ_act, 7.09 for the delay, 7.51 for τ_tail, and 2.16 for I _H, as illustrated by the lines. (B) Arrhenius plots of the data in A. Plotted against 1,000/temperature (°K⁻¹) are the natural logarithm of 1/delay (○), 1/τ_act (•), 1/τ_tail (▴), and I _H (♦). The slopes, determined by linear regression, correspond with E _a values of 41.7 kcal/mol for τ_act, 33.0 kcal/mol for the delay, 33.3 kcal/mol for τ_tail, and 13.0 kcal/mol for I _H, as illustrated by the lines.

Comparison among Different Cells and Mammalian Species

Fig. 5 illustrates the temperature dependence of the four parameters studied in several types of cells. Several features are immediately apparent. First, the three kinetic parameters, τ_act, delay, and τ_tail are all highly temperature sensitive. A second result that is somewhat unusual in temperature studies on ion channels is that there are no obvious changes in the slopes of these curves. The data were well described by a straight line on the graphs, giving a single Q ₁₀ value over the entire temperature range. Q ₁₀ values from experiments like these are summarized in Table I. The third result evident in both Fig. 5 and Table I is that the three kinetic parameters have nearly the same Q ₁₀. The similarity of Q ₁₀ values for the three kinetic parameters explains why the general appearance of the currents appeared to simply scale with temperature (compare Figs. 1 and 2).

Figure 5.

Temperature dependence of H⁺ current parameters in several cell types. ( A) Temperature dependence of the amplitude and gating kinetics of H⁺ currents in a human neutrophil at pH_o 7.0//pH_i 5.5. From V_hold = −60 mV, pulses were applied to +20 mV with a duration 0.4–8.0 s according to the temperature range. The rising current at +20 mV was fitted by a delay (○), followed by a single exponential to obtain τ_act (•) and I _H (♦). The tail current upon repolarization to −60 mV was fitted by a single exponential to obtain τ_tail (▴). The delay was the least well defined parameter. The slopes, determined by linear regression, correspond with Q ₁₀ values of 4.46 for τ_act, 6.82 for the delay, 4.53 for τ_tail, and 2.33 for I _H, as illustrated by the lines. There was noticeable hysteresis in this experiment, as the temperature was first increased from room temperature (19°C) to 37°C, decreased to 11°C, and then returned to room temperature. As a result of this hysteresis, there is a certain amount of arbitrariness in the evaluation of these data. (B) THP-1 cell at pH_o 7.0//pH_i 5.5. Pulses were applied from V_hold = −60 to +50 mV, and then −30 mV. (C) BV-2 cell at pH_o 7.0//pH_i 5.5. Pulses were applied from V_hold = −80 to −30 mV, and then −80 mV. (D) Inside-out patch from an alveolar epithelial cell at pH_o 7.5//pH_i 6.5. Pulses were applied from V_hold = −60 to +20 mV, and then −40 mV. Because the currents in patches were much smaller than whole-cell currents, the kinetic parameters are less well determined, but I _H is probably more reliable because depletion effects are minimized (see text).

The H⁺ current amplitude increased substantially with temperature. However, its measurement was complicated by several factors. At low temperature, activation was very slow, and the pulses were sometimes not long enough to reach steady state. We extrapolated the fitted exponential rise to obtain I _H. At high temperatures, the currents were quite large and we sometimes observed decay of outward currents above ∼30°C. H⁺ channels do not inactivate (DeCoursey and Cherny, 1994b ), and this decay is almost certainly the result of increased pH_i due to the large efflux of H⁺ comprising current flow (see discussion). Other factors that could artifactually decrease I _H at high temperature include spontaneous clogging of the pipette tip and movement of the cell relative to the pipette due to thermal expansion of the copper support for the chamber (used to transfer heat to the preparation). Because many of these complications can be avoided or minimized using the inside-out patch configuration, we considered this approach to provide the most reliable estimate of the temperature dependence of I _H.

Inside-Out Patch Experiments

Several measurements were made in inside-out patches excised from rat alveolar epithelial cells. Although the smaller current amplitudes compared with whole-cell measurements made the extraction of kinetic parameters less precise, the problems associated with pH_i changes due to depletion of protonated buffer by H⁺ currents are greatly reduced. Fig. 6 illustrates families of H⁺ currents at several temperatures in an inside-out patch. The parameters that could be extracted are plotted in Fig. 5 D, as was done for whole cell data. At higher temperatures, the time-independent “leak” current appears to increase. Because the I _H amplitude is obtained by fitting the current to a delay plus a single exponential, it reflects only the time-dependent component of outward current. If some part of the initial jump in outward current at higher temperature reflects H⁺ current, for example if the decay of capacity current obscures the initial rise in I _H at higher temperatures where activation becomes rapid, then the Q ₁₀ of I _H will be underestimated by this procedure. We could not resolve tail currents well enough to estimate τ_tail reliably over a large temperature range in most patches. The values of τ_act, summarized in Table I, are generally similar to those from whole-cell experiments. Notably different is I _H. The H⁺ current amplitude in patches continued to increase at higher temperatures (instead of saturating above ∼30°C). The Q ₁₀ extracted from patches even in the higher temperature range (>20°C, Table I) was larger than for whole-cell experiments. Because the use of excised patches minimizes depletion problems, we believe that these data are more reliable than those obtained in whole-cell experiments.

Figure 6.

H⁺ current families at 10 ( A), 20 (B), and 30°C (C) in an inside-out patch from an alveolar epithelial cell at pH_o 7.5// pH_i 6.5. In each family, V_hold was −60 mV, and pulses to −20, 0, and +20 mV are illustrated. Note the changes in time calibration. The same current calibration applies to all parts.

The I _H data from patches exhibited clear nonlinearity of the type observed to a lesser extent in whole cell I _H data. In Fig. 7, I _H data from three patches with different current amplitudes are plotted. The Q ₁₀ is 2–3 at 20–30°C, but much larger (4–6) at temperatures below 20°C. The curvature is in the direction that would be attenuated in an Arrhenius plot; however, the Arrhenius plots in Fig. 7 B are still clearly nonlinear, with E _a ∼15 kcal/mol at high temperatures and ∼30 kcal/mol at low temperatures. Activation energies clearly vary depending on the temperature range studied. In Tables I we list values from above and below 20°C.

Figure 7.

Nonexponential temperature dependence of I _H in three inside-out patches from alveolar epithelial cells. ( A) I _H in three patches (one is also plotted in Figs. 5 D and 6). Because the plots are not linear, we arbitrarily fitted the data at <21 (○, •), 21–35 (⋄, ♦), and >35°C (□). Lines determined by linear regression are drawn through the points and Q ₁₀ values are given near the relevant sections of data. (B) The same data in an Arrhenius plot. Although the curvature is slightly less than in A, the plot clearly is steeper at low temperatures. Dots inside the symbols identify the data points used to determine the lines shown. E _a values for the selected sections of data are given near the data.

discussion

The main results are: (a) the rate of activation of the g _H is highly temperature sensitive. The Q ₁₀ for both the delay and τ_act was about the same, ranging from 6 to 9 in various cells. (b) The rate of deactivation also has a high Q ₁₀ of 6–8, practically identical to that for activation. (c) There were no obvious break points in the temperature dependence of the three kinetic parameters studied. (d) The Q ₁₀ of the H⁺ conductance is high, >2 in whole-cell measurements, and 2.8 in inside-out patches >20°C and 5.3 at <20°C. (e) The Arrhenius plot of I _H is nonlinear, being steeper at low temperature. (f) The temperature dependence of both H⁺ currents and H⁺ channel gating kinetics is quite similar in different mammalian cells.

H⁺ Channel Gating Is Steeply Temperature Dependent

Table I summarizes the temperature dependence of three kinetic parameters reflecting channel opening (τ_act and delay) and closing (τ_tail). For all cells studied, the mean Q ₁₀ values were similar, both from one cell type to another, and, more remarkably, for all three kinetic parameters. For other ion channels, opening and closing (τ_act and τ_tail) do not as a rule have the same Q ₁₀ (Table II), and in most cases the Q ₁₀'s of inactivation (or block) and recovery appear to be radically different. The Q ₁₀ values in Table IA for H⁺ currents range from 6 to 9, which inspection of Table II shows is at the upper end of reported values for gating of various ion channels. Most channel gating processes have Q ₁₀ values near 3, generally taken to indicate significant conformational rearrangement of the channel molecule. A high Q ₁₀ for K⁺ channel inactivation was ascribed to interaction between two peptide moieties, at least one of which evidently has a low probability of adopting the correct conformation to permit binding (Murrell- Lagnado and Aldrich, 1993). Alamethicin pore formation (listed as τ_act in Table II) has a Q ₁₀ of 9 at low temperatures. This result is intriguing because alamethicin is believed to form channels in which 6–10 molecules assemble in the membrane in a barrel-stave arrangement (Boheim and Kolb, 1978), reminiscent of one of the hypothetical physical depictions of our gating model, in which several channel protomers assemble in the membrane to form a functional channel (Cherny et al., 1995). Another intriguing parallel is the high Q ₁₀ of a slow gating process in a Cl⁻ channel that, like the H⁺ channel, is gated by its permeant ion, interpreted as reflecting channel subunit interaction (Pusch et al., 1997). In general, the high Q ₁₀ for H⁺ channel gating is compatible with substantial conformational changes in the channel.

Table II.

Q₁₀ Values for Ion Channel Permeation and Gating

Channel		°C		Conductance		τact		τtail		τi		τrecovery		Reference
KIR (frog muscle)		3.5–17.5		1.67		2.45		—		—		—		Almers, 1971
(tunicate oocyte)		5–20		1.44*		—		—		3.41V *		—		Ohmori, 1978
(starfish oocyte)		1–26		1.62H–5.8L		—		—		—		—		Hagiwara and Yoshii, 1980
(guinea pig myocyte)		5–37		1.15		1.45		—		—		—		Martin et al., 1995
(cat cardiac myocyte)		5–37		1.22		1.82		—		—		—		Martin et al., 1995
KV (Xenopus laevis)		5–20		1.2		3.2		2.8		—		—		Frankenhaeuser and Moore, 1963
(Myxicola axon)		5–14		—		2.40		—		3.02β		1.70β		Schauf and Bullock, 1982
(rat muscle)		1–37		1.42		2H–6L		1.7H–11.5L		—		—		Beam and Donaldson, 1983
(human T-cell)		27–37		1.56		3.31		7.09		3.87		9.81		Lee and Deutsch, 1990
(human T-cell)		20–25		1.18*		2.9		—		2.2		—		Pahapill and Schlichter, 1990
ShB K+ peptide		5–20		—		—		—		5.0176		<1.1176		Murrell-Lagnado and Aldrich, 1993
Shaker K+		5–20		1.51		3.14		—		7.2		1.57		Nobile et al., 1997
KCa (human RBC)		0–47		1.50		—		—		—		—		Grygorczyk, 1987
Na+ (X. laevis)		5–20		1.3		1.8		1.7		—		—		Frankenhaeuser and Moore, 1963
(squid axon)		0–16		—		2.35		—		2.7H–4.3L		—		Kimura and Meves, 1979
(rabbit nerve)		0–25		1.7H–4.7L		—		—		3H–33L		—		Chiu et al., 1979
(neuroblastoma)		5.6–14		—		—		—		1.3α *		1.3α *		Yamamoto and Yeh, 1984
(frog muscle)		0–22		—		2.4		—		3.0H–5.3L		—		Kirsch and Sykes, 1987
(rabbit muscle)		0–22		—		2.3		—		3.4H–9.1L		—		Kirsch and Sykes, 1987
AchR (BC3H-1)		10–40		1.26H–1.55L *		3.6*		—		—		—		Dilger et al., 1991
Ca2+ (muscle)		—		1.3–1.6*		∼3.0		∼3.0		—		—		McDonald et al., 1994
CIC-0		9–40		1.4*		—		2.2		∼40		—		Pusch et al., 1997
Alamethicin		−1–32		1.28–1.31		2.9H–9.0L		2.04		—		—		Boheim and Kolb, 1978
Gramicidin (K+, Na+)		3–23		1.38,* 1.34*		—		3.1*		—		—		Hladky and Haydon, 1972
Gramicidin (Na+)		10–40		1.52*		3.09		2.62		—		—		Bamberg and Läuger, 1974
Gramicidin (H+)		15–22		1.33*		—		—		—		—		Akeson and Deamer, 1991
H+ (snail neuron)		10–25		2.1		—		—		—		—		Byerly and Suen, 1989
(mammalian cells)		5–44		2.8H, 5.3L		6–9		6–8		—		—		This study

For a variety of ion channels, Q ₁₀ values are listed for the conductance, and for kinetic parameters reflecting gating transitions: activation, deactivation, and inactivation (in some cases block). Q ₁₀ values not given in original references were calculated from Arrhenius activation energy values or other available data (see materials and methods).  

^*Values for single channel currents, which are not complicated by possible interactions between gating and conductance. Several measurements reflect block, rather than intrinsic gating: ^vvoltage-dependent Na⁺ block,  

¹⁷⁶block by the inactivation peptide, ^βblock and unblock by nonyltriethylammonium ions, ^αblock and unblock by 9-aminoacridine. ^H Q ₁₀ at higher temperatures, ^L Q ₁₀ at lower temperatures.  

Table IA.

Q₁₀ Values for Voltage-gated H⁺ Channels (Mean ± SD)

Cell type		I H		τact		Delay		τtail
PMN		3.06 ± 0.48 (5)		6.1 ± 1.2 (5)		7.1 ± 1.5 (5)		6.4 (1)
THP-1		2.05 ± 0.10 (4)		6.8 ± 2.1 (8)		7.5 ± 2.0 (7)		7.8 ± 1.6 (6)
BV-2		2.07 ± 0.42 (4)		8.9 ± 2.0 (4)		8.8 ± 1.6 (4)		7.8 ± 0.3 (3)
HL-60		2.22 ± 0.47 (3)		6.3 ± 0.8 (3)		5.9 (2)		7.0 (2)
Rat Mφ		2.96 ± 0.98 (3)		7.3 ± 2.6 (3)		8.5 ± 3.7 (3)
Type II		2.35 ± 1.2 (15)		7.4 ± 2.0 (16)		7.0 ± 1.1 (9)		6.2 ± 1.7 (10)
i-o patch		2.8 ± 0.4 (5), >20°5.3 ± 1.1 (4), <20°		8.4 ± 2.0 (6)				5.6 (1)

The average value for the entire temperature range studied in each cell is shown. The temperature dependence of I _H in inside-out patches was often nonlinear (on semilog axes), thus we give values at high or low temperatures. See text for further discussion. In whole-cell data, the nonlinearity was less than the scatter in the data. We excluded data deemed to be unreliable or poorly determined (due to inadequate pulse duration or presumed depletion of protonated buffer from the cell, etc.). PMN, human neutrophils (polymorphonuclear cells); Mφ, rat alveolar macrophage; Type II, rat alveolar epithelial cells (type II when isolated); i-o patch, inside-out patches from rat alveolar epithelial cells. In one outside-out patch from an alveolar epithelial cell, Q ₁₀ values were I _H 1.8, τ_act 7.2, and delay 5.2. Most cells were studied at pH_o//pH_i = 7.0//5.5, but the ranges were type II pH_o 7.0–8.0, pH_i 5.5–6.5; PMN pH_i 5.5–6.0; BV-2 pH_o 5.5–7.0.  

We proposed a model of H⁺ channel gating in which opening requires deprotonation of an externally accessible site(s), followed by a conformational change that shifts the accessibility of the protonation site(s) to the internal side, and finally stabilization of the open configuration by protonation from the inside (Cherny et al., 1995). This model illustrated how gating could be regulated by voltage and the pH gradient, ΔpH (pH_o − pH_i). Although the model is hypothetical, it is difficult to conceive of a mechanism that does not incorporate the general ideas of regulatory protonation sites whose accessibility switches from one side of the membrane to the other. The voltage dependence of gating in our model could arise either from voltage-dependent proton binding to sites inside “proton wells” analogous to those in H⁺ ATPases (Mitchell and Moyle, 1974) or from a voltage-dependent conformational change, as is more typical of voltage-gated ion channels. The protonation/deprotonation reactions at the internal site are rate determining, with the conformational change being rapid and in quasi-equilibrium. Because deuterium slowed activation threefold with only minor effects on deactivation, we suggested that a voltage-dependent closing step might precede the internal deprotonation step (DeCoursey and Cherny, 1997).

In this context, the similarity of Q ₁₀ values for τ_act, delay, and τ_tail was surprising. Although we cannot rule out the possibility that several processes could have the same high E _a, the simplest explanation is that the same energy barrier is rate determining for all three parameters. The energy wells on either side of the barrier must be relatively symmetrical. The E _a for this process is evidently 30–38 kcal/mol, which is substantially larger than any of the proton-related processes listed in Table III. Specifically, the E _a is much larger than 7 kcal/mol for ionization of the imidazole group of histidine (Reeves, 1977), a candidate for the external regulatory protonation site, proposed on the basis of deuterium isotope effects on gating (DeCoursey and Cherny, 1997). In a linear gating scheme, the delay presumably reflects early events in the opening process, τ_act reflects the entire gating sequence, and τ_tail must reflect the final transition between the open state and a neighboring closed state. It appears paradoxical that the same process could determine the relatively rapid tail current decay and the slower activation. A possible explanation for the similarity of E _a for all three kinetic parameters is that each of several channel subunits must undergo an identical or similar complex first-order conformational change during opening, but a reverse transition in only one subunit is sufficient to close the channel. This is essentially the Hodgkin-Huxley (1952) model for Na⁺ and K⁺ channel gating. This hypothesis would also explain the surprising similarity of E _a for the delay, τ_act, and τ_tail. In a multiple independent subunit channel, the ratio of delay to τ_act is fixed (R.W. Aldrich and F.T. Horrigan, personal communication).

Table III.

Activation Energy for Various Proton Events at 18–25°C (or in Ice)

Property		E a (kcal/mol)		Reference
H+ conductance in water		2.6		Robinson and Stokes, 1959
Hydrogen bond strength in water (H2O–H2O)		2.6		Walrafen et al., 1996
Water rotation in water (dielectric relaxation)		4.5		Eigen and DeMaeyer, 1958 *
Water rotation in ice(dielectric relaxation)		8.4		Glasstone et al., 1941
		∼13		Bjerrum, 1952
Proton hopping in ice		9.5		Collier et al., 1984
Bjerrum orientational defect migration in ice		12.0		Collier et al., 1984
Entry of Bjerrum fault into HBC		≤8.0		Nagle et al., 1980
Entry of ionic defect into HBC		∼10–20		Nagle et al., 1980
Self-energy cost of H3O+ permeating a membrane‡		58.6		Parsegian, 1969
Ionization of histidine imidazole		7		Reeves, 1977
Hydrolysis (deprotonation of water)		15.5–16.5		Eigen and DeMaeyer, 1958
Hydration of CO2/dehydration of HCO3 −		17.9–15.6		Sanyal and Maren, 1981
H+ channel conductance (excised patches)		18H, 27L		This study
H+ channel gating (τact, delay, τtail)		30–38		This study

^*Based on several original references cited in the review. HBC, hydrogen-bonded chain; ^Llow temperatures (<20°C); ^Hhigh temperatures (>20°C).  

^‡Assumes dielectric constant ε = 2 and ionic radius = 1.38 Å.  

The temperature dependence of gating was nearly linear in Arrhenius plots.

All three of the kinetic parameters measured had roughly linear temperature dependence over the range 6–42°C. For a constant Arrhenius activation energy, E _a, the temperature dependence in simple semi-logarithmic plots (e.g., Figs. 4 A, 5, and 7 A) is slightly nonlinear, becoming steeper at low temperatures. Our data do not resolve the fine distinction between linearity and the predicted Arrhenius curvature, and appeared linear on both types of plots (compare Fig. 4, A and B). Many studies of other ion channels describe break points in conductance (Lass and Fischbach, 1976; Chiu et al., 1979; Hagiwara and Yoshii, 1980; Quartararo and Barry, 1988) or gating kinetics (Schwarz, 1979; Chiu et al., 1979; Kirsch and Sykes, 1987), which occur at 4–20°C. Others report no clear break points, although the Q ₁₀ increases at lower temperatures (Boheim and Kolb, 1978; Kimura and Meves, 1979; Kukita, 1982; Beam and Donaldson, 1983; Pahapill and Schlichter, 1990). Breakpoints in Arrhenius plots are generally taken to indicate phase transitions of membrane lipids. Krasne et al. (1971) reported that “freezing” artificial bilayer membranes abolished the conductance mediated by the carriers nonactin and valinomycin, but had little effect on the conductance of the gramicidin channel. Here we saw no consistent or reliable evidence of a break point in the temperature dependence of any kinetic parameter. The absence of a break point could mean that H⁺ channel gating is relatively insensitive to the fluidity of the surrounding membrane (see Beam and Donaldson, 1983). A more likely explanation is that the membranes of the cells studied do not exhibit sharp phase transitions in the temperature range studied. The linearity of the Arrhenius plots suggests that the same process is rate determining over the entire temperature range.

Arrhenius plots of I_H are nonlinear.

In contrast to the kinetic parameters, I _H usually changed more steeply at low temperatures, and tended to saturate at high temperature (>30°C). In cells in which I _H saturated, the currents often decayed during the pulse (not shown). H⁺ channels do not inactivate, and this decay is almost certainly the result of increased pH_i due to the large efflux of H⁺ during current flow. Large I _H decreases the driving force by increasing pH_i, as has been demonstrated by changes in V _rev (DeCoursey, 1991; DeCoursey and Cherny, 1994b ), or deduced from pH_i measured by microelectrodes (Thomas and Meech, 1982; Meech and Thomas, 1987) or fluorometric dyes (Kapus et al., 1993). During even moderate depolarizations at high temperature, there was sometimes evidence of depletion. Our interpretation is that high temperature exacerbates the depletion of protonated buffer from the cell (and consequent increase in pH_i), in spite of the high (100 mM) concentration of buffer in all solutions. Thus, the apparent saturation of I _H at high temperature is not ascribable to events occurring near the channel. Higher Q ₁₀ values were obtained for I _H measured in inside-out patches than in whole-cell experiments, whereas Q ₁₀'s for gating kinetics were similar. The most likely explanation is that depletion of protonated buffer due to H⁺ efflux is less problematic in excised patches because there are much smaller diffusion barriers between either side of the membrane and an effectively infinite volume of buffered solution.

Nevertheless, in inside-out patches, which would be less subject to depletion effects, Arrhenius plots of I _H exhibited distinct curvature (Fig. 7 B). The similar temperature dependence of Arrhenius plots of I _H in different patches in which I _H differs by an order of magnitude speaks against bulk depletion (of protonated buffer from the enclosed volume at the tip of the pipette) as a cause of the nonlinearity. Although there was no obvious break point, we cannot rule out the possibility that the membrane fluidity affects I _H. Another interpretation is that nonlinearity of Arrhenius plots of conductance reflects the temperature dependence of the hydration of ions (Kuyucak and Chung, 1994). If entry into the channel requires at least partial dehydration, it will be facilitated at higher temperatures where ions are less hydrated. Entry of a proton into a hydrogen-bonded chain (HBC, see below), which is the putative nature of the H⁺ channel conduction pathway, by definition requires complete dehydration. However, the E _a for breaking a hydrogen bond between water molecules (Table I), even a first shell hydrogen bond with E _a approximately twice that of a second shell hydrogen bond (Agmon, 1996), is too low to account for the E _a of permeation. Finally, nonlinearity of the Arrhenius plot for I _H may indicate that different processes are rate determining in different temperature ranges. For example, the rate-determining step might be hydrolysis or entry of the ionic defect into the channel at high temperature, but permeation at lower temperatures.

I_H Has Abnormally Strong Temperature Dependence

The average Q ₁₀ for I _H in whole-cell measurements was 2.1–3.1 in various mammalian cells, and was higher in patches (Table IA). For reasons discussed above, we consider Q ₁₀ values from inside-out patches to be more reliable for I _H (but less reliable for the kinetic parameters). The Q ₁₀ in patches averaged ∼2.8 at >20°C and increased to 5.3 at <20°C (Table IA). As discussed in the context of Fig. 6, overestimation of the leak current would tend to decrease the apparent Q ₁₀. Temperature effects on the pK _a of buffers will affect these values by changing both the absolute pH and ΔpH. The decrease in pH_i at higher temperature will tend to increase I _H, presumably by ∼1.7-fold/U (DeCoursey and Cherny, 1995, 1996a ). Most of the measurements were made with Bes externally and Mes internally, for which ΔpH will decrease at higher temperatures, essentially offsetting the increase in RT/F. Correcting for the decrease in pH_i at higher temperature lowers the Q ₁₀ values to 2.0–2.9 in whole-cell and 2.6–5.0 in excised patch measurements. These values greatly exceed practically all values reported for ion permeation through other channels (Table II), and thus require some explanation.

An increase in I _H with temperature could reflect increased single-channel conductance or open probability, P _open. If the opening and closing rates had different temperature dependence, P _open would vary with temperature. Three observations indicate that P _open does not change with temperature. First, the g _H–V relationship was not convincingly shifted. Second, the kinetic parameters of gating (delay, τ_act, and τ_tail) and the I _H waveform in general all appeared to simply scale uniformly with temperature. The temperature dependence of neither τ_act nor τ_tail was detectably voltage dependent. Finally, the H⁺ current variance at 20°C increases sharply with depolarization, and then plateaus or decreases with further depolarization (V.V. Cherny and T.E. DeCoursey, unpublished observations), suggesting that for large depolarizations P _open > 0.8 at 20°C, which would severely limit any possible increase at higher temperatures by this mechanism. None of the arguments is conclusive, and none rules out mechanisms in which the number of functional channels changes with temperature. Insertion of channels at high temperature by vesicle fusion can be ruled out because lowering the temperature rapidly reverses the effects of temperature on I _H. Finally, we cannot eliminate the possibility that a rapid gating process (i.e., “flicker”) that is perhaps not in the normal opening pathway might alter the effective unitary current with some arbitrary temperature dependence. In the discussion that follows, we assume that the temperature dependence of I _H reflects changes in unitary conductance.

The H⁺ current is not limited by bulk diffusion.

Limitations to channel permeation can occur at several stages, as delineated for gramicidin by Andersen (1983). The rate-limiting step could occur during diffusion to the mouth of the channel, entry into the channel, permeation through the pore, the exit step, or diffusion away on the distal side. For H⁺ channels, additional possible rate-limiting steps include buffer diffusion, protonation/deprotonation reactions, and hydrolysis. Because varying the external or internal buffer concentrations from 1 to 100 mM changed I _H less than twofold (DeCoursey and Cherny, 1996b ), neither diffusion nor protonation/deprotonation of buffer limits I _H. The present results appear to rule out the possibility that diffusion of free H⁺ is rate determining. This conclusion is consistent with the larger deuterium isotope effect on H⁺ channel currents than on conduction in bulk solution (DeCoursey and Cherny, 1997).

Temperature dependence of H⁺ conduction in water.

The electrical conductivity (ionic mobility) of H⁺ is anomalously higher than that of any other cation, by a factor of ∼5 (Eigen and DeMaeyer, 1958; Robinson and Stokes, 1959). This observation is explained by the unique conduction mechanism for H⁺. The proton in aqueous solution exists mainly (96–99% of the time) in association with a particular water molecule as a hydronium ion, H₃O⁺ (Conway et al., 1956). Any of the three protons may leave this molecule to conduct current. Protons thus hop from one water molecule to the next (de Grotthuss, 1806) by a mechanism referred to as Grotthuss, water wire, or prototropic transfer (Lengyel and Conway, 1983). The activation energy for H⁺ conduction is lower than for other ions, and decreases rapidly with increasing temperature. The Q ₁₀ for H⁺ conductivity, λ⁰, decreases from 1.2 between 5 and 15°C to 1.11 between 35 and 45°C (Landolt-Börnstein, 1960). The conductivity of H⁺ traditionally has been separated into ordinary hydrodynamic conduction (that expected if H₃O⁺ diffused as an invariant molecular species like other ions) and “excess” prototropic conductivity of H⁺; e.g., λ_H ⁺ − λ_Na ⁺ (Hückel, 1928). Hydrogen bonds between molecules facilitate H⁺ conduction by the Grotthuss mechanism. The excess prototropic conduction decreases strongly with increased temperature: (λ_HCl − λ_KCl)/λ_KCl is 2.26 at 273°K and 1.07 at 373°K (Lengyel and Conway, 1983), because the extent of hydrogen bonding in water is decreased by thermal motion (Ewell and Eyring, 1937; Morgan and Warren, 1938). The validity of the common practice of subtracting hydrodynamic from total to obtain the “excess” H⁺ conductance has been questioned recently, on the basis that little conventional hydrodynamic conductance can occur due to the strength of first-shell hydrogen bonds, which trap the H₃O⁺ ion in a densely hydrogen-bonded network of water molecules (Agmon, 1996). In this view, all H⁺ conduction occurs by prototropic transfer. H⁺ permeation through channels most likely occurs by this mechanism.

Permeation is not equivalent to diffusion in bulk solution.

The conductance of most cation channels is weakly temperature sensitive (Table II). A higher E _a has been reported for a lymphocyte K⁺ channel, 8.2 kcal/mol or twice that of free diffusion (Lee and Deutsch, 1990), and even higher values for inward rectifier K⁺ channels, although these higher values are from macroscopic measurements that may reflect factors other than changes in single-channel current amplitude. The Q ₁₀ of the conductivity of physiological monovalent cations (Na⁺ and K⁺) in aqueous solutions is ∼1.2–1.3 between 5 and 35°C, while that of H⁺ is only 1.14–1.20 (Robinson and Stokes, 1959). The similarity of the Q ₁₀ for aqueous diffusion of ions and open channel conductance suggests that ions permeate channels in an environment approximating aqueous diffusion (e.g., Horn, 1984; Stein, 1986). This implies that there are not large energy barriers in the permeation pathway, and the ion should permeate at a rate roughly comparable with its diffusion in bulk solution. The conductance of various channels is somewhat less than calculated from the bulk diffusion coefficient, given the dimensions of the pore (Stein, 1986). Calculated using the Poisson-Nernst-Planck approach, the effective diffusion coefficient of ions inside channels during permeation is roughly an order of magnitude lower than in bulk solution (Chen et al., 1997). Part of the higher E _a for conduction through ion channels than bulk solution may reflect the energetic cost of partial dehydration of the ion; the effective hydration number of ions in solution decreases at higher temperatures, facilitating entry into the channel (Kuyucak and Chung, 1994). The mobility of H⁺ in gramicidin channels, which are single-file water-filled pores (Levitt et al., 1978; Finkelstein and Andersen, 1981), at high [HCl] is not much lower than in bulk HCl solution, suggesting that this water-filled pore offers little additional intrinsic resistance (Cukierman et al., 1997). H⁺ current through single gramicidin channels has a Q ₁₀ of 1.33 (4.8 kcal/mol) at 1 M HCl (Akeson and Deamer, 1991), about twice that of the mobility of H⁺ in bulk solution. Akeson and Deamer (1991) speculated that misaligned hydrogen bonds between waters in the pore might increase the E _a for proton hopping. The recent proposal that the rate-determining step in H⁺ conduction in water is the breaking of second hydration shell hydrogen bonds of strength 2.5 kcal/mol (Agmon, 1995) leads to the idea that entry of H⁺ into a channel must require breaking a first shell hydrogen bond, which would be about twice as strong (Agmon, 1996), consistent with the conclusion that H⁺ permeation through gramicidin is entirely diffusion limited (Decker and Levitt, 1988). The Q ₁₀ for H⁺ permeation reported here is substantially larger, especially considering the uniquely low Q ₁₀ of H⁺ conduction in aqueous solution. Evidently, the rate-limiting step in H⁺ permeation through voltage-gated H⁺ channels is thermodynamically distinct from diffusion.

What is the rate-limiting step in permeation?

Table III compares E _a for voltage-gated H⁺ channels with various processes involving protons. We focus on parameters related to hydrogen bonding and to the two separate processes believed to be required for H⁺ passage through an HBC, namely a hopping step (ionic defect migration) and a turning step (Bjerrum L defect migration, or reorientation/rotation of the elements in the HBC to “reload” for the next H⁺) (Nagle and Morowitz, 1978; Nagle and Tristram-Nagle, 1983). The E _a found for H⁺ permeation through voltage-gated channels, 18–27 kcal/mol, is much larger than the E _a for H⁺ diffusion, 2.6 kcal/mol, and more than double the free energy of water rotation in ice, 8.4 kcal/mol (Glasstone et al., 1941). Of the few processes in Table III with E _a in the range observed here, hydrolysis is intriguing because Kasianowicz et al. (1987) proposed this mechanism to account for the problematic supply of sufficient protons to support the large H⁺ fluxes observed in protonophore-doped membranes. Voltage-gated H⁺ currents verge on being large enough to require this or some other special mechanism to supply H⁺ to the channel (DeCoursey and Cherny, 1996b ).

Could hydrolysis provide enough protons to conduct H⁺ current?

The hydrolysis mechanism is effectively a proton transfer reaction in the energetically unfavorable direction from water, with pK _a 15.7, to a hypothetical protonation site at the inner mouth of the channel, whose pK _a is unknown but likely much lower. If we assume that the reverse reaction is rapid and diffusion limited and occurs at 2.3 × 10¹⁰ M⁻¹ s⁻¹ (Eigen and Hammes, 1963), then the forward reaction rate is determined by the pK _a of the channel (Bell, 1973; Eigen, 1964). The maximum single-channel H⁺ current assuming that all protons come from hydrolysis is then only 0.04 fA for His (histidine); pK _a 6.0), 6.2 fA for Cys (cysteine; pK _a 8.18), and 477 fA for Tyr (tyrosine; pK _a 10.07). The elementary current through H⁺ channels in neutrophils was estimated at ∼1 fA (DeCoursey and Cherny, 1993), and more recent estimates are somewhat larger (V.V. Cherny and T.E. DeCoursey, unpublished observations). Thus the hypothesis that hydrolysis provides most of the protons is plausible only if the entry site has an effective pK _a ≥ 8 (i.e., Cys, Tyr, Lys, Arg). A speculative mechanism that might overcome the limited intrinsic rate of hydrolysis assumes that the H⁺ channel is a metalloprotein. The zinc ion at the catalytic center of carbonic anhydrase greatly lowers the pK _a of the H₂O molecule bound to it, facilitating hydrolysis, as well as electrostatically repelling the nascent proton from the resulting OH⁻ (Liang and Lipscomb, 1988). An attractive feature of hydrolysis is that it would occur at a rate relatively independent of pH, and this could account for the near pH independence of the g _H (Byerly et al., 1984; Demaurex et al., 1993; DeCoursey and Cherny, 1994b , 1995, 1996a ; Cherny et al., 1995).

Entry of the proton into the HBC is not rate limiting.

Entry of the ionic defect into an HBC should have a substantial E _a (Nagle et al., 1980; Table III), comprising the Born electrostatic energy required to insert a charge into a low dielectric membrane/channel and the chemical energy required to protonate a group on the HBC (John F. Nagle, personal communication). The transmembrane movement of each electronic charge e during H⁺ conduction across an HBC is divided into two parts, reducing the Born energy. In ice (Scheiner and Nagle, 1983), 0.64 e is carried across during the H⁺ hopping step and the other 0.36 e is carried during the “turning” step as the HBC reorients to permit the next transfer. The Born energy f ² q ²/(2 a ε) amounts to 7 kcal/mol under reasonable assumptions (Nagle et al., 1980): the fractional charge f = 0.5 because we do not know the nature of the HBC, q = the electronic charge, ionic radius a = 3 Å, and the dielectric constant ε = 2. The chemical energy for a proton to enter the HBC is (pH − pK) × 1.34 kcal/mol. If the group that comprises the mouth of the channel has a much lower pK _a than the ambient pH, entry will be thermodynamically unfavorable and require a high E _a. Generating the large E _a that we observe (Tables IB and III by this mechanism would require a large difference (pH_i − pK) on the order of 8–15 U. The forward rate constant for channel protonation would be too low to result in much current, and we therefore rule out the entry step as rate limiting in permeation.

Table IB.

Activation Energy, E_a (kcal/mol), for Voltage-gated H⁺ Channels (Mean ± SD)

Cell type		I H		τact		Delay		τtail
PMN		18.7 ± 1.2(5)		30.6 ± 3.5(5)		33.3 ± 4.1(5)		31.6 (1)
THP-1		12.5 ± 1.0 (4)		33.4 ± 5.3(8)		35.0 ± 5.0 (7)		35.9 ± 3.9(6)
BV-2		12.6 ± 3.3(4)		38.4 ± 3.7(4)		38.1 ± 3.2(4)		36.4 ± 0.4 (3)
HL-60		13.9 ± 4.1(3)		32.6 ± 2.5(3)		32.2 (2)		32.7 (2)
Rat Mφ		18.5 ± 5.6(3)		34.1 ± 5.3(3)		36.5 (2)
Type II		13.6 ± 6.0(15)		34.3 ± 4.4(16)		33.7 ± 2.0(9)		31.3 ± 4.5 (10)
i-o patch		18.3 ± 2.2(5), >20°27.0 ± 3.6(4), <20°		36.0 ± 4.2(6)				30.0 (1)

Same data as in Table IA expressed in terms of activation energy. The values are not directly interchangeable because different temperature ranges were used in different experiments.  

Permeation is rate determining.

Many types of evidence point to H⁺ permeation through the channel as being rate determining for voltage-gated H⁺ channel current. Even if hydrolysis could provide sufficient protons, it seems unlikely to be rate limiting. I _H does not saturate at large voltages except at low intracellular buffer concentration, and in this situation the apparent saturation probably reflects bulk pH_i changes (DeCoursey, 1991). If increasing the voltage increases the current, then the rate-determining step must be voltage dependent. Entry into or exit from the pore could conceivably appear voltage dependent if permeation occurred as a collective event, a possibility suggested by the high proton polarizability of numerous hydrogen-bonded systems (Zundel, 1992). However, entry/exit could not appear voltage dependent if this were the rate-limiting step. Permeation across an HBC might involve a large E _a. Because both the hopping and turning steps in HBC conduction carry fractional charges (Scheiner and Nagle, 1983), both would be voltage dependent and either could be rate determining.

A high energy barrier to proton permeation might be traversed by tunneling. In this case, the deuterium isotope effect on permeation would likely be large (e.g., 67) (Conway et al., 1956; Crooks, 1977), whereas we observed only a 1.9 H⁺/D⁺ ratio (DeCoursey and Cherny, 1997). The Arrhenius slope should also be somewhat steeper in deuterium (Bahnson and Klinman, 1995). In preliminary attempts, we observed E _a for permeation (and gating) in D₂O that were in the upper range of values in protium solutions. More careful investigation of this question is warranted, but at present there is not strong evidence that tunneling is rate limiting.

Although its high E _a appears to place H⁺ channel permeation in the realm of pumps and carriers, H⁺ currents require neither ATP nor co- or counter-ions. A simple carrier mechanism for permeation seems unlikely. Unless the deprotonated form of the carrier is effectively uncharged, it will tend to accumulate on one side of the membrane at extreme voltages, giving rise to a bell-shaped voltage dependence, as recently described for H⁺ translocation by the voltage sensor of K⁺ channel (Starace et al., 1997). We conclude that permeation through the H⁺ channel is an arduous undertaking for a proton, with a large E _a that intrinsically limits the conductance of this channel.

Are H⁺ channels water-filled pores?

We have suggested that voltage-gated H⁺ channels are unlikely to be water-filled membrane-spanning pores (DeCoursey and Cherny, 1994b , 1995, 1997; Cherny et al., 1995). Three types of evidence support this conclusion. (a) Voltage-gated H⁺ channels are extremely selective, with no detectable permeability to cations other than H⁺ or D⁺, and permeability ratios P _H/P _cation > 10⁶ − 10⁸, calculated from deviations of V _rev from E _H (Kapus et al., 1993; Demaurex et al., 1993; DeCoursey and Cherny, 1994b , 1997; Cherny et al., 1995). A water-filled pore would be expected to have detectable permeability to other cations because H₃O⁺ and K⁺ have nearly identical radii. (b) The unitary H⁺ channel conductance appears to be near saturation at pH 7.5, eight orders of magnitude lower [H⁺] than at saturation of H⁺ current through other water-filled ion channels (DeCoursey and Cherny, 1994b ). (c) The H⁺/D⁺ conductance ratio is 1.9 at 20°C (DeCoursey and Cherny, 1997), much greater than 1.35 in the prototypical water-filled channel gramicidin (Akeson and Deamer, 1991). Some uncertainty is introduced by the possibility that the water molecules in a pore are constrained by interactions with the walls (e.g., Nagle et al., 1980; Gutman et al., 1992). Molecular dynamics simulations indicate that rotational relaxation rates for water molecules confined inside narrow channels are reduced compared with bulk (Sansom et al., 1996). Ab initio molecular orbital calculations (Scheiner, 1981) show that the E _a for proton transfer between hydrogen-bonded chains of water molecules increases dramatically and superlinearly if the inter- oxygen distance is increased or the bond angles are deformed, and theoretically could be as large as found here. The deuterium isotope effect on conduction is much larger in ice than in liquid water (Kunst and Warman, 1980). Table III shows that the E _a for some of the steps likely involved in H⁺ conduction through a water-filled pore (water rotation, proton hopping, and defect migration) is increased severalfold in ice. Even so, the E _a observed here for I _H remains about double any of these values, suggesting that if the H⁺ channel were a water-filled pore, then it must constrain the water molecules more tightly than in ice. a and b above remain hard to reconcile with the idea of a water-filled pore, although waters rigidly frozen inside the channel could prevent other cations from permeating. On balance, we favor the idea that the channel does not contain a continuous chain of waters that span the membrane.

Hydrogen-bonded chain.

The alternative to a water-filled pore is a hydrogen-bonded-chain, a continuous “proton wire” comprising some combination of side groups of amino acids and possibly intercalated water molecules. (We imply the presence of substituents other than water in our use of the term HBC, although a pure “water wire” is formally just a special type of HBC). The HBC mechanism was proposed by Nagle and colleagues for other biological H⁺ channels such as those in bacteriorhodopsin and in H⁺ATPases of mitochondria and chloroplasts (Nagle and Morowitz, 1978; Nagle and Tristram-Nagle, 1983). Comparison of the Q ₁₀ for H⁺ translocation through other membrane proteins (Table IV) generally suggests that H⁺ transporters that involve conduction via hydrogen-bonded chain mechanisms that include protein groups (such as bacteriorhodopsin, the H⁺ channel of proton pumps, and MotA) tend to have substantially higher Q ₁₀ than does H⁺ permeation through the water-filled gramicidin pore. The high Q ₁₀ observed here for I _H suggests the existence of significant energy barriers in the permeation pathway. Although we consider a simple water wire to be unlikely, the hydrogen-bonded chain comprising the permeation pathway certainly could include intercalated water molecules, as demonstrated recently for bacteriorhodopsin (Pebay-Peyroula et al., 1997). The M2 viral proton channel may comprise a water-filled pore with a single constriction, occluded by His groups that shuttle protons by a tautomerization (ring flipping) mechanism (Pinto et al., 1997). Although the temperature dependence of its conductance is not known, the rate-determining step in CO₂ catalysis by carbonic anhydrase is an intramolecular proton transfer from Zn-bound water to His (Liang and Lipscomb, 1988; Taoka et al., 1994), with E _a ∼8 kcal/mol (Ghannam et al., 1986). In summary, the high Q ₁₀ of H⁺ permeation strengthens the case that the voltage-gated H⁺ channel is not a water-filled pore like other ion channels. Entry into the channel may consist of simple protonation of the end of an HBC. This may explain the paucity of inhibitors of this conductance—there is no pore to occlude. The main inhibitors of H⁺ currents are polyvalent cations, which may bind to the putative proton entry site or near enough to it to lower the local [H⁺] electrostatically.

Table IV.

Q₁₀ Values for Other H⁺ (or Non-H⁺)^* Transporters

Transporter		Range		Q 10		Reference
		(°C)
Passive currents
H+ conductvity, water		18–25		1.17		Robinson and Stokes, 1959
H+/OH− permeability, renal		25–40		1.30		Ives, 1985
Gramicidin: H+ current		15–22		1.33		Akeson and Deamer, 1991
Gramicidin: Na+ current*		0–25		1.56*		Althoff et al., 1989
CF0 H+ channel conductance		0–25		1.89		Althoff et al., 1989
Water channel H2O flux*		4–37		1.24		Dempster et al., 1992
Carriers
Na+-H+ antiport		25–37		1.22		Graber et al., 1992
		25–40		1.85		Ives, 1985
Nonactin		42–48		4.23		Krasne et al., 1971
Valinomycin*		0–25		2.61*		Althoff et al., 1989
Na+ glutamate co-transport		8–18		1.95		Schwartz and Tachibana, 1990
Malonate flux (mitochondrial anion channel)*		5–45		1.3–13		Lie et al., 1996
Glucose facilitated diffusion (protozoan)*		20–33		2.33*		Wille et al., 1996
Intramolecular H+ transfer, carbonic anhydrase II		5–30		1.6		Ghannam et al., 1986
Proton shuttle on K+ channel voltage sensor		16–30		2.6		Starace et al., 1997
Pumps (turnover rate)
H+-ATPase		13–40		2.1		Bidani et al., 1994
MotA H+ flux		16–32		2.1–2.5		Meister et al., 1987; Blair and Berg, 1990
Bacteriorhodopsin		5–40		1.33–3.37‡		Cao et al., 1995
Na,K-ATPase*		5–37		3.0–5.7*		Ellory and Willis, 1982
Na,K-ATPase*		5–35		2.4H–5.3L *		Hakao and Gadsby, 1986; Apell, 1997

^*These measurements are not for H⁺ transport.  

^‡Range of activation enthalpies for five kinetic components of H⁺ transfer in the M intermediate and for H⁺ release.  

Physiological relevance.

At room temperature, mammalian voltage-gated H⁺ channels open very slowly in comparison with most ion channels, although other slow channels exist, such as the cardiac delayed rectifier. Mammalian H⁺ channels and those in molluscan neurons differ mainly in activation kinetics (DeCoursey, 1991, 1998), the latter opening in a few milliseconds (Byerly et al., 1984). The strong temperature dependence of gating means that mammalian H⁺ channels activate 20–40× faster at body temperature than at room temperature. When the high Q ₁₀ of I _H is also considered, it is clear that H⁺ channels are capable of rapid and highly efficient acid extrusion. The combined effect of the high Q ₁₀ for I _H and for gating means that the g _H will be activated much faster at body temperature than at room temperature, where most studies of H⁺ currents have been done.

Comparisons among different cells and mammalian species.

A final point to emerge from this study is that the temperature sensitivity of H⁺ currents and several kinetic measures of H⁺ channel gating are quite similar in human neutrophils, THP-1 monocytes, and promyelocytic HL-60 cells, mouse BV-2 microglial cells, and rat alveolar epithelial cells and macrophages. A recent study reported highly temperature sensitive H⁺ currents in murine mast cells, with a Q ₁₀ of 6.0 or 9.9 for the outward current at the end of voltage ramps at pH_i 5.5 or 7.3, respectively (Kuno et al., 1997). This high sensitivity appeared to distinguish the H⁺ channel in mast cells from that in other cells for which little data had been published. However, the H⁺ current amplitude at the end of a voltage ramp depends on both the conductance and gating kinetics—at low temperatures, fewer channels will open during the ramp. In the present study, we distinguished between effects of temperature on gating and on open channel conductance. Once this separation was made, it became apparent that the temperature sensitivity of both conductance and gating is similar in all cells in which these properties have been studied. Although there are distinct varieties of H⁺ channels (DeCoursey, 1998), their temperature sensitivity does not differ obviously. Byerly and Suen (1989) reported a Q ₁₀ of 2.1 for whole-cell I _H in snail neurons. Because activation is very rapid in Lymnaea, this value is a relatively pure reflection of I _H uncontaminated by gating effects, and is well within the range observed for the Q ₁₀ of I _H in mammalian cells (Table IA). These observations provide no evidence for significant differences in either the mechanism of H⁺ permeation or the rate-determining steps in gating in various types of H⁺ channels.

Abbreviations used in this paper: E

_a

activation energy

E_H

Nernst potential for H⁺

g_H

H⁺ chord conductance

HBC

hydrogen-bonded chain

I_H

extrapolated H⁺ current amplitude

V_hold

holding potential

V_rev

measured reversal potential