The Calcium Sensitivity of Individual Secretory Vesicles Is Invariant with the Rate of Calcium Delivery

Abstract

Differences in the calcium sensitivity of individual secretory vesicles can explain a defining feature of calcium-regulated exocytosis, a graded response to calcium. The role of the time dependence of calcium delivery in defining the observed differences in the calcium sensitivity of sea urchin egg secretory vesicles in vitro was examined. The calcium sensitivity of individual secretory vesicles (i.e., the distribution of calcium thresholds) is invariant over a range of calcium delivery rates from faster than micromolar per millisecond to slower than micromolar per second. Any specific calcium concentration above threshold triggers subpopulations of vesicles to fuse, and the size of these subpopulations is independent of the time course required to reach that calcium concentration. All evidence supports the hypothesis that the magnitude of the free calcium is the single controlling variable that determines the fraction of vesicles that fuse, and that this fraction is established before the application of calcium. Submaximal responses to calcium cannot be attributed to alterations in the calcium sensitivity of individual secretory vesicles arising from the temporal properties of the calcium delivery. Models that attempt to explain the cessation of fusion using changes in the distribution of calcium thresholds arising from the rate of calcium delivery and/or adaptation are not applicable to this system, and thus cannot be general.

introduction

Calcium has long been recognized as an essential intracellular messenger involved in many pivotal biochemical pathways. The biochemically relevant information attributed to this ionic species is believed to be encoded in the concentration and spatio-temporal properties of the calcium signal. The relationship that exists between calcium and the regulated response has been attributed to the complexity of the calcium signal triggering the physiological response (Knight and Baker, 1987). In this paper, we focus on one of the temporal properties of the calcium signal, the rate of calcium delivery. The role of the time dependence of calcium delivery in defining the observed differences in the calcium sensitivity of sea urchin egg secretory vesicles was examined. No evidence was found to support the hypothesis that the calcium sensitivity of individual secretory vesicles is dependent upon the rate of calcium delivery.

Since a graded response to calcium represents a defining feature of calcium-regulated exocytosis, several classes of limiting mechanisms have been proposed. These include heterogeneity in the calcium sensitivity of individual vesicles, calcium-dependent inactivation, and rate-dependent inactivation through a calcium-dependent intermediate (Knight and Baker, 1982). Recently, adaptation has been proposed as a property of calcium-regulated exocytosis in presynaptic terminals in which the sensitivity of synaptic vesicles to calcium was reported to decrease in response to either multiple exposures or different rates of calcium (Hsu et al., 1996). Our result that the calcium sensitivity of secretory vesicles is invariant with the rate of calcium delivery supports the hypothesis that the calcium sensitivity of individual vesicles within a population of exocytotic vesicles is heterogeneous before initiating the fusion process (Blank et al., 1998) and that the magnitude of the calcium stimulus is the single controlling variable that determines which subpopulations of vesicles enter the fusion process. These results are incompatible with several classes of models that have been used to describe calcium-regulated exocytosis.

materials and methods

Materials and methods related to the use of the two specimens of sea urchins, Stronglyocentrotus purpuratus and Lytechinus pictus are described in the companion paper (Blank et al., 1998). The rate of calcium delivery was varied using either perfusion or UV photolysis of DM-nitrophen (Kaplan and Ellis-Davies, 1988). The time-dependent increase in calcium at the sample is referred to as a calcium “ramp” even if the change in calcium activity with time was not linear. Since the calcium concentration can never change instantaneously, there will always exist a period of time over which the calcium concentration varies. Turbulent exchange of solutions within the flow chamber, described in the companion paper (Blank et al., 1998) and referred to as a calcium “step,” corresponds to a calcium ramp occurring in <300 ms.

Calcium ramps generated using a gradient maker (385; Bio-Rad Laboratories, Hercules, CA) and a peristaltic pump (7445-10 with 7013-20 Head; Cole Parmer Inst. Co., Vernon Hills, IL) operating at a flow rate of 3.5 ml/min and total volumes of 40, 80, or 120 ml correspond to linear gradients of total calcium lasting ∼11, 23, and 34 min, respectively. Light scattering from a dilute suspension of 0.1 μm polystyrene latex spheres was used to verify the linearity of the ramp with respect to the mixing of the two compartments. The calcium activity along the ramp ranged from nominally zero to >10 mM and was roughly linear in pCa as determined by discrete sampling at different time points and subsequent measurement using a calcium electrode as described previously (Blank et al., 1998). If both the initial solution composition and the rate of removal from the gradient mixer are kept constant, then the temporal response of the sample to ramps created using different total volumes can be compared by renormalizing time to the beginning and ending of the ramp. This normalization procedure provides a relationship between the calcium concentration at the sample and the fusion response. Fusion change in response to a calcium ramp is designated the “dynamic response.” Ramps are useful for comparing manipulations that are believed to alter the calcium dependence of exocytosis and conditions where the calcium dependence of exocytosis may be different. However, depending upon the rate of delivery, it may be inappropriate to use calcium ramps to determine the steady state calcium dependence of vesicle fusion or the kinetics of fusion.

For a given ramp protocol, variability between experiments was observed. These differences were due to errors in precisely defining the zero time point, reproducing the exact volume flow rate, and perhaps to variability in the distribution of thresholds between preparations. The pH of samples taken at different time points dropped by a maximum of only 0.15 U for the standard solutions containing 50 mM PIPES, and was constant for solutions containing 100 mM PIPES. Increasing pH buffering capacity did not affect the fusion response to the calcium ramp. Since treatment with pH 6.0 solutions (but not pH 6.4) results in vesicles that do not fuse (data not shown), care must be taken to avoid conditions that lead to acidification of the preparation as pH-dependent effects could be mistaken for calcium-dependent effects.

Calcium ramps generated using photolysis of DM-nitrophen, as described in Shafi et al. (1994), correspond to an ∼60 μM change over ∼1 s, a rate of delivery intermediate between turbulent exchange and slow perfusion. Photolysis of DM-nitrophen was required to evaluate the relationship between changes in calcium concentration and the first fusion event after an initial fusion response, because transient flexing of the chamber during turbulent exchange alters the optical path. The change in optical path during turbulent exchange makes it difficult to evaluate when the first fusion event occurs because the high volume flow (∼8 ml/s) lasts, typically, for 0.5 s. This limitation does not exist with photolysis.

Free calcium concentrations are estimated using the fluorescent indicator, Rhod-2 (Molecular Probes, Inc., Eugene, OR) and calibrated as described previously (Shafi et al., 1994). Error in the estimation of the free calcium concentration arises primarily from error in K _d, contributions from fluorescence beyond the plane of focus, and misregistration between the planes of UV and fluorescence excitation and emission. Propagation of the error in K _d (4.0 ± 0.8 μM; Shafi et al., 1994) leads to an error of ∼0.2 pCa U. The other two optical properties are expected to bias the determinations towards an underestimation of the calcium concentration. For calcium concentrations in the neighborhood of the midpoint of the calcium activation curve, the uncertainty in K _d introduces an uncertainty in the estimation of the free calcium concentration by a factor of ∼2. In the photolysis double challenge experiments, light scattering and fluorescence were monitored simultaneously during a transient increase in calcium (first challenge) and increases to high concentrations (>500 μM, second challenge). The first detectable fusion event during the second challenge was correlated with the calcium concentration. The criteria for the first detectable fusion event was the first light scattering (% fusion) value outside the envelope defined by ±5% fusion. This range in fusion, ±5% fusion, corresponded to the steady state peak to peak noise in the light scattering signal. This criteria represents a conservative estimate for detection and places an upper limit on the calcium concentration required for subsequent fusion in the photolysis double-challenge protocol. The results from a total of 30 perfusion ramps and 48 photolysis ramps are reported.

results

The average dynamic response of S. purpuratus and L. pictus to an 11-min ramp in the total calcium is shown in Fig. 1 A. The dynamic response of L. pictus, compared with S. purpuratus, is shifted in time, indicating that higher calcium concentrations are required for the same response (Fig. 1 B). The time to 50% response is significantly different between the two species (4.75 ± 0.12 and 5.40 ± 0.19 min for S. purpuratus, n = 6, and L. pictus, n = 2, mean ± SEM or range, respectively). This phenotypic variation with species is consistent with the shift in the calcium activity curves measured using step changes in calcium (Blank et al., 1998). For the same rate of calcium delivery, S. purpuratus is more sensitive to calcium than L. pictus.

Figure 1.

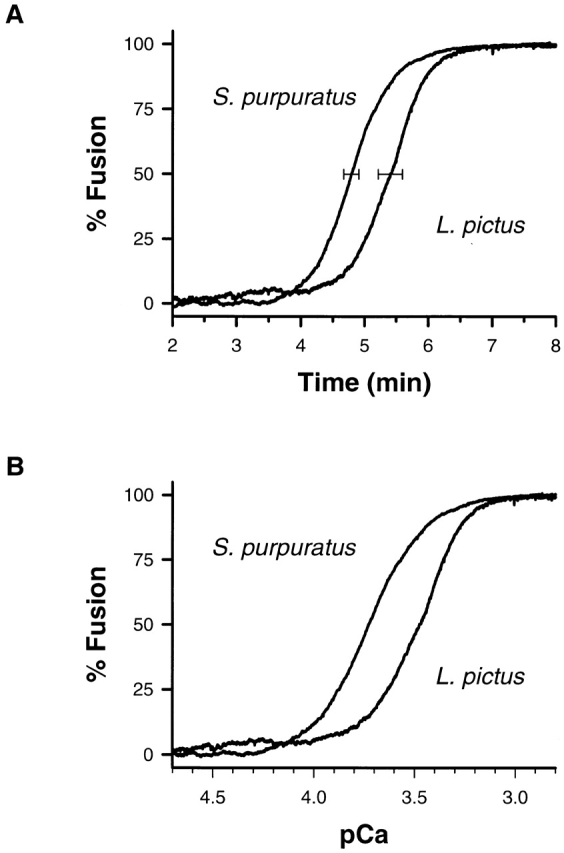
Average dynamic response of S. purpuratus and L. pictus to an 11-min ramp. (A) The time dependence between 2 and 8 min is shown. The time to 50% response is significantly different between the two species. (B) The same response with the time axis normalized to represent the calcium concentration in the chamber is shown.

The dynamic responses observed using these ramps were shifted along the pCa axis compared with the stable, submaximal responses obtained with step changes in the calcium concentration (Blank et al., 1998). This shift is expected if overlap between the characteristic times associated with the exocytotic process and the calcium ramp is significant because the dynamic response is strongly influenced by the convolution of the calcium delivery with the underlying fusion kinetics. Vesicle fusion, detected at a later time, may have entered the fusion process at an earlier time in response to a lower calcium concentration. Whether this shift is secondary to the relationship between calcium and the extent of fusion was tested. If the calcium-delivery history has no effect on the steady state extent of fusion, then interrupting the ramp and holding the calcium concentration constant should result in extents of fusion identical to those produced by step changes to the same calcium concentration.

The dynamic response to an 11-min ramp with and without interruption is shown in Fig. 2. Interrupted ramps resulted in 70 ± 9% (mean ± SEM, n = 3) fusion at a calcium concentration of ∼60 μM. Interrupting the ramp and maintaining the preparation at this calcium concentration produced submaximal extents of fusion that are indistinguishable from those produced by step changes to the same calcium concentration. This is indicated by the overlap of the interrupted ramp data with the calcium activation curve described by the log-normal cumulative distribution function (this paper, see Fig. 8 A, ▪; Blank et al., 1998, Fig. 7 A). For these experiments, the more highly buffered solution (6 mM EGTA, 6 mM HEDTA, 3 mM nitrilotriacetic acid) was used. To what extent, if any, is the behavior of the unfused vesicles altered by the kinetics of calcium delivery?

Figure 2.

Interrupted ramp. Interrupting a calcium ramp (arrow) and maintaining this calcium concentration (solid line) results in submaximal extents of fusion that are indistinguishable from those produced by step changes to the same calcium concentration. See Fig. 8 A.

Figure 8.

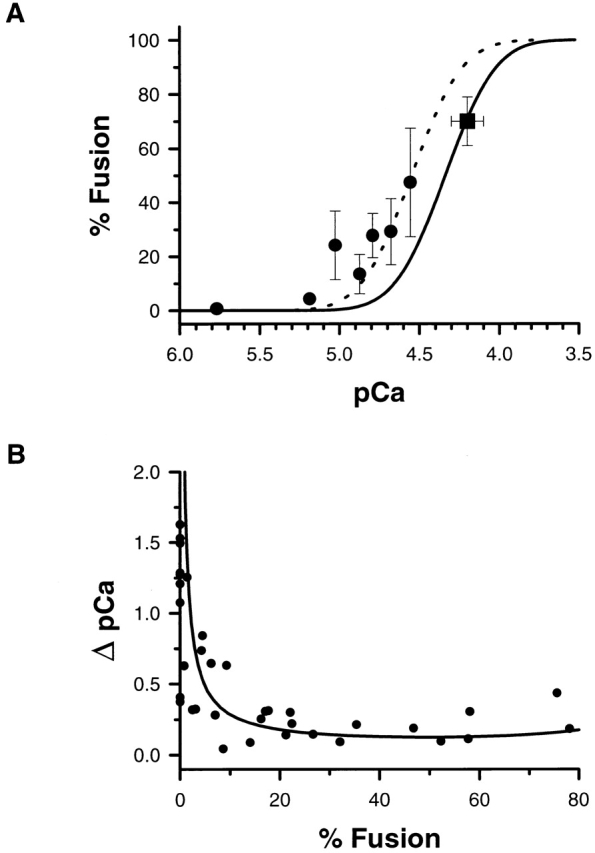
(A) Overlap between the extent of fusion after an interrupted ramp (▪) and the underlying calcium activity curve derived from step changes in the calcium concentration (solid line). Overlap between the extent of fusion after short pulses of UV (•) and the underlying calcium activity curve derived from step changes in the calcium concentration shifted by 0.2 pCa units (dotted line). This shift in the activity curve is consistent with the known errors in determining the free calcium concentration using Rhod-2 fluorescence and is not significant. (B) The change in calcium (ΔpCa) required to detect a 10% change in fusion beginning at any initial value of fusion is shown (solid line). The curve is derived from the log-normal cumulative distribution function that describes the calcium activation curve (d% fusion/d pCa) and the points represent the data from individual photolysis experiments.

Figure 7.

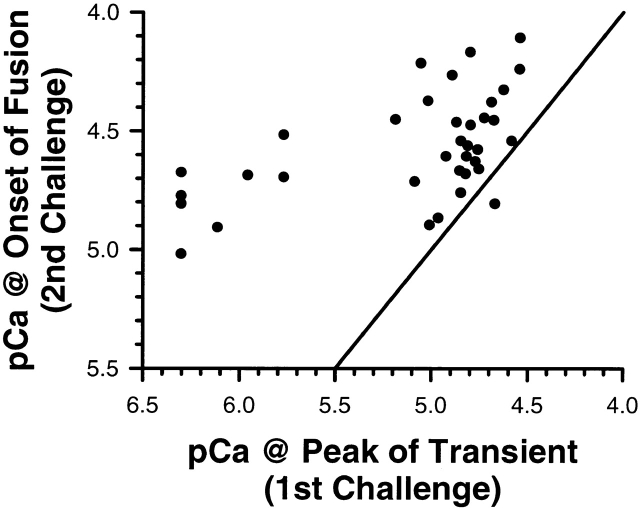
Correlation between calcium challenges. The correlation between the calcium in the first challenge and the calcium at the onset of fusion after the second challenge is shown. All points, except one, lie to the left of the identity line, indicating that a higher calcium concentration is required for subsequent fusion.

After the establishment of a stable, submaximal extent of fusion, the calcium ramp was continued and the exocytotic response of the remaining vesicles was compared with the response obtained from a continuous ramp. When the time axis is rescaled to the concentration of calcium present at the sample, no systematic shifts in the response are observed for interrupted and continuous ramps. The pCa at 85% fusion in the dynamic responses of the interrupted and continuous ramp are identical (pCa_85% = 3.88 ± 0.05). As a further test, the shape of the dynamic response was compared by rescaling the time axis after continuation of the interrupted calcium ramp. The rescaled plot of the final 30% fusion for interrupted and continuous ramps is shown in Fig. 3 A. The slope of the cross-correlation between the fusion response for interrupted and continuous ramps using normalized time as the parametric variable is 1.01 ± 0.00 (Fig. 3 B). There are no significant differences between the dynamic response of the remaining unfused vesicles in either a continuous or interrupted calcium ramp.

Figure 3.

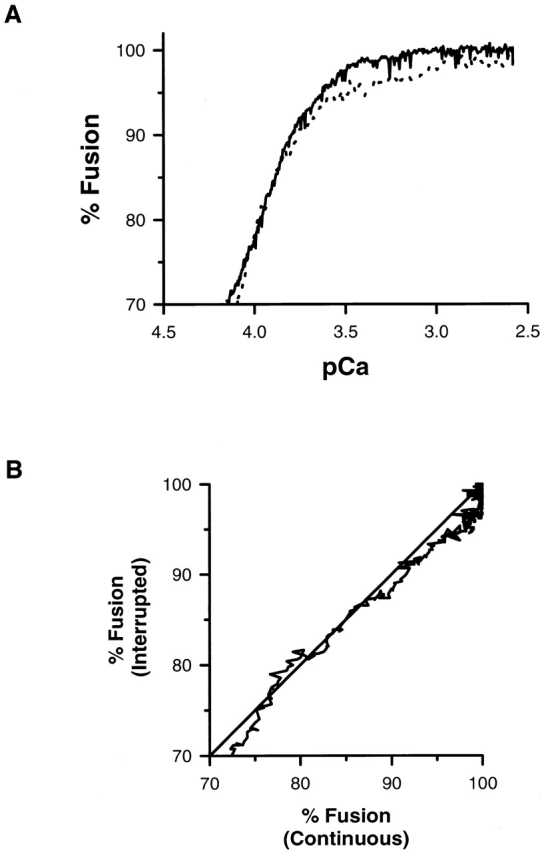
Continuation of an interrupted ramp. (A) The dynamic response of the remaining unfused vesicles is not altered when the ramp is continued. (B) The slope of the cross-correlation between the last 30% fusion response for interrupted (solid line) and continuous (dotted line) ramps using normalized time as the parametric variable is not significantly different from one. The identity line is included for comparison.

If the cessation of fusion occurs because a specific population of vesicles is removed through fusion, then changing the rate at which a defined concentration of calcium is delivered may alter the fusion kinetics but not the underlying relationship between calcium and the extent of fusion. This hypothesis was tested by altering the buffering properties of the solution, total concentration of calcium in the second chamber of the gradient maker, or increasing the ramp duration from 11 to 34 min. Examples of the dynamic response to both 11- and 23-min ramps are shown in Fig. 4 A. When the time axis is rescaled to the concentration of calcium present at the sample, no systematic shifts in the response are observed and 100% fusion is always obtained (Fig. 4 B). The difference in pCa at 50% fusion in the dynamic response to the two ramps is not significant (pCa_50% = 3.49 ± 0.05 and 3.57 ± 0.05 for 11- and 23-min ramps, respectively, P < 0.05). As a further test, the shape of the dynamic response was compared by rescaling the time axis about 50% fusion after renormalizing the time axis by the gradient volumes. This converts the time axis to an axis proportional to the extent of the ramp where 0 and 1 correspond to the concentrations at the beginning and end of the ramp. If the dynamic response is invariant to the delivery rate, then the slope of the cross-correlation between the two different fusion responses will be one. The slope of the cross-correlation between the fusion response at the two different calcium-delivery rates using normalized time as the parametric variable is 0.97 ± 0.00; the fusion response is invariant to a factor of two in the rate of calcium delivery.

Figure 4.

Response to a calcium ramp generated by perfusion. (A) The dynamic response to calcium ramps of identical magnitude but different rates of delivery. (B) The difference in pCa at 50% fusion in the dynamic response to the two ramps is not significant. The slope of the cross-correlation between the fusion response at the two different calcium-delivery rates using normalized time as the parametric variable is consistent with no significant differences between the dynamic response for 11- and 23-min ramps.

Calcium ramps generated using different UV excitation intensities resulted in calcium ramps intermediate between turbulent exchange and slow perfusion. Examples of the average dynamic response to different photolysis-derived ramps (n = 6) is shown in Fig. 5 A. The UV excitation intensity was varied using a glass plate. No systematic shifts in the response are observed when the time axis is rescaled to the concentration of calcium present at the sample using time as the parametric variable; the two traces overlap (Fig. 5 B). The dynamic response was not altered by changes in the rate of calcium delivery intermediate between turbulent exchange and slow perfusion.

Figure 5.

Response to a calcium ramp generated by photolysis. (A) The dynamic response to calcium ramps of identical magnitude but different rates of delivery. (B) The dynamic response as a function of calcium is identical for the two different rates of delivery. For clarity, only every 10th data point is plotted. The solid and open symbols correspond to the faster and slower ramps, respectively. The sample time was 5 ms for fluorescence and light scattering with an offset of 2.5 ms between the two data channels. The data represents the average of six individual trials. The error in % fusion is less than the thickness of the trace (SEM < 1%). The standard error in the averaged calcium values is <0.1 pCa.

If vesicles respond only to the magnitude of the calcium stimulus, then the calcium concentration associated with the first detectable fusion event after a stable, submaximal response must be greater then the concentration that produced the initial fusion response. This hypothesis was tested using photolysis double challenge experiments. Calcium transients resulting from the photolysis of DM-nitrophen lead to stable, submaximal extents of fusion (Fig. 6 A). After a return to base-line calcium concentrations, a ramp in the calcium concentration was used to initiate fusion of the remaining vesicles. The concentration of calcium associated with the first detectable fusion event after this second challenge was correlated with the calcium concentration present at the peak of the first challenge (Fig. 6 B). In 35 of 36 cases, the first detectable fusion event always occurred at a higher calcium concentration independent of the calcium rate of delivery in the second challenge (Fig. 7). That the data is shifted to the left of the identity line is expected because in these experiments the noise envelope for % fusion is approximately ±5% (Fig. 6 B). The one anomalous event may be due to the stable, submaximal response not being reached before initiating the second calcium challenge. The calcium concentration associated with the first detectable fusion event after a stable, submaximal fusion response is greater than the concentration that produced the initial fusion response. However, does the change in calcium required to detect the first fusion event, but monitored using the fluorescent indicator Rhod-2, agree with the steady state calcium activation curve derived from rapid perfusion (turbulent exchange) of solutions with defined calcium concentrations?

Figure 6.

Double challenge with photolysis of DM-nitrophen. (A) The release of calcium after photolysis of DM-nitrophen leads to submaximal extents of fusion. The time-dependent changes in the calcium concentration during the two challenges are indicated. The calcium concentration during the second challenge increases to concentrations >60 μM (data not shown). Calcium concentration is monitored using Rhod-2 fluorescence. (B) The calcium at the onset of fusion after the second challenge is indicated by point 3. The horizontal lines define the peak-to-peak noise envelope and the first detectable fusion event is indicated. Point 1 marks the beginning of UV irradiation, point 2 marks the time at which the calcium concentration matches the peak transient (first challenge), and point 3 marks the onset of fusion. The data were collected using a sample time of 0.02 s with an offset of 0.01 s between light scattering and fluorescence data.

Results from photolysis, interrupted perfusion, and turbulent exchange are summarized in Fig. 8 A. The solid line represents the log-normal cumulative distribution function previously shown to parameterize the calcium activation curve (Blank et al., 1998). A shift of ∼0.2 pCa U in this distribution function describes the average data derived from photolysis in which the relationship between peak fusion and calcium was monitored using the fluorescent indicator Rhod-2 (Fig. 8 A, dotted line). However, this shift is not considered significant because the error in K _d alone is sufficient to account for a difference of 0.2 pCa U in a single determination and <0.1 pCa U for averaged data. If the calcium concentrations were systematically underestimated, then comparing the change in calcium required to detect the first fusion event as a function of the initial level of fusion with the same quantity derived from the cumulative distribution function provides an alternative method for comparing the response to calcium step changes and photolytic release. The translational invariance of the calcium activation curve along the pCa axis justifies this approach.

The change in calcium required for a subsequent 10% change in fusion, starting from any initial level of fusion, was derived from the slope of the log-normal cumulative distribution. The infinitesimal change in calcium with fusion, 1/(d% fusion/d pCa), for a log-normal cumulative distribution function is d pCa/d% fusion = 0.01 · (2π)^0.5 · W · exp({[pCa + log(10^-6 M)]/(2W)}²).

The relationship between (d pCa/d% fusion) and % fusion was derived from a parametric plot of (d pCa/d% fusion) and % fusion using pCa as the parametric variable. When multiplied by 10%, this relationship describes the change in calcium associated with a 10% change in fusion, or ΔpCa per 10% fusion. The solid line in Fig. 8 B represents this function. A 10% change in fusion was chosen because the noise in the light scattering signal of the photolysis experiments corresponded to ∼10% peak to peak and represents the minimum change detectable in these experiments. When the initial extent of fusion is low or high, a large change in calcium is required for a subsequent 10% change in fusion, while in the transition region, small changes in calcium are required. The change in calcium required to detect the first fusion event in the photolysis experiments (Fig. 8, •) is in agreement with the relationship derived from the calcium activation curve for rapid perfusion of solutions with defined calcium concentrations (Fig. 8 B, solid line). In the linear region of the calcium activation curve, a change in calcium of 0.22 ± 0.03 pCa U (mean ± SEM, n = 14) is sufficient for additional subpopulations to fuse. The agreement between photolysis, step perfusion, and ramp perfusion data, despite the very different time courses associated with the calcium delivery, is consistent with the hypothesis that the concentration of free calcium is the single controlling variable that determines the fraction of the vesicles that fuse.

discussion

By combining slow perfusion of calcium in a chamber optimized for microscopic examination with rapid production of calcium by photolysis of chelator, we have tested the often-debated suggestion that stimulus–secretion coupling depends on the rate of calcium delivery. The calcium sensitivity of individual secretory vesicles was invariant to calcium delivery rates from faster than micromolar per millisecond to slower than micromolar per second. All experimental evidence supports the hypothesis that vesicles respond to the magnitude of the calcium stimulus independent of the time course over which it is delivered. No evidence was found to support the hypothesis that a decrease in the calcium sensitivity of individual secretory vesicles arising from the temporal properties of the calcium delivery is a limiting mechanism in establishing a graded response to calcium. These results have profound implications for models that attempt to explain the mechanism of calcium-regulated exocytosis.

Elimination of Models for Calcium-triggered Exocytosis

The properties of sea urchin egg secretory vesicle exocytosis in vitro in response to both multiple solution exchange protocols and different rates of calcium delivery are incompatable with several classes of kinetic reactions that have been incorporated into models of calcium-regulated exocytosis. Kinetic reactions that are not applicable are summarized here (1) A → B (two-state reaction); (2) A → B → C (consecutive reaction); (3) A → B → C with A, B → I_irreversible or A, B ↔ I_reversible (consecutive reaction with inhibitory branches); (4) A_i ↔ A_i* (i = 1, 2, ...) and B_j → B_j* (j = 1, 2, ...) (parallel reactions with fusion ∝ A_i*^N B_j*^M); and (5) adapting quantity.

All homogeneous population models (reactions 1, 2, and 3) with or without reversible or irreversible inhibitory states fail to describe the properties of this calcium-triggered exocytotic system. The first two models are simple linear reaction schemes in which reactant A is converted to product in one or two steps. If fusion is proportional to the concentration of product, then there can be no submaximal levels of fusion because all reactants are converted to product. Including an inhibitory branch in the reaction (reaction 3) does not alter the final outcome of a linear reaction scheme, conversion to product, unless the branch is irreversible. However, an irreversible branch means that the pool of reactants that are irreversibly inhibited can never take part in the reaction. This property is not observed: there was no irreversible loss in the ability of the remaining vesicles to fuse (this paper and Blank et al., 1998). Parallel reaction models (reaction 4) in which fusion is proportional to the product of individual transitions allows for submaximal conversion if one class of transitions is reversible. However, this model has the property of reset through the reversible transition. Removing calcium would reset the reversible transition such that a second challenge of the same concentration would result in fusion of the remaining vesicles to the same fractional extent as before. This property is not observed: the first detectable fusion event after the development of a stable, submaximal response occurs at a higher calcium concentration than the concentration that produced the initial response. All attempts to reveal a limiting reaction other than a decrease in the number of vesicles in different subpopulations were unsuccessful.

Adaptation (reaction 5) has been proposed as a property of calcium-triggered exocytosis in presynaptic terminals (Hsu et al., 1996). Models based on an adapting quantity that is proportional to a linear combination of receptor states predict that the removal of calcium should lead to recovery of sensitivity, and the activity of the adapting quantity should be dependent upon the rate of change of calcium (Segel et al., 1986; Knox et al., 1986). The previous paper (Blank et al., 1998) demonstrated that the fusion process cannot be reset: two identical pulses separated in time failed to elicit the same response. Here, we demonstrate that the same extent of fusion is achieved for different rates of delivery of the same calcium concentration. Together, these results rule out these kinetic models based on an adapting quantity that is proportional to a linear combination of receptor states.

One can speculate that the existence of multiple, calcium-dependent states in the exocytotic process before fusion may be branch points for calcium-dependent inactivation. For example, calcium could have a dual effect on a “priming” state where the main kinetic branch proceeds to fusion and a second branch leads to a nonfusing state that can proceed to fusion only by a second calcium- dependent path with a higher threshold for calcium. An extension of this process could lead to multiple, nonfusing states where each state has an alternate kinetic pathway requiring higher concentrations of calcium for subsequent fusion. Calcium could create a distribution of nonfusing, “priming” states, each state having a pathway to fusion with differing calcium requirements. The question of heterogeneity would be shifted from an initial population of vesicles with different calcium thresholds to a calcium-induced population of priming states. Each priming state would have alternate fusion pathways with different calcium requirements. However, the data are difficult to reconcile with this proposal. If these nonfusing states are in equilibrium with “upstream” states, then the removal of calcium should reset the system. Removal of calcium does not reset the system. One would have to postulate, post hoc, that only the forward rate of reaction creating the nonfusing state was calcium dependent and that the backward reactions were dependent on factors no longer available; in essence, locking the system into new, calcium-dependent, metastable states with the potential to proceed to fusion with different, but higher, concentrations of calcium. Without detailed knowledge of the calcium triggering event, it is difficult to evaluate these complicated kinetic alternatives. However, there exists a simpler description of the kinetics of exocytosis that is consistent with the observed behavior. We have proposed that the number and distribution of activated fusion complexes underlie the control of the rate and extent of triggered exocytosis (Vogel et al., 1996). This model has been extended and describes the kinetics of fusion in response to all experimental calcium challenges (single, double, and ramp) used to date (Blank, P.S., S.S. Vogel, J. Malley, and J. Zimmerberg, manuscript in preparation).

In summary, we have determined that the calcium sensitivity of individual secretory vesicles is invariant with the rate of calcium delivery. The graded responses observed in calcium-regulated exocytosis are explained by earlier differences in the calcium sensitivity of individual secretory vesicles (Blank et al., 1998), and these differences in calcium sensitivity are not modulated by the rate of calcium delivery over a range faster than millimolar per second to slower than micromolar per second. Our working hypothesis is that differences in calcium sensitivity, together with a stochastic variability in the number of fusion complexes active on individual vesicles, explains the kinetics and extent of calcium-regulated exocytosis. Exocytosis occurs when a vesicle has at least one fusion complex active; the rate of exocytosis is a function of the number of active fusion complexes per vesicle. Exocytosis ceases after all the vesicles with active fusion complexes have fused: the release of this subpopulation of vesicles explains the graded response to calcium.