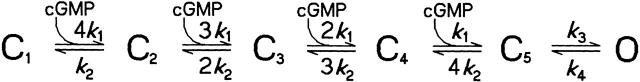Gating by Cyclic Gmp and Voltage in the α Subunit of the Cyclic Gmp–Gated Channel from Rod Photoreceptors

Abstract

Gating by cGMP and voltage of the α subunit of the cGMP-gated channel from rod photoreceptor was examined with a patch-clamp technique. The channels were expressed in Xenopus oocytes. At low [cGMP] (<20 μM), the current displayed strong outward rectification. At low and high (700 μM) [cGMP], the channel activity was dominated by only one conductance level. Therefore, the outward rectification at low [cGMP] results solely from an increase in the open probability, P _o. Kinetic analysis of single-channel openings revealed two exponential distributions. At low [cGMP], the larger P _o at positive voltages with respect to negative voltages is caused by an increased frequency of openings in both components of the open-time distribution. In macroscopic currents, depolarizing voltage steps, starting from −100 mV, generated a time-dependent current that increased with the step size (activation). At low [cGMP] (20 μM), the degree of activation was large and the time course was slow, whereas at saturating [cGMP] (7 mM) the respective changes were small and fast. The dose–response relation at −100 mV was shifted to the right and saturated at significantly lower P _o values with respect to that at +100 mV (0.77 vs. 0.96). P _o was determined as function of the [cGMP] (at +100 and −100 mV) and voltage (at 20, 70, and 700 μM, and 7 mM cGMP). Both relations could be fitted with an allosteric state model consisting of four independent cGMP-binding reactions and one voltage-dependent allosteric opening reaction. At saturating [cGMP] (7 mM), the activation time course was monoexponential, which allowed us to determine the individual rate constants for the allosteric reaction. For the rapid rate constants of cGMP binding and unbinding, lower limits are determined. It is concluded that an allosteric model consisting of four independent cGMP-binding reactions and one voltage-dependent allosteric reaction, describes the cGMP- and voltage-dependent gating of cGMP-gated channels adequately.

INTRODUCTION

Cyclic GMP-gated (CNG)¹ channels play a central role in vertebrate phototransduction by controlling the flow of cations across the plasma membrane of rod and cone photoreceptors. While the principal physiological properties of the rod cGMP-gated channel have been known for some time (for reviews see Yau and Baylor 1989; Eismann et al. 1993; Zimmerman 1995; Finn et al. 1996), several basic questions about its mechanism of opening and closing remain unresolved.

The light-sensitive current flowing through cGMP-gated channels shows a pronounced outward rectification (Bader et al. 1979) and is almost constant within the range of voltages at which rod photoreceptors operate (−30 to −70 mV). This outward rectification, which is greatly alleviated in the absence of divalent cations, has been attributed to the voltage-dependent blockage by external Ca²⁺ and Mg²⁺ (Matthews 1986; Stern et al. 1986; Yau et al. 1986; Zimmerman and Baylor 1992). At low cGMP concentrations ([cGMP]), however, the current–voltage (IV) relation is outwardly rectifying even in the absence of divalent cations on both sides of the membrane (Kaupp and Altenhofen 1992). This effect could account for a major fraction of the outward rectification of the light-sensitive current in intact rods because, in the dark, [cGMP] is only a few micromolar and is further decreased by light (Yau et al. 1986).

The cGMP-dependent rectification could be generated either by a voltage-dependent incidence of subconductance levels (sublevels) at unchanged open probability or by a voltage-dependent open probability at unchanged single channel conductance. The first mechanism is particularly appealing, because the cGMP-gated channel is cooperatively activated by binding of several cGMP molecules (for review see Kaupp 1995; Yau and Baylor 1989). At low [cGMP], sublevels could correspond to opening of partially liganded channels. In fact, several investigators have noticed sublevels preferentially at subsaturating [cGMP] (Hanke et al. 1988; Ildéfonse and Bennett 1991; Taylor and Baylor 1995; Ruiz and Karpen 1997).

Presently used kinetic models for the gating of CNG channels assume either that the channel has to be fully liganded to open (linear state models; Karpen et al. 1988; Tanaka et al. 1989; Gordon and Zagotta 1995; Varnum et al. 1995) or that opening may already occur in the partially liganded channel (allosteric models; Il-défonse et al., 1992; Goulding et al. 1994; Varnum and Zagotta 1996) according to the Monod-Wyman-Changeux model that describes allosteric transitions in proteins (Monod et al. 1965).

In an effort to understand the cGMP-dependent rectification, we studied single-channel and macroscopic currents. In the single-channel experiments, we took advantage of the superior resolution of thick-walled glass pipettes and the slower open-close kinetics of homooligomeric α subunits compared with the fast “flickery” kinetics of the native channels (Haynes et al. 1986; Zimmerman and Baylor 1986; Matthews and Watanabe 1987; Taylor and Baylor 1995). We show that subconductance states are extremely rare events at all [cGMP] and that the outward rectification is caused by an increased open probability of the channel at positive compared with negative voltages. Macroscopic currents were measured under steady state conditions and in response to voltage steps to relate the absolute open probability of the channels to both the [cGMP] and voltage. Assuming four cGMP binding reactions, the experimental data can be described adequately with both an allosteric and a sequential model with slight superiority of the allosteric model.

MATERIALS AND METHODS

Oocyte Preparation

Ovarian lobes were resected from Xenopus laevis under anesthesia (0.3% 3-aminobenzoic acid ethyl ester, Ms-222) and transferred to a Petri dish containing Barth medium containing (mM): 84 NaCl, 1 KCl, 2.4 NaHCO₃, 0.82 MgSO₄, 0.33 Ca(NO₃)₂, 0.41 CaCl₂, 7.5 Tris-HCl, pH 7.4. Stage V and VI oocytes were isolated mechanically or by incubation for 20–30 min in a Ca²⁺-free Barth medium containing 1 or 2 mg/ml collagenase. Within 2–7 h after isolation, RNA specific for the α subunit of the cGMP-gated channel from rod photoreceptors (Kaupp et al. 1989; here referred to as cGMP-gated channel) was injected into oocytes through glass micropipettes (15–20 μm diameter). The injected volume was 30–50 nl containing either ∼0.5 ng/μl RNA (single-channel experiments) or ∼50 ng/μl RNA (macroscopic currents). Oocytes were stored at 18°C overnight and defolliculated manually 20–28 h after isolation. Oocytes were further incubated for 3–7 d after injection at 18°C until experimental use. Before patching, the vitelline membrane of the oocytes was mechanically removed after exposing the cells to a hypertonic solution containing (mM): 200 aspartate, 20 KCl, 1 MgCl₂, 5 EGTA, 10 HEPES-KOH, pH 7.4.

Recording Technique

Skinned oocytes were transferred to the experimental chamber, which was mounted on the stage of an inverted microscope. The patch pipettes were pulled from borosilicate glass tubing. The tips were coated with Sylgard 184^® (Dow Corning Corp.). The bath and pipette solutions contained (mM): 140 KCl, 10 EGTA, 10 HEPES, pH 7.4.

Macroscopic currents were recorded with a conventional patch-clamp technique (Hamill et al. 1981). The glass tubing had an outer diameter of 2.0 mm and an inner diameter of 1.0 mm. The pipette resistance after fire polishing was 2–3 MΩ. The patches contained between several hundred and 2,000 active channels generating currents of as much as 2 nA at +100 mV. Currents of such magnitude may generate significant accumulation and depletion of ions near the membrane (Zimmerman et al. 1988). When working with the same solution at both sides of the patch, a sensitive test for such concentration changes is to step the voltage from remote values (e.g., +100 mV) to 0 mV. Any concentration change would then cause a transient rebound current. We tried to keep the patch as close at the pipette tip as possible by minimizing suction. Under those conditions, it was possible to record ionic currents without noticeable rebound current at 0 mV. Only such patches are included in this study.

Single-channel currents were recorded with a patch-clamp technique with improved resolution using short (8-mm total length) and thick-walled patch pipettes that were pulled from borosilicate glass tubing with an external and internal diameter of 2.0 and 0.5 mm, respectively. These pipettes were not fire polished. The technique of preparation of the thick-walled pipettes has been previously described in detail (Benndorf 1994, Benndorf 1995). The resistance of the pipettes used here was 30–50 MΩ. The thick-walled pipettes were used repeatedly by breaking the tips at the bottom of the chamber (Böhle and Benndorf 1994). The resistance of broken pipettes was 10–35 MΩ.

All ionic currents through cGMP-gated channels were recorded in inside-out patches that were excised ∼30 s after the formation of a seal. The seal resistance exceeded 4 GΩ with the conventional patch pipettes and 50 GΩ with the thick-walled patch pipettes. cGMP-gated channels were activated by replacing the bath solution with a bath solution containing 3′,5′-cyclic guanosine monophosphate. Each excised patch was first exposed to a solution containing 700 μM cGMP to determine either the amplitude of the macroscopic current in macropatches or the number of active channels in single-channel experiments. Only patches were accepted in which removal of cGMP caused complete disappearance of channel activity.

Recording was performed with an Axopatch 200A amplifier (Axon Instruments). Single-channel recordings were filtered online at a cut-off frequency of 2 or 5 kHz and were further filtered to the indicated final cut-off frequency with a Gaussian filter algorithm. Macroscopic currents were filtered at a cut-off frequency of 10 kHz.

Data Acquisition and Analysis

Recording and analysis of the data was performed on a PC-80486 with the ISO2 software (MFK Niedernhausen). Single-channel traces were sampled at 25 kHz, traces with macroscopic currents were sampled either at 10 kHz (20, 70, and 700 μM cGMP, 12-bit resolution) or 50 kHz (700 μM and 7 mM cGMP). Macroscopic currents were corrected for leak and capacitive components by subtracting respective currents in the absence of cGMP in the bath solution. All macroscopic currents considered herein are averages of 10–20 consecutive recordings.

Amplitude histograms were built either in a conventional way, including all sampling points, or by using the variance-mean technique described by Patlak 1988 to improve resolution. In the latter case, transition points were eliminated by shifting a window of defined length along the traces, plotting the variance as function of mean current within the window, and discarding all original sampling points with variances above a defined threshold. The windows used here were 280 μs long. The threshold variance was set to the variance of the background noise.

The fits were performed with a derivative-free Levenberg-Marquardt algorithm. Statistical data are given as mean ± SD.

RESULTS

Outward Rectification Is Caused by Voltage-dependent P_o

To test whether at low [cGMP] rectification is caused by a voltage-dependent incidence of sublevels at unchanged P _o or by a voltage-dependent P _o at unchanged single channel conductance, we recorded single-channel activity at high (70 μM) and low (7 μM) [cGMP] (Fig. 1). At both [cGMP], the unitary current level was similar. The corresponding amplitude histograms were fitted with sums of Gaussian functions. The fit shows that at 7 μM cGMP the channels operated with the same conductance as at 70 μM. The same result was obtained in three other patches. Smaller or larger levels than the mean open level (sub- or superlevels, respectively) were observed only extremely rarely. Therefore, the higher degree of outward rectification of the IV relation at low versus high [cGMP] must be caused by a voltage-dependent open probability at unchanged single-channel current.

Figure 1.

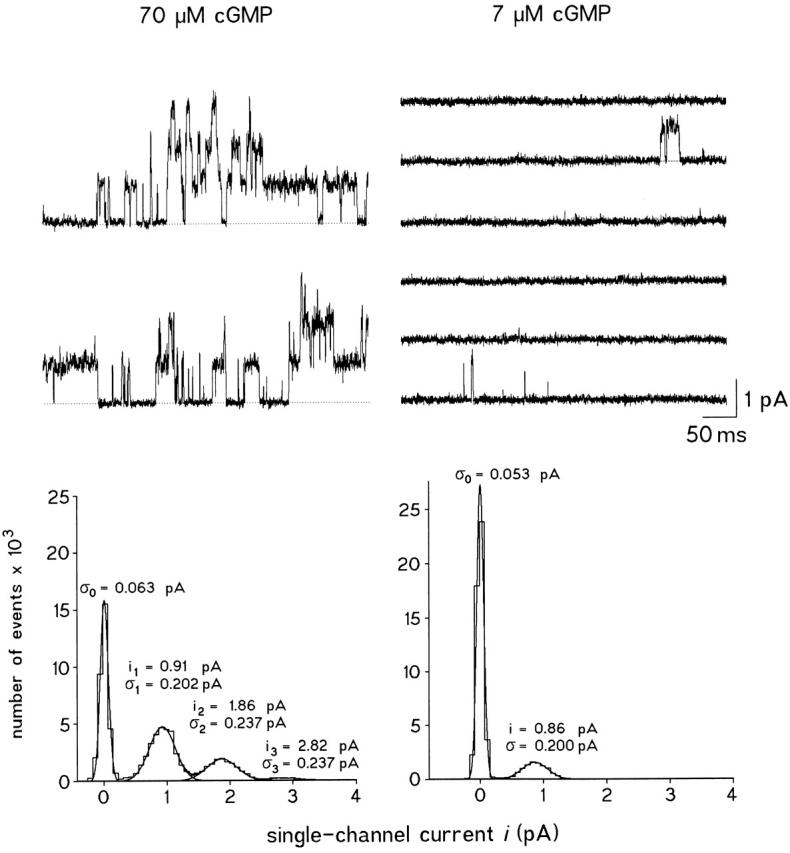
Single-channel currents and corresponding amplitude histograms in a patch containing at least three CNG channels at 70 (left) and 7 (right) μM cGMP. The patch was held at +50 mV. The individual traces of 500-ms duration were recorded in intervals of 1 s. The final cut-off frequency was 1 kHz. The amplitude histograms were formed with the variance-mean technique with a window width of 280 μs (seven sampling points). The distributions were fitted with sums of either four or two Gaussian functions. The respective single-channel currents i and standard deviations σ are indicated. At 70 μM cGMP, the amplitude histograms were formed from consecutive traces, whereas at 7 μM cGMP only nonempty traces were used. Significant sublevel openings were not present.

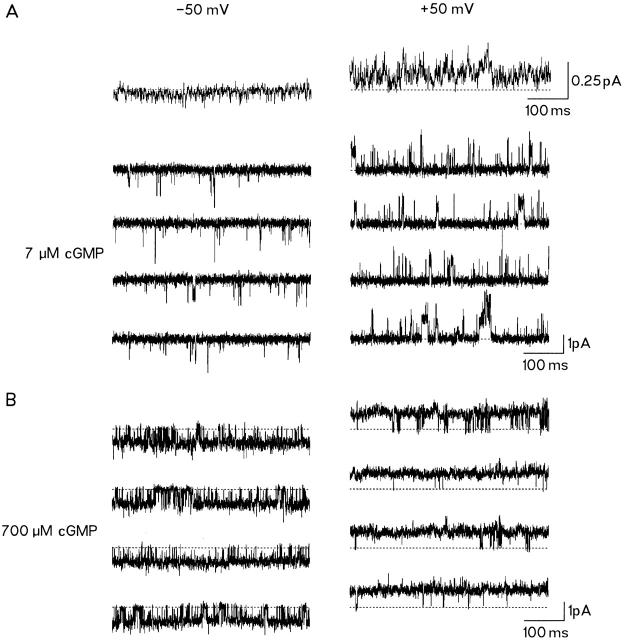
Fig. 2 A shows representative single-channel currents at 7 μM cGMP at both −50 and +50 mV from a patch containing at least three channels. Comparison of the channel activity at the two voltages suggests two differences: at +50 mV, the frequency of openings was increased and longer events appeared more often than at −50 mV. The average currents (Fig. 2 A, top) indicate noticeable outward rectification. Amplitude histograms showed only the fully open level at each voltage (not shown). The open probability was evaluated in the following way: Gaussian curves were fitted to the amplitude histograms that contained all sampling points. The ratio between the area under the open level peak and the total area provides nP _o; for the patch in Fig. 2, top, it was 0.041 at +50 mV and 0.026 at −50 mV. The ratio P _o,rel = P _o (+50 mV)/P _o (−50 mV) yields a relative measure of P _o at +50 mV with respect to that at −50 mV (assuming that n is constant). P _o,rel was 1.6 for the example shown in Fig. 2 A. The P _o,rel at ±50 mV favorably compares with the ratio of the ensemble average currents I₊₅₀/I₋₅₀ of 1.8. Together with the results of the previous paragraph, it has to be concluded that the pronounced outward rectification at low [cGMP] is primarily caused by an increase of P _o at more positive voltages.

Figure 2.

Voltage-dependent activity of cGMP-gated channels at 7 and 700 μM cGMP. The final filter frequency was 2 kHz. (A) 7 μM cGMP. The voltage was stepped repetitively between −50 and +50 mV every 3 s. In each 3-s interval, three traces were recorded for 500 ms. The patch contained at least three channels. The corresponding ensemble averaged currents (top, calculated from 12 individual traces each) show outward rectification. (B) 700 μM cGMP. The patch contained only one channel. Although the P _o at −50 mV is also smaller than that at +50 mV (for values see text) the degree of outward rectification is lower than at 7 μM cGMP.

Fig. 2 B shows recordings at 700 μM cGMP from a patch that contained only one active channel. From amplitude histograms, P _o at +50 and −50 mV was calculated to be 0.97 and 0.81, respectively; hence P _o,rel was 1.2. Since the single-channel current was only less different at +50 than at −50 mV (0.90 ± 0.17 vs. 0.84 ± 0.17 pA), the moderate outward rectification at saturating [cGMP] is also generated by the voltage dependence of P _o.

Gating Kinetics of Single CNG Channels as Function of Voltage and [cGMP]

The previous section suggests that a larger P _o at positive compared with negative voltages is caused by longer and more frequent opening events. We therefore analyzed the open-time distribution at ±50 mV as function of [cGMP]. At 70 and 700 μM cGMP, only patches containing one active channel were used, whereas at 7 and 20 μM cGMP, patches with several channels were used for the analysis to obtain a sufficiently large number of events. In these patches, the incidence of overlapping opening events was below 5%, which only negligibly modified the open-time distribution.

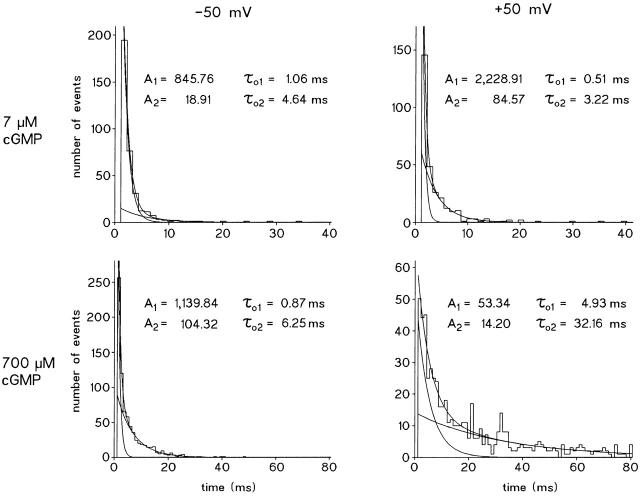
Fig. 3 shows open-time histograms of recordings from two patches (7 and 700 μM cGMP; ±50 mV). All distributions were well described by the sum of two exponentials with contributions A₁ and A₂ and the time constants τ_o1 and τ_o2, respectively. Consider the open time distribution at 7 μM cGMP and −50 mV. The vast majority of openings had a mean lifetime of roughly 1 ms; a small fraction [A₂/(A₁ + A₂) ≈ 2%] of longer events had a mean lifetime of roughly 5 ms. At +50 mV, the mean open times of these two kinetically distinct events were either unchanged or even slightly shorter, but the channel opened more often and the longer opening events occurred more frequently [A₂/(A₁ + A₂) ≈ 4%]. In the presence of 700 μM cGMP, the lifetimes of both short and long opening events were not much different when V_m was −50 mV. Longer opening events occurred roughly four times more frequently [A₂/(A₁ + A₂) ≈ 8%] than in the presence of 7 μM cGMP at the same voltage. However, switching the voltage from negative to positive values at 700 μM cGMP had a pronounced effect on gating kinetics: both τ_o1 and τ_o2 increased by roughly five- to sixfold and the contribution of the longer openings increased dramatically [A₂/(A₁ + A₂) ≈ 21%].

Figure 3.

Open-time histograms at 7 and 700 μM cGMP and +50 and −50 mV each. The data were obtained from a multichannel patch at 7 μM cGMP and a single-channel patch at 700 μM cGMP. The distributions were fitted with sums of two exponentials yielding the indicated contributions A_n and open-time constants τ_n. The combination of high [cGMP] and positive voltage caused a dramatic prolongation of both time constants. Filter, 2 kHz.

Fig. 4 summarizes the results from nine similar experiments at [cGMP] of 7, 20, 70, and 700 μM. In Fig. 4 A, the time constants for the fast (τ_o1) and slow (τ_o2) exponentials are plotted as function of [cGMP]. The vertical lines connect data points of the same exponential and from the same patch at −50 (squares) and +50 (circles) mV. At 7 and 20 μM [cGMP], τ_o1 and τ_o2 do not significantly depend on voltage. At the higher concentrations of 70 and 700 μM, both τ_o1 and τ_o2 are significantly larger at +50 than at −50 mV (not clearly visible in the diagram for τ_o1 at 70 μM cGMP). The voltage-dependent increase of τ_o1 and τ_o2 at high [cGMP] would suggest that the outward rectification becomes more pronounced at high rather than at low [cGMP], assuming an equal number of openings at both voltages. This contrasts with the experimental finding that outward rectification is steeper at low compared with high [cGMP]. The resolution of this apparent contradiction is that channels at low [cGMP] open much more often at +50 than at −50 mV. Since the evaluation of the contributions A₁ and A₂ at low [cGMP] was complicated by a variable number of channels in the patches, we evaluated for equal time intervals at each voltage the ratios A₁ (+50 mV)/A₁ (−50 mV) and A₂ (+50 mV)/A₂ (−50 mV). These ratios are independent of the number of channels. Fig. 4 B shows a plot of these ratios as function of [cGMP]. As anticipated, both ratios are largest at the lowest [cGMP] and smallest at the highest [cGMP]. At 7 μM cGMP, this implies that the channels open much more often at +50 than at −50 mV. Furthermore, the ratio A₂ (+50 mV)/A₂ (−50 mV) is approximately twice as large as the ratio A₁ (+50 mV)/A₁ (−50 mV). At [cGMP] of 70 and 700 μM, both ratios fall to values far below unity, indicative of a significantly smaller number of openings at +50 compared with −50 mV. This matches the longer open times at +50 compared with −50 mV. From Fig. 4, three conclusions may be derived. (a) At high [cGMP], the low number of openings at +50 compared with −50 mV approximately compensates for the long openings. This result explains why rectification of the macroscopic current is weak. (b) At low [cGMP], τ_o1 and τ_o2 are independent of voltage, but the number of events in the distribution of both the fast and the slow openings considerably increases. The slow component A₂ is about twice as voltage dependent as the fast component A₁. The steep outward rectification is therefore solely caused by a significant increase of the number of openings at positive voltages. (c) The fact that a large increase of τ_o1 and τ_o2 could be reached only at high [cGMP], and positive voltage implies a high degree of coupling between cGMP binding and voltage-dependent gating.

Figure 4.

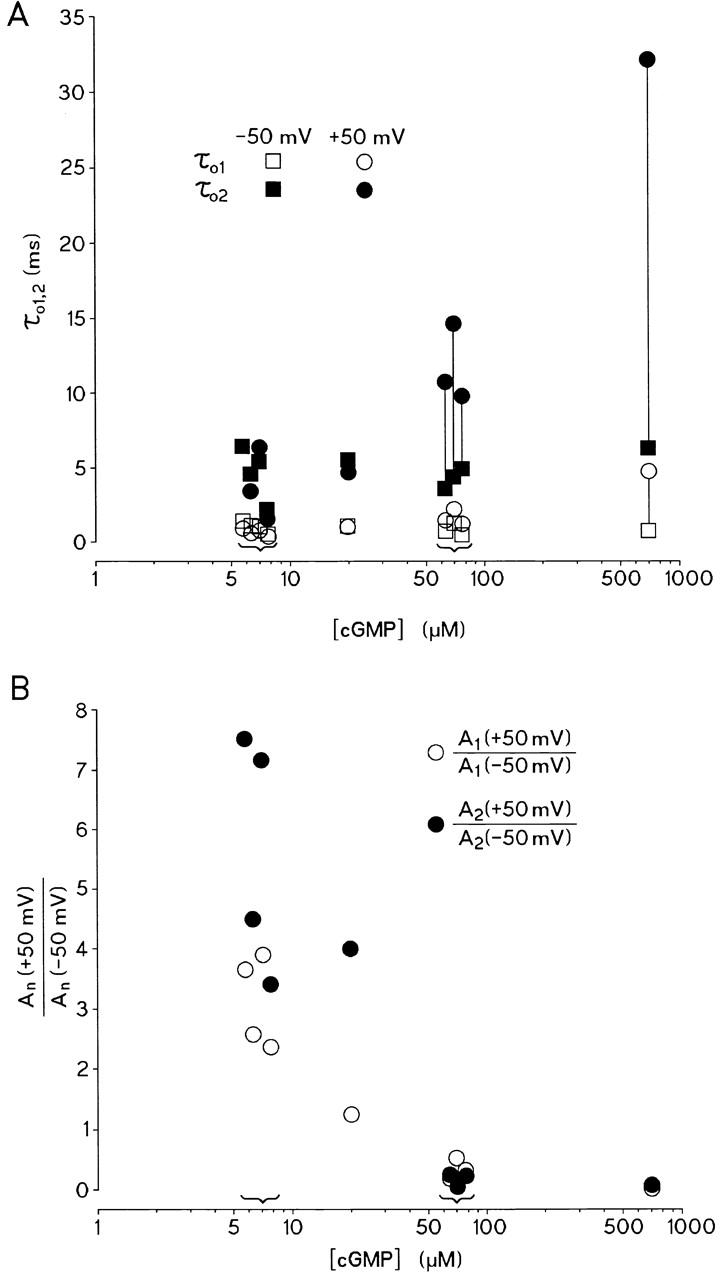
Dependence of open times on [cGMP]. All data were filtered at 2 kHz. (A) Fast open time τ_o1 and slow open time τ_o2 of single cGMP-gated channels as function of [cGMP]. Kinetic constants were measured at 7, 20, 70, and 700 μM cGMP and at −50 and +50 mV. Parentheses indicate values at 7 and 70 μM, respectively. 16–63 traces of 500-ms duration were analyzed. When switching from −50 to +50 mV, both τ_o1 and τ_o2 increased at 70 μM cGMP and even more so at 700 μM cGMP, whereas at 7 and 20 μM cGMP, no statistically significant increase of either τ_o1 and τ_o2 was observed. (B) Voltage-dependent incidence of the relative contribution of fast and slow exponential in the open-time histograms as function of [cGMP]. Plotted is the ratio A_n (+50 mV)/A_n (−50 mV). At low [cGMP], A₂ (+50 mV)/A₂ (−50 mV) is larger than A₁ (+50 mV)/A₁ (−50 mV), suggesting that the contribution of the slow exponential is more influenced by voltage than that of the fast exponential.

Although the single-channel analysis provided criteria for appropriate kinetic models, the variability of the single-channel data did not allow a more precise analysis of the gating mechanism. We therefore performed experiments in macroscopic currents.

Voltage-dependent Gating in Macroscopic Currents

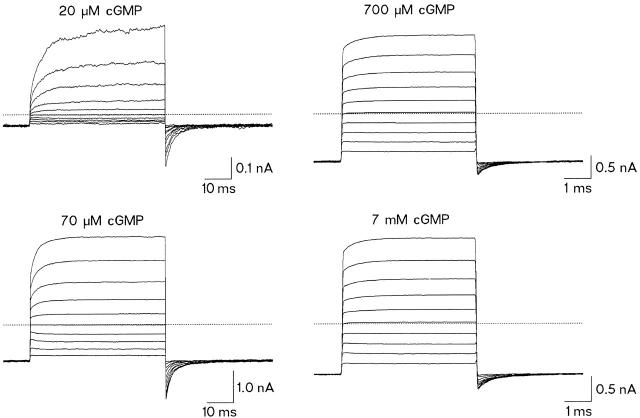
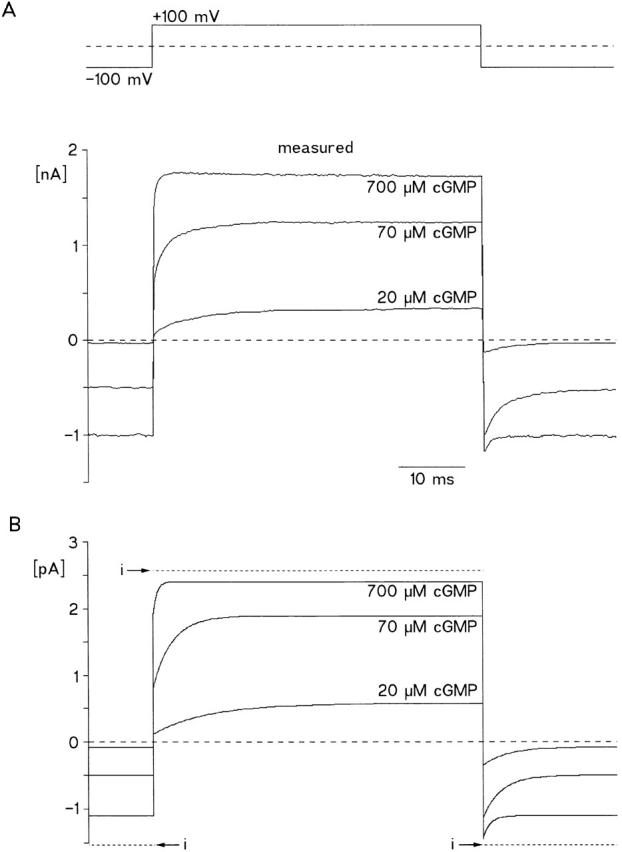
Upon stepping the holding voltage of −100 mV to positive test voltages, two current components were observed at all [cGMP]: an instantaneous outwardly directed current was followed by a time-dependent current that increased to a new steady state level (Fig. 5). When the voltage was returned to −100 mV, an inwardly directed instantaneous current was followed by a tail current that relaxed to the same current level as observed before the depolarizing step. In terms of P _o, these observations may be interpreted as follows. The amplitude of the instantaneous current at the beginning of the test pulse is determined by P _o at the holding voltage, whereas the amplitude of the steady state current at the end of the test pulse is determined by P _o at the test voltage. In addition, the time-dependent current at the test voltage represents extent and kinetics of channel gating from P _o at the holding voltage to P _o at the test voltage (voltage-dependent activation). After stepping back to the holding voltage, the amplitude of the instantaneous current is determined by P _o at the test voltage, whereas the amplitude of the steady state current is determined by P _o at the holding voltage. Hence, the tail current at the holding voltage represents the extent and kinetics of the channel gating when changing from P _o at the test voltage to P _o at the holding voltage (voltage-dependent deactivation). At the test voltage, the amplitude ratio of the steady state current with respect to the instantaneous current must equal the amplitude ratio of the instantaneous tail current with respect to the steady state current at the holding voltage. This ratio is defined by how many times P _o at the test voltage is larger than P _o at the holding voltage.

Figure 5.

Voltage dependence of macroscopic currents through cGMP-gated channels at different [cGMP]. Recordings at 20 and 70 μM cGMP were obtained from one patch and at 700 μM and 7 mM cGMP from another patch. The membrane voltage V_m was stepped from −100 mV to another voltage between −80 and +100 mV in 20-mV increments. The duration and frequency of pulses were either 50 ms and 2 Hz (20 and 70 μM cGMP) or 4 ms and 10 Hz (700 μM and 7 mM cGMP), respectively. Traces represent the average of 10–20 consecutive current recordings. Each trace was corrected for capacitive and small leakage currents by subtracting a current that was averaged from 5–10 control traces recorded in the absence of cGMP.

At 20 μM cGMP, the amplitude of the activating current component was clearly larger than that of the instantaneous current component, whereas at 7 mM cGMP it was much smaller. This indicates a stronger effect of voltage on channel gating at low compared with high [cGMP]. Fig. 5 also shows that the kinetics of the activating and deactivating current component became greatly accelerated at increased [cGMP], but was largely independent of voltage (see also below).

Dose–Response Relation of Steady State P_o at +100 and −100 mV

To discriminate between different state models describing the gating of CNG channels, the relation between the absolute P _o and [cGMP] was determined. Because in single-channel recordings determination of P _o does not provide the required accuracy, we measured the dose–response relation of P _o in macroscopic currents with three different methods as follows:

(a) At large P _o, its exact value can be determined by the analysis of stationary noise. The noise variance σ² is related to the amplitude of the mean current I by:

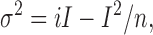1

where i denotes the single-channel current and n the total number of channels. The single-channel current i was determined from single-channel recordings, σ² and I were determined from macroscopic currents. The background noise variance was subtracted. These two measurements then yield ni, the maximum current that is obtained when all channels are open. The ratio I/(ni) gives the P _o at the respective [cGMP]. The contribution of shot noise and Johnson noise to the total noise was calculated to be negligible. For large values of P _o, the variability in the results was remarkably low. This is illustrated by the dose–response relationship of Fig. 6 A, where the small error bars (SD) are hidden in the respective symbols for the data at +100 mV/700 μM [cGMP], +100 mV/7 mM [cGMP], and −100 mV/7 mM [cGMP]. The data at −100 mV/700 μM [cGMP] and +100 mV/70 μM [cGMP] were also determined with the noise analysis, albeit the SD was larger.

Figure 6.

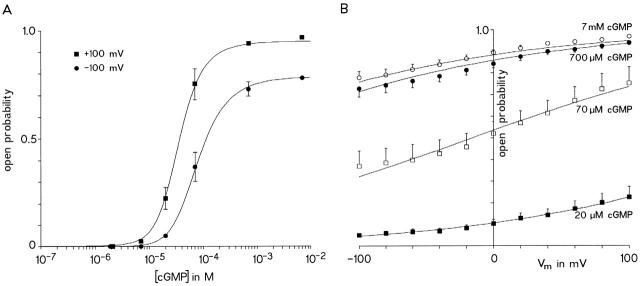
Voltage and [cGMP] dependence of macroscopic current. (A) Dose–response relationships for the channel activation by cGMP at +100 and −100 mV. The error bars indicate SD; for several conditions, SD is smaller than the size of the symbols. Three different types of measurements were used to determine the dose–response relationships (see text). Each data point was calculated from 4–10 individual experiments. The data points at the two voltages were simultaneously fitted with the allosteric model (Fig. 1; see text for parameters). (B) P _o/V_m relationships at 20, 70, and 700 μM, and 7 mM [cGMP]. In the diagram, the data points at −100 and +100 mV were taken from A. The data points for all other voltages were obtained from the instantaneous tail currents at −100 mV after test pulses to the indicated voltages at the abscissa (compare Fig. 5). The error bars indicate SD that was computed according to the error propagation law. The curves provide the best simultaneous fit to all data with the allosteric model (see text for parameters).

(b) The data points at +100 mV/7 μM [cGMP], −100 mV/7 μM [cGMP], and +100 mV/20 μM [cGMP] were obtained by recording first the steady state current in multichannel patches and thereafter at +100 mV/700 μM [cGMP]. The amplitudes of the currents at the lower concentrations were normalized in each individual patch with respect to the amplitude of the current at 700 μM [cGMP] measured in the same patch. The mean was calculated at each concentration and final values in the diagram were obtained by considering that P _o was 0.93 at +100 mV/700 μM [cGMP].

(c) The data points at −100 mV/70 μM [cGMP] and −100 mV/20 μM [cGMP] were calculated from voltage step protocols as shown in Fig. 5. As described in the previous section, the amplitude ratios were formed from the instantaneous current with respect to the steady state current after stepping to +100 mV and from the steady state current with respect to the instantaneous current after stepping back to −100 mV. Finally, the mean ratios at 20 and 70 μM [cGMP] were multiplied with the values of the respective data points at +100 mV.

Fig. 6 A shows that at −100 mV the dose–response relation constructed in this way saturated at significantly lower P _o and was slightly shifted to higher [cGMP] with respect to the dose–response relation at +100 mV.

Selection of Model and Fit to Steady State Data

The experimental data provide five constraints for a kinetic model. (a) Even at the highest [cGMP] (700 μM or 7 mM) and the most positive voltage (+100 mV), P _o does not reach unity. This observation implies that channels close by a reaction whose equilibrium is independent of [cGMP]. (b) At −100 mV, the maximal P _o value at saturating [cGMP] is considerably lower than that at +100 mV. A corollary of this observation is that one voltage-dependent reaction must exist that follows the binding of cGMP. (c) The effect of voltage on P _o is large at low [cGMP] and small at high [cGMP]. This result can be explained by coupling between the action of [cGMP] and voltage. (d) In a total of 24 experiments similar to those illustrated in Fig. 5, the time course of activation did not show any delay. This observation indicates that only a single voltage-dependent reaction is rate limiting for channel opening. (e) The channels operate with only a single conductance.

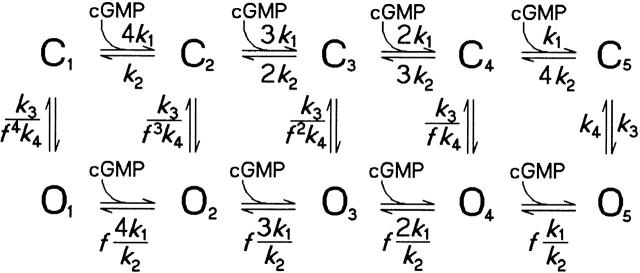
With these constraints, two types of models are reasonable: allosteric and sequential models. Fig. 1 illustrates an allosteric model with four cGMP binding reactions as used previously to describe gating of CNG channels (Goulding et al. 1994). The opening reaction was assumed to be voltage dependent. The rate constant for an individual cGMP-dependent reaction is given by m[cGMP]k ₁ with m = 1…4. The reverse reaction is given by (4 − m + 1)k ₂. The voltage-dependent rate constants k ₃ and k ₄ were assumed to be k _3,0exp (0.5zFV_m/RT) and k _4,0exp (−0.5zFV_m/RT), respectively. k _3,0 and k _4,0 are the rate constants at V_m = 0 mV; F is the Faraday constant, V_m the transmembrane voltage, R the gas constant, T the absolute temperature, z the effective gating charge, and f the allosteric factor. The value of 0.5 indicates a symmetric barrier for the voltage-dependent reaction. This assumption is without relevance for all fits of steady state properties. T was 298 K. For the fit of the dose–response relations, the allosteric factor was set to 10 because with our model this value predicts a spontaneous P _o (in the absence of cGMP) of 10⁻⁴, similar to the measured value of 1.25 × 10⁻⁴ (Tibbs et al. 1997). The three free parameters were k ₁/k ₂, k _3,0/k _4,0, and z. The curves in Fig. 6 A illustrate that the allosteric model describes the data well, which also confirms the assumption of four cGMP binding reactions because the number of binding sites determines the steepness of the dose–response relation. The parameters were k ₁/k ₂ = 2.00 × 10⁴ M⁻¹, k _3,0/k _4,0 = 8.24, z = 0.21.

Scheme S1.

Fig. 2 shows a corresponding sequential model with four cGMP binding reactions in which the channel has to be fully liganded before a voltage-dependent reaction causes opening (termed “G₄O model”). The meaning of all parameters and constants is the same as in the allosteric model, apart from the absence of the allosteric factor f. The sequential model equals the allosteric model in the limit that the allosteric factor reaches infinity. We tried to fit the dose–response relations with sequential models including between two and five cGMP binding reactions. Fits with similar quality as with the allosteric model were obtained with the binding of three cGMP molecules (termed “G₃O model”) and four cGMP molecules, whereas the fits were worse with two and five cGMP molecules. The parameters from the fit with the G₄O model are k ₁ /k ₂ = 2.65 × 10⁴ M⁻¹, k _3,0/k _4,0 = 7.95, z = 0.22 (fit not shown).

Scheme S2.

To test whether the allosteric, the G₃O, and the G₄O models correctly predict P _o for voltages between −100 and +100 mV, we evaluated the amplitude of deactivating tail currents at −100 mV, following respective test pulses. P _o was determined by relating the tail current amplitude at +100 and −100 mV to the respective P _o values obtained above. This analysis was performed at 20, 70, 700 μM, and 7 mM cGMP (Fig. 6 B). The plot of the data points as function of the test pulse voltage shows that the voltage dependence was steepest in the negative branch of the voltage range at high [cGMP] and in the positive branch at low [cGMP]. These four P _oV relations were fitted simultaneously with each of the three models. The allosteric model (Fig. 1), which included the allosteric factor f as fourth free parameter, yielded k ₁/k ₂ = 1.9607 × 10⁴ M⁻¹, k _3,0/k _4,0 = 7.84, z = 0.23, f = 10.24 (curves in Fig. 6 B). Interestingly, the fit converged with an allosteric factor close to the value assumed above. A similarly reasonable fit was obtained with the G₃O model (k ₁/k ₂ = 1.63 × 10⁴ M⁻¹, k _3,0/k _4,0 = 7.77, z = 0.23). In contrast, with the G₄O model the predicted P _o value was too small at positive voltages and 20 μM cGMP. Assuming independent binding of four cGMP molecules, this result shows that the allosteric model is superior over the corresponding sequential G₄O model.

Determination of the Rate Constants

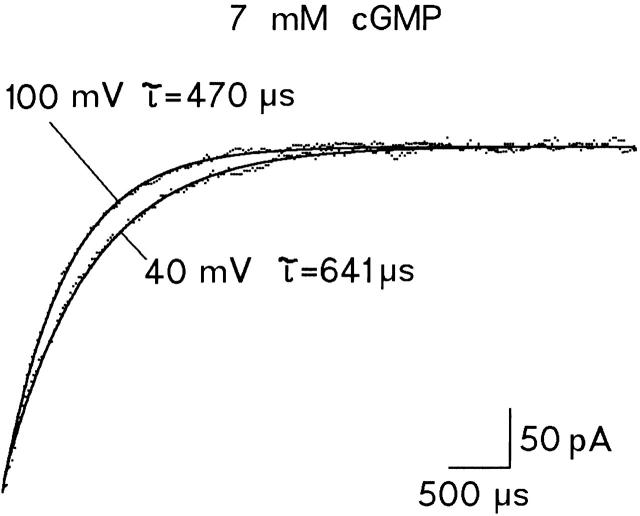
The fit of the dose–response relations yielded only values for the ratios k ₁/k ₂ and k _3,0/k _4,0. The individual rate constants of the voltage-dependent reaction (k _3,0 and k _4,0) were determined as follows: at the saturating [cGMP] of 7 mM (Fig. 3), it is reasonable to assume that all channels are fully liganded. In our models, voltage-dependent activation should then obey a monoexponential time course with the time constant τ = 1/(k ₃ + k ₄). Fig. 7 shows normalized time courses of the activating component of current at +40 and +100 mV and 7 mM [cGMP] together with theoretical curves of best fits with a single exponential. Monoexponential functions described the measured time courses adequately. In all experiments, these time course were slower at +40 mV compared with +100 mV. As time constants τ, we obtained 535 ± 116 μs and τ = 436 ± 41 μs (mean ± SD; n = 4), respectively. For the allosteric model, the values of k _3,0 and k _4,0 were then calculated with k _3,0/k _4,0 = 7.84 and z = 0.23 according to:

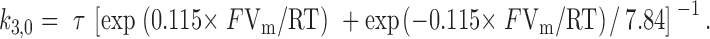2

Figure 7.

Time course of the activation at saturating [cGMP] (7 mM). The activation time course was fitted with a single exponential yielding the indicated time constants τ. The measured current at +40 mV was scaled to the current at +100 mV.

All symbols have the same meaning as described above. From the τ value at +100 mV, we calculated k _3,0 = 1.39 × 10³ s⁻¹ and k _4,0 = 1.67 × 10² s⁻¹. Similar values of the rate constants k _3,0 and k _4,0 were obtained from the τ value at +40 mV. Similar values were also obtained for the G₃O and G₄O models.

Knowing k _3,0 and k _4,0, we attempted to determine the parameters k ₁ and k ₂, rather than their ratio, by simultaneously fitting the allosteric model to current traces after voltage steps at three different [cGMP] (Fig. 8 A). Although there was only one free parameter left, the fit did not converge and therefore did not allow us to derive a unique set of rate constants. However, it did allow us to estimate a lower limit for the rate constants k ₁ and k ₂. A reasonable description of the measured traces was obtained with k ₁ > 3 × 10⁷ M⁻¹ s⁻¹ and k ₂ > 1.5 × 10³ s⁻¹ (with k ₁/k₂ < 22 × 10⁴ M⁻¹). The consequence is that for all tested [cGMP] between 20 μM and 7 mM, neither the rate of cGMP binding nor that of cGMP unbinding is limiting for the time course of voltage-dependent activation and deactivation. Fig. 8 B shows theoretical currents calculated with the allosteric model; k ₁ and k ₂ were set to 3 × 10⁷ M⁻¹ s⁻¹ and 1.5 × 10³ s⁻¹, respectively. The theoretical currents were scaled with respect to the measured single-channel current i at ±100 mV (dotted lines). Simulation of current traces as shown in Fig. 8 A with both the G₃O and the G₄O models yielded similarly reasonable results (not shown).

Figure 8.

Comparison of computed with measured currents at three [cGMP] and voltage steps of 50-ms duration from −100 to +100 mV. (A) Measured currents. The currents at 70 and 700 μM cGMP were recorded from the same patch. The current at 20 μM [cGMP] was recorded from another patch and it was scaled with the ratio of currents at 700 μM [cGMP] in the two patches. (B) Computed currents. P _o was calculated with the allosteric model (Fig. 1) and then scaled with the mean single channel current (dotted lines; −1.6 pA at −100 mV; 2.6 pA at +100 mV). The parameters were: k ₁ = 3 × 10⁷ M⁻¹ s⁻¹, k ₂ = 1.5 × 10³ s⁻¹, k _3,0 = 1.39 × 10³ s⁻¹, k _4,0 = 1.67 × 10² s⁻¹, z = 0.23.

DISCUSSION

Subconductance Levels

Previous studies reported the occurrence of sublevels (Zimmerman and Baylor 1986; Hanke et al. 1988; Haynes et al. 1986; Ildéfonse and Bennett 1991; Taylor and Baylor 1995; Ruiz and Karpen 1997). In our experiments, the incidence of sublevels was very low at all [cGMP]; hence, sublevels cannot significantly contribute to macroscopic currents through the rod cGMP-gated channel α subunit. This conclusion also holds for the salamander rod cGMP-gated channel, which maximally spends 5–10% of its time in a state of small conductance of <5–6 pS (Taylor and Baylor 1995). Sublevels in the salamander channel occurred more frequently at low [cGMP] and were virtually absent at [cGMP] > 50 μM (Taylor and Baylor 1995). The native rod cGMP-gated channel is composed of two distinct subunits, a smaller α subunit and a larger β subunit (Kaupp et al. 1989; Körschen et al. 1995). The β subunit is also engaged in ligand binding (Brown et al. 1993), pore formation, and gating (Chen et al. 1994; Körschen et al. 1995), suggesting that cGMP-dependent sublevels observed in the native channel are imparted by the β subunit. Ruiz and Karpen 1997, however, observe a high incidence of two sublevels that contribute roughly 50% to P _o of the heterologously expressed α subunit (see Fig. 3 b in Ruiz and Karpen 1997). These authors also show that sublevels result from channel species that have fewer than the maximal number of four cGMP molecules bound. The reason for the significant differences between their and our observations is not clear.

Voltage Dependence of Open Times

Changing the voltage at low [cGMP] primarily affects the frequency of opening and the relative abundance of longer open periods, whereas the two mean open times are largely equal. The finding of two components in the open-time distribution implies the existence of at least two open states. In the modeling strategy, these open states were lumped to one open state because of a lack of stringent criteria on how to include these open states in the model (see below).

At low [cGMP], and correspondingly small P _o, the open times were independent of voltage (Fig. 3 and Fig. 4). This result does not conflict with the voltage-dependent gating described in the macroscopic currents because the relatively low degree of voltage dependence found in the macroscopic currents (z = 0.22) is hidden in the variability of the open time histograms.

At high [cGMP], P _o increased to large values. Changing then the voltage from negative to positive values increased the mean open times dramatically and, concomitantly, decreased the frequency of openings. The increase of the open times at high [cGMP] and positive voltage cannot be explained by an unbinding reaction of cGMP from the channel, which should be independent of the [cGMP]. The most likely interpretation of the prolonged open times at elevated [cGMP] is that they result from unresolved closures due to an immediate reopening when the channel is fully liganded. Hence, the rate constant of the voltage-dependent opening reaction must be very rapid. In conclusion, the single channel experiments suggest a kinetic model in which channel opening is the result of one or more cGMP binding steps followed by at least one voltage-dependent step. However, the variability of the single-channel data did not allow us to derive stringent criteria for modeling of the cGMP- and voltage-dependent gating. This was only possible with macroscopic currents.

Dose–Response Relation of the Absolute P_o Obtained from Macroscopic Currents

A plot of the normalized current through CNG channels (response) as function of the [cGMP] (dose) is the standard and most simple procedure to determine both the [cGMP] of half maximum activation and the number of the cGMP molecules binding to a channel (for review, see Kaupp 1995; Finn et al. 1996). The exact measurement of P _o is not trivial. In the single channel experiments, the accuracy is limited by the typical variability inherent in single-channel measurements. In macroscopic currents, determination of P _o requires knowledge of the limiting P _o value at saturating [cGMP]. We determined P _o at saturating (and also slightly lower) [cGMP] with stationary noise analysis because at high P _o its value does not critically depend on the exact value of the single-channel current I. The position of the dose–response relation at −100 mV was determined with respect to that at +100 mV by evaluating the instantaneous and steady state currents at one voltage (either −100 or +100 mV). In this way, the error introduced by the uncertainty in the determination of the IV relation of the single-channel current was avoided. As a consequence, our dose–response relations for the absolute value of P _o at +100 and −100 mV provided more constraints to discriminate among kinetic models than normalized relations used previously.

Strategy of Modeling

In our modeling strategy, we tested an allosteric model with four cGMP binding reactions (Fig. 1) and two sequential models containing three (G₃O model) or four (G₄O model; Fig. 2) cGMP binding reactions. All three models fitted the steady state dose–response relations of the absolute P _o at +100 and −100 mV (compare Fig. 6 A) and they produced reasonable time-dependent currents in response to voltage steps (compare Fig. 8). However, when fitting the P _oV relations (Fig. 6 B), the allosteric and G₃O models were superior to the G₄O model. Including furthermore that CNG channels may open even in the absence of cGMP (Tibbs et al. 1997) and that four α subunits, containing one cGMP-binding site each (Kaupp et al. 1989), form one functional CNG channel (Gordon and Zagotta 1995; Liu et al. 1996), the allosteric model seems to be more adequate than each of the sequential models. Interestingly, the allosteric factor f was determined to be very similar to that obtained from measurements in the absence of cGMP.

With respect to the rate constants describing cGMP binding (k ₁) and unbinding (k ₂), our models allowed us only to determine the ratio k ₁/k ₂ and to estimate lower limits for the absolute values. The reason for this indeterminateness is that in the case of rapid binding and unbinding the activation time course is defined by the relative occupancy of the last closed states before opening in conjunction with the kinetics of the C ⇔ O transition.

The finding of two open times, suggesting at least two open states, was not included in our models because we did not have sufficient criteria to specify a model with two open states. In all our models, τ_o calculates to be 1/k ₄. At +50 and −50 mV, the predicted values for τ_o are 7.2 and 4.8 ms. Interestingly, these values approximately match the range of the slow mean open time τ_o2 in the single-channel recordings. It may therefore be speculated that the C ⇔ O transition, whose closing reaction generates τ_o2, notably contributes to the voltage-dependent activation. With respect to the fast closing reactions corresponding to τ_o1, one possibility is that the open channel closes to an additional closed state, similar to a channel block.

For the allosteric model, we can exclude that the rate constants of the transitions O₄ ⇒ C₄ and O₅ ⇒ C₅ correspond directly to 1/τ_o1 and 1/τ_o2, respectively, because at saturating [cGMP], when only C₅ ⇔ O₅ is occupied, the channel should open predominantly with long openings, also at negative voltages. For the fit of the open time histograms (compare Fig. 4), this would mean that A₂ × τ_o2 >> A₁ × τ_o1. This relation was not observed.

Comparison with Previous Work

Linear state models were repeatedly used to interpret gating of CNG channels (e.g., Tanaka et al. 1989; Gordon and Zagotta 1995; Varnum et al. 1995). Voltage dependence of this gating was studied in channels of retinal rods by Karpen et al. 1988 who analyzed relaxation kinetics of macroscopic currents in response to voltage steps. These authors proposed a linear state model similar to the G₃O model used here: during the process of activation, three cGMP molecules sequentially bind to the channel and only the fully liganded channel may open by a voltage-dependent reaction. Both the experimental results and several assumptions used for modeling were different between the results of Karpen et al. 1988 in native channels of salamander rods and the present results in homooligomeric channels formed from α subunits only. (a) At all [cGMP], the activation time course in the native channels was severalfold faster than that in our currents. The reason for this difference is not clear. Possible explanations are: different subunit compositions (heterooligomeric channels formed by α and β subunits versus homooligomeric channels formed by the α subunit only) and different species (salamander retinal rods versus bovine α subunit). (b) We related our models to measured absolute values of steady state P _o, whereas Karpen et al. 1988 used relative currents with respect to the current at saturating concentrations. (c) In the model of Karpen et al. 1988, cGMP binding to the three binding sites was not assumed to be independent. In contrast, our model was based on the assumptions of independent cGMP binding. To our knowledge, more detailed experimental data to differentiate between the cGMP-binding reactions are not available. (d) In the model of Karpen et al. 1988, the entire voltage sensitivity was attributed to the closing reaction, whereas we used models with a symmetric barrier for the voltage-dependent reaction.

In the case of experimental evidence for opening of partially liganded channels, allosteric models are favored for interpretation (Ildéfonse et al. 1992; Goulding et al. 1994; Varnum and Zagotta 1996). These models generally allow opening from all closed states and the probability for opening increases in proportion to the number of ligands bound. A special case of such a model was used by Taylor and Baylor 1995 to interpret single-channel data of CNG channels of salamander rods: during the process of activation, three cGMP molecules sequentially bind to the channel and the channel may open in a voltage-dependent reaction with either two or three cGMP molecules bound. In contrast to Karpen et al. 1988, the entire voltage sensitivity was attributed to the rate constant of the opening reaction. It is noteworthy that the time constant of relaxation at saturating [cGMP] was only 22 μs (Taylor and Baylor 1995). This value basically agrees with the fast kinetics reported by Karpen et al. 1988 in the same channels, but is much faster than the corresponding activation kinetics observed in our homooligomeric channels (τ = 535 μs at +40 mV). An explanation for the faster activation time course in the native cells is that they contain additional factors (possibly subunits) that are not present in our experiments.

Interestingly, an allosteric model of the type used herein was also successful to describe the gating of large conductance Ca-activated K⁺ channels (Cox et al. 1997). These channels show several structural and functional similarities with the CNG channels: they belong to the same S4 helix–containing superfamily and they are activated by both voltage and the binding of a ligand to the COOH terminus. Though there is also an essential difference in function (Ca-activated K⁺ channels can be activated by voltage nearly maximally even in the absence of Ca²⁺, whereas CNG channels can practically not be activated in the absence of cGMP), the usefulness of the allosteric model to describe gating properties in both channel types suggests a uniform gating process.