Functional Triads Consisting of Ryanodine Receptors, Ca²⁺ Channels, and Ca²⁺-Activated K⁺ Channels in Bullfrog Sympathetic Neurons

Abstract

Fluorescent ryanodine revealed the distribution of ryanodine receptors in the submembrane cytoplasm (less than a few micrometers) of cultured bullfrog sympathetic ganglion cells. Rises in cytosolic Ca²⁺ ([Ca²⁺]_i) elicited by single or repetitive action potentials (APs) propagated at a high speed (150 μm/s) in constant amplitude and rate of rise in the cytoplasm bearing ryanodine receptors, and then in the slower, waning manner in the deeper region. Ryanodine (10 μM), a ryanodine receptor blocker (and/or a half opener), or thapsigargin (1–2 μM), a Ca²⁺-pump blocker, or ω-conotoxin GVIA (ω-CgTx, 1 μM), a N-type Ca²⁺ channel blocker, blocked the fast propagation, but did not affect the slower spread. Ca²⁺ entry thus triggered the regenerative activation of Ca²⁺-induced Ca²⁺ release (CICR) in the submembrane region, followed by buffered Ca²⁺ diffusion in the deeper cytoplasm. Computer simulation assuming Ca²⁺ release in the submembrane region reproduced the Ca²⁺ dynamics. Ryanodine or thapsigargin decreased the rate of spike repolarization of an AP to 80%, but not in the presence of iberiotoxin (IbTx, 100 nM), a BK-type Ca²⁺-activated K⁺ channel blocker, or ω-CgTx, both of which decreased the rate to 50%. The spike repolarization rate and the amplitude of a single AP-induced rise in [Ca²⁺]_i gradually decreased to a plateau during repetition of APs at 50 Hz, but reduced less in the presence of ryanodine or thapsigargin. The amplitude of each of the [Ca²⁺]_i rise correlated well with the reduction in the IbTx-sensitive component of spike repolarization. The apamin-sensitive SK-type Ca²⁺-activated K⁺ current, underlying the afterhyperpolarization of APs, increased during repetitive APs, decayed faster than the accompanying rise in [Ca²⁺]_i, and was suppressed by CICR blockers. Thus, ryanodine receptors form a functional triad with N-type Ca²⁺ channels and BK channels, and a loose coupling with SK channels in bullfrog sympathetic neurons, plastically modulating AP.

INTRODUCTION

Intracellular Ca²⁺ ([Ca²⁺]_i) in neurons plays important roles in exocytosis, regulation of cell membrane excitability, cell growth, and gene expressions (see review by Berridge 1998). To achieve these actions effectively, Ca²⁺-sensing molecules responsible for these functions should exist close to sources of the Ca²⁺. At presynaptic terminals, voltage-gated Ca²⁺ channels are coupled with proteins involved in exocytosis of neurotransmitters (Llinás et al. 1992; Heidelberger et al. 1994; Stanley 1997). In some sorts of neurons, specific types of voltage-gated Ca²⁺ channels are closely located to specific kinds of Ca²⁺-activated K⁺ channels, presumably for the effective regulation of cell membrane excitability (Marrion and Tavalin 1998).

These regulatory actions of Ca²⁺ can be amplified, if Ca²⁺-induced Ca²⁺ release (CICR; Endo et al. 1970) via Ca²⁺ release channels augments the rise in [Ca²⁺]_i created near the primary source of Ca²⁺, as known in muscles (reviewed by Endo 1977; Kuba 1994; Berridge 1998; Verkhratsky and Petersen 1998). In several types of neurons, CICR is known to generate rhythmic membrane hyperpolarizations (Kuba and Nishi 1976) and the afterhyperpolarization (AHP) of an action potential (AP; Kuba et al. 1983; Kawai and Watanabe 1989; Sah and McLachlan 1991; Yoshizaki et al. 1995; Cohen et al. 1997; Tanabe et al. 1998) and to modulate transmitter exocytosis (Smith and Cunnane 1996; Narita et al. 1998). There is little evidence, however, for the close functional coupling of ryanodine receptors to both the Ca²⁺-sensing target molecules and Ca²⁺ channels providing Ca²⁺ to trigger CICR, although the functional coupling of ryanodine receptors, voltage-gated Ca²⁺ channels and exocytotic machinery was recently reported (Narita et al. 2000).

In bullfrog sympathetic ganglion cells, CICR occurs in response to the action of caffeine (Kuba and Nishi 1976; Hernández-Cruz et al. 1990) or a long (>200 ms) depolarization (Kuba et al. 1992; Friel and Tsien 1992; Hua et al. 1993). This activation of CICR appears to take place predominantly in the cytoplasm within 5 μm from the cell membrane and around the nucleus (Hua et al. 2000). In the present study, we have investigated where, how and in what timing CICR occurs in response to Ca²⁺ entry evoked by APs and what types of Ca²⁺-dependent K⁺ channels are activated by CICR in bullfrog sympathetic neurons, using whole-cell patch-clamp and confocal laser-scanning fluorescence imaging techniques. To minimize the exogenous buffering effect of a Ca²⁺ indicator, we used Oregon green BAPTA-1 at a concentration (10 μM) much lower than the concentrations used in the previous studies (50 ∼ 100 μM, Fura-2 or Indo-1; Nohmi et al. 1992; Hua et al. 1993).

The results demonstrated that CICR indeed occurs in the submembrane region in response to Ca²⁺ influx via N-type Ca²⁺ channels activated during the spike of an AP. This CICR directly shapes the spike repolarization of the AP by opening BK-type Ca²⁺-dependent K⁺ channels (BK channels) and the AHP of the AP by activating SK-type Ca²⁺-dependent K⁺ channels (SK channels). The activation of BK channels was gradually decreased during repetition of APs by the graded reduction of CICR, broadening the spike duration. Whereas the CICR-dependent SK channel activity was also decreased during repetitive APs, the total activation of SK channels was increased by the increase in Ca²⁺ entry due to the prolonged spike duration and the accumulation of Ca²⁺. Ryanodine receptors thus form a functional triad with N-type Ca²⁺ channels and BK channels and a loose coupling with SK channels in bullfrog sympathetic ganglion cells, which plastically modulate the cell membrane excitability. Part of these findings was published in abstract form (Akita and Kuba 1999a,Akita and Kuba 1999b).

MATERIALS AND METHODS

Cell Preparations

Adult bullfrogs (Rana catesbeiana) were killed by pithing. Neurons of paravertebral sympathetic ganglia were dissociated and cultured as previously described (Hua et al. 1993). In brief, after dissociation in the presence of collagenase (3 mg/ml; Sigma-Aldrich) and trypsin (0.5 mg/ml; Sigma-Aldrich), neurons were placed on coverglasses and incubated at room temperature over 1 wk. The culture medium was based on L-15 (diluted to 70%; GIBCO BRL), supplemented with 6% fetal calf serum (Nakashibetsu), 20 ng/ml nerve growth factor (Wako Chemicals, Inc.) and 50 μg/ml gentamicin (GIBCO BRL). Large, spherical cells, 40–60 μm in diameter along their long axis and presumably B cell origin, were selected for the experiments.

Electrophysiology

A whole-cell patch-clamp technique (Hamill et al. 1981) was applied to cultured neurons at room temperature by using single electrode amplifiers (8100-1 from Dagan Corp., Minneapolis, MN; or CEZ-3100 from Nihon-Kohden, Tokyo, Japan). Patch electrodes (6–8 MΩ) were filled with a solution containing (mM): 120 K-aspartate; 7 KCl; 2 MgCl₂; 4 Na₂ATP; 0.3 Na₃GTP; 10 HEPES, and 0.01 Oregon green BAPTA-1 (OGB-1), pH 7.2. The composition of Ringer's solution was (mM): 115 NaCl; 2.5 KCl; 1 MgCl₂; 2 CaCl₂; 5 HEPES, and 10 D-glucose, pH 7.2. Voltage-gated Ca²⁺ currents were recorded in a solution containing (mM): 119 TEA-Cl; 2 CaCl₂; 5 HEPES; 10 D-glucose; supplemented with 100 nM tetrodotoxin, pH 7.2, using patch pipettes filled with a solution, in which K⁺ was replaced by Cs⁺. The liquid junction potential of Ringer's solution to the K⁺-based electrode solution and that of the TEA-based solution to the Cs⁺-based electrode solution were 11 and 20 mV, respectively.

APs were evoked by brief current pulses of 1–2 ms duration to avoid overlapping the first derivatives of the spike repolarization with the current pulses. The derivative of the spike of AP was taken to estimate the membrane current underlying spike repolarization. The rate of spike repolarization showed either single or double negative peaks. When BK channels were blocked by iberiotoxin (IbTx), the spike repolarization occasionally became diphasic in the cells, which normally showed a monophasic spike repolarization (see Fig. 10 B, b). Furthermore, IbTx predominantly decreased the initial negative peak of the diphasic derivative of spike repolarization in a considerable number of cells (see Fig. 10 A, b). The initial peak was therefore analyzed to estimate the relative change in the BK channel component of spike repolarization. The data were stored on DAT tapes through TEAC RD-135T recorder, and then analyzed with software (pCLAMP6 from Axon Instruments, Inc.; or Excel from Microsoft Co.). The current and voltage records were filtered at 3–5 kHz with a 4-pole Bessel filter (NF Corporation) before the analysis. Drugs were applied by extracellular perfusion. To avoid photolysis, nifedipine was applied under the nearly dark condition except for laser light for line scanning.

Figure 10.

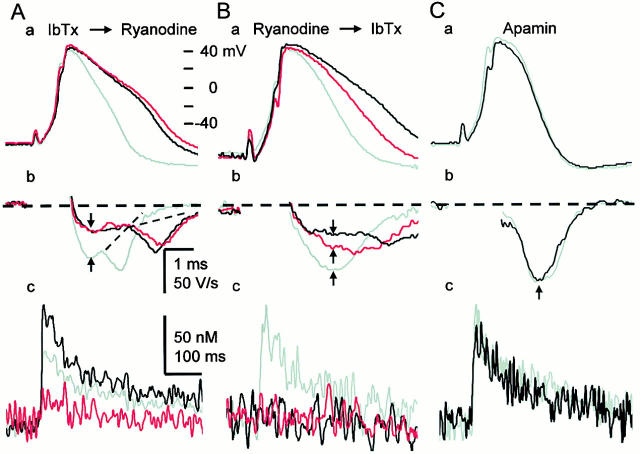
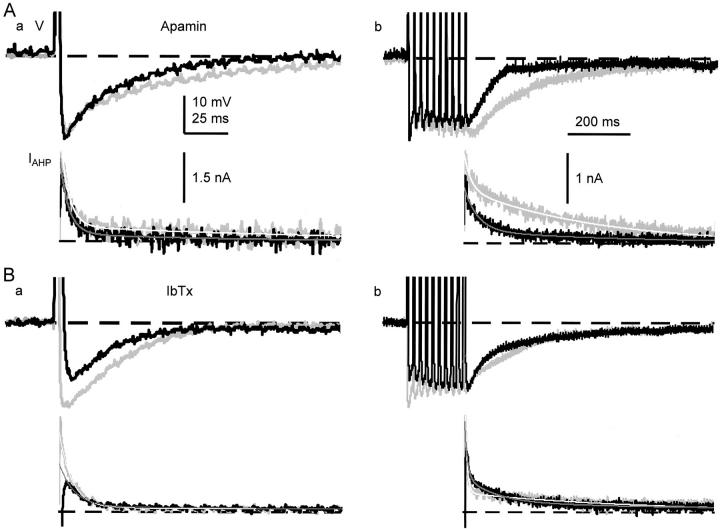
CICR activates BK channels during the spike repolarization. (A) Effects of sequential applications of IbTx and ryanodine on the spike (a), its first derivatives (b), and a single AP-induced Ca²⁺ transient (c). Ca²⁺ transients were measured within the region of 2 μm below the plasma membrane and shown in net changes in [Ca²⁺]_i. IbTx (100 nM) was first applied for 10 min, and then ryanodine (10 μM) was applied for 5 min. Gray traces indicate the records before the application of blockers, whereas black and red traces represent those after the application of IbTx and ryanodine, respectively. The derivatives of the spike during current stimulation were omitted. Vertical arrows indicate the points at which the rates of spike repolarization were measured. Dotted lines were drawn to illustrate no apparent changes in the second component of the rate of spike repolarization by the drugs. (B) Effects of sequential applications of ryanodine and IbTx on the spike (a), its first derivatives (b), and a single AP-induced Ca²⁺ transient (c). Ryanodine was first applied for 10 min, and then IbTx was applied for 10 min. Gray traces indicate the records before the application of the blockers, whereas red and black traces represent those after the application of ryanodine and IbTx, respectively. (C) Effects of apamin (100 nM) on the spike repolarization of AP (a and b) and the Ca²⁺ transient (c). Gray and black traces are the records before and 10 min after the application of apamin, respectively.

To record the current underlying AHP (I_AHP), a bridge current clamp mode was electronically switched to a voltage clamp mode at the end of the spike of AP (hybrid clamp; Lancaster and Adams 1986). For analysis, the current obtained was fitted to an exponential decaying function with a nonlinear least square fitter (Levenberg-Marquadt routine) of software (Mathcad2000; Mathsoft Inc.). The switching was made at the time when the spike repolarization of a single AP or the last of repetitive APs reached the holding potential level (−50 mV) to avoid a capacitative surge. The timing of the switching was determined under the control condition but fixed throughout a series of the experiment. This yielded comparison of I_AHPs (i.e., membrane conductance) under different conditions at the same timing after the beginning of Ca²⁺ entry and the resultant CICR. When the duration of the spike of an AP became longer in some conditions, however, there was a positive shift of membrane voltage relative to the holding potential at the time of the switching. In this case, the starting point of the fitting was set at 1–2 ms after the switching and the amplitude of I_AHP was estimated at the time of the switching by extrapolation. Another drawback was that the comparison of voltage-sensitive components of the current at the same voltage level became not possible due to the voltage shift. The switching at the higher voltage and the faster timing (1–2 ms at most) might overestimate the initial amplitude of the current relaxation of voltage-gated K⁺ currents relative to that expected to be obtained at −50 mV. On the other hand, it was possible that a component of the voltage-sensitive K⁺ conductance that would have been activated during the rest of repolarization phase (that was abolished by voltage-clamping) was lost in the record of the current relaxation produced at the earlier switching. Thus, these two opposite effects could be compromised. The extent of this overestimation would be less than the difference between the amplitude of I_AHP at the time of switching and the amplitude at the time, at which the prolonged spike repolarization was expected to reach −50 mV. The difference was 28%, for instance, when IbTx prolonged the fast decay time constant of the I_AHP evoked by 1 AP to 8 ms (see Fig. 14 B, b).

Figure 14.

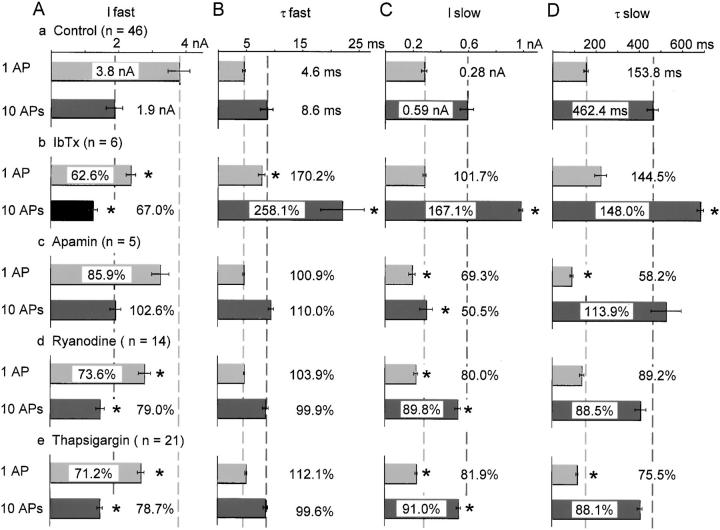
Effects of IbTx, apamin, ryanodine and thapsigargin on two components of I_AHP. The time course of I_AHP was fitted by the equation, I_AHP = I_fast× exp(−t/τ_fast) + I_slow × exp(−t/τ_slow) [nA]. (A and B) The amplitude and time constants of fast I_AHP. (C and D) The amplitude and time constants of slow I_AHP. Effects of the blockers are shown in percentages of control, reflected in the relative length of bars for the control. Pale and dark gray dashed lines indicate 100% level of control for each component of I_AHPs after 1 AP and 10 APs, respectively. Asterisks (*) indicate that changes are significantly different from the corresponding control values (P < 0.01). Numerical values are shown only for the mean in or outside each column, whereas the SEM is shown by a horizontal bar.

[Ca²⁺]_i Measurement

Neurons were loaded with a Ca²⁺ indicator, OGB-1 (10 μM), through a patch pipette. Equilibrium of OGB-1 loaded was attained 15–20 min after the opening of a membrane patch. Neurons were scanned with blue laser (488 nm, 0.45 mW) using a confocal scan unit (MRC-600; Nippon BIO-RAD Laboratories) attached to an inverted microscope (TMD-300; water immersion 40× objective, NA 1.15; Nikon). The diameter of the confocal aperture was set to be 3.1 mm, yielding the lateral and axial resolutions of 0.15 and 1.25 μm, respectively (measured at the half maximum decay length of the fluorescence of a 0.21-μm fluorescent bead). The whole image of a neuron was initially obtained by a X-Y scan mode, and then the neuron was line-scanned at the time resolution of 2 or 4 ms across the cell soma.

The in vivo K _d of OGB-1 was determined by the modified version of a calibration method (Tokimasa et al. 1997). In brief, cells were immersed in a pseudo-intracellular solution (PIS) containing each [Ca²⁺]_i (0, 0.1, 0.3, 1, and 100 μM) and 20 μM digitonin for 25 min. The cells were then incubated in digitonin-free PIS containing 10 μM OGB-1 for 15 min. After removal of the PIS, the cells were briskly rinsed once with dye-free PIS and then covered with liquid paraffin. The fluorescence intensity in the submembrane region (within 5 μm beneath the cell membrane) of the cytosol was averaged over six to seven cells, and then plotted against [Ca²⁺]_i values. The K _d of OGB-1 thus determined was 438 nM (F_min/ F_max = 0.123), whereas the K _d in vitro measured in the same PIS was 215.4 nM (F_min/ F_max = 0.085).

The ratio of fluorescence intensity (F) of OGB-1 during and after the application of electrical pulses or a drug to that before the application (F₀) was taken for conversion of fluorescence intensity to [Ca²⁺]_i values. Since no spatial gradient of the resting [Ca²⁺]_i in this cell was already checked by confocal laser microscopy with two-wavelength Ca²⁺ indicators in the previous study (Nohmi et al. 1992), this procedure canceled out the spatial inhomogeneous distribution of the Ca²⁺ indicator in the cells (see Fig. 2A and Fig. B). [Ca²⁺]_i values were calculated according to the following equation:

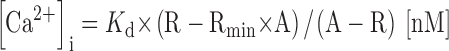1

where R (= F/F₀) is the ratio; R_min = F_min/F_max; A = (K _d + [Ca²⁺]_i(0)/(K _d × R_min + [Ca²⁺]_i(0)) and [Ca²⁺]_i(0) is the resting basal [Ca²⁺]_i value in the absence of CICR blockers. During the acute period of the actions of ryanodine or thapsigargin, however, some cells showed the inhomogeneous rise in the basal [Ca²⁺]_i higher in the submembrane region than in the deeper cytoplasm, presumably due to a localized Ca²⁺ release (see Fig. 2 C and results).

Figure 2.

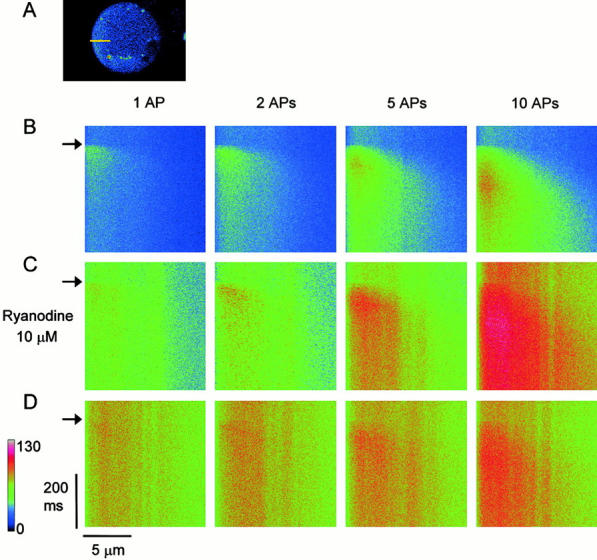
The inward spread of Ca²⁺ transients evoked by single or repetitive APs in the submembrane region of the cytoplasm. (A) The X-Y scanned fluorescence image of a ganglion cell. A yellow bar shows the scanned line of 12 μm across the cytoplasm with no nucleus. (B) Line-scanned fluorescence images of Ca²⁺ transients evoked by 1, 2, 5, and 10 APs at 50 Hz. The left side edge of each image corresponds to the plasma membrane of the cell. An AP or a train of APs was elicited at the time marked by arrows. (C) The line-scanned images of AP-induced Ca²⁺ transients recorded at 5 min after the application of ryanodine (10 μM). (D) The images taken at 10 min after the application. Note that ryanodine initially increased the basal level of [Ca²⁺]_i and enhanced AP-evoked Ca²⁺ transients (C), and then diminished the transients in this cell (D). A color bar represents fluorescence intensity in an arbitrary unit. Each line-scanned image is the average of five scanned images obtained every 20 s.

The calculation of [Ca²⁺]_i values depended critically on the assumption of [Ca²⁺]_i(0). In this study, [Ca²⁺]_i(0) was assumed to be 96 nM, according to the mean value measured with Fura-2 in the previous study (Nohmi et al. 1992). In most cases, the maximum increase in the fluorescence ratio induced by single or repetitive AP(s) was in the range of 0.3 ∼ 0.5, which was equivalent to [Ca²⁺]_i values of 170 ∼ 225 nM. These values of [Ca²⁺]_i were far less than the in vivo K _d of OGB-1. Thus, most [Ca²⁺]_i values obtained can be considered in the linear range of the conversion formula. After the application of ryanodine or thapsigargin, the resting [Ca²⁺]_i was increased (see results). In some cells, the converted value of AP-evoked [Ca²⁺]_i rise in the presence of the drugs sometimes reached the range of micromolar. This is almost out of the range of [Ca²⁺]_i values measurable with OGB-1 fluorescence. Nevertheless, since no signs of the saturation of OGB-1 fluorescence were seen in this study (compare the image for 10 APs in Fig. 2 C and that in Fig. 2 D), the high converted value of the [Ca²⁺]_i was considered to be due to the wrong assumption of [Ca²⁺]_i(0). In these cases, the [Ca²⁺]_i(0) value was set to be 34 nM, the lower bound value estimated in the previous study (Nohmi et al. 1992).

The propagation (wave) velocity of a Ca²⁺ transient in the submembrane region of the cell was measured as follows. The time courses of a Ca²⁺ transient were measured at two points of different distances (a few micrometers) from the cell membrane in the fast propagation phase of the cytoplasm. The distance between these points was then divided by the difference between the peak times of the Ca²⁺ transients, yielding the velocity of Ca²⁺ wave. The rate of rise of a Ca²⁺ transient was defined as the quotient of the peak amplitude to the peak time. For the accurate measurement of the rate of rise, the signal-to-noise ratio of Ca²⁺ transients was decreased by averaging them over the whole region of the fast propagating region within 1–2 μm from the plasma membrane (except for Fig. 6 B, b; see legend). Photobleaching of OGB-1 was negligible during the course of line scan and therefore not considered in analyses.

Figure 6.

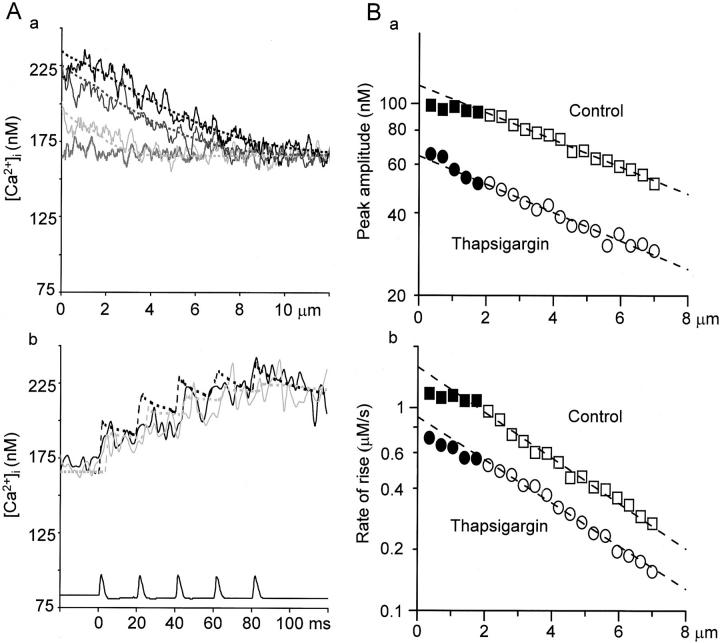
Effects of thapsigargin on the spatial and temporal characteristics of a five AP-induced Ca²⁺ transient and their simulation. (A) The spatial (a) and temporal (b) profiles of the 5APs-evoked Ca²⁺ transient in the presence of thapsigargin and their simulation. Decreasing Ca²⁺ release and no Ca²⁺ uptake at Ca²⁺ stores was assumed in the simulations as in Fig. 4, Aa and Ba. The values assumed for all the parameters were the same as those in Fig. 4 (A and B, a) except for the amplitude of Ca²⁺ release (which was the half of the initial value of the control; 0.9 nA) and the increased basal [Ca²⁺]_i (166 nM). (A, a) Continuous lines show the profiles of [Ca²⁺]_i in the presence of thapsigargin (2 μM, 10 min) after the generation of first (pale gray), third (dark gray), and fifth AP (black) indicated by the vertical arrows in Fig. 5 A, b. The shaggy, gray line shows the basal [Ca²⁺]_i. Dotted lines represent the simulated spatial profiles of [Ca²⁺]_i. (A, b) The temporal profiles of [Ca²⁺]_i identical to traces 1 and 2 in Fig. 5 C, b (solid black and gray) and their simulation (dotted black and gray). (B) The spatial decay in the peak amplitude and the rate of rise of five APs-induced Ca²⁺ transients toward the deeper cytoplasm. The peak amplitudes (a) and the rates of rise (b) of AP-induced Ca²⁺ transients in the absence (squares) and presence of thapsigargin (2 μM; circles) were plotted against the distances from the cell membrane in semi-logarithmic scale. The rate of rise in this figure was defined as the linear regression slope from the beginning of the rise to the peak. The values in the fast propagation phase are shown by closed symbols, whereas those in the slow phase are shown by open symbols. The dashed lines show the results of single exponential fitting over the points in the slow phase. Note that the points in the fast phase for both parameters deviate from the fitting in control and the deviation become small after the treatment with thapsigargin.

Computer Simulations

AP-induced Ca²⁺ dynamics involving CICR was simulated based on the rapid buffering and linearized approximation of the diffusion equation (Wagner and Keizer 1994; Zador and Koch 1994). The approximation was justified for the range of changes in [Ca²⁺]_i far below the in vivo K _d of OGB-1. In this situation, the effective diffusion coefficient (D_eff) is expressed as (D_Ca + D_m × β_m)/(1 + β_m + β_f), where D_Ca is the diffusion coefficient of free Ca²⁺ (223 μm²/s; Allbritton et al. 1992), whereas D_m is that of the mobile buffer. β_m and β_f are buffering capacities of mobile and fixed buffers (Neher and Augustine 1992). Only the Ca²⁺ indicator was assumed to be the mobile buffer under the whole-cell patch-clamp. β_m can be expressed as [B_m]_T/K_m, where [B_m]_T and K_m are the total concentration (10 μM) and the K _d of the Ca²⁺ indicator. The spherical model cell of 20-μm radius was compartmentalized into 100 concentric shells of 0.2-μm width. Time (0.1-ms step) and spatial integration over the compartments were performed on MathCad2000 software with Crank-Nicolson scheme (Crank and Nicolson 1947).

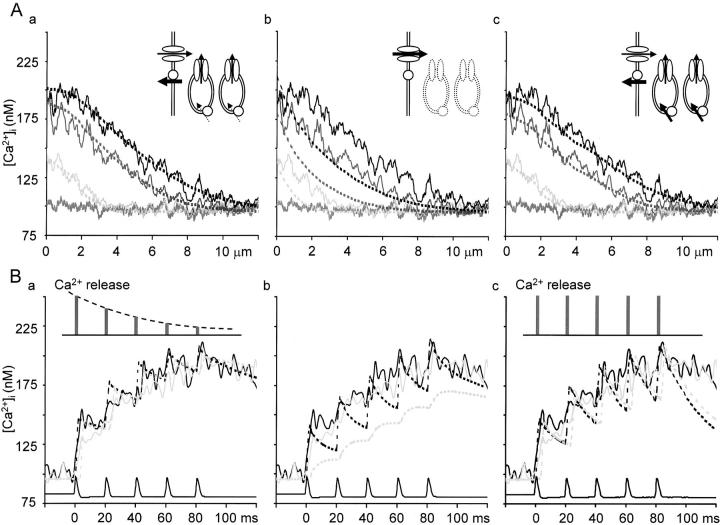
To reproduce the temporal and spatial dynamics of the initial phase (120 ms) of 5APs-evoked Ca²⁺ transients, we tried three types of simulation under different assumptions. In the first type of simulation (Fig. 4A and Fig. B, a), Ca²⁺ entry, Ca²⁺ release, fixed and mobile buffers, Ca²⁺ extrusion, but not Ca²⁺ uptake, were considered. Ca²⁺ flux of constant amplitude (1.5 nA) and duration (1 ms) every 20 ms was involved in the outermost shell for Ca²⁺ entry through voltage-gated Ca²⁺ channels. To mimic Ca²⁺ release, Ca²⁺ flux of constant duration (1 ms) was incorporated to take place every 20 ms in each shell in the region 4 μm beneath the plasma membrane. (Although this formulation does not represent the real mechanism of CICR, it is appropriate at least to test whether the additional source of Ca²⁺ plays a role in the spatial and temporal characteristics of AP-induced Ca²⁺ transients recorded experimentally.) The timing of the flux in each shell was delayed by 0.5 ms from the outer adjacent shell. The amplitude of the flux was assumed to decrease exponentially (time constant; 50 ms) until the end of the fifth pulse. The distribution of the sources of Ca²⁺ release was divided into two parts of 2 μm in depth; the outer high-density region and the inner low-density region. The initial amplitude of the flux in each shell was set to be 8.8 × 10⁻⁹ μmol/s (equivalent to 1.7 nA of Ca²⁺ current) in the high-density region and 4.4 × 10⁻⁹ μmol/s (equivalent to 0.85 nA of Ca²⁺ current) in the low-density region. Noncooperative, Michaelis-Menten type Ca²⁺ pumps and leakage at the cell membrane were included in the outermost shell (Sala and Hernández-Cruz 1990). The maximum speed of the pump at the cell membrane was set to be 1.4 × 10⁻⁴ μmol/cm² × s. The Ca²⁺ concentration for its half-maximal activation was 0.83 μM. Endogenous fixed rapid buffers were assumed only in the submembrane region of 4 μm in depth. β_f was set to be 75 (Neher and Augustine 1992). D_m of 120 μm²/s yielded the best result, a slightly higher value than that of fura-2 in axons of Aplysia neurons (102.5 μm²/s; Gabso et al. 1997).

Figure 4.

The spatial and temporal profiles of a 5APs-evoked Ca²⁺ transient and their reconstruction by computer simulation. (A) The spatial profiles of the Ca²⁺ transient and their simulation. Pale gray, dark gray, and black lines show the profiles of [Ca²⁺]_i averaged over 10-ms periods after the generation of first, third, and fifth AP indicated by the vertical arrows in Fig. 3 B, b. The abscissas show the distances from the plasma membrane. Each trace was smoothed by the spatial running average over 0.2 μm. Shaggy, gray lines show the basal [Ca²⁺]_i. Dotted lines show the simulated spatial profiles of [Ca²⁺]_i under different assumptions, representing the results of temporal average over the same periods as the corresponding experimental traces. The assumptions are illustrated by the drawings in insets, including voltage-gated Ca²⁺ channel (ellipses) and a Ca²⁺-pump (a circle) at the cell membrane and Ca²⁺ release channels (vertical ellipses) and Ca²⁺ pumps (circles) at the endoplasmic reticulum (ER) membrane. Arrows indicate the direction of Ca²⁺ flux via these channels and pumps, the width of which reflects the relative amount of the flux to each other, defined in the modeling. See materials and methods for the details of parameters. (A, a) Simulation assuming Ca²⁺ release of decreasing amplitude from the submembrane ER. The magnitude of Ca²⁺ release was assumed to decrease exponentially. Dashed arrows beside the pumps on ER indicate that there must be a small amount of Ca²⁺ pump flux in the actual system, although they were not explicitly included in the modeling (see results). (A, b) Simulation assuming only the diffusion process for the transport of Ca²⁺ in the cytoplasm. (A, c) Simulation assuming Ca²⁺ release of constant amplitude and Ca²⁺ uptake at the ER. (B) Computer simulation of the time courses of the initial phase of the Ca²⁺ transient. Pale gray and black lines show the time courses of Ca²⁺ transients identical to the traces 1 and 2 in Fig. 3 D, b. Dotted lines represent the results of simulation averaged over the three neighboring shells (0.6-μm wide) at the regions corresponding to the experimental records. Assumptions used in the simulation B (a–c) were the same as those of A (a–c), respectively. Voltage traces of APs triggering the Ca²⁺ transient are shown at the bottom. The relative magnitudes of Ca²⁺ release assumed are shown in B (a and c).

The second type of simulation (see Fig. 4A and Fig. B, Fig. b) incorporated only Ca²⁺ entry at the plasma membrane and the mobile buffer (for the Ca²⁺ indicator) in the cytoplasm. Ca²⁺ release, endogenous fixed buffers (except for the outermost shell), Ca²⁺ extrusion and uptake were not included. A greater flux was assumed for Ca²⁺ entry (3.2 nA). Other parameters were the same as in the first type.

The third type of simulation (see Fig. 4A and Fig. B, Fig. c) incorporated Ca²⁺ entry, Ca²⁺ release, fixed and mobile buffers, Ca²⁺ extrusion and uptake. The amount of Ca²⁺ entry was the same as in the first type of simulation. Ca²⁺ release was similarly defined as those of the first type, but the magnitude was fixed constant during its repetition. The maximum rate of Ca²⁺ pumping at Ca²⁺ storing organelles was assumed 64% (0.9 × 10⁻⁴ μmol/cm² × s) of that at the cell membrane with the same affinity. The area occupied by the pumps in each compartment was assumed equal to the surface area of the cell for the outer 2-μm region and its half for the deeper 2-μm region. Other parameters were the same as those in the first type.

Chemicals

Thapsigargin, ryanodine, and nifedipine were purchased from Wako Chemicals, Inc. Iberiotoxin, apamin, ω-conotoxin GVIA, digitonin, TEA, and HEPES were from Sigma-Aldrich. OGB-1 and BODIPY FL-X ryanodine were from Molecular Probes. TTX was from Alomone Labs.

Statistics

Each data is shown by mean ± SEM. Student's paired t test was performed for statistical comparison with Microsoft Excel software.

RESULTS

CICR Occurs in the Submembrane Regions

Localization of Ryanodine Receptors in Bullfrog Sympathetic Neurons

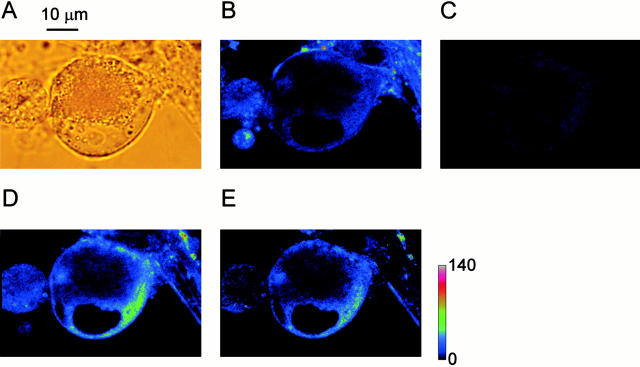
Ryanodine receptors in bullfrog sympathetic neurons were stained with fluorescent ryanodine, BODIPY FL-X ryanodine (0.5 μM). To subtract nonspecific binding of fluorescent ryanodine, the following protocol was adopted. Ganglion cells in culture (Fig. 1 A) were first incubated in a solution containing both fluorescent ryanodine (0.5 μM) and ryanodine (10 μM) for 10 min. Under this condition, there was weak fluorescence in narrow regions close to the cell membrane and perinuclear regions (Fig. 1 B). After washing with Ringer's solution for 30 min (Fig. 1 C), fluorescent ryanodine (0.5 μM) alone was applied for 8 min. This procedure gave strong fluorescence in almost the same cytoplasmic regions (Fig. 1 D) as those showing weak fluorescence in Fig. 1 B. The subtraction of the image in Fig. 1 B from that in Fig. 1 D showed a similar distribution of the fluorescence (Fig. 1 E) to those in Fig. 1B and Fig. D, indicating the negligible nonspecific binding of fluorescent ryanodine in the cytoplasm of ganglion cells. Thickness of the submembrane distribution ranged from 1 to 3 μm in most cases (n = 14). With some cells, as in Fig. 1, the distribution of ryanodine receptors was also recognized around the inner boundary of the nucleus. In such cases, the perinuclear fluorescence was likely to reach the submembrane region, comprising a wider (5–6 μm) distribution of the fluorescence. This indicates the intracellular network of Ca²⁺ stores endowed with ryanodine receptors, which may transmit Ca²⁺ signals from the cell membrane toward the nucleus. In this study, we focus on the mode of CICR activation in the submembrane region related to the modulation of cell membrane excitability, whereas the mechanism of CICR activation in the perinuclear region will be reported elsewhere.

Figure 1.

Distribution of ryanodine receptors stained with fluorescent ryanodine in a cultured bullfrog sympathetic ganglion cell. (A) A bright-field image of a ganglion cell. Note the nucleus with a clear nucleolus in its center facing the lower edge of the cell. (B) The fluorescence image obtained at 10 min after the combined application of 10 μM ryanodine and 0.5 μM BODIPY FL-X ryanodine. (C) After washout of the dye and ryanodine with Ringer's solution for 30 min. (D) After reapplication of 0.5 μM BODIPY FL-X ryanodine alone for 8 min. (E) The image obtained by the subtraction of the image B from the image D. Negative values were clipped to zero. A color-coding bar shows fluorescence intensity in an arbitrary unit.

Fast and Slow Propagation of a Ca²⁺ Transient in the Cytoplasm Evoked by an AP or APs

A region of the cytoplasm within 12 μm from the cell membrane (Fig. 2 A) was line-scanned with a confocal laser microscope before, during, and after current pulse stimulation. This provided the time courses of single-dimensional changes in fluorescence evoked by 1–10 APs (50 Hz), representing those of [Ca²⁺]_i (Ca²⁺ transients; Fig. 2, B–D). Ca²⁺ transients initially occurred in the cytoplasm just beneath the cell membrane and spread toward the deeper cytoplasm. The propagation front of the increased [Ca²⁺]_i showed two phases; fast and slow. The fast propagation front was almost flat and clearly demarcated from the resting fluorescence, spanning 1.5–2 μm beneath the plasma membrane (Fig. 2 B). The width of the fast phase was analogous to that of the distribution of ryanodine receptors identified by fluorescent ryanodine (Fig. 1 E). On the other hand, the slow phase following the fast phase showed the dull front plane of the propagation and became wider as the number of APs was increased (Fig. 2 B and 3 B).

Regenerative Activation of CICR in the Fast Propagation Front of a Ca²⁺ Transient

Similarity between the width of the distribution of ryanodine receptors and that of the fast propagation phase of a Ca²⁺ transient suggests the regenerative activation of CICR during the fast propagation. The time courses of a single AP-induced Ca²⁺ transient at discrete points in the fast propagating region were quite similar. The amplitude and rate of rise of the single AP-induced Ca²⁺ transient only slightly decreased with an increase in distance from the cell membrane and slightly delayed in peak time (traces 1 and 2 in Fig. 3D and Fig. E, a). The peak amplitude of the Ca²⁺ transient induced by a single AP or the first of APs in a train was on average 58.5 ± 13.3 nM (n = 31). Likewise, the time courses of a five AP-induced Ca²⁺ transient in the fast propagation phase followed a similar trend (traces 1 and 2 in Fig. 3D and Fig. E, Fig. b; see filled squares in Fig. 6 B). The peak amplitude of a five APs-induced Ca²⁺ transient within the fast phase was 167.2 ± 28.8 nM.

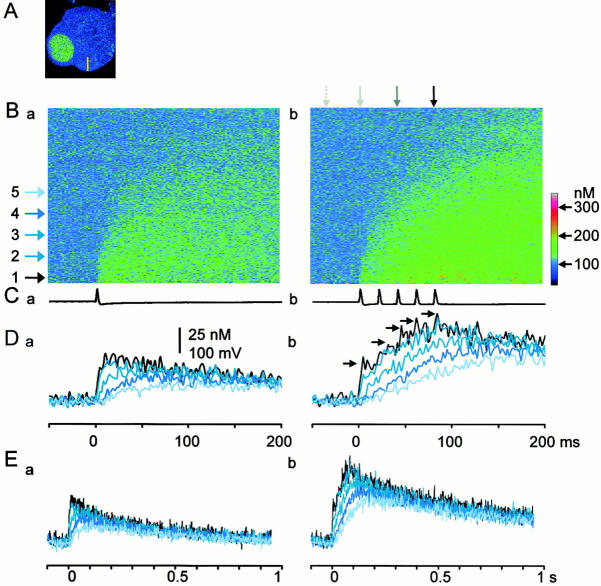
Figure 3.

Temporal profiles of the inward spread of AP-evoked Ca²⁺ transients. (A) The X-Y scanned image of a ganglion cell. A yellow bar indicates the line (12 μm) scanned across the cytoplasm. (B) The fluorescence ratio images of the inward spreads of Ca²⁺ transients evoked by 1 AP (a) and 5 APs (b). Line-scanned fluorescence images recorded with single and five APs were divided by the image without stimulation. The lower edge of each image corresponds to the plasma membrane. Each image is the average of five scanned images obtained every 20 s. Horizontal arrows spaced every 1.5 μm indicate the positions, at which the time courses of Ca²⁺ transients in D and E were measured. Vertical arrows above the image (b) point the times, at which the spatial profiles of the increased [Ca²⁺]_i shown in Fig. 4 A were taken. The arrows represent the timings of before, the first, third, and fifth AP generations, respectively. A color coding bar is expressed in [Ca²⁺]_i values. (C) Voltage traces of an AP and APs given during the line-scans shown in B. (D and E) Time courses of Ca²⁺ transients at the points indicated by the horizontal arrows in B. The time scale in D is identical to those of the images in B and voltage records in C. Each trace is the average of pixel values over 0.5 μm. The black arrows in Db were added to note the progressive decrease in the amplitude of the [Ca²⁺]_i rise during the course of APs.

The characteristics of the propagation of Ca²⁺ transients are also shown in their spatial profiles (Fig. 4 A). As APs were successively delivered on the cell, the spatial profiles of [Ca²⁺]_i within 2 μm beneath the plasma membrane, corresponding to the fast propagation region, became gradually flat. Computer simulation assuming only the diffusion process without fixed buffers and extrusion processes (both of which should slow Ca²⁺ diffusion) for intracellular Ca²⁺ dynamics failed to demonstrate the formation of the flat propagation region (Fig. 4 A, b). Instead, the simulation including the additional sources of Ca²⁺ in the submembrane region nicely reproduced the experimental data (Fig. 4 A, a). With this assumption of the additional sources of Ca²⁺, the time courses of 5APs-induced Ca²⁺ transients were also reconstructed well (Fig. 4 B, a), whereas the assumption of no additional Ca²⁺ sources failed to reproduce them (Fig. 4 B, b). Thus, the flat gradient of the rise in [Ca²⁺]_i in the submembrane region must be caused by the activation of additional sources of Ca²⁺ during the fast propagation, namely the regenerative activation of CICR, producing a “Ca²⁺ wave” in the fast phase. The propagation velocities of the Ca²⁺ wave (see materials and methods) evoked by a single and five APs were 183.7 ± 17.8 μm/s and 142.5 ± 15.9 μm/s (n = 31), respectively.

Blockade of the Fast Ca²⁺ Wave Propagation by Ryanodine and Thapsigargin

The final test of the activation of CICR in the submembrane region is to observe the actions of blockers of Ca²⁺ release or uptake on AP-induced Ca²⁺ transients. Ryanodine (10 μM) or thapsigargin (1–2 μM) raised the basal level of [Ca²⁺]_i (Fig. 2C and Fig. D). The magnitudes of the increases were 65.8 ± 26.6 nM (n = 11) or 58.8 ± 22.3 nM (n = 12), respectively, at 10 min after the application. Although the increased basal [Ca²⁺]_i remained over 30 min in most cells, some cells showed recovery and/or reduction of the basal level within 30 min by 17.9 ± 4.3 nM (4/15) or 9.2 ± 2.4 nM (3/15) from the base level of the control even in the presence of ryanodine or thapsigargin, respectively. Sometimes a transitory, spatially inhomogeneous increase in the basal [Ca²⁺]_i occurred during the course of the application of CICR blockers (Fig. 2 C; 1AP and 2APs). Its extent differed from cell by cell, but it finally disappeared in most cases (Fig. 2 D).

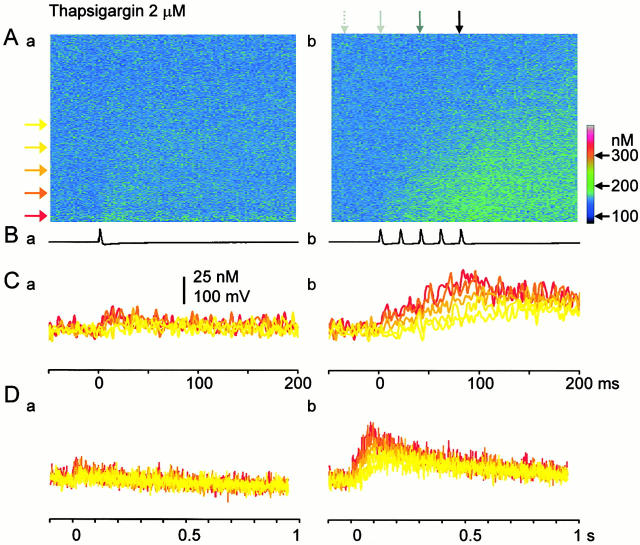
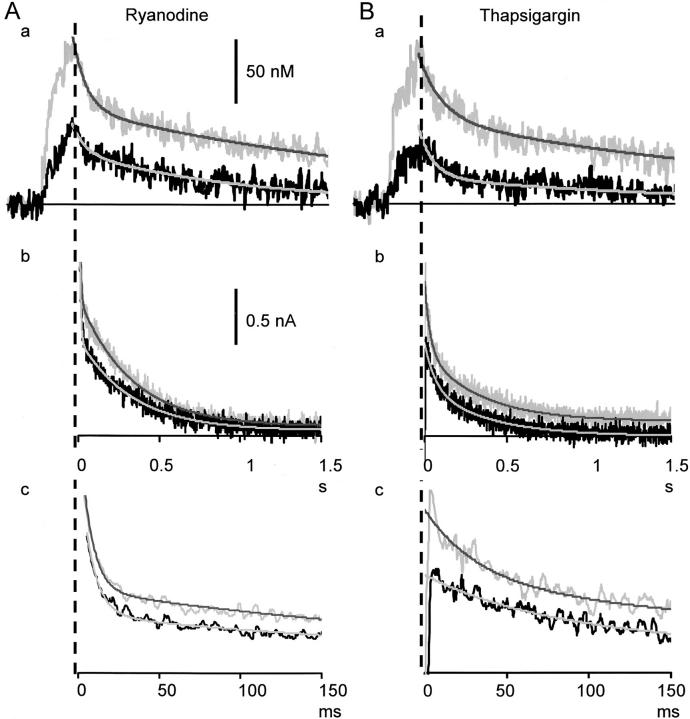
Ryanodine (10 μM) decreased Ca²⁺ transients in the submembrane region evoked by a single AP or the first AP in a train to 49.1 ± 9.1% of the control, and the total amplitude of five APs-induced Ca²⁺ transients to 50.1 ± 7.2% at 10 min after its application (see Fig. 7 C, a for a single AP-induced Ca²⁺ transient). Likewise, thapsigargin (1–2 μM) depressed Ca²⁺ transients evoked by a single AP or the first AP in a train to 46.6 ± 10.7%, and the total amplitude of five APs-Ca²⁺ transients to 50.4 ± 8.9% at 10 min after the application (Fig. 5, Fig. 6 B, and 7, A and B, a). The rate of rise in [Ca²⁺]_i by a single AP or the first AP in a train was also reduced similarly to 47.0 ± 7.6% by ryanodine and to 42.1 ± 8.9% by thapsigargin. Under this condition, the Ca²⁺ wave in the fast phase disappeared leaving only the slow, waning mode of propagation (Fig. 5 and Fig. 6). The full blocking action of ryanodine or thapsigargin on AP-induced Ca²⁺ transients was seen within 1–3 min in some cells, but mostly it took over 30 min. The actions of CICR blockers were not due to the saturation of Ca²⁺ indicators (see materials and methods, and also Fig. 2 legend) and the decrease in Ca²⁺ entry caused by the action of the blockers on voltage-gated Ca²⁺ channels (see the next section and Fig. 8). Computer simulation with the assumption of the reduction in Ca²⁺ release to 50% of the control and the increased basal level of [Ca²⁺]_i with unchanged Ca²⁺ entry also reproduced the effects of CICR blockade on the time course and the spatial spread of five APs-induced Ca²⁺ transients (Fig. 6 A).

Figure 7.

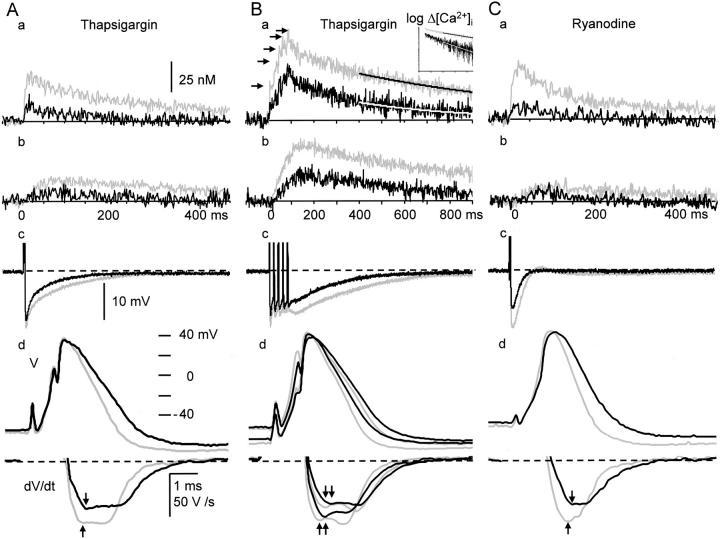
Effects of thapsigargin and ryanodine on the spikes and AHP of APs and the accompanying Ca²⁺ transient. (A) Effects of thapsigargin on single APs and Ca²⁺ transients. (a) and (b); single AP-induced Ca²⁺ transients measured at 0–1 μm (a) and 5–6 μm (b) from the plasma membrane. They consist of averaged pixel values over the regions obtained from five ratio images taken at 20-s intervals. Each Ca²⁺ transient is shown by the net change in [Ca²⁺]_i. Thapsigargin increased the basal [Ca²⁺]_i by 23 nM in this cell. (c) The AHPs of APs in the same time scale as the Ca²⁺ transients. (d) Spikes and their rates of fall of the APs. Gray and black traces indicate the records before and 10 min after the application of thapsigargin (1 μM), respectively. The derivatives of the spikes during current stimulation were omitted. Vertical arrows indicate the points at which the rates of spike repolarization were compared. (B) Effects of thapsigargin on repetitive APs and Ca²⁺ transients. Explanations are essentially the same as those in A except for the following points. The spikes of the first and fifth APs and their derivatives are shown in d. The spikes of shorter duration and their greater derivatives in gray and black traces correspond to those of the first APs. Smooth lines superimposed on the Ca²⁺ traces in a show the results of single exponential fittings over a period beginning at 400 ms after the first of stimuli, at which the spatial gradient of [Ca²⁺]_i disappeared. The inset in a shows the same decay time course of the [Ca²⁺]_i in semi-logarithmic scale. Black horizontal arrows in a note progressive decreases in the amplitude of [Ca²⁺]_i rises induced by individual APs. (C) Effects of ryanodine (10 μM) on the spike and AHP of a single AP and the accompanying Ca²⁺ transient. Ryanodine increased the basal [Ca²⁺]_i by 85 nM from the control level in this cell. Explanations are the same as those in A.

Figure 5.

Effects of thapsigargin on AP-evoked Ca²⁺ transients. (A–D) The inward spreads and time courses of Ca²⁺ transients induced by a single AP (a) and five APs (b) in the presence of thapsigargin (2 μM). Explanations are the same as those in Fig. 3B–E except that the data were taken in the presence of thapsigargin. Note that the basal [Ca²⁺]_i increased by thapsigargin corresponds to cold colors for the clearer demonstration of Ca²⁺ transients. However, the difference in the [Ca²⁺]_i level from the control is shown in the scaling of the color cord.

Figure 8.

No effects of thapsigargin and ryanodine on Ca²⁺ currents and their rundown and no restoring effect of high Ca²⁺ on the Ca²⁺ transients suppressed by CICR blockers. (A) The time courses of Ca²⁺ current rundown in the absence and presence of thapsigargin or ryanodine. A depolarizing voltage pulse from −75 to 0 mV (10–50 ms of the pulse duration) evoked Ca²⁺ currents. Open circles with a vertical bar indicate the mean ± SEM of the peak amplitudes of Ca²⁺ currents in the absence of a blocker (n = 24), whereas triangles and squares with a vertical bar are those in the presence of thapsigargin (1 μM; n = 19) and ryanodine (10 μM; n = 13), respectively. Each data point for CICR blockers was normalized to the amplitude before the application of the blockers. Dashed lines are the results of single exponential fitting with time constants of 29.2 min for the control, 30.0 and 30.2 min for those in the presence of thapsigargin and ryanodine, respectively. (B) No restoring effect of high extracellular Ca²⁺ on the Ca²⁺ transients suppressed by CICR blockers. Upper and lower traces represent Ca²⁺ transients (in fluorescence ratio change (ΔF/F₀); to show the less possibility of the dye saturation) and Ca²⁺ currents induced by voltage pulses of 50 ms from −75 to 0 mV (shown in the middle trace) at 15 (a), 25 (b), 30 (c), and 35 min (d) after the opening of a membrane patch. Ca²⁺ transients were measured from the region of 5-μm width beneath the cell membrane. Ryanodine (10 μM) was applied immediately after the record (a). The extracellular Ca²⁺ concentration ([Ca²⁺]_o) was raised to 10 mM after the end of the record (c).

The spatial gradient of Ca²⁺ transients induced by one or five APs disappeared at 400–500 ms after the beginning of stimuli (Fig. 3 E). The decay time course of an increased [Ca²⁺]_i over that period would reflect the rate of Ca²⁺ clearance in the cytoplasm, i.e., Ca²⁺ extrusion and uptake. The blockade of Ca²⁺ pump or the opening of ryanodine receptors on Ca²⁺ stores is then expected to retard the rate of this Ca²⁺ clearance. Unexpectedly, however, both ryanodine and thapsigargin shortened the decay time constant of the AP-induced Ca²⁺ transient over 400 ms after the beginning of stimuli in most cases (Fig. 7 B, a and inset). The decay time constant of the five APs-transient (822.9 ± 98.4 ms) decreased to 72.8 ± 14.2% (P < 0.01) by the application of ryanodine for 10 min and to 70.2 ± 12.3% (P < 0.01) by thapsigargin. One possible explanation might be that CICR remains to be activated to some extent after the end of Ca²⁺ entry and is eliminated by the blockers. Alternatively, Ca²⁺ release from mitochondria, which may normally occur during the late decay phase of Ca²⁺ transient following Ca²⁺ uptake during the rising phase (Colegrove et al. 2000), could be reduced for the suppression of Ca²⁺ transients under the blockade of CICR. This issue needs to be studied.

Reduction of Ca²⁺ Entry Does Not Explain the Depressant Actions of CICR Blockers

Run-down of Ca²⁺ current (I_Ca) during the course of whole-cell recording or the blockade of voltage-gated Ca²⁺ channels by CICR blockers might explain the depressant actions of the drugs on the Ca²⁺ transients. We first examined the run-down of I_Ca induced by a voltage pulse (10–50 ms). The rate of run-down of I_Ca varied among cells and patch-clamp conditions. The amplitude of I_Ca decreased on average by 15–20% (n = 24) at 8 min after the opening of the membrane patch (Fig. 8 A) and so was the accompanying Ca²⁺ transient (by 23.2 ± 6.5%, n = 8; data not shown). These reductions were much smaller than the decrease (50%) in AP-induced Ca²⁺ transients produced by ryanodine or thapsigargin (Fig. 7, A–C, a). Next, we examined effects of ryanodine (10 μM) and thapsigargin (1–2 μM) on I_Ca and its run-down. The blockers affected neither the amplitude nor the rate of run-down of I_Ca (Fig. 8 A). In some cells, the depressant effects of ryanodine or thapsigargin on the amplitude of Ca²⁺ transients appeared long after its application (Fig. 8 B, c). Even in these cells, where the I_Ca run-down proceeded to a fair extent, the amplitude of Ca²⁺ transient was not recovered after raising the extracellular Ca²⁺ and restoring the amplitude of the I_Ca (Fig. 8 B, d). Accordingly, the depressant actions of ryanodine and thapsigargin did not result from the reduction of I_Ca due to its blockade or run-down. The results also indicate that the principal mechanism of the increase in [Ca²⁺]_i evoked by an AP or APs is CICR in bullfrog sympathetic ganglion cells, similar to the mechanism in cardiac muscles. This is also supported by the successful simulation of AP-induced Ca²⁺ transients with the assumption of a large Ca²⁺ release 17 times greater than Ca²⁺ entry (see materials and methods).

Graded Reduction of the Submembrane CICR during Repetitive APs

Another remarkable feature of APs-induced Ca²⁺ transients was the progressive decrease in the rises in [Ca²⁺]_i produced by individual APs during repetitive stimulation. The amplitude and rate of rise in [Ca²⁺]_i evoked by the first AP were the largest and those by the subsequent APs became progressively smaller (Fig. 3 D, b, and Fig. 7 B, a). The amplitude of the rise evoked by the fifth AP (25.2 ± 3.9 nM) was 43.4 ± 3.6% of the first. Similarly, the rate of rise in [Ca²⁺]_i induced by the first AP was 7.1 ± 1.5 μM/s, whereas that induced by the fifth AP was 46.7 ± 5.5% of the first.

There are several possible mechanisms for the progressive decrease in the [Ca²⁺]_i rise. The acceleration of Ca²⁺ uptake into Ca²⁺ stores, say via thapsigargin-sensitive pumps, might have reduced the net Ca²⁺ flux during the later part of stimuli. This is unlikely, however, according to the simulation assuming the Ca²⁺ entry and release of constant magnitude and the Michaelis-Menten type Ca²⁺ pumping in the submembrane region, the strength of which was adjusted so that the peak [Ca²⁺]_i values reached by the individual simulated Ca²⁺ rises were matched to those of the experimental data. Although the simulation apparently reproduced the spatial profiles of [Ca²⁺]_i averaged over the period of 10 ms after the first and third AP (Fig. 4 A, c), it was unable to reconstruct the progressive reduction in amplitude and the decay phase of the individual [Ca²⁺]_i rise (Fig. 4 B, c). Varying the pump speed, cooperativity or the affinity for Ca²⁺ also failed to improve the large discrepancy between the results of simulation and the observations (not shown). Mitochondrial Ca²⁺ uptake that responds to the microdomains of high [Ca²⁺]_i (Rizzuto et al. 1998) is also unlikely for the mechanism of the progressive reduction of Ca²⁺ transients, since its operation could be regarded as the rapid buffering system (i.e., β_f in our simulation) for its fast kinetics (see reviews by Carafoli 1987 and Rizzuto et al. 1999).

Another possible mechanism would be the progressive decline in Ca²⁺ release during repetition of APs. This was again tested by computer simulation assuming the exponential decay in Ca²⁺ release flux until the end of repetitive pulses. This simulation not only yielded the progressive reduction in the amplitude of individual Ca²⁺ rises during repetitive APs, but also reproduced the spatial profiles of the Ca²⁺ transient and the decay phases of the individual Ca²⁺ rises (Fig. 4A and Fig. B, a). (Thapsigargin-sensitive Ca²⁺ pumps were not explicitly included to yield the best fitting, indicating that such a pumping would have so small and slow kinetics that it should not actually affect the time course of the Ca²⁺ transient during the short period of stimulation.) Thus, the inherent property of Ca²⁺ release appears to be involved in the progressive decrease in Ca²⁺ rises during repetitive APs. This may be the inactivation of Ca²⁺ release (Fabiato 1985) or Ca²⁺ depletion. Ca²⁺ depletion, however, may have not occurred during repetition of 5–10 APs, since CICR blockers largely increased the basal [Ca²⁺]_i (Fig. 2C and Fig. D) and took longer time to cease CICR. We will report the details of the property of the inactivation of CICR elsewhere.

Ca²⁺ Influx through N-type Ca²⁺ Channels Triggers CICR

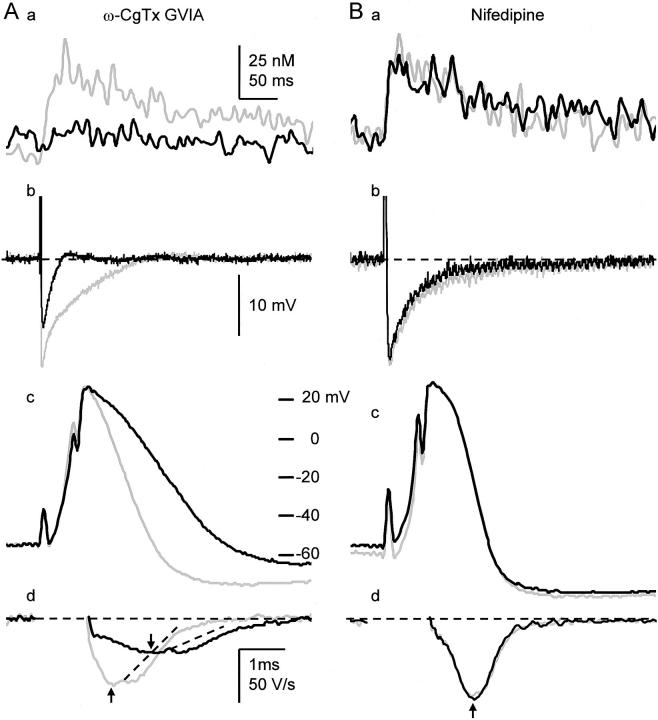
Bullfrog sympathetic ganglion cells are endowed predominantly with N-type Ca²⁺ channels, and less with L- and other types of Ca²⁺ channels (Jones and Marks 1989a; Elmslie et al. 1994). ω-CgTx at 1 μM drastically blocked Ca²⁺ transients induced by a single AP to 18.3 ± 6.5% (n = 8; Fig. 9 A, a) and those by 10 APs to 32.2 ± 8.2% (not shown) at 10 min. Nifedipine (20 μM), however, did not affect single AP-induced Ca²⁺ transients (96.6 ± 12.9%, n = 6; Fig. 9 B, a) and slightly reduced 10 APs-induced Ca²⁺ transients to 79.6 ± 8.22% (n = 6), which was the same as that caused by the run-down of I_Ca (see above). Thus, Ca²⁺ entry via N-type Ca²⁺ channels activates CICR in bullfrog sympathetic neurons.

Figure 9.

N-type Ca²⁺ channels are involved in the generation of AP-induced Ca²⁺ transients, spike repolarization and AHP of APs. (A) Effects of ω-CgTx (1 μM) on a single AP-induced Ca²⁺ transient (a), AHP (b), the spike (c), and its first derivatives (d) of the AP. AHPs are shown in the same time scale in a. Gray and black traces are the records before and 10 min after the application of ω-CgTx (1 μM), respectively. Ca²⁺ transients were measured from the region of 2-μm width beneath the cell membrane. The derivatives of the spikes during current stimulation were omitted. Vertical arrows indicate the points at which the rates of spike repolarization were compared. Dotted lines were drawn to illustrate no apparent changes in the second component of the rate of spike repolarization by ω-CgTx. (B) Effects of nifedipine (20 μM) on the Ca²⁺ transient, AHP, the spike and its first derivatives of a single AP. Explanations are the same as those in A.

Passive Propagation of Ca²⁺ Transients in the Deeper Cytoplasm

As single or five APs-induced Ca²⁺ transients spread into the region deeper than a few micrometers from the plasma membrane, they decreased progressively in amplitude, rate of rise, and peak time (traces 3–5 in Fig. 3B, Fig. D and Fig. E; open squares in Fig. 6 B). The passive property of Ca²⁺ propagation in the slow phase was clearly shown in the spatial and temporal profiles of the rise in [Ca²⁺]_i (Fig. 3 and Fig. 4 A). During the train of stimuli, the spatial profiles in the slow phase showed gradual decreases in [Ca²⁺]_i toward the center of the cell (Fig. 4 A). As the amplitude of the rise in [Ca²⁺]_i in the fast phase decreased after the end of the stimuli, the [Ca²⁺]_i in the deeper region of the slow phase slowly increased until the spatial gradient of [Ca²⁺]_i disappeared (traces 3–5 in Fig. 3 D), and then decayed over hundreds of milliseconds to several seconds (Fig. 3 E). Thus, only the buffered Ca²⁺ diffusion process would contribute to the propagation in the deeper cytoplasm. Computer simulation with no assumption of Ca²⁺ release, fixed Ca²⁺ buffering and pumping in the deeper cytoplasm also reconstructed well the spatial profiles of the rise in [Ca²⁺]_i both in the absence and presence of CICR blockers (Fig. 4 A and 6 A, a).

The passive property of the propagation can also be demonstrated by the spatial decay in the amplitude and rate of rise of a five APs-induced Ca²⁺ transient (Fig. 6 B, a and b). The spatial decay of the amplitude and rate of rise were fitted by single exponentials, yielding their “length constants” (λ_amp and λ_r) in the slow propagation phase. λ_amp and λ_r were found to be 6.4 ± 0.6 μm and 3.4 ± 0.3 μm, respectively. Theses length constants were not significantly affected by ryanodine and thapsigargin (99.1 ± 2.3% or 99.7 ± 2.0% of the control for λ_amp and 100.5 ± 3.8% or 102.5 ± 3.8% for λ_r, respectively; Fig. 6 B). The results also support the predominance of the diffusion process in the deeper cytoplasm.

CICR Shapes the Spike Repolarization and AHP of APs

Possible target molecules of CICR in the submembrane region would be two types of Ca²⁺-activated K⁺ channels: BK channels (Adams et al. 1982) facilitating the spike repolarization and SK channels generating AHP of APs (Pennefather et al. 1985). Thus, it is possible that CICR shapes directly the spike and AHP of an AP that triggers CICR.

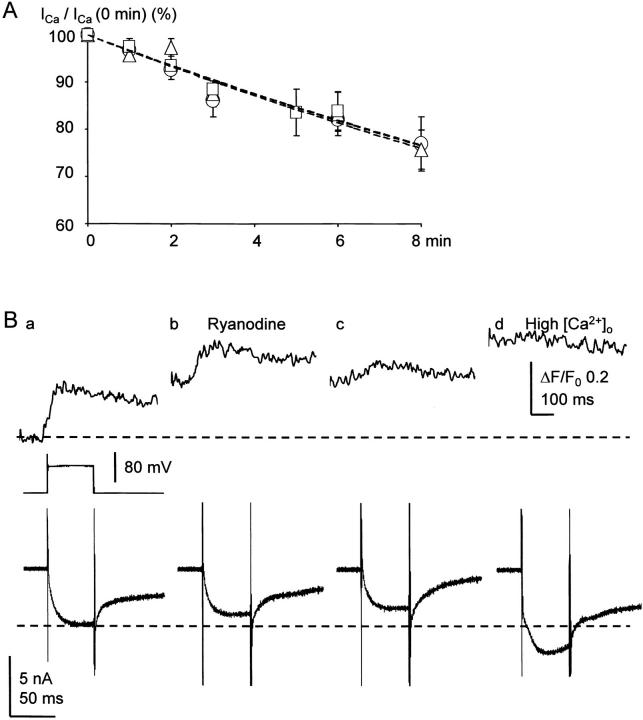
Blocking CICR gave three modes of actions in shaping APs. First, the maximum rate of spike repolarization of an AP or the first AP in a train was reduced to 79.1 ± 8.3% (P < 0.01, n = 11) of the control (−76.7 ± 6.9 V/s, n = 37) by ryanodine (10 μM; Fig. 7 C, d) and to 81.9 ± 4.4% (P < 0.01, n = 12) by thapsigargin (1 ∼ 2 μM; Fig. 7 A, d) after their application for 10 min. Those of the fifth spike in a train at 50 Hz were 70.1 ± 5.8% (not shown) and 70.3 ± 4.1% (Fig. 7 B, d), respectively. These reductions were not due to the run-down of any types of ion channels because of intracellular perfusion, since there was no change in the slope of spike repolarization during the same period in the absence of the blockers (102.7 ± 1.4%, P > 0.1, n = 14; not shown). Second, the amplitude of the AHP of an AP was decreased to 85.5 ± 6.8% (n = 11, P < 0.01) of the control (20.4 ± 0.9 mV) by ryanodine (Fig. 7 C, c and d) or to 88.9 ± 2.8% (n = 12; P < 0.01) by thapsigargin (Fig. 7 A, c and d). Those of the fifth AP in a train at 50 Hz were 85.9 ± 5.2% (not shown) and 86.4 ± 3.7% (Fig. 7 B, c) of the control (17.2 ± 1.1 mV), respectively, the degree of which were not significantly different from those of a single AP (P > 0.1). Third, the half decay time of the AHP of an AP was shortened to 85.7 ± 9.3% (control, 34.0 ± 4.7 ms) by ryanodine (Fig. 7 C, c) or to 80.1 ± 11.7% by thapsigargin (Fig. 7 A, c). Those of the fifth AP in a train were 86.1 ± 7.8% (control, 144.6 ± 28.7 ms) by ryanodine (not shown) or to 78.7 ± 7.2% by thapsigargin (Fig. 7 B, c). Again, the extent of the decrease was not different from that of a single AP (P > 0.1).

Spike-triggered CICR Activates BK-type Ca²⁺-dependent K⁺ Channels for Spike Repolarization

It is likely that the broadening of the spike of AP and the reduction in the amplitude of AHP under the blockade of CICR are caused by the reduction in BK channel activity, for the known role of BK channels in spike repolarization. To examine how many fractions of spike repolarization is attributed to BK channel activity, we first examined the effect of IbTx on spike repolarization. IbTx (100 nM) markedly prolonged the spike of an AP, decreased its maximum rate of fall to 49.0 ± 3.7% (n = 13) at 10 min after the application (black traces in Fig. 10 A, a and b) and enhanced the single AP-induced Ca²⁺ transient in the submembrane region (Fig. 10 A, c, black trace). In many cells, the derivative of spike repolarization was diphasic (Fig. 10 A, see also Fig. 7 B and 9 A). IbTx decreased its initial phase, but not the late phase (Fig. 10 A, b). In contrast, a blocker of SK channel, apamin (100 nM), had no effect on spike repolarization (100.0 ± 2.7%, P > 0.1, n = 5; Fig. 10 C, a and b) and Ca²⁺ transients (Fig. 10 C, c). Thus, the activation of BK channel contributes to 50% of the rate of spike repolarization, predominantly to its initial phase. In the presence of IbTx, ryanodine had little effects on the spike of AP (n = 5, P > 0.1; red traces in Fig. 10 A, a and b), although it considerably suppressed the accompanying Ca²⁺ transient (Fig. 10 A, c, red trace). Furthermore, blocking Ca²⁺ entry by ω-CgTx (1 μM) reduced the rate of spike repolarization, preferentially its initial phase, to 52.2 ± 2.6% (n = 7, Fig. 9 A, c and d), whereas nifedipine had no effect (100.1 ± 1.0%, P > 0.1, n = 8, Fig. 9 B, c and d). Thus, only the BK channel participates in the Ca²⁺-dependent K⁺ current for spike repolarization in response to Ca²⁺ entry via N-type Ca²⁺ channels and the resultant CICR. (Enhancement of the AP-induced Ca²⁺ transient by blocking BK channels with IbTx is obviously caused by an increase in Ca²⁺ entry.)

Next, we asked how many fractions of BK channels are activated by CICR for spike repolarization. We first blocked the CICR-activated component of spike repolarization with ryanodine or thapsigargin. Then, we eradicated all the remaining BK channel activity with IbTx. As already shown (Fig. 7 C, d), ryanodine reduced the rate of spike repolarization to 80% (red traces in Fig. 10 B, a and b), and the subsequent application of IbTx further decreased it to 50% (black traces). The sequential depressant actions of ryanodine and IbTx occurred preferentially on the initial phase of spike repolarization so that its monophasic shape changed to diphasic one (Fig. 10 B, b, see also Fig. 7 A), indicating the involvement of the CICR-dependent activation of BK channels in the initial phase of spike repolarization. Combination of the applications of thapsigargin and IbTx showed similar results (not shown). As the rate of voltage change (i.e., the first derivatives) reflected the actual membrane current, these values yielded the fraction of BK channels activated by CICR, which was at least 40% ([100 − 80] × 100/[100 − 50]). It may be noted that the Ca²⁺ current component of spike repolarization, which is in the opposite direction, would have been negligible, as estimated from the difference between the effects of ω-CgTx and IbTx (<3% [52–49%]; no statistical significance).

Decrease in CICR-dependent BK Channel Activity during a Train of APs

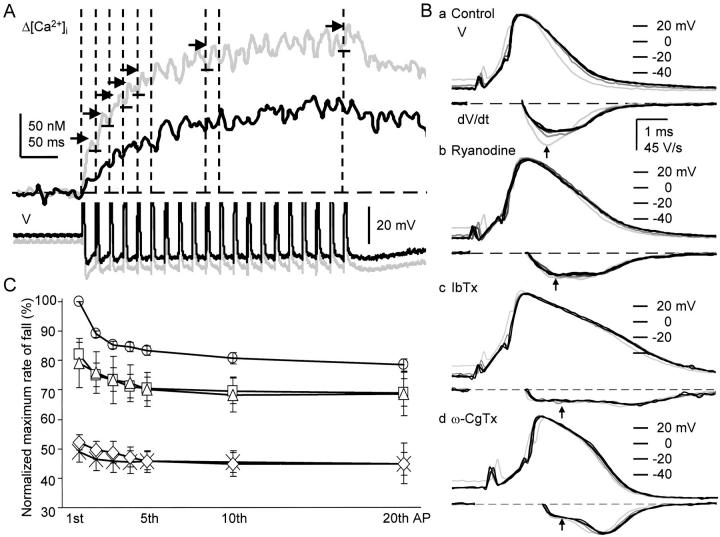
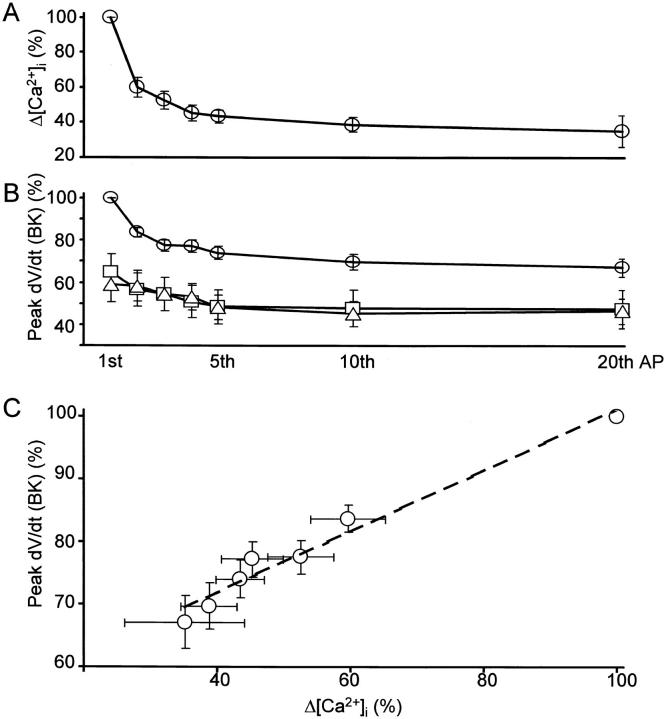
The progressive decrease in each AP-induced [Ca²⁺]_i rise in the submembrane region during a 5APs-train (Fig. 3 D, b, and Fig. 7 B, a and b) suggests the waning of BK channel activation by CICR during repetitive APs. We explored this possibility in detail by evoking a train of 20 APs at 50 Hz. During repetition of APs, the spike of AP broadened progressively (Fig. 11 B, a). The rate of spike repolarization decreased and attained a plateau value of 79.0 ± 2.2% at the tenth to twentieth AP (Fig. 11B and Fig. C, circles). The peak of the corresponding rise in [Ca²⁺]_i evoked by each AP in a train also decreased with the progress of stimulation and reached a plateau value of 35.2 ± 9.0% of the first (Fig. 11 A and 12 A). On the other hand, repetition of APs in the presence of ω-CgTx (1 μM) or IbTx (100 nM) decreased the rate of spike repolarization only by 5% (from 50% to 44.8 ± 3.8% or 44.9 ± 6.8%, respectively, at the twentieth spike; Fig. 11 B, c and d, and diamonds and crosses in Fig. 11 C, respectively). These results obviously indicate that the spike broadening during repetitive generation of APs results predominantly from the progressive reduction in BK channel activity and less from that in other K⁺ currents (compare Aldrich et al. 1979; Ma and Koester 1996). The subtraction of the rates of repolarization in the presence of IbTx from those in the absence of IbTx yielded the time course of changes in the BK channel component of spike repolarization during repetitive APs (open circles in Fig. 12 B). The magnitude of the BK channel component was significantly correlated with that of the corresponding rise in [Ca²⁺]_i evoked by each AP (Fig. 12 C). The maximum reduction of BK channel activation ascribed to AP repetition was 32% ([100 − 79 − 5] × 100/50; Fig. 12 B).

Figure 11.

Reduction in the rate of spike repolarization and the accompanying Ca²⁺ transients during repetitive APs. (A) Time courses of increases in [Ca²⁺]_i induced by 20 APs in the submembrane region and the accompanying AHPs. Upper records are the net increases in [Ca²⁺]_i (Δ[Ca²⁺]_i) within 2 μm from the plasma membrane, whereas lower records are the AHPs. Gray and black traces are those before and 10 min after the application of ryanodine (10 μM), respectively. Each trace of the records of [Ca²⁺]_i changes was the average of two records and smoothed by a moving average over 6 ms. Vertical dashed lines indicate the timing of the first to fifth, tenth, and twentieth spike, corresponding to each of those of AP-evoked Δ[Ca²⁺]_i. Horizontal short arrows and bars were added to note the decrease in the individual Δ[Ca²⁺]_i during the repetitive APs. (B) The first, second, fifth, tenth, and twentieth APs and their first derivatives in a 50-Hz train in the absence and presence of ryanodine, IbTx and ω-CgTx. (a)Control APs; (b) APs recorded at 10 min after the application of ryanodine (10 μM). (c) APs recorded at 10 min after the application of IbTx (100 nM) following ryanodine. (d) APs in the presence of ω-CgTx (1 μM) applied for 10 min in another cell. The derivatives of the spike during the rising phase were omitted. Vertical arrows indicate the points at which the rates of spike repolarization were measured. (C) Reduction in the rate of spike repolarization during repetitive APs. The maximum rate of fall of each spike was normalized to that of the first in the absence of blockers. The mean ± SEM of pooled data obtained before (circles, n = 31) and after the application of ryanodine (10 μM, squares, n = 11), thapsigargin (1–2 μM, triangles, n = 12), ω-CgTx (1 μM, diamonds, n = 8) and IbTx (100 nM, crosses, n = 13) were plotted and bound with straight lines.

Figure 12.

Correlation of BK channel activity to individual AP-induced rise in [Ca²⁺]_i during repetition of APs. (A) Changes in each AP-induced increase in [Ca²⁺]_i in the submembrane region (Δ[Ca²⁺]_i) during a train of 20 APs at 50 Hz. Each change in Δ[Ca²⁺]_i was normalized to that evoked by the first AP in a train in the absence of blockers. (B) Changes in IbTx-sensitive fraction of the maximum rate of spike repolarization (peak dV/dt [BK]) in the absence (open circles; n = 14) and the presence of ryanodine (squares; 10 μM, 10 min, n = 7) or thapsigargin (triangles; 1–2 μM, n = 7). The maximum rate of spike repolarization in the presence of IbTx was subtracted from each of those in the absence of IbTx. This procedure yielded the IbTx-sensitive component of spike repolarization in the presence and absence of CICR blockers. All the data were normalized to the maximum fractional decrease of the first AP in the presence of IbTx (50% of the control; see Fig. 11 C). (C) Correlation between Δ[Ca²⁺]_i shown in A and peak dV/dt (BK) shown in B. Error bars indicate the means ± SEM. A dashed line in C expresses the slope of linear regression (0.57).

Ryanodine (10 μM) or thapsigargin (1 ∼ 2 μM) decreased the extent of the reduction in the rate of spike repolarization induced by repetitive APs, which was only 12% (from 79.1% to 68.5 ± 7.4% or from 81.9% to 69.0 ± 4.7%, respectively, at the twentieth spike). Accordingly, the maximum net decreases in the BK channel component under these circumstances were 14% ([12 − 5] × 100/50; open triangles and squares, respectively, in Fig. 12 B). These results strongly indicate that the spike broadening during repetitive APs results from the progressive reduction of CICR in the submembrane region evoked by each AP. The lesser extent of the broadening in the presence of the blockers could be explained by the same type of decrease in residual CICR. These progressive decreases in each of AP-induced Ca²⁺ transients as well as BK channel activation during repetitive APs could not be due to the inactivation of Ca²⁺ channels because of their slow inactivation property (Jones and Marks 1989b). (Ryanodine or thapsigargin reduced the amplitude of each AP-induced rise in [Ca²⁺]_i and the plateau level during the course of stimulation [Fig. 11 A]. However, the faithful quantitative measurement of the individual AP-induced rises in [Ca²⁺]_i was not possible because of the high noise level due to the high background fluorescence.) Consequently, the sum of the reduction in the ryanodine- or thapsigargin-sensitive component of the spike repolarization of the first AP (40%) and that brought about by repetition of APs in the presence of CICR blockers (14%) provides an estimate of the total fraction of BK channels activated by CICR for spike repolarization, which was 54%. The remaining fraction of Ca²⁺-dependent spike repolarization must therefore depend on another source of Ca²⁺, i.e., Ca²⁺ entry.

The Shift in Predominance from BK to SK Channels for AHP Generation during Repetitive APs

Shortening of AHP by suppression of CICR (Fig. 7, A–C, c) suggests that CICR also regulates SK channels. Apamin (100 nM), a SK channel blocker (Pennefather et al. 1985; Tanaka et al. 1986), reduced the half-decay time of AHP of an AP to 72.2 ± 9.1%, but not the amplitude (99.8 ± 2.8% of the control, n = 5; Fig. 13 A, a). In contrast, IbTx (100 nM) markedly decreased the amplitude of AHP following a single spike to 76.5 ± 3.5% (n = 7) and the half decay time to 81.8 ± 5.7% (Fig. 13 B, a). This indicates that the initial component of AHP of an AP is produced by the activation of BK channels, whereas the later component is caused by the activation of SK channels. In addition, ω-CgTx suppressed both the amplitude (50.7 ± 4.8%) and half-decay time of AHP of an AP (48.1 ± 6.1%, n = 8, Fig. 9 A, b), whereas nifedipine did not affect the AHP (peak amplitude; 100.2 ± 1.1%, half-decay time; 91.5 ± 9.3%, n = 8, Fig. 9 B, b). Ca²⁺ entry via N-type Ca²⁺ channels and the subsequent CICR thus activate Ca²⁺-dependent K⁺ channels that contribute to 50% of AHP formation of an AP.

Figure 13.

Changes in the magnitude of the contribution of BK and SK channels to the generation of AHP during repetitive stimuli. (A) Effects of apamin on the AHPs and I_AHPs following single (a) and 10 (b) spikes. Gray and black traces are the records before and 10 min after the application of apamin (100 nM). (B) Effects of IbTx on the AHPs and I_AHPs following single (a) and 10 (b) spikes. Gray and black traces are the records before and 10 min after the application of IbTx (100 nM). Each smooth line on the I_AHP shows the result of double exponential fitting (see Fig. 14 for the amplitude and time constant of each component).

This mode of AHP generation, however, changed with repetition of APs due to the progressive decrease in BK channel activity. IbTx (100 nM), which significantly reduced the amplitude of the first AHP (Fig. 13 B, a), did not affect the amplitude of the tenth AHP (105.0 ± 3.8%) and reduced the half-decay time only slightly (74.6 ± 9.3%; Fig. 13 B, b). On the other hand, apamin (100 nM), which did not affect the amplitude of the first AHP (Fig. 13 A, a), decreased that of the tenth AP to 89.0 ± 5.1% and markedly the half-decay time to 49.3 ± 4.8% (Fig. 13 A, b). Thus, SK channel activity increased during repetitive APs, compensating for the reduction in BK channel activity in AHP formation. This increase in SK channel activity as well as the decrease in BK channel activity was also recognized in the membrane current underlying the AHP (I_AHP).

The time course of I_AHP was best fitted with a double exponential function in most cases. The amplitude of the fast decay component of I_AHP (fast I_AHP) following a single AP was decreased after repeating 10 APs at 50 Hz (Fig. 14 A, a), whereas the decay time constant was increased (Fig. 14 B, a). On the other hand, the amplitude of the slow component of I_AHP (slow I_AHP) was increased after repeating 10 APs (Fig. 14 C, a). Under this condition, the time constant of the slow I_AHP was also increased (Fig. 14 D, a).

IbTx (100 nM) reduced the amplitude of the fast I_AHP following 1 AP and 10 APs (Fig. 13 B and Fig. 14 A, b) and increased their time constants (Fig. 14 B, b). In contrast, apamin (100 nM) had no significant effects on the fast I_AHP (Fig. 14A and Fig. B, Fig. c). Thus, BK channel activity is largely involved in the fast I_AHP. The lesser contribution of BK channel activity to the fast I_AHP (38% for 1 AP and 33% for 10 APs; see Fig. 14 A, b) than that estimated from the rate of repolarization (51% for 1 AP and 34% for 10 AP; see above) may indicate the faster decay in BK channel activity during spike repolarization than other voltage-gated K⁺ currents. (Prolongation of the time constant of fast I_AHP by repeating repetitive APs or the action of IbTx would reflect the longer time constants of other K⁺ channel currents, which became apparent after the reduction of BK channel component.) Ryanodine and thapsigargin decreased the amplitude of the fast I_AHP (Fig. 14 A, d and e), indicating again the activation of BK channels by CICR.

Apamin applied for 10 min decreased the amplitude of the slow I_AHP following 1 and 10 APs (Fig. 13 A) to 69 and 50%, respectively (Fig. 14 C, c). In contrast, IbTx did not affect the amplitude of the slow I_AHP after a single AP (Fig. 14 C, b). Thus, SK channel is involved in the slow I_AHP and its fraction was increased from 31 to 50% by repetition of APs. (IbTx increased the amplitude of the slow I_AHP after 10 APs (Fig. 14 C, b) and the time constants of the slow I_AHPs after single and 10 APs (Fig. 14 D, b). These increases can be accounted for by an increase in Ca²⁺ entry due to the broadened spike duration; see the following section.) These results together with those in preceding paragraphs demonstrate that the shift in predominance from BK to SK channels for AHP formation occurs during repetition of APs.

Changes in the Mode of SK Channel Activation during Repetitive APs

The foregoing results demonstrated that the component of SK channel activity in AHP formation increased during a train of APs, whereas BK channel activity decreased progressively due to the reduction of CICR. Since the suppression of AHP by ryanodine or thapsigargin (Fig. 7, A–C, c) suggests that SK channels are also activated by CICR, the CICR-dependent component of SK channel activity is expected to decrease during repetitive stimulation. This was the case.

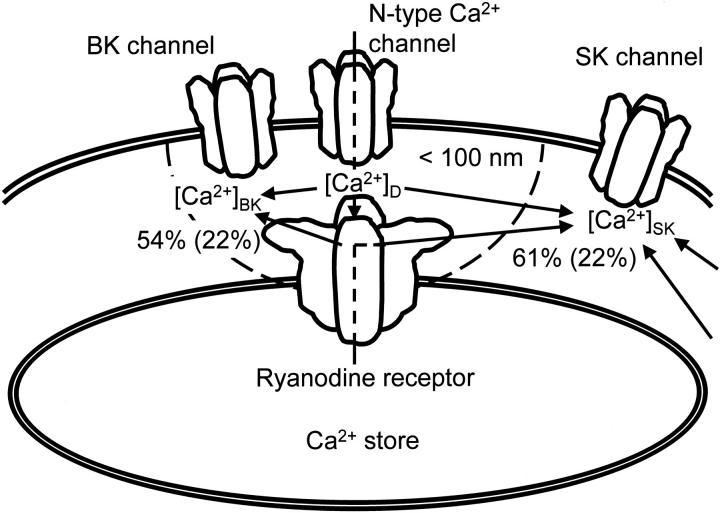
Ryanodine (10 μM) and thapsigargin (1 μM) reduced the amplitude of the slow I_AHP (reflecting SK channel activity) after a single AP by 19% and 18%, respectively, whereas they decreased the amplitude after 10 APs by 11% and 9% (Fig. 14 C, d and e, and Fig. 15A and Fig. B, Fig. b and Fig. c, respectively). The difference between those of single and 10 APs in each condition is statistically significant (P < 0.01). Since the apamin-sensitive SK channel component of the slow I_AHP amplitude were 31% for a single AP and 50% for 10 APs (see above), the CICR-dependent fraction of SK channel activity were calculated to be 61% (19/31) and 22% (11/50), respectively (Fig. 16). Thus, the CICR-dependent SK channel activity decreases with repetition of APs as in the case of BK channels. The increase in the total activity of SK channels during repetitive APs must then be explained by other mechanisms.

Figure 15.

Comparison of the decay time courses of AP-induced Ca²⁺ transients and the accompanying I_AHPs and effects of ryanodine and thapsigargin on them. (A) Effects of ryanodine on the Ca²⁺ transient within 2 μm from the plasma membrane (a) and the corresponding I_AHP (b and c) induced by 10 spikes. Gray and black traces are the records before and 10 min after the application of ryanodine (10 μM). I_AHPs are shown in different time scales (b and c). The time scale of b is the same as that of the Ca²⁺ transient in a. Each of smooth lines on the Ca²⁺ transients and I_AHPs shows the result of double exponential fitting to the decay phase of each trace after the end of current stimuli. (B) Effects of thapsigargin (1 μM) on the Ca²⁺ transient (a) and the I_AHP (b and c) induced by 10 spikes. Other explanations are the same as those in A.

Figure 16.

A scheme to illustrate spatial relationships among ryanodine receptor, N-type Ca²⁺ channel, BK, and SK channels. [Ca²⁺]_D means the [Ca²⁺]_i in the Ca²⁺ microdomain closed to the orifices of N-type Ca²⁺ channel and ryanodine receptor Ca²⁺ release channel. [Ca²⁺]_BK and [Ca²⁺]_SK are the Ca²⁺ concentrations involved in the activation of BK and SK channels, respectively. Arrows indicate the pathways of Ca²⁺ entering via N-type Ca²⁺ channels or ryanodine receptors. Numbers with percents indicate the fraction of the contribution of CICR to the activation of BK or SK channel involved in a single AP generated sparsely, whereas the numbers in parentheses are those during a sustained high frequency induction of APs.

Two mechanisms can be deduced for the increase in SK channel activity as follows: First, this increase in SK channel activity in contrast to the decrease in BK channel activity indicates that SK channel is not activated by the [Ca²⁺]_i in the microdomain sensed by BK channel (see discussion). Furthermore, the duration of the activation of SK channels, reflected in the time courses of the slow I_AHP and AHP, were comparable (albeit shorter; see below) to that of the accompanying submembrane rise in [Ca²⁺]_i and both were concomitantly shortened by CICR blockers (Fig. 7 B, c, and Fig. 15A and Fig. B, Fig. b). The Ca²⁺-sensing molecule, calmodulin, which couples with SK channels (Xia et al. 1998), thus senses the mixed, accumulated rise of [Ca²⁺]_i in the submembrane region during a train of APs (Fig. 16; see discussion). Since the accumulated rise of [Ca²⁺]_i is less affected by changes in individual Ca²⁺ entry or release during their repetitive activation than the rise in the Ca²⁺ microdomains, the total activity of SK channels should be less sensitive to changes in CICR and be increased by the cumulative effect of total Ca²⁺ entry and release. Second, total Ca²⁺ entry induced by repetitive APs must be increased by the spike broadening, as supported by the enhancement of AP-induced Ca²⁺ transients by IbTx (Fig. 10 A, c) and the slowly inactivating property of N-type Ca²⁺ channel (Jones and Marks 1989b). This increase in Ca²⁺ entry should maintain the averaged rise in [Ca²⁺]_i and enhance SK channel activation, thus compensating for the decrease in CICR during the repetitive APs.

Finally, another evidence suggests that SK channels are likely to respond to the higher [Ca²⁺]_i accumulated in the submembrane region. The time constant of the slow I_AHP of 10 APs (0.46 s; Fig. 14 D, a, 15) was shorter than that of the slow decay component of 10 APs-induced Ca²⁺ transients in the submembrane cytoplasm (1.66 ± 0.13 s, n = 35). It was still smaller than those of the Ca²⁺ transients in the presence of ryanodine (0.76 ± 0.09 s, n = 14; Fig. 15 A, b) or thapsigargin (1.10 ± 0.13 s, n = 21; Fig. 15 B, b). Thus, the activation of SK channels disappears before the decay of an increased [Ca²⁺]_i in the submembrane region. This indicates that the Ca²⁺ sensor of SK channels have relatively low Ca²⁺ affinity and sense the higher [Ca²⁺]_i in the submembrane space (see discussion).

DISCUSSION

Activation of CICR by an Action Potential in the Submembrane Cytoplasm

The present study demonstrates that Ca²⁺ influx accompanying an AP activates CICR in the submembrane region of cultured bullfrog sympathetic ganglion cells. AP-induced Ca²⁺ transients were regeneratively propagated at constant amplitude and rate of rise in the submembrane region (a few micrometers), whose width was almost identical to that of the distribution of ryanodine receptors revealed by fluorescent ryanodine. The propagation was blocked by ryanodine, thapsigargin, or ω-CgTx. The Ca²⁺ transient initiated in the submembrane region spread toward the deeper cytoplasm with decreasing in amplitude and the rate of rise, reflecting the passive buffered diffusion of Ca²⁺. Furthermore, computer simulation assuming Ca²⁺ release in the submembrane region with Ca²⁺ entry at the cell membrane nicely reconstructed the spatial and temporal profiles of AP-induced Ca²⁺ dynamics.

Previous attempts (Nohmi et al. 1992) to prove the involvement of CICR in the AP-induced Ca²⁺ transients in intact bullfrog sympathetic ganglion cells were not successful. In that study, Ca²⁺ transients induced by repetitive APs were little affected by ryanodine (10 μM), although caffeine-induced [Ca²⁺]_i oscillation was completely blocked under the same condition. There are three technical reasons for the failure to reveal the activation of CICR by APs in the previous study. First, in contrast to the high time resolution (500 Hz) in the present study, fluorescence was measured at 0.5 Hz for the experiments to observe the effects of ryanodine in the previous study (see Methods in Nohmi et al. 1992). Second, averaged fluorescence changes were measured through an objective of low NA (0.5 or 0.75) predominantly from the core cytoplasm (more precisely from the square inscribed to the center of a cell image; Nohmi et al. 1992). Under those conditions, the fast regenerative phase of AP-induced Ca²⁺ transient in the submembrane region would have not been fully resolved and partly blunted, although the extent of an increase in the measured [Ca²⁺]_i would have been enhanced by CICR. The situation is quite a contrast to that in the present study, in which confocal imaging with a high NA (1.15) objective was used. Third, in contrast to a low concentration (10 μM) of OGB-1 in the present study, a high concentration (∼50 μM) of Fura-2 was used in the previous study (Nohmi et al. 1992). This large amount of exogenous Ca²⁺ buffer would have retarded the regenerative activation of CICR. Studies using 50 μM of Indo-1 or Fura-2 (and also 1 mM EGTA in patch pipettes) showed that a long depolarizing pulse (>200 ms), high K⁺-induced depolarization or the action of caffeine activated the submembrane CICR (Hua et al. 1993, Hua et al. 2000). Rather long lasting Ca²⁺ entry seemed to be needed to overcome the exogenous buffering effects of Indo-1 and EGTA. Ca²⁺ entry during the later part of long depolarization (during which exogenous buffers would have been saturated) therefore activated CICR. In support of this, CICR that was activated by a voltage pulse increased with an increase in the total amount of Ca²⁺ entry in the previous studies. In addition, depolarizing pulse (100 ms)-induced Ca²⁺ transients were facilitated by repeating pulses (Hua et al. 1993). The activation of CICR by caffeine appears to be less affected by exogenous Ca²⁺ buffers, since the activation occurs as a result of an increase in the Ca²⁺ sensitivity of ryanodine receptors (compare to Endo 1975).

The activation of CICR by Ca²⁺ entry accompanying a single AP was also found in other neurons. Ca²⁺ transients through the activation of CICR by a single AP were reported in rabbit vagal afferent neurons (Cohen et al. 1997) and rat CA1 pyramidal neurons (Sandler and Barbara 1999). The ryanodine- or thapsigargin-sensitive component of AHP following a single AP was seen in rat sympathetic ganglion cells (Kawai and Watanabe 1989), guine pig vagal motoneurons (Sah and McLachlan 1991), rabbit otic ganglion cells (Yoshizaki et al. 1995), rabbit vagal afferent neurons (Moore et al. 1998), and rat CA3 pyramidal neurons (Tanabe et al. 1998). Thus, the functional coupling of voltage-gated Ca²⁺ channels to ryanodine receptors appears to be the common mechanism in a variety of neurons. The strength of such a coupling, however, may vary among these neurons. The coupling of Ca²⁺ channels and ryanodine receptors in bullfrog sympathetic neurons seems to be as strong as the coupling in cardiac muscles (see below). However, N-type Ca²⁺ channels, instead of L-type, are involved in the coupling.

The Functional Triad Consisting of Ryanodine Receptors, N-type Ca²⁺ Channels and BK Channels

The present study showed that blocking CICR by ryanodine or thapsigargin reduced the rate of spike repolarization of an AP. The extent of the blockade by either of the CICR blockers was 40% of that brought about by ω-CgTx or IbTx. CICR also decreased during repetition of APs, further decreasing the rate of the spike repolarization by 12–14% under the effect of CICR blockers. If we assume that the remaining CICR in the presence of CICR blockers disappeared during the repetitive APs, at least 54% of the population of BK channels is activated by CICR in response to Ca²⁺ entry through N-type Ca²⁺ channels. The rest of population (46%) was directly activated by the Ca²⁺ entry (Fig. 16).

There are two limiting conditions required for the effective couplings of ryanodine receptors to Ca²⁺ channels and BK channels. First, the time delay for the sequential activation of ryanodine receptors and BK channels after the entry of Ca²⁺ through N-type Ca²⁺ channels must be less than the time period from the peak of spike to the maximum rate of the spike repolarization. This latency, which was 0.64 (0.53 ∼ 0.82) ms in this study, would provide the upper bound for the sum of the distance for Ca²⁺ diffusion between N-type Ca²⁺ channels and ryanodine receptors and that between ryanodine receptors and BK channels. The diffusion time of 0.64 ms for Ca²⁺ would give the diffusion path of 196 nm [= (6Dt)^1/2 = (6 × 10⁻⁷ cm²/s × 0.64 ×10⁻³ s)^1/2], yielding 98 nm of the distance from ryanodine receptor to Ca²⁺ channels or BK channels (assuming the equivalent distances for the two diffusion paths). The time delay for the activation of BK channels by CICR would be even shorter, because the effect of CICR blockers on APs had already appeared around the peak of the spike (Fig. 7). The distances between ryanodine receptor to Ca²⁺ channels and BK channels could therefore be much shorter than this value.

The second limiting condition for the effective coupling may be the Ca²⁺ affinity of BK channels. The Ca²⁺ sensitivity of BK channel was reported to be >10 μM at +20 ∼ −40 mV (Barrett et al. 1982; Smart 1987; McManus and Magleby 1991). This indicates that BK channels are activated by the high [Ca²⁺]_i in Ca²⁺ microdomains ([Ca²⁺]_BK ≈ [Ca²⁺]_D in Fig. 16) produced by both Ca²⁺ entry through Ca²⁺ channels and Ca²⁺ release via ryanodine receptors, rather than the [Ca²⁺]_i in the bulk phase of the cytoplasm measured. Such a low Ca²⁺ sensitivity of BK channels obviously requires the close proximity of BK channels to ryanodine receptors. Assuming rapid Ca²⁺ buffering, numerical analysis of the [Ca²⁺]_i in the Ca²⁺ domain predicted that the range of an increased [Ca²⁺]_i >10 μM within 1 ms after instantaneous Ca²⁺ entry at a point was ∼100 nm from the Ca²⁺ source (see Fig. 1 of Smith 1996; Smith et al. 1996). This value is similar to that estimated from the temporal limitation (see above). Thus, ryanodine receptors in bullfrog sympathetic neurons must be closely coupled to both N-type Ca²⁺ channels and BK channels within this distance (Fig. 16).

The findings in bullfrog sympathetic neurons are consistent with the earlier observations of spontaneous miniature transient outward currents (SMOCs) due to the activation of BK channels by presumptive spontaneous Ca²⁺ release (Brown et al. 1983; Satin and Adams 1987). Similar transient outward currents in smooth muscle cells were nicely correlated with the occurrence of localized spontaneous Ca²⁺ transients, Ca²⁺ sparks (Pérez et al. 1999; Zhu Ge et al. 1999). Moreover, SMOCs in mudpuppy parasympathetic neurons were blocked by Ca²⁺ channel antagonists, nifedipine and ω-CgTx, as well as ryanodine (Merriam et al. 1999). This indicates the existence of a similar coupling of ryanodine receptors to Ca²⁺ channels and BK channels in the parasympathetic neurons, although the mode of CICR activation by Ca²⁺ influx was not selective as in bullfrog sympathetic neurons.

Functional Coupling of Ryanodine Receptors to N-type Ca²⁺ Channels and SK Channels at the Plasma Membrane

CICR triggered by Ca²⁺ entry accompanying the spike of AP activates another type of Ca²⁺-dependent K⁺ channels, SK channels, and participates in the generation of AHP. This was indicated in the reduction of the apamin-sensitive components of AHP and the slow I_AHP by thapsigargin or ryanodine. This is consistent with the previous findings in the same (Kuba et al. 1983) or other (Kawai and Watanabe 1989; Sah and McLachlan 1991; Yoshizaki et al. 1995; Moore et al., 1997; Tanabe et al. 1998) types of neurons.

As already described in the results, the increase in the total SK channel activity during repetitive APs and its slow decay (reflected in AHP and slow I_AHP), which are comparable with the time course of repetitive APs-induced Ca²⁺ transient, suggest that SK channels would sense the mixed, accumulated rise of [Ca²⁺]_i during the train of APs. This mode of activation of SK channel can be achieved only by the location of SK channels somehow remote from both Ca²⁺ channels and ryanodine receptors. This is consistent with the previous observations. The intracellular injection of EGTA shortened the duration of AHP with no change in the peak amplitude (Kuba et al. 1983; Tanaka and Kuba 1987), indicating the distance of more than 100 nm (Naraghi and Neher 1997) between the site of CICR and SK channels (Fig. 16). However, the activity of SK channels should reflect a relatively high level of [Ca²⁺]_i in the submembrane region, since the decay time course of I_AHP was shorter than that of the submembrane [Ca²⁺]_i rise (Fig. 15). The affinity of the Ca²⁺ sensing molecule forming complex with SK channels was reported to be 0.3 μM (Xia et al. 1998), which is greater than the peak of AP-induced Ca²⁺ transients measured in this study. In this context, SK channels could be regarded to couple functionally with N-type Ca²⁺ channels and ryanodine receptors, but less tightly than BK channels.

Plastic Modulation of Cell Membrane Excitability by the Functional Coupling

The activation of BK and SK channels by CICR in response to Ca²⁺ entry through N-type Ca²⁺ channels and its dependence on the frequency of APs may flexibly regulate the cell membrane excitability under the physiological condition. For sparsely coming presynaptic inputs, the fast spike repolarization of an AP through the activation of BK channels by CICR would prepare for the brisk subsequent firing of the neuron. This effect of CICR, activating 52 ∼ 54% of the population of BK channel, however, is not maintained for repeated high-frequency synaptic inputs. The magnitude of CICR decreases during the course of repetitive APs presumably due to inactivation of CICR. This reduces the activation of BK channel by CICR to a level, for instances, less than 20 ∼ 23% at 50 Hz, broadening the spike of AP (Fig. 11; see also Fig. 16). Under this condition, the broadened spike would prolong the refractory period of Na⁺ channels at the axon hillock, limiting the rate of impulse transmission to target cells.

On the other hand, the broadened spike increases the duration of N-type Ca²⁺ channel activation. This increases the amount of Ca²⁺ entry, thereby compensates for the decrease in CICR and maintains the averaged total rise in [Ca²⁺]_i around SK channels for their activation. Thus, the AHP following repetitive APs is prolonged in spite of the reduced CICR. The long-lasting AHP produced mainly by the SK channels activation increases the threshold for the subsequent firing. These modes of activation of BK and SK channels by CICR during repetitive nerve activity may favor intermittent bursting discharges. Consequently, this bullfrog sympathetic neuron regulates its membrane excitability by shifting the dependence of spike and AHP formation over two different kinds of Ca²⁺-activated K⁺ channels, through changing the extent of CICR. The efficacy of this mechanism would be variable among the cells, depending on the density of ryanodine receptors or the amount of Ca²⁺ stores.

Functional coupling between two types of ion channels has been known for those between ryanodine receptors and L-type Ca²⁺ channels or Ca²⁺-dependent K⁺ channels (Pérez et al. 1999; Zhu Ge et al. 1999) in muscles. There are also several lines of evidence for more or less similar functional couplings in neurons. Selective activation of SK channels by L-type Ca²⁺ channels and that of BK channels by N-type Ca²⁺ channels were reported in hippocampal neurons (Marrion and Tavalin 1998) and their opposite roles in rat superior cervical ganglion (Davies et al. 1996). The regulation of L-type Ca²⁺ channels at the cell membrane by ryanodine receptors was reported in mouse cerebellar granule cells (Chavis et al. 1996). There is no evidence, however, for the functional coupling of three types of ion channels. The coupling of ryanodine receptor to N-type Ca²⁺ channel and Ca²⁺-activated K⁺ channel in bullfrog sympathetic neurons would be the first evidence for the functional coupling of ion channels, which operates in a cascade of Ca²⁺ entry, Ca²⁺-induced Ca²⁺ release and Ca²⁺-activated opening of K⁺ channel within a short period of time (<1 ms). Moreover, the graded reduction of the submembrane CICR during repetitive APs provides plasticity in the strength of this coupling, which seems to be also the first evidence for the plastic modulation of cell functions by CICR. Furthermore, the modulation of Ca²⁺ channels by adrenaline, acetylcholine, and other neurotransmitters are known in bullfrog sympathetic neurons (Kuba and Koketsu 1976; Minota and Koketsu 1977; Bley and Tsien 1990; Elmslie et al. 1990). Such modulation should affect the extent of the submembrane CICR due to the close coupling. Thus, the functional triad formed by ryanodine receptors, Ca²⁺ channels, and Ca²⁺-activated K⁺ channels operates as one of the important mechanisms of postsynaptic plasticity in bullfrog sympathetic neurons and may provide a novel mechanism in general for the plastic regulation of cell membrane excitability in various kinds of cells.