Conjoint Control of Hippocampal Place Cell Firing by Two Visual Stimuli

Abstract

To better understand how hippocampal place cell activity is controlled by sensory stimuli, and to further elucidate the nature of the environmental representation provided by place cells, we have made recordings in the presence of two distinct visual stimuli under standard conditions and after several manipulations of these stimuli. In line with a great deal of earlier work, we find that place cell activity is constant when repeated recordings are made in the standard conditions in which the centers of the two stimuli, a black card and a white card, are separated by 135° on the wall of a cylindrical recording chamber. Rotating the two stimuli by 45° causes equal rotations of place cell firing fields. Removing either card and rotating the other card also causes fields to rotate equally, showing that the two stimuli are individually salient. Increasing or decreasing the card separation (card reconfiguration) causes a topological distortion of the representation of the cylinder floor such that field centers move relative to each other. We also found that either kind of reconfiguration induces a position-independent decrease in the intensity of place cell firing. We argue that these results are not compatible with either of two previously stated views of the place cell representation; namely, a nonspatial theory in which each place cell is tuned to an arbitrarily selected subset of available stimuli or a rigid map theory. We propose that our results imply that the representation is map-like but not rigid; it is capable of undergoing stretches without altering the local arrangement of firing fields.

INTRODUCTION

Place cells are hippocampal pyramidal cells that discharge intensely only when a rat's head is in a certain place in its environment and for this reason were proposed to be units of a neural navigational system (O'Keefe and Dostrovsky 1971). Elementary considerations make it clear that the location-specific firing of place cells can be reliable over long times only if the place cells have access to sensory information from stable landmarks in the environment. In the absence of such information, the locations of the regions of intense activity (“firing fields”) would necessarily drift relative to the environment. Thus, detection of self-motion is insufficient for long term stability of place cells; either continuous or sufficiently frequent intermittent reference to fixed features of the environment is necessary for stationary place cell firing (Knierim et al. 1998; Save et al. 2000).

Shortly after the discovery of place cells, O'Keefe and colleagues began investigating how location-specific activity is controlled by environmental stimuli. A seminal study by O'Keefe and Conway 1978 used a “controlled cue environment” in which were placed a T-maze and four prominent stimuli. When the stimuli and T-maze were rotated as a rigid set by 90° on some trials and 180° or 270° on other trials, each firing field rotated equally, establishing that the fields are controlled by local, identifiable stimuli. O'Keefe and Conway 1978 then tested the effects of eliminating combinations of the controlled cues and found that many fields stayed intact after any single cue or any pair of cues was deleted. O'Keefe and Conway concluded that the location-specific firing of place cells is not triggered by any single stimulus or by any special pair of stimuli. Instead, location-specific firing can be supported by a framework made up of “multiple, replaceable stimuli.” According to the theory of O'Keefe and Nadel 1978, the place cells form a rigid map of the environment.

In the experiment of O'Keefe and Conway 1978, the stimuli remain fixed relative to each other. What happens when two sets of stimuli are put into conflict was explored by Shapiro et al. 1997 and Tanila et al. 1997. The “distal stimuli” consisted of large objects on the curtains of a controlled cue environment. The “local stimuli” were odors and floor textures on the arms of a “plus-maze” in the center of the controlled cue chamber. Baseline recordings with the local and distal cues in the positions used during training were compared with recordings made after the distal and local cues were rotated 90° in opposite directions. The responses of place cells were sorted into four classes. (a) The majority of cells became silent or had fields that jumped from their baseline location to a new, unpredictable location. It was argued that such cells are tuned to combinations of distal and local cues and therefore undergo violent changes in firing properties when the crucial stimuli are out of register. (b) Cells whose firing rotated with the distal cues. (c) Cells whose firing rotated with the local cues. (d) Cells whose fields stayed fixed in the laboratory frame. Additional manipulations suggested that some cells are tuned to individual distal or local stimuli. Overall, Shapiro et al. 1997 concluded that each individual cell responds to an arbitrarily selected combination of available stimuli and that the stimulus combination can shift if initially critical stimuli are altered or deleted. Moreover, Tanila et al. 1997 found that individual cells of simultaneously recorded ensembles could respond in discordant ways to the double rotation.

Thus, stimulus control over place cell activity has been described in at least two different ways. In the rigid map scheme, every cell is controlled by a set of stimuli that defines a global spatial reference system. If sufficiently many of these stimuli are available, the reference system is intact and the firing fields of all cells remain fixed relative to each other. In this scheme, deleting individual stimuli or small stimulus subsets has no effect on any place cell; the distribution of fields in the environment is unchanged and therefore the place cell representation is undisturbed. In the contrasting, combinatorial scheme, each cell is controlled by a selected subset of the stimuli in the environment. Therefore, virtually any stimulus manipulation is expected to affect the discharge of some cells; deleting a stimulus or putting it into conflict with other stimuli should affect those cells that happen to be “tuned” to the specified stimulus and leave unchanged all other cells.

These alternative pictures have important implications with regard to the nature of the place cell representation of the environment. The idea that multiple, replaceable stimuli establish a spatial reference frame suggests that the place cell representation has an internal structure, perhaps based on the recurrent CA3–CA3 connections, that permits firing field positions to remain consistent with each other after certain cue changes. The contrasting idea that combinations of selected stimuli control the activity of individual cells suggests that the place cells are independent of one another, and may reflect the parallel processing of arbitrary relationships (Eichenbaum et al. 1999). Thus, important aspects of the representation of the environment may remain intact even if relative positions of firing fields are preserved only weakly or not at all.

Is either picture accurate? Recent studies indicate that neither correctly describes how firing fields transform after all changes in the environment. For example, when one of three white cards on the walls of a square chamber was removed, no major disruptions of firing fields were seen, as expected from the rigid map model (Hetherington and Shapiro 1997). Nevertheless, changes in field properties varied with the distance between a field and the removed card, a result at odds with the simplest form of the rigid map model. O'Keefe and Burgess 1996 looked at firing fields in a square chamber of side S, a vertically oriented rectangular chamber S by 2S, a horizontally oriented rectangle 2S by S, and a large square chamber 2S by 2S. They used a combinatorial approach to describe how shape changes affected firing fields. In their analysis, fields were affected by combinations of two or three walls. The results of O'Keefe and Burgess 1996, however, indicated the existence of at least one map-like feature—the importance of a wall for a firing field depended on the distance from a wall to the field. Additional studies by Sharp et al. 1990 and Skaggs and McNaughton 1998 indicate that some place cells may have similar fields in two visually similar parts of an apparatus (in line with the combinatorial view), but that other cells may reliably fire in only one of the two regions, perhaps based on the use of position tracking by self-motion information (consistent with a spatial representation). Similar conclusions can be drawn from the study of Gothard et al. 1996.

We conclude that the nature of stimulus control over place cell firing fields is not fully understood and requires continued investigation. To this end, we have done experiments using simple initial conditions and subtle changes in the relationship between stimuli (Fig. 1). The experimental chamber was a 76-cm diameter gray cylinder on whose inner wall were attached a white and a black cue card that each occupied 45° of arc and whose middles were separated by 135°. The salience of each card was demonstrated by removing the other card; place cell firing was virtually unchanged in the presence of only one card. We then asked how firing fields were affected if the angular distance between the two cards was made either smaller or greater by 25°. These “reconfigurations” did not cause fields to disappear nor to move over large distances as occurs in remapping (Muller and Kubie 1987; Thompson and Best 1989; Bostock et al. 1991; Kentros et al. 1998), allowing us to look for patterns of field movements across the cell sample.

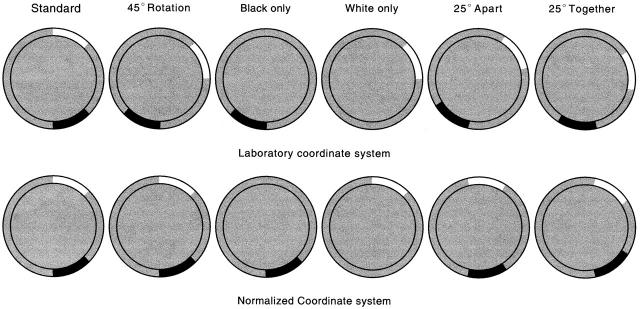
Figure 1.

Summary of experimental design. Each circular image represents an overhead view of the 76-cm diameter, 51-cm high recording cylinder. The inner circle is the cylinder floor that is covered with gray paper that is renewed after each recording session. The gray annulus is a foreshortened view of the cylinder wall; the white and black annular sectors represent the two 45° cue cards. The upper row of images show how the cue cards were arranged in the laboratory coordinate system during recording sessions. The 3:00 o'clock position is the origin of the angular coordinate. In the standard condition at left, the centers of the two cue cards are at +62.5° (white card) and −62.5° (black card) and are symmetrically placed above and below the horizontal diameter of the cylinder. In the other experimental conditions, the cue cards are rotated or removed as shown by the annular sectors. Rotations of the cue cards are superimposed after either cue removal (white only, black only) or card reconfiguration (apart, together) to determine whether firing fields follow the cards or are locked to uncontrolled cues that are stationary in the environment. The bottom row of images (“normalized coordinate”) shows the appearance of the cylinders after the superimposed rotation has been subtracted. All angular values in this paper and the next are in the normalized frame.

Some possible outcomes of this experiment conform closely to the rigid map model and some to the combinatorial model. For example, firing fields might all rotate by an equal amount if they all followed the white card, the black card, or some average of the angular positions of the two cards. Cases in which fields do not move relative to each other are expected from the rigid-map model. Alternatively some fields might move with the black card even as others move with the white card and yet others move with some average of the angular positions of the two cards. Cases in which fields move relative to each other as if following different groups of stimuli are expected from the combinatorial model.

In line with the recent work cited above, our results are not well predicted by either the rigid map or the combinatorial model. We will present evidence that every field is affected by both cards, as expected from the rigid map model, but that fields move relative to each other, as expected from the combinatorial model. Thus, relative field positions appear to undergo a topological transformation such that neighboring fields strongly tend to move in similar ways, whereas the distances between fields that are far from each other in general tend to change. This topological distortion is accompanied by an overall, position-independent decrease in firing rate. The combined reconfiguration and card removal results lead us to conclude that the hippocampal representation of the environment is map-like in the sense that local adjacency relationships are preserved in circumstances where overlapping or even coincident fields could move relative to each other. At the same time, this map-like representation appears to have global elastic properties since distances between widely separated fields are not fully preserved. In the discussion, we argue that the map-like representation depends on a template of the environment that may be stored in the recurrent CA3 → CA3 synapses and that topological distortion caused by reconfiguration reflects conflict between the expected and actual stimulus patterns. A system with these properties has many of the features of an attractor network (Redish and Touretzky 1997; Samsonovich and McNaughton 1997).

METHODS

The behavioral, surgical, electrical recording, and rat-tracking methods used in this paper are similar to those used in earlier work from this laboratory (Muller and Kubie 1987; Muller et al. 1994) and are only briefly summarized. The focus is therefore on methods specific to this work.

Experimental Conditions

The recording chamber was a 76-cm diameter, 51-cm high gray cylinder centered on the floor of a 2.5 × 2.5 m room and could be surrounded by a cylindrical curtain 2 m in diameter. Lighting was supplied by four 25-watt bulbs arranged on the corners of a square 2 m above the apparatus floor. The cylinder was placed on gray photographic backdrop paper that was changed after each training and recording session. Four items in addition to the lights were 2 m overhead. (a) A vertically oriented video camera whose optical axis was collinear with the cylinder center. The camera was used to view the rat's behavior and to automatically track the rat's position. (b) A 25-channel commutator that made electrical connections between the rat's head and the laboratory. The commutator prevented kinking of the recording cable. (c) A counterweight system that kept the recording cable off the floor when the rat was near the cylinder center and that easily fed out cable as the rat moved to the cylinder edge. (d) A pellet feeder that dispensed 25-mg food pellets at a rate of ∼3/min in a pseudorandom schedule with a minimum interval of 10 s and a maximum interval of 1 min. The pellet feeder made an audible noise each time it operated. The pellets were made to scatter over the apparatus floor by dropping them onto four layers of coarse wire mesh set at 45° angles below each other.

Subjects and Training

The subjects were five male Long Evans rats whose ad lib weights were between 300 and 350 g. The rats were housed one per cage and maintained on a 12:12 h light:dark cycle in the departmental animal colony. After arrival, the rats were handled for a few minutes per day for 3–5 d to accustom them to the experimenter. They were then food deprived to 85% of their ad lib weight and trained to forage for food pellets scattered by the feeder. This training was divided into two parts. Preoperative training lasted 3 or 4 d, depending on how rapidly the rat learned to run everywhere in the apparatus. For each training day, the rat was put into the cylinder three times for pellet chasing sessions that lasted 15 min. During preoperative training, a single white cue card that occupied 90° of arc was attached to the cylinder wall. The cylindrical curtains were not drawn and the room door was left open.

After preoperative training, recording electrodes were implanted as described below. The rat was allowed 1 wk to recover after surgery and training was resumed with the following changes. (a) The single white card in the cylinder was replaced with two cards, a white card and a black card that each occupied 45° of arc and whose centers were separated by 135°. The black card was actually very dark gray (Color-aid GRAY 2.5; Color Aid Corp.) and the white card was very light gray (Color-aid GRAY 9.5; Color Aid Corp.) and were selected so that the reflectance ratio between the black card and the gray cylinder wall was equal to the reflectance ratio between the gray wall and the white card. (b) The cylindrical curtain was closed to visually isolate the cylinder from the rest of the laboratory. (c) The door to the recording room was closed.

Postoperative training was accomplished in four or five training sessions per day for a week. Each session lasted 15 or 30 min and the time between sessions was at least 30 min. For 30-min training sessions, both cards were present at the outset. After 10 min, either the white or the black card was removed for 10 min without otherwise interrupting the session. After 10 more min, the card was returned to its former position. In experimental sessions, all changes of card configuration were made when the rat was outside the recording room. Specifically, for experimental sessions with single cards, the rat was put into the cylinder with one card already removed.

Card Configurations

Once training was complete, the recording electrodes were screened several times per day for place cell activity. Once one or more place cells were isolated, recordings were made with the cards in one of the six configurations summarized in Table . Either a white card only or a black card only session is called a card removal session. Either a cards-apart or a cards-together session is called a reconfiguration session. The positions of the cards in each stimulus configuration are shown in Fig. 1. Regardless of its type, each session lasted either 16 min or, in a few cases, 32 min.

Table 1.

Arrangements of Cur Cards Inside the Recording Cylinder

Configuration	Card positions
Standard	The middles of the black and white cards were separated by 135°, with the black card clockwise to the white card. The cards were arranged such that they were symmetrically placed above and below the diameter that runs from 3:00 (0°) to 9:00 (±180°) o'clock. Thus, the middle of the white card was at +67.5° and the middle of the black card was at −67.5°. The standard configuration was the only one in which the angular positions of the cards were always fixed.
Rigid rotation	The two cards were treated as if they were rigidly connected to each other. For a rotation, both cards were moved 45°, either clockwise or counterclockwise. This manipulation tested whether the combined cards determined the angular position of place cell firing fields.
Black card only	The white card was removed and the black card was rotated 45° clockwise or counterclockwise. This manipulation tested whether the black card alone was sufficient to support place cell firing and furthermore whether its angular position could control the angular positions of firing fields.
White card only	The black card was removed and the white card was rotated 45° clockwise or counterclockwise. This manipulation tested whether the white card alone was sufficient to support place cell firing and furthermore whether its angular position could control the angular positions of firing fields.
Cards apart	The purpose was to increase the separation between the cards from 135° to 160°. This was accomplished in one of two ways. In the first, the white card was rotated 45° clockwise and the black card was rotated 70° clockwise; in the second, the white card was rotated 45° counterclockwise and the black card was rotated 20° counterclockwise. The superimposed rotations ensured that neither card nor the midpoint between the cards stayed at the same angular position in the laboratory frame.
Cards together	The purpose was to decrease the separation between the cards from 135° to 110° and was accomplished either by rotating the white card 45° clockwise and the black card 20° clockwise, or by rotating the white card 45° counterclockwise and the black card 70° counterclockwise. Again, the additional rotations ensured that neither card nor the midpoint between the cards was at the same angular position in the laboratory frame.

Additional description is given in Fig. 1

The sequence of recording sessions was determined by the following rules. (a) The first session on any experimental day was always a standard session. (b) During each experimental day, all odd numbered sessions were standard sessions, so that every session of another type was bracketed by a pair of standard sessions. (c) Nonstandard sessions were run with priority decreasing in the sequence: apart = together, black only = white only, rigid rotation. Rigid rotation sessions were of lowest priority because previous experience indicates that a single card controls the angular position of firing fields (Muller and Kubie 1987) and initial recordings after rigid rotations cards indicated their combined salience. Reconfiguration sessions were of highest priority because they directly address the question of how two cues conjointly control the firing fields of place cells. Thus, standard sessions were most common, followed by reconfigurations, single-card sessions, and rotation sessions. It must be emphasized that each rat saw each card configuration many times since each rat was exposed to each configuration after a new set of place cells were isolated. We looked for time-order effects and could detect none; to the best of our knowledge, the effect on place cells of any stimulus reconfiguration depends only on the reconfiguration and not on the sequence of recording sessions. The possibility of time-order effects is not considered further in these papers.

Five of the six changes in stimulus conditions included a rotation of whichever cards were present. In this way, we tested whether the cards exert stimulus control over the angular position of firing fields or if instead the fields are tied to uncontrolled, static background cues. We found that every field rotated with the single card or with both cards. This control of firing fields by the cards justifies the use of a card-centered angular coordinate instead of a laboratory centered angular coordinate. When both cards were present, the zero of the card-based angular coordinate was defined as the midpoint between the centers of the two cards, and this zero was placed at 3:00 o'clock in the view of the overhead TV camera. When only one card was present, the zero of the card-based coordinate was the angle at which the midpoint between the two cards would have been had the center of the removed card been in its standard position (135° away) relative to the center of the remaining card. The relationship of the card-centered and laboratory centered coordinate frames is summarized in Fig. 1.

Surgical and Electrophysiological Methods

For single cell recordings, 10 microwire electrodes were implanted under Nembutal (40 mg/kg) anesthesia (Kubie 1984). These 25-μm electrodes form a bundle threaded through a piece of stainless steel tubing. Each wire is attached to a pin on the outside of a circular connector. The tubing is attached to the center pin of the connector and serves as animal ground as well as a guide for the microwires. The connector, tubing, and wires are moved down in the brain by turning screws attached to the connector into nylon cuffs that are attached to the rat's skull. The tips of the bundle are implanted above the dorsal CA1 pyramidal cell layer 3.8 mm posterior to bregma and 2.8 mm lateral to the central suture according to the atlas of Paxinos and Watson 1986. With this placement, the electrodes penetrate the CA1 cell layer ∼1 mm ventral to their initial placement. In some rats, recordings were made from CA3 as well as from CA1 by continuing to advance the electrodes. We saw no differences between CA1 and CA3 place cells and this question is not further addressed in these papers.

To greatly reduce movement artifacts, we amplified the signal from each microwire at the animal's head with a unity gain preamplifier. A miniature cable connected the headstage to the rotating part of the overhead commutator. The fixed part of the commutator was connected to a patch panel that allowed different wires to be attached to final amplifiers. The microwire signals were amplified 10,000× and bandpass filtered between 100 Hz and 10 kHz. The signals from microwires that had unit activity of sufficient amplitude (at least 200 μV) were digitized at 40 kHz, candidate waveforms were clipped out and stored on a disk. Later, the candidate waveforms were sorted by characteristic features (for example, peak voltage, waveform duration, and so on) into time series, each of which was taken to be generated by a single cell. The sorting was done with modified Datawave software (Kubie et al. 1996).

Once the electrodes were below the CA1 pyramidal cell layer in some rats and below the CA3 cell layer in others, the rat was given a lethal dose of Nembutal (80 mg/kg) and perfused through the heart first with saline, and then with 4% formaldehyde. The brain was removed and cut into 40-μm frozen sections to visualize the electrode track and its termination. For each rat, the electrode track passed through the CA1 cell layer and the depth at the end of the track was equal to the depth estimated from turning the drive screws.

Data Analysis

To locate the rat's head with the overhead TV camera, a headlight was tracked at 60 Hz with a special purpose analogue-to-digital converter. The light position was determined in a 256 × 256 array of square pixels that were 0.65 cm on a side. To compute firing rate as a function of position and for all other numerical calculations, the positional resolution was reduced to 64 × 64 pixels, each 2.6 cm on a side.

The primary measure of place cell activity is the “positional firing rate distribution,” the time-averaged firing rate in each pixel. This is obtained by dividing the number of spikes detected in each pixel by the total time the rat's head was detected in that pixel. Color coded “firing-rate maps” were created to visualize the positional firing-rate distribution for each place cell. In the color code, white is used for pixels that were never visited by the rat and yellow for pixels in which the positional firing rate was exactly zero for the entire session. Greater-than-zero rates are encoded in increasing order, orange, red, green, blue, purple, such that the number of pixels in a color category is 0.8× the number of pixels in the next lower category. Maps are shown with a color key that indicates the median firing rate in each color category.

Cells were included in the analysis only if inspection of their firing-rate maps showed the tight positional confinement of firing to distinct “firing fields” that are characteristic of place cells. A firing field was defined as a group of at least nine contiguous pixels such that each pixel had a firing rate greater than zero and shared at least one side with another pixel in the field. Spikes fired outside a field were suppressed so that numerical analyses were done on fields. Cells were studied as long as their waveform did not change >30% from the preceding session for a set of parameters that included peak and trough amplitude. Waveforms judged to be stable in this way almost invariably had firing fields in virtually the same location across standard sessions. In a few cases, a place cell had two (7/76 cells) or three (2/76 cells) stable firing fields. Each field for multiple-field cells was analyzed separately so that the number of fields in the sample was 87 (see Table ).

Table 2.

Fitting Pattern Parameters for Pairs of Standard Sessions

	Standard 1	Standard 2	Difference	Paired t	P
Grand rate	1.20 ± 2.05	1.24 ± 2.04	0.044 ± 0.879	0.292	0.77
Field rate	5.11 ± 4.09	4.99 ± 4.46	−0.113 ± 2.50	0.420	0.68
Centroid rate	12.5 ± 11.0	13.1 ± 13.5	0.562 ± 11.8	0.442	0.66
Size	678 ± 502	739 ± 629	61.0 ± 397	1.43	0.16
Coherence	1.06 ± 0.28	1.01 ± 0.276	−0.046 ± 0.259	1.65	0.10
Information	3.36 ± 1.18	3.29 ± 1.24	−0.062 ± 0.840	0.682	0.50

The first and second standard sessions were separated by a card manipulation session. The mean values for the six parameters did not change in a reliable way between the two sessions, as indicated by the high probability for the paired t test for each parameter. Note that the difference between the parameter means for the two sessions (Standard 1 and Standard 2) is not exactly equal to the mean of the differences (Difference). The same lack of exact agreement between the difference of the means and the mean difference occurs also in Table Table Table Table .

Measuring the Properties of Firing Fields

In principle, the cue card manipulations could affect place cell activity in several ways, including the location, size, shape, and discharge rate of firing fields. It was therefore necessary to use numerical methods to determine which changes took place. Throughout the paper values are reported as the mean ± SD. We measured seven field properties: (1) location of the field center, (2) overall firing rate, (3) firing rate inside the field, (4) firing rate at the field center, (5) field size, (6) field smoothness estimated with coherence, and (7) spatial information per spike. The seven measures were defined as follows:

(1) Location of the field center. A primary interest is how firing fields move after a stimulus manipulation. To measure this movement, we locate the field center under standard conditions and after changing the cards. The field-center displacement is then a vector whose tail is at the field center location in the standard conditions and whose head is at the field center location in the altered conditions.

We tried three methods of locating the field center; namely, the “centroid” pixel, the “distance-weighted center” pixel, and the “peak rate” pixel.

The coordinates of the centroid pixel are defined by and . The X (Y) coordinate of the centroid is the mean X (Y) position of pixels in the field weighted by the firing rate in the pixel.

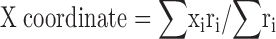1a

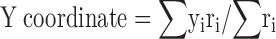1b

To find the distance-weighted center, the rate in each pixel is mapped onto a 1/distance weighted average. Thus, for each target pixel, the distance to each other pixel is divided into the rate for the other pixel and the average is taken across all other pixels. The distance-weighted center is the target pixel with the highest such average.

The peak rate pixel is also found by considering each pixel in turn. The rate assigned to each candidate pixel is the sum of the spikes in the pixel and its eight nearest neighbors divided by the total time spent in the pixel and its eight nearest neighbors. The peak rate pixel is that pixel that is assigned the highest rate by this 3 × 3 “boxcar” average.

How should the measure of field center be selected? Since fields are reproducible under fixed conditions (Muller and Kubie 1987; Thompson and Best 1990), we take the best measure of field-center position to be that which minimizes the average field displacement for pairs of standard sessions. The average center displacement for 87 fields was 3.1 cm for the centroid, 4.3 cm for the distance-weighted center, and 6.7 cm for the peak-rate center. Accordingly, all of our measures of field location and displacement are based on the centroid. It is important to emphasize, however, that our results were not strongly affected by using either of the other central tendency measures. Specifically, the pattern of displacement vectors for reconfigurations is substantially the same for field peak as for field centroid (not shown). The importance of choice of field center measure is raised again in the next paper (Fenton et al. 2000).

(2) The overall firing rate is the total number of spikes fired by the cell divided by the recording time. Rates are given in spikes/second.

(3) The field rate is the total number of spikes fired in the field divided by the total time spent in the field.

(4) The field centroid rate is the rate in the field centroid pixel.

(5) Field size is the number of pixels in the field.

(6) Coherence is a nearest-neighbor 2-D autocorrelation of firing rate (Muller and Kubie 1989) and is calculated in three steps. First, parallel lists are constructed for the firing rate in each pixel and the average firing rate in the eight nearest neighbors; the average is the sum of the number of spikes in the neighbors divided by the sum of the time spent in the neighbors. Next, the product–moment correlation between the two lists is calculated. Coherence is the z-transform of this correlation and estimates the local smoothness of the field.

(7) Spatial information is defined by (Skaggs et al. 1993). Spatial information estimates how much a single spike fired by a cell reduces the uncertainty of the rat's location and is measured in bits per spike.

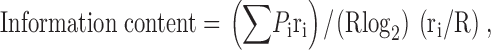2

where r_i is the mean rate in pixel i; R is the overall mean rate; P _i is the probability of finding the rat in pixel i and P _i = t _i/T where t _i is the time spent in pixel i and T is the total recording time.

RESULTS

A key finding in this study is that none of the cue card manipulations induced the major, violent changes in positional firing patterns of individual place cells that are characteristic of remapping. The stability of fields after each card manipulation is illustrated for a pair of simultaneously recorded place cells in Fig. 2, where the rate maps are shown after subtracting rotations, using the normalized angular coordinate. By inspection, the firing field of each cell is nearly the same after each manipulation, as in the standard session. In general, the effects of the card manipulations are not convincingly detectable by inspection of firing rate maps, and more sensitive methods of description are therefore required.

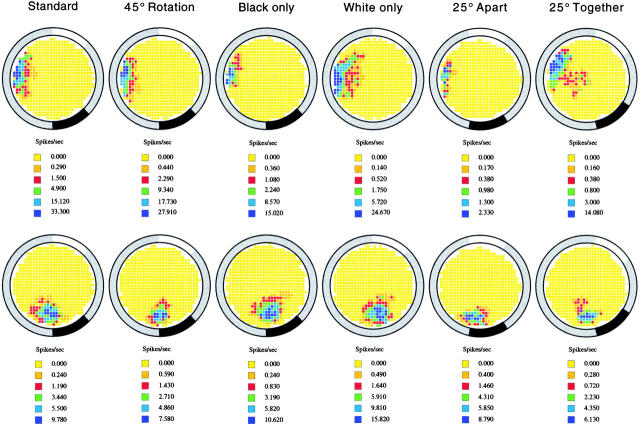
Figure 2.

Example color-coded firing rate maps in each experimental condition for a pair of simultaneously recorded place cells. The firing rate in yellow pixels was exactly zero over the entire recording session. Firing rates for the median pixel in the other color categories are shown in the key below each map; additional details of the color code are given in methods. In these maps, the firing field has been isolated by setting to zero the rate in any out-of-field pixels in which one or more action potentials occurred. By inspection of these maps, it is clear that the firing field of both cells was not disrupted in a major way by any of the manipulations. This stability held for all except one cell in a single standard session and forms the background of our analysis of the way in which card manipulations affected firing fields.

To provide such a description, we first characterize firing field properties seen in standard sessions. Next, we consider field changes between pairs of standard sessions. Since firing fields are stable in a fixed environment (Muller and Kubie 1987; Markus et al. 1994), variations in field properties between pairs of standard sessions provide a baseline for estimating the effects of card manipulations. Finally, we consider in sequence how fields are affected by rotating both cards by the same amount (equal rotations), how they are affected by removing one card or the other, how they are affected by moving the cards apart to increase their angular separation, and finally how fields are affected by moving the cards together to decrease their angular separation. This analysis leads us to conclude that field properties are unchanged after equal card rotations and card removals and are changed only by the apart and together (“reconfiguration”) manipulations.

Characteristics of Firing Fields in Standard Conditions

Qualitatively, firing fields recorded in the presence of a 45° white card and a 45° black card separated by 135° appear the same as fields recorded with other card configurations (Muller and Kubie 1987; Sharp et al. 1990; Bostock et al. 1991; Hetherington and Shapiro 1997). In standard sessions, the average field size was 678 ± 502 cm², so that the average field occupied 17% of the apparatus area. The large standard deviation indicates that fields vary considerably in size, in agreement with earlier work (Muller and Kubie 1987).

The intensity of location-specific firing was estimated in three ways (see methods). The mean overall rate in standard sessions was 1.20 ± 2.05 spikes/s. The mean in-field rate was 5.11 ± 4.09 spikes/s. The mean firing rate in the field centroid pixel was 12.5 ± 11.0 spikes/s. We also found that the information content in standard sessions was 3.36 ± 1.18 bits/spike and that the mean coherence of the positional firing patterns was 1.06 ± 0.28.

In addition to characterizing average field properties, we asked about the distribution of firing field centroids inside the cylinder, which can be seen in Fig. 4 (below). First we used the Rayleigh vector to see if there was a tendency of field centers to occur in a particular range of angles inside the cylinder. The length of the Rayleigh vector was 0.102 (n = 87). The probability that a vector this long or greater would occur by chance is 0.37, revealing no trend of the centroids to cluster. A chi-square test also indicated that the centroids were evenly distributed at all angles [P(X² > 0.18; df = 11) ∼1.0]. Nevertheless, there appears to be a higher than expected number of field centers near 45°, in the vicinity of the clockwise edge of the white card. This tendency can be seen in Fig. 4 A as well as B, 1 and 2 (below), and is reminiscent of the tendency of fields to occur in front of large rectangular stimuli, described by Hetherington and Shapiro 1997. We also looked for a tendency of centroids to occur inhomogeneously as a function of distance from the cylinder center. The Kolmogorov-Smirnov test revealed no such tendency [d = 0.10; P(d > 0.10) = 0.287]. A chi-square test dividing the cylinder into 13 annuli agreed that the distribution of centroids as a function of distance from the center was flat [P(X² > 0.20; df = 12) = ∼1.0]. Finally, a two-dimensional version of the Kolmogorov-Smirnov test (Press et al. 1992) revealed no tendency of centroids to be clustered in the cylinder [d = 0.16; P(d > 0.16) = 0.08]. We conclude that the visible density of field centers near the clockwise edge of the white card is hard to detect statistically and that fields are not far from evenly distributed in the apparatus.

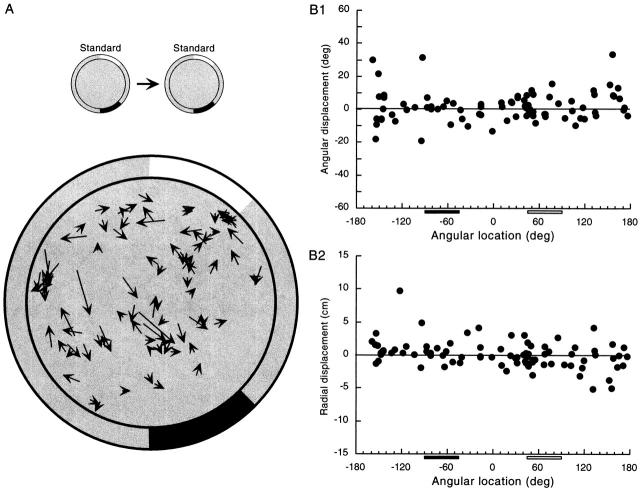
Figure 4.

Constancy of field centroid position in pairs of standard sessions. (A) Displacement vectors for 87 fields. In general, the vectors are quite short, indicating that the field centroid position was reproducible. In addition, there is no organization to the vector directions; displacements of neighboring fields are unrelated to each other. (B) In agreement with the impression gained from the displacement vectors, plots of the angular (1) and radial (2) vector components reveal no tendency for fields in certain angular ranges to move in coordinated fashion. Note that both the displacement vector presentation and the vector component plots show a higher than expected density of fields along the radius aimed at the clockwise white card edge, especially near the cylinder wall. The origins of this apparent inhomogeneity are unclear.

Reproducibility of Fields between Pairs of Standard Sessions

The experimental design involves comparisons of firing field properties in a standard session and the next session, which is always a card manipulation session done on the same day. It is therefore important to test whether there is any tendency of field properties to change as a function of time. To this end, we compare field properties in the first pair of standard sessions done for each cell. These sessions were always done on the same experimental day and were separated by a single card manipulation session, so that if time effects are important they should be seen more clearly than for pairs of successive sessions.

Table summarizes the mean values of several properties of 87 firing fields in each of two standard sessions, the mean pairwise difference of each property and the result of a paired t test. It is clear from Table that there is no systematic tendency of field properties to change between pairs of standard sessions. This overall stability of firing fields is the background against which we will measure the effects of card manipulations.

In addition to comparing field properties, we also characterized how the centroid moved between pairs of sessions, again to provide a baseline to measure field movements caused by card manipulations. Methods of describing movements of field centroids are summarized in Fig. 3, and results are given for pairs of standard sessions in Fig. 4. In Fig. 4 A, each arrow represents the movement of a field centroid such that the arrow tail is the centroid position in the first standard session and the arrowhead is the centroid position in the second standard session. The relatively short lengths of the arrows indicate that fields did not move very much; the mean distance was 2.9 ± 2.3 cm. Moreover, there does not appear to be any pattern to movements since the direction of arrows is independent of their position in the cylinder. This impression is confirmed with a Rayleigh test that shows that there is no tendency of the movement directions to cluster near a certain angle (mean vector length = 0.106; P ∼ 0.37).

Figure 3.

Methods for showing how card manipulations affected positions of firing field centroids. Each of the two heavy vectors represents the displacement of the field centroid from a standard session to a second session. The tail of each heavy vector is the field centroid position in the initial standard session; the head of the vector is the field centroid position in a later session. Displacement vectors are shown for different conditions in A of Fig. 4 Fig. 5 Fig. 6 Fig. 7. In the second method of summarizing field centroid movements, the angular and radial components of the vector for each field are computed and plotted against the normalized angular coordinate. Plots of the angular displacement vector component against direction are shown for different conditions in B, 1 of Fig. 4 Fig. 5 Fig. 6 Fig. 7; corresponding plots of the radial vector component are shown in B, 2 of the same figures.

The second way of summarizing centroid movements is to plot the angular (Fig. 4 B, 1) and radial (B, 2) components of the displacement vectors as a function of the angular position of the field in the first standard session. The angular positions of the black and white cards are drawn under the x axes as a filled and an open bar. The impression that there is no pattern of centroid movement between pairs of standard sessions obtained from Fig. 4 A is confirmed in B, where it is seen that angular displacements and radial displacements are independent of the angular location of the centroid in the first standard session. Thus, the mean angular displacement [mean = −0.495 ± 33.5°; t = 0.86; P(t ≥ 0.86) = 0.39] and mean radial displacement [mean = 0.190 ± 2.07 cm; t = 0.14; P(t ≥ 0.14) = 0.89] are not reliably different from zero. Furthermore, there was no tendency for either component of the displacement vectors to be reliably greater than or less than the median value in a certain angular range, as shown with runs tests [angular displacement: median = −1.47°; z = 0.75; P(z ≥ 0.75) = 0.81; radial displacement: median = 0.10 cm; z = 0.54; P(z ≥ 0.54) = 0.94]. In summary, the good reproducibility of field properties and locations between pairs of standard sessions allows us to detect subtle changes caused by card manipulations.

Control over Firing Field Position by Equal Card Rotations

Previous work showed that rotations of a single white card or a single black card caused equal rotations of firing fields (Muller and Kubie 1987; Bostock et al. 1991). To establish that the card pair exerted similar strong stimulus control, we therefore ran at least one equal card rotation session for each rat. These equal card rotations had the expected effect of causing equal field rotations. The mean departure of centroid rotation for nine fields was not different from zero [mean error = 0.90 ± 5.9°; t = 0.46; df = 8; P(t ≥ 0.46) = 0.66]. The mean absolute departure of field centroid rotation from the ideal was 4.6° ± 3.5°. We did not do rigid rotations for each cell set to reduce the number of required sessions, thereby increasing the likelihood that the cells would remain discriminable and that the rat would continue to run during more informative card removals and reconfigurations.

Changes in Field Properties and Positions Caused by Removing One Card

To test whether each card was individually salient, sessions were run in which one card or the other was removed. We begin by considering separately one-card sessions done in the presence of only the white card and others done only in the presence of the black card. We will show that the properties of place cells in the presence of either card are the same as in standard sessions. We will further show that rotations of either card cause equal rotations of firing fields regardless of their position in the apparatus.

The properties of 18 firing fields recorded in the presence of only the white card are compared with their properties in preceding standard sessions in Table . In no case was there a reliable difference in any field property. Similarly, in Table , the properties of 30 fields recorded in the presence of only the black card are compared with their properties recorded in preceding standard sessions. Once again, there was no reliable difference for any property.

Table 3.

Firing Pattern Parameters for a Standard Session and a Succeeding White Card Only Session

	Standard	White Card	Difference	Paired t	P
Grand rate	2.86 ± 3.94	3.00 ± 4.32	0.139 ± 0.927	0.636	0.53
Field rate	8.48 ± 6.81	7.68 ± 6.56	−0.802 ± 3.29	1.03	0.32
Centroid rate	16.25 ± 12.33	16.33 ± 16.38	0.073 ± 11.5	0.027	0.98
Size	995.6 ± 817.5	1124.3 ± 997.6	19.3 ± 75.0	1.09	0.29
Coherence	1.12 ± 0.244	1.084 ± 0.284	−0.032 ± 0.280	0.489	0.63
Information	2.98 ± 1.55	2.78 ± 1.59	−0.204 ± 1.17	0.744	0.47

The high values of probability for all parameters indicates that removing the black card had no detectable effect on any of these field properties.

Table 4.

Firing Pattern Parameters for a Standard Session and a Succeeding Black Card Only Session

	Standard	Black card	Difference	Paired t	P
Grand rate	2.27 ± 3.15	2.61 ± 4.15	0.339 ± 2.91	0.627	0.54
Field rate	6.84 ± 6.53	6.21 ± 5.00	−0.669 ± 3.693	0.922	0.36
Centroid rate	15.28 ± 12.47	12.57 ± 9.60	−2.922 ± 10.09	1.46	0.15
Size	917.0 ± 683.2	994.6 ± 930.2	79.43 ± 846.9	0.503	0.62
Coherence	1.083 ± 0.302	1.090 ± 0.302	0.003 ± 1.002	0.135	0.89
Information	2.86 ± 1.17	2.88 ± 1.41	0.035 ± 1.002	0.138	0.89

The high values of probability for all parameters indicates that removing the white card had no detectable effect on any of these field properties.

As an aside, we note that the mean values of all three firing rate measures in both the white and black card sessions and their preceding standard sessions (Table and Table ) are somewhat higher than for the standard sessions in Table . There is, however, no tendency for any property to change when either card is removed.

Because the field properties in the presence of either card do not change compared with preceding standard sessions, it is convenient to combine white and black card sessions into a card removal group. To further test whether this is reasonable, we directly compared field properties in white card sessions to properties in black card sessions. When this was done for the samples of 30 black card sessions and 18 white card sessions, no reliable difference was found in any field property (values not given). We also asked about pairwise differences for the 16 fields that were recorded in the presence of each card alone. There were no differences according to pairwise t tests for any measure. Therefore, field centroid movements seen in black card only and white card only sessions are combined.

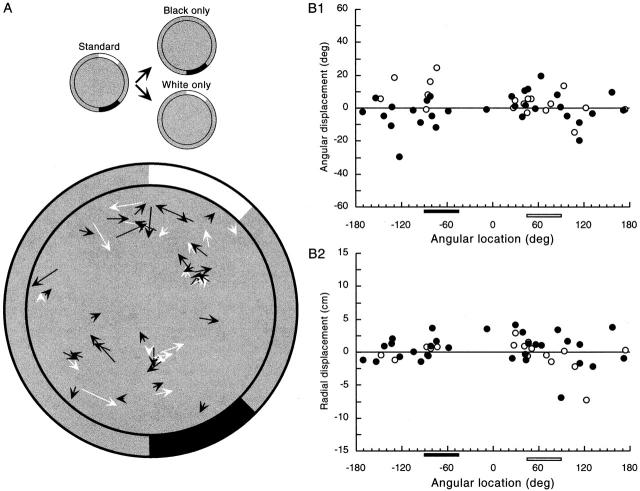
In parallel with Fig. 4, Fig. 5 contains two descriptions of how removing one card affected the position of field centroids. The centroid displacement vectors shown in Fig. 5 A are once again short (mean = 3.6 ± 2.4 cm). The length of the Rayleigh vector is also short and indicates no clustering of displacement vector directions at any angle [mean = 29.2°, variance = ± 93.4°, r = 0.18, (P(r ≥ 0.18) > 0.20]. Field centroid movements were also assessed by plotting the angular (Fig. 5 B, 1) and radial (B, 2) components of the displacement vectors as a function of angular position within the cylinder. Inspection of the displacement vector components reinforces the notion that there is no systematic tendency of centroids to rotate or to move radially when one card is removed. Neither the mean angular displacement [−1.92° ± 10.01°; t = 1.08; P(t ≥ 1.09) = 0.28] nor the mean radial displacement [0.21 ± 2.07 cm; t = 0.59; P(t ≥ 0.59) = 0.56] were reliably different from zero. According to runs tests, there was also no tendency of the angular or radial displacement vector components to reliably occur in certain angular ranges within the cylinder [angular displacement: median = −1.11°; z = 0.00; P(z ≥ 0.00) = 1.0; radial displacement: median = 0.27 cm; z = 0.00; P(z ≥ 0.00) = 1.0]. Thus, within the accuracy of our measurements, each of the two cue cards separately exerts nearly ideal stimulus control over the angular positions of firing fields. When either card is rotated, fields everywhere in the apparatus rotate by an equal amount, as if all the fields were rigidly connected to each other and in turn to the remaining cue card.

Figure 5.

Cue removal does not affect the position of field centroids. (A) The white arrows (white card only) and black arrows (black card only) represent displacement vectors associated with card removal. As was true for pairs of standard sessions, the displacement vectors are short, indicating that card removal leaves the field centroid position alone. In addition, there is no apparent organization to the directions of the displacements. (B) Plotting the angular and radial vector field displacements against the normalized angular coordinate did not reveal any underlying pattern to displacement of field centroids. The paucity of fields in the short arc between the cards is due only to choices about which fields were recorded during removal sessions.

Following the work of Hetherington and Shapiro 1997, we also asked if there were systematic changes of firing rates, field size, coherence, or information content as a function of distance of a field away from the removed card or as a function of distance away from the remaining card. Possible effects of distance were looked for in two ways. First, we calculated the correlation between distance from a card and change in field properties. Second, we divided fields into those closer to a card than the radius of the cylinder and those further away (unequal areas). In contrast to the finding of Hetherington and Shapiro 1997 that field size increased and firing rate decreased for fields near a removed stimulus, we saw no systematic relationship between field property changes and distance from either the position of the removed card or the remaining card.

Changes in Field Properties and Positions Caused by Moving the Cards Apart or Together

Having found that the two cards are equally salient when only one is present, we next asked how field centroids moved when the separation between the cards was increased or decreased by 25°. This creates a kind of conflict for the place cell system since the altered separation between the cards would require fields to be in two positions at once. Our goal was to see how this conflict was resolved. We first show that several field properties were changed by the apart and together card manipulations and then describe the field movements themselves.

A total of 47 fields were recorded after the cards were moved apart by 25°; the properties of these fields in the apart session and in the preceding standard session are summarized in Table . Thus, increasing the card separation caused a decrease in all three firing rate measures and a reduction in coherence. Field size was unchanged. Moreover, given constant field size, it is not surprising that information content was unchanged since information content measures the reduction of uncertainty of the animal's position available from a single spike.

Table 5.

Firing Pattern Parameters for a Standard Session and a Succeeding Card-apart Session

	Standard	Apart	Difference	Paired t	P
Grand rate	0.767 ± 0.718	0.615 ± 0.614	−0.152 ± 0.459	2.096	0.04
Field rate	4.95 ± 2.95	3.932 ± 2.686	−1.013 ± 2.26	2.840	0.007
Centroid rate	12.77 ± 11.07	8.224 ± 8.695	−4.542 ± 12.37	2.323	0.03
Size	549.8 ± 361.1	543.0 ± 402.2	−6.76 ± 267.2	0.160	0.87
Coherence	1.072 ± 0.266	0.957 ± 0.285	−0.115 ± 0.270	2.695	0.01
Information	3.59 ± 1.09	3.57 ± 1.12	−0.025 ± 0.876	0.180	0.86

The probabilities for the t values indicate reliable decreases in three different measures of firing rate. Coherence also decreased, suggesting that the field was noisier. There was no change in field size. As expected for unchanged field size, the information per spike is unaffected by moving the cards apart.

A total of 64 fields were recorded after the cards were moved together. Means for the properties of these fields in together sessions and in the preceding standard session are shown in Table . Decreasing the distance between the cards also produced decreases of all three firing rate measures, although the decrease of the grand rate is only a trend. In addition to the decreased firing rates, we also observed a small decrease in the pairwise coherence that approaches significance at the 0.05 level. Once again, field size and information content were unaffected.

Table 6.

Firing Pattern Parameters for a Standard Session and a Succeeding Card-together Session

	Standard	Together	Difference	Paired t	P
Grand rate	0.747 ± 0.792	0.61 ± 0.63	−0.136 ± 0.673	1.55	0.13
Field rate	4.03 ± 2.420	3.45 ± 2.06	−0.577 ± 1.502	2.95	0.005
Centroid rate	12.09 ± 11.51	7.46 ± 7.65	−4.635 ± 10.62	3.35	0.001
Size	593.7 ± 361.1	576.3 ± 52.2	−17.4 ± 398.7	0.34	0.74
Coherence	1.046 ± 0.285	0.979 ± 0.225	−0.067 ± 1.056	1.95	0.06
Information	3.55 ± 1.18	3.49 ± 1.16	−0.059 ± 1.056	0.43	0.67

The probabilities for the t values indicate decreases in three different measures of firing rate, although the decrease in grand rate is only a trend. The decrease in coherence was also only a trend, suggesting that the field was noisier. There was no change in field size nor information per spike.

In addition to comparing field properties between both kinds of reconfigured session and corresponding preceding standard sessions, we also compared field properties between apart and together sessions. We first compared the properties of 47 fields recorded in apart sessions and 64 fields recorded in together sessions and saw no reliable differences. We also compared the properties of 27 fields recorded in both apart and together sessions and again saw no differences. Thus, the apart and together manipulations affect field properties in the same way.

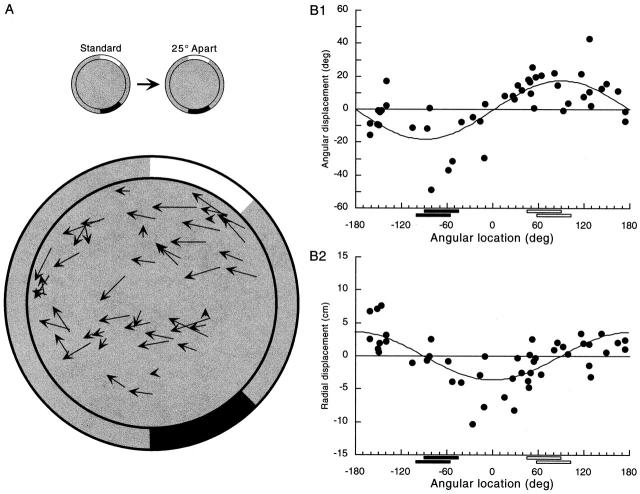
The field centroid movements caused by moving the cards apart and together are shown, respectively, in Fig. 6 and Fig. 7. The field displacement vectors for the apart manipulation (Fig. 6 A) show a clear organization. Fields in general moved in the direction of movement of the imaginary line that connects the centers of the cards, although fields near the wall at 9:00 o'clock (180°) showed little displacement; we will consider possible reasons for this pattern in the discussion. In addition to an overall motion of the displacement vectors, there also appears to be a relatively smooth shift in their directions in the vicinity of the white and black cards.

Figure 6.

Differential movements of field centroids caused by increasing the card separation by 25°. (A) In contrast to the constancy of field position in standard sessions or after removal of either card, there is a distinct pattern to the movements of field centroids when the cards are moved apart. The overall tendency is for field centroids to shift in the direction of movement of the line that connects the two card centers; with the chosen coordinate system, this tendency is for fields to move horizontally. In addition, there is a trend for fields near the white card to rotate along with the card, with little change in the distance from the cylinder center. A similar trend for fields near the black card to rotate with the black card is visible but more evident in the component plotted in B. (B) The curves on the graphs are sine functions fitted by eye. (1) The plot of the angular component of displacement vectors for field centroids shows that centroids in the sector delimited by each card tend to rotate with that card, whereas centroids in the small or large sector between the cards tend not to rotate. (2) The plot of the radial component of displacement vectors shows that fields near either card did not tend to move inward or outward relative to the cylinder center. In contrast, fields in the small arc between the cards tended to move towards the cylinder center, whereas those in the large arc between the cards tended to move away from the cylinder center.

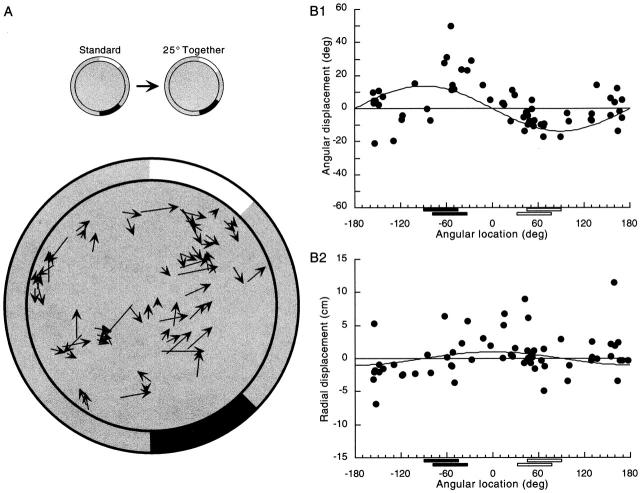
Figure 7.

Differential movements of field centroids caused by decreasing the card separation by 25°. (A) To a first approximation, the pattern of field centroid movements caused by moving the two cards closer together is similar to but in the opposite direction of the movements caused by moving the cards apart. The magnitude of the effect is, however, weaker than in the case of the apart manipulation. (B) The curves on the graphs are sine functions fitted by eye. (1) The variation of the angular component of the displacement vectors is clear and has the same pattern as for the together manipulation; field centroids near either card tend to rotate with that card, whereas fields in the sectors between the cards tend not to rotate. (2) An overall tendency of fields in the sectors between the two cards to move relative to the cylinder center is visible but weaker than was the case for the apart manipulation. This effect is most evident from the preponderance of positive radial displacement components in the small arc between the cards.

The nature of this feature of the displacement vector pattern is revealed by plotting the angular and radial components of the vectors (Fig. 6 B). First, there is a clear tendency of fields near each cue card to rotate along with the card (Fig. 6 B, 1). In contrast, fields in either the small sector or the large sector between the cue cards tend not to rotate at all. The impression that similar angular displacements occur at similar angular positions around the cylinder is confirmed with a runs test [median angular displacement component = 3.63°; z = 3.98; P(z ≥ 3.98) = 6.8 × 10⁻⁵]. There is also a clear tendency of fields in either the small or large sector between the cards to move radially such that fields to the right of the center move towards the center (negative radial displacements) and fields to the left of the center move away from the center (positive radial displacements; Fig. 6 B, 2). In contrast, fields near either cue card tend to show no radial displacement at all. The impression that similar radial displacements occur at similar angular positions around the cylinder is also confirmed with a runs test [median radial displacement component = 0.22 cm; z = 3.95; P(z ≥ 3.95) = 7.8 × 10⁻⁵]. Thus, moving the cards apart causes field centroids to move relative to each other; it is as if the area inside the cylinder undergoes a topological stretch. To illustrate the pattern of field displacements, sine functions have been drawn in Fig. 6 B, 1 and 2.

The displacement vectors caused by moving the cards together are shown in Fig. 7 A. There is a clear tendency for field centroids to move in the opposite direction to the movements caused by the apart manipulation so that once again the fields follow the motion of the imaginary line that connects the centers of the cards. Interestingly, as with moving the cards apart, fields near the wall at 9:00 o'clock do not tend to move towards the cylinder center. We will consider this issue in the discussion.

Additional features of the pattern of field movements after together manipulations are shown by plotting the components of the displacement vectors against angular field position. In agreement with the effects of moving the cards apart, fields near each card rotate along with the card (Fig. 7 B, 1), whereas fields in the sectors between the cards show little angular movement. The tendency for similar angular displacements to occur at similar angular positions around the cylinder is confirmed with a runs test (median angular displacement component = −0.76°; z = 3.59; P(z ≥ 3.59) = 3.3 × 10⁻⁴). In contrast to the apart manipulation, however, a runs test reveals no clear clustering of radial movements as a function of angular field position (see Fig. 7 B, 2). Nevertheless, there appears to be a tendency of fields in the small arc between the cards to move away from the cylinder center. Overall, it is clear that the magnitudes of the radial displacements are smaller for the together than for the apart manipulation. Testing this impression and considering its implications are deferred to the next paper (Fenton et al. 2000).

DISCUSSION

To reinvestigate how place cells represent the environment, we made recordings as rats ran around inside a gray cylindrical apparatus with two distinct stimuli, a white card and a black card, pasted on the apparatus wall. There were four main findings. (a) In agreement with earlier work (Muller and Kubie 1987; Thompson and Best 1990), firing fields are stable for days when place cells are repeatedly recorded with the two cards in standard positions. (b) Equal rotations of the two cards on the cylinder wall caused firing fields to rotate by the same amount. Firing fields were otherwise unaltered by such rigid rotations. This nearly ideal control of firing fields by specific stimuli is also in agreement with previous work (O'Keefe and Conway 1978; Muller and Kubie 1987; Sharp et al. 1990; Gothard et al. 1996; Cressant et al. 1997). (c) The only effect of removing one card and rotating the other was to cause uniform rotations of all firing fields. Thus, removal of one card did not cause firing fields to move relative to each other, nor were their firing rates or local smoothness affected. (d) Changing the angular distance between the cards by unequal rotations had several major effects on firing fields. First, fields in different parts of the cylinder moved in different ways so that distances between field centroids were topologically altered. Second, place cell firing rates decreased regardless of whether the cards were moved closer together or further apart. Finally, as measured by coherence, the local smoothness of fields decreased regardless of their position in the environment. We consider the significance of each of these results in turn.

In the experimental design, standard sessions were alternated with all other session types to test whether card manipulations induced permanent changes in positional firing patterns. No such changes could be seen by inspection of firing rate maps, an impression confirmed with numerical estimates of variations in firing field locations and properties under constant conditions. The mean displacement of the field centroid pixel was only 2.9 cm, or ∼4% of the cylinder diameter. The mean fractional change of in-field firing rate was ∼20%, a small value relative to the range of in-field firing rates across place cells. The reproducibility of firing fields in standard conditions provides a baseline against which to measure changes induced by card manipulations.

The constancy of place cell activity in the standard cylinder has another and critical implication: for the firing patterns to be reproducible in a given environment and to be completely different but also reproducible in other environments (Muller and Kubie 1987; Thompson and best, 1990; Kentros et al. 1998), there must be stored for each an environment-specific “template.” Only one template can be used at a time; the others coexist in a latent form and are not expressed. The process by which a given environment is recognized is outside the scope of our current treatment; we are interested in how a template, once activated, permits each place cell to fire in its stable firing field. We believe that formation of such environment-specific templates requires the participation of synaptic plasticity mechanisms (Kentros et al. 1998; Rotenberg et al. 2000). But even if each template is preestablished during development (McNaughton et al. 1996; Samsonovich and McNaughton 1997), reproducibility of place cell activity means that the correct template is activated by a recognition process. The existence of environment-specific templates forms an essential part of our theory of how stimuli control place cell activity.

The reproducibility of firing fields under constant circumstances may mean that the sensory information necessary to reactivate the template and to allow reliable location-specific firing for individual cells is supplied by the cue cards, by uncontrolled background stimuli, or by both. We asked about the relative importance of the cards by rotating them through equal angles on the wall of the cylinder. Such rotations caused the centroids of all fields to rotate uniformly through the same angle, establishing the salience of the card pair. That stimulus control by the cards is prepotent is suggested by our inability to detect any other effect of equal rotation of the two cards. The uniform rotation of all fields and the otherwise unchanged properties means that the fundamental features of the across-cell representation of the environment, including distances between firing fields, are unchanged by equal card rotations; it is as if the field centroids are connected by rigid rods so that the whole representation rotates as a unit.

Our next question was whether both cards had to be present for the environmental template to be activated, and, if not, whether stimulus control was exerted exclusively by one card or the other, or if both cards were individually salient. Removal of one card and rotation of the other caused uniform rotations of firing fields, regardless of the position of the firing field in the environment; no other changes in firing field properties were detected. Thus, either card could be removed without interfering with recognition of the environment or with reliable location-specific firing of place cells. As was true of equal card rotation, removal of one card left intact all properties of the representation, including distances between all pairs of field centroids; once again the representation acted as a rigid unit. The ability of each card to control firing field position shows that neither card overshadowed or blocked the other during or after the initial experience in the environment. It is also possible, however, that stimulus control is exerted exclusively by only one card when both are present, that control over all fields might be exerted by an average of the positions of the two cards, or that some cells are controlled by one card, some cells are controlled by the other card, and yet other cells by the two cards together.

We examined these possibilities by doing card reconfiguration sessions in which the angular distance between the cards was either increased (in “apart sessions”) or decreased (in “together sessions”). Two general kinds of outcomes are possible. (a) All fields undergo precisely the same rotation and are otherwise unchanged. Outcomes in which the entire representation rotates as a rigid unit imply that the resolution of the conflict in card position is based on the selection of a single angular reference. (b) Fields move relative to each other; other field properties may or may not be changed. Outcomes in which distances between field pairs are topologically distorted suggest that fields are differentially controlled by the two stimuli. We found that either kind of card reconfiguration caused fields to move relative to each other and caused the strength and local smoothness of fields to decrease. Note that the observed topological distortion occurred without changing apparatus shape (compare the individual cell data of O'Keefe and Burgess 1996).

The two most important parts of this study are therefore in apparent conflict since they support two very different interpretations of the place-cell representation. On one hand, removal of either card leaves the representation unchanged, precisely what is expected from the rigid map model in which no single component of the stimulus constellation is critical for any single cell. On the other hand, changing the angular distance between the cards has clear effects on individual firing fields and distorts the overall representation, results that are compatible with the combinatorial model in which individual cells are independently tuned to arbitrary sets of stimuli selected from the stimulus constellation.

Before turning to a new model that is compatible with both card removal and reconfiguration, it is important to show how the rigid map and combinatorial models fail to account for the entire set of results. First, the rigid map model is at odds with the reconfiguration manipulation since the field centroid positions of individual cells are clearly controlled by individual stimuli. Specifically, after reconfigurations, fields near a card move as if they are rigidly attached to that card, whereas fields between the two cards act as if they are controlled about equally by the two cards. In any simple interpretation of the rigid map model, inconsistencies should be resolved in a way that allows the representation to remain an undistorted unit. Thus, in agreement with the work of O'Keefe and Burgess 1996, Tanila et al. 1997, Skaggs and McNaughton 1998, and Knierim et al. 1998, our results indicate that the basic rigid map model is incorrect.

At first glance, the combinatorial model fares better since it not only seems to be compatible with the reconfiguration results, but can also account for the effects of card removal. In this explanation, each cell in the standard environment is tuned primarily to either the white card, the black card, or both cards. Following Shapiro et al. 1997, the tuning of each cell can switch when its primary stimulus is removed so that, in the presence of only one of two salient stimuli, all cells are controlled by that stimulus. We emphasize that the proposed process of switching from the primary to a secondary stimulus with no changes in other field properties is an additional, ad hoc assumption for the combinatorial model. Nevertheless, there is no fundamental inconsistency between the main model and this additional requirement.

Why then do we reject the combinatorial model? It is mainly because additional analysis of the reconfiguration experiments indicates that the combinatorial model does not account for the entire range of results. First, although movements of field centroids indicate that some cells are primarily tuned to the white card, some to the black card, and some to the two cards combined, the combinatorial model in no way predicts or accounts for the fact that there is a spatial pattern to the tuning. Thus, it would require yet another new assumption to explain why fields near each card act as if they are controlled by that card, whereas fields between the cards are tuned to the combination of the cards and therefore show radial rather than rotational movements during reconfigurations. The finding that the salience of a card depends on the distance between the card and the field means that fields cannot move relative to each other in arbitrary ways, but instead that the mapping of the environment onto the place cells has a distinct spatial flavor. The fact that field movements are systematic and smoothly distributed with position forms the basis of the theory presented in the next paper (Fenton et al. 2000).

A second major discrepancy between the reconfiguration data and the combinatorial model involves changes in the properties of individual cells. If single cells are indeed tuned to a specific card or a combination of the cards, we would expect there to be no detectable change in properties for cells whose centroid position is controlled by the nearby card. In reality, we see that decreases in firing rate and coherence are homogeneous across the apparatus surface. These decreases in field intensity and quality suggest that both cards are important for all fields, even for fields whose centers move in register with one card or the other. Thus, it is possible to use field properties to detect the influence of each card on all place cells. Taken together, the smooth, cohesive motions of fields induced by reconfigurations and the position-independent importance of each card leads us to believe that the combinatorial model ignores a true spatial organization to the place-cell representation of the environment.

What do we propose to supplant the rigid map and combinatorial models? We suggest that a template is constructed during the animal's initial experience in a given environment. When the animal is put back in the environment, an unspecified recognition process decides whether the current surroundings are familiar or novel. We imagine that the decision rules are very complex and depend on the behavioral requirements in the environment as well as the immediate sensory information (Markus et al. 1995; Zinyuk et al. 2000). We do not consider further what happens if a new template must be built. In the present case, the fact that firing fields were unaltered by equal card rotations and card removals and only subtly altered by card reconfigurations indicates that the same template was used in all experimental circumstances. The fact that the template remains intact despite changes in the stimulus constellation suggests that the template is indeed a neural entity with an integrity of its own (Muller et al. 1991, Muller et al. 1996; Samsonovich and McNaughton 1997). We therefore speculate that blocking synaptic plasticity mechanisms would not change the effects of any card manipulations.

When an environment is recognized as familiar, its template is activated. By activation, we mean that the hippocampus proper and especially CA3 becomes an environment-specific autoassociative network (Lisman 1999; Rolls 1996; Mizumori et al. 1989). This network is environment specific because discharge is confined to an environment-specific subset of the pyramidal cells—those that are place cells in the environment. Moreover, if discharge is confined to this “active subset” of pyramidal cells, the set of synapses that contribute to processing in the network is greatly reduced; only synapses made onto pyramidal cells in the active subset or onto interneurons control processing.

What happens when the template is active and the rat is at a certain place in the environment? We consider a separate case for each experimental condition. In the standard cylinder, there is an exact match between the current view of the environment and information stored in the autoassociator. Consequently, only those place cells whose fields contain the rat's current position discharge; the discharge rate of each cell is a function of the distance between the rat's position and the centroid of the cell's field (Zipser 1985; Sharp 1991; Wan et al. 1993; Burgess and O'Keefe 1996; O'Keefe and Burgess 1996). When the rat moves to another position, the sensory input pattern changes and the distribution of activity across the output of the autoassociator (the place cells) changes in parallel. When the cards are rotated equally, everything is the same because stimulus control by the two cards is ideal within our experimental error.

When one card is removed, the sensory input pattern no longer matches the template. Nevertheless, the remaining card exerts ideal stimulus control over all firing fields, regardless of their position in the cylinder. Furthermore, firing rates and coherence do not change. Thus, removal of a demonstrably salient stimulus has no detectable effect on place cells. This is possible because the autoassociative network performs nearly ideal completion of the input stimulus pattern.

Why then do fields move relative to each other and degrade when card reconfigurations are made? We imagine that fields move because the place where the best fit occurs between the current input pattern and the template has moved from its original location. The degradation of firing patterns occurs because the closeness of the best fit between the input pattern and the template is decreased; there is no place at which all of the information about the stimuli simultaneously match the learned input pattern of the template.

We view the proposed operations of an autoassociator on the stimulus patterns after card removal and card reconfiguration as examples of a more general transformation. For instance, if the contrast of, say, the black card against the gray wall is reduced when the card separation is changed, then we might find that the magnitude of the topological stretch of the environment and the reduction of firing rates are proportionally decreased. Alternatively, the combined effect of contrast reduction and card reconfiguration might suddenly become equivalent to card removal at some threshold contrast. Experiments of this sort allow distinctions to be made among different classes of autoassociator (attractor) models.

A key question about this picture is whether the effects of card removals and reconfigurations can be reproduced with an anatomically realistic network model in which the synaptic weights are set for the standard environment, and then not modified. It is also worth noting that an alternative to the view that the pattern completion/distortion operations take place in the hippocampus is that it is the input to the hippocampus that is modified in the stated ways. These alternatives can be distinguished by recording cells in entorhinal cortex and dentate gyrus and possibly earlier in the pathways that process sensory information.

It is our intention to build a neural network model to see what properties it must have to account for our results. We have, however, already taken a parallel approach in which we model the effects of card removal and reconfiguration with a formal mathematical model (Fenton et al. 2000). This strictly empirical model is built to account for the effects of removing one card or the other and for changing the separation between the cards. It takes the form of a vector field equation that describes how field centroids move under the stated conditions. We then test the ability of the vector field equation to predict effects on firing patterns in addition to movements of field centroids.