Abstract
The effects of 0.3–10 nM extracellular protons (pH 9.5–8.0) on ouabain-sensitive rubidium influx were determined in 4,4′-diisocyanostilbene-2, 2′-disulfonate (DIDS)-treated human and rat erythrocytes. This treatment clamps the intracellular H. We found that rubidium binds much better to the protonated pump than the unprotonated pump; 13-fold better in rat and 34-fold better in human erythrocytes. This clearly shows that protons are not competing with rubidium in this proton concentration range. Bretylium and tetrapropylammonium also bind much better to the protonated pump than the unprotonated pump in human erythrocytes and in this sense they are potassium-like ions. In contrast, guanidinium and sodium bind about equally well to protonated and unprotonated pump in human red cells. In rat red cells, protons actually make sodium bind less well (about sevenfold). Thus, protons have substantially different effects on the binding of rubidium and sodium. The effect of protons on ouabain binding in rat red cells was intermediate between the effects of protons on rubidium binding and on sodium binding. Remarkably, all four cationic inhibitors (bretylium, guanidinium, sodium, and tetrapropylammonium) had similar apparent inhibitory constants for the unprotonated pump (∼5–10 mM). The K d for proton binding to the human pump, with the empty transport site facing extracellularly is 13 nM, whereas the extracellular transport site loaded with sodium is 9.5 nM, and with rubidium is 0.38 nM. In rat red cells there is also a substantial difference in the K d for proton binding to the sodium-loaded pump (14.5 nM) and the rubidium-loaded pump (0.158 nM). These data suggest that important rearrangements occur at the extracellular pump surface as the pump moves between conformations in which the outward facing transport site has sodium bound, is empty, or has rubidium bound and that guanidinium is sodium-like and bretylium and tetrapropylammonium are rubidium-like.
Keywords: pH clamp, tetrapropylammonium, ion transport, Na(+)-K(+)-exchanging ATPase, red blood cells
INTRODUCTION
The sodium pump harnesses the energy of ATP hydrolysis to move sodium ions out of cells and potassium ions into cells. Extensive kinetic studies of the pump have provided important evidence in support of the current kinetic model (Blostein, 1999; Apell and Karlish, 2001). An important feature of the model is that the exchange of sodium and potassium is ping-pong, that is, intracellular sodium ions bind, are occluded, and then released to the outside. After this half cycle is finished, extracellular potassium ions bind, are occluded, and then released to the inside. During the sodium half-cycle, the terminal phosphate from ATP is catalytically transferred to the pump, forming a phosphointermediate. During the potassium half-cycle, the phosphointermediate is hydrolyzed.
Like all enzymes, the sodium pump has an optimal proton concentration. In open membranes, where the proton concentration on both sides is varied, the optimal proton concentration is roughly around the physiological range (40 nM or pH 7.4) (Skou, 1979). Skou (1979) has shown that increasing the proton concentration favors the conformation that binds potassium and lowering the proton concentration favors the conformation that binds sodium. These ATPase studies were done on open membranes and thus it is not possible to discern whether the effect is due to intracellular protons or extracellular protons or both. On the other hand, sidedness can be strongly inferred from the studies with eosin, even in an unsided preparation (Skou and Esmann, 1980). In the absence of ATP, eosin binds to the ATP site and can be used to monitor the potassium and sodium forms. These studies clearly showed that intracellular protons favored the potassium conformation. Equivalently, the results can be stated as saying that the K d for protons binding to a particular residue changes depending on whether intracellular potassium or sodium is bound to the pump. In this way, the state of this residue can provide information about different pump conformations.
An increase in extracellular proton concentration from 40 nM has been shown to lead to proton transport (Polvani and Blostein, 1988; Dissing and Hoffman, 1990; Goldshleger et al., 1990). Only a few studies have examined the effect of decreasing extracellular proton concentration on sodium/potassium exchange by the sodium pump. Breitweiser et al. (1987), in squid axons, showed clearly that the predominant effect of protons in the pH range from 6 to 8 was at the intracellular surface (at saturating extracellular potassium). Recently, Salonikidis et al. (2000) showed that protons altered the Km for potassium on the outside and influenced the rate of the intermediate charge movement step during sodium release.
Several organic cations are thought to bind to the potassium site, including tetrapropylammonium and bretylium (Kropp and Sachs, 1977; Dzimiri and Almotrefi, 1992). Bretylium competes with potassium (Dzimiri and Almotrefi, 1992). At low concentrations, tetrapropylammonium and potassium compete and extracellular sodium makes tetrapropylammonium inhibit better (Kropp and Sachs, 1977). This effect of extracellular sodium is difficult, if not impossible, to explain by an interaction of sodium at the transport site. This is one piece of kinetic evidence in support of an extracellular sodium modifier site (Kropp and Sachs, 1977). Karlish and coworkers (David et al., 1992; Or et al., 1993) have found that guanidinium and related compounds are sodium-like in interactions on the cytoplasmic surface.
In this paper, we examine the effects of extracellular protons, in the range of 0.3–10 nM (pH 9.5–8.0), on rubidium influx. Rubidium is a convenient potassium congener. Red blood cells allow us to clamp the intracellular proton concentration so that only the extracellular H concentration is varied. We compared the effect of extracellular protons on the inhibition by bretylium, guanidinium, sodium, and tetrapropylammonium. Remarkably, all these ions have similar apparent inhibitory constants for the unprotonated pump. In contrast, the protonated pump has dramatically different apparent inhibitory constants for these four ions. Protons decrease the apparent Ki for tetrapropylammonium 13.4-fold, for bretylium 8.1-fold, and for guanidinium and sodium only 1.1- and 1.35-fold, respectively. Protons also decreased the kinetic constant for rubidium 34-fold in human red cells. Thus, bretylium and tetrapropylammonium are rubidium-like and guanidinium is sodium-like. In rat red cells, protons also decreased the kinetic constant for rubidium (13-fold); in contrast, protons increased the kinetic constant for sodium (7.1-fold). Protons only slightly affected ouabain binding by decreasing the Ki 2.2-fold. Importantly, protons greatly improved the binding of extracellular rubidium relative to sodium in both rat and human red cells. These data suggest that important rearrangements occur at the extracellular pump surface as the pump moves between conformations in which the outward facing transport site has sodium bound, is empty, or has potassium bound.
MATERIALS AND METHODS
Human blood was obtained from a consenting volunteer into a heparinized tube. Rat blood was obtained from Pel-Freez (Arkansas). After removal of plasma and white cells, the red cells were washed three times in a solution of 165 mM NaCl. Cells were stored at least overnight at 4°C and for up to 1 wk. The overnight storage ensures that the Na concentration in the cell is nearly saturating (typically ∼40 mM in our hands). On the day of the measurement, the cells were incubated in a solution containing 150 mM NaCl, 20 mM HEPES, and 10 mM glucose for 1 h in order to be sure the ATP concentrations were restored. K was omitted in order to keep the cell Na high. The cells were treated with 0.1 mM 4,4′-diisocyanostilbene-2, 2′-disulfonate (DIDS)* in the same media for 15 min. Normal red blood cells rapidly equilibrate protons, primarily via chloride/bicarbonate exchange. DIDS inhibits this exchange and the residual proton flux is very small (Jennings, 1978; Wieth et al., 1980). The substantial buffering capacity of hemoglobin easily prevents any intracellular proton concentration change due to the small proton influx. Thus, it is possible, using DIDS treated red blood cells, to clamp the intracellular pH and vary only the extracellular pH (Xu and Roufogalis, 1988; Milanick, 1990; Dissing and Hoffman, 1990; Xu et al., 2000.). In control experiments, we measured the pH in lysed DIDS-treated red cells before and after incubation for 10 min at pH 9.28 (the highest pH used in these studies). After the incubation, the cells were washed in unbuffered Mg(NO3)2 and then lysed and the pH measured with a pH electrode. There was no significant difference in the intracellular pH.
After the DIDS treatment, the cells were then washed three times in 110 mM Mg(NO3)2 and placed into flux media. Nitrate was used so that there would be no chloride-dependent rubidium flux, thus reducing the ouabain-insensitive component of the flux. The media contained 0.1 mM DIDS, 0.3 mM Rb (except Fig. 7 where the indicated concentrations were used), 86Rb, 62 mM Mg(NO3)2, and 100 mM N-methyl-D-glucamine TAPS, titrated to the indicated proton concentrations. The final concentration of red cells was <1%. The tubes were incubated at 37°C for 10 min. The flux was stopped by adding ice cold 137 mM Na2SO4 and the cells spun down. They were washed two additional times in the same media and the amount of 86Rb in the pellet determined with a scintillation counter. In preliminary experiments, we found that the ouabain-insensitive flux was independent of the proton concentration, thus we only measured the flux in the presence of ouabain at the lowest proton concentration studied in each experiment (0.5 nM except for one experiment in Fig. 3) and used that measurement to determine the ouabain-sensitive flux at all proton concentrations.
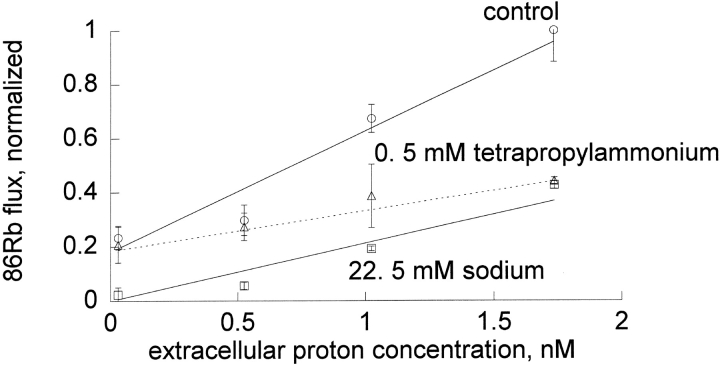
Figure 7.
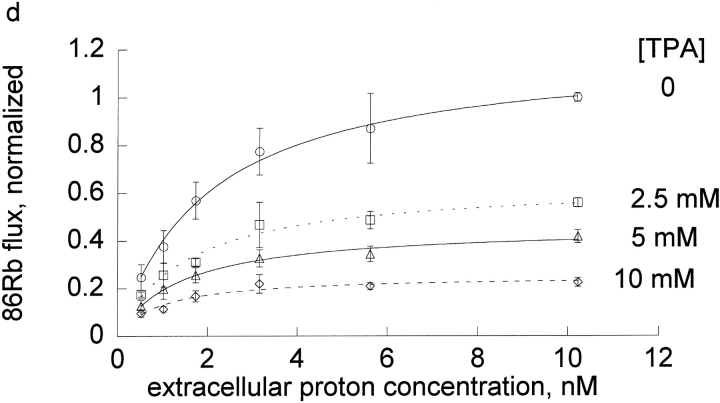
Extracellular protons influence the inhibition by sodium more than the inhibition by tetrapropylammonium. Ouabain-sensitive 86Rb influx was determined as described in materials and methods in DIDS-treated red blood cells. Shown are the mean and standard deviation of a representative experiment of a total of three that were done under these conditions. In this experiment, the slope in the absence of inhibitor (circle) was 0.447 ± 0.055, in the presence of 0.5 mM tetrapropylammonium (triangle) was 0.149 ± 0.032, and in the presence of 22.5 mM sodium (square) was 0.212 ± 0.006. The slope of flux versus proton concentration was statistically significantly different for tetrapropylammonium and for sodium in all three experiments.
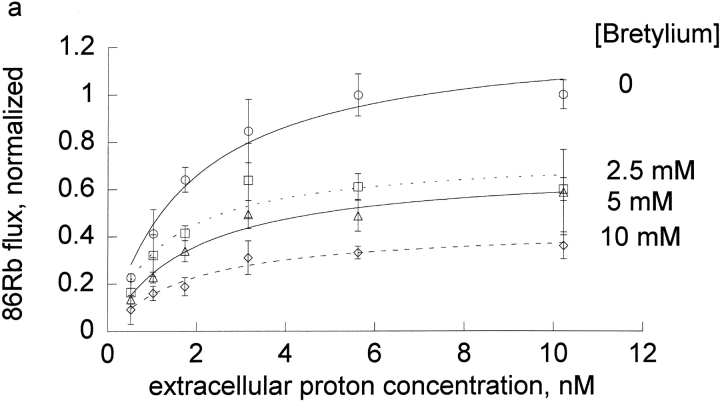
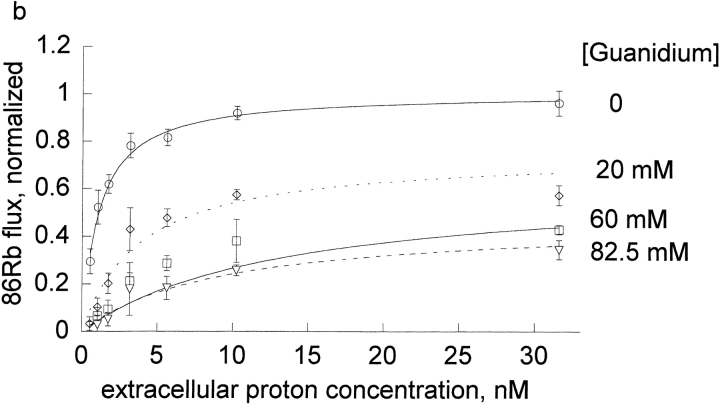
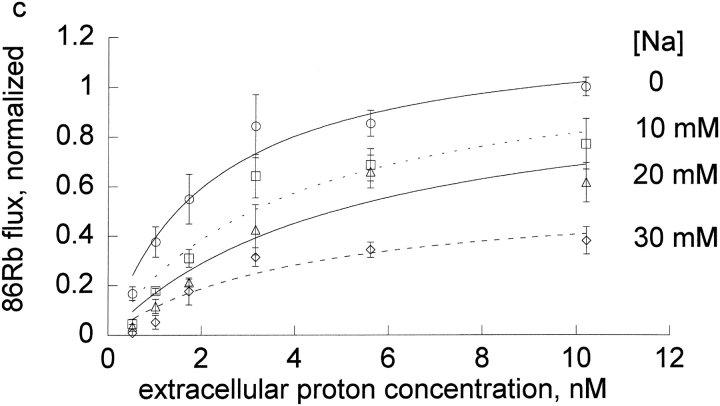
Figure 3.
Extracellular proton activation of 86Rb influx at different inhibitor concentrations. Ouabain-sensitive 86Rb influx was determined as described in the methods in DIDS treated human red blood cells at 0.3 mM rubidium. Three complete experiments were run for each inhibitor, which included all the proton concentrations shown in the figures and all 4 inhibitor concentrations as indicated in each panel and the data pooled as indicated in the legend to Fig. 1.The data (not the means) were fit to the equation, v = H/[A + B × H] at each inhibitor concentration. The replots of A and B versus I are shown in Fig. 4, a and b.
Kinetic Analysis
For this analysis, we assume that the binding of rubidium and each inhibitor are mutually exclusive. (Competition is a subset of mutually exclusive.) The equation also assumes that both the inhibitor (I) and the proton (H) can be bound to the pump and that they can bind in random order. Protons and rubidium (Rb) are also assumed to bind in random order.1 The data were analyzed using the following equation with Kaleidagraph Software (Synergy Software, Reading, PA).
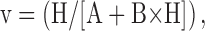 |
where A = c + d × I and B = e + f × I and c = LRb × KH/KRb (1 + KRb/Rb); d = LRb × KH/Rb × (I/Ki); e = 1 + LRb/Rb; f = (LRb/Rb) × (I/Li).
This equation is essentially the same as in Segel (1975) except for the use of LRb and Li instead of α × KRb and β × Ki. In general, the constants are functions of rate constants from many steps in the cycle. However, if the binding of proton, rubidium, and inhibitor were in rapid equilibrium and if the rate limiting step followed their binding (e.g., rubidium deocclusion), then KH is the dissociation constant for protons and KRb and LRb are the dissociation constants for rubidium for the unprotonated pump and protonated pump, respectively. Ki and Li are the dissociation constants for the inhibitors (bretylium, guanidinium, ouabain, sodium, and tetrapropylammonium) for the protonated and unprotonated pump, respectively.
All experiments were done in triplicate. We used individual data from each experiment for fitting but plotted the average value and standard error for each set of triplicates at each concentration for clearer display.
Materials
Guanidium (guanidine) nitrate (AC215310010) was purchased from Fisher Scientific and all reagents were obtained from Fisher Scientific or Sigma-Aldrich.
RESULTS
In all the following experiments, ouabain-sensitive 86Rb influx was determined in DIDS-treated red blood cells as a function of the extracellular proton concentration. We measured the pH of DIDS-treated cells and found that after 10 min in a pH 9.2 medium, the pH inside the red cells changed by <0.1 pH units, thus confirming that the intracellular proton concentration was effectively clamped at 40 nM (pH 7.4) for at least 10 min in DIDS-treated red cells. This is expected because DIDS-treated red cells have a very low proton permeability and the buffer capacity of hemoglobin is very high (unpublished data).
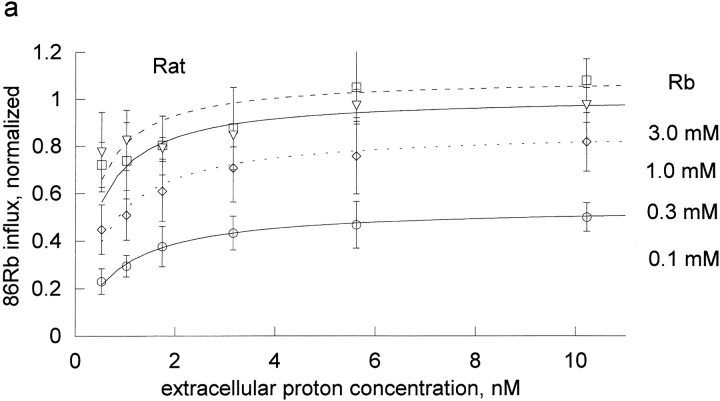
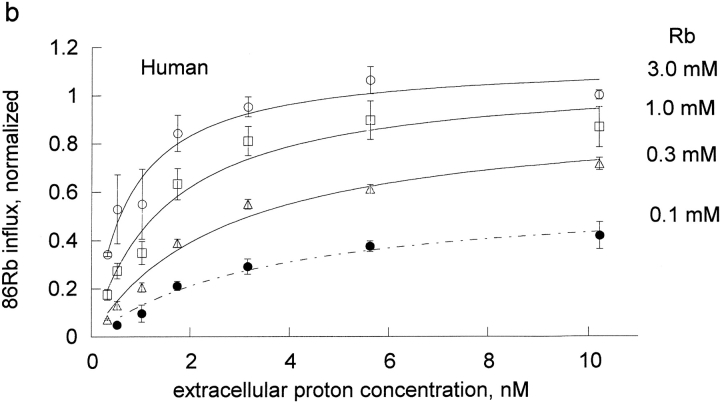
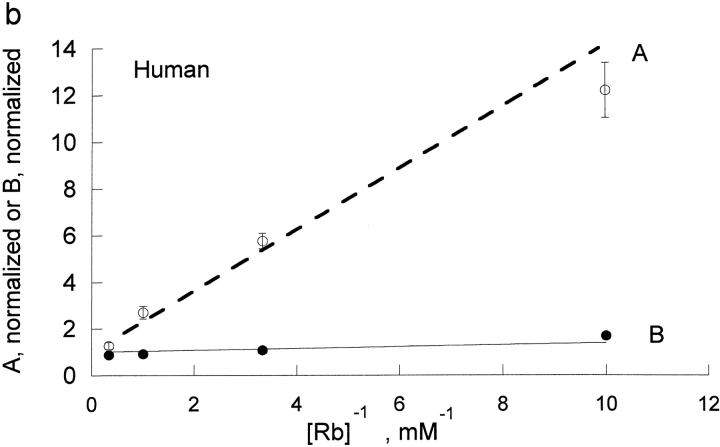
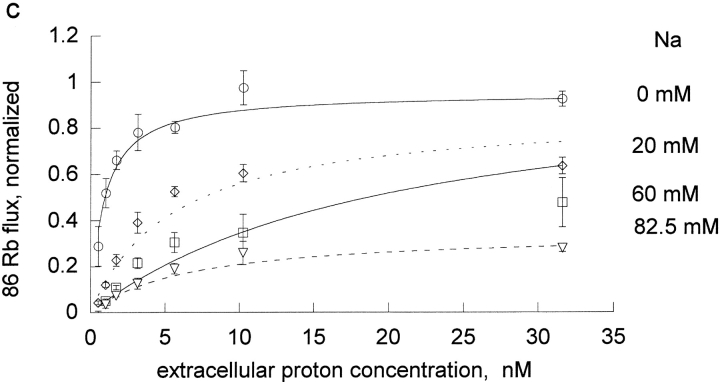
The effect of rubidium on proton activation of the pump was determined in human and rat red blood cells (Fig. 1) . If protons and rubidium were competing at the rubidium transport site, or were mutually exclusive, then rubidium would increase the K1/2 for protons, which is not observed. Rather, rubidium decreased the apparent K1/2 for protons in both species. To determine the kinetic constants for rubidium binding to the unprotonated pump, KRb, and the protonated pump, LRb, we fit these data to the equation, flux = H/[A + B × H], where A and B are functions of 1/Rb. The equation H/[A + B × H] is equivalent to the more conventional Vmax H/[Km + H] with A = Km/Vmax and B = 1/Vmax. One advantage of the A and B formulation is that A contains the kinetic constants in the absence of H and B contains the kinetic constants at saturating H. In particular, A contains the kinetic constant for rubidium binding to the unprotonated pump (KRb) and B contains the kinetic constant for binding to the protonated pump (LRb). This means that the kinetic constants are more directly calculated from A and B and this approach avoids the artifactual compilation of errors that would occur if we first fit to find Km and Vmax and then calculated Km/Vmax.
Figure 1.
Extracellular proton activation of 86Rb influx as a function of rubidium. Ouabain-sensitive Rb influx was determined as described in materials and methods in DIDS-treated red blood cells. The DIDS treatment effectively clamps the intracellular proton concentration, so that the observed effect is due to extracellular protons. Three complete experiments were run for both rat (a) and human (b) red cells. Each experiment included all the proton concentrations shown in the figures and all 4 rubidium concentrations as indicated in each panel. The data on each day were normalized to the flux at the highest proton and rubidium concentrations. The data from the 3 experiments were then pooled and the mean and standard deviations are shown. The data (not the means) were fit to the equation, v = H/[A + B × H] at each rubidium concentration. The replots of A and B versus 1/Rb are shown in Fig. 2.
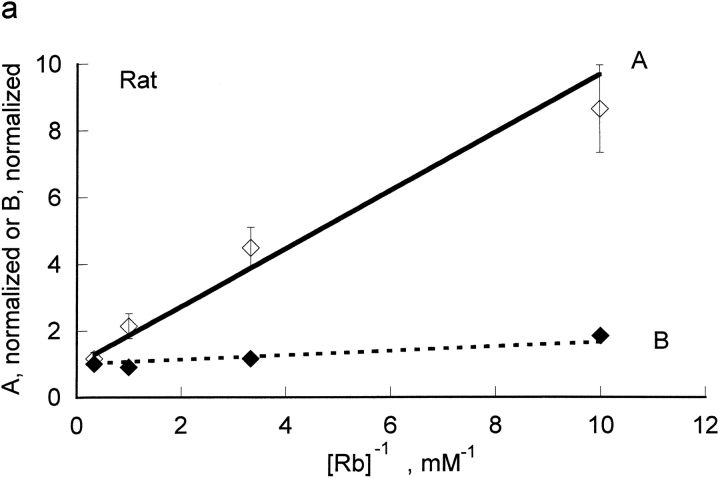
The kinetic constants were obtained from a replot of A and B versus the reciprocal of the Rb concentration (Fig. 2) . In the rat red cells, from the slopes and intercept we determine that KRb, a measure of rubidium binding to the unprotonated pump, is 0.87 ± 0.1 mM and that LRb, a measure of rubidium binding to the protonated pump, is 0.066 ± 0.006 mM. Thus, protons substantially improve the binding of rubidium to the pump; in a simple rapid equilibrium model protons make rubidium bind ∼13-fold better in rat red cells. KH, a measure of proton binding to the pump in the absence of rubidium, was 2.11 nM in the rat and was about sixfold greater in human, 13 nM. In human, protons had an even greater effect on the binding of rubidium; in a simple rapid equilibrium model protons make rubidium bind ∼34 fold better in human red cells. This is the result of a higher kinetic constant for rubidium in the absence of protons, KRb = 1.32 ± 0.07 mM, and a lower kinetic constant for rubidium in the presence of protons, LRb = 0.0387 ± 0.0074 mM. Thus, it is clear that in both species, contrary to the expectation that protons and rubidium might compete, protons make rubidium bind substantially better.
Figure 2.
Replot of A and B versus 1/[Rb]. The values of A and B were determined from the data in Fig. 1. The values for A have been normalized so that the y intercept is 1. By doing this, the slope of the line for A is proportional to KRb; in the rapid equilibrium case, this reflects rubidium binding to the unprotonated pump. As shown in materials and methods, the line for B is theoretically expected to have a y intercept of 1. The slope for B is proportional to LRb; in the rapid equilibrium case, this reflects rubidium binding to the protonated pump. Clearly, protons greatly increase the affinity of the pump for rubidium. The slopes were 0.868 ± 0.101 for A (open diamonds) and 0.066 ± 0.0059 for B (closed diamonds) for rat red blood cells (a) and were 1.32 ± 0.07 for A (open circles) and 0.0387 ± 0.0074 for B (closed circles) for human red blood cells (b).
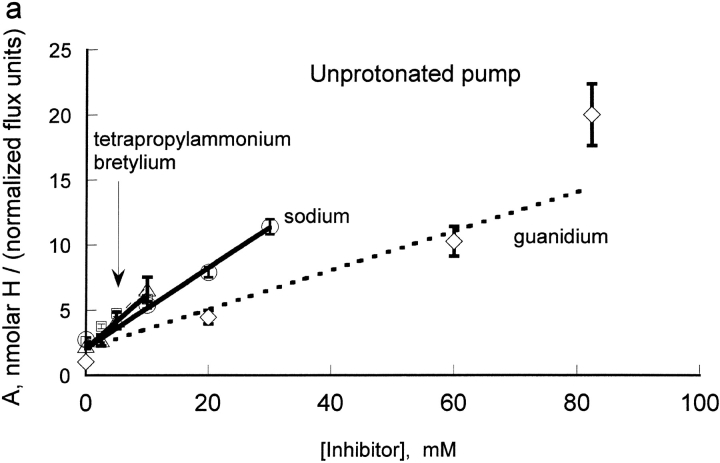
We wanted to determine if protons had similar effects on the binding of other cationic inhibitors. Thus, we compared the effect of extracellular protons on the inhibition by four cations in human red cells: bretylium, guanidinium, sodium, and tetrapropylammonium at a fixed concentration of rubidium (0.3 mM). On each day, we measured the flux at seven different extracellular proton concentrations (0.3–10.3 nM) and four different inhibitor concentrations (0–10 mM for tetrapropylammonium and bretylium, 0–30 mM for sodium, 0–82.5 mM for guanidinium). The results for the four cationic inhibitors are shown in Fig.3.
To compare the inhibition constants for binding to the unprotonated pump (Ki) and to the protonated pump (Li), we fit the data to the equation: H/[A + B × H]. In this formulation, A contains the inhibitor constant for binding to the unprotonated pump and B contains the inhibitor constant for binding to the protonated pump. Fig. 4 A shows a replot of A = c + d × I versus I for the four inhibitors. As shown in methods, the conventional kinetic equation has H and Rb terms in both numerator and denominator, as they are activators, and inhibitor terms only in the denominator. Thus, replots for the activator, Rb, are linear in the reciprocal of the rubidium concentration and replots for the inhibitors are linear in the inhibitor concentration. The y intercept values for the four inhibitors studied in human red blood cells are very similar, as expected because c = LRb × Kh/KRb × (1 + KRb/Rb), which merely reflects the properties of the transporter without inhibitor bound. Remarkably, the slopes for all these inhibitors are also very similar, despite the great structural differences. The slopes are equal to LRb × KH/(Rb × Ki). The only term that depends upon the inhibitor is Ki, which is the inhibitory constant for the unprotonated pump. (With rapid equilibrium and the rate-limiting step following proton and rubidium binding, Ki would be the K d.) Since the slopes are so similar, we conclude that all these ions bind to the unprotonated pump with similar Ki.
Figure 4.
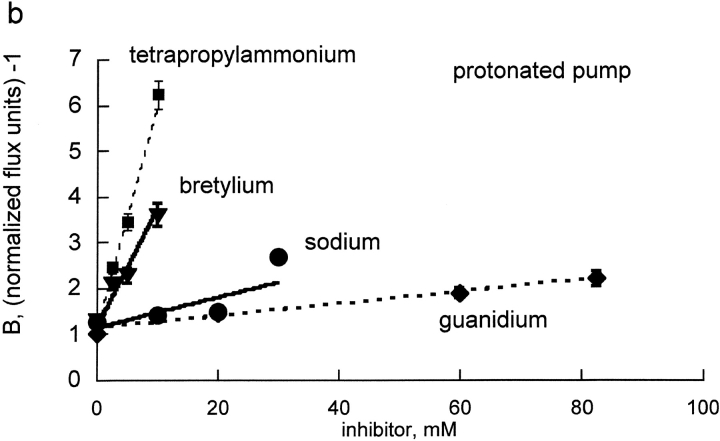
(a) Replot of A for bretylium, guanidinium, sodium, and tetrapropylammonium versus inhibitor concentrations. The values of A were determined from the plots in Fig. 3. The slope of this line is proportional to the Ki for each inhibitor, for binding to the unprotonated pump. All four lines have similar slope, implying that all four inhibitors bind with similar affinity to the unprotonated pump. The slopes were: bretylium (triangles), 0.392 ± 0.078; guanidinium (diamonds), 0.175 ± 0.014; sodium (circles), 0.271 ± 0.037; tetrapropylammonium (squares), 0.364 ± 0.063. (b) Replot of B for bretylium, guanidinium, sodium, and tetrapropylammonium versus inhibitor concentrations. The values of B were determined from the plots in Fig. 3. The slope of this line is proportional to the Li for each inhibitor, for binding to the protonated pump. Clearly Na and guanidinium have very little affinity for the protonated pump and bretylium and TPA have substantial affinity. The slopes were: bretylium (triangles), 0.282 ± 0.019; guanidinium (diamonds), 0.016 ± 0.001; sodium (circles), 0.040 ± 0.006; tetrapropylammonium (squares), 0.517 ± 0.016.
Fig. 4 B shows a replot of B = e + f × I vs. I for the four cationic inhibitors. Once again, the y intercept values, e, are very similar, as expected because the y intercept should merely reflect the properties of the transporter without inhibitor bound. Strikingly the slopes are very different. The slopes include the factor LRb/rubidium and the respective Li for inhibitor binding to the protonated pump. Clearly, the protonated pump has different apparent affinities for these inhibitors; the protonated pump binds bretylium and tetrapropylammonium about an order of magnitude better than guanidinium and sodium.
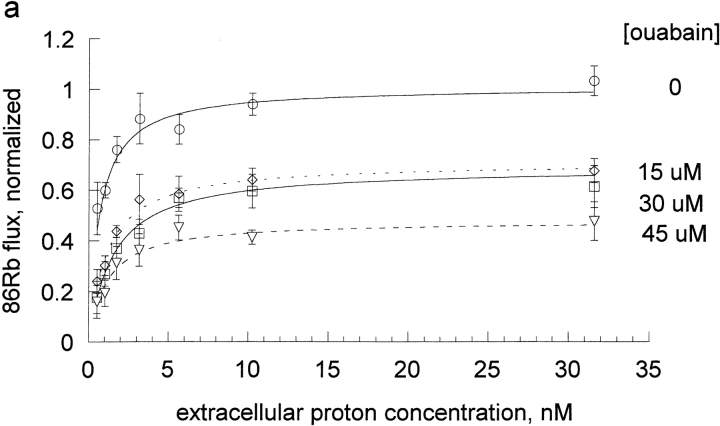
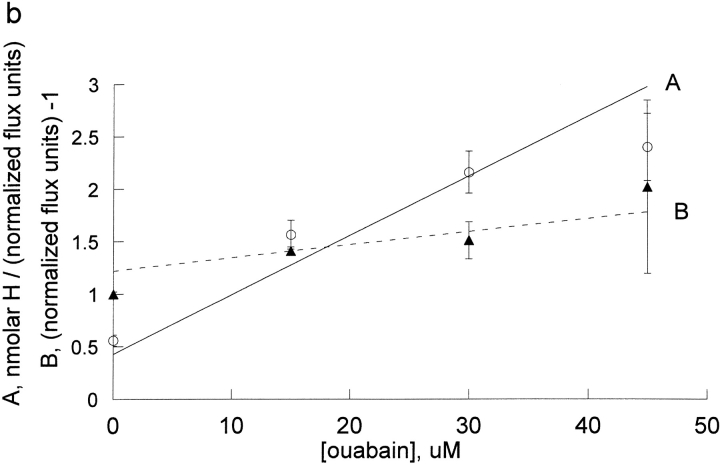
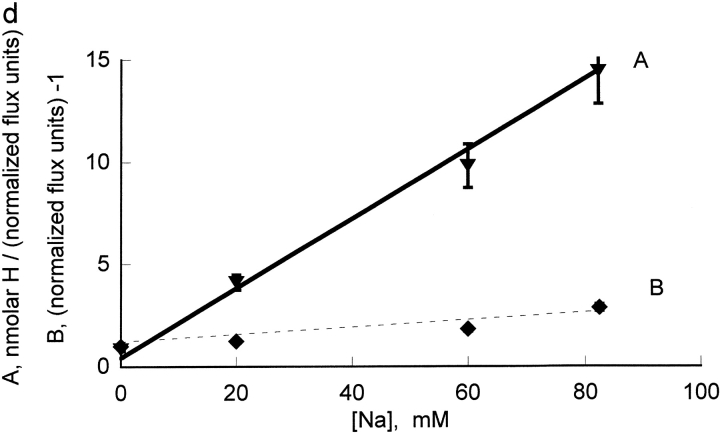
We also wanted to examine an extracellular inhibitor that would not bind at the transport site and we chose to examine ouabain. Because ouabain binding and dissociation are slow in human red blood cells and we wished to apply steady-state inhibition analysis, ouabain inhibition was examined in rat red blood cells. The effect of ouabain on the proton activation curves is shown in Fig. 5 A and the replot of A and B versus ouabain is shown in Fig. 5 B (note that the x-axis is micromolar in this case and not millimolar as was the case for the cationic inhibitors). We also determined the kinetic constants for Na inhibition of Rb influx in rat red cells (Fig. 5, C and D); the analysis was similar to that presented for human red blood cells above, except that higher Na concentrations (0, 20, 60, and 82.5 mM) were used, in order to get significant inhibition.
Figure 5.
The effect of ouabain and sodium on the proton activation of Rb influx in DIDS treated rat red blood cells. The experimental procedure was similar to that described in Fig. 3 and the results of 3 separate experiments pooled as described in Fig. 3. The data were fit to the equation, v = H/[A + B * H] at each inhibitor concentration (panels a and c) and the values of A and B replotted vs. I (panels b and d). Note that the x axis for ouabain is in micromolar in this panel b, reflecting the substantially higher affinity for ouabain than for the sodium and the inhibitors in Fig. 4. The slope for ouabain binding in the absence of protons was 0.0566 ± 0.0043 and in the presence of protons was 0.0124 ± 0.0023. The slope for ouabain binding in the absence of protons was 0.17 ± 0.011 and in the presence of protons was 0.12 ± 0.012.
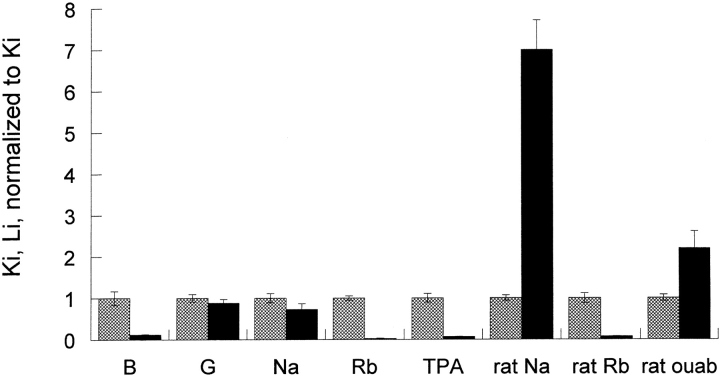
The slopes of the lines in the replots of Fig. 4 and Fig. 5, B and D, for binding to protonated and unprotonated pump cannot be directly compared because the slopes include the kinetic constants for Rb binding to the unprotonated pump (A) and the protonated pump (B). The inhibitory constants t for the unprotonated pump and protonated pump were calculated from the Rb kinetic constants determined in Figs. 1 and 2 and the replot slopes determined in Figs. 4 and 5 using the equations in materials and methods. As can be seen in Fig. 6 , protons have little or no effect on sodium and guanidinium kinetic constants and have a very large effect on bretylium, tetrapropylammonium, and rubidium kinetic constants binding in human pumps. The effect on ouabain binding in rat is intermediate between sodium and rubidium.
Figure 6.
The effect of protonation on the kinetic constants for bretylium, guanidinium, ouabain, rubidium, and sodium. The values of Ki and Li were calculated as indicated in the text and normalized to the value of Ki. The cations fall into two categories: category one includes tetrapropylammonium, bretylium, and rubidium. Their kinetic constants are substantially decreased by protonation. In a simple model where these kinetic constants reflect the affinity, this implies that protons make these ions bind much better. Category two includes guanidinium and sodium. In human, their kinetic constants are little changed by protonation; in rat, the kinetic constant for sodium is substantially increased. Ouabain is intermediate between sodium and rubidium in rat.
These results make what may appear to be a paradoxical prediction in human pumps: even though the inhibition constants for sodium are only slightly altered by protons, the inhibition by sodium will be strongly pH dependent and even though the inhibition constants for tetrapropylammonium depend strongly on protons, the tetrapropylammonium inhibition will be nearly pH independent. This paradoxical prediction was tested in the experiments shown in Fig. 7, where the effect of extracellular protons on the inhibition by tetrapropylammonium and sodium was determined in the same experiment. It can be seen that protons have little effect on the inhibition by tetrapropylammonium. In contrast, protons dramatically reduce the inhibition by sodium. Clearly, it would be misleading to conclude from these experiments, however, that protons decrease the inhibition constant for sodium and have no effect on the inhibition constant for tetrapropylammonium. It is misleading because protons are also affecting rubidium binding (compare control line).
The summary data in Fig. 6 show that protons increase the binding of rubidium and tetrapropylammonium approximately equally. When the proton concentration increases, one would expect tetrapropylammonium to bind better in the absence of rubidium. In our flux experiments, we necessarily examine the competition between rubidium and tetrapropylammonium. Since protons make both rubidium and tetrapropylammonium bind better, the outcome is essentially no effect of proton concentration on tetrapropylammonium inhibition of pump flux. In contrast, protons have little effect on sodium binding, but as protons increase, rubidium binds better, so sodium cannot bind, and therefore there is less inhibition as protons increase. This analysis rests on the reasonable assumption that rubidium and tetrapropylammonium and sodium bind in a mutually exclusive manner in this concentration range. (Competition at a common site is a subset of mutually exclusive models.)
DISCUSSION
In this paper we have shown that protons alter the inhibition by tetrapropylammonium and bretylium differently from guanidinium and sodium. We have determined that the inhibitory constants for these ions are similar for the unprotonated carrier. In contrast, the protonated pump binds tetrapropylammonium and bretylium about an order of magnitude better than sodium and guanidinium. In addition, rubidium binds ∼13-fold and 34-fold better to the protonated pump in rat and human pumps, respectively. Ouabain binds with higher affinity than the other inhibitors and while protons slightly decrease the binding, the effect is less than observed for sodium and in the opposite direction from that of rubidium. These data suggest that there is an extracellular titratable residue whose environment depends upon which ion is bound to the extracellular transport site.
Two previous studies have examined the effect of extracellular protons in the alkaline range on the sodium/potassium exchange mediated by the sodium pump. Our results are consistent with these studies. In squid giant axons, Breitweiser et al. (1987) and, in Xenopus oocytes, Salonikidis et al. (2000) found that, at saturating extracellular K, extracellular proton concentration had little effect on the pump. As shown in Fig. 2, our results are consistent with models in which extracellular protons have only a slight effect on Vmax. Salonikidis et al. (2000) also studied the effect of protons at less than saturating extracellular potassium and they found that an increase in proton concentration from 10 to 100 nM (pH 8 to 7) caused a twofold increase in apparent Km when the membrane potential was zero. In contrast, we find that from 0.5 to 10 nM (pH 9.3 to 8.0) the apparent Km for Rb decreases. This difference could reflect a species or temperature dependent difference. Alternatively, a plot of Km vs. pH could be bell shaped, with a plateau at pH 8.0 and each study examined a different half of the bell-shaped curve.
Skou (1979) in ATPase measurements where the proton concentration varied on both sides found that protons increase the affinity for potassium. This is similar to our results. It is difficult to determine whether the ATPase effects observed by Skou were at intracellular or extracellular sites. Our data are consistent with the interpretation that they could occur at extracellular sites. In contrast, the proton dependence of eosin binding clearly reflects intracellular sodium and potassium binding sites and it is simplest to imagine that the proton effects are also intracellular (Skou and Esmann, 1980). The eosin binding studies clearly show that protons increase the affinity for intracellular potassium and our results clearly show that extracellular protons increase the affinity for extracellular rubidium. Interestingly, Breitweiser et al. (1987) found that intracellular protons increase the affinity for extracellular rubidium.
Since protons also made rubidium bind about an order of magnitude better, tetrapropylammonium and bretylium behave like rubidium, and guanidinium behaves like sodium with respect to their proton dependence.
Rat Versus Human
The fundamental finding that protons affect the binding of rubidium and sodium differently is found in both human and rat red cells. Although the kinetic parameters for Rb binding are slightly different in the rat and the human, protons make Rb bind better in both species, but the effect is larger in human. In contrast, protons have little effect on sodium binding in humans, but have a larger effect (and in the opposite direction as for rubidium) in rat.
Another way to examine the data is to ask how do sodium and potassium alter the proton interaction with the pump. Protons bind ∼13-fold better to the rat pump than to the human pump in the absence of sodium and potassium (unloaded pump). In human pumps, protons bind ∼34-fold better to the rubidium-loaded pump than unloaded pump and about equally well (1.34-fold) in the presence or absence of sodium (sodium-loaded pump vs. unloaded pump). Thus, protons bind ∼34/1.34 = 25-fold better to the rubidium-loaded pump than to the sodium-loaded pump and it is this property that is closely matched in rats: protons bind ∼13-fold better to the rubidium-loaded pump than the unloaded pump and about sevenfold less well to the sodium-loaded pump than the unloaded pump. Thus, in rat there is also a substantial preference (13 × 7 = 91-fold) in proton binding to the rubidium-loaded pump than to the sodium-loaded pump.
Ouabain Versus Cations
Although we were able to classify the cationic inhibitors into two classes: those which bound much better to the protonated pump and those that bound about the same, or less well, to the protonated pump than to the unprotonated pump, ouabain did not seem to fit into either class. Potassium is known to be antagonistic to ouabain binding. It is interesting that rubidium decreased the kinetic constant for protons 13-fold, but ouabain had an effect, while small, in the opposite direction, increasing the kinetic constant for protons 2.2-fold. The effect of ouabain was in the same direction as the effect of sodium (to increase the kinetic constant for protons), but sodium had a much greater effect (sevenfold). These values are consistent with the idea that the pump conformation is different with ouabain bound than with rubidium or sodium bound.
Models for Proton Regulation of the Pump
There are two classes of models to consider for the effect of protons: (a) protons alter extracellular cation dissociation constants or (b) protons alter a rate constant for steps not involving extracellular cation binding and dissociation (e.g., sodium translocation or the opening of the Rb occlusion gate to the inside). We consider each of these models in turn.
Protons Alter the Extracellular Cation Dissociation Constant
In this model, protons bind to an extracellular residue and alter the binding of extracellular cations. For simplicity, we will assume that the Ki values are the K d values. In models where Ki does not equal K d, the additional rate constants in Ki reflect properties of the pump that are independent of the inhibitor and thus will not alter the conclusions about how the inhibitors are different. Also we assume that sodium is a dead end inhibitor, like tetrapropylammonium, bretylium, and guanidinium. This is a reasonable assumption because the red cells will have a low concentration of ADP, so that the ADP release step, which occurs during the sodium efflux half cycle, is essentially irreversible (Kaplan, 1985).
Our analysis clearly shows that protons greatly decrease the apparent K d for tetrapropylammonium, rubidium and bretylium and have only a slight effect on sodium and guanidinium. This seems a little puzzling if all these ions are going to the same site. However, the analysis can also be stated as, the K d for protons depends upon which cation is bound to the site. This is easy to picture if the protonated residue is outside of the transport pocket. A change of K d implies that the residue has an altered environment. It would not be surprising that there would be allosteric differences in the extracellular protein surface depending on whether tetrapropylammonium, rubidium, bretylium, guanidinium, or sodium are bound. The relative changes of K d for these different states are shown in Fig. 8 . This model is the simplest explanation of our data and provides an important distinction between the sodium conformation and the potassium conformation.
Figure 8.
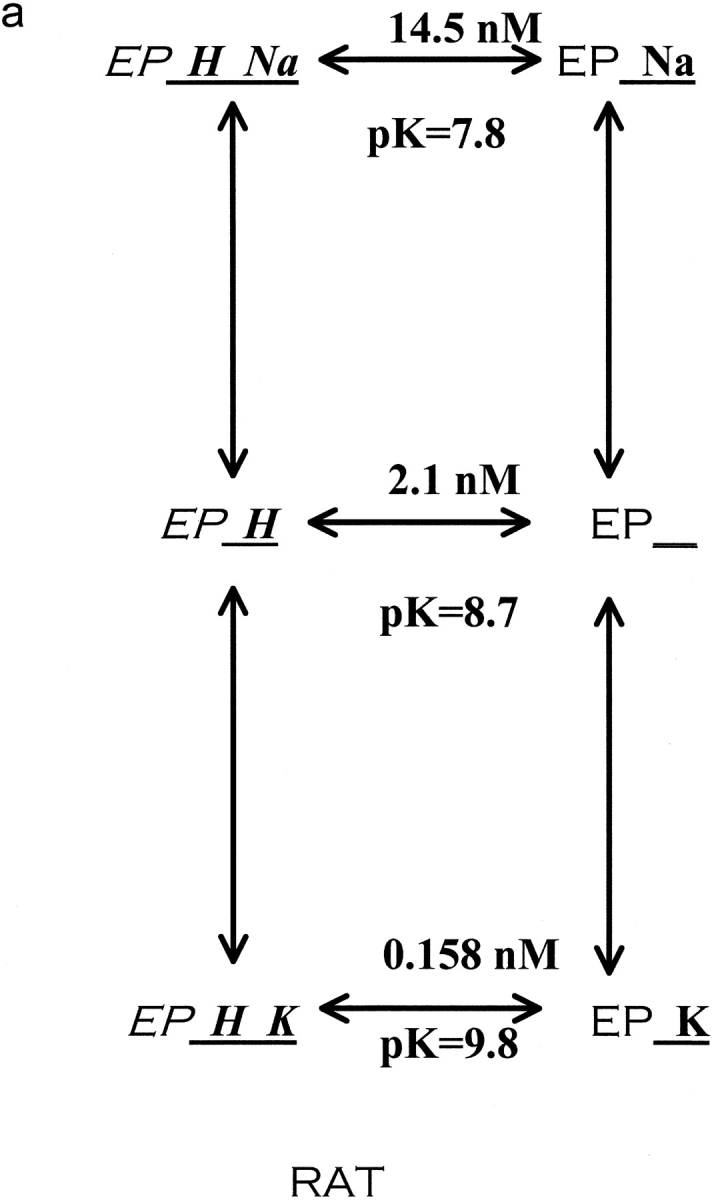
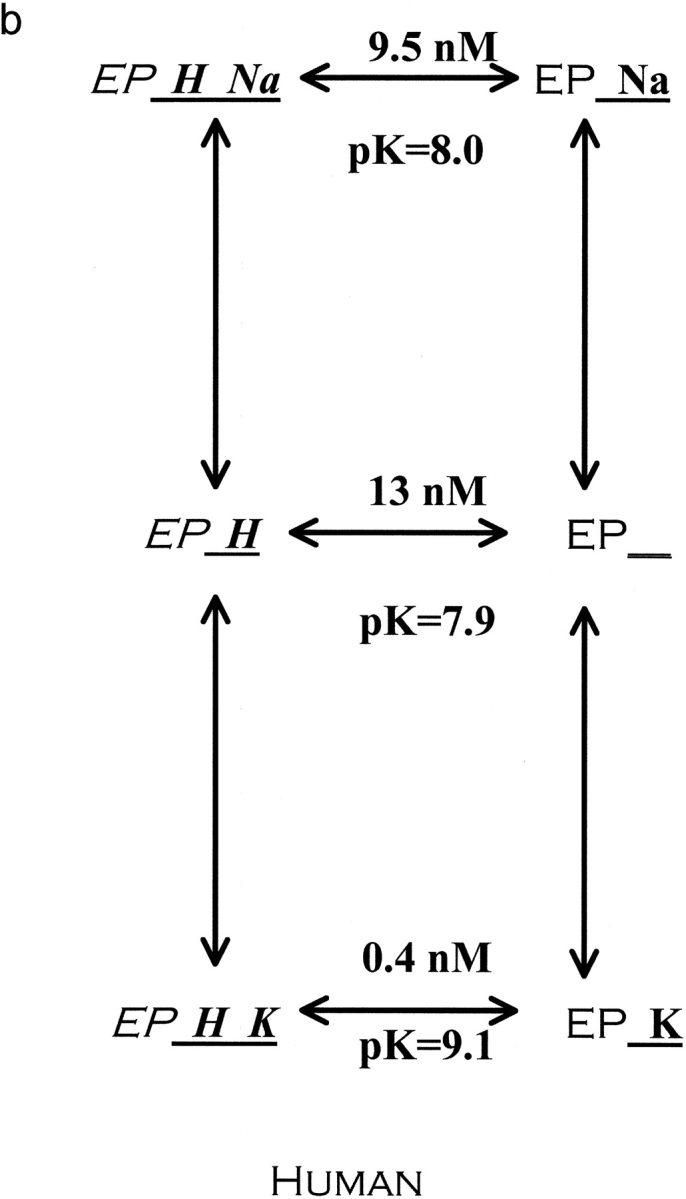
Reaction scheme for extracellular cations binding to the Na pump. The scheme depicted describes the enzyme conformation that has just translocated and released Na to the extracellular space. We have purposefully omitted references to E1 and E2 as they are sometimes used to describe different pump conformations. Also, this model assumes that rubidium and sodium are mutually exclusive. Rubidium binds much better to the protonated pump than the unprotonated pump, 13-fold better in rat (a) and 34-fold better in human (b). In contrast, sodium binds only 1.34-fold better to the protonated pump than the unprotonated pump in human. In rat, the effect of protons is in the opposite direction, making sodium bind sevenfold less well. In both species, the addition of protons greatly increases the selectivity of the pump for rubidium over sodium. Stated another way, the pK changes substantially in both species when rubidium binds instead of sodium. The reaction scheme shows the K d values for proton binding to the different cation loaded, outward facing, conformations and also the pK values. Values obtained from Figs. 2, 4, 5, and 6, using the equations in materials and methods as described in the text.
Figs. 6 and 8 illustrate our finding that extracellular cationic inhibitors of the Na pump fall into two classes: those whose inhibition is greatly increased by protonation of the pump (tetrapropylammonium and bretylium) and those whose inhibition is virtually unaffected by protonation (sodium and guanidinium). In contrast, ouabain binding does not fall into either category, which is not surprising since it does not bind at the transport site. Nevertheless, ouabain binding does alter the K d for protons.
Because extracellular sodium ions potentially have three different roles other models are possible. There are three different types of interactions that have been proposed for extracellular sodium. (a) Extracellular sodium is a product of the forward pump cycle and therefore would bind as a product inhibitor. (Note that no Na/Na exchange is likely under our conditions because these are well fed red blood cells and the ADP should be low [Kaplan, 1985].) (b) Extracellular sodium can substitute for potassium on the forward pump cycle, in which case the pump stoichiometry is 3Na/2Na and the flux is electrogenic (Cornelius and Skou, 1985). In wild-type pumps, this rate is very slow. (c) Extracellular sodium has been proposed to bind to a modifier site. Two examples are the effect of sodium to increase the binding of tetrapropylammonium and to decrease the inhibition by vanadate (Kropp and Sachs, 1977; Sachs, 1987).
Could the effect of sodium observed here be at the putative modifier site? If so, then there is no need (based on the current data) to design a model in which proton binding alters the transport site affinity for rubidium differently from sodium. Why? The K d for the extracellular residue is 13 nM for the empty, outward-facing transport site, and changes substantially (at least eightfold) when the transport site is loaded with tetrapropylammonium, bretylium, or potassium. One can conveniently assume that a similar change takes place when sodium binds to the transport site, since in this modifier site model, that effect was not studied here. In this modifier site model, the K d changes only slightly when sodium or guanidinium is bound at the modifier site. Thus, in the modifier-site model, a large pK change of the residue occurs because its local environment is substantially altered when any of the tested ions are bound to the transport site but only slightly altered when sodium or guanidinium is bound to the modifier site. In addition, this model requires that the binding of sodium to its modifier site increases the affinity for tetrapropylammonium (Kropp and Sachs, 1977), and that the binding of proton to its modifier site also increases the affinity for tetrapropylammonium but that protons and sodium do not compete at this site. In addition, since guanidinium has an effect similar to sodium, it would appear that guanidinium goes to the modifier site in this model.
Proton Switch?
Could the proton be important in determining if the pump treats extracellular sodium as a product inhibitor or treats extracellular sodium as a potassium surrogate? This is an interesting possibility and makes important predictions about the pH dependence of 3Na/3Na exchange versus 3Na/2Na exchange. Because, in wild-type pump, the 3Na/2Na exchange is very slow, it may not be possible to test this directly. In the E779A mutant, 3Na/2Na exchange is nearly as fast as 3Na/2K exchange and is readily measured (Koster et al., 1996; Peluffo et al., 2000). It is possible that this mutant results in a change of the K d for the extracellular proton site. This change of K d would then alter the bias of the pump from sodium-as-product to sodium-as-surrogate-potassium. Experiments are in progress to test this model.
Elegant data from several labs clearly provides evidence for a conformational difference in the pump when it binds extracellular sodium compared with extracellular potassium (Gadsby et al., 1993; Hilgemann, 1994, 1997; DeWeer et al., 2001). The binding of two sodium ions causes an access well to close and then the third extracellular sodium ion must traverse this well to its binding site.2 Our data that the K d for proton changes provides clear evidence for a conformational difference in the pump when it binds extracellular sodium compared with extracellular potassium. It would be most economical if the conformation change that the proton detects and the access well conformational change were the same conformational change. We consider two cases: that the protonated residue is inside the access well and that it is outside the access well.
Could the K d change observed here reflect the change of environment of a residue inside the access well? We think that is unlikely. For this model, we assume that, under our conditions, the binding of sodium closes the access well. This closing would be expected to alter the local environment of residues inside the access well and yet we did not observe a change of K d for proton in the presence of sodium compared with the K d for proton for the empty transport site.
Could the K d change observed here reflect the change of environment of a residue outside the access well that occurs when the access well closes or opens? This also seems unlikely. Start by considering the empty outward facing transport site. It has a K d of 13 nM. In this model, when sodium binds, the access well closes and yet the K d remains nearly the same (12 nM). On the other hand, when potassium binds (and presumably the access well does not close) there is a large change of K d (to 0.4 nM). Thus, the large change of K d occurs on potassium binding, not sodium binding, but the access well changes on sodium binding and presumably not potassium binding. What does occur on potassium binding is occlusion of potassium. But a similar change of K d occurs with tetrapropylammonium and bretylium (to 1.6 and 1 nM respectively). Tetrapropylammonium does not become occluded (Forbush, 1988), so the change of K d occurs before the conformational change for occlusion.
Protons Alter a Rate Constant
An alternative model of the effect of protons on rubidium is that protons alter a rate constant that is not involved with extracellular cation binding. For this analysis, we start with the fact that an increase in extracellular proton concentration causes a decrease in the apparent Km for rubidium. In general Km is not equal to the K d for rubidium, but rather reflects a number of rate constants in the cycle. Thus, in theory, it is possible for protons to alter the Km by altering another step in the cycle and not the binding or release of extracellular potassium. Consider a model with two rate limiting steps, sodium efflux and potassium influx, and that the binding of proton and potassium occurs between these steps and is rapid. In this case, it is easy to show that decreasing the sodium efflux rate–limiting step or increasing the potassium influx rate limiting step causes a decrease in the apparent Km for rubidium. In fact, Forbush and Klodos (1991) have shown, in an unsided preparation, that protons alter the rate-limiting step, causing a decrease in the sodium efflux half cycle and an increase in the rate of potassium deocclusion. This is exactly in the opposite direction to what is required by our results. Thus it seems very likely that the proton effects observed by Forbush and Klodos (1991) reflect intracellular proton effects, as would be expected from the work of Skou (1979), Skou and Esmann (1980), and Breitweiser et al. (1987).
In conclusion, we have found that tetrapropylammonium and bretylium have rubidium-like effects on extracellular proton binding that are different than the sodium-like effects of guanidinium. In addition, protons bind at least 25-fold better to the rubidium-loaded pump than to the sodium-loaded pump in both human and rat red blood cells. This change in K d for extracellular protons reflects a conformational change due to extracellular cation binding and seems unlikely to be related to the conformational change that opens the access well.
Acknowledgments
We thank Allan C. Powe and Craig Gatto for very helpful comments on the kinetic analysis and the manuscript. We thank Betty Jo Wilson for doing some of the preliminary experiments.
This work was supported by National Institutes of Health grant DK37512.
Footnotes
Abbreviations used in this paper: DIDS, 4,4′-diisocyanostilbene-2, 2′-disulfonate.
We did attempt to fit the data to an ordered model. A model in which protons must bind before rubidium or tetrapropylammonium binds provided an adequate fit of most of the data, but was not as good a fit (in terms of sum of squares of the error) as a random order model. Although our data are better fit by the random ordered model, we do not feel we have completely eliminated such an elegant model as the ordered model for proton binding before rubidium and tetrapropylammonium. We have chosen to present a random ordered model for our analysis as this is the most conservative approach; an ordered model in which protons must bind before rubidium or tetrapropylammonium could be considered a subset of the random ordered model, where protons increase binding infinitely, in contrast to the 34- and 13-fold observed here.
Strictly speaking, the binding of two potassium ions could also cause an access well to close, but in this case, no ion can traverse the well and thus there is no electrical measurement to detect the access well. But at some point in the cycle it must close so that it is closed when the first sodium is released to the outside.
References
- Apell, H.J., and S.J. Karlish. 2001. Functional properties of Na,K-ATPase, and their structural implications, as detected with biophysical techniques. J. Membr. Biol. 180:1–9. [DOI] [PubMed] [Google Scholar]
- Blostein, R. 1999. Jeanne Mannery Fisher Memorial Lecture 1998. Structure-function studies of the sodium pump. Biochem. Cell Biol. 77:1–10. [DOI] [PubMed] [Google Scholar]
- Breitweiser, G.E., A.A. Altamirano, and J.M. Russell. 1987. Effects of pH changes on sodium pump fluxes in squid giant axon. Am. J. Physiol. Cell Physiol. 253:C547–C554. [DOI] [PubMed] [Google Scholar]
- Cornelius, F., and J.C. Skou. 1985. Na+-Na+ exchange mediated by (Na+ + K+)-ATPase reconstituted into liposomes. Evaluation of pump stoichiometry and response to ATP and ADP. Biochim. Biophys. Acta. 818:211–221. [DOI] [PubMed] [Google Scholar]
- DeWeer, P., D.C. Gadsby, and R.F. Rakowski. 2001. Voltage dependence of the apparent affinity for external Na(+) of the backward-running sodium pump. J. Gen. Physiol. 117:315–328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- David, P., H. Mayan, H. Cohen, D.M. Tal, and S.J. Karlish. 1992. Guanidinium derivatives act as high affinity antagonists of Na+ ions in occlusion sites of Na+,K(+)-ATPase. J. Biol. Chem. 267:1141–1149. [PubMed] [Google Scholar]
- Dissing, S., and J.F. Hoffman. 1990. Anion-coupled Na efflux mediated by the human red blood cell Na/K pump. J. Gen. Physiol. 96:167–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dzimiri, N., and A.A. Almotrefi. 1992. Inhibition of myocardial Na(+)-K(+)-ATPase activity by bretylium: role of potassium. Arch. Int. Pharmacodyn. Ther. 318:76–85. [PubMed] [Google Scholar]
- Forbush, B. III. 1988. The interaction of amines with the occluded state of the Na,K-pump. J. Biol. Chem. 263:7979–7988. [PubMed] [Google Scholar]
- Forbush, B. III, and I. Klodos. 1991. Rate-limiting steps in Na translocation by the Na/K pump. Soc. Gen. Physiol. Ser. 46:210–225. [PubMed] [Google Scholar]
- Gadsby, D.C., R.F. Rakowski, and P. De Weer. 1993.Extracellular access to the Na,K pump: pathway similar to ion channel. Science. 260:100–103. [DOI] [PubMed] [Google Scholar]
- Goldshleger, R., Y. Shahak, and S.J. Karlish. 1990. Electrogenic and electroneutral transport modes of renal Na/K ATPase reconstituted into proteoliposomes. J. Membr. Biol. 113:139–154. [DOI] [PubMed] [Google Scholar]
- Hilgemann, D.W. 1994. Channel-like function of the Na,K pump probed at microsecond resolution in giant membrane patches. Science. 263:1429–1432. [DOI] [PubMed] [Google Scholar]
- Hilgemann, D.W. 1997. Recent electrical snapshots of the cardiac Na,K pump. Ann. NY Acad. Sci. 834:260–269. [DOI] [PubMed] [Google Scholar]
- Jennings, M.L. 1978. Characteristics of CO2-independent pH equilibration in human red blood cells. J. Membr. Biol. 40:365–391. [DOI] [PubMed] [Google Scholar]
- Kaplan, J.H. 1985. Ion movements through the sodium pump. Annu. Rev. Physiol. 47:535–544. [DOI] [PubMed] [Google Scholar]
- Koster, J.C., G. Blanco, P.B. Mills, and R.W. Mercer. 1996. Substitutions of glutamate 781 in the Na,K-ATPase alpha subunit demonstrate reduced cation selectivity and an increased affinity for ATP. J. Biol. Chem. 271:2413–2421. [DOI] [PubMed] [Google Scholar]
- Kropp, D.L., and J.R. Sachs. 1977. Kinetics of the inhibition of the Na-K pump by tetrapropylammonium chloride. J. Physiol. 264:471–487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milanick, M.A. 1990. Proton fluxes associated with the Ca pump in human red blood cells. Am. J. Physiol. Cell Physiol. 258:C552–C562. [DOI] [PubMed] [Google Scholar]
- Or, E., P. David, A. Shainskaya, D.M. Tal, and S.J. Karlish. 1993. Effects of competitive sodium-like antagonists on Na,K-ATPase suggest that cation occlusion from the cytoplasmic surface occurs in two steps. J. Biol. Chem. 268:16929–16937. [PubMed] [Google Scholar]
- Peluffo, R.D., J.M. Arguello, J.B. Lingrel, and J.R. Berlin. 2000. Electrogenic sodium-sodium exchange carried out by Na,K-ATPase containing the amino acid substitution Glu779Ala. J. Gen. Physiol. 116:61–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polvani, C., and R. Blostein. 1988. Protons as substitutes for sodium and potassium in the sodium pump reaction. J. Biol. Chem. 263:16757–16763. [PubMed] [Google Scholar]
- Sachs, J.R. 1987. Inhibition of the Na,K pump by vanadate in high-Na solutions. Modification of the reaction mechanism by external Na acting at a high-affinity site. J. Gen. Physiol. 90:291–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salonikidis, P.S., S.N. Kirichenko, L.V. Tatjanenko, W. Schwarz, and L.A. Vasilets. 2000. Extracellular pH modulates kinetics of the Na(+),K(+)-ATPase. Biochim. Biophys. Acta. 1509:496–504. [DOI] [PubMed] [Google Scholar]
- Segel, I.H. 1975. Enzyme Kinetics. John Wiley and Sons, New York. 285 pp.
- Skou, J.C. 1979. Effects of ATP on the intermediary steps of the reaction of the (Na+ + K+)-ATPase. IV. Effect of ATP on K0.5 for Na+ and on hydrolysis at different pH and temperature. Biochim. Biophys. Acta. 567:421–435. [DOI] [PubMed] [Google Scholar]
- Skou, J.C., and M. Esmann. 1980. Effects of ATP and protons on the Na:K selectivity of the (Na+ + K+)-ATPase studied by ligand effects on intrinsic and extrinsic fluorescence. Biochim. Biophys. Acta. 601:386–402. [DOI] [PubMed] [Google Scholar]
- Wieth, J.O., J. Brahm, and J. Funder. 1980. Transport and interactions of anions and protons in the red blood cell membrane. Ann. NY Acad. Sci. 341:394–418. [DOI] [PubMed] [Google Scholar]
- Xu, W., B.J. Wilson, L. Huang, E.L. Parkinson, B.J. Hill, and M.A. Milanick. 2000. Probing the extracellular release site of the plasma membrane calcium pump. Am. J. Physiol. Cell Physiol. 278:C965–C972. [DOI] [PubMed] [Google Scholar]
- Xu, Y.H., and R.D. Roufogalis. 1988. Asymmetric effects of divalent cations and protons on active Ca2+ efflux and Ca2+-ATPase in intact red blood cells. J. Membr. Biol. 105:155–164. [DOI] [PubMed] [Google Scholar]