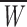Abstract
The gating properties of channels responsible for the generation of persistent Na+ current (I NaP) in entorhinal cortex layer II principal neurons were investigated by performing cell-attached, patch-clamp experiments in acutely isolated cells. Voltage-gated Na+-channel activity was routinely elicited by applying 500-ms depolarizing test pulses positive to −60 mV from a holding potential of −100 mV. The channel activity underlying I NaP consisted of prolonged and frequently delayed bursts during which repetitive openings were separated by short closings. The mean duration of openings within bursts was strongly voltage dependent, and increased by e times per every ∼12 mV of depolarization. On the other hand, intraburst closed times showed no major voltage dependence. The mean duration of burst events was also relatively voltage insensitive. The analysis of burst-duration frequency distribution returned two major, relatively voltage-independent time constants of ∼28 and ∼190 ms. The probability of burst openings to occur also appeared largely voltage independent. Because of the above “persistent” Na+-channel properties, the voltage dependence of the conductance underlying whole-cell I NaP turned out to be largely the consequence of the pronounced voltage dependence of intraburst open times. On the other hand, some kinetic properties of the macroscopic I NaP, and in particular the fast and intermediate I NaP-decay components observed during step depolarizations, were found to largely reflect mean burst duration of the underlying channel openings. A further I NaP decay process, namely slow inactivation, was paralleled instead by a progressive increase of interburst closed times during the application of long-lasting (i.e., 20 s) depolarizing pulses. In addition, long-lasting depolarizations also promoted a channel gating modality characterized by shorter burst durations than normally seen using 500-ms test pulses, with a predominant burst-duration time constant of ∼5–6 ms. The above data, therefore, provide a detailed picture of the single-channel bases of I NaP voltage-dependent and kinetic properties in entorhinal cortex layer II neurons.
Keywords: persistent Na+ current, single channel, entorhinal cortex, stellate cells, patch clamp
INTRODUCTION
The persistent Na+ current (I NaP) is widely expressed in a variety of neuronal populations of the central nervous system (CNS)* (French and Gage, 1985; Stafstrom et al., 1985; French et al., 1990; Chao and Alzheimer, 1995; Uteshev et al., 1995; Kay et al., 1998; Magistretti and Alonso, 1999). Its distinctive biophysical properties consist of a scarce, or absent, tendency to inactivate during sustained depolarizations and a low threshold of activation (for review see Taylor, 1993; Crill, 1996). I NaP has recently been the object of considerable interest in both biophysical and functional studies on central neurons. It is now well established that, due to its persistent nature and its recruitment as a consequence of small depolarizations, I NaP significantly contributes to basic aspects of neuronal integrative functions, such as amplification and processing of synaptic inputs (Deisz et al., 1991; Schwindt and Crill, 1995; Stuart and Sakmann, 1995; Lipowsky et al., 1996), and is implicated in the generation of specific patterns of neuronal electrical activity and responsiveness, including subthreshold oscillations (Alonso and Llinás, 1989; Amitai, 1994; Takakusaki and Kitai, 1997; Pape and Driesang, 1998), spontaneous firing (Pennartz et al., 1997; Takakusaki and Kitai, 1997; Bevan and Wilson, 1999; Bennett et al., 2000; Taddese and Bean, 2002), burst firing (Franceschetti et al., 1995; Parri and Crunelli, 1998; Brumberg et al., 2000), depolarizing afterpotentials (Azouz et al., 1996), and plateau potentials (Llinás and Sugimori, 1980; Jahnsen and Llinás, 1984; Sandler et al., 1998). Given the fundamental integrative functions of dendrites (Johnston et al., 1996; Reyes, 2001), the demonstration that the conductance and channels underlying I NaP are expressed by dendrites of central neurons (Schwindt and Crill, 1995; Lipowsky et al., 1996; Magistretti et al., 1999b) further emphasizes the importance of the same current in information processing and integration.
A well-characterized role of I NaP in controlling the subthreshold electrical activity of central neurons is found in the stellate cells of entorhinal cortex (EC) layer II. The I NaP expressed by these neurons (Magistretti and Alonso, 1999) has been demonstrated to interplay with the hyperpolarization-activated cation current, I h (Dickson et al., 2000), to generate subthreshold membrane-potential oscillations in a frequency range corresponding to the theta band (Alonso and Llinás, 1989; Klink and Alonso, 1993; Dickson et al., 2000). These subthreshold theta oscillations critically influence spike patterning in response to small, sustained depolarizations (Alonso and Klink, 1993). Theta-patterned spike discharge underlain by subthreshold oscillations generated at the single-cell level is likely to be propagated, at the EC-network level, by the reciprocal connections developed by layer II stellate cells (Lingenhöhl and Finch, 1991; Klink and Alonso, 1997). Indeed, a local generator of theta rhythmicity has been demonstrated to exist in EC layer II (Alonso and García-Austt, 1987a,b), and theta population activity is prominently expressed in the EC and other parahippocampal structures (Bland and Colom, 1993). In turn, the theta rhythm is believed to be required for the proper implementation of the memory function of the parahippocampal region (PHR) (Winson, 1978; Buzsaki, 1996), and, in particular, to exert major modulatory effects on cellular events, such as long-term potentiation, that may represent elementary correlates of the ongoing PHR memory processes (Larson and Lynch, 1986; Larson et al., 1986; Greenstein et al., 1988; Alonso et al., 1990; Huerta and Lisman, 1996; Hölscher et al., 1997).
Due to the ability of I NaP to generate membrane bistability and plateau potentials (e.g., Klink and Alonso, 1993; Johnston et al., 1994), this current has also been implicated in the basic pathophysiological mechanism of epileptogenesis (Segal, 1994; for review see Ragsdale and Avoli, 1998). In addition, since I NaP can sustain long-lasting Na+ influxes, thus promoting steady increases of intracellular Na+ (and secondarily also Ca2+) concentration, considerable attention has been devoted to its possible contributions to neurodegeneration processes (Taylor and Meldrum, 1995).
Despite the major interest raised by I NaP properties and functions, the single-channel correlates of this current have long remained elusive. This is not entirely surprising, since I NaP is normally only a minimal fraction of total voltage-dependent Na+ currents expressed by neuronal membranes (Taylor, 1993; Crill, 1996), which is likely to hamper attempts to identify the underlying single-channel activity. In a recent study performed in EC layer II principal neurons (Magistretti et al., 1999a), the single-channel activity responsible for the I NaP expressed by the same cells has been found to consist in channel openings characterized by: (a) relatively high opening probability, maintained for long periods of time (tens of minutes), during prolonged (500-ms) depolarizing test pulses; and (b) a single-channel conductance of ∼20 pS, significantly higher than observed in channel openings underlying the classical, transient voltage-dependent Na+ current (I NaT).
In the present work we further developed our previous studies on the channels responsible for I NaP generation by undertaking a thorough analysis of their fine gating properties in EC layer II principal neurons. Our results allowed us to provide a detailed description of the single-channel bases of I NaP voltage dependence and kinetic properties.
MATERIALS AND METHODS
Cell Preparation
Young-adult Long-Evans rats (P25-P35) were killed by decapitation according to a procedure approved by the Animal Care Committee of the Montreal Neurological Institute, and compliant with the Canadian and international laws on animal research. The brain was quickly removed under hypothermic conditions, blocked on the stage of a vibratome (Pelco), and submerged in an ice-cold cutting solution containing (in mmol/l): 115 NaCl, 5 KCl, 4 MgCl2, 1 CaCl2, 20 PIPES, and 25 D-glucose (pH 7.4 with NaOH, bubbled with pure O2). Horizontal slices of the retrohippocampal region were cut at 350–400 μm. Layer II of medial EC was then dissected from each slice. Neurons were acutely isolated from the tissue fragments thus obtained following an enzymatic and mechanical dissociation procedure described elsewhere (Magistretti and de Curtis, 1998).
Single-channel Recordings
The recording chamber was mounted on the stage of an inverted microscope (see below). After seeding into the recording chamber, cells where initially perfused with a standard HEPES buffer containing (in mmol/l): 140 NaCl, 5 KCl, 10 HEPES (free acid), 2 CaCl2, 2 MgCl2, 25 glucose, pH 7.4 with NaOH, bubbled with pure O2. The pipette solution contained (in mmol/l): 130 NaCl, 35 TEA-Cl, 10 HEPES-Na, 2 CaCl2, 2 MgCl2, 5 4-AP, pH 7.4 with HCl. Single-channel patch pipettes had resistances ranging from 10 to 35 MΩ when filled with the above solution, and were always coated with Sylgard® (Dow Corning) from the shoulder to a point as close as possible to the tip, so as to minimize stray pipette capacitance. After obtaining the cell-attached configuration, the extracellular perfusion was switched to a high-potassium solution containing: 140 K-acetate, 5 NaCl, 10 HEPES (free acid), 4 MgCl2, 0.2 CdCl2, 25 glucose, pH 7.4 with KOH, so as to hold the neuron resting membrane potential at near 0 mV. Recordings were performed at room temperature using an Axopatch 200B amplifier (Axon Instruments, Inc.). Capacitive transients and linear current leakage were minimized online by acting on the respective built-in compensation sections of the amplifier. To elicit voltage-gated Na+-channel currents, 50-, 500-, or 20-s depolarizing voltage steps were delivered one every 5, 5.6, or 40 s, respectively. The holding potential was −100 mV.
Whole-cell Recordings
For these experiments, dissociated cells were initially perfused with the same solution as described in the previous paragraph. After washout of cell debris, cell perfusion was switched to a solution suitable for Na+-current isolation, containing: 100 NaCl, 40 TEA-Cl, 10 HEPES (free acid), 2 CaCl2, 3 MgCl2, 0.2 CdCl2, 5 4-AP, 25 glucose, pH 7.4 with NaOH, bubbled with pure O2. The intrapipette solution contained (in mmol/l): 110 CsF, 10 HEPES-Na, 11 EGTA, 2 MgCl2, pH 7.25 with CsOH. When filled with the above solution, the patch pipettes had a resistance of 3–5 MΩ. Cells were observed at 400× magnification with an Axiovert 100 microscope (ZEISS). Tight seals (>100 GΩ) and the whole-cell configuration were obtained by suction (Hamill et al., 1981). Series resistance was on average 13.5 ± 3.1 MΩ (n = 5), and was always compensated by ∼70% with the amplifier's built-in compensation section. Voltage-clamp recordings were performed at room temperature (∼22°C) using an Axopatch 1D amplifier (Axon Instruments, Inc.). The holding potential was −80 mV.
Data Acquisition
Voltage protocols were commanded and current signals were acquired with a Pentium PC interfaced to an Axon TL1 interface, using the Clampex program of the pClamp 6.0.2 software package (Axon Instruments, Inc.). Current signals were filtered on-line (using the amplifier's built-in low-pass filter) and digitized at different frequencies according to the specific experimental aim. In single-channel experiments, filtering and acquisition frequencies were 5 and 100 kHz, respectively, for 50-ms depolarizing protocols; 2 and 10 kHz, respectively, for 500-ms depolarizing protocols; 1 and 2 kHz, respectively, for 20-s depolarizing protocols. In whole-cell experiments, filtering and acquisition frequencies were 10 and 20 kHz, respectively.
Data Analysis
Single-channel recordings were analyzed using Fetchan, pStat, and Clampfit (from the pClamp 6.0.5 software package; Axon Instruments, Inc.). Residual capacitive transients were nullified by off-line subtracting fits of average blank traces. Residual leakage currents were carefully measured in trace regions devoid of any channel openings, and digitally subtracted.
Channel dwell times were determined by applying a standard half-amplitude crossing protocol using Fetchan. No minimum-duration threshold for detection of state transitions was imposed. Dwell-time histograms were constructed, in some cases, as double-linear plots. However, logarithmic plots represent a suitable and powerful tool for data display and analysis in the presence of different exponential components widely separated in terms of time constants, and the slowest of which are represented by relatively few samples (see Blatz and Magleby, 1986; Sigworth and Sine, 1987; McManus et al., 1987). Hence, logarithmic plots were routinely used for the analysis of intraburst open and closed times as well as burst duration, and in these cases data were binned logarithmically. To do this, lower and upper bin limits were first set according to a logarithmic scale that yielded 11.4 bins/decade. To avoid arbitrary over- or underestimations of the calculated numbers of events per millisecond, upper limit values were then approximated to the nearest tenth of a millisecond above, so as to make each bin width equal an integer multiple of the sampling interval routinely used (100 μs). After data binning, numbers of events (n i) were divided by the corresponding bin widths (δt i), and the natural logarithm of n i/δt i ratios was calculated. The values thus obtained were plotted as a function of x = ln t to construct log–log frequency-distribution graphs (see Fig. 2 A2 and B2). Exponential fitting of log-log histograms was performed by applying the following function (McManus et al., 1987):
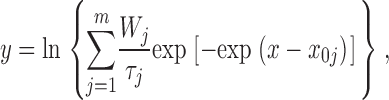 |
(1) |
where x
0j = ln τj, and W
j and τj are the weight coefficient and time constant, respectively, of each exponential component. Therefore, Eq. 1 corresponds to a double logarithmic transform of a sum of exponential functions. The above fittings were performed using the fitting routine of Origin 6.0 (MicroCal Software), based on a minimum χ2 method. To better highlight single exponential components as straight lines, logarithmically binned histograms constructed as described above were also displayed on a linear, rather than logarithmic, time scale, thereby obtaining log-linear graphs (see Fig. 2 A3 and B3). Theoretical mean dwell times (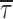 ) were derived from the exponential fitting functions according to the relationship:
) were derived from the exponential fitting functions according to the relationship:
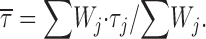 |
(2) |
Figure 2.
Display and analysis of intraburst open- and closed-time data. (A) Frequency-distribution diagrams of intraburst open times at −10 mV. Data were collected from nine different patches. (B) Frequency-distribution diagrams of intraburst closed times at −10 mV. Data were from the same nine patches used for A. A1 and B1 show histograms constructed after linear binning of original data and displayed on a double-linear scale (bin width, 0.4 ms in A1; 0.1 ms in B1). A2 and B2 are log-log histograms. Data were binned logarithmically (11.4 bins/decade), and the natural logarithm of the numbers of observations per ms [ln(n/ms)] was plotted as a function of time in a logarithmic scale. Smooth, enhanced lines are third (A2) or second (B2) order exponential functions obtained by applying the fitting function of Eq. 1 (materials and methods). Smooth, dotted lines are the single exponential components shown separately. Fitting parameters are specified in Table I. A3 and B3 are log-linear plots of the same data. Data were binned logarithmically as above, and the quantity ln(n/ms) was plotted as a function of time in a linear scale. The x value of each point is the logarithmic midpoint of the corresponding bin. Continuous and dotted lines are the same functions as in the two previous panels: single exponential components appear here as straight lines.
Ensemble-average traces were constructed using Clampfit (Axon Instruments, Inc.). Clampfit was also used to analyze whole-cell recordings. The decay phases of ensemble-average or whole-cell currents were fitted with m-order exponential functions in the form:
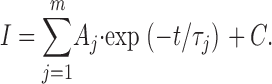 |
Fittings to data points made by applying other nonlinear functions, including the Boltzmann relation in the form: y = A/{1 + exp[(V m − V 1/2)/k]}, were performed using Origin 6.0. Average values are expressed as mean ± SE. Statistical significance was evaluated by means of the two-tail Student's t test for paired or unpaired data.
RESULTS
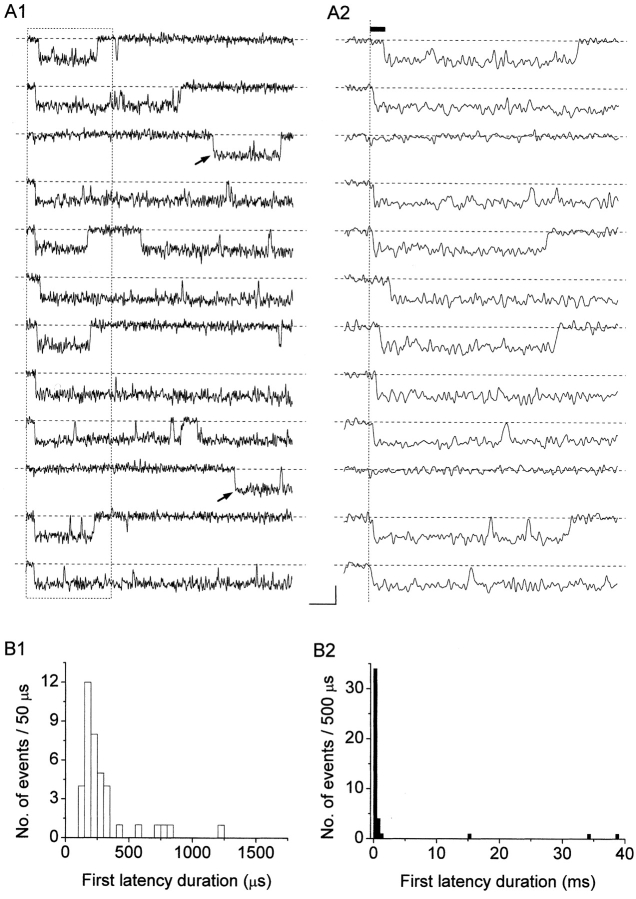
Na+-channel activity was studied in cell-attached membrane patches of entorhinal cortex layer II principal neurons. The cell-attached configuration was chosen in order to preserve the intracellular environment existing in intact cells, thus obtaining recording conditions closer to the physiological situation. Channel openings were routinely elicited by delivering 500-ms depolarizing pulses at variable test potentials (−50 to 0 mV). The application of these depolarizing protocols evoked, in most patches, a prominent, early Na+-channel activity that decayed within a few ms after the start of the test pulse. In addition to these expected, transient Na+-channel openings, in 56 out of 68 patches prolonged early openings and/or late openings were frequently observed (see Fig. 1) . We have shown elsewhere that this “persistent” Na+-channel activity represents an elementary correlate of the macroscopic persistent Na+ current (I NaP) expressed by these cortical neurons (Magistretti et al., 1999a; Magistretti and Alonso, 1999). The persistent Na+-channel activity consisted of more or less prolonged burst events in which repetitive openings of variable duration were separated by brief closings. The analysis of closed times at various test voltages (see below) revealed the existence of two relatively fast time constants (τ c(fast)1 and τ c(fast)2) plus a much slower time constant (τ c(slow)). τ c(slow) values were ∼65–95 times larger than the slowest τ c(fast)2 values observed, and therefore τ c(slow) was considered as related to the interburst closing process. The average values of τ c(fast)2 and τ c(slow) were such that the duration threshold between intraburst and interburst closing events was set at 10 ms (namely, an interval ∼6–10 times higher than the slowest τ c(fast)s observed). Since most recordings were obtained from multichannel patches, only those bursts in which no sign of superimposed (multiple) openings was apparent were considered. Among these, only bursts of >10 ms in duration were selected for analysis (Fig. 1, arrows). This was done to exclude from our analysis late openings of brief duration that classical, fast Na+ channels can occasionally produce (Alzheimer et al., 1993).
Figure 1.
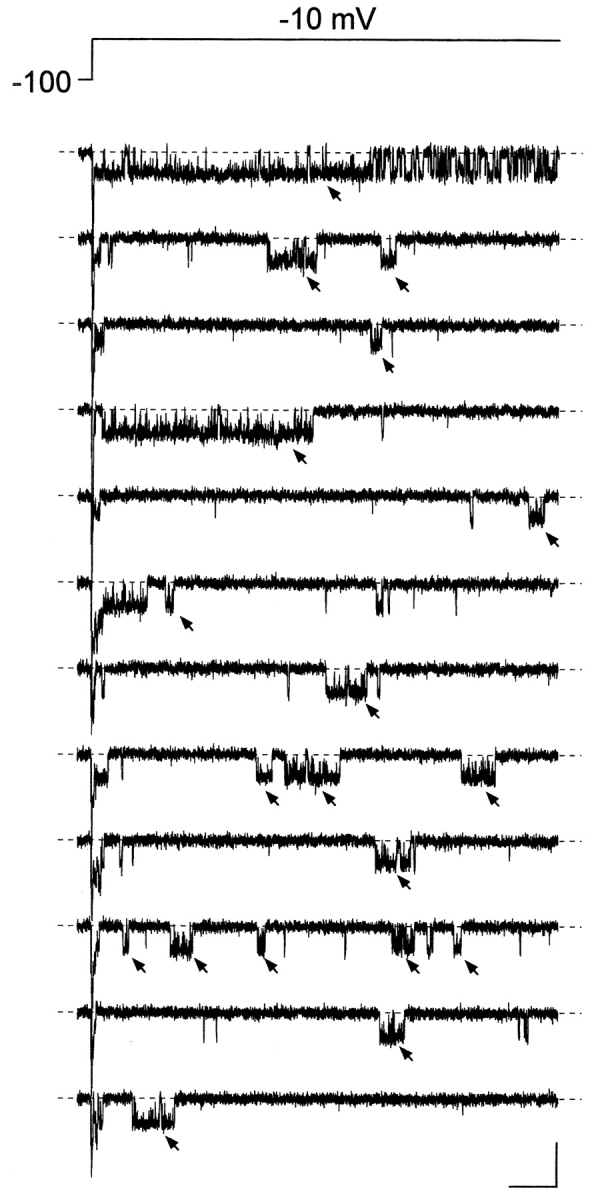
Persistent Na+ channel activity consists in prolonged and/or delayed burst openings. The figure shows twelve consecutive current sweeps recorded in response to 500-ms depolarizing pulses at −10 mV (top trace) in a representative cell-attached patch (patch A8716). The interpulse interval was 5.1 s. The arrows point to burst openings that were selected for analysis due to their characteristics (see the text for details). Calibration bars, 2 pA, 50 ms.
Analysis of Openings and Closings within Bursts
The properties of opening and closing events within bursts were first analyzed. After deriving dwell-time event lists for both in each patch (see materials and methods), frequency-distribution diagrams were constructed. For each test potential, data from different patches were pooled together in a single overall histogram, rather than used to create separate histograms for each patch, for two reasons: (a) most patches were multichannel patches, which implies that in such cases it was not possible to attribute the late bursting activity to a single channel rather than several, different channels, and (b) the above approach provided an internal compensation for the different numbers of observations obtained from different patches.
Fig. 3 illustrates the results of open-time analysis. The repetitive openings within individual bursts appeared to be short and frequent at negative membrane potentials (V
ms), and more prolonged and stable at increasingly positive V
ms (Fig. 3 A, insets). The analysis of open-time frequency distributions allowed for a precise quantification of this behavior. Inspection of log-linear plots clearly revealed, at all test potentials, the presence of three exponential components (see Fig. 2 A3). Fittings of log-log plots performed applying Eq. 1 (see materials
and
methods) confirmed that the best concordance with experimental data was achieved using a third-order exponential function (see Fig. 2 A2). Application of higher-order exponential functions did not add to the quality of fit. Fig. 3 (main panels) shows the open-time histograms obtained at all test potentials, here displayed as double-linear plots to highlight the actual numbers of observations, along with fitting functions derived as explained above. All of the three time constants found (τ
o(b)1 − τ
o(b)3)1 proved to be prominently voltage dependent (Table I) and increased by ∼12 (τ
o(b)1), 20 (τ
o(b)2), or 8 (τ
o(b)3) times from −50 to 0 mV. The mean open time (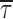 o(b)), calculated on the basis of fitting parameters as explained in materials
and
methods (Eq. 2), was also strongly voltage dependent (Fig. 3 B, open symbols), showing an e-fold increase (over an estimated pedestal level of 0.47 ms) per every 11.8 mV of depolarization.
o(b)), calculated on the basis of fitting parameters as explained in materials
and
methods (Eq. 2), was also strongly voltage dependent (Fig. 3 B, open symbols), showing an e-fold increase (over an estimated pedestal level of 0.47 ms) per every 11.8 mV of depolarization.
Figure 3.
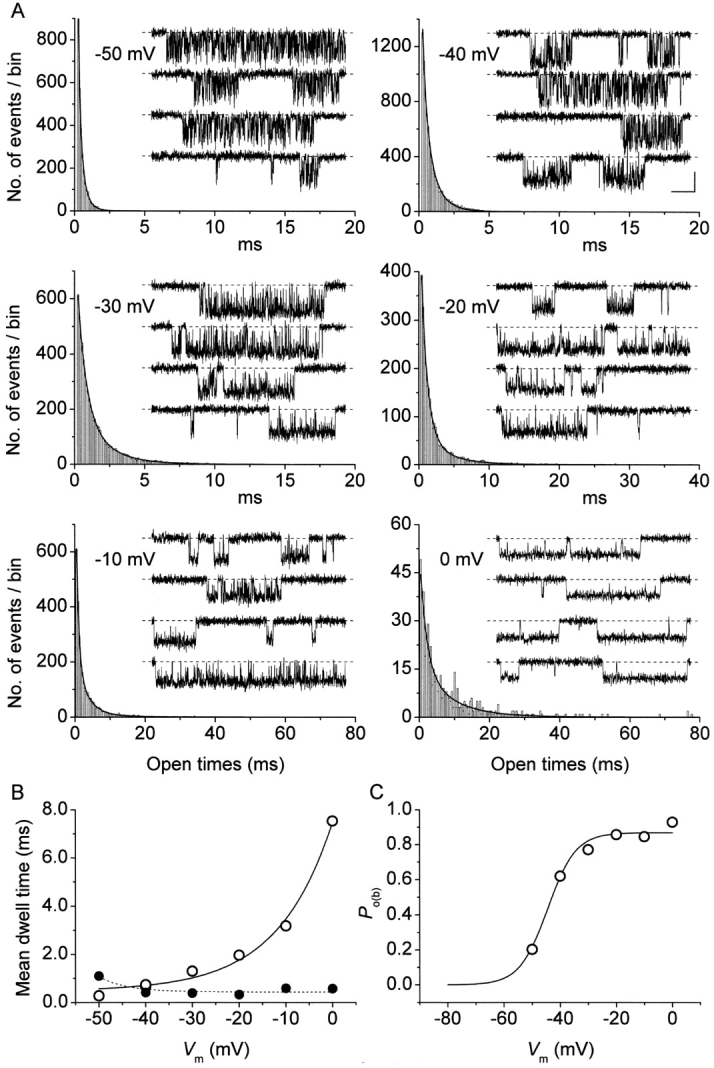
Open times are strongly voltage dependent. (A) Frequency distributions of open times at six different membrane potentials (−50 to 0 mV). Each histogram has been constructed pooling together data from 4 to 10 different patches. Data are shown binned linearly and plotted on a double-linear scale (bin width = 0.1 ms at −50 to −30 mV; 0.2 ms at −20 mV; 0.4 ms at −10 and 0 mV). Note the different time scales used. Smooth lines are best third order exponential fittings obtained applying Eq. 1 to log-log plots of the same data binned logarithmically (see materials
and
methods, and Fig. 2). Fitting parameters are specified in Table I. For each test potential, exemplary 210-ms current-trace segments were selected from 500-ms sweeps recorded in a single representative patch (patch B8708), and are shown in the inset of the corresponding panel (calibration bars: 1 pA, 25 ms). (B) Plot of mean open time (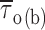 , calculated from fitting parameters as explained in the text) as a function of membrane potential (open circles). The continuous line is the best fitting to data points obtained applying the exponential function
, calculated from fitting parameters as explained in the text) as a function of membrane potential (open circles). The continuous line is the best fitting to data points obtained applying the exponential function 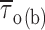 = A · exp(V
m/h) + C, which returned the following fitting parameters: A = 7.0 ms, h = 11.8 mV, C = 0.47 ms. Filled circles are mean intraburst closed times (
= A · exp(V
m/h) + C, which returned the following fitting parameters: A = 7.0 ms, h = 11.8 mV, C = 0.47 ms. Filled circles are mean intraburst closed times (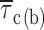 : see Fig. 4) measured in the same patches, shown here for comparison. (C) Voltage dependence of average intraburst opening probability (P
o(b)), calculated from
: see Fig. 4) measured in the same patches, shown here for comparison. (C) Voltage dependence of average intraburst opening probability (P
o(b)), calculated from 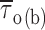 and
and 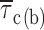 as explained in the text. The continuous line is the best Boltzmann fitting to data points. Fitting parameters are: A = 0.869, V
1/2 = −44.5 mV, k = −5.02 mV.
as explained in the text. The continuous line is the best Boltzmann fitting to data points. Fitting parameters are: A = 0.869, V
1/2 = −44.5 mV, k = −5.02 mV.
TABLE I.
Intraburst Open and Closed States
| Intraburst open states | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vm |
|
τo(b)1 |
|
τo(b)2 |
|
τo(b)3 | n T | |||||
| mV | ||||||||||||
| −50 | 0.552 | 0.15 | 0.439 | 0.391 | 0.009 | 2.607 | 1,993 | |||||
| −40 | 0.349 | 0.301 | 0.637 | 0.816 | 0.014 | 2.957 | 7,892 | |||||
| −30 | 0.482 | 0.611 | 0.5 | 1.839 | 0.019 | 4.622 | 5,849 | |||||
| −20 | 0.613 | 0.837 | 0.339 | 3.093 | 0.048 | 8.281 | 2,984 | |||||
| −10 | 0.407 | 0.646 | 0.494 | 3.11 | 0.1 | 13.864 | 3,337 | |||||
| 0 | 0.312 | 1.819 | 0.597 | 8.136 | 0.09 | 23.328 | 554 | |||||
| Intraburst closed states | ||||||||||||
| Vm |
|
τo(b)1 |
|
τo(b)2 | n T | |||||||
| mV | ||||||||||||
| −50 | 0.517 | 0.63 | 0.483 | 1.585 | 2,093 | |||||||
| −40 | 0.935 | 0.348 | 0.065 | 1.278 | 5,586 | |||||||
| −30 | 0.956 | 0.324 | 0.044 | 1.746 | 3,047 | |||||||
| −20 | 0.853 | 0.228 | 0.147 | 0.899 | 1,145 | |||||||
| −10 | 0.819 | 0.37 | 0.181 | 1.543 | 1,334 | |||||||
| 0 | 0.783 | 0.314 | 0.217 | 1.5 | 169 | |||||||
Kinetic parameters obtained from the analysis of frequency distribution diagrams of intraburst open times (top) and intraburst closed times (bottom) of persistent Na+ channel openings. Data were from 10 different patches. Open-time and closed-time histograms were fitted with triple or double exponential functions, respectively (see materials
and
methods, Eq. 1). The fitting parameters thus obtained at various test potentials (V
m), namely time constants (τs) and relative weight coefficients (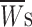 ), are specified. Relative weight coefficients were calculated as:
), are specified. Relative weight coefficients were calculated as: 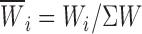 . n
T is the total number of observations in each histogram.
. n
T is the total number of observations in each histogram.
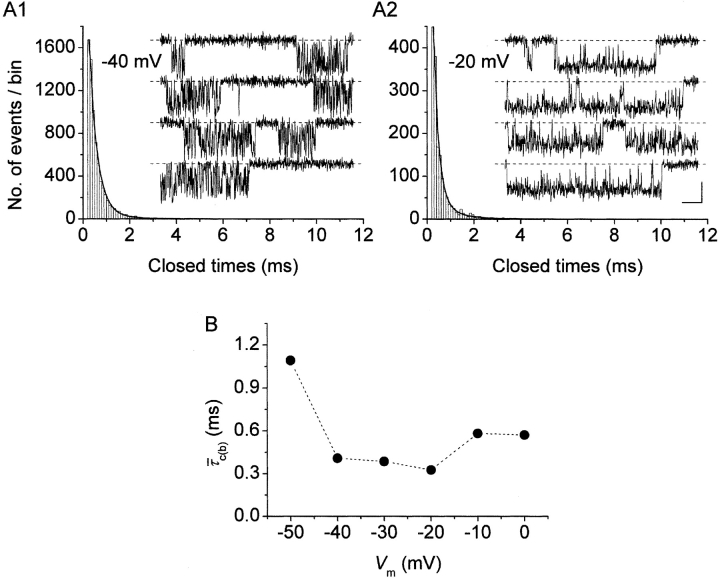
In comparison to open times, the duration of closings within bursts appeared much less voltage dependent (Fig. 4 A, insets). Closed-time histograms could be best fitted by the sum of two exponential functions at all test potentials (Figs. 2 B2 and 4 A, main panels). Both time constants found (τ
c(b)1 − τ
c(b)2) were basically voltage independent (Table I). The calculated intraburst mean closed time (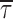 c(b)) also showed very scarce voltage dependence, at least between −40 and 0 mV (Fig. 4 B, filled symbols). Only at −50 did
c(b)) also showed very scarce voltage dependence, at least between −40 and 0 mV (Fig. 4 B, filled symbols). Only at −50 did 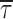 c(b) appear to increase somewhat (on average, by ∼2.4 times) with respect to the values observed at more positive voltage levels.
c(b) appear to increase somewhat (on average, by ∼2.4 times) with respect to the values observed at more positive voltage levels.
Figure 4.
Intraburst closed times are scarcely voltage dependent. (A) Frequency distributions of intraburst closed times at two exemplary membrane potentials (−40 mV in A1, −20 mV in A2). The histograms have been constructed pooling together data from seven (−40) or nine (−20) different patches. Data are shown binned linearly and plotted on a double-linear scale (bin width = 0.1 ms). Smooth lines are the best second-order exponential fittings obtained applying Eq. 1 to log-log plots of the same data binned logarithmically (see the materials
and
methods, and Fig. 2). Fitting parameters are specified in Table I. For both test potentials, exemplary 100-ms current-trace segments were selected from 500-ms sweeps recorded in a single representative patch (patch D8716), and are shown in the inset of the corresponding panel over an expanded time scale (calibration bars: 1 pA, 10 ms). (B) Plot of mean intraburst closed time (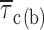 , calculated from fitting parameters as explained in the text) as a function of membrane potential.
, calculated from fitting parameters as explained in the text) as a function of membrane potential.
Having measured intraburst mean open and closed times, we were able to directly derive the probability of a channel to be open within a bursting event (P o(b)) by applying the following relation:
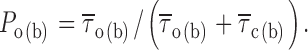 |
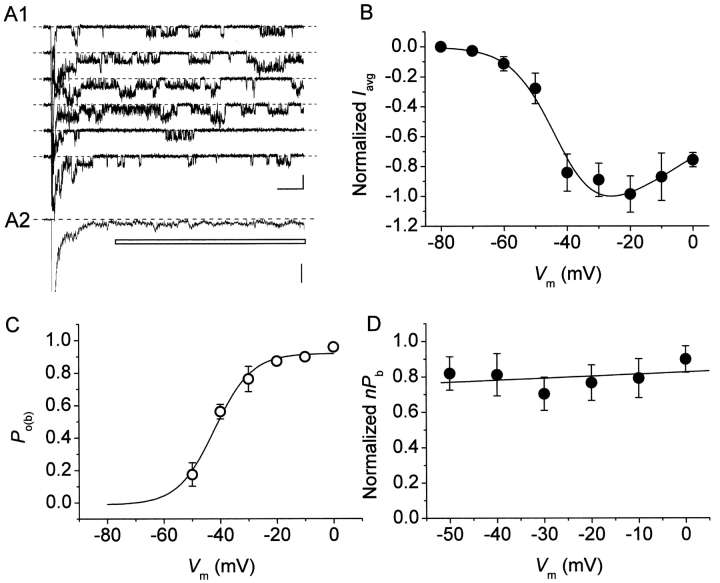
P o(b) values thus obtained were then plotted as a function of membrane potential (Fig. 3 C), which revealed a progressive increase of P o(b) at increasingly positive voltages, with a nearly saturating level at V ms positive to −20 mV. Fitting the data points with a single Boltzmann function returned a plateau P o(b) level of ∼0.87, a V 1/2 of about −44.5 mV, and a slope coefficient (k) of about −5 mV. Remarkably, the V 1/2 and k values thus found were extremely similar to those already reported for the activation voltage dependence of the whole-cell conductance underlying the macroscopic I NaP (Magistretti and Alonso, 1999).
Analysis of Interburst Closed Times
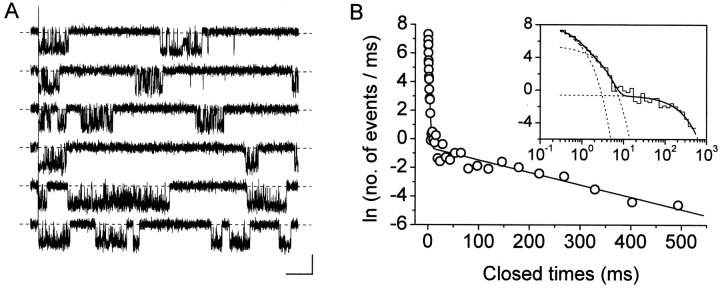
The quantitative analysis of closing periods between bursts requires the isolation of channel activity that may be attributed to an individual channel only, or, alternatively, to a known number of channels behaving identically. As mentioned above, most patches recorded in this study were multichannel patches. In these cases no assumptions could be made as to the number of channels responsible for “persistent” openings (from this point on, “NaP channels” for brevity), and, hence, no analysis of interburst closings could be performed. In two patches, however, only one single NaP channel appeared to be present. Indeed, despite the relatively high opening probability found in these patches (0.18 ± 0.04 during 500-ms depolarizing pulses at −10 mV), superimposed persistent openings were never observed in a total of 180 sweeps.2 In these patches, therefore, inter-burst closed times, in addition to intraburst closed times, could be analyzed. Current traces recorded in response to 500-ms depolarizing pulses were used for this analysis (Fig. 5 A). The overall closed-time distribution obtained for the test potential of –10 mV is shown in Fig. 5 B. The log-log histogram could be best fitted with a third-order exponential function (Fig. 5 B, inset), with two fast time constants (τ c(fast)1 and τ c(fast)2) of 0.351 and 1.215 ms, respectively, and a much slower one (τ c(slow)) of 115.5 ms. Similar measurements could also be performed in the same patches for the test potentials of −20 and −30 mV (not depicted): exponential fittings of closed-time histograms returned τ c(slow) values of 81.0 and 88.3 ms, respectively. The ratios between τ c(slow) and the slowest τ c(fast) were 95.1, 94.3, and 144.8 at −10, −20, and −30 mV, respectively. These data clearly indicate the existence of at least one long-lasting nonconductive state that interrupts and separates burst events generated by single NaP channels.3
Figure 5.
Analysis of interburst closed times. (A) Selected 500-ms sweeps from a patch in which the activity of a single NaP channel was recorded in isolation (patch F8711). The traces have been chosen to show the occurrence of reopenings and illustrate inter-burst intervals. Test potential was −10 mV. Calibration bars, 1 pA, 50 ms. (B) Frequency distribution of total closed times at −10 mV. The graphs have been constructed pooling together data from two single-channel patches. Data were binned logarithmically and in the main panel are shown in a log-linear plot. In the inset, the same data are shown as a log-log histogram. In both panels, the smooth, continuous line is the best third-order exponential fitting obtained applying Eq. 1 to the log-log plot. Dotted lines are the single exponential components of the fitting function shown separately. Fitting parameters are: W 1 = 1094.29, τ c1 = 351.2 μs; W 2 = 291.57, τ c2 = 1.215 ms; W 3 = 63.42, τ c3 = 115.53 ms.
Analysis of First Latencies
The possibility of performing a quantitative analysis of first latencies is subject to the same limitations discussed for interburst closed times. In the same two patches mentioned in the previous paragraph, in each of which only one NaP channel appeared to be active, we were able to analyze the latencies of first openings occurring in response to step depolarizations at −10 mV. To this purpose, 50-ms current sweeps acquired at 100 kHz and on-line filtered at 5 kHz were used. The sweeps selected for this analysis were devoid of transient Na+-channel openings, as confirmed by the absence of short, fast-decaying transients at the beginning of ensemble-average traces (see below, and Fig. 9 A2). The results are illustrated in Fig. 6 . Most first latencies appeared remarkably short. More than 75% of the first latencies observed were <350 μs, and >90% were shorter than 1.25 ms (Fig. 6 B1). In addition, much more delayed first openings were occasionally observed (Fig. 6 A1, arrows, and B2). Due to the limited number of observations, however, it was not possible to derive specific time-constant values from the analysis of first-latency frequency distribution.
Figure 9.
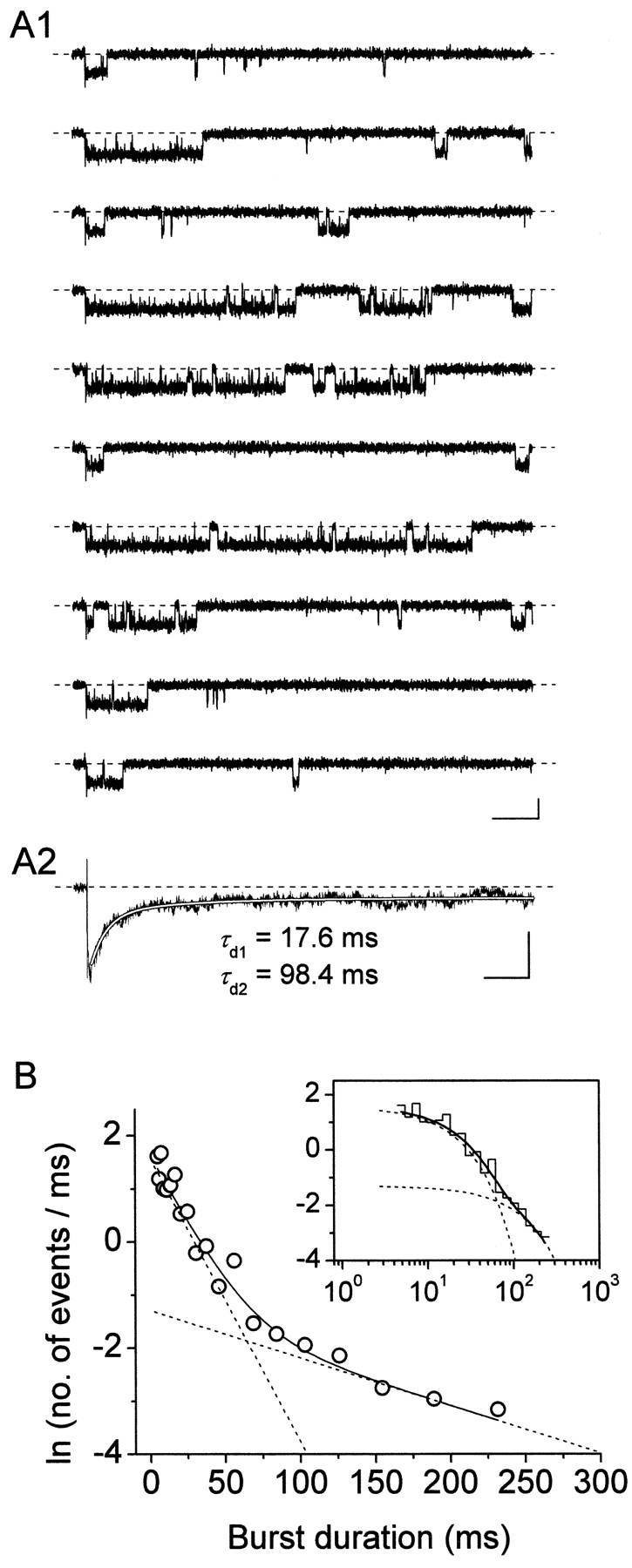
Burst-duration time constants result in very similar macroscopic relaxation time constants in ensemble-average traces. (A) Kinetic properties of the ensemble-average current derived, for the test potential of −10 mV, from patches showing the activity of single NaP channels in isolation. A1 shows exemplary traces recorded in response to 500-ms depolarizing pulses at −10 mV in the same patch as in Fig. 5, A2 shows the trace obtained by averaging 34 such traces from the two single-channel patches available. The smooth, blank line in A2 is the best biexponential fitting to data points (time-constant values are specified nearby). Calibration bars, 1 pA, 50 ms (A1); 400 fA, 50 ms (A2). (B) Frequency distribution of burst durations at −10 mV for the two single-channel patches illustrated above. The graphs have been constructed pooling together data from the same two patches used for A2. Data were binned logarithmically and in the main panel are shown in a log-linear plot. In the inset, the same data are shown as a log-log histogram. In both panels, the smooth, continuous line is the best second-order exponential fitting obtained applying Eq. 1 to the log-log plot. Dotted lines are the single exponential components of the fitting function shown separately. Fitting parameters are: W 1 = 90.21, τ b1 = 18.71 ms; W 2 = 30.68, τ b2 = 111.92 ms.
Figure 6.
Analysis of first latencies at −10 mV. (A) Selected sweeps showing persistent Na+ channel openings in isolation from a representative patch (patch H8710). Single-channel currents recorded in response to 50-ms depolarizing step pulses at −10 mV are shown in A1. A2 shows a detail, over an expanded time scale, of the first 15 ms of the same traces as in A1 (corresponding to the segments included in the dotted-line box of A1). The arrows in A1 remark two channel openings characterized by remarkably long first latencies. The filled bar in A2 indicates the first latency of the channel opening occurring in the top trace, determined starting from the depolarization's zero time point (dotted vertical line). Calibration bars, 1 pA, 5 (A1) or 1.5 (A2) ms. (B) Frequency distribution of first latencies at −10 mV. Data have been obtained in a total of 42 sweeps from two different patches, and are shown binned linearly and plotted on a double-linear scale. B1 highlights the initial part of the distribution (up to 1.75 ms). B2 shows the whole frequency distribution (with a different bin width).
Burst Analysis
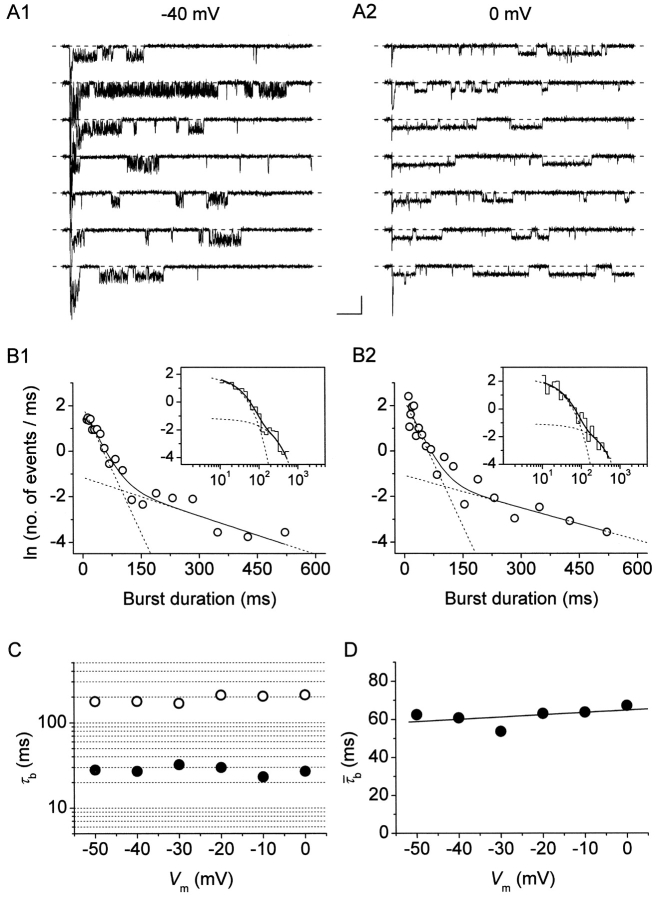
We then examined the periods of channel activity characterized by repetitive, bursting openings to analyze burst duration and its possible voltage dependence. In most patches, burst openings occurring at a given test potential (starting form the usual holding level of −100 mV) were typically relatively short as compared with the duration of the depolarizing pulses applied (500 ms), but long-lasting bursts were also occasionally observed (see Figs. 1, 7 A, and 9 A1). In six patches a complete analysis of burst duration over a wide range of membrane potentials could be performed. Overall frequency-distribution diagrams were constructed for each test potential. Fig. 7 B shows log-linear and log-log plots obtained for the test potentials of −40 and 0 mV. The frequency distribution of burst duration was biexponential at all V
ms. Both burst-duration time constants (τ
b1 and τ
b2) appeared remarkably voltage independent over the entire membrane-potential range explored (−50 to 0 mV), and fluctuated around values of ∼28 and ∼190 ms, respectively (Fig. 7 C). Mean burst duration (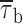 ), calculated on the basis of fitting parameters in the same way as explained for mean open and closed times (materials
and
methods, Eq. 2), was also largely voltage independent (Fig. 7 D).
), calculated on the basis of fitting parameters in the same way as explained for mean open and closed times (materials
and
methods, Eq. 2), was also largely voltage independent (Fig. 7 D).
Figure 7.
Analysis of burst duration. (A) Selected current traces recorded in response to 500-ms depolarizing pulses at −40 mV (A1) or 0 mV (A2) in a representative patch (patch D8708). Calibration bars, 2 pA, 50 ms. (B) Frequency distributions of burst duration at V
m = −40 mV (B1) and 0 mV (B2). Each graph has been constructed pooling together data from five different patches. Data were binned logarithmically and in the main panels are shown as log-linear plots. In the insets, the same data are shown as log-log histograms. In all panels, the smooth, continuous line is the best second-order exponential fitting obtained applying Eq. 1 to log-log plots. Dotted lines are the single exponential components of fitting functions shown separately. Fitting parameters are: W
1 = 192.16, τ
b1 = 26.98 ms; W
2 = 55.83, τ
b2 = 177.47 ms (−40 mV); W
1 = 258.22, τ
b1 = 27.03 ms; W
2 = 72.26, τ
b2 = 210.83 ms (0 mV). (C) Plot of burst-duration time constants (τ
bs) as a function of membrane potential. Filled and empty circles are τ
b1 and τ
b2 values, respectively. Note the logarithmic scale of the y axis. (D) Voltage dependence of mean burst duration (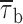 , calculated from fitting parameters as explained in the text).
, calculated from fitting parameters as explained in the text).
Since mean burst duration was found to be basically constant over a wide range of membrane potentials, and the same appeared to be true for interburst closed times (see above), at least at −30 to −10 mV, the probability of NaP channels to dwell in a “bursting state” (P b) would be expected to be also relatively voltage independent. To test this hypothesis, the problem of estimating P b was approached starting from the following relationship:
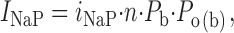 |
where i NaP is the amplitude of unitary persistent Na+-channel openings at a given potential, and n is the number of channels. The product of the two factors, P b and P o(b), expresses the probability of a NaP channel to be open at any time point. n · P b can thus be derived as:
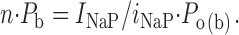 |
(3) |
On the basis of Eq. 3, we reconstructed n · P b values in the six patches used for burst-duration analysis. I NaP amplitude was estimated from the amplitude of the persistent component of ensemble-average currents (I avg; Fig. 8 A). Importantly, the voltage dependence of the I avg thus obtained (Fig. 8 B) was very similar to that typical of the whole-cell I NaP (Magistretti et al., 1999a; Magistretti and Alonso, 1999). Moreover, the voltage dependence of P o(b) measured in these patches closely paralleled that observed analyzing all of the available patches (compare Fig. 8 C with Fig. 3 C). n · P b was thus calculated applying Eq. 3 at each test potential, then n · P b values were normalized for the maximum value observed in each patch and averaged among patches. The plot of average, normalized n · P b as a function of V m (Fig. 8 D) clearly shows that this parameter was basically constant over the whole voltage range considered (−50 to 0 mV).
Figure 8.
The probability of NaP channels to dwell in a “bursting state” is largely voltage-independent. (A) Measurement of I NaP amplitude from ensemble-average currents (EACs). A1 shows exemplary traces recorded in response to 500-ms depolarizing pulses at −30 mV in a representative multichannel patch (patch C8703), A2 shows the trace obtained by averaging 20 such traces from the same patch. The horizontal bar marks the part of the trace the points of which were averaged to derive the amplitude of EAC's persistent component (I avg). Calibration bars, 2 pA, 50 ms (A1); 1 pA (A2). (B) Plot of average I avg amplitude, measured in EACs, as a function of membrane potential (n = 6). The continuous line is the best fitting to data point obtained applying the following function: I avg = A/{1 + exp[(V m – V 1/2)/k]} · (V m – V Na), were V Na is the average, extrapolated reversal potential of persistent Na+-channel openings as derived from the same six patches (54.5 mV). Fitting parameters are: V 1/2 = −42.2 mV, k = −6.8 mV. (C) Values of intraburst opening probability (P o(b)) were derived from each of the same six patches as in B, averaged, and plotted as a function of membrane potential. The continuous line is the best Boltzmann fitting to data points. Fitting parameters are: A = 0.92, V 1/2 = −42.0 mV, k = −6.6 mV. (D) Voltage dependence of average, normalized nP b (see text). nP b values were derived for the same six patches as in B and C.
Relationships between Burst Duration and INaP Decay Kinetics
Our analysis of burst duration has shown that the transition process from burst openings to long-lasting nonconductive state(s) occurs with two major time constants (τ bs) that in a voltage range between −40 and 0 mV are relatively voltage independent and average ∼28 and ∼190 ms. Assuming that first latencies are normally negligible as compared with burst durations (which is indeed the case at −10 mV: see above) and that burst durations are in turn far exceeded by inter-burst closed times, early burst openings would be expected to produce, in macroscopic I NaPs, inactivation time constants similar to, or somewhat smaller than, the observed τ bs. To directly test this idea we constructed ensemble-average traces from single-channel recordings obtained in patches displaying only NaP-channel activity (Fig. 9) . Fig. 9 A2 shows the ensemble-average trace obtained, for the test potential of −10 mV, from the two patches, in each of which only one single NaP channel appeared to be present. In these two patches, the analysis of burst duration returned two τ bs of 18.7 and 111.9 ms (Fig. 9 B). The ensemble-average current showed a decay phase that could be best fitted with a double exponential function (Fig. 9 A2), with time constants (τ d1 and τ d2) equal to 17.6 and 98.4 ms. These values are in good agreement with those of the τ bs found in the same patches. Indeed, considering that the mean closed time (τ c(ib)) of interburst closings occurring between short/medium-duration burst openings was found to be 115.5 ms at −10 mV (see above), the macroscopic relaxation time constant generated by τ b1 can be predicted to equal τ b1 · τ c(ib)/[τ b1 + τ c(ib)] = 16.1 ms, a value which compares favorably with that of the measured τ d1 (17.6 ms). Very similar results were obtained in an additional patch in which NaP-channel activity was recorded in isolation at various test potentials (−50 to 0 mV). These data show that burst-duration time constants characterizing the persistent Na+-channel activity can actually generate very similar, or slightly smaller, relaxation time constants in the corresponding macroscopic currents.
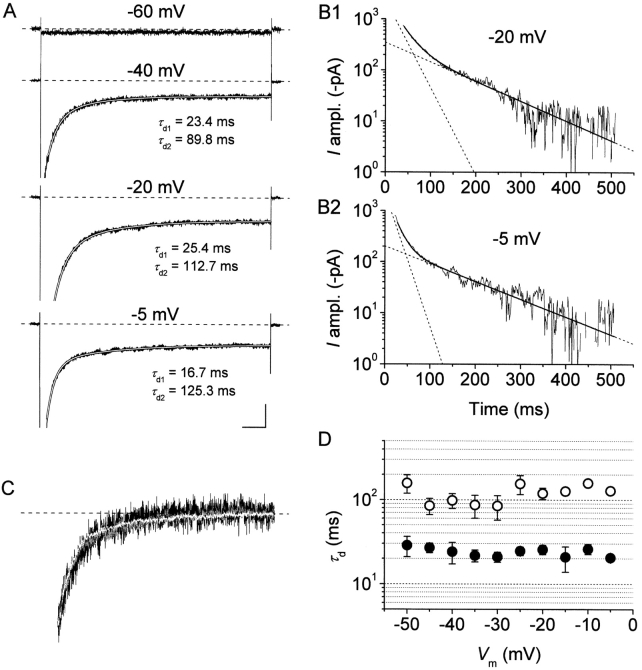
As a further step, we analyzed the decay kinetics of whole-cell I NaPs. We considered the decay phase of Na+ currents recorded in response to 500-ms depolarizing steps starting from 20–30 ms after the test pulse's onset, so as to exclude fast decay components due to the classical, fast Na+ current, I NaT. At test potentials positive to −55 mV, I NaP decay could be consistently fitted by second-order exponential functions (Fig. 10, A and B) . In the same voltage region, the decay time constants (τ ds) showed no apparent voltage dependence and fluctuated around values of ∼24 ms and ∼120 ms, respectively (Fig. 10 D). These values are not far from those found, in single-channel experiments, for the two major burst-duration time constants, which is in agreement with the hypothesis that I NaP τ ds mainly reflect mean burst durations. Consistently with this view, in the same membrane-potential region the overall I NaP decay kinetics appeared remarkably voltage independent (Fig. 10 C), a behavior that paralleled the relative voltage independence of single-channel mean burst durations (see Fig. 7 C). At test potentials negative to −50 mV, whole-cell I NaPs appeared much more sustained and largely nondecaying (Fig. 10 A, top trace). A similar behavior was also observed in ensemble-average traces from single-channel recordings (not depicted, but see Fig. 6 A in Magistretti et al., 1999a). Given the difficulty to obtain reliable measures of various single-channel kinetic parameters (i.e., first latencies, interburst closed times) at such negative voltage levels, the exact single-channel bases of the latter phenomenon could not be elucidated.
Figure 10.
I NaP fast and intermediate decay time constants closely parallel burst-duration time constants characteristic of persistent Na+-channel openings. (A) Whole-cell Na+ currents recorded in response to 500-ms depolarizing pulses at four different test potentials in a representative neuron (cell 96315). The traces are shown to highlight the I NaP component (part of the peak transient component at −40 to −5 mV has been blanked). The decay phases of the three lower traces (starting at 20–30 ms from the onset of the depolarizing test pulse) have been best fitted with a second order exponential function (smooth, blank lines). The time constants values returned by fittings are specified close to each trace. Calibration bars, 100 (−60 mV) or 200 (the remaining potentials) pA, 50 ms. (B) The two lower traces of A and the corresponding fitting functions are shown sign-inverted, subtracted of their offset components, and plotted on a logarithmic y axis to highlight the correspondence between second order exponential fitting functions and the experimental traces. Smooth, enhanced lines are the total fitting functions, dotted lines are the single exponential components shown separately. (C) Average I NaP traces obtained from five cells for three different test potentials (−45 mV, black trace; −25 mV, blank trace; −5 mV, gray trace) are shown normalized in amplitude and superimposed to highlight the similarities in their decay kinetics. Current traces were subtracted of their offset components and normalized for the amplitude measured at 40 ms from the onset of the depolarizing test pulse (the parts preceding the above time point have been omitted). Same time scale as in A. (D) Voltage dependence of I NaP “fast” and “intermediate” decay time constants (τ d1 and τ d2: filled and open circles, respectively) as obtained from the protocol illustrated in A and B (n = 5). Note the logarithmic scale of the y axis.
Effects of Long-lasting Depolarizations on Interburst Intervals and Burst Duration
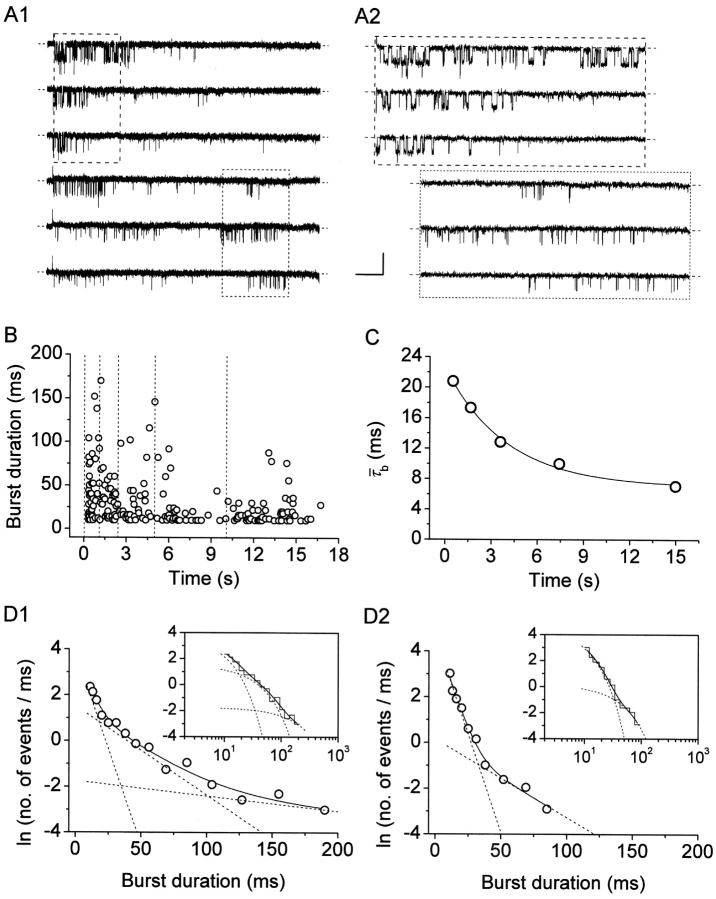
We have already demonstrated elsewhere that, besides faster kinetics decay processes, the whole-cell I NaP also undergoes a slow inactivation that develops during long-lasting depolarizations with moderately voltage-dependent time constants of ∼2.5–6.5 s (Magistretti and Alonso, 1999). This slow inactivation was shown to be paralleled by a progressive rarefaction of channel openings during prolonged depolarizations. We now provide a more detailed description of the single-channel correlates of the above phenomenon. Fig. 11 illustrates the data obtained in one representative patch and the results of our analysis. During the application of 20-s depolarizing pulses, the occurrence of burst openings was observed to decrease in frequency over time, such that most bursts were clustered within the first few seconds from the pulse's starting point (Fig. 11 A1). A further, quantitative description of the bases of this phenomenon would require a direct analysis of interburst closed times and their time course during long-lasting depolarizations, which, however, could not be performed because all of the patches from which these data were obtained were multichannel patches.
Figure 11.
Prolonged depolarizations induce longer interburst closings and shorter burst openings. (A) Single-channel recordings obtained applying long-lasting (20-s) depolarizing pulses at −20 mV in a representative patch (same patch as in Fig. 7 A). A1 shows six selected 20-s current sweeps in their entire length. 5-s segments were extracted from either the initial (dashed-line box) or the final (dotted-line box) part of the same sweeps, and shown in A2 over an expanded time scale to highlight the different mean duration of burst openings. Calibration bars, 2 pA, 2 s (A1) or 490 ms (A2). (B) Scatter plot of burst duration versus time during the application of 20-s depolarizing pulses at −20 mV. Data are from the same patch illustrated in A. Burst durations were plotted as a function of the starting point of each burst. The vertical, dotted lines mark the limits between the regions in which the plot was subdivided, and from each of which data values were extracted and used to construct burst-duration histograms (see D1 and D2). (C) Time course of mean burst duration, 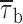 , during long-lasting (20-s) depolarizing pulses at −20 mV. Data points are
, during long-lasting (20-s) depolarizing pulses at −20 mV. Data points are 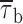 values derived from burst-duration histograms (see D1 and D2) constructed for the five regions in which the experimental traces were subdivided (see B). The continuous line is the best exponential fitting to data points. Fitting parameters are: A = 15.61 ms, τ = 4.01 s, C = 6.95 ms. (D) Frequency distributions of burst duration in early (D1) and late (D2) phases of 20-s depolarizing pulses at −20 mV. Each graph has been constructed pooling together data from five different patches. The data shown in D1 and D2 were collected from the first and the last, respectively, of the periods in which burst-duration time courses were subdivided (see B). Data were binned logarithmically and in the main panels are shown as log-linear plots. In the insets, the same data are shown as log-log histograms. In all panels, the smooth, continuous line is the best third- (D1) or second- (D2) order exponential fitting obtained applying Eq. 1 to log-log plots. Dotted lines are the single exponential components of fitting functions shown separately. Fitting parameters are: W
0 = 274.08, τ
b0 = 6.01 ms; W
1 = 118.19, τ
b1 = 25.79 ms; W
2 = 26.57, τ
b2 = 151.4 ms (D1); W
0 = 612.28, τ
b0 = 5.83 ms; W
1 = 34.09, τ
b1 = 29.26 ms (D2).
values derived from burst-duration histograms (see D1 and D2) constructed for the five regions in which the experimental traces were subdivided (see B). The continuous line is the best exponential fitting to data points. Fitting parameters are: A = 15.61 ms, τ = 4.01 s, C = 6.95 ms. (D) Frequency distributions of burst duration in early (D1) and late (D2) phases of 20-s depolarizing pulses at −20 mV. Each graph has been constructed pooling together data from five different patches. The data shown in D1 and D2 were collected from the first and the last, respectively, of the periods in which burst-duration time courses were subdivided (see B). Data were binned logarithmically and in the main panels are shown as log-linear plots. In the insets, the same data are shown as log-log histograms. In all panels, the smooth, continuous line is the best third- (D1) or second- (D2) order exponential fitting obtained applying Eq. 1 to log-log plots. Dotted lines are the single exponential components of fitting functions shown separately. Fitting parameters are: W
0 = 274.08, τ
b0 = 6.01 ms; W
1 = 118.19, τ
b1 = 25.79 ms; W
2 = 26.57, τ
b2 = 151.4 ms (D1); W
0 = 612.28, τ
b0 = 5.83 ms; W
1 = 34.09, τ
b1 = 29.26 ms (D2).
In addition, we also noticed that during prolonged depolarizations the mean duration of burst openings tended to become shorter (Fig. 11 A2). Plots of burst duration as a function of depolarization time confirmed this observation (Fig. 11 B). Burst duration was therefore analyzed in more detail in different phases of long-lasting depolarizations. To do this, five subsequent intervals of geometrically increasing duration were defined in the 20-s test pulses applied (see Fig. 11 B). The openings occurring in the different intervals were considered separately, and for each interval one burst-duration histogram was constructed (Fig. 11 D). The analysis of these histograms revealed mean burst durations (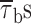 ) much shorter in the case of “late” openings as compared with “early” openings, with
) much shorter in the case of “late” openings as compared with “early” openings, with 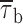 values of 7.1 ms in the last 10 s versus 20.8 ms in the first second.
values of 7.1 ms in the last 10 s versus 20.8 ms in the first second. 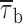 decrease over time could be described by a single exponential function plus an offset component (Fig. 11 C). At −20 mV, the time constant of
decrease over time could be described by a single exponential function plus an offset component (Fig. 11 C). At −20 mV, the time constant of 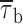 decrease was 4.0 s, and the relative amplitude of the offset component was ∼0.31. As reported elsewhere (Magistretti and Alonso, 1999), the slow inactivation process of both the macroscopic I
NaP and ensemble-average traces obtained from single-channel recordings was characterized by time constants somewhat faster (2.6–3.2 s at −20 mV) and offset components of considerable lower relative amplitude (<0.15 at −20 mV). Hence, it can be concluded that the time-dependent decrease of burst duration observed during prolonged depolarizations cannot entirely account for the kinetics of I
NaP slow inactivation, and, consequently, that a time-dependent increase of interburst closed times must give a major contribution to the same process.
decrease was 4.0 s, and the relative amplitude of the offset component was ∼0.31. As reported elsewhere (Magistretti and Alonso, 1999), the slow inactivation process of both the macroscopic I
NaP and ensemble-average traces obtained from single-channel recordings was characterized by time constants somewhat faster (2.6–3.2 s at −20 mV) and offset components of considerable lower relative amplitude (<0.15 at −20 mV). Hence, it can be concluded that the time-dependent decrease of burst duration observed during prolonged depolarizations cannot entirely account for the kinetics of I
NaP slow inactivation, and, consequently, that a time-dependent increase of interburst closed times must give a major contribution to the same process.
Further, our analysis of burst duration as a function of time revealed, in the histograms constructed for “late” openings, the predominance of a fast time constant (τ b0, equal to ∼6 ms) (Fig. 11 D2) that was much less represented in the histograms constructed for “early” openings (Fig. 11 D1). Indeed, in the last 10 s of 20-s depolarizing pulses, the relative amplitude coefficient of this fast exponential component was 0.947, as compared with a value of 0.654 observed during the first second.4 These results demonstrate that prolonged depolarizations promote the transition of NaP channels to short-duration “bursting” state(s). Consistently with these findings, we noticed that standard, 500-ms depolarizing test pulses delivered from holding potentials positive to −80 mV, rather than the usual level of −100 mV, evoked a NaP-channel activity characterized by markedly shorter burst openings than normally observed (not depicted). Data obtained with such experiments in four patches at V m = −20 mV were used to construct an overall burst-duration histogram, which revealed the appearance of a predominant fast time constant equal to 5.41 ms, and therefore similar to the above τ b0.
DISCUSSION
The present study provides a detailed analysis of the gating properties of the channels mainly responsible for persistent Na+-current (I NaP) generation (“NaP channels”) in EC layer II neurons. The achievement of this aim was hindered by the extreme difficulty to encounter patches showing the activity of single NaP channels in isolation, and hence to obtain reliable estimations of some specific single-channel parameters. This is not unexpected, since I NaP is normally a tiny fraction (0.002–0.02) of total whole-cell, voltage-gated Na+ currents (Taylor, 1993; Crill, 1996). Nonetheless, our results allowed us to unveil and describe in detail several basic properties of NaP channels, including their bursting behavior, and, perhaps most significantly, to elucidate the single-channel bases of I NaP voltage dependence and kinetic properties.
Voltage Dependence of Intraburst Open and Closed Times
First of all, our data show that, differently from intraburst closed times, intraburst open times are characterized by a very pronounced voltage dependence, with an e-fold increase of mean open time per every ∼12 mV of depolarization. This observation may have implications of some importance in clarifying the mechanistic processes involved in I NaP generation. In single-channel studies on native neurons, persistent Na+ channel openings underlying the macroscopic I NaP have been proposed to derive from a specific population of “persistent” Na+ channels (on the basis of conductance data: Magistretti et al., 1999a), or, alternatively, from the occasional, transient switch of otherwise typical, “fast” Na+ channels to a noninactivating gating modality (“modal gating”: Alzheimer et al., 1993). Open times of classical, neuronal Na+ channels, however, are known to be largely voltage independent and uniformly short over a wide range of V ms (Aldrich et al., 1983; Barres et al., 1989; Kirsch and Brown, 1989). In the latter hypothesis, therefore, it should be assumed that the inactivation process, rather than becoming transient and extremely short-lived, does not proceed at all. For instance, in a “ball-and-chain” model of the inactivation process (Armstrong et al., 1973; Bezanilla and Armstrong, 1977; Armstrong and Bezanilla, 1977), the lack of inactivation could be the consequence of a failure of the inactivating ball either to maintain the inactivated state (the ball does reach its binding site but does not “stick” onto it for long), or, alternatively, to induce it (the ball does not have any tendency to reach its binding site any more). Only the latter possibility is compatible with our single-channel data. A voltage-dependent behavior of open times similar to that we describe here was observed in long-lasting burst events that are occasionally produced in membrane patches from skeletal muscle fibers (Patlak and Ortiz, 1986), ventricular myocytes (Ju et al., 1994), and neocortical neurons (Alzheimer et al., 1993), and that have been attributed to modal gating of classical Na+ channels by Patlak and Ortiz (1986) and Alzheimer et al. (1993). Also in these cases, it was concluded that only a transient failure of the inactivation process is a mechanism compatible with the kinetic properties of such bursting events (Patlak and Ortiz, 1986; Alzheimer et al., 1993). Indeed, removal of Na+ channels' fast inactivation, obtained with proteolytic treatment, animal toxins, or organic gating modifiers, unveils a prominent voltage dependence of open times within burst openings (Horn et al., 1984; Kohlhardt et al., 1987; Quandt, 1987; Cukierman, 1991). Hence, it seems that, under the “modal gating” hypothesis, prolonged periods of “persistent” activity of individual channels (that we did observe in our recordings: see Magistretti et al., 1999a,b) would require significant functional modifications (and, therefore, probably also structural rearrangements) of the molecular components that govern the inactivation process within the same channels. Interestingly, expression in Xenopus oocytes of various brain or skeletal muscle Na+ channel α subunits (Nav1.2A, Nav1.3, Nav1.4) in the absence of β subunits produces I Nas with abnormally slow decay kinetics (discussed by Chang et al., 1996; Makita et al., 1996; Goldin, 1999) resulting from an exaggerated Na+ channel bursting activity (Moorman et al., 1990; Zhou et al., 1991), the normal phenotype being recovered by coexpression with β1 subunits.
An additional consequence of our data is that the closings occurring within bursts are not compatible with transient, short forays to a “classical” inactivated state, but rather represent transitions to different, short-lived closed states. Our analysis identified at least two distinct closed states, as well as three open states, within bursts. Because all of the dwell-time histograms used for this analysis were constructed pooling together data from several different patches, in most of which more than one channel was active, the question could be raised whether individual channels can generate the three open states and the two closed states corresponding to the time constants observed, or, rather, distinct channel subsets are responsible for these different kinetic states. This issue will be the subject of a separate paper (unpublished data).
Properties of Bursts
Differently from intraburst open times, the duration of burst openings, as well as the probability of NaP channels to be in a “bursting” state, were found to be largely voltage independent in the range of membrane potentials we investigated. The frequency distribution of burst durations could be described by two relatively voltage-independent time constants (τ b1 and τ b2) of ∼28 and ∼190 ms, the faster of which was typically much more represented. Therefore, most bursts were of “medium” duration, whereas long-lasting burst events (underlying the slow time constant, τ b2) were of less frequent observation. “Medium-duration” burst openings were encountered in the majority of sweeps in >80% of the patches examined. By contrast, in frog skeletal muscle (Patlak and Ortiz, 1986) and mammalian neocortical neurons (Alzheimer et al., 1993), late Na+-channel activity has been reported to consist in either brief reopenings (“background activity”) or rarely occurring, long-lasting bursts that often exceeded the duration of the depolarizing pulses applied (500 ms). In our recordings, “long-duration” bursting activity was prevalent in a minority of patches, and in such cases it appeared remarkably persistent (see Magistretti et al., 1999a,b). This diversity of bursting behaviors encountered in EC neurons and its bases will be also described in more detail elsewhere (unpublished data).
Whatever the mechanisms underlying the above diversity in bursting activity, the prevalence of “medium”-duration bursts (or, after prolonged depolarizations, short-duration bursts; see below) over long-lasting bursts is likely to add to the relatively high conductance of NaP channels in determining the “noisy” nature of I NaP (White et al., 1998; Agrawal et al., 2001). Indeed, for given values of steady current and channel conductance, discontinuous openings would generate higher levels of stochastic channel noise than sustained openings. In turn, membrane-potential fluctuations resulting from channel noise may have major impacts on neuronal dynamics (see White et al., 2000). Modeling and experimental data have shown that current noise can enhance membrane resonance in response to oscillatory inputs (White et al., 1998), increase excitability (Ho and Destexhe, 2000), influence spike timing reliability (Mainen and Sejnowski, 1995; Tang et al., 1997; Hunter et al., 1998), and improve signal detection and information transfer (Douglass et al., 1993; Levin and Miller, 1996). In particular, it has been proposed that the subthreshold membrane potential fluctuations caused by I NaP activation in EC layer II neurons may play a role, through a resonance phenomenon, in facilitating oscillatory dynamics and/or spike timing reliability (White et al., 2000), thereby influencing the learning and memory functions of the EC.
Further, we found that the average duration of burst openings also depends on the duration of the depolarization applied to elicit NaP channel activity, as well as on the foregoing holding potential. In both cases, sustained depolarizations favored the appearance of predominant, short burst events the frequency distribution of which was largely described by a fast time constant (τ b0) of ∼5–6 ms. This implies that burst duration, and hence I NaP amplitude and fluctuations, not only are functions of absolute membrane potential, but also depend on the modalities by which a given V m level is reached and maintained. Such properties may confer more complexity than previously thought onto the ability of I NaP to influence the integrative functions of central neurons, both in a sub- and near-threshold range of membrane potentials, and at more positive voltage levels (see the introduction).
Finally, our data give strong support to the idea that the kinetics of the fast and intermediate decay components observed in whole-cell I NaP during step depolarizations largely reflect the burst-duration time constants characteristic of the underlying single-channel activity. The relative voltage independence of both τ b1 and τ b2 are indeed consistent with the scarce voltage dependence of I NaP fast and intermediate decay time constants. By contrast, the kinetics of the slow component of I NaP decay (or “slow inactivation”) turned out to result from time-dependent changes in both interburst-interval duration and burst-opening duration. In this case, the inactivation process is accompanied by voltage-dependent transitions of NaP channels to interburst closed state(s) characterized by longer durations as compared with those prevalently occurring during short depolarizations.
Single-channel Bases of INaP Voltage Dependence
A remarkable result of the present study is the finding that the strong voltage dependence of open times within bursts is almost entirely responsible for the voltage-dependent properties of macroscopic I NaP. Indeed, the voltage dependence of the opening probability within bursts closely paralleled that of the conductance underlying I NaP, with nearly identical kinetic parameters returned by Boltzmann fittings of the respective plots. By contrast, both mean burst duration and the estimated probability of NaP channels to dwell in a bursting state were found to be largely voltage independent. This implies that, whatever the molecular mechanisms underlying I NaP generation, depolarization itself is not a primary factor in either promoting or prolonging “persistent” bursting channel openings, but rather determines the temporal balance between conductive and nonconductive states within each burst opening. Therefore, a single mechanism, namely the increase of dwell times in intraburst open states with increasing depolarizations, appears to confer upon I NaP its voltage dependence in a range of membrane voltages where the same currents exert its characteristic effects on neuronal electroresponsiveness.
In a recent study on histaminergic tuberomammillary neurons (Taddese and Bean, 2002) it has been proposed, on the basis of whole-cell current recordings, that the same channels that generate the fast, transient Na+ current (I NaT) also entirely account for I NaP, and, more importantly, that no particular structural or functional specialization at the typical, “fast” Na+ channels' charge, not even modal gating, is necessary to explain the presence of a persistent Na+ current. The authors of that study propose an allosteric kinetic model of Na+ channel gating that includes a series of closed states in equilibrium with as many inactivated states, and a single open state in equilibrium with an additional inactivated state. In this model, transitions between closed states are voltage dependent (in a “cooperative” manner), whereas the transitions from the open state to the two nonconductive states communicating with it are not. Proper implementation of such a kinetic scheme was able to reproduce the properties and voltage dependence of both macroscopic I NaT and I NaP in those neurons. Clearly, the above model does not apply to the here-studied case of EC layer II neurons, because: (a) in that model, the open times of Na+ channels are voltage independent, whereas we have demonstrated that, in our case, open times of NaP channels are strongly voltage dependent and account almost entirely for I NaP voltage dependence; (b) in the model, conversely, dwell times in nonconducting (closed or inactivated) states are strongly voltage dependent and entirely account for the voltage dependence of the persistent Na+-current fraction; on the contrary, we show that in EC layer II neurons the voltage dependence of NaP-channel closed times is minor; and (c) finally, the model cannot reproduce a bursting behavior of channel openings responsible for the persistent Na+ current fraction, whereas we show that such a behavior is a prominent and distinctive feature of the channel activity that underlies I NaP in EC layer II neurons. Obviously, it is possible that different mechanisms are used in different neuronal systems to generate a macroscopic I NaP, according to the functional needs specific of each neuronal type. A highly specialized mechanism able to produce burst openings characterized by the peculiar kinetic properties that we have described must be dominant in EC layer II neurons, but is likely to operate in other CNS neuronal populations as well, including EC layer V neurons (Agrawal et al., 2001), neocortical neurons (Alzheimer et al., 1993), hippocampal neurons (Masukawa et al., 1991; Segal and Douglas, 1997), cerebellar Purkinje cells (Sugimori et al., 1994), and also tuberomammillary neurons (Uteshev et al., 1995).
A Kinetic Model for NaP Channels?
Due to the limitations discussed previously in the present paper, some specific aspects (i.e., first latencies, interburst closed times) of the channel activity responsible for I NaP generation in the neurons under study could not be investigated in detail. As a consequence, our data do not allow us to elaborate an exhaustive, reliable model of the kinetic properties of the same channel activity. However, they do enable us to point out some key features that will have to be taken into account in future models of NaP channel gating behavior. NaP channel openings have been shown to occur in bursts, separated from each other by prolonged dwellings in interburst closed state(s). During burst events, repetitive transitions take place between multiple open states (at least three) and closed states (at least two). The occurrence of a burst could be viewed as the transition of a channel to a “bursting state.” Since three time constants (τ b0-τ b2) were found to describe burst duration, at least three different “bursting states” could be proposed to exist. Mean burst duration was found to be largely voltage independent, whereas mean open time within bursts (and hence the number of openings per burst) displayed strong voltage dependence. The most parsimonious interpretation of these findings is to assume that transitions to interburst closed states can occur with equal probability from any of the intraburst open and closed states. It is actually this probable functional equivalence of intraburst states, as far as the migration to interburst closed states is concerned, that supports the idea of the existence of “bursting states,” induced and maintained independently of open-closed state transitions, as the physical substrate of burst events.
Concluding Remarks
Considerable effort has been placed to elucidate the biophysical and molecular mechanisms underlying persistent Na+ currents in brain neurons. This is not surprising, due to the important roles played by this current in basic neuronal integrative functions, such as processing of synaptic potentials, generation of spontaneous and pacemaker activity, and firing-pattern shaping, as well as in pathological processes such as epileptogenesis and neurodegeneration (see the introduction). In spite of this effort, the issue has not yet been fully elucidated in any neuronal type, and there is plenty of controversy about the potential underlying mechanisms (Huguenard, 2002). A source of information that will probably turn out to be important is the functional analysis of Na+ channel subunits expressed in heterologous cell systems in the attempt to reproduce the properties of I NaP and the underlying channels. The present study represents a necessary step for future comparisons between persistent Na+ channel activity in native neurons and heterologously reconstructed Na+ channels able to generate sustained, threshold Na+ currents.
Footnotes
Abbreviations used in this paper: CNS, central nervous system; EC, entorhinal cortex; PHR, parahippocampal region.
Events <100 μs (the sampling interval of the long-lasting depolarizing protocols here applied) were missed in our dwell-time analysis. This limitation could affect our estimations of mean open and closed times. The algorithms that can be employed to correct such errors (e.g., Colquhoun and Sigworth, 1983) could not be applied here, since the fastest time constants observed (see Table I) were not long enough as compared to the limit of resolution of the measurements, which is one of the basic requirements for these corrections being applicable. Therefore, the time constants we report are uncorrected, and should be interpreted as upper bonds for the exact, real values.
In this case, if two channels opening with equal probability were responsible for the persistent activity observed, ∼5% of the opening time would be predicted to consist of superimposed openings. However, the possibility that multiple channels, each opening sporadically, generated single bursts in these patches, although unlikely, cannot be unequivocally ruled out. As a consequence, our estimation of mean interburst closed time (τ c(slow)) should be taken as a lower limit for true value(s). It is also worth to note that, if the τ c(slow) value we provide is underestimated, the criterion we used to discriminate between intra- and interburst closings (see the first paragraph of results) would be even safer.
Again, we stress that in the present context the expression “NaP channels” is used for brevity and does not necessarily imply the existence of a specific population of Na+ channels exclusively devoted to persistent Na+ current generation. It is simply meant to indicate those channels the openings of which produce the “persistent” Na+ channel activity here studied and underlie the macroscopic I NaP.
It is worth noting that τb0 was prominently represented also in the initial phases of 20-s depolarizing pulses, although to a lesser extent than in later phases, whereas it was virtually absent, even in the same patches, when 500-s depolarizing pulses delivered from −100 mV were considered (see above). This explains the much shorter 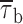 values found in the initial phases of 20-s traces as compared to those observed in 500-ms protocols. The reason for this discrepancy could be that repetitive, long-lasting depolarizing pulses induce a “short-lived” bursting behavior, and that full recovery from this process requires longer repolarizations than the inter-episode time (20 s) that separated the single 20-s pulses in the protocol we applied.
values found in the initial phases of 20-s traces as compared to those observed in 500-ms protocols. The reason for this discrepancy could be that repetitive, long-lasting depolarizing pulses induce a “short-lived” bursting behavior, and that full recovery from this process requires longer repolarizations than the inter-episode time (20 s) that separated the single 20-s pulses in the protocol we applied.
References
- Agrawal, N., B.M. Hamam, J. Magistretti, A. Alonso, and D.S. Ragsdale. 2001. Persistent sodium channel activity mediates subthreshold membrane potential oscillations and low-threshold spikes in entorhinal cortex layer V neurons. Neuroscience. 102:53–64. [DOI] [PubMed] [Google Scholar]
- Aldrich, R.W., D.P. Corey, and C.F. Stevens. 1983. A reinterpretation of mammalian sodium channel gating based on single channel recording. Nature. 306:436–441. [DOI] [PubMed] [Google Scholar]
- Alonso, A., M. de Curtis, and R. Llinás. 1990. Postsynaptic Hebbian and non-Hebbian long-term potentiation of synaptic efficacy in the cortex in slices and in the isolated adult guinea pig brain. Proc. Natl. Acad. Sci. USA. 87:9280–9284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alonso, A., and E. García-Austt. 1987. a. Neuronal sources of theta rhythm in the entorhinal cortex of the rat. I. Laminar distribution of theta field potentials. Exp. Brain Res. 67:493–501. [DOI] [PubMed] [Google Scholar]
- Alonso, A., and E. García-Austt. 1987. b. Neuronal sources of theta rhythm in the entorhinal cortex of the rat. II. Phase relations between unit discharges and theta field potentials. Exp. Brain Res. 67:502–509. [DOI] [PubMed] [Google Scholar]
- Alonso, A., and R. Klink. 1993. Differential electroresponsiveness of stellate and pyramidal-like cells of medial entorhinal cortex layer II. J. Neurophysiol. 70:128–143. [DOI] [PubMed] [Google Scholar]
- Alonso, A., and R.R. Llinás. 1989. Subthreshold Na+-dependent theta-like rhythmicity in stellate cells of entorhinal cortex layer II. Nature. 342:175–177. [DOI] [PubMed] [Google Scholar]
- Alzheimer, C., P.C. Schwindt, and W.E. Crill. 1993. Modal gating of Na+ channels as a mechanism of persistent Na+ current in pyramidal neurons from rat and cat sensorimotor cortex. J. Neurosci. 13:660–673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amitai, Y. 1994. Membrane potential oscillations underlying firing patterns in neocortical neurons. Neuroscience. 63:151–161. [DOI] [PubMed] [Google Scholar]
- Armstrong, C.M., and F. Bezanilla. 1977. Inactivation of the sodium channel. II. Gating current experiments. J. Gen. Physiol. 70:567–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong, C.M., F. Bezanilla, and E. Rojas. 1973. Destruction of sodium conductance inactivation in squid axons perfused with pronase. J. Gen. Physiol. 63:375–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azouz, R., M.S. Jensen, and Y. Yaari. 1996. Ionic basis of spike after-depolarization and burst generation in adult rat hippocampal CA1 pyramidal cells. J. Physiol. 492:211–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barres, B.A., L.L.Y. Chun, and D.P. Corey. 1989. Glial and neuronal forms of the voltage-dependent sodium channel: Characteristics and cell-type distribution. Neuron. 2:1375–1388. [DOI] [PubMed] [Google Scholar]
- Bennett, B.D., J.C. Callaway, and C.J. Wilson. 2000. Intrinsic membrane properties underlying spontaneous tonic firing in neostriatal cholinergic interneurons. J. Neurosci. 20:8493–8503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bevan, M.D., and C.J. Wilson. 1999. Mechanisms underlying spontaneous oscillation and rhythmic firing in rat subthalamic neurons. J. Neurosci. 19:7617–7628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezanilla, F., and C.M. Armstrong. 1977. Inactivation of the sodium channel. I. Sodium current experiments. J. Gen. Physiol. 70:549–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bland, B.H., and L.V. Colom. 1993. Extrinsic and intrinsic properties underlying oscillation and synchrony in limbic cortex. Prog. Neurobiol. 41:157–208. [DOI] [PubMed] [Google Scholar]
- Blatz, A.L., and K.L. Magleby. 1986. Quantitative description of three modes of activity of fast chloride channels from rat skeletal muscle. J. Physiol. 378:141–174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brumberg, J.C., L.G. Nowak, and D.A. McCormick. 2000. Ionic mechanisms underlying repetitive high-frequency burst firing in supragranular cortical neurons. J. Neurosci. 20:4829–4843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki, G. 1996. The hippocampo-neocortical dialogue. Cereb. Cortex. 6:81–92. [DOI] [PubMed] [Google Scholar]
- Chang, S.Y., J. Satin, and H.A. Fozzard. 1996. Modal behavior of the μ1 Na+ channel and effects of coexpression of the β1-subunit. Biophys. J. 70:2581–2592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao, T.I., and C. Alzheimer. 1995. Do neurons from rat neostriatum express both a TTX-sensitive and a TTX-insensitive slow Na+ current? J. Neurophysiol. 74:934–941. [DOI] [PubMed] [Google Scholar]
- Colquhoun, D., and F.J. Sigworth. 1983. Fitting and statistical analysis of single channel records. Single Channel Recording. B. Sakmann and E. Neher, editors. Plenum Publishing Co., New York and London. 191–263.
- Crill, W.E. 1996. Persistent sodium current in mammalian central neurons. Annu. Rev. Physiol. 58:349–362. [DOI] [PubMed] [Google Scholar]
- Cukierman, S. 1991. Inactivation modifiers of Na+ currents and the gating of rat brain Na+ channels in planar lipid membranes. Pflugers Arch. 419:514–521. [DOI] [PubMed] [Google Scholar]
- Deisz, R.A., G. Fortin, and W. Zieglgänsberger. 1991. Voltage dependence of excitatory postsynaptic potentials of rat neocortical neurons. J. Neurophysiol. 65:371–382. [DOI] [PubMed] [Google Scholar]
- Dickson, C.T., J. Magistretti, M.H. Shalinsky, E. Fransén, M. Hasselmo, and A. Alonso. 2000. Properties and role of I h in the pacing of subthreshold oscillations in entorhinal cortex layer II neurons. J. Neurophysiol. 83:2562–2579. [DOI] [PubMed] [Google Scholar]
- Douglass, J.K., L. Wilkens, E. Pantazelou, and F. Moss. 1993. Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature. 365:337–340. [DOI] [PubMed] [Google Scholar]
- Franceschetti, S., E. Guatteo, F. Panzica, G. Sancini, E. Wanke, and G. Avanzini. 1995. Ionic mechanisms underlying burst firing in pyramidal neurons: intracellular study in rat sensorimotor cortex. Brain Res. 696:127–139. [DOI] [PubMed] [Google Scholar]
- French, C.R., and P.W. Gage. 1985. A threshold sodium current in pyramidal cells in rat hippocampus. Neurosci. Lett. 56:289–293. [DOI] [PubMed] [Google Scholar]
- French, C.R., P. Sah, K.J. Buckett, and P.W. Gage. 1990. A voltage-dependent persistent sodium current in mammalian hippocampal neurons. J. Gen. Physiol. 95:1139–1157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenstein, Y.J., C. Pavlides, and J. Winson. 1988. Long-term potentiation in the dentate gyrus is preferentially induced at theta rhythm periodicity. Brain Res. 438:331–334. [DOI] [PubMed] [Google Scholar]
- Goldin, A.L. 1999. Diversity of mammalian voltage-gated sodium channels. Molecular and Functional Diversity of Ion Channels and Receptors. B. Rudy and P. Seeburg, editors. New York Academy of Sciences, New York. 84–88. [DOI] [PubMed]
- Hamill, O.P., A. Marty, E. Neher, B. Sakmann, and F.J. Sigworth. 1981. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflugers Arch. 391:85–100. [DOI] [PubMed] [Google Scholar]
- Ho, N., and A. Destexhe. 2000. Synaptic background activity enhances the responsiveness of neocortical pyramidal neurons. J. Neurophysiol. 84:1488–1496. [DOI] [PubMed] [Google Scholar]
- Hölscher, C., R. Anwyl, and M.J. Rowan. 1997. Stimulation on the positive phase of hippocampal theta rhythm induces long-term potentiation that can be depotentiated by stimulation on the negative phase in area CA1 in vivo. J. Neurosci. 17:6470–6477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn, R., C.A. Vandenberg, and K. Lange. 1984. Statistical analysis of single sodium channels. Effects of N-bromoacetamide. Biophys. J. 45:323–335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huerta, P.T., and J.E. Lisman. 1996. Low-frequency stimulation at the troughs of θ-oscillation induces long-term depression of previously potentiated CA1 synapses. J. Neurophysiol. 75:877–884. [DOI] [PubMed] [Google Scholar]
- Huguenard, J.R. 2002. Sodium channels: grit, determination, and persistence. Neuron. 33:492–494. [DOI] [PubMed] [Google Scholar]
- Hunter, J.D., J.G. Milton, P.J. Thomas, and J.D. Cowan. 1998. Resonance effect for neural spike time reliability. J. Neurophysiol. 80:1427–1438. [DOI] [PubMed] [Google Scholar]
- Jahnsen, H., and R. Llinás. 1984. Ionic basis for the electro-responsiveness and oscillatory properties of guinea-pig thalamic neurones in vitro. J. Physiol. 349:227–247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston, A.R., N.K. MacLeod, and M.B. Dutia. 1994. Ionic conductances contributing to spike repolarization and after-potentials in rat medial vestibular nucleus neurones. J. Physiol. 481:61–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston, D., J.C. Magee, C.M. Colbert, and B.R. Christie. 1996. Active properties of neuronal dendrites. Annu. Rev. Neurosci. 19:165–186. [DOI] [PubMed] [Google Scholar]
- Ju, Y.-K., D.A. Saint, and P.W. Gage. 1994. Inactivation-resistant channels underlying the persistent sodium current in rat ventricular myocytes. Proc. R. Soc. Lond. B Biol. Sci. 256:163–168. [DOI] [PubMed] [Google Scholar]
- Kay, A.R., M. Sugimori, and R. Llinás. 1998. Kinetic and stochastic properties of a persistent sodium current in mature guinea pig cerebellar Purkinje cells. J. Neurophysiol. 80:1167–1179. [DOI] [PubMed] [Google Scholar]
- Kirsch, G.E., and A.M. Brown. 1989. Kinetic properties of single sodium channels in rat heart and rat brain. J. Gen. Physiol. 93:85–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klink, R., and A. Alonso. 1993. Ionic mechanisms for the subthreshold oscillations and differential electroresponsiveness of medial entorhinal cortex layer II neurons. J. Neurophysiol. 70:144–157. [DOI] [PubMed] [Google Scholar]
- Klink, R., and A. Alonso. 1997. Morphological characteristics of layer II projection neurons in the rat medial entorhinal cortex. Hippocampus. 7:571–583. [DOI] [PubMed] [Google Scholar]
- Kohlhardt, M., U. Frobe, and J.W. Herzig. 1987. Properties of normal and non-inactivating single cardiac Na+ channels. Proc. R. Soc. Lond. B Biol. Sci. 232:71–93. [DOI] [PubMed] [Google Scholar]
- Larson, J., and G. Lynch. 1986. Induction of synaptic potentiation in hippocampus by patterned stimulation involves two events. Science. 232:985–988. [DOI] [PubMed] [Google Scholar]
- Larson, J., D. Wong, and G. Lynch. 1986. Patterned stimulation at the theta frequency is optimal for the induction of hippocampal long-term potentiation. Brain Res. 368:347–350. [DOI] [PubMed] [Google Scholar]
- Levin, J.E., and J.P. Miller. 1996. Broadband neural encoding in the cricket cercal sensory system enhanced by stochastic resonance. Nature. 380:165–168. [DOI] [PubMed] [Google Scholar]
- Lingenhöhl, K., and D.M. Finch. 1991. Morphological characterization of rat entorhinal neurons in vivo: soma-dendritic structure and axonal domains. Exp. Brain Res. 84:57–74. [DOI] [PubMed] [Google Scholar]
- Lipowsky, R., T. Gillessen, and C. Alzheimer. 1996. Dendritic Na+ channels amplify EPSPs in hippocampal CA1 pyramidal cells. J. Neurophysiol. 76:2181–2191. [DOI] [PubMed] [Google Scholar]
- Llinás, R., and M. Sugimori. 1980. Electrophysiological properties of in vitro Purkinje cell somata in mammalian cerebellar slices. J. Physiol. 305:171–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magistretti, J., and M. de Curtis. 1998. Low-voltage activated T-type calcium currents are differently expressed in superficial and deep layers of guinea pig piriform cortex. J. Neurophysiol. 79:808–816. [DOI] [PubMed] [Google Scholar]
- Magistretti, J., and A. Alonso. 1999. Biophysical properties and slow-voltage dependent inactivation of a sustained sodium current in entorhinal cortex layer-II principal neurons: A whole-cell and single-channel study. J. Gen. Physiol. 114:491–509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magistretti, J., D.S. Ragsdale, and A. Alonso. 1999. a. High conductance sustained single channel activity responsible for the low threshold persistent Na+ current in entorhinal cortex neurons. J. Neurosci. 19:7334–7341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magistretti, J., D.S. Ragsdale, and A. Alonso. 1999. b. Direct demonstration of persistent Na+ channel activity in dendritic processes of mammalian cortical neurones. J. Physiol. 521:629–636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mainen, Z.F., and T.J. Sejnowski. 1995. Reliability of spike timing in neocortical neurons. Science. 268:1503–1506. [DOI] [PubMed] [Google Scholar]
- Makita, N., P.B. Bennett, and A.L. George. 1996. Molecular determinants of β1 subunit-induced gating modulation in voltage-dependent Na+ channels. J. Neurosci. 16:7117–7127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masukawa, L.M., A.J. Hansen, and G. Sheperd. 1991. Distribution of single-channel conductances in cultured rat hippocampal neurons. Cell. Mol. Neurobiol. 11:231–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McManus, O.B., A.L. Blatz, and K.L. Magleby. 1987. Sampling, log binning, fitting, and plotting durations of open and shut intervals from single channels and the effects of noise. Pflugers Arch. 410:530–553. [DOI] [PubMed] [Google Scholar]
- Moorman, J.R., G.E. Kirsch, A.M. VanDongen, R.H. Joho, and A.M. Brown. 1990. Fast and slow gating of sodium channels encoded by a single mRNA. Neuron. 4:243–252. [DOI] [PubMed] [Google Scholar]
- Pape, H.C., and R.B. Driesang. 1998. Ionic mechanisms of intrinsic oscillations in neurons of the basolateral amygdaloid complex. J. Neurophysiol. 79:217–226. [DOI] [PubMed] [Google Scholar]
- Parri, H.R., and V. Crunelli. 1998. Sodium current in rat and cat thalamocortical neurons: role of a non-inactivating component in tonic and burst firing. J. Neurosci. 18:854–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patlak, J.B., and M. Ortiz. 1986. Two modes of gating during late Na+ channel currents in frog sartorius muscle. J. Gen. Physiol. 87:305–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pennartz, C.M., M.A. Bierlaagh, and A.M. Geurtsen. 1997. Cellular mechanisms underlying spontaneous firing in rat suprachiasmatic nucleus: involvement of a slowly inactivating component of sodium current. J. Neurophysiol. 78:4811–4825. [DOI] [PubMed] [Google Scholar]
- Quandt, F.N. 1987. Burst kinetics of sodium channels which lack fast inactivation in mouse neuroblastoma cells. J. Physiol. 392:563–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ragsdale, D.S., and M. Avoli. 1998. Sodium channels as molecular targets for antiepileptic drugs. Brain Res. Brain Res. Rev. 26:16–28. [DOI] [PubMed] [Google Scholar]
- Reyes, A. 2001. Influence of dendritic conductances on the input-output properties of neurons. Annu. Rev. Neurosci. 24:653–675. [DOI] [PubMed] [Google Scholar]
- Sandler, V.M., E. Puil, and D.W. Schwarz. 1998. Intrinsic response properties of bursting neurons in the nucleus principalis trigemini of the gerbil. Neuroscience. 83:891–904. [DOI] [PubMed] [Google Scholar]
- Schwindt, P.C., and W.E. Crill. 1995. Amplification of synaptic current by persistent sodium conductance in apical dendrite of neocortical neurons. J. Neurophysiol. 74:2220–2224. [DOI] [PubMed] [Google Scholar]
- Segal, M.M. 1994. Endogenous bursts underlie seizurelike activity in solitary excitatory hippocampal neurons in microcultures. J. Neurophysiol. 72:1874–1884. [DOI] [PubMed] [Google Scholar]
- Segal, M.M., and A.F. Douglas. 1997. Late sodium channel openings underlying epileptiform activity are preferentially diminished by the anticonvulsant phenytoin. J. Neurophysiol. 77:3021–3034. [DOI] [PubMed] [Google Scholar]
- Sigworth, F.J., and S.M. Sine. 1987. Data transformations for improved display and fitting of single-channel dwell time histograms. Biophys. J. 52:1047–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stafstrom, C.E., P.C. Schwindt, M.C. Chubb, and W.E. Crill. 1985. Properties of persistent sodium conductance and calcium conductance of layer V neurons from cat sensorimotor cortex in vitro. J. Neurophysiol. 53:153–170. [DOI] [PubMed] [Google Scholar]
- Stuart, G., and B. Sakmann. 1995. Amplification of EPSPs by axosomatic sodium channels in neocortical pyramidal neurons. Neuron. 15:1065–1076. [DOI] [PubMed] [Google Scholar]
- Sugimori, M., A.R. Kay, and R. Llinás. 1994. The persistent Na+ channel in cerebellar Purkinje cells has a single channel conductance distinct from the inactivating current. Soc. Neurosci. Abstr. 20:63. [Google Scholar]
- Taddese, A., and B.P. Bean. 2002. Subthreshold sodium current from rapidly inactivating sodium channels drives spontaneous firing of tuberomamillary neurons. Neuron. 33:587–600. [DOI] [PubMed] [Google Scholar]
- Takakusaki, K., and S.T. Kitai. 1997. Ionic mechanisms involved in the spontaneous firing of tegmental pedunculopontine nucleus neurons of the rat. Neuroscience. 78:771–794. [DOI] [PubMed] [Google Scholar]
- Tang, A.C., A.M. Bartels, and T.J. Sejnowski. 1997. Effects of cholinergic modulation on responses of neocortical neurons to fluctuating input. Cereb. Cortex. 7:502–509. [DOI] [PubMed] [Google Scholar]
- Taylor, C.P. 1993. Na+ currents that fail to inactivate. Trends Neurosci. 16:455–460. [DOI] [PubMed] [Google Scholar]
- Taylor, C.P., and B.S. Meldrum. 1995. Na+ channels as targets for neuroprotective drugs. Trends Pharmacol. Sci. 16:309–316. [DOI] [PubMed] [Google Scholar]
- Uteshev, V., D.R. Stevens, and H.L. Haas. 1995. A persistent sodium current in acutely isolated histaminergic neurons from rat hypothalamus. Neuroscience. 66:143–149. [DOI] [PubMed] [Google Scholar]
- White, J.A., J.T. Rubinstein, and A.R. Kay. 2000. Channel noise in neurons. Trends Neurosci. 23:131–137. [DOI] [PubMed] [Google Scholar]
- White, J.A., R. Klink, A. Alonso, and A.R. Kay. 1998. Noise from voltage-gated ion channels may influence neuronal dynamics in the entorhinal cortex. J. Neurophysiol. 80:262–269. [DOI] [PubMed] [Google Scholar]
- Winson, J. 1978. Loss of hippocampal theta rhythm results in spatial memory deficit in the rat. Science. 201:160–163. [DOI] [PubMed] [Google Scholar]
- Zhou, J.Y., J.F. Potts, J.S. Trimmer, W.S. Agnew, and F.J. Sigworth. 1991. Multiple gating modes and the effect of modulating factors on the μI sodium channel. Neuron. 7:775–785. [DOI] [PubMed] [Google Scholar]