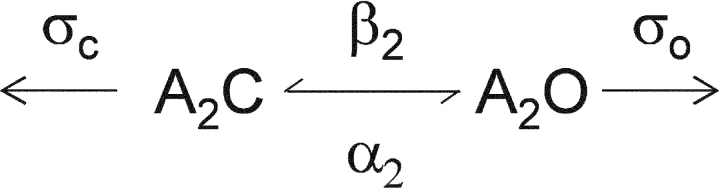The Role of Loop 5 in Acetylcholine Receptor Channel Gating

Abstract

Nicotinic acetylcholine receptor channel (AChR) gating is an organized sequence of molecular motions that couples a change in the affinity for ligands at the two transmitter binding sites with a change in the ionic conductance of the pore. Loop 5 (L5) is a nine-residue segment (mouse α-subunit 92–100) that links the β₄ and β₅ strands of the extracellular domain and that (in the α-subunit) contains binding segment A. Based on the structure of the acetylcholine binding protein, we speculate that in AChRs L5 projects from the transmitter binding site toward the membrane along a subunit interface. We used single-channel kinetics to quantify the effects of mutations to αD97 and other L5 residues with respect to agonist binding (to both open and closed AChRs), channel gating (for both unliganded and fully-liganded AChRs), and desensitization. Most αD97 mutations increase gating (up to 168-fold) but have little or no effect on ligand binding or desensitization. Rate-equilibrium free energy relationship analysis indicates that αD97 moves early in the gating reaction, in synchrony with the movement of the transmitter binding site (Φ = 0.93, which implies an open-like character at the transition state). αD97 mutations in the two α-subunits have unequal energetic consequences for gating, but their contributions are independent. We conclude that the key, underlying functional consequence of αD97 perturbations is to increase the unliganded gating equilibrium constant. L5 emerges as an important and early link in the AChR gating reaction which, in the absence of agonist, serves to increase the relative stability of the closed conformation of the protein.

INTRODUCTION

At cholinergic synapses, transmitter molecules induce acetylcholine receptor channels (AChRs) to change from a closed- to an open-channel conformation. The driving energy for this reaction is the ∼10⁴-fold higher affinity of the open-channel conformation for ACh at each of the two transmitter binding sites (TBS) (Karlin, 1967; Jackson, 1989). Our objective is to understand the molecular motions that link the closed- and open-channel AChR structures, which is the gating reaction mechanism.

The adult, vertebrate neuromuscular AChR is a heteropentamer (α₂βδɛ) in which the two TBS are located ∼30 Å above the plane of the membrane at the α-δ and α-ɛ subunit interfaces (Valenzuela et al., 1994; Unwin, 2000; Karlin, 2002). The crystal structure of AChBP, a homologue of the AChR extracellular domain (Brejc et al., 2001), predicts that this region of the AChR is almost entirely composed of β-strands and connecting loops. The α-subunit (“+”) side of the TBS contains three such loops (Fig. 1) : L5 (the β₄–β₅ linker), which contains binding segment A; L8 (the β₇–β₈ linker), which contains binding segment B; and L10, (the β₉–β₁₀ linker) which contains binding segment C. L5 is the focus of this report.

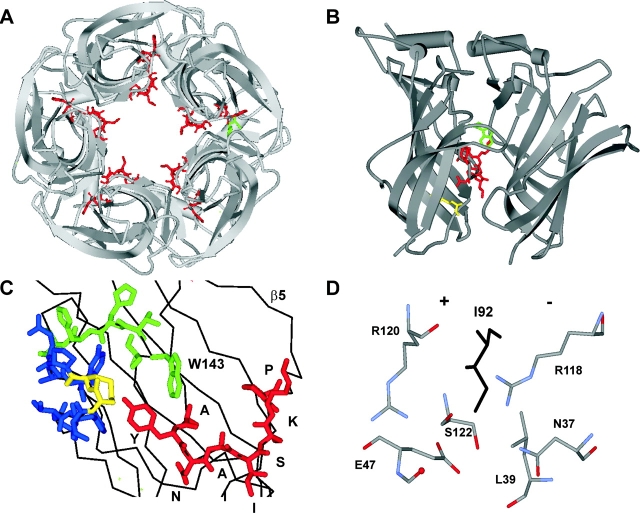
Figure 1.

Structure of L5 in AChBP. (A) View along the fivefold axis of symmetry, from the Cys-loop (in AChR, from the membrane). L5 (binding segment A) is red, and W143 at the TBS is green. The apex residue I92 (which aligns with αD97 in AChRs) projects into the lumen. (B) View perpendicular to the fivefold axis of symmetry (“+” side, left). L5 (red) lies at the subunit interface and spans the distance between the TBS (W143, green) and the Cys-loop disulfide (yellow). (C) View of the TBS, from the “−” side. L5 is red (apex residue is I92), L8 (binding segment B) is green, and L10 (binding segment C) is blue (disulfide is yellow). See Table I for sequences. (D) Close up of I92 at a subunit interface. Atoms from three side chains and one backbone carbonyl on the “+” side and three side chains on the “−” side are within 6 Å of the δC of I92 (black).

L5 is a nine-residue segment (LYNNADGDF in the mouse α-subunit) that is located between the TBS and the disulfide bond of the signature “Cys-loop” (β₆–β₇ linker), along a subunit interface (Fig. 1). The tyrosine at position 93 is an integral part of the TBS (Galzi et al., 1990; Cohen et al., 1991; Brejc et al., 2001). After mutation of αY93 the macroscopic dose–response curve is right-shifted (Aylwin and White, 1994; Sullivan and Cohen, 2000), mainly because of slower ligand-association and channel-opening rate constants (Auerbach et al., 1996; Akk et al., 1999). At positions αN95 and αA96, cysteine-mutations cause a leftward shift in the dose–response curve (Sullivan and Cohen, 2000). In the GABA_AR, another member of the cys-loop receptor family, βY97 (sequence alignment with mouse AChR: αV91) and βL99 (αY93) contribute to the TBS and the mutation βL99C causes a large increase in spontaneous opening when expressed as a β₂-homomer (Boileau et al., 2002). Although there is little conservation of L5 residues between AChRs and GABA_ARs (Table I) , these studies suggest that L5 plays a similarly important role in the activation of these related receptors.

TABLE I.

Sequence Alignment of L5

		β4___________β5			β4___________β5
AChBP	:	LAAYN-AISKPEV	AChBP	:	LAAYN-AISKPEV
M.alpha1	:	VVLYNNADGDFAI	X.lealpha1	:	LVLYNNADGDFAI
M.alpha2	:	IVLYNNADGEFAV	G.gaalpha1	:	LVLYNNADGDFAI
M.alpha3	:	IVLYNNADGDFQV	B.toalpha1	:	IVLYNNAVGDFQV
M.alpha4	:	IVLYNNADGNFAV	D.mealpha1	:	IVLYNNADGNYEV
M.alpha5	:	IVLFDNADGRFEG	C.elalpha1	:	VVLYNNADGNYQV
M.alpha6	:	IVLYNNAVGDFQV	L.mialpha1	:	IVLTNNSEGNFEV
M.alpha7	:	ILLYNSADERFDA	H.5HT3AS	:	ILINEFVDVGKSP
M.alpha9	:	ILLAMTVFQLMVA	M.5HT3AS	:	ILINEFVDVGKSP
M.beta1	:	VLLNNNDGNFDVA	H.5HT3B	:	IIINEFVDIERYP
M.beta2	:	IVLYNNADGEFAV	M.5HT3B	:	IIINEFVDVERSP
M.beta3	:	IVLFENADGRFEG	H.GABAA1	:	TFFHNGKKSVAHN
M.beta4	:	IVLYNNADGTYEV	M.GABAA1	:	TFFHNGKKSVAHN
M.deltal	:	IVLENNNDGSFQI	H.GABAB1	:	TYFLNDKKSFVHG
M.epsilon1	:	IVLENNIDGQFGV	M.GABAB1	:	TYFLNDKKSFVHG
M.gamma1	:	IVLENNVDGVFEV	H.GABAD1	:	TFIVNAKSAWFHD
M.mualpha1	:	VVLYNNADGDFAI	M.GABAD1	:	TFIVNAKSAWFHD
R.noalpha1	:	VVLYNNADGDFAI	H.GABAGS	:	TFFRNSKKADAHW
H.saalpha1	:	LVLYNNADGDFAI	M.GABAGS	:	TFFRNSKKADAHW
T.caalpha1	:	LVLYNNADGDFAI	H.GlyA1	:	LFFANEKGAHFHE
A.caalpha1	:	IVLYNNADGNYEV	M.GlyA1	:	LFFANEKGAHFHE

Sequence-alignment of L5 in AChBP and subunits from pentameric, “cys-loop” receptor channels. The line marks L5 in AChBP. In AChRs, the tyrosine (in mouse α₁, Y93) forms a part of the ACh binding pocket. The apex of L5 is at residue I92 in AChBP and is in bold. See Fig. 1 for structures.

We have investigated the effects of mutations to every residue in L5 of the AChR α-subunit, with a particular focus on the putative apex residue αD97. Selected L5 residues in the other subunits were also examined. We used single-channel kinetic analysis to define the consequences of a mutation in terms of the fundamental equilibrium and rate constants for ligand binding (to both closed and open AChRs), channel gating (of both unliganded and fully-liganded AChRs), and desensitization. The results suggest that in the α-subunit, L5, serves as a “latch” that decreases the unliganded gating equilibrium constant, which is an important determinant of both the amplitude and the time course of the response to transmitter at the synapse.

MATERIALS AND METHODS

Expression

cDNA clones of α, β, δ, and ɛ subunits of mouse AChR in pRBG4 were transiently expressed in human embryonic kidney cells (HEK 293) by transfection with calcium phosphate. A total of 3.5 μg of DNA per 35-mm culture dish was used in the subunit ratio 2:1:1:1(α:β:δ:ɛ). The medium was changed after 24 h and electrophysiological recording began another 24 h later. All mutations were made using the QuikChange TM site-directed mutagenesis kit (Stratagene) and were confirmed by dideoxy sequencing.

Single-channel Recordings and Analysis

Patch-clamp recordings were done in the cell-attached configuration. Pipettes were pulled from borosilicate capillaries, coated with Sylgard (Dow Corning) and fire polished to a resistance of 10–15 MΩ. Dulbecco's phosphate buffered saline (in mM: 137 NaCl, 0.9 CaCl₂, 2.7 KCl, 1.5 KH₂PO₄, 0.5 MgCl₂, and 8.1 Na₂HPO₄, pH 7.3) was used in both the bath and pipette. The potential of the pipette was held at 70 mV which, in the cell-attached configuration, corresponds to a membrane potential of approximately −100 mV. Single-channel currents were recorded using an Axopatch 200B amplifier (Axon Instruments, Inc.). The data were digitized at a sampling rate of 100 kHz after low-pass filtering to 20 kHz (8-pole Bessel). All kinetic analyses were done using QuB software (www.qub.buffalo.edu). Idealization of the currents into noise-free closed and open intervals was done using the segmental k-means algorithm (SKM) at full bandwidth and using a simple CO model (both rate constants = 100 s⁻¹), or by a half-amplitude threshold-crossing algorithm after additional low-pass filtering to 2–5 kHz. A “cluster” was defined as a series of openings separated by closed intervals all of which were shorter than a critical duration, τ_crit. τ_crit was defined using a method that minimizes the total number of misclassified events (Jackson et al., 1983). Model-based analyses of the idealized intervals were done using a maximum interval likelihood method (Qin et al., 1996) with an imposed dead time of 25–90 μs.

Activation Kinetics

Rate and equilibrium constants were estimated either by fitting dose–response curves or from model-based kinetic analyses. One estimate of the diliganded channel opening rate constant (β₂) was obtained by fitting the effective opening rate (β′) versus concentration of agonist (A) data to the following empirical equation:

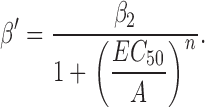(1)

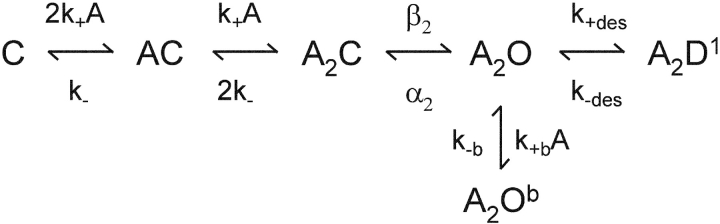
β′ is the inverse of the slowest component of the closed interval dwell time that scales with agonist concentration. This value asymptotically approaches the diliganded opening rate constant at high agonist concentration. P_open was defined as the fraction of time the channel is open within a cluster. The P_open versus agonist concentration profile was fitted by Eq. 2, which was derived from Scheme I :

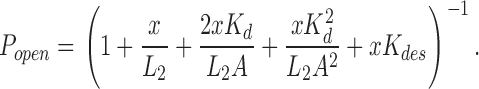(2)

SCHEME I.

In this and all other analyses we assumed that the two transmitter binding sites are equivalent and independent with respect to agonist affinity (Salamone et al., 1999). K_d (k_-/k₊) is the agonist dissociation equilibrium constant for each binding site in closed AChRs, L₂ (β₂/α₂) is the diliganded gating equilibrium constant, x = (1 + A/K_b)⁻¹ where K_b (k_−b/k_+b) is the dissociation equilibrium constant for channel block (2 mM for ACh and 20 mM for choline at −100 mV), and K_des (k_+des/k_−des) is the equilibrium constant for short-lived desensitization (0.05 for ACh and ignored for choline) (Elenes and Auerbach, 2002). The only free parameters in the fit of the P_open dose–response curves were K_d and L₂.

Scheme I was also used to estimate both the binding and gating rate constants.

The estimated rate constants were k₊ and k₋ (the association and dissociation rate constants for a single TBS) and β₂ and α₂ (the channel-opening and -closing rate constants for diliganded AChRs). Single-channel dwell times, obtained at several concentrations of agonist, were fitted jointly, i.e., one set of rate constants for all concentrations with k₊ scaled linearly by the agonist concentration. In some cases, the diliganded opening rate constant (β₂) was constrained to be the value obtained from Eq. 1.

It is difficult to estimate activation rate constants for wt AChRs activated by ACh because the β₂ is large and the lifetime of A₂C is near the limit of the instrumentation bandwidth (∼10 μs). Therefore, in order to study the mutants which had β₂-values that are even larger than the wt, we used the weak agonist choline for which (in wt AChRs) the channel-opening rate constant is 500 times slower than for ACh (Zhou et al., 1999; Grosman and Auerbach, 2000a). For some mutants, only the opening and closing rate constants (β₂ and α₂) were measured using 20 and 0.4 mM choline (to avoid channel block by the agonist), respectively. To correct for choline dissociation from open AChRs, a values of 200 s⁻¹ was subtracted from the α₂ estimate (Cymes et al., 2002).

For constructs in which β₂ was slower than the wt, the activation rate constants were estimated from a joint fit of single-channel interval dwell times obtained at several different ACh concentrations.

Desensitization

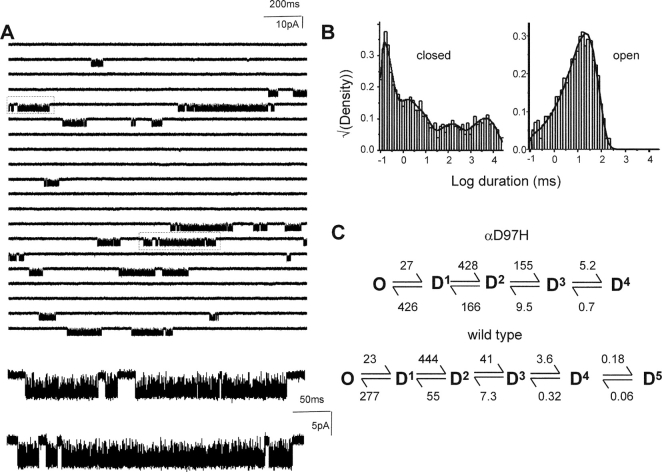
Single-channel currents were recorded in the presence of 100 μM ACh. To incorporate all silent intervals, before idealization (by a half-amplitude threshold criterion) extraneous noise was removed (by eye) and replaced with the baseline (Elenes and Auerbach, 2002). Interval durations were fitted by a kinetic model having one conducting and five coupled nonconducting states, using an imposed dead time of 100 μs. One of the nonconducting states was proximal to the open state (to reflect channel activation; not shown in Fig. 6), whereas the remaining four were distal to the open state (Elenes and Auerbach, 2002).

Figure 6.

αD97H does not affect desensitization. (A) Low time-resolution view of currents elicited by 100 μM ACh. Below, higher time-resolution view of boxed clusters. (B) Dwell time histograms that pertain to all intervals in the record. The fastest closed-interval component reflects activation and the remaining four components reflect desensitization. (C) The desensitization rate constants were similar to those estimated for wt AChRs (Elenes and Auerbach, 2002; see Table V).

Agonist Dissociation from the Open State

The principles underlying the method of estimating the rate constant for agonist dissociation from open AChRs have been described previously (Grosman and Auerbach, 2001). Briefly, when the channel-opening rate constant is large, an apparent open interval is in fact a “burst” of individual openings (Colquhoun and Hawkes, 1977). The burst lifetime, τ_b, represents the joint lifetime of diliganded-closed and -open states, {A₂C + A₂O}:

β₂ and α₂ are the diliganded opening and closing rate constants, and σ_C and σ_O are the sum of all exit rate constants that terminate a burst from the diliganded-closed and open-states, respectively. The two processes that contribute to σ_C and σ_O are desensitization and agonist dissociation. Desensitization from A₂C is slow (Auerbach and Akk, 1998), so we can substitute the diliganded AChR agonist dissociation rate constant, k₋₂ (with equal binding sites, as in Scheme I, k₋₂ = 2k₋) in place of σ_C. However, desensitization and agonist dissociation from A₂O are of similar magnitude and σ_O must be taken as the sum of these two processes. When the lifetime of A₂C is brief (i.e., when the sum k₋₂ + β₂ is large), the burst lifetime (Scheme II) is:

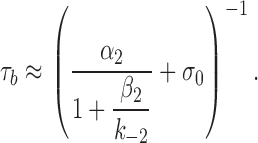(3)

SCHEME II.

In wild-type AChRs, where α₂ ≈ 2,000 s⁻¹ and β₂/k₋₂ ≈ 1, bursts terminate mainly by agonist dissociation from A₂C. Under this condition, [α₂/(1 + β₂/k₋₂)] >> σ_O and burst termination from the open state can be ignored. Accordingly, the burst lifetime can be described by Eq. 4 (Colquhoun and Hawkes, 1977).

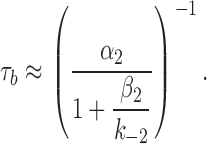(4)

To estimate the rate constant for agonist dissociation from open AChRs, we first measured τ_b for constructs having various side chains at position α97 plus a distant, background mutation in the δ-subunit (in the M2 segment, at position 265 or 268), which does not influence agonist binding (Grosman and Auerbach, 2001). The purpose of these mutations is to slow closing and speed opening (to known extents), so that the term [α₂/(1 + β₂/k₋₂)] approaches zero. At this limit, τ_b ≈ σ_O ^-1. That is, when the channel opening rate is very large or when the channel closing rate is very slow (or both), the inverse of the burst lifetime is an estimate of the sum of the rate constants for ACh dissociation from the open state plus desensitization.

Single-channel currents were elicited by a low concentration (1 μM) of ACh. Usually, the burst lifetimes were described by three exponential components that probably reflect un-, mono-, and diliganded AChRs. The time constant of the slowest (diliganded) component was taken as τ_b. The asymptotic limit of τ_b (and hence, σ_O ⁻¹) was estimated for the AChR mutant series. For each construct, the values of β₂ and α₂ with ACh as the agonist were calculated from the corresponding values measured with choline as the agonist (Table II; see also Grosman and Auerbach, 2000a; Cymes et al., 2002) and were used as fixed parameters in Eq. 3. One important assumption was that the only difference between these two agonists is that AChRs activated by choline open 500-times more slowly than AChRs activated by ACh (Grosman et al., 2000b). Given this a priori knowledge of β₂ and α₂, a fit of the experimental τ_b-values by Eq. 3 yielded estimates of the two remaining free parameters, k₋₂ and σ_O. Because σ_o is a sum, the rate constant for dissociation from the open-state dissociation was then estimated by subtracting the rate constant for desensitization from the open state, which was obtained in another set of experiments using model-based kinetic analyses (see above).

Unliganded Gating Kinetics

The spontaneous activity of mutants was studied in cell-attached patches. To prevent contamination by agonist a separate pipette assembly (holder, Ag/AgCl electrode and filling needle) that had never been exposed to agonists was used. After replacement of noisy sections, currents were idealized as described above. Because the number of channels in each patch was not known, a quantitative measure of the unliganded gating equilibrium constant was not possible. The inverse of the mean closed duration (τ_c) was defined as the opening frequency of the patch, which is a function of both the single-channel opening rate constant and the number of channels in the patch. The open probability per patch was calculated as τ_o/(τ_o + τ_c), where τ_o is the open-interval time constant.

Kinetics of Hybrid Mutant Receptors

Single-channel currents were recorded from cells transfected with both wild-type and mutant α-subunits (1:1 ratio). After idealization (half-amplitude method), clusters of openings were defined using τ_crit = 50 ms. Clusters with overlapping channel activity or with fewer than 10 open intervals were discarded. A stability plot of cluster P_open revealed four distinct populations, which were defined within QuB using the SKM algorithm. Clusters that were within ±1.5 SD of their respective population means were selected for idealization (using SKM) and rate constant estimation.

αD97P and αD97G

The starting model was a cycle having two closed and two open states (up to eight free parameters). Constraints on the rate constants were added progressively, and these were incorporated into the model only if their inclusion increased the log likelihood of the fit by >10 units.

RESULTS

A Mutational Scan of L5 Residues

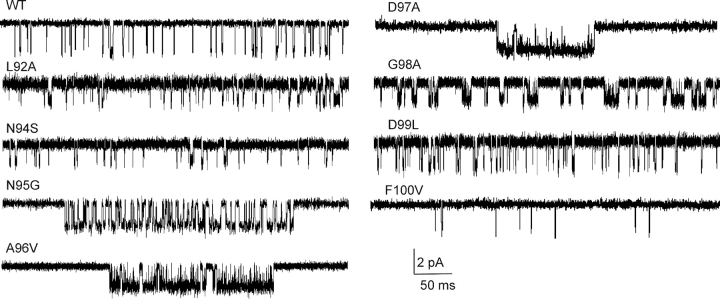
We measured the diliganded gating equilibrium constant, L₂, for AChR constructs having mutations to an L5 residue in both α-subunits (positions 92–100; Fig. 2) . Starting with the NH₂ terminus of L5, at position L92 an alanine substitution had no measurable effect on gating. Mutations of Y93 have been shown previously to cause up to ∼10-fold reductions in L₂ (Auerbach et al., 1996; Akk et al., 1999; Akk, 2001). N94S had wild-type gating behavior. At position N95, serine and glycine mutations each caused a fairly small (∼7.5-fold) increase in L₂. At position A96, substitution of a valine caused a 129-fold increase in L₂, but there was no effect of a glycine substitution. The mutation αD97A caused a large, 168-fold increase in L₂. At position αG98, substitution of an alanine caused 132-fold increase in L₂, but substitution of a valine had no measurable effect. The mutation αD99L had no effect on channel gating. Although this survey is by no means exhaustive, the overall pattern suggests that the three central residues of L5 in the α-subunit, positions 96–98 (ADG), can be significant determinants of the gating equilibrium constant. We therefore concentrated our efforts on the central residue αD97, which aligns in sequence with AChBP I92, located at the apex of L5 (Fig. 1). The AChR α-subunit contains a single amino acid insertion in L5 after Y93 (AChBP Y89), so there is some uncertainty in the actual position of αD97 in AChRs.

Figure 2.

Mutational scan of α-subunit L5 residues. Currents were recorded at 20 mM choline (open is down; filtered at 2 kHz for display). Several mutations in this loop increase the cluster open probability because they increase the diliganded equilibrium gating constant L₂. Of the 27 α-subunit L5 mutants that were studied, αD97A caused the largest increase in L₂ (168-fold). L5 mutations in the non-α-subunits had no effect on gating.

αD97 Mutant Series

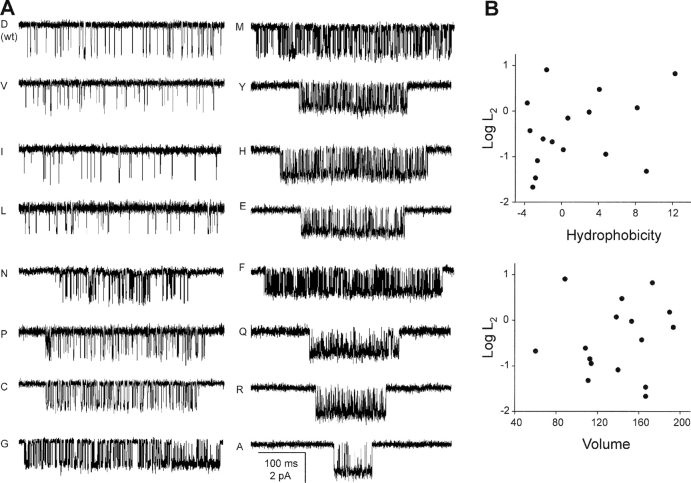
Fig. 3 A shows example currents from fully liganded AChRs having different side chains at position αD97. Of the 17 substitutions that we examined (Table II) , 12 increased L₂ and 3 had little or no effect. The remaining two mutants, S and T, resulted in complete loss of activity (no openings apparent in >30 patches at various agonist concentrations). Presumably these mutations prevented expression, gating, or both. Aside from these two side chains, which notably both contain an −OH group that can participate in hydrogen bonding, there was no correlation between the side chain hydrophobicity or volume and the effect on L₂ (Fig. 3 B).

Figure 3.

αD97 mutations increase diliganded gating. (A) Example clusters elicited by a saturating concentration (20 mM) of choline. Most mutations increase the cluster P_open, mainly by reducing the closed-interval durations. (B) There is no apparent correlation between side chain hydrophobicity or volume and the effect on the diliganded gating equilibrium constant, L₂ (Table II).

TABLE II.

Gating Parameters for α97 AChR Mutants Activated by Choline

α97	β2	α2	L2	L2-ratio (mut/wt)
	s−1	s−1
I	60	2,801	0.022	0.45
L	91	2,684	0.034	0.71
D (wt)	100	2,100	0.048	—
V	161	1,974	0.082	1.71
N	268	2,379	0.113	2.37
P1	322	2,276	0.141	2.97
G1	421	2,105	0.200	4.20
C	531	2,172	0.244	5.13
M	835	2,255	0.370	7.78
G2	570	942	0.605	2.37
P2	1,396	2,276	0.613	12.88
Y	1,396	1,992	0.701	14.72
H	1,840	1,938	0.949	19.94
E	2,967	2,076	1.429	24.78
F	2,748	1,831	1.501	31.52
Q	6,006	2,016	2.979	62.56
R	10,951	1,653	6.624	139.12
A	13,793	1,719	8.023	168.50

The diliganded channel opening (β₂) and closing (α₂) rate constants were estimated from single-channel currents elicited by 20 and 0.4 mM choline, respectively. The diliganded gating equilibrium constant was calculated as the ratio β₂/α₂. Proline and glycine substitutions have two distinct kinetic modes, denoted by subscripts. The values are means from ≥3 patches. A REFER analysis of these data is shown in Fig. 8. G₂ kinetics were measured only at 20 mM choline. Because of unresolved channel block, the α₂ value shown in the table is twice the apparent closing rate constant.

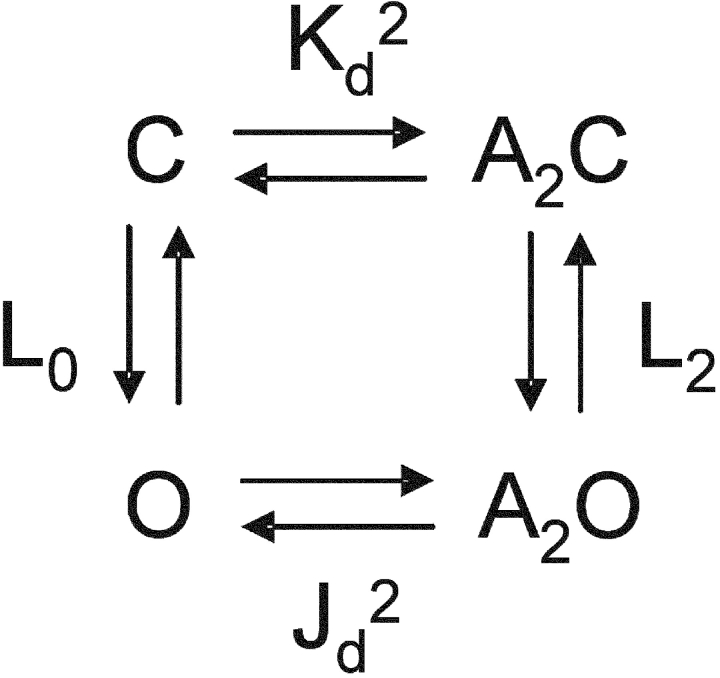
Like conformational changes in other allosteric proteins, AChR gating can be interpreted using the framework of a thermodynamic cycle (Karlin, 1967). Assuming that the two transmitter binding sites are independent and equivalent (Salamone et al., 1999),

For this cycle to satisfy detailed balance, the ratio of the diliganded/unliganded gating equilibrium constants (L₂/L₀) must equal the ratio of the closed/open dissociation equilibrium constants (K_d/J_d) at each of the two transmitter binding sites. Thus, the changes in L₂ that were apparent with mutations of position αD97 may reflect changes in any or all of three fundamental equilibrium constants, L₀, K_d, and/or J_d:

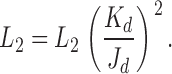(5)

At the neuromuscular synapse the peak response is approximately proportional to (1 + L₂ ⁻¹)⁻¹ and Eq. 3 approximately describes the decay time constant of the current. Because L₂ (= β₂/α₂) is proportional to L₀, the unliganded gating equilibrium constant is a key determinant of both the amplitude and the time course of the synaptic response.

Our first objective was to measure the fundamental binding and gating equilibrium constants, as well as the parameters for desensitization, in some of the αD97 mutants.

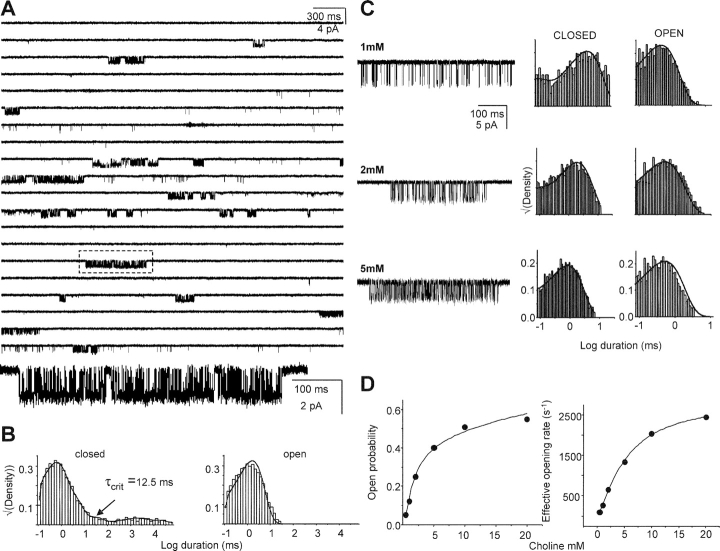
Activation Kinetics of αD97E and αD97H

We recorded single-channel currents using a range of choline concentrations for two mutant constructs, αD97E and αD97H (Fig. 4) . The equilibrium constants for activation obtained from fitting P_open dose–response profiles (Fig. 4 D) and from model-based, single-channel kinetic analyses (Table III) were self-consistent. For αD97E and αD97H, respectively, the equilibrium gating constants were 2.9 ± 0.7 and 1.1 ± 0.5 from dose–response analysis versus 1.3 ± 0.2 and 1.2 ± 0.1 from kinetic modeling. These mutant L₂ values are >20 times greater than the wt value, 0.05. For these two mutants, the equilibrium dissociation constants (mM) were 3.2 ± 0.6 and 2.1 ± 0.3 from dose–response analysis versus 2.1 ± 0.3 and 2.8 ± 0.2 from modeling. These mutant K_d values are similar to the wt value, ∼2 (Zhou et al., 1999). We conclude that substituting an E or an H in place of the wt D at position α97 substantially increases the diliganded gating equilibrium constant (mainly by increasing the channel opening rate constant), but does not significantly alter the dissociation equilibrium constant for choline to closed AChRs. We therefore hypothesize that increases in L₂ that were observed for the entire αD97 mutation series arise from changes in either or both of the equilibrium constants L₀ and J_d. Below, we present results indicating that mutation of residue F100 does not change the K_d for ACh.

Figure 4.

Kinetic analysis of αD97E. (A) Low time-resolution view of currents elicited by 20 mM choline. The openings are clustered (boxed cluster shown on an expanded time scale, below). The single-channel current amplitude is reduced approximately by half because of open-channel blockade by choline. (B) Interval duration histograms for the entire record. Clusters of openings were defined and selected for further kinetic analysis using the indicated value of τ_crit. (C) Example clusters and interval duration histograms elicited by different choline concentrations. The solid lines over the histograms are density functions calculated from the rate constants of the model, obtained from a joint fit of a single model to all concentrations, with the association rate constant scaled linearly by the concentration. (Table III). (D) Dose–response analysis. The solid lines are the fits by Eq. 1 and 2. From the P_open data, K_d = 3.2 mM and L₂ = 2.9. From the saturation of the effective opening rate data, β₂ = 2,875 s⁻¹ (wt values are K_d ≈ 2 mM, L₂ = 0.05, and β₂ = 100 s⁻¹).

TABLE III.

Kinetics of Binding and Gating in AChRs Activated by Choline

Construct	k+	k−	Kd	β2	α2	L2
	mM−1 s−1	s−1	mM	s−1	s−1
wt	—	—	2	100	2,100	0.047
αD97H	1,055 ± 40	2,993 ± 141	2.84 ± 0.24	3,189 ± 168	2,759 ± 149	1.15 ± 0.14
αD97E	2,839 ± 187	6,070 ± 467	2.14 ± 0.32	3,024 ± 131	2,293 ± 214	1.31 ± 0.21

The binding and gating rate constants (mean ± SD) were estimated by jointly fitting interval durations from different concentrations of choline (one patch each at 1, 2 and 5 mM) using Scheme I (see Fig. 4). K_d was calculated as the ratio k₋/k₊. The K_d value for choline in wt receptors is from (Zhou et al., 1999).

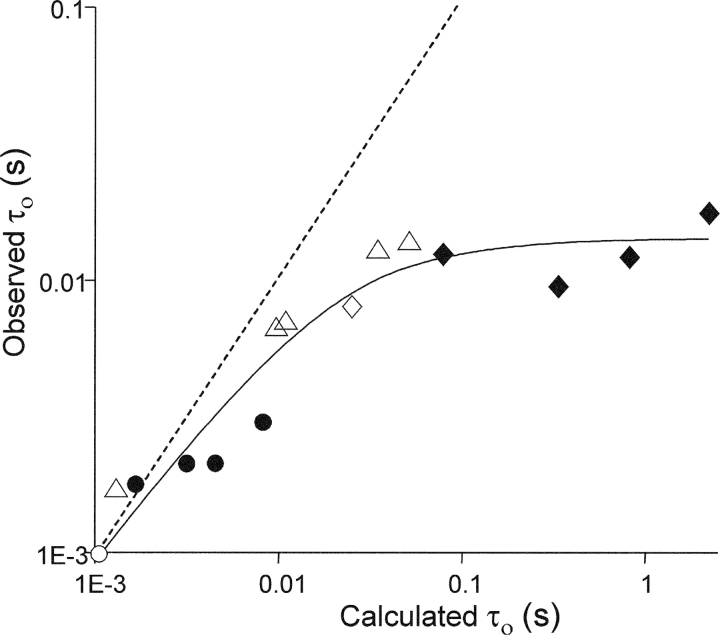
Dissociation and Desensitization from Open AChRs for αD97 Mutants

As described in the materials and methods, the first step in estimating the rate constant for agonist dissociation from open AChRs is to measure the lifetime of bursts of openings (τ_b) elicited by 1 μM ACh from AChRs having background mutations that decreased α₂ (the main effect) and increased β₂ to known extents (Table IV) . In addition, these constructs contained a mutation of residue αD97. As expected, the observed and calculated (Eq. 4) burst durations deviate from each other because the mutations increase the opening rate constant to such an extent that burst termination from the open state (by dissociation or desensitization), which is not incorporated into Eq. 4, becomes significant.

TABLE IV.

Agonist Dissociation from Diliganded-open AChRs

Construct	β2 ACh	α2 ACh	τb (observed)	τb (calculated)
	s−1	s−1	ms	ms
Wild-type	50,000	2,000	0.99	1.05
δS12′G	60,700	1,807	1.67	1.30
δS12′C	108,950	346	6.42	9.85
δS12′T	129,770	351	6.87	11.03
δS12′V	149,030	125	12.62	34.37
δS12′N	192,410	102	13.77	51.52
δL9′T	50,000	84	8.00	25.07
αD97N	134,000	2,379	1.79	1.67
αD97C	265,500	2,172	2.12	3.16
αD97M	417,500	2,255	2.13	4.54
αD97Y	698,000	1,992	3.01	8.25
δL9′T-αD97C	265,500	87	12.31	79.43
δL9′T-αD97E	1,226,000	82	9.38	341.53
δL9′T-αD97Q	3,000,000	81	11.97	835.17
δL9′T-αD97A	6,895,000	69	17.59	2,230.96

The channel-opening (β₂) and -closing (α₂) rate constants with ACh as the agonist were calculated from the corresponding measured values for choline (Table II) assuming Φ = 1 for the transmitter binding sites. The wild-type AChR β₂ and α₂ values are from Salamone et al. (1999). τ_b (observed) is the burst duration measured at 1 μM ACh. τ_b (calculated) was generated using Eq. 4, the β₂ and α₂ values in the table, and k₋₂ = 45,216 s⁻¹ (see Fig. 5 and materials and methods).

Fig. 5 shows that the inverse of the asymptotic limit of τ_b (14.3 ms), which is equal to the sum of the rate constants for agonist dissociation and desensitization from open AChRs, is the same for AChRs with and without substitutions at αD97, 70 ± 6 s⁻¹. That is, we were unable to detect a difference in the sum of these rate constants in AChRs having wt or mutated α97 side chains. From the same dataset we estimate k₋₂ (2k₋ in Scheme I) = 45,200 ± 15,600 s⁻¹ for both wt and mutant α97 AChRs. This value is in excellent agreement with k₋₂ values estimated by completely different methods (43,800 to 57,400 s⁻¹) (cited in Grosman and Auerbach, 2001), which further supports our hypothesis that agonist binding to closed AChRs is not altered significantly by mutation of αD97.

Figure 5.

αD97 mutations do not affect agonist dissociation from diliganded-open AChRs. Currents were elicited by 1 μM ACh from AChRs having wt/mutations (open/filled) at α97. Different background mutations were used (○, wt; ⋄, δL265T; Δ, δS268G, C, T, V or N) that had known effects on the gating rate constants (Table IV). The α97 side chains were D (δS268 series and δL265T); N, C, M, Y (wt background); and C, E, Q, A (δL265T background). The x-axis is the burst lifetime (τ_b) calculated assuming that there is no exit path from the diliganded-open state (Eq. 4), and the y-axis is the experimentally measured value of τ_b. The points deviate from the dashed line (slope = 1) because of agonist-dissociation and desensitization from diliganded-open AChRs. The solid line is a fit by Eq. 3, with the parameters k_-2 = 45,216 ± 15,551 s⁻¹ and σ_O = 70.3 ± 3.5 s⁻¹.

To separately estimate the open-state dissociation and desensitization rate constants, we measured directly the desensitization entry and recovery rate constants for the αD97H and αD97E mutants. In these experiments, the fastest closed-interval component reflects activation and the remaining four components reflect desensitization. In these mutants, shut intervals were fitted by four desensitized components, whereas in wild-type AChRs five desensitized components are required (Elenes and Auerbach, 2002). We suspect that this difference is attributable to the fact that the total recording time using the αD97 mutants (∼20 min) was significantly shorter than those using the wild-type (up to 2 h) and therefore few events from the slowest component were present. All of the desensitization rate constants were similar in the mutant and wt AChRs (Fig. 6 and Table V) . Specifically, the rate constant for desensitization from open AChRs was 39 s⁻¹ in the mutant, and 33 s⁻¹ in the wt.

TABLE V.

Desensitization Kinetics of Wild-type and αD97 Mutant AChR

α97	k01	k10	k12	k21	k23	k32	k34	k43
wt	33 ± 12	326 ± 133	293 ± 80	48 ± 6	39 ± 1	6.8 ± 0.6	3.3 ± 0.3	0.33 ± 0.01
E	37 ± 1	286 ± 26	146 ± 18	24 ± 10	17 ± 7	1.27 ± 0.4	0.92 ± 0.4	0.25 ± 0.12
H	41 ± 7	311 ± 86	257 ± 92	80 ± 42	77 ± 39	5.7 ± 1.8	3.29 ± 1	0.53 ± 0.15

Closed and open intervals in the record were fitted using the linear model shown in Fig. 6. Rate constants are s⁻¹. The wt values are from Elenes and Auerbach (2002). The values are means ± SEM for three patches activated by 100 μM ACh.

The rate constant for ACh dissociation from open αD97A AChRs was calculated as the difference between σ_O (70 ± 3.5 s⁻¹) and this open-state desensitization rate constant. The resulting value, 31 s⁻¹, is similar to that for wt AChRs, 24 s⁻¹ (Grosman and Auerbach, 2001). These results suggest that αD97 substitutions do not substantially change the rate constants for either ACh dissociation or desensitization from diliganded-open AChRs, or for ACh dissociation from diliganded-closed AChRs.

By the process of elimination (Eq. 5), we hypothesize that αD97 mutations have a single functional consequence, to change the unliganded gating equilibrium constant L₀. That is, our studies suggest that the changes in L₂ that are apparent with the αD97 mutant series mainly reflect parallel changes in L₀. One important caveat is that we are unable to measure the association rate constant to open AChRs, thus our results showing an unchanging open-channel dissociation rate constant cannot be unequivocally translated into an unchanging equilibrium constant J_d.

Unliganded Gating

To further explore this hypothesis, we studied the qualitative effects of αD97 mutations on spontaneous gating, i.e., in the absence of added agonists (Fig. 7 and Table VI) . Wild-type AChRs produce very little activity in the absence of agonist (Jackson, 1984; Grosman and Auerbach, 2000b) and our hypothesis predicts that relative levels of activity generated by the AChR mutants should roughly mirror the relative increases in L₂ (Table II; Eq. 5). In cell-attached patches the number of channels generating the spontaneous activity is not known, so we were able to make only a qualitative comparison between these two sets of experimental results.

Figure 7.

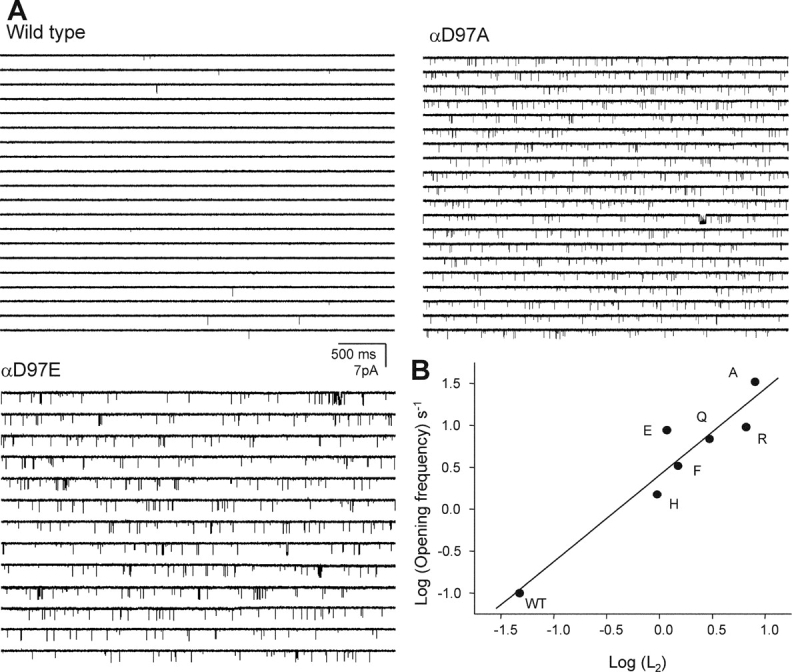
Unliganded gating of αD97 mutants. (A) Spontaneous openings in wild-type, αD97E, and αD97A mutant AChRs. (B) The log of the spontaneous opening frequency (Table VI) is correlated with the log of the diliganded gating equilibrium constant (L₂, from Table II) (R = 0.95).

TABLE VI.

Unliganded Gating Parameters of Wild-type and αD97 Mutants

α97 construct	Opening frequency	Open probability (×104)	τo	n
	s−1		ms
wt	0.10 ± 0.01	0.07 ± 0.01	0.07 ± 0.02	3
H	1.5 ± 0.54	1.02 ± 0.23	0.08 ± 0.01	3
E	8.81 ± 2.66	12.5 ± 4.87	0.14 ± 0.03	4
F	3.29 ± 0.82	1.97 ± 0.30	0.06 ± 0.01	4
Q	6.90 ± 1.61	5.61 ± 2.92	0.08 ± 0.01	4
R	9.55 ± 1.35	10.3 ± 1.82	0.10 ± 0.01	3
A	33.2 ± 11.4	34.6 ± 12.9	0.10 ± 0.01	6

The opening frequency (per patch; mean ± SEM) was estimated as the inverse of mean duration of closed intervals (τ_c). The open probability (per patch) was calculated as the τ_o/(τ_o + τ_c), where τ_o is the mean duration of open intervals; n is the number of patches. The effect of the mutation on the opening frequency correlates with its effect on L₂ (Fig. 7).

The opening frequency, patch open probability, and the mean open duration are shown for the agonist-free experiments in Table VI. As expected, all of the tested mutants of αD97 increased the opening frequency and the open probability within a patch. Fig. 7 B shows that for six αD97 mutants there was a correlation between the spontaneous gating parameters and the magnitude of the L₂ change, which is consistent with the hypothesis that the primary effect of αD97 mutations is to change L₀.

The Rate-equilibrium Free Energy Relationship of αD97

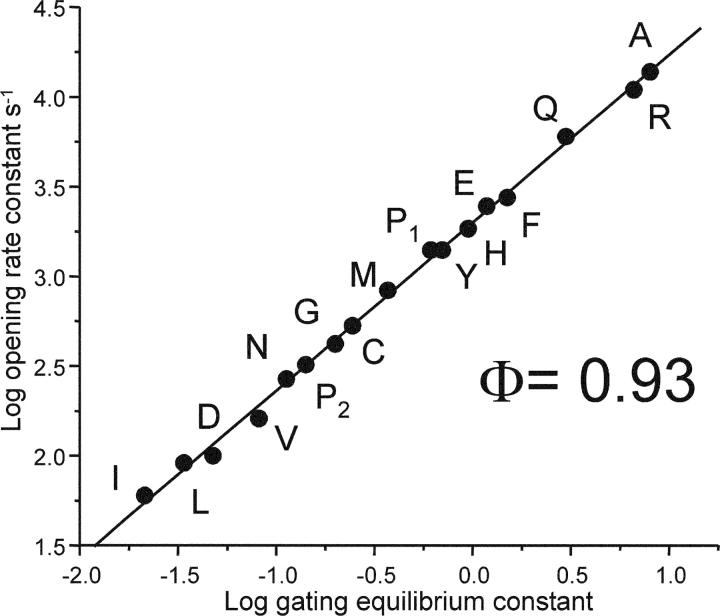
Insofar as a change in the free energy of a reaction following a perturbation reflects a change in the local structure, the observation that αD97 mutations cause large changes in L₂ suggests that the environment of this residue is significantly different in the closed versus the open conformation. The opening rate constants and the diliganded gating equilibrium constants were plotted for the αD97 mutant series as a rate-equilibrium free energy relationship (REFER; Fig. 8) . The slope of the linear fit, Φ, reports the reaction progress of the perturbed region relative to the global transition state, and has values ranging from 0 (closed-like) to 1 (open-like). The Φ-value of αD97 was 0.935 ± 0.012. This value indicates that the side chain of α97 is almost completely open-like at the gating transition state, i.e., that it moves “early” in the gating reaction. The transmitter binding sites, which can be perturbed simply by changing the agonist, also have a Φ-value of 0.93 (Grosman et al., 2000b). Hence, during the gating reaction the movement of αD97 occurs essentially in synchrony with the low-to-high affinity change at the TBS.

Figure 8.

REFER plot for the αD97 mutant series. The Φ-value (the slope) is 0.936 ± 0.012, which is the same as that for the transmitter binding site (Φ = 0.931 ± 0.035). The Φ-value indicates that α97 moves early (relative to the transition state) during channel-opening, in synchrony with the low-to-high affinity change at the transmitter binding site. The subscripts for proline refer to its two kinetic modes.

Hybrid αD97 Mutants

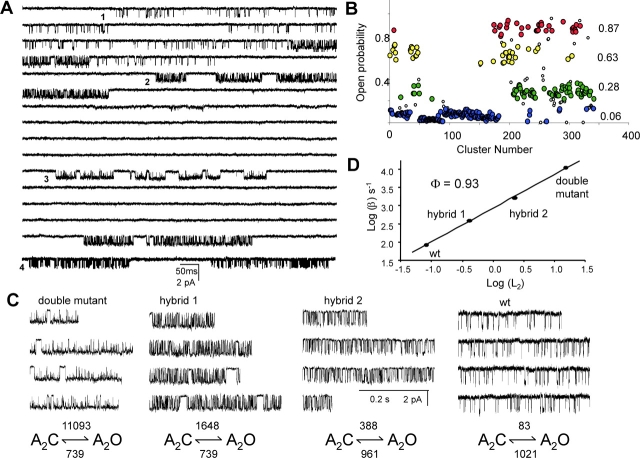
Each AChR pentamer has two α-subunits, and we sought to measure the contributions of each of the αD97 mutations in order to test for possible differences in the role of L5 at the α–ɛ and α–δ subunit interfaces. From previous experiments (Akk et al., 1996), we expected that HEK cells cotransfected with equal amounts of wild-type and αD97A mutant cDNAs (along with wild-type β-, δ-, and ɛ-subunits) would give rise to four different AChR populations that differed in their α-subunit composition: wt-wt, αD97A-wt, wt-αD97A, and αD97A-αD97A. Currents elicited by a saturating concentration of choline indeed exhibited four different patterns of activity based on cluster open probability (P_open; Fig. 9) . The clusters with highest and lowest P_open corresponded to those of pure mutant and the pure wild type AChRs. We presume that the two populations of clusters with intermediate P_open values represent the two hybrid classes.

Figure 9.

Hybrid αD97A receptors. (A) Single-channel currents elicited by 20 mM choline showing heterogeneous clusters in a cell transfected with both wild-type and αD97A mutant α subunits. Four different types of clusters are apparent (numbered 1–4). The data are continuous except for the bottom trace (which is from the same patch). (B) A plot of cluster open probabilities (P_open) for all the clusters in the patch (τ_crit = 50 ms). Four distinct populations are apparent. The highest P_open population corresponds to the double αD97A mutant (red) and the lowest to the wild-type (blue). Clusters from hybrid AChRs (one wild-type α-subunit and one D97A α-subunit) are yellow and green. The open symbols represent clusters that were >1.5 SD from their population means and were not analyzed further. (C) High resolution views of clusters. The diliganded opening and closing rate constants for each type of cluster are shown below (the apparent closing rate constants are reduced ∼2-fold because of channel block by choline). ΔΔG₀ values (kcal mol⁻¹) for channel gating, computed as 0.59 ln(L₂ ^wt/L₂ ^mut), are: 3.09 (double mutant), 1.96 (hybrid 1), 0.95 (hybrid 2). The ΔΔG₀ values for the two hybrids are different, which indicates that the residue contributes unequally toward gating at the α–δ and α–ɛ subunit interfaces. The sum of ΔΔG₀ values of the two hybrids is close to that of the double mutant, which indicates that the two sites contribute independently to the overall gating reaction. (D) REFER analyses for each cluster population. The two α97 residues move synchronously in the gating reaction.

The gating kinetics of each population was examined in isolation. The L₂ values of the two hybrids differed by ∼5.5 fold, which corresponds to an ∼2-fold difference in the change in free energy of the gating reaction (ΔΔG₀). However, the sum of the ΔΔG₀ values for the two hybrids was equal to that caused by the double αD97A mutant. That is, the αD97A mutations in the two α-subunits have unequal consequences with respect to the gating equilibrium constant, but their contributions are independent. From our experiments we cannot identify the α subunit (α–δ or α–ɛ) that corresponds to each of the hybrid populations.

We also explored whether we could detect any asynchrony in the movement of the two (nonindentical) αD97 residues during the gating reaction. A REFER analysis of the four sub-populations of AChRs is shown in Fig. 9 D. All populations fall on the same line, which indicates that they have the same Φ-value (0.93). We conclude that during gating, L5 at the α–ɛ and α–δ interfaces move in synchrony.

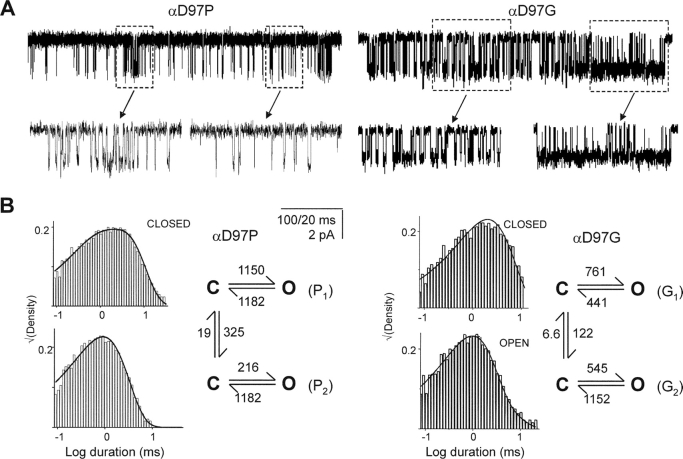
αD97P and αD97G

Two of the α97 mutants did not exhibit simple closed-open kinetics within clusters. With proline at this position, the single-channel kinetics required two, rather than one, closed state, and with glycine, two open and two closed states were needed. Inspection of the current traces for both of these mutants led us to suspect that within a cluster, an AChR was switching between two kinetic modes that had distinct gating rate constants (Fig. 10) .

Figure 10.

αD97P and αD97G display modal gating kinetics. (A) Example clusters elicted by 20 mM choline. High and low periods of activity (boxed areas) are apparent and are shown at higher resolution, below. (B) Closed and open interval dwell time histograms and superimposed curves calculated from the corresponding models. For αD97P, the closing rate constants were constrained to be equal. For both mutants, the closing rate constants are ∼2-fold slower than the low concentration measurements (Table II) because of unresolved, fast channel block by choline.

The αD97P currents were best described by gating models with two opening, but only one closing, rate constant. The opening rate constants (and the L₂ values) for the two modes differed by ∼5.3-fold. We could not distinguish whether these two “modes” were coupled through the open or the closed states (or both). The lower P_open mode predominated (∼90%), with a transition from the slow- to the fast-opening mode occurring, on average, only every ∼50 ms. The αD97G currents were described by gating models with two opening and two closing rate constants. The L₂ values for the two modes differed by ∼3.6-fold, mainly due to a difference in closing rate constants. For this mutant, the two “modes” were mostly coupled through the closed states. The lower P_open mode predominated (92%), with transitions to the higher P_open mode occurring, on average, only every 200 ms.

We speculate that these “modes” arise from spontaneous fluctuations in the AChR structure (Popescu and Auerbach, 2003). Although the location and extent of this perturbation(s) is not known, the Φ-value of 1 for αD97P modal behavior suggests that it may occur at a site(s) that moves early in the gating reaction, perhaps within L5 itself. The smaller Φ-value (0.22) for the αD97G fluctuation may reflect a later-moving and/or a more distant site, but Φ-values estimated from single perturbations can be misleading because the effect of a perturbation on the transition state is not always a linear combination of its effects on the ground states (a “catalytic” effect; for an example see (Cymes et al., 2002). Without additional experiments, the most likely source of the primary fluctuation(s) that gives rise to modal behavior in these mutants, αD97G and αD97A, is a local change in the conformation of the backbone.

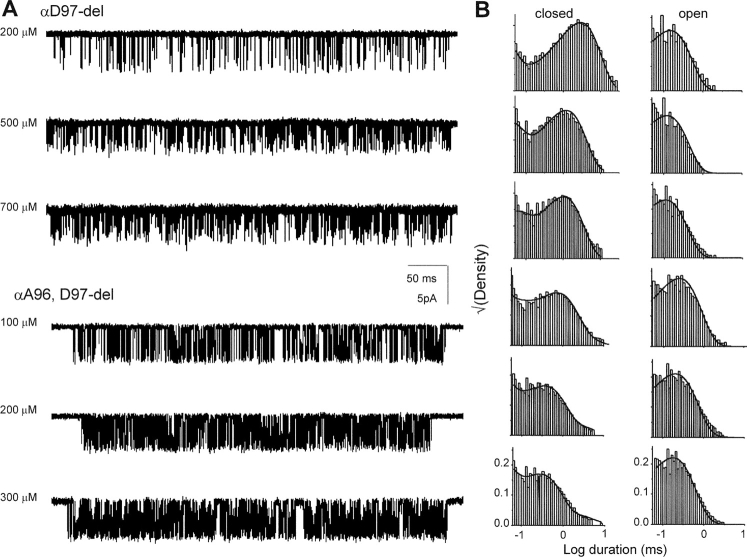
L5 Deletions

In addition to point substitutions at αD97, we investigated the effects of deleting this residue, both alone and in combination with deletions of its flanking amino acids A96 and G98 (Fig. 11) . These perturbations are different in character from simple substitutions because the backbone, in addition to the side chain, is altered.

Figure 11.

L5 deletion mutants. (A) Single channel currents elicited by various concentrations of ACh. (B) Interval histograms. The solid lines are from the global fit using Scheme I (Table VI).

Unlike the side chain substitutions, deletion of αD97 reduced L₂ 40-fold, mainly because of a reduction in the opening rate constant (Table VII) . Because of the smaller opening rate constant, we were able to use single-channel, model-based kinetics analyses to estimate the association and dissociation rate constants using ACh as the agonist. Both of these rate constants were modestly reduced in αD97-del, but the overall effect on the equilibrium dissociation constant was small (<2.5-fold). Thus, the major consequence of this deletion was to reduce L₂, presumably by reducing L₀.

TABLE VII.

Rate and Equilibrium Constants of Loop 5 Deletion Mutants Activated by ACh

Construct	k+	k−1	Kd	β2	α2	L2
	μM−1 s−1	s−1		s−1	s−1
wt	167 ± 2	24,745 ± 257	148	50,000	2,100	23.8
Del 97	42 ± 4	15,099 ± 1,185	359	3,928 ± 132	6,704 ± 744	0.59
Del 97-98	63 ± 2	5,008 ± 135	79	7,715 ± 174	4,045 ± 131	1.91

The binding and gating rate constants were estimated by jointly fitting interval durations elicited by different concentrations of ACh, using Scheme I (see Fig. 11). K_d was calculated as the ratio k₋/k₊. Wild type values are from (Salamone et al., 1999).

The double deletion of αD97 and αG98 also reduced L₂, but only by 12.5-fold. As with the single deletion, the ACh association and dissociation rate constants were reduced in the double-deletion mutant, but the change in the equilibrium dissociation constant was small (<2-fold; Table VII). Deletion of all three residues (96, 97, and 98) resulted in the complete loss of expression of functional channels.

The Φ-values of single- and double-deletion perturbations were 0.68 and 0.74, respectively, which are significantly lower than that of the αD97 side chain (Fig. 7). One possible interpretation of these Φ-values is that in the deletion mutants, L5 moves later in gating (relative to the transition state) than it does in the wt. However, these are only two-point REFER analyses (one point for the wt and one for the mutant) and our confidence in the Φ-estimates is low. Without additional perturbations we cannot exclude the possibility that a deletion has an independent, destabilizing (“anticatalytic”) effect on the transition state that results in a lower apparent Φ-value.

Other Mutations

The point mutation αF100V, unlike the others we examined, reduced L₂ and could therefore be studied using ACh as the agonist. Fig. 12 shows clusters and the corresponding intracluster dwell times for this mutant. The opening rate constant estimated from the saturation of the effective opening rate dose–response curve is ∼6 times slower than the wild-type. P_open dose–response curve analyses indicate that this mutation reduced L₂ ∼5-fold, but left K_d essentially unchanged (189 vs. 150 μM; mutant vs. wt). From model-based kinetic analyses, the one-site ACh association and dissociation rate constants were estimated to be 7.8 × 10⁷ M⁻¹s⁻¹ and 16,845 s⁻¹, respectively (corresponding to a K_D of 215 μM, similar to the value obtained from the dose–response analysis), which are each within a factor of ∼2 of the wild-type values (Akk and Auerbach, 1996; Salamone et al., 1999). With regard to gating, the mutation had no effect on the closing rate constant. Thus we conclude that αF100, like all other L5 residues (except αY93), serves mainly to set the unliganded gating equilibrium constant and has little influence on agonist binding.

Figure 12.

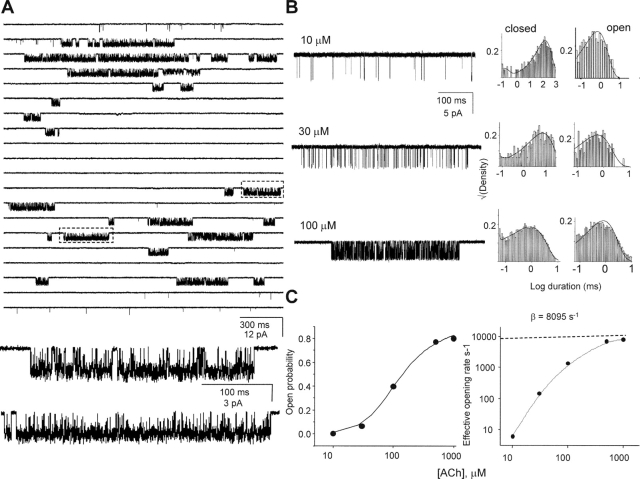
Kinetic analysis of αF100V. (A) A continuous single-channel current trace of αF100V activated by 1 mM ACh. Boxed areas are shown below at higher resolution. (B) Current traces elicited at different concentrations of ACh and the corresponding interval duration histograms. The solid lines are from the global fit using Scheme I (k₊ = 7.8 × 10⁷ M⁻¹s⁻¹ and k₋ = 16,845 s⁻¹, corresponding to a K_D of 215 μM). (C) Macroscopic dose–response analyses. Left, cluster P_open vs. [ACh]. Solid line is fit by Eq. 2 (L₂ = 5.27 ± 0.9 and K_D 189 ± 31 μM). Right, effective opening rate vs. [ACh]. The high-concentration limit is an estimate of β₂ (8,095 s⁻¹).

Finally, a small number of mutations were studied in L5 of the non-α-subunits (Table VIII) . None of these had any measurable effect on the gating equilibrium constant.

TABLE VIII.

Gating Rate Constants for Mutations in Loop A of Non-α-subunits Activated by Choline

Construct	β2	α2*
	s−1	s−1
wt	100	1,100
β-subunit
D97A	72	1,320
D97V	85	762
G98A	49	861
G98V	80	471
δ-subunit
N98V	62	437
N98A	36	1,335
D99A	146	630
D99V	117	561
ɛ-subunit
D97A	64	645
D97V	103	933

Channel opening (β₂) and closing (α₂*) rate constants were measured at a saturating concentration of choline (20 mM). Because channel block prolongs the apparent open-interval lifetimes, α₂* values are ∼2-fold smaller than the α₂ values measured at low choline concentrations (see Table II).

DISCUSSION

Loop 5 of the α-subunit emerges as an early and important link in the chain of events that constitutes AChR gating. Mutations of this region, which is adjacent to the transmitter binding site, have large effects on channel gating but little or no effect on agonist binding or desensitization. Our results suggest that the most significant role of L5 in the α-subunit is to regulate the unliganded gating equilibrium constant, L₀.

We arrived at this conclusion mainly by eliminating the possibility that the αD97 mutations increased the diliganded gaiting equilibrium constant L₂ by increasing the ratio of the closed/open dissociation equilibrium constants (Eq. 5). In two constructs using choline as the agonist (97E, 97H), and in three constructs using ACh as the agonist (97-del, 97/98-del, and 100 V), K_d was <2.5-fold different from the wt. Moreover, the dissociation rate constant from closed AChRs activated by ACh for seven mutations of αD97 (A, R, E, Q, M, C, and Y) was indistinguishable from that of the wt (Fig. 5). This is strong evidence that the changes in L₂ that were apparent with perturbations of positions 97, 98, and 100 did not arise from parallel changes in the closed-channel affinity. So far, the only L5 residue that has been shown to influence closed-channel binding is αY93. In AChBP the hydroxyl-group of the homologous residue, Y89, is <6 Å from W143, which forms the floor of the TBS (Fig. 1).

The only other affinity-based mechanism that might account for the observed increases L₂ is, then, a parallel decrease in the open-channel dissociation equilibrium constant, J_d. In the specific case of αD97A, Eq. 5 predicts that the 168-fold increase in L₂ could be accounted for by a 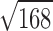= 13-fold reduction in J_d at each of the two TBS, i.e., from ∼10 nM in the wt (Grosman and Auerbach, 2001) to <1 nM. We were unable to measure the equilibrium constant J_d directly, but instead were limited to measuring the open-channel dissociation rate constant, which turned out to be indistinguishable between the αD97 mutants and the wt (31 s⁻¹ vs. 24 s⁻¹, respectively).

If a reduction in open-channel dissociation was the sole consequence of the αD97 mutations, then we would have obtained a very different result. Accordingly, we can calculate the expected τ_b-value with Eq. 3 using the values for the gating rate constants (Table II), an open channel dissociation rate constant = 31 s⁻¹/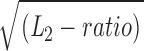, and a desensitization rate constant of 39 s⁻¹. The four αD97-δL9'T double mutants (Table IV) would be expected to have an average τ_b value of 21 ms, instead of the observed average value of only 13 ms. This difference is significant and is ∼10 times larger than the accuracy of our τ_b measurements. We therefore reject the hypothesis that the changes in L₂ that are apparent with perturbations of positions 97 arise from parallel changes in the open-channel dissociation rate constant.

We have no information regarding the open-channel association rate constant and therefore we cannot unambiguously link the open-channel dissociation rate constant with the open-channel dissociation equilibrium constant. This gap in our knowledge places some uncertainty on our conclusion that mutations of αD97 have no effect on the agonist affinity of open AChRs. However, the positive correlation between the level of spontaneous activity and the magnitude of L₂ for six αD97 mutants (Fig. 7) provides additional support to our conclusion that mutations of this residue act mainly by increasing L₀.

Functional Considerations

Of the 27 different α-subunit point substitutions that we examined, 16 increased gating, 8 had little or no effect, 1 (αF100V) reduced gating, and 2 did not expresses as functional AChRs. If we attribute these effects on gating exclusively to changes in L₀, this pattern implies that wild-type AChRs have nearly maximized the extent to which the α-subunit L5 favors the stability of unliganded-closed AChRs. We note, however, that the deletion of the putative apex residue αD97 decreased gating, presumably by increasing the relative stability of unliganded-closed AChRs even further, but this perturbation changed the backbone and also had modest effects on the kinetics of ligand binding.

While mutation of L5 residues in both α-subunits cause up to a 168-fold increase in L₂ (Table II), the largest effect we observed for a single mutation was an ∼27-fold increase in the gating equilibrium constant for one of the αD97A hybrid constructs (Fig. 10). Although the relationship between energy and structure is complex, the magnitude of effect suggests that this residue experiences a significant change in its local environment between closed and open conformations. However, point mutations of single residues in the AChR membrane domain can cause a 1,000-fold change in L₀ (Grosman et al., 2000b) so from this perspective, the L5 contributions to the relative stability of unliganded-closed AChRs is not large.

What makes the L5 special is its proximity to the TBS. Point mutations of many residues in the extracellular domain of the α-subunit have been examined, and most that affect gating do so by decreasing, rather than increasing, L₂. For some of these, this decrease has been shown to arise, at least in part, from a decrease in L₀ (Grosman et al., 2000a). The regions of greatest sensitivity are the TBS (Akk et al., 1999; Karlin, 2002; Sine, 2002), the Cys-loop (Shen et al., 2003), and, in GABA_AR, the β1-β2 linker (Kash et al., 2003). The magnitudes of the changes in L₂ caused by mutations of these extracellular residues is similar to those caused by mutations of the α-subunit L5, but the direction of the change is opposite. So far, L5 and the M2-M3 linker (Grosman et al., 2000a) are the only extracellular regions of the AChR that have been shown to increase the probability of spontaneous gating. In particular, our results suggest that the putative apex of the α-subunit L5, residues 96–98 (ADG), is an important region with respect to maintaining the high stability of unliganded-closed AChRs.

The relative timing of αD97 movement during the gating reaction was assessed using REFER analysis. This residue had a Φ-value of 0.93, which is indistinguishable from that of the TBS itself. This indicates that L5 in both α-subunits move early in the gating reaction, approximately in synchrony with the TBS.

The relative contributions to gating of L5 in the two α-subunits were probed by examining the separate effects of point αD97A mutations in the α-ɛ and α-δ subunits. The energetic contributions to gating at these two sites differed by 5.5-fold, but there was no evidence for coupling. A similar pattern was observed for the mutant αD200N in L8 (fivefold difference and no coupling; Akk et al., 1996). These results indicate that in the vicinity of the TBS the energetic contributions to gating are different at the two subunit interfaces by ∼1.6 k_BT, although they do not allow us to identify which α−subunit makes the greater contribution.

10 mutations to the putative apex of L5 in the β-, ɛ-, and δ-subunits were without effect on gating, leading us to specify the role of L₀-regulator only to the α-subunit. It appears that these non-α-residues do not experience a significant change in their structure or local environment as a consequence of gating.

Structural Considerations

The functional evidence points to L5 in the α-subunit, and particularly its three putative apex residues (ADG), acting as a “latch” that, in the absence of agonists, holds the channel closed and reduces the probability of spontaneous opening. It is extremely useful to combine structural and functional information in order to deduce reaction mechanism. However, we only have an x-ray structure for AChBP, which does not “gate” and whose L5 primary sequence is poorly conserved with those of AChRs (Table I). In particular, the apex residue is an isoleucine in AChBP, but a highly conserved aspartate in the AChR. One caveat is that AChRs contain an amino acid insertion in αL5 after Y93, so there is some uncertainty about the location of αD97.

The functional evidence points to at least the three apex residues forming a concerted structure that acts as a “latch.” In the αD97 mutant series, we were unable to correlate the effect of the side chain on gating with any particular chemical or structural parameter (Fig. 3 B). At this position, substitution of any side chain (including a glycine) either had no effect or increased gating, whereas the deletion of both the backbone and side chain of αD97 resulted in a large (40-fold) decrease in gating. Further deletion of residue 96 resulted in a partial restoration of gating (L₀). Finally, two substitutions of α97, proline and glycine, were special in that they generated multiple gating modes (that interconvert on the ∼0.1 s time scale), presumably because these residues allow unusual backbone configurations. This pattern of behavior is complex and more structural information is needed before we can form a hypothesis about the forces that hold the latch closed. One important clue is that substitution of serine or threonine at α97, which can participate in hydrogen bonds, resulted in a complete loss of expression of functional channels.

We can speculate on the general sequence of events surrounding L5 of the α-subunit during the initial stages of AChR gating. When the two TBS are empty, the AChR is almost always in its closed conformation: The two binding sites have a low affinity for ACh (∼150 μM), the two α-subunit L5 “latches” are in positions that favor the closed conformation, and ion permeation is forbidden. When transmitter molecules occupy the TBS, residues in the immediate vicinity, perhaps including αY93, move. One consequence of these movements is that the TBS affinity increases by ∼4 orders of magnitude. We speculate that another effect is that there is a nearly synchronous movement of atoms in other L5 residues. In particular, the putative apex residues ADG move to a position that reduces the relative stability of the AChR closed conformation. We cannot distinguish whether this movement causes the loss of a favorable interaction (with respect to keeping the channel closed), the generation of an unfavorable one, or both. Regardless, we hypothesize that the motion of the apex of L5 allows other parts of the protein to move, and so on, until the channel becomes ion-permeable. During channel closing, the sequence of events is reversed.

It is of course important to define the intraprotein interactions that constitute the closed-channel and open-channel complements of this latch, but as yet there is little structural, chemical modification, or mutagenesis data to guide our thinking. In AChBP, atoms from only six different side chains (three from each side of the subunit interface) and one backbone carbonyl lie within 6 Å of the δ1-carbon of I92 (Fig. 1 D). It is interesting to note that some of these (i.e., the homologous residues in AChRs) are at or near sites that influence channel gating, for example the β1-β2 linker (Kash et al., 2003; Miyazawa et al., 2003), the cys-loop disulfide (Shen et al., 2003), and the ɛ-subunit vicinal prolines (Ohno et al., 1996). In addition to these potential interaction loci, it is conceivable that the M2-M3 extracellular linker, which also regulates L₀ (Grosman et al., 2000a) interacts with αD97. This linker is absent in AChBP, but cysteine labeling and structural studies suggest that both in GABA_ARs (Horenstein et al., 2001) and AChRs (Miyazawa et al., 2003) it may project into the extracellular space by >10 Å. It will be important to pinpoint the location of αD97 and the M2-M3 linker in AChRs in order to ascertain whether these regions interact directly or whether the movement of L5 impacts on other residues that in turn impact on the M2-M3 linker. Interestingly, some of these potential sites of interaction with L5 move significantly later in the channel-opening reaction than does αD97 (e.g., Φ∼0.7 for αS269; Grosman et al., 2000a) and thus may be part of the next sequential movement of the gating “conformational wave.”

In the above scenario, agonist-driven movements of αY93 cause a movement of the apex residues of L5. However, our experimental results indicate that mutations to αD97 do not cause a significant change in K_d. Such asymmetry is perhaps not surprising if the intervening residues (94–96) are in a flexible loop. In addition, there are multiple determinants to K_d and it is possible that the αD97 perturbations cause changes in the position of αY93, but these alone are too small to register as a significant change in agonist affinity. In fact, the apex deletion constructs do have small but measurable effects on ligand binding, both with respect to equilibrium (2.5-fold) and rate constants (fivefold).

AChR gating appears to be an organized and sequential movement of protein domains within each of which the atoms move essentially in synchrony. L5 and the TBS belong to one such dynamic domain, which is perhaps the first to move during channel opening. We speculate that the apex of L5 is at the boundary of this domain, which spans at least 15 Å and is likely to include other (perhaps more distant) residues in the α- (Unwin et al., 2002; Miyazawa et al., 2003) and ɛ/δ-subunits. We propose that that center of mass of the TBS-L5 gating domain moves essentially as a rigid body (in effect, as a “nanotectonic plate” that has a uniform Φ-value) and that this movement coaxes conformational changes in adjacent gating domains. In this sense, L5 may resemble the S4-S5 linker of K channels (Jiang et al., 2003), which couples changes in the conformation of the voltage sensor to changes in the structures of elements that form, or that in turn are coupled to, the gate.

SCHEME III.