Unique Inner Pore Properties of BK Channels Revealed by Quaternary Ammonium Block

Abstract

Potassium channels have a very wide distribution of single-channel conductance, with BK type Ca²⁺-activated K⁺ channels having by far the largest. Even though crystallographic views of K⁺ channel pores have become available, the structural basis underlying BK channels' large conductance has not been completely understood. In this study we use intracellularly applied quaternary ammonium compounds to probe the pore of BK channels. We show that molecules as large as decyltriethylammonium (C₁₀) and tetrabutylammonium (TBA) have much faster block and unblock rates in BK channels when compared with any other tested K⁺ channel types. Additionally, our results suggest that at repolarization large QA molecules may be trapped inside blocked BK channels without slowing the overall process of deactivation. Based on these findings we propose that BK channels may differ from other K⁺ channels in its geometrical design at the inner mouth, with an enlarged cavity and inner pore providing less spatially restricted access to the cytoplasmic solution. These features could potentially contribute to the large conductance of BK channels.

INTRODUCTION

The crystallization of several bacterial K⁺ channels (Doyle et al., 1998; Jiang et al., 2002a, 2003; Kuo et al., 2003) has provided unprecedented tangible ground for the interpretation of numerous functional studies. These structural data have reshaped our understanding of how ion channels assemble and function. One of the most interesting findings from these prokaryotic channel structures is that the general organization of the ion permeation pathway, or the pore, appears similar among different channels. Additionally, pharmacological (MacKinnon et al., 1998) and chimaeric studies (Patten et al., 1999; Lu et al., 2001) have indicated that the ion conduction pore is conserved among K⁺ channels. Correspondingly, it has been proposed that all K⁺ channels may share similar mechanisms for ion selectivity and gating transitions in the pore region. On the other hand, functional studies from many eukaryotic K⁺ channels have suggested that the properties of the pore may vary significantly among different channels. For example, the single-channel conductance of K⁺ channels varies from ∼5 to ∼300 pS under similar recording conditions, and a variety of pore blockers demonstrate very different blocking affinities and kinetics among K⁺ channels (Hille, 2001). The reasons underlying these differences have been largely elusive.

One useful tool to functionally probe the pore of K⁺ channels is a group of tetraethylammonium (TEA) analogs collectively referred to as quaternary ammoniums (QAs). Based on their elegant studies on the blockage of squid axon K⁺ channels by intracellular QAs, Armstrong and his colleagues were able to propose some topological properties of K⁺ channel pores long before any structural information about ion channels was available (Armstrong and Binstock, 1965; Armstrong, 1969, 1971; Armstrong and Hille, 1972). These features included a physical gate at the cytoplasmic face of the pore, a wide inner mouth large enough to hold bound drug, and a constriction on the outside. Numerous functional and recent structural studies on K⁺ channels have corroborated these hypotheses (Hille, 2001).

All voltage-gated and inwardly rectifying K⁺ channels were found to be sensitive to QAs applied to the intracellular side; and QA molecules have been well established as open-channel blockers, which have access only to channels that are open. Furthermore, most of the channels tested share similar patterns in their responses to internal QAs in spite of different apparent affinities (Armstrong, 1971; French and Shoukimas, 1981; Taglialatela et al., 1991; Choi et al., 1993; Guo and Lu, 2001), suggesting that all K⁺ channels may share similar geometry around the pore.

Large conductance Ca²⁺-activated K⁺ (BK) channels have by far the largest single-channel conductance among all K⁺ channels. The mechanism for its large conductance is not well understood. Whereas negative charges near the inner mouth help to enhance cation entrance rates (Brelidze et al., 2003; Nimigean et al., 2003; Brelidze and Magleby, 2004), it is also likely that the topology of ion permeation pathway in BK channels may differ from those in many other K⁺ channels. In the absence of a crystal structure, we have employed QA molecules to functionally probe the pore of BK channels and compare the results with the QA block of other K⁺ channels. It has been long known that BK channels can be effectively blocked by internal QAs (Yellen, 1984; Villarroel et al., 1988), but the blockage has not been described in detail or compared with other channels. In the present study we show that the blockage of BK channels by QAs differs significantly from that of other K⁺ channels. Our results may reflect different accessibility to the channel pore from the inside of the membrane, possibly as a result of a unique topological organization in BK channels, tailored for large conductance.

MATERIALS AND METHODS

Channel Expression

For all experiments with BK channels the mbr5 clone of the mouse homologue of the slo gene (mslo) (Butler et al., 1993) was expressed in Xenopus laevis oocytes. The clone was modified and transcribed into cRNA as previously described (Cox et al., 1997). For appropriate levels of expression, 0.05–5 ng of cRNA was injected into oocytes. Recordings were usually performed within 3–7 d after injection. For experiments with Shaker channels ShB Δ6-46 cRNA was instead injected into oocytes.

Electrophysiology

All recordings were performed in the inside-out patch clamp configuration (Hamill et al., 1981). Electrodes for recordings of macroscopic currents were made from VWR borosilicate micropipettes (Cat. No. 53432–921; VWR Scientific), whereas those for single-channel recordings were made with WPI thick wall borosilicate capillary tubing (Cat. No. PG52150-4; World Precision Instruments). All electrodes were coated with wax (Sticky Wax, Kerr Corporation) and fire polished before use. Pipette access resistance in the bath solution was kept between 0.8–1.2 MΩ for all macroscopic recordings. Voltage errors due to series resistance were estimated as <10 mV and not corrected. All experiments were performed at 22°C.

Data acquired with an Axopatch 200-A patch-clamp amplifier (Axon Instruments, Inc.) were low pass filtered at 10 kHz with its 4-pole Bessel filter. Resistive and capacitive feedback modes were used for macroscopic and single-channel recordings, respectively. The ITC-16 hardware interface (Instrutech) and Pulse acquisition software (HEKA Electronik) were used to sample the records at 20-μs (macroscopic) or 10-μs (single channel) intervals and to store data in a Macintosh G3 computer system. Capacitive transients and leak currents were subtracted from macroscopic currents via the use of P/5 leak subtraction protocol with a leak holding potential of −120 mV. Four to eight consecutive current series under identical conditions were usually averaged for analysis to increase the signal to noise ratio. Experiments with visible time-dependent rundown of currents were excluded from analysis. With QUB software (Qin et al., 1996), single-channel records were baseline-corrected and idealized using half-amplitude threshold analysis. In dwell time histograms, dwell times greater than two times the calculated dead time (∼18 μs) were used for exponential fitting. Simulation, statistical analysis, graphing, and curve fitting were performed with Igor Pro Software (WaveMetrics, Inc.). Nonlinear least-squared fits were performed using the Levenberg-Marquardt algorithm.

Solutions

Pipette (extracellular in inside-out configuration) solution contained (in mM): 140 KMeSO₃, 20 HEPES, 2 KCl and 2 MgCl₂, pH 7.20. Bath (intracellular) solution: 136 KMeSO₃, 20 HEPES, 6 KCl and 0.1 CaCl₂, pH 7.20). In the absence of added Ca²⁺ buffer, 0.1 mM added CaCl₂ in the bath solution resulted in a free Ca²⁺ concentration of 110 μM, as measured with a Ca²⁺ electrode (Orion Research, Inc.) (Bers, 1982). In some experiments low Ca²⁺ internal solution was used to control the open probability of BK channels. For this purpose, 5 mM HEDTA and 0.99 mM CaCl₂ were added into intracellular solution and the free Ca²⁺ concentration was measured to be 0.85 μM with the Ca²⁺ electrode. To chelate contaminant Ba²⁺, 40 μM fresh (+)-18-crown-6-tetracarboxylic acid (18C6TA) was added to the internal solution just before recording (Diaz et al., 1996; Neyton, 1996; Cox et al., 1997).

A sewer pipe flow system (DAD-12; Adams and List Assoc., Ltd.) was used to constantly perfuse internal solution onto inside-out patches. Frozen aliquots of Ba²⁺ chelator and channel blockers were thawed and added at the appropriate amount into internal solutions before they were loaded into different reservoirs of the flow system. Computer-controlled switches allow for complete solution changes around the patches in <1 s.

Chemicals

Decyltriethylammonium (C₁₀) was a gift from Dr. Clay Armstrong. Tetrabutylammonium (TBA) was obtained from Alfa Aesar. All other chemicals were ordered from Sigma-Aldrich.

RESULTS

Previous studies on K⁺ channels with internal QAs have established these molecules as open-channel blockers. One of the key observations suggesting that these molecules can only block open channels is the time-dependent block of the K⁺ current. Particularly when large QAs are applied from inside, K⁺ currents first activate normally then decay during the depolarization pulse (Fig. 1 A). This can be explained if closed channels remain unblocked and can be opened normally with depolarization, but are blocked by QAs after opening. This phenomenon has been observed with almost all types of voltage-gated and inwardly rectifying K⁺ channels that have been tested in the literature (Armstrong, 1971; French and Shoukimas, 1981; Taglialatela et al., 1991; Choi et al., 1993; Guo and Lu, 2001). However, to our surprise, we found that BK type K⁺ currents demonstrated rather different responses to large QA molecules. Fig. 1 B shows examples of macroscopic BK K⁺ currents in response to the application of a long tail TEA analogue, decyltriethylammonium (C₁₀). A significant fraction of currents was blocked by C₁₀, but there was no sign of time dependence in the blockage. This was true with different concentrations of C₁₀ and at different membrane potentials (Fig. 1 B, a–c).

Figure 1.

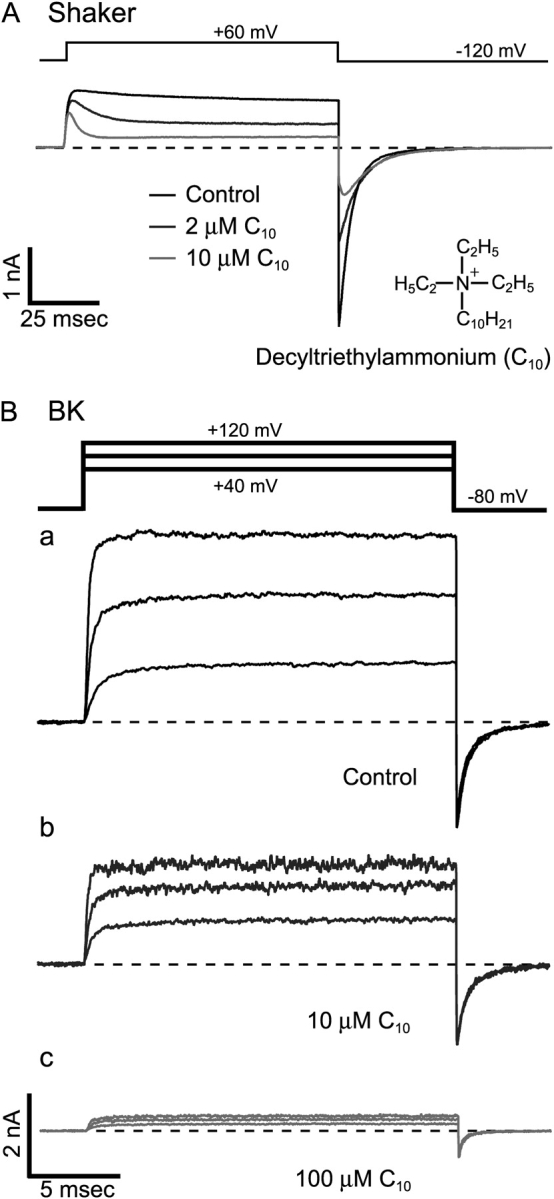
No time dependence in the blockage of BK currents by C₁₀. (A) Time-dependent block of Shaker K⁺ channels by C₁₀. Macroscopic K⁺ currents were recorded from an inside-out patch from an oocyte expressing Shaker B Δ6-46 channels. Under voltage clamp, currents were elicited by depolarization of the membrane potential to 60 mV from a holding potential at −120 mV. Application of 2 μM (dark gray trace) and 10 μM C₁₀ (light gray trace) resulted in reductions of current from the control level (black trace). (B) Macroscopic K⁺ currents carried by BK channels and their responses to C₁₀. Currents were recorded under voltage clamp from an inside-out patch from an oocyte expressing mslo BK channels. Currents were elicited by depolarizations of the membrane potential to 40, 80, and 120 mV from a holding potential at −80 mV. Currents before (black) and after the application of 10 μM (dark gray) and 100 μM C₁₀ (light gray) are shown with the same scale in a, b, and c, respectively. Current traces in this and all other figures represent the average of 4–8 consecutive series. The dashed lines indicate the zero current level in this and all other figures with macroscopic current traces.

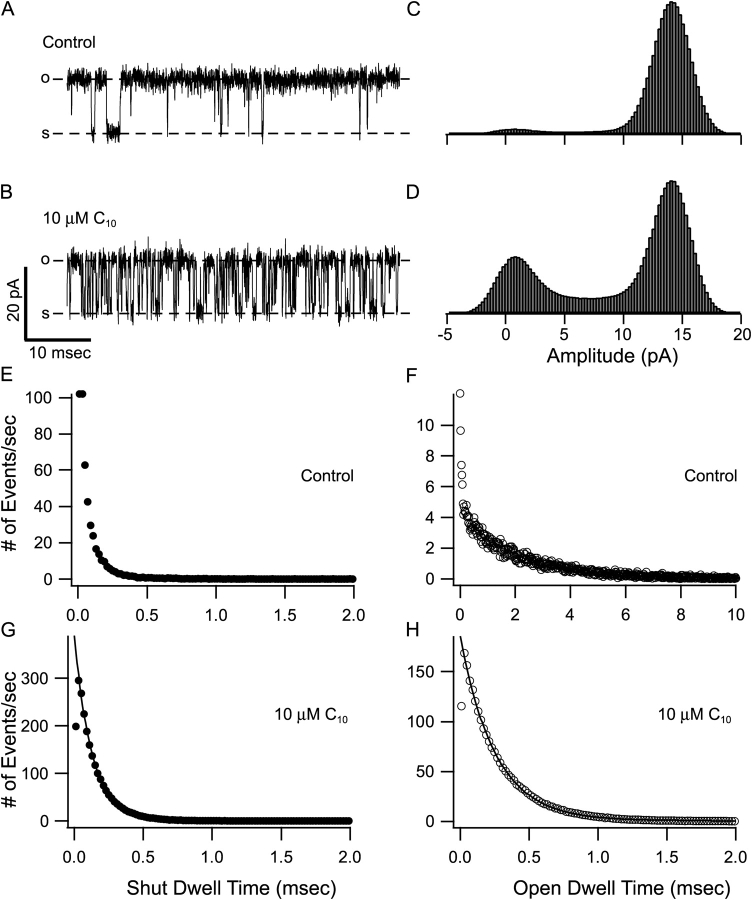
However, the lack of obvious time dependence in the blockage does not necessarily mean that C₁₀ is not an open-channel blocker for BK channels. For the onset of block to be visible in the time course of K⁺ current, it has to be a relatively slow process compared with the activation of channels. For example, small QA molecules such as TEA are known to be very fast blockers and they do not produce time-dependent block in some other K⁺ channels (Taglialatela et al., 1991; Choi et al., 1993). To identify the reasons for the lack of time dependence in C₁₀ block, we used single-channel recordings to directly measure the kinetics of the C₁₀ block in BK channels. Examples of single BK currents at 60 mV before and after the application of 10 μM C₁₀ are shown in Fig. 2, A and B . In the control trace, long openings are separated by occasional brief closures. When C₁₀ is applied from inside, many more brief transitions between open and shut levels emerge in the record. With the assumption that C₁₀ does not directly affect channel gating, these numerous new transitions must be due to the block and unblock of the channel while it is open. In the presence of 10 μM C₁₀, most of the transitions reach the fully open or shut level and can be easily resolved in the records. The all-point amplitude histogram in the presence of C₁₀ has identical peak amplitudes with control, although the calculated open probability (P_o) decreases from ∼0.95 to ∼0.65 (Fig. 2, C and D). To obtain quantitative kinetic information of C₁₀ block we idealized the single-channel records using half-amplitude threshold analysis and analyzed the distribution of dwell times (Fig. 2, E–H). Shown in Fig. 2, E and F, are dwell time histograms for shut and open states of control records, and Fig. 2, G and H, for records after the application of 10 μM C₁₀. In the presence of C₁₀, since the vast majority of the transitions reflect blocking and unblocking events of an open channel, the dwell time distributions should be dominated by how long the open channel remains blocked or unblocked before another transition occurs. As shown in Fig. 2, G and H, both the shut and the open dwell time histograms can be approximated well with a single exponential function, consistent with a two-state blocking scheme: O(pen) ↔ B(locked), while transitions between closed and open states are rare and can be neglected. As in all two-state models, the time constants from the single exponential fitting should measure the reciprocal of either the on rate (open dwell time) or off rate (shut dwell time) for C₁₀ block of a single BK channel (Yellen, 1984). Because of the inaccuracy in estimation of the durations for very brief transitions, only dwell times longer than twice the calculated dead time were used for the fitting. This also helped reduce the effect of flickery brief closures native to BK channels (Fig. 2, A and E). On the other hand, in the presence of C₁₀, some of the block or unblock events are too short to be resolved. This is likely to result in a slight overestimation of average dwell time at both open and shut levels, i.e., an underestimation of the rate constants.

Figure 2.

C₁₀ block of BK currents demonstrates fast kinetics at single-channel level. A and B are representative segments of single BK currents before and after the application of 10 μM C₁₀. Currents were recorded at 60 mV from an inside-out patch containing a single BK channel. The dashed lines labeled with “o” and “s” indicate open and shut levels. All-point amplitude histograms for 30 s of recording before and 100 s of recording after the application of 10 μM C₁₀ are shown in C and D, respectively. Single-channel traces were idealized with half-amplitude threshold analysis. E and F show the distribution of shut and open dwell time from the idealization of 30 s of control record, while G and H from 100 s of record in the presence of 10 μM C₁₀. For the ease of comparison, the y-axis in E–H was converted to number of events per second. Note the different x-axis scale in F. Data in G and H were each fitted (solid lines) with a single exponential function: y = Aexp(−x/τ) + b. Calculated dead time for half-amplitude threshold analysis at 10 kHz is 17.9 μs. Only dwell times >40 μs were used for fitting. Data in G were fitted with A = 389, b = 0.44 and τ = 127 μs. Data in H were fitted with A = 185, b = 0.45 and τ = 253 μs.

Using the method shown in Fig. 2, the block and unblock rate constants in 10 μM C₁₀ were measured at different membrane potentials from six patches, each containing a single BK channel, with the mean values plotted in Fig. 3 A. Within the voltage range shown, both the on and off rates of C₁₀ block demonstrate clear voltage dependence. The data were fitted to the following equation:

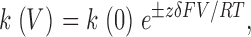(1)

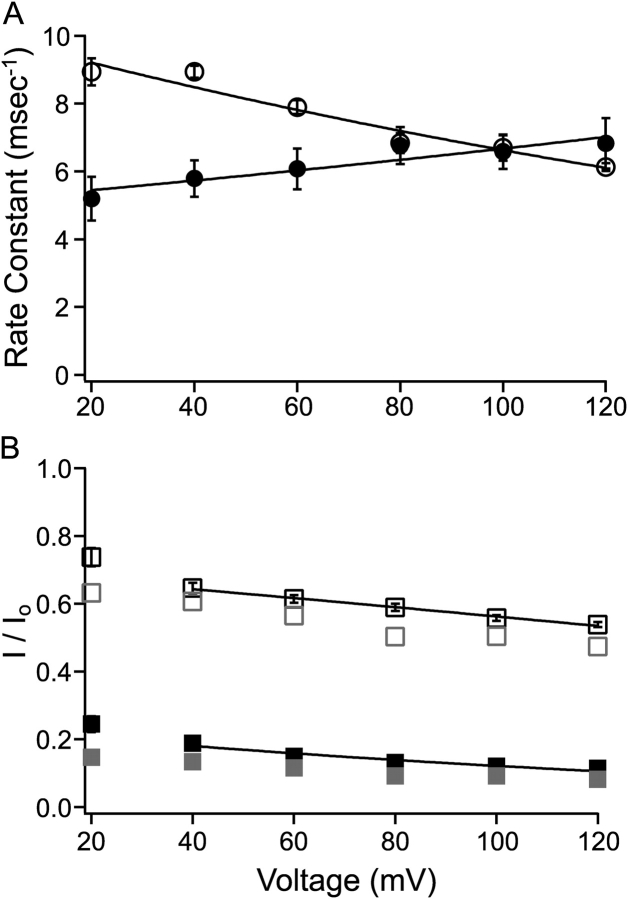
where k(0) represents rate constant at 0 mV, z is the valence of C₁₀ (+1), δ the effective electrical distance, V membrane potential, F Faraday's constant, R the universal gas constant, and T temperature. With 10 μM C₁₀, values used to fit data were k(0) = 5.18 ms⁻¹, δ = 0.06 (on rate), and k(0) = 10.00 ms⁻¹, δ = 0.10 (off rate), respectively. This method of measurement requires that most of the transitions reflect block and unblock of an open channel, this condition may not be satisfied at more negative membrane potentials where openings in the control records are short. Indeed the dwell time histograms progressively deviate from single exponential distributions at potentials lower than 20 mV. For this reason those single exponential time constants were not included for the fitting, and those values obviously deviate from the fitted function in Fig. 3 A.

Figure 3.

Single-channel kinetics corresponds with macroscopic measurements. (A) With the method shown in Fig. 2, on (filled circles) and off (open circles) rate constants for C₁₀ block were determined at various membrane potentials from six inside-out patches, each containing a single BK channel. Each measurement was made from 60 to 100 s of single-channel recording, and each dwell time histogram included 120,000 to 250,000 events. Each point represents the mean ± SEM. Voltage dependence of the rate constants was fitted (solid lines) with Eq. 1 (see text). Values for the fitting in this figure are: k(0) = 5.18 ms⁻¹, δ = 0.06 (block rate) and k(0) = 10.00 ms⁻¹, δ = 0.10 (unblock rate). Rate constants measured at more negative potentials than 20 mV clearly deviated from the shown voltage dependence. For reasons specified in the text, those values were not shown or included in the fitting. (B) Remaining fractions of steady-state macroscopic BK currents in the presence of 10 (open black squares, n = 15) or 100 μM C₁₀ (filled black squares, n = 6) are plotted against membrane potential. Error bars representing SEM are plotted with the mean values, but are often smaller than the symbols. Voltage dependence in the remaining fraction of macroscopic currents was fitted (solid lines) with Eq. 2 (see text). Values at 20 mV and below could not be measured reliably due to very small currents at these potentials, therefore they were not included in the fitting. Indeed the measurements at these potentials apparently deviate from the fitting of voltage dependence. Values used to fit the data are as following: K(0) = 22.6 μM, δ = 0.14 (10 μM C₁₀) and K(0) = 29.9 μM and δ = 0.19 (100 μM C₁₀). Gray symbols in B represent the predicted fraction of remaining steady-state currents with a two-state: O↔B blocking reaction using average on and off rates in A. Note in this prediction no dependence of block on open probability was taken into consideration. In the case of 100 μM C₁₀, 10 times the on rate in 10 μM C₁₀ was used.

As a way to verify the rate constants shown in Fig. 3 A, we compared single-channel kinetic parameters with the level of block in macroscopic BK currents. Fig. 3 B shows the remaining fractions of steady-state currents in response to 10 and 100 μM C₁₀ as a function of membrane potential. If our measurements of the on and off rates are accurate, they should be able to predict the amount of block in macroscopic currents. Indeed, the calculated amounts of remaining current (Fig. 3 B, gray symbols) from our measured on and off rates according to a two-state blocking reaction: O↔B are reasonably close to the values seen in macroscopic currents. The apparent overestimation in the amount of block may reflect some inaccuracy in our kinetic measurements; but on the other hand, it could also be a result of complications in macroscopic recordings such as voltage errors due to series resistance or incomplete leak subtraction. Importantly, the voltage dependence of our measured on and off rates correctly predicts the voltage dependence of fractional block. The voltage dependence of block was fitted with the Woodhull (1973) equation:

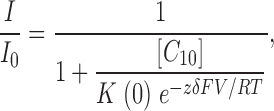(2)

where I/I ₀ is the remaining fraction of the current in the presence of C₁₀, [C ₁₀] the concentration of C₁₀ (10 or 100 μM), K(0) the block equilibrium constant at 0 mV, and all other parameters have the same meanings as in Eq. 1. Effective electrical distances δ obtained from the fitting of block at 10 and 100 μM C₁₀ are 0.14 and 0.19, respectively. These values are close to the sum of δ values for our measured on (0.06) and off rates (0.10), as they should be for a two-state block mechanism.

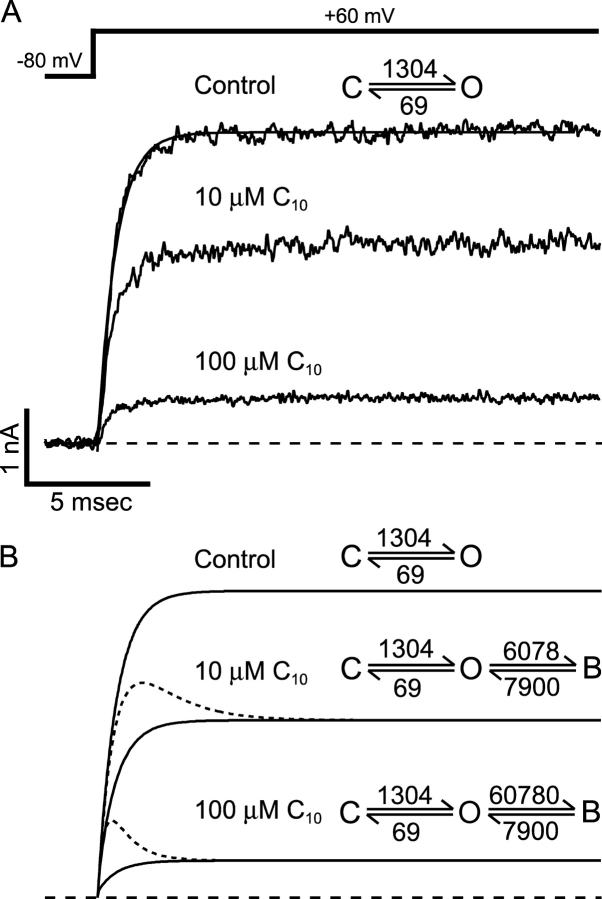
The favorable comparison in Fig. 3 assures that our estimations of rate constants for C₁₀ block are close to their true values. These rates are ∼20 or more times higher than reported for other K⁺ channels under similar conditions (Swenson, 1981; Choi et al., 1993). Can these values then explain the lack of time dependence in C₁₀ block of macroscopic BK currents? In Fig. 4 , we use simulations to address this question. Fig. 4 A shows an example of BK currents at 60 mV before and after the application of 10 or 100 μM C₁₀. With a delay of ∼100 μs, the activation of BK current can be well fitted by single exponential time course (Cui et al., 1997). Therefore, for our purposes the opening of BK channel can be simplified as a two-state reaction: C(losed) ↔ O(pen). If a P_o of 0.95 is assumed at 60 mV, apparent rate constants for the C↔O transition can be estimated by fitting the control current with a single exponential function. The calculated rate constants are shown in Fig. 4 A. With the assumption that the gating kinetics remain unchanged, we added a blocked state according to the open-channel block mechanism, with block and unblock rate constants from mean values shown in Fig. 3 A at 60 mV (10 times the on rate was used in simulation of 100 μM C₁₀) (Fig. 4 B). The simulations of currents in the presence of C₁₀ (solid lines in Fig. 4 B) under this scheme have very similar time course and final values to the recorded currents in Fig. 4 A. Furthermore, if we decrease both the on and off rate constants for the block by 20-fold without changing affinity, the resulting simulations (dotted lines) are very reminiscent of the time-dependent block of other K⁺ channels by C₁₀ (Fig. 1 A). These simulations indicate that fast kinetics can completely account for the lack of time dependence in the C₁₀ block of BK currents. Therefore, all the data presented so far are consistent with C₁₀ being a very fast open-channel blocker for BK channels.

Figure 4.

Fast kinetics can account for the lack of time dependence in C₁₀ block of BK channels. (A) An example of macroscopic BK currents before and after the application of 10 and 100 μM C₁₀. Currents were elicited by depolarization of membrane potential to 60 mV from −80 mV under voltage clamp. The smooth line in A is the fit of the control trace to a single exponential function I = I _max (1 − exp(−(t − t ₀)/τ)), where I _max is the maximal current level, t ₀ is the delay in the activation process (Cui et al., 1997), and τ is activation time constant. Values used for the fit are I _max = 4.03 nA, t ₀ = 89 μs, and τ =728 μs. If we assume a two-state activation process: C↔O with opening rate α and closing rate β, then (1/ τ) = α + β, and P _o = α/(α + β). By assuming a P _o of 0.95 at 60 mV we can calculate the values for the forward and backward rates: α = 1,304 s⁻¹ and β = 69 s⁻¹. (B) Gating parameters from A were used for the simulations of currents according to the open-channel block mechanism: C↔O↔B. Block and unblock rate constants are from mean values at 60 mV in Fig. 3 A. Parameters used in the simulations are shown on the top of each trace (solid lines). 10 times the on rate is used in the simulation of 100 μM C₁₀. Dotted lines are simulations when both the block and unblock rates are decreased by 20-fold with the C↔O gating parameters remaining unchanged.

Another important feature of open-channel blockers is that they often slow the deactivation process of channels at repolarization. According to the scheme shown in Fig. 4 B, the blocked channels can't close until they are unblocked first. On average, it will take longer for all channels to return to the closed state, yielding a slower macroscopic deactivation process at repolarizing membrane potentials. Consistent with this classical open-channel block model, tail currents were slowed by large QA molecules in other K⁺ channels (Fig. 1 A) (French and Shoukimas, 1981; Choi et al., 1993; Clay, 1995). However, in our study we observed the opposite effect by C₁₀ on macroscopic BK currents. As shown in Fig. 5 A, tail currents at −80 mV before and after the application of 10 and 100 μM C₁₀ can be well fitted by single exponential functions (dark lines in the box). In this example, the time constants are 649 μs (control), 545 μs (10 μM C₁₀), and 450 μs (100 μM C₁₀), meaning that deactivation is in fact made faster in the presence of C₁₀. When the tail currents are scaled to the same peak amplitude (Fig. 5 B), it is clearly visible that C₁₀ speeds up the process of deactivation. This effect is in direct contrast with the prediction of an open-channel block mechanism. In Fig. 5 C, we illustrate by simulation the prediction of this C↔O↔B scheme. The rate constants for the C↔O transition at repolarization were calculated from the fitting of the tail current in the control trace in Fig. 5 A, assuming that 99% of channels are closed at equilibrium at −80 mV. The rate constants for the O↔B transition were extrapolated from the fitting in Fig. 3 A, since at such negative potentials direct measurements of rate constants are not reliable because the openings are short even in the absence of C₁₀. Fig. 5 C shows the simulations of tail currents in the presence of 10 or 100 μM C₁₀. The predicted tail currents clearly become slower in the presence of C₁₀ so that they cross with the control trace. Single exponential fittings of the simulated tail currents resulted in time constants of 649 μs (control), 865 μs (10 μM C₁₀), and 2.603 ms (100 μM C₁₀), respectively. The slowing of deactivation is more evident when the tail currents are normalized to their peak amplitudes (Fig. 5 C).

Figure 5.

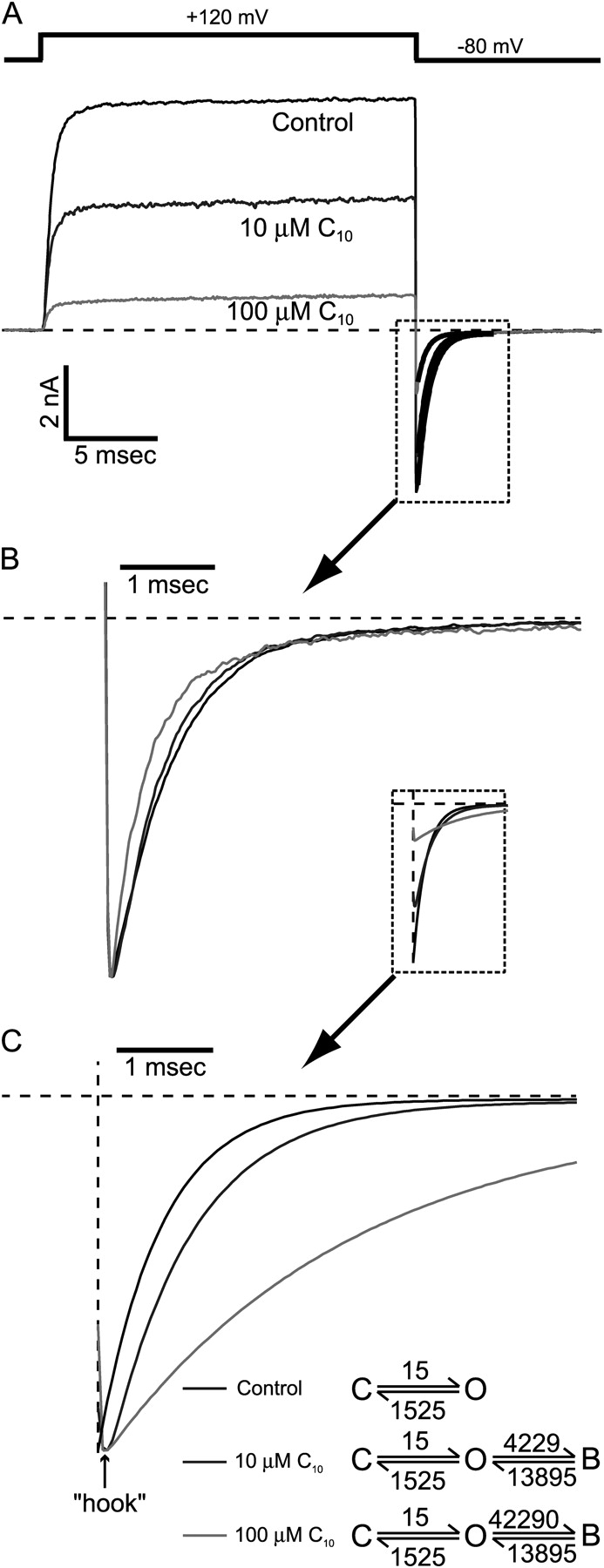
C₁₀ does not slow down the deactivation of BK channels. (A) Macroscopic BK currents were recorded from an inside-out patch under voltage clamp. Membrane potential was first depolarized to 120 mV to open all the channels then repolarized to −80 mV. Control current is shown in black and currents in the presence of 10 and 100 μM C₁₀ are shown in dark gray and light gray, respectively. All tail currents can be well fitted with a single exponential function (black traces in the dotted box). The time constants from the fitting are 649 μs (control), 545 μs (10 μM C₁₀) and 450 μs (100 μM C₁₀). (B) Tail currents within the dotted box in A are normalized to the same peak amplitude. (C) Simulations of tail currents according to the open-channel block mechanism: C↔O↔B. In control trace, if we assume a two-state deactivation process: C↔O with opening rate α and closing rate β, then (1/τ) = α + β, and P _o = α/(α + β). With the time constant τ from the single exponential fitting and by assuming a P _o of 0.01 at −80 mV, we can calculate the values for the forward and backward rates: α =15 s⁻¹ and β =1,525 s⁻¹. C₁₀ block and unblock rate constants at −80 mV are extrapolated values based on the voltage dependence of rate constants in Fig. 3 A, because accurate measurements of rate constants were not possible at negative potentials. The initial conditions for simulations of tail currents were determined by the level of steady-state block at 120 mV. The simulations of tail currents in the presence of 10 and 100 μM C₁₀ are shown in dark and light gray, together with the control trace (black) in the dotted box. 10 times the on rate was used for the simulation of 100 μM C₁₀. Single exponential fitting (not depicted) of the simulated tail currents yielded time constants of 649 μs (control), 865 μs (10 μM C₁₀), and 2.603 ms (100 μM C₁₀). Normalized tail currents to the same peak amplitude clearly demonstrate the slowing in deactivation.

Considering the possible inaccuracy in the extrapolation of the O↔B rate constants, we also tried simulations with different block and unblock rate values. We found that higher rate constants predicted slower deactivation. However, even when we decreased the rates by 10-fold from the values in Fig. 5 C, the model still predicted a significant slowing of tail currents (not depicted). Interestingly, simulated tail currents in the presence of C₁₀ show a “hook” at the beginning, similar to what was originally observed by Armstrong and Binstock (1965) with squid axon K⁺ channels and later by others with other K⁺ channels. This hook appears because the net unblock of channels is faster than channel closure so that K⁺ current increases before it decreases due to deactivation. In contrast, no signs of such hooks were observed in our recorded BK tail currents in the presence of C₁₀ (Fig. 5 B).

Speeding of the deactivation of BK channels by C₁₀ was observed at all tested membrane potentials lower than −20 mV, where the tail currents can be fitted reliably. After maximal activation at 120 mV, membrane potential was stepped down to different values. Tail currents across all negative potentials can be fitted well with single exponential functions (Fig. 6 A). As shown in Fig. 6 B, time constants of tail currents decrease by a similar factor at all potentials in response to C₁₀ in a concentration-dependent manner. The speeding of tail currents was not merely an artifact due to smaller currents after block, because the time constants of tail currents were not sensitive to their sizes when different fractions of channels are activated from the same patch by depolarizations to different potentials.

Figure 6.

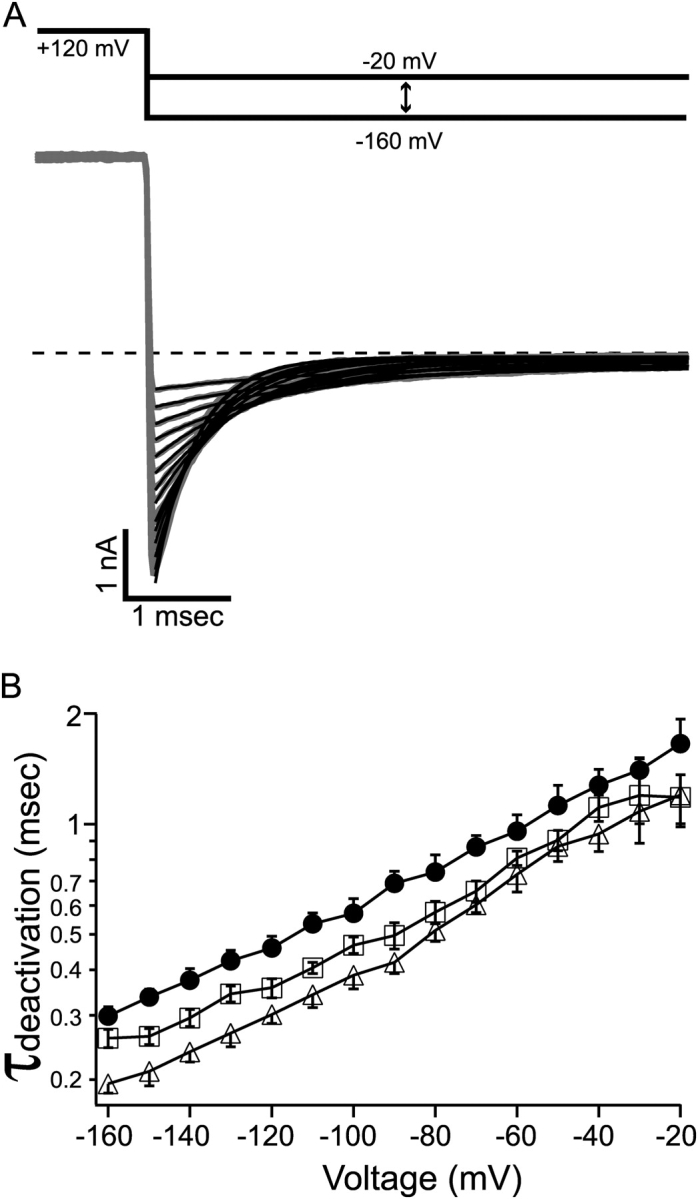
Deactivation of BK channel was speeded by C₁₀ at all negative membrane potentials. (A) Macroscopic BK currents (gray traces) were recorded from an inside-out patch under voltage clamp. Membrane potential was first depolarized to 120 mV to open all the channels then repolarized to various levels between −160 and −20 mV at 10-mV steps. Tail currents at each potential were fitted with single exponential function (black lines). Tail currents in the presence of 10 or 100 μM C₁₀ (not depicted) can also be well fitted with single exponential functions at all negative potentials. (B) Deactivation time constants as measured in A are shown for control (filled circles), 10 μM C₁₀ (open squares), and 100 μM C₁₀ (open triangles). Each point represents the mean and SEM determined from 6–8 patches. The measurements of deactivation time constants in the absence and presence of C₁₀ are from the same patches. The lines connecting the data points have no physical meanings.

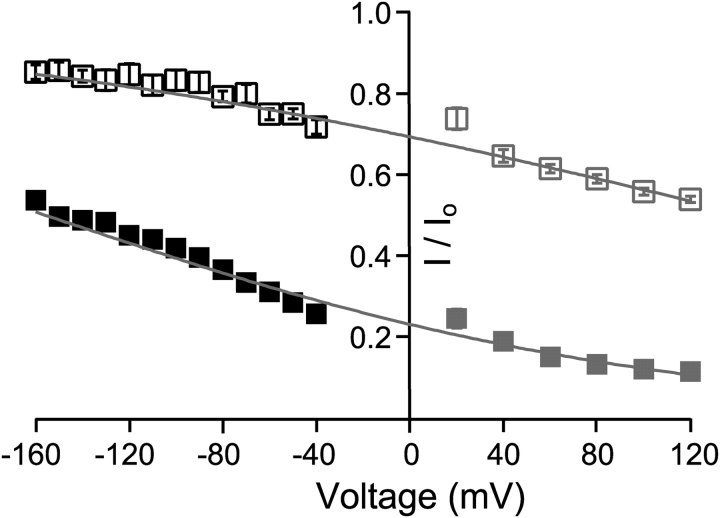
Why does C₁₀ speed up the deactivation process rather than slowing it down? It is known that extremely slow open-channel blockers can result in an apparent speeding of tail currents, because a very slow component due to unblock is too small to detect in this case (Colquhoun et al., 1979). However, several lines of evidence suggest that this mechanism doesn't underlie the effect of C₁₀ on BK currents. First, based on the voltage dependence of the rate constants, the extrapolated values suggest that C₁₀ remains a very fast blocker at negative membrane potentials in spite of the decrease in apparent affinity. Second, if C₁₀ becomes an extremely slow blocker at negative potentials, then the beginning of the tail currents should have the same amount of block as in the steady-state currents before repolarization, because it takes a long time for the block to reach a new equilibrium. Fig. 7 clearly shows that it is not the case. Peak tail currents at negative potentials are much less blocked than the steady-state currents in the preceding depolarization (120 mV). Gray markers and lines are from Fig. 3 B, indicating levels of block in steady-state currents at more positive potentials. Interestingly, the fitting of voltage-dependent steady-state block at positive potentials can predict the level of block in peak tail currents at negative potentials. This suggests that C₁₀ is an extremely fast blocker at negative potentials so that the block at the beginning of repolarization reaches its new equilibrium right away. This can explain the lack of a “hook” in the tail currents, because the process of developing a new equilibrium is too fast to resolve in our measurement. Expanded views at the beginning of tail currents show that they always peak at the same time point with or without C₁₀ (unpublished data). Additionally, the fact that the voltage dependence holds across a wide range of voltage corroborates our measurement of voltage dependence in C₁₀ block.

Figure 7.

Reduction of peak tail currents suggests fast block at negative membrane potentials. Remaining fractions of steady-state currents shown in Fig. 3 B are replotted in gray (10 μM C₁₀: open squares; 100 μM C₁₀: filled squares), with the fitting of voltage dependence (gray lines) extrapolated into the negative membrane potentials. The black symbols are the remaining fractions of peak tail currents after the application of 10 μM (open squares) or 100 μM C₁₀ (filled squares). Each data point represents the mean ± SEM determined from 6–7 patches. Note that error bars are often smaller than the symbols.

The last line of evidence against the explanation by slow block at negative potentials came from our experiments with another QA molecule, tetrabutylammonium (TBA). At around half block concentration (500 μM), TBA resulted in faster block kinetics compared with 10 μM C₁₀. Single-channel current rarely reaches the fully open or shut level, precluding direct measurement of kinetics (Fig. 8 A). TBA block of macroscopic BK currents demonstrated a similar voltage dependence as C₁₀, with a δ value of ∼0.2 (Fig. 8 B). To measure the effect of TBA on deactivation, tail currents at various membrane potentials were fitted with single exponential functions and the time constants are plotted in Fig. 8 C. As in the case of C₁₀, TBA speeds up the deactivation of BK channels at all negative potentials. In light of the similar effect by the faster blocker TBA, the faster tail currents are unlikely the result of extremely slow block.

Figure 8.

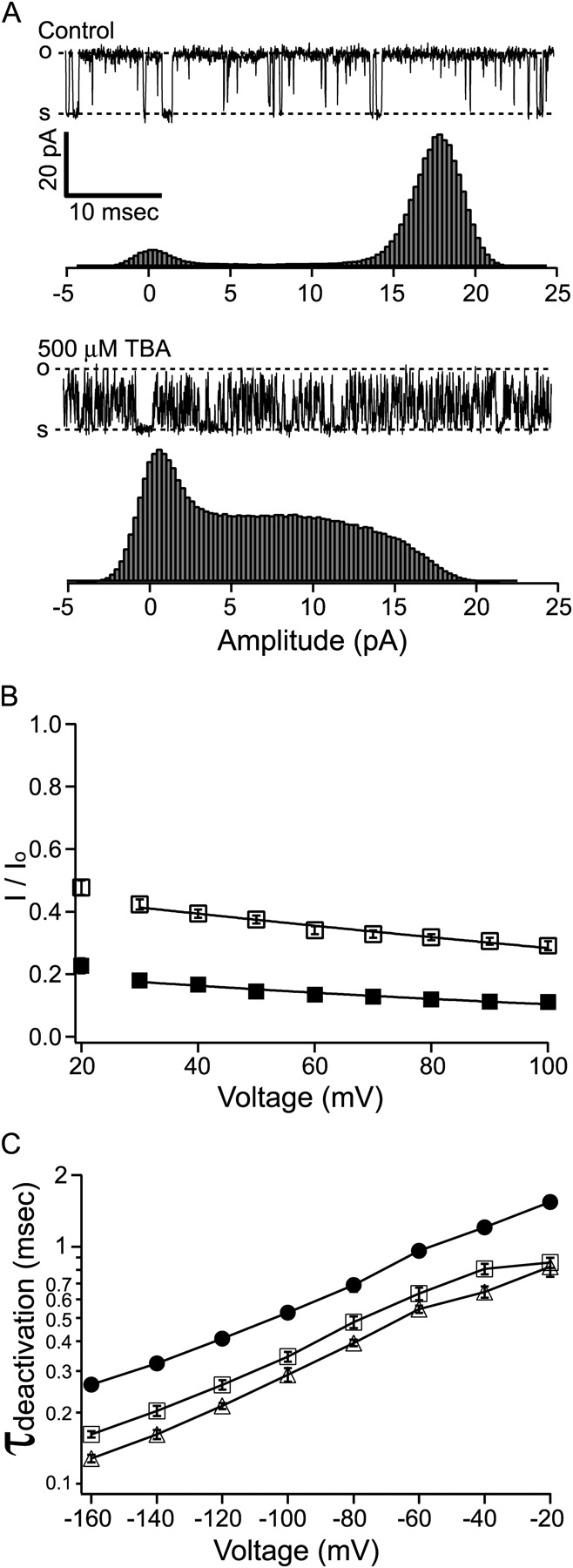
Block of BK channels by tetrabutylammonium (TBA). (A) Sample single-channel records before and after the application of 500 μM TBA (this concentration of TBA blocks ∼50% of steady-state current at 60 mV) are shown on top of all-point amplitude histograms, each constructed from 30 s of recording. The dashed lines labeled with “o” and “s” represent open and shut levels. Because the current rarely reaches the fully open level in the presence of TBA, the open level is determined from the control trace from the same patch. (B) Remaining fractions of steady-state macroscopic BK currents in the presence of 1 mM TBA (open squares) and 5 mM TBA (filled squares) are plotted against membrane potential. Each data point represents the mean ± SEM determined from 6–7 patches. Error bars are often smaller than the symbols. Voltage dependence of TBA block was fitted with Eq. 2 (solid lines) with [TBA] replacing [C₁₀]. Data at 30 mV and above were included for the fitting, which yielded the following parameters: K(0) = 0.90 mM, δ = 0.21 (1 mM TBA) and K(0) = 1.37 mM, δ = 0.22 (5 mM TBA). (C) TBA speeds up the deactivation of BK channels. Tail currents at various negative potentials were fitted with single exponential functions as in Fig. 6. Deactivation time constants before (filled circles) and after the application of 1 mM (open squares) and 5 mM TBA (open triangles) are plotted against membrane potential. Each point represents the average from 6–7 patches. Most error bars representing SEM are smaller than the symbols. The lines connecting the data points have no physical meanings.

The direct conflict of our tail current data with the prediction by the classic open-channel block mechanism suggests that this model needs to be modified for BK channels. For fast blockers to speed up the deactivation process, blocked channels must be able to close directly without unblocking first. Moreover, blocked channels must close faster than the unblocked ones in order to produce an overall faster deactivation. Fig. 9 illustrates two ways in which blocked channels can close directly. Fig. 9 A recapitulates the classic open-channel block mechanism, where channels can't close with a bound QA blocker. This was explained by a “foot in the door” model, which means that the blocker physically prevents the channel gate from being closed (Yeh and Armstrong, 1978). A straightforward modification of this model for BK channels is to propose a larger cavity around QA binding site so that the bound blocker no longer physically interferes with the channel gate (Fig. 9 B). This has been proposed for other K⁺ channels under certain circumstances (Armstrong, 1971; Holmgren et al., 1997) as the “trapping” mode, because when the channel closes, the gate traps the bound QA blocker, which can't leave the cavity until the gate is open again. As a more dramatic modification of the model, it is possible that the accessibility of QA blockers to their binding sites from inside the membrane is not restricted by the channel gate, which is referred to as “free access” model in Fig. 9 C. This will mean that the gate of BK channel is not located between the QA binding site and the cytoplasmic solution, the commonly proposed position for channel gates in most other K⁺ channels (Hille, 2001). These two mechanisms could be potentially distinguished by whether trapping occurs at repolarization. However, unfortunately, due to the very fast block kinetics of QAs in BK channels, trapping would not be detected if it indeed happens. Previous characterizations of trapping behavior all relied on a slow unblock phase that trails channel activation (Armstrong, 1971; Miller, 1987; Holmgren et al., 1997). For this reason we could not rule out the possibility suggested in Fig. 9 C, but we do favor the mechanism in Fig. 9 B as discussed in the next section. Regardless of the actual mechanism, if a blocked channel can close faster than an unblocked one, the model will indeed predict a faster tail current depending on the concentration of QA blockers.

Figure 9.

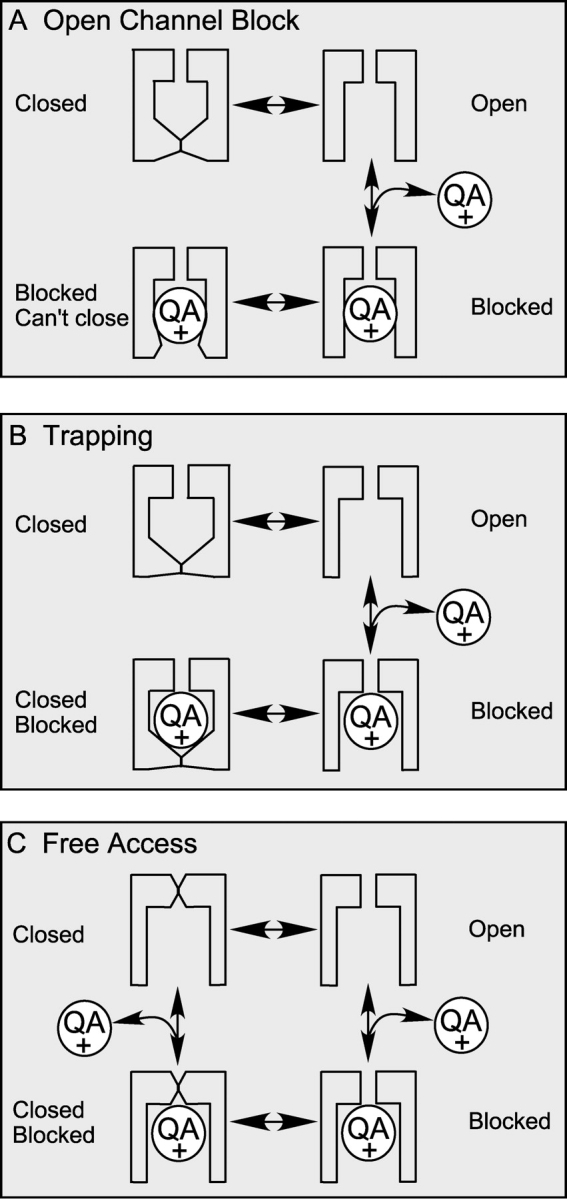
Classic open-channel block mechanism needs modification to account for the block of BK channels by QAs. (A) Classic open-channel block scheme, in which a blocked channel can't close until it is unblocked first. (B) The “trapping” scheme, in which the channel can close with a bound blocker by trapping it inside. In this model, the blocker cannot enter or leave a channel when it is closed. (C) “Free access” scheme, in which the accessibility of the blocker to its binding site is not dependent on the conformation of the channel gate. Channels can be blocked or unblocked in either open or closed conformation. However, this mechanism does not exclude differences in binding affinity or kinetics between closed and open conformation. Therefore, the block may not be truly “independent” on gating.

Whether a blocked channel can directly close also has implications for the dependence of steady-state block on open probability. For the classic open-channel block mechanism:

(K _g and K _d are the equilibrium constants for the gating and blocking reaction, respectively), the degree of block depends on both gating and blockage (Choi et al., 1993). In the absence of blocker, open probability

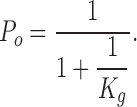(3)

At equilibrium in the presence of QA blocker

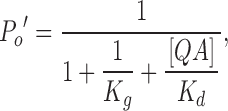(4)

where [QA] is the concentration of QA blocker. The remaining fraction of current in the presence of QA is thus

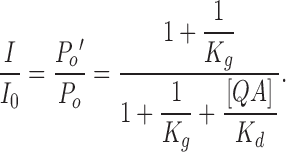(5)

When K _g >> 1, P _o ≈ 1 and most channels are open,

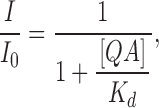(6)

which provides a measurement of the true blockage equilibrium constant. All the data presented so far satisfy this condition. Particularly in Fig. 7 the remaining fractions of currents at negative potentials reflect the true blockage equilibrium constants because they were measured at the beginning of tail currents, where the open probability is still close to unity.

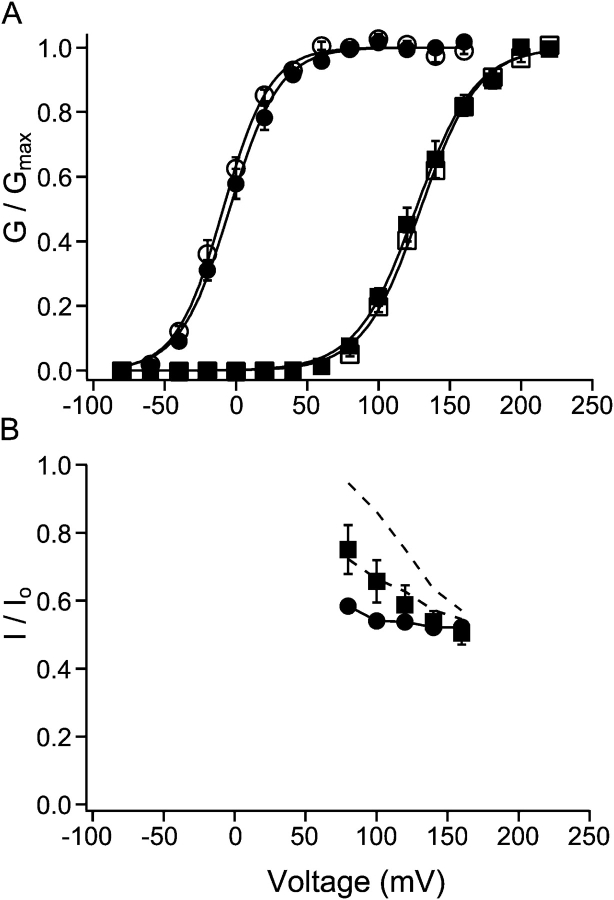
However, when P _o is significantly less than unity, the fraction of block is dependent on both the gating and blockage equilibrium according to Eq. 5. Note that both gating and blockage of BK channels are dependent on voltage. To directly study the dependence of blockage on open probability independently of voltage, we compared the degree of block at the same voltage in channels with different P _o. For this purpose, we measured the remaining fractions of steady-state currents in the presence of C₁₀ with either 110 μM Ca²⁺ or 0.85 μM Ca²⁺ in the internal solution. This low Ca²⁺ concentration resulted in a right shift in the conductance versus voltage relationship (G-V) for BK channels by ∼140 mV (Cui et al., 1997) compared with high Ca²⁺, whereas the shift in the G-V relationship caused by the presence of C₁₀ is minimal (Fig. 10 A). The remaining fractions of currents with both Ca²⁺ concentrations are plotted against membrane potentials between 80 and 160 mV in Fig. 10 B. Below 80 mV currents were too small with 0.85 μM internal Ca²⁺, and at voltages >160 mV complications resulting from saturation or calcium block will likely induce large errors in our measurement (Cox et al., 1997). In the case of 110 μM internal Ca²⁺, because P _o is close to unity within this voltage range (Fig. 10 A), the remaining fraction of current reflects the true blockage equilibrium constant according to Eq. 6. By comparison, less block occurs in 0.85 μM internal Ca²⁺ with the same concentration of C₁₀ at the same voltages, suggesting that the blockage of BK currents is indeed dependent on P_o. To test whether the classic open-channel block mechanism can fully explain the data, we used Eq. 5 to predict the remaining fractions of currents in 0.85 μM internal Ca²⁺ with K _g calculated from the low Ca²⁺ G-V relationship in Fig. 10 A (Eq. 3) and K _d from the remaining fractions of currents in 110 μM internal Ca²⁺ (Eq. 6). As the top dashed line in Fig. 10 B shows, this prediction obviously underestimates the level of block by C₁₀ at these potentials in 0.85 μM internal Ca²⁺.

Figure 10.

Dependence of steady-state block on open probability. (A) Relative conductance of macroscopic BK currents as a function of membrane potential. Membrane potential was depolarized to various levels followed by repolarization at −80 mV. To determine relative conductance at different potentials, amplitude of tail currents at 80 μs after the beginning of repolarization was measured and normalized to the maximum. Open and filled circles are data points with 110 μM Ca²⁺ in the internal solution before and after the application of 10 μM C₁₀. Open and filled squares are data points with 0.85 μM Ca²⁺ in the internal solution before and after the application of 10 μM C₁₀. Each point represents the mean ± SEM from six patches. Data with 110 and 0.85 μM Ca²⁺ were from the same patches. Each set of data were fitted (solid lines) with the Boltzmann function G=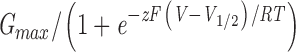 and then normalized to the maximum of the fit. In this function V _1/2 is the membrane potential at which half of the channels are open, z is the apparent equivalent gating charge, while all other parameters have their normal meanings. Values used to fit the data are as following: 110 μM Ca²⁺: V _1/2 = −9.0 mV and z = 1.56 (before C₁₀); V _1/2 = −4.4 mV and z = 1.46 (10 μM C₁₀); 0.85 μM Ca²⁺: V _1/2 = 129.5 mV and z = 1.27 (before C₁₀); V _1/2 = 126.3 mV and z = 1.23 (10 μM C₁₀). (B) Remaining fractions of steady-state currents at various potentials in the presence of 10 μM C₁₀ with either 110 (filled circles) or 0.85 μM Ca²⁺ (filled squares) in the internal solution. Each point represents the average from the same six patches in A, and the error bars are SEM. The solid line connecting filled circles has no physical meaning. The top dashed line is the prediction for 0.85 μM Ca²⁺ based on the C↔O↔B scheme, with true blocking equilibrium determined from level of block at 110 μM Ca²⁺ and open probability from A. The middle dashed line is the prediction for 0.85 μM Ca²⁺ based on the C↔O↔B↔BC scheme, with true blocking equilibrium determined from data at 110 μM Ca²⁺ and a factor of θ = 2 in the change of gating equilibrium when blocker is bound (see text for details).

We wanted to find out whether this discrepancy could be explained if a blocked channel can directly close as proposed in Fig. 9. In the following scheme:

BC represents a blocked and closed state. If we assume the binding of a blocker changes the gating equilibrium by a factor of θ, K _g′ = θK _g, then at equilibrium in the presence of QA blocker,

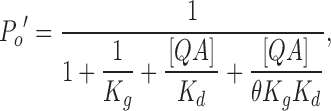(7)

thus the remaining fraction of current

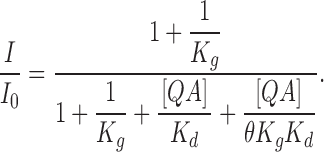(8)

When θ is infinitely large, which means that the channel never reaches the BC state, Eq. 8 reduces to the form for the classic open-channel block mechanism (Eq. 5). When θ = 1, i.e., the gating equilibrium is not affected by binding with QA blocker, Eq. 8 reduces to Eq. 6, which means that the blockage is not dependent on open probability. A θ value of ∼2 yields the prediction that agrees approximately with the data in 0.85 μM internal Ca²⁺ (the middle dashed line in Fig. 10 B). Energetically this means that binding of QA stabilizes the open-channel configuration by ∼0.7 kT, where k is Boltzmann's constant, and T is the absolute temperature, which is a rather small change in free energy. As mentioned earlier, the closing rate of blocked BK channels is increased by the binding of a QA blocker. A stabilization of the open-channel configuration by a blocker must then mean that the opening rate of a blocked and closed channel is increased even more. Altogether, Fig. 10 suggests that BK channels can close with a bound QA blocker in the pore. On the other hand, the dependence of block on open probability doesn't help rule out the mechanism in Fig. 9 C. In that model such dependence can be explained by the differences in QA binding affinity between closed and open channels.

DISCUSSION

Fast Kinetics of QA Block in BK Channels

Our results demonstrate that internal large QA molecules such as C₁₀ have ∼20 or more times faster blocking kinetics in BK channels than in any other K⁺ channels that have been tested. In previous studies, the size of QAs and their entry rates into the channel have been employed to estimate the dimension of the inner pore (or its narrowest part between the QA binding site and intracellular solution) when the channel is open (Armstrong, 1971; French and Shoukimas, 1981; Swenson, 1981; Guo and Lu, 2001). These studies suggest a rather narrow inner pore between the cavity and the cytoplasmic solution. For example, Guo and Lu (2001) show that experimental on rates for all QA molecules in inward rectifier channels are well below the estimated diffusion limit, implying that the inner pore in these channels may spatially restrict the entry of QA molecules. In agreement with this, Yellen's lab showed recently that the inner pore in Shaker channel is narrow in the open state (Webster et al., 2004). However, this picture may be very different in BK channels based on our kinetic measurement of QA block. QA molecules as large as C₁₀ have an estimated on rate of 5,000 s⁻¹ at 0 mV and 10 μM concentration, which translates into 5 × 10⁸ M⁻¹s⁻¹, approaching the commonly estimated diffusion limit of on rates of 10⁸–10⁹ M⁻¹s⁻¹ (Guo and Lu, 2001). 500 μM TBA resulted in even faster apparent blocking kinetics. These values suggest that in BK channels the inner pore may not pose a significant energy barrier for large QA molecules to access their binding site from the cytoplasmic solution. In other words, BK channels may have significantly larger inner pores compared with other K⁺ channels. This would apply to the open state in the trapping model (Fig. 9 B) and to both the open and closed states in the free access model (Fig. 9 C).

Even larger internal open-channel blockers may be potentially useful to estimate the dimensions of BK channel inner pore. When synthesized Shaker B (ShB) amino-terminal ball peptide is intracellularly applied to trypsin-treated BK channels in rat adrenal chromaffin cells, the block shows no time dependence (Solaro and Lingle, 1992), suggesting that even the bulky ball peptide can access its binding site without much restriction. Of course in this case it is not clear whether it's because the ball peptide also has faster block kinetics than activation or, as the authors suggested, the binding site is accessible whether the channel is open or closed. Single-channel studies of BK channels blocked by ball peptide revealed two kinetically different behaviors: a short block (on rate at ∼10⁷ M⁻¹s⁻¹) and a long block (on rate at ∼10⁴ M⁻¹s⁻¹), both slower than the prediction by diffusion controlled rates (Foster et al., 1992; Toro et al., 1992).

The size of the inner pore in BK channels may have a large impact on their conductance. BK channels have by far the largest single-channel conductance among all K⁺ channels. The mechanism for its large conductance is not completely understood, although a ring of negative charges near the inner mouth were found to contribute partly (Brelidze et al., 2003; Nimigean et al., 2003; Brelidze and Magleby, 2004). Our results suggest that another factor that improves the conductance in BK channels could be the larger dimension of the inner pore. By comparison with other K⁺ channels, the permeation of K⁺ ions may be less restricted by the inner pore of BK channels and approaches the diffusion limit, thus allowing more ions to pass through in a unit of time.

Without crystal structures, we can only speculate about the structural bases underlying the differences in the spatial restriction of the inner pore between BK channels and other K⁺ channels such as Shaker. One possibility is that the “tetramerization” or T1 domain (Kreusch et al., 1998), which exists only in K_v-type channels (with conductance 10–30 pS), such as Shaker, but not in high-conductance K⁺ channels (with conductance 100–300 pS), such as BK and bacterial KcsA channels, could potentially pose a significant barrier for ion permeation. However, when the crystallized portion of the T1 domain is deleted from Shaker B channel, single-channel conductance remains unchanged or even decreases slightly. Furthermore, internal TEA block is not affected by the deletion and blockage by Shaker B ball peptide has slightly lower on rate compared with control (Kobertz and Miller, 1999). These findings argue against the possibility that T1 domain functions as a cytoplasmic ion filter in the permeation pathway of Shaker type K_v channels. Another obvious possibility lies in the differences in the S6 transmembrane segments lining the pore, because mutational and chimaeric modifications in the S6 segment of Shaker channels have profound effects on the single-channel conductance and internal QA block (Lopez et al., 1994; Zei et al., 1999; Ding and Horn, 2002). Potentially, the conformation adopted by the S6 segments in the open state can determine the degree of spatial constriction on the ion permeation pathway by the inner pore. In the picture of open conformation suggested by the structure of bacterial MthK channel, the pore-lining segments undergo a hinge motion at a conserved glycine to splay the inner pore wide open (Jiang et al., 2002b). However, recent metal bridge modification studies show that Shaker channels maintain a narrow entrance to the internal cavity even in the open state, in contradiction to the prediction by MthK structure (Webster et al., 2004). Interestingly, the single-channel conductance of MthK channels is ∼200 pS (at −100 mV in 150 mM K⁺) (Jiang et al., 2002a), close to that of BK channels and ∼10 times higher than that of Shaker channels. Therefore it is possible that large conductance K⁺ channels such as BK and KcsA adopt the wide-open conformation suggested by the MthK structure, while small conductance ones such as Shaker open in a significantly different way, in which the four S6 segments maintain a limiting constraint on ion permeation even in the open state.

Trapping or Different Gate?

In contrast to the classic open-channel block mechanism, our data show that the deactivation of BK channels is not slowed by QAs in spite of the fast block kinetics. To explain our data, BK channels must be able to close with a bound QA blocker. In Fig. 9 we proposed two possible schemes whereby this can be achieved: a trap door mechanism, or a free access mechanism. Although our data don't provide information to rule out the second possibility, we currently favor the trapping hypothesis because it requires only minor revision from the structure of other K⁺ channels.

Trapping of QAs was first reported by Armstrong (1971) with nonyltriethylammonium (C₉) in K⁺ channels from squid axon. Although no trapping is evident in normal Shaker K⁺ channels, a point mutation at I470C makes the channel capable of trapping both TEA and C₁₀ (Holmgren et al., 1997). Because I470 corresponds to a residue in bacterial KcsA channel structure that lines the internal cavity, where the QAs are supposed to bind (Zhou et al., 2001), it was proposed that the smaller cysteine side chain makes the cavity larger, enough to fit a QA molecule when the channel is closed (Melishchuk and Armstrong, 2001). In a different type of study, Miller (1987) showed that Ba²⁺ can be trapped inside BK channels by a cytoplasm-facing gate from the intracellular solution, although his study didn't indicate the relative position of the gate to the QA binding site. From these indirect lines of evidence, we tentatively propose that BK channels may possess a gate at a similar location as in other K⁺ channels, likely at the “bundle crossing” of S6 segments (MacKinnon, 2003), but have an enlarged cavity such as proposed for the Shaker I470C mutant. However, our data don't allow us to completely rule out the possibility that the QA binding site is not occluded from the intracellular solution by channel closure, as illustrated in Fig. 9 C. In addition, fast kinetics can also be easily explained if a gate is not present between QA binding site and intracellular solution. Indeed, when Clay (1995) found that TEA didn't result in slower tail currents in squid axon K⁺ channels, he interpreted his data as suggesting that TEA is not a “state-dependent” blocker, although the same data can also be explained by a complete trapping model (Holmgren et al., 1997).

The Mechanism for Faster Deactivation

Regardless of the actual mechanism via which blocked BK channels can close, they have to be able to close faster than unblocked channels in order to speed up the overall deactivation process. The speeding of tail currents was observed with different types of QAs at different concentrations. The degree of speeding by QAs was similar at different membrane potentials or with different internal Ca²⁺ concentrations (unpublished data). We also tried changing extracellular K⁺ concentration, which did not interfere with the speeding of tail currents significantly (unpublished data). At present the actual mechanism that makes a blocked channel close faster is completely elusive to us. One straightforward hypothesis is that the blocker itself, upon binding to the channel, modifies the gating kinetics and/or equilibrium. For example, it has been reported that QA blockers can modify the kinetics of C-type inactivation in Shaker K⁺ channel in the absence of permeant ions (Baukrowitz and Yellen, 1996a,b). Of course, other secondary mechanisms of QAs such as interaction with occupancy of permeant ion binding sites may also contribute.