Elimination of the Slow Gating of Clc-0 Chloride Channel by a Point Mutation

Abstract

The inactivation of the ClC-0 chloride channel is very temperature sensitive and is greatly facilitated by the binding of a zinc ion (Zn²⁺) from the extracellular side, leading to a Zn²⁺-induced current inhibition. To further explore the relation of Zn²⁺ inhibition and the ClC-0 inactivation, we mutated all 12 cysteine amino acids in the channel and assayed the effect of Zn²⁺ on these mutants. With this approach, we found that C212 appears to be important for the sensitivity of the Zn²⁺ inhibition. Upon mutating C212 to serine or alanine, the inactivation of the channel in macroscopic current recordings disappears and the channel does not show detectable inactivation events at the single-channel level. At the same time, the channel's sensitivity to Zn²⁺ inhibition is also greatly reduced. The other two cysteine mutants, C213G and C480S, as well as a previously identified mutant, S123T, also affect the inactivation of the channel to some degree, but the temperature-dependent inactivation process is still present, likewise the high sensitivity of the Zn²⁺ inhibition. These results further support the assertion that the inhibition of Zn²⁺ on ClC-0 is indeed due to an effect on the inactivation of the channel. The absence of inactivation in C212S mutants may provide a better defined system to study the fast gating and the ion permeation of ClC-0.

Introduction

The ClC-0 chloride channel from Torpedo electric organ is thought to be a homodimeric protein containing two ion-permeating pores (Miller and White 1984; Middleton et al. 1994, Middleton et al. 1996; Ludewig et al. 1996). Two different gating mechanisms, fast and slow gating, have been known to control the opening of this channel (for review, see Miller and Richard 1990; Pusch and Jentsch 1994; Foskett 1998). Each pore of the channel can independently open and close on a millisecond time scale, via the fast-gating process. The slow gate, on the other hand, controls the two pores at the same time, with an average transition time on the order of seconds. The opening of the slow gate allows the pore openings to be controlled by the two fast gates, whereas its closure shuts two pores simultaneously and results in a long-lived, zero-conductance inactivated state. At the single-channel level, the inactivated intervals thus interrupt the millisecond opening–closing transitions, leading to a burst-like behavior of channel opening.

Several factors, such as membrane potential and temperature, as well as the chloride ion have been shown to affect the slow gating. Early studies on the channel purified from Torpedo electric organ revealed that the slow gate of the channel favors a nonconducting (inactivated) state upon membrane depolarization (White and Miller 1979; Miller and White 1980; Miller 1982), much like the inactivation process of voltage-gated cation channels. Moreover, the operation of the slow gate is also affected by the chloride gradient across the channel pore (Richard and Miller 1990), and reduction of the extracellular chloride concentration favors the inactivated state (Chen and Miller 1996). Recently, it was found that the slow-gating process of ClC-0 is extremely temperature dependent (Pusch et al. 1997; Chen 1998). The inactivation rate of the channel is speeded up by ∼40-fold as the temperature is increased by 10°C. It was argued based on the high temperature dependence that the gating process may involve a large conformational change in the channel structure (Pusch et al. 1997). We have recently found that the extracellular zinc ion (Zn²⁺) inhibits the wild-type ClC-0 channel with a similar degree of temperature dependence, leading to a conclusion that Zn²⁺ inhibits the channel by inducing the closure of the slow gate (Chen 1998).

That the slow gating may be a very complex process and may involve different parts of the channel protein is also suggested by mutational studies. Several single-point mutations scattered around the whole channel sequence as well as deletion mutations of the COOH terminus of the channel have been shown to alter the voltage dependence or the kinetics of the slow gating (Ludewig et al. 1996, Ludewig et al. 1997a; Fong et al. 1998). Taking advantage of the finding that Zn²⁺ inhibits the channel via an effect on the slow gate, we probe the channel's inactivation process with extracellular Zn²⁺. In the present study, we focus on cysteine residues because of numerous examples of the involvement of cysteine residues in forming the Zn²⁺-binding site (Fersht 1985; Backx et al. 1992; Yellen et al. 1994). With this approach, we have now found that C212 of ClC-0 is important in controlling the Zn²⁺ sensitivity of the channel. Mutation of C212 to serine or alanine greatly reduces the Zn²⁺ sensitivity. At the same time, the mutations appear to eliminate the slow-gating process. These results further support the assertion that the high apparent affinity of Zn²⁺ to inhibit ClC-0 is indeed due to the effect on the slow gating of the channel.

Materials and Methods

Mutagenesis and Channel Expression

Site-specific mutants were generated using recombinant PCR mutagenesis. All 12 cysteine residues of ClC-0 were mutated, one at a time, to serine except C39, C100, and C213, where the substituted amino acids were arginine, threonine, and glycine, respectively. Wild-type ClC-0 (Jentsch et al. 1990) and all the mutants were constructed in the expression vector pBlueScript and the regions generated by PCR were sequenced completely to exclude errors introduced by the polymerase. Capped RNAs of ClC-0 and all the mutants were synthesized from ScaI-linearized DNA (New England Biolabs Inc.) with T3 polymerase (Ambion Inc.). Xenopus oocytes were prepared and injected with RNAs as previously described (Chen 1998).

Macroscopic Current Recording of the Xenopus Oocyte

Whole oocyte ClC-0 current was recorded with a two-electrode voltage clamp amplifier (725C; Warner Instruments) and digitized with Digidata 1200 data acquisition board and pClamp6 software (Axon Instruments). Detailed recording techniques and the confirmation of successful channel expression in Xenopus oocytes have been described (Chen 1998).

To assay the sensitivity of Zn²⁺ inhibition, the bath (external) solution containing Zn²⁺ was ND 96 containing (mM): 96 NaCl, 2 KCl, 1 MgCl₂, 0.3 CaCl₂, 5 HEPES, pH 7.6. The solution to wash out Zn²⁺ had an additional 1 mM CaCl₂ and 1 mM EGTA. The membrane potential of the oocyte was held at −30 mV and the current was monitored with a 100-ms voltage pulse to +40 mV, given every 4–8 s. The steady state P _o–V curve of the fast gate and the activation curve of the slow gate were constructed following previously described protocols (Pusch et al. 1995, Pusch et al. 1997; Chen 1998). In brief, for the P _o–V curve of the fast gate, a −120-mV voltage step was first given to activate the slow gate. The fast gate was then examined with a voltage pulse to +50 mV, followed by different test voltages from +50 or +60 mV to −170 or −160 mV in −20-mV steps. The tail current was measured at −100 mV and the extrapolated value to the beginning of the pulse was normalized to that obtained with the +70- or +80-mV test pulse, yielding the relative P _os at the corresponding membrane potential in the test period. To construct the activation curve of the slow gate, a 7-s prepulse from 0 to −130 or −150 mV in −10-mV steps was given to reach a quasi–steady state opening of the slow gate. The oocyte current was then examined by a 0.8-s test pulse at +40 mV. The current measured at the end of the 0.8-s test pulse was normalized to the maximal value obtained from each oocyte. Because of a paradoxical behavior of the slow gate at membrane potentials more negative than −120 mV (Ludewig et al. 1997a; Chen 1998; Fong et al. 1998), only data points in the voltage range from −120 to 0 mV were shown. Because the channel does not close completely even at very negative membrane potential (Chen and Miller 1996; Ludewig et al. 1997a), records were not leak-subtracted.

ZnCl₂ (J.T. Baker, Inc.) was dissolved in water as 100 mM stock solution, and then added to the ND96 solution to obtain the indicated concentration. The temperature of the bath solution was monitored and controlled by a heater controller (TC 324A; Warner Instruments).

Excised Inside-Out Patch Recording

Inside-out patches (Hamill et al. 1981) were obtained with glass electrodes fire-polished to a resistance of 2–7 MΩ. Single-channel currents were recorded with an Axopatch 200B (Axon Instruments) amplifier. The output of the amplifier was filtered at 200 Hz (−3 dB corner frequency, four-pole Bessel; Dagan Corp.) and digitized at 1 kHz by a Microstar DAP 800 acquisition board (Microstar Laboratories, Inc.) installed in a Pentium computer using home-written software (Chen and Miller 1996). The external (pipette) solution contained (mM): 110 N-methyl-d-glucamine (NMDG)^–Cl, 5 MgCl₂, 1 CaCl₂, 5 HEPES, pH 7.6. The bath solution contained (mM): 110 NaCl, 5 MgCl₂, 5 HEPES, 1 EGTA, pH 7.6. To display the slow-gating transition with long single-channel trace, every 500 sampling points (equivalent to 0.5 s) were averaged and shown as one data point (see Fig. 6 Fig. 7 Fig. 8). In such a compressed time window, the fast-gating transition is no longer visible, but any inactivation event with duration longer than ∼200 ms can be seen as an upward deflection (e.g., see Fig. 6 A). The displays of the fast gating are the original recording traces sampled at 1 kHz.

Figure 6.

Single-channel recordings of (A) Wild-type ClC-0, (B) C213G, and (C) C480S. Continuous recording from excised inside-out patch at a holding potential of −50 mV. The top of each panel shows a 4-min recording in a compressed time window. The bottom is with an expanded time window starting at the position indicated by the arrow. Note that two C213G channels were present in the patch. The temperature during recording was ∼23–25°C.

Figure 7.

(A and B) Single-channel recordings of C212S and C212A. Continuous recording for 5 min in each case at a holding potential of −50 mV. The top of each panel is in a compressed time window. a–d are the recordings starting at the indicated points (arrows) with an expanded time window. The scale bars for the compressed and expanded time windows in A also apply to B. No inactivation event was discernible in both A and B throughout the whole recordings. Temperature was ∼23–24°C. (C) Comparison of cumulative dwell-time distributions of the events at conductance levels D (□), M (•), and U (▴) between wild-type ClC-0 (left) and C212S (right). The recording trace of the wild-type channel used for analysis is the same as the 4-min trace in Fig. 6 A. For C212S, the analyzed trace is the first 4-min recording shown in A. All events in each of the three levels were used for analysis. The numbers of events in levels D, M, and U are: (wild type) 1,399, 7,009, and 5,612; and (C212S) 1,731, 7,822, and 6,092, respectively.

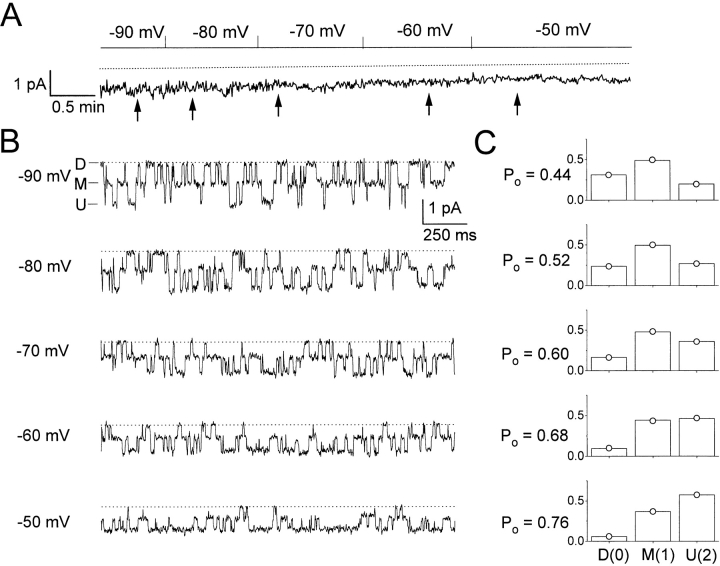
Figure 8.

Binomial distribution of the three current levels in C212S. (A) Continuous 6-min single-channel recording trace at various membrane voltages. Same channel as the one shown in Fig. 7 A. The recording at −50 mV corresponds to the first ∼100-s recording in Fig. 7 A. (B) Representative 2-s recording traces starting at the positions indicated by arrows in A. (C) Open probability of the fast gate (P _o) and the probabilities of the three current levels, f _D, f _M, and f _U, at membrane potentials from −90 (top) to −50 (bottom) mV. The analysis was made on the corresponding regions shown in A, with the length of each segment being: 44 s (−90 mV), 62 s (−80 mV), 70 s (−70 mV), 72 s (−60 mV), and 106 s (−50 mV). The measured state probabilities, f _D, f _M, and f _U, are represented by bars, whereas ○'s denote f ₀, f ₁, and f ₂, the predicted values of state probabilities calculated from P _o.

Data Analysis

Data analysis for macroscopic current was conducted with software programs in pClamp6 (Axon Instruments) and Origin 4.0 (Microcal Software, Inc.). Analysis of the single-channel recording trace was performed with a home-written program (Chen and Miller 1996). Due to a small single-channel current amplitude at voltages close to the reversal potential, the single-channel traces were further digitally filtered at 200–300 Hz, leading to a final filter frequency at ∼140–170 Hz (−3 dB). Missed events were not corrected.

The methods for calculating the open probability and the opening and closing rate constants of the fast gate (see Fig. 9) have been described previously (Miller 1982; Hanke and Miller 1983; Miller and White 1984; Chen and Miller 1996). For the wild-type channel, except where indicated, the inactivation events were first eliminated by eye to isolate the bursts of channel openings. The bursts of channel activity always show three equally spaced conductance states, labeled D, M, and U, corresponding to the opening of 0, 1, and 2 pores, respectively. The probability for the channel to stay at each state, f _D, f _M, and f _U, and the time constants of the dwell-time histograms for those events in the three levels, τ_i, were determined. The open probability of the fast gate was then calculated from the observed state probabilities:

1

Figure 9.

Comparison of single-channel properties of wild-type ClC-0 and C212S. The parameters of the fast gate were calculated from and the single-channel current amplitudes were measured from all-points amplitude histograms. (A) Steady state voltage dependence of the open probability of the fast gate. (B) Opening rate constants of the fast gate as a function of membrane potential. (C) Closing rate constants of the fast gate. (D) Single-channel I–V curves. ○ and ▴ are the current amplitudes of one-pore opening, whereas □ and ▾ are those of two-pore openings. In all panels, solid symbols represent wild-type ClC-0, whereas open symbols are C212S.

The time constants of the distributions, τ_i, were used to determine the opening and closing rate constants, α and β, respectively, of each individual pore:

2

and

3

The gating parameters, P _o, α, and β, for C212S were calculated in the same way except that no event at level D (or nonconducting level) was eliminated. Single-channel current amplitudes were measured from all-points amplitude histograms.

To test the binomial distribution of the three current levels in C212S, theoretical values of the state probabilities were calculated from P _o based on binomial distribution:

4a

4b

and

4c

These calculated values were compared with the measured state probabilities f _D, f _M, and f _U, as shown in Fig. 8 C.

All curve fittings were performed with an unweighted least-squares method. Results are presented as mean ± SEM.

Results

We started with examining the expressions of various cysteine mutants as well as studying their slow-gating behaviors. Fig. 1 A shows the positions of the 12 cysteine residues of ClC-0 based on the putative membrane topology. Among these mutations, 9 of 12 cysteine mutants generated voltage-dependent chloride current similar to that of the wild-type channel. Fig. 2 A shows the quasi–steady state activation curve of the slow gate of wild-type ClC-0. Consistent with previous studies (Pusch et al. 1997; Chen 1998), the open probability of the slow gate is higher at more hyperpolarized membrane potentials. This voltage dependence of the slow gating is different in C212S, C213G, and C480S. These mutants reveal either no voltage dependence (C212S; Fig. 2 B), a reverse voltage dependence with lower open probability at negative potential (C213G; Fig. 2 C), or only slight voltage dependence (C480S; Fig. 2 D). As shown in Fig. 1 B, C212 and C213 of the Torpedo channel are also conserved in ClC-1 and ClC-2, but this conservation occurs only within this branch of the channel family. The channel in the closest branch, for example, ClC-Ka, already loses this conservation. C480 has less conservation, with a corresponding cysteine present only in ClC-1, but not ClC-2. The significance of the conservation of these cysteine residues remains to be determined.

Figure 1.

(A) Positions of cysteine residues of ClC-0. The membrane topology of the top panel was drawn according to Schmidt-Rose and Jentsch 1997, whereas the bottom panel was drawn according to Fahlke et al. 1997. Placing the D8–D9 linker in intracellular side (bottom), however, violates the fact that there is a glycosylation site in this linker (Middleton et al. 1994). (B) Alignment of the amino acid sequences of D5 and D11 from several ClC channels. Stars on top of the sequences denote C212, C213 (in D5), and C480 (in D11) of ClC-0.

Figure 2.

Quasi–steady state activation curves of the slow gate. (A) Wild-type (WT) ClC-0; temperature: 23.7–23.8°C . (B) C212S; temperature: 25.9–27.1°C . (C) C213G; temperature: 20.1–21.1°C . (D) C480S; temperature: 21.5–22.1°C The solid line connecting the adjacent points is a straight line. Insets are the steady state P _o–V curve of the fast gate .

The Zn²⁺ sensitivities of wild-type ClC-0 and the three cysteine mutants are compared in Fig. 3. All of the channels except C212S have a relatively high sensitivity to Zn²⁺ inhibition, with half effective concentrations <10 μM. The remaining current after the inhibition by saturating Zn²⁺ concentration is usually <10–20% of the total current. In contrast, C212S has a lower sensitivity for zinc inhibition. The dose–response curve of zinc inhibition reveals a K _1/2 of ∼50 μM. The most striking observation, however, is the maximal inhibition by Zn²⁺. With a Zn²⁺ concentration as high as 3 mM, the maximal inhibition is <40%.

Figure 3.

Sensitivity of wild-type ClC-0 and cysteine mutants to extracellular Zn²⁺ inhibition. (A) Inhibition by 10 μM extracellular Zn²⁺ on the steady state current of the wild-type channel (WT), C212S, C213G, and C480S. Down- and upward arrows indicate the application and washout of 10 μM Zn²⁺, respectively. Dotted lines represent zero-current level. (B) Dose-dependent inhibition of Zn²⁺ for the four channels shown in A. All data points were the average of 3–11 determinations. The current amplitude was normalized to the value right before the application of Zn²⁺. Solid curves were drawn according to a Langmuir function: , with values of K _1/2 and I _∞: (wild type) 1.0 μM and 0.87; (C212S) 47.5 μM and 0.33; (C213G) 3.5 μM and 0.78; (C480S) 9.3 μM and 0.88.

Thus, there seems to be at least two different ways for Zn²⁺ to inhibit these channels. The one with higher apparent affinity (K _1/2 < 10 μM) in wild-type ClC-0, C213G, and C480S is eliminated by a mutation at C212. This Zn²⁺ effect has previously been shown to be due to an effect on the entropy of the free energy involved in the slow-gating transition. Because a change of entropy is equivalent to a change in temperature in terms of their contributions to the free energy of the inactivation process (Chen 1998), we examine the slow gating with the temperature-jump experiment as shown in Fig. 4. For the wild-type channel, raising the temperature of the bath solution leads to an initial increase in the current amplitude, followed by a current reduction (Fig. 4 A). The initial increase of the current is likely due to a larger single-channel conductance, whereas the current reduction is due to the closure of the slow gate (Pusch et al. 1997). In the three mutants shown here (Fig. 4, B–D), only C212S does not show the current reduction phase, suggesting that the slow gating of C212S may be eliminated by a single conserved mutation, thus rendering the channel insensitive to the Zn²⁺ inhibition. The conclusion is further supported by examining the temperature dependence of the current increase upon raising the temperature. The Q₁₀ of the current increase seen with C212S is ∼1.4 (Fig. 5), a value similar to the temperature dependence of the diffusion rate (Hille 1992). Thus, the increase of the steady state current in C212S upon temperature jump appears to result from the increase of the single-channel conductance.

Figure 4.

Temperature dependence of macroscopic current. The temperatures T₁ and T₂ were (°C): (A) Wild-type ClC-0, 22.0 and 28.7 . (B) C212S, 22.0 and 28.8 . (C) C213G, 20.7 and 30.0 . (D) C480S, 22.3 and 28.5 . All current values were normalized to the amplitude of the first data point and the dotted lines represent the zero-current level.

Figure 5.

Temperature dependence of the macroscopic current of C212S. (A) Temperature-jump experiments showing different degrees of the increase in the steady state current. All current amplitudes are normalized to the value of the first point and the dotted lines are the zero-current level. All data points were from the average of four measurements. (B) Temperature-dependent increase of the whole oocyte current. I₁ was measured right before the increase of the temperature, whereas I₂ was measured near the end of the temperature jump. The solid line is the best fit to a linear equation , with a fitted . Data points were from the average of four to six measurements.

To examine whether the inactivation of C212 mutants is indeed eliminated, we employed single-channel recordings on inside-out membrane patches excised from Xenopus oocytes. In these recordings, symmetrical chloride concentrations were applied on both sides of the membrane patch and the membrane potential was held at −50 mV. In the wild-type channel, there is a gating transition with average time on the order of seconds, a typical inactivation process (Fig. 6 A) that is also present in C213G and C480S (Fig. 6B and Fig. C). The probability of the inactivated state and the kinetics of the slow-gating process in C213G and C480S, however, are different from those of wild-type ClC-0. Although an accurate determination of the inactivation probability may require a longer recording trace because of the slow behavior of the process, several minutes of the recording can provide a rough estimate. For C213G, the inactivation probability is usually >50%. For C480S, the probability of the inactivation state is rather small (∼0.1–5%), consistent with the small amount of current reduction in the temperature-jump experiment (Fig. 4 D). In the C212 mutants, the slow-gating transitions of both C212S and C212A are absent (Fig. 7A and Fig. B). In all our recordings with good quality (∼100 min for C212S, ∼20 min for C212A), we did not observe any nonconducting event with duration longer than 500 ms. There are, however, very rare occasions of long closings of an individual pore (Fig. 7 B, arrowheads) as described previously in the wild-type channel (Ludewig et al. 1997b).

The absence of a relatively long nonconducting event in the C212 mutants, though indicative of a change in the slow-gating process, may not truly reflect the absence of the inactivation event. One could argue that the inactivation event may be shortened by the mutation so that it is not possible to differentiate the closed from the inactivated state based on the duration of nonconducting events. This situation was recently found in the ClC-1 channel, in which the average time of the slow-gating transition is only threefold larger than that of the fast-gating process, rendering a clear dissection of these two gating processes rather difficult (Saviane et al. 1999). However, it was shown in the same study that if all nonconducting events were considered as closed rather than inactivated states, the dwell-time distribution of these events could not be described by a single-exponential function and the probabilities of the three current levels of ClC-1 would depart from a binomial distribution. We therefore analyzed the single-channel recording trace of C212S in more detail. Fig. 7 C shows that, without eliminating any nonconducting event, the dwell-time distribution of zero-current events of C212S is well described by a single-exponential function, whereas that of the wild-type channel is not. In addition, the three current levels of C212S follow a perfect binomial distribution (Fig. 8). These results indicate that the nonconducting events of C212S indeed do not include inactivation events. Most (or all) of them appear to result from the simultaneous closure of the two independent fast gates.

The effect of C212 mutation appears to be quite specific for the slow-gating process of the channel. The fast-gate open probability (Fig. 9 A), the rate constants of the activation (opening rate, Fig. 9 B), and the deactivation (closing rate, Fig. 9 C) of the fast gate as well as the single-channel conductance (Fig. 9 D) are almost identical between wild-type ClC-0 and C212S. The elimination of the slow gating in C212S, therefore, explains why the channel is not sensitive to Zn²⁺ inhibition.

Thus, probing the channel's inactivation process with Zn²⁺ indicates that the high affinity block of the channel by Zn²⁺ is present only when the inactivation process exists. We have also tested this hypothesis with a previously identified slow-gating mutant, S123T (Ludewig et al. 1996). Although the voltage dependence of the slow gating was altered, inactivation events were still present in this mutant as examined at the single-channel level (Ludewig et al. 1996). Fig. 10 shows the voltage and temperature dependence of the slow gating as well as the Zn²⁺ sensitivity of S123T. Although the voltage dependence is reversed, the temperature dependence of the slow gating is obviously present, likewise the high apparent affinity for Zn²⁺ inhibition. These results are consistent with the hypothesis that the effect of Zn²⁺ is on the temperature-dependent process of the slow gating.

Figure 10.

Probing the slow gate of S123T. (A) Quasi–steady state activation curve off the slow gate. (B) Temperature dependence of the macroscopic current from the whole oocyte. (C) Dose-dependent inhibition of the channel by extracellular Zn²⁺. The solid curve is drawn according to the Langmuir function described in Fig. 3, with K _1/2 and I_∞: 1.72 μM and 0.85 .

Discussion

The present study was initiated with an intention to search for the possible Zn²⁺-binding site responsible for the extracellular Zn²⁺ inhibition (Chen 1998). We started with mutating all cysteine residues of ClC-0 one at a time, followed by examining their Zn²⁺ sensitivity. We have indeed found a cysteine mutant with an altered Zn²⁺ sensitivity. As shown in Fig. 3, a conserved point mutant C212S still retains >60% of the current after applying 3 mM extracellular Zn²⁺. On the other hand, the inhibition of Zn²⁺ on the wild-type channel, which has been shown to be due to an effect on the slow gating of the channel, has an apparent affinity of only ∼1 μM (Fig. 3; see also Chen 1998).

Thus, it seems that there are at least two ways for Zn²⁺ to inhibit the channel. Zn²⁺ at a low micromolar concentration induces the closure of the slow gate of ClC-0, resulting in the steady state current inhibition (Chen 1998). On the other hand, the partial inhibition seen on C212S requires a higher concentration of Zn²⁺. The on and off rates of this partial inhibition have little temperature dependence (data not shown), a phenomenon also different from that found in the wild-type channel (Chen 1998). Although we do not understand the exact mechanism for the partial inhibition of C212S, there are several possibilities. First, the inhibition of C212S by high concentrations of Zn²⁺ may be due to a mechanism totally unrelated to the slow gating, such as a reduction of the single-channel conductance or a change of an unrelated gating process. On the other hand, it is equally possible that the Zn²⁺ inhibition of C212S is on the remaining inactivation process. For example, if the inactivation process of wild-type ClC-0 is composed of multiple sequential steps, it is fully conceivable that a high concentration of Zn²⁺ is necessary for the channel to achieve the first step of very short-lived closure, which is followed by a highly temperature-dependent gating step leading to a deep inactivated state. For the C212S mutant, because the latter step is removed, Zn²⁺ is unable to drive the channel into the deep inactivated state.

Although we have found that mutation of a cysteine residue appears to greatly reduce the sensitivity of the channel to Zn²⁺ inhibition, we are unable to conclude that C212 is responsible for the Zn²⁺ binding site for an obvious reason. Mutation at the C212 position appears to eliminate the slow-gating transition, it is thus expected that the channel loses its sensitivity to Zn²⁺ inhibition if the effect of Zn²⁺ is indeed on the slow gate. In the >100-min recordings we made on C212S and C212A with good quality, we did not observe any nonconducting event with duration longer than 500 ms. We did, however, observe long closings of an individual pore, which was also found in the wild-type channel (Fig. 7 B). It was speculated that such rarely occurring channel behavior that deviates from the binomial distribution may be due to a different gating process (Ludewig et al. 1997b). The conserved mutation at the 212 position appears not to alter this obscure gating mechanism.

Inspection of the single-channel recording trace thus provides a direct way to evaluate the presence of the long-lived inactivated state. Nonetheless, one may argue that the duration of the inactivation events could be shortened by the mutation and it may then be difficult to visually dissect the inactivated from the closed events. However, if the nonconducting level of C212S indeed contains two populations of events that do not have the same average event duration, the dwell time of these nonconducting events would not have revealed a single-exponential distribution (Fig. 7 C). Furthermore, analysis of the single-channel recording trace of C212S without eliminating any nonconducting event reveals that the three current levels follow a perfect binomial distribution (Fig. 8). This indicates that if the slow gate of C212S or C212A is still present, its probability at the nonconducting state must be extremely low.

We have also applied the same three tests to examine the slow gating of S123T, a previously identified mutant of slow gating (Ludewig et al. 1996). Consistent with the previous report, the voltage dependence of the slow gating for this mutant has been altered, but the channel still retains relatively high sensitivity to Zn²⁺ inhibition and shows a current reduction phase in the temperature-jump experiment (Fig. 10). This is consistent with previous results that the channel still showed prominent inactivation at the single-channel level (Ludewig et al. 1996).

The high sensitivity of Zn²⁺ inhibition on the slow-gating mutants correlates well with the temperature dependence of the macroscopic current reduction and the presence of the inactivation process. These results thus provide further support to the conclusion that the inhibition of ClC-0 by low concentration of Zn²⁺ is due to the facilitation of the inactivation process via a change in the entropy of the free energy involved in the slow-gating process (Chen 1998). The conserved change of cysteine to serine or alanine at position C212 appears to have a rather specific effect on the slow gating of the channel. The steady state P _o–V curve and the kinetics of the fast-gating process of C212S does not show significant difference from those of the wild-type channel (Fig. 2A and Fig. B, insets). The single-channel recording not only confirms this conclusion, but also reveals that the conductance of C212S is the same as that of wild-type ClC-0 (Fig. 7 C and 9). The only difference that we can so far identify between the wild-type channel and C212S is the presence of the inactivated state. That a single conserved mutation of ClC-0 specifically eliminates a gating transition with a very high activation energy (Pusch et al. 1997; Chen 1998) raises an interesting question regarding the underlying inactivation mechanism. Clearly, C212 by itself does not account for the structural basis of the slow gating because mutations at other places in the channel alter the properties of the slow gating (Ludewig et al. 1996, Ludewig et al. 1997a; Fong et al. 1998). Furthermore, the residue is conserved in ClC-1 (Fig. 1 B), but this muscle chloride channel shows a common gate very different from the slow gating of ClC-0 in the gating kinetics and voltage dependence (Saviane et al. 1999). The slow-gating transition of ClC-0 is thought to be related to the chloride flux across the channel pore (Richard and Miller 1990). Although C212S does not show difference in the single-channel conductance from the wild-type channel, the possibility that the 212 position is located in the channel pore has not been ruled out, given the nearby regions in ClC-1 channel were implicated as pore segments (Fahlke et al. 1997). It would be interesting to further examine this possibility by studying the permeation properties of C212 mutants with respect to different permeant ions.