Ph-Dependent Inhibition of Voltage-Gated H⁺ Currents in Rat Alveolar Epithelial Cells by Zn²⁺ and Other Divalent Cations

Abstract

Inhibition by polyvalent cations is a defining characteristic of voltage-gated proton channels. The mechanism of this inhibition was studied in rat alveolar epithelial cells using tight-seal voltage clamp techniques. Metal concentrations were corrected for measured binding to buffers. Externally applied ZnCl₂ reduced the H⁺ current, shifted the voltage-activation curve toward positive potentials, and slowed the turn-on of H⁺ current upon depolarization more than could be accounted for by a simple voltage shift, with minimal effects on the closing rate. The effects of Zn²⁺ were inconsistent with classical voltage-dependent block in which Zn²⁺ binds within the membrane voltage field. Instead, Zn²⁺ binds to superficial sites on the channel and modulates gating. The effects of extracellular Zn²⁺ were strongly pH_o dependent but were insensitive to pH_i, suggesting that protons and Zn²⁺ compete for external sites on H⁺ channels. The apparent potency of Zn²⁺ in slowing activation was ∼10× greater at pH_o 7 than at pH_o 6, and ∼100× greater at pH_o 6 than at pH_o 5. The pH_o dependence suggests that Zn²⁺, not ZnOH⁺, is the active species. Evidently, the Zn²⁺ receptor is formed by multiple groups, protonation of any of which inhibits Zn²⁺ binding. The external receptor bound H⁺ and Zn²⁺ with pK _a 6.2–6.6 and pK _M 6.5, as described by several models. Zn²⁺ effects on the proton chord conductance–voltage (g _H–V) relationship indicated higher affinities, pK _a 7 and pK _M 8. CdCl₂ had similar effects as ZnCl₂ and competed with H⁺, but had lower affinity. Zn²⁺ applied internally via the pipette solution or to inside-out patches had comparatively small effects, but at high concentrations reduced H⁺ currents and slowed channel closing. Thus, external and internal zinc-binding sites are different. The external Zn²⁺ receptor may be the same modulatory protonation site(s) at which pH_o regulates H⁺ channel gating.

INTRODUCTION

Voltage-gated proton channels differ from other voltage-gated ion channels, not only in their extreme selectivity for H⁺, but also in the regulation of their gating by pH_o and pH_i. The mechanism of permeation is believed to differ radically from traditional ion channels, which comprise water-filled pores through which ions diffuse: proton channels appear to conduct H⁺ by a Grotthuss-like mechanism of hopping across a hydrogen-bonded chain spanning the membrane (DeCoursey and Cherny 1994, DeCoursey and Cherny 1995, DeCoursey and Cherny 1997, DeCoursey and Cherny 1998; Cherny et al. 1995). If ion channels are defined narrowly as water-filled pores, then proton channels are not ion channels, although they conduct protons passively down their electrochemical gradient, and independently of other ionic species. In spite of these fundamental differences, it is remarkable how closely proton channels resemble other voltage-gated channels. H⁺ channels activate upon depolarization with a sigmoidal time course, deactivate exponentially, and exhibit a Cole-Moore effect (DeCoursey and Cherny 1994) practically indistinguishable from the behavior of delayed rectifier K⁺ channels (Cole and Moore 1960). Low pH_o shifts the voltage-activation curves of both H⁺ channels and other ion channels toward positive potentials and slows activation at a given voltage. Voltage-gated proton channels characteristically are inhibited by extracellular polyvalent cations. The transition metals Zn²⁺ and Cd²⁺ have been used most frequently (Thomas and Meech 1982; Byerly et al. 1984; Barish and Baud 1984; Mahaut-Smith 1989; DeCoursey 1991; Kapus et al. 1993; Demaurex et al. 1993; DeCoursey and Cherny 1993; Humez et al. 1995; Gordienko et al. 1996; Nordström et al. 1995), but Cu²⁺, Ni²⁺, Co²⁺, Hg²⁺, Be²⁺, Mn²⁺, Al³⁺, and La³⁺ have similar effects (Thomas and Meech 1982; Meech and Thomas 1987; Byerly and Suen 1989; Bernheim et al. 1993; DeCoursey and Cherny 1994; Eder et al. 1995). To the extent that each has been explored, all of these metal cations shift the voltage dependence of activation (channel opening) to more positive potentials and slow the opening rate (Byerly et al. 1984; Barish and Baud 1984; Meech and Thomas 1987; Mahaut-Smith 1989; DeCoursey 1991; DeCoursey and Cherny 1993; Demaurex et al. 1993; Kapus et al. 1993; Nordström et al. 1995; Gordienko et al. 1996). These effects resemble those of polyvalent cations on other ion channels (e.g., Frankenhaeuser and Hodgkin 1957; Hille 1968; Stanfield 1975; Gilly and Armstrong 1982; Spires and Begenisich 1992, Spires and Begenisich 1995; Arkett et al. 1994). Closer examination reveals differences, however. The H⁺ channel is much more sensitive to external ZnCl₂ than are voltage-gated K⁺ channels, which require 1,000-fold higher concentrations to produce comparable effects in squid (Spires and Begenisich 1992), 10–100-fold higher concentrations in frog skeletal muscle (Stanfield 1975), and 100-fold higher concentrations in Shaker (Spires and Begenisich 1994). In addition, the effects of ZnCl₂ on squid axon K⁺ channels are similar for addition to either side of the membrane and internally applied ZnCl₂ is quite potent (Begenisich and Lynch 1974). In contrast, we find that ZnCl₂ has qualitatively different effects on H⁺ channels depending on the side of application and thus binds to distinct external and internal sites.

The effects of metal cations on H⁺ currents have been characterized variously as voltage-dependent block, voltage shifts induced by electrostatic effects on the voltage sensor, and specific binding to the channel. These interpretations invoke different mechanisms. Voltage-dependent block suggests that the metal ion enters the channel and crosses part of the membrane potential field to reach its block site in the pore. Here we explore the effects of ZnCl₂, one of the more potent inhibitors of H⁺ channels, as a prototypical metal inhibitor. We find that voltage-dependent block is not a viable mechanism. Prominent effects of Zn²⁺ reflect specific binding that allosterically alters gating.

A key feature of the inhibition of H⁺ currents by Zn²⁺ is a profound pH dependence, which has not been described previously. Lowering pH_o decreases the effectiveness of ZnCl₂. Competition between Zn²⁺ and H⁺ has been noted previously for other channels, including Cl⁻ (Hutter and Warner 1967; Spalding et al. 1990; Rychkov et al. 1997) and K⁺ (Spires and Begenisich 1992, Spires and Begenisich 1994). We consider whether the pH_o dependence indicates that (a) the active form is not Zn²⁺ but ZnOH⁺, (b) Zn²⁺ and H⁺ compete for the same binding site, or (c) there is noncompetitive inhibition; i.e., protonated channels have a lower affinity for Zn²⁺. We conclude that the external Zn²⁺ receptor is formed by three or more protonation sites, perhaps comprising His residues, that together coordinate one Zn²⁺.

MATERIALS AND METHODS

Rat Alveolar Epithelial Cells

Type II alveolar epithelial cells were isolated from adult male Sprague-Dawley rats using enzyme digestion, lectin agglutination, and differential adherence, as described in detail elsewhere (DeCoursey et al. 1988; DeCoursey 1990), with the exception that we now use elastase without trypsin to dissociate the cells. The rats were anesthetized using sodium pentobarbital. In brief, the lungs were lavaged to remove macrophages, elastase was instilled, and then the tissue was minced and forced through fine gauze. Lectin agglutination and differential adherence further removed contaminating cell types. The preparation at first includes mainly type II alveolar epithelial cells, but after several days in culture the properties of the cells are more like type I cells. H⁺ currents were studied in approximately spherical cells up to several weeks after isolation.

Solutions

Solutions contained 100 mM buffer supplemented with tetramethylammonium (TMA) methanesulfonate (TMAMeSO₃) to bring the osmolarity to ∼300 mOsm. One exception was the pH_o 7.0 solution made with 70 mM PIPES. External solutions contained 2 mM CaCl₂ or 2 mM MgCl₂. Internal solutions contained 2 mM MgCl₂ and 1 mM EGTA. Solutions were titrated to the desired pH with TMA hydroxide (TMAOH) or methanesulfonic acid (solutions using BisTris as a buffer). A stock solution of TMAMeSO₃ was made by neutralizing TMAOH with methanesulfonic acid. TPEN (N,N,N ′,N ′-tetrakis(2-pyridylmethyl)ethylenediamine) was purchased from Sigma Chemical Co.

Buffers and Their Metal Binding Properties

The following buffers were used near their negative logarithm of the acid dissociation constant (pK _a) (at 20°C) for measurements at the following pH: pH 5.0, Homopipes (homopiperazine-N,N ′-bis-2-(ethanesulfonic acid), pK _a 4.61); pH 5.5–6.0 Mes (pK _a 6.15); pH 6.5 BisTris (bis[2-hydroxyethyl]imino-tris[hydroxymethyl]methane, pK _a 6.50); pH 7.0 PIPES (pK _a 6.80); pH 7.5–8.0 HEPES (pK _a 7.55). Buffers were purchased from Sigma Chemical Co., except for Homopipes (Research Organics). Buffers such as Tricine and BES that reportedly complex strongly with transition metals (Good et al. 1966) were avoided. We could not find information in the literature on the Zn²⁺ or Cd²⁺ binding properties of the buffers used. Therefore, we measured the binding constants for a number of buffers, according to the method described by Good et al. 1966. This consisted of titrating the buffer alone, and then together with an equimolar amount of the metal salt (usually 10 mmol in a 100-ml vol). The binding constant was calculated from the relationship ():

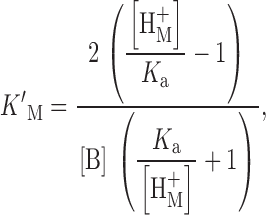1

where K ′_M is the metal binding constant, K _a is the proton dissociation constant defined in Fig. 3 (−pK _a value), [H⁺ _M] is the H⁺ concentration at the midpoint of the titration curve in the presence of the metal being tested and [B] is the total buffer concentration. The higher the affinity of the buffer for metal, the greater the shift in the titration curve. Table gives the results.

Scheme S3.

Table 1.

Affinity Constants of Buffers for Divalent Metals at 20°C

	pK a at 20°C	Metal binding constant (log K′M)
Buffer	Measured (nominal)	Cu2+	Zn2+	Cd2+	Ca2+	Ni2+
Homopipes	4.51 ± 0.04 (8)	—	0.8 (2)	0.9 (3)	NS (1)	0.2 (2)
	[4.61]
Mes	6.23 ± 0.05 (7)	—	0.8 (2)	1.2 (2)	NS	0.4 (2)
	[6.15]	NS*			0.7*
BisTris	6.52 ± 0.06 (8)	—	2.2 (2)	1.9 (2)	2.0 (2)	3.3 (2)
	[6.46]
PIPES	6.96‡ ± 0.07 (10)	—	1.1 (3)	0.6 (3)	1.1 (2)	1.3 (2)
	[6.80]	NS*			NS*
BES	7.18 ± 0.07 (7)	—	1.7 (2)	1.6 (2)	—	2.5 (2)
	[7.17]	3.5*			NS*
HEPES	7.55 ± 0.09 (9)	—	NS (2)	1.3 (4)	NS (1)	0.8 (2)
	[7.55]	NS*			NS*
Tricine	8.16 ± 0.04 (8)	—	5.2 (2)	4.3 (2)	2.3 (2)	5.7 (2)
	[8.15]	7.3*			2.4*

Note that this table gives the metal binding constant, K ′_M, as used for this purpose by Good et al. 1966, which is the inverse of K _M, as defined in Fig. 2. Thus, log K ′_M is the same as pK _M; i.e., a large number means high affinity binding. The pK _a values for buffers measured at the same time as metal binding determinations are given as mean ± SD (n) to indicate the variability of the measurements. Nominal pK _a values [n] are apparent “practical” values at 20°C and 0.1 M (Perrin and Dempsey 1974), except that for Homopipes, which was taken from the manufacturer's literature. K ′_M values were measured at room temperature (20–22°C) and calculated as described in materials and methods from the change in pK _a of the buffer titrated in the absence or presence of equimolar ZnCl₂ or other metal (Good et al. 1966). Values were calculated from the average shift in pK _a in (n) determinations, thus errors are not given. For NS entries, the measured pK _a values ± metal were indistinguishable. Values of log K ′_M < 1 are effectively negligible, because log K ′_M = 0.7 if ΔpK _a is 0.02 U, a barely detectable difference. *K ′_M values for Ca²⁺ and Cu²⁺ from Good et al. 1966 are given for comparison. ^‡The pK _a given is pK ₂ for titrating the acid, with pK ₁ occurring at pH < 3 (Good et al. 1966).

Good et al. 1966 reported that the affinity of several buffers for Ca²⁺ was generally about five log units weaker than that for Cu²⁺. A notable exception is Mes, which binds Ca²⁺ weakly but Cu²⁺ negligibly (Good et al. 1966). We find that Zn²⁺ is bound roughly two log units more weakly than Cu²⁺, consistent with the lower affinity binding of Zn²⁺ than Cu²⁺ to various ionizable groups on proteins (Breslow 1973). One exception to this rule is that PIPES did bind Zn²⁺ weakly, whereas Cu²⁺ was bound negligibly (Good et al. 1966). All buffers bound Cd²⁺ detectably and to roughly the same extent that they bound Zn²⁺. It should be noted that Table lists log metal dissociation constant (K _M) values, and that a value <1.3 indicates that >50% of the total metal remains unbound. Thus, much of the binding indicated is rather weak and does not preclude using these buffers in studies of metals.

Solubility of Zn(OH)₂ and Other Metal Dihydroxides

An upper limit to the concentration of ZnCl₂ is set by the limited solubility of Zn(OH)₂ (K _sp ≥ ∼4 × 10⁻¹⁷; Lide 1995). The maximal soluble concentrations: ∼40 μM at pH 8, ∼4 mM at pH 7, and ∼400 mM at pH 6, were not approached during experiments. We encountered solubility problems when titrating the buffers to test for metal binding (above). For this purpose, we usually used 10 mM ZnCl₂, and in fact the solutions began to precipitate just above pH 7. To extend the pH range, buffers with higher pK _a were titrated at 1 instead of 10 mM. The dihydroxide of Cd²⁺ is somewhat more soluble (K _sp 5.27 × 10⁻¹⁵; Lide 1995) than that of Zn²⁺, and the maximal attainable concentration is ∼5 mM at pH 8, so solubility was less of a problem. However, when the metal titrations exceeded pH ∼8, precipitation commenced.

Electrophysiology

Conventional whole-cell, cell-attached patch, or inside-out patch configurations were used. Inside-out patches were formed by lifting the pipette into the air briefly. Micropipettes were pulled using a Flaming Brown automatic pipette puller (Sutter Instruments, Co.) from EG-6 glass (Garner Glass Co.), coated with Sylgard 184 (Dow Corning Corp.), and heat polished to a tip resistance ranging typically from 3 to 10 MΩ. Electrical contact with the pipette solution was achieved by a thin sintered Ag-AgCl pellet (In Vivo Metric Systems) attached to a Teflon-encased silver wire. A reference electrode made from a Ag-AgCl pellet was connected to the bath through an agar bridge made with Ringer's solution. The current signal from the patch clamp (List Electronik) was recorded and analyzed using a Laboratory Data Acquisition and Display System (Indec Corp.). Seals were formed with Ringer's solution (mM: 160 NaCl, 4.5 KCl, 2 CaCl₂, 1 MgCl₂, 5 HEPES, pH 7.4) in the bath, and the zero current potential established after the pipette was in contact with the cell. Bath temperature was controlled by Peltier devices, and monitored by a resistance temperature detector element (Omega Scientific) in the bath.

Because the voltage dependence of H⁺ channel gating depends strongly on ΔpH, the threshold for activation ranging from −80 to +80 mV at ΔpH 2.5 and −1.5, respectively (Cherny et al. 1995), the holding potential, V_hold, must be adjusted appropriately. V_hold was set sufficiently negative to the threshold of activation at each ΔpH to avoid Cole-Moore effects (DeCoursey and Cherny 1994), but positive enough to avoid unnecessarily large voltage steps.

Conventions

We refer to pH in the format pH_o//pH_i. In the inside-out patch configuration, the solution in the pipette sets pH_o, defined as the pH of the solution bathing the original extracellular surface of the membrane, and the bath solution sets pH_i. Currents and voltages are presented in the normal sense; that is, upward currents represent current flowing outward through the membrane from the original intracellular surface, and potentials are expressed by defining the original bath solution as 0 mV. Current records are presented without correction for leak current or liquid junction potentials.

Data Analysis

The time constant of H⁺ current activation, τ_act, was obtained by fitting the current record by eye with a single exponential after a brief delay (DeCoursey and Cherny 1995) ():

2

where I ₀ is the initial amplitude of the current after the voltage step, I _∞ is the steady state current amplitude, t is the time after the voltage step, and t _delay is the delay. The H⁺ current amplitude is (I ₀ − I _∞). No other time-dependent conductances were observed consistently under the ionic conditions employed. Tail current time constants, τ_tail, were fitted to a single exponential ():

3

where I ₀ is the amplitude of the decaying part of the tail current.

Data are presented as mean ± SD or SEM, as indicated. Significance of differences between groups was calculated by two-tailed student's t test.

RESULTS

Effects of Extracellular ZnCl₂ on H⁺ Currents

The inhibition of H⁺ currents by external ZnCl₂ is illustrated in Fig. 1. The H⁺ current elicited by a pulse to +10 mV is reduced in a concentration-dependent manner by ZnCl₂. The rate the current turns on during a depolarizing voltage pulse is slower, as seen more clearly in Fig. 1 B, where the currents are scaled to the same value at the end of the pulse. Another effect (explored below) is to shift the voltage dependence of H⁺ channel gating to more positive voltages. To some extent, the reduced H⁺ current amplitude and slower activation can be attributed to this voltage shift. One implication is that any attempt to quantitate the apparent “block” of H⁺ currents by ZnCl₂ by measuring the current at the end of a pulse will be arbitrary because the result depends strongly on the length of the pulse and the voltage selected for the measurement. The apparent extent of block at the end of the pulses in Fig. 1 would be greatly reduced if longer test pulses were applied and especially if a more positive test potential were selected.

Figure 1.

(A) Effects of ZnCl₂ on the H⁺ current elicited by a 4-s pulse to +10 mV in a cell studied at pH 7.0//5.5. The inset shows the pH of the pipette and bath solutions. (B) The same currents scaled to the same value at the start and end of the 4-s pulse, illustrating the slowing of the activation time course. The steps in the 10 μM record are due to the resolution of the A–D converter.

Zn²⁺ Block Is Not Voltage Dependent

If ZnCl₂ binds with rapid kinetics to a site in the H⁺ channel within the membrane electrical field, this should manifest itself in the instantaneous current–voltage relationship. The control instantaneous current–voltage (I-V) relationship in Fig. 2 A (•) exhibits moderate outward rectification, consistent with previous studies (Byerly et al. 1984; Kapus et al. 1993; Bernheim et al. 1993; Cherny et al. 1995; DeCoursey and Cherny 1996). The instantaneous I-V relationship in the presence of 10 μM ZnCl₂ (▪) is also plotted. The currents are reduced even though the prepulse was 40 mV more positive. After both sets of currents are scaled to match at +100 mV (Fig. 2 B), the currents superimpose, indicating that there is no rapid voltage-dependent block. In some experiments with CdCl₂, there was a suggestion that the inward currents were reduced preferentially, but this effect was too small to be sure of, even with data spanning 200 mV. Thus, metals have negligible effects on the instantaneous I-V relation of H⁺ channels.

Figure 2.

(A) Instantaneous current–voltage relationships in a cell studied at pH 7.0//6.5 before (•) and after (▪) addition of 10 μM ZnCl₂ to the bath. A prepulse to +40 mV for control and +100 mV in the presence of ZnCl₂ was applied to open H⁺ channels, followed by a test pulse to the voltage on the abscissae. The current at the start of the test pulse, after the capacitive transient, is plotted. (B) Data from A after correction for the current at the end of the prepulse, and normalized to be equal at +100 mV. Dividing the test current by that at the end of the prepulse corrects for variation in the activation of the g _H during different prepulses. The symbols have the same meaning as in A.

The effects of ZnCl₂ and other metals might reflect voltage-independent interaction of the metal with the channel or nearby membrane. By binding to or screening negative charges near the external side of the H⁺ channel, metals could bias the membrane potential sensed by the channel's voltage sensor (Frankenhaeuser and Hodgkin 1957). In the simplest scenario, the voltage-dependent properties of the channel will simply shift along the voltage axis. Fig. 3 A illustrates proton chord conductance (g _H)–V relationships in one cell in the absence (dashed lines) or presence of 100 μM ZnCl₂ (⋄), 10 mM NiCl₂ (▵), or several concentrations of CdCl₂ (solid symbols). When shifted along the voltage axis, the g _H-V relationships appear quite similar (Fig. 3 B), consistent with this mechanism. These metals may reduce the limiting g _H (g _H,max) slightly, although for the data shown here this effect was smaller than the variability in the control measurements. At higher metal concentrations, some reduction in g _H,max usually became evident, but was difficult to measure accurately. In Fig. 3 C, the g _H-V relationships are plotted on linear axes, scaled to the same g _H,max to illustrate their similar shape and slope. The predominant effect is a simple voltage shift.

Figure 3.

Effects of divalent metals on the g _H-V relationship are incompatible with the idea of voltage-dependent block. (A) The g _H-V relationships in a cell studied in the presence of several metals: controls (dashed lines), 0.1 mM CdCl₂ (•), 1 mM CdCl₂ (▾), 10 mM CdCl₂ (▪), 10 mM NiCl₂ (▵), and 0.1 mM ZnCl₂ (⋄). The sequence was control, all CdCl₂ concentrations, control, NiCl₂, ZnCl₂, and control. (B) The same g _H-V relationships in A shifted along the voltage axis so that they superimpose at small g _H. Other than small differences in the limiting g _H,max, the shape of the voltage dependence appears similar. The voltage shifts applied were: 0, +8, and +34 mV for 0.1, 1.0, and 10 mM CdCl₂, respectively, +15 mV for NiCl₂ and +18 mV for ZnCl₂. (C) The same g _H-V relationships plotted on linear axes and scaled to have similar g _H,max appear to simply shift along the voltage axis. The scale factor was determined by taking the ratio of g _H in the presence of metal to that at +80 mV in the first control measurement. To compensate for the apparent voltage shift (compare A and B), the g _H value used for this purpose for the metal data was shifted by 10 mV (1 mM CdCl₂, 10 mM NiCl₂), 20 mV (ZnCl₂), or 30 mV (10 mM CdCl₂). All scale factors were <2.5. (D) The steepness of the apparent voltage dependence of “block” by divalent cations is similar to that of the g _H-V relationship itself. The data in C are plotted as a ratio of the g _H in the presence of metal to that in its absence, at each voltage, using the same symbols as other parts of this figure. There is no block at any voltage at 0.1 mM CdCl₂ (•). The control g _H-V relationship (C, dashed line) was fitted to a simple Boltzmann distribution and normalized to its fitted maximum. The slope factors of Boltzmann fits were 12.5 mV for control, and for metal ranged from 8 to 13 mV in fits constrained to limit at 1.0.

Even though there is no rapid voltage-dependent block (Fig. 2), the apparent voltage shift might conceivably reflect a slow block/unblock process. If we estimate the steady state voltage dependence of this apparent ZnCl₂ block in the usual manner by plotting the ratio I _H(ZnCl₂)/I _H(control), the apparent block is quite steep. Fig. 3 D shows the ratios for the same experiment as in other parts of this figure. These curves have similar slopes: a simple Boltzmann fit gives slope factors 8–13 mV. However, if the actual effect is a simple voltage shift of the g _H-V relationship, then the apparent steepness of the “voltage-dependent block” will be identical to the steepness of the Boltzmann relationship in the absence of Zn²⁺. This being the case, the data in Fig. 3 D strongly suggest that metals shift the voltage sensed by the channel rather than binding to the channel in a voltage-dependent manner.

ZnCl₂ Slows H⁺ Channel Opening

A prominent effect of ZnCl₂ is to slow the activation of H⁺ currents. We quantified this effect by fitting the turn-on of current during depolarizing pulses to a single exponential, after a delay. This procedure provides a reasonable fit under most conditions. In the presence of ZnCl₂, both the delay and τ_act were increased by roughly the same factor. We focussed mainly on metal effects on τ_act, which are illustrated in Fig. 4 for the same cell shown in Fig. 3. Because the τ_act-V relationship is nearly exponential (linear on semi-log axes), it is not possible to distinguish whether τ_act is slowed or its voltage dependence is shifted, or both. In the simplest case of a Huxley-Frankenhaeuser-Hodgkin voltage shift, all kinetic parameters should be shifted equally along the voltage axis. To explore the extent to which this model might apply, the τ_act data in Fig. 4 B were “corrected” by the voltage shift determined for the g _H-V relationship (Fig. 3 B). To a rough approximation, the τ_act effect in CdCl₂ and NiCl₂ appears to be explainable by this simple voltage shift. Closer examination of Fig. 4 B and other data (not shown) at high CdCl₂ concentrations indicates that CdCl₂ slows activation somewhat more than is accounted for by the shift of the g _H-V relationship, consistent with a previous study of CdCl₂ on H⁺ currents (Byerly et al. 1984). In contrast, ZnCl₂ slows channel opening dramatically, and far beyond its shift of the g _H-V relationship. The effects of ZnCl₂ are dominated by an interaction with the H⁺ channel that results in τ_act slowing, beyond a simple voltage shift of all parameters.

Figure 4.

Effects of metals on the activation time constant, τ_act, in the same cell studied at pH 6.0//5.5 as in Fig. 3. (A) The voltage dependence of τ_act is plotted in the presence of CdCl₂, NiCl₂, and ZnCl₂ at concentrations indicated in the figure (mM). Four control data sets are plotted as dashed lines. The sequence was control twice, CdCl₂, control, NiCl₂, ZnCl₂, and control. (B) The data in the presence of metals is shifted to more negative voltages, according to the shift of the g _H-V relationship observed in this cell (in Fig. 3). For clarity, only data at 10 mM CdCl₂ (▪), 10 mM NiCl₂ (▵), and 0.1 mM ZnCl₂ (⋄) are plotted. Note that the slowing of τ_act by CdCl₂ and NiCl₂ appears ascribable to a simple voltage shift, whereas ZnCl₂ has an additional slowing effect.

ZnCl₂ and CdCl₂ Have Minor Effects on H⁺ Channel Closing

The tail current decay seemed faster in the presence of external ZnCl₂ or CdCl₂. However, attempts to evaluate metal effects on H⁺ channel closing were hampered by the tendency of metals to reduce H⁺ currents and by the weak voltage dependence of the closing rate (Cherny et al. 1995). The latter property (τ_tail changes e-fold in ∼50 mV) means that a 35-mV shift of the τ_tail-V relationship would change τ_tail at a given voltage by a factor of only two. Examination of data on ZnCl₂ and CdCl₂ in a number of cells under different conditions gave the impression that the τ_tail-V relationship may have been shifted in the positive direction at most by roughly the amount that the g _H-V relationship was shifted, but little effect was seen in some experiments.

pH Dependence of Metal Effects

Fig. 5 illustrates the effects of ZnCl₂ on H⁺ currents at three pH_o. ZnCl₂ reduces the H⁺ current at each voltage, slows activation, and shifts the voltage dependence of activation to more positive voltages. At each pH_o, the effects are similar, but the concentration of ZnCl₂ required to produce these effects is much greater at low pH_o. In this sense, lowering pH_o decreases the efficacy of ZnCl₂. To quantitate the effects of ZnCl₂, we measured τ_act and calculated the ratio of τ_act in the presence of ZnCl₂ to that in its absence in the same cell at the same voltage. In most cells, this ratio was the same at all voltages, thus the effect of ZnCl₂ is a uniform voltage-independent slowing. Average ratios at several pH_o are plotted in Fig. 6 and can be thought of as reflecting the “apparent potency” of ZnCl₂ at various pH_o. The concentration required to slow τ_act twofold is (μM) 0.22 at pH_o 8, 0.46 at pH_o 7, 5.4 at pH_o 6, 89 at pH_o 5.5, and 1,000 at pH_o 5. The apparent potency of ZnCl₂ (estimated for a fourfold slowing of τ_act where the curves are parallel) decreased only 2.3-fold between pH_o 8 and 7, 10-fold between pH_o 7 and 6, and 103-fold between pH_o 6 and 5.

Figure 5.

The effects of ZnCl₂ are strongly dependent on pH_o. Families of voltage-clamp currents are shown at pH_o 7.0, 6.0, and 5.0, with pH_i 5.5, recorded in the absence (left-most family in each row) and presence of the indicated concentration of ZnCl₂. Data in each row are from the same cell, were recorded during an identical family of voltage pulses, and the same calibration bars apply. The cell at pH_o 7.0 was held at −60 mV, and pulses were applied from −40 to +20 mV in 10-mV increments. The cell at pH_o 6.0 was held at −20 mV and pulses applied from +10 to +70 mV in 10-mV increments. The cell at pH_o 5.0 was held at −20 mV and pulses applied from +50 to +100 mV in 10-mV increments.

Figure 6.

(A) Slowing of τ_act by ZnCl₂ depends strongly on pH_o (▿, pH_o 8; •, ○, 7; ▪, □, 6.0; ♦, 5.5; ▴, pH_o 5) but is independent of pH_i. Open symbols indicate cells studied at pH_i 6.5, solid symbols at pH_i 5.5. Families of H⁺ currents were recorded in the absence and presence of ZnCl₂ in each cell. The H⁺ currents were fitted by a single exponential after a delay and the τ_act data plotted versus voltage, as illustrated in Fig. 4. The ratio of τ_act in the presence of ZnCl₂ to that in its absence was measured at several voltages and averaged for each cell. When the voltage range did not overlap (as occurred for only a few cells at high [ZnCl₂]), the control value was extrapolated from τ_act data at the highest voltages studied. The mean ratios from three to five different cells at each pH_o//pH_i are plotted along with SD bars. The dashed line indicates a ratio of 1.0, which means that no effect was observed. (B) The data in A are replotted after correcting for measured metal binding by the buffers used (Table ). The corrections apply to measurements using PIPES and Mes, for which detectable binding of ZnCl₂ was measured. The calculated correction factors that give the fraction of total applied [ZnCl₂] that is unbound by buffer are: 0.576 for pH_o 7.0, 0.798 for pH_o 6.0, and 0.90 for pH_o 5.5, calculated from [M]_free/[M]_total = 1/(1 + K ′_M[B⁻]), where the deprotonated buffer concentration [B⁻] was calculated by the Henderson-Hasselbalch equation according to the buffer pK _a and pH. No correction was applied at pH_o 8.0 or 5.0 because no binding of ZnCl₂ to HEPES or Homopipes, respectively, was detected (Table ).

Most of the buffers used bind Zn²⁺ detectably (Table ). In Fig. 6 B, the data from Fig. 6 A are replotted after correcting the metal concentrations for binding by buffer. The correction factors are given in the legend. The main effect is to reduce the shift in apparent potency between pH_o 7 and 8. After correction, the concentration required to slow τ_act twofold is (μM) 0.22 at pH_o 8, 0.27 at pH_o 7, 4.3 at pH_o 6, 80 at pH_o 5.5, and 1,000 at pH_o 5. The apparent potency of ZnCl₂ (again estimated for a fourfold slowing of τ_act where the curves are parallel) decreased 1.3-fold between pH_o 8 and 7, 14-fold between pH_o 7 and 6, and 129-fold between pH_o 6 and 5.

Measurements made in the same external solutions with different pipette pH gave no indication that pH_i affects the interaction between externally applied ZnCl₂ and τ_act. As illustrated in Fig. 6, there was no obvious difference in the effects of ZnCl₂ at constant pH_o in cells studied with pH_i 5.5 (solid symbols and continuous lines) or at pH_i 6.5 (open symbols and dashed lines). This result is consistent with externally applied ZnCl₂ exerting its effect at the external side of the membrane.

Besides slowing activation, metals also shift channel opening to more positive voltages. This voltage shift was estimated from graphs of the g _H-V relationships in the absence or presence of metal and is plotted in Fig. 7. This parameter was somewhat arbitrary and less well defined than τ_act, because it required extrapolating the fitted time course of H⁺ current and measuring V_rev in each solution (whenever pH_o was changed). Nevertheless, the pH_o sensitivity of the g _H-V relationship to ZnCl₂ (solid symbols) qualitatively resembles that of τ_act. In fact, the interaction between ZnCl₂ and pH_o manifested in the g _H-V relationship appears to be somewhat stronger than that for the τ_act-V relationship. The concentration of ZnCl₂ required to produce a 20-mV depolarizing shift of the g _H-V relationship was 0.13 μM at pH_o 8.0, 0.77 μM at pH_o 7.0, 54 μM at pH_o 6.0, 470 μM at pH_o 5.5, and 12.4 mM (by extrapolation) at pH_o 5.0. The apparent potency of ZnCl₂ thus decreased sixfold between pH_o 8 and 7, 70-fold between pH_o 7 and 6, and 230-fold between pH_o 6 and 5. The larger difference between the effective potency of ZnCl₂ between pH 7 and pH_o 8 requires a higher pK _a for the steady state conductance measurement than for the kinetic τ_act measurement (see discussion).

Figure 7.

The shift in the voltage dependence of activation of the g _H produced by ZnCl₂ or CdCl₂ depends strongly on pH_o. Mean shift ± SD are plotted for two to seven determinations in each condition (91 total). Filled symbols connected by solid lines represent ZnCl₂ and open symbols with dashed lines indicate CdCl₂ measurements, and the numbers indicate pH_o. The shift was estimated by plotting g _H-V relationships and measuring the apparent voltage shift for comparable levels of g _H. The estimate was made arbitrarily when g _H was large enough to be reliably determined, but always at <50% of g _H,max because any reduction in g _H,max (which might have a different mechanism) would contaminate the measurement. ZnCl₂ and CdCl₂ concentrations have been corrected for buffer binding as described in Fig. 6. The calculated unbound fraction of CdCl₂ was 0.672 at pH_o 7 and 0.626 at pH_o 6. Because pH_i had no detectable effect on externally applied metals (Fig. 6), we combined results here for pH_i 5.5 and 6.5. For all data at pH_o 8.0, pH_i was 6.5, measurements at pH_o 7 and 6 include both pH_i 5.5 and 6.5, and for all data at pH_o 5.5 or 5.0, pH_i was 5.5.

Effects of Intracellular ZnCl₂ on H⁺ Currents

Effects of internally applied ZnCl₂ were studied in the whole-cell configuration and in inside-out patches. Fig. 8 illustrates families of H⁺ currents in cells studied at pH 6.5//6.5 without (A) and with (B) 2.5 mM ZnCl₂ added to the pipette solution. The H⁺ currents appear generally similar, although closer inspection reveals that the tail currents decayed more slowly in the cell with internal ZnCl₂. The pipette solution contained 1 mM EGTA and BisTris buffer (which will bind ∼90% of the Zn²⁺ under these conditions, Table ), so the addition of 2.5 mM ZnCl₂ results in a free [Zn²⁺] ∼170 μM. Fig. 8 C illustrates that addition of the pH 6.5 ZnCl₂ containing pipette solution to the bath dramatically reduced the H⁺ current at +50 mV. This result makes it clear that ZnCl₂ applied externally is much more effective than when applied internally. Several cells were studied with 2.5 mM ZnCl₂ in the pipette at pH_i 7.5. HEPES buffer does not bind ZnCl₂ detectably (Table ), hence the free [ZnCl₂] was ∼1.5 mM. In these cells, the H⁺ currents also appeared normal (data not shown).

Figure 8.

High concentrations of intracellular ZnCl₂ have only subtle effects on H⁺ currents. The families of H⁺ currents at pH 6.5//6.5 were recorded in a control cell (A) and with 2.5 mM ZnCl₂ in the pipette solution (B), and are scaled according to membrane capacity. The measured V_rev was +4 mV in A and +1 mV in B. Note the slower tail current decay with ZnCl₂ in the pipette. Considering binding of ZnCl₂ to 1 mM EGTA and 100 mM BisTris in the pipette solution, the free [Zn²⁺] was ∼170 μM. (C) Identical 8-s pulses to +50 mV were applied before and after addition of the pipette solution used in B to the bath, in the same cell shown in A, demonstrating the dramatic effects of this solution applied externally. The threshold for activating outward H⁺ current shifted from +30 to +60 mV after adding ZnCl₂ to the bath (determined using high gain and 5-mV increments). (D) Average (mean ± SEM) H⁺ current–voltage relationships normalized according to membrane capacity, in 6–10 control cells (•), 9–14 cells studied with 2.5 mM ZnCl₂ added to the pipette solution (▪), and 3 cells studied with 2.5 mM CdCl₂ in the pipette solution (⋄), all at pH 6.5//6.5. *Values for ZnCl₂ at +80 and +100 mV differ significantly from control (P < 0.05).

Our impression was that there was nothing unusual in the behavior of the g _H in these experiments. H⁺ currents were studied after allowing at least 5–10 min equilibration of the ZnCl₂-containing pipette solution. The amplitude of I _H did not change consistently during the experiment. The mean I _H normalized to the input capacity (Fig. 8 D) was reduced significantly (P < 0.05) at +80 and +100 mV in cells studied with 2.5 mM ZnCl₂ in the pipette, on average after 29 min in whole-cell configuration. Internal ZnCl₂ at high concentrations reduces I _H, but this effect is not very pronounced.

Fig. 9 illustrates mean τ_act values in cells studied at pH 6.5//6.5 with (▪) and without (□) 2.5 mM ZnCl₂ in the pipette solution. No difference in the kinetics of H⁺ current activation was detected. However, channel closing was significantly slower in cells studied with internal ZnCl₂. Fig. 9 shows mean values of τ_tail in cells studied with internal ZnCl₂ (•) and in control cells (○). The deactivation rate on average was 3.1-fold slower with internal ZnCl₂ (measured between −50 and +10 mV). In three cells studied with 2.5 mM CdCl₂ added to the pipette solutions, the average slowing of τ_tail was 1.8-fold at 10 voltages from −80 to +20 mV (P < 0.05 at each voltage) (not shown). Applied internally, ZnCl₂ thus slows closing without affecting activation. In contrast, externally applied ZnCl₂ slowed activation and, if anything, accelerated deactivation. Clearly the internal and external sites of action of ZnCl₂ are functionally quite different.

Figure 9.

Effects of intracellular ZnCl₂ on the mean (±SEM) activation time constant, τ_act, and deactivation time constant, τ_tail, in cells studied at pH 6.5//6.5. Tail current decay was fitted with a single exponential in three to nine control cells (○) and in four to eight cells studied with 2.5 mM ZnCl₂ added to the pipette solution (•). All τ_tail values with ZnCl₂ in the pipette differ significantly from control (P < 0.01). Values of τ_act obtained by fitting a single exponential after a delay are plotted from 10–12 control cells (□) and from four to nine cells studied with 2.5 mM ZnCl₂ added to the pipette solution (▪).

A concern during these experiments was the extent to which ZnCl₂ in the pipette solution actually diffused into the cell. ZnCl₂ diffusion into the cell will be slowed by binding to cytoplasmic proteins, acting as fixed buffers. That measurable effects on τ_tail were seen is evidence that the ZnCl₂ diffused into the cells to a significant extent. The mobility of ZnCl₂ is not unusually small (Robinson and Stokes 1959). V_rev values were consistent with the applied ΔpH (pH 6.5//6.5, Nernst potential = 0 mV), suggesting that buffer from the pipette solution diffused into the cell. In 11 cells studied with 2.5 mM ZnCl₂ in the pipette, V_rev averaged −1.3 ± 2.4 mV (mean ± SEM). To confirm that ZnCl₂ entered the cell, we used TPEN, a membrane-permeant metal chelator with a high affinity for Zn²⁺ (Arslan et al. 1985). Shortly after addition of 250 μM TPEN to cells studied with ZnCl₂-containing pipette solutions, the tail current kinetics became more rapid. On average, the ratio of τ_tail before/after TPEN was 1.65 ± 0.32 (mean ± SD, n = 7), measured at pH 6.5//6.5 at −20 or −40 mV. This is in qualitative agreement with the threefold slowing of τ_tail observed in the groups of cells studied with or without internal ZnCl₂ (Fig. 9). Addition of TPEN to three cells studied with metal-free pipette solutions did not affect τ_tail detectably.

Measurements in Excised Patches

Inside-out patches were studied at pH_o 7.5 or 6.5 (pipette pH) and pH_i 6.5 (bath pH). Addition of 2.5 mM ZnCl₂ to the bath (∼170 μM free Zn²⁺) reduced the H⁺ current amplitude (Fig. 10 B). This effect of ZnCl₂ was reversible upon washout (Fig. 10 C). The reduction of H⁺ currents was similar to that observed in whole-cells dialyzed with ZnCl₂ containing pipette solutions (Fig. 8 D), suggesting that similar concentrations were reached in the whole-cell experiments. There was no clear shift of the voltage dependence of gating. If anything, there was sometimes a small shift to more negative voltages. A small hyperpolarizing shift might be explainable by the slight lowering of pH after addition of ZnCl₂ to the solution (0.023 U calculated, 0.05 U measured), due to displacement of protons from buffer. In some inside-out patches, the H⁺ currents decreased progressively and gradually after addition of ZnCl₂. Spontaneous rundown may account for this largely irreversible loss of H⁺ current. In summary, the inside-out patch data support the conclusion that effects of internally applied ZnCl₂ differ qualitatively as well as quantitatively from those of externally applied ZnCl₂. Internal application of high concentrations of ZnCl₂ produces only modest effects.

Figure 10.

Effects of intracellular ZnCl₂ on H⁺ currents in an inside-out patch studied at pH 6.5//6.5. The first family (A) was recorded within 5 min after forming the inside-out patch. The family in B was recorded starting 2.5 min after addition of 2.5 mM ZnCl₂, and the family in C was recorded starting 1.5 min after washout. In all parts, the cell was held at −40 mV, and 16-s pulses were applied in 20-mV increments. Calibration bars in A apply to all families.

Effects of CdCl₂ on H⁺ Currents

Although we intended to study ZnCl₂ as a prototype for the effects of all polyvalent cations on H⁺ currents, there were subtle differences between the effects of ZnCl₂ and CdCl₂. Both metals slowed activation and shifted the g _H-V relationship to more positive voltages. However, to a first approximation, the effects of CdCl₂ could be viewed as a simple shift of all parameters to more positive voltages. “Correction” of the τ_act–V relationships in Fig. 4 according to the shift observed in the g _H-V relationship in Fig. 3 normalized the data for CdCl₂, but not for ZnCl₂. In other words, ZnCl₂ has a pronounced additional slowing effect. Examination of τ_act data in individual cells revealed that ZnCl₂ effects could usually be approximated as uniform slowing at all voltages, whereas the relative slowing by CdCl₂ sometimes decreased for larger depolarizations. As a result of this subtle difference, there was not a unique “slowing factor” for CdCl₂, and we did not try to plot CdCl₂ data in Fig. 6. The slowing of τ_act by CdCl₂ was strongly pH_o dependent, however. To a first approximation, the pH_o dependence of CdCl₂ was similar to that of ZnCl₂.

Another difference between metals is evident in Fig. 7. The shifts of the g _H-V relationships indicate that CdCl₂ is ∼30× less potent at either pH_o 7 or 6. In contrast, the slowing of τ_act by 100 μM ZnCl₂ exceeded that by 10 mM CdCl₂ over most voltages (Fig. 4 A), and thus there is a >100-fold difference in potency for this effect. Thus the relative potency of the two metals for slowing τ_act and shifting the g _H-V relationship differs. Perhaps distinct binding sites are involved in these effects, and the relative affinities of the metals for the sites differ. ZnCl₂ has a high affinity for the site that slows activation, whereas most of the effects of CdCl₂ are consistent with binding to a “nonspecific” site that shifts the apparent membrane potential sensed by the H⁺ channel.

DISCUSSION

Polyvalent cations and protons have similar effects on many ion channels (Hille 1968; Woodhull 1973; Kwan and Kass 1993; Arkett et al. 1994), perhaps because they bind to similar sites. It has been postulated that the function of voltage-gated proton channels requires at least two distinct types of protonation sites. Conduction likely occurs via a hydrogen-bonded chain (Nagle and Morowitz 1978; DeCoursey and Cherny 1994, DeCoursey and Cherny 1995, DeCoursey and Cherny 1997, DeCoursey and Cherny 1998, DeCoursey and Cherny 1999a,DeCoursey and Cherny 1999b), in which case the entryway of the “channel” is a protonation site, where H⁺ must bind to initiate permeation. The second type of protonation sites are allosteric regulatory sites (Byerly et al. 1984) that govern the strong ΔpH (ΔpH = pH gradient = pH_o − pH_i) dependence of gating; i.e., the 40 mV/U shift in the voltage-activation curve with changes in either pH_o or pH_i (Cherny et al. 1995). The ΔpH-dependent gating mechanism was explained economically by assuming identical internally and externally accessible regulatory protonation sites (Cherny et al. 1995). More recent evidence suggests the internal and external sites have distinct chemical properties (DeCoursey and Cherny 1997).

Given this background, H⁺ channels might be affected by Zn²⁺ in several ways. (a) Binding at or near the entry to the channel should inhibit H⁺ current by preventing H⁺ binding or reducing the local [H⁺] available to enter the channel. The attenuation of g _H,max at high metal concentrations might reflect local H⁺ depletion by this mechanism. However, most of the effects of metals are not compatible with metal binding to and occluding the channel entry. (b) Binding to a site remote from the entry but which is sensed by the voltage sensor of the channel could shift the position of the voltage dependency of gating, the most simple mechanism of which would result in all voltage-dependent parameters shifting equally along the voltage axis. This mechanism is consistent with most of the effects of Cd²⁺ and Ni²⁺. (c) Binding near the allosteric sites on either side of the membrane might reduce the local [H⁺] electrostatically, and hence affect gating in the same manner as an increase in pH. The effects of metals are in the wrong direction for this mechanism to apply. (d) Finally, metal binding to the allosteric protonation sites might have a similar effect on gating as protonation of these sites, and might thus mimic the effects of low pH near the site. The details of the effects in this case are hard to predict, because due to differences in binding kinetics and steric factors, Zn²⁺ can hardly be expected to mimic a single H⁺, or even two H⁺. Nevertheless, most of the effects of Zn²⁺ can be explained by assuming that it binds to the same regulatory sites as protons, and has the same effects as protons in our model (Cherny et al. 1995). Thus, Zn²⁺ (or H⁺) binding at the external site prevents channel opening, and Zn²⁺ (or H⁺) binding at the internal site prevents channel closing.

Zn²⁺ Is Not a Voltage-dependent Blocker of H⁺ Channels

Although polyvalent cation effects on H⁺ currents in various cells are quite similar, some authors have characterized these effects as modification of the voltage dependence of gating (Byerly et al. 1984; Barish and Baud 1984; DeCoursey 1991; Kapus et al. 1993; DeCoursey and Cherny 1993, DeCoursey and Cherny 1994; DeCoursey and Cherny 1996; Demaurex et al. 1993), whereas others describe the effects as voltage-dependent block (Bernheim et al. 1993; Gordienko et al. 1996). These views are not equivalent. The voltage dependence of ionic block is generally assumed to arise from the entry of the blocker into the channel pore partway across the membrane potential field, where it gets stuck, physically occluding the pore. Interpreted in terms of voltage-dependent block, metal binding affinity depends strongly on voltage (Bernheim et al. 1993; Gordienko et al. 1996), whereas effects due to binding to a modulatory site can be explained with a fixed K _M. Because the instantaneous I-V relation was simply scaled down by ZnCl₂ with no detectable voltage dependence (Fig. 2), we ruled out the possibility of rapidly reversible binding of Zn²⁺ to a site within the membrane potential field.

Even though there is no rapidly reversible block, the more obvious effects of ZnCl₂ could be due to a slow time-dependent block/unblock. Five arguments oppose the idea that the slow activation of H⁺ current in the presence of Zn²⁺ reflects voltage-dependent unbinding of Zn²⁺ from the channel. (a) If τ_act in the presence of metals (several seconds) reflects the unblock rate, then block must have very slow kinetics. If we assume that pK _M = 6.5 (Fig. 11) and that the binding rate of Zn²⁺ is 3 × 10⁷ M⁻¹ s⁻¹, a characteristic rate of complex formation between Zn²⁺ and proteins (Eigen and Hammes 1963), then the unbinding rate is 9.5 s⁻¹. Thus, Zn²⁺ probably binds and unbinds in a fraction of a second. If the kinetics are rapid, effects should have been manifested in the instantaneous I-V relation. (b) In normal drug-receptor reactions, the unblock rate is independent of concentration. However, increasing the concentration of ZnCl₂ slowed H⁺ current activation progressively. There was no indication that two populations of gating behavior resulted, as would be predicted if ZnCl₂ modified a fraction of channels that then opened slowly, with the remaining channels opening at the normal rate. A single exponential (after a delay) continued to fit the data at all [ZnCl₂]. Thus it appears that ZnCl₂ binds and unbinds the channel repeatedly during a single pulse, with the slowing effect related to the fraction of time ZnCl₂ is bound to the channel. (c) The steady state voltage dependence of this apparent Zn²⁺ block, defined as the ratio I _H(Zn²⁺)/I _H(control), is quite steep: a simple Boltzmann fit gives slope factors 8–13 mV (Fig. 3 D). In terms of traditional voltage-dependent block mechanisms (Woodhull 1973), if z is the charge on the blocking ion and δ is the fraction of the membrane potential sensed by the ion at the block site, then zδ ≥ 2.0, which implies that Zn²⁺, Cd²⁺, and Ni²⁺ traverse ≥100% of the membrane field to reach the block site. Several examples of δ > 1.0 for ionic blockade exist in the K⁺ channel literature and are traditionally explained by interaction between permeant ions in a multiply occupied channel (e.g., Hille and Schwarz 1978). Because it is unlikely for a hydrogen-bonded–chain conduction mechanism to support multiple protons simultaneously, especially at physiological pH (DeCoursey and Cherny 1999a), explaining the high zδ observed for divalent cation “blockade” is problematic. (d) If ZnCl₂ simply shifted the g _H-V relationship along the voltage axis, then the apparent steepness of the block, defined as the ratio I _H(Zn²⁺)/I _H(control), will be precisely identical to the steepness of the g _H-V relationship in the absence of Zn²⁺. The slopes of the fractional block curves, 8–13 mV (Fig. 3D), and control g _H-V relationships, 8–10 mV (DeCoursey and Cherny 1994; Cherny et al. 1995), are the same, consistent with a simple voltage shift. (e) Finally, any part of the H⁺ channel conductance pathway comprised of hydrogen-bonded chain would not allow Zn²⁺ passage; thus the possibility for voltage-dependent block by Zn²⁺ could exist only in an aqueous vestibule. We conclude that polyvalent cations do not exert their effects by entering into the pore, but instead bind to sites on the channel that are accessible to the solution and outside of the membrane potential field. Binding must be specific because different divalent cations have very different concentration dependencies. For example, effects of micromolar concentrations of Zn²⁺ are seen in the presence of millimolar [Ca²⁺]_o or [Mg²⁺]_o.

Figure 11.

Comparison of the τ_act data replotted from Fig. 6 with the slowing predicted by , assuming that the H⁺ channel cannot open while Zn²⁺ is bound to its receptor (see text for details). The meaning of the symbols is the same as in Fig. 6, and all curves are the predictions for pK _a 6.3, pK _M 6.5, and cooperativity factor a = 0.03.

Byerly et al. 1984 proposed that divalent cations bind specifically to a site on the external side of H⁺ channels, based on their observation that the g _H-V relationship was shifted less by CdCl₂ than was the τ_act–V (actually t _1/2-V) relationship. For epithelial H⁺ channels, the disparity in effects on channel opening compared with the g _H-V relationship was even more pronounced for ZnCl₂ than for CdCl₂. A similar sequence of voltage shifts by ZnCl₂ (τ_act-V > g _H-V > τ_tail-V) was seen for K⁺ channels (Gilly and Armstrong 1982). Their interpretation was that Zn²⁺ binds to a site on the external side of the channel that is exposed to the bath solution only when the channel is closed. This is precisely the nature of the proposed external modulatory protonation site in our model of H⁺ channel gating (Cherny et al. 1995). The site must be deprotonated before the channel can open, and during the opening process the site “disappears” and the same site (or a distinct site) appears on the internal side of the membrane. It was necessary to assume that the protonation sites were not accessible to both sides of the membrane at the same time to account for the ΔpH dependence of gating.

Zn²⁺ Is the Active Species of Zinc

In solution, zinc exists as several chemical species, whose relative proportions depend strongly on pH. One plausible explanation for the increased apparent potency of ZnCl₂ at higher pH is that ZnOH⁺, rather than the divalent form, is the species acting on H⁺ channels. As pH is increased, the proportion of ZnCl₂ in monohydroxide form, ZnOH⁺, increases 10-fold/U, up to ∼pH 8 (Baes and Mesmer 1976). The absolute concentration of ZnOH⁺ is a small fraction of the total, and >90% of ZnCl₂ is divalent at pH < 8.0, hence [Zn²⁺] remains relatively constant (Baes and Mesmer 1976). Spalding et al. 1990 concluded that ZnOH⁺ was the active form for Cl⁻ currents in muscle. The “consensus” potency sequence for inhibiting H⁺ currents by divalent metal cations, Cu < Zn > Ni > Cd > Co > Mn > Ba, Ca, Mg < 0 (DeCoursey 1998), is intriguingly similar to the tendency of these cations to hydrolyze (Perrin and Dempsey 1974) (indicated by their pK _a): Cu (8.0) > Co (8.9), Zn (9.0) > Ni, Cd (9.9) > Mn (10.6) > Mg (11.4) > Ca (12.6) > Ba (13.4).

The pK _a sequence generally reveals the proportion of total metal in monohydroxide form at a given pH. If the monohydroxide form were active, then the apparent potency for all of these metals should increase ∼10-fold per unit increase in pH, and the pH dependence should saturate around the pK _a. We show here that the apparent potency of both ZnCl₂ and CdCl₂ increase at higher pH, and the pH_o dependence saturates for ZnCl₂. However, saturation occurs at a pH that is too low by ∼1 U, and the change at low pH_o is at least 100-fold/U (Fig. 5 Fig. 6 Fig. 7), both inconsistent with the hypothesis that the monohydroxide form is active. If ZnOH⁺ were the active form, an additional mechanism (e.g., competition with H⁺) would be required to enhance the pH sensitivity of its effects. Several polyhydroxide forms of zinc (with net negative charge) also are increasingly represented at high pH, but we rule these out as candidates for interaction with the H⁺ channel because (a) it seems unlikely that anions and protons would compete for the same sites, and (b) the fraction of all of these forms combined at pH 5 is <10⁻¹² of the total ZnCl₂ present (Baes and Mesmer 1976). In conclusion, the most probable form of ZnCl₂ active on H⁺ channels is the divalent form.

Model of the Interaction between Zn²⁺ and H⁺ that Slows Activation

The explores the predictions of several possible mechanisms of competition between Zn²⁺ and H⁺ for hypothetical binding sites on H⁺ channels. The pH_o dependence of Zn²⁺ effects on τ_act are reasonably compatible with Models 4, 5, or 6 (see Fig. 13 for all models). These models assume that the external Zn²⁺ receptor on proton channels is formed by multiple protonation sites that are accessible to the external solution and that coordinate the binding of a single Zn²⁺. If H⁺ and Zn²⁺ compete directly for the same site(s), then at least two to three protonation sites must exist. If H⁺ and Zn²⁺ bind to different sites, then there must be substantial interaction between them, and the range of the pH dependence indicates that protonation of one site lowers the affinity of the remaining site(s) for Zn²⁺ by a factor ∼30. Similar binding constants reproduce the pH dependence of Zn²⁺ effects using any of several models: pK _M is 6.5 and pK _a is 6.2–6.6 and is somewhat model dependent.

Figure 13.

The probability that the metal receptor is occupied by a metal ion as predicted by various models with different assumptions about the interaction between H⁺ and Zn²⁺. To relate the occupancy of the metal receptor to data such as in Fig. 6, it is necessary to assume a specific mechanism, as discussed in the text. On the other hand, the pK _a value is set by the pH_o at which the effect saturates, and is relatively insensitive to this relationship. Binding constants for H⁺ and Zn²⁺, pK _a, and pK _M, respectively, are defined in the text. (A) Model 1 (pK _a 6.6 and pK _M 6.5, from ) assumes simple competition between H⁺ and Zn²⁺ for a single site. At low pH, the concentration of Zn²⁺ required to produce a given occupancy increases 10-fold per unit decrease in pH. (B) Model 2 (pK _a 6.6 and pK _M 6.5, from ) describes noncompetitive inhibition, in which H⁺ and Zn²⁺ bind independently to separate sites. These curves superimpose if scaled up. (C) Model 3 (pK _a 6.6 and pK _M 6.5, from ) assumes that the effect is the same whether H⁺ or Zn²⁺ is bound to the site. If the pH 5 curve is scaled to the pH 9 curve, the former is shifted to the right ∼10-fold. (D) Model 4 (pK _a 6.6 and pK _M 6.5, from ) assumes two identical protonation sites that combine to coordinate one Zn²⁺ ion. Pure competition is assumed, in that protonation of either site prevents Zn²⁺ binding. (E) Model 5 (pK _a 6.2 and pK _M 6.5, from ) is identical to Model 4 except that there are three independent sites, protonation of any of which prevents Zn²⁺ binding. The pK _a was adjusted to reproduce the 10-fold change in apparent potency of Zn²⁺ observed between pH 6 and 7 (Fig. 6), but the apparent potency of Zn²⁺ changes too much between pH 6 and 5 (∼285-fold, compared with 100-fold for the data in Fig. 6), and ∼850-fold between pH 5 and 4, approaching the low pH limit of a 1,000-fold change. (F) Model 6 (pK _a 6.3, pK _M 6.5, and a = 0.03, from ) assumes three sites, but the protonation of one site lowers the affinity of the next site(s) to 0.03 of the original affinity. In essence, the fully protonated channel has a much lower affinity for Zn²⁺ (apparent pK _M ∼ 1.3) so that the effect of pH on Zn²⁺ saturates at either high or low pH. With this interaction factor (a = 0.03), decreasing pH from 4 to 3 lowers the Zn²⁺ affinity less than twofold, and lowering pH to <3 has no further effect.

To apply the model equations in the to real data, it is necessary to define the effect that metal binding has on channel behavior. By making one assumption, we can define the entire body of τ_act data in Fig. 6. We assume that when Zn²⁺ is bound to its receptor on the H⁺ channel, the channel cannot open. For the simplest case of a two-state channel, with Fig. 1:

Scheme S1.

where α is the opening rate and β is the closing rate, the time constant is (α + β)⁻¹. Because the slowing of τ_act was voltage independent, β evidently is negligibly small in the voltage range measured, hence τ_act ≈ α⁻¹. The opening rate will be slowed by the factor (1 − P _Zn), where P _Zn is the probability that the receptor is occupied by Zn²⁺ (the occupancy plotted in Fig. 13). Thus the observed time constant will be ∼[α (1 − P _Zn)]⁻¹, and the ratio of τ_act in the presence of ZnCl₂ to that in its absence will be simply (1 − P _Zn)⁻¹. Given these assumptions, τ_act is slowed by a factor of 2.0 at the K _M of Zn²⁺.

In Fig. 11, the τ_act data from Fig. 6 are replotted with smooth curves superimposed that assume Model 6, in which the Zn²⁺ receptor is formed by three protonation sites and protonation of each site reduces the affinity of the receptor for Zn²⁺ by a factor a. We selected Model 6 because it comes closest to embodying the pH dependence observed. The entire set of theoretical curves is determined by the assumption that a Zn²⁺-bound channel cannot open, and by pK _M = 6.5, pK _a = 6.3, and cooperativity factor a = 0.03. Setting a to 0.03 produces an ∼100-fold change in apparent Zn²⁺ potency between pH 5 and 6 that resembles the τ_act data. With a = 0.01, the shift was too large, and at a = 0.1 the shift was too small. We could not collect data at pH 4, which might have revealed whether the saturation of the effect at very low pH predicted by this model () occurs. The agreement is generally excellent, although the slope of the data appears shallower than that defined by the theory. Expressed in terms of Zn²⁺ activity rather than concentration, calculated with to the Davies equation (Stumm and Morgan 1981) at the ionic strength of all solutions used, ∼0.13 M, the pK _M is 7.0.

Model of the Interaction between Zn²⁺ and H⁺ that Shifts the g_H-V Relationship

The effects of ZnCl₂ on the g _H-V relationship were modeled in a similar manner as the effects on τ_act. Fig. 12 shows the predictions of Model 6 (as in Fig. 11), with parameters adjusted to match the ZnCl₂ data from Fig. 7, which are superimposed. Several differences in the g _H-V data compared with the τ_act data (Fig. 11) required different parameters. It was necessary to assume that more than two protonation sites were involved because the shift between pH_o 6 and 5 was ∼230, whereas 100 is the maximum possible shift for a two-site model. pK _M in all equations is defined by the metal concentration–response relationship at high pH_o, where binding is unaffected by pH. pK _a is somewhat model dependent, and is defined by the pH_o at which the interaction between metal and H⁺ saturates. For a given model, this is set by the size of the shift in the high pH_o region. Thus, in Fig. 12, pK _a is 7.0 because this produces a sixfold shift between pH_o 8 and 7, as observed in the data. Finally, it was necessary to assume some interaction between binding sites, because pure competition in a three-site model predicts too large a shift at low pH_o. The value of the interaction factor, a, is established by the entire shift over the pH_o range from 8 to 5. This shift was 10⁵ in the data, and a = 0.01 matched this value. Setting a = 0.02 reduced the range to 3 × 10⁴ and at a = 0 (pure competition) the range was too large, 4 × 10⁵. The mechanistic interpretation is that protonation of one of the sites lowers the affinity of the Zn²⁺ receptor 100-fold. Assuming the same model, the affinity of Cd²⁺ for the external metal receptor is lower than that of Zn²⁺ by ∼2 U (roughly pK _M 6).

Figure 12.

Optimized model predictions for the effect of ZnCl₂ on the g _H-V relationship (shown in Fig. 7). is assumed for reasons described in the text, but with somewhat different parameters than in Fig. 11, where the τ_act effect is modeled: pK _M is 8.0, pK _a is 7.0, and a = 0.01. The model implies that the external Zn²⁺ receptor consists of three protonation sites, and that protonation of one site reduces the affinity of Zn²⁺ for the receptor 100-fold.

A depolarizing shift in the g _H-V relationship at low P _open can be approximated as a reduction of P _open by a constant fraction. Because the slope factor of the g _H-V relationship fit by a simple Boltzmann function is ∼10 mV (DeCoursey and Cherny 1994; Cherny et al. 1995), an e-fold reduction in P _open should produce a 10-mV depolarizing shift. In Fig. 12, we use Model 6 under the assumption that the channel cannot open when Zn²⁺ is bound. The voltage shift is given by ln(1 − P _Zn)⁻¹ × 10 mV. The g _H-V data were best described by pK _M = 8.0, pK _a 7.0, and a = 0.01. Expressed in terms of Zn²⁺ activity rather than concentration, pK _M is 8.5.

The g _H-V data were best described by pK _M = 8.0, pK _a 7.0, and a = 0.01 (Fig. 12), whereas the optimal values for the same model of τ_act data were pK _M = 6.5, pK _a 6.3, and a = 0.03 (Fig. 11). The different parameter values describing the interactions observed for the g _H-V relationship and τ_act may reflect that the former is a steady state parameter and the latter a kinetic one. Alternatively, distinct metal binding sites may be involved in slowing τ_act and shifting the g _H-V relationship, as suggested by the greater relative potency of ZnCl₂ (compared with other metals) for the slowing effect. If so, the “nonspecific” site at which polyvalent metals shift all voltage-dependent parameters simply has a higher pK _a than the site that regulates τ_act. Another possibility is that the Zn²⁺ receptor has a higher affinity for both protons and Zn²⁺ when the channel is open. This idea is incompatible with the external Zn²⁺ receptor being comprised of the regulatory protonation sites that govern gating in our model, because these sites become inaccessible to the external solution when the channel is open (Cherny et al. 1995). We saw no evidence of decay of H⁺ current in the presence of metals, which would be expected if metals bound (with resolvable kinetics) preferentially to open channels. A final possibility is that fitting the τ_act and g _H-V data simply provides two ways to estimate the binding parameters of the Zn²⁺ receptor.

Evidence that Metals Bind to the External Site that Regulates pH-dependent Gating

The modeling exercise indicates that protons and polyvalent cations (at least Zn²⁺ and Cd²⁺) compete for a common site at the external surface of the H⁺ channel. Furthermore, the metal receptor can also bind two or more H⁺, and protonation inhibits metal binding. The best fit was achieved with the assumption that three protonation sites coordinate one Zn²⁺. We propose that metal binds to the same external modulatory sites at which extracellular protons regulate the gating of H⁺ channels. Extracellular metals and protons have qualitatively similar effects on channel gating. Both slow activation (increase τ_act), shift the voltage-activation curve (g _H-V relation) to more positive potentials, and have relatively small effects on the channel closing rate. In our model (Cherny et al. 1995), the ΔpH dependence of gating arises from the requirement that three externally accessible sites must be deprotonated for the channel to open. The agreement between the numbers of protonation sites involved in gating and Zn²⁺ binding may be serendipitous, but lends support to both models.

Internal Metal Binding Site

Although metals produce dramatic effects on H⁺ currents at quite low concentrations for external application, internally applied ZnCl₂ or CdCl₂ also altered H⁺ currents. Deactivation was slowed with no effect on τ_act, and H⁺ current amplitude was reduced. Because internally applied ZnCl₂ had relatively weak effects, we could not study them in as much detail, and could not determine whether Zn²⁺ and H⁺ compete for internal sites. Nevertheless, in our model (Cherny et al. 1995), the first step in channel closing is deprotonation at internally accessible sites. Thus, the slowing of deactivation by internal ZnCl₂ with no effect on the opening rate is qualitatively consistent with the idea that Zn²⁺ binds to the same internal protonation sites that help regulate gating.

Because the effects of internal and external addition were qualitatively different, distinct metal binding sites must exist at the inner and outer surfaces of the channel. In contrast, ZnCl₂ has similar effects whether applied externally or internally to K⁺ channels, on ionic currents (Begenisich and Lynch 1974; Spires and Begenisich 1992, Spires and Begenisich 1994) as well as on gating currents (Spires and Begenisich 1995), leading Spires and Begenisich 1995 to conclude that Zn²⁺ can reach its binding site in the channel from either side of the membrane. The dissimilarity of effects on H⁺ channels leads us to conclude that there are distinct internal and external sites and, furthermore, that negligible quantities of these metals applied internally reach the external binding site. Not only is there no evidence that ZnCl₂ can cross the membrane, the lack of effects of pH_i on external ZnCl₂ effects (Fig. 6) indicates that intracellular protons do not affect the local pH near the external Zn²⁺ receptor. Thus, H⁺ channels are less promiscuous than are K⁺ channels. In turn, this conclusion supports the concept that voltage-gated proton channels are not water-filled pores that might conduct detectable amounts of Zn²⁺ or Cd²⁺ (or perhaps ZnOH⁺ or CdOH⁺), but instead comprise a hydrogen-bonded chain. The extremely high selectivity of H⁺ channels is another argument for this conduction mechanism (DeCoursey and Cherny 1994, DeCoursey and Cherny 1998, DeCoursey and Cherny 1999a,DeCoursey and Cherny 1999b).

The Chemical Nature of the Protonation Sites on H⁺ Channels

To account for the ΔpH dependence of the voltage activation curve of the H⁺ channel, we originally proposed identical external and internal protonation sites with pK _a 8.5 (Cherny et al. 1995). Deprotonation at the external site was the first step in channel opening, and deprotonation at the internal site was the first step in channel closing. That deuterium substitution slowed activation threefold with negligible effects on closing suggested that the external and internal sites were chemically different, with the external site likely composed of His, Lys, or Tyr residues and the internal site possibly a sulfhydryl group, presumably Cys (DeCoursey and Cherny 1997). A classical example of His forming a Zn-binding site is carbonic anhydrase, in which zinc is coordinated between three His residues (and one OH⁻) to form the catalytic site of this metalloenzyme (Silverman and Vincent 1983). Chelators can remove this zinc and it can then be replaced by various other ligands, which bind with a relative potency Hg >> Cu > Zn > Cd, Ni > Co > Mn (Silverman and Vincent 1983), a sequence similar to that reported for metal inhibition of H⁺ currents (see above). The data presented here are compatible with the idea that the Zn²⁺ binding site is the same site at which external protons regulate gating. In this regard, it is intriguing that pH_o acting on extracellular His residues shifts the voltage dependence of the gating of a plant K⁺ channel (Hoth et al. 1997). Protonation of this stomatal guard cell channel shifts the activation curve toward more positive voltages, just as the g _H-V relation of voltage-gated proton channels is shifted to the right at lower pH_o. Because this K⁺ channel is activated by hyperpolarization, it is activated by low pH_o, whereas the voltage-gated proton channel is activated by depolarization and thus is inhibited by low pH_o. Zinc binding sites have been created in α-hemolysin channels by introducing His residues (Walker et al. 1994; Kasianowicz et al. 1999). The external Zn²⁺ receptor on H⁺ channels binds Zn²⁺ with a substantially higher affinity, pK _M ∼6.5, than the “normal” association constant for 1:1 binding of Zn(II) to His, pK _M 2.5 (Breslow 1973). The higher affinity is compatible with our conclusion that multiple His (or other ionizable groups) coordinate the binding of a single Zn²⁺. The Zn²⁺ dissociation constant for carbonic anhydrase, in which three His coordinate one Zn²⁺, is 4 pM (Kiefer et al. 1993). The typical pK _a of His in proteins ranges from 6.4 to 7.2 (Breslow 1973), encompassing the pK _a values derived from most of the models tested here. Thus, many types of evidence point to His as a likely candidate for forming the external Zn²⁺ receptor.

Henderson 1998 demonstrated recently that mutation of any of three His residues to Leu in a putative transmembrane domain abolished the H⁺ conductance associated with NADPH oxidase in neutrophils. This intriguing result may support the identity of the external modulatory site as His. However, epithelial and phagocyte H⁺ channels differ significantly (DeCoursey 1998), and some phagocyte H⁺ channels have a higher sensitivity to ZnCl₂ (Bánfi et al. 1999). Furthermore, the role of one or more of the His might be in conduction, forming part of the hydrogen-bonded chain, rather than in regulation of gating.

The much weaker deuterium isotope effect on H⁺ channel closing than on opening led to the suggestion of Cys as a candidate for the internal regulatory protonation site because sulfhydryl groups typically have smaller pK _a shifts in D₂O (DeCoursey and Cherny 1997). The weak effects of internal ZnCl₂ reported here, however, must be reconciled with the typically high affinity binding of Zn²⁺ to Cys (Breslow 1973). If Cys does help form the internal site, steric constraints may allow proton or deuteron binding, but disfavor close approach by Zn²⁺.

Pathophysiological Significance

Because they are more sensitive to polyvalent metal cations than most other ion channels, H⁺ channels would be among the first to register effects of metal poisoning. Human plasma zinc levels are maintained at ∼15 μM (Cornelis and Versieck 1980), most of which is complexed with plasma proteins or phosphates. However, the g _H-V relationship is quite sensitive to Zn²⁺ at physiological pH with a distinct shift at <0.1 μM ZnCl₂ (Fig. 7). ZnCl₂ or CdCl₂ suppress the respiratory burst—the release of bactericidal reactive oxygen species—in human neutrophils in vitro, presumably by inhibiting H⁺ currents (Henderson et al. 1988). Inhalation of zinc oxide produces metal fume fever, apparently by elevating plasma interleukin-6 (a pyrogen produced by granulocytes) levels (Fine et al. 1997). Voltage-gated proton channels in alveolar epithelium may contribute to CO₂ extrusion by the lung (DeCoursey 2000). Volume regulation of alveolar epithelial cells is inhibited by high concentrations of ZnCl₂ (Jones et al. 1982). This evidence is circumstantial, but worth worrying about.

Competition between Zn²⁺ and H⁺

If Zn²⁺ is the sole form of ZnCl₂ active on H⁺ channels, then the strong pH_o sensitivity of its effects (5 6) could be explained in two ways. Zn²⁺ and H⁺ might compete for the same site on the channel, or protonation of the channel might lower its affinity for Zn²⁺. Several classes of mechanisms encompassing both possibilities can be envisioned. Here we will explore the extent to which the stoichiometry of the apparent competition between metal and protons defines the nature of the metal receptor. To make this analysis as model-independent as possible, we will simply consider the probability that Zn²⁺ is bound to its receptor. In the discussion we assumed specific mechanisms by which metals slow H⁺ channel activation (11) or shift the g _H-V relationship (12), and determine the model parameters given those assumptions.

If one Zn²⁺ (M) competes with one H⁺ (H) for the same binding site or receptor (R), each will have a dissociation constant, defined in 2 and 3, respectively (the brackets indicating concentration have been omitted):

Scheme S2.

and

as K _M = k _b/k _f and K _a = k ₂/k ₁.

We define pK _M the way pK _a is defined, as the negative logarithm of K _M. Note that K _M as defined here is the inverse of the metal-buffer binding constant defined by Good et al. 1966, thus we indicate their parameter as K ′_M (). The fraction of channels with metal bound to them is given by a “simple competition” model:

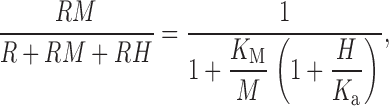A1

where the number of free, metal-bound, or protonated receptors is R, RM, or RH, respectively (see Spires and Begenisich 1992). , illustrated in 13 A, predicts that, well below the pK _a, the apparent potency of metal will decrease 10-fold per unit decrease in pH (Clark 1926). An example in which such a relationship holds is the affinity of zinc for the bc ₁ complex, which decreases 10-fold per unit decrease in pH between pH 7 and 5 (Link and von Jagow 1995). agrees with the ∼10-fold reduction in potency seen between pH_o 7 and 6, but the decrease in apparent potency of Zn²⁺ between pH_o 6 and 5 is closer to 100-fold (6). Therefore, this model must be abandoned.

We next consider noncompetitive inhibition, in which Zn²⁺ and H⁺ bind independently to different sites, and the effect is observed only when Zn²⁺ and not H⁺ is bound. This “noncompetitive inhibition” model is:

A2

In , metal simply becomes ineffective at low pH (13 B). Furthermore, the “threshold” concentration of metal is the same at all pH. In contrast, the data exhibit large effects of Zn²⁺ at low pH_o, where the concentration–response relationship appears simply to shift to higher [Zn²⁺] (5 and 6). Furthermore, the threshold concentration that produces detectable effects changes radically with pH. Therefore, we rule out purely noncompetitive models.

The simple competition model could be altered to reflect that Zn²⁺ and H⁺ have qualitatively similar effects when bound to H⁺ channels. Both cations slow activation at a given voltage, and shift the voltage-activation curve to more positive potentials. The formulation of this “both Zn²⁺ and H⁺ effective” model is ():

A3

As is apparent from 13 C, if there is competitive binding and Zn²⁺ and H⁺ have the same effects, then at low pH_o there will be little further effect of adding metal because all the sites are already protonated. There is a small shift of the threshold [Zn²⁺], but this occurs at the expense of reducing the maximal effect. At least this simple form of the “both effective” class of models is incompatible with the data.

A more complicated model is necessary to explain the ∼100-fold shift in apparent potency of Zn²⁺ between pH_o 6 and 5. One possibility is that each channel has multiple protonation sites near enough to each other that two can coordinate a single Zn²⁺. The divalency of Zn²⁺ suggests this idea naturally. A channel that coordinates Zn²⁺ between His and Asp side groups has been described (Kasianowicz et al. 1999). We model this possibility by assuming that the Zn²⁺ receptor can bind two protons. Protonation of either site prevents Zn²⁺ binding. The metal occupancy will be given by (2 H⁺ and 1 Zn²⁺ compete):

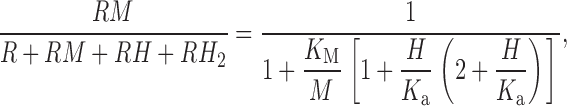A4

assuming that the two protonation sites are identical and independent. Here K _a = k ₂/k ₁, with k ₁ and k ₂ defined in the two partial reactions of the degenerate two-step system (Bernasconi 1976) (4 and 5):

Scheme S4.

Scheme S5.

and

13 D shows the prediction of , assuming that pK _a = 6.6 and pK _M = 6.5. The values of pK _a and pK _M are established from the pH range at which the pH_o sensitivity of Zn²⁺ diminishes, and from the position of the concentration–response curve at high pH_o, respectively. In , the apparent efficacy of Zn²⁺ decreases 100-fold/U at low pH_o, consistent with the shift observed between pH 6 and 5. The equation describes the τ_act data (6) fairly well, although the calculated shift between pH 6 and 5 is only 70 rather than 100, because the low pH_o behavior is not fully manifest at these relatively high pH_o. It might be expected that protonation of the first site would lower the proton affinity of the second site. We modeled this by lowering the pK _a of the second protonation reaction, but there were only subtle differences in the predicted behavior for two sites with identical pK _a compared with two sites with 1 U different pK _a having the same average value.

If the H⁺ channel were a trimer or tetramer, there might reasonably be three or four equivalent protonation sites. Assuming that protonation of any site prevents metal binding, this purely competitive model is described by (see Perez-Cornejo et al. 1998):

A5

In , the shift in apparent Zn²⁺ potency at low pH_o is 10³ for n = 3 and 10⁴ for n = 4. Although the data do not exhibit a shift that large, the three-site model 5 (13 E, “H⁺ and 1 Zn²⁺ compete”) can simulate the data tolerably well using pK _a 6.2 and pK _M 6.5 because the 1,000-fold/U shift is attained only at lower pH than the range of the data.

One final variant will be considered, in which the channel has multiple protonation sites that interfere with Zn²⁺ binding, either allosterically or electrostatically. Protonation of each successive site lowers the affinity of the metal binding site for Zn²⁺, but protonation and Zn²⁺ binding are not mutually exclusive. The general “indirect interaction, multimeric site” model is (Perez-Cornejo et al. 1998):

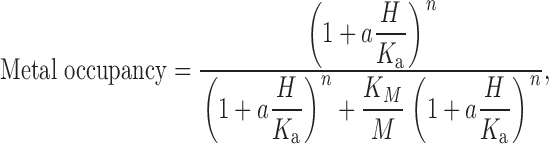A6

where factor a is a cooperativity factor that is unity for completely independent binding of H⁺ and Zn²⁺, decreases as the metal affinity is reduced, and becomes 0 when there is pure competition (in which case reduces to ). This model behaves as though, in the limit of high and low pH, the affinity of the site for Zn²⁺ is high or low, respectively. Thus, the shift in apparent metal potency saturates at both high and low pH in contrast with purely competitive Models 1, 4, and 5 (13), which saturate at high pH only.