Rapid Activation of the Cardiac Ryanodine Receptor by Submillisecond Calcium Stimuli

Abstract

The local control concept of excitation–contraction coupling in the heart postulates that the activity of the sarcoplasmic reticulum ryanodine receptor channels (RyR) is controlled by Ca²⁺ entry through adjoining sarcolemmal single dihydropyridine receptor channels (DHPRs). One unverified premise of this hypothesis is that the RyR must be fast enough to track the brief (<0.5 ms) Ca²⁺ elevations accompanying single DHPR channel openings. To define the kinetic limits of effective trigger Ca²⁺ signals, we recorded activity of single cardiac RyRs in lipid bilayers during rapid and transient increases in Ca²⁺ generated by flash photolysis of DM-nitrophen. Application of such Ca²⁺ spikes (amplitude ∼10–30 μM, duration ∼0.1–0.4 ms) resulted in activation of the RyRs with a probability that increased steeply (apparent Hill slope ∼2.5) with spike amplitude. The time constants of RyR activation were 0.07–0.27 ms, decreasing with spike amplitude. To fit the rising portion of the open probability, a single exponential function had to be raised to a power n ∼ 3. We show that these data could be adequately described with a gating scheme incorporating four sequential Ca²⁺-sensitive closed states between the resting and the first open states. These results provide evidence that brief Ca²⁺ triggers are adequate to activate the RyR, and support the possibility that RyR channels are governed by single DHPR openings. They also provide evidence for the assumption that RyR activation requires binding of multiple Ca²⁺ ions in accordance with the tetrameric organization of the channel protein.

INTRODUCTION

In mammalian heart, the process of excitation–contraction (E-C)¹ coupling is mediated by calcium-induced Ca²⁺ release (CICR, Fabiato and Fabiato 1979; Bers 1991; Stern and Lakatta 1992). It has been postulated that Ca²⁺ entering through single L-type Ca²⁺ channels (dihydropyridine receptor channels, DHPRs) locally controls the activity of the release units, composed of Ca²⁺ release channels/ryanodine receptors (RyRs, Cannell et al. 1995; López-López et al. 1995; Santana et al. 1996; Shorofsky et al. 1998) located in the membrane of the sarcoplasmic reticulum (SR) across a 20-nm wide junctional gap. Single DHPR activity is characterized by brief openings (∼0.2 ms) separated by relatively long closures (∼10 ms, Rose et al. 1992). When the channel opens, Ca²⁺ in its vicinity immediately rises to levels above 10 μM; when the channel closes, the local Ca²⁺ gradient dissipates rapidly (microseconds) due to Ca²⁺ diffusing away (Simon and Llinás 1985; Stern 1992a; Naraghi and Neher 1997; Soeller and Cannell 1997). Thus, according to the local control concept of CICR, the physiological trigger of calcium release must be a rapid and transient elevation of Ca²⁺ to above 10 μM lasting <0.5 ms.

The gating properties of the RyRs have been studied after reconstitution of the channels into lipid bilayers. All these studies have been performed under stationary Ca²⁺ conditions (Rousseau and Meisner 1989; Ashley and Williams 1990; Chu et al. 1993; Sitsapesan and Williams 1994; Zahradníková and Zahradník 1995; Copello et al. 1997), or during sustained changes in Ca²⁺ produced by photolysis of “caged calcium” (Györke and Fill 1993; Györke et al. 1994; Valdivia et al. 1995; Zahradníková et al. 1999a) or mechanical solution exchange (Schiefer et al. 1995; Sitsapesan et al. 1995; Laver and Curtis 1996; Laver and Lamb 1998). These studies, although yielding important information on channel behavior, do not reveal how the RyR responds to the brief Ca²⁺ stimuli that are likely to initiate E-C coupling in vivo.

In the present study, we used the photolabile Ca²⁺ chelator DM-nitrophen (DMN) to produce brief Ca²⁺ elevations that mimic the waveform of Ca²⁺ changes associated with openings of single DHPRs. Photolysis liberates Ca²⁺ from the DMN-Ca complex much faster then free DMN binds Ca²⁺ (Zucker 1993; Ellis-Davies et al. 1996; Escobar et al. 1997). Thus, Ca²⁺ released from the photolyzed DMN will be free for some time until it rebinds to unphotolyzed DMN, producing a brief (<1 ms) Ca²⁺ overshoot. Our results show that application of such brief “Ca²⁺ spikes” to RyR channels in bilayers results in rapid and transient activation of the channels. The probability that a single RyR will be activated is determined by the amplitude and duration of the Ca²⁺ trigger signal. These results support the possibility that activation of release units is triggered by single DHPR events, and that DHPR–RyR coupling can be the subject of physiological modulation and pathological failure.

METHODS

Bilayer Experiments

Heavy SR microsomes were prepared from canine left ventricles by standard procedures (Dettbarn et al. 1994). Single SR Ca²⁺ release channels were reconstituted by fusing heavy SR microsomes into planar lipid bilayers as described previously (Györke and Fill 1993; Györke et al. 1994). The experimental solution contained 400 mM CsCH₃SO₃, 10 mM CsHEPES, and 1 mM glutathione, pH 7.4. The bilayer chamber was designed to minimize the background current noise during recordings with high temporal resolution. The bilayer aperture had a diameter of 0.1 mm, resulting in bilayer capacitance of 50–70 pF. Single-channel currents were measured using a patch-clamp amplifier (Axopatch 200A; Axon Instruments), filtered at 2–10 kHz, and digitized at 5–100 kHz. Data acquisition and analysis were performed using pClamp (version 6.0.1; Axon Instruments) and Origin (version 5.0; Microcal Software). The experimental variance was estimated according to Landau and Páez 1997. Peak open probability was defined as the intersection of the fits of the ascending and descending parts of the ensemble open probability (by exponential association function raised to the power n _a, and by monoexponential function, respectively).

Flash Photolysis Experiments

Fast changes of the Ca²⁺ concentration in the microenvironment of the reconstituted channel were performed by flash photolysis of DM-nitrophen (Calbiochem Corp.) as described previously (Györke and Fill 1993; Györke et al. 1994). Intense, 9-ns long UV laser flashes produced by a pulsed, frequency-tripled, Nd:YAG laser (Spectra-Physics) were applied through a fused silica fiber optics (450 μm diameter) positioned perpendicular to the bilayer surface (100 μm diameter) so that the whole volume between the fiber optics and the bilayer was illuminated evenly and instantaneously. The amplitude and time course of Ca²⁺ after the flash were determined from the concentration of total and free DMN and Ca²⁺, and from the proportion of DMN photolyzed during the flash according to the reaction scheme shown below in Fig. 1 A. The total concentration of DMN was kept at 3 mM. The concentration of steady state free Ca²⁺ was determined with a Ca²⁺-selective minielectrode (Györke et al. 1994). The local Ca²⁺ changes near the bilayer were calibrated by transforming the bilayer aperture into a Ca²⁺ electrode, using Ca²⁺ ionophore resin (Györke et al. 1994). The potential of the Ca²⁺ electrode was measured with 0.2 mV precision using the patch-clamp amplifier in current-clamp mode. The increase in free steady state Ca²⁺ after photolysis was plotted as a function of flash intensity and free Ca²⁺ before the flash to construct a calibration curve (see Fig. 1 B). The proportion of DMN photolyzed at a given free Ca²⁺ and flash intensity was calculated from the pre- and post-flash steady state free Ca²⁺, using parameters taken from the literature (Ellis-Davies et al. 1996; Escobar et al. 1997; Table ). The time course of Ca²⁺ concentration changes in a particular experiment was reconstructed from the above data, using the published set of differential equations and kinetic parameters of DM-nitrophen complexation and photolysis (Ellis-Davies et al. 1996; Escobar et al. 1997). Computations were performed with a program written in Mathematica (version 3.0; Wolfram Research).

Figure 1.

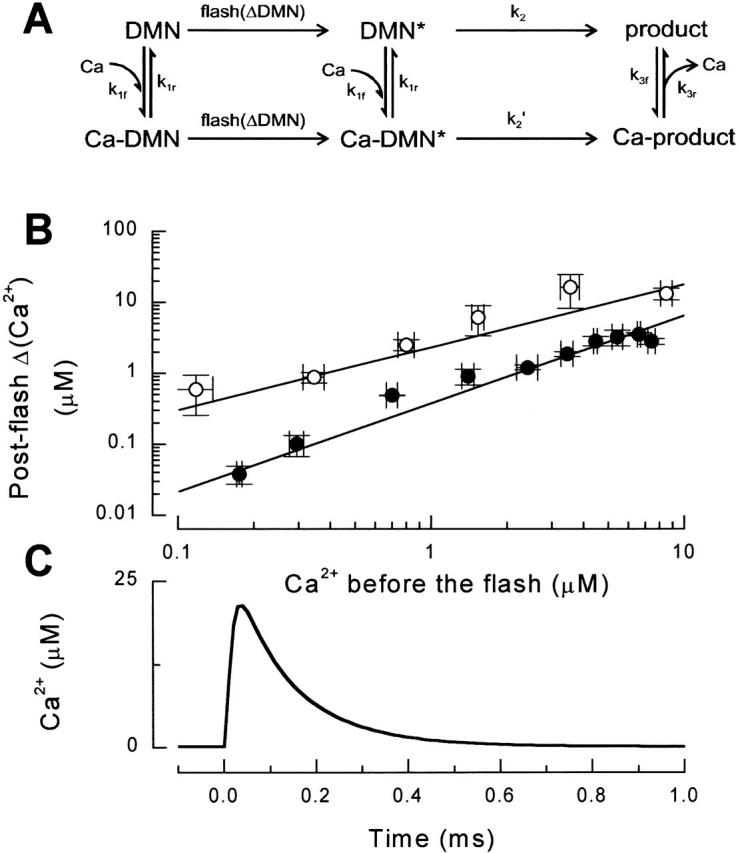
Defining the properties of the rapid Ca²⁺ spikes. (A) The reaction scheme of DMN complexation and photolysis (Ellis-Davies et al. 1996). The light-induced transitions of DMN into the activated states are assumed to be irreversible and instantaneous, and only a fraction of DMN (ΔDMN; 0.5–2% in our experiments) undergoes this reaction step. Other transitions in the scheme are reversible. (B) The increase in steady state Ca²⁺ after the flash plotted as a function of preflash steady state Ca²⁺ in five independent experiments. The total DMN concentration was always 3 mM. Different symbols denote different power settings of the laser flash. For a given flash energy the log–log plot of ΔCa²⁺ vs. Ca²⁺ was linear and was used to precalibrate flash energy in a given experiment. (C) The time course of a typical calcium spike reconstructed from the pre- and postflash steady state Ca²⁺ concentrations. The on and off portions of the calcium profile could be fitted by monoexponential functions, giving τ_on = 6.5 ± 1.5 μs and τ_off = 106 ± 1 μs.

Table 1.

The Rate Constants of DMN Complexation and Photolysis Used for Calculating the Time Course of Free Ca²⁺ during the Spike

Description	Constant	Value
Ca-binding on rate—DMN	k 1F	80 μM−1 s−1
Ca-binding off rate—DMN	k 1R	0.40 s−1
Decomposition of DMN	k 2	80000 s−1
Ca-binding on rate—photolyzed DMN	k 3F	80 μM−1 s−1
Dissociation constant—photolyzed DMN	K3*	3 mM

See Ellis-Davies et al. 1996 and Escobar et al. 1997. *K₃ = k _3R/k _3F.

Modeling of RyR Gating

To simulate the RyR response to Ca²⁺ spikes, we used our previously published minimal gating model of RyR with one Ca²⁺ binding step (Zahradníková and Zahradník 1996; see Fig. 5 and Model 1Ca in Table ). As alternative models, we used extensions of Model 1Ca, incorporating consecutive binding of two to five Ca²⁺ ions. It was assumed that Ca²⁺ binding sites are identical and behave independently. Subsequent gating steps are possible only if all calcium binding sites are occupied (Table , Model 2Ca–Model 5Ca). The rate constants of transitions not involving Ca²⁺ binding were unchanged. In models with multiple Ca²⁺ binding steps, the ratios of the on and off rates for calcium binding were calculated from the apparent peak and steady state calcium sensitivities of the channel P _o (see Zahradníková and Zahradník 1996) to provide a mean value identical to that of Model 1Ca. The on rates were optimized for best description of the rate of RyR activation.

Figure 5.

Description of the calcium dependence of the kinetics and amplitude of the ensemble open probability by different models of RyR gating. (A–E) Superposition of the experimental channel responses (thin noisy lines; data from the experiment shown in Fig. 4) and theoretical responses of the models (thick lines): Model 1Ca (A), Model 2Ca (B), Model 3Ca (C), Model 4Ca (D), and Model 5Ca (E). (F) The relationship between the peak open probability and the Ca²⁺ spike amplitude. The symbols with their standard deviations represent measured peak open probability at different levels of peak calcium during the spike. The lines represent the theoretical dose–response curves () for models with one to five Ca²⁺ binding sites. Labels correspond to the number of Ca²⁺ binding steps in the model.

Table 2.

Rate Constants of RyR Models Used for Simulation of Channel Activity

Rate constant	Model 1Ca	Model 2Ca	Model 3Ca	Model 4Ca	Model 5Ca	Unit
k on	1.0 × 103	9.2 × 102	8.2 × 102	7.1 × 102	7.1 × 102	μM−1· s−1
k off	1.0 × 105	1.4 × 104	5.5 × 103	3.0 × 103	2.0 × 103	s−1
k Cn01			1.0 × 104			s−1
k Cn02			1.0 × 100			s−1
k 01Cn			5.0 × 102			s−1
k 02Cn			5.0 × 10−1			s−1
k 01Cn + 1			2.0 × 100			s−1
k CN + 101			6.7 × 10−1			s−1
k 02Cn + 1			3.0 × 103			s−1
k CN + 102			1.0 × 102			s−1
k Cn + 1I			5.0 × 10−1			s−1
k ICn + 1			1.5 × 100			s−1

Single-channel activity in response to Ca²⁺ stimuli was simulated using the program SCESim (Zahradníková et al. 1999b). Channel kinetics were described by a matrix of transition rates between individual channel states (Colquhoun and Hawkes 1983). The time course of theoretical Ca²⁺ spikes for selected initial DMN saturation and percentage of DMN photolyzed were first calculated with 10-μs resolution, and then used as input for channel gating simulations.

The theoretical time course of channel open probability during and after the Ca²⁺ spike was calculated in Mathematica (Wolfram Research) by combining the differential equations for DMN complexation and photolysis (Ellis-Davies et al. 1996; Escobar et al. 1997) with those describing channel kinetics (Zahradníková and Zahradník 1996).

The analysis of statistical significance of differences between models was performed by χ² tests, according to the procedure described by Landau and Páez 1997. The values of χ² were determined from the sum of squares of differences between experimental data and model prediction, and from the experimental variance. The models that did not pass the χ² test at P = 0.01 were rejected.

The apparent calcium sensitivity of peak open probability in response to a Ca²⁺ spike was described by a general equation (, see Zahradníková and Zahradník 1996):

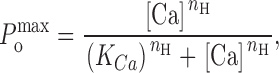1

where K _Ca is apparent calcium sensitivity of the channel, and n _H is the apparent Hill slope. In general, the apparent Hill slope may not necessarily correspond to the actual number (n) of Ca²⁺ binding sites. Specifically, n _H < n when the activation path contains a Ca²⁺-independent closed state (as with our models of RyR), even if the binding sites are equivalent and independent.

RESULTS

Generation of Rapid Ca²⁺ Stimuli for Activation of RyR

Single cardiac RyR channels were reconstituted at a steady state Ca²⁺ concentration of 20 μM. After incorporation of a single RyR, DMN (3 mM) was added to the cytoplasmic (cis) side of the channel. The free Ca²⁺ was titrated to 75–150 nM. Identical precalibrated photolytically induced Ca²⁺ spikes were applied to the channel. After each UV pulse, resting conditions were reestablished by stirring the solution in the cis chamber for at least 30 s. The laser flash-induced Ca²⁺ spike is too fast to be directly measured by any available method, including measurements using the fastest Ca²⁺ indicators (Ellis-Davies et al. 1996; Escobar et al. 1997). Therefore, the amplitude and time course of photolytic Ca²⁺ changes were reconstructed from the pre- and post-flash steady state free Ca²⁺ (see methods). In 21 independent experiments, the calculated free Ca²⁺ rose virtually instantaneously (τ_on = 6–18 μs) to 9–30 μM, and then decayed with a τ_off = 106–200 μs to a final level of 105–190 nM. Ca²⁺ was elevated to over 5 μM for 0.1–0.4 ms and to over 1 μM for 0.3–0.7 ms. A typical example of such a Ca²⁺ spike is shown in Fig. 1 C. The amplitude and duration of this Ca²⁺ stimulus is similar to that expected to occur near a RyR channel during a single brief opening of an adjacent DHPR channel (Rose et al. 1992; Stern 1992a; Stern 1992b; Soeller and Cannell 1997).

Kinetics of RyR Response to Rapid Ca²⁺ Stimuli

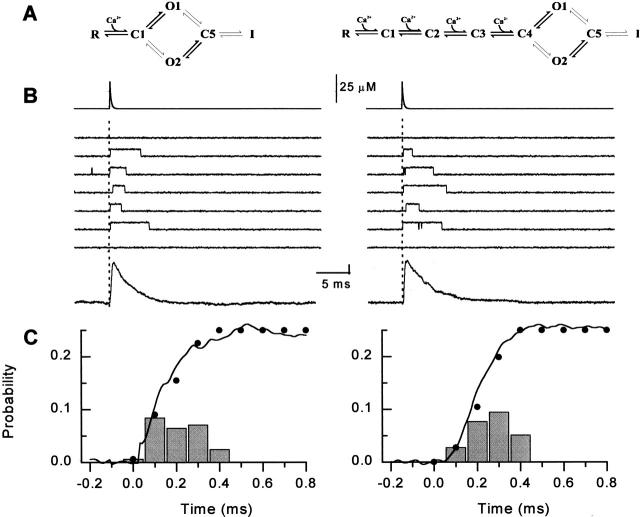
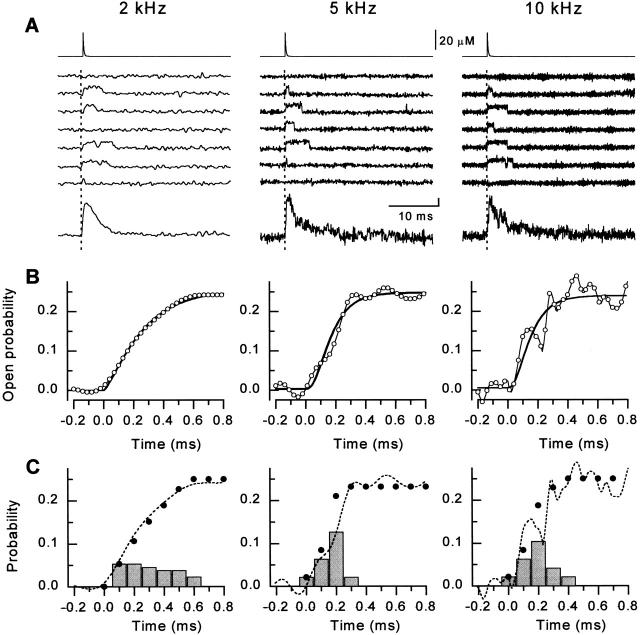
We recorded single RyR channel activity in response to such brief free Ca²⁺ stimuli (Fig. 2 and Table ). The required temporal resolution was achieved by recording at a sampling rate of 100 kHz and cut-off filter setting ≥5 kHz. Before the flash, the channels exhibited essentially no activity. The channels responded to the Ca²⁺ stimulus in ∼25% of the episodes. The activity evoked by DMN photolysis consisted mostly of single openings, after which the channel stayed closed until the end of the episode (Fig. 2 A). To quantify the time course of channel activity, at least 32 single channel records obtained from an individual channel were combined to generate ensemble averages (Fig. 2 A, bottom).

Figure 2.

Activation of the RyR channel by rapid Ca²⁺ spikes produced by flash photolysis of DM-nitrophen measured at three different bandwidths (left to right: 2, 5, and 10 kHz, respectively). (A, top) Time course of the reconstructed calcium spikes applied to the bilayer. (Middle) Sets of representative single channel records measured at +40 mV. The flash was applied at t = 0 ms (dotted lines). (Bottom) Ensemble currents constructed from 32–64 individual episodes. The vertical calibration denotes 20 and 1 pA for the center and bottom. (B) Exponential fits to the rising phase of the ensemble P _o (expanded scale). Only every third point of P _o is plotted for clarity (○). The continuous lines were obtained by fitting the data by the function:P _o=P _max1−e ^{−tτ_a n_a},where τ_a was 0.22 ± 0.01, 0.10 ± 0.01, and 0.09 ± 0.02 ms and n was 1.4 ± 0.4, 3.0 ± 0.5, and 2.8 ± 0.9 for 2, 5, and 10 kHz bandwidths, respectively. (C) The probability density of first latency (bars), the respective cumulative first latency distributions of channel openings (•), and open probability (dashed lines; same curve as ○ in B) at 2, 5, or 10 kHz.

Table 3.

Properties of the Open Probability Transient Induced by the Ca Spike

Parameter		Filter cutoff frequency
		2 kHz*	5 kHz‡	10 kHz‡
t o	Average open time	2.22 ± 0.18 ms	1.93 ± 0.24 ms	1.41 ± 0.05 ms
τa	Activation time constant	0.34 ± 0.02 ms§	0.16 ± 0.03 ms	0.14 ± 0.03 ms
n a	Exponent of activation	1.77 ± 0.46§	2.96 ± 0.74	2.48 ± 0.42
t d	Time constant of deactivation	3.14 ± 0.85 ms	3.03 ± 0.34 ms	3.47 ± 0.60 ms
P o	Peak open probability	0.32 ± 0.08	0.24 ± 0.03	0.22 ± 0.01

*n = 5; ^‡ n = 3; ^§significantly different from the data measured at 5 and 10 kHz bandwidth (P < 0.05).

Channel open probability transiently increased upon photolysis of DMN. The time course of activation was best fit by a single exponential association function raised to the power n _a (see Fig. 2, legend). The rising portions of P _o on expanded time scale are shown in B (○) along with the fits (solid lines). At 2 kHz bandwidth, the rise of P _o was relatively slow (τ_a = 0.22 ms, n _a = 1.4). Expanding the bandwidth to 5 kHz resulted in a significant decrease in the rise time of P _o (τ_a = 0.10 ms). In addition, a notable delay between the application of the laser flash and the ascent of P _o became evident (n _a = 3). Increasing the filter cutoff frequency to 10 kHz had no further impact on the observed rate of channel activation (τ_a= 0.09; n _a = 2.8). Therefore, the temporal resolution of our measurements at 5 and 10 kHz was adequate to resolve the kinetics of RyR activation. The rising phase of P _o at both 5 and 10 kHz was best fit by an exponential function with a power close to 3 (solid line), strongly suggesting that binding of several Ca²⁺ ions must occur before the channel can open.

To further quantify the kinetics of the channel response, we analyzed the distribution of the first latencies of channel openings induced by the laser flash (Fig. 2 C). The cumulative first latency distributions (•) closely corresponded to the time courses of the rising phases of the respective ensemble open probabilities at each bandwidth (dashed lines). This confirms that the delay observed in the open probabilities at ≥5 kHz reflects channel behavior and is not merely an artifact introduced by experimental noise. Consistent with the observed time course of ensemble open probabilities, the distributions of first latencies showed no delay at 2 kHz bandwidth. At both 5 and 10 kHz, they exhibited a prominent rising phase and peaked at ∼0.2 ms. The average channel open time was 1.9 ± 0.2 ms at 2–10 kHz. Deactivation of the channel after the Ca²⁺ spike had a monoexponential time course (τ_d = 3.2 ± 0.4 ms). It was much slower than channel activation or the decay of the Ca²⁺ spike and was independent of the bandwidth.

RyR Response to Transient versus Sustained Ca²⁺ Stimuli

Previous studies of RyR activation by photolysis of DMN (Györke and Fill 1993, Györke and Fill 1994; Valdivia et al. 1995) showed only sustained RyR responses decaying (i.e., adapting) with a time constant of ∼1 s and displayed no brief responses demonstrated in the present study. To explore the relationship between the rapid and sustained responses, we performed measurements of RyR activity during two sequential laser flashes of equal intensity (Fig. 3 A, top). It can be seen that while the first flash elicited predominantly single openings (Ca²⁺ spike response), the second pulse triggered mostly multiple openings (adaptation response). The corresponding changes in free [Ca²⁺] (continuous line) calculated from the Ca²⁺ electrode response (dashed line) using published parameters of complexation and photolysis of DMN (Ellis-Davies et al. 1996) are also presented (Fig. 3 A). The first flash elicited a Ca²⁺ spike followed by a small steady [Ca²⁺] elevation; the second flash elicited a similar Ca²⁺ spike, which was followed by a steady [Ca²⁺] elevation to a significantly higher level. The increase in steady component of the Ca²⁺ signal during successive flashes is due to a gradual increase in the saturation of DMN by Ca²⁺, leaving less DMN for rebinding of Ca²⁺ after the flash. These results clearly show that the adaptation behavior is determined by the steady component of the [Ca²⁺] signal.

Figure 3.

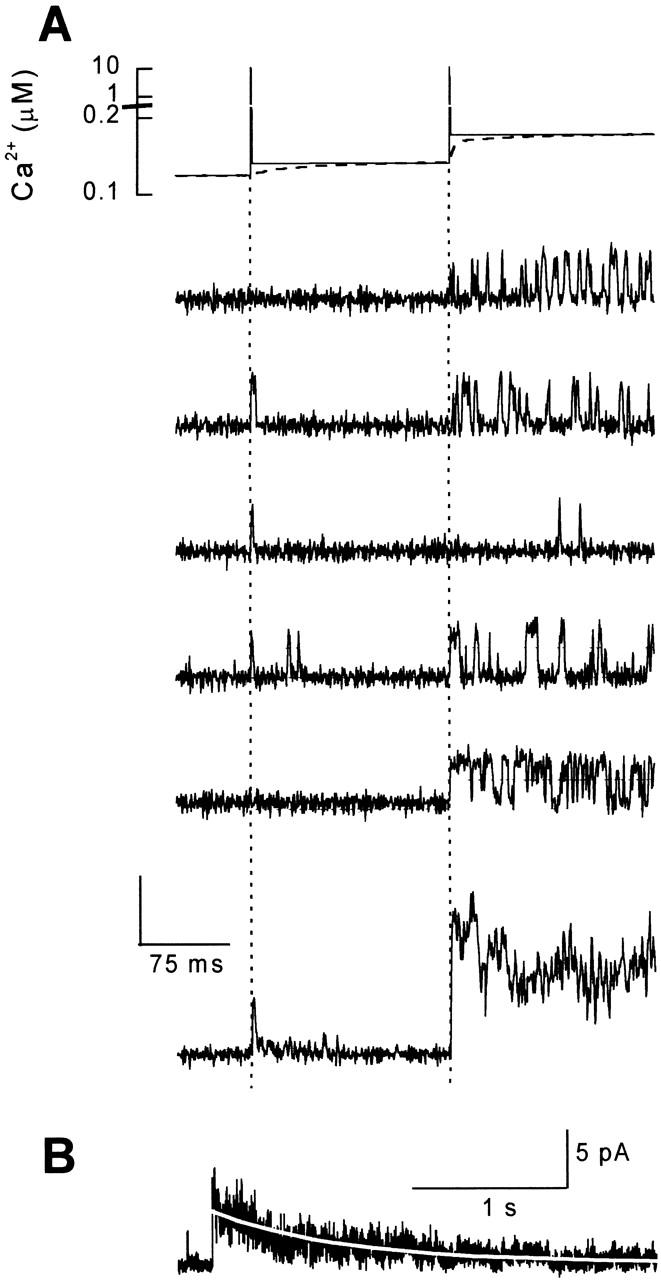
Response of single RyR channels to a sequence of two identical laser flashes. (A, top) The time course of the Ca²⁺ stimuli estimated by the calcium cup electrode (dashed line) and calculated from the pre- and postflash steady state Ca²⁺ concentrations (full line). (Middle) Representative single-channel records measured at +40 mV. The flashes were applied at t = 60 and 230 ms (dotted lines). Only the first 400 ms of 3.2-s-long traces are shown. (Bottom) Ensemble current constructed from 54 episodes. The vertical calibration denotes 20 and 5 pA for the center and bottom, respectively. (B) The time course of the ensemble current at a compressed time scale. Open probability in response to the second laser flash decayed monoexponentially with a time constant of 880 ms (white line).

RyR Response to Ca²⁺ Spikes of Different Magnitudes

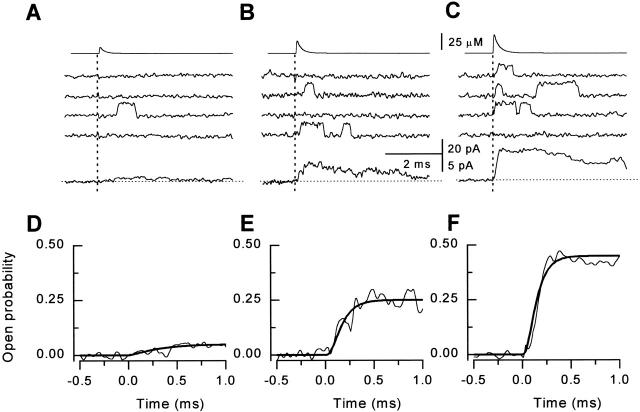
To further characterize the activation of RyRs by Ca²⁺ spikes, we measured RyR activity in response to laser flashes of different intensities. Fig. 4A–C, shows channel responses to laser flashes of low, intermediate, and high intensity along with the corresponding calculated free [Ca²⁺] spikes in a representative experiment. In this experiment, the amplitude of the Ca²⁺ spike was estimated to be 9.3, 18.3, and 27.4 μM for low, intermediate, and high intensity pulses, respectively. The Ca²⁺ spikes decayed with time constants of 0.17, 0.18, and 0.20 ms, respectively. Ca²⁺ was elevated to over 5 μM for 0.13, 0.27, and 0.34 ms, and to over 1 μM for 0.4, 0.6, and 0.7 ms, respectively. As can be seen, low-intensity flashes caused channel openings only in relatively few occasions (peak P _o ∼ 0.06); increasing flash energy increased the probability of activation (peak P _o ∼ 0.25 and 0.50, respectively). Interestingly, in all cases the responses were composed of isolated openings with a similar duration. The time constants of activation, determined by fitting single exponential association function raised to the power n to the ensemble averages, progressively decreased with increasing the energy of the laser pulse (τ_a = 0.27, 0.09, and 0.07 ms; n _a = 3.5, 2.5, and 2.4, respectively; Fig. 5, D–F). Similar results were obtained in five other experiments. These results are summarized in Fig. 6 F, which plots the peak P_o of the channel as a function of spike amplitude. The [Ca²⁺] dependence of P_o could be described by with a K_Ca value of 29 ± 1 μM and an apparent Hill slope of 2.5 ± 0.2. The high values of the activation exponent and of the Hill slope further indicate that activation of the RyR channel requires binding of several calcium ions.

Figure 4.

Response of single RyR channels to spikes of different amplitude. In A–C, the flash energy setting was 45, 47.5, and 50, respectively, corresponding to peak Ca²⁺ concentrations of 9, 18, and 27 μM. (Top) Time course of the reconstructed calcium spikes applied to the bilayer. (Middle) Sets of representative single channel records measured at +40 mV. The flash was applied at t = 0 ms (dotted lines). (Bottom) Ensemble currents constructed from 32–96 individual episodes. (E–F) Exponential fits to the rising phase of the ensemble P _o (expanded scale), corresponding to A–C, respectively. The time course of activation was best described by the equation:P _o=P _max1−e ^{−tτ_a n_a},where τ_a = 0.27 ± 0.06, 0.09 ± 0.02, and 0.07 ± 0.01 ms, and n _a = 3.5 ± 1.4, 2.5 ± 0.8, and 2.5 ± 0.3 for the ensemble averages in A–C, respectively.

Figure 6.

Simulation of RyR responses to Ca²⁺ spikes using RyR gating models with one or four Ca²⁺ binding sites. (A) The gating schemes for Model 1Ca (left) and Model 4Ca (right; the rate constants are given in Table ). (B, top) The time course of the calcium spikes. (Middle) Sets of representative simulated single channel episodes filtered at 10 kHz. (Bottom) Ensemble currents constructed from 128 individual episodes. The vertical calibration denotes 20 and 1 pA for the center and bottom, respectively. The dotted lines denote the time of application of the Ca²⁺ spikes. (C) The probability density of first latency (bars) along with the respective cumulative first latency distributions (•) of channel openings. The ensemble open probabilities are overlaid (solid lines).

Gating Mechanisms of RyR Channel during Brief Ca²⁺ Stimuli

To better understand the mechanisms of activation and deactivation of RyR in response to Ca²⁺ spikes, we performed single channel simulations using our published minimal model of RyR gating (Zahradníková and Zahradník 1996) with two open and three closed states and one Ca²⁺ binding step (Fig. 5 A, left; Table , Model 1Ca). Similar to experimental observations, the simulated responses consisted mostly of single, ∼2-ms long openings (Fig. 5 B). However, other features of simulated channel activity were at odds with the experimental data. For example, contrary to real channels, simulated channels exhibited substantial basal activity. In addition, the ensemble P _o or the distribution of the first latencies of the simulated responses (Fig. 5 C) showed no delay after the Ca²⁺ spike, seen with experimental data.

The excessive background activity and a lack of delay between the Ca²⁺ spike and RyR activation could be ascribed again to the possibility that binding of more than one Ca²⁺ ion is required to produce channel opening. Considering the tetrameric organization of the RyR, we extended our minimal RyR model by including four sequential Ca²⁺ binding steps (Fig. 5 A, right; Table , Model 4Ca). The ensemble P _o generated using the extended model showed essentially no spontaneous openings before the Ca²⁺ spike. After the Ca²⁺ spike, it exhibited a significant delay, similar to the experimentally observed behavior (Fig. 5 B). Furthermore, the first latency distribution (Fig. 5 C) yielded a peak near 0.25 ms, close to the experimentally observed value of 0.2 ms. These results suggest that activation of the RyR by Ca²⁺ spikes may indeed involve binding of multiple, perhaps as many as four, Ca²⁺ ions to the channel.

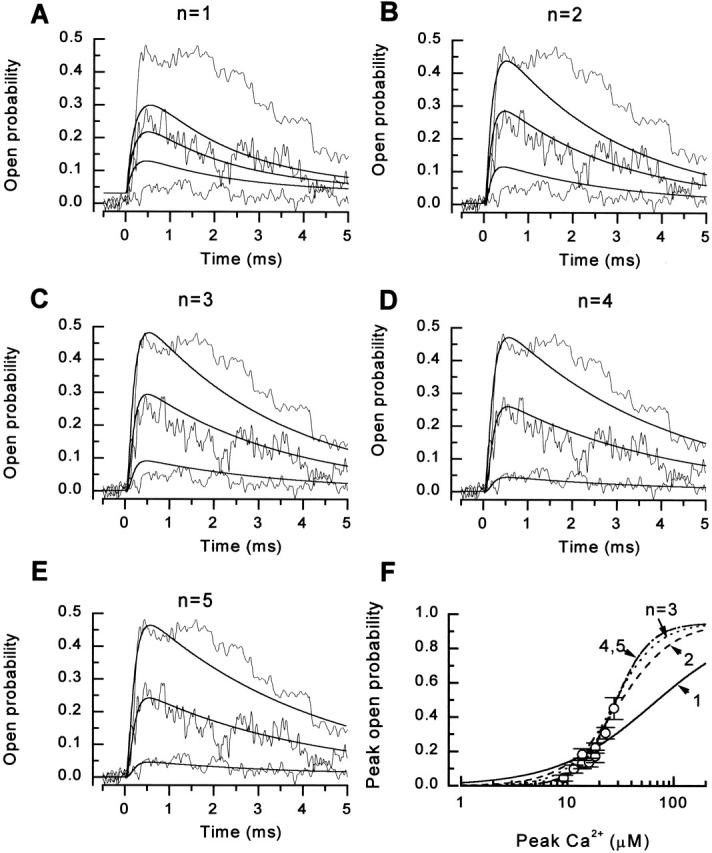
To further elucidate how many Ca²⁺ binding steps are involved in channel activation, we carried out theoretical simulations using models with different numbers of Ca²⁺ binding sites. We compared the abilities of the models with different numbers of Ca²⁺ binding sites to reproduce the experimentally observed kinetics of RyR activation. This approach is illustrated in Fig. 6A–E, for the experiment shown in Fig. 4 and for models with one to five Ca²⁺ binding steps, respectively. Differences between the models were statistically analyzed by the χ² test, applied to the whole data set of six experiments. The χ² values were determined from the sum of squares of differences between experimental data and predictions of the particular model, and from the experimental variance (Landau and Páez 1997). We obtained χ² values of 17,120, 9,821, 6,712, 4,667, and 4,711 (4,510 degrees of freedom) for models with one, two, three, four, and five Ca²⁺ binding sites, respectively. Models with less than four calcium binding sites have failed the χ² test at the significance level P = 0.01, while models with four and five Ca²⁺ binding sites passed the test and can be considered, therefore, compatible with the data. These tests strongly suggest that binding of at least four Ca²⁺ ions are necessary for RyR activation.

Fig. 6 F shows theoretical Ca²⁺–P _o dependence curves obtained from the above series of models along with the Ca²⁺–P _o dependence curve obtained from experimental data. The apparent Hill slopes of the theoretical [Ca²⁺]–P _o relationships yielded by the models with one, two, and three Ca²⁺ binding steps (0.97 ± 0.15, 1.69 ± 0.02, and 2.09 ± 0.01, respectively) were significantly different from those derived from experimental data (2.5 ± 0.2) at significance levels of 0.0001, 0.001, and 0.05, respectively. Therefore, these models are not compatible with the experimental results. Models with four and five Ca²⁺ binding steps (apparent Hill slopes 2.6 ± 0.1 and 2.6 ± 0.1, respectively) were not significantly different from the experimental data even at P = 0.5. Therefore, the response of the RyR to Ca²⁺ spikes can be described by our minimal model of the RyR modified by including a total of four Ca²⁺ binding steps.

Theoretical Dependency of RyR Response on Amplitude-duration Characteristics of Ca²⁺ Stimulus

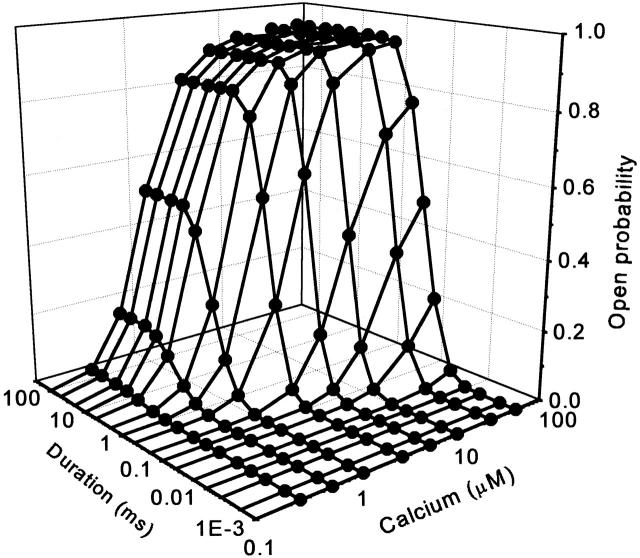
The chemistry of DMN limits flash-photolysis experiments to a rather narrow range of amplitude-duration characteristics of Ca²⁺ spikes. In contrast, the parameters of local Ca²⁺ signals associated with the activity of DHPRs vary widely. Therefore, to gain further insight into the dependence of the channel activation on the characteristics of the trigger signal, we performed simulations in response to a broad range of rectangular Ca²⁺ pulses using Model 4Ca with four Ca²⁺ binding sites described above. The properties of the Ca²⁺ pulse in the physiological range of durations and amplitudes had a profound effect on peak open probability of the RyR, as illustrated in Fig. 7. Calcium elevations lasting <10 μs had negligible probability to open the RyR in the whole amplitude range. To increase the peak open probability from 5 to 95%, the amplitude of the calcium pulse has to be increased by ∼10-fold for any pulse duration. Prolongation of the Ca²⁺ pulses above 1 ms was not effective in increasing peak P _o of the RyR. In the high Ca²⁺ pulse amplitude range (>10 μM), the dependence of peak P _o on pulse duration was very steep for short pulse durations (0.1–0.5 ms).

Figure 7.

Simulated peak open probabilities of Model 4Ca with four Ca²⁺ binding sites (Table ) in response to rectangular Ca²⁺ pulses, plotted as a function of pulse amplitude and duration. The x axis represents the amplitude of free Ca²⁺ concentration during the pulse, the y axis represents the duration of the pulse, and the z axis represents the peak open probability of the channel estimated from the ensemble average of 4,096 episodes.

DISCUSSION

In the present study we measured the kinetics of activation of cardiac SR Ca²⁺ release channels/RyRs using fast Ca²⁺ concentration spikes produced by photolysis of DM-nitrophen. The Ca²⁺ spikes mimic the profile of Ca²⁺ produced by openings of single DHPRs in the vicinity of the RyRs. Thus, our results show, for the first time, how single RyRs might respond to a physiological trigger signal.

Under our experimental conditions (∼100 nM resting Ca²⁺ and 3 mM DMN), the reconstructed Ca²⁺ spikes were characterized by an activation time constant of ∼15 μs, a duration of ∼0.1–0.4 ms (at 5 μM Ca²⁺) and a peak amplitude of 10–30 μM (Fig. 1 C). Application of such Ca²⁺ pulses resulted in activation of the RyR with 5–50% probability, depending on spike magnitude. The activity of RyR was characterized by isolated single openings with duration of ∼2 ms. It is important that in our experiments we used Cs⁺ instead of Ca²⁺ as the charge carrier. Besides improving the signal-to-noise ratio, this allowed us to determine the parameters of channel kinetics without potential side effects related to “feed-through” influences of luminal Ca²⁺ at the cytosolic activation and inactivation sites (Tripathy and Meissner 1996).

Previous studies using caged Ca²⁺ did not yield channel activation in response to Ca²⁺ spikes (Györke and Fill 1993, Györke and Fill 1994; Györke et al. 1994; Valdivia et al. 1995). These negative results can be ascribed to lower concentrations of the calcium cage, low time resolution of the measurements, and the presence of a laser flash artifact that could have concealed the occasional, brief channel openings in response to the flash. In the above studies, the effective trigger signal consisted of both a transient (i.e., spike) and a sustained component. The reported time constants of channel activation were 1–2 ms. Our present experiments with improved time resolution showed that rapid Ca²⁺ spikes can activate the channel with much faster kinetics (activation time constant ∼0.15 ms).

We believe that our measurements yield the true response time of the channel because channel activation displayed a distinct delay, and the kinetics of the RyR response were unaffected by increasing the filter cutoff frequency from 5 to 10 kHz. The lifetime of isolated RyR channel openings induced by Ca²⁺ spikes (t _o ∼ 2 ms) was substantially longer than the average channel open time (∼1 ms) reported under similar conditions at steady state (Zahradníková and Zahradník 1995). However, it was similar to the average channel open time within the high activity (H) gating mode (Zahradníková and Zahradník 1995). The deactivation rate obtained from ensemble averages of the channel responses to the Ca²⁺ spike was ∼3 ms, and it corresponded approximately to the average channel open time. These results provide further evidence for the idea that the H-mode activity is the preferred initial regime of channel operation upon activation (Zahradníková and Zahradník 1996; Zahradníková et al. 1999a).

In previous studies with photolysis of DMN and NP-EGTA, the RyRs activated rapidly, and then the P _o decayed slowly, by a process termed adaptation (Györke and Fill 1993; Valdivia et al. 1995). It has been argued that adaptation might simply be a result of the spontaneous deactivation of the RyR after its activation by the rapid Ca²⁺ spike (Lamb et al. 1994). Our direct measurements of the RyR response to Ca²⁺ spikes indicate that the deactivation of the RyR after a Ca²⁺ spike is too fast to account for the adaptation phenomenon. Further, our results with double flashes that induce Ca²⁺ waveforms with similar transient but different steady components (Fig. 3) showed that the adaptation response is evoked only by the Ca²⁺ signal with a large steady component. Thus, it appears that the type of response of the RyR (i.e., rapid or prolonged) is determined by the steady component of the photolytic Ca²⁺ change.

The kinetics and [Ca²⁺] dependence of the response of the RyRs to Ca²⁺ spikes could be well described by our minimal model of RyR (Zahradníková and Zahradník 1996) with two open and three closed states modified by including three additional (a total of four) Ca²⁺-dependent closed states (Fig. 5 A). We have shown previously that the minimal model reproduces reasonably well the main aspects of channel behavior, including modal gating activity, under both stationary and nonstationary conditions (Zahradníková and Zahradník 1996; Zahradníková et al. 1999a). This model consists of three sets of states (i.e., gating modes) connected by slow transitions. The results of our present study with improved time resolution allowed us to refine the state structure of the high activity mode corresponding to the activation path of the channel.

The existence of multiple Ca²⁺ binding steps in the RyR activation path is consistent with the results of analysis of closed time distributions of steady state recordings at low [Ca²⁺], yielding at least five closed states (Sitsapesan and Williams 1994). Importantly, the four-Ca²⁺ binding site model is also consonant with the molecular structure of the RyR, a protein composed of four homologous subunits with each monomer carrying at least one Ca²⁺ binding site (Coronado et al. 1994).

Based on our model simulations, we suggest that the response of the RyR to a Ca²⁺ spike includes the following steps. (a) Sequential binding of four Ca²⁺ ions to the channel promotes transition from closed states (R–C4) to an open state (O1). The need for binding of four Ca²⁺ ions to open the channel accounts for the delay in channel activation, for the negligible P _o at basal [Ca²⁺], and for the fact that spikes do not always cause channel opening. (b) After termination of the spike, Ca²⁺ dissociates from the channel and the channel deactivates by returning first to the closed states (C4–C1) and eventually to the resting state. Transitions between states C4–O2 and O1–C2 are very slow (∼1 s; Zahradníková and Zahradník 1995); consequently, the probability of the channel entering these late states during brief Ca²⁺ spikes is low. Thus, as we have previously predicted (Zahradníková and Zahradník 1996), the channel has just enough time to enter the fast access states of the H-mode, but not the slow access states of the L-mode when challenged by brief, calcium spike–like stimuli. The slow transitions between states C4–O2 and O1–C2 can only occur when Ca²⁺ remains elevated in the vicinity of the channel (Zahradníková et al. 1999a; Fig. 3). In this respect, our gating model could be simplified by omitting the slow access states (O2, C5, and I) and still be able to account for most results with brief Ca²⁺ spikes. However, such a truncated model would clearly become inadequate for describing channel behavior in response to sustained Ca²⁺ elevations when the initial passage to rapid access states is followed by a transition to slow access states, accounting for the phenomenon of RyR adaptation (Zahradníková et al. 1999a; Fig. 3). Neither would the truncated model be able to describe steady state activity characterized by modal behavior; i.e., random transitions between periods of high and low activity (Zahradníková and Zahradník 1995, Zahradníková and Zahradník 1996).

Our results have important ramifications for understanding CICR in vivo. It has been suggested that during E-C coupling Ca²⁺ entering through single L-type Ca²⁺ channels locally controls the activity of the Ca²⁺ release channels, presumably arranged into functionally independent release units (Stern 1992b; Cannell et al. 1995; López-López et al. 1995; Shorofsky et al., 1997). One important premise of the local control theory is that the RyR must be fast enough to track the fast Ca²⁺ changes associated with single DHPR openings (see introduction). The results of the present study show that brief (<0.5 ms) trigger Ca²⁺ signals are adequate to activate RyRs and are consistent with the possibility that RyR channels are controlled by single DHPR events. Such rapid activation could also provide a means for effective cross-activation of neighboring Ca²⁺ release channels within a single release unit, thus accounting for the synchronization of multiple RyRs during a Ca²⁺spark (Bridge et al. 1999). At the same time, the presence of four Ca²⁺ binding sites that must be occupied for channel opening would tend to reduce activation by global background Ca²⁺ while still enabling the local Ca²⁺ increase in the diadic cleft to activate the channels efficiently (Stern 1992b; Stern et al. 1999).

We showed that Ca²⁺ spikes with an estimated amplitude of 10–30 μM, which mimic single DHPR-related signals, have a 5–50% probability of inducing RyR activation. The results of our simulations in a wider range of amplitudes and durations of the Ca²⁺ elevations demonstrate that the probability of activation of a single RyR is graded with the amplitude as well as duration of the triggering Ca²⁺ pulse. These results are consistent with a DHPR–RyR coupling arrangement that could be the subject of physiological modulation and pathological failure in the heart (Gomez et al. 1997). The relatively low efficiency of activation of single RyRs by brief Ca²⁺ stimuli could also reflect the importance of clustering of RyRs in the junctional gap, which would be expected to improve responsiveness of the RyRs (Cannell and Soeller 1997). While our data suggest that the lower and shorter Ca²⁺ elevations produced by DHPR openings trigger RyR activation with a relatively low probability, the resulting longer RyR openings of higher amplitude can be expected to activate the neighboring RyRs with a much higher probability, giving rise to the stereotypical spatio-temporal shape of a calcium spark (Cannell et al. 1995; López-López et al. 1995; Bridge et al. 1999).