Autoregulation of renal blood flow in the conscious dog and the contribution of the tubuloglomerular feedback

Abstract

1. The aim of this study was to investigate the autoregulation of renal blood flow under physiological conditions, when challenged by the normal pressure fluctuations, and the contribution of the tubuloglomerular feedback (TGF).

2. The transfer function between 0.0018 and 0.5 Hz was calculated from the spontaneous fluctuations in renal arterial blood pressure (RABP) and renal blood flow (RBF) in conscious resting dogs. The response of RBF to stepwise artificially induced reductions in RABP was also studied (stepwise autoregulation).

3. Under control conditions (n = 12 dogs), the gain of the transfer function started to decrease, indicating improving autoregulation, below 0.06-0.15 Hz (t = 7-17 s). At 0.027 Hz a prominent peak of high gain was found. Below 0.01 Hz (t > 100 s), the gain reached a minimum (maximal autoregulation) of -6.3 ± 0.6 dB. The stepwise autoregulation (n = 4) was much stronger (-19.5 dB). The time delay of the transfer function was remarkably constant from 0.03 to 0.08 Hz (high frequency (HF) range) at 1.7 s and from 0.0034 to 0.01 Hz (low frequency (LF) range) at 14.3 s, respectively.

4. Nifedipine, infused into the renal artery, abolished the stepwise autoregulation (-2.0 ± 1.1 dB, n = 3). The gain of the transfer function (n = 4) remained high down to 0.0034 Hz; in the LF range it was higher than in the control (0.3 ± 1.0 dB, P < 0.05). The time delay in the HF range was reduced to 0.5 s (P < 0.05).

5. After ganglionic blockade (n = 7) no major changes in the transfer function were observed.

6. Under furosemide (frusemide) (40 mg + 10 mg h⁻¹ or 300 mg + 300 mg h⁻¹ i.v.) the stepwise autoregulation was impaired to -7.8 ± 0.3 or -6.7 ± 1.9 dB, respectively (n = 4). In the transfer function (n = 7 or n = 4) the peak at 0.027 Hz was abolished. The delay in the LF range was reduced to -1.1 or -1.6 s, respectively. The transfer gain in the LF range (-5.5 ± 1.2 or -3.8 ± 0.8 dB, respectively) did not differ from the control but was smaller than that under nifedipine (P < 0.05).

7. It is concluded that the ample capacity for regulation of RBF is only partially employed under physiological conditions. The abolition by nifedipine and the negligible effect of ganglionic blockade show that above 0.0034 Hz it is almost exclusively due to autoregulation by the kidney itself. TGF contributes to the maximum autoregulatory capacity, but it is not required for the level of autoregulation expended under physiological conditions. Around 0.027 Hz, TGF even reduces the degree of autoregulation.

The ample capacity of the kidney for the autoregulation of blood flow has been well characterized for artificially induced stepwise changes of mean perfusion pressure (Shipley & Study, 1951; Kirchheim, Ehmke, Hackenthal, Lowe & Persson, 1987). However, under physiological conditions, the mechanisms of autoregulation are challenged more dynamically by pressure fluctuations distributed over a wide range of frequencies (Marsh, Osborn & Cowley, 1990; Persson, Ehmke, Kohler & Kirchheim, 1990). Therefore, knowledge about the temporal characteristics of this regulation is of major interest. With the aid of the transfer function between renal perfusion pressure and blood flow it has been shown that the regulation is based on at least two mechanisms of different response times (Daniels, Arendshorst & Roberds, 1990; Holstein Rathlou, Wagner & Marsh, 1991; Cupples, Novak, Novac & Salevsky, 1996). In those investigations in which only one mechanism was found the frequency ranges tested were either too high (Sakai, Hallman & Marsh, 1986) or too low (Wittmann, Nafz, Ehmke, Kirchheim & Persson, 1995) to detect both mechanisms. In most of the studies using transfer function analysis, the pressure fluctuations were artificially produced by external forcing or by induction of atrial fibrillation. The few studies which have applied the transfer function to the spontaneous fluctuations (He & Marsh, 1993; Cupples et al. 1996) were done in anaesthetized rats. Apart from the influence of anaesthesia on the spectrum of the spontaneous pressure fluctuations (Robinson, Buyck & Galletly, 1994), the finding of differences in the transfer spectrum, even under two related anaesthetics (Cupples et al. 1996), suggests that this method should be applied in the conscious animal. Although this has been done on conscious dogs by Marsh et al. (1990) and Wittmann et al. (1995), in the first of these studies the frequency range of interest did not include the frequency responses of either of the two regulating mechanisms, and the second used artificially induced pressure oscillations and was thereby limited to frequencies slower than the fast response.

Therefore, the first aim of the present study was to characterize the autoregulation of renal blood flow in conscious dogs when challenged by the normal spectrum of blood pressure fluctuations under physiological conditions in a frequency range embracing the characteristic frequencies of the two regulatory mechanisms. This includes the determination of the temporal characteristics and the regulatory efficiency under these conditions, the comparison of this regulatory efficiency to that in response to stepwise, artificially induced pressure changes, and the delineation of autonomic nervous and intrarenal autoregulatory contributions to the transfer spectrum.

There is today wide agreement that the underlying mechanisms of this regulatory behaviour can probably be attributed only to the action of the myogenic response and tubuloglomerular feedback (TGF) (Schnermann & Briggs, 1989; Takenaka, Harrison Bernard, Inscho, Carmines & Navar, 1994; Feldberg, Colding Jorgensen & Holstein Rathlou, 1995). However, their relative contributions to the capacity of renal blood flow autoregulation has long been a matter of debate. While TGF undoubtedly exerts a clear regulatory influence (Schnermann, Wright, Davis, Stackelberg & Grill, 1970), it does not seem to be the only mechanism responsible for blood flow regulation, since autoregulatory responses occur also in non-filtering kidneys (Sadowski & Wocial, 1977). Neither can the vasoconstriction in response to a sudden reduction in perirenal pressure (Clausen, Oien & Aukland, 1992) be explained by TGF. Micropuncture experiments allow more direct block of TGF and they have shown, that although TGF contributes to the regulation of single nephron filtration rate, considerable regulatory activity remains when this mechanism is abolished (Moore, Schnermann & Yarimizu, 1979). In similar studies, the contribution of TGF has been estimated to account for about 50 % of the total regulatory capacity (Moore et al. 1979; Schnermann, Briggs & Weber, 1984). Nevertheless, the extrapolation of these findings to the autoregulation of total renal blood flow under physiological conditions remains difficult because there are intricate interactions between adjacent nephrons (Kallskog & Marsh, 1990), as well as between TGF and the myogenic response (Haeberle, 1988; Schnermann & Briggs, 1989). Furthermore, the exact strength of these interactions still remains ill defined. Therefore, the contribution of the two mechanisms has been assessed under more physiological conditions by the use of the transfer function between pressure and flow. In one of these studies, the blockade of TGF by ureteral occlusion failed to change the transfer function below 0.03 Hz (Daniels & Arendshorst, 1990), and thus suggested that the contribution of TGF in this frequency range might be negligible. On the other hand, a study on conscious dogs, in which TGF had been eliminated by furosemide (frusemide) (Wittmann et al. 1995), suggested that TGF was the only active mechanism.

Thus, the second aim of this investigation was to characterize the importance of TGF for the regulation of renal blood flow under physiological conditions, when it is challenged by the normal spectrum of pressure fluctuations.

For the approach to these two aims, the transfer function was calculated from the spontaneous fluctuations of pressure and flow in conscious resting dogs. For comparison, the regulatory efficiency was also identified by measuring the blood flow response to stepwise artificially induced reductions of the renal artery pressure. Autonomic nervous and intrinsic autoregulatory influences were delineated by determining the transfer spectra during ganglionic blockade and nifedipine, respectively. In order to define the role of TGF, the transfer function under spontaneous fluctuations and the regulatory efficiency in response to artificially induced pressure changes were investigated before and after inhibition of TGF by furosemide.

METHODS

All data were derived from fifty-two experiments on twenty-three conscious chronically instrumented foxhounds (23-35 kg body weight), held on a standard dog diet (SSNIFF, Soest, Germany or ALMA 5003, Botzenhardt, Kempten, Germany) and kept under an artificial light-dark cycle (06.00-18.00 h light, 18.00-6.00 h dark). All experiments and procedures were done in accordance with the national law for the care and use of research animals (licence no. 37-9185.81/105/94).

Surgical procedures

The dogs were surgically prepared under sterile conditions. After premedication with atropine (0.5 mg s.c.; Braun, Melsungen, Germany) and propionylpromazine (Combelen®, 0.64 mg kg⁻¹s.c.; Bayer, Leverkusen, Germany) anaesthesia was induced using sodium pentobarbitone (Nembutal®, 20 mg kg⁻¹i.v.; Sanofi, Libourne Cedex, France) and maintained using halothane (Fluothane®, 0.8-1.0 %; Zeneca, Planckstadt, Germany) and N₂O (0.5 l min⁻¹) in O₂. Through a left flank incision the left renal artery and the abdominal aorta were exposed retroperitoneally. A polyurethane catheter was implanted into the renal artery or the abdominal aorta, or both. An ultrasonic transit time flow probe (Transonic, Ithaca, NY, USA) was placed on the renal artery. In fourteen of the dogs an inflatable cuff was implanted around the same artery distal to the flow probe in order to allow for controlled reduction in renal perfusion pressure and determination of the zero flow offset of the flow probe. Four of the dogs also received a pressure transducer (Konigsberg P5-S-N; Konigsberg, Pasadena, CA, USA; accurate frequency response up to 1 kHz, as indicated by manufacturer), which was inserted into the aorta about 2-5 cm distal to the aortic catheter and which allowed assessment of the frequency response characteristics of the catheters. The free ends of the catheters and cables were run subcutaneously to the animal's neck, where they were exteriorized. At least 10 days recovery were allowed before the experiments were begun. During the first 9 days, the dogs received a combination of benzylpenicilline and sulphatolamide (Tardomycel®; Bayer; 3 ml s.c. every 3rd day). The catheters were flushed every second or third day and filled with a solution of heparin (1700 i.u. ml⁻¹) and cephtazidim (Fortum®, 16 mg ml⁻¹; Glaxo, Bad Oldesloh, Germany) in physiological saline (0.9 % NaCl) solution.

Measurements

All experiments were done between 07.30 and 15.00 h, while the dogs were resting on their right side, as trained previously. Arterial blood pressure (ABP) (renal and/or aortic) was measured using pressure transducer(s) (Statham P23Db or P23XL; Gould, Valley View, OH, USA) with calibrated amplifiers (Gould Pressure Processor) connected to the catheters. Renal blood flow (RBF) was measured using the implanted flow probe connected to the flowmeter (Transonic T 106 or T 108), the output of which was low-pass filtered below 10 Hz by the built-in analog filter. The phase shift caused by the filter is a constant delay of only 3.8 ms. ABP and filtered RBF were continuously recorded on a computer (80286, or 80386+, using Labtech Note Book software, v. 7.11; Labtech, Wilmington, MA, USA) at a sampling rate of 20 Hz, after A/D conversion (DAS-16; Keithley-Metrabyte, Taunton, MA, USA). The frequency response of the catheters was tested in the four dogs that received a pressure transducer in addition to the arterial catheter. The transfer function between the blood pressure signal from the implanted transducer to that measured via the catheter simultaneously at 20 Hz for 2 h, showed a flat response up to at least 0.6 Hz with a corner frequency at 1.0 ± 0.2 Hz (0.6-1.8 Hz) and -3 dB attenuation at 3.2 ± 1.2 Hz (0.8-7 Hz). As higher frequencies were even more attenuated, the sampling rate of 20 Hz was most probably sufficient to avoid significant aliasing in the ABP data. Therefore, no analog filter was used for this signal.

Experimental protocols

Transfer function analysis

In order to analyse the transfer function (T) of renal blood flow autoregulation under physiological conditions, renal arterial blood pressure (RABP) and renal blood flow (RBF) were continuously recorded for a duration of 3 h (13 500 s), while the dogs were quietly resting as described above. The recordings were done under five different conditions as follows.

T-Ctrl (n = 12)

In the control group (Ctrl), these recordings were performed without any further intervention.

T-Nife (n = 5)

The recordings were done during a continuous infusion of the calcium channel blocker nifedipine (Nife) (Adalat pro infusione®, Bayer) at 24 ml h⁻¹ (1.4 μg kg⁻¹ min⁻¹) into the renal arterial catheter. In preliminary experiments in two dogs, nifedipine was infused at increasing rates (1-48 ml h⁻¹, i.e. ∼0.06-2.9 μg kg⁻¹ min⁻¹) for 5 min each. The half-effective dose for the decrease of renal vascular resistance (RVR) was at 6 ml h⁻¹ (i.e. 0.36 μg kg⁻¹ min⁻¹) and saturation at 24-48 ml h⁻¹ (i.e. 1.4-2.9 μg kg⁻¹ min⁻¹). In order to keep systemic effects small, the 24 ml h⁻¹ dose was chosen. In one dog, 48 ml h⁻¹ were given in an additional experiment for a duration of 2 h. Similar results to those with the lower dose in the same dog were obtained. The recordings for the calculation of the transfer functions were started 5 min after the beginning of the infusion.

T-Hexa (n = 7)

To eliminate possible autonomic nervous influences on RBF, these dogs received the ganglionic blocking agent hexamethonium bromide (Hexa) (Sigma-Aldrich) as a 5 mg kg⁻¹i.v. bolus, immediately followed by a continuous i.v. infusion of 5 mg kg⁻¹ h⁻¹. Recordings were started 20 min after the bolus.

T-Furo-I (n = 7)

In order to inhibit the function of TGF, furosemide (Furo) (Lasix®; Hoechst AG, Frankfurt am Main, Germany) was given as a bolus of 40 mg i.v. followed by a continuous i.v. infusion of 10 mg h⁻¹ (in 10 ml h⁻¹ saline) starting 20 min after the bolus. Recordings for the transfer functions were begun a further 10 min later. At least 20 min before the bolus was given a bladder catheter was inserted through the urethra. The voided urine volume was documented every 15 min. This volume was replaced i.v. by an infusion of physiological saline solution containing 4 mmol l⁻¹ KCl, the rate of which was adjusted if necessary every 15 min. Care was taken not to infuse more volume than voided (including the vehicle for furosemide). Plasma levels of Na⁺ and K⁺ were determined electrochemically (NOVA 11+; Nova Biomedical, Rödermark, Germany) from blood samples drawn from the arterial catheter before the administration of furosemide and at the end of the experiment. In two of the dogs, urine samples were taken immediately, 2 h and 4 h after the recordings had been started. Determination of the furosemide concentration by HPLC was generously performed by Dr U. Milbert (Hoechst AG, Frankfurt am Main, Germany).

T-Furo-II (n = 4)

In order to study possible dose dependency, in this group very high doses of furosemide were used: 300 mg (∼10 mg kg⁻¹) bolus followed 20 min later by a continuous i.v. infusion of 300 mg h⁻¹. Six instead of 4 mmol l⁻¹ KCl were added to the replacement fluid. Urine samples were taken from three of the dogs. Otherwise the protocol was similar to that for the T-Furo-I group.

Stepwise autoregulation

In order to assess the autoregulatory capacity in response to stepwise artificially induced pressure reductions (S), RABP and RBF were measured while RABP was reduced by a controlled inflation of the implanted cuff. After a control period RABP was reduced to 90, 80, 70, 60, 50, and 40 mmHg for 5 min at each value. Mean values of RBF and RABP were calculated from the last 2 min of each pressure step and from all 5 min of the control period. For the determination of renal arterial occlusion pressure (RABP₀) and zero offset of the flowmeter (RBF₀) the renal artery was totally occluded for 30 s. The four following protocols were performed.

S-Ctrl (n = 4)

In the control group a 35 min precontrol period was allowed before the experiment was started, to match the protocol to the following groups.

S-Nife (n = 3)

Nifedipine was infused into the renal artery at the same dose as in the T-Nife group (24 ml h⁻¹ (1.4 μg kg⁻¹ min⁻¹)). After a precontrol period of 25 min, i.e. 5 min before the control period, the infusion was started.

S-Furo-I (n = 4)

After insertion of the bladder catheter and after a 5 min precontrol period, a bolus of 40 mg furosemide i.v. was given. Fifteen to 20 min later a continuous i.v. infusion of 10 mg kg⁻¹ furosemide was started. Thirty minutes after the bolus, the control period was begun. Physiological saline solution with 4 mmol l⁻¹ KCl was infused i.v. according to voided urine volume. In three dogs, urine samples were taken at 10 min and 2 h after the start of the infusion for determination of furosemide concentration.

S-Furo-II (n = 4)

Following the same protocol as for S-Furo-I, 300 mg furosemide i.v. was given as a bolus, and 300 mg h⁻¹ as a constant i.v. infusion. Six instead of 4 mmol l⁻¹ KCl was dissolved in the replacement fluid. Urine samples were taken from three dogs.

If several protocols were performed on the same dog, the order in which these were done was different for each dog. At least 1 day of recovery was allowed after administration of hexamethonium and at least 1 week after furosemide. After all experiments planned for a respective dog had been done, or if serious complications or technical failures occurred, the dog was killed by an overdose of sodium pentobarbitone i.v.

Data analysis

Transfer function

In principle, the transfer function compares the fluctuations in the output signal of a control system to those in its input signal. The gain of the transfer function grossly corresponds to the ratio of the amplitude of the output divided by that of the input signal of a respective fluctuation. Thus, if RBF is taken as the output and RABP as the input a low gain means that the fluctuation in RBF is small compared with that in RABP, and hence reflects a high regulatory efficiency. In a rigid tube without regulatory responses, the relative changes of RABP and RBF would be equal and thus the gain (if calculated from normalized values of RBF and RABP) should be 1 (0 dB). Due to the underlying fourier transformation the transfer function gives a spectrum of gain values as a function of the frequency of the respective fluctuation. Strictly speaking, this method is only valid for a linear control system. However, if the coherence between input and output, which is a measure of congruence of the two signals yielding values between 0 and 1, is higher than 0.5, sufficient linearity may be assumed, to justify the application of this method.

All calculations were performed off-line on a 80486 computer with programs specifically designed by U. W. and A. J. For the calculation of the transfer function, the 20 Hz data files were digitally low-pass filtered (cut-off frequency, 3.5 Hz; finite impulse response, order 50) and then reduced 4 : 1 to a rate of 5 Hz. This will produce aliasing in the frequency range above 1.5 Hz, a range not relevant for the present investigation. However, it keeps the ratio of sampling to cut-off frequency small, thereby improving the accuracy in the passing range of the filter, and also keeps the cut-off frequency with the inherent undulation far outside of the frequency range of interest. These 5 Hz data were split into eight blocks of 8192 data points each (∼27 min). In dogs with a renal artery occluder RBF₀ and RABP₀ were determined in separate experiments. In all experiments, the same RABP₀ value of 16 mmHg (mean from all determinations was 15.5 ± 0.8 mmHg, n = 15) was subtracted from each RABP value. RBF was corrected by subtracting the individual RBF₀ if determined for that dog. No correction was made if the RBF₀ was unknown. For each block (RABP - 16 mmHg) and (RBF - RBF₀) were normalized by dividing the data by the respective mean values of the block, in analogy to the index of Semple & De Wardener (1959). The transfer function spectra were calculated by dividing the cross-spectral density between the normalized values of (RABP - 16 mmHg) and (RBF - RBF₀) by the autospectral density of normalized (RABP - 16 mmHg) for each block, using the Blackman-Tukey algorithm. All gain values were converted into decibels (20 × log(gain)) before further calculations. A single gain spectrum was calculated for each experiment by averaging all consecutive spectra. If ABP or RBF recordings contained obvious artifacts (e.g. clotting of catheters, transient interruption of nifedipine infusion), the respective data blocks were discarded (a total of 6 blocks, maximally 2 blocks per experiment were discarded). For each experimental group a single mean spectrum was calculated from the averaged spectra. The DC component and the lowest two frequencies of each spectrum were discarded. Because of the strong linear trend of RBF during the high dose of furosemide, all transfer spectra were calculated after a linear trend correction had been applied to every block of RABP and RBF data. The phase spectra between RABP and RBF were derived from the ratio between imaginary and real part of the (not trend corrected) transfer spectra. Also, the mean phase spectra for each dog were converted into spectra of time delays by dividing by the product of 2π and the respective frequency. Mean delay spectra were calculated by averaging all delay spectra for each group. Spectra of the power spectral density of ABP (Blackman-Tukey algorithm) and of the coherence between ABP and RBF were calculated from the same blocks of 8192 values. Mean spectra were derived from all blocks and all dogs of each group. The DC component and the two lowest frequencies were discarded. The transfer function between the normalized values of (RABP - 16 mmHg) and renal vascular resistance (RVR) was calculated in the same way as described for RBF and RABP. RVR was derived by dividing (RABP - 16 mmHg) by (RBF - RBF₀). In order to avoid a possible distortion of RVR by capacitive effects with each heart beat (∼1 Hz), the 5 Hz data of RABP and RBF were further low-pass filtered below 0.5 Hz, before the RVR and the transfer function were calculated. In order to estimate the absolute magnitude of the spontaneous fluctuations of RABP (D_RABP) corresponding to the frequency range below 0.01 Hz, the 5 Hz data files of RABP were first converted into 0.1 Hz data by block averaging fifty consecutive values each. Further smoothing was done by a sliding average over ten values each, without further reduction of the sampling rate. These 0.1 Hz files were split into thirty-two blocks of forty-one values each (corresponding to 410 s or 0.002 Hz). From each block the difference between the highest and the lowest ABP value was determined, and averaged for all blocks and all dogs of each group. Heart rate (HR) was determined off-line automatically from the pulse intervals detected in the 20 Hz ABP data.

Stepwise autoregulation

The autoregulatory index (AI) between 90 and 70 mmHg was calculated as described by Semple & De Wardener (1959). In each dog RBF was corrected by subtracting the individual RBF₀ measured at the end of the same experiment. For RABP₀ in every dog the same value of 16 mmHg was taken, for the sake of analogy to the transfer gain. The relative change in RBF was calculated from the difference between the RBF values at 90 mmHg (RBF₉₀) and 70 mmHg (RBF₇₀), divided by the mean value of the corrected RBF: (RBF₉₀ - RBF₇₀)/(½× (RBF₉₀+ RBF₇₀) - RBF₀). The relative change in RABP was derived in the same way: (RABP₉₀ - RABP₇₀)/(½× (RABP₉₀+ RABP₇₀) - 16 mmHg). The AI was calculated by dividing the relative change in RBF by the relative change in RABP and was then converted into a percentage. In analogy to the transfer gain, the values were also converted into decibels (20 × log(AI)).

In the S-Furo-II group, RBF slowly increased over time (see Results). As the pressure steps were applied in descending order, this effect might have overestimated or even totally feigned autoregulatory behaviour. In order to exclude such an effect RVR was calculated from (RABP - 16 mmHg) and (RBF - RBF₀) at the beginning and end of the experiment. Under the assumption of a linear change of RVR over time, this change was subtracted from the actual RVR and new RBF values were recalculated from (RABP - 16 mmHg) and the corrected RVR. In the S-Furo-II group, all measured RBF values were replaced by these new values.

Statistical methods

Statistical significance between the groups was tested by Student's t test for unpaired samples. For comparisons within the groups, the paired t test was used. A P value of 0.05 was considered significant. All values are expressed as means ±s.e.m.

RESULTS

Transfer function

The transfer function was calculated from the spontaneous fluctuations in RABP and RBF during 3½ h of continuous recordings in conscious resting dogs. The overall mean values during this period are shown in Table 1. The spontaneous fluctuations occurring under these control conditions are demonstrated in Fig. 1. Three different types of dynamic response of RBF can be seen. (i) Fast changes in the RABP which also occurred in the RBF signal (position 1). (ii) Slower changes in RABP which were not paralleled by changes in RBF, indicating effective regulation (position 2). (iii) Following one of the rapid pressure changes, oscillations in RBF with a cycle length of ∼30 s which did not appear in the RABP signal (position 3). The mean power density spectra of the RABP fluctuations from all control experiments are shown in Fig. 2. The absolute magnitude of the low frequency fluctuations, estimated by averaging the maximum changes for the smoothed 410 s blocks, was about 9 mmHg (Table 2B). The mean coherence was greater than 0.5 for all frequencies in all experimental groups (Fig. 3). The transfer function from the control group is shown in Fig. 4, where the gain is plotted as a function of the frequency in Fig. 4A. As described in Methods, the gain gives a measure of the regulatory efficiency with a small gain indicating a high degree of regulatory efficiency. The transfer spectrum displays a constant high gain, i.e. low or lacking regulatory efficiency, for frequencies above about 0.06 Hz. Note that the gain in this range exceeded 0 dB. Below a corner frequency of 0.06-0.15 Hz, the gain decreased, indicating improvement of the regulation with decreasing frequencies. Below about 0.01 Hz, corresponding to fluctuations with cycle lengths of longer than 100 s, gain approached a low plateau. Negative values indicate effective autoregulation in this frequency range. Between 0.0034 and 0.01 Hz the mean gain was -6.3 dB (Table 2). Between 0.01 and 0.1 Hz in each control experiment a characteristic region of higher gain was found, the peak was centred around 0.027 ± 0.009 Hz. The phase between RABP and RBF is depicted in Fig. 4B, a positive value indicates that the RBF change preceded that of RABP. This was the case for virtually all frequencies assessed. There were two phase maxima (at 0.010-0.015 Hz and 0.06-0.08 Hz), which reached about π/4. Note that the phase was significantly different from π/2. Below both phase maxima there were two regions of decreasing phase. Within these regions the time delay remained more or less constant (Fig. 4C), reaching 1.7 and 14.3 s, respectively (Table 3). The phase between RABP and RVR (Fig. 9) was negative both at the corner frequency and at 0.027 Hz, indicating that RVR lagged behind RABP, but the amounts were similar to the those of the phase between RABP and RBF and hence also smaller than π/2.

Table 1.

Mean haemodynamic data during the 3½ h recordings

Group	n	RABP (mmHg)	HR (beats min−1)	RBF(ml min−1)
T-Ctrl	12	103 ± 3	81 ± 4	214 ± 20
T-Nife	5	91 ± 5 *	136 ± 8 *	223 ± 35
T-Hexa	7	100 ± 4	120 ± 2 *	223 ± 25
T-Furo-I	7	105 ± 5	66 ± 2 *	197 ± 22
T-Furo-II	4	115 ± 3 *	97 ± 8	403 ± 68 *

^*Significantly different from T-Ctrl (P < 0·05). n, number of dogs.

Figure 1. Original traces of RABP and RBF.

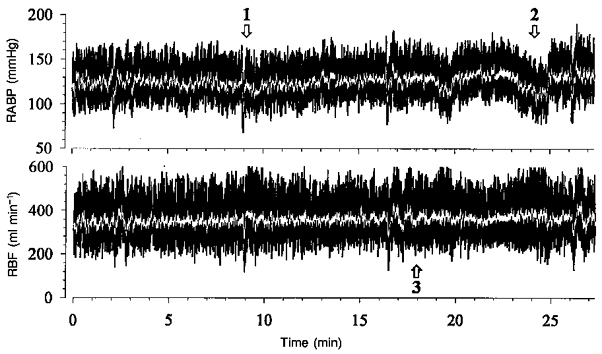
Transfer functions (black traces) and moving averages over 2 s (white traces) calculated from filtered 5 Hz data from one of the 27 min peroids during a control experiment. Note that the spontaneous fluctuations comprise fast changes in RABP, which are paralleled by those of RBF (1). There are also slower fluctuations, which are not followed by RBF (2). Finally, oscillations of RBF can be seen at a cycle length of ∼30 s, which are not present in the RABP (3). Abscissa values in the lower panel apply also to the upper panel.

Figure 2. Mean spectra of the spontaneous fluctuations in RABP.

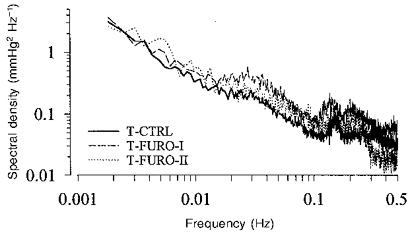
Under control conditions (T-Ctrl, n = 12) there is a characteristic distribution with a prominent representation in the low frequency range (note logarithmic scales). During infusion of furosemide at the lower dose (T-Furo-I, n = 7), the pressure fluctuations were slightly enhanced vs. control above 0.01 Hz, but were not significantly different at lower frequencies. With the higher dose of furosemide (T-Furo-II, n = 4) the spectral density was not changed, except above 0.3 Hz.

Table 2.

Autoregulatory efficiency

	A. Stepwise autoregulation			B. Transfer function
Group	n	AI (%)	AI (dB)	n	DRABP (mmHg)	Gain (dB)
Ctrl	4	11 ± 13	-19·5 *	12	9 ± 1 †	-6·3 ± 0·6 †
Nife	3	82 ± 11	-2·0 ± 1·1	5	5 ± 1	+0·3 ± 1·0
Furo-I	4	41 ± 1	-7·8 ± 0·3	7	10 ± 1 †	-5·5 ± 1·2 †
Furo-II	4	50 ± 9	-6·7 ± 1·9	4	10 ± 1 †	-3·8 ± 0·8 †

A, artificially induced stepwise reductions in RABP. Autoregulatory index (AI) between 90 and 70 mmHg is given as a percentage and in decibels. In one group (indicated by asterisk) mean AI (dB) was calculated from the mean value of AI (%). B, transfer function from spontaneous fluctuations. Average gain between 0·0034 and 0·01 Hz calculated from the original or from trend-corrected data. The magnitude of the spontaneous pressure fluctuations (D_RABP) in this frequency range is estimated by the mean of the maximum change of RABP found in blocks of 410 s of low-pass filtered data.

^†P < 0·05 compared with nifedipine.

Figure 3. Coherence between RABP and RBF.

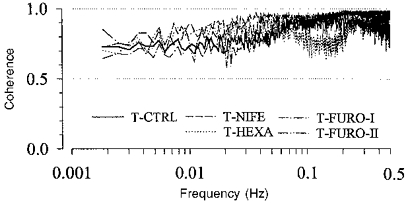
T-Ctrl, n = 12; T-Nife, n = 5; T-Hexa, n = 7; T-Furo-I, n = 7; T-Furo-II, n = 4. In all groups the coherence was higher than 0.5 for all frequencies.

Figure 4. Transfer function between RABP and RBF under normal conditions.

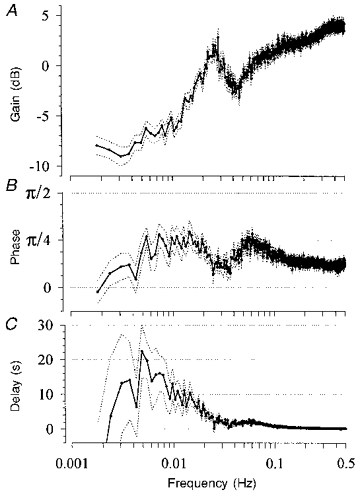
Means (continuous lines) ±s.e.m. (dotted lines) from twelve conscious resting dogs. A, gain starts to decrease below a corner frequency of 0.06-0.15 Hz and approaches a minimum level below 0.01 Hz. In between, there is a peak of higher gain at 0.027 Hz. B, the phase between RABP and RBF shows two maxima at 0.07 and at 0.013 Hz that reach π/4. C, time delay below 0.07 and 0.013 Hz remained more or less constant at 2 s, and 10-20 s, respectively. Abscissa values in C apply also to A and B.

Table 3.

Time delay between RABP and RBF

		Time delay
Group	n	LF range (s)	HF range (s)
T-Ctrl	12	14·3 ± 3·9	1·7 ± 0·2
T-Nife	5	11·2 ± 3·0	0·5 ± 1·1 *
T-Hexa	7	15·9 ± 2·5	2·0 ± 0·2
T-Furo-I	7	-1·1 ± 3·4 *	2·7 ± 0·1 *
T-Furo-II	4	-1·6 ± 2·4 *	1·4 ± 0·1

The time delay, calculated from the phase of the transfer function, was more or less constant in the low and high frequency ranges (0·0034-0·01 Hz and 0·03-0·08 Hz, respectively) (Fig. 4C). For each experiment, all delays within each of these ranges were averaged, the given values are the group means of these average values.

^*Significantly different from T-Ctrl (P < 0·05).

Figure 9. Phase relations during infusion of furosemide at the lower dose.

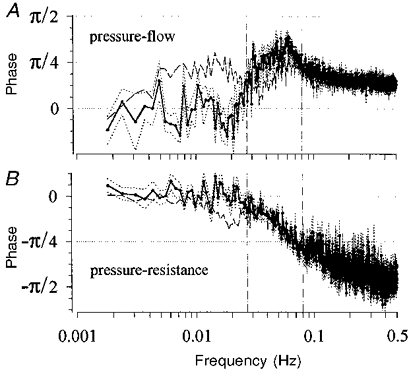
A, phase between RABP and RBF. In comparison with control (dashed line, n = 12), the phase in the vicinity of 0.027 Hz (left vertical line) is reduced to 0 under furosemide (mean (continuous line) ±s.e.m. (dotted lines); n = 7). The phase around the corner frequency (0.06-0.15 Hz, right vertical line at 0.08 Hz) may have been slightly increased, but was significantly smaller than π/2. B, phase between RABP and RVR. The phase difference in the vicinity of 0.027 Hz (left vertical line), present under normal conditions (dashed line) was abolished to 0 during furosemide (mean (continuous line) ±s.e.m. (dotted lines)). The phase at the corner frequency (right vertical line) was not affected by furosemide and was also significantly smaller than π/2.

Stepwise autoregulation

There was highly effective autoregulation for artificially induced stepwise reductions of RABP down to 70 mmHg (S-Ctrl, Fig. 5). The autoregulatory index in response to the reduction in RABP from 90 to 70 mmHg was 11 % (Table 2). In one of the dogs RBF was even higher at 70 than at 90 mmHg. Because conversion into decibels cannot be done in this single case, the mean AI in decibels for this group was derived from direct conversion of the mean AI expressed as a percentage. Thus -19.5 dB (Table 2) is a minimum estimate for the amount of attenuation.

Figure 5. Autoregulation in response to stepwise artificially induced pressure reductions.

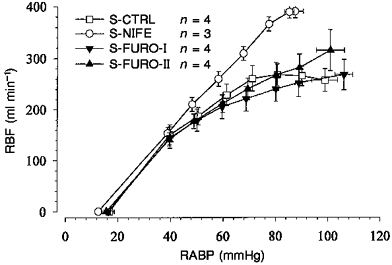
Under control conditions (S-Ctrl, n = 4) there was perfect autoregulation above 70 mmHg. With intrarenal nifedipine (S-Nife, n = 3) the RBF was linearly related to RABP, indicating absence of autoregulation. During both doses of furosemide (S-Furo-I, n = 4; S-Furo-II, n = 4), the autoregulation was somewhat impaired compared with that for S-Ctrl, but was still more efficient than that for S-Nife. Note the identical zero flow intercepts (RABP₀) at ∼16 mmHg.

Ca²⁺ channel blockade

The same experiments were done during intrarenal infusion of nifedipine, which should abolish the renal regulatory capacity. Nifedipine caused hypotension and tachycardia (Table 1). RBF did not change significantly. The magnitude of the low frequency pressure fluctuations (D_RABP in Table 2) was somewhat smaller than that during control. In the experiments in which RABP was reduced stepwise during nifedipine (S-Nife, Fig. 5), RBF varied proportionately with RABP, so that RBF was higher than in the S-Ctrl group for RABP values above 60 mmHg, but the RABP-RBF relation below this threshold remained unchanged. AI was higher than 82 %, corresponding to 2 dB attenuation (AI (%) and AI (dB) in Table 2). The transfer function showed a constant high gain down to 0.007-0.01 Hz, the mean gain being close to 0 dB above 0.0034 Hz (Fig. 6A and Table 2). There was a sharp decrease of the gain below 0.0034 Hz (Fig. 6A). Note that the time delay between 0.03 and 0.08 Hz was reduced significantly close to 0 s (Table 3). The delay between 0.0034 and 0.01 Hz was not significantly changed (Table 3). However, the delay was not constant but increased with decreasing frequencies due to a rather constant phase. Both phase maxima were abolished.

Figure 6. Gain of the transfer function under nifedipine or ganglionic blockade.

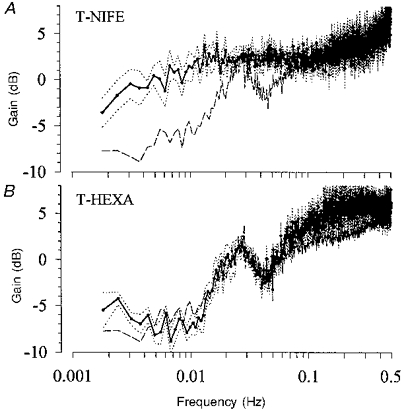
A, after abolition of the autoregulation by nifedipine (T-Nife, mean (continuous line) ±s.e.m. (dotted lines), n = 5), the gain was higher than 0 dB down to 0.005-0.009 Hz, decreased slightly below 0.01 Hz and sharply below 0.0034 Hz. The dashed line depicts the gain of the control group from Fig. 4. B, the inhibition of autonomic nervous influences by hexamethonium (T-Hexa, mean (continuous line) ±s.e.m. (dotted lines), n = 7) caused only minor increases in the gain at the highest and the lowest frequencies compared with control (dashed line).

Ganglionic blockade

In order to inhibit a possible impact of the autonomic nervous system, experiments were conducted during ganglionic blockade. Heart rate (HR) increased to 120 beats min⁻¹, while RABP and RBF did not change significantly (Table 1). The transfer function is depicted in Fig. 6B. At the lowest frequencies shown, there was a slight increase in the gain values. In the range above 0.1 Hz, the gain values were also slightly higher than those in the control group, but the corner frequency was not overtly changed. The remaining spectrum and the time delays were not altered (Table 3).

Furosemide

In order to investigate the contribution of TGF, experiments were performed during the infusion of furosemide. Under the lower dose of furosemide, the concentration found in the urine after 2 h was 2.5 × 10⁻⁵ M, while it was about 10 times higher under the larger dose (Table 4). In both cases the urinary concentration seemed to decrease over time (Table 4). Both doses impaired the autoregulation in response to stepwise RABP changes (Fig. 5) as indicated by AI values of -7.8 and -6.7 dB, respectively (Table 2).

Table 4.

Concentrations of furosemide in the urine

Time	[Furo-I] (10−5 mol l−1)	[Furo-II] (10−5 mol l−1)
0 h	5·9 ± 1·8	41·4 ± 7·6
	n = 4	n = 5
2 h	2·5 ± 0·1	32·8 ± 2·4
	n = 5	n = 5
4 h	2·7	23·6 ± 3·9
	n = 1	n = 3

Concentrations during infusion of furosemide at the lower dose (Furo-I) and the higher dose (Furo-II) measured 0, 2 and 4 h after the start of the experimental period (30 min after furosemide). Data at 0 h and 2 h are pooled from continuous recordings (groups T-Furo-I and T-Furo-II) and from experiments with stepwise reductions of RABP (S-Furo-I and S-Furo-II). Data at 4 h are from continuous recordings only.

In the transfer function experiments with the lower dose of furosemide, mean HR was slightly smaller than in the control group, but mean RABP and RBF were not different (Table 1). Urine volume was 11.7 ± 0.1 ml min⁻¹. The substituted volume lagged behind the excreted urine volume by a rather constant difference of about 220 ml min⁻¹. Plasma K⁺ concentration fell from 3.9 ± 0.1 mmol l⁻¹ before to 3.5 ± 0.1 mmol l⁻¹ at the end of the experiment (P < 0.05), while Na⁺ was not affected (157 ± 2 to 158 ± 2 mmol l⁻¹). The blood pressure spectrum after furosemide was somewhat elevated in the range above 0.01 Hz (Fig. 2), but the lower frequency power (Fig. 2) and the magnitude of low frequency fluctuations (D_RABP in Table 2) were not different from control. In the transfer spectrum (Fig. 7A) the peak of the gain found at 0.027 Hz in the control group was totally abolished. Note that the downward slope of the gain below the corner frequency more closely resembled 20 than 40 dB per decade of frequency (see additional lines in Fig. 7A). The mean gain between 0.0034 and 0.01 Hz was significantly smaller than in the T-Nife group (Table 2). The gain values of the subsequent blocks (Fig. 8) demonstrate that at no time was the gain significantly different from that of the control group. The phase difference between RABP and RBF, present under normal conditions below 0.027 Hz was abolished to 0 (Fig. 9A). The phase in the vicinity of the upper corner frequency was close to π/4 rather than π/2 (Fig. 9A). The same was true for the phase between RABP and RVR (Fig. 9B). The delay between RABP and RBF in the low frequency range was significantly reduced to values close to 0 s, while the delay at 0.03-0.08 Hz was prolonged (Table 3).

Figure 7. Gain of the transfer function under furosemide.

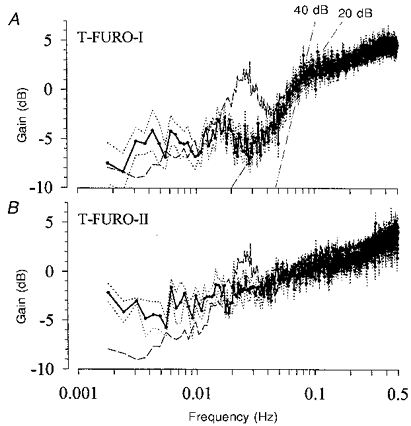
A, under the lower dose (T-Furo-I, mean (continuous line) ±s.e.m. (dotted lines), n = 7) the peak at 0.027 Hz was totally abolished, but the rest of the transfer spectrum was only slightly changed compared with control (dashed line). There may be a peak of higher gain at 0.018 Hz. Note that the slope of the drop in gain, below the corner frequency, resembled 20 rather than 40 dB per decade of frequency. B, under the higher dose (T-Furo-II, mean (continuous line) ±s.e.m. (dotted lines), n = 4) the peak at 0.027 Hz was also abolished, although the gain was not as much reduced as with the higher dose. The gain below 0.01 Hz was slightly higher than in control (dashed line), but still lower than 0 dB.

Figure 8. Time course of the transfer gain between 0.0034 and 0.01 Hz.

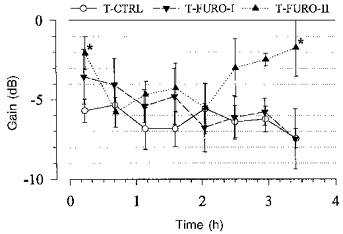
The gain was averaged between 0.0034 and 0.01 Hz from the single spectra of the eight consecutive blocks. Under the lower dose of furosemide (T-Furo-I, n = 7) there was a slight decreasing trend over time, but at no time was the gain significantly different from that of the control (T-Ctrl, n = 12). Under the higher dose (T-Furo-II, n = 4) the gain increased during the second half of the experiment and was significantly higher than control in the last spectrum. The gain in the first spectrum also was higher than the control. *P < 0.05 vs. T-Ctrl.

With the higher dose of furosemide mean RBF was greatly elevated (Table 1). This was due to a strong linear increase of RBF throughout the whole recording period (from 274 ± 52 ml min⁻¹ within the first 27 min to 499 ± 94 ml min⁻¹ during the last 27 min, P < 0.05). Urine volume was 2-3 times as high as under the lower dose and also increased over time (24.5 ± 2.8 ml min⁻¹ during the first 30 min to 36.8 ± 2.6 ml min⁻¹ during the last 30 min of the experiment, P < 0.05). The difference between infused and voided volume was between 200 and 350 ml. Plasma K⁺ concentration decreased from 4.1 ± 0.2 mmol l⁻¹ before to 3.2 ± 0.2 mmol l⁻¹ at the end of the experiment (P < 0.05), while Na⁺ concentration remained unchanged (156 ± 2 to 157 ± 2 mmol l⁻¹). Except for a moderate attenuation at the highest frequencies shown, the spectral power for blood pressure in the remaining frequency range (Fig. 2) and the magnitude of low frequency RABP fluctuations (D_RABP in Table 2) were not different from the control group. In the transfer function the typical gain peak was abolished, although the gain was not so reduced as with the smaller dose (Fig. 7B). Although the low frequency gain may have been somewhat higher, it was still significantly lower than with nifedipine (Table 2). After trend correction the gain in the low frequency range was even lower (-4.9 ± 0.7 dB). The delay in the low frequency range was greatly reduced to around 0 s, whereas the high frequency delay was not affected (Table 3). During the second half of the experiment, the gain values of the sequential blocks (Fig. 8) increased over time, so that the last value was significantly higher than that in the control group. The first value was also significantly higher than that in control. After trend correction (data not shown), the gain values under the higher dose of furosemide were further lowered by about 1 dB, so that then only the gain of the last block was higher than the control.

DISCUSSION

The normal regulation of renal blood flow

The spontaneous fluctuations of blood pressure are considerably different from white noise or pure sinusoidal waves. In accordance with previous reports (Marsh et al. 1990; Just, Wagner, Ehmke, Kirchheim & Persson, 1995) there was a prominent representation in the low frequency range (Fig. 2). In order to investigate the regulation of renal blood flow under this natural challenge, the transfer function analysis was applied to the spontaneous fluctuations of RABP and RBF. Although the renal autoregulation is known to comprise a considerable share of non-linearities (Yip & Holstein Rathlou, 1996), the application of this linear method is still justified because of the high coherence present at all frequencies (Fig. 3).

The transfer function was very similar to that found in response to forced fluctuations of RABP in anaesthetized rats (Sakai et al. 1986; Holstein Rathlou et al. 1991) and conscious dogs (Wittmann et al. 1995). Moreover, there was also a remarkable accordance to the transfer function in response to fluctuations provoked by atrial fibrillation (Sakai et al. 1986; Daniels et al. 1990) or those occurring spontaneously (He & Marsh, 1993; Cupples et al. 1996) in anaesthetized rats.

The presence of the corner frequency at 0.1 Hz, the oscillation at 0.027 Hz (Fig. 4A), as well as the finding of two different delay times (Fig. 4C), indicates, in accordance with previous reports (Daniels et al. 1990; Holstein Rathlou et al. 1991; Cupples et al. 1996), that this regulation is brought about by at least two mechanisms. The apparent corner frequency at 0.3-0.4 Hz (Fig. 4A) is not considered to be derived from a true regulatory activity, since there was no change in the phase in this frequency range.

The faster of these mechanisms seems to respond at a natural frequency of 0.06-0.15 Hz and to produce a delay of about 2 s. The most likely candidate for this mechanism appears to be the myogenic response. Interestingly, the vasoconstriction in response to a sudden reduction of the perirenal pressure in rats (Clausen et al. 1992), which is most easily explained by the myogenic response, showed a delay of 0.3-2.5 s, and sometimes produced an overshoot lasting 2-5 s, which would be compatible with a response cycle of 4-10 s or a natural frequency of 0.1-0.25 Hz.

The phase between pressure and flow, as well as that between pressure and resistance, was smaller than π/2 both at the corner frequency and in the vicinity of the oscillation at 0.027 Hz (Figs 4B and 9). This is also in accordance with previous studies (Daniels et al. 1990; Holstein Rathlou et al. 1991; Wittmann et al. 1995; Cupples et al. 1996). This behaviour highlights interesting implications: a first order linear control system will at its natural frequency produce a phase of π/4. However, such a system is based on a first order linear differential equation and hence does not allow for a rate-sensitive component. In a second order control system, which includes such a component, the phase at the natural frequency, which is at or slightly above the corner frequency, will amount to π/2 (Foellinger, 1992). Moreover, a first order system would reduce the gain by 20 dB per decade of frequency, whereas a second order system would attain a slope of 40 dB per decade (Foellinger, 1992). These criteria are more reliable, if the total regulation consists of only one regulating system, which probably was the case during the infusion of furosemide. Under these conditions, the phase between RABP and RBF (Fig. 9A), as well as that between RABP and RVR (Fig. 9B), was significantly smaller than π/2 at the corner frequency. Also, the slope of the gain between RABP and RBF was 20 rather than 40 dB per decade (Fig. 7A). This was also the case for the gain between RABP and RVR (data not shown). The shallow slope of the gain under the higher dose of furosemide (Fig. 7B) may be derived from additional effects due to direct vascular actions of furosemide (Kreye, Bauer & Villhauer, 1981) or to the changes in plasma K⁺ concentration (Table 4). Therefore, the present data suggest that, at least for the faster mechanism, a rate-sensitive component, which has been described for the myogenic response in isolated arterioles (Davis & Sikes, 1990), does not seem to play a dominating role in regulating renal arterioles in the conscious animal. However, under anaesthesia with halothane, when compared with isoflurane, a steeper slope of the gain and a larger phase close to π/2 have been observed (Cupples et al. 1996), suggesting that the contribution of the rate-sensitive component may be exaggerated under this type of anaesthesia.

The peak of the gain around 0.03 Hz has been observed in previous studies in rats (Daniels et al. 1990; Holstein Rathlou et al. 1991; Cupples et al. 1996) and in dogs (Wittmann et al. 1995). Because similar oscillations can also be found in tubular pressure (Leyssac & Baumbach, 1983; Holstein Rathlou et al. 1991), as well as in tubular flow and chloride concentration (Holstein Rathlou & Marsh, 1989), this peak has been argued to reflect the action of TGF. The present study provides further evidence for this interpretation, because this peak was totally abolished by both doses of furosemide (Fig. 7), while the remaining transfer spectrum was only slightly changed. A similar effect on the transfer function can also be detected in the data of an earlier study, in which TGF had been blocked by ureter occlusion (Daniels et al. 1990). The fact that in the present study the gain was not so reduced with the higher dose as with the lower dose of furosemide, may be explained by an additional TGF-independent impairment of autoregulation due to direct vascular effects of furosemide (Kreye et al. 1981) or due to the changes in plasma K⁺ concentration. The loss of the peak does not seem to be attributable to a change in the challenge, because it was also observed under the higher dose, in which the pressure spectrum was not altered. However, during the lower dose there was an enhancement of the pressure fluctuations, but there is no apparent reason why a higher challenge per se should have led to a decrease in the gain, i.e. to an improvement of the regulatory efficiency. Moreover, the increase of the challenge was not confined exactly to the frequency of the peak.

The phase (Fig. 9) and delay (Table 3) between RABP and RBF below 0.01 Hz were also eliminated by furosemide and are therefore probably attributed to TGF as well. Interestingly, the slower component of the two successive responses of the vascular resistance observed after a sudden increase in perfusion pressure in rats, which has been ascribed to TGF, started after a delay of 12-15 s (Young & Marsh, 1981). A similar delay of 10.5 s has been found between oscillations in proximal tubular pressure and distal tubular chloride concentration in rats (Holstein Rathlou & Marsh, 1989). A delay of 11 s appeared to pass before the stop flow pressure started to rise after tubular perfusion had been stopped in dogs (Bell, Thomas, Williams & Navar, 1978). A somewhat longer latency of 18 s has been reported in rats, when this response had been provoked by sudden changes in the tubular perfusion pressure (Daniels & Arendshorst, 1990).

The normal regulatory efficiency

The transfer function demonstrates that the regulatory activity starts to become effective below the corner frequency of 0.06-0.15 Hz, indicating that it can respond to fluctuations of pressure with cycle lengths as short as 7-17 s. The high gain values above the corner frequency, exceeding 0 dB, which have also consistently been reported by other authors (Sakai et al. 1986; Daniels et al. 1990; Holstein Rathlou et al. 1991; Wittmann et al. 1995; Cupples et al. 1996), can probably be explained as a capacitive effect due to the high compliance of the renal vascular bed. For a cycle length of more than 100 s the gain approached a maximum level of regulatory efficiency, which is maintained down to at least 0.0018 Hz (9 min cycle length) in our study. It has been demonstrated to extend to fluctuations as long as 6-8 h by other authors (Marsh et al. 1990). The gain value of -6.3 dB in this frequency range (Table 2) is similar to the values found by other authors in the transfer function in dogs (Marsh et al. 1990; Wittmann et al. 1995) and rats (Daniels et al. 1990; Holstein Rathlou et al. 1991; Cupples et al. 1996). This indicates that the fluctuations of RBF are reduced to only about half the amplitude of those for RABP. This is a poor regulatory effect compared with the much stronger regulatory capacity usually found when investigating responses to stepwise artificially induced reductions of RABP (Shipley & Study, 1951; Navar, Champion & Thomas, 1986; Ogawa & Ono, 1986; Kirchheim et al. 1987). The same strength of regulation has been confirmed in the present study, when tested in the mentioned stepwise way (Fig. 5, AI in Table 2).

Thus, there is obviously a strong capacity available for the regulation of renal blood flow. However, the maximum gain of the transfer function suggests that this ability is only partially employed under resting physiological conditions.

Contribution of intrarenal regulating mechanisms

Because the transfer function was calculated from spontaneous fluctuations the possibility that the changes in RABP are brought about, or accompanied, by events which simultaneously alter RVR in the same direction cannot be excluded. In such a case changes in RBF would be smaller than those in RABP and hence the transfer gain would be low. Such responses would certainly contribute to the overall regulation of RBF, but the gain of the transfer function would then not be a reliable indicator of the autoregulatory activity by the kidney itself.

Therefore, the same experiments were done during infusion of nifedipine, which is known to block the autoregulatory responses selectively, while leaving other determinants of renal vascular tone functional (Navar et al. 1986; Ogawa & Ono, 1986). The proportional decrease of RBF to stepwise reduction of RABP (Fig. 5) demonstrates the abolition of the autoregulation in the present study. The high gain in the transfer function down to at least 0.0034 Hz and the eliminated delay between 0.03 and 0.08 Hz under the same dose of nifedipine therefore suggest that the regulation above 0.0034 Hz, detected in the transfer function, is due in large part to autoregulation by the kidney itself.

Contribution of the autonomic nervous system

In order to delineate the contribution of the most probable of the possible extrarenal factors to the regulation, the autonomic nervous system was inhibited by ganglionic blockade. Under these conditions the transfer spectrum differed from the control group only slightly (Fig. 6B), suggesting that the neurogenic influence is marginal in the investigated frequency range. Only below 0.0034 Hz, the autonomic nerves may partially contribute to the regulation of RBF. The slight elevation of the gain in the range above the corner frequency would be compatible with a higher vascular compliance. This is not in contradiction to the limited vasoconstrictory influence of the renal nerves (Kirchheim, Ehmke & Persson, 1989), because resistance and compliance may well be derived from different parts of the vascular tree.

Taken together the effects of nifedipine and ganglionic blockade suggest that above 0.0034 Hz the regulation of RBF is brought about almost exclusively by mechanisms intrinsic to the kidney itself and does not depend on neurogenic or other extrarenal influences. Thus, it seems safe to conclude that the transfer spectra of all other experimental groups in which no measures were taken to exclude extrarenal influences probably reflect the characteristics of the intrarenal regulatory mechanisms only.

Contribution of the tubuloglomerular feedback to the autoregulatory efficiency

In order to investigate the relative contribution of TGF to the autoregulatory efficiency, we attempted to block this mechanism by an intravenous infusion of furosemide. Under these conditions the autoregulatory capacity in response to stepwise reductions of RABP was impaired providing an attenuation of RBF changes by only -7.8 and -6.7 dB, respectively. However, it was not totally abolished, as can be seen by comparison with the results under nifedipine. Note that without the applied correction for the slow trend of RBF under the high dose of furosemide (see Methods), the difference compared with that under nifedipine would have been even more pronounced in this group.

In the transfer function the gain between 0.0034 and 0.01 Hz may have been somewhat elevated compared with the control, but it was still significantly more negative than that under nifedipine, indicating that the autoregulatory efficiency had only slightly been impaired. Care was taken not to infuse more volume than that lost in the urine in order to avoid an attenuation of TGF due to volume expansion (Persson, Schnermann & Wright, 1979). In comparison to the control group it should be taken into consideration that the normal urine production (0.7 ml min⁻¹; Ehmke et al. 1992) amounts to ∼170 ml within 4 h. We did not take into account a possible change of the renal interstitial pressure. This most probably was elevated under furosemide (Willassen & Ofstad, 1979). Note that this is not in contradiction to the unchanged values of RABP₀ found during renal artery occlusion in the present study, since these measurements are certainly not sensitive to changes derived from differences in tubular flow rate. The consideration of a higher value for RABP₀ in the calculation of the transfer function would have led to even lower gain values under furosemide.

It should be emphasized that the resulting gain below 0.01 Hz was similar to the gain values found under the artificial stepwise reductions of RABP (AI in Table 2). Moreover, there is also a remarkable similarity to the gain values found by other authors, when TGF was blocked. The regulatory capacity for single nephron filtration rate after interruption of tubular flow still provided an attenuation compared with a non-responsive model by -4.4 dB under furosemide and -9.9 dB after interruption of tubular flow (Moore et al. 1979). In a similar study, this regulation was capable of attaining a ‘magnification’ of 0.50 to 0.54, i.e by -6.0 to -5.3 dB, when the tubular flow had been interrupted (Schnermann et al. 1984). In isolated juxtamedullary nephrons, in which TGF had been blocked by furosemide, the glomerular blood flow changed by only 13 % when the arterial pressure rose from 101 to 124 mmHg, corresponding to a gain of -4.1 dB (Takenaka et al. 1994). In model calculations, the fractional compensation of flow changes between 110 and 77 mmHg did still reach 0.42-0.80, i.e. -7.5 to -1.9 dB, even when TGF was not included (Aukland & Oien, 1987). In another model (Feldberg et al. 1995) TGF-independent regulation was able to reduce RBF changes to 5.6 % for each kilopascal of pressure change at a mean of 12.5 kPa, corresponding to a gain of -3.1 dB.

Even though the massive diuretic response, the disappearance of the gain peak, as well as the loss of the phase and delay below 0.01 Hz, all suggest that TGF had been impaired, they do not prove that it had been completely blocked. The concentration of furosemide at the macula densa required for complete block of TGF in rats is known to be about 5 × 10⁻⁵ M, but partial inhibition may be achieved above 10⁻⁶ M and half-effective blockade is reached at 1 × 10⁻⁵ M (Mason, Kain, Welsch & Schnermann, 1981; Gutsche, Brunkhorst, Muller Ott, Franke & Niedermayer, 1984). In order get an estimate of the furosemide concentration at this location in the conscious dog, we measured furosemide in the voided urine (Table 4). Under the assumption that the urine, and thus furosemide, is concentrated by about 1 : 20 on its way from the macula densa (Koushanpour, Tarica & Stevens, 1971), the local concentrations probably were 10⁻⁶ M for the lower and 2 × 10⁻⁵ M for the higher dose. Although it thus cannot be excluded that we may have failed to achieve a total block, the concentrations under the higher dose were at least well within the steep portion of the dose-response curve. Consequently, if TGF had contributed significantly to the regulatory efficiency, both the differences in the furosemide concentration between the two doses, as well as those over time, should have led to respective differences in the gain. As can be seen from Fig. 8, there was neither a consistent difference in gain between the two different doses of furosemide nor a clear decreasing trend in gain over time, during which the drug's concentration waned rather. Under the higher dose the gain even rose with time despite the decreasing concentration. This progressive loss of autoregulatory efficiency may rather be explained by direct vascular effects of furosemide, which are known to develop slowly over 1-3 h (Kreye et al. 1981), or by the increase in the plasma K⁺ concentration. Note that the gain values during the higher dose of furosemide would be even lower after trend correction.

Therefore, although TGF is a major contributing factor towards the total strength of RBF autoregulation, there still remains considerable regulatory capacity in the absence of this mechanism. This residual ability seems to be sufficient for the maintenance of the level of autoregulation, which is usually expended under resting physiological conditions.

Conclusions

This study shows that in the conscious resting dog the regulation of renal blood flow can respond to pressure fluctuations as fast as 0.1 Hz or 7-17 s cycle length. Maximum regulatory efficiency is achieved for pressure changes slower than 100 s cycle length (0.01 Hz), and is maintained for cycle lengths of at least 9 min (0.0018 Hz). This regulation reduces the flow changes, which are evoked by the fluctuations in pressure, by about 50 %. It is also confirmed that in the conscious resting dog this regulation is brought about by at least two mechanisms. The faster one of these responds at 0.1 Hz with a delay of 2 s, and therefore most probably corresponds to the myogenic response. The rate-sensitive component probably plays a minor role. The slower mechanism shows an oscillation at 0.027 Hz and produces a delay of 14 s, and thus seems to reflect TGF. This interpretation is confirmed by the fact that both features are abolished by furosemide. The transfer function thus provides a method to assess the integrity of TGF under physiological conditions.

For fluctuations faster than 5 min this regulation is brought about almost exclusively by the autoregulation of the kidney itself. Therefore, the transfer function calculated from the spontaneous fluctuations of pressure and flow in this frequency range probably reliably reflects this autoregulation.

Furthermore, we would like to conclude, that the ample regulatory capacity, which is obviously available in the kidney, is only partially employed under resting physiological conditions. Although TGF considerably contributes to the maximal strength of renal blood flow autoregulation, this contribution is not required to maintain the limited amount of regulatory capacity, which is usually expended under resting physiological conditions. The delay below 0.01 Hz and its susceptibility to furosemide strongly suggests that TGF does exert some influence on renal blood flow in this frequency range, when TGF is functional. However, a more exact quantification of the contribution of this influence to the autoregulation under normal conditions, cannot be gained from the methods applied in this study.

The presence of the peak of high gain in the normal transfer spectrum implies that the TGF somewhat ameliorates the autoregulatory efficiency in this frequency range. Therefore, the results of this study raise questions as to whether the main purpose of the TGF is the autoregulation of renal blood flow. Other tasks, such as the adjustment of filtration and reabsorption to the demands of fluid and electrolyte homeostasis (Moore, 1984), may be more important. Since the constancy of flow per se may not be essential, the impairment of its regulation would be a small price to pay for the sake of more important functions.