Estimating rat renal medullary interstitial oncotic pressures and the driving force for fluid uptake into ascending vasa recta

Abstract

1. We have investigated the potential contribution of medullary interstitial oncotic pressure to the net balance of forces influencing fluid movement through the walls of the ascending vasa recta (AVR) in the exposed papillae of 2-week-old Sprague-Dawley rats.

2. Using a capillary zone electrophoresis (CZE) assay, hyaluronan (HA) concentrations were measured in fresh tissue slices from the renal papilla. HA content per wet weight of tissue decreased from tip to base of the papilla, but as a function of cell-free interstitial space (IS) HA concentration was relatively constant at 1.6 μg HA per mg IS up to 1600–1800 μm from the tip. Thereafter the concentration fell rapidly to near zero levels.

3. The volume of the IS was determined using a transmission electron micrographic study of the papilla in age-matched rats. Total interstitial volume (i.e. IS + IC, the interstitial cell volume), as a function of total tissue volume, decreased only slightly between 0 and 1800 μm (i.e. from about 40 to 35%). IS and IC were found to be reciprocally related with IS decreasing from 21.8 to 10.2%, while IC increased from 18.3 to 25.2% over the 1800 μm.

4. Total interstitial oncotic pressures were estimated as the sum of the oncotic pressure due to HA alone plus the oncotic pressure of albumin (A) in an HA matrix. Taking into account reflection coefficients to HA and A, there was an effective oncotic pressure (Eπ) of between 3.46 and 6.0 cmH₂O on the interstitial side of the AVR. Under free flow conditions an Eπ in this range is sufficient to result in a net inward driving force of between 5.4 and 9.3 cmH₂O, sufficient to account for current estimates of water reabsorption by the AVR.

5. HA concentrations in the papilla increased over the first 3 weeks of life from 0.313 ±0.09 μg (mg wet weight of slice)⁻¹ (mean ± s.e.m.) at 1 week to 0.563 ±0.06 at 3 weeks of age (P > 0.01), in parallel with an age-dependent increase in mean urine osmolarity. It is suggested that the increasing interstitial concentrations of HA may contribute to the development of urinary concentrating ability, which occurs concurrently.

In the final stages of urine concentration water is filtered from the collecting ducts into the inner medullary interstitium, and is then reabsorbed by the ascending vasa recta (AVR) for return to the circulation. The high hydraulic permeability (L_p) of the AVR and a reflection coefficient (σ) to serum albumin of 0.7 (MacPhee & Michel, 1995b) both favour fluid reabsorption into the AVR; but it has not yet been established whether fluid movement is driven by hydrostatic or oncotic pressure differences. We have previously calculated that a hydrostatic pressure difference of only a few centimetres of water could account for the necessary fluid movement (MacPhee & Michel, 1995b), but is this what occurs in vivo? This problem has recently been discussed for fluid uptake into cortical peritubular capillaries from the cortical interstitium by Aukland and colleagues (Aukland, Bogusky & Renkin, 1994).They concluded that only a driving force due to hydrostatic pressure can explain fluid reabsorption in certain situations (e.g. perfusion with colloid-free solutions), and that such a mechanism is a possible explanation even under normal conditions. At that time, they assumed that due to the absence of (known) medullary lymphatics, interstitial protein concentrations would be high, unless the AVR are impermeable to protein - which we can now confirm not to be the case (σ for albumin is 0.7, MacPhee & Michel, 1995b).

It was suggested more than 35 years ago by Koefoed & Knudsen, (1961) at the First International Congress in Nephrology that a colloid degradation system (e.g. hyaluronan-hyaluronidase) may drive the countercurrent mechanism in the kidney. A few years later Pinter (1967) pointed out that interstitial glycosaminoglycans (GAGs) might be involved in urine concentration due to their ability to bind large amounts of water and because the osmotic pressure of hyaluronan (HA)-protein solutions is greater than the sum of either component alone (Laurent & Ogston, 1963).

HA is the major GAG of the extracellular matrix in the inner medulla; biochemical analyses have indicated that HA accounts for about 96% of the total GAGs secreted by rat papillary slices in vitro (Pitcock, Lyons, Brown, Rightsel & Muirhead, 1988). HA obtained from most tissues has a molecular weight of several millions, and is a very long chain molecule. The molecular weight is highest when it is first synthesized and gradually diminishes both with the lifespan of the molecule and with the lifespan of the animal (Vasa, Saporito, Saraswathi, Tesoriero & Manley, 1983). In solution it has the ability to trap large quantities of water (litres per gram) to form a gel-like substance, the exact amount of water being a function of its molecular weight. It is this property of HA that has led to its special interest for renal physiologists, as large volumes of water are continuously flowing through the medullary interstitium during urine concentration.

The experiments described in this paper were designed to investigate the concentration of matrix GAGs in the interstitium of young Sprague-Dawley rats age matched with those used for the study of the hydraulic permeability (L_p) and albumin reflection coefficient of the AVR (MacPhee & Michel, 1995b), in order that each of the Starling forces operating across the AVR will have been measured in the same rat model.

The colloid osmotic pressure of the interstitial matrix is related both to the concentration of GAGs that form the matrix and the concentration of albumin (A) and other plasma proteins which have entered the matrix as a result of both convection and diffusion from the vasa recta and the medullary capillaries. To determine the concentration of HA in the interstitium it is necessary to know both its content and volume of distribution. Tissue HA content was measured at several distances from the papillary tip, to determine whether HA gradients existed in the interstitium, as have been proposed for electrolyte gradients, and to take into account the changing volume of the interstitium. In this study we have also considered the partition coefficient for albumin in an HA solution, as well as the reflection coefficient to serum albumin, in order to calculate the effective oncotic pressure (Eπ) of albumin-HA mixtures across the AVR wall. In a separate set of experiments, interstitial volume was measured in age-matched rats from electron micrographs of the papilla, at the same distances from the tip (i.e. ‘levels’), as used for the molecular analyses of HA content.

An additional set of preliminary experiments was designed to investigate the related question of whether or not the HA levels vary with the age and concentrating ability of the rat. Studies were performed at 1, 2 and 3 weeks of age in order to determine whether the concentration of HA might be related to the maturation of the urine concentrating mechanism.

METHODS

Animals

Sprague-Dawley rats were obtained from Harlan-Olac, Oxford as females with a litter of at least ten female pups (cross-fostered). Litters arrived several days prior to the experiments in order to allow time for the animals to settle into their new surroundings. Rats were maintained on SDS-CRM rat chow (SDS, Witam, Essex) and the pups were used at 1, 2 and 3 weeks of age for the studies on HA content and at 2 weeks of age for the interstitial volume measurements. Rat weights were 13.3 ± 1.2, 24.4 ± 2.2 and 42.1 ± 1.4 g (means ±s.d.) at 7, 14 and 21 days of age, respectively. Kidneys were removed under anaesthesia induced by an intraperitoneal injection of 0.1–0.2 ml of a mixture of Hypnorm (0.315 mg ml⁻¹ fentanyl citrate and 10 mg ml⁻¹ fluanisone), Hypnovel (5 mg ml⁻¹ midazolam hydrochloride) and water, made up in the proportions 1 : 1 : 2 by volume. Supplementary anaesthesia was given if required, by subcutaneous injection of small amounts of the anaesthetic mixture. Rats were killed at the end of the procedure by an intracardiac overdose of anaesthetic. Experiments were performed in accordance with Home Office guidelines.

Electron microscopy (EM)

Papillae were immediately dissected from the kidneys under a stereomicroscope and fixed by overnight immersion in 2.5% glutaraldehyde in 0.1 M cacodylate buffer pH 7.2–7.4. Weights of kidneys and papillae were not taken as this would have introduced delays and enhanced evaporation of the specimens. After washing, the tissue was postfixed with 1% osmium tetroxide for 2 h, washed, and dehydrated with alcohol according to standard procedures. Tissues were embedded in Spurrs resin, taking care to arrange the papilla so the tip could be cut in cross-section. Sections were cut at 200 μm intervals from 200 to 1800 μm from the tip to the base of the papilla (towards the outer medulla); not all levels were available in each rat (see Results). Collection of sections was stopped at 1800 μm as by this point the papilla was beginning to widen and structures could no longer be cut in cross-section across the entire medulla. Sections were places on grids (200 mesh) and stained with osmium tetroxide (0.1% v/v).

Photographs were taken at a magnification of × 3400 using a Phillips 401 electron microscope and the negatives were enlarged to a print size of 18.5 × 24 cm to give a final magnification of × 8 160. On average, twelve grid squares were photographed on each tissue section, distributed across the full width of the tissue at each level for each animal. A total of six kidneys from six rats at up to nine levels with a total of 495 prints were analysed.

Analysis of relative areas/volumes of the various structures in the medulla was done by placing a grid of 17 × 21 = 357 points over the photograph and each point characterized as falling on a vasa recta, collecting duct, interstitial cell, interstitial space or loop of Henle. On average, the fractional cross sectional areas of objects are equivalent to their fractional volume; a proof of this relationship has been provided by Aherne & Dunhill (1982).

Determination of HA concentration by capillary zone electrophoresis (CZE)

Pilot experiments were done using the HA-binding region assay developed by Fosang, Hey, Carney & Hardingham (1990). Results suggested that HA concentration decreased in slices further from the papillary tip (e.g. towards the outer medulla; data not shown). The amount of tissue required for a single assay allowed us to divide a papilla into a maximum of three slices. In order to increase our discrimination of HA at various distances from the papillary tip we decided to utilize a CZE assay.

Kidneys were removed under anaesthesia and the papillae quickly dissected free of the cortex under a Wild M10 stereomicroscope. Using a sharp scalpel each papilla was cut into five slices and the slices were then blotted gently to remove surface fluid and weighed on a fine balance. Slices from the same level from up to six kidneys were accumulated until 1–2 mg of tissue were obtained and then the slices were analysed together.

Such slices, which weighed 0.285 ± 0.0010 mg (mean ±s.e.m., n = 109 slices), could be cut and weighed in a mean time of 25.3 ± 0.09 s (mean ±s.e.m.) as determined by an independent observer. During this time the slices lost a mean of 14.9% in weight (as suggested by back extrapolation from losses in the following seconds). Values given in Table 2 are raw data and were not adjusted for this possible loss, as at least some of this must be due to evaporation of fluid still clinging to the surface of the organ.

Table 2.

Age-dependent changes in HA content of papillas of 1- to 3-week-old Sprague-Dawley rats

Level	1 week old	2 weeks old	3 weeks old
1. Tip	0.313 ± 0.09a	0.44 ± 0.02b	0.563 ± 0.06c
2.	0.219 ± 0.02	0.41 ± 0.05	0.46 ± 0.018
3.	0.157 ± 0.05	0.145 ± 0.05	0.21 ± 0.05
4.	0.015 ± 0.007	0.145 ± 0.08	0.18 ± 0.026
5. Base	0.018 ± 0.013	0.01 ± 0.007	0.078 ± 0.01
6. Control	0.0	0.0	0.0
Number of rats	12	11	11
Number of kidneys	24	22	22
Urine osmolarity	311.9 ± 15.3d	502 ± 43.5 e	613.95 ± 29.9f
Number of rats	27	71	10
Range	140–538	172–1731	205–1258

HA content was measured in μg HA (mg wet weight of slice)⁻¹, and urine osmolarity in mosmol l⁻¹. Values are means ±s.e.m.P values are: a vs. b = > 1 < 2%, b vs. c = < 0.01, d vs. e = < 0.01.

Briefly, tissue slices were placed immediately after weighing in 20 μl of chondroitinase (Sigma) buffer (50 mM Tris-Cl and 60 mM sodium acetate, pH 8.0, 0.0002 U chondroitinase (μg HA)⁻¹) for digestion overnight at 37°C. After the overnight digestion, samples were centrifuged at 1100 r.p.m. for 3 min in a 1 ml tube in an Eppendorf centrifuge in order to sediment the remnants of the slices. The supernatants were collected for determination of HA oligosaccharides according to the method of Carney & Osbourne (1991), with the only difference being that no borate was added to the running buffer, a modification which enhanced the separation of HA from other components of the renal medulla. This modification was suggested by Dr M. Crossman of the Advanced Biotechnology Centre, Charing Cross Hospital, London during earlier trials, work which is consistant with this study (MacPhee & Crossman, 1995); these data were not included in these results. HA was assessed against a standard curve produced using HA (250 μg ml⁻¹) from the Unsaturated Dissaccharide Kit, Seikagaku, Kogyo, Co. Ltd, Japan.

Statistics

Results are expressed as means ±s.e.m. Comparisons were made using Student's unpaired t test and significance was set at P < 0.05.

RESULTS

Capillary zone electrophoresis assay for HA

The HA concentration was assessed in 1-, 2-, and 3-week-old rats. Table 1 gives the accumulated results from fifty-four kidneys from twenty-seven 2-week-old rats, and Table 2 the results of a separate study at 1, 2, and 3 weeks of age showing an age-dependent increase in HA. There is a clear trend for the HA levels to decrease with distance from the tip, falling to near zero (undetectable levels, i.e. < 0.01 μg (mg wet weight)⁻¹) by 1500–1800 μm from the tip.

Table 1.

Capillary zone electrophoresis assay

Level	[HA] (μg (mg wet wt)−1)
1. Tip	0.337 ± 0.02
2.	0.344 ± 0.02
3.	0.207 ± 0.02
4.	0.150 ± 0.02
5. Base	0.05 ± 0.01
6. Control	0.02 ± 0.007

Two-week-old Sprague-Dawley rats were used. Values are means ±s.e.m. Control is the same level as base, but without enzyme digestion. Twenty-seven rats and fifty-four kidneys were used.

Electron microscopic determination of interstitial volumes

Using the standard stereological technique of point counting (Aherne & Dunhill, 1982), the percentage of total area (and hence of volume) consisting of cell-free interstitial space or area occupied by the interstitial cells was identified on electron micrographs. Micrographs were taken at random across the entire cross-section of the papilla over the nine levels (Fig. 1A and B) and results of the measurement of the interstitium reported in Table 3. Note that the volume occupied by cells and cell-free space has a reciprocal relationship and that this begins to plateau at about 1400 μm from the tip (Fig. 2). As a result, the proportion of the total interstitium occupied by the cell-free interstitial space (IS) is steadily decreasing, while the total volume of the interstitium remains relatively constant at 35–40%.

Figure 1. Transmission electron micrographs of renal medulla.

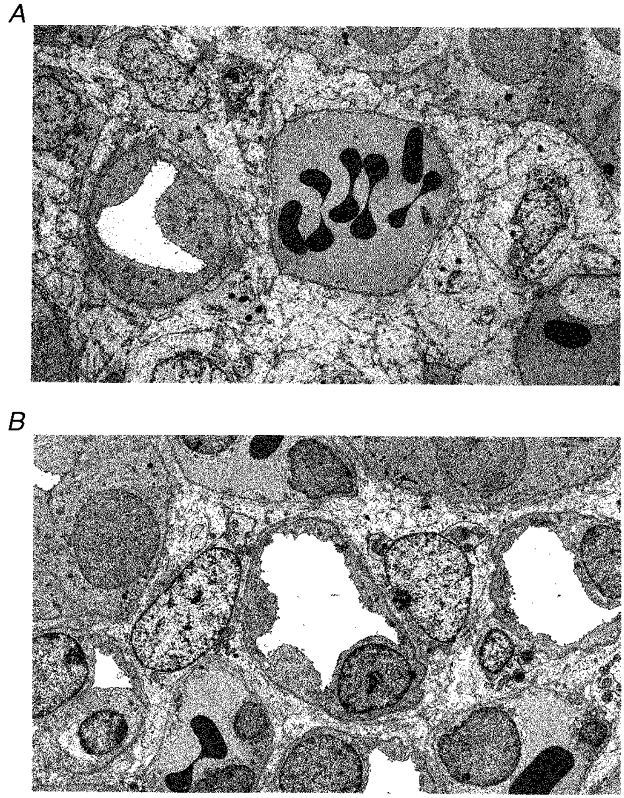
A, micrograph taken at 400 μm from the papillary tip. Note the wide interstitial spaces and vasa recta large enough to contain numerous red blood cells (RBCs). B, 1400 μm from the tip the interstitial space is less prominant, the vasa recta are smaller and parts of four LH are visible, two on the left margin, one central and one to the centre right. Three vasa recta containing RBCs are visible. Final magnification, × 4000.

Table 3.

Calculated HA concentrations

Level (μm)	IS (vol%)	[HA] (μg (mg wet wt slice)−1)	[HA] (μg (mg IS)−1)	[HA] (μg (mg IS + IC)−1)
0–400	20.8	0.337 ± 0.02	1.62	0.677
400–800	17.1	0.344 ± 0.02	2.01	0.819
800–1200	13.0	0.207 ± 0.02	1.59	0.618
1200–1600	9.4	0.150 ± 0.02	1.6	0.767
1600–1800	10.2	0.050 ± 0.007	0.005	0.500

IS, cell-free interstitial space; wt, weight; IC, interstitial cell; vol%, percentage of total tissue volume; and HA, hyaluronan. Values are means ±s.e.m.

Figure 2. The relationship between interstitial cell (IC) volume and the cell-free interstitial space (IS) in the rat papillary interstitium as a percentage of total tissue volume.

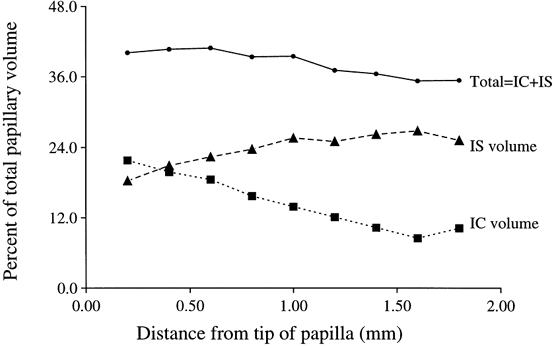
IC and IS have a reciprocal relationship, which plateaus off at about 1.5 mm from the papillary tip, while total volume remains roughly between 35 and 40%.

Calculation of HA concentration in the interstitium

Our calculations assume that the HA we are measuring was located entirely in the intercellular interstitial spaces in vivo. This assumption is based on work carried out by Prehm (1984) when he demonstrated that HA is produced at the plasma membrane and extruded extracellularly. Since we now have estimates of the cell-free interstitial volume in rats of the same age and at the same levels within the inner medulla we can determine a local HA concentration. This will be in μg HA (mg wet wt of whole papillary slice)⁻¹ divided by the percentage cell-free IS (Table 3). HA concentrations were similarly measured at 1, 2 and 3 weeks of age in a separate experiment (Table 2). Tissue concentrations of HA showed an age-dependent increase over the 3 week period. The tendency for the HA concentration to fall to near undetectable levels about 2 mm from the tip was maintained at 3 weeks of age.

Calculation of the effective oncotic pressure of mixtures of HA and A

During our previous studies on interstitial fluid protein concentration we used Moyses (1986) estimation of the oncotic pressure of albumin (π_A):

(1)

When C_A is 0.91 ± 0.06 g dl⁻¹ (0.134 mmol l⁻¹) (MacPhee & Michel, 1995b), the oncotic pressure π_A will be 3.69 cmH₂O. Note that C_A= 0.91 g dl⁻¹ is an estimate of the mean albumin concentration for the whole papilla; any tip to base gradients in albumin concentration will therefore not be evident. Secondly, C_A it is not a measure of total interstitital protein, only of free albumin, as an unknown quantity of albumin will remain associated with HA by electrostatic charges (Niedermeier, Gramling & Pigman, 1966; Peitzsch & Reed, 1992). Centrifugation at the low forces used is unlikely to release water or albumin closely associated within an HA gel matrix. Bound albumin will be constantly in flux with free albumin and so both will be part of the total pool of albumin in the papilla, as measured by other means. It is the free albumin, however, that will contribute to oncotic pressure across the AVR wall. In addition, other plasma proteins will be present in the IS to varying degrees depending on their reflection coefficients (σ) at the AVR wall, which have not yet been measured. Their concentrations in the IS will be proportional to, but likely to be much lower than that in the plasma. Therefore, we can estimate the total protein concentration (C_P) to be equal to C_A/0.6 = 1.52 g dl⁻¹ (assuming A is 60% of plasma protein). When C_P is 1.52 g dl⁻¹, π_P will be 4.14 cmH₂O. In addition to plasma proteins, other interstitial proteins may be present, such as those associated with proteoglycans; their contribution is not known but is assumed here to be small.

The osmotic pressure (π) of HA (π_HA) alone is:

(2)

as determined by Wiederhielm, Fox & Lee (1976), where C is the concentration in g per 100 ml (0.16 g (100 ml)⁻¹) and yields π in mmHg.

Wiederhielm et al. (1976) modelled the interaction of HA and albumin and found that the exclusion effects of HA caused the osmotic pressure of a mixture of HA and albumin to be greater than the sum of the two parts. He then compared measured values for HA-A mixtures with his theoretical results and concluded that the data supported the conclusion that the mixture could be regarded as a two compartment system. A reasonable estimate of the partition coefficient (Λ) for A (i.e. the proportion of the space in an HA solution available for A) in an HA solution can be made using the approximation of Michel (1984); in brief,

(3)

where V_f is the volume fraction of HA in the system and V_x is the volume from which A is excluded, i.e.:

(4)

where r_HA is the radius of HA = 0.5 nm (HA is assumed to be cylindrical), and r_A is the radius of A = 3.8 nm (albumin is assumed to be an oblate ellipsoid). V_f for HA will equal the mean specific volume × concentration of HA = 0.65 × 0.16 g (100 ml)⁻¹= 0.00104; and therefore Λ will be 0.9269. The adjusted concentration of A in an HA matrix will be:

for our minimal estimate of C_P (C_min), and

for our maximal estimate of π (π_max is 6.4 cmH₂O). A mixture of HA and protein will then have a total osmotic pressure somewhere between:

and

The total effective oncotic pressure (Eπ) takes into account the reflection coefficients (σ) to HA and A at the AVR wall. As the σ for HA is unknown but probably high (HA has a molecular weight close to 10⁶), a σ of 1 was assumed in these calculations (see Discussion). The reflection coefficient to albumin (σ= 0.718) has been previously determined during reabsorption experiments in vivo (MacPhee & Michel, 1995b). The Eπ_min will then equal the osmotic pressure (OP) of HA alone (0.81 ×σ_HA= 0.81 cmH₂O) + the OP of A in the HA mixture (3.69 ×σ_A= 2.65), i.e.:

and

Due to the high permeability of AVR to water and protein the reflection coefficients to salts and urea are assumed to be correspondingly low. Experiments performed by Pallone (1991) also suggest that osmotic gradients due to salt and urea gradients are negligible in the AVR.

DISCUSSION

Interstitial volumes

Estimates of interstitial volume have previously been made on adult male Sprague-Dawley rats (Knepper, Danielson, Saidel & Post, 1977) using 5 μm sections stained with Haematoxylin and Eosin and a similar point counting system. Interstitium, however, was defined as any space not occupied by either renal tubules or vasculature, and therefore did not distinguish between interstitial cells (IC) and cell-free interstitial space (IS). Knepper and colleagues found that the total interstitial space decreased from about 22% (interpolated from his Fig. 1) near the papillary tip to about 10%; this can be compared with the small decrease from about 40 to 35% seen in the papilla of young rats in this study. Knepper's results also differ markedly in this respect from those of Pfaller (1982) who found that in adult Wister rats total interstitial volume decreased from 33 to 22% over approximately the same distance. The similarity between the values seen in young Sprague-Dawley rats in this study and those of adult Wistar rats in Pfaller's suggests that the finding of larger interstitial volumes may be a result of the use of electron microscopy versus light microscopy, rather than the age or strain of the rats.

In the case of the young Sprague-Dawley rats, IS and IC were found to have a reciprocal relationship over the first 1400 μm from the tip, reaching a plateau thereafter. The young rats had double the volume of interstitial cells (IC) seen in adult rats, accounting for the difference in the total interstitial volumes. One explanation might be that during the first few weeks of life while the urinary concentrating mechanism is maturing, IC are especially active in production of HA and other glycosaminoglycans (GAGs), and are therefore either much larger or greater in number than in the adult rat. Since IC and IS can be calculated separately, it was therefore possible to calculate the local interstitial concentration of HA in the free interstitial space and hence estimate its local contribution to the total oncotic pressure of the interstitium.

It must also be asked what effect the sudden decrease in HA concentration near the base of the papilla (Table 4) might have on fluid and protein movement through the interstitium. Such a sharp decrease in the concentration of HA may result in a local decrease in albumin concentration in the IS favouring diffusion upwards (other things being equal), i.e. towards the outer medulla with its lymphatic drainage at the cortico-medullary junction. In addition, at this point albumin will no longer be bound to HA and this may alter the electrostatic charge gradients in the interstitium (Niedermeier et al. 1966; Peitzsch & Reed, 1992), and hence the diffusion rates through the interstitium. It would certainly be helpful to be able to dissect the albumin gradients as well as the HA gradients in the inner medulla.

Table 4.

Solving for interstitial hydrostatic (P_i) and oncotic (π_i) pressures

a) Solving for Pi using our calculated πi (min: where Cp=[A]= 0.91 g dl−1)
Under conditions such that fluid flux = 0			Then under free flow conditions
Interstitium		AVR lumen	Interstitium		AVR lumen
Pi=?	←	Pc= 12.7*	Pi= 1.4	←	Pc= 6.0*
Eπmin= 3.46	→	Eπc= 17.6* (5% BSA)	Eπi= 3.46	→	Eπc= 18.5* (plasma)
Pi will = 1.4 cmH2O			Net inward pressure = 9.3 cmH2O
b) Solving for Pi using our calculated πi (max: where Cp=[A/0.6]= 1.52 g dl−1)
Under conditions such that fluid flux = 0			Then under free flow conditions
Interstitium		AVR lumen	Interstitium		AVR lumen
Pi=?	←	Pc= 12.7*	Pi=−1.1	←	Pc= 6.0*
Eπmax= 6.0	→	Eπc= 17.6* (5% BSA)	Eπmax= 6.0	→	Eπc= 18.5* (plasma)
Pi will =−1.1 cmH2O			Net inward pressure = 5.4 cmH2O
c) Solving for πi using our experimentally determined Pi
Under conditions such that fluid flux = 0			Then under free flow conditions
Interstitium		AVR lumen	Interstitium		AVR lumen
Pi= 0.9*	←	Pc= 12.7*	Pi= 0.9*	←	Pc= 6.0*
Eπi=?	→	Eπc= 17.6* (5% BSA)	Eπi= 5.8	→	Eπc= 18.5* (plasma)
Eπi will = 5.8 cmH2O			Net inward pressure = 7.6 cmH2O

^*Data from MacPhee & Michel, 1995b.

Calculation of estimated osmotic pressure of HA and albumin mixtures

Since HA has been estimated to constitute 96% of GAGs produced by the renal medullary interstitial cells (Pitcock et al. 1988), the minor contribution of other GAGs to the oncotic pressure (π) in the medullary interstitial matrix has been ignored in the calculations. The second main contributor to total interstitial π will be the interstitial proteins. These consist of proteins carried into the interstitium by convection with water, and those diffusing into the interstitium through the walls of the vasa recta. The reflection coefficient for albumin (σ_A) has been estimated to be 0.59–0.78 in the AVR (and 0.718 during reabsorption experiments) of Sprague-Dawley rats (Pallone, 1992; MacPhee & Michel, 1995b), and close to 1 in the DVR (Pallone, 1992). Reflection coefficients for the larger macromolecules (e.g. fibrinogen and globulins) have not yet been measured in the AVR, but they are likely to be fairly close to 1 and therefore make only a minor contribution to interstitial oncotic pressure. Thus our value for π_{HA + A} of between 3.46 and 6.0 cmH₂O may slightly underestimate the total oncotic pressure in the interstitium.

The quantification of albumin in the medullary interstitium itself has been difficult. Qualitative studies using radioisotopes (Lassen, Longley & Lilienfield, 1958), fluoresence (Pomerantz, Slotkoff & Lilienfield, 1965) and Evans Blue (Wilde & Vorburger, 1967) have demonstrated a considerable pool of extravascular albumin. In previous experiments the mean albumin concentration in the papillary tissue fluid was found to be approximately 0.91% albumin (see MacPhee & Michel, 1995b). Levick (1994) has pointed out in the context of a discussion of albumin flux across the synovium that sieving effects may contribute to local accumulation of albumin on the abluminal surface, forming a barrier as fluid is drawn into the vessel through small ‘pores’ (of whatever type). This will tend to raise the local albumin concentration near the point of entry of fluid and so diminish the oncotic pressure gradient across the wall, with the result that hydrostatic pressure gradients will have a relatively greater effect. Using a different approach Pallone (1994) hypothesized that in hydropenic Munich- Wister rats the luminal contents of segments of AVR isolated by wax blocks would equilibrate rapidly with the interstitium; his estimate of interstitial protein concentration was 3.4 ± 0.5 g dl⁻¹.

Various estimates have also been made for the contribution of hydrostatic pressure to the balance of Starling forces across the AVR. Using our calculated Eπ for HA + A in the IS (Table 4a) of 3.46 cmH₂O, this suggests that during our in vivo reabsorption experiments interstitial hydrostatic pressure (P_i) must have been about 1.4 cmH₂O. If Eπ was as high as our maximal estimate (Table 4b) P_i becomes negative (−1.1), reducing the net inward driving force to 5.4 cmH₂O. The rhythmic contractions of the ureter may result in intermittent alterations in these values, and possibly large variations in pressure; unfortunately no measurements have been made with the renal pelvis intact due to technical difficulties.

Both of these estimates of P_i (i.e. −1.1 and 1.4) are lower than that of > 3.8 cmH₂O obtained by Pallone (1994) and considerably lower than that of 9.1 cmH₂O found by Garcia-Estañ & Roman (1989) using implanted capsules in adult Sprague-Dawley rats. In the latter case it was noted at the end of the experiment that the implanted capsules were actually located close to the cortico-medullary junction, and it may be that these values are close to cortical interstitial pressures. No experiments have been done using capsules in the inner medulla (i.e. the first 2 mm of the papillary tip). The low interstitial pressures found in this study are, however, consistent with values obtained by the authors using a totally different method, i.e. an estimate of 0.9 cmH₂O based on the difference between in vitro and in vivo closing pressures of the AVR (MacPhee & Michel, 1995a).

The balance of Starling forces across the AVR

During previous in vivo micropuncture experiments a segment of an AVR was perfused with Evans Blue-albumin solution with an oncotic pressure similar to plasma (MacPhee & Michel, 1995b), and the pressure in the micropipette supplying the albumin adjusted so that no blue dye was visible in the interstitium. At this balance point the intraluminal pressure will equal the sum of the interstitial hydrostatic and oncotic pressures (P_i and π_i). Using our new estimate of π_i from this study, we can then estimate P_iin vivo in the exposed papilla (see Table 4 and below). Knowing π_i we can now estimate the net inward pressure for fluid reabsorption that will probably exist under normal (free flow) conditions in the same vessels. We can check these results for internal consistency by using our independent and experimentally determined estimate of P_i (MacPhee & Michel, 1995b), and solving for π_i.

Our present data (Table 4) suggest that under free flow conditions in the AVR and using our estimate of Eπ_i based on measured concentrations of HA and A there is a net inward driving force of between 5.4 and 9.3 cmH₂O available for fluid reabsorption. Using our previous experimental estimate of P_i of 0.91 cmH₂O (Table 4c), and solving for Eπ_i, we obtained 5.8 cmH₂O, which would result in a net inward pressure of 7.6 cmH₂O in a free flow situation. The validity of these results is enhanced by noting that both our experimental estimates of what interstitial oncotic pressure must be in vivo, and our calculated oncotic pressure based on measured HA and albumin concentrations, yield internally consistent results (between 5.4 and 9.3, and 7.6 cmH₂O) in terms of net inward driving pressures for fluid flux in the AVR. A further internal consistency is found in that our estimate of Eπ_i= 5.8 cmH₂O (from Table 4c), based on the experimentally determined P_i, could result from a C_P of 1.64 g dl⁻¹ (i.e. a C_A of 0.98), which is very close to our measured value of 0.91.

HA concentration changes with age and concentrating ability

The finding of an increasing HA concentration over the first 3 weeks postnatally which parallels the increasing mean urine osmolarity supports the idea of a relationship between HA content and concentrating ability. One interesting example of an association between HA and concentrating ability is found in the Brattleboro (BB) strain of rat which has a hereditary defect in concentrating ability. In the homozygous rat (DI/DI), antidiuretic hormone (ADH) is very low, associated with greatly reduced levels of interstitial GAGs (< 20% control) in the papillary interstitium, as determined by staining of sections with Azur Blue dyes (McAuliffe, 1980). Another change noted in BB rats was a decrease in size and presence of cell processes of type I interstitial cells and an increase in type II cells. McAuliffe has suggested that lack of stimulation of the IC by ADH in BB rats may lead to decreased production of GAGs, and that reduced levels of GAGs (with their high negative charge) may alter the tip to base gradients of small solutes such as Na⁺ and so alter interstitial osmolality and hence the concentrating mechanism. In contrast to the mechanism proposed by Koefoed & Knudsen (1961), i.e. a driving force generated by the continual turnover of HA, it may be that it is the concentration of HA present in the interstitium at any given place and time that determines, in conjunction with albumin etc., the total interstitial colloid oncotic pressure and hence driving force for fluid reabsorption and therefore the efficiency of the concentrating mechanism. Certainly, a role for the turnover rate may be important and needs to be investigated further, not only in normal animals but in those with concentrating defects. Another potential role for HA is in the endothelial cell junctions (Aukland et al. 1994), as well as in the fenestrae or the glycocalyx, where the shrinking or swelling of GAGs may influence the permeability of the capillary wall.

In summary, new estimates of medullary interstitial volume and of inner medullary interstitial HA content have been made in age-matched rats to facilitate calculations of local papillary hyaluronan concentrations. The EM study suggests that interstitial cells and interstitial space have a reciprocal relationship over the first 1800 μm of the rat papillary tip, such that the total interstitial volume is kept relatively constant (35–40%), along with the hyaluronan concentration (0.16 g dl⁻¹). HA concentration tends to drop off sharply to near zero between 1600 and 1800 μm from the tip in rats of 1, 2, and 3 weeks of age. Over the first 3 weeks of life HA concentrations in the tip region are increasing slowly in parallel with the increase in mean urine osmolarities. Knowing the HA concentration, we can now estimate its contribution alone, and in combination with serum albumin, to the total oncotic pressure of the inner medullary interstitium. As a result, we estimate, based on our calculated values for HA, that the effective oncotic pressure of the interstitial fluid is between 3.46 and 6.0 cmH₂O, resulting in vivo in a net inward force of 3.46–9.3 cmH₂O available for driving fluid reabsorption into the AVR.