Abstract
Stimulation of the carotid sinus nerve causes an increase in inspiratory (I) and expiratory (E) neural activities. If central respiratory oscillation is generated by an attractor-cycle process, an increase in its activity can be caused by a centrifugal perturbation of state. We evaluated this hypothesis by comparing the respiratory oscillator's phase responses to carotid sinus nerve stimulations in cats to the phase responses of an attractor-cycle oscillator, the Bonhoeffer-van der Pol (BvP) equations, subjected to centrifugal perturbations.
We recorded phrenic activity in seven anaesthetized, vagotomized, glomectomized, paralysed and servo-ventilated cats. Carotid sinus nerve (CSN) stimulation with 0.5–0.8 s electrical pulse trains increased the immediate cycle period and delayed the onset of breaths after stimulation in a highly predictable manner, with the exception that strong stimuli (25 Hz, 0.25–0.90 V) caused unpredictable responses when given at the I-E or the E-I transitions. The resetting plots exhibited focal gaps corresponding to these unpredictable responses, and the size of the gaps increased with increases in the strength of CSN stimulation. Type 0 resetting was not achieved despite the large perturbations in rhythm induced by CSN stimulation.
Centrifugal perturbations of the BvP oscillator resulted in phase responses which were similar to those found in the animal experiments. The BvP cycle had two critical phases at which phase resetting was highly irregular and neighbouring state trajectories were highly divergent. The resetting plots had focal gaps that increased in size with increases in the strength of perturbation. The gaps did not represent true discontinuity because at higher computational resolution the resetting plots appeared to be steep but smooth portions of topological Type 1 resetting curves.
These studies support the concept that brief carotid sinus nerve stimulations cause a transient outward displacement of the central respiratory state away from its attractor cycle, in contrast to the unidirectional displacements that accompany midbrain reticular or superior laryngeal nerve stimulations. The findings define particular geometrical relationships between oscillatory state trajectories of the rhythm generator and perturbed state trajectories induced by inputs to the oscillator. These relationships provide a framework for developing and testing the validity of neural models of the respiratory oscillator.
Certain properties of oscillation can be addressed by studying the impact on rhythm of a discrete perturbation. When the respiratory oscillatory process is so perturbed by a brief stimulus, the oscillator eventually recovers its previous rhythm although its phase may be reset relative to the control rhythm. The amount of resetting depends upon several factors: the strength of the stimulus, the time in the cycle at which it is given (Paydarfar, Eldridge & Kiley, 1986; Paydarfar & Eldridge, 1987; Kitano & Komatsu, 1988; Eldridge, Paydarfar, Wagner & Dowell, 1989; Lewis, Bachoo, Polosa & Glass, 1989: Oku & Dick, 1995; Paydarfar, Gilbert, Poppel & Nassab, 1995), as well as the level of respiratory activity, i.e. respiratory drive (Eldridge et al. 1989). The findings can be related in a general way to the geometry of the oscillatory trajectories in state space (see Eldridge et al. 1989; Lewis, Glass, Bachoo & Polosa, 1992; Ogilvie, Gottschalk, Anders, Richter & Pack, 1992: Baconnier, Benchetrit, Pachot & Demongeot, 1993; Gottschalk, Ogilvie, Richter & Pack, 1994; Sammon, 1994; Paydarfar & Buerkel, 1995). Specific neural models of the respiratory oscillator can be excluded if their phase responses are qualitatively dissimilar to the experimental responses (Winfree, 1980; Glass & Winfree, 1984).
We previously studied phase resetting of respiratory rhythm by brief (< 1 s) stimuli given at various times in the cycle, using either stimulations of the superior laryngeal nerve (SLN) which inhibits inspiration and leads to early expiration (Paydarfar et al. 1986), or stimulations of midbrain reticular formation (MR) which activates inspiration (Paydarfar & Eldridge, 1987; Eldridge et al. 1989). In both cases, weak stimuli caused little phase resetting and the latency from stimulus to subsequent cycles (called the cophase, θ) fell by one cycle as the stimulus time (called the old phase, φ) was advanced through the entire cycle, i.e. there was a topological Type 1 phase resetting pattern (e.g. Fig. 1A and B). Strong stimuli caused large perturbations of respiratory rhythm and there was no net change in the cophase as the old phase increased one full cycle, i.e. there was a topological Type 0 phase resetting (e.g. Fig. 1D and E). Stimuli with intermediate strength resulted in a phase singularity, recorded as highly variable latencies to the next cycles for stimuli given at a single old phase (e.g. Fig. 1C); the same stimulus given at all other times in the cycle resulted in highly predictable phase resetting.
Figure 1. Toplogical types of phase resetting of respiratory rhythm.
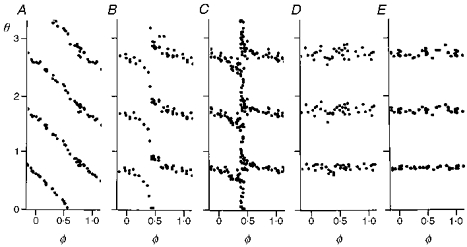
Plots of phase resetting of respiratory rhythm in one cat. Midbrain reticular formation was stimulated for 1 s with increasing strengths: 10 (A), 20 (B), 25 (C), 30 (D) and 100 Hz (E). Old phase (φ) is the time from the onset of inspiration to the onset of the stimulus. Cophase (θ) is the time from offset of the stimulus to the onset of a rescheduled breath, shown for three successive breaths. Old phase and cophase are in cycle units, i.e. 1 is the period of the control cycle before stimulation. A and B, the cophase has a net change of 1 as the old phase is varied through one full cycle (Type 1 resetting). D and E, the cophase has a net change of 0 as the old phase is varied through one full cycle (Type 0 resetting). C, there is unpredictable resetting with stimuli given only at a specific old phase (0.4, near the I-E transition). This response identifies the oscillator's phase singularity. Adapted from Paydarfar & Eldridge (1987).
We found that MR stimulation and SLN stimulation resulted in the same qualitative pattern of phase resetting; but a salient difference was the time in the cycle at which the phase singularity was located. The inspiratory facilitatory input (MR stimulation) resulted in a singularity at the transition from inspiration to expiration, whereas the inspiratory inhibitory input (SLN stimulation) evoked the same unpredictable singular response at the transition from expiration to inspiration. The experimental data support the idea that endogenous respiratory rhythm follows attractor-cycle dynamics, that MR stimulations are unidirectional and shift the oscillator's trajectories toward the inspiratory state regardless of the respiratory phase at stimulation, and that the SLN stimulations are also unidirectional but propel the trajectories toward the expiratory state.
Brief stimulations from the carotid body (CB) or carotid sinus nerve (CSN) also affect respiratory timing; inspiratory stimuli can prolong inspiration (Howard, Bromberger- Barnea, Fitzgerald & Bane, 1969; Black & Torrance, 1971; Eldridge, 1972a, b; Black, Goodman, Nail, Rao & Torrance, 1973) and stimuli given during expiration can prolong expiration (Black & Torrance, 1971; Eldridge, 1972a, b; Eldridge, 1976), although very late expiratory stimuli can actually shorten the expiratory period by initiating the next inspiration (Eldridge, 1972a, b; Remmers, Richter, Ballantyne, Bainton & Klein, 1986). These studies clearly show that a single brief CSN stimulus can shift the immediate respiratory cycle. However, in preliminary studies we found that such stimuli did not lead to replication of the resetting patterns found with MR or SLN stimuli. We thought that the reason might lie in the fact that, unlike MR and SLN inputs which cause pure inspiration facilitation or inspiration inhibition, respectively, CSN stimulation increases the respiratory neural activity that exists at the time of stimulation, i.e. stimulation during inspiration increases inspiratory activity (Howard et al. 1969; Black & Torrance, 1971; Eldridge, 1972a, b; Black et al. 1973), whereas stimuli given during expiration increase expiration, as shown by increased electrical activity of expiratory muscles and increased depth of expiration (Eldridge, 1976). In other words, the CSN input is stimulatory in both halves of the cycle.
We hypothesized therefore that the CSN input does not cause a unidirectional perturbation of the central respiratory state but rather always causes an outward displacement of the oscillator's state from its attractor cycle, i.e. a centrifugal perturbation. The present study evaluates this hypothesis. We examined in animals the patterns of respiratory phase resetting that follow brief CSN stimuli given at various times in the respiratory cycle, and with various intensities. The findings were then compared with those computed from equations of a generic attractor cycle subjected to similar perturbations of a drive parameter. The results support the concept that carotid sinus nerve input acts as a centrifugal perturbator of the central respiratory state, rather than causing unidirectional perturbations as produced by midbrain or superior laryngeal nerve input. The findings define particular geometrical relationships between oscillatory state trajectories of the rhythm generator and perturbed state trajectories induced by inputs to the oscillator. These relationships provide a framework for developing and testing the validity of neural models of the respiratory oscillator.
METHODS
Animal studies
General preparations
Studies were performed in seven adult cats weighing between 2.8 and 4.8 kg. Anaesthesia was induced with inhaled ether, and maintained with a mixture of chloralose (40 mg kg−1) and urethane (250 mg kg−1) given as a single dose through a femoral vein. The trachea was cannulated, and the animal was placed supine on a table with a rigid head mount. The femoral artery was cannulated for continuous recording of blood pressure using a strain-gauge transducer. Body temperature was monitored with a rectal thermistor and kept between 37 and 38°C by means of a servo-controlled heating mat. Vagosympathetic trunks were isolated and cut bilaterally. One phrenic nerve root (C5) was exposed in the neck, cut, desheathed, and placed on a bipolar recording electrode immersed in mineral oil. Phrenic nerve activity was amplified (model P-15; Grass Instrument Co), half-wave rectified and integrated for each 100 ms period. The animals were ventilated with 100% O2 using a volume-cycled ventilator and paralysed with gallamine triethiodide, 3 mg kg−1i.v. initially, followed by a continuous infusion at the rate of 3 mg kg−1 h−1 to maintain paralysis. The adequacy of anaesthesia was confirmed by continuous monitoring of blood pressure and respiratory frequency throughout the experiments; there were no bursts of hypertension or tachypnoea. End-tidal PCO2 was monitored through the tracheal cannula, using an infrared CO2 analyser (Beckman LB-2). In order to minimize changes in end-tidal CO2, the motor of the ventilator was servo-controlled (Smith, Mercer & Eldridge, 1978) by the animal's end-tidal PCO2. The control system was set to maintain a constant (± 0.5 mmHg) end-tidal PCO2.
Carotid sinus nerve preparation and electrical stimulation
The region of the carotid artery bifurcation was exposed unilaterally. The carotid sinus nerve was freed from surrounding tissue by blunt dissection, crushed distally, placed on bipolar stimulating electrodes and covered with mineral oil. The opposite carotid sinus nerve was exposed and cut. After the surgical procedures had been completed, end-tidal PCO2 was raised 3–4 mmHg above the threshold for rhythmic phrenic activity. Initially, the carotid sinus nerve was stimulated electrically with a continuous monophasic train of 0.5 ms pulses generated at 25 Hz, and the phrenic nerve response was recorded. The stimulus voltage was increased gradually to determine the level at which evoked phrenic nerve activity did not increase further. This voltage level varied from cat to cat (0.25–0.9 V). In all experiments, peak integrated phrenic activity was expressed as a percentage of the estimated maximum (Eldridge, Gill-Kumar & Millhorn, 1981): 80% maximum phrenic chemoresponse was determined by increasing end-tidal PCO2 to 30 mmHg above threshold, and the addition of continuous maximal CSN stimulation at this level further raised phrenic activity to 95% of the absolute maximum response of the respiratory controller.
The onset of neural inspiration was designated as the time when integrated phrenic activity increased to a level that was twice the baseline noise level. Brief stimulations at various times in the respiratory cycle were accomplished by short monophasic trains of 0.5 ms pulses. Throughout each experiment the train duration was kept constant: 0.8 s in five animals, 0.6 s in one animal, and 0.5 s in one animal. Stimulus strength was varied by changing the pulse frequency (5 animals) or pulse voltage (2 animals).
Experimental protocol
Each brief CSN stimulus was preceded by ten control breaths, during which end-tidal PCO2 and neural respiratory output remained constant (± 0.5 mmHg end-tidal PCO2; ± 5% change in respiratory period). After each stimulus, an additional four to ten breaths were recorded. Initially, a specific stimulus strength was selected and given at various times in the respiratory cycle. An attempt was made to give at least one stimulus in each 5% increment of the respiratory cycle. This was usually achieved within 45 min. On completion of this set of runs, the stimulus strength was increased or decreased and the protocol was repeated. At the end of each experiment the animal was killed by lethal i.v. injection of sodium pentabarbitone (100 mg kg−1).
Computer model studies
We studied the Bonhoeffer-van der Pol (BvP) equations (Fitzhugh, 1961):
where 1 - 2b/3 < a < 1; 0 < b < 1; and b < c2.
The solutions of the differential equations were estimated by computer, using Runge-Kutta fourth order difference equation approximation (Δt = 0.01), setting a = 0.7, b = 0.8, c = 3.0. For −0.3452 > z > −1.4023 the approximated BvP trajectories in the x-y plane converge to a stable attractor cycle. The singular point is the point of intersection of the x and y nullclines (dx/dt = dy/dt = 0). The position of the singular point can be moved relative to the attractor cycle by changing z (Paydarfar & Buerkel, 1995), unlike the van der Pol oscillator which has an immobile centrally located singular point. The cubic term of the BvP equation was scaled to alter the numerical amplitude of oscillation by replacing the x3/3 term with x3/3d (Eldridge, 1991; Paydarfar & Buerkel, 1995); increasing the drive component (d) results in an increase in oscillator drive by increasing the amplitude of the attractor cycle (see Fig. 6A). The effect on BvP trajectories of transient centrifugal perturbations was computed by increasing d from 1 to (1 +Δd) for 1/4 of a full cycle. The phase of rhythm is determined by setting an activity threshold (yt) and by determining the time at which y(t) activity crosses from below to above this threshold. The analogy to respiration is that the yt threshold divides the cycle into inspiratory-like and expiratory-like activity, and the crossing times represent the onsets of inspiration. Cophase and old phase are computed (see Fig. 1 legend) relative to the perturbation in drive.
Figure 6. BvP oscillator's state response to transient centrifugal perturbations.
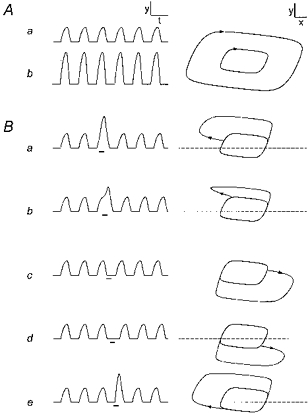
A, increasing d from 1 (run a) to 6 (run b) causes an increase in the amplitude of the rhythm, expressed as y(t) (left), and the size of the x-y attractor cycle (right tracing). B, transient increase in d for 1/4 cycle causes perturbations in rhythm (y vs. t) and trajectories (y vs. x) that depends on the old phase of stimulation. φ= 0.1 (a), 0.3 (b), 0.5 (c), 0.7 (d), and 0.9 (e). Direction of perturbation is centrifugal, outwardly displacing the stimulated portion of the cycle. Dashed horizontal line is y threshold (yt= 0.7) corresponding to zero amplitude and above which rhythmic activity is apparent. z =−0.875. Scale bars (arbitrary units): x = 1, y = 1, t = 10.
RESULTS
Animal experiments
Effects of strong carotid sinus nerve stimuli
An example of the effect on phrenic activity of a prolonged stimulus train (30 s; pulse frequency, 25 Hz; pulse duration, 0.5 s; pulse strength, 0.5 V; end-tidal PCO2, 4.1 mmHg above apnoeic threshold of 28.3 mmHg) is shown in Fig. 2A. This was a strong stimulus because it caused peak integrated phrenic activity to increase from 36 to 92% of its maximum. The average response (7 animals) to strong CSN stimulation was to increase phrenic activity from 29 to 72% of maximum, with small and inconsistent changes of rate in these vagotomized animals. When continuous stimulation was given for 30 s, short-term potentiation of respiration occurred, leading to an increased post-stimulus level of phrenic activity, compared with control (Fig. 2A), which decayed gradually to control over some minutes (Wagner & Eldridge, 1991).
Figure 2. Effect on phrenic activity of CSN stimulation.
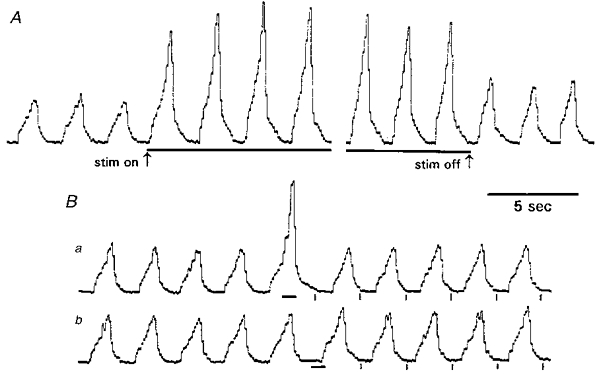
A, example of effect on phrenic rhythm of strong CSN stimulation (horizontal bars), given for 30 s (pulse frequency, 25 Hz; duration, 0.5 ms; strength, 0.5 V). Note the presence of short-term potentiation of rhythm after offset of stimulation. B, effect on phrenic rhythm of 0.8 s CSN stimulation (horizontal bars), otherwise with same pulse parameters as used in A. Stimulation during inspiration (a) facilitates amplitude and duration of the concomitant inspiration; the same stimulus prolongs the expiratory period when given during expiration (b). The stimulus has no lasting effects on subsequent respiratory amplitudes and periods, but delays the time of onset of breaths subsequent to stimulation relative to that expected from extrapolation of the control rhythm (vertical marks below phrenic rhythm).
Figure 2B shows the effect on phrenic activity of the same CSN stimulus but with a duration of only 0.8 s. Brief stimulation during inspiration (Fig. 2Ba) led to increased amplitude and duration of that inspiration. The same stimulus, when given during expiration (Fig. 2Bb), caused prolongation of the expiration with only a small effect on the initial part of the subsequent inspiration. Both stimuli in Fig. 2B delayed the times of onset of breaths subsequent to stimulation, i.e. reset the phase of rhythm. Unlike the longer durations of stimulation, brief (0.5–0.8 s) stimuli did not cause measurable short-term potentiation of respiration in any of the experiments.
Phase resetting of respiratory rhythm
Figure 3 shows examples in one animal of the effects of weak and strong CSN stimulation given at various times in the respiratory cycle. Figure 3A shows that the weak (10 Hz) stimulus (0.8 s, 0.7 V, 0.5 ms) had little effect on respiratory rhythm no matter when it was given in the cycle (runs a-i). The phase resetting plot of the full set of forty-one runs for this weak stimulus is shown in Fig. 3B. The dotted diagonal lines show the relationship that would be seen for a 0.8 s stimulus having no effect at all on phase (‘no resetting’). CSN stimuli given during most of the cycle caused only a small delay in the rescheduled rhythm (by up to 15% of the control cycle period, or 0.15 units of cophase). However, for stimuli given near the phase of transition between inspiration and expiration (φ=0.41 ± 0.01, e.g. Fig. 3A, run e), the inspiratory onsets were slightly earlier than for the projected unperturbed rhythm. This is a Type 1 resetting pattern as would be expected with a weak stimulus.
Figure 3. Resetting of respiratory rhythm by brief CSN stimulation.
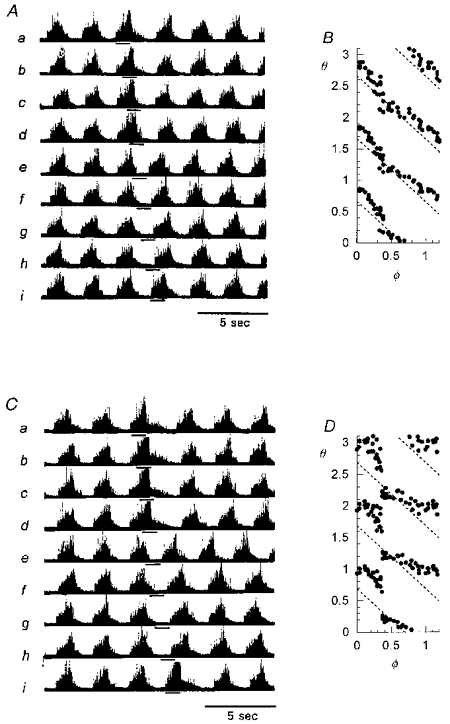
Phase resetting patterns for weak (A and B: 10 Hz, 0.8 s, 0.7 V, 0.5 ms) and strong (C and D: 25 Hz, 0.8 s, 0.7 V, 0.5 ms) CSN stimulation (runs a-i, horizontal bars), in the same cat as shown in Fig. 1. The stimulated cycle period is prolonged and post-stimulus breaths are delayed for all stimuli except those given at the transition between inspiration and expiration (φ=0.41 ± 0.01), e.g. run e in C. Dotted diagonal lines show the θvs.φ relationship for a stimulus having no effect on phase.
In Fig. 3C, all stimulus parameters were the same except the pulse frequency, which was increased to 25 Hz. This is a strong stimulus which caused large shifts in respiratory rhythm, prolonging the stimulated cycle and all cophases when given during most phases of inspiration and expiration. The conspicuous exception again was a shortening of the cycle and all cophases for stimuli given near the phase of transition between inspiration and expiration (e.g. run e). The phase resetting plot of Fig. 3D quantifies the effect in the full set of runs with strong stimuli. Despite the strong stimulus, the resetting pattern did not convert to Type 0 resetting.
Figure 4A-C shows resetting plots in another cat for a CSN stimulus (0.6 s, 25 Hz, 0.5 ms) with three different strengths (A, 0.42 mA; B, 0.6 mA; C, 1.0 mA). The plots show resetting patterns similar to the first example (Fig. 3); there is an abrupt drop in cophase (by up to 0.5 units) for CSN stimuli given near φ= 0.4. In addition, there is a second smaller gap in cophase (by 0.2 units) near φ= 0.9 for the strongest CSN stimulus (1 mA, Fig. 4C). Again there is no evidence of Type 0 resetting.
Figure 4. Graded resetting of respiratory rhythm by CSN stimulation.
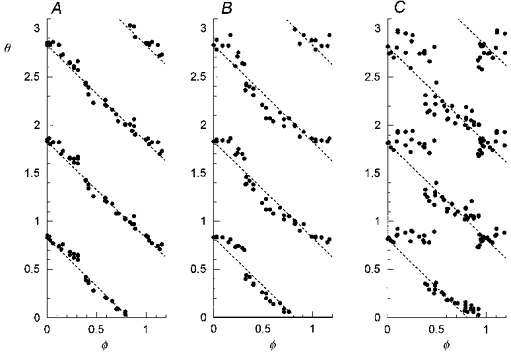
Resetting plots in another cat, for a CSN stimulus with three different strengths (A, 0.42 mA; B, 0.6 mA; C, 1.0 mA). The plots are similar to the example in Fig. 2; in addition there is a sharp drop in θ of 0.2 near φ= 0.9, corresponding to a shortening of the expiratory period when the stimulus was given in late expiration.
We found a second abrupt drop in cophase in four animals; in all instances this occurred within an old phase range of 0.8–1.0, was present only for stimuli of greatest strength, and was less prominent than the cophase gap near φ= 0.4. Figure 5 shows resetting plots for the strongest CSN stimuli in three other animals, showing either a single cophase gap (Fig. 5B and C) or two gaps (Fig. 5A). The level of end-tidal PCO2, the control phrenic amplitude or period, and the respiratory response to continuous maximum CSN stimulation were no different (P > 0.1, unpaired Student's t test) in the group of four animals with two cophase gaps, compared with the three animals with a single gap.
Figure 5. Variations of strong resetting of rhythm by CSN stimulation in three cats.
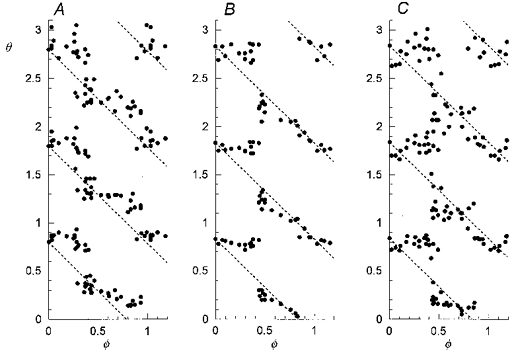
Examples of phase resetting by strong CSN stimulation in three other animals, showing apparent discontinuities in θ for stimuli given near the I-E transition (A-C) and for stimuli given near the E-I transition (A). Stimulus durations, 0.8 s (A and C) or 0.5 s (B).
Comment on animal studies
We began these studies with the premises that: (a) the respiratory oscillation is generated by a non-linear attractor-cycle oscillator and (b) brief CSN stimulation increases the neural activity, inspiratory or expiratory, that exists at the time of stimulation, i.e. a transient increase of respiratory ‘drive’. We postulated that Type 0 resetting by CSN stimulation is impossible because the perturbation impacts centrifugally upon the oscillator (see Discussion). Indeed, Type 0 resetting was not achieved in any of the seven experiments, even when there were large shifts in rhythm induced by near-maximal CSN stimuli.
Computational studies of the BvP system
Effect on oscillation of increasing drive (d)
The BvP oscillator's response to increasing d is shown in Fig. 6A. Increasing d from 1 (run a) to 6 (run b) causes an increase in the amplitude of the rhythm (expressed as y(t), left tracing), and the size of the x-y attractor cycle (right tracing). The dashed horizontal line represents the y activity threshold (yt= 0.7). Transient increase in d for 1/4 of the cycle period causes a transient increase in the amplitude of y(t) activity if the perturbation is given when y(t) is above yt, illustrated in Fig. 6B (run a). The perturbed x-y trajectory travels away from the attractor cycle, loops around and rejoins the attractor cycle after the perturbation. The same perturbation, given when y(t) is below yt (defined as expiratory like), causes a similar displacement of the x-y trajectory but in the opposite direction, i.e. driving the state further below the yt threshold. The effect on the cycle period in both cases is to delay the onset of the subsequent cycle; an exception is found in Fig. 6B (run e) where a stimulus begun in late expiration causes early onset and subsequent increase in the amplitude of inspiration.
Phase resetting by transient perturbations
We computed the relationships among old phase (φ), cophase (θ), and perturbation strength (Δd) of the approximated BvP oscillator. Perturbation of state was imposed for 1/4 cycle. For z =−0.875, the attractor cycle is symmetrical and its singular point is centrally located. The resetting curves (Fig. 7A-C) are of topological Type 1, i.e. cophase decreases by one cycle as old phase increases by one cycle. Increasing the strength of perturbation (for control d = 1; Δd values: A, 0.3; B, 1.5; C, 5) causes increasing deviation of the resetting curves away from the diagonal dotted line, the ‘no resetting’ line which corresponds to no effect on phase. For old phases of 0.3 and 0.8 the slope of the resetting curve becomes progressively steeper as the strength of perturbation increases. The resetting curve for the strongest perturbation (Fig. 7C), when computed with increments in the old phase of 0.01 (continuous curve), has two gaps that can be filled in by computing the cophase for old phase increments of 0.001 (open circles). The abrupt fall in cophase over tiny increments of old phase corresponds to highly divergent trajectories away from the attractor cycle. Figure 8 illustrates this effect, showing perturbations in y(t) rhythm (left) and x-y trajectories induced by perturbations (Δd = 5) given at old phases corresponding to the edges of the gap. The examples show the abrupt shift in effect of the perturbation at these sites from prolongation of the cycle (A and C), to shortening of the cycle (B and D).
Figure 7. Phase resetting of the BvP oscillator by transient centrifugal perturbations.
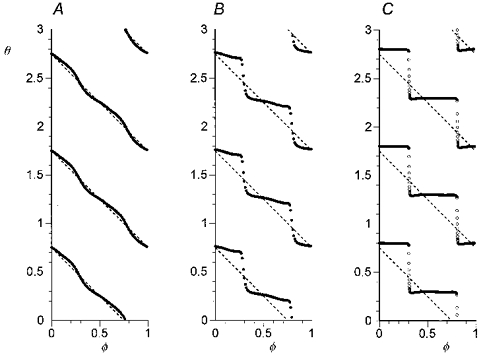
Increasing the perturbation strength (Δd values: A, 0.3; B, 1.5; C, 5) causes increasing deviations of cophase above and below the dotted line which depicts plot for stimulus having no effect on phase. Resetting curve C (Δd = 5), when computed with Δφ= 0.01 (continuous curve), has two apparent discontinuities (near φ= 0.3 and φ= 0.8) which can be filled in by computing at higher resolution (Δφ= 0.001, open circles). Duration of perturbation is 1/4 cycle. z =−0.875. yt= 0.7.
Figure 8. BvP state and rhythm responses to critically timed perturbations.
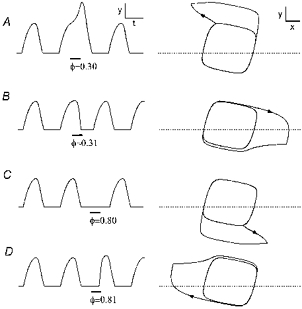
There are divergent trajectories for perturbations (Δd = 5 for 1/4 cycle) given at old phases near the apparent discontinuities of the resetting curve (e.g. see Fig. 7C). The rescheduled cycle after perturbation is delayed (A and C) or foreshortened (B and C) with only slight changes in φ near 0.3 or 0.8. z =−0.875. yt= 0.7. Scale bars (arbitrary units): x = 1, y = 0.5, t = 5.
Changing the z-value of the BvP model alters the position of the singular point relative to the attractor cycle. We found that such changes strongly influence the steepness of the resetting curves above and below the ‘no resetting’ line. For example, if the singular point is positioned near the top and within the attractor cycle by setting z =−1.3, the resetting curve is extremely steep at φ= 0.35, and the remaining resetting curve is smooth, i.e. there is only one apparent discontinuity similar to some of the animal experiments (see Fig. 5).
Comment on computational studies
These numerical experiments show that a centrifugal perturbation of the BvP attractor-cycle oscillation cannot induce Type 0 resetting, even with extremely strong pertubations. The resetting patterns are Type 1, and at low resolution there are gaps in cophase similar to those shown in the animal experiments, although at high resolution these gaps fill in. The position of the gaps in the cycle (i.e. old phase) and the size of the gap (i.e. jump in cophase) is influenced by the geometry of the oscillator's phase space, notably the position of the singular point with respect to the attractor cycle.
DISCUSSION
Endogenous respiratory rhythm viewed as an attractor cycle
The endogenous rhythm of the brainstem respiratory oscillator is usually fairly regular (with a preferred amplitude and period) and the effects of brief stimuli are transient. In order to obtain an understanding of accessible respiratory states, the oscillator can be probed with perturbations over a wide range of stimulus strengths and given at small time increments within the cycle. Recent experiments on perturbation of respiratory rhythm by stimuli that inhibit or facilitate inspiratory activity have led to the following observations. (1) Perturbations having particular combinations of strength and timing relative to the cycle induce a highly variable latency in the resumption of the rhythm after stimulation (Paydarfar et al. 1986; Paydarfar & Eldridge, 1987; Kitano & Komatsu, 1988; Lewis et al. 1989; Oku & Dick, 1992). This post-stimulus delay can exceed the pre-stimulus respiratory period (Paydarfar & Eldridge, 1987). (2) The relationships among cophase, old phase, and stimulus strength can be characterized by a helicoidal surface (Paydarfar et al. 1986; Paydarfar & Eldridge, 1987), the highly variable responses falling along the axis of the helicoid. (3) Increasing respiratory drive reduces the ability of a stimulus to reset the phase of respiratory rhythm (Eldridge et al. 1989). These observations are core features of oscillators governed by attractor-cycle dynamics (Winfree, 1980). An attractor cycle, also known as an attracting limit cycle, can be depicted as a closed loop in state space of two or more dimensions. The near-steady state oscillation is viewed as a trajectory that closely follows this smooth, closed loop and a discrete perturbation of the rhythm corresponds to a transient displacement off the loop. The region in state space consisting of paths that lead back to the attractor cycle is the basin of attraction to the cycle. States that are not within this basin constitute the oscillator's phaseless set. The helicoid resetting surface, with an axis representing irregular phase resetting and bounded by topological Type 0 and Type 1 resetting curves (see above), is characteristic of oscillators whose phaseless set is bounded by an attractor cycle (Winfree, 1980).
Experimental study
The present study looked at the impact of CSN stimulation on the timing of respiratory rhythm. The stimulations prolonged the duration of the stimulated cycle and usually delayed the onset of cycles subsequent to stimulation, although stimulation near the I-E and E-I transitions caused highly variable responses, including prolongation of the cycle period, shortening, or no effect. The stimulation caused true resetting of the phase of the respiratory oscillator, the amount being a function of stimulus time in the cycle and stimulus strength. However, despite inflicting large shifts in rhythm it was not possible to achieve Type 0 resetting even with the strongest CSN stimuli.
The BvP oscillator model
We also modelled the effect of a CSN-like stimulation in the Bonhoeffer-van der Pol oscillator (Fitzhugh, 1961) which is a two-dimensional attractor-cycle oscillator whose phaseless set is a singular point. The BvP can be perturbed with unidirectional stimuli, similar to those used in the midbrain studies (Paydarfar & Eldridge, 1987) and with strong stimuli yields the same Type 0 resetting (Eldridge, 1991) found with those experimental stimuli. The model can also be perturbed by an increase of respiratory ‘drive’ (Eldridge et al. 1989), by increasing the factor d in our equation, which results in an increase of amplitude of the attractor cycle regardless of the time in the cycle at which it is exhibited (Fig. 6). Thus, the CSN-like stimulus displaces the oscillator's state away from its attractor cycle and the singular point, which is within the attractor cycle. The phase resetting curves in the model were of topological Type 1, i.e. cophase decreased by one as stimulus old phase increased by one full cycle (Winfree, 1980) and it was not possible to obtain Type 0 resetting. The findings were thus similar to those of the experimental preparation.
Apparent discontinuities of phase resetting in the BvP model reflect steep zones of the cophase vs. old phase curves which are continuous when the resolution of computation is increased. Over these small intervals of old phase, perturbations induce highly divergent trajectories. Such an effect is not a universal property of attractor-cycle systems. For example, trajectories of radial isochron clocks (Winfree, 1980; Hoppensteadt & Keener, 1982; Glass & Winfree, 1984) converge back to the attractor cycle in a highly symmetrical fashion, and the resetting curve for a radial perturbation would coincide with the ‘no resetting’ line, even for perturbations inflicting arbitrarily large radial displacements.
Distinction between centrifugal and unidirectional perturbations
Thus, the findings in both the animal experiments and the model show that CSN input acts on the respiratory oscillator differently than other inputs that readily induce Type 0 resetting, for example, following strong electrical stimulations of the superior laryngeal nerve (Paydarfar et al. 1986; Lewis et al. 1989; Oku & Dick, 1992) or midbrain reticular formation (Paydarfar & Eldridge, 1987; Eldridge et al. 1989). We proposed that the distinguishing feature of CSN stimulation is that it increases the central neural respiratory activity that exists at the time of stimulation, whereas the previously studied Type 0-inducing stimuli cause the same directional effect on neural respiratory activity regardless of the stimulus time in the cycle. In geometrical terms, the action of the CSN stimulus can be viewed as a centrifugal perturbation.
Although all three methods of stimulation are capable of inflicting large shifts in respiratory rhythm, only CSN stimulation failed to cause Type 0 resetting. This difference can be understood as a more general property of attractor-cycle oscillators, not limited to the BvP, as illustrated in Fig. 9. Consider a phase resetting experiment on an attractor-cycle oscillator with loop trajectory C, and an internal phaseless set (black dot). A discrete perturbation displaces the trajectory to a new state. If such perturbations are given at all phases of C, the set of new states constitute the shifted cycle C′. In Fig. 9A we illustrate the fact that Type 0 resetting cannot be achieved with centrifugal perturbations of an attractor with an internal phaseless set; no matter how strong, the shifted cycle (C′) always encloses the phaseless set and cophase must decrease one cycle as the old phase advances through one full cycle, i.e. Type 1 resetting (see Winfree, 1980 and Glass & Winfree, 1984 for the topological basis for this claim). In contrast, Fig. 9B illustrates the fact that a large perturbation which displaces the trajectory towards a specific sector of state space can result in a shifted cycle that does not encompass the phaseless set. Consequently, cophase has no net change as old phase varies through the full cycle, i.e. Type 0 resetting. Midbrain reticular stimulation, by acting as an inspiratory, facilitatory stimulus irrespective of the stimulus phase (Paydarfar & Eldridge, 1987), causes phase resetting behaviour that is consistent with this view (Fig. 9B). Superior laryngeal nerve stimulation also achieves Type 0 resetting and apparently acts as the obverse of reticular stimulation, inhibiting inspiratory activity (Paydarfar et al. 1986) and depolarizing stage I expiratory neurones (Remmers et al. 1986; Richter, Ballantyne & Remmers, 1987). These observations support the idea that the shifted cycle induced by strong superior laryngeal nerve stimulation lacks the phaseless set, and is on the side of the attractor cycle that is opposite to the shifted cycle induced by reticular stimulation.
Figure 9. Two distinct forms of strong state perturbations of an attractor cycle.
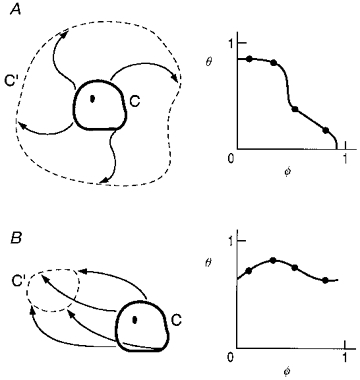
Perturbations (arrows), displace the attractor cycle (C), and the locus of states at the end of perturbation initiated at all φ is the shifted cycle (C′). A, centrifugally shifted cycle C′ encircles the phaseless set (dot) and the resetting curve must be Type 1 (right). B, perturbation towards a sector of state space results in a shifted cycle C′ (left) that does not encircle the phaseless set (dot). Resetting curve must be Type 0 resetting (right).
Other considerations
Other dynamic schemes could explain some of the resetting plots taken in isolation (see discussion of Paydarfar & Buerkel, 1995). It has been argued that because some resetting plots appear discontinuous, the respiratory oscillator might be governed by discontinuous dynamics like that exhibited by integrate-and-fire and other discrete models that show instantaneous jumps in activity during the steady-state oscillation (Lewis et al. 1989). While this hypothesis has not been disproven, we should point out that experiments with midbrain reticular stimulation (Paydarfar & Eldridge, 1987) showed a series of resetting plots with the appearance of continuity and these plots were of much higher resolution than those which have apparent discontinuities. Furthermore, a transient apneusis was triggered by midbrain stimuli with specific combinations of strength and time in the cycle, and these combinations are those corresponding to a ‘break point’ between Type 1 and Type 0 resetting. To our knowledge, such stimulus-evoked dysrhythmias have not been demonstrated in integrate-and-fire or discrete models.
Another approach to modelling the respiratory oscillator might be the creation of ‘realistic’ model equations that replicate the activities of various pools of neurones. This was not our concern in the present investigation. Rather, we have analysed a simple generic model of oscillation, the BvP equations, in order to infer the directional impact on the respiratory oscillation induced by CSN stimulations. Therefore, inferences from the model regarding in vivo respiration are qualitative and based on the phase of the cycle, a threshold of activity, and direction of perturbation with respect to the state of activity. The concept of centrifugal perturbation of the oscillator's state should be reflected in the activities of rhythm generated neurones. Although these neurones have not been fully characterized, transient increase in peripheral chemoreceptor activity has been shown to increase the activities of some medullary respiratory neurones that are active at the time of stimulation (Lipski, Trzebski, Chodobska & Kruk, 1984) and to depolarize the membrane potential of some of both inspiratory and expiratory neurones (Lawson, Richter, Ballantyne, Lalley, Bischoff & Kuhner, 1989).
We would point out that alterations in the attractor-cycle and singular point geometry strongly influence the deviation of the resetting curve above and below the ‘no resetting’ line. For example, placement of the singular point near the attractor cycle results in strong focal deviations in the resetting curve for stimuli given near the phase at which the attractor cycle is closest to the singular point. In the animal experiments, the greatest deviation from the ‘no resetting’ line was for stimuli given near the I-E transition. This observation raises the possibility that the respiratory oscillator's phaseless set may be situated off-centre, on the inspiratory side of the activity threshold. However, the structure of the phaseless set, and its location relative to the attractor cycle may be strongly influenced by a variety of factors, such as the type and strength of anaesthesia, presence of respiratory afferent feedback, and degree of central chemoreceptor stimulation. The tendency for infants to develop sporadic expiratory apnoea raises the possibility that the underdeveloped respiratory oscillator's phaseless set is situated on the expiratory side of the activity threshold (Paydarfar & Buerkel, 1997).
Technical questions include the possibility that electrical stimulation of the CSN may have activated baroreceptive fibres along with those from the chemoreceptors. At the voltages used, we found the pressor responses to be small or absent, perhaps due in part to our use of chloralose anaesthesia which blunts baroresponses (Neil, Redwood & Schweitzer, 1949), but this does not rule out an effect of barofibre stimulation on respiratory rhythm. Two observations argue against an important, if any, influence of barofibre stimulation on respiratory timing. First, the phrenic responses to CSN stimulation described in the present study, although more discrete (allowing for reliable measurements of phase response) are otherwise the same as those induced by chemical stimulation of the chemoreceptors by injection of solutions saturated with 100% CO2 or bicarbonate into the carotid sinus (Black & Torrance, 1971; Eldridge, 1972a, b). Reliable phase resetting experiments would not be possible with chemical stimulation of the carotid body because timing of perturbation is not well defined, and the stimulus strength is not reliably constant (Eldridge, 1972b). Second, inspiratory inhibitory effects that typify baroreceptor stimulation were not observed (Biscoe & Sampson, 1970; Saupe, Smith, Henderson & Dempsey, 1995).
Short-term potentiation of rhythm was not observed in our resetting experiments. This is not surprising because the durations of CSN stimulation (0.6–0.8 s) used in the present study were much shorter than the 9 s time constant for development of short term potentiation of respiratory rhythm (Wagner & Eldridge, 1991). However, recurrent CSN stimuli may lead to substantial activation of short-term potentiation (Wagner & Eldridge, 1991) and affect the oscillator's phase response (Lewis et al. 1992).
Conclusion and prospects
We have shown that perturbations of respiratory drive induced by carotid sinus nerve stimulation can be geometrically represented as a centrifugal perturbation of the central neural respiratory state, i.e. it is the equivalent of a transient outward deflection of the trajectory away from its attractor cycle and phaseless set, followed by a return toward the same attractor. Because of this feature, Type 0 resetting, which is found with unidirectional stimuli such as midbrain reticular or superior laryngeal nerve stimulation, is not possible with carotid sinus nerve stimulation. We propose that because centrifugal perturbations always drive the oscillator away from its phaseless set, dysrhythmias in that state can be terminated by CSN stimulation (Paydarfar & Buerkel, 1995).
Neural models of the respiratory oscillator can be evaluated by comparing their phase resetting properties with the experimental resetting plots (e.g. see Ogilvie et al. 1992; Gottschalk et al. 1994; Sammon, 1994; Oku & Dick, 1995). In this regard, the BvP model is useful only for highlighting qualitative features of resetting that relate to the dynamics of the respiratory oscillator. On the other hand, models that are based on postulated neural mechanisms can be excluded if their phase resetting behaviour is topologically different from the experimental resetting plots. For example, Sammon (1994) recently proposed a neural model of respiratory states, in which eupnoea is geometrically represented as an attractor cycle that circumnavigates a region lacking a phaseless set; there are two singular points outside this region. We propose that an oscillator with this geometry of state has phase resetting properties which are topologically different from those exhibited by an oscillator in which the phaseless set is within the boundary of the attractor cycle. Therefore, further analysis of Sammon's (1994) model with respect to phase resetting may provide a critical test of its validity.
Acknowledgments
We thank Lynn Houser for technical support, Drs Zibin Chen and Paul Wagner for assistance in performing some of the experiments, Dr Robert Banzett for helpful criticism and discussion and Mr Daniel Buerkel for assistance in preparing the figures. This work was supported in part by funding from the National Institutes of Health (grants HL 49848 and HL 17689).
References
- Baconnier PF, Benchetrit G, Pachot P, Demongeot J. Entrainment of the respiratory rhythm: a new approach. Journal of Theoretical Biology. 1993;164:149–162. doi: 10.1006/jtbi.1993.1145. [DOI] [PubMed] [Google Scholar]
- Biscoe TJ, Sampson SR. An analysis of the inhibition of phrenic motoneurones which occurs on stimulation of some cranial nerve afferents. Journal of Physiology. 1970;209:375–393. doi: 10.1113/jphysiol.1970.sp009170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Black AMS, Goodman NW, Nail BS, Rao PS, Torrance RW. The significance of the timing of chemoreceptor impulses for their effect upon respiration. Acta Neurobiologiae Experimentalis. 1973;33:139–147. [PubMed] [Google Scholar]
- Black AMS, Torrance RW. Respiratory oscillations in chemoreceptor discharge in the control of breathing. Respiration Physiology. 1971;13:221–237. doi: 10.1016/0034-5687(71)90092-2. [DOI] [PubMed] [Google Scholar]
- Eldridge FL. The importance of timing on the respiratory effects of intermittent carotid sinus nerve stimulation. Journal of Physiology. 1972a;222:297–318. doi: 10.1113/jphysiol.1972.sp009798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldridge FL. The importance of timing on the respiratory effects of intermittent carotid body chemoreceptor stimulation. Journal of Physiology. 1972b;222:319–333. doi: 10.1113/jphysiol.1972.sp009799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldridge FL. Expiratory effects of brief carotid sinus nerve and carotid body stimulations. Respiration Physiology. 1976;26:395–410. doi: 10.1016/0034-5687(76)90009-8. 10.1016/0034-5687(76)90009-8. [DOI] [PubMed] [Google Scholar]
- Eldridge FL. Phase resetting of respiratory rhythm - experiments in animals and models. In: Haken H, Koepchen HP, editors. Springer Series in Synergetics, Rhythms in Physiological Systems. Vol. 55. Berlin: Springer-Verlag; 1991. pp. 165–175. [Google Scholar]
- Eldridge FL, Gill-Kumar P, Millhorn DE. Input-output relationships of central neural circuits involved in respiration in cats. Journal of Physiology. 1981;311:81–95. doi: 10.1113/jphysiol.1981.sp013574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldridge FL, Paydarfar D, Wagner PG, Dowell RT. Phase resetting of respiratory rhythm: effect of changing respiratory ‘drive’. American Journal of Physiology. 1989;257:R271–277. doi: 10.1152/ajpregu.1989.257.2.R271. [DOI] [PubMed] [Google Scholar]
- Fitzhugh R. Impulses and physiological states in theoretical models of nerve membrane. Biophysical Journal. 1961;1:445–465. doi: 10.1016/s0006-3495(61)86902-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glass L, Winfree AT. Discontinuities in phase-resetting experiments. American Journal of Physiology. 1984;246:R251–258. doi: 10.1152/ajpregu.1984.246.2.R251. [DOI] [PubMed] [Google Scholar]
- Gottschalk A, Ogilvie MD, Richter DW, Pack AI. Computational aspects of the respiratory pattern generator. Neural Computation. 1994;6:56–68. [Google Scholar]
- Hoppensteadt FC, Keener JP. Phase locking of biological clocks. Journal of Mathematical Biology. 1982;15:339–349. doi: 10.1007/BF00275692. [DOI] [PubMed] [Google Scholar]
- Howard P, Bromberger-Barnea B, Fitzgerald RS, Bane HN. Ventilatory responses to peripheral nerve stimulation at different times in the respiratory cycle. Respiration Physiology. 1969;7:389–398. doi: 10.1016/0034-5687(69)90022-x. 10.1016/0034-5687(69)90022-X. [DOI] [PubMed] [Google Scholar]
- Kitano S, Komatsu A. Central respiratory oscillator: phase-response analysis. Brain Research. 1988;439:19–30. doi: 10.1016/0006-8993(88)91457-6. 10.1016/0006-8993(88)91457-6. [DOI] [PubMed] [Google Scholar]
- Lawson EE, Richter DW, Ballantyne D, Lalley PM, Bischoff A, Kuhner A. Peripheral chemoreceptor inputs to medullary inspiratory and postinspiratory neurons of cats. Pflügers Archiv. 1989;414:523–533. doi: 10.1007/BF00580987. [DOI] [PubMed] [Google Scholar]
- Lewis JE, Bachoo M, Polosa C, Glass L. The effects of superior laryngeal nerve stimulation on the respiratory rhythm: phase-resetting and aftereffects. Brain Research. 1989;517:44–50. doi: 10.1016/0006-8993(90)91005-2. [DOI] [PubMed] [Google Scholar]
- Lewis JE, Glass L, Bachoo M, Polosa C. Phase resetting and fixed-delay stimulation of a simple model of respiratory rhythm generation. Journal of Theoretical Biology. 1992;159:491–506. doi: 10.1016/s0022-5193(05)80693-9. [DOI] [PubMed] [Google Scholar]
- Lipski J, Trzebski A, Chodobska J, Kruk P. Effects of carotid chemoreceptor excitation on medullary expiratory neurons in cats. Respiration Physiology. 1984;57:279–291. doi: 10.1016/0034-5687(84)90077-x. [DOI] [PubMed] [Google Scholar]
- Neil E, Redwood CRM, Schweitzer A. Pressor responses to electrical stimulation of the carotid sinus nerve in cats. Journal of Physiology. 1949;109:259–271. doi: 10.1113/jphysiol.1949.sp004390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogilvie MD, Gottschalk A, Anders K, Richter DW, Pack AI. A network model of respiratory rhythmogenesis. American Journal of Physiology. 1992;263:R962–975. doi: 10.1152/ajpregu.1992.263.4.R962. [DOI] [PubMed] [Google Scholar]
- Oku Y, Dick TE. Phase resetting of the respiratory cycle before and after unilateral pontine lesion in cat. Journal of Applied Physiology. 1992;72:721–730. doi: 10.1152/jappl.1992.72.2.721. [DOI] [PubMed] [Google Scholar]
- Oku Y, Dick TE. Paradoxical phase response at late expiration by superior laryngeal nerve stimulation. NeuroReport. 1995;6:379–383. doi: 10.1097/00001756-199501000-00037. [DOI] [PubMed] [Google Scholar]
- Paydarfar D, Buerkel DM. Dysrhythmias of the respiratory oscillator. Chaos. 1995;5:18–29. doi: 10.1063/1.166067. [DOI] [PubMed] [Google Scholar]
- Paydarfar D, Buerkel DM. Sporadic apnea: paradoxical transformation to eupnea by perturbations that inhibit inspiration. Medical Hypotheses. 1997;49:19–26. doi: 10.1016/s0306-9877(97)90246-2. [DOI] [PubMed] [Google Scholar]
- Paydarfar D, Eldridge FL. Phase resetting and dysrhythmic responses of the respiratory oscillator. American Journal of Physiology. 1987;252:R55–62. doi: 10.1152/ajpregu.1987.252.1.R55. [DOI] [PubMed] [Google Scholar]
- Paydarfar D, Eldridge FL, Kiley JP. Resetting of mammalian respiratory rhythm: existence of a phase singularity. American Journal of Physiology. 1986;250:R721–727. doi: 10.1152/ajpregu.1986.250.4.R721. [DOI] [PubMed] [Google Scholar]
- Paydarfar D, Gilbert RJ, Poppel CS, Nassab PF. Respiratory phase resetting and airflow changes induced by swallowing in humans. Journal of Physiology. 1995;483:273–288. doi: 10.1113/jphysiol.1995.sp020584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remmers JE, Richter DW, Ballantyne D, Bainton CR, Klein JP. Reflex prolongation of stage I expiration. Pflügers Archiv. 1986;407:190–198. doi: 10.1007/BF00580675. [DOI] [PubMed] [Google Scholar]
- Richter DW, Ballantyne D, Remmers JE. The differential organization of medullary post-inspiratory activities. Pflügers Archiv. 1987;410:420–427. doi: 10.1007/BF00586520. [DOI] [PubMed] [Google Scholar]
- Sammon M. Geometry of respiratory phase switching. Journal of Applied Physiology. 1994;77:2468–2480. doi: 10.1152/jappl.1994.77.5.2468. [DOI] [PubMed] [Google Scholar]
- Saupe KW, Smith CA, Henderson KS, Dempsey JA. Respiratory and cardiovascular responses to increased and decreased carotid sinus pressure in sleeping dogs. Journal of Applied Physiology. 1995;78:1688–1698. doi: 10.1152/jappl.1995.78.5.1688. [DOI] [PubMed] [Google Scholar]
- Smith DM, Mercer RR, Eldridge FL. Servo control of end-tidal CO2 in paralyzed animals. Journal of Applied Physiology. 1978;45:133–136. doi: 10.1152/jappl.1978.45.1.133. [DOI] [PubMed] [Google Scholar]
- Wagner PG, Eldridge FL. Development of short-term potentiation of respiration. Respiration Physiology. 1991;83:129–140. doi: 10.1016/0034-5687(91)90098-4. [DOI] [PubMed] [Google Scholar]
- Winfree AT. The Geometry of Biological Time. New York: Springer-Verlag; 1980. [Google Scholar]


