Abstract
The tension and sarcomere length responses induced by ramp stretches (at amplitudes of 1–3 % fibre length (Lo) and speeds of 0.01–12 Lo s−1) were examined at different temperatures (range, 10–35 °C) in resting intact muscle fibre bundles isolated from the soleus (a slow-twitch muscle) and extensor digitorum longus (a fast-twitch muscle) of the rat. Some observations are also presented on the effects of chemical skinning on passive viscoelasticity at 10 °C.
As previously reported, the tension response to a ramp stretch, in different preparations and under various conditions, could be resolved into a viscous (P1), a viscoelastic (P2) and an elastic (P3) component and showed characteristic differences between slow and fast muscle fibres.
Chemical skinning of the muscle fibres led to a decrease in the amplitude of all three tension components. However, the fast-slow fibre differences remained after skinning. For example, the viscosity coefficient derived from P1 tension data decreased from 0.84 ± 0.06 before skinning to 0.44 ± 0.06 kN s m−2 after skinning in fast fibres; the corresponding values in slow fibres were 2.1 ± 0.08 and 0.87 ± 0.09 kN s m−2, respectively.
Increasing the experimental temperature from 10 to 35 °C led to a decrease in all the tension components in both fast and slow muscle fibre bundles. The decrease of P1 (viscous) tension was such that the viscosity coefficient calculated using P1 data was reduced from 0.84 ± 0.1 to 0.43 ± 0.05 kN s m−2 in fast fibres and from 2.0 ± 0.1 to 1.0 ± 0.1 kN s m−2 in slow fibres (Q10 of ∼1.3 in both).
In both fast and slow muscle fibre preparations, the plateau tension of the viscoelastic component (P2) decreased by 60–80 % as the temperature was increased from 10 to 35 °C giving P2 tension a Q10 of ∼1.4 in slow fibres and ∼1.7 in the fast fibres. Additionally, the relaxation time of the viscoelasticity decreased from 11.9 ± 1 ms (fast) and 43.1 ± 1 ms (slow) at 10 °C to 3 ± 0.5 ms (fast) at 25 °C and 8.7 ± 0.6 ms (slow) at 35 °C (Q10 of ∼2.0 in slow and ∼2.5 in fast fibres).
The fast-slow fibre differences in passive viscoelasticity remained at the high physiological temperatures. The physiological significance of such fibre-type differences and their possible underlying mechanisms are discussed.
In resting intact muscle fibres, the tension response to a ramp stretch consists of three components, a viscous (P1), a viscoelastic (P2) and an elastic (P3) component, identified on the basis of their sensitivity to stretch velocity (Bagni, Cecchi, Colomo & Garzella, 1995; Mutungi & Ranatunga 1996b). The structural bases underlying each of the components within a sarcomere are not fully understood but from these studies it is clear that none of the components arises from cycling cross-bridges. The viscous tension is thought to arise from viscous resistance to stretch between thick and thin filaments in each half sarcomere, whereas the viscoelasticity and elasticity may result from other structural elements such as the gap filament and the cytoskeleton. Our experiments on intact mammalian muscle fibre bundles showed that these passive tension components were characteristically different between fast and slow fibres; in general, the amplitude of all three tension components was larger and the relaxation time of the viscoelastic component 3–4 times longer in the slow than in the fast muscle fibres (Mutungi & Ranatunga 1996c). The above experiments were done at low temperature (∼10°C) and it would be important to know whether such differences exist at high (physiological) temperatures (∼35°C). Moreover, the temperature dependence of the passive tension components would also enhance our understanding of the viscoelasticity in resting muscle fibre. With that primary rationale in mind, we examined the characteristics of the tension response to ramp stretch in intact rat fibre bundles at different temperatures ranging from 10 to 35°C. Additionally, some experiments were performed at 10°C before and after chemical skinning in an attempt to establish the molecular basis of the fast-slow fibre difference in the viscous (P1) component. Our results show that the tension components decrease in amplitude with heating and after skinning, but the fast-slow fibre differences remain under both conditions.
Some preliminary data from this study were presented to The Physiological Society (Mutungi & Ranatunga, 1995).
METHODS
Adult male rats (body weight of ∼200 g) were killed with an overdose of sodium pentobarbitone (Sagatal, Rhone Meriux Ltd, Harrow, Essex, UK) injected intraperitoneally and the soleus (a slow-twitch muscle) and extensor digitorum longus (a fast-twitch muscle) were carefully removed. Small bundles containing up to ten muscle fibres were isolated under a dissecting microscope using dark-field illumination. Considerable care was taken in removing damaged fibres to ensure that those which extended from end to end in a bundle were intact and electrically excitable.
The recording system and the general methodology used in the experiments were basically the same as those described in previous studies (see Mutungi & Ranatunga, 1996a, b, c). The details of the tension transducer and of the servo motor are given in Ranatunga (1994) and Mutungi & Ranatunga (1996a), respectively. Briefly, a fibre bundle preparation was set up in a flow through a stainless-steel chamber (volume, ∼2 ml) that was perfused (0.5 ml min−1) with Ringer solution containing (mm): NaCl, 109; KCl, 5; MgCl2, 1; CaCl2, 4; NaHCO3, 24; NaH2PO4, 1; sodium pyruvate, 10 and 200 mg l−1 of bovine fetal serum; the solution was continuously bubbled with 95 % O2 and 5 % CO2. The temperature control (± 0.1°C) or change was done by means of a Peltier device fitted underneath the muscle chamber and it was monitored with a thermocouple placed inside the chamber. In addition, the sarcomere length change in a 2 mm region of the bundle near the tension transducer was monitored using He-Ne laser diffraction (see Mutungi & Ranatunga, 1996a, c). Unless it is mentioned otherwise, the initial sarcomere length of the preparations used in the experiments was between 2.6–2.8 μm. A fibre bundle was stimulated with single supramaximal stimuli at a rate of 1/90 s, and small stretches were interposed in between twitches during some cycles. The resting tension responses to ramp stretches of 100–300 μm in amplitude (∼1–3 % of initial fibre length, L0) and at different velocities were examined at 10°C before and after warming the preparations to 20, 25 and 35°C. All the experiments performed at high temperature and a few at 10°C were carried out in the presence of 10 mm 2,3-butanedione-2-monoxime (BDM) in the Ringer solution. In both fibre types, the addition of 10 mm BDM inhibited active contractions and abolished stretch activation seen at high temperatures (see Mutungi & Ranatunga, 1996a), but had no effect on the stretch-induced passive tension response.
Experiments were also done to examine the main effects of chemical skinning on the passive tension components in fast and slow fibres: the relaxing solutions used for these experiments were similar to those described by Fortune, Geeves & Ranatunga (1989) and Ranatunga (1994) and they contained 5–10 mm MgATP and 15–20 mm EGTA (pH 7–7.1; ionic strength, 180–200 mm). The experiments were done at 10°C and a full set of data at a range of stretch velocities was initially collected from a preparation before skinning. Then the Ringer solution was quickly replaced with skinning solution containing 0.5 % Brij (Brij 58, Aldrich; Fortune et al. 1989) while the preparation was still connected to the recording assembly. A preparation remained exposed to skinning solution for 1 h before a second set of passive tension responses was recorded in standard relaxing solution, for comparison with the responses from the intact preparation. In some experiments, the preparations were left in skinning solution overnight and the same protocol carried out the following day. The results obtained from these preparations were similar to and were pooled with the results from the preparations skinned for 1 h.
The length signal (from the motor), the sarcomere length signal (from the diffractometer) and the tension transducer signal were collected via a CED 1401 laboratory interface using Signal Averager software (Cambridge Electronic Design Ltd., Cambridge, UK) and stored in a Tandon computer (Target 386 SX40); up to ten responses were averaged at low stretch velocities (< 1 Lo s−1) in order to increase the signal-to-noise ratio: single traces were used at speeds higher than 4–5 Lo s−1. The description and analysis of the tension response is shown in Fig. 1 and is essentially as described previously by Mutungi & Ranatunga (1996b, c). Initial analyses of the tension response for measuring the peak tension, the steady tension after relaxation (P3, measured 300–400 ms after the peak) and the tension at breakpoint (P1 tension) were made using the Signal Averager software (see Fig. 1A); P2 tension was estimated as peak tension - (P3+P1) (see Fig. 1D). Further analyses of the data, involving curve fitting to P2 data, subtraction of P3 curve using the sarcomere length record (see Mutungi & Ranatunga, 1996b) were done using Fig.P software (Biosoft, Cambridge, UK). The curve fitted to the P2 tension versus reciprocal stretch duration was the equation given by Bagni et al. (1995) and in our previous papers (see Mutungi & Ranatunga, 1996b, c): such curve fitting provided the relaxation time and the plateau tension of the viscoelastic (P2) component.
Figure 1. General features of the tension response to a ramp stretch and its analysis.
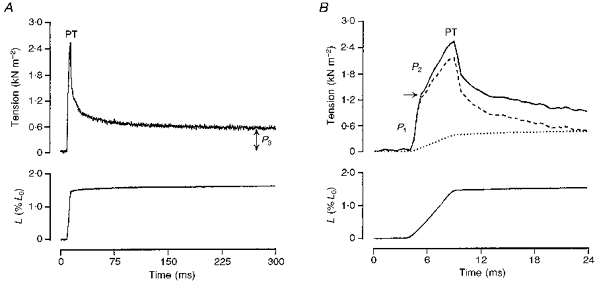
The tension response (upper trace) induced by a moderately fast ramp stretch (bottom trace; L, fibre length) are displayed at two time scales in A and B. In A, the tension rises rapidly during the stretch to reach a peak (PT) at the end of the ramp. Thereafter, it decays in a complex manner to reach a plateau (P3) tension at the stretched length when sarcomere length remains relatively constant. The rising phase of the tension response in B consists of an initial rapid tension rise to a break (arrow; P1) and a slower tension rise (P2). The dotted trace in B is sarcomere length record normalized to P3 tension and represents the net P3 tension response. Subtracting the P3 tension from the original tension response gives the difference trace (dashed line) which in this case consists of P1 and P2 tension components. All traces are from a fast-twitch muscle fibre bundle at 10 °C.
RESULTS
The effects of chemical skinning (at 10°C)
The basic aim in these experiments was to determine the major changes produced in the viscous and viscoelastic components when the muscle fibres in a preparation were skinned by detergent treatment. On exposure to the skinning solution, a preparation lost its excitability within seconds as evidenced by the loss of the active twitch responses regularly initiated by electrical stimuli. After skinning the preparation for 1 h, the steady resting tension at any given initial sarcomere length (range, 2.1–3.4 μm) was reduced by between 30–60 % in different preparations as compared with that in the intact preparation. When subjected to a ramp stretch at different stretch speeds, the passive tension response in the skinned preparation remained qualitatively similar to that of an intact preparation; there was, however, a clear reduction in the overall amplitude of the tension response. This can be seen from the experimental tension records from the fast-twitch muscle fibre bundle shown in Fig. 2A (upper traces), where the tension response after skinning is superimposed on that recorded before skinning (i.e. in the intact preparation). The responses were induced by the same standard ramp stretch, as can be seen from the resultant, superimposed, sarcomere length records (lower traces). In each response, the tension rises to reach a peak at the end of the ramp; thereafter it decays to a steady level (P3) at the stretched length when sarcomere length remains relatively constant. In both tension records, a close examination of the rising phase of the tension response shows that it contains an initial break (arrows). The tension at this break (breakpoint tension, P1), P3 tension and the peak tension (PT) were measured and used in calculating the P2 tension as peak tension - (P1+P3).
Figure 2. Effects of chemical skinning.
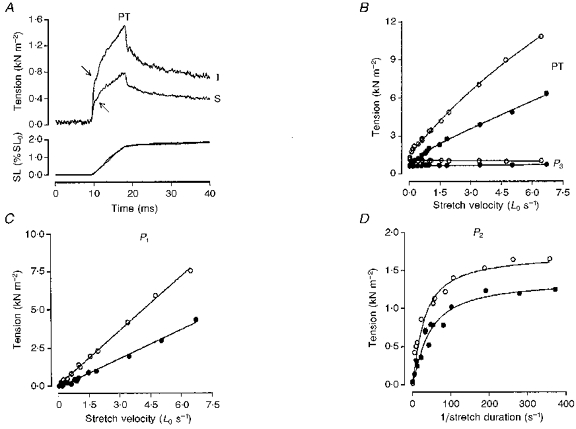
A shows the tension (top trace) and sarcomere length (SL; bottom trace) responses to a moderately fast ramp stretch in a fast-twitch muscle fibre bundle recorded before (intact, I) and after chemical skinning (S). During a stretch, the tension rises rapidly at first to a break (P1; arrows) and then slowly to reach a peak (PT) at the end of the ramp. Thereafter, it decays in a complex manner to a plateau (P3) at the stretched length when the sarcomere length remains relatively constant. In B and C the PT, P3 and P1 tensions from another fast-twitch muscle fibre bundle obtained before (^) and after (•) chemical skinning are plotted against stretch velocity. Note that in both intact and skinned preparations P3 tension is relatively insensitive to stretch speed (elastic) while P1 tension increases in direct proportion to stretch velocity (viscous). The slope calculated from the fitted regression line in C (P < 0.001) represents a viscosity coefficient of 1.19 kN s m−2 before skinning and 0.63 kN s m−2 after chemical skinning. In D, P2 tension (calculated as PT - (P1+P3)) is plotted against reciprocal stretch duration as suggested by Schoenberg (1988) for the analysis of viscoelasticity. The fitted curves represent the equation used by Bagni et al. (1995) for the analysis of viscoelasticity and they give a relaxation time for the viscoelasticity of 14.4 ms before and 12.9 ms after chemical skinning. Note that the amplitude of the tension response and all its components is decreased on chemical skinning.
The tension data collected from a fast-twitch muscle fibre bundle for a range of stretch velocities are shown in Fig. 2B, C and D, where open symbols are data collected before and filled symbols represent those collected after chemical skinning. In Fig. 2B, the peak (PT) and P3 tensions are plotted against ramp stretch velocity and shows that in both the intact and the skinned preparations P3 tension is relatively insensitive to stretch velocity (elastic) while PT increases with stretch speed. However, both tensions are depressed in the latter preparation. Figure 2C shows P1 tension plotted as a function of stretch velocity and one can see that the breakpoint (P1) tension values measured before skinning as well as after chemical skinning increase in direct proportion with stretch velocity (viscous), but the slope of the relation is decreased in the skinned preparation. The fitted lines represent the calculated linear regression to each set of data; the slope of which denotes the viscosity coefficient (in kN s m−2 per Lo). The data show that the viscosity coefficient is clearly lower in the skinned fibres (see figure legend). P2 tension data collected before and after chemical skinning are plotted against the reciprocal of stretch duration in Fig. 2D (since the stretch amplitude was constant, the reciprocal stretch duration is directly proportional to stretch velocity); in both cases, tension increases with velocity up to a plateau (viscoelastic; i.e. a viscous element in series with an elastic element), but its plateau tension level is depressed after chemical skinning. Analysis of the P2 tension data by curve fitting (see Mutungi & Ranatunga, 1996c) gave a somewhat shorter relaxation time for the viscoelasticity in the skinned preparation (see figure legend). Further skinning of the preparations had no significant effect on the tension response.
Similar results were obtained in experiments on slow-twitch muscle fibre bundles as can be seen from the data illustrated in Fig. 3. From the plots of the various tension components against either stretch velocity (Fig. 3A and B) or the reciprocal of stretch duration (Fig. 3C), it is clear that the amplitudes of the various component tensions are larger in the slow-twitch than in the fast-twitch muscle fibres. However, as in the fast-twitch muscle fibre preparations, the amplitudes of the various tension components are depressed on chemical skinning. Also included in the plots is the data obtained in the presence of 4 % dextran (average molecular weight, 500 000) in the relaxing solution (•). The addition of 4 % dextran to the bathing medium led to a small but significant increase in all the tension components, but it did not reverse the values to their control levels.
Figure 3. Velocity dependence of the various tension components in a slow-twitch muscle fibre bundle before (triangles) and after (circles) chemical skinning.
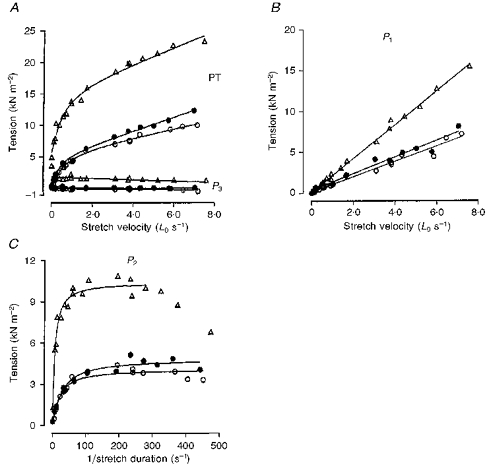
The data are presented in the same way as in Fig. 2B, C and D. In this preparation P1 tension analysis gives a viscosity coefficient of 2.05 kN s m−2 (per Lo) before skinning and 0.93 kN s m−2 (per Lo) after chemical skinning. The curve fitted to P2 tension has a relaxation time of 48 ms in the intact fibre and 29.6 ms after chemical skinning. •, data from the skinned preparation obtained in the presence of 4 % dextran in the relaxing solution. Note that chemical skinning reduces the tension amplitude at all velocities and that the addition of 4 % dextran improves the amplitudes only marginally.
The effects of chemical skinning on both fast- and slow-twitch muscle fibres are summarized in Table 1. The data show that after skinning, the viscosity coefficient is reduced by about ∼50–65 %, the plateau P2 tension is decreased by ∼65 % and the relaxation time of viscoelasticity (P2) is decreased by ∼25–50 % of their control values in the two fibre types. Our results are qualitatively similar to those reported by Bagni et al. (1995) from single frog fibres, which showed large reductions in the passive tension components following mechanical skinning. Skinning of frog muscle fibres is known to result in expansion of the filament lattice (Matsubura & Elliot, 1972; Goldman & Simmons, 1986) and, in skinned mouse muscle fibres, addition of ∼3 % dextran to the relaxing solution is thought to restore the filament lattice spacing to intact fibre dimensions (see Matsubara, Umazume & Yagi, 1985). In a few experiments, the effects of adding 4 % dextran on the tension response to a ramp stretch was examined after a preparation was skinned. As shown in Fig. 3 and Table 1, this resulted in a small but significant increase in the amplitudes of both the viscous (P1) and the viscoelastic (P2) tensions, but 4 % dextran did not restore their amplitudes to the intact fibre levels. In view of different dextran concentration levels used in other studies (Maughan & Godt, 1981; Gulati & Babu, 1985; Ford, Nakagawa, Desper & Seow, 1991), it would be interesting to extend these observations to higher concentrations of dextran. Nevertheless, our observations indicate that the changes obtained after skinning may be due to a leakage of intracellular constituents (such as globular proteins) leading to decreased viscosity. However, it is interesting to note that the fast-slow fibre differences in P1 and in P2 components remained in the skinned fibre preparations despite the overall reductions in their amplitudes.
Table 1.
A summary of the effects of chemical skinning on the characteristics of the various tension components in fast- and slow-twitch muscle fibre bundles
| η (kN s m−2 (Lo)−1) | P2 (kN m−2) | P2 (ms) | P3 (kN m−2) | |||||
|---|---|---|---|---|---|---|---|---|
| Before | After | Before | After | Before | After | Before | After | |
| Fast | 0.90 ± 0.06 | 0.44 ± 0.06 | 189 ± 14 | 72 ± 8 | 14 ± 0.6 | 12 ± 0.8 | 0.98 ± 0.2 | 0.65 ± 0.1 |
| 0.52 ± 0.05* | 79 ± 3* | 12.8 ± 1* | 0.7 ± 0.03* | |||||
| Slow | 2.1 ± 0.2 | 0.73 ± 0.09 | 736 ± 37 | 258 ± 16 | 46 ± 0.9 | 27.6 ± 2 | 2.8 ± 0.2 | 0.18 ± 0.08 |
| 1.13 ± 0.1* | 346 ± 48* | 24 ± 3* | 0.17 ± 0.03* | |||||
The data represent mean ±s.e.m. obtained from 8 fast- and 7 slow-twitch muscle fibre bundles before and after chemical skinning (initial sarcomere length, 2.7 μm; temperature, 10 °C).
Data obtained in the presence of 4 % dextran in the relaxing solution (n= 3 fast- and 3 slow-twitch muscle fibre bundles). η is the viscosity coefficient from P1 tension analyses; P2 (kN m−2) is the plateau tension of the viscoelastic component; P2 (ms) the relaxation time of the viscoelastic component; P3 (kN m−2) is the elastic tension measured 300 ms or more after the start of the stretch. Note that chemical skinning leads to a 50 % or more drop in the characteristics of all the tension components.
Chemical skinning also led to a fibre type-dependent decrease in P3 (elastic) tension. The decrease in P3 was greater in the slow-twitch fibres (∼95 %) than in fast-twitch fibres (∼40 %). At certain stretch speeds the tension response of slow-twitch muscle fibre preparations (at 10°C) exhibited a more complex behaviour, in that there was a delayed tension rise at the stretched length (see Fig. 4C and D). The delayed tension rise following stretch was similar to that previously reported in intact (fast- and slow-twitch) muscle fibre preparations at 35°C (see Mutungi & Ranatunga, 1996a). Indeed, like in the intact fibre experiments at 35°C, the addition of 10 mm BDM in the relaxing solution abolished this behaviour. However, 10 mm BDM had no effect on the characteristics of the other tension components. Skinned fast-twitch muscle fibres (at 10°C) never showed a delayed tension rise after stretch and the addition of 10 mm BDM had no effect on its tension response (see Fig. 4A and B).
Figure 4. Effects of chemical skinning and 10 mm 2,3-butanedione-2-monoxime (BDM) on the tension responses to a ramp stretch in a fast- and a slow-twitch muscle fibre bundle.
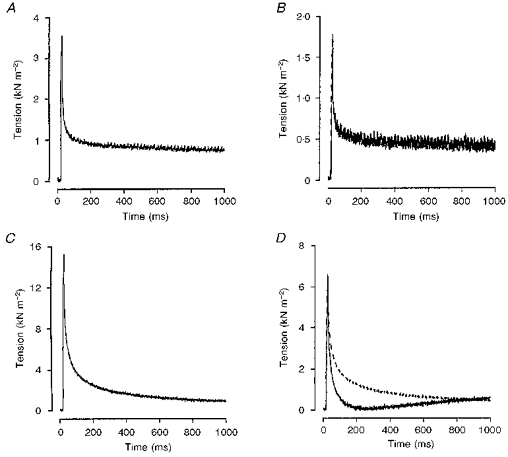
The tension response to a ramp stretch in a fast- (A and B) and slow-twitch (C and D) muscle fibre bundle before (A and C) and after 2 h of chemical skinning (B and D): temperature, 10 °C. The dotted traces in B and D are the tension responses recorded from the skinned fibre bundles in the presence of 10 mm BDM. Note the fibre type-dependent effects of chemical skinning on P3 tension. In the slow-twitch muscle fibre, there is a delayed tension rise after the initial tension relaxation. The addition of 10 mm BDM into the relaxing solution reversibly abolished this behaviour (dotted trace in D). No delayed tension rise was observed in the fast-twitch fibre records and the addition of 10 mm BDM had no effect on the tension response as evidenced by the complete superimposition of the two traces in B.
Tension responses at different temperatures
In a number of experiments, the passive tension response to a standard ramp stretch was examined during warming from 10 to 35°C and during subsequent cooling back to 10°C; the main finding was that the tension response decreased in amplitude at the higher temperature but remained qualitatively similar and the changes were reversible. This is illustrated in Fig. 5 which shows the tension response (upper) induced by a moderately fast ramp stretch (lower) recorded from a slow-twitch muscle fibre bundle at 10°C (A, before warming), 35°C (B) and at 10°C again (C, after cooling); the peak amplitude is reversibly reduced by ∼50 % in warming from 10 to 35°C.
Figure 5. Reversibility of the temperature effects.
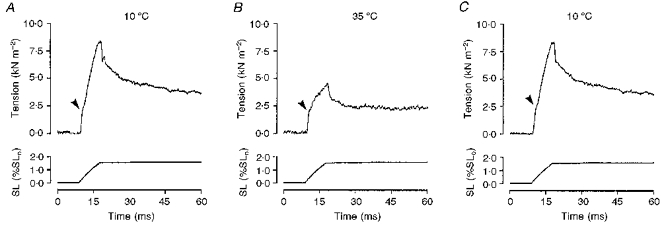
The tension response (upper trace) to a ramp stretch (bottom trace; SL, sarcomere length) in a slow-twitch muscle fibre bundle at 10 °C before (A) and after (C) warming to 35 °C (B). Note that warming the preparation reduces the size of the tension response and the effects are completely reversible. Arrowheads indicate the break, corresponding to P1 tension, seen on the rising phase of the tension response.
Figure 6 shows tension responses (T, upper traces) recorded from a fast-twitch muscle fibre bundle at three different temperatures (10, 25 and 35°C). Shown superimposed on each tension trace is the sarcomere length response (SL, dashed curve) with its amplitude normalized to the steady tension at the stretched length (P3); since P3 is elastic tension, the normalized sarcomere length record corresponds to P3 tension response to stretch (see Mutungi & Ranatunga, 1996b, c). The second trace (Dif, dotted curve) superimposed on the tension response, is the difference between the original tension record and the P3 curve and it contains P1 (initial break) and P2 components only. It can be seen that, when examined in this manner and using the same standard stretch, the tension that is most reduced by warming is that of the P2 component i.e. the tension rise above P1 (arrows) in the difference trace.
Figure 6. Effects of temperature.
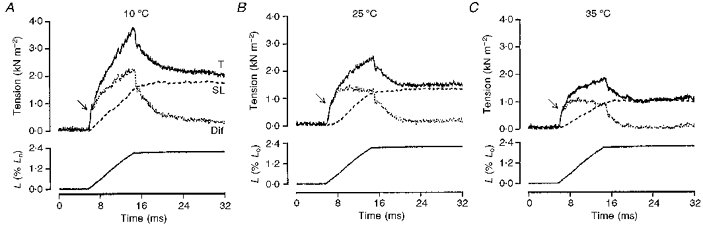
The tension response (continuous line; T) to a ramp stretch (bottom trace) in a fast-twitch muscle fibre bundle at 10 (A), 25 (B) and 35 °C (C). The dashed line (SL) is the sarcomere length trace with its amplitude normalized to the steady P3 tension measured 400 ms or more after the stretch; it represents the change of elastic tension (P3) during stretch (see Mutungi & Ranatunga, 1996b). The dotted trace (Dif) shows the difference trace obtained by subtracting the P3 tension (SL) from the original tension trace (T). Note that at all temperatures, the difference trace consists of P1 and net P2 components separated by a break (arrows); also, at this stretch velocity warming the preparation markedly reduces the P2 amplitude (compare A with B and C).
Figure 7 shows, from a slow-twitch fibre bundle, the data collected for a range of stretch velocities at two different temperatures. In Fig. 7A, PT and P3 tensions measured at 10°C before (^) and after (▴) warming to 35°C (•) are plotted against stretch velocity. At both temperatures PT increases with stretch velocity while P3 is relatively insensitive to stretch speed (elastic), but both tensions are reduced at the higher temperature. In Fig. 7B, the P1 tension measured during the same experiments is plotted against stretch velocity; the line through each set of points is the calculated linear regression. At all three temperatures, the breakpoint tension (P1) increases in direct proportion with stretch velocity, but the slope of the relation (viscosity coefficient) is clearly lower at the higher temperature (see legend). The P2 tension is shown in Fig. 7C and is plotted against the reciprocal of the stretch duration. P2 tension increases with velocity up to a plateau (viscoelastic) but its plateau amplitude is decreased at the higher temperature; the calculated relaxation time was also decreased at the higher temperature. Note that the changes seen on warming the preparation were reversible.
Figure 7. Velocity dependence of the various tension components at different temperatures.
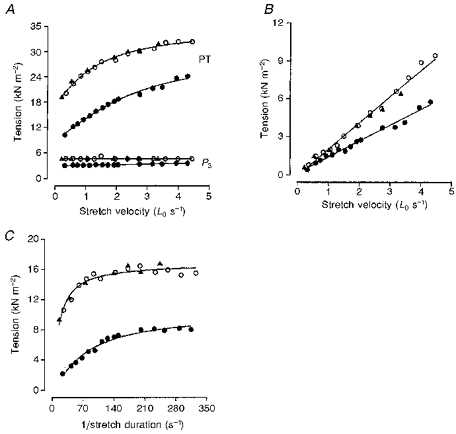
Data are from a slow-twitch muscle fibre preparation obtained at 10 °C before (^) and after (▴) warming the preparation to 35 °C (•). A shows PT and P3 tension obtained at both temperatures plotted against stretch velocity. In B, P1 tension obtained at both temperatures is plotted against stretch velocity. The slope of the fitted regression lines (P < 0.001) corresponds to a viscosity coefficient of 2.1 kN s m−2 at 10 °C and 1.25 kN s m−2 at 35 °C. In C, P2 tension (calculated as PT minus the sum of P1 and P3 tensions) at 10 and 35 °C is plotted against reciprocal stretch duration. The fitted curves (as in Fig. 2) give relaxation times of ∼41 ms at 10 °C and ∼8 ms at 35 °C.
Figure 8 shows plots of data from a fast-twitch muscle fibre bundle in which the tension response to the same standard ramp stretch was examined at a range of temperatures. Data obtained at two different initial sarcomere lengths (2.6 μm, velocity 6.7 Lo s−1, open symbols and 3.0 μm, 6 Lo s−1, filled symbols) are shown. The breakpoint tension (P1), peak tension and the P3 tension were measured from each record, while P2 tension was calculated as a difference (see Methods). As reported previously (see Mutungi & Ranatunga, 1996b, c), the amplitudes of the tension components are larger at the longer sarcomere length. The results show that increasing the temperature from 10 to 35°C led to decreases (20–50 %) in peak tension and P3 tension (Fig. 8A) and in P1 (breakpoint) tension (Fig. 8B) at both sarcomere lengths. On the other hand, increasing the temperature over the same range has a more marked effect on the P2 tension (Fig. 8C); indeed, the P2 tension amplitudes of fast-twitch fibres at 35°C were too small for curve fitting and confident analyses of the viscoelastic component. The more pronounced effect on the P2 amplitude at a given standard stretch velocity indicates that the relaxation time of viscoelasticity may be decreased with increased temperature (see below).
Figure 8. Effect of temperature on the amplitudes of the tension components induced by a standard ramp stretch.
PT and P3 tensions (A), P1 tension (B) and net P2 tension (C) from a fast-twitch muscle fibre bundle plotted against temperature. The preparation was held at an initial sarcomere length of either 2.6 μm (open symbols) or 3.0 μm (filled symbols): the same ramp stretch was used (the stretch velocity was stretched at 6.7 Lo s−1 for 2.6 μm and 6.0 Lo s−1 for 3.0 μm). Note that the amplitude of all the tension components drops as the temperature is increased and that net P2 tension shows the largest drop, being almost absent at 35 °C at both sarcomere lengths.
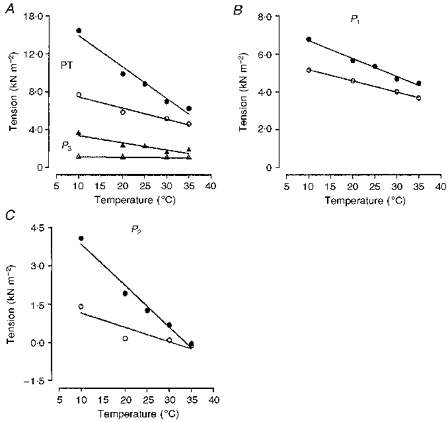
Experiments similar to the one depicted in Fig. 7 were carried out on ten fast-twitch and nine slow-twitch muscle fibre bundles to determine the temperature dependence of the various parameters, and the pooled data are illustrated in Fig. 9. Circles and triangles denote data from fast-twitch fibres and slow-twitch fibres, respectively, and open and filled symbols represent data at two different sarcomere lengths (∼2.7 μm and ∼3.0 μm, respectively). Figure 9A shows the temperature dependence of the viscosity coefficient (from P1 tension analyses), Fig. 9B shows the relaxation time of viscoelasticity and Fig. 9C shows the plateau tension of the viscoelastic component (from P2 analyses); the mean ±s.e.m. values are plotted on logarithmic ordinates against temperature on the abscissa. In both fibres and at both sarcomere lengths, warming from 10 to 35°C led to a ∼50 % reduction in the viscosity coefficient derived from P1 data. For example, the viscosity coefficient (at sarcomere length of ∼2.7 μm and as kN s m−2 of fast-twitch fibres decreased from 0.84 ± 0.1 (mean ±s.e.m.) at 10°C to 0.43 ± 0.1 at 35°C while that of slow-twitch muscle fibres dropped from 2.02 ± 0.1 at 10°C to 1.04 ± 0.1 at 35°C. These changes correspond to a temperature coefficient (Q10) of ∼1.3. The dashed line in Fig. 9A represents the linear regression fitted to the data given by Felix (1972) for the viscosity of water (multiplied by 105) at different temperatures (range, 10–35°C; the similarity in its slope to the other lines suggests that the viscosity of water also has a similar temperature dependence. The temperature dependence of the plateau viscoelastic (P2) tension (plotted as a Young's modulus in Fig. 9C) is higher for fast-twitch muscle fibres (∼1.7) than for slow-twitch fibres (∼1.4). The relaxation time of the viscoelastic component shows a much greater temperature sensitivity (Fig. 9B) than the viscosity coefficient or the plateau P2 tension. At a sarcomere length of 2.7 μm, the relaxation time of fast-twitch muscle fibres decreased from ∼12 ± 1 ms at 10°C to ∼3 ± 0.5 ms at 25°C giving a Q10 of ∼2.5; in slow-twitch muscle fibres the values were 43.1 ± 1 ms at 10°C and 8.7 ± 1 ms at 35°C, corresponding to a Q10 of ∼2.0. As stated above, no relaxation time could be calculated in fast muscle fibres at 35°C as the net P2 component was small.
Figure 9. Temperature dependence of the various tension components.
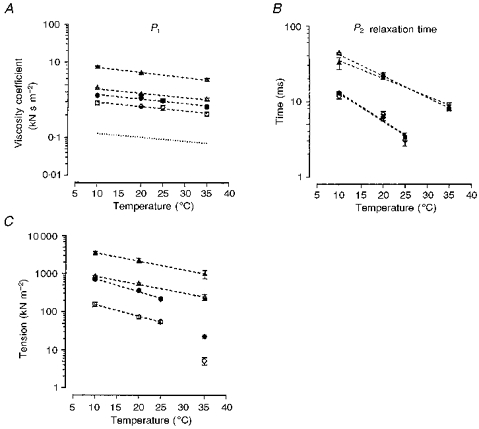
The viscosity coefficient obtained from analyses of P1 tension (A), the relaxation time of P2 tension analyses (B) and plateau P2 tension (C) (expressed as a Young's modulus) are plotted against temperature (note that the vertical axes are logarithmic); the lines are fitted regressions to the pooled data but the symbols denote the mean and the vertical bars the s.e.m. Circles are data from fast-twitch fibres; triangles, data from slow-twitch fibres; open symbols at sarcomere length of 2.7 μm; and filled symbols at 3.0 μm. The dotted line in A represents the change in the viscosity of pure water at atmospheric pressure multiplied by 105 (data are from Felix, 1972). Note that all the lines in A have approximately the same slope, suggesting similar temperature dependence, Q10 of ∼1.3: the relaxation time of the viscoelasticity (P2) has a higher Q10 of 2.4 in the fast-twitch muscle fibres and of 2.0 in the slow-twitch muscle fibres. P2 tension has an intermediate Q10 of 1.5–1.7 in the two fibre types. In fast-twitch muscle fibres, the plateau P2 tension at 35 °C could not be accurately estimated by curve fitting (see text): the symbols denote values obtained from the average measurements at three stretch speeds within the plateau region and these were not used in the calculation of the Q10 given above.
DISCUSSION
The present study confirms our previous findings (see Mutungi & Ranatunga, 1996b, c) that the tension response to a ramp stretch in both fast- and slow-twitch resting mammalian (rat) muscle fibres at 10°C consists of only three components - a viscous (P1), a viscoelastic (P2) and an elastic (P3) component and that each has characteristics specific to the muscle fibre type (fast-twitch or slow-twitch). The physical dimensions, such as the fibre length and the cross-sectional area, were comparable between the two fibre type bundle preparations (see Mutungi & Ranatunga, 1996c); hence, the observed differences between them cannot be ‘artefactual’ arising from propagation effects etc., but reflect true differences arising from within the muscle fibres.
In many experiments, 10 mm BDM, which abolished active contractions in rat muscle fibres (Fryer, Neering & Stephenson, 1988; Mutungi & Ranatunga, 1996a) was used in order to remove the tension components (e.g. delayed tension rise) resulting from cycling cross-bridges. Since the particular tension components (P1, P2 and P3) were not affected by BDM (see Fig. 7 in Mutungi & Ranatunga, 1996b), actively cycling cross-bridges do not contribute to the components of the tension response. However, whether 10 mm BDM would prevent formation of weakly attached cross-bridges remains uncertain (McKillop, Fortune, Ranatunga & Geeves, 1994; Regnier, Morris & Holmsher, 1995). Nevertheless, it is pertinent to note that our results are basically similar to those reported by Bagni et al. (1995) from single frog muscle fibres in which they did not find any mechanical evidence of weakly attached cross-bridges. In both frog (Bagni et al. 1995) and rat (Mutungi & Ranatunga, 1996b, c) muscle fibres, the amplitudes of all the tension components increased with increasing sarcomere length. For example, in mammalian muscle fibres, increasing the sarcomere length from ∼2.6 to ∼3 μm reduced tetanic tension by 30–50 %, whereas the amplitudes of the resting tension components were nearly doubled.
The present study shows that the amplitudes of the tension components are decreased after chemical skinning and when the temperature is raised; however, the fast-slow fibre differences persist both in the skinned fibre preparations and in the intact fibres at high physiological temperatures. We discuss below the possible significance of our findings.
Effects of skinning
Our results show that, when the muscle fibres were chemically skinned and immersed in a standard relaxing solution, the amplitudes of all three passive tension components, and in both fibre types, were significantly reduced. The results are basically similar to those obtained in frog muscle fibres, which also showed a substantial drop in the amplitude of the various passive tension components after mechanical skinning (Goldman & Simmons, 1986; Bagni et al. 1995). Since permeabilization of muscle fibres will lead to the loss of some cytoplasmic constituents that contribute to myoplasmic viscosity, a reduction in the viscosity coefficient was expected: at least in our preparations, an expansion of filament lattice spacing after skinning is probably not a major factor, since addition of 4 % dextran did not have a large restorative effect. Quantitatively, the decrease of ∼50 % reported in this study is lower than the ∼70–80 % drop in viscosity coefficient observed when single intact frog muscle fibres were mechanically skinned; in these fibres the viscosity coefficient dropped from 53.5 N s m−2 (per Lo) before skinning to 15 N s m−2 (per Lo) after skinning (see Bagni et al. 1995).
P1 tension is thought to arise from the viscous resistance to inter-filamentary sliding in each half sarcomere. Although the cytoplasm is assumed to be dilute and to have viscosity properties similar to those of pure water, recent studies suggest that the fluid phase of the cytoplasm of living tissue culture cells may be as crowded as a 13 % dextran solution (Kao, Abney & Verkman, 1993). Additionally, the cytoplasm may have a protein concentration as high as 200–300 mg ml−1, although the proportion of these proteins which are in the fluid phase is not known (Luby-Phelps, 1994). It is possible that the frictional resistance to inter-filamentary (thick and thin filament) sliding arising from the overcrowding of macromolecules may be the cause of the viscous tension component we observe in resting muscle fibres subjected to ramp stretch. Therefore, the large drop in the viscosity coefficient of mechanically skinned frog fibres (Bagni et al. 1995) as compared with that of chemically skinned fibres may be due to the loss of more myoplasmic macromolecules in the former than in the latter fibres. However, as to the size and concentration of these macromolecules, the amounts lost during chemical skinning and why the fast-slow difference remains in skinned fibres immersed in the same bathing medium remain unclear.
In both fibre types, chemical skinning leads to an ∼60 % drop in the amplitude of P2 tension and significantly reduces its relaxation time by 15 % in fast-twitch muscle fibres and by 40 % in slow-twitch muscle fibres (see Table 1). Such changes may be expected, if indeed the viscoelastic tension (P2) partly arises from viscous-like resistance in an elastomer-like structural element, such as the gap filament, in a sarcomere (see below).
The elastic (P3) component in slow-twitch muscle fibres seems to be the most sensitive to chemical skinning and shows an ∼95 % drop in amplitude after the fibres are chemically skinned for 1 h or more. On the other hand, P3 tension drops by only ∼50 % in fast-twitch muscle fibres. Mutungi & Ranatunga (1996b, c) suggested that P3 tension in resting mammalian muscle fibres may reside in the cytoskeleton. If this hypothesis is correct, then the present results suggest that the cytoskeleton of fast- and slow-twitch muscle fibres is affected differently by chemical skinning. Another possibility is that the elastic tension in slow-twitch muscle fibres resides mainly in the sarcolemma, with little or no contribution from the other parallel elastic elements, while in fast-twitch muscle fibres P3 resides mainly in the non-sarcolemmal parallel elastic elements.
Effects of temperature
The results presented in this study show that the amplitude of all three component tensions is reduced to varying degrees as the experimental temperature is raised from 10 to 35°C. The viscoelastic component seems to be the more sensitive to temperature than the elastic and viscous components (see Figs 5 and 7).
In both fibre types viscosity coefficient, derived from P1 analyses, is halved as the experimental temperature is increased from 10 to 35°C. This gives it a temperature dependence (Q10) of ∼1.3 which is very similar to the Q10 for the viscosity of pure water (∼1.27) (Felix, 1972 and references therein), suggesting that although the myoplasm may be highly overcrowded with macromolecules (see above) and may show fast-slow muscle fibre type differences, temperature seems to affect its ‘viscous-like resistance’ to movement in a similar way to that of pure water.
The viscosity coefficients obtained at 35°C and at a sarcomere length of 2.7 μm were 0.4 kN s m−2 for fast-twitch fibres and 1.04 kN s m−2 for slow-twitch fibres: the values will be lower at resting sarcomere length of 2.5 μm (see Mutungi & Ranatunga, 1996b), probably about 0.25 kN s m−2 in the fast and 0.65 kN s m−2 in the slow fibres. Thus, at the maximum shortening velocity (Vmax) of 12 Lo s−1 in fast-twitch fibres and ∼7 Lo s−1 in slow-twitch fibres (Ranatunga, 1984), the internal resistance would be ∼3–5 kN m−2, which is ∼1–2 % of their maximum tetanic tensions (∼250 kN m−2). The viscous resistance at Vmax at 35°C is ∼3 times higher than that which we calculated for these fibres at 10°C (∼1 kN m−2 at Vmax; see Mutungi & Ranatunga, 1996b, c). Thus, as previously suggested then (Mutungi & Ranatunga, 1996b, c), an increase of internal resistance to filament sliding arising from passive viscous properties in muscle cannot be the cause of the marked reduction in Vmax observed in these fibres at the low temperatures (see Ranatunga, 1984). However, whether the level of viscous resistance to filament sliding at 35°C, as reported in this study, can influence the force-velocity relation (see Worthington & Elliot, 1996) and/or significantly limit the Vmax remains uncertain; it seems, however, that the effect would be greater in the slow-twitch muscle fibres both due to higher internal resistance and greater curvature of the force-velocity relation.
Present results show that as temperature is increased from 10 to 35°C, the plateau tension of the viscoelastic component (net P2 normalized to stretch amplitude) decreased by ∼70 % in slow-twitch muscle fibres and by ∼90 % in fast-twitch fibres. Additionally, its relaxation time decreased from ∼12 ms at 10°C to ∼3 ms at 25°C in fast-twitch fibres and from ∼44 ms at 10°C to ∼8 ms at 35°C in slow-twitch fibres (Q10 of 2.0–2.5). These Q10 values compare well with those reported previously for maximum shortening velocity in these fibres (2–2.5, see Ranatunga, 1984). Therefore, the passive viscoelasticity of resting muscle and active cross-bridge cycling rate seem to have the same thermal dependence. Indeed, the difference in the P2 relaxation time between fast- and slow-twitch muscle fibres at 10°C was the same as the difference in the time courses of their active contractions (see Introduction) suggesting that passive viscoelasticity and active cross-bridge cycling rate in these fibres may somehow be coupled. As suggested previously (see Mutungi & Ranatunga, 1996b, c), a coupling of this nature may be important for the efficient transmission of muscle power during active contractions especially during lengthening/shortening cycles.
The viscoelasticity (net P2 tension) may arise from either the cytoskeleton (Bagni et al. 1995) or from the gap-filament (De Tombe & Ter Keurs, 1992; Mutungi & Ranatunga, 1996b, c), since the sarcomere length and BDM experiments show no evidence of cycling cross-bridge involvement. The isolated connectin (= titin) protein molecules, which form the gap filament, exhibit long-range elasticity in their force extension characteristics (Wang, McCarter, Wright, Beverly & Ramirez-Mitchell, 1991) and it has been demonstrated recently that they can unfold at extreme and slow stretches (Rief, Gautel, Oesterhelt, Fernadez & Gaub, 1997; Kellermayer, Smith, Granzier & Bustamante, 1997; Tskhovrebova, Trinick, Sleep & Simmons, 1997). Folding/unfolding is one possible mechanism to explain viscoelasticity, although under the more restricted physiological sarcomere length range employed here (< 3 μm) it seems unlikely to be the major mechanism. Alternatively, or additionally, the viscoelastic tension can arise from the gap filament protein molecules behaving like an elastomer in a viscous medium, and hence it has two components, one arising from the interaction of molecular segments with the myoplasmic medium and the other from their configuration (entropic) changes. One may further speculate that such elastomer-like behaviour is within the more extensible region of the titin molecules (PEVK region, Labeit & Kolmerer, 1995). The decrease of viscoelastic force and the decrease of relaxation time with decreased viscosity (skinned fibres) and with increase of temperature may be qualitatively accounted for on the basis of such a mechanistic viscoelastic model for the gap filament. Additionally, fast- and slow-twitch fibre differences would reflect the fact that the extensible region of the titin molecule is longer in the slow-twitch than in the fast-twitch muscle fibres.
Acknowledgments
We thank The Wellcome Trust for funding this research.
References
- Bagni MA, Cecchi G, Colomo F, Garzella P. Absence of mechanical evidence for attached weakly binding cross-bridges in frog relaxed muscle fibres. Journal of Physiology. 1995;482:391–400. doi: 10.1113/jphysiol.1995.sp020526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Tombe PP, Ter Keurs HEDJ. An internal viscous element limits unloaded velocity of sarcomere shortening in rat myocardium. Journal of Physiology. 1992;454:619–642. doi: 10.1113/jphysiol.1992.sp019283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felix F. Water: a Comprehensive Treatise, vol. 1, the Physical Chemistry of Water. London: Plenum Press; 1972. chap. 10. [Google Scholar]
- Ford LE, Nakagawa K, Desper J, Seow C. Effect of osmotic compression on the force-velocity properties of glycerinated rabbit skeletal muscle cells. Journal of General Physiology. 1991;97:73–88. doi: 10.1085/jgp.97.1.73. 10.1085/jgp.97.1.73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortune NS, Geeves MA, Ranatunga KW. Pressure sensitivity of active tension in glycerinated rabbit psoas muscle fibres: effects of ADP and phosphate. Journal of Muscle Research and Cell Motility. 1989;10:113–123. doi: 10.1007/BF01739967. [DOI] [PubMed] [Google Scholar]
- Fryer MW, Neering IR, Stephenson DG. Effects of 2,3-butanedione monoxime on the contractile activation properties of fast- and slow-twitch rat muscle fibres. Journal of Physiology. 1988;407:53–75. doi: 10.1113/jphysiol.1988.sp017403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman Y, Simmons RM. The stiffness of frog skinned muscle fibres at altered filament spacing. Journal of Physiology. 1986;378:175–194. doi: 10.1113/jphysiol.1986.sp016213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gulati J, Babu A. Critical dependence of calcium-activated force on width in highly compressed skinned fibres of frog. Biophysical Journal. 1985;48:781–787. doi: 10.1016/S0006-3495(85)83836-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kao HP, Abney JR, Verkman AS. Determinants of the translational mobility of a small solute in cell cytoplasm. Journal of Cell Biology. 1993;120:175–184. doi: 10.1083/jcb.120.1.175. 10.1083/jcb.120.1.175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kellermayer MSZ, Smith SB, Granzier HL, Bustamante C. Folding-unfolding transitions in single titin molecules characterized with laser tweezers. Science. 1997;276:1112–1116. doi: 10.1126/science.276.5315.1112. 10.1126/science.276.5315.1112. [DOI] [PubMed] [Google Scholar]
- Labeit S, Kolmerer B. Titins: Giant proteins in charge of muscle ultrastructure and elasticity. Science. 1995;270:293–296. doi: 10.1126/science.270.5234.293. [DOI] [PubMed] [Google Scholar]
- Luby-Phelps K. Physical properties of cytoplasm. Current Opinion in Cell Biology. 1994;6:3–9. doi: 10.1016/0955-0674(94)90109-0. [DOI] [PubMed] [Google Scholar]
- McKillop DFA, Fortune NS, Ranatunga KW, Geeves MA. The influence of 2,3-butanedione 2-monoxime (BDM) on the interaction between actin and myosin in solution and in skinned muscle fibres. Journal of Muscle Research & Cell Motility. 1994;15:309–318. doi: 10.1007/BF00123483. [DOI] [PubMed] [Google Scholar]
- Matsubara I, Elliot GF. X-ray diffraction studies on skinned single fibres of frog skeletal muscle. Journal of Molecular Biology. 1972;72:657–669. doi: 10.1016/0022-2836(72)90183-0. [DOI] [PubMed] [Google Scholar]
- Matsubara I, Umazume Y, Yagi N. Lateral filamentary spacing in chemically skinned murine muscles during contraction. Journal of Physiology. 1985;360:135–149. doi: 10.1113/jphysiol.1985.sp015608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maughan D, Godt RE. Inhibition of force production in compressed skinned muscle fibres of the frog. Pflügers Archiv. 1981;390:161–163. doi: 10.1007/BF00590200. [DOI] [PubMed] [Google Scholar]
- Mutungi G, Ranatunga KW. Effects of temperature on the visco-elasticity of intact, relaxed, fast (rat) muscle fibres. Journal of Physiology. 1995;487.P:153P. [Google Scholar]
- Mutungi G, Ranatunga KW. The tension relaxation after stretch in resting mammalian muscle fibers: Stretch activation at physiological temperatures. Biophysical Journal. 1996a;70:1432–1438. doi: 10.1016/S0006-3495(96)79702-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mutungi G, Ranatunga KW. The visco-elasticity of resting intact mammalian (rat) fast muscle fibres. Journal of Muscle Research and Cell Motility. 1996b;17:357–364. doi: 10.1007/BF00240933. [DOI] [PubMed] [Google Scholar]
- Mutungi G, Ranatunga KW. The viscous, viscoelastic and elastic characteristics of the resting fast and slow mammalian (rat) muscle fibres. Journal of Physiology. 1996c;496:827–836. doi: 10.1113/jphysiol.1996.sp021730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. The force-velocity relation of rat fast- and slow-twitch muscles examined at different temperatures. Journal of Physiology. 1984;351:517–529. doi: 10.1113/jphysiol.1984.sp015260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranatunga KW. Thermal stress and Ca-independent contractile activation in mammalian skeletal muscle fibers at high temperatures. Biophysical Journal. 1994;66:1531–1541. doi: 10.1016/S0006-3495(94)80944-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regnier M, Morris C, Holmsher E. Regulation of the crossbridge transition from a weakly to a strongly bound state in skinned rabbit muscle fibres. American Journal of Physiology. 1995;269:C1532–1539. doi: 10.1152/ajpcell.1995.269.6.C1532. [DOI] [PubMed] [Google Scholar]
- Rief M, Gautel M, Oesterhelt F, Fernandez JM, Gaub HE. Reversible unfolding of individual immunoglobulin domains by AFM. Science. 1997;276:1109–1112. doi: 10.1126/science.276.5315.1109. [DOI] [PubMed] [Google Scholar]
- Schoenberg M. Characterization of the myosin adenosine triphosphate (M.ATP) crossbridge in rabbit and frog skeletal muscle fibers. Biophysical Journal. 1988;54:135–148. doi: 10.1016/S0006-3495(88)82938-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tskhovrebova L, Trinick J, Sleep J, Simmons RM. Elasticity and unfolding of single molecules of the giant muscle protein titin. Nature. 1997;387:308–312. doi: 10.1038/387308a0. [DOI] [PubMed] [Google Scholar]
- Wang K, McCarter R, Wright J, Beverly J, Ramirez-Mitchell R. The regulation of skeletal muscle stiffness and elasticity by titin isoforms: A test of the segmental extension model of resting tension. Proceedings of the National Academy of Sciences of the USA. 1991;88:7101–7105. doi: 10.1073/pnas.88.16.7101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worthington CR, Elliot GF. Muscle contraction: the step size distance and the impulse-time per ATP. International Journal of Biological Macromolecules. 1996;18:123–131. doi: 10.1016/0141-8130(95)01070-x. [DOI] [PubMed] [Google Scholar]


