Abstract
An investigation into the distribution of light intensity across the rat retina was carried out on excised, intact rat eyes exposed to Ganzfeld illumination from a helium-neon laser (543 nm).
Some of the light entering the eyes exits through the sclera where its intensity can be monitored with an optical ‘pick-up’ that samples the intensity coming from a small region of external sclera and underlying retina. The spatial resolution of the pick-up is such that it samples light that has passed through ca 2% of the rods in the rat eye.
Some of the laser light is absorbed by the rod pigment, rhodopsin, which gradually bleaches. Bleaching in the retina, in turn, causes an exponential increase in intensity emanating from the sclera. By monitoring this intensity increase, we are able to measure two important parameters in a single bleaching run: the local rhodopsin concentration and the local intensity falling on the rods.
With an ocular transmission photometer, we have measured both the local intensity and the local rhodopsin concentration across wide regions of rat retina. Both pigmented and albino rats were studied.
The distributions of rhodopsin and intensity were both nearly uniform; consequently, the product, (rhodopsin concentration) × (intensity), was similarly nearly equal across the retina. This means that the initial rate of photon absorption is about the same at all retinal locations.
Interpreted in terms of photostasis (the regulation of daily photon catch), this means that the rate of photon absorption is about the same in each rod, viz. 14 400 photons absorbed per rod per second. Since this rate of absorption is sufficient to saturate the rod, one possible purpose of photostasis is to maintain the rod system in a saturated state during daylight hours.
Although physiological optics is a subject of considerable interest to many workers, there is not unanimous agreement about the way in which light intensity is distributed across the vertebrate retina. Some studies show that measured intensity distributions are different from those predicted by models, and, indeed, even the models frequently disagree with each other (cf. Gross, 1932; Fitzke, 1981; Young, 1981; Kooijman, 1983; Kooijman & Witmer, 1986; Pflibsen, Pomerantzeff & Ross, 1988). The one point on which there is concurrence is that a vertebrate eye, confronted with a uniformly lighted field, will experience the highest intensity at the posterior pole and the lowest at the periphery. However, a persistent question remains: what is the distribution of intensity from pole to periphery? In this work we have answered that question for the rat eye.
The albino rat is a very popular animal for studies of the retina, and a schematic eye for the rat exists (Hughes, 1979). Beyond that, however, no information has been published (to our knowledge) about the light intensity distribution in the rat eye. Making such measurements would not only provide new information about the eye of this popular research subject, but also have important implications for studies of retinal light damage in rats (see Rapp & Williams, 1980) and for the theory of photostasis (Penn & Williams, 1986).
Rapp & Williams (1980) showed that the rat retina has a region in the superior mid-periphery that is exquisitely sensitive to light-induced damage, the ‘sensitive area’. Is this because the retina absorbs more light there than elsewhere?Penn & Williams (1986), using microspectrophotometry (MSP), showed that the rods in this area, in rats raised under conditions of low light intensity, do have greater light-absorbing efficiency than those in other parts of the retina. Thus, the question would seem to have been answered: more light-absorbing efficiency, more light damage. However, this paper will show that greater light-absorption efficiency is not necessarily synonymous with absorbing more photons in this region of the rat retina.
As regards photostasis, we have discovered that rats, both pigmented and albino, all absorb the same number of photons in their rods every day. This is the case over a broad range of light intensity and day length in the habitats in which they have been born and raised (Penn & Williams, 1986; Williams, Baker & Dodge, 1994; Parker & Williams, 1995). The ‘photostasis number’, or number of photons absorbed per eye per day, for rats is 1.2 × 1016 (± 20%).
An especially interesting interpretation of this number obtains if one considers the rate of absorption per rod implied by this dose of photons: 1016 absorptions per eye per 12 h light period, distributed over the number of rods in the rat eye (1.75 × 107 (± 15%); Lashley, 1932; Cone, 1963), translates to 11 000-15 000 photons per rod per second. These rates are in the mid-range of those that reportedly saturate the rods and keep them saturated (Aguilar & Stiles, 1954; Pirenne, 1962; Alpern, Rushton & Torii, 1969). Thus, we postulate that a property of photostasis is to render the scotopic visual system saturated during the daylight hours.
However, an important caveat attends this postulate and prompts the present work: the rate of absorption per rod cited above is the mean rate which we have calculated from whole-eye rhodopsin measurements; in short, it says nothing about individual rods. To suggest, as we now do, that photostasis results in the saturation of ‘the rod system’ is to imply that all or at least most of the rods are absorbing at this rate. What if, for example, a moderate fraction of the rods was absorbing at a very high rate, and the others at near-zero rates (to pick an extreme case)? The mean rate could come out as calculated above but the scotopic system would not be functionally saturated, i.e. some rods could still function upon absorbing light. If our postulate is to be sustained, all rods should absorb at nearly the same rate and this rate should lie in the range reported to saturate the rods, viz. 8000-20 000 photons absorbed per rod per second (Pirenne, 1962).
This paper reports results which support our hypothesis that photostasis mechanisms have the capability of keeping most if not all rods at saturation. In order to provide such support, we have built an ocular transmission photometer (OTP) which measures both rhodopsin concentration and light intensity in small regions across the rat retina without interfering with the normal optics of the eye (Williams & Webbers, 1995). In order to calculate the rate of photon absorption in any particular, small region of the retina it is necessary to measure both rhodopsin concentration and light intensity in that region because the absorption rate is given by Φ×I×R, where Φ, the photosensitivity of bleaching, is constant and I and R are the local light intensity and local rhodopsin concentration, respectively.
The results of this study show that most, if not all, rods absorb photons at nearly the same rate when the rat eye is exposed to Ganzfeld illumination. They further suggest a new way to think about scotopic and photopic vision, namely that the duplex retina has evolved such that the number of photons absorbed by the rods over the daylight hours is regulated at just the ‘correct’ (photostasis) level to saturate the scotopic system.
METHODS
Animals
All experiments have been done according to NIH guidelines for the care and use of animals. Sprague-Dawley albino and Long- Evans hooded (pigmented) rats were used in these studies. All rats were raised in either 3 or 200 lx light, on a 12 h cycle. All work was done on fully dark-adapted (overnight) rats. The retinas of the albinos had previously been studied in vitro (microspectrophotometrically) as regards the regional light absorption properties of their retinas (Penn & Williams, 1986), and, thus, serve in several respects as models for what is observed in these experiments.
Apparatus
The ocular transmission photometer (OTP) monitors the intensity of light transmitted through excised eyes (Williams & Webbers, 1995). Intense, actinic bleaching light, passing through the normal optics of an eye, traverses all of the ocular media including the photoreceptor-retinal pigment epithelium-choroid complex. A fraction of that which is not absorbed or scattered exits through the sclera where it is sampled by a fine-tipped ‘optical pick-up’ which touches the external surface of the sclera. The pick-up is, in turn, optically coupled to a photon-counting system where photon rates are measured, log transformed, recorded and displayed against time. The bleaching beam from a ‘green’ He-Ne laser (543 nm) delivers up to 1015 photons per second to the eye by way of a Ganzfeld whose intensity distribution has been shown to be very uniform (Williams & Webbers, 1995). Achieving this uniformity was important: we had to be sure that any non-uniformities in the intensity distributions found inside the eyes were not determined by non-uniform intensity distributions outside the eyes.
The mature rat retina normally has 1.75 × 107 rods (Lashley, 1932; Cone, 1963) and subtends an area of 80-90 mm2 (Hughes, 1979). Scale drawings of the pick-up, sclera, choroid and retina, done with appropriate refractive indices, showed that the optical pick-up collects light from an area of retina of about 1.6 mm2 (Williams & Webbers, 1995). This area corresponds to about 2% of the rods in the rat retina. The pick-up is attached to a goniometer, calibrated in 10 deg steps out to 70 deg from the optic nerve.
Protocol
Rats were killed in dim red light by CO2 asphyxiation followed by exsanguination. An eye was then excised, trimmed of debris, and introduced into the OTP such that it ‘viewed’ the inside of the Ganzfeld. Then, under visual control in red light, the stump of the optic nerve was aligned with a reference pointer that was fixed at 0 deg, and the optical pick-up was lowered so as to make contact with the sclera. A sensitive electronic ‘touch-down’ detector was used to prevent the experimenter from distorting the sclera by advancing the pick-up too far. This procedure was aimed at preserving the alignment of photoreceptor cells underneath the pick-up, and it was apparently successful since the present results on albino rats were found to agree very well with axial absorbances of albino rat rods calculated from side-on measurements with a microspectrophotometer (MSP) (Penn & Williams, 1986).
The procedure for all OTP measurements was as follows. An eye was suddenly exposed to the full intensity of the laser-lighted Ganzfeld. Simultaneously, the photon-counting system began to monitor the light transmitted through the sclera at the chosen location. Photons were collected using bin sizes of 800 ms and stored for later display as log(counts s−1), a parameter that is proportional to absorbance and therefore to concentration. The intensity of this transmitted light increased with time as rhodopsin inside the eye bleached. The asymptotic, ‘total’ change in log(counts s−1), Δ, was directly proportional to the rhodopsin concentration per unit area that had been present in the dark-adapted eye at the given location (Williams & Webbers, 1995). For the bleaching of rhodopsin to reach near-asymptotic levels, a run typically lasted 300-500 s.
The data were stored as the log(counts s−1) vs. time, plotted and then fitted with a simple exponential of the form:
(Williams & Webbers, 1995). From the curve fit, we obtained both the total absorbance change, Δ, and the time constant of bleaching, τ. The value of Δ, measured at 543 nm, when multiplied by 2 is equivalent to the absorbance change at 500 nm, the λmax of rat rhodopsin. τ is inversely proportional to the light intensity falling on the rods at the location. For rat rods, this change in absorbance (less than 0.2 absorbance units) is well fitted by a simple exponential function of time and corresponds to ‘Case 2' of Dartnall's (1957) method of photometric curves. Thus, one run provides both of the parameters of interest: 1/τ, proportional to the local intensity, and Δ, proportional to the local, dark-adapted rhodopsin concentration per unit area. The product, Δ(1/τ), which is proportional to the initial rate of photon absorption, is then calculated for the retinal region being examined.
In some runs, the bleaching was not complete but this did not obviate the use of the data because we used the curve-fitting routine to obtain the best-fit values of Δ and τ. In a test to decide if complete bleaching was essential to obtaining correct τ and Δ, we did four runs in which the bleaching was complete and for which τ and Δ were obtained. Then we simulated incomplete bleaching by deleting up to half of the data bins from the end of the runs (ca 3 tau units) and then re-fitted exponential functions to these truncated curves. The fitted values from these truncated functions were within 2% of those obtained from the complete curves. That is, incompleteness in the bleaching functions caused no problem. A similar test showed that missing the initial points on some of the curves (ca 0.5 tau units) posed no problem for the curve-fitting routine. We attribute these convient features firstly to the excellent signal-to-noise ratio of the OTP, and secondly to the fact that the bleaching produces simple exponential functions, and our forcing the data to conform to such functions leaves no ambiguity in the result. The curve-fitting routine also reliably determined the value of the absorbance at time zero, a necessary condition for the calculation of Δ. The correctness of this was again verified by simulation, in this case by deleting several initial data points from runs in which time zero points were available.
Tests were done to determine if photoproducts interfere with the observed results: using rats that had been perfused with NH2OH-saline, we found that Δ was the same with or without NH2OH. Thus, photoproducts did not interfere with the observed Δ (see Dartnall, 1953). This was expected, mainly because 543 nm bleaching/measuring light is not appreciably absorbed by long-lived photoproducts. On the other hand, when we used 500 nm light in the Ganzfeld and no NH2OH, we found smaller and less consistent values of Δ, suggesting that photoproducts were being produced. With NH2OH and 500 nm light, the Δ values were consistent and equal to the ones obtained with the 543 nm light (except that the latter had to be multiplied by 2, as described above; see also Williams & Webbers, 1995).
RESULTS
Typical changes in absorbance: pigmented and albino eyes
Figure 1 shows typical time courses of bleaching, obtained from eyes of albino (top curve) and pigmented rats (bottom curve). Curves fitted to the data are exponential functions, described above. The total absorbance changes, Δ, determined from the fitted values of these curves were 0.158 and 0.179 absorbance units for the albino and pigmented eyes, respectively. These values, although from small regions of these retinas, are in good agreement with the finding that pigmented rats have about the same amount of rhodopsin per eye as do albinos when both have been raised in dim light, as these have been (cf. Battelle & LaVail, 1978; Penn & Williams, 1986; Williams, et al. 1994). Note that, while the curve for the albino retina was essentially asymptotic at 300 s, the curve for the pigmented eye was still rising appreciably at that time. The τ values of these functions, from curve fitting, were 85 and 143 s, respectively. Although the intensity in the Ganzfeld was the same for both of these eyes, rhodopsin in the pigmented eye bleached about half as fast as it did in the albino. The simplest interpretation of this is that the intensity experienced by the rods in the pigmented eye is about half that in the albino eye. Indeed, a factor of 2 was predicted by Rapp & Williams (1980), who showed that about twice as much light in the pigmented rat eye was required to produce the same degree of retinal light damage as in the albino. It was suggested then that the reason for this difference was that light, having passed once through the rods of an albino eye, would be scattered back through those rods again, effectively increasing the exposure (see Discussion). In the pigmented eye, of course, the heavily melanized epithelium and choroid layers absorb photons that escape absorption by the rods, and there is very little back scatter.
Figure 1. Typical absorbance changes with time in the 543 nm bleaching/measuring light.
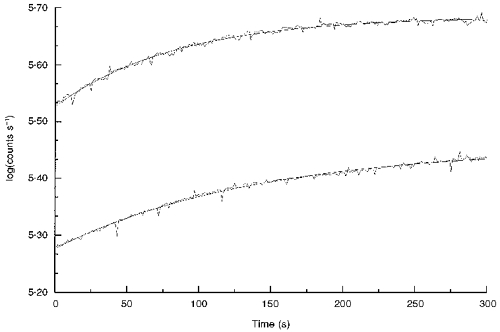
Each curve was obtained by monitoring intensity transmitted through the sclera of eyes when the pick-up was set at 30 deg from the optic nerve in the superior hemisphere. The top curve is from the eye of an albino rat and the bottom curve from the eye of a pigmented rat, both animals having been born and raised in low intensity light (3 lx). The smooth lines drawn through the traces are best-fit exponential functions from which values of Δ and 1/τ are obtained.
Albino rats, low intensity light history
Figure 2 shows a summary of results obtained from albino rat eyes, the animals having been raised in dim (3 lx), cyclic light. The top line in the figure is the local Δ, measured across 70 deg of the superior retina. The mean observed change was 0.160, which is equivalent to 0.32 absorbance change at 500 nm. Notice that there was a slight rise in this line at 30 deg. The results of microspectrophotometry by Penn & Williams (1986) are in excellent agreement with both the mean absorbance change across these angles and with the slight elevation of absorbance in this retinal region for rats raised in dim light.
Figure 2. Plot of Δ, 1/τ and Δ(1/τ) from albino rats raised in low intensity light.
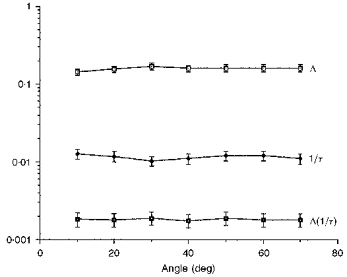
Values were obtained from measurements across the superior hemispheres of retinas of albino rats that had been born and raised in 3 lx cyclic light. The bottom-most function is the product Δ(1/τ), proportional to the initial rate of photon absorption at the angles shown. Each Δ and 1/τ is the mean of at least 6 measurements and the error bars are the standard errors. The top-most curves are almost flat and this causes the bottom-most curve to be flat also.
The middle line in Fig. 2 depicts the 1/τ intensity parameter at these six retinal locations; note that it decreased slightly over this range of angles and that there was a slight dip in the line at 30 deg. The former is consistent with published results from other species which show that intensity falls off with eccentricity (Gross, 1932; Young, 1981; Kooijman & Witmer, 1986). However, the fall-off is not very steep in the albino rat eye.
Point-by-point multiplication of these two lines gives the bottom line in this figure, Δ(1/τ). This line was virtually flat. A least-squares line, fitted to these points, sloped gently towards the periphery (slope = -3%). The flatness of the line shows that the initial rate of photon absorption is almost the same across the 70 deg of these retinas.
Albino rats, high intensity light history
Similarly, Fig. 3 shows that nearly flat functions were obtained from albino rats that had been raised in (‘bright’) 200 lx light. The mean rhodopsin absorbance over these 40 deg was 0.092, a value which is less than that found in rats raised in dim light (Fig. 2), and is consistent with the fact that albinos with this kind of light history are known to have less rhodopsin in their eyes than do rats raised in 3 lx light. The ratio of mean Δ values in Figs 2 and 3 was 1.73. Measured by detergent extraction methods, the ratio of whole-retina rhodopsin levels in the dark-adapted eyes of rats raised in 3 and 200 lx light is 1.74 (Penn & Williams, 1986). The mean OTP Δ is also in excellent agreement with the MSP results of Penn & Williams (1986), and with their observation that no local elevations of absorbance are seen in these bright light-raised rats. Furthermore, this reduction of absorbance by the rods is a manifestation of rod outer segment (ROS) renewal and is adaptive vis-à-vis habitat intensity (Schremser & Williams, 1995a, b).
Figure 3. Plot of Δ, 1/τ and Δ(1/τ) from albino rats raised in high intensity light.
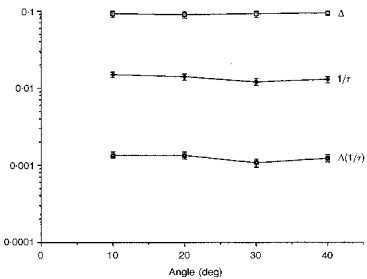
Values were measured across the inferior retina of albino rats that had been raised in the relatively intense 200 lx cyclic lighting. Such rats are known to have about 2/3 rhodopsin per eye, as do rats raised in 3 lx. The Δ values are, accordingly, lower, but the intensity parameter, 1/τ, is identical to that shown in Fig. 2. This is expected if the bleaching of the rods conforms to Dartnall's Case 2 of photometric curves, wherein there is neither self-screening nor photoproduct interference. The points are the means from 4 eyes, on average, and error bars are the standard errors.
The 1/τ values were statistically no different from those measured in the 3 lx albinos (P < 0.30). This is as expected if the determination of intensity by this method truly conforms to Dartnall's Case 2 (no self-screening and no photoproduct screening).
The locus of the product Δ(1/τ) in Fig. 3 was nearly flat. This shows that the initial photon absorption rates are nearly equal across the area measured here.
The combined results shown in Figs 2 and 3 indicate that the OTP is capable of sorting out the rhodopsin concentration from the intensity parameter (cf. Dartnall, 1957) and of giving reproducible intensity readings from eye to eye even when rhodopsin concentrations differ.
Pigmented rats, low intensity light history
Figure 4 shows results obtained from Long-Evans pigmented rats which had been born and raised in dim (3 lx), cyclic light. The mean rhodopsin concentrations were statistically indistinguishable from those of the albinos raised in dim light (P < 0.6). This agrees with our unpublished results and with those of Battelle & LaVail (1978). Again, a region of slightly elevated absorbance was seen, but in this strain of rat it appeared nearer to 20 deg than to 30 deg (Fig. 2).
Figure 4. Plot of Δ, 1/τ and Δ(1/τ) from pigmented rats raised in low intensity light.
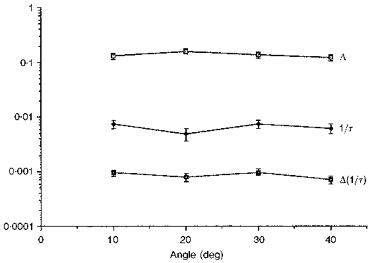
Values were determined at 4 locations across the superior hemispheres of retinas of pigmented rats that had been born and raised in 3 lx cyclic light. The points are the means from at least 3 eyes and error bars are the standard errors. The functions are again relatively flat, especially the lowest one, namely the rate of absorption curve.
The intensity parameter, 1/τ, was less flat than in Figs 2 and 3 and, as discussed, had about half the value of those shown in those figures. That it was less flat here is not surprising, since the interior of a pigmented eye acts less like an integrating sphere than does an albino eye. However, the product, Δ(1/τ), was nearly flat (slope = -3%) and this, in turn, means that there are nearly equal rates of photon absorption across this region of pigmented retina.
DISCUSSION
The present results show the existence of a strikingly uniform distribution of intensity across wide regions of the rat retina. The uniformity is somewhat greater in the albino eye than in the pigmented eye, perhaps because the albino eye scatters light internally and in effect promotes the uniformity: it acts like an imperfect integrating sphere itself. On the other hand, the melanin inside a pigmented eye prevents much of the scatter. This observation establishes not only the distribution of initial absorption rates in the two kinds of eye but also explains why twice as much light is needed for inducing equal damage in the pigmented eye (Rapp & Williams, 1980).
Whether the intensity distribution in the pigmented eye is steeper than in the albino is, at this time, moot because we cannot measure beyond about 40 deg in the pigmented eye. This is because an unusual pupillary response is present in the pigmented eyes that persists in these eyes upon excision (Williams et al. 1994). This response is circadian-like and, although weakest at night, vestigial responses are present frequently enough to interfere with some of the runs. Furthermore, small constrictions from the fully dilated state have an effect on the retinal illumination in the periphery of the retina but not in the more central areas (Kooijman, 1983). Thus, the only results presented here are those from (i) central/mid-peripheral retinas; and (ii) eyes with fully dilated pupils and in which we confirmed by visual inspection before and after a run that there was no detectable reduction in pupil diameter during OTP measurement. These constraints have thus far limited our measurements to angles of 40 deg or less in pigmented eyes.
We had some indication from earlier MSP studies that Δ might be rather flat across the retina. However, in order to arrive at that conclusion in those experiments (Penn & Williams, 1986) we calculated the axial absorbance of rat rods across the retina by multiplying regional measurements of ROS length by corresponding ‘side-on’ MSP determinations of rhodopsin absorbance. The OTP gives a direct measurement of axial absorbance, and the present results are in excellent agreement with those earlier calculations.
Our original paper on photostasis showed that the rhodopsin contained in an eye is inversely proportional to the light intensity of the habitat and, thus, it might be reasonable to suggest that local intensity in a single eye might regulate the local rhodopsin concentration. There may be a ‘photostasis within a photostasis’ wherein the number of photons absorbed by the whole eye is regulated, and at the same time each rod is also responding to its local light intensity in such a way as to regulate its absorption. However, in this study when we did a statistical analysis (Student's paired t tests) on the Δ functions we found that the ‘rise’ in absorbance at 20-30 deg was not significantly higher than other points in that function (P = 0.080). Similarly, neither was the ‘dip’ in the 1/τ functions (P = 0.083). Thus, the question of point-by-point ‘compensatory’ behaviour in these functions awaits further study. We suggest that several simultaneous measurements on the same eye with multiple pick-ups might answer this question because the trend towards ‘compensation’ appears to exist but is washed out when averaged data are used.
Although we used a very ‘unnatural’ visual field - a uniformly lighted Ganzfeld - to demonstrate uniform absorption rates, the fact is that these eyes developed in normal animals raised in normally lighted cages (not uniform Ganzfelds). These rats, free to move about in their cages, obviously did not experience uniform intensity in all directions. Yet, the way their retinas developed was such that the light-absorbing properties were very uniform. If local intensity regulates local rhodopsin concentration, and if the intensity from moment to moment is non-uniform, then perhaps the exposure of rods is time averaged in such a way that over the entire (daily?) exposure all rods receive approximately the same dose of light.
Interpreting the ‘photostasis number’ (1016 photons absorbed per eye per day) in terms of rate of absorption, it seems likely that most if not all rods contribute equally to the absorption of that number. Thus, our postulate, stated in the Introduction, is supported: one function of photostasis is to render the rod system saturated during daytime exposures to photopic levels of light.
Rod saturation, determined in psychophysical experiments, has been reported to occur over a range of photon absorption rates that bracket the ones we find from photostasis considerations (Aguilar & Stiles, 1954; Pirenne, 1962; Alpern et al. 1969). These rates, whether derived from psychophysics or from photostasis, are similar to, and in some cases the same as, those found in electrophysical studies of single mammalian rods (Baylor, Nunn & Schnapf, 1984; Nakatan, Tamura & Yau, 1991; Kraft, Schneeweiss & Schnapf, 1993). Two of these studies have now suggested that saturation of rod vision can be attributed to saturation of the rod cells themselves (Baylor et al. 1984; Kraft et al. 1993). Perhaps mammalian rods, generally, display saturation at or near the ‘photostasis’ rates. If so, it implies that the photostasis number for mammals is the product of the number of rods per eye times (about) 15 000 photons absorbed per rod per second times the number of seconds in the lights-on period.
The OTP provides a method for determining the local intensity across the retina. In addition, the intensity being measured is the functional intensity for bleaching rhodopsin in situ. Methods which employ physical probes inserted into bleached eyeballs through the sclera almost certainly disrupt some aspects of the physiological optics of the eye (see Kooijman & Witmer, 1986). Furthermore, such methods assess primarily the optics anterior to the photoreceptors. If antenna or light-guiding properties exist in these cells (Wijngaard, 1981), the OTP might disclose them, but invasive methods might interfere with them. In this study we made no attempt to determine if these are important in the rat eye, partly because we had earlier hints that such effects in the rat retina are probably not large (Williams & Webbers, 1995) and partly because we made no effort to maintain ocular pressure in the rat eyes. With regard to the latter, our results are subject to the same criticism levelled at some earlier work by others on larger eyes in which pressure was not maintained (cf. Kooijman & Witmer, 1986). However, the rat eye is relatively small and has a relatively large lens: about one-third of the volume of the eye is occupied by the lens which would help prevent collapse simply because it fills such a large fraction of the eye (Hughes, 1979). Such collapse would cause the disorientation of the photoreceptors relative to the lens, pupil and cornea. In fact, judging from our earlier work, collapse of the eyeball, with concomitant destruction of good optics, does not seem to be a problem in the present work. For example, the excellent agreement with Penn & Williams (1986), who used MSP methods that required strict orientation of ROSs relative to the electric vector of an MSP measuring beam, indicates that not maintaining ocular pressure here had no major deleterious effects on photoreceptor orientation.
The OTP uses only one wavelength of bleaching/measuring light and with it we cannot assess the possibility that cones (ca 2% of the visual cells in the rat retina) are contributing to the measurements reported here. However, there are two reasons why we think that cones do not make a significant contribution to the observations. (i) The present results agree with those of Penn & Williams (1986), whose measured spectra were clearly those of rhodopsin. (ii) Cones comprise only about 2% of the visual cells in the rat and are not concentrated in any one location. Dispersed in this way, they would not contribute much to the absorbance changes we report. Indeed, Kemp, Faulkner & Jacobson (1988), using a reflectance technique, have shown that in the cat area centralis, where cones are relatively concentrated, absorbance changes from cones amounted to no more than 5% of the total change; the remainder was from rods. If cones contribute so little in that situation, their contribution here is probably undetectable.
References
- Aguilar M, Stiles W S. Saturation of the rod mechanism of the retina at high levels of stimulation. Optica Acta. 1954;1:59–65. [Google Scholar]
- Alpern M, Rushton W A H, Torii S. Encoding of rod signals from rods. Nature. 1969;223:1171–1172. doi: 10.1038/2231171a0. [DOI] [PubMed] [Google Scholar]
- Battelle B-A, LaVail M M. Rhodopsin content and rod outer segment length in albino rat eyes: modification of dark-adaptation. Experimental Eye Research. 1978;26:487–497. doi: 10.1016/0014-4835(78)90134-3. [DOI] [PubMed] [Google Scholar]
- Baylor D A, Nunn B J, Schnapf J L. The photocurrent, noise and spectral sensitivity of rods of the monkey Macaca fascicularis. Journal of Physiology. 1984;357:575–607. doi: 10.1113/jphysiol.1984.sp015518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cone R A. Quantum relations of the rat electroretinogram. Journal of General Physiology. 1963;46:1267–1286. doi: 10.1085/jgp.46.6.1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dartnall H J A. The interpretation of spectral sensitivity curves. British Medical Bulletin. 1953;9:24–30. doi: 10.1093/oxfordjournals.bmb.a074302. [DOI] [PubMed] [Google Scholar]
- Dartnall H J A. The Visual Pigments, chap. 3. London, New York: Methuen & Co., Wiley & Sons; 1957. [Google Scholar]
- Fitzke F W. Optical properties of the eye. Investigative Ophthalmology and Visual Science. 1981;(suppl. 20):144. [Google Scholar]
- Gross K. Ueber vergleichende helligkeitsmessungen am albinotischen kaninchenauge. Zeitschrift FuerSinnephysiologie. 1932;62:38–43. [Google Scholar]
- Hughes A. A schematic eye for the rat. Vision Research. 1979;19:569–588. doi: 10.1016/0042-6989(79)90143-3. 10.1016/0042-6989(79)90143-3. [DOI] [PubMed] [Google Scholar]
- Kemp C M, Faulkner D J, Jacobson S G. The distribution and kinetics of visual pigments in the cat retina. Investigative Ophthalmology and Visual Science. 1988;29:1056–1065. [PubMed] [Google Scholar]
- Kooijman A C. Light distribution on the retina of a wide-angle theoretical eye. Journal of the Optical Society of America. 1983;A 73:1544–1550. doi: 10.1364/josa.73.001544. [DOI] [PubMed] [Google Scholar]
- Kooijman A C, Witmer F K. Light distribution on the retina of human and rabbit eyes: calculations and ‘in vitro’ measurements. Journal of the Optical Society of America. 1986;A 76:57–64. doi: 10.1364/josaa.3.002116. [DOI] [PubMed] [Google Scholar]
- Kraft T W, Schneeweiss D M, Schnapf J L. Visual transduction in human rod photoreceptors. Journal of Physiology. 1993;464:747–765. doi: 10.1113/jphysiol.1993.sp019661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lashley K S. The mechanism of vision. V. Journal of Comparative Psychology. 1932;13:173–185. [Google Scholar]
- Nakatani K, Tamura T, Yau K-W. Light adaptation in retinal rods of the rabbit and two other non-primate mammals. Journal of General Physiology. 1991;97:413–435. doi: 10.1085/jgp.97.3.413. 10.1085/jgp.97.3.413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker C, Williams T P. The effects of daylength on photostasis. Investigative Ophthalmology and Visual Science. 1995;(suppl. 36):515. [Google Scholar]
- Penn J S, Williams T P. Photostasis: Regulation of daily photon-catch by rat retinas in response to varous cyclic illuminances. Experimental Eye Research. 1986;43:915–928. doi: 10.1016/0014-4835(86)90070-9. 10.1016/0014-4835(86)90070-9. [DOI] [PubMed] [Google Scholar]
- Pflibsen K P, Pomerantzeff O, Ross R N. Retinal illuminance using a wide-angle model of the eye. Journal of the Optical Society of America A. 1988;5:146–150. doi: 10.1364/josaa.5.000146. [DOI] [PubMed] [Google Scholar]
- Pirenne M H. Liminal brightness increments. In: Davson H, editor. The Eye. New York and London: Academic Press; 1962. pp. 159–174. [Google Scholar]
- Rapp L M, Williams T P. A parametric study of retinal light-damage in albino and pigmented rats. In: Williams T P, Baker B N, editors. Effects of Constant Light on Visual Processes. New York: Plenum Press; 1980. pp. 135–159. [Google Scholar]
- Schremser J-L, Williams T P. Rod outer segment renewal as a mechanism for adaptation to a new intensity environment. I Rhodopsin levels and ROS length. Experimental Eye Research. 1995a;61:17–24. doi: 10.1016/s0014-4835(95)80054-9. [DOI] [PubMed] [Google Scholar]
- Schremser J-L, Williams T P. Rod outer segment renewal as a mechanism for adaptation to a new intensity environment. II Rhodopsin synthesis and packing density. Experimental Eye Research. 1995b;61:25–32. doi: 10.1016/s0014-4835(95)80055-7. [DOI] [PubMed] [Google Scholar]
- Wijngaard W. Theoretical considerations of optical interactions in an array of retinal receptors. In: Enoch J M, Tobey F L, editors. Vertebrate Photoreceptor Optics. Berlin: Springer Verlag; 1981. pp. 301–322. [Google Scholar]
- Williams T P, Baker B N, Dodge J. Pigmented rats, pupillary reflex and photostasis. Investigative Ophthalmology and Visual Science. 1994;(suppl. 35):1608. [Google Scholar]
- Williams T P, Webbers J P. Photometer for measuring intensity and rhodopsin distributions in intact eyes. Applied Optics. 1995;34:5720–5724. doi: 10.1364/AO.34.005720. [DOI] [PubMed] [Google Scholar]
- Young R W. A theory of central retinal disease. In: Sears M L, editor. New Directions in Ophthalmic Research. New Haven, CT, USA,: Yale University Press; 1981. pp. 237–270. [Google Scholar]


