Endogenous pacemaker activity of rat tumour somatotrophs

Abstract

1. Cells derived from a rat pituitary tumour (GC cell line) that continuously release growth hormone behave as endogenous pacemakers. In simultaneous patch clamp recordings and cytosolic Ca²⁺ concentration ([Ca²⁺]_i) imaging, they displayed rhythmic action potentials (44.7 ± 2.7 mV, 178 ± 40 ms, 0.30 ± 0.04 Hz) and concomitant [Ca²⁺]_i transients (374 ± 57 nM, 1.0 ± 0.2 s, 0.27 ± 0.03 Hz).

2. Action potentials and [Ca²⁺]_i transients were reversibly blocked by removal of external Ca²⁺, addition of nifedipine (1 μM) or Ni²⁺ (40 μM), but were insensitive to TTX (1 μM). An L-type Ca²⁺ current activated at -33.6 ± 0.4 mV (holding potential (V_h), −40 mV), peaked at -1.8 ± 1.3 mV, was reduced by nifedipine and enhanced by S-(+)-SDZ 202 791. A T/R-type Ca²⁺ current activated at -41.7 ± 2.7 mV (V_h, -80 or -60 mV), peaked at -9.2 ± 3.0 mV, was reduced by low concentrations of Ni²⁺ (40 μM) or Cd²⁺ (10 μM) and was toxin resistant. Parallel experiments revealed the expression of the class E calcium channel α1-subunit mRNA.

3. The K⁺ channel blockers TEA (25 mM) and charybdotoxin (10–100 nM) enhanced spike amplitude and/or duration. Apamin (100 nM) also strongly reduced the after-spike hyperpolarization. The outward K⁺ tail current evoked by a depolarizing step that mimicked an action potential reversed at −69.8 ± 0.3 mV, presented two components, lasted 2–3 s and was totally blocked by Cd²⁺ (400 μM).

4. The slow pacemaker depolarization (3.5 ± 0.4 s) that separated consecutive spikes corresponded to a 2- to 3-fold increase in membrane resistance, was strongly Na⁺ sensitive but TTX insensitive.

5. Computer simulations showed that pacemaker activity can be reproduced by a minimum of six currents: an L-type Ca²⁺ current underlies the rising phase of action potentials that are repolarized by a delayed rectifier and Ca²⁺-activated K⁺ currents. In between spikes, the decay of Ca²⁺-activated K⁺ currents and a persistent inward cationic current depolarize the membrane, activate the T/R-type Ca²⁺ current and initiate a new cycle.

The GC cell line, which is derived from a rat pituitary tumour (subclone of the GH₃ strain) (Tashjian, Yasumura, Levine, Sato & Parker, 1968), represents a homogeneous in vitro model of tumour somatotrophs. In contrast to GH₃ cells, they release growth hormone (GH) (Masur, Holtzman & Bancroft, 1974) but not prolactin (Bancroft, 1973). Under standard culture conditions, they do not express receptors for growth hormone-releasing hormone (GHRH) (Lin, Lin, Chang & Rosenfeld, 1992) but display functional somatostatin receptors mainly of the sst₁ and sst₂ subtypes (Mounier et al. 1995). In keeping with these observations, both somatostatin and octreotide, a long-acting preferential agonist at sst₂ receptor subtypes, inhibit basal GH release from GC cells (Mounier et al. 1995).

In order to understand the mechanisms underlying the sustained release of GH by GC cells in the absence of external stimulation, we analysed their membrane activity and cytosolic Ca²⁺ concentration ([Ca²⁺]_i) changes during long-lasting (1–2 h) simultaneous recordings of membrane potential and [Ca²⁺]_i. We report that GC cells spontaneously oscillate and we provide a complete analysis of the voltage, ionic and pharmacological dependency of the membrane potential and [Ca²⁺]_i oscillations. The Ca²⁺ and K⁺ currents underlying these oscillations have been analysed in patch clamp and a computer model of pacemaker activity is proposed.

Comparison with results obtained in normal somatotrophs in culture (Kwiecien, Tseeb, Kurchikov, Kordon & Hammond, 1997) suggests that: (i) both normal and tumour rat somatotrophs share the same pacemaker mechanism, (ii) normal somatotrophs behave mainly as ‘conditional pacemakers’, their activity being turned on by GHRH, while (iii) GC cells behave as ‘endogenous pacemakers’, their activity being spontaneous probably as a result of a permanent mechanism that favours the oscillatory state. The closest model to this pacemaker activity is that of the sino-atrial node cells of mammals (Irisawa, Brown & Giles, 1993).

METHODS

GC cell culture

The GC cell line (D. Gourdji; INSERM U159, Paris, France) was maintained routinely as a monolayer in complete medium composed of Dulbecco's modified Eagle's Medium-Ham's F12 medium (DMEM-F12; Seromed Biockrom, Berlin, Germany) supplemented with heat-inactivated horse and fetal calf serum (15 % v/v HS and 2.5 % v/v FCS; Sigma), glutamine (2 mM; Seromed) and antibiotics (100 i.u. ml⁻¹ penicillin and 100 μg ml⁻¹ streptomycin; Seromed). Cultures were incubated at 37°C in a humidified atmosphere containing 6 % CO₂. Cells were harvested by trypsin-EDTA (0.02–0.05 % w/v; Seromed) treatment and seeded at densities of 20 000–40 000 cells per dish of 35 mm diameter. They were cultured in low-serum medium composed of DMEM-F12 supplemented with 2.4 % (v/v) HS, 0.4 % (v/v) FCS, 10 mM Hepes, antioxidants (5 mg ml⁻¹ glutathione and 5 mg ml⁻¹ ascorbic acid), 0.1 % (w/v) bovine serum albumin (BSA; Boehringer Mannheim, Meylan, France), and glutamine and antibiotics at the same concentration as above. For fluorescence experiments the bottom of each dish was replaced with a 0.13–0.17 mm thick glass (Deckgläser; Poly Labo, Paul Block & Cie, Strasbourg, France). Experiments were performed after 2–8 days of incubation.

Extracellular solutions and drug applications

During the recording session, GC cells were perfused at 2–5 ml min⁻¹ with control Krebs solution containing (mM): 140 NaCl, 5 KCl, 2 CaCl₂, 1 MgCl₂, 5 Hepes, 5 NaHepes, and 10 glucose, pH 7.4. The osmolarity was adjusted to 320–330 mosmol l⁻¹. Other external solutions were locally applied through a concentric double pipette, one pipette allowing rapid delivery of drugs by gravity near the recorded cell (at 100 μl min⁻¹) and the other allowing rapid cessation of drug delivery by suction through a negative pressure circuit. Another suction pipette placed on the other side of the recorded cell allowed the rapid removal of the drug from the medium bathing the cell.

Current clamp recordings

Recordings were only made from single cells; cells that were part of a chain were not studied. Patch clamp electrodes (6–12 MΩ; Clark Electromedical) were immersed briefly in the internal solution (mM): 120 potassium gluconate, 20 KCl, 2 MgCl₂, and 10 Hepes, pH 7.4. They were backfilled with the same solution containing amphotericin B (100 μg ml⁻¹) kept at 4°C and made fresh every 2 h from the stock solution (20 mg ml⁻¹ in dimethylsulphoxide (DMSO), prepared before each experiment). The Ca²⁺-free solution was prepared by adding 1 mM EGTA to a Ca²⁺-free Krebs solution. The Na⁺-free and low-Na⁺ solutions were prepared by substituting TrisCl for NaCl in the Krebs solution and the pH was adjusted with TrisOH. Membrane potential was recorded at room temperature (20–22°C) with an Axopatch 200A (Axon Instruments) using the perforated whole-cell configuration with electrical access to the cell interior provided by the perforated patch of membrane. Typically, the final access resistance was 25–75 MΩ and was uncompensated. It stabilized after 10 min of recording and remained stable for the duration of the experiment (1–1.5 h). Data were stored on a digital tape recorder (DTR 1204).

Voltage clamp recordings

To record the L-type Ca²⁺ current, single cells were perfused with a Ba-TEA or a Ca-TEA solution containing (mM): 100 NaCl, 25 TEACl, 5 CsCl, 10 BaCl₂ or CaCl₂, 1 MgCl₂, 10 Hepes, and 10 glucose, pH 7.4. To record the T/R-type Ca²⁺ current, cells were perfused either with the preceding Ba-TEA solution or with a Ca-TEA solution containing (mM): 75 NaCl, 50 TEACl, 5 CsCl, 10 CaCl₂, 1 MgCl₂, 10 Hepes, 10 glucose; and 1 μM TTX, pH 7.4. The Ca²⁺-free solutions were prepared by adding 1 mM EGTA to a Ca²⁺-free TEA solution. The Na⁺-free solutions were prepared by replacing NaCl with TrisCl in the Ba-TEA or Ca-TEA solutions and the pH was adjusted with TrisOH. For perforated whole-cell recordings, patch pipettes were briefly immersed in the internal solution (mM): 120 potassium gluconate or CsCH₃O₃S, 20 CsCl, 2 MgCl₂, and 10 Hepes, pH 7.4 adjusted with CsOH. They were backfilled with the same solution containing amphotericin B as described above. For whole-cell recordings, patch pipettes were filled with a solution containing (mM): 140 caesium fluoride, 2 MgCl₂, 10 EGTA, and 10 Hepes, pH 7.4 adjusted with CsOH. Membrane currents were recorded at room temperature with an Axopatch 200A in response to voltage commands. They were filtered at 10 kHz. Leak currents were estimated from negative voltage steps and subtracted from all traces. In some current-voltage curves, series resistance errors were graphically corrected according to Marty & Neher (1995).

Measurements of cytosolic Ca²⁺ concentration

Cells were incubated for 15–20 min at room temperature with 1 μM fura-2 AM (acetoxymethyl ester form of the fluorescent dye fura-2, diluted from a 1 mM stock solution in DMSO; Molecular Probes) in the extracellular recording medium with 0.01 % Pluronic F-127 (Molecular Probes). The fura-2 AM-containing solution was then replaced by the recording medium for 30 min before experimentation. Measurements were performed on a Nikon Diaphot 300 microscope (Nikon, France). Each cell was alternately excited at wavelengths of 340 and 380 nm by using interference filters mounted on a computer-driven rotating wheel (λ10; Sutter Instruments, Norato, CA, USA). The fluorescence emitted from single cells in response to excitation at 340 nm (F₃₄₀) and 380 nm (F₃₈₀) was measured at 510 nm by means of a third interference filter and an intensified charge-coupled device (CCD) camera (Isis II; Photonic Science, Robertbridge, UK). The ratio (R = F₃₄₀/F₃₈₀) was displayed at a frequency digitized at 1–3 Hz by the Axon Imaging Workbench (AIW) system (Axon Instruments). Sometimes, to allow more rapid display, the ratio was performed only once every fifty measurements and F₃₈₀ was displayed at 10 Hz. Cytosolic free Ca²⁺ concentrations were determined from the equation:

where K_D is equal to 224 nM, R_min is the ratio of fluorescence intensities from wavelengths 340 and 380 nm for a minimal Ca²⁺ concentration inside the cell, R_max is the ratio of fluorescence intensities from wavelengths 340 and 380 nm for a maximal Ca²⁺ concentration inside the cell and S_f,380/S_b,380 is the ratio of Ca²⁺-free and Ca²⁺-bound fura-2 fluorescences at 380 nm (Grynkiewicz, Poenie & Tsien, 1985). The system was calibrated by recording the fluorescence ratio between 340 and 380 nm excitation light from cells recorded in the whole-cell configuration with pipettes containing 100 μM fura-2 and different ratios of CaEGTA/EGTA chosen to give minimal and maximal concentrations of free Ca²⁺ and concentrations covering the physiological range of [Ca²⁺]_i. Background fluorescence signals obtained in the cell-attached mode before whole-cell recordings were subtracted. The Ca²⁺ buffering capacity of fura-2 was estimated from comparison of electrophysiological recordings in fura-2 AM-loaded and non-loaded GC cells. The criteria used were spike amplitude, duration, frequency and after-spike hyperpolarization (AHP). Preparations in which any one of these parameters was different from the control were discarded. Therefore, the parameters for the retained cells in the two preparations were not significantly different (see Results).

Polymerase chain reaction (PCR) amplification

Total RNA was isolated from GC cell cultures by using the TRIzol protocol (Gibco) derived from Chomczynski & Sacchi (1987). The total RNA was first treated with DNase (1.5 U, 15 min, 37°C; Gibco) to remove any residual genomic DNA. cDNA templates for amplification by PCR were synthesized by reverse transcription (RT) of total RNA (2 μg) either with (RT+) or without (RT-) Moloney's murine leukaemia virus reverse transcriptase (Superscript II; Gibco) with random hexanucleotide primers (Gibco) and 24-deoxynucleoside 54-triphosphates (dNTPs; 2 mM) for 50 min at 42°C in the buffer (supplied by the manufacturer; Gibco). PCR was carried out using synthetic oligonucleotides as primer (purchased from Eurogentec) with sequences chosen on the basis of the rat calcium channel α1E-subunit sequence (GenBank, sequence L15453):

sense primer: 5′-CCTGTCATGGAAACTGTGACC-3′

antisense primer: 5′-CCATCAGACTGTTGGTCCTCC-3′.

The primer construction is specific for both the rat and mouse α1E-subunit sequences. The cDNA mixture was supplemented with 2.5 U Taq polymerase (Thermus aquaticus YT1; Gibco), 25 pmol of each primer, 5 μl 10 × PCR buffer (100 mM Tris-HCl pH 8.4, 20 mM MgCl₂, 500 mM KCl), 10 mM dNTP mix and water to bring the final volume to 50 μl. The reaction mixture was overlaid with 50 μl mineral oil (Promega) and incubated in a thermal cycler (Eppendorf) for thirty cycles each consisting of 1 min denaturation at 94°C, 1 min hybridization at 50°C, and 45 s polymerization at 72°C. After amplification, 10 μl of PCR product was run on an ethidium bromide-stained gel (1.5 % agarose). The PCR product was a fragment of 308 nucleotides. PCR on the RT- product served as a control for the DNase treatment quality.

Computer simulation

The model used in these simulations followed the methodology now standard in the field (Traub, Jefferys, Miles, Whittington & Toth, 1994) based on the equations originally employed by Hodgkin & Huxley (1952) with the exception that all the equations have been recast into the same form by a reparameterization. Because the cells were compact and essentially isopotential, only a single compartment was used. The values of all the parameters are shown in Tables 2 and 3. The mathematical system described here is essentially dimensionless: an appropriate set of units for the particular application is given in Table 1. The currents are assumed to follow Hodgkin-Huxley style dynamics with the extension that the gating variables may also depend on the calcium concentration. It should be noted here that the calcium model used is dimensionless and that its parameters are degenerate. No attempt has been made at this stage to quantitatively relate the very complex calcium dynamics of these cells to the drastically simplified model used. Collectively, the parameters for calcium buffering and diffusion and for calcium-activated channels give a sensible form for calcium-dependent processes, but individually they have no absolute significance.

Table 2.

Channel	Ion	Conductivity (Gk)
L	Ca2+	1.23
KV	K+	0.87
BKCa	K+	1.72
T	Ca2+	1.13
SKCa	K+	0.41
Cationic leak	cations	0.19

K_V, delayed rectifier K⁺ channel; BK_Ca, high-conductance Ca²⁺-sensitive K⁺ channel; SK_Ca, small-conductance Ca²⁺-sensitive K⁺ channel.

Table 3.

Gate	Channel	α	β	γ	δ	ε	μ	ν	p	Ca pool
1	L	−0.130	1	0	−30.6	680	0.19	0.57	1	—
2	L	0.060	1	0	−27.8	8.7	0.66	0.66	2	—
3	KV	0.084	1	0	−5.6	170	0.31	0.45	1	—
4	BKCa	0.023	1	1.8	0.2	1	1.0	1.1	1	1
5	T	0.096	1	0	−37.0	1	0.66	0.55	2	—
6	T	−0.087	1	0	−42.5	1	0.35	0.21	1	—
7	SKCa	0.27	0	1	3.7	1	1	1	1	3

Table 1.

Variable	Unit
Cmem	μF cm−2
G	μA cm−2 mV−1
V	mV
E	mV
t	ms
β	mV−1
ε	ms
A	μm
B	ms
C	ms
D	μA mV−1μM−1
y	μm

All other quantities are dimensionless. For definitions see Computer simulation.

The compartment is uniquely specified by its membrane capacitance, C_mem, the densities, G_k (k = 1…N_ch) of its N_ch channel types, expressed as conductance per unit area and the reversal potentials, E_i, for each of the four ions Na⁺, K⁺, Ca²⁺ and Cl⁻. Each channel, k, has N_g,k gates, governed by gating variables X_i,k (i = 1…N_g,k).

The potential V of the compartment satisfies:

(1)

for integer powers p_i,k. The apparent reversal potential E_I,k (where subscript I,k denotes the ion to which channel k is permeable) at potential V is derived from the actual reversal potential using the Goldman-Hodgkin-Katz constant field equations.

The gating variables have time dependence (omitting subscript i and k on X, its equilibrium value X_e and the gate constants α, β, γ, δ, ɛ, μ and ν):

(2)

with the steady-state open fraction X_e(V, [Ca²⁺]) satisfying:

(3)

where y is the dimensionless calcium concentration (see below) in the region in which the channel is located.

The calcium dynamics are based on a simple domain model. The membrane area was divided into N_p concentric patches with outer-boundary area fraction b_i and calcium concentration y_i, linked by diffusion rates d_i. The same buffering time constant B and base calcium level A apply to all regions, with calcium currents G_Ca,i scaled to concentration changes by C and diffusion parameters scaled globally by D. Thus:

(4)

Patch (i - 1) lies entirely within patch i but the topology of the enclosure can be varied: small d_i corresponds to low diffusion, implying a small boundary which in the limit would be a single circular subregion; large d_i corresponds to rapid diffusion, which would be the case if the enclosed area were composed of many distinct regions, giving a larger total contact length. In the present case, calcium entry is only allowed into region 1: G_Ca,i = 0 for i = / 1. Calcium-dependent channels may be located in any region by choosing which calcium variable to include in eqn (3). This is given in the column ‘Ca pool’ of Table 3.

The remaining parameters of the model, not defined in Table 3 are: C_mem = 1.0 μF cm⁻²; reversal potentials: K⁺, -81 mV; Ca²⁺, 49 mV; cationic leak, -30 mV; calcium: A = 10⁻⁵, B = 830, C = 170, D = 25, b₁ = 0.036, b₂ = 0.22, d₁ = 31, d₂ = 12 (A, B, C, D, b₁, b₂, d₁ and d₂ are dimensionless).

Chemicals

TTX and apamin were purchased from Latoxan. All other chemicals were purchased from Merck or Sigma. ω-Agatoxin IVA was a generous gift from Dr Saccomano, Pfizer Central Research (Groton, USA) and was prepared as described in Mintz, Adams & Bean (1992).

Statistics

All values are presented as means ±s.e.m. Student's paired t tests were used for the statistical comparison of two groups. P < 0.05 was considered significant: * 0.05 < P > 0.01; ** 0.01 < P > 0.001; ***P < 0.001.

RESULTS

The data reported in this paper are based on 258 GC cells recorded in current clamp and 210 cells recorded in voltage clamp.

Pacemaker activity and spontaneous [Ca²⁺]_i transients

After 2–3 days in culture, all recorded GC cells exhibited spontaneous rhythmic action potentials of constant frequency, in the absence of external stimulation (Fig. 1A). When measured on a sample of ten GC cells subjected to patch clamping alone, rhythmic action potentials (Fig. 1A, inset) had a mean frequency of 0.38 ± 0.05 Hz (range, 0.18–0.65), peaked to a mean potential of -10.1 ± 1.2 mV (range, -16 to -3.9 mV) and were followed by an AHP to -55.0 ± 1.4 mV (range, -60 to -48 mV) with two components (Fig. 1A, AHP₁ and AHP₂). The mean amplitude of action potentials measured from their peak to the following AHP₁ was 44.9 ± 1.9 mV (range, 38.3–54 mV). Their average width measured at mid-amplitude (half-width) was 180 ± 21 ms (range, 94–334 ms). The histogram of the interspike intervals was fitted by a single Gaussian curve (Fig. 1B; mean interspike interval, 3.2 ± 0.5 s; range, 1.5–6 s), showing that GC cells behave as regularly spiking cells. Between two consecutive spikes, the membrane spontaneously depolarized from the peak of the AHP₁ to the threshold potential of the following spike (-41.6 ± 1.1 mV; range, -46 to -38 mV; n = 10) defined as a break in the upstroke velocity of the spike (Fig. 1A, single arrow). This phase of slow depolarization was called pacemaker depolarization by analogy with pacemaker activity of cardiac cells (DiFrancesco, 1993). The pacemaker depolarization either immediately triggered the following spike or, upon repolarization from AHP, stabilized around −40 mV for a few seconds. During this period of relative potential stability, subthreshold membrane fluctuations that failed to evoke action potentials were observed (Fig. 1A, double arrow and inset). The injection of a constant current pulse (-3 or -10 pA; n = 5) allowed calculation of a 2- to 3-fold increase in membrane resistance (from 0.85 ± 0.17 to 1.94 ± 0.21 GΩ) during the interspike interval (Fig. 1C). This experiment, performed in whole-cell configuration to minimize access resistance, suggested that a decrease in conductance underlies the slow pacemaker depolarization.

Figure 1. Pacemaker activity of GC cells.

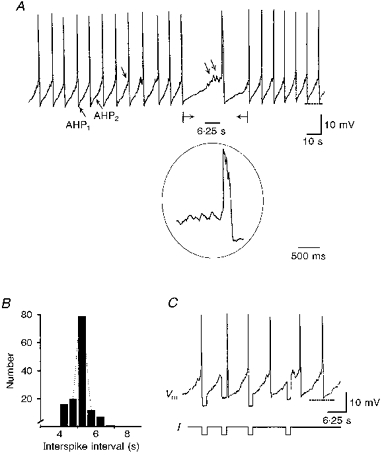
A, perforated whole-cell patch clamp recording of the spontaneous activity of a GC cell. In the period between the horizontal arrows, the trace speed was increased. Inset, the same spike displayed at a greater speed. AHP, after-spike hyperpolarization. See text for explanation of single and double arrows. B, histogram of the duration of the interspike intervals of the cell shown in A is fitted by a single Gaussian curve (mean duration, 4.9 ± 0.5 s; n = 135; bin width, 1 s). C, injection of negative current pulses (I, -10 pA) during the slow pacemaker depolarization showed that membrane resistance increased from 0.4 to 1.2 GΩ (whole-cell recording). V_m, membrane potential. The dashed lines in A and C indicate a V_m of -53 and -51 mV, respectively.

The pacemaker activity in fura-2 AM-loaded GC cells had similar characteristics to that of non-loaded cells (compare Figs 1A and 2A). Spikes had a mean amplitude of 44.7 ± 2.7 mV (range, 39–53 mV), a mean half-width of 178 ± 40 ms (range, 96–322 ms) and were followed by an AHP to -52.7 ± 2.2 mV (range, -60 to -47 mV; n = 8). A spontaneous [Ca²⁺]_i transient (mean amplitude, 374 ± 57 nM; range, 143–631 nM) corresponded to each spontaneous spike. The transients were evoked from a basal level of 173 ± 20 nM (range, 97–252 nM) and lasted 5 times longer than spikes (mean half-width, 1.0 ± 0.2 s; n = 5; Figs 2A and 3A). Pacemaker activity and [Ca²⁺]_i transients had similar mean frequencies (0.3 ± 0.04 and 0.27 ± 0.03 Hz, respectively). Histograms of the interspike intervals (mean interval, 3.5 ± 0.4 s; range, 2.5 to 4.7 s; n = 5; Fig. 2B, left) and that of the intervals between [Ca²⁺]_i transients (mean interval, 3.4 ± 0.4 s; range, 2.4–4.6 s; n = 5; Fig. 2B, right) were both fitted by a single Gaussian curve and gave mean intervals that were not significantly different. Simultaneous recordings of membrane potential and [Ca²⁺]_i transients also allowed comparison of the kinetics of the two signals (Fig. 3A). The mean time to peak of action potentials (measured from threshold to peak) was 164.3 ± 7.2 ms while that of [Ca²⁺]_i transients was 5 times longer (872.5 ± 64.6 ms; n = 5). The decay of the [Ca²⁺]_i transients was fitted (after the first 0.5 s) by a monoexponential with a decay time constant τ of 2.33 ± 0.28 s (n = 5; Fig. 3A, inset).

Figure 2. Simultaneous recordings of pacemaker activity and cytosolic Ca²⁺ oscillations.

A, simultaneous recordings of pacemaker activity (top) and [Ca²⁺]_i transients (bottom) from a single GC cell loaded with fura-2 AM (perforated whole-cell). In this and subsequent figures, ratio means the ratio of fluorescence intensities for excitation wavelengths of 340 and 380 nm (frequency of ratio acquisition, 3 Hz). B, histograms of the duration of the interspike interval (left) and of the intervals between [Ca²⁺]_i transients (right) were fitted by a single Gaussian curve (mean duration, 4.3 ± 0.5 s (n = 46) and 4.1 ± 0.9 s, (n = 27), respectively; bin width, 0.5 s).

Figure 3. Time correspondence between pacemaker activity and cytosolic Ca²⁺ oscillations - voltage dependence of pacemaker activity.

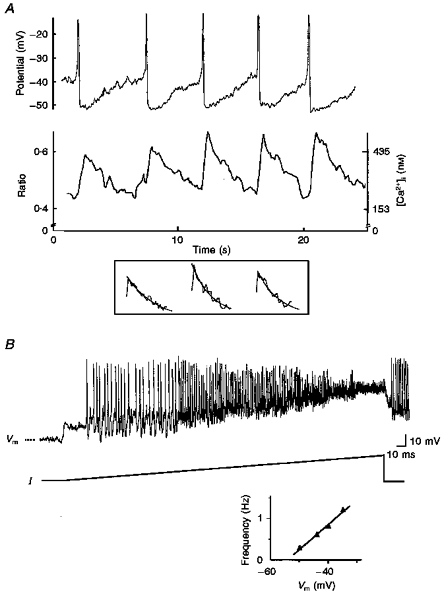
A, both membrane potential (top) and cytosolic Ca²⁺ oscillations (bottom) are shown on a rapid time base. During each slow pacemaker depolarization, cytosolic Ca²⁺ oscillations (frequency of ratio acquisition, 10 Hz) decayed to a basal level of 180 nM. The decay of the [Ca²⁺]_i transients was fitted by a monoexponential. The three transients shown in the inset correspond to the second, third and fifth transient shown in the bottom trace. Decay time constants (τ) from left to right were 3.2, 2.1 and 2.3 s. B, injection of a continuous depolarizing current of increasing amplitude (from -4 to +23 pA, I). The dashed line indicates -50 mV. At the end of the recording the current injection was stopped and pacemaker activity recovered. The bottom graph shows the linear relation between spike frequency and membrane potential measured at the level of the AHP₁.

Voltage- and Ca²⁺-sensitivity of the pacemaker activity

When the membrane was hyperpolarized to more than -50.2 ± 2.5 mV, spikes (Fig. 3B) and [Ca²⁺]_i transients were completely suppressed. At potentials more depolarized than -31.7 ± 4.4 mV spikes became too small to be distinguished from noise (Fig. 3B). In all cells tested, the pacemaker activity was present in a narrow range of membrane potentials (15.0 ± 2.5 mV; n = 8). In this narrow range, spike frequency increased linearly with membrane potential (Fig. 3B, graph). These results show that voltage-sensitive currents participate in pacemaking and [Ca²⁺]_i transients. Application of a Ca²⁺-free external solution (1–2 min; n = 5; Fig. 4A), or the L-type Ca²⁺ channel blocker nifedipine (1–3 μM; 10–60 s duration; n = 7; Fig. 4B) temporarily stopped spontaneous firing and [Ca²⁺]_i transients. The membrane potential stabilized at -30 ± 3 mV upon removal of external Ca²⁺, and at -35.0 ± 2.9 mV during nifedipine-evoked silence. Basal [Ca²⁺]_i was decreased to 125 ± 28 nM in both cases. Inorganic Ca²⁺ channel blockers such as Cd²⁺ (1 mM, 5–200 s) or Ni²⁺ (30–40 μM, 10–100 s; Fig. 4C) stopped the firing. During Cd²⁺ application, spike amplitude progressively decreased to an undetectable level as the membrane potential depolarized to -25.6 ± 4.0 mV (n = 5, not shown). A different effect was produced by Ni²⁺: the spike frequency decreased and then the cell stopped firing at a mean potential of -42 ± 3 mV (n = 5; Fig. 4C). All these effects were reversible in 2–4 min. Complete disappearance of spikes and [Ca²⁺]_i transients in the absence of external Ca²⁺ or when L-type Ca²⁺ channels were pharmacologically blocked suggested that the rising phase of spontaneous rhythmic spikes and [Ca²⁺]_i transients result, at least in part, from spontaneous Ca²⁺ entry through L-type Ca²⁺ channels.

Figure 4. Ca²⁺ dependence of pacemaker activity and [Ca²⁺]_i transients.

A, simultaneous recordings of membrane potential (top) and cytosolic Ca²⁺ oscillations (bottom) during (Ca²⁺ free, 1 min 50 s) and after removal of external Ca²⁺. Pacemaker activity stopped at a V_m of -26 mV. Concomitantly, the amplitude of [Ca²⁺]_i transients decreased without change in the basal [Ca²⁺]_i level. Upon washout, both activities recovered (frequency of ratio acquisition, 1 Hz). B, nifedipine (20 s) reversibly stopped pacemaker activity at a V_m of -38 mV. C, Ni²⁺ (100 s) reversibly stopped pacemaker activity at a V_m of −40 mV. Dashed lines indicate -48 mV (B) and -50 mV (C).

The slowly inactivating, high-voltage-activated (HVA) Ca²⁺ current and action potential upstroke

Figure 5A shows the slowly inactivating HVA current (bottom traces) recorded in the presence of external Ba²⁺ in response to depolarizing steps (top trace). The mean cell capacitance was 12.8 ± 0.5 pF (n = 20). The time to peak varied from 36.6 ± 8.5 ms (at -25 mV) to 9.3 ± 0.9 ms (at 5 mV). The current-voltage relation (n = 6; Fig. 5B) and the steady-state activation curve (n = 5; Fig. 5E, •) were obtained from records as in Fig. 5A. The amplitude of the HVA current was measured at the end of the step (sustained HVA current). The sustained HVA current activated at -33.6 ± 0.4 mV, was half-activated at V_½ of -18.7 ± 1.5 mV and peaked around -10 to 0 mV (n = 5). When recorded in the presence of external Ca²⁺ (10 mM), it showed some inactivation (Fig. 5C, left). Removal of external Ca²⁺ (n = 5; Fig. 5C, right) or Ba²⁺ (n = 5, not shown) strongly decreased the HVA current at all potentials tested. At -10 mV it was decreased by 89 ± 7 % (n = 5; Fig. 5C). Steady-state voltage-dependent inactivation was studied by varying the holding potential (V_h) for 1 min before applying a test pulse to 0 mV (Fig. 5D). The amplitude of the sustained HVA current during the test pulse was plotted against V_h to give the inactivation curve (n = 5; Fig. 5E, ○). The sustained current began to inactivate at -37.7 ± 0.8 mV, was half-inactivated at -30.2 ± 0.8 mV and totally inactivated at -19.9 ± 4.3 mV (n = 5).

Figure 5. Voltage dependence of the HVA Ba²⁺ or Ca²⁺ current.

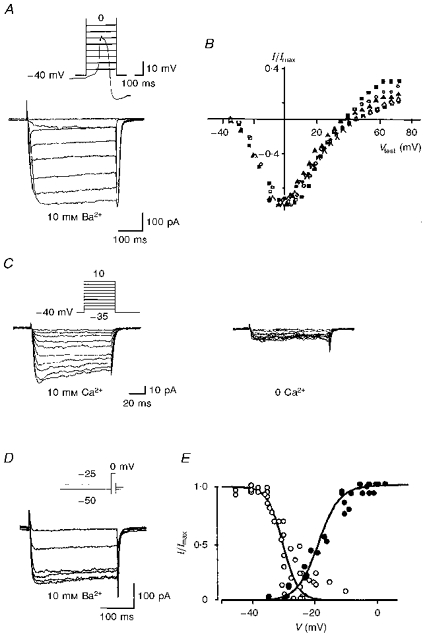
All recordings were performed in the perforated whole-cell configuration at a holding potential (V_h) of −40 mV in the presence of 10 mM Ba²⁺ (A, B, D and E) or Ca²⁺ (C). A, HVA currents (bottom traces) recorded in response to command steps from -35 to +35 mV. The first voltage steps are superimposed on a spontaneous Ca²⁺ spike recorded in the same cell in current clamp mode (top trace). After the 100 ms command step, repolarization to −40 mV resulted in an inward tail current. Cell capacitance was 12.2 pF. B, current-voltage relation of the sustained HVA current summarized for six cells. For comparison across cells, currents were normalized (I/I_max) to the current at 0 mV, a voltage at which maximal current (I_max) was recorded. V_test, test potential. C, HVA currents recorded in the presence (left) or in the absence (0 Ca²⁺, right) of 10 mM external Ca²⁺. D, HVA currents recorded in response to a 250 ms command step to 0 mV from holding potentials varying from -50 to -25 mV. E, inactivation-activation curve of the HVA current. ○, sustained current amplitude, normalized to the maximal sustained current obtained at a V_h of −40 to -50 mV, plotted against V_h (from data illustrated in D; n = 5). Data were fitted with a smooth curve derived from the Boltzmann relation: I/I_max = [1 + exp ((V - V_½)/k)]⁻¹, where the potential at half-maximal inactivation (V_½) = -30 mV and the slope factor (k) = 2.3 mV. •, sustained current amplitude, normalized to maximal current obtained at a V_test of 0 mV, plotted against V_test (from data illustrated in A; n = 5). Data were fitted with a smooth curve: I/I_max = [1 + exp(-(V - V_½)/k)]⁻¹, where V_½ of activation = -19 mV and k = 4 mV.

Cadmium (300 μM; n = 13), or the dihydropyridine antagonist of L-type channels, nifedipine (1–3 μM; n = 6), respectively, totally depressed (Fig. 6A) or reduced (Fig. 6B) the sustained HVA current at all potentials tested. At 0 mV, nifedipine reduced the current by 64 ± 9 % (n = 6) while the dihydropyridine agonist S-(+)-SDZ 202 791 (1 μM) enhanced it by 32 ± 8 % (n = 10; Fig. 6C). Both dihydropyridines also altered the voltage dependence, the peak HVA current being shifted to the right with nifedipine (Fig. 6B) and to the left with S-(+)-SDZ 202 791 (not shown). The P-type channel blocker ω-agatoxin IVA paradoxically increased the HVA current by 37 ± 11 %, an effect that could not be attributed to cytochrome C used to prepare the toxin solution (Fig. 6C). Ni²⁺ (40 μM, not shown; n = 7), the N-type channel blocker ω-conotoxin GVIA and TTX had no effect while replacement of external Na⁺ with Tris significantly increased the HVA current by 19 ± 6 % (10 mM external Ca²⁺; Fig. 6C). All these results strongly suggested that the slowly inactivating HVA current is a L-type Ca²⁺ current.

Figure 6. Pharmacology of the HVA Ba²⁺ current.

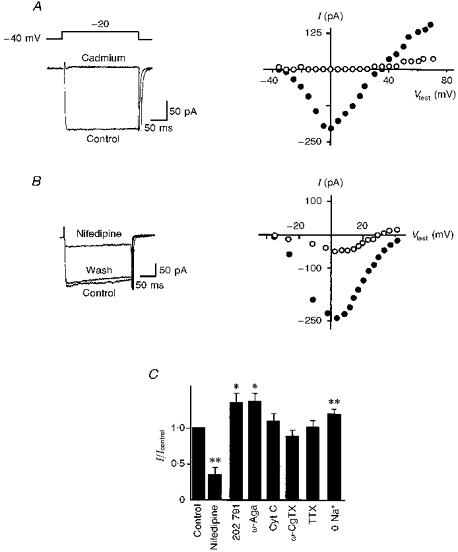
A, HVA currents in response to a depolarizing step to -20 mV before (Control) and during cadmium (300 μM) application (left) and the current-voltage relation of the sustained HVA current from the same cell (right) before (•) and during (○) cadmium application (ramp command, 2.5 mV ms⁻¹). B, HVA currents in response to a depolarizing step to -20 mV before (Control), during and after (Wash) application of nifedipine (3 μM; left) and the current-voltage relation of the sustained HVA current from the same cell (right) before (•) and during (○) nifedipine application (currents have been graphically corrected). C, histogram of the amplitude of the sustained HVA Ba²⁺ current at 0 mV under control conditions, in the presence of nifedipine (3 μM, n = 6), S-(+)-SDZ 202 791 (202 791; 1 μM, n = 10), ω-agatoxin IVA (ω-Aga; 250 nM, n = 5), cytochrome C (Cyt C; 1 mg ml⁻¹, n = 6), ω-conotoxin GVIA (ω-CgTX; 1 μM, n = 9), TTX (1 μM, n = 6) and in the absence of external Na⁺ (0 Na⁺, n = 11). Currents were normalized (I/I_control) to the current under control conditions (I_control). Perforated whole-cell configuration; 10 mM external Ba²⁺; V_h, −40 mV. * 0.05 < P > 0.01; ** 0.01 < P > 0.001.

The rapidly-inactivating, medium voltage-activated (MVA), toxin-resistant Ca²⁺ current and action potential upstroke

Figure 7A shows the MVA currents (bottom traces) recorded in response to depolarizing steps from a V_h of -60 mV (top trace) when Ca²⁺ (10 mM) was used as a charge carrier (whole-cell configuration). The criterion for assuming that the L-type Ca²⁺ current had disappeared (usually 10–20 min after seal formation) was that essentially no inward current was activated under the same conditions when test pulses were applied from a V_h at −40 mV. The V_h was fixed at -60 mV in order to study activation properties of the transient current from a potential close to the maximal current recorded during pacemaker activity (the maximal hyperpolarization during AHP was around -60 mV). The current-voltage relation (V_h, -60 mV; n = 6; Fig. 7B) and activation curve (V_h, -80 mV; n = 6; Fig. 7D, ▪) showed that detectable transient current appeared at -41.7 ± 2.7 mV, was half-activated at -25.4 ± 3.1 mV and peaked around -10 to -5 mV. The MVA current reached a peak after a delay varying from 10 to 3 ms depending on the amplitude of the voltage step (9.9 ± 2.0 ms at −40 mV and 2.8 ± 0.2 ms at -10 mV; n = 5). The time course of inactivation was well described by a single exponential function (τ = 12.5 ± 1.2 ms at -15 mV; n = 5) when the current had a small amplitude (< -150 pA). For larger currents (> -150 pA), the time course of inactivation at -15 mV was described by a double exponential (τ₁ = 1.6 ± 0.3 ms and τ₂ = 20.6 ± 2.5 ms; n = 6). In the presence of external Ba²⁺ (10 mM), the MVA current had a small amplitude and its time course of inactivation was fitted by a monoexponential at all potentials tested (τ = 12.3 ± 0.7 ms at -15 mV; n = 6; not shown). Steady-state inactivation was studied by varying the V_h from -80 to -20 mV for 700 ms before activating the transient current by a subsequent 60 ms command step to 0 mV (Fig. 7C). The transient current began to inactivate at -78.3 ± 0.9 mV, was half-inactivated at -57.7 ± 0.7 mV and fully inactivated around -35 to -30 mV (Fig. 7D, □; n = 7). The activation-inactivation curves showed very little overlap (Fig. 7D). The time and voltage dependence of removal of inactivation was examined by varying the duration of the hyperpolarizing step at -60 or -100 mV before a subsequent test to -10 mV. Results obtained with these two protocols were not significantly different. The time course of recovery from inactivation showed that the transient current had recovered by 50 % after 191 ± 51 ms at -60 or -100 mV (n = 9; Fig. 7E). After a time (2 s) close to the mean interspike interval (3.2 ± 0.5 s), the transient current had recovered by 94 ± 2 % (n = 5).

Figure 7. Voltage dependence of the fast-inactivating MVA current.

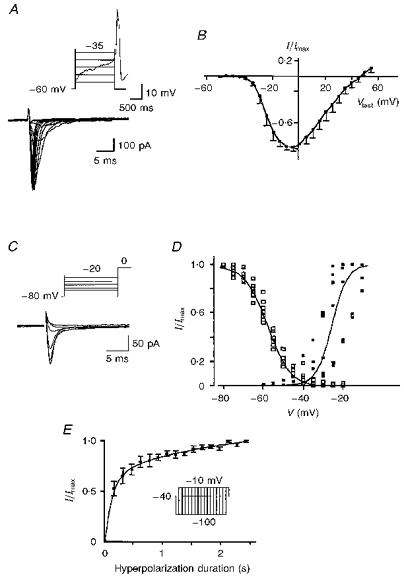
MVA Ca²⁺ currents recorded in the whole-cell configuration in the presence of 10 mM external Ca²⁺ after run-down of the L-type current. A, MVA currents (bottom traces) in response to command steps from -55 to +15 mV (V_h = -60 mV). The first voltage steps are superimposed on a spontaneous Ca²⁺ spike recorded in the same cell in current clamp mode (top trace). B, current-voltage relation for the peak MVA current (V_h = -60 mV, n = 6). Currents were normalized (I/I_max) to the maximal current (I_max) recorded at 0 mV. C, currents in response to a V_test of 0 mV from holding potentials varying from -80 to -20 mV. D, inactivation-activation curve: ▪: V_½ of activation, -25 mV (k = 4 mV, n = 6); □: V_½ of inactivation, -58 mV (k = 5.7 mV, n = 7). E, plot of the relative peak MVA current amplitude generated by a voltage step to -10 mV against the duration of the preceding hyperpolarizing step to -100 mV (n = 5). The maximal amplitude (I_max) is that evoked following a 2400 ms hyperpolarizing step.

Low concentrations of Ni²⁺ (40 μM; Fig. 8A) or Cd²⁺ (10 μM; Fig. 8B) reversibly reduced the MVA current at all potentials tested. At 0 mV the peak current was reduced by 56 ± 8 % in 40 μM Ni²⁺ (n = 18) or 36 ± 12 % in 10 μM Cd²⁺ (n = 7) (Fig. 8D). In contrast, ω-conotoxin GVIA, ω-agatoxin IVA and nifedipine had no effect (Fig. 8D). Removal of external Na⁺ did not significantly affect the MVA current (Fig. 8D) while removal of external Ca²⁺ reversibly decreased the MVA current (Fig. 8C) at all potentials examined. The mean decrease at the peak (test potential (V_test) = -20 to -10 mV) was -77 ± 12 % (n = 7). All these results suggested that the MVA current is a Ca²⁺ current with a threshold of activation and steady-state inactivation lying between those of the T-type and the HVA currents. MVA current presents a higher permeability to Ca²⁺ than to Ba²⁺, a sensitivity to low concentrations of both Ni²⁺ and Cd²⁺ and a resistance to L-, N- and P-type channel blockers.

Figure 8. Pharmacology of the MVA Ca²⁺ current.

A and B, MVA Ca²⁺ whole-cell current in response to a depolarizing step from -50 to +20 mV in the absence (Control) and in the presence of 40 μM Ni²⁺ (A) or 10 μM Cd²⁺ (B). C, removal of external Ca²⁺ (0 Ca²⁺) strongly reduced the control MVA current (Control). D, histogram of the amplitude of the normalized peak MVA currents at 0 mV in the absence (Control), in the presence of Ni²⁺ (40 μM, n = 18), Cd²⁺ (10 μM, n = 7), ω-conotoxin GVIA (ω-CgTX; 1 μM, n = 8), nifedipine (3 μM, n = 7), ω-agatoxin IVA (ω-Aga; 250 nM, n = 9) or cytochrome C (Cyt C; 1 mg ml⁻¹, n = 8) and in the absence of external Na⁺ (0 Na⁺; n = 5). * 0.05 < P > 0.01; ***P < 0.001. E, detection of the α1E-subunit in GC cells. A cDNA fragment of 308 nucleotides was either synthesized (RT+) or not (RT-) by the reverse transcriptase and amplified by using α1E-specific primers (sense and antisense) in embryonic day 13 dorsal root ganglion (DRG) neurones, in GC cells, in cortical neurones from 2-month-old rats (Cortex) and in plasmid containing the complete cDNA sequence of rat α1E. The PCR generated a single band of identical size in each case.

Since the class E calcium channel α1-subunit (α1E)-mediated current (Ellinor et al. 1993) has similar properties to those of the present MVA Ca²⁺ current, we investigated the presence in GC cells of the mRNA coding for the α1E-subunit. Figure 8E shows that PCR amplification of the α1E-clone yielded an expected fragment of 308 nucleotides in length, confirming the efficiency of the primers. The oligonucleotide specificity of the RT-PCR on rat neuronal tissues was confirmed by specific amplification of a similar fragment in cortical neurones from 2-month-old rats and in embryonic day 13 rat dorsal root ganglion neurones as previously described (Hilaire, Diochot, Desmadryl, Richard & Valmier, 1997). Amplification of cDNA prepared from GC cell RNA also produced a fragment of 308 nucleotides in length. The specificity of amplification was enhanced by use of the Genetics Computer Group program (Wisconsin package version 9.1; GCG, Madison, WI, USA) and the primer was tested on α1A-, α1B-, α1C- and α1D-clones as negative controls (not shown). We concluded that the α1E-subunit mRNA was present in GC cells.

K⁺ currents, action potential downstroke and after-spike hyperpolarization

Addition of TEA (5 s to 2 min), at a concentration (25 mM) that reduces the delayed rectifier K⁺ current and Ca²⁺-activated K⁺ currents, had different effects depending upon the initial membrane potential. When applied at the control membrane potential (Fig. 9A) it significantly increased spike amplitude by 65 ± 20 % (from 48.9 ± 2.3 to 72.6 ± 2.4 mV) and spike duration by 589 ± 155 % (from 170 ± 12 to 1203 ± 337 ms) and decreased spike frequency by 63 ± 6 % (from 0.33 ± 0.04 to 0.13 ± 0.03 Hz) (n = 6). The same effects were observed on [Ca²⁺]_i transients which peaked to 1875 ± 177 nM from a basal level of 399 ± 18 nM (n = 5) in TEA (Fig. 9A). The decay of the increased [Ca²⁺]_i transients was fitted by a double exponential (τ₁ = 0.46 ± 0.06 s and τ₂ = 6.9 ± 2.0 s). In other cells, the same concentration of TEA induced a long-duration Ca²⁺ spike with a plateau (7–30 s) at -4.4 ± 0.9 mV (n = 5; Fig. 9B). In contrast, at slightly more hyperpolarized potentials (during a continuous current injection of -1 to -3 pA), the same TEA application stopped firing at a mean potential of -49.7 ± 3.4 mV (n = 4, not shown). Both effects could be obtained on the same cell depending upon initial membrane potential. Charybdotoxin (CTX; 100 nM, 3–4 min; n = 10), significantly increased the spike amplitude by 27 ± 8 % (from 48.8 ± 3.4 to 60.1 ± 2.9 mV) and the first component of the AHP (AHP₁, from -54.5 ± 1.4 to -55.7 ± 1.4 mV; P < 0.005; Fig. 10A) but did not significantly change spike duration (119 ± 11 ms in control vs. 137 ± 19 ms in CTX) and frequency (0.47 ± 0.06 Hz in control vs. 0.54 ± 0.07 Hz in CTX). Apamin (100 nM, 10 min; n = 6) significantly increased spike duration by 101 ± 29 % (from 202 ± 44 to 385 ± 56 ms) and strongly decreased the first component of the AHP (from -51 ± 3 to -45 ± 2 mV; Fig. 10B) but did not significantly affect spike amplitude (45 ± 2 mV in control vs. 39 ± 4 mV in apamin) or spike frequency (0.38 ± 0.04 Hz in control vs. 0.46 ± 0.09 Hz in apamin). When CTX and apamin were applied at the same time (100 nM of each, 30 s to 3 min; n = 6), they evoked long-duration Ca²⁺ spikes (range, 205–8200 ms) with a plateau at -15 to -8 mV (Fig. 10C), which suddenly repolarized even during the toxin application period (not shown). In contrast, external Cs⁺ (3–10 mM, n = 6) had no effect.

Figure 9. Effect of TEA on pacemaker activity and [Ca²⁺]_i transients.

A, application of TEA (25 mM, 1 min 50 s) increased spike amplitude (from 45 to 80 mV) and duration (from 115 to 538 ms) and decreased spike frequency (from 0.23 to 0.10 Hz). In the same cell the amplitude of [Ca²⁺]_i transients was concomitantly increased by a factor of 5. B, in another GC cell, TEA application (25 mM, 20 s) induced a long-lasting (18 s) Ca²⁺ spike that transiently peaked to a V_m of +6 mV, had a plateau phase at a V_m of -8 mV and repolarized after the end of TEA application to V_AHP1 of -53 mV. The dashed line indicates a V_m of -50 mV.

Figure 10. Effect of blockers of Ca²⁺-activated K⁺ currents on pacemaker activity.

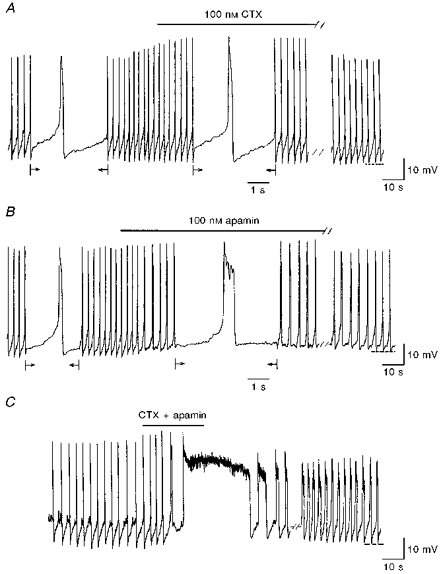
A, application of charybdotoxin (CTX; 100 nM, 3 min) increased spike amplitude (from 49 to 63 mV) and, in this cell, spike duration (from 160 to 210 ms). B, application of apamin (100 nM, 10 min) increased spike duration (from 166 to 398 ms) and strongly decreased the AHP₁ (from -56 to -50 mV). C, application of both toxins at the same concentration (100 nM, 30 s) induced a long-lasting (30 s) spike with a plateau at a V_m of -10 mV. Note that just before the long-lasting spike, the AHP₁ was replaced by an after-spike depolarization. Upon washout, the activity did not totally recover. Recordings in A-C were obtained from three different GC cells. The dashed lines indicate -52 mV (A), -54 mV (B) and -50 mV (C). Arrows in A and B indicate the intervals during which the trace speed was increased. Note that in C the trace speed was constant during the whole recording.

The slow pacemaker depolarization

To test the hypothesis that the 2- to 3-fold increase in membrane resistance observed in the interspike interval (see Fig. 1C) corresponds to a decrease in the outward currents, the time course of the outward tail current activated after a depolarization was studied. Figure 11A shows the outward tail currents (middle traces) recorded at potentials from -90 to −40 mV following a 200 ms depolarizing pulse to 0 mV (to mimic an action potential, top trace) in control Krebs solution (perforated whole-cell configuration). The outward tail current reversed at −69.8 ± 0.3 mV (n = 12), a potential close to the estimated reversal potential for K⁺ ions and its decay was fitted by two exponentials (bottom graph). It was completely suppressed by Cd²⁺ (400 μM; Fig. 11B), thus showing that it resulted from Ca²⁺-activated K⁺ currents. Under control conditions, at a V_h of −40 mV, this Ca²⁺-activated K⁺ tail current decayed with two time constants (τ₁ = 291 ± 20 ms (n = 5) and τ₂ = 2137 ± 741 ms (n = 5)) and could be separated into two components (I_tail1 = 18.3 ± 3.4 pA (n = 5) and I_tail2 = 35.7 ± 3.5 pA (n = 5); Fig. 11C, top trace (Control) and middle graph). Apamin (100 nM) selectively decreased I_tail1 by 54 ± 18 % and τ₁ by 72 ± 11 % but did not significantly affect τ₂ or I_tail2 (Fig. 11C, top trace (Apamin) and bottom graph).

Figure 11. Time course and pharmacology of the outward tail currents.

A, currents recorded in response to a 200 ms voltage step to -10 mV followed by a 3 s repolarizing step from -90 to −40 mV (top trace). Upon repolarization, outward tail currents were recorded (middle traces). In the same cell, the outward tail current recorded at −40 mV was fitted by a double exponential (τ₁ = 344 ms and τ₂ = 2500 ms; bottom graph). B, the outward tail current recorded at −40 mV (Control) was completely suppressed in the presence of Cd²⁺ (400 μM). C, the outward tail currents recorded at −40 mV in the absence (Control) or presence of apamin (100 nM) (upper traces). Middle and bottom graphs show semilogarithmic plots of the tail current amplitude against time in control and during application of apamin. The fast component (○) and the slow component (•) were separated on the observation that after 1 s only the slow component was present. The points between 1 and 2.4 s were fitted by linear regression and the initial fast decaying component (○) isolated by subtraction of the extrapolated slower component (•) from the total tail current.

Removal of external Na⁺ induced an immediate block of spontaneous spikes, hyperpolarized the membrane to -61.0 ± 3.5 mV (n = 9), blocked [Ca²⁺]_i transients and decreased basal [Ca²⁺]_i to 49.4 ± 15.3 nM. These effects lasted throughout the application of the Na⁺-free solution and pacemaking progressively recovered upon washout (Fig. 12). In contrast, TTX, which blocks voltage-sensitive Na⁺ channels (1–10 μM, 1–10 min; n = 5) had no significant effect on the amplitude (49.5 ± 1.8 mV in TTX vs. 49.5 ± 2.1 mV in control) or frequency (0.27 ± 0.04 Hz in TTX vs. 0.26 ± 0.05 Hz in control) of spontaneous spikes (Fig. 13A). When the extracellular Na⁺ concentration was progressively lowered, a decrease in spike frequency was first observed. Spike frequency significantly decreased by 30 ± 8 % (n = 5) and by 52 ± 10 % (n = 7 out of 12) when external Na⁺ was lowered to 90 mM (Fig. 13B, top trace) or to 40 mM (Fig. 13B, middle trace), respectively. For the other five cells in 40 mM external Na⁺ and for all the cells tested in 15 or 5 mM Na⁺ (n = 18), spontaneous firing was totally blocked at a membrane potential of -48 ± 2 mV (n = 23; Fig. 13B, bottom trace).

Figure 12. Effect of external Na⁺ removal on pacemaker activity and [Ca²⁺]_i transients.

Removal of external Na⁺ (Na⁺ free, 1 min 40 s) stopped pacemaker activity and hyperpolarized the membrane to -64 mV. In the same cell, concomitant [Ca²⁺]_i transients disappeared and the basal [Ca²⁺]_i level decreased from around 150 to 50 nM (rate of ratio acquisition, 3 Hz). Upon washout, both activities recovered.

Figure 13. Effect of TTX and low external Na⁺ solutions on pacemaker activity.

A, TTX (1 μM, 10 min) had no effect on pacemaker activity. B, in another cell, application of external solutions containing 90 mM Na⁺ (35 s, top trace), 40 mM Na⁺ (30 s, middle trace) and 5 mM Na⁺ (35 s, bottom trace), progressively increased AHP₁ amplitude, decreased spike frequency and stopped pacemaker activity at -42 mV (middle trace) or -50 mV (bottom trace). The dashed lines indicate -51 mV (A), -52 mV (B, top trace), -50 mV (B, middle trace) and -49 mV (B, bottom trace).

Computer simulation of pacemaker activity

In order to quantitatively examine the interplay of the currents characterized here, a simple model has been constructed, based as far as possible on the experimental data. It is fully described in the Methods section. The model employs six different currents. Initially activation and inactivation curves were taken from the experimental data. They, and the relative channel densities, were then adjusted in order to reproduce the current clamp recordings as closely as possible. In particular, negative shifts of about 10 mV were imposed on the Ca²⁺ currents to approximate the differences between recordings in high Ca²⁺ or Ba²⁺ and under physiological conditions. Substantial leeway was also allowed in reducing the current densities of L- and T/R-type currents for the same reason. For example, the L-current density was reduced by a factor of 6 (from -35 pA pF⁻¹ in 10 mM Ba²⁺ in Fig. 5A to -6 pA pF⁻¹ in the model). The resulting model is intended to reproduce the median properties of the population of cells rather than to be a realistic representation of a particular cell.

In the model (Fig. 14), the action potential results mainly from the L-type Ca²⁺ current. Spike repolarization was the most difficult part in the model. It was achieved by a voltage- and Ca²⁺-activated K⁺ current (BK), the delayed rectifier K⁺ current (I_K(V)) and a voltage-independent Ca²⁺-activated K⁺ current (SK) and depended on a ‘feedback deactivation’ of the L-type Ca²⁺ current in the presence of these outward K⁺ currents (Reuveni, Friedman, Amitai & Gutnick, 1993). By ‘feedback deactivation’, we mean that once the plateau drifts below a certain potential (as calcium accumulation augments SK current) the deactivation of the L current is self-sustaining. A small hyperpolarization causes further deactivation which in turn gives a further hyperpolarization. BK current acts first to interrupt the rising phase of the spike whereas SK current acts rather later and underlies the AHP that immediately follows the spike. In combination with the delayed rectifier, either of the two Ca²⁺-activated K⁺ currents is sufficient to repolarize the cell (Figs 9A and B and 15B and C). The blockade of BK or SK current did not mimic exactly the effect of CTX or apamin since it significantly enhanced spike frequency. This can be explained by: (i) the fact that the toxins did not completely block these currents in experiments, and (ii) the presence of an apamin-insensitive Ca²⁺-activated K⁺ current that participated in the outward tail current after a spike (see Fig. 11C) but was not included in the model. Therefore in the model, without BK or SK current, the leak current depolarized the membrane faster between spikes and increased spike frequency. To mimic the effect of CTX or apamin we had to reduce the cationic leak current by 75 % when no SK current was present. This suggests that the apamin-insensitive Ca²⁺-activated K⁺ current participates in the interspike interval by counterbalancing the leak inward cationic current.

Figure 14. Computer simulation of control pacemaker activity.

Traces labelled a show modelled [Ca²⁺]_i transients and currents during three cycles of pacemaker activity and traces labelled b show, on an expanded time scale, modelled currents during a spike. Aa, control pacemaker activity and Ab, control spike. B, [Ca²⁺]_i transients. Ca and Cb, L-type Ca²⁺ current. Da and Db, T-type Ca²⁺ current and I_K(V) (delayed rectifier K⁺ current). Ea and Eb, Ca²⁺-activated K⁺ currents: BK (dashed line) and SK (continuous line). Fa and Fb, cationic leak current.

Figure 15. Computer simulations of the effect of the blockade of currents.

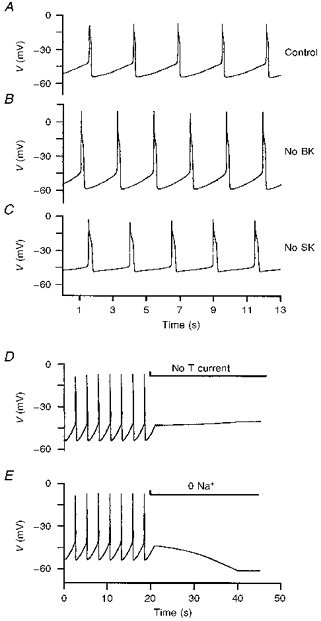
A, control pacemaker activity. B, blockade of the voltage and Ca²⁺-activated K⁺ current (BK) to mimic the effect of CTX. C, blockade of the Ca²⁺-activated K⁺ current (SK) to mimic the effect of apamin. D, progressive blockade (introduced uniformly between 20 and 40 s, i.e. no effect at 20 s and full effect at 40 s) of the T-type Ca²⁺ current to mimic the effect of Ni²⁺ application (40 μM). E, progressive shift of the reversal potential of the leak cationic current to -60 mV (from 20 to 40 s) to reproduce the effect of Na⁺ removal.

The T-type Ca²⁺ current helps to depolarize the membrane to the threshold potential for L-type Ca²⁺ current activation, at the end of the interspike interval, since the threshold for the T-current is 8–10 mV more hyperpolarized than that of the L-current. Without T-current, the cell stops firing at −40 mV (compare Fig. 14C and 15D). In the model, in the absence of the T-current, as the cationic leak current depolarizes the membrane, early Ca²⁺ entry through L-channels is sufficient to forestall a spike by activating BK current. However, this behaviour depends critically on the relative slopes of the activation curves of the L and BK currents. If the BK current activation is made steeper (i.e. α for gate 4 in Table 3 changed from 0.023 to 0.04) keeping V_½ constant, then the model does show spikes in the absence of the T-current.

The cationic leak current serves in the model to produce the steady depolarization between spikes to the threshold of the L-current, to generate the next spike. Its reversal potential was set at -30 mV as suggested by the membrane potential value in the absence of external Ca²⁺ or when Ca²⁺ channels were blocked (see Fig. 4). Since it reverses at -30 mV, it is outward at the peak of the spike and participates in its repolarization. The experimental procedure of Na⁺ removal was mimicked in the model by shifting the reversal potential of the leak cationic current to -60 mV. If we assume that the cationic leak current is carried by K⁺, Na⁺ and Ca²⁺ ions, Na⁺ removal does not eliminate this current but makes its reversal potential more hyperpolarized and therefore hyperpolarizes the membrane to around -60 mV, as observed in current clamp recordings (compare Figs 12 and 15E).

DISCUSSION

The present study shows that the GC cell line, a model of rat tumour somatotrophs, displays cycles of regularly spaced Ca²⁺ action potentials with concomitant [Ca²⁺]_i transients. Within each cycle the action potentials and the slow pacemaker depolarization in between spikes have been separately analysed. On the basis of the experimental data and computer simulations, we propose that the rising phase of action potentials and that of [Ca²⁺]_i transients result mainly from Ca²⁺ entry through L-type Ca²⁺ channels. Ca²⁺-activated K⁺ current and a delayed rectifier current repolarize the membrane to the AHP. The slow pacemaker depolarization that allows regenerative activity results from the decay of Ca²⁺-activated K⁺ currents superimposed on a background Na⁺-sensitive (cationic) inward current. This depolarizes the membrane to the threshold potential for the T/R-type Ca²⁺ current that in turn activates the L-type Ca²⁺ current and initiates a new cycle. Such transient and recurrent Ca²⁺ entry has been proposed as an effective way to maintain exocytosis over long periods of time while avoiding large intracellular Ca²⁺ levels that may damage the cell. It would thus underlie the continuous GH secretion by GC cells.

Action potentials and [Ca²⁺]_i transients

To participate in the rising phase of Ca²⁺ spikes, the Ca²⁺ current(s) should activate around spike threshold and not inactivate during the time course of the rising phase of action potentials. The T/R-type Ca²⁺ current fulfils the former condition, while the L-type Ca²⁺ current fulfils the latter. The role of a L-type current in the rising phase of action potentials and [Ca²⁺]_i transients was suggested by the disappearance of both oscillations during nifedipine application, while that of the T/R-type was suggested by the blocking effect of low concentrations of Ni²⁺ on pacemaker activity. Therefore both currents could participate in the rising phase of action potentials. It is important to note that, under high external Ba²⁺ or Ca²⁺ as in our recordings, the current-voltage relations were probably shifted along the voltage axis to positive values, due to the screening effect of Ba²⁺ or Ca²⁺ on the negative surface charges (Hagiwara & Ohmori, 1982). Therefore, the threshold of activation of T/R- and L-type Ca²⁺ currents in GC cells are likely to be more negative in physiological saline as set in the model. We propose that the T/R-type current activates during the last phase of the pacemaker depolarization. It helps to depolarize the membrane to the threshold potential of the L-type current and then inactivates in tens of milliseconds. In addition, it deinactivates during the time course of the interspike interval due to hyperpolarization of the membrane during the AHP. The L-type current is the main current underlying the rising phase of action potentials, due to its slow inactivation even in the presence of external Ca²⁺.

Separate use of CTX and apamin showed that the Ca²⁺-activated BK (sensitive to CTX) and SK (sensitive to apamin) currents (Sah, 1996) have different repolarizing functions. BK current would interrupt the rising phase of Ca²⁺ spikes while SK current would participate in spike repolarization and in the AHP₁. The fact that spikes still repolarized in the presence of both CTX and apamin suggested that toxin-sensitive Ca²⁺-activated K⁺ currents are not fully responsible for the spike downstroke. The delayed rectifier K⁺ current of GC cells would also play a role in spike repolarization since it activates around -10 mV but would not participate in the AHP as it deactivates rapidly, in less than 10 ms (Authors' unpublished observation).

The L- and T/R-type currents described here have similar properties to those reported in GH-related cell lines including the mammosomatotroph GH₃ cells (Hagiwara & Ohmori, 1982; Armstrong & Matteson, 1985; Simasko, Weiland & Oswald, 1988; Scherübl & Hescheler, 1991; Herrington & Lingle, 1992; Zong, Yassin & Tanabe, 1995), GH₄ cells (Cohen & McCarthy, 1987) and human growth-hormone producing pituitary adenoma cells (Yamashita, Matsunaga, Shibuya, Teramoto, Takakura & Ogata, 1988). The major difference concerns the inactivation of the T/R-type current, which is faster in GC cells. This T/R-type current presents characteristics, a medium range of activation and a resistance to toxins, close to those of the R-type current characterized in cerebellar granule cells or to those generated by expression of the cloned α1E-subunit in oocytes (Zhang et al. 1993; Williams et al. 1994; Hilaire et al. 1997). This strongly suggests that the α1E-subunit mRNA that we detected in GC cells may be related to the T/R-type Ca²⁺ current recorded in this preparation.

The slow pacemaker depolarization

During the interspike interval, the increase in membrane resistance probably results from both the fast and slow deactivation of Ca²⁺-activated K⁺ currents (as shown in K⁺ tail current recordings). The fact that the membrane depolarizes in the interspike interval from the peak of the AHP to the threshold potential for Ca²⁺ spike initiation indicates that the net current during the pacemaker slow depolarization is inward since a decreasing outward current cannot by itself depolarize the membrane (Irisawa et al. 1993). The model proposed that a cationic leak inward current depolarizes the membrane in the interspike interval. The presence of such a background Na⁺-sensitive current, also described in GH₃ cells (Simasko, 1994), was suggested by the hyperpolarizing effect of external Na⁺ removal. It must be stressed that, due to the high input membrane resistance of GC cells (around 1 GΩ), even a very small inward current can significantly change the level of membrane depolarization. In cells that spontaneously fire Ca²⁺ spikes, a persistent depolarizing drive is essential to maintain the membrane potential close to the threshold potential for Ca²⁺ spike initiation.

Comparison of pacemaker activities in tumour and normal somatotrophs

Related GH cell lines such as the mammosomatotrophs GH₃, GH₃B₆ or GH₄C₁ cells also display spontaneous activity (Table 4 and see review by Corette, Bauer & Schwarz, 1995). There is a general agreement that action potentials result from Ca²⁺ entry through L-type channels. The failure of some authors to detect the Na⁺ dependency (Table 4) could be due to insufficient Na⁺ depletion of the local cell environment, in line with our demonstration that the Na⁺ concentration should fall below 40 mM to be effective.

Table 4.

Comparison of quantitative characteristics, ionic sensitivity and pharmacology of spikes and [Ca²⁺]_i transients recorded from GH-related cell lines (GH₃ or GH₄C₁ and GC)

A. Spikes
Parameter	GH3/GH4C1	GC10
Amplitude (mV)	47.6 1	44.9 ± 1.9
Peak (mV)	−12.4 ± 3.2 1	−10.1 ± 1.2
Duration (ms)	184 ± 44 1	—
Half-width (ms)	—	180 ± 21
Threshold (mV)	−44.5 ± 0.9 1	−41.6 ± 1.1
Time to peak (ms)	—	164.3 ± 7.2
Upstroke (V s−1)	1.55 ± 0.30 1	—
AHP (mV)	−60.0 ± 1.5 1	−55.0 ± 1.4
Frequency (Hz)	—	0.38 ± 0.05
Interspike interval (ms)	3509 ± 1147 1	3200 ± 500
0 Ca2+	blockade 2	blockade
Inorganic Ca2+ channel blockers	blockade 234	blockade
Nifedipine	blockade 3	blockade
0 Na+	no effect 46	hyperpolarization
	hyperpolarization 3	—
TTX	no effect 346	no effect

B. [Ca2+]i transients
Parameter	GH3/GH4C1	GC 10
Basal level (nM)	123 ± 41 7	173 ± 20
Amplitude (nM)	236 ± 31 7	374 ± 57
Half-width (ms)	—	1000 ± 200
Time to peak (ms)	240 ± 16	872.5 ± 64.6
Frequency (Hz)	0.3 8	0.27 ± 0.03
0 Ca2+	blockade579	blockade
Cadmium	blockade 9	—
Nifedipine	decrease 7	blockade
	blockade 95	—

¹Simasko, 1991

²Mollard, Vacher, Dufy & Barker, 1988

³Simasko, 1994

⁴Kidokoro, 1975

⁵Schlegel et al. 1987

⁶Taraskevich & Douglas, 1980

⁷Mollard, Guérineau, Audin & Dufy, 1989

⁸Iijima, Sand, Sekiguchi & Matsumoto, 1990

⁹Bresson, Fahmi, Sartor, Dufy & Dufy-Barbe, 1991

¹⁰this study.

Between pacemaker activity of rat tumour somatotrophs (present paper) and that of normal rat somatotrophs (Kwiecien et al. 1997) there are only quantitative differences. Both somatotrophs display action potentials with similar voltage- and ionic dependencies and Na⁺-dependent pacemaker depolarizations. This last characteristic can have important functional implications for the pituitary in vivo, an organ in which the extracellular space is restricted. Changes in external Na⁺ concentration as a result of the activation of the Na⁺-Ca²⁺ exchanger during the decay of [Ca²⁺]_i transients would exert a retrograde inhibition on somatotrophs by decreasing firing frequency, Ca²⁺ entry and subsequent GH release. The quantitative differences between pacemaker activities of tumour and normal somatotrophs, such as spike duration, AHP amplitude and regularity of interspike intervals could be explained by the presence of stronger repolarizing K⁺ currents in GC cells or by different magnitudes of Ca²⁺ or background cationic currents.

The major difference between these two cells is the dependency on GHRH: in normal somatotrophs pacemaking is triggered or potentiated by GHRH while in GC cells it is spontaneous. Therefore, according to the terminology of Selverston, Miller & Wadepuh (1983), normal somatotrophs behave as ‘conditional pacemakers’ (Kwiecien et al. 1997) while GC cells behave as ‘endogenous pacemakers’ (this study). We propose that normal somatotrophs have developed a mechanism that locks the membrane in a non-oscillatory state in the absence of external stimulation. Such an ‘oscillation clamp’ would be relieved by GHRH in normal somatotrophs and would be absent in GC cells.

Comparison with other pacemaker cells

Comparison of the present pacemaker mechanism with that of other pacemaker cells shows that the closest model to tumour somatotrophs is that of sino-atrial node cells (Irisawa et al. 1993). However, a major difference concerns the presence in heart node cells but not in GC cells of a Cs⁺-sensitive, hyperpolarization-activated inward cationic current (I_f or I_h) that provides a depolarization of the membrane in the interspike interval (in normal somatotrophs and the GH₃ cell line, Simasko & Sankaranarayanan (1997) described an I_h-like current but it activated at potentials more hyperpolarized than these cells can achieve). In heart node cells, the role of both hyperpolarization-activated inward current (I_f) and Na⁺-dependent inward background current (I_b,Na) is to control and stabilize pacemaker frequency (DiFrancesco, 1993). For example, when the external Na⁺ concentration is lowered, I_b,Na is reduced and the membrane hyperpolarizes. As a result, I_f is activated more strongly and depolarizes the membrane. This process continues until the additional activated I_f balances the reduced I_b,Na. Therefore, I_f protects sino-atrial node cells from frequency changes induced by changes in other depolarizing currents. In contrast, in GC cells, due to the absence of I_f, a decrease in external Na⁺ concentration can strongly reduce firing frequency. The function of pacemaker activity in the two types of cells is quite different: in sino-atrial node cells it allows heart beating while in GC cells it allows hormone secretion. In the first preparation, it seems important to avoid important frequency changes during perturbations of external ionic concentrations while in the second preparation these changes might contribute to the modulation of hormone release.