Electrophysiological characterization of Na⁺ currents in acutely isolated human hippocampal dentate granule cells

Abstract

1. Properties of voltage-dependent Na⁺ currents were investigated in forty-two dentate granule cells (DGCs) acutely isolated from the resected hippocampus of twenty patients with therapy-refractory temporal lobe epilepsy (TLE) using the whole-cell patch-clamp technique.

2. Depolarizing voltage commands elicited large, rapidly activating and inactivating Na⁺ currents (140 pS μm⁻²; 163 mm extracellular Na⁺) that were reduced in amplitude by lowering the Na⁺ gradient (43 mm extracellular Na⁺). At low temperatures (8–12 °C), the time course of Na⁺ currents slowed and could be well described by the model of Hodgkin & Huxley.

3. Na⁺ currents were reversibly blocked by tetrodotoxin (TTX) and saxitoxin (STX) with a half-maximal block of 4.7 and 2.6 nm, respectively. In order to reduce series resistance errors, the Na⁺ current was partially blocked by low toxin concentrations (10–15 nm) in the experiments described below. Under these conditions, Na⁺ currents showed a threshold of activation of about −50 mV, and the voltages of half-maximal activation and inactivation were −29 and −55 mV, respectively.

4. The time course of recovery from inactivation could be described with a double-exponential function (time constants, 3–20 and 60–200 ms). The rapid and slow time constants showed a distinct voltage dependence with maximal values around −55 and −80 mV, respectively. These properties contributed to a reduction of the Na⁺ currents during repetitive stimulation that was more pronounced with higher stimulation frequencies and also showed a dependence on the holding potential.

5. In summary, the most striking features of DGC Na⁺ currents were the large current density and the presence of a current component showing a slow recovery from inactivation. Our data provide a basis for comparison with properties of Na⁺ currents in animal models of epilepsy, and for the study of drug actions in therapy-refractory epilepsy.

Na⁺ channels are large glycoproteins that form voltage-dependent, Na⁺-permeable pores through the membranes of excitable cells (Hille, 1992). Na⁺ channels play a central role in the regenerative electrical properties of neurons and muscle cells. At resting membrane potentials, most Na⁺ channels are in a closed resting state. The channels open in reponse to depolarization, resulting in inward Na⁺ flux, and then rapidly convert to a non-conducting inactivated state. Repolarization of the membrane removes inactivation, converting the channels back to the resting state.

With respect to epilepsy, Na⁺ channels are particularly relevant since they are a primary target for established anticonvulsant drugs (Upton, 1994; MacDonald & Kelly, 1995): carbamazepine and phenytoin, for example, reduce the Na⁺ current amplitude in voltage-clamp experiments, shift the voltage dependence of steady-state inactivation in the hyperpolarizing direction, and slow the recovery from inactivation. In addition, transcript levels of different sodium channel subtypes seem to be altered in human epilepsy (Lombardo, Kuzniecky, Powers & Brown, 1996) and in the kainate model of epilepsy (Gastaldi, Bartolomei, Massacrier, Planells, Robaglia-Schlupp & Cau, 1997). One candidate mechanism governing Na⁺ channel expression may be a feedback regulation by electrical activity that has been demonstrated in vitro and in vivo in neuronal and muscle preparations (Brodie, Brody & Sampson, 1989; Offord & Catterall, 1989; Dargent & Couraud, 1990; Duff, Offord, West & Catterall, 1992). Furthermore, Na⁺ channel density can be affected by chronic treatment with antiepileptic agents (Sashihara, Yanagihara, Izumi, Murai & Mita, 1994). Although these points underscore the importance of voltage-gated Na⁺ channels in human epilepsy and animal models of epilepsy, little is known about the electrophysiological properties of Na⁺ channels from human brain. The availability of tissue following epilepsy surgery has hitherto permitted the analysis of Na⁺ channels in isolated cortical pyramidal cells (Cummins, Xia & Haddad, 1994). In the present study, we have analysed the properties of Na⁺ channels in human hippocampal dentate granule cells (DGCs). Such data are important, since the hippocampus is severely affected by the epileptogenic process in patients with therapy-refractory temporal lobe epilepsy (TLE). We have limited our analysis to a clinicopathologically homogeneous group of patients with TLE, showing segmental neuron loss and synaptic reorganization accompanied by severe gliosis (Ammon's horn sclerosis; Margerison & Corsellis, 1966).

METHODS

Patient data

All recordings were made on acutely isolated human hippocampal DGCs from surgical specimens of twenty patients (mean age at surgery, 32 ± 9 years) with drug-resistant TLE. The mean duration of the TLE was 13 ± 11 years. The mean age at the onset of seizures was 19 ± 11 years. All patients suffered from complex partial seizures, with additional simple partial seizures (10 patients), and additional secondary generalized seizures (13 patients). The surgical removal of the hippocampus was clinically indicated in every case to achieve seizure control (Wyllie, 1993).

We cannot exclude the possibility that chronic drug treatment over a period of many years might have effects on Na⁺ current properties. However, prior to epilepsy surgery, most patients undergo several different therapeutic regimens with different combinations of antiepileptic drugs for up to thirty-four years. Based on the history of antiepileptic medication over periods as long as this, different patient groups are difficult to discriminate. At the time of presurgical evaluation, a monotherapy with carbamazepine was carried out in twelve patients and a combination of anticonvulsants including carbamazepine, valproate, lamotrigin, phenobarbital, gabapentin, vigabatrin, phenytoin and oxcarbazepine was administered in seven patients. When the properties of the Na⁺ currents were compared between patient groups with carbamazepine monotherapy and combination therapies, no significant differences could be found. The comparison of patients treated with agents acting primarily on Na⁺ currents and patients treated with other drugs was not possible in this study, since only one patient underwent a monotherapy with gabapentine. Measurements from this patient are included in the determination of the TTX concentration-response curve only. In all cases, the epilepsy was idiophathic and histopathological evaluation revealed solitary Ammon's horn sclerosis with severe astrogliosis and neuronal loss in the CA1, CA3 and CA4 subfields, and relative sparing of CA2 (Margerison & Corsellis, 1966; Wolf et al. 1993).

Informed consent was obtained from all patients for additional electrophysiological evaluation. All procedures were approved by the Ethics Committee of the University of Bonn Medical Centre and conform to standards set by the Declaration of Helsinki (1989).

Preparation of acutely isolated DGCs

Human hippocampal specimens were placed in ice-cold saline containing (mm): NaCl, 90; KCl, 3; MgSO₄, 2; CaCl₂, 2; sodium pyruvate, 1; Hepes, 10; glucose, 10; and sucrose, 105 (pH 7.4, 100 % O₂), immediately after surgical removal. Coronal slices (thickness, 400 μm) were prepared from the corpus of hippocampal specimens with a vibratome (Ted Pella Inc., Redding, CA, USA) and stored in a chamber with bicarbonate-buffered artifical cerebrospinal fluid (21°C) containing (mm): NaCl, 124; KCl, 3; NaH₂PO₄, 1.25; CaCl₂, 2; MgCl₂, 2; NaHCO₃, 26; and glucose, 10. The pH was adjusted to 7.4 by gassing the solution with carbogen (5 % CO₂, 95 % O₂). The time of slice preparation following surgical removal was 10-20 min. In this storage chamber, slices could be stored for up to 10 h.

After an equilibration period of 60 min, the first section was transferred to a tube with 5 ml saline containing (mm): NaCl, 126; KCl, 2.5; CaCl₂, 2; MgCl₂, 2; NaH₂PO₄, 1.25; Pipes, 26; and glucose, 10 (titrated to pH 7.4 with NaOH). Pronase (protease type XIV, 2 mg ml⁻¹; Sigma) was added to the oxygenated medium (100 % O₂). After an incubation period of 25 min at 28°C, the slice was washed in the identical ice-cold saline. Afterwards, the dentate gyrus was dissected and triturated with fire-polished Pasteur pipettes of decreasing aperture. The cell suspension was transferred to a 35 mm tissue culture Petri dish (Nunc, Wiesbaden-Biebrich, Germany) and mounted on the stage of an inverted microscope (Telaval, Zeiss, Jena, Germany). The isolated neurons were allowed to settle for 5-10 min and were subsequently washed with extracellular solution (160 mm Na⁺). Isolated cells showed a round or ovoid small soma with a single process reminiscent of DGC morphology in situ. Another type of neuron occurring in low numbers in the preparation showed a multipolar morphology with several processes emanating from the soma. Only neurons with a typical DGC morphology were included in this study.

Recording solutions and electrodes

The bath and superfusion solution contained (mm): NaCl, 120; KCl, 2.5; CaCl₂, 2; MgCl₂, 2; Pipes, 26; 4-aminopyridine, 4; and CdCl₂, 0.03 (pH 7.4 with NaOH). The Na⁺ concentration introduced by adjusting the pH was determined to be 43 ± 2 mm. In some experiments, the Na⁺ concentration in the extracellular solution was decreased by replacing NaCl (80 or 120 mm) with isomolar amounts of choline chloride. These bath solutions as well as solutions containing the toxins tetrodotoxin (TTX) and saxitoxin (STX) at concentrations of 1, 3, 10, 30 and 100 nm were applied by local perfusion with a seven-barrelled superfusion pipette placed at a distance of 100-250 μm from the cell body.

The pipette solution contained (mm): caesium methanesulphonate, 80; CaCl₂, 1; MgCl₂, 5; TEA, 20; Hepes, 10; EGTA, 11; adenosine 5′-triphosphate (disodium salt), 10; and guanosine 5′-triphosphate (lithium salt), 0.5 (pH 7.3 with CsOH). All experiments were carried out at room temperature (21-23°C), unless otherwise stated. The bath could be cooled by a Peltier element (bath chamber, Luigs and Neumann GmbH, Hofheim, Germany; temperature controller, List). The temperature of the solution in the chamber, measured by a thermistor 0.5-1.0 mm away from the voltage-clamped membrane, was taken as the test temperature. The osmotic pressure was adjusted with sucrose to 303 ± 5 mosmol l⁻¹ for the external solutions and to 295 ± 6 mosmol l⁻¹ for the internal solution (OM 801, Vogel, Giessen, Germany). Recording pipettes were fabricated from borosilicate glass capillaries (o.d., 1.5 mm; i.d., 1 mm; Science Products, Hofheim, Germany) on a Narishige puller P83 and fire polished with a microforge (MF-900, Narishige Inc., Tokyo, Japan) to a final resistance of 2-3 MΩ. Pipettes were coated with Sylgard to improve capacitance compensation during measurements between 8 and 12°C.

A liquid junction potential of 7 ± 1 mV (n= 3) was measured between the internal and external solutions (Barry & Lynch, 1991). All voltages presented were corrected for this liquid junction potential (Neher, 1995).

Patch clamp recording and data analysis

Membrane currents were measured with the patch-clamp technique in the whole-cell recording configuration. Current signals were amplified (Axoclamp-200A, Axon Instruments), filtered at 5 kHz (-3 dB, 4-pole low-pass Bessel filter), unless otherwise stated, and sampled at 20 kHz or more by an interface (DigiData 2000, Axon Instruments) connected to a computer (Intel 486, 66 MHz) using the pCLAMP software (Axon Instruments).

A holding potential of -57 mV was chosen, which is near the physiological resting membrane potential of human DGCs (Isokawa, Avanzini, Finch, Babb & Levesque, 1991). Tight-seal whole-cell recordings were obtained according to the method of Hamill, Marty, Neher, Sakmann & Sigworth (1981) (seal resistance > 1GΩ; uncompensated series resistance, R_s, 3.5-4.5 MΩ). To improve the voltage control during activation of Na⁺ current, series resistance and capacitance compensation (60-70 %) were employed. The membrane surface was estimated from whole-cell capacitance (read from the dial of the Axopatch-200A, 10.6 ± 1.4 pF) assuming a value of 1 μF cm⁻². The maximal Na⁺ conductance (140 pS μm⁻²) and Na⁺ current density (1000 pA pF⁻¹) were very high. Thus, without compensation, the maximal residual voltage error defined by R_sI_max approached 10-20 mV.

Thus, it was necessary to reduce the Na⁺ current amplitude by one or a combination of the following three methods. (1) Reduction of the holding voltage (-55 to -50 mV) and/or reduction of the prepulse voltage (-77 mV). (2) Addition of low concentrations (10–15 nm) of TTX or STX to the superfusion solution. (3) Alternatively, the Na⁺ gradient was decreased by lowering the extracellular Na⁺ concentration to 43 or 83 mm. Under these conditions, the maximal residual voltage error estimated as above did not exceed 3 mV. Method (1) was used for the investigation of the concentration-dependent effects of TTX and STX. Unless stated otherwise, residual capacitance transients and leak conductance were subtracted by means of a P/4 protocol (Bezanilla & Armstrong, 1977). All fits were done using the NFit software (University of Texas, Galveston, USA). Statistical comparison was performed with Student's two-tailed t test at a significance level of 0.05. Unless stated otherwise, all results are presented as means ±s.d.

RESULTS

In all neurons under investigation, rapidly activating and inactivating Na⁺ currents could be elicited by depolarizing voltage commands when other voltage-dependent inward and outward currents were blocked by Cs⁺, TEA⁺ and Cd²⁺. During the first few minutes after establishing the whole-cell configuration, the Na⁺ currents increased in amplitude by 72 ± 17 % (n= 5). Thereafter, Na⁺ currents remained stable for the duration of the experiment in most cells (up to 40 min), while some cells showed a slow run-down.

With an extracellular Na⁺ concentration of 163 mm, Na⁺ current amplitudes were very large (Fig. 1), such that series resistance errors could not be avoided in most experiments. Reduction of the extracellular Na⁺ concentration to 43 mm decreased the current to 21 ± 5 % of control (n= 5, Fig. 1Aa). Under these conditions, Na⁺ currents exhibited a typical voltage-dependent activation with a threshold of activation between -60 and -50 mV and a peak conductance of about -20 mV (Fig. 1B). Current-voltage (I-V) curves for the peak Na⁺ currents were fitted with the following equation:

(1)

where V is the test potential, V_Na is the Na⁺ reversal potential and G(V) is the conductance derived from the following Boltzmann equation:

(2)

where $\overline{G}$ is the maximum Na⁺ conductance, V₅₀^m is the voltage where $\overline{G}$ (V)is half of $\overline{G}$, and k_m indicates the steepness of channel activation on membrane voltage. Alternatively, the data from the I-V relationship were plotted as normalized conductance G(V)/$\overline{G}$ (Fig. 1C, filled circles). The data points for the conductance were obtained by dividing the peak current by the driving force and by $\overline{G}$. On average, the voltage of half-maximal activation was -29 ± 3 mV (n= 3, 43 mm Na⁺). For comparison, equivalent data from the neuron in Fig. 1Aa measured with 163 mm Na⁺ are shown (open circles). In this particular cell, ideal recording conditions permitted an adequate resolution of voltage dependence (Armstrong & Gilly, 1992) that was not possible in most other recordings performed with a high Na⁺ gradient.

Figure 1. Na⁺ currents in human DGC.

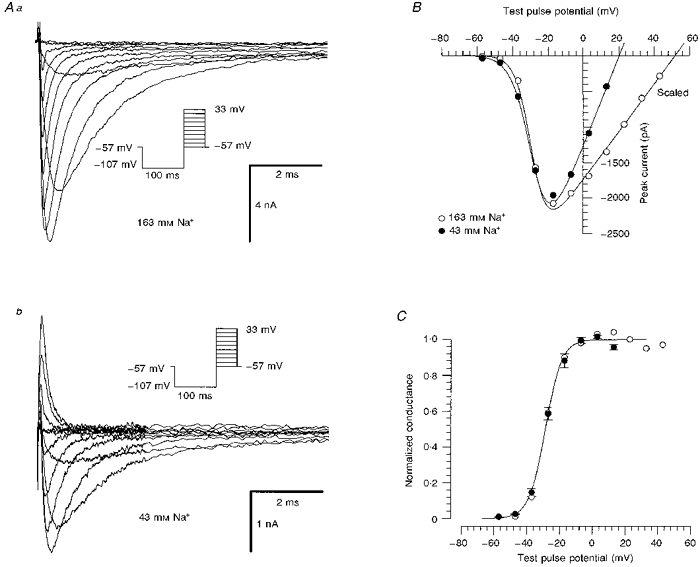
Aa, currents from a human DGC elicited by the activation protocol shown in the inset. Extracellular Na⁺ concentration was 163 mm. The current traces were filtered at 10 kHz. The cell capacitance was 10.5 pF, and a series resistance of 2.5 MΩ was compensated by 70 %. Ab, same cell as in Aa. Reduction of extracellular [Na⁺] (to 43 mm) decreased the current amplitude. B, current-voltage relationship of the peak Na⁺ current for the currents in Aa (163 mm Na⁺, ○) and Ab (43 mm Na⁺, •). The currents in the solution containing 163 mm Na⁺ are scaled down by a factor of 5. The data points were fitted with a modified Boltzmann function (eqn (1)), yielding k_m of 4.5 and 5.5 mV, ₅₀ V^mof -29 and -28 mV, and V_Na of 52 and 17 mV for high and low Na⁺ concentrations, respectively. C, comparison of normalized conductances calculated for the cell in Aa (163 mm Na⁺, ○) with the conductances averaged from 3 DGCs recorded in 43 mm Na⁺ solution (•, k_m= 5.0 ± 0.5 mV and $V_{50}^{\text{m}}=-29\pm 2\text{mV}$). The smooth curve through the data points was calculated from the mean values of these parameters.

Properties of time-dependent activation and inactivation

At room temperature, the kinetics of time-dependent activation and inactivation of STX-treated Na⁺ currents were extremely rapid, with times to peak of less than 500 μs. Therefore, it was probable that the activation of the current traces was contaminated by a time delay between onset of the clamp step and complete membrane depolarization. Current traces obtained in this configuration could not be adequately described with the model of Hodgkin & Huxley (1952), so we fitted the inactivation kinetics with monoexponential functions only. In order to slow the activation of the current, we investigated the Na⁺ currents of four DGCs at 8–12°C (Fig. 2A). At this temperature, current traces were smaller, so that a reduction of the extracellular Na⁺ concentration to 83 mm was sufficient to ensure adequate voltage-clamp conditions. The properties of voltage-dependent activation $(V_{50}^{\text{m}}=\text{ 28 }\pm \text{ 3 mV})$ were not significantly different from measurements performed with a low extracellular Na⁺ concentration (43 mm) at room temperature. In order to illustrate the activation of the Na⁺ currents with higher resolution, the currents in Fig. 2Aa are shown on a logarithmic time scale in Fig. 2Ab. Now these currents could be well described with the model of Hodgkin & Huxley (1952):

(3)

where g_Na would be the maximum Na⁺ conductance of the channels achieved in the absence of inactivation, and τ_m and τ_h are the time constants of activation and inactivation, respectively. Current traces measured at 8–12°C were best fitted when a time delay between voltage step and commencement of the activation process was taken into account. Therefore, the term on the right-hand side of eqn (3) was modified by substituting t - t_sfor t. The mean delay value (t_s) was 190 ± 90 μs. Time-to-peak values predicted by the Hodgkin-Huxley equation were consistent with the values observed from current traces (Fig. 2B).

Figure 2. Properties of time-dependent activation and inactivation at 8 °C.

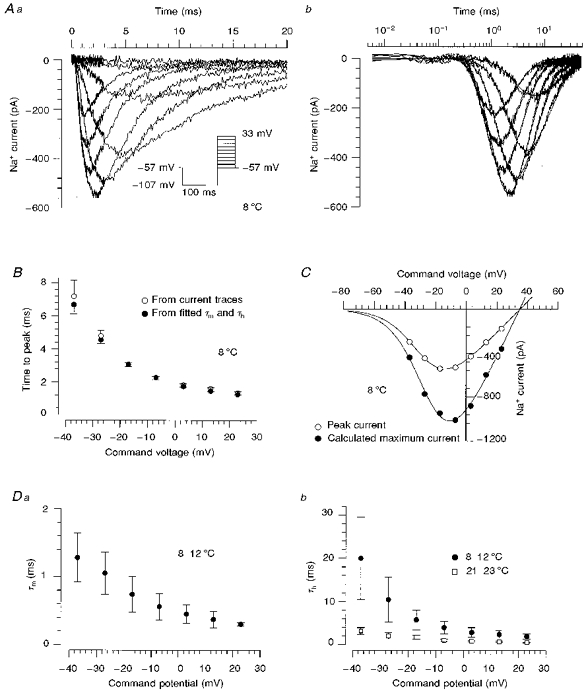
Aa, time course of Na⁺ currents elicited with an activation protocol in a human DGC at 8 °C with 83 mm NaCl in the extracellular solution. The traces were filtered at 10 kHz. The initial 3 ms following the onset of the voltage jump were sampled with a small sample interval of 6 μs, and the remaining parts of the traces with a sample interval of 50 μs. Ab, current traces obtained at 7 potentials (-38 to 22 mV) were fitted according to the Hodgkin-Huxley model (eqn (3)) including a time delay, t_s, (smooth lines). The data are plotted on a logarithmic time scale in order to show the activation phase clearly. B, comparison of time-to-peak τ_mln(1 + 3τ_h/τ_m) (•), predicted by the Hodgkin-Huxley equation, and the time to peak observed from current traces (○). These data were obtained from 4 measurements of one human DGC. C, current-voltage relationships derived from the Hodgkin-Huxley fitted maximum Na⁺ current g_Na(V - V_Na) (•) and from peak Na⁺ current amplitudes (○). The smooth curves represent fits (eqn (1)) with k_m of 7.2 and 7.7 mV, V₅₀^m of −23 and −28 mV, $\overline{G}$ of 23 and 12 pA mV⁻¹, and V_Na of 35 and 34 mV for the fitted maximum current and peak current, respectively. D, the voltage dependence of activation (Da) and inactivation (Db) time constants (n= 4). Recordings were performed at 8–12 °C (•) or at room temperature (□).

Current-voltage relationships derived from the peak Na⁺ current amplitudes and from fitted peak amplitudes of the Na⁺ currents g_Na(V - V_Na) were fitted with eqn (1) (Fig. 2C), yielding a potential of half-maximal activation of -28 ± 2 mV and -25 ± 1 mV, respectively. The ratio of Na⁺ conductances $\overline{G}$_peak/$\overline{G}$_fit was 0.52 ± 0.03. The activation time constant, τ_m, was faster than the inactivation time constant, τ_h, at all command potentials (Fig. 2Da and Db). A slowing of the inactivation rate of the Na⁺ current at 8–12°C compared with room temperature was clearly apparent (Fig. 2Db). Our attempts to remove the inactivation of the Na⁺ current enzymatically by intracellular perfusion of 0.25 mg ml⁻¹ papain resulted in a complete run-down of Na⁺ current within 15 min without any alteration of inactivation.

Effects of TTX and STX

We employed an additional method of reducing Na⁺ currents measured with 163 mm extracellular Na⁺ by applying the Na⁺ channel toxins STX and TTX. STX (Fig. 3A and B) and TTX (not shown) reversibly and rapidly reduced Na⁺ current amplitude in a concentration-dependent manner. In these measurements, the holding potential was set to more depolarized levels (between -55 and -50 mV) in order to reduce Na⁺ current amplitude further.

Figure 3. Suppression of Na⁺ currents by TTX and STX.

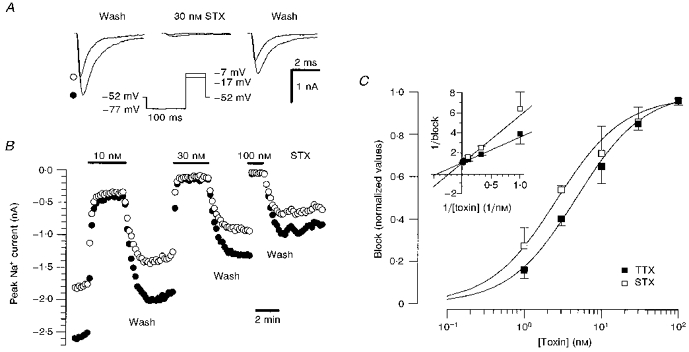
A, Na⁺ current traces before, during and after 30 nm STX application. Currents were evoked by test pulses to -17 mV (•) and to -7 mV (○). B, time course of block of peak Na⁺ current in a human DGC during superfusion with a range of STX concentrations. Symbols represent different test pulse potentials as in A. Test pulses were applied at 10 s intervals. The cell showed a fast run-down and the block effect was estimated with respect to the mean of the current amplitude value before and after application of the toxin. C, concentration-response curves for block of Na⁺ current by TTX (▪) and STX (□). The value of the current amplitude during toxin application was compared with the mean amplitude in control solutions before and after application of toxin. Block values were averaged for each toxin concentration (STX, 8 cells; TTX, 7 cells). For the determination of EC₅₀ values, the data points were transformed into a Lineweaver-Burk plot (see inset). The EC₅₀ values (STX, 2.6 ± 0.2 nm; TTX, 4.7 ± 0.6 nm) were determined by fitting a linear regression to the data points, taking into account the standard error of the mean values (Press, Teukolsky, Vetterling & Flannery, 1994).

To exclude significant shifts in the current-voltage dependence following toxin application, we employed test pulses to two different command voltages near the voltage of maximal inward current (−7 and −17 mV, Fig. 3A and B). The proportion of block was not significantly different at these two test voltages. Figure 3C illustrates the concentration-dependent suppression of Na⁺ conductance by STX and TTX. The EC₅₀ values were derived from Lineweaver-Burk plots by fitting a linear regression to the data points weighted by the standard error of the mean (see inset: STX, 2.6 ± 0.2 nm; TTX, 4.7 ± 0.6 nm). Na⁺ currents were completely blocked by toxin concentrations of 100 nm.

Voltage dependence of activation and inactivation

In further experiments, concentrations of STX or TTX between 10 and 15 nm were added, which blocked around 70 % of the peak Na⁺ current amplitude. Under these conditions, voltage errors due to series resistance were acceptable with a maximal residual voltage error of 3 mV. The voltage dependence of the Na⁺ currents was not affected by varying the toxin concentration. Na⁺ currents demonstrated voltage-dependent activation properties not significantly different from those measured with 83 or 43 mm extracellular Na⁺ (Fig. 1) in the absence of toxin, showing a threshold for activation of between -50 and -40 mV (Fig. 4A), and a voltage of half-maximal activation of -29 ± 4 mV (n= 4, Fig. 4B). Na⁺ currents depended on the prepulse potential, consistent with classical steady-state inactivation (Fig. 4C). The data points could be well fitted with a Boltzmann function equivalent to eqn (2), with a voltage of half-maximal inactivation of -55 ± 2 mV (n= 3, Fig. 4D). The dependence on the prepulse potential was smooth, with an e-fold change in current amplitude per 6 mV.

Figure 4. Voltage dependence of activation and inactivation.

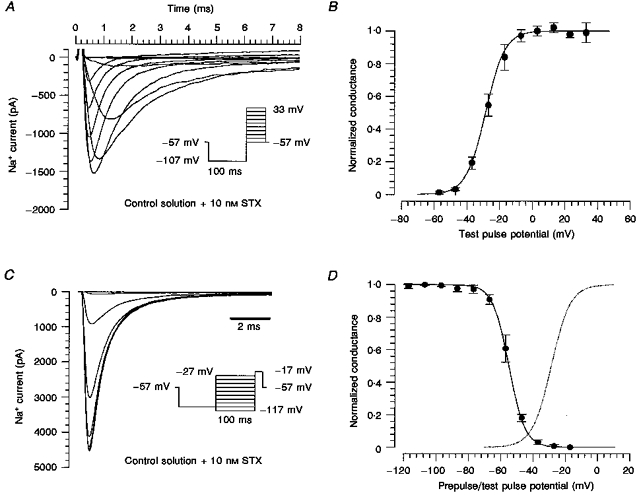
A, currents of a human DGC elicited by the activation protocol shown in the inset. The extracellular Na⁺ concentration was 163 mm. The current amplitude was reduced with 10 nm STX. B, mean values of the normalized conductance of 4 DGCs. The smooth curve through the data points was calculated from the mean values of the parameters obtained by fitting a modified Boltzmann function to the data points, with k_m= 5.9 ± 0.4 mV and $V_{50}^{\text{m}}=-29\pm 4\text{mV}$ (for comparison, see Fig. 1B). C, steady-state voltage-dependent inactivation of Na⁺ currents in a human DGC measured with test pulses to -17 mV following 100 ms conditioning prepulses that were incremented by 10 mV steps from -117 to -27 mV. The prepulses were preceded by a 100 ms pulse at -107 mV to remove slow inactivation. D, conductances were obtained from the peak currents, normalized and fitted with the Boltzmann equation (eqn (2), with $V_{50}^{\text{m}}$ and k_m replaced by $V_{50}^{\text{h}}$ and k_h, respectively). The voltage of half-maximal inactivation, $V_{50}^{\text{h}}$, was -55 ± 2 mV, and k_h was -5.6 ± 1.1 mV (n= 3). The dotted line shows the fitted activation curve from B.

Recovery from inactivation and frequency-dependent reduction of Na⁺ current

The time course of recovery from inactivation of Na⁺ current was investigated with double-pulse experiments at different recovery potentials (-107 to -47 mV) (Fig. 5Aa, inset). These experiments were carried out in the presence of low concentrations of STX (10–15 nm) at room temperature (with 163 mm Na⁺). With interpulse intervals of up to 100 ms, the time course of recovery from inactivation could be described with a single exponential (Fig. 5Aa). However, during this period only 87 ± 8 % (n= 25) of the Na⁺ channels recovered from inactivation, indicating a second, slower process. To obtain complete recovery from inactivation, experiments were performed with a maximal recovery time of 10 s. In this case, the data points could be fitted with two time constants (Fig. 5Ab). Maximal values of the rapid and slow time constant were obtained at membrane potentials of approximately -52 and -77 mV, respectively (Fig. 5Ba and Bb). The fraction of the slower time constant varied (5-75 %) with applied potential, resulting in a mean value of 20 ± 18 % (n= 26) when averaged over the entire potential range (-107 to -47 mV).

Figure 5. Recovery of Na⁺ currents from inactivation.

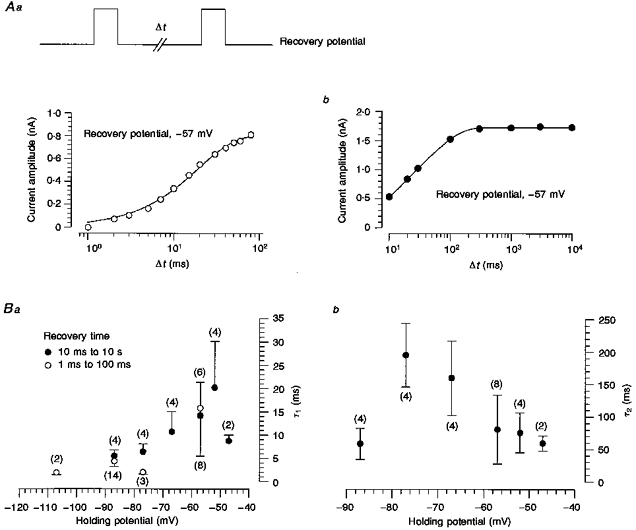
A, the recovery of the Na⁺ current was investigated with two-pulse protocols choosing recovery potentials ranging from -107 to -47 mV. The membrane was depolarized (-17 mV) for 14 ms and no leak subtraction was applied. The membrane holding potential was adjusted to the recovery potential 20 s before starting the stimulation protocol. The current amplitude of the test pulse was investigated following different recovery times limited by a maximal time of 100 ms (Aa) or 10 s (Ab, a different cell). Data from Aa were fitted with a monoexponential function a[1 - exp(t/τ₁)], yielding a time constant of 18.9 ms. Data from Ab were fitted with a double-exponential recovery curve a₁[1 - exp(t/τ₁)]+a₂[1 - exp(t/τ₂)], with time constants τ₁ and τ₂ of 12 and 60 ms, respectively, and a₁ and a₂ values of 670 and 1060 pA, respectively. Ba, the voltage dependence of the recovery time constant derived from experiments with recovery times of 1-100 ms (○), and the shorter recovery time constant obtained from experiments with recovery times of 10 ms to 10 s (•). Bb, the voltage dependence of the second, longer time constant derived from double-exponential fits as shown in Ab. The error bars in Ba and Bb represent the standard error of the mean. Numbers in parentheses are numbers of cells.

The peak current amplitude was reduced by repetitive depolarization of the DGCs (Fig. 6A). A stimulation frequency of 5 Hz caused a gradual reduction, while increasing the stimulation frequency to 20 or 50 Hz initiated a more rapid and pronounced reduction (Fig. 6B). In contrast, no diminution of Na⁺ current amplitude was found with a stimulation frequency of 0.1 Hz (not shown). The decrease of the peak current was found to be voltage dependent, showing a significantly larger reduction at a holding potential of -57 mV than at -77 mV for all stimulation frequencies (Fig. 6C).

Figure 6. Na⁺ currents are diminished by repetitive depolarization.

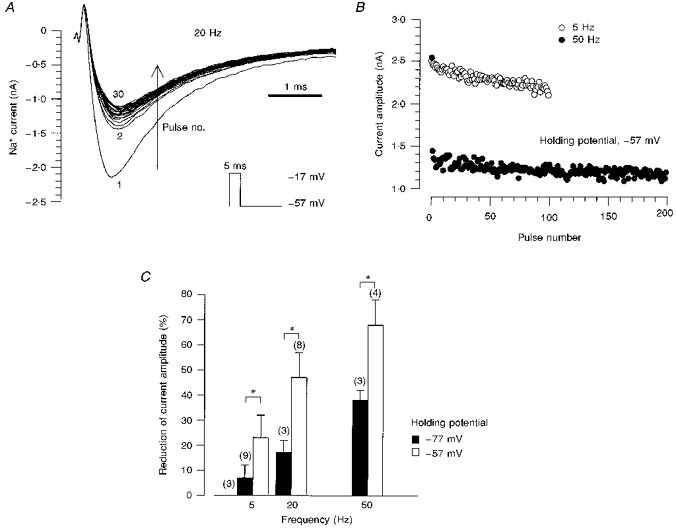
A, the cell membrane was depolarized 100 times for 5 ms with a frequency of 20 Hz (first 30 current traces shown). The membrane holding potential (-57 mV) was adjusted to the recovery potential 20 s before the start of the stimulation protocol. No leak subtraction was applied. B, current amplitudes of traces elicited by membrane depolarizations for 5 ms with frequencies of 5 and 50 Hz. The holding potential was -57 mV. C, the proportional reduction of the current amplitude increased with depolarization frequency. For the various stimulation frequencies, the reduction was significantly larger at a holding potential of -57 mV than at -77 mV, as indicated by the asterisks. Numbers in parentheses represent the number of cells.

DISCUSSION

The synaptic properties of human hippocampal DGCs have been investigated in a number of studies employing conventional sharp microelectrodes as well as patch-clamp recordings in the slice (Isokawa et al. 1991; Isokawa, Levesque, Babb & Engel, 1993; Williamson, Spencer & Shepherd, 1993). In addition, recent studies have taken advantage of the unique possibility of isolating neurons suitable for patch-clamp recordings from human hippocampal specimens. Whereas the properties of voltage-dependent calcium and potassium currents (Beck, Steffens, Heinemann & Elger, 1997b; Beck, Clusmann, Kral, Schramm, Heinemann & Elger, 1997a) have been investigated in human DGCs, the properties of voltage-gated Na⁺ currents in this region are unknown.

In this study, we were able to elicit large, rapidly activating and inactivating voltage-dependent Na⁺ currents in all neurons under investigation. In our recording configuration, a non-inactivating component of the Na⁺ current could not be observed. As the Na⁺ currents in these cells were extremely large, the amplitudes of Na⁺ currents had to be reduced in order to diminish voltage errors due to series resistance. We were able to reduce the peak amplitude of Na⁺ currents about 4-fold by lowering the extracellular Na⁺ concentration to 43 mm.

Description with the Hodgkin-Huxley model

Under conditions of reduced extracellular Na⁺, we attempted to describe Na⁺ currents with a Hodgkin-Huxley equation. However, at room temperature the activation time course could not be resolved satisfactorily. In order to slow the time course of Na⁺ currents, we reduced the bath temperature to 8–12°C. Under these conditions, Na⁺ currents could be well described by a Hodgkin-Huxley equation, with an inactivation time constant that was much slower than the activation time constant. It could be concluded from the ratio of Na⁺ conductances ${\overline{G}}_{\text{peak}}/{\overline{G}}_{\text{fit}}$ that, in this model, abolishing the inactivation would theoretically lead to an approximately 2-fold increase in current amplitude. In the absence of evidence that abolishing inactivation by application of proteolytic enzymes increases the inward current amplitude, it is also possible that other models with opposite ratios of activation and inactivation time constants might predict the same time course of Na⁺ conductance (Hille, 1992).

Toxin sensitivity of Na⁺ currents

In most further analyses of kinetic parameters, Na⁺ currents were reduced with STX/TTX. Na⁺ currents in isolated human DGCs showed EC₅₀ values comparable to those measured in acutely isolated human axons (TTX, 1-10 nm; Scholz, Reid, Vogel & Bostock, 1993) and human neocortical pyramidal neurons (STX, 2.3 nm; Cummins et al. 1994). In cloned rat brain IIa channels, Satin, Limberis, Kyle, Rogart & Fozzard (1994) found EC₅₀ values between 10 and 15 nm for TTX, and between 2 and 4 nm for STX at potentials from -110 to -60 mV. Kaneda, Oyama, Ikemoto & Akaike (1989) reported an EC₅₀ value for TTX of 10 nm for Na⁺ channels in isolated rat hippocampal CA1 neurons.

Comparison with other preparations

The voltage dependence of Na⁺ channels in human DGCs was similar to data obtained in other human and rat preparations. Other groups have examined hippocampal and neocortical pyramidal neurons of patients with TLE (M. Vreugdenhil & W. J. Wadmann, personal communication; Cummins et al. 1994) and pyramidal and non-pyramidal cells from the neocortex of mature rats (Huguenard, Hamill & Prince, 1988; Cummins et al. 1994). These groups found half-maximal values of activation of about -33 mV, which are in good agreement with the values reported here, while the half-maximal values of inactivation (-66 mV, on average) are about 10 mV more negative than ours. Another group (Sah, Gibb & Gage, 1988) found more negative half-maximal values of activation and inactivation (-40 and -75 mV, respectively) in hippocampal CA1 neurons of guinea-pig. In contrast, the properties of recovery from inactivation were clearly different from those reported in numerous other preparations. In addition to fast voltage-dependent recovery time constants (3-20 ms), which are in good agreement with values reported for Na⁺ channels of cardiocytes, skeletal muscle or brain (Huguenard et al. 1988; West, Scheuer, Maechler & Catterall, 1992; Schneider et al. 1994; Wang, George & Bennet, 1996), we observed a significant contribution of a second, 4 to 31 times larger (depending on the potential) time constant. Such a slow recovery from inactivation has traditionally only been reported after more prolonged conditioning depolarizations (Patlak, 1991). More recently, however, a slow recovery from inactivation has been observed following a train of ten short (2 ms) depolarizations as well as following a single depolarization in rat hippocampal CA1 pyramidal neurons (Jung, Mickus & Spruston, 1997). A slowing of inactivation rates can also be observed following intracellular application of various proteolytic enzymes (Bezanilla & Armstrong, 1977; Gonoi & Hille, 1987). We cannot totally exclude the possibility that the enzymatic isolation procedure performed in our study might contribute towards a slow recovery from inactivation. However, such effects have not been observed in other similar preparations (Steinhäuser, Tennigkeit, Matthies & Gündel, 1990; Cummins et al. 1994). Furthermore, varying the concentration of pronase during incubation did not change the Na⁺ current properties under these conditions.

Compared with the double-exponential recovery from inactivation, it is somewhat surprising that the onset of inactivation of Na⁺ currents could be well approximated by a single time constant in the Hodgkin-Huxley equation. However, experiments have been previously reported where monoexponential decay in Na⁺ current traces was accompanied by double-exponential kinetics when the inactivation time course was measured with double-pulse protocols (French & Horn, 1983).

Following determination of these recovery time constants, we investigated the reduction of current amplitude by repetitive depolarization with appropriate frequencies. The recovery times of the various stimulation frequencies (5, 20, 50 Hz) we used here were 195, 45 and 15 ms. With the longest interstimulus intervals (195 ms, 5 Hz) the rapid component of inactivation should be fully recovered. Therefore, the gradual reduction of current amplitude may be ascribed to the slow process of recovery from inactivation. With higher stimulation frequencies (20 and 50 Hz), we observed a more pronounced and rapid reduction of current amplitude, in line with a possible additional contribution of the rapid recovery from inactivation. This hypothesis is strengthened by the parallel voltage dependence of the fast recovery time constant and of the peak amplitude reduction at a stimulation frequency of 50 Hz. However, the following points make the interpretation of these data problematic. Firstly, the rapid recovery time constant might be increased due to the membrane being in a prolonged depolarized state with high stimulation frequencies. A decrease of the Na⁺ gradient by repetitive loading of the intracellular space might also affect recovery from inactivation. Integration of four current traces with a mean peak amplitude of 2.2 ± 0.1 nA leads to a mean charge movement of (5.0 ± 1.1) × 10⁻¹² C. Assuming a spherical neuron (radius, ∼10 μm) and a homogeneous distribution of Na⁺, this charge flow corresponds to only arround 10 μm (Faraday constant, ∼10⁵ C mol⁻¹).

In recent investigations of the somatic and dendritic Na⁺ currents from rat CA1 pyramidal neurons, Colbert, Magee, Hoffman & Johnston (1997) and Jung et al. (1997) found a voltage-dependent reduction of Na⁺ current amplitude by repetitive (20 and 50 Hz), short (2 ms) depolarizations, which was more pronounced in the dendrites. Our data compare well to the properties of the somatic Na⁺ currents in these neurons. We cannot exclude the possibility that Na⁺ channels on distal dendritic portions that were mostly truncated in our preparation may show biophysical properties different from those described here.

Possible effects of chronic TLE

The current densities observed in human DGCs were large (around 1000 pA pF⁻¹) compared with densities observed in non-focal cortical pyramidal cells from patients with TLE or in normal adult rat cortical neurons (both around 600 pA pF⁻¹; Cummins et al. 1994). Changes in the expression of Na⁺ channel α-subunit mRNA have been observed in animal models as well as in human epilepsy. For instance, neonatal Na⁺ channel isoforms showed an upregulation following kainate-induced status epilepticus in the dentate gyrus and the hippocampal CA1 area (Gastaldi et al. 1997). In addition, a pronounced change in the ratio of type SCN1A and SCN2A subunit mRNAs was detected in the hippocampus of patients with temporal lobe epilepsy with less distinctive changes in the temporal lobe neocortex (Lombardo et al. 1996). Apart from a regulation of Na⁺ channel transcripts due to the epileptogenic process, an influence of antiepileptic medication on Na⁺ channel expression cannot be excluded in human studies, since the patients are usually under a full anticonvulsant drug regimen at the time of operation. Indeed, administration of phenytoin to El mice (Sashihara et al. 1994) increases Na⁺ channel density in brain synaptic membranes. In addition, chronic blockade of Na⁺ channels leads to an upregulation of Na⁺ channel expression in cultured rat myotubes (Brodie et al. 1989). The mechanism responsible for such an effect may consist of a negative feedback control of Na⁺ channel expression by the intracellular Na⁺ concentration (Brodie et al. 1989; Dargent & Couraud, 1990). If such a mechanism is relevant in human epilepsy, we would expect differences between patient groups treated with antiepileptic drugs known to act on Na⁺ channels and those treated with drugs lacking effects on Na⁺ channels. Since all except one patient received at least one drug acting on Na⁺ channels, we were not able to address this issue in the present study.

In summary, we have described the properties of a TTX and STX-sensitive fast Na⁺ current in human DGCs. The most striking features of these currents were the large current density and the presence of a current component showing a slow recovery from inactivation. The relationship of these data to electrophysiological characteristics of Na⁺ currents in non-epileptic human DGCs remains unclear. Similarly, the functional consequences of these biophysical properties for signal integration (Colbert et al. 1997; Jung et al. 1997) of DGCs (in situ at 37°C) will be the subject of further studies. However, these data provide an important basis for comparison with the properties of Na⁺ currents in animal models of epilepsy, and for the study of mechanisms of action of drugs intended for clinical use in therapy-refractory epilepsy.