Submillisecond kinetics and low efficacy of parallel fibre-Golgi cell synaptic currents in the rat cerebellum

Abstract

1. The whole-cell configuration of the patch clamp technique was used to record from Golgi cells in thin slices of the rat cerebellum (P12-P25). Their active membrane properties and the input that they receive from the parallel fibres were characterized.

2. Most cells were filled with biocytin and morphologically identified by the presence of a large axonal arbor restricted to the granular layer. The morphological parameters of eighteen of the best-preserved cells were quantified.

3. A slow capacitive current transient, characteristic of the Golgi cell axon, was used to identify Golgi cells whenever their morphology could not be preserved.

4. Golgi cells fire action potentials spontaneously at 3 ± 1.7 Hz (n = 17). Their firing frequency increases linearly with the amplitude of depolarizing current pulses and displays marked adaptation.

5. When hyperpolarized Golgi cells display an anomalous rectification which is blocked by 2 mm CsCl, indicating the presence of an I_h-like current.

6. Golgi cells receive a spontaneous excitatory input from parallel fibres. This input is composed of small amplitude, mostly monoquantal, EPSCs. Chemical stimulation of granule cells by locally applied kainate evokes tetrodotoxin (TTX)-dependent events with similar properties.

7. The parallel fibre-Golgi cell EPSCs have both AMPA and NMDA components. The NMDA component is blocked by 1 mm external magnesium at -60 mV and decays with time constants of 31 ± 9 ms and 170 ± 15 ms (at +61 mV in the presence of magnesium).

8. In the presence of 10 μM internal spermine, the AMPA component of the spontaneous EPSCs is markedly slowed (0.96 ± 0.25 ms to 1.86 ± 0.47 ms; n = 4) and reduced in amplitude (49 ± 7 %; n = 4) when depolarizing the cell from -70 mV to +61 mV.

9. The decay kinetics of individual AMPA EPSCs were found to be variable, in part because of dendritic filtering. A more detailed analysis reveals that the synaptic AMPA conductances are regulated during development and close faster at days P19-P25 than at days P13-P16.

10. These data suggest that the efficacy of the parallel fibre-Golgi cell input is rather low. This places strong constraints on the conditions in which the inhibitory feedback exerted by the Golgi cell can be operational.

11. The possibility is considered that the Golgi cell-granule cell circuit shows an oscillatory behaviour. This hypothesis is discussed in relation to the models of Albus and Marr.

Inhibitory interneurones are found in all regions of the central nervous system. For many years their main function has been viewed as limiting excitation and sharpening the spatial coding through lateral inhibitory circuits (Eccles, 1967), but in recent years it has been proposed that the inhibitory interneurones participate in more diverse and complex functions, like temporal coding on a millisecond time scale and synchronization of neuronal populations (Buzsáki & Chrobak, 1995; Singer, 1996). Recent studies using new approaches (patch-clamp, paired recordings, imaging) have indeed confirmed the importance of local inhibitory interneurones in the temporal coding of information in the hippocampus and thalamus and shown that understanding the significance of a given local inhibitory circuit requires the detailed knowledge of the connectivity and of the physiological properties of the cells and synapses involved (Buhl, Halasy & Somogyi, 1994; Miles, Toth, Gulyás, Hájos & Freund, 1996; Buhl, Tamás, Szilagyi, Stricker, Paulsen & Somogyi, 1997; Kim, Sanchez-Vives & McCormick, 1997).

In the cerebellum, the inhibitory interneurones are separated into two classes, the interneurones of the molecular layer (basket and stellate cells) and the interneurones of the granular layer, among which the Golgi cells (Golgi, 1883) are the most conspicuous. The molecular layer interneurones have been intensely studied within the framework of the hypotheses proposed for their role in spatial coding (Eccles, Ito & Szentágothai, 1967) but recent work has also suggested that they play a role in temporal coding (Callaway, Lasser-Ross & Ross, 1995; Haüsser & Clark, 1997). Golgi cells have been comparatively neglected. The anatomical evidence indicates that their dendrites extend both in the granular layer, where they are contacted by mossy and climbing fibres, and in the molecular layer, where they receive an input from both the parallel fibres and molecular layer interneurones (Palay & Chan-Palay, 1974). The Golgi cell axon ramifies profusely in the granular layer to contact thousands of granule cells at the level of the glomeruli (Hámori & Szentágothai, 1966). It has been abundantly demonstrated that these synapses use GABA as a transmitter (see Brickley, Cull-Candy & Farrant, 1996). These morphological and electrophysiological data suggest the existence of an inhibitory feedback circuit from the Golgi cells onto the granule cells. Indeed early studies, using in vivo extracellular and intracellular recordings, showed that a strong stimulation of the parallel fibres induces a depression of the transmission of the mossy fibre excitatory input to the Purkinje cells, possibly through the excitation of Golgi interneurones and subsequent inhibition of the granule cells (Eccles, Llinás & Sasaki, 1964; Eccles, Llinás & Sasaki, 1966).

The inhibition exerted by Golgi interneurones over granule cells is central to the operation performed at the mossy fibre-granule cell synapse, the key relay of excitatory inputs to the cerebellum. Extracellular recordings of the activity of Golgi cells in vivo have indicated that, in the behaving animal, the activity of Golgi cells varies according to the phase of the movement. The range of firing frequencies encountered goes from 0 to 100 Hz (Edgley & Lidierth, 1987). This frequency modulation must arise from the nature, organization and temporal pattern of the excitatory and inhibitory inputs received by the Golgi cells. These inputs have only been briefly described in two reports using patch clamp and intracellular recordings in slices (Midtgaard, 1992; Dieudonné, 1995). In particular the efficacy of individual parallel fibre inputs on Golgi cells, which is an important parameter of the granule cell-Golgi cell feedback circuit, is not known.

In the present paper patch-clamp recordings from identified Golgi cells in cerebellar rat slices were used to characterize the electrical properties of the Golgi cells and the excitatory input that they receive from the parallel fibres. One of the central questions addressed was: how many parallel fibre inputs would be necessary to modulate the firing frequency of Golgi cells in the range of frequencies encountered in vivo? As will be seen, the synaptic currents produced by the parallel fibres are surprisingly brief and small in young animals and become even briefer in adults. The data obtained suggest that the efficacy of the parallel fibre-Golgi synapses is low compared with that of the synapses of parallel fibres onto molecular layer interneurones. It is therefore unlikely that variations in the frequency of the parallel fibre input can solely account for the modulation of the Golgi cell firing frequency. This study also reveals that Golgi cells express an I_h-like current favouring rhythmic activity. This suggests that the feedback circuit on the granule cells includes oscillatory components, as already shown for circuits involving interneurones in other structures (Buzsáki & Chrobak, 1995). A model is proposed, in which the Golgi cell serves to encode the intensity of mossy fibre input into a frequency of occurrence of bursts of granule cell activity. This dynamic model differs in many points from the ‘static’ models of Marr (1969) and Albus (1971).

METHODS

Slice preparation

Cerebellar thin slices were prepared from male Wistar rats aged 12-25 days following the method originally described by Llinás & Sugimori (1980) with slight modifications (Llano, Marty, Armstrong & Konnerth, 1991). Briefly, animals were decapitated and the cerebellum was dissected and immediately cooled to 0°C. A parasagittal cut was made in the paravermis and parasagittal slices 200-300 μm thick were cut from the vermis with a microslicer (Dosaka, Japan). They were kept at 34°C for 1-9 h before being transferred to the recording chamber. On some occasions slices were allowed to cool slowly from 34°C to room temperature (20-24°C) 1 h after slicing.

Slices were visualized using a × 40 water-immersion objective (0.75 NA, Axioskop, Carl Zeiss) and infrared optics (illumination filter 750 nm, and a Sony CCD camera from which the infrared blocking filter had been removed). Large Golgi cells were visually selected for recording as previously explained (Dieudonné, 1995). Their identification was later confirmed on the basis of their characteristic morphology and/or passive electrical properties (see the paragraph Morphological reconstruction and Figs 1 and 2).

Figure 1. Morphological features of a Golgi cell recorded at P16.

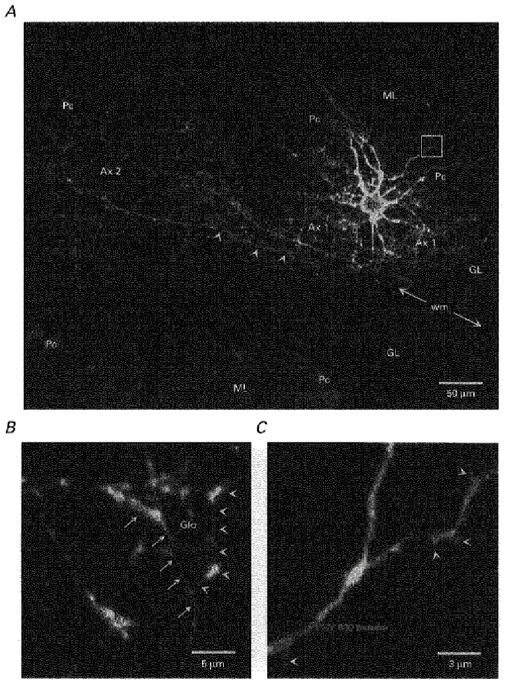
A Golgi cell was filled with biocytin during patch-clamp recording and revealed with avidin-FITC. Purkinje cells were labelled as described in Methods. A, parasagittal projection of the cell reconstructed from serial confocal images taken every 1 μm through the whole depth of the dendritic and axonal shafts. This cell occupies the terminal portion of a lobule as shown by the localization of the Purkinje cell bodies (Pc). The cell body (cb), the basolateral dendrites (not clearly identifiable at this scale), the main axonal plexus (Ax 1) and a secondary axonal plexus (Ax 2) are all found in the granular layer (GL). The secondary plexus arises from two main axonal trunks, one of which (indicated by arrowheads) runs into the white matter (wm). Apical dendrites form a fan-shaped dendritic arbor in the molecular layer (ML). B, detail of the axonal plexus constructed from optical sections taken every 0.2 μm. Glo indicates the putative location of a glomerulus encircled by numerous varicose branches of the axon (in front of the projection plane, arrows, and behind, arrowheads). C, detail of the apical dendrites in the molecular layer constructed from optical sections taken every 0.2 μm at the location indicated by a white box in A. Note the short protrusions of the dendrites (arrowheads).

Figure 2. Passive electrical properties associated with the Golgi cell axon.

A, current transients were evoked by a hyperpolarizing voltage pulse of 10 mV (from -70 mV, CsCl based internal solution) in the cell shown in Fig. 1 (top recording) and in the cell shown in Fig. 2B (bottom recording). The slowest component of the transients is fitted by a single exponential function (line superimposed on data points) and its integral is plotted as a bold line. B, the parasagittal projection of this putative Golgi cell lacking its axon was produced as in Fig. 1. The neurites seen in the granular layer (GL) are basolateral dendrites, as attested by their large diameter and tortuosity. Scale bar, 25 μm. C, comparison of the slow transient integral of 41 putative Golgi cells grouped according to their morphology. ‘No axon’ labels a group of 8 cells for which no axonal plexus was preserved. ‘Damaged axon’ represents a group of 6 cells for which the Golgi type II axon had been greatly damaged and reduced in extension. D, same protocol as in A for a Golgi cell perfused with an internal solution containing blockers of voltage-dependent channels (see Methods) for 1 min and 4 min (superimposed traces).

Patch-clamp recording

All experiments were performed at room temperature. The recording chamber was continuously perfused at a rate of 1.5 ml min⁻¹ with the following saline solution (mm): 125 NaCl, 2.5 KCl, 2 CaCl₂, 1 MgCl₂, 1.25 NaH₂PO₄, 26 NaHCO₃ and 25 glucose, bubbled with a mix of 95 % O₂-5 % CO₂ (pH 7.4). The same solution was used during the dissection and slicing. Tetrodotoxin (TTX, Sigma), strychnine (Sigma) and gabazine (RBI) were bath applied. To remove the external calcium ions an external solution containing no added calcium, 3 mm MgCl₂ and 100 μM EGTA was used. Granule cells were stimulated chemically by local application of kainic acid (Tocris Cookson, Bristol, UK) dissolved in a Hepes-buffered solution of the following composition (mm): 140 NaCl, 2.5 KCl, 2 CaCl₂, 1 MgCl₂ and 30 Hepes; pH adjusted to 7.3 with NaOH. Kainate was pressure applied from a patch pipette placed in the granule cell layer near to the recorded Golgi cell.

Pipettes had a resistance of 2-4 MΩ for whole-cell voltage-clamp recordings and a resistance of 5-10 MΩ for current-clamp recordings. The pipette capacitance was compensated for once the seal was obtained, in the cell-attached configuration. For most recordings, cells were voltage clamped at -70 mV with the following internal solution (mm): 142 CsCl, 10 Hepes, 1 EGTA, 5 MgCl₂, 0.1 CaCl₂, 4 NaATP and 0.4 NaGTP; pH adjusted to 7.3 with N-methyl-D-glucamine (NMDG). The series resistance was kept between 3 and 10 MΩ during voltage-clamp recordings and around 15 MΩ in the current-clamp mode. EPSCs were also recorded at depolarized potentials (+61 mV). An internal solution containing blockers of voltage-dependent channels was used to limit the amplitude of the whole-cell currents activated by depolarization. This solution contained (mm): 123 CsOH, 100 D-gluconic acid, 17.5 TEA, 10 Hepes, 5 QX-314, 10 EGTA, 1 CaCl₂, 5 MgCl₂, 4 NaATP and 0.4 NaGTP; pH adjusted to 7.3 with CsOH. Two physiological internal solutions were used for current-clamp recordings. The first solution (KG internal solution) contained (mm): 144 potassium gluconate, 10 Hepes, 0.2 EGTA and 3 MgCl₂; the pH was adjusted to 7.3 with KOH. The second solution (KGC internal solution) contained (mm): 115 potassium gluconate, 22 KCl, 10 Hepes, 1 EGTA, 0.1 CaCl₂, 5 MgCl₂, 4 NaATP and 0.4 NaGTP; pH adjusted to 7.3 with KOH. Membrane potentials were corrected for liquid junction potentials when they exceeded 2 mV (of the order of the maximal voltage drop across the series resistance).

Data analysis

pCLAMP 6 software (Axon Instruments) was used for the acquisition of all recordings. For the analysis of EPSC amplitudes and decay time constants, recordings were filtered at 2 kHz and digitized at 10 kHz. For the analysis of EPSC rise times, recordings were filtered at 5 kHz and digitized at 25 kHz. Current clamp recordings were filtered at 10 kHz and acquired at 50 kHz. Spontaneous EPSCs were detected automatically using the ACS software kindly provided by P. Vincent (Institut des Neurosciences, Paris). All the events detected were subjected to visual inspection. The EPSCs were fitted using the N05 software kindly provided by S. Traynelis (Salk Institute of Biological Studies, La Jolla, CA, USA).

Morphological reconstruction

In most experiments biocytin (2 mg ml⁻¹) was added to the internal solution. At the end of whole-cell recordings the patch pipette was slowly moved away from the cell in order to obtain an outside-out patch and to reseal the cell membrane. This was not always successful, particularly at the end of long recordings. The slice was then fixed at 4°C in phosphate-buffered saline (PBS: 150 mm) containing 4 % w/w paraformaldehyde (and sometimes 0.05 % v/v glutaraldehyde). After 12 h to 2 weeks of fixation, biocytin was revealed using avidin coupled to fluoresceine isothiocyanate (FITC) or the ABC elite kit (Vector Laboratories Inc., Burlingame, CA, USA). In the latter case slices were preincubated for 10 min in 10 % methanol, 89 % PBS and 1 % H₂O₂ to remove endogenous peroxidase activity. They were then permeabilized for 30 min with 0.4 % Triton PBS and incubated for 2 h with the avidin derivatives. Peroxidase activity was revealed by incubation in a Tris solution containing 0.015 % w/v diaminobenzidine, 0.15 % w/v nickel ammonium sulphate and 0.4 μl ml⁻¹ of a 1 % H₂O₂ solution. Slices were preincubated for 20 min in a similar solution without H₂O₂.

For fluorescence imaging, slices were mounted in Vectashield (Vector Labs) and for transmitted light observation they were mounted in Mowiol (Hoechst). The images presented in this article are parasagittal projections of all or parts of FITC-revealed Golgi cells. The software Imagespace (Molecular Dynamics) running on an Indy workstation (Silicon Graphics) was used to reconstruct the cells from sections taken with an epifluorescence confocal microscope (Sarastro 2000, Molecular Dynamics). Serial confocal images were taken every 0.2 to 1 μm and projections were obtained by superposition of the different images accompanied by a 3D Gaussian deconvolution. To show the position of the recorded cells relative to the different layers of the cerebellar cortex, Purkinje cells were labelled with an anti-calbindin primary antibody (SWant, Bellinzona, Switzerland) and a CY₃-coupled secondary antibody. The CY₃ fluorescence photomultiplier detector was set at such a level that only the brightest parts of the Purkinje cells, that is the cell bodies, were visible.

RESULTS

The morphology of most of the cells recorded resembles that of Golgi cells previously described by anatomical methods

The classification of cerebellar interneurones began in the late 19th century with studies using the Golgi impregnation technique. In the granular layer of the cerebellar cortex Golgi (1883) first distinguished two subgroups of large neurones, a classification that was confirmed in later studies. The cells of the first class have a rounded or polygonal soma, which lies in the granular layer or at the border of the Purkinje cell layer, and a stellate shape of the dendritic arborization. They were named Golgi cells after their discoverer (see Palay & Chan-Palay, 1974). It is the most abundant interneurone of the granular layer. The second class of cells defined by Golgi are characterized by their fusiform soma lying just under the Purkinje cell layer and their bipolar dendrites which run for long distances at the upper limit of the granular layer. They were generally named Lugaro cells (Lugaro, 1894; Fox, 1959; Lainé & Axelrad, 1996). The Golgi cell is clearly distinguished from the Lugaro cell by its extensive and densely bifurcated Golgi type II axonal plexus, which is restricted to the granular layer (Golgi, 1883; Palay & Chan-Palay, 1974), whereas the Lugaro axonal plexus is sparse and extends in both the molecular and granular layers (Fox, 1959; Lainé & Axelrad, 1996).

More recently immunohistochemical studies have improved, and somewhat modified the classification of granular layer interneurones. Using systematic monoclonal antibody screening procedures, the group of Hockfield has produced antibodies selective for Golgi cells, Lugaro cells and a new type of interneurone of the granular layer: the unipolar brush cell (Hockfield, 1987; Sahin & Hockfield, 1990). These observations demonstrated that unipolar brush cells and Lugaro cells are not abnormal forms of granule cells and Golgi cells, respectively. They also showed that Lugaro cells are more numerous than previously thought, and that many of them do not lie just underneath the Purkinje cell layer, as classically described, but deeper in the granular layer. As a consequence the position and shape of the cell body does not allow an unambiguous distinction between Lugaro cells and Golgi cells. Nevertheless all immunohistochemically defined Lugaro cells present three features of the first-recognized fusiform cells, which clearly distinguish them from Golgi cells: their dendrites do not enter the molecular layer, their axons are poorly ramified and they extend in both the granular and molecular layers.

In this study infrared microscopy was used to visualize the cell bodies of putative Golgi cells in thin slices of the rat cerebellum. These cell bodies are easily distinguished by their size from those of the surrounding granule cells and of the unipolar brush cells, but not from those of the Lugaro cells. This preliminary identification was therefore confirmed by morphological reconstruction. Golgi cells were found in every cerebellar lobule. They were located at various depths within the granular layer but the majority of them were found close to the Purkinje cell layer. As shown in Fig. 1A, the most striking feature of Golgi cells is their extensive neuritic plexus in the granular layer. A part of this plexus is shown at higher magnification in Fig. 1B It is composed of very fine beaded fibres, which are characteristic of the Golgi cell axon. The preservation of a large Golgi type II axon was used as a morphological criterion to identify Golgi cells. In some places the axon wraps around some elongated structures where it forms numerous varicosities, and which correspond to glomeruli (indicated in the Fig. 1B by Glo) (Hámori & Szentágothai, 1966). The initial segment of the main axon is characterized by its rectilinear course and its smooth contours. It could be identified in all the cells injected. This main axon descends directly towards the white matter, giving out numerous collaterals on its way. It does not enter into the white matter directly, but when reaching it, bifurcates into horizontal branches. These branches can run for hundreds of micrometres at the limit of or inside the white matter (see Table 1). In many instances, they formed secondary plexuses at some distance from the cell body. As can be seen in Fig. 1A, these secondary plexuses are much less dense than the axonal plexus found in the region of the cell body. These observations (see Table 1) suggest that the existence of several axonal plexuses is a feature of most, if not all, Golgi cells. The functional consequences of this organization are unknown.

Table 1.

Morphological features of the cerebellar Golgi cells

		Mean ±s.d.	Min	Max
Somata	Vertical diameter (μm)	16 ± 4	8	25
	Horizontal diameter (μm)	17 ± 5	10	28
	Deformation index	1.0 ± 0.3	0.63	1.9
	Position in the granular layer (% from white matter to Purkinje)	80 ± 14	57	100
Apical dendrites	Number of primary apical dendrites	2.1 ± 0.9	1	4
	Number of dendritic branches entering the Purkinje cell layer	2.8 ± 1.3	1	5
	Number of dendritic branche terminations in the molecular layer	11.2 ± 4.0	4	17
	Width of the apical dendritic arbor (μm)	191 ± 79	50	310
Basolateral dendrites	Number of basolateral dendrites born from the cell body	4.1 ± 1.4	2	7
	Number of branches born from primary apical dendrites	2.7 ± 1.7	0	5
Axon	Number of preserved axonal plexus	1.4 ± 0.7	1	3
	Width of the main plexus (μm)	230 ± 100	40	410
	Identification of the axon initial segment from the cell body	18/18 cells
	Presence of an axonal branch runing into the white matter	9/18 cells

Morphological data were gathered from the 18 best-preserved Golgi cells filled with biocytin. In all these cells particular attention was paid to the preservation of the apical dendritic tree. In some cases basolateral dendrites may have been cut away from the soma but their proximal portion could still be recognized and included in the statistics. The axonal arbor of all the cells was well preserved but it is very likely that in most cells some of its distal parts were lacking because a main axonal trunk had been cut when making the slice. The deformation index of the soma is the vertical diameter divided by the horizontal diameter measured parallel to the Purkinje cell layer. The number of primary apical dendrites is the number of dendrites arising from the cell body which emit at least one branch entering the molecular layer. The width of the dendritic arbor was the maximal extension measured parallel to the Purkinje cells layer. The main axonal plexus was identified as that containing the most dense axonal arborization. It was surrounding the cell body and its limits were sharp when the axon was well preserved. Axon collaterals giving rise to more dispersed arborizations away from the cell body were counted as secondary plexuses.

Palay & Chan-Palay (1974) have reported that Golgi cells have a main axon originating from the cell body and several secondary axons which originate from the Golgi cell dendrites in the granular layer. In many cases varicose axon-like neurites originating from dendrites in the granular layer, similar to the secondary axons described by Palay & Chan-Palay, were observed. In contrast to the main axon, they lacked the characteristic initial segment and could not be followed easily over long distances. It is impossible to ascertain with the techniques used, whether they represent secondary axons or thin and thorny dendritic branches.

Four to ten dendrites emerge from the cell body of Golgi cells (see Table 1). They can be divided into two categories, apical and basolateral. Apical dendrites, generally stout and straight, rise towards the Purkinje cell layer, branching several times as they cross it. They may divide again once or twice in the molecular layer, where they form a diffuse, fan-shaped, dendritic arborescence. A segment of the apical dendrites of the cell presented in Fig. 1A is shown in Fig. 1C at larger scale. Sparse, short and stout spine-like protrusions are visible. They have been described previously using the Golgi impregnation technique. These protrusions, as well as the shaft of the dendrite, are the sites of synaptic contacts with the parallel fibres. In addition to the apical dendrites, several basolateral dendrites originate from the cell body. These are contorted, branch several times and always remain into the granular layer. It must be noted that, on their way through the granular layer, the main trunks of the apical dendrites can give several branches similar in all aspects to basolateral dendrites (see Table 1).

Neurones having the classical dendritic morphology of Lugaro cells were occasionally recorded during the course of this study. Their ‘apical’ dendrites were curving under the Purkinje cell layer and were mostly restricted to the granular and Purkinje cell layers. In some instances their most distal dendrites seemed to penetrate the very bottom of the molecular layer (Sahin & Hockfield, 1990; Lainé & Axelrad, 1996). In many cases thin axons were seen in the granular layer, but never formed a dense axonal plexus. Some of the axons reached the white matter directly without branching whereas others, after several bifurcations, ascended to the molecular layer.

The Golgi cell axon capacitive transient is a simple electrophysiological criterion for separating Golgi cells from other large interneurones of the granular layer

The whole-cell configuration of the patch-clamp technique was used to record from putative Golgi neurones in the granular layer. The holding potential was set at -70 mV. Hyperpolarizing voltage pulses (10 mV) elicited a current transient which decayed with both fast (in the millisecond range) and slow (tens of milliseconds, called hereafter the third component of the decay) kinetics. The fast part of the capacitive transient was correctly fitted by the sum of a fast and a slow exponential function (first and second components). The statistics for their time constants and integrals (expressed as an equivalent capacitance) are given in Table 2. At the beginning of the recordings the fastest exponential component of the cell capacitance was cancelled. To improve the control of the membrane potential the access resistance was compensated (70-90 %). The time constant of the second exponential component was subsequently reduced to 66 ± 13 % (n = 43) of its initial value, indicating that the two electrically equivalent resistance-capacitance (RC) circuits are connected in series (see Table 2).

Table 2.

Passive electrical parameters of cerebellar Golgi cells

Parameters	τ1 (μs)	a1 (pA)	τ2 (μs)	a2 (pA)	τ′2 (μs)	(τ′2/τ2) × 100	C1 (pF)	C′1 (pF)	C2 (pF)
Mean ±s.d.	140 ± 50	450 ± 180	690 ± 230	490 ± 170	450 ± 170	66 ± 13	6 ± 3	23 ± 8	32 ± 11
Min	60	190	280	230	200	43	2.4	12	15
Max	300	900	1170	971	940	95	15.7	44	58

Passive electrical parameters were measured in 43 Golgi cells dialysed with a CsCl internal solution. The capacitive transient evoked by a 10 mV (dV) hyperpolarizing voltage pulse was fitted by three exponential functions. The slowest component, corresponding to the axonal capacitive transient (see Fig. 2) is not described in this table. τ₁, a₁, τ₂ and a₂ are the time constants and amplitudes of the exponentials fitted to the capacitive transient. τ‘₂ is the time constant of the intermediate component remaining after cancellation of the first component and compensation (generally 80%) of the series resistance R_s. C₁ is an underestimate of the capacitance of the first component, calculated as τ₁×a₁. A closer approximation of this capacitance can be obtained assuming that the cell is composed of two resistance-capacitance compartments in series:

Similarly C₂, calculated as τ₂×a₂ underestimates the capacitance of the distal electrical component.

The slow part of the current transient evoked by hyperpolarizing voltage pulses (third component) could be fitted by a single exponential function. Its time constant was 18 ± 11 ms (range: 3-59 ms; n = 36) and its amplitude was 40 ± 25 pA (range: 4-100 pA; n = 36). The number of charges carried by this relaxation are given by the integral of the fitted exponential function or by the amplitude of the integral of the current transient. Both methods gave similar values, which were highly variable from cell to cell (range: 20-2430 fC). This variability is illustrated in Fig. 2A

The transients shown in Fig. 2A, which have very different amplitudes, were recorded from the cells shown in Fig. 1 (top recording) and Fig. 2B (bottom recording). The two cells have very similar dendritic profiles but strikingly different axonal extensions, which suggests that the slow transient is associated with the presence of the axon. This supposition was supported by the analysis of the other cells: the amplitude of the slow transient was consistently correlated with the presence of a Golgi type II axonal plexus in all the cells examined. A summary is presented in Fig. 2C. In the two morphologically identified Lugaro cells recorded with the same internal solution one of the slow capacitive transients was too small to be measured and the other carried 10 fC. From the sample of Fig. 2C we conclude that a slow current relaxation carrying more than 150 fC is a distinctive feature associated with the large and ramified axonal plexus of Golgi cells. Conversely, all the cells having a smaller transient (some of which may have been Golgi cells with a severed axon, and some Lugaro cells) were removed from the present study.

The amplitudes of the slow transients were similar when the cells were dialysed with an internal solution containing blockers of voltage-dependent conductances (Fig. 2D) and they did not disappear in the presence of the following blockers in the external solution: 1 mm 4-aminopyridine (4-AP), 10 mm TEACl, 2 μM TTX and 200 μM BaCl₂ (data not shown). This indicates that the slow transient current is mainly due to the passive charge of the axonal membrane capacitance. With the standard solution the mean integral of the transient was 770 fC (n = 36). This charge would correspond to the clamp of a large portion of the ramified axon. The initial descending segment of the axon can be represented by a cable with a radius r_a = 0.5 μm, a maximum length of 200 μm and a specific membrane capacitance C_m = 1 μFcm⁻². If the capacitive charge was coming mainly from this initial unramified segment, it should be at most 450 fC (not taking into account the space-clamp problems into the axon). Thus, it is expected that the total capacitive charge depends on the density and extension of the axonal plexus.

Dependence of Golgi cells’ firing frequency on depolarizing current injection

When recorded in the cell-attached configuration, most Golgi cells generated spontaneous action potentials. Their mean spike frequency was 3.0 ± 1.7 Hz (n = 17; from 0.62-5.7 Hz). Their activity was regular in most cases but pauses in the activity were observed in two Golgi cells recorded after P20 and occasionally Golgi cells were encountered that were silent during the cell-attached recording time. This may be correlated with the results of Wall & Usowicz (1997) who, recording from granule cells, observed that the frequency of TTX-dependent IPSCs (assumed to originate from Golgi cells) is dramatically reduced in older animals.

The active membrane properties of Golgi cells (P12-P19) were studied in the whole-cell configuration using the potassium gluconate intracellular solutions described in Methods. Cells were held around -75 mV in the current- clamp mode with a holding current ranging from -30 to 0 pA (mean -7 pA; n = 8). In the majority of cells, stepping to +30 pA was sufficient to generate spikes. Figure 3A presents the typical response of a Golgi cell to depolarizing current pulses of 1 s duration. As in all Golgi cells, the firing frequency adapted during the pulse. The evolution of the instantaneous firing frequency during three current pulses of increasing intensity is plotted in Fig. 3B The ratio of the instantaneous firing frequency for the first spike and at the steady state is 3.5, 3.8 and 5.2 for the current pulses of 55, 165 and 265 pA, respectively. This adaptation was slower and less pronounced when Golgi neurones were recorded with an internal solution of higher Ca²⁺-buffering power (1 mm vs. 0.2 mm EGTA; see Methods), whereas the initial firing frequency was unchanged. This suggests that part of the adaptation is a calcium-dependent process possibly due to calcium-dependent potassium channels. These channels are well known to generate a long-lasting post-train AHP produced by strong depolarizing current pulses. This type of AHP is present in Golgi cells, as shown in Fig. 3A (300 pA current pulse).

Figure 3. Active electrical properties of the Golgi cells.

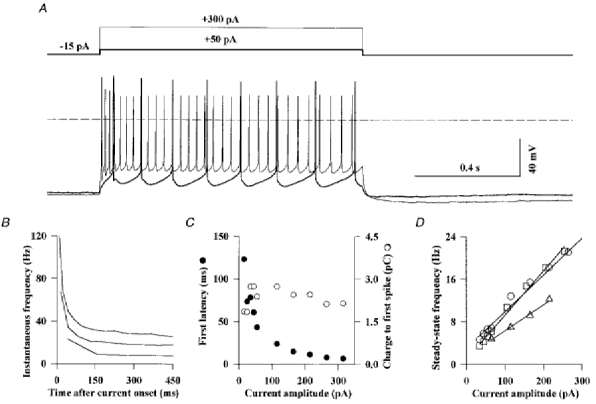
Golgi cells were recorded in the current-clamp mode of the whole-cell patch-clamp configuration with the KG internal solution (see Methods) and in the presence of 10 μM NBQX, 1 μM strychnine and 20 μM gabazine. A, firing behaviour of a Golgi cell in response to 1 s depolarizing current pulses of 50 pA (thick line) and 300 pA (thin line). B, plot of the instantaneous firing frequency during current pulses of +40 pA, +150 pA and +250 pA (from bottom to top) for the cell shown in A. The instantaneous firing frequency was defined as the reciprocal of the interval (in seconds) between one spike and that preceding it. For the first spike it was defined as the inverse of the time from the beginning of the pulse to the beginning of the spike. C, the latency of the first spike during a depolarizing current pulse (•) and the product of this latency by the pulse amplitude (total charge to generate the first spike, ^) are plotted against the pulse amplitude. Same cell as in A. D, the steady-state firing frequency, measured between 300 and 500 ms after pulse onset, is plotted against the current pulse amplitude for three cells. The slopes of the linear regression lines are 49, 69 and 83 Hz nA⁻¹.

Figure 3C shows that the latency of the first spike was inversely proportional to the intensity of the depolarizing current step, so that the total charge necessary to reach the threshold of the first action potential was independent of the current pulse intensity (Fig. 3C). Thus, despite the non- linearity of the voltage-dependent processes leading to the generation of a propagated action potential, the Golgi cell behaves like a linear charge integrator. Figure 3D shows that the steady-state firing frequency of Golgi cells is proportional to the current pulse amplitude. The linear regressions gave a mean slope of 70 ± 20 Hz nA⁻¹ for three cells perfused with an internal solution of low Ca²⁺-buffering power and of 230 ± 50 Hz nA⁻¹ for five cells perfused with the high Ca²⁺-buffering power internal solution.

Golgi cells express I_h

The response of a Golgi cell to hyperpolarizing current pulses is shown in Fig. 4A. The recording is characterized by a sag, the size of which increases with hyperpolarization. The ratio of peak to steady-state hyperpolarization varied from cell to cell and depended on the current pulse amplitude. This type of sag in current clamp recordings is generally associated with the presence of the I_h current which, by activating slowly at hyperpolarized potentials, promotes a hyperpolarization-induced depolarization. At the end of hyperpolarizing current pulses I_h stays activated for tens of milliseconds and is responsible for a rebound depolarization above the initial membrane potential. In Fig. 4A this depolarization is subthreshold for the current pulse of -50 pA and triggers action potentials for the large current pulse of -300 pA.

Figure 4. Electrical response of Golgi cells to hyperpolarizing current pulses.

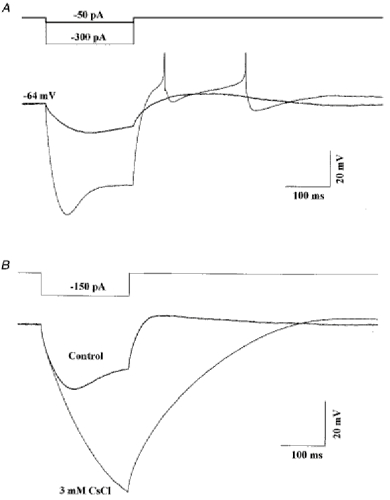
A, the cell was held at -64 mV by a steady current injection of -40 pA and further hyperpolarized for 200 ms periods by current pulses of -50 pA (thick line) and -300 pA (thin line). The sodium spikes generated during the rebound depolarization are truncated. B, same cell as in A recorded in the presence of TTX (1 μM) in the bath (thick line). After addition of CsCl (3 mm) both the sag and rebound depolarization evoked by a -150 pA current pulse were suppressed (thin line). The holding potentials were -70 mV for the control and -74 mV in the presence of CsCl. Recording conditions as in Fig. 3.

I_h is characterized pharmacologically by its sensitivity to low millimolar concentrations of Cs⁺ ions in the external medium (Pape, 1996). This can be used to distinguish I_h from inward rectifying potassium currents, which are not blocked by external Cs⁺ ions. As shown in Fig. 4B, both the sag during a hyperpolarizing current pulse and the rebound depolarization of the Golgi cell were blocked by addition of 3 mm CsCl to the external medium. The comparison of the two traces indicates that I_h activation can be detected after about 30 ms, and seems to be nearly complete after 200 ms. This fast activation is partially masked by the charge of the cell capacitance, and particularly of the axonal capacitance, so that a sag of modest amplitude corresponds in fact to a very large depolarizing effect of the I_h current. When I_h is blocked, hyperpolarizing current pulses lead to very large hyperpolarizations and the calculated value for the input resistance is of the order of 0.5 GΩ. The comparison of the steady-state hyperpolarization in the presence and absence of I_h indicates that it is the main component of the membrane conductance at hyperpolarized potentials.

Fast spontaneous synaptic events are glutamatergic EPSCs

The spontaneous synaptic activity recorded from Golgi cells voltage clamped at -70 mV is shown in Fig. 5A. Synaptic events were detected automatically as described in Methods. All the events detected were aligned on their first rising point and are displayed on an expanded time scale on the right of the traces. Synaptic events could be divided into two groups with very different kinetic properties: slow events, lasting tens of milliseconds, previously characterized as inhibitory GABAergic and glycinergic IPSCs (Dieudonné, 1995), and fast events, decaying within a few milliseconds and assumed to be glutamatergic EPSCs. When saturating concentrations of GABA_A and glycine receptor antagonists (1 μM strychnine and 20 μM gabazine) were added to the external solution (Fig. 5B), the slow events disappeared but the fast events were unaffected. They were blocked by subsequent superfusion with 10 μM 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX; Fig. 5C), as expected for glutamatergic EPSCs mediated by AMPA-type receptors. This spontaneous excitatory activity was very stable in amplitude and frequency, even during long-lasting recordings. The mean peak amplitude of spontaneous EPSCs was 38 ± 9 pA (n = 21) at -70 mV with a CsCl internal solution and 47 ± 11 pA (n = 11) at -76 mV with a potassium gluconate solution. The mean frequency of EPSCs was 1.6 ± 1.5 Hz (range: 0.15-6.3 Hz; n = 32).

Figure 5. Pharmacological separation of excitatory and inhibitory spontaneous synaptic currents.

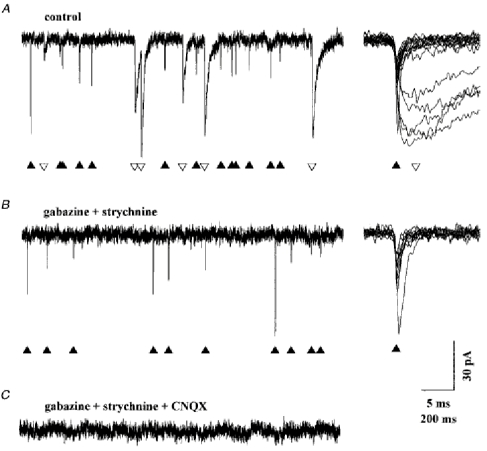
Golgi cell dialysed with the CsCl internal solution. Holding potential -70 mV. Synaptic events were detected automatically as described in Methods. All the events detected in the sections of recordings displayed in the left part of the figure were aligned at their first rising point, superimposed and displayed on an expanded scale on the right. ▴ are placed under the fast decaying events and ▿ are placed under the slow decaying event. A, in the absence of blocker in the external solution the spontaneous activity is composed of fast and slow events. B, the slow events are blocked by 20 μM gabazine and 1 μM strychnine. C, the fast events are blocked by the further addition of 10 μM CNQX.

Most spontaneous EPSCs recorded in Golgi cells are due to release of a single quantum at the parallel fibre-Golgi cell synapses

Figure 6 illustrates the effect of TTX (0.4 μM) on the spontaneous excitatory activity. In Fig. 6A each bar represents an EPSC. In this cell TTX reduced the frequency of the spontaneous EPSCs to 54 % of the control. On average the frequency fell to 80 ± 26 % (n = 3) of the control. Removal of the external calcium did not further decrease the EPSC frequency (96 ± 8 %; n = 3). These results indicate that most of the spontaneous EPSCs are miniature events that require neither action potential nor presynaptic calcium entry.

Figure 6. Effect of TTX on the spontaneous excitatory activity.

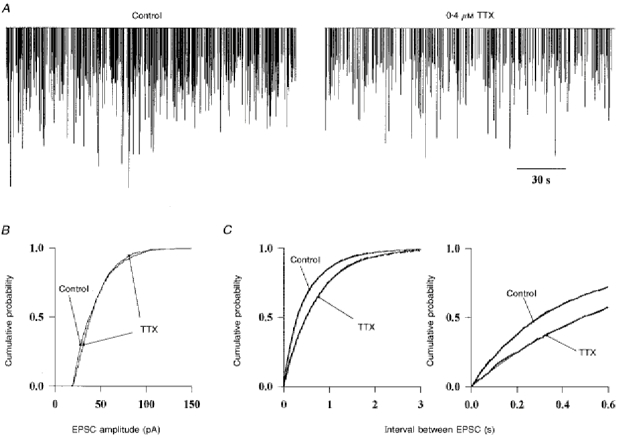
A, the fast EPSCs were recorded in the presence of 20 μM gabazine and 1 μM strychnine in the bath and detected as in Fig. 5. Each event is represented by a vertical bar proportional to its amplitude to allow the visualization of the activity over long recording periods (3 min). TTX (0.4 μM) reduces the frequency of occurence of EPSCs. B, cumulative amplitude histogram of the EPSCs before and after addition of TTX to the bath. Data were pooled from 3 different Golgi cells. C, the interval between consecutive EPSCs was calculated in the same 3 cells. The cumulative frequency distributions obtained before and after addition of TTX are plotted at two time scales. The data were obtained from stretches of recordings of the same duration in all the cells. The sum of two exponential functions with time constants of 0.24 s and 0.67 s was fitted to the experimental points in control conditions (thin line). Only one exponential function of time constant 0.71 s was necessary to fit the data after addition of TTX.

The amplitude distribution of the EPSCs was not significantly affected by TTX (Fig. 6B). This could indicate that the TTX-dependent EPSCs are mostly monoquantal. Alternatively, multiquantal release may occur but may be masked if, at a single release site the postsynaptic receptors are saturated by a single quantum.

The cumulative density functions of inter-event intervals measured before and during TTX application are plotted in Fig. 6C The data points obtained in the presence of TTX are fitted by a single exponential function, as expected for independent miniature events occuring at random, according to a Poisson process. To describe the data obtained under control conditions it is necessary to add a second exponential function with a faster time constant. The presence of this second exponential component indicates that TTX-dependent EPSCs do not occur independently of each other but appear in bursts. Bursts are not apparent in the recordings of Fig. 6A because their internal frequency is not very different from the average frequency. In other cells the bursts were clearly distinguished on a background of low average frequency. As most granule cells are normally inactive in the slice, in part because they receive inhibition from the Golgi cells but no excitation from the cut mossy fibres, the present results probably indicate that one or a few damaged granule cells, firing in bursts, are responsible for all the TTX-dependent activity.

The vast majority of excitatory synapses formed on Golgi cells are made by parallel fibres which contact the apical dendrites, and only a few are made by mossy fibres or climbing fibres which contact the cell body and the basolateral dendrites and which are silent in the slice. It is therefore very likely that most of the spontaneous EPSCs recorded in Golgi cells result from release events at parallel fibre synapses. To test further this hypothesis, kainate was applied locally to the granule cell layer. This chemical stimulation is expected to excite granule cells selectively, because mossy and climbing fibres, isolated from their cell body in the slice, are not thought to express glutamate-gated channels. As shown in Fig. 7A, a puff of kainate (40-100 μM) evoked numerous TTX-dependent EPSCs in the Golgi cell. As shown on an expanded time scale in Fig. 7B, this kainate-evoked activity was composed of fast synaptic currents. The spontaneous EPSCs and the kainate-evoked EPSCs from five Golgi cells were pooled and compared. As shown in Fig. 7C the amplitude ranges of both populations are very similar. However, there is an excess of large amplitude events in the kainate-evoked population. This might happen either if the frequency of evoked EPSCs is too high, so that some events occur too close to each other to be discriminated or, if there is a population of truly multiquantal TTX-dependent events. To distinguish between these two hypotheses the histogram of the intervals between kainate-evoked EPSCs was constructed. As expected, most of the EPSCs were randomly distributed in time, as shown by the exponential decay of the interval histogram. However, in addition to the randomly occuring events, there was a significant population of EPSCs separated by less than 4 ms and thus representing nearly synchronous unitary events (marked by an asterisk in Fig. 7B). A large number of these double events, because they were separated by less than 0.5 ms, were detected as single EPSCs (and are therefore absent from the histogram). As there is no known mechanism that can synchronize granule cells (inhibition is blocked) these double events, which include the events larger than the spontaneous ones in the histogram of Fig. 7C, are truly multiquantal. Such large multiquantal events were not present in significant proportion in the spontaneous activity described in Fig. 6 for two reasons: TTX-dependent EPSCs represented only a fraction of the spontaneous activity and they probably arose from a small and possibly unrepresentative sample of granule cells, which might not have included a cell with multiquantal contacts.

Figure 7. Synaptic events evoked by local application of kainate onto the granular layer.

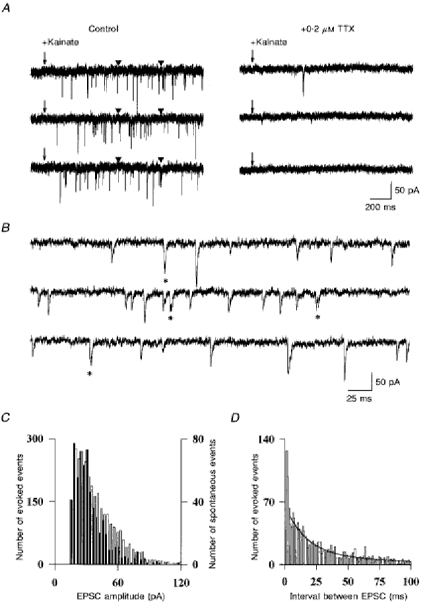
A, kainate (40 μM) was pressure applied near the Golgi cell at the time indicated by the arrow. It was possible to find places where no kainate receptors were activated in the postsynaptic cell. The responses to three consecutive applications are shown. Left: control. Right: kainate-evoked EPSCs are blocked by addition of 0.2 μM TTX in the bath. Arrowheads indicate the beginning and the end of the recordings enlarged in B. B, kainate-evoked events are displayed on an expanded time scale. Double events with a latency under 3 ms are indicated by asterisks. C, amplitude distribution of spontaneous events (filled bars) and kainate-evoked events (open bars) in the same cells. Data pooled from three cells. D, histogram of the intervals between two consecutive kainate evoked EPSCs. The sum of two exponential functions was fitted to the data for events separated by more than 4 ms (continuous line), showing the excess of events in the 0-3 ms range.

AMPA and NMDA components of parallel fibre EPSCs

EPSCs were recorded at positive and negative membrane potentials with an internal solution containing blockers of voltage-dependent channels. The voltage dependence of their AMPA and NMDA components was studied in the presence of external Mg²⁺ ions (1 mm) and internal spermine (10 μM). In the Golgi cells presenting enough spontaneous activity a ‘mean parallel fibre spontaneous EPSC’ was generated by averaging the EPSCs aligned at their first rising point. Such a mean EPSC for a Golgi cell clamped at +61 mV is presented in Fig. 8A. The NMDA component is clearly identified as a prominent slow component which was completely blocked by 100 μM dl-2-amino-5-phosphonovaleric acid (dl-APV; Fig. 8B). The decay of the NMDA component was well fitted by two exponential functions of time constants 31 ± 9 and 170 ± 15 ms (n = 4). On average the faster NMDA component represented 33 ± 25 % (n = 4) of the peak NMDA current. APV had no effect on the EPSCs recorded at hyperpolarized potentials, showing that the NMDA receptors present at the synapse are completely blocked by Mg²⁺ ions.

Figure 8. Parallel fibre EPSCs at hyperpolarized and depolarized potentials.

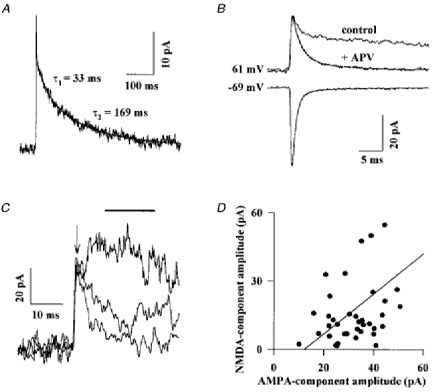
Golgi cells were recorded with an internal solution containing blockers of voltage-dependent channels (see Methods) and successively maintained at +61 mV or at - 69 mV. A, the mean EPSC recorded at +61 mV is displayed at a slow time scale. The initial AMPA component is seen as a spike. The slower NMDA component is fitted by the sum of two exponential functions (smooth line). B, mean EPSCs recorded from the same cell and displayed on an expanded time scale. ‘Control’ corresponds to the trace shown in A. Addition of 100 μM dl-APV blocked the slow NMDA component of the EPSC without affecting the initial peak. Isolated AMPA components at -69 mV and +61 mV are fitted by the sum of two exponential functions with time constants of 0.83 ms and 3.87 ms (at -69 mV) and 1.8 ms and 7.74 ms (at 61 mV). The slow component contributed respectively to 10 and 22 % of the peak amplitude. C, three representative EPSCs are superimposed. The arrow indicates the time of the peak current and the bar indicates the time window for averaging of the peak NMDA current. D, the amplitudes of the AMPA and of the NMDA components of individual EPSCs were measured as described in the text and plotted against each other. The line corresponds to a significant (P < 0.05) linear correlation between the two amplitudes.

At hyperpolarized potentials, with the internal solution containing blockers, the mean (AMPA) EPSCs were well fitted by a single exponential function, but the fit was generally improved when two exponential functions were used. The decay time constants of the EPSC shown in Fig. 8B are 0.82 and 4.7 ms. In four cells recorded in the same conditions the mean values were 0.96 and 4.9 ms. The voltage dependence of the AMPA component of EPSCs was assessed in the presence of 100 μM dl-APV (Fig. 8B). The fast and slow decay time constants were both increased by depolarization to +61 mV, by 186 % and 164 %, respectively. The relative amplitude of the slow component was increased from 10 ± 2.5 % at -69 mV to 26 ± 3 % at +61 mV. This effect cannot be explained by poorer clamp conditions due to the activation of voltage-dependent conductances at depolarized potentials because this would lead to the opposite effect, that is an apparent decrease of the decay time constant of the EPSCs. The kinetics of the AMPA components of parallel fibres EPSCs are thus both very fast and strongly voltage dependent.

Spermine (10 μM) is known to block selectively some AMPA receptors from the cytoplasmic side at depolarized potentials (Bowie & Mayer, 1995). The rectification of spontaneous EPSCs in the presence of internal spermine was calculated as the ratio of the peak amplitude of the mean EPSC at -69 mV and +61 mV. This value was 0.7 ± 0.12 (n = 5). Due to the rectification, many of the smallest EPSCs detected at -69 mV will fall under the detection threshold at +61 mV. This is seen as an apparent decrease in the EPSC frequency at positive potentials. To correct this threshold artefact, the same number of the largest EPSCs were averaged at -69 mV and at +61 mV. The corrected rectification index is 0.49 ± 0.07 (same five cells), indicative of a low calcium permeability at these receptors (Washburn, Numberger, Zhang & Dingledine, 1997).

As can be seen in Fig. 8B, the peak of the averaged EPSC at depolarized potentials is not affected by the addition of APV. This shows that AMPA channels are fully activated before any substantial activation of the NMDA channels occurs. It is therefore possible to compare the relative sizes of the AMPA and NMDA components of single EPSCs without too much cross-contamination. The amplitude of the AMPA component was taken as the peak current in the first millisecond following the onset of the synaptic current (arrow on top of the traces of Fig. 8C). The amplitude of the NMDA component was taken as the mean value of the current recorded between 10 ms (when the AMPA component has decayed to less than 10 % of its peak) and 25 ms after the EPSC onset (bar on top of the traces of Fig. 8C). As shown in Fig. 8C, three EPSCs having the same AMPA component can have very different NMDA components. Nevertheless, in the four cells studied, there was a statistically significant (P < 0.05) correlation between the amplitude of the AMPA and NMDA components of individuals EPSCs (Fig. 8D). The average slope (0.6 ± 0.4) and the significance of the correlation might be underestimated since, as shown below, the peak amplitude of the AMPA component of EPSCs occuring at distal synapses is reduced by dendritic filtering, which probably does not affect the slower NMDA component to the same extent.

Variability of the kinetic properties of the AMPA component of individual EPSCs

The EPSC presented in Fig. 9A is the average of 175 spontaneous EPSCs recorded from a Golgi cell voltage clamped at -70 mV with a CsCl-based internal solution during a period of 3 min. Its decay is quite well fitted by a single exponential function with a time constant of 1.2 ms (mean time constant 1.06 ± 0.26 ms; n = 24). The good voltage clamp achieved with this internal solution might explain the discrepancy with Fig. 8B. Six individual EPSCs, recorded from the same Golgi cell, are shown in Fig. 9B. Their decays, which are fitted by single exponential functions, show a very large dispersion. As shown in the histogram of Fig. 9C, which illustrates the distribution of the time constants for all the individual EPSCs recorded in this experiment, the most frequently encountered decay time constant was close to 0.9 ms and the extremes in this cell were 0.51 and 3.26 ms. Similar histograms were obtained in fourteen other Golgi cells and normalized by dividing the number of events in each bin by the total number of events in the histogram. These normalized histograms were averaged to obtain the histogram of Fig. 9D, where the mean and s.e.m. are plotted for each bin. It is clear from the s.e.m. that dispersion exists in all the cells but that there is some heterogeneity between cells in the proportion of events in the different bins. For example there are many fewer events under 0.6 ms in the cell presented in Fig. 9C than in the average histogram of Fig. 9D.

Figure 9. Kinetic variability of the AMPA component of spontaneous EPSCs.

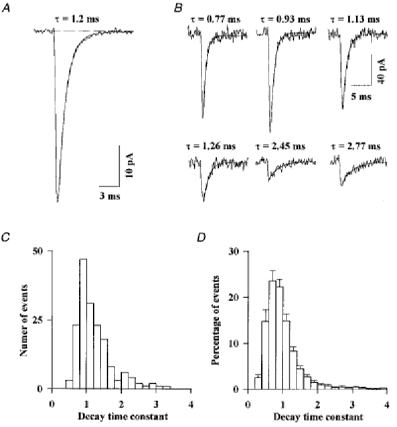
A, all the EPSCs detected in a Golgi cell were aligned at their first rising point and averaged. The decay of the mean EPSC is well fitted by a single exponential function (smooth line). The dashed line indicates the baseline current. B, in the same cell individual EPSCs were fitted by a single exponential function. The six examples displayed in B are representative of the variability of the decay kinetics between EPSCs. C, histogram of the decay time constants for the EPSCs of the cell used in A and B. D, the histograms were obtained as in C for 14 Golgi cells were scaled and averaged. Error bars represent the s.d. of the percentage of all events in a given bin.

The dispersion of the EPSC kinetics, as well as the differences between cells, could be due to dendritic filtering and/or to some variability in the synaptic AMPA conductance kinetics.

The kinetics of parallel fibre EPSCs are affected by dendritic filtering

The EPSCs recorded in the Golgi cell are fast (compare with the values given in the review by Bettler & Mulle, 1995). As a result, the kinetics of the EPSCs fall within the range of the kinetics of clamp of the distal compartment of the Golgi cells (see Table 2), and it is likely that both space- and voltage-clamp limitations in the dendrites affect the measurement of the decay time constant of EPSCs and are partly responsible for its variability. Indeed, in four Golgi cells tested, the apparent kinetics of all the EPSCs slowed when the speed of the voltage clamp is reduced by turning off the access resistance compensation (data not shown). Furthermore, when large events were selected, in order to limit the interference of baseline noise with rise-time measurements, a small but significant correlation was found between their 20-80 % rise time and their decay time constant (data not shown). The data presented here are thus in agreement with morphological data locating the parallel fibres synapses on the apical dendritic arbor in the molecular layer, away from the well-clamped cell body.

In these voltage-clamp conditions, a correlation between the distance of parallel fibre synapses from the cell body and the decay time constant of the EPSC is expected. To test this prediction neighbouring granule cells were stimulated by puffs of kainate at different locations in the granular layer. As the apical dendrites of the Golgi cell have the shape of a fan, the granule cells most lateral to the Golgi cell body are expected to contact the most distal parts of the dendrites. Indeed, the events evoked when stimulating the most lateral granule cells had a decay time constant similar to that of the slowest spontaneous events (2.2 ± 0.6 ms; mean ± s.d). The mean decay time constants of the evoked EPSCs became progressively faster as the stimulation pipette was brought closer to the cell body (1.5 ± 0.4 ms; mean ±s.d.; 2 cells).

Despite the fact that the above results suggest that dendritic filtering influences the decay of EPSCs, no correlation was found between the mean decay of EPSCs (heterogeneity between cells) and the passive electrical properties of the cells. There was no significant correlation between the mean decay time constant of EPSCs and the second capacitive time constant (presumably that of the distal dendritic compartment) measured in twenty Golgi cells (data not shown). There was also no significant correlation between the mean decay time constant of EPSCs and the input resistance of the cell, contrary to what would be expected if the dendritic clamp was dominated by the shunt due to dendritic conductances. Although it is not known which fraction of the membrane conductance comes from the apical dendrites and how distal apical dendrites contribute to the capacitive transient, these data suggest that dendritic filtering is not the only factor responsible for the variability of the EPSC kinetics between cells.

Distal EPSCs carry more charge than proximal ones

Although some synaptic charge is lost when dendritic filtering occurs, as a consequence of voltage escape in the dendrite and of shunt through dendritic conductances, the charge of the EPSC recorded at the soma in a Golgi cell is probably not very different from the charge of the EPSC that would be recorded with a perfect clamp of the synapse. Taking 100 pF as the total capacitance of a Golgi cell (see Table 2 and Fig. 2) and 0.5 GΩ as its input resistance, one finds a specific membrane resistivity of 5 × 10⁴Ω cm². With a value of 100 Ω cm for the specific intracellular resistivity and a mean radius of the apical dendrites of 0.5 μm, the space constant of the apical dendrites can be estimated to be close to 1100 μm. As apical dendrites are generally shorter than 300 μm their electrotonic length would be smaller than 0.25. With similar parameters Spruston, Jaffe, Williams & Johnston (1993) calculated that the loss of charges at the most distal synapses of an ideal cable having an electrotonic length of 0.5 is smaller than 20 %. Thus in Golgi cells dendritic filtering occurs at nearly constant charge content. The product of the EPSC time constant (τ) and amplitude (a) represents a good approximation of this charge (q). Therefore, if all EPSCs are similar, the relation between the peak amplitude of an EPSC measured at the soma and its filtered decay time constant should be hyperbolic (a = q/τ⇒ that for each group of events having similar τ: mean a = mean q/τ, where ‘mean q’ is a constant).

To test this prediction, the amplitude of 3850 EPSCs recorded from twenty Golgi cells was plotted against the value of the decay time constant (Fig. 10A). As expected, the largest EPSCs tended to be fastest, and at first sight the relation between the peak of the EPSCs and their decay time constant corresponded approximately to the hyperbola that would be produced by dendritic filtering. However, it will be shown in the following analysis that the distribution observed is in fact significantly different from the distribution that would be produced by dendritic filtering of a population of synaptic AMPA conductances whose amplitudes and kinetics are independent of the position of the synapse on the dendrite.

Figure 10. Slow EPSCs carry more charge than fast ones.

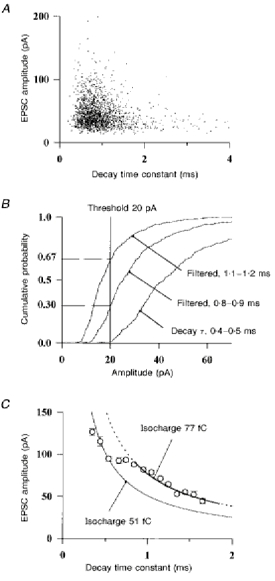
A, the peak amplitudes of 3850 EPSCs recorded from 20 Golgi cells are plotted against their fitted decay time constant. B, the cumulative density function for the amplitude of those events displayed in A which had a decay time constant between 0.4 and 0.5 ms is displayed (right curve). Dendritic filtering was simulated by dividing the amplitudes of these events by the appropriate factors, 0.45/0.75 and 0.45/1.15, providing the theoretical density functions (middle and left curves) expected for events filtered to 0.7-0.8 ms and to 1.1-1.2 ms, respectively. The proportion of events falling under the detection threshold of 20 pA are read on the left. C, the number of events with a decay time constant falling in each bin of 0.1 ms was corrected for detection threshold effects as indicated in the text. The mean amplitudes of the largest 10 % (corrected) of EPSCs are plotted against their mean decay time constant. Error bars are s.e.m. The mean amplitude of the events in the bin 0.4-0.5 ms corresponds to an isocharge of 51 fC (hyperbolic function in these co-ordinates, see text). Another ‘isocharge’ hyperbolic function of 77 fC was fitted to the points between 0.8 and 1.7 ms.

The exact relation between the amplitude and the decay time constant of the EPSCs in the population of Fig. 10A is difficult to assess because slow (and small) events will fall under the threshold used for detection of EPSCs. In a first attempt to correct for this problem, the analysis can be restricted to the largest events. The events can be grouped according to their decay time constant in bins of 0.1 ms and the mean amplitude of the 10 % of events having the largest amplitudes in each bin can be calculated. However, the result obtained by this direct calculation would still contain an error because the number of events in the slower bins would be underestimated, due to detection threshold effects. To correct the number of events in each bin, the cumulative density function for the amplitude of the EPSC in the bin 0.4-0.5 ms was plotted (Fig. 10B, right curve). The detection threshold had been set to 20 pA. One can a priori assume that these rapid events represent proximal, lightly filtered events. If all such proximal events had been filtered without loss of charge to acquire a decay time constant of 0.75 ms their peak amplitude would have been divided by 0.75/0.45 = 1.67. The corresponding predicted amplitude distribution is plotted in Fig. 10B (middle curve). Only 70 % of the EPSCs would have remained over the detection threshold. This means that if x events are detected in the bin 0.7-0.8 ms when recorded from the soma, x/0.7 were above threshold before filtering. For events with a decay time constant between 1.1 and 1.2 ms the remaining proportion is 33 % (left curve) and x/0.33 is the corrected number of events.

The mean amplitudes of the largest events in each bin, corrected as described above, are displayed in Fig. 10C. Contrary to what was expected from the premise of this analysis, the points are not placed along a single hyperbolic function. EPSCs with a decay time constant ranging from 0.3 to 0.6 ms carry on average 51 fC. In contrast, an isocharge of 77 fC can be fitted to the mean amplitudes of the events slower than 0.8 ms. Slow synaptic events carry about 1.5 times more charge than fast events. This indicates that the properties of the synaptic conductances may contribute to the variability of the EPSC kinetics in a cell and between cells.

The excess of charge carried by slow EPSCs probably arises from slow kinetics of AMPA conductances at newly formed synapses

The Golgi cells used for this study were obtained from animals between P13 and P25, that is at an age when parallel fibres are still forming new synapses on the distal part of the Golgi cell dendrites (Altman & Bayer, 1997). Therefore the heterogeneity of synaptic currents could reflect a developmental heterogeneity of the parallel fibre synapses. In this case large distal EPSCs would reflect the characteristics of immature synapses forming on growing Golgi cell dendrites.

To address this developmental issue, the kinetic properties of spontaneous EPSCs were compared between two age groups: P13-P16 and P19-P25. A correlation was found between the mean kinetics of the EPSC and the age of the rat. As shown in Fig. 11A, the mean of the decay time constants in the age group P13-P16 is 1.05 ± 0.04 ms (n = 12) and is significantly faster (P < 0.003; f test) than the mean of the decay time constants in the age group P19-P25, 0.85 ± 0.03 ms (n = 7). The cumulative density functions for the decay time constants of 1883 EPSCs recorded from twelve cells between P13 and P16 and of 1953 EPSCs recorded from seven cells between P19 and P25 are plotted in Fig. 11B. The median of these distributions is 0.95 ms for young cells and 0.75 ms for old cells. The EPSCs decaying with a time constant faster than 0.7 ms (that is corresponding to the ‘fast’ isocharge in Fig. 10D) represent 44 % of all the EPSCs in old animals whereas they represent only 19 % in young animals. On the contrary EPSCs with a time constant slower than 1 ms (corresponding to the predominance of the ‘slow’ isocharge) represent 23 % of all the EPSCs in old animals and 45 % in young animals. The mean amplitude of the EPSCs is not different for the two age groups, as shown in Fig. 11C.

Figure 11. The kinetics of spontaneous EPSCs change during development.

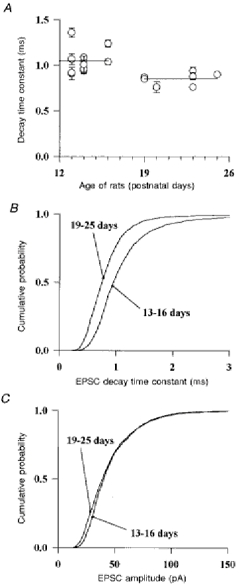
The properties of spontaneous EPSCs, recorded from 13 Golgi cells from P13-P16 rats and 7 Golgi cells from P19-P25 rats and arising mostly at parallel fibre-Golgi cell synapses are compared. A, the mean decay time constant of the detected EPSCs was calculated for each cell and plotted against the age of the rat. Error bars represent the s.e.m. The two lines represent the means of the decay time constants for the two age groups. A significant difference (P < 0.05) was found between these two values. B and C, cumulative distribution of the decay time constants (B) and of the peak amplitudes (C) of the EPSCs in the two age groups.

The results illustrated in Figs 10 and 11 suggest that during development a decrease in the decay time constant of synaptic conductances occurs at parallel fibre-Golgi cell synapses.

DISCUSSION

Golgi cells form an homogeneous class of interneurones

Since the first description of the Golgi cell, morphologists have tried to distinguish subtypes within that class of interneurones. Ramon y Cajal (1911) proposed a subdivision of the Golgi cell into four subtypes, based on the position and size of their cell body and on the projection of their axon. The size and the density of the axonal arbor of the Golgi cells recorded in the present study was indeed variable. In particular, many of these cells extend long axon collaterals which have a tendency to enter the white matter and to form secondary plexuses removed from the cell body. The heterogeneity of those secondary plexuses may account for the early classification by Cajal but does not seem to correspond to populations of Golgi cells with different electrophysiological properties.

More recently, Neki, Ohishi, Kaneko, Shigemoto, Nakanishi & Mizuno (1996) have demonstrated that 90 % of the interneurones of the granular layer express mGluR2 and that the remaining 10 % express mGluR5. The mGluR5-positive interneurones include, according to their description in both text and figures, typical bipolar Lugaro cells and chandelier cells, a recently described interneurone of the Purkinje cell layer (Lainé & Axelrad, 1994). Nevertheless, the authors propose that these populations correspond to two different subtypes of Golgi cells. There is no electrophysiological correlate to support such a claim and it seems more likely that mGluR5 is a marker of non-Golgi interneuronal types which have already been classified. This would explain why in glomerular structures of the granular layer, where Golgi cells axons project, one sees mGluR2 immunoreactivity but no mGluR5 immunoreactivity.

All the Golgi cells recorded in this study share common features. Their apical dendrites have a stout trunk which climbs directly towards the molecular layer above the cell body and begins to ramify upon entering the Purkinje cell layer. They extend for long distances in the whole depth of the molecular layer. Basolateral dendrites, restricted to the granular layer, are thin and contorted. The passive and active electrophysiological properties of the recorded cells also appear remarkably constant. Their discharge frequency accommodates during depolarizing current pulses. They display rebound depolarization after hyperpolarizing current pulses, due to the activation of I_h. Finally, they generally fire spontaneous action potentials in the slices of young animals and their firing frequency decreases and may fall to zero in the adult.

Organization of the parallel fibre-Golgi cell connection

It has been assumed that parallel fibres are the major source of excitation for Golgi cells. The activity of groups of nearby Golgi and Purkinje cells has been recorded simultaneously during locomotor activity in the awake cat (Edgley & Lidierth, 1987), and it was found that the peaks of activity were in phase. Since the activity recorded from Purkinje cells was that elicited by parallel fibres (only simple spikes were analysed), the observation implies that the Golgi cell activity and the parallel fibre activity are high at the same time, which supports the classical idea that the firing of Golgi cells is, at least in part, controlled by the activity of the same parallel fibres which contact the nearby Purkinje cells.

The Golgi cell has generally been considered as mediating feedback inhibition of granule cells, but it is not known whether the granule cells inhibited by a given Golgi cell are those which are responsible for the excitation of that Golgi. Given the length of the parallel fibres, a granule cell could contact a Golgi cell at a great transverse distance. The converse is not true, because a Golgi cell will only inhibit the granule cells situated in the narrow parasagittal band occupied by its axon. The kainate stimulation experiments (Fig. 7) show that granule cells situated inside the axonal field extension of a Golgi cell can indeed contact that same cell. Whether or not these granule cells are among those inhibited by the Golgi cell needs to be investigated.

In the cerebellum, all the dendritic trees encountered in the molecular layer are organized in parasagittal planes orthogonal to parallel fibres. Furthermore electron microscopy suggests that most contacts formed by parallel fibres include a single release site (Palay & Chan-Palay, 1974, p. 90). These predictions from the anatomical data were confirmed by the electrophysiological analysis which shows that most parallel fibre EPSCs are monoquantal. The fact that in a few cases double release events are triggered by the chemical stimulation of a granule cell (see Fig. 7) may be explained by the observation that some Golgi cells grow dendrites in two different parasagittal planes but in close parasagittal superimposition (Fig. 1), which could allow a parallel fibre to contact successively two dendrites.

Weak efficacy of the parallel fibre input on Golgi cell firing activity

In awake cats at rest Golgi cells fire regularly at frequencies varying from 5 to 40 Hz and their firing frequency can reach 100 Hz during movement (Edgley & Lidierth, 1987). Can these modulations of the Golgi cells’ activity be due to the parallel fibre input? If this is the case how many EPSCs per second do they require? It has been shown in the present article that parallel fibres EPSCs carry on average 55 fC in the juvenile rat (P19-P25) and that the slope of the relation between the steady-state firing frequency and the intensity of depolarizing current pulses is 230-70 Hz nA⁻¹, depending on the native calcium buffering capacity of the Golgi cell. Therefore a steady current of 400-1400 pA would be necessary to cover the range of firing rate (100 Hz) of the Golgi cells, which corresponds to an increase of 7000-25000 Hz on the frequency of the parallel fibre EPSP.

An alternative calculation of the in vivo excitatory drive can be proposed, if it is assumed that the Golgi cell returns to a potential close to -75 mV between two action potentials. We have seen that under these conditions the charge necessary to reach the threshold is constant and of the order of 2 pC. This means that about forty parallel fibres would have to fire in between two spikes, that is in less than 10 ms at the highest firing frequency. This implies a peak activity of 4000 Hz at parallel fibre synapses.

Both calculations are underestimates because they do not take into account the inhibitory input onto Golgi cells. The second calculation also neglects the shunting and hyperpolarizing action of the K⁺ currents active during the AHP. It must be noted that all the recordings in this study have been made at room temperature. Preliminary experiments performed at 34°C indicate that the slope of the input-output relation is not changed whereas EPSCs are faster, increasing the frequency of the parallel fibre input necessary to drive the Golgi cells.

All the evaluations made above suggest that the sensitivity of Golgi cells to parallel fibre input is unexpectedly low, in the order of the sensitivity of Purkinje cells to this same input recorded in comparable conditions (Barbour, 1993). In contrast it has been shown that, for interneurones of the molecular layer, the input of a single parallel fibre can evoke an action potential (Barbour, 1993).

Alternative models for parallel fibre control over Golgi cells

In addition to the parallel fibre input, Golgi cells also receive a direct excitatory input from the mossy fibres and the climbing fibres. Electrophysiological data describing these inputs are lacking. A calyx-like ending formed by one of these afferences, called the en marron synapse, is found on the cell body of many Golgi cells. Such large contacts with many release sites are generally associated with strong excitatory inputs. It is therefore possible that the firing pattern of Golgi cells is determined mainly by mossy and climbing fibre pattern of activity. In his model Marr (1969) stated that Golgi cells set the granule cell threshold for the mossy fibre. According to the present data, this assumption would have to be reversed to say that it is the activity in the parallel fibres and molecular layer interneurones that sets the threshold of Golgi cells for mossy fibre input. This has the great advantage that it allows the Golgi cell to fire only after a substantial amount of mossy fibre information has been transferred to the granule cells.

A precise temporal coding of information is important at all levels of the brain and particularly in the cerebellum, which is thought to exert a fine control over the motor activity. In many systems such precise coding has been associated with synchronous oscillatory behaviour. Several recent results support the existence of such oscillations in the cerebellum. Oscillatory activity has been found in some regions of the cerebellar cortex and in cerebellothalamic inputs (Courtemanche & Lamarre, 1997; Timofeev & Steriade, 1997). Synchronization of action potentials in Golgi cells has also been found in vivo, suggesting that Golgi cells participate in this global oscillatory behaviour (Vos, Maex & De Schutter, 1997). Finally the work of Edgley & Lidierth (1987), already discussed in the first section of Discussion, shows that the activity of Golgi cells, far from inhibiting the parallel fibre input to Purkinje cells, is in fact coincident with it. This result, which cannot be interpreted if Golgi cells keep granule cells silent, is coherent with an oscillatory model.

The present study gives an insight into the cellular mechanisms by which such oscillatory activity could be generated. As shown in Fig. 4, Golgi cells express I_h (see also, for turtle Golgi cells, Midtgaard, 1992) which has been associated with oscillatory behaviour in other systems (see Pape, 1996). The activation of I_h in Golgi cells is very fast (compare Fig. 4 with Pape, 1996) and it could already occur during the hyperpolarization following an action potential, leading to a rebound depolarization. The potential for oscillations is also encoded in the retroinhibitory granule cell-Golgi cell circuit itself and in the feed-forward inhibition coming from the basket cells. In a recent model Maex, Vos & De Schutter (1996) showed that the frequency of the rhythm spontaneously generated by this part of the cerebellar circuit depends on the amount of excitation of granule cells by the mossy fibres.

It thus appears that the granule cell-Golgi cell circuit may function as an oscillator which encodes the mean activity of the mossy fibre input into a frequency of oscillation, more specifically into a frequency of bursts of parallel fibre inputs to Purkinje cells. As Golgi cells integrate a constant number of charges before firing an action potential (Fig. 3), each burst of granule cell activity may include a similar number of events. This would preserve the calculation and discrimination potency of the Purkinje cells even at high firing rates, as predicted by both Marr (1969) and Albus (1971).

In conclusion parallel fibres are unlikely to provide the main excitatory drive of Golgi cells in vivo. More probably they modulate the Golgi cell activity, either by setting the threshold of activation by mossy/climbing fibre input and/or by the modulation of the frequency of the spontaneous oscillatory behaviour of the Golgi cell-granule cell-molecular layer interneurone circuit.

Properties of the AMPA and NMDA conductances at parallel fibre to Golgi cell synapses

The kinetics of synaptic currents recorded in the central nervous system is quite variable and in many cells the voltage clamp conditions do not allow the determination of the real kinetics of synaptic conductances. The fast decay kinetics of the AMPA components of the parallel fibre EPSCs onto Golgi cells resembles the submillisecond kinetics encountered at some synapses studied under good voltage clamp conditions (Forsythe, 1994; Zhang & Trussell, 1994; Isaacson & Walmsley, 1995; Silver, Colquhoun, Cull-Candy & Edmonds, 1996; Geiger, Lübke, Roth, Frotscher & Jonas, 1997). Many attempts have been made, using the single cell reverse transcriptase-polymerase chain reaction (RT-PCR) technique (for example Angulo, Lambolez, Audinat, Hestrin & Rossier, 1997), to correlate the channel kinetics in patches excised from identified cells in brain slices to the pattern of mRNA expression for AMPA subunits in these cells. However the situation in vivo is complicated by the fact that a given cell usually expresses many subunits which seem to be selectively directed to particular synapses and which impart different properties to the different synaptic inputs. It has been shown in the present work that, in older animals, the AMPA component of the parallel fibre EPSC onto Golgi cells has a faster decay than in younger animals, but a similar peak amplitude. This may indicate that the identity of the AMPA subunits present at a given synaptic site is developmentally regulated. This type of developmental process might have complicated the single cell studies, most of which were done in immature animals or in culture. Although this is the first report of a developmental change for AMPA receptors at an identified synapse, developmental regulations have already been reported for other receptors and in particular for NMDA receptors, which also get faster with development (Carmignoto & Vicini, 1992; Hestrin, 1992).

Given the very slow membrane time constants of most central neurones, the functional role of subtle (in the millisecond range) regulations in the kinetics of EPSCs remains a mystery. It has been shown that fast kinetics of synaptic conductances can influence the temporal summation of EPSPs at the soma. Alternatively subtle modifications in the kinetics of synaptic conductances, as described in this paper, can change the mean charge carried by the EPSCs and therefore the slope of the input-output relationship for the parallel fibre control over Golgi cells.