Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
. 1998 Aug 15;511(Pt 1):265–272. doi: 10.1111/j.1469-7793.1998.265bi.x

Delayed production of adenosine underlies temporal modulation of swimming in frog embryo

Nicholas Dale 1
PMCID: PMC2231108  PMID: 9679180

Abstract

  1. To investigate the dynamics of adenosine production in the spinal cord during motor activity, and its possible contribution to the temporal modulation of motor patterns, a sensor sensitive to adenosine at concentrations as low as 10 nm was devised.

  2. When pressed against the outside of the spinal cord, the sensor detected slow changes in the levels of adenosine during fictive swimming that ranged from 10 to 650 nm. In four embryos where particularly large signals were recorded due to favourable probe placement, the adenosine levels continued to rise for up to a minute following cessation of activity before slowly returning to baseline. In the remaining thirteen embryos, levels of adenosine started to return slowly to baseline almost immediately after activity had stopped.

  3. Inhibitors of adenosine uptake increased the magnitude of the signal recorded and slowed the recovery following cessation of activity.

  4. A realistic computational model of the spinal circuitry was combined with models of extracellular breakdown of ATP to adenosine. ATP and adenosine inhibited, as in the real embryo, the voltage-gated K+ and Ca2+ currents, respectively. The model reproduced the temporal run-down of motor activity seen in the real embryo suggesting that synaptic release of ATP together with its extracellular breakdown to adenosine is sufficient to exert time-dependent control over motor pattern generation.

  5. The computational analysis also suggested that the delay in the rise of adenosine levels is likely to result from feed-forward inhibition of the 5′-ectonucleotidase in the spinal cord. This inhibition is a key determinant of the rate of run-down.

Intrinsic temporal modulation, or run-down, is a common feature of many motor patterns. Following a triggering stimulus, rhythmic motor patterns undergo a characteristic temporal sequence: they run down in frequency and strength before spontaneously terminating (e.g. McClellan & Grillner, 1983; Robertson et al. 1985; Iwahara et al. 1991; Dale & Gilday, 1996). Whereas most studies have concentrated on the neuronal mechanisms of pattern generation, the mechanisms that control run-down have been largely overlooked. In the frog embryo, pharmacological evidence suggests run-down of swimming is controlled by the opposing actions of ATP and adenosine (Dale & Gilday, 1996). ATP, which is released from spinal neurons, inhibits K+ currents and increases excitability, while adenosine inhibits Ca2+ currents thereby reducing excitability. Nevertheless these actions by themselves are insufficient to exert temporal control of motor pattern generation unless the ratio of ATP and adenosine (and thus the balance of their actions) varies as a function of time. A delay in the appearance of adenosine relative to the release of ATP can be introduced if adenosine is produced from the breakdown of ATP in the extracellular space. This delay (and the time-dependent actions of the two competing transmitters) will be greatly extended if feed-forward inhibition by ADP of the 5′-ectonucleotidase that converts AMP to adenosine, originally described in the endothelium (Gordon et al. 1986; Slakey et al. 1986), is also present. Direct measurement of the time course of adenosine production during motor activity is therefore a key test of whether the purine transmitters can indeed exert temporal regulation of motor pattern generation. By designing and utilizing a sensor sensitive to adenosine I have measured adenosine production during motor activity. These results demonstrate that the appearance of adenosine is indeed delayed and that this delay is characteristic of its production in the extracellular space from synaptically released ATP. By utilizing a computational model I have found that feed-forward inhibition of the 5′-ectonucleotidase is very likely to be present in the spinal cord and that this has a major role in determining the temporal progression of motor activity.

METHODS

Adenosine sensor

The sensor worked on the principle of successively converting adenosine to inosine, to hypoxanthine and thence to uric acid with the evolution of H2O2.

graphic file with name tjp0511-0265-m1.jpg (1)
graphic file with name tjp0511-0265-m2.jpg (2)
graphic file with name tjp0511-0265-m3.jpg (3)

Similar methods using oxidative enzymes to allow detection of substances amperometrically have been widely described (e.g. Sakura & Buck, 1992; Berners et al. 1994). The three enzymes, adenosine deaminase, nucleoside phosphorylase (both from calf spleen, Sigma) and xanthine oxidase (bacterial, Sigma), required for this process were loaded into single- and dual-barrelled sensor probes obtained from Sycopel International (Jarrow, Tyne and Wear, UK). Each barrel consisted of a 230 μm diameter semipermeable glass membrane enclosing a Pt working electrode (4 mm exposed), a Ag counter electrode and a Ag-AgCl reference electrode. The dual-barrelled probes could be used as a quasi-differential device, in that enzymes were loaded into only one barrel and the difference signal between the two barrels was measured. In this case the reference and counter electrodes of one barrel were connected to the equivalent electrodes in the other barrel. The probes were controlled by a potentiostat (Biosensor Driver, Sycopel International; one for each barrel for the dual probes) that held the working electrode at +650 mV to detect H2O2 (e.g. Murphy & Galley, 1994). For the dual probes the output of the two controlling sensors was fed into a simple differential amplifier to provide a signal that was proportional to the difference between the two probes. Calibration and testing of the probe took place in a vessel (7 ml volume). The probe was immersed in saline that was constantly stirred. The adenosine concentration in the vessel was changed by adding concentrated aliquots to raise the overall concentration to known levels. Successive amounts of adenosine were added to give a calibration curve. Other agents (e.g. coformycin and inosine) were also added in this way.

Measuring adenosine release during fictive swimming

Stage 37/38 Xenopus embryos were prepared for recording by means of well-established techniques. In brief, in accordance with the UK Animals (Scientific Procedures) Act (1986) embryos were anaesthetized in MS-222 (1 mg ml−1) until they no longer responded to skin stimuli. The dorsal fin was then slit and they were treated with α-bungarotoxin (0.077 mg ml−1) until immobilized. The trunk skin was then removed and the muscles overlying one side of the spinal cord from the hindbrain to the obex were removed to expose the spinal cord. The animal was pinned in a small chamber (0.5 ml volume) so that the lateral side of the exposed cord was uppermost. Ventral root recordings were made from the intermyotome clefts (Kahn & Roberts, 1982) and the sensor probe was laid along the length of the exposed cord. For dual probes the barrel with enzymes was in contact with the cord, while the reference barrel was necessarily further away (due to the size of the probe relative to the spinal cord). Thus the dual probe recordings were not true differential recordings. Nevertheless the difference signal was more stable and less prone to drift and environmental disturbance. The ventral root recording and output from the sensor drivers were plotted on a thermal array recorder (Graftek). Unlike the in vitro measurements, the fluid in the recording chamber was kept stationary except during solution changes. The saline for physiological recordings contained (mm): 115 NaCl, 2.4 NaHCO3, 3 KCl, 2 CaCl2, 1 MgCl2, 1 or 2 sodium phosphate, 10 Hepes; pH 7.4.

Computational model

The computational model was based upon that previously described (Dale, 1995a,b). However, the version used in this work runs on a Unix platform and can simulate networks of a few hundred neurons. The voltage-gated channels and kinetics of the ligand-gated channels were the same as those described by previously published equations and parameters (Dale, 1995a,b). Each neuron had a membrane capacitance of 10 pF, an input resistance of 1 GΩ, and the following voltage-gated conductances (whole-cell conductance or permeability given in parentheses): fast Na+ (300 nS); Ca2+ (mean ±s.d. 9 × 10−10± 5 × 10−10 cm s−1); fast K+ (7.5 × 10−10 cm s−1); slow K+ (3 × 10−10 cm s−1); and Na+-dependent K+ (50 nS). For these simulations a network of 200 dual excitatory-inhibitory neurons was formed with 100 neurons equally spaced on each side of a portion of simulated spinal cord 2 mm long. Synaptic connections between the neurons were made randomly according to predefined biologically plausible rules: no neuron could synapse to itself; excitatory synapses could only be made to neurons on the same side; while all inhibitory synapses could only be made to neurons on the opposite side. Neurons were given ascending and descending axons 800 μm long and synapses could only be made within the length of the axon. The probability of making a synapse varied with the position of soma of the presynaptic neuron according to the relation 0.4/(1 +d/1000) where d is the position in micrometres in the rostro-caudal axis of the simulation. The unit conductance for a single synaptic connection was 0.25 nS for the NMDA receptor-mediated synapses, 0.5 nS for the AMPA receptor-mediated synapses and 2 nS for the glycinergic synapses. Axons were give a conduction velocity of 200 μm s−1. swimming was triggered by synaptic inputs that lasted around 150 ms and mimicked the glutamatergic excitation that the spinal sensory systems are known to generate (Clarke & Roberts, 1984; cf. Dale, 1995b).

To incorporate the modulation by ATP and adenosine, it was assumed that ATP was released in a spike- and Ca2+-dependent manner. The rate of ATP release therefore depended upon the presynaptic voltage according to the equation:

graphic file with name tjp0511-0265-mu1.jpg

where Kr is the rate of release, Kmax the maximal rate and V the presynaptic voltage. To model the conversion of ATP in the extracellular space the methods and equations of Slakey et al. (1986) were adapted. In brief, the breakdown of ATP was considered as four coupled irreversible reactions (through ADP, AMP and finally adenosine) that followed simple Michaelis-Menten kinetics. The feed-forward inhibition was modelled by competitive inhibition by ADP (Slakey et al. 1986). Michaelis constants (Km) and maximum velocities (Vm) were scaled from those presented in Slakey et al. (1986), maintaining the same ratios. For breakdown of ATP, ADP and AMP the Vm and Km values were: 2.2 μM s−1 and 33.3 μM; 0.32 μM s−1 and 9.5 μM; and 0.3 μM s−1 and 0.94 μM, respectively. In addition a simple first order reaction was added to simulate uptake of adenosine with a Vm of 0.1 μM s−1 and a Km of 1 μM. To simplify matters, diffusion of ATP and its breakdown products was ignored and it was assumed that the kinetics of inhibition of the voltage-gated currents were very rapid and could be described by steady-state equations. The fast and slow components of the delayed rectifier were inhibited by ATP according to the equation 1/(1 +Ki/[ATP]), where Ki was set at 5 μM. The maximum inhibition by ATP was set as 20 % in line with physiological evidence. Adenosine modulated the Ca2+ current according to the equation 1/(1 +Ki/[adenosine]) with Ki set at 5 μM and the maximum inhibition set at 50 %. The equations were integrated with a Cash-Karp embedded Runge-Kutta-Fehlberg algorithm (Press et al. 1992). The simulations ran on a Sun Ultra 170E Creator. For reasons of computational felicity and economy, the rates of production of ATP and its conversion were made deliberately faster than those likely to occur physiologically so that run-down could be studied in simulations lasting a few seconds rather than minutes. Even so, simulations of 2-8 s of activity could take 1-5 h to complete.

Analysis of simulations

The activity of all 200 neurons in the simulation was analysed automatically. A threshold crossing method was used to determine when neurons fired action potentials. These timings were then used to calculate the cycle period of activity. In addition, for each cycle of activity in the simulation, the number of neurons that fired on each side of the network was counted (automatically via a threshold crossing method) and divided by 100 to give the proportion active on one side of the simulation per cycle.

RESULTS

Adenosine sensor

I devised an adenosine sensor based on an enzyme cascade that successively converted adenosine to inosine, then xanthine which was oxidized to uric acid with the evolution of H2O2 which could be detected electrochemically. This allowed rapid and sensitive detection of adenosine at concentrations as low as 10 nm (Fig. 1). The sensor gave a linear response from 10 nm to 2 μM (Fig. 1). As electrochemical sensors can react non-specifically with several metabolites (notably ascorbate and urate), it was important to devise a method that established the dependence of the probe current on the activity of adenosine deaminase. Coformycin was therefore utilized (Agarwal & Parks, 1978) to block the first enzyme of the detection cascade, adenosine deaminase (Fig. 1) and test the specificity of the probe signal.

Figure 1. In vitro calibration and characterization of the adenosine sensor.

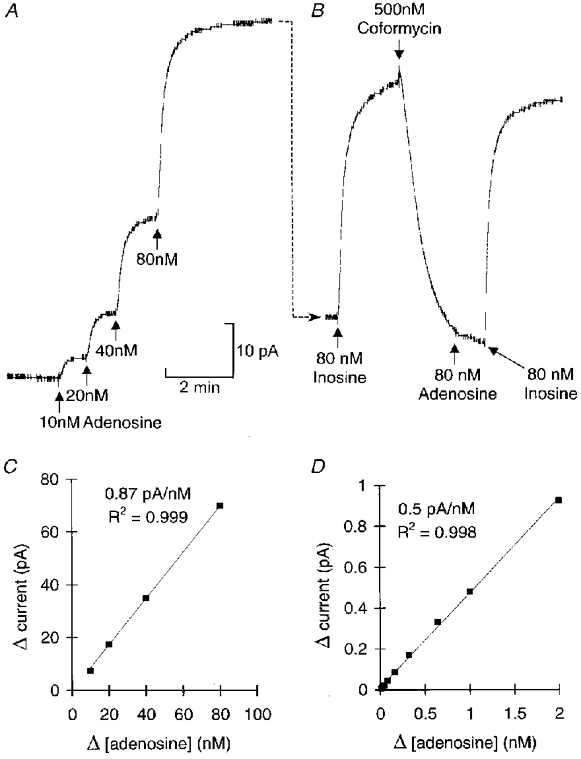
Figure 1

Open in a new tab

A, successive amounts of adenosine were added to the bath at each arrow to raise the concentration of adenosine in the bath by the amount indicated under each arrow. The speed of response by the probe is determined in large by mixing in the bath. The change in probe current resulting from each application of adenosine is plotted in C This shows that the probe responds in a linear fashion. B, in the same experiment 80 nm inosine was added (immediately after the 80 nm adenosine). The response to inosine (substrate for the second enzyme in the cascade) was about 25 % bigger than the response to the same amount of adenosine, indicating some loss of efficiency in the probe. Coformycin (500 nm), a specific blocker of adenosine deaminase, was added. This rapidly reduced the probe current (due to the continued presence of adenosine in the bath) and greatly attenuated the response to subsequent addition of adenosine. However, the response to inosine was unaffected. Thus coformycin only disables the first part of the cascade but leaves the rest intact making it a good test for the specificity of the device. D, after the coformycin had been washed out, the sensitivity of the probe to adenosine recovered (although it was still slightly lower than in C). This calibration shows that the response to adenosine was linear from 10 nm to 2 μm.

Adenosine release during fictive swimming

The sensor was next used to monitor the production of adenosine during locomotor activity in the Xenopus embryo. When the probe was aligned with the ventral portion of the spinal cord, clear responses occurred during motor activity (Fig. 2). The ventral cord also contains the densest staining for 5′-ectonucleotidase activity (N. Dale & C. Gardner, unpublished observations). The probe current slowly rose during swimming and then, after the activity had ceased, gradually fell back to baseline over a period of several minutes (Table 1). This current was almost certainly due to release of adenosine from the spinal cord, since block of adenosine deaminase by 50 nm coformycin greatly reduced the signal from the probe (n= 6). The signals recorded from the probe were variable depending upon the placement of the probe relative to the spinal cord. They corresponded to increases in adenosine concentration ranging from 10 to 100 nm with a mean change of 58 nm (n= 13, Fig. 2A, Table 1). In four additional experiments, the change in adenosine levels was much larger and ranged from 150 to nearly 650 nm (mean change 377 nm, Fig. 2B, Table 1). These large signals could also be blocked with coformycin (Fig. 2B) and were presumably recorded because the probe was fortuitously placed very close to the source of adenosine production. In these four cases, the levels of adenosine continued to rise for 15-72 s beyond the end of the episode to achieve a peak level twice that measured at the end of the episode before falling back to baseline (Table 1). This is exactly the behaviour expected if adenosine is produced from a pool of AMP that accumulates in the extracellular space and persists after neural activity has finished.

Figure 2.

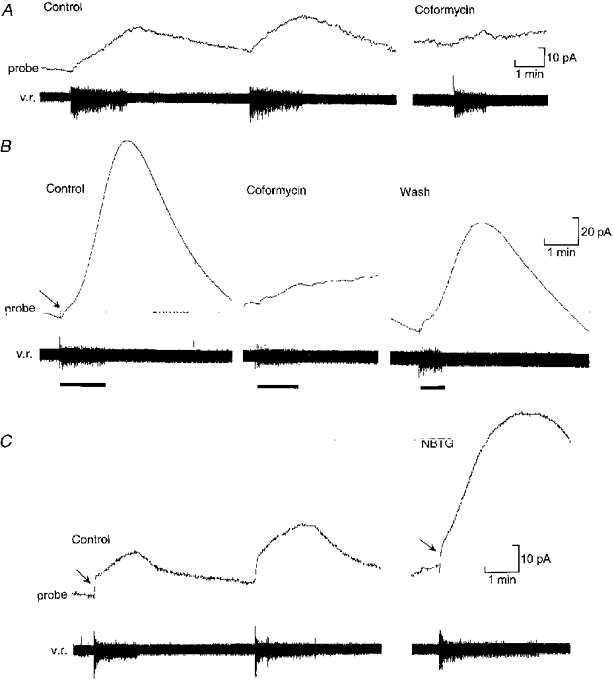
Figure 2

Open in a new tab

The sensor probe can detect adenosine released from the spinal cord during fictive locomotion

A, production of adenosine during two consecutive episodes of swimming monitored by a ventral root recording (v.r.). Note the slow rise in the probe current (equivalent to a change in concentration of about 60 nm) and the slow decay after the end of the swimming episode. The record on the right shows that application of 50 nm coformycin blocks most of the probe current, indicating that the signal is largely due to the release of adenosine. B, example (from another preparation) where favourable placement of the probe relative to the spinal cord resulted in a massive signal equivalent to a change in adenosine concentration of about 370 nm. A fast component to the probe current (arrow) can be seen at the beginning of the swimming activity. The probe signal continued to rise for about 50 s after the end of the swimming episode. Application of 50 nm coformycin blocked the probe current, but left a small fast component. The large slowly developing component of the probe current was thus specifically due to the release of adenosine. C, blockers of adenosine uptake greatly enhance the release of adenosine from the spinal cord. In the control (left) the probe current involved both fast (arrow) and slow components, the slow component being equivalent to a rise in adenosine concentration of around 64 nm. After application of 1 μM NBTG (right) to block adenosine uptake, the fast component (arrow) was unchanged, but the slow component was greatly increased in amplitude and rate of rise (equivalent to a change of about 150 nm).

Table 1.

Magnitude and time course of adenosine production during swimming

Type n Change in [adenosine] (nm) Half-decay time (s) Delay to peak (peak-end) (s) Ratio (peak/end)
Small 13 58 ± 6 90.0 ± 19.3 6.5 ± 4.8 1.1 ± 0.1
Large 4 377 ± 106 104.0 ± 16.8 49.0 ± 12.3 2.0 ± 0.4
Open in a new tab

The data are divided into two groups according to the size of adenosine response (see text). The ‘half-decay time’ is the time for the adenosine level to fall to half its peak value; the ‘delay to peak’ refers to the delay between the end of the swimming episode and the peak of the adenosine response; and the ‘ratio’ is the peak concentration of adenosine divided by that measured at the end of the episode of swimming. All values expressed as the mean ± S.E.M. with nthe number of preparations.

Adenosine uptake limits the rise in levels during swimming

To test whether adenosine uptake systems could play a role in limiting the rise of adenosine during locomotor activity, the effects of nitrobenzylthioguanosine (NBTG), a blocker of adenosine uptake (Thorn & Jarvis, 1996), were studied. At 1 μM, NBTG had two effects (Fig. 2C): it greatly enhanced the magnitude (means 60 ± 9 and 175 ± 44 nm in control and NBTG, respectively, n= 5) and rate of the rise in adenosine concentration (means 37 ± 7 and 101 ± 34 nm min−1 in control and NBTG, respectively, n= 5); and it slowed the recovery after the cessation of motor activity (in 3 of 5 preparations the probe signal did not decay to half-peak within 5 min). These results suggest that adenosine uptake plays an important role both in slowing and limiting the rise in adenosine concentrations during activity and terminating the actions of this modulator.

Computational analysis of temporal modulation

During a locomotor episode in the Xenopus embryo, all neurons of the spinal circuitry start and end their activity together (Arshavsky et al 1993). As there is no sub-population of neurons that continues to fire after cessation of motor activity, the observation that adenosine levels can rise for up to a minute after the end of an episode of swimming rules out the possibility that adenosine is released synaptically. Instead, the time course of adenosine production is characteristic of conversion of ATP to adenosine in the extracellular space with feed-forward inhibition of the 5′-ectonucleotidase that converts AMP to adenosine. To examine this possibility further, I borrowed the kinetic analysis performed on ectoATPases in the endothelium (Gordon et al 1986; Slakey et al 1986) and incorporated it into a realistic computational model of the Xenopus embryo motor circuitry (Dale, 1995a,b) which has successfully predicted the influence of synaptic conductances on cycle period (Dale, 1995b) and the roles of K+ currents in repetitive firing and motor pattern generation (Kuenzi & Dale, 1998). It was assumed that ATP was released as a cotransmitter in a spike- and Ca2+-dependent manner and the model was utilized to investigate whether the known actions of ATP and adenosine were sufficient to exert temporal control and whether the strength of feed-forward inhibition could influence the rate of run-down.

For run-down to occur in the model, it proved necessary to incorporate some of the natural variability found between neurons. This was done in a simplified way by making the magnitude of the Ca2+conductance vary randomly between the model neurons in a Gaussian manner. All other conductances and properties were identical in the 200 neurons of the simulation. When ‘swimming’ was started in the model (by sensory excitation, see Methods), run-down of the motor pattern occurred: the cycle periods lengthened progressively before activity spontaneously stopped (Fig. 3B). Without the incorporation of the purinergic modulation no run-down or spontaneous termination occurred during the simulations. Interestingly, the firing of some neurons in the simulation became less reliable as activity proceeded (Fig. 3B) so that action potentials ‘dropped out’ in a manner akin to that described for the real circuit (Sillar & Roberts, 1993; Fig. 3A). Crucially the duration of episodes of activity became steeply dependent on the feed-forward inhibition as this was strengthened (Fig. 3C). The sensitivity of episode duration to the feed-forward inhibition suggests that physiological regulation of this inhibition could be a powerful way of changing the duration of motor activity. The modelling also revealed that if the rate of ATP release was increased, the rate of run-down was much slower except when the feed-forward inhibition was very weak (Fig. 3C). This result occurs for two reasons: firstly, because the greater levels of ATP reduce the K+ currents (Dale & Gilday, 1996) to a greater extent and thus cause greater excitability in the neural circuit; and secondly, because more ADP accumulates which in turn gives rise to stronger inhibition of the 5′-ectonucleotidase and thus slower accumulation of adenosine (Fig. 3).

Figure 3. Computational model incorporating release of ATP and its conversion to adenosine reproduces run-down of the motor pattern.

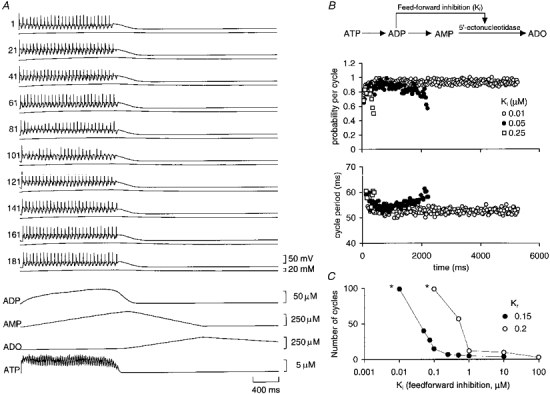
Figure 3

Open in a new tab

A, the activity of every 20th neuron from a simulation of 200 neurons (neurons 1-100 and 101-200 are on opposing sides of the simulated circuit). The trace underlying the membrane potential record for each neuron is the intracellular concentration of Na+. Underneath the neural records are traces that show the release of ATP, the build-up of ADP and AMP, and the production of adenosine (ADO). The feed-forward inhibition was set at 0.075 μM. Note how the peak adenosine production was greatly delayed relative to swimming activity. B, schema showing the break-down of ATP to adenosine and feed-forward inhibition of the 5′-ectonucleotidase by ADP (top). Run-down of the motor pattern can be seen in a decay in the probability of firing (middle) and a lengthening in the cycle period of activity (bottom). Data are shown for three strengths of feed-forward inhibition, showing a case with essentially no run-down (Ki= 0.01 μM) and two other cases where the feed-forward inhibition was weaker and allowed much more rapid run-down. C, the duration of motor activity in the model depends strongly on the strength of feed-forward inhibition. Once Ki reached a certain strength, episode length was steeply dependent upon its magnitude. Data are shown for two rates of ATP release (Kr). Note that run-down proceeds more slowly for all strengths of Ki at the faster rate of ATP release. The asterisks indicate that the number of cycles counted for these data points was terminated by the length of the simulation and not by the occurrence of run-down in the model.

DISCUSSION

These results are the first direct demonstration that adenosine is produced by the spinal cord during motor activity. This is an important finding since, although earlier studies strongly suggest that adenosine regulates motor pattern generation (Dale & Gilday, 1996), it remained unclear whether there was any time dependence to the actions of adenosine The demonstration that adenosine levels rise slowly, and with a characteristic delay, shows that this transmitter will indeed exert time-dependent control on the motor circuitry. In addition, the computational modelling strongly suggests that the known actions of ATP and adenosine, together with breakdown of synaptically released ATP in the extracellular space are sufficient to generate temporal modulation of motor pattern generation. swimming in the marine mollusc Tritonia also exhibits run-down and spontaneous termination. However, a rather different mechanism has been proposed that depends upon a decaying extrinsic drive to the pattern-generating circuit as well as synaptic interactions within the circuit including slow summation of inhibition (Getting & Dekin, 1985). Nevertheless the involvement of further mechanisms in mediating run-down of swimming in Tritonia, such as purinergic modulation, cannot be excluded.

Feed-forward inhibition by ADP of the 5′-ectonucleotidase has been described for the endothelium (Gordon et al 1986; Slakey et al 1986) and in cholinergic synaptosomes derived from the striatum (James & Richardson, 1993). The physiological function of this inhibition has remained unclear, although the general notion that it may serve to separate temporally the appearance of ATP and adenosine has been proposed (James & Richardson, 1993). This study provides the first insight into the physiological significance of this phenomenon in the central nervous system. The strength of the feed-forward inhibition is a key determinant of the rate of run-down of the motor pattern. If ATP and adenosine were to regulate self-sustaining reverberatory activity in brain circuits, the feed-forward inhibition could similarly determine the time dependence of decay of that reverberatory activity. Since run-down is very sensitive to the magnitude of the feed-forward inhibition, physiological modulation of this step is an attractive mechanism for changing the intrinsic temporal progression of activity within neural circuits.

There is a second more subtle, but very important, consequence of the feed-forward inhibition. In an escape behaviour such as swimming, stronger activation of the locomotor network will cause a greater proportion of neurons to be active (and result in a greater rate of ATP release). For an escape behaviour this should result in activity that runs down more slowly and lasts longer. However, without feed-forward inhibition this will not occur because the rate of adenosine production will be simply proportional to the rate of ATP release. Thus stronger activation would cause both a greater rate of ATP release and faster run-down, a potentially disastrous consequence. With feed-forward inhibition present, the greater accumulation of ADP that results from stronger activation of the network will slow the appearance of adenosine and will indeed result in slower run-down.

A further problem with intrinsic mechanisms for run-down is that they will tend to provide only very stereotyped temporal progressions in circuit activity. This raises the problem of how flexibility can be provided when circumstances might, for example, require an extension of activity within the circuit beyond that normally allowed by the purinergic feedback system. The presence of both feed-forward inhibition and adenosine uptake potentially allows resetting of the system. If a circuit is partway through its run-down sequence and a further excitatory stimulus arises that activates more neurons and thus a greater rate of ATP release, more ADP will be produced. This in turn will inhibit the 5′-ectonucleotidase more strongly. If adenosine uptake is sufficiently rapid, this will result in a paradoxical fall in the levels of adenosine: in effect, a resetting of run-down.

Acknowledgments

I thank the Royal Society and The Wellcome Trust for generous support.

References

  1. Agarwal RP, Parks RE. Adenosine deaminase from human erythrocytes. Methods in Enzymology. 1978;51:502–507. doi: 10.1016/s0076-6879(78)51069-0. [DOI] [PubMed] [Google Scholar]
  2. Arshavsky YI, Orlovsky GN, Panchin YV, Roberts A, Soffe SR. Neuronal control of swimming locomotion: analysis of the pteropod mollusc Clione and embryos of the amphibian Xenopus. Trends in Neurosciences. 1993;16:227–232. doi: 10.1016/0166-2236(93)90161-e. 10.1016/0166-2236(93)90161-E. [DOI] [PubMed] [Google Scholar]
  3. Berners MOM, Boutelle MG, Fillenz M. Online measurement of brain glutamate with an enzyme/polymer coated tubular electrode. Analytical Chemistry. 1994;66:2017–2021. doi: 10.1021/ac00085a016. [DOI] [PubMed] [Google Scholar]
  4. Clarke JDW, Roberts A. Interneurones in the Xenopus embryo spinal cord: sensory excitation and activity during swimming. The Journal of Physiology. 1984;354:345–362. doi: 10.1113/jphysiol.1984.sp015380. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Dale N. Kinetic characterization of the voltage-gated currents possessed by Xenopus embryo spinal neurons. The Journal of Physiology. 1995a;489:473–488. doi: 10.1113/jphysiol.1995.sp021066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Dale N. Experimentally derived model for the locomotor pattern generator in the frog embryo. The Journal of Physiology. 1995b;489:489–510. doi: 10.1113/jphysiol.1995.sp021067. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Dale N, Gilday D. Regulation of rhythmic movements by purinergic neurotransmitters in frog embryos. Nature. 1996;383:259–263. doi: 10.1038/383259a0. 10.1038/383259a0. [DOI] [PubMed] [Google Scholar]
  8. Getting PA, Dekin MS. Mechanisms of pattern generation underlying swimming in Tritonia. IV. Gating of central pattern generator. Journal of Neurophysiology. 1985;53:466–480. doi: 10.1152/jn.1985.53.2.466. [DOI] [PubMed] [Google Scholar]
  9. Gordon EL, Pearson JD, Slakey L. The hydrolysis of extracellular adenine nucleotides by cultured endothelial cells from pig aorta. Journal of Biological Chemistry. 1986;261:15496–15504. [PubMed] [Google Scholar]
  10. Iwahara T, Atsuta Y, Garcia-Rill E, Skinner RD. Locomotion induced by spinal cord stimulation in the neonatal rat in vitro. Somatosensory Motor Research. 1991;8:281–287. doi: 10.3109/08990229109144751. [DOI] [PubMed] [Google Scholar]
  11. James S, Richardson PJ. Production of adenosine from extracellular ATP at the striatal cholinergic synapse. Journal of Neurochemistry. 1993;60:219–227. doi: 10.1111/j.1471-4159.1993.tb05841.x. [DOI] [PubMed] [Google Scholar]
  12. Kahn JA, Roberts A. The central nervous origin of the swimming motor pattern in embryos of Xenopus laevis. Journal of Experimental Biology. 1982;99:185–196. doi: 10.1242/jeb.99.1.185. [DOI] [PubMed] [Google Scholar]
  13. Kuenzi FM, Dale N. The pharmacology and roles of two K+ channels in motor pattern generation in the Xenopus embryo. Journal of Neuroscience. 1998;18:1602–1612. doi: 10.1523/JNEUROSCI.18-04-01602.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. McClellan AD, Grillner S. Initiation and sensory gating of ‘fictive’ swimming and withdrawal responses in an in vitro preparation of the lamprey spinal cord. Brain Research. 1983;269:237–250. doi: 10.1016/0006-8993(83)90133-6. 10.1016/0006-8993(83)90133-6. [DOI] [PubMed] [Google Scholar]
  15. Murphy LJ, Galley PT. Measurement in vitro of human plasma glycerol with a hydrogen peroxide detecting microdialysis enzyme electrode. Analytical Chemistry. 1994;66:4345–4353. doi: 10.1021/ac00095a035. [DOI] [PubMed] [Google Scholar]
  16. Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical Recipes in C: The Art of Scientific Computing. 2. Cambridge: Cambridge University Press; 1992. [Google Scholar]
  17. Robertson GA, Mortin LI, Keifer J, Stein PSG. Three forms of the scratch reflex in the spinal turtle: central generation of motor patterns. Journal of Neurophysiology. 1985;53:1517–1534. doi: 10.1152/jn.1985.53.6.1517. [DOI] [PubMed] [Google Scholar]
  18. Sakura S, Buck RP. Amperometric processes with glucose oxidase embedded in the electrode. Biochemistry and Bioenergetics. 1992;28:387–400. volume343ofJournal of Electroanalytical Chemistry. [Google Scholar]
  19. Sillar KT, Roberts A. Control of frequency during swimming in Xenopus embryos: a study on interneuronal recruitment in a spinal rhythm generator. The Journal of Physiology. 1993;472:557–572. doi: 10.1113/jphysiol.1993.sp019962. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Slakey L, Cosimini K, Earls JP, Thomas C, Gordon EL. Simulation of extracellular nucleotide hydrolysis and determination of kinetic constants for ectonucleotidases. Journal of Biological Chemistry. 1986;261:15505–15507. [PubMed] [Google Scholar]
  21. Thorn JA, Jarvis SM. Adenosine transporters. General Pharmacology. 1996;27:613–620. doi: 10.1016/0306-3623(95)02053-5. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES