Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
. 1998 Nov 15;513(Pt 1):251–261. doi: 10.1111/j.1469-7793.1998.251by.x

The arterial baroreceptor reflex of the rat exhibits positive feedback properties at the frequency of Mayer waves

Delphine Bertram 1, Christian Barrès 1, Guy Cuisinaud 1, Claude Julien 1
PMCID: PMC2231264  PMID: 9782175

Abstract

  1. Modelling studies have led to the proposal that Mayer waves (∼0.4 Hz in rats) could result from a resonance phenomenon in a feedback control loop. In this study, we investigated the presence of a resonance frequency in the arterial baroreceptor reflex loop, i.e. a particular frequency at which arterial pressure feeds back positively to the baroreceptors.

  2. Frequency responses of mean arterial pressure (MAP) to aortic depressor nerve (ADN) stimulation were studied in fifteen urethane anaesthetized, ventilated rats with cardiac autonomic blockade. The ADN was stimulated using rectangular trains of impulses (2 ms, 100 Hz) delivered at frequencies ranging from 0.1 to 1 Hz. Phase angles between impulses and MAP were calculated using cross-spectral analysis based on a fast Fourier transform algorithm.

  3. Rhythmic ADN stimulation induced regular MAP oscillations at the expected frequencies that were attenuated by α-adrenoceptor blockade and abolished after ganglionic blockade. The relationship between impulse and MAP oscillations was characterized by a strong coherence and a positive phase shift at low frequencies, indicating that impulses led MAP with respect to the out-of-phase pattern. Deviation of the phase from the out-of-phase behaviour was mainly due to the presence of a fixed time delay (∼0.8 s) between ADN stimuli and MAP changes. Phase angles fell to zero at 0.42 ± 0.02 Hz.

  4. In rats, the arterial baroreceptor reflex exhibits a resonance frequency close to the frequency of spontaneously occurring Mayer waves. The reflex therefore seems the most likely origin for the Mayer waves.

In almost all mammalian species studied thus far, arterial pressure-time series exhibit regular oscillations at frequencies lower than those for respiration. These low frequency oscillations are usually referred to as Mayer waves (Mayer, 1876). The average frequency is fairly constant among individuals and is close to 0.1 Hz in humans, dogs (Pagani et al. 1986) and cats (Di Rienzo et al. 1991), and 0.4 Hz in rats (Rubini et al. 1993; Brown et al. 1994). Mayer waves are usually attributed to cyclic changes in sympathetic vasomotor tone. It has been shown that Mayer waves are coupled with well-defined oscillations in the activity recorded directly from sympathetic nerves in humans (Pagani et al. 1997) and rats (Brown et al. 1994). Moreover, in rats, Mayer waves are strongly attenuated after acute α-adrenoceptor blockade (Japundzic et al. 1990; Cerutti et al. 1991; Rubini et al. 1993) or chronic chemical sympathectomy (Cerutti et al. 1991; Daffonchio et al. 1995; Julien et al. 1995).

In the past decade, Mayer waves have been the focus of a large number of studies (for review see Persson, 1997), especially because their amplitude was proposed as an indicator of sympathetic modulation of vascular tone (Malliani et al. 1991). Despite continuing effort, there is still no general agreement as to whether Mayer waves originate from the autonomous activity of a central oscillator or from a resonance phenomenon in a reflex control loop. The former hypothesis was put forward after the demonstration that in anaesthetized cats, spontaneous slow oscillations of preganglionic sympathetic nervous activity could be observed in the absence of concomitant changes in arterial pressure (Preiss & Polosa, 1974). More recently, it was reported that in vagotomized dogs, blood flow in the vascularly isolated hindlimb exhibited self-sustained oscillations even when carotid sinus pressure was held constant (Grasso et al. 1995). Although both studies suggest the involvement of a central oscillator in the genesis of Mayer waves, it must be noted that the period of the oscillations reported in these studies (20–25 s) is longer than that of the 10 s oscillations occurring spontaneously in conscious cats (Di Rienzo et al. 1991) and dogs (Pagani et al. 1986).

The involvement of a resonance phenomenon in the genesis of low frequency oscillations of arterial pressure was proposed as early as 1951 by Guyton & Harris. Later on, the hypothesis was refined by introducing computer-simulated models of the short-term control of arterial pressure. It was proposed that a resonance phenomenon in the arterial baroreceptor reflex loop could generate regular, self-sustained oscillations of arterial pressure, mainly because of the delay in the vascular responses to sympathetic modulation (DeBoer et al. 1987; Madwed et al. 1989; Burgess et al. 1997b). Experimental support for this hypothesis came from studies in sino-aortic baroreceptor denervated animals, which demonstrated a reduction in sympathetically mediated oscillations of arterial pressure (Di Rienzo et al. 1991; Cerutti et al. 1994; Jacob et al. 1995), and a selective uncoupling from corresponding fluctuations in vascular conductances (Julien et al. 1995). Although these studies strongly suggested an important role for the arterial baroreceptor reflex in the synchronization of arterial pressure oscillations in the Mayer band, they did not provide unequivocal evidence that the oscillations are actually generated by the reflex. Indeed, chronically after baroreceptor denervation, fluctuations of arterial pressure in the frequency band containing the Mayer waves are reduced by only 30–50 % (Di Rienzo et al. 1991; Cerutti et al. 1994; Julien et al. 1995). In addition, it has been shown in denervated rats that the residual oscillations in this band are of sympathetic origin, as they disappear after ganglionic blockade (Cerutti et al. 1994). These observations, therefore, are not entirely conclusive as to the exact role of arterial baroreceptors, since incomplete denervation or reinnervation of baroreceptor areas, as well as sensitization of other cardiovascular reflexes, could well account for the residual variability in the Mayer band.

The aim of the present study was to determine whether the arterial baroreceptor reflex of the rat actually exhibits a resonance frequency, i.e. a particular frequency at which arterial pressure is fed back positively to the baroreceptors. We therefore characterized the phase relationship between rhythmic stimulation of the aortic depressor nerve and the resulting oscillations of arterial pressure. The aortic nerve was chosen because it contains only baroreceptor sensory afferents in the rat (Sapru et al. 1981). Because there is strong evidence that heart rate oscillations tend to oppose, rather than reinforce arterial pressure oscillations of ∼0.4 Hz in rats (Cerutti et al. 1991, 1994), all experiments were performed under cardiac autonomic blockade. Finally, to ascertain that arterial pressure oscillations induced by aortic nerve stimulation were mediated by the sympathetic nervous system, experiments were repeated after sequential blockade of α-adrenoceptors and ganglionic transmission.

METHODS

All experiments were carried out according to the guidelines of the local animal ethics committee.

Surgical procedures

Twenty male Sprague-Dawley rats (300–400 g; Iffa-Credo, L'Arbresle, France) were used. Animals were anaesthetized with urethane (1.2 g kg−1i.p.) and placed on a heating blanket to maintain rectal temperature at 37 ± 0.2°C (mean ±s.e.m.). Supplemental doses of urethane (0.1 g kg−1i.v.) were given whenever required, as assessed by the foot pinch reflex. A polyethylene catheter was inserted into the lower abdominal aorta through the left femoral artery. Two polyethylene catheters were also inserted into the inferior vena cava via the left femoral vein for the administration of drugs. The trachea was cannulated and the rat was ventilated at 2–2.5 ml per stroke with a mixture of oxygen and a small amount of room air (∼20 %). The cycling rate was set at 72 cycles min−1 (1.2 Hz) so as to avoid interference with arterial pressure oscillations that could be evoked by the fastest rate of aortic nerve stimulation (see below). Under these conditions, arterial pH was 7.36 ± 0.01, and the arterial partial pressures of O2 and CO2 were 265 ± 9 and 32 ± 1 mmHg, respectively (n = 5 rats). The left aortic depressor nerve was isolated at its junction with the superior laryngeal nerve, placed on a bipolar platinum- iridium electrode, and insulated with silicon gel (Silgel 604A and 604B, Wacker-Chemie, Munich, Germany).

Arterial pressure recording

The arterial catheter was connected to a precalibrated pressure transducer (TNF-R; Ohmeda, Bilthoven, The Netherlands) through a two-way stopcock, which allowed the continuous infusion of a 5 % glucose solution (0.5 ml h−1). The arterial pressure signal was fed simultaneously to an amplifier-recorder (Model 8802; Gould, Cleveland, OH, USA) and to a personal computer (486 DX2/66) equipped with an analog-to-digital converter board (AT-MIO-16; National Instruments, Austin, TX, USA). Using LabVIEW 3.1.1 software (National Instruments), the arterial pressure curve was sampled at 500 Hz.

Aortic nerve stimulation

The nerve was stimulated with trains of rectangular impulses (2 ms, 100 Hz) delivered by a stimulator (Model S88; Grass, Quincy, MA, USA). Voltage intensity was initially determined as the intensity inducing reproducible depressor responses of about 40 mmHg. This voltage was then used throughout each experiment. To verify that responses to aortic nerve stimulation did not change with time, 30 s continuous trains of impulses were applied at regular intervals until the end of the experiment. In each rat, the arterial pressure response to step stimulation was calculated as the mean of two to three randomly chosen responses. To generate oscillations in arterial pressure, rhythmic stimulation was applied to the aortic nerve. At each modulation frequency (0.1–1 Hz), the nerve was stimulated during one half cycle (5–0.5 s) at the beginning of each cycle, so that the same total number of impulses was delivered at any frequency. Stimulation trials lasted 4 min and were separated by a time interval sufficient to allow full recovery of arterial pressure, usually 3–4 min. The different modulation frequencies were applied in random order. The output signal of the stimulator was sampled at 2000 Hz by the computer.

Pharmacological protocols

Aortic nerve stimulation was performed while the rats were under cardiac autonomic blockade. This was achieved by the combined i.v. administration of atropine methyl nitrate and atenolol (2 mg kg−1 each, both from Sigma-Aldrich). Pilot experiments indicated that under these conditions, depressor responses to methacholine hydrochloride (2.5 μg kg−1i.v.; Sigma) were attenuated from 58 ± 5 to 5 ± 2 mmHg (n = 5) and the tachycardia provoked by isoprenaline hydrochloride (1 μg kg−1i.v.; Sigma) was reduced from 89 ± 4 to 10 ± 2 beats min−1 (n = 5). Administration of blockers was repeated every hour so as to ensure effective blockade across the whole study.

In some animals, the role of α-adrenoceptors was evaluated by repeating the same protocol of stimulation after administration of phentolamine hydrochloride (5 mg kg−1i.v.; Sigma). This dose has been shown previously to abolish completely pressor responses to phenylephrine hydrochloride (3 μg kg−1i.v.; Sigma) for at least 1 h (Lo et al. 1991). As phentolamine had a profound depressor effect, arterial pressure was immediately restored to the baseline level by means of a continuous infusion of angiotensin II acetate (200–500 ng kg−1 min−1i.v.; Sigma), with infusion rates ranging from 0.5 to 2 ml h−1. Finally, to examine the possible contribution of non-autonomic factors, aortic nerve stimulation was performed after ganglionic blockade with chlorisondamine hydrochloride (2.5 mg kg−1i.v.; Ciba-Geigy) combined with angiotensin II infusion. In this latter case, modulation frequencies were 0.1, 0.4 and 0.8 Hz.

At the end of the experiments, animals were killed with an i.v. overdose of sodium pentobarbitone.

Data analysis

Off-line processing of data was performed on a workstation (SPARCstation 1; Sun Microsystems, Mountain View, CA, USA). For each cardiac cycle, the computer calculated mean arterial pressure and heart rate. The output signal of the stimulator was resampled at 10 Hz by computing mean values over 100 ms consecutive periods.

Spectral analysis was used to quantify mean arterial pressure oscillations evoked by rhythmic stimulation of the aortic depressor nerve (Cerutti et al. 1991). Beat-to-beat time series were sampled at 10 Hz after linear interpolation. For each 4 min test period, three data sets of 1024 points (102.4 s) overlapping by half were processed. Power spectral density was calculated using a fast Fourier transform algorithm after removal of the linear trend and application of a Hanning window. Spectra obtained for the three data sets were averaged. The frequency resolution was 0.00976 Hz. The spectral modulus, which has been proposed for estimating the absolute amplitude of an oscillation (Laude et al. 1995), was calculated as the square root of the area under the peak, which usually covered three consecutive frequency components. In the following text, the amplitude of an oscillation refers to the total excursion of the curve, i.e. the double amplitude of the corresponding sine wave.

To study the temporal relationship between aortic nerve stimulation and mean arterial pressure oscillation, phase angles between impulses and mean arterial pressure were calculated using cross-spectral techniques, as previously described in detail (Cerutti et al. 1994; Julien et al. 1995). Briefly, coherence and phase angle were estimated using overlapped Fourier transform processing. Phase angles were taken at the peak coherence frequency. A positive phase angle at a given frequency indicates that fluctuations in the input (impulses) precede those in the output (mean arterial pressure), with respect to the out-of-phase pattern.

Statistics

To evaluate differences in mean values and oscillatory responses of mean arterial pressure, two-way analysis of variance for repeated measures with pharmacological treatment and modulation frequency as factors, was performed. Results are presented as means ±s.e.m.

results

Prestimulation levels of mean arterial pressure and heart rate were 103 ± 4 mmHg and 361 ± 6 beats min−1, respectively (n = 15 rats).

Mean arterial pressure responses to step stimulation of the aortic depressor nerve

Continuous 30 s aortic nerve stimulation induced depressor responses that were usually biphasic with an initial decrease larger than the late, steady-state response. The maximum decrease in mean arterial pressure reached 42 ± 4 mmHg (n = 15 rats). As the animals were under cardiac autonomic blockade, step stimulation of the aortic nerve induced minimal changes in heart rate (−3 ± 1 beats min−1).

The latency of the depressor response was estimated as follows. The upper and lower arterial pressure limits before the start of stimulation were determined, allowing for any fluctuation due to respiration. Then, the first diastolic pressure that fell below the lower limit after the onset of stimulation was identified. The time elapsed between the first impulse delivered by the stimulator and the first low diastolic pressure was taken as the onset latency of the depressor response to aortic nerve stimulation. In two of fifteen rats, the output signal of the stimulator could not be recorded for technical reasons. In the remaining thirteen rats, the decrease in mean arterial pressure was delayed by 0.86 ± 0.02 s from the onset of aortic nerve stimulation.

Quantitative assessment of mean arterial pressure oscillatory responses to rhythmic stimulation of the aortic depressor nerve

As illustrated in Fig. 1, rhythmic aortic nerve stimulation induced regular oscillations of mean arterial pressure at the expected frequencies, which appear as sharp, well-defined peaks in the power spectra. The oscillatory responses of mean arterial pressure decreased steeply with increasing modulation frequency of the aortic nerve. In six of fifteen rats, there was no clear peak in the mean arterial pressure power spectrum when the modulation frequency was set at 1 Hz.

Figure 1. Effect of rhythmic aortic nerve stimulation on arterial pressure.

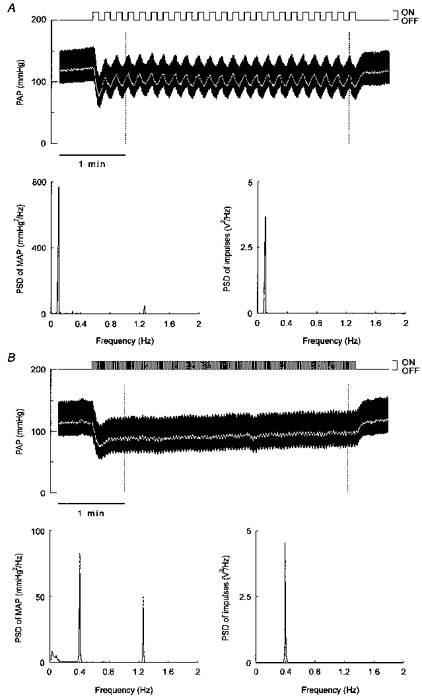
Figure 1

Open in a new tab

Original recordings of pulsatile arterial pressure (PAP, upper panels) obtained during rhythmic stimulation of the left aortic depressor nerve in a urethane anaesthetized rat. Rectangular trains of impulses (voltage intensity, 0.9 V) were delivered by a stimulator at frequencies of 0.1 (A) and 0.4 (B) Hz. At each modulation frequency, power spectral analysis was applied to mean arterial pressure (MAP, white trace) data collected over the 205 s periods delimited by the dotted lines. The power spectral density (PSD) peak located at about 1.2 Hz in the MAP spectrum (lower left panels) is due to the mechanical ventilation of the rat. Spectral analysis was also applied to the output signal of the stimulator presented above the arterial pressure traces (lower right panels). Note that although the peak heights differed at the two modulation frequencies, the peak areas were almost identical (0.0546 and 0.0543 V2 at 0.1 and 0.4 Hz, respectively).

The linear relationship between the spectral modulus of the peaks and the absolute amplitude of the oscillations was evaluated using either computer-generated sine waves or experimental mean arterial pressure data. Figure 2 shows that the results obtained using simulated and experimental data were in excellent agreement. Therefore, the slope of the theoretical regression line was used to derive the absolute amplitude of mean arterial pressure oscillations from the modulus of the corresponding peaks in the power spectrum.

Figure 2. Relationship between the absolute amplitude of an oscillation and its corresponding spectral modulus.

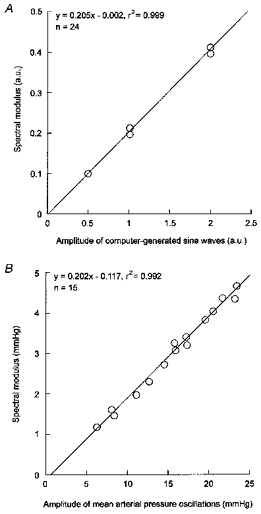
Figure 2

Open in a new tab

Linear regression analysis was applied to either computer-simulated sine waves (A) or experimental mean arterial pressure data (B). A, for each amplitude (expressed in arbitrary units, a.u.), the computer generated 500 Hz time series at eight different frequencies (0.1–1 Hz). B, mean arterial pressure data were obtained in fifteen rats during rhythmic stimulation of the aortic depressor nerve at 0.1 Hz. The amplitude of the stimulation-induced mean arterial pressure oscillations was measured directly using beat-to-beat values displayed on the computer screen. In all cases, the spectral modulus was calculated from 205 s time series (see Methods).

Mechanism of mean arterial pressure oscillatory responses to rhythmic stimulation of the aortic depressor nerve

The effects of sequential blockade of α-adrenoceptors and ganglionic transmission were assessed in seven of fifteen rats. The prestimulation levels of mean arterial pressure measured after phentolamine and chlorisondamine administration combined with angiotensin II infusion (103 ± 5 and 102 ± 8 mmHg, respectively) did not differ significantly from that observed during cardiac autonomic blockade alone (99 ± 9 mmHg). As shown in Fig. 3, mean arterial pressure oscillations were attenuated by about 50 % after phentolamine administration (P < 0.05), and were abolished after chlorisondamine administration.

Figure 3. Role of α-adrenoceptors and ganglionic transmission in the mean arterial pressure oscillations induced by rhythmic aortic nerve stimulation.

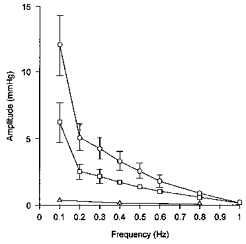
Figure 3

Open in a new tab

In the same seven rats under cardiac autonomic blockade, rhythmic stimulation of the aortic depressor nerve was performed before (○) and after sequential blockade of α-adrenoceptors with phentolamine (□) and ganglionic transmission with chlorisondamine (▵). Here and in subsequent figures symbols and error bars indicate means ± s.e.m.

Coherence and phase angle between aortic nerve stimulation and mean arterial pressure oscillations

The relationship between mean arterial pressure and impulses was characterized by a strong coherence (> 0.90), except at 1 Hz (Fig. 4A). The corresponding phase angles were positive at low frequencies, indicating that impulses led mean arterial pressure with respect to the out-of-phase pattern (Fig. 4B). Phase angles showed a clear tendency to decrease linearly from 0.1 to 0.8 Hz. The presence of a linear trend was confirmed in each of the thirteen rats by means of linear regression analysis (Table 1). Using these regression lines, it was established that phase angles fell to 0 at 0.42 ± 0.02 Hz. Therefore, at this particular frequency, mean arterial pressure oscillations were in phase with aortic nerve stimulation.

Figure 4. Cross-spectral analysis between mean arterial pressure and aortic nerve stimulation.

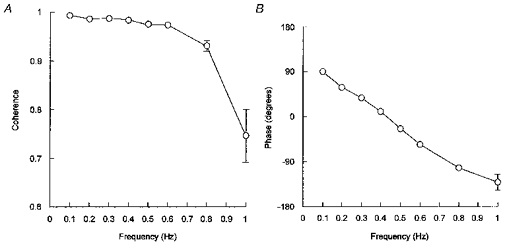
Figure 4

Open in a new tab

In each rat (n = 13), coherence (A) and phase angle (B) were computed with the impulses delivered by the stimulator as the input signal and mean arterial pressure as the output signal.

Table 1.

Linear regression analysis between modulation frequency and phase angle in thirteen rats

Rat no. r Slope (deg Hz−1) y-Axis intercept (deg) x-Axis intercept (Hz)
1 0.985 −324 140 0.43
2 0.989 −339 120 0.36
3 0.986 −283 116 0.41
4 0.991 −282 134 0.48
5 0.982 −240 122 0.51
6 0.997 −312 136 0.43
7 0.993 −314 122 0.39
8 0.995 −334 115 0.34
9 0.985 −284 129 0.45
10 0.996 −273 92 0.34
11 0.993 −284 109 0.38
12 0.986 −288 120 0.42
13 0.993 −269 139 0.52
Mean 0.990 −294 123 0.42
s.e.m. 0.001 8 4 0.02
Open in a new tab

The phase angle was computed between impulses delivered by the stimulator (input signal) and mean arterial pressure (output signal). The regression analysis included phase angles obtained at seven different modulation frequencies ranging from 0.1 to 0.8 Hz.

In a separate group of five rats, it was verified that the remaining intact baroreceptors did not significantly distort the phase relationships between mean arterial pressure oscillations and aortic nerve stimulation. Surgical denervation of sino-aortic baroreceptors was performed as previously described (Zhang et al. 1995) and the aortic nerve used for stimulation was cut as far caudal as possible. Phenylephrine hydrochloride (6 μg kg−1i.v.) was administered before and after denervation. The cardiac baroreceptor reflex sensitivity was estimated as the ratio of the peak change in heart rate to the peak change in mean arterial pressure. It was altered from −0.56 ± 0.07 to 0.35 ± 0.24 beats min−1 mmHg−1, thus confirming the completeness of denervation. Phase angles between impulse frequency and arterial pressure oscillations did not differ significantly from those obtained in intact rats at any frequency. Linear regression analysis applied to individual phase angles in the 0.1–0.8 Hz range indicated that phase fell to 0 at 0.43 ± 0.03 Hz in sino-aortic baroreceptor denervated rats. This value does not differ significantly (Mann-Whitney U test) from that obtained in baroreceptor-intact animals.

Characterization of mean arterial pressure oscillatory responses to rhythmic stimulation of the aortic depressor nerve in the low frequency range

The frequency-dependent attenuation of mean arterial pressure oscillations suggested the presence of a low-pass filter between baroreceptor afferent activity and arterial pressure. These low-pass filter properties were further characterized in seven of fifteen rats by stimulating the aortic nerve at additional frequencies below 0.1 Hz (0.06–0.09 Hz) and at 0.15 Hz. A Bode plot, which allows a simple graphic analysis of the frequency responses of a system (Gille et al. 1991), was constructed (Fig. 5). In each rat, the amplitude of mean arterial pressure oscillations (A) was normalized by the peak depressor response to step stimulation of the aortic nerve (B). The attenuation (loss = 20 log(A/B), expressed in dB) was plotted against the modulation frequency on a logarithmic scale (Fig. 5). In each rat, a linear fit was applied to the data between 0.06 and 0.6 Hz (r= 0.988± 0.003). The mean slope of individual fitted lines was −24.1 ± 1.5 dB decade−1. Although this value slightly deviated from the theoretical slope of −20 dB decade−1, the system was approximated to a first-order physical system with a corner frequency located at 0.045 ± 0.002 Hz (Fig. 5). In such a system, phase angles would decline steeply from 180 deg and then tend to a constant value of 90 deg, unless a fixed time delay was present between the input and the output. In this latter case, phase angles would keep decreasing with a linear slope (Fig. 6A). The behaviour of the experimental phase, i.e. a steep decline at low frequencies followed by a linear decrease, was seemingly consistent with this hypothesis (Fig. 6B). However, the model phase angle fell to 0 at 0.33 Hz. To obtain a resonance frequency of 0.4 Hz, the model had to be changed either by increasing the corner frequency to 0.21 Hz or by decreasing the fixed time delay to 0.67 s.

Figure 5. Bode plot of the oscillatory responses of mean arterial pressure to rhythmic stimulation of the aortic depressor nerve.

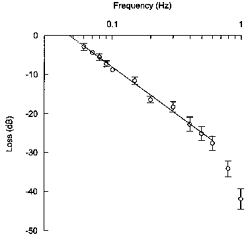
Figure 5

Open in a new tab

In each rat (n = 7), mean arterial pressure oscillations were normalized with respect to the maximum depressor response to step stimulation of the aortic nerve. Undamped oscillations would yield a null attenuation (0 dB). Normalized oscillatory responses tended to decrease linearly from 0.06 to 0.6 Hz with a slope close to −20 dB decade−1, which is the hallmark of a first-order low-pass filter. In such a system, the corner frequency can be estimated as the intersection of the line with the x-axis. The corner frequency is the frequency at which the amplitude of the oscillatory responses of the output signal starts to decrease precipitously. From individual regression lines, it was established that the corner frequency was 0.045 ± 0.002 Hz.

Figure 6. Linear modelling of phase angles between impulses and mean arterial pressure.

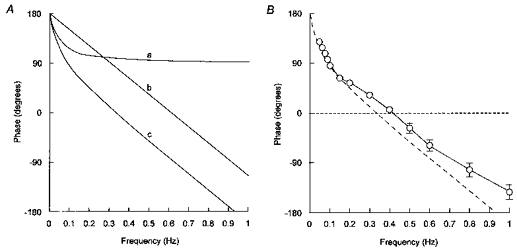
Figure 6

Open in a new tab

A, theoretical phase functions computed for physical systems containing either a first-order low-pass filter alone (a), a fixed time delay alone (b), or both in series (c). A first-order low-pass filter is defined by its corner frequency (fc, in Hz) and produces a phase shift of -tan−1(f/fc). A fixed time delay (T, in s) produces a phase shift of −360Tf. In a linear feedback system combining a first-order low-pass filter and a fixed time delay in series, phase angle (Φ) decreases from 180 deg according to the following equation: Φ(f) = 180 - tan−1(f/fc) - 360Tf. B, experimental phase angles (n = 7) together with the theoretical phase function (dashed line) corresponding to curve c in A (with fc = 0.045 Hz and T = 0.82 s).

The fixed time delay was calculated from the slope of the individual regression lines given in Table 1 (Saul et al. 1991). The value of 0.82 ± 0.02 s obtained from this calculation did not differ significantly (Student's t test for paired comparisons) from that obtained by the time domain approach (0.86 ± 0.02 s, see first paragraph of Results).

discussion

The present study provides direct experimental evidence for the existence of a resonance frequency near 0.4 Hz in the baroreceptor reflex loop of the rat, which therefore has the potential for generating self-sustained oscillations at this frequency. The study also suggests that this characteristic of the reflex is mainly the consequence of a fixed time delay of ∼0.8 s between baroreceptor afferent activity and arterial pressure.

Control theory teaches that every negative feedback system containing time lags is prone to oscillate because, as frequency increases, the output signal is progressively delayed from the input signal until, at a particular frequency, it is fed back positively, i.e. the output is in phase with the input (Gille et al. 1991). The resonance frequency depends on the phase shift generated by the fixed time delays and the dynamic behaviour of the components of the feedback loop, and is therefore an intrinsic characteristic of the system. These theoretical considerations have been applied to the arterial baroreceptor reflex and various models predicting the arterial pressure Mayer waves have been proposed (Madwed et al. 1989; Burgess et al. 1997b). However, the existence of a resonance frequency in the arterial baroreceptor reflex has never been proven experimentally. To address this issue, we examined the phase function between aortic depressor nerve stimulation and resulting oscillations of arterial pressure in anaesthetized rats.

Arterial pressure oscillations evoked by rhythmic aortic nerve stimulation were entirely mediated by the sympathetic nervous system, because they were abolished after ganglionic blockade. On the other hand, it was observed that these oscillations contained a significant contribution from non-adrenergic factors, as they were attenuated by only 50 % after phentolamine administration. This observation accords with previous studies in conscious rats reporting that acute α-adrenoceptor blockade does not completely abolish arterial pressure variability in the Mayer band (Japundzic et al. 1990; Cerutti et al. 1991). The residual arterial pressure oscillations observed under α-adrenoceptor blockade could be secondary to the release of cotransmitters of noradrenaline, such as neuropeptide Y, which may have been facilitated by the angiotensin II (Pernow & Lundberg, 1989), infused throughout the phentolamine experiment to maintain vascular tone.

Arterial pressure oscillations progressively attenuated as the modulation frequency of the aortic nerve was increased. At 1 Hz, arterial pressure oscillations had almost completely disappeared. Accordingly, Stauss & Kregel (1996) reported that rhythmic stimulation of the splanchnic sympathetic nerve was not translated into oscillations of mesenteric vascular resistance at frequencies above 1 Hz in conscious rats. In addition, it was shown by the same group (Stauss et al. 1997) that stimulation of the hypothalamic paraventricular nucleus can elicit oscillations of splanchnic nerve activity up to modulation frequencies of 2 Hz, whereas the mesenteric vasoconstrictor response is negligible at frequencies beyond 1 Hz. Both studies support the hypothesis that in our preparation, the frequency-dependent attenuation of arterial pressure oscillations is attributable to the slow response of the arterial smooth muscle to sympathetic modulation.

The attenuation of arterial pressure oscillatory responses with increasing modulation frequency was associated with a progressive decrease in phase angles. As outlined above, this deviation of the phase angle from the expected value of 180 deg in a negative feedback system could be due to the presence of fixed time delays and/or to the phase shift generated by the dynamic behaviour of its components. Linear trends in the phase function were identified in the frequency range 0.1–0.8 Hz, indicating the presence of a fixed time delay of about 0.8 s. A similar value was obtained by examining the onset latency of the depressor responses to step stimulation of the aortic nerve. This time lag included both the latency of nervous pathways and the delay in the vascular response to sympathetic modulation. The former is in the order of 0.15–0.3 s (Seller, 1991). The neuroeffector delay can be estimated from a recent study in conscious rats where it was reported that during acute exposure to behavioural stress, a change in renal sympathetic nervous activity is followed by a change in arterial pressure after a delay of 0.4–0.6 s (Burgess et al. 1997a). The 0.8 s latency we report here is therefore consistent with the existing data in the literature. It must be noted that this estimation of the overall delay in the baroreceptor reflex is based on the assumption that the transduction delay of the arterial baroreceptors themselves is negligible (Charlton & Baertschi, 1982) compared with the total delay introduced by the other components of the reflex arc.

This 0.8 s time delay generates a phase shift of 180 deg, and hence results in a null phase at around 0.6 Hz (Fig. 6A). Therefore, an additional phase lag is required to explain the null phase that was observed at 0.42 Hz. At modulation frequencies below 0.1 Hz, the phase function showed a steep decline that could reflect the properties of a low-pass filter. The Bode plot of the oscillatory responses allowed estimation of the order and the corner frequency of the filter (Fig. 5). The features of the gain function resembled those of a first-order low-pass filter with a corner frequency located at 0.045 Hz. Interestingly, a similar value of 0.05 Hz has been reported for the corner frequency of the baroreceptor reflex loop in anaesthestized rabbits (Ikeda et al. 1996). In the model combining a first-order low-pass filter with a fixed time delay in series, about one-half of the phase shift at the resonance frequency is generated by the low-pass filter, the other half being produced by the time delay (Fig. 6A). The model provided a reasonable approximation of experimental data (Fig. 6B). It is of note that in the model, the main characteristic of the low-pass filter, i.e. its corner frequency, has a weak influence on the value of the resonance frequency compared with that of the time delay. Figure 7 shows the resonance frequency as a function of the corner frequency for two different time delays in the arterial baroreceptor reflex: 0.8 s, which is the value suggested by the present study in rats, and 2.5 s, which is the value reported in humans using neck suction (Eckberg, 1980) or electrical stimulation of the carotid sinus nerves (Borst & Karemaker, 1983). For a wide range of corner frequencies, the model predicts reasonably well the actual frequency of Mayer waves, i.e. 0.4 Hz in rats and 0.1 Hz in humans. However, it must be reiterated that this simple linear model slightly underestimated the resonance frequency in the present study, mainly due to a breaking in the experimental phase function between 0.1 and 0.2 Hz (Fig. 6B). The model has therefore to be improved, especially by incorporating non-linearities, which are likely to be present at various levels in complex biological systems such as the baroreceptor reflex (Kitney, 1979).

Figure 7. Theoretical relationship between the corner frequency and the resonance frequency.

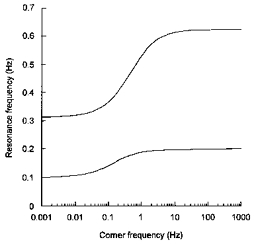
Figure 7

Open in a new tab
The graph shows resonance frequency as a function of corner frequency (fc) in a linear feedback system containing a first-order low-pass filter and a fixed time delay (T) in series, for two different values of the time delay (upper curve, 0.8 s; lower curve, 2.5 s). The resonance frequency was obtained by successive iterations of the following equation:
graphic file with name tjp0513-0251-mu1.jpg

The present data indicate that the time delay in the baroreceptor reflex is the critical element which determines the resonance frequency of the entire control loop. Therefore, interspecies differences in the frequency of the Mayer waves are probably the result of interspecies differences in the time delay. As the latency of the central nervous pathways is relatively constant among species (Seller, 1991), it is likely that differences in the overall delay are due to different latencies in the efferent sympathetic limb of the reflex. Different body sizes will result in different conduction times as conduction velocity in postganglionic sympathetic nerves is about 1 m s−1 in both humans (Fagius & Wallin, 1980) and rats (Yamazaki et al. 1990). Differences in neuroeffector delays could also be involved. In humans, the frequency response of cutaneous blood flow to electrical stimulation of skin sympathetic fibres suggests that the transmission from peripheral sympathetic nerves to the vasculature is slower than in rats (Stauss et al. 1998).

The present study establishes on an experimental basis that one essential condition, i.e. the existence of a resonance frequency at 0.4 Hz, is fulfilled for an oscillation to be self-generated in the arterial baroreceptor reflex loop of the rat. The theory predicts that, depending on the open loop gain at this frequency, the oscillation will vanish (gain < 1) or grow (gain > 1) until a limit is reached and the oscillation continues at a stable amplitude. The limit imposed on the oscillation amplitude reflects non-linearities in the effector response, e.g. saturation phenomena, and is subject to modulation by extrinsic factors. In the present study, anaesthesia and artificial ventilation resulted in almost complete elimination of spontaneous 0.4 Hz oscillations (data not shown), which suggests that the open loop gain of the baroreceptor reflex was decreased (Bedran-de-Castro et al. 1990; Brown et al. 1994). In conscious animals also, the presence or absence of Mayer waves depends on the experimental conditions. For example, it has been shown that Mayer waves are normally absent in conscious rabbits unless placed in a hypoxic environment, which results in the appearance of regular oscillations of arterial pressure and renal sympathetic nervous activity at 0.3 Hz (Janssen et al. 1997). Future studies will have to establish whether the amplitude of Mayer waves can be used as a reliable index of the baroreceptor reflex gain.

Acknowledgments

We wish to express our appreciation to Andrei Cividjian for helpful discussions and valuable advice. We also thank Dr Roland Favier and Professor Guy Annat for kindly providing part of the equipment. D. B. is the recipient of a research fellowship from the Ministère de l'Education Nationale, de l'Enseignement Supérieur et de la Recherche.

References

  1. Bedran-de-Castro MT, Farah VM, Krieger EM. Influence of general anesthetics on baroreflex control of circulation. Brazilian Journal of Medical and Biological Research. 1990;23:1185–1193. [PubMed] [Google Scholar]
  2. Borst C, Karemaker JM. Time delays in the human baroreceptor reflex. Journal of the Autonomic Nervous System. 1983;9:399–409. doi: 10.1016/0165-1838(83)90004-8. [DOI] [PubMed] [Google Scholar]
  3. Brown DR, Brown LV, Patwardhan A, Randall DC. Sympathetic activity and blood pressure are tightly coupled at 0.4 Hz in conscious rats. American Journal of Physiology. 1994;267:R1378–1384. doi: 10.1152/ajpregu.1994.267.5.R1378. [DOI] [PubMed] [Google Scholar]
  4. Burgess DE, Hundley JC, Li S-G, Randall DC, Brown DR. Multifiber renal SNA recordings predict mean arterial blood pressure in unanesthetized rat. American Journal of Physiology. 1997a;273:R851–857. doi: 10.1152/ajpregu.1997.273.3.R851. [DOI] [PubMed] [Google Scholar]
  5. Burgess DE, Hundley JC, Li S-G, Randall DC, Brown DR. First-order differential-delay equation for the baroreflex predicts the 0.4-Hz blood pressure rhythm in rats. American Journal of Physiology. 1997b;273:R1878–1884. doi: 10.1152/ajpregu.1997.273.6.R1878. [DOI] [PubMed] [Google Scholar]
  6. Cerutti C, Barrarrès C, Paultre C-Z. Baroreflex modulation of blood pressure and heart rate variabilities in rats: assessment by spectral analysis. American Journal of Physiology. 1994;266:H1993–2000. doi: 10.1152/ajpheart.1994.266.5.H1993. [DOI] [PubMed] [Google Scholar]
  7. Cerutti C, Gustin M-P, Paultre C-Z, Lo M, Julien C, Vincent M, Sassard J. Autonomic nervous system and cardiovascular variability in rats: a spectral analysis approach. American Journal of Physiology. 1991;261:H1292–1299. doi: 10.1152/ajpheart.1991.261.4.H1292. [DOI] [PubMed] [Google Scholar]
  8. Charlton JD, Baertschi AJ. Responses of aortic baroreceptors to changes of aortic blood flow and pressure in rat. American Journal of Physiology. 1982;242:H520–525. doi: 10.1152/ajpheart.1982.242.4.H520. [DOI] [PubMed] [Google Scholar]
  9. Daffonchio A, Franzelli C, Radaelli A, Castiglioni P, Di rienzo M, Mancia G, Ferrari AU. Sympathectomy and cardiovascular spectral components in conscious normotensive rats. Hypertension. 1995;25:1287–1293. doi: 10.1161/01.hyp.25.6.1287. [DOI] [PubMed] [Google Scholar]
  10. DeBoer RW, Karemaker JM, Strackee J. Hemodynamic fluctuations and baroreflex sensitivity in humans: a beat-to-beat model. American Journal of Physiology. 1987;253:680–689. doi: 10.1152/ajpheart.1987.253.3.H680. [DOI] [PubMed] [Google Scholar]
  11. Di rienzo M, Parati G, Castiglioni P, Omboni S, Ferrari AU, Ramirez AJ, Pedotti A, Mancia G. Role of sinoaortic afferents in modulating BP and pulse-interval spectral characteristics in unanesthetized cats. American Journal of Physiology. 1991;261:H1811–1818. doi: 10.1152/ajpheart.1991.261.6.H1811. [DOI] [PubMed] [Google Scholar]
  12. Eckberg DL. Nonlinearities of the human carotid baroreceptor-cardiac reflex. Circulation Research. 1980;47:208–216. doi: 10.1161/01.res.47.2.208. [DOI] [PubMed] [Google Scholar]
  13. Fagius J, Wallin BG. Sympathetic reflex latencies and conduction velocities in normal man. Journal of the Neurological Sciences. 1980;47:433–448. doi: 10.1016/0022-510x(80)90098-2. 10.1016/0022-510X(80)90098-2. [DOI] [PubMed] [Google Scholar]
  14. Gille J-C, Decaulne P, Pélegrin M. Dynamique de la Commande Linéaire. 9. Paris: Dunod; 1991. [Google Scholar]
  15. Grasso R, Rizzi G, Schena F, Cevese A. Arterial baroreceptors are not essential for low frequency oscillation of arterial pressure. Journal of the Autonomic Nervous System. 1995;50:323–331. doi: 10.1016/0165-1838(94)00103-q. [DOI] [PubMed] [Google Scholar]
  16. Guyton AC, Harris JW. Pressoreceptor-autonomic oscillation: a probable cause of vasomotor waves. American Journal of Physiology. 1951;165:158–166. doi: 10.1152/ajplegacy.1951.165.1.158. [DOI] [PubMed] [Google Scholar]
  17. Ikeda Y, Kawada T, Sugimachi M, Kawaguchi O, Shishido T, Sato T, Miyano H, Matsuura W, Alexander J, Jr, Sunagawa K. Neural arc of baroreflex optimizes dynamic pressure regulation in achieving both stability and quickness. American Journal of Physiology. 1996;271:H882–890. doi: 10.1152/ajpheart.1996.271.3.H882. [DOI] [PubMed] [Google Scholar]
  18. Jacob HJ, Ramanathan A, Pan SG, Brody MJ, Myers GA. Spectral analysis of arterial pressure lability in rats with sinoaortic deafferentation. American Journal of Physiology. 1995;269:R1481–1488. doi: 10.1152/ajpregu.1995.269.6.R1481. [DOI] [PubMed] [Google Scholar]
  19. Janssen BJA, Malpas SC, Burke SL, Head GA. Frequency-dependent modulation of renal blood flow by renal nerve activity in conscious rabbits. American Journal of Physiology. 1997;273:R597–608. doi: 10.1152/ajpregu.1997.273.2.R597. [DOI] [PubMed] [Google Scholar]
  20. Japundzic N, Grichois M-L, Zitoun P, Laude D, Elghozi J-L. Spectral analysis of blood pressure and heart rate in conscious rats: effects of autonomic blockers. Journal of the Autonomic Nervous System. 1990;30:91–100. doi: 10.1016/0165-1838(90)90132-3. [DOI] [PubMed] [Google Scholar]
  21. Julien C, Zhang Z-Q, Cerutti C, Barrarrès C. Hemodynamic analysis of arterial pressure oscillations in conscious rats. Journal of the Autonomic Nervous System. 1995;50:239–252. doi: 10.1016/0165-1838(94)00095-2. [DOI] [PubMed] [Google Scholar]
  22. Kitney RI. A nonlinear model for studying oscillations in the blood pressure control system. Journal of Biomedical Engineering. 1979;1:89–99. doi: 10.1016/0141-5425(79)90063-3. [DOI] [PubMed] [Google Scholar]
  23. Laude D, Weise F, Girard A, Elghozi J-L. Spectral analysis of systolic blood pressure and heart rate oscillations related to respiration. Clinical and Experimental Pharmacology and Physiology. 1995;22:352–357. doi: 10.1111/j.1440-1681.1995.tb02014.x. [DOI] [PubMed] [Google Scholar]
  24. Lo M, Julien C, Barrarrès C, Boomsma F, Cerutti C, Vincent M, Sassard J. Blood pressure maintenance in hypertensive sympathectomized rats. I. Adrenal medullary catecholamines. American Journal of Physiology. 1991;261:R1045–1051. doi: 10.1152/ajpregu.1991.261.4.R1045. [DOI] [PubMed] [Google Scholar]
  25. Madwed JB, Albrecht P, Mark RG, Cohen RJ. Low-frequency oscillations in arterial pressure and heart rate: a simple computer model. American Journal of Physiology. 1989;256:H1573–1579. doi: 10.1152/ajpheart.1989.256.6.H1573. [DOI] [PubMed] [Google Scholar]
  26. Malliani A, Pagani M, Lombardi F, Cerutti S. Cardiovascular neural regulation explored in the frequency domain. Circulation. 1991;84:482–492. doi: 10.1161/01.cir.84.2.482. [DOI] [PubMed] [Google Scholar]
  27. Mayer S. Studien zur Physiologie des Herzens und der Blutgefässe. Über spontane Blutdruckschwankungen. Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften. 1876;74:281–307. [Google Scholar]
  28. Pagani M, Lombardi F, Guzzetti S, Rimoldi O, Furlan R, Pizzinelli P, Sandrone G, Malfatto G, Dellell'Orto S, Piccaluga E, Turiel M, Baselli G, Cerutti S, Malliani A. Power spectral analysis of heart rate and arterial pressure variabilities as a marker of sympatho-vagal interaction in man and conscious dog. Circulation Research. 1986;59:178–193. doi: 10.1161/01.res.59.2.178. [DOI] [PubMed] [Google Scholar]
  29. Pagani M, Montano N, Porta A, Malliani A, Abboud FM, Birkett C, Somers VK. Relationship between spectral components of cardiovascular variabilities and direct measures of muscle sympathetic nerve activity in humans. Circulation. 1997;95:1441–1448. doi: 10.1161/01.cir.95.6.1441. [DOI] [PubMed] [Google Scholar]
  30. Pernow J, Lundberg JM. Modulation of noradrenaline and neuropeptide Y (NPY) release in the pig kidney in vivo: involvement of alpha 2, NPY and angiotensin II receptors. Naunyn-Schmiedeberg's Archives of Pharmacology. 1989;340:379–385. doi: 10.1007/BF00167038. [DOI] [PubMed] [Google Scholar]
  31. Persson PB. Spectrum analysis of cardiovascular time series. American Journal of Physiology. 1997;273:R1201–1210. doi: 10.1152/ajpregu.1997.273.4.R1201. [DOI] [PubMed] [Google Scholar]
  32. Preiss G, Polosa C. Patterns of sympathetic neuron activity associated with Mayer waves. American Journal of Physiology. 1974;226:724–730. doi: 10.1152/ajplegacy.1974.226.3.724. [DOI] [PubMed] [Google Scholar]
  33. Rubini R, Porta A, Baselli G, Cerutti S, Paro M. Power spectrum analysis of cardiovascular variability monitored by telemetry in conscious unrestrained rats. Journal of the Autonomic Nervous System. 1993;45:181–190. doi: 10.1016/0165-1838(93)90050-5. [DOI] [PubMed] [Google Scholar]
  34. Sapru HN, Gonzalez E, Krieger AJ. Aortic nerve stimulation in the rat: cardiovascular and respiratory responses. Brain Research Bulletin. 1981;6:393–398. doi: 10.1016/s0361-9230(81)80009-3. [DOI] [PubMed] [Google Scholar]
  35. Saul JP, Berger RD, Albrecht P, Stein SP, Chen MH, Cohen RJ. Transfer function analysis of the circulation: unique insights into cardiovascular regulation. American Journal of Physiology. 1991;261:H1231–1245. doi: 10.1152/ajpheart.1991.261.4.H1231. [DOI] [PubMed] [Google Scholar]
  36. Seller H. Central baroreceptor reflex pathways. In: Persson PB, Kirchheim HR, editors. Baroreceptor Reflexes: Integrative Functions and Clinical Aspects. Heidelberg: Springer-Verlag; 1991. pp. 45–74. [Google Scholar]
  37. Stauss HM, Anderson EA, Haynes WG, Kregel KC. Frequency response characteristics of sympathetically-mediated vasomotor waves in humans. American Journal of Physiology. 1998;274:H1277–1283. doi: 10.1152/ajpheart.1998.274.4.H1277. [DOI] [PubMed] [Google Scholar]
  38. Stauss HM, Kregel KC. Frequency response characteristic of sympathetic-mediated vasomotor waves in conscious rats. American Journal of Physiology. 1996;271:H1416–1422. doi: 10.1152/ajpheart.1996.271.4.H1416. [DOI] [PubMed] [Google Scholar]
  39. Stauss HM, Persson PB, Johnson AK, Kregel KC. Frequency-response characteristics of autonomic nervous system function in conscious rats. American Journal of Physiology. 1997;273:H786–795. doi: 10.1152/ajpheart.1997.273.2.H786. [DOI] [PubMed] [Google Scholar]
  40. Yamazaki Y, Karakida T, Homma S. Conduction velocity of motor nerve and cervical sympathetic and vagus nerve in streptozotocin diabetic rats. Neuroscience Letters. 1990;113:29–33. doi: 10.1016/0304-3940(90)90489-v. [DOI] [PubMed] [Google Scholar]
  41. Zhang Z-Q, Barrarrès C, Julien C. Involvement of vasodilator mechanisms in arterial pressure lability after sino-aortic baroreceptor denervation in rat. The Journal of Physiology. 1995;482:435–448. doi: 10.1113/jphysiol.1995.sp020530. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES