Ryanodine Receptor Adaptation

In the heart, depolarization during the action potential activates voltage-dependent Ca²⁺ channels that mediate a small, localized Ca²⁺ influx (I_Ca). This small Ca²⁺ signal activates specialized Ca²⁺ release channels, the ryanodine receptors (RyRs), in the sarcoplasmic reticulum (SR). This process is called Ca²⁺-induced Ca²⁺ release (CICR). Intuitively, the CICR process should be self-regenerating because the Ca²⁺ released from the SR should feedback and activate further SR Ca²⁺ release. However, the CICR process is precisely controlled in the heart and, consequently, some sort of negative control mechanism(s) must exist to counter the inherent positive feedback of the CICR process. Defining the nature of this negative control has been a focus of investigation for decades. Several mechanisms have been suggested including all of the following: Ca²⁺-dependent inactivation, adaptation, stochastic attrition, “fateful” inactivation, SR Ca²⁺ depletion, and coupled RyR gating. These mechanisms are generally regarded as being mutually exclusive (i.e., alternative). An emerging and more sophisticated view is that the required negative control is probably provided by a synergy of mechanisms, not a single mechanism.

In this perspective, we focus on the origin of Ca²⁺-dependent inactivation and adaptation of single cardiac RyR channels. Specific concerns about the adaptation phenomenon are addressed and a comprehensive unifying view of RyR Ca²⁺ regulation is forwarded. We conclude that the steady-state Ca²⁺ dependence, high Ca²⁺ inactivation and low Ca²⁺ adaptation are three distinct manifestations of the same underlying mechanism, Ca²⁺-dependent modal RyR channel gating.

Ca²⁺ -dependent Inactivation

Fabiato 1985 was the first to propose the existence of Ca²⁺-dependent inactivation. He proposed that inactivation of SR Ca²⁺ release is due to slow Ca²⁺ binding to a high affinity inactivation site on the SR Ca²⁺ release channel. He showed, in a skinned cardiac cell preparation, that SR Ca²⁺ release was substantially inactivated at steady-state Ca²⁺ concentrations as low as 60 nM. He argued that this conventional absorbing Ca²⁺-dependent inactivation leaves the SR Ca²⁺ release process refractory. Recovery from this refractory state requires removal of the Ca²⁺ stimulus and time. One important tenet of conventional Ca²⁺-dependent inactivation is that it should be evident in both the stationary and nonstationary behavior of the channel. Another important tenet of conventional inactivation is that it will be essentially an all-or-none process (i.e., any channel will be either inactivated or not) at the single channel level. Thus, a second incremental Ca²⁺ stimulus would not be expected to reactivate an inactivated (i.e., refractory) channel regardless of stimulus amplitude or duration.

Historically, studies on intact and permeabilized cells present contradictory evidence concerning the existence of Ca²⁺-dependent inactivation (Fabiato 1985; Nabauer and Morad 1992). More recently, Lukyanenko and Györke 1999 showed that elevation of resting Ca²⁺ levels increased the frequency of spontaneous Ca²⁺ sparks, which are thought to arise from bursts of SR Ca²⁺ release channel activity. The conclusion was that SR Ca²⁺ release (RyR) channel activity in cells is not depressed by a high affinity Ca²⁺-dependent inactivation. There are also no signs of high affinity Ca²⁺-dependent inactivation (e.g., occurring at <0.1 mM Ca²⁺) in studies of steady-state single RyR channel behavior (e.g., Györke and Fill 1993; Zahradníková and Zahradník 1995). Interestingly, there is evidence supporting the existence of low affinity inactivation that occurs at very high Ca²⁺ concentrations (>1 mM; Laver et al. 1995). It is not clear whether such high cytoplasmic Ca²⁺ concentrations are ever reached in the cell.

Ca^{2 +}-dependent Adaptation

Györke and Fill 1993 were the first to explore the complex dynamics of RyR channel Ca²⁺ regulation. They showed that fast Ca²⁺ stimuli rapidly activated (τ ∼1 ms) single RyR channels in planar bilayers to a high open probability (P_o) level. The P_o then slowly and spontaneously decayed. This was surprising because the Ca²⁺ stimuli generated a sustained Ca²⁺ elevation of ∼1 μM, and there was no evidence of steady-state Ca²⁺-dependent inactivation at that Ca²⁺ concentration. To test if the spontaneous decay was mediated by conventional Ca²⁺-dependent inactivation, Györke and Fill 1993 applied a second incremental Ca²⁺ stimulus to the apparently “inactivated” RyR channels. The second Ca²⁺ stimulus reactivated the apparently inactivated channels. These data suggested that the spontaneous decay was mediated by some unknown mechanism. This unknown mechanism was not apparent at steady-state and did not leave the channel refractory. Györke and Fill 1993 coined the term adaptation to describe this unexpected RyR channel behavior. Valdivia et al. 1995 confirmed the rate and extent of adaptation using a similar method. There is now substantial experimental evidence that adaptation is a manifestation of Ca²⁺-dependent modal gating (for details see RyR Adaptation and Modal Gating).

The Györke and Fill 1993 RyR adaptation hypothesis was controversial. Lamb et al. 1994 suggested that the decrease in channel activity might just reflect slow RyR deactivation following the very fast, large Ca²⁺ spike that was present on the leading edge of the applied Ca²⁺ stimuli. The merits of this theoretical concern were experimentally addressed. These studies indicate that the fast Ca²⁺ spike has no impact on the much slower (1,000-fold slower) adaptation phenomenon. They also indicate that the impact of the fast Ca²⁺ spike is limited to accelerating the closed to open transition of the channel (i.e., essentially super-charging the Ca²⁺ stimuli). The evidence supporting this conclusion is described later in Ca² + Spike Concern.

The nonstationary dynamics of RyR Ca²⁺ regulation have also been explored using other methodologies (Schiefer et al. 1995; Sitsapesan et al. 1995; Laver and Curtis 1996; Laver and Lamb 1998). These studies also report a relatively fast Ca²⁺ activation followed by a slow spontaneous decay in channel activity. However, the slow spontaneous decay is interpreted as conventional Ca²⁺-dependent inactivation, not adaptation. Some investigators have evoked the original Lamb et al. 1994 concern to suggest that inactivation, not adaptation, warrants further investigation. We disagree and suggest that our focus should be on reconciling the diverse RyR data sets based on their intrinsic empirical value instead of simply defending a particular interpretation. The merits of each view are discussed later in Mechanical Solution Change Studies.

RyR Adaptation and Modal Gating

Under steady-state conditions, the opening of single RyR channels occurs in bursts. These bursts fall into two categories (i.e., high and low open probability; P_o). These bursts do not occur randomly, but, instead, they are temporally clustered into distinct modes of RyR channel gating (i.e., high- and low-P_o modes). Several groups have now reported the existence of modal RyR channel gating (Zahradníková and Zahradník 1995; Armisén et al. 1996; Villalba-Galea et al. 1998; Saftenku et al. 2000).

Stationary single RyR channel activity exhibits three distinct gating modes (Zahradníková and Zahradník 1995). At intermediate Ca²⁺ concentrations (∼10 μM), the high P_o mode (H-mode) is characterized by periods of frequent and long openings. The low P_o mode (L-mode) is marked by periods of infrequent and short openings. The inactivated mode (I-mode) corresponds to periods where no opening events occur. A simple Markovian model of RyR modal gating was proposed by Zahradníková and Zahradník 1996 that predicts that upon a small fast Ca²⁺ elevation the P_o of a RyR channel residing in the H-mode will rapidly increase before the channel has time to relax to a new equilibrium between all three modes. The result is a rapid rise of channel activity that spontaneously decays over time. A second prediction is that the response of a single RyR channel to fast Ca²⁺ elevation will depend on which mode the channel happens to be in at the moment the stimulus is applied. In other words, a single channel fluctuates spontaneously between modes with different capacities to respond to a Ca²⁺ stimulus. For example, if a channel happens to be in the L- or I-mode (40% probability at 1 μM Ca), then the probability of a high Po response will be reduced to ∼17% because of the relatively long dwell times of these modes. Another prediction is that a single RyR channel will respond transiently and repeatedly to small fast incremental Ca²⁺ elevations. This realization lead Zahradníková and Zahradník 1996 to propose that modal gating may explain the adaptation phenomenon observed by Györke and Fill 1993. For years, this proposal was based on theory, not experimental evidence. Recently, Zahradníková et al. 1999a defined the evolving temporal correlations between the three RyR gating modes during the adaptation phenomenon and experimentally established that modal gating and the adaptation phenomenon are likely related.

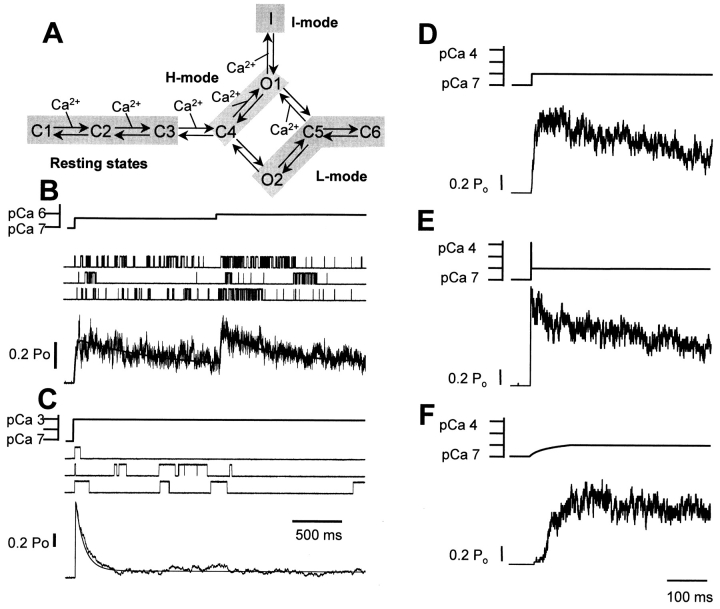
There are certain aspects of the Zahradníková and Zahradník 1996 model, however, that do not entirely reproduce the adaptation phenomenon. Our view is that these discrepancies indicate that the modal gating model needs refinement. Others have viewed these discrepancies as evidence against adaptation. Villalba-Galea et al. 1998 refined and expanded the original Zahradníková and Zahradník 1996 modal gating model to better reproduce various aspects of RyR gating behavior. The Villalba-Galea et al. 1998 form of the model incorporates an additional Ca²⁺-dependent transition that shifts channel gating to the H-mode as the amplitude of the Ca²⁺ perturbation becomes greater. In addition, the model includes a Ca²⁺-dependent transition to the inactivated state to better reproduce high Ca²⁺ (>1 mM) inhibition. The specific Markovian model presented by Villalba-Galea et al. 1998 is illustrated in Fig. 1 A. The simulated response of a single RyR channel to Ca²⁺ stimuli like those applied by Györke and Fill 1993 is presented in Fig. 1 B. The Ca²⁺ stimuli (Fig. 1 B) did not contain the fast Ca²⁺ spike. The model predicts that single RyR channels display rapid activation followed by a slow, spontaneous decay in channel activity. The spontaneous decay occurs at Ca²⁺ levels (<1 μM) that are well below those known to induce Ca²⁺-dependent inactivation under steady-state conditions (e.g., >1 mM). A second incremental Ca²⁺ stimulus induces a second transient of channel activity. Thus, a specific kinetic scheme (Fig. 1 A) can reproduce the fundamental hallmarks of the adaptation phenomenon (Györke and Fill 1993) in the absence of the fast Ca²⁺ spike.

Figure 1.

(A) The modal gating kinetic scheme (Villalba-Galea et al. 1998) shows the Ca²⁺-dependent transitions involved in RyR activation, modal gating (C4-O1-C5 and C5-O2-C4), and inactivation (O1-I, C1-C2, C2-C3, C3-C4, and C4-O1). The rate constants for the transitions between states are listed in Table . (B) Single-channel recordings simulated using the Monte Carlo method. The Ca²⁺ stimulus, sample single-channel sweeps, and an ensemble record generated from 100 sweeps are shown. These simulations show that each of two consecutive fast incremental Ca²⁺ elevations (<1 μM) generate transient bursts of channel activity. (C) Single RyR response to a single large Ca²⁺ elevation to 1 mM. The Ca²⁺ stimulus, sample single-channel sweeps, and an ensemble record are shown. (D) Single RyR response to a fast small Ca²⁺ elevation to 1 μM. Only the Ca²⁺ stimulus and an ensemble record are shown. (E) Single RyR response to a fast small Ca²⁺ elevation to 1 μM with a large (100 μM) Ca²⁺ spike at its leading edge. Only the Ca²⁺ stimulus and an ensemble record are shown. (F) Single RyR response to a 100-ms ramp-like Ca²⁺ elevation to 1 μM. Only the Ca²⁺ stimulus and an ensemble record are shown.

Recently, the Williams' group has reported highly variable Ca²⁺-dependent modal RyR gating (Saftenku et al. 2000). They found that elevating the steady-state Ca²⁺ concentrations increases the P_o within the L-mode and also increases the probability of the channel being in the H-mode. They suggest that this observation is inconsistent with the adaptation hypothesis. However, it is not clear, how this behavior might preclude the possibility of adaptation. The Villalba-Galea et al. 1998 model described above, in agreement with the results of Saftenku et al. 2000, clearly predicts a Ca²⁺-dependent increase in H-mode probability. It also predicts a Ca²⁺-dependent increase in P_o during the H-mode, but not during the L-mode. Like the Saftenku et al. 2000 abstract, Zahradníková et al. 1999a showed a Ca²⁺-dependent increase in P_o during the L-mode but found that this increase was significant but minor (<5% P_o) at Ca²⁺ concentrations where the adaptation phenomenon occurs (i.e., between 0.5 and 20 μM Ca). It is the Ca²⁺-dependent increase in P_o during the H-mode, not during the L-mode, that drives the adaptation phenomenon.

How does Ca²⁺-dependent modal gating work? At low Ca²⁺ concentrations (100 nM), the states with the highest probability of being occupied are C1, C2, and C3 and, consequently, the channel will be closed most (97%) of the time. After a small Ca²⁺ elevation, the channel will move initially into the C4 and O1 states, inducing long openings and short closures (H-mode), and then into the C5, O2, and C6 states, inducing short openings and long closures (L-mode). Interestingly, the larger the Ca²⁺ stimulus, the longer the channel spends in the H-mode. The Ca²⁺-dependent transition that connects C5 with O1 shifts the model to the H-mode during large Ca²⁺ stimuli. At high Ca²⁺ concentrations (e.g., >1 mM), the Ca²⁺-dependent transition between the O1 and I states will move the channel into the nonconducting I state (I-mode).

At any steady-state Ca²⁺ level, there will be a dynamic equilibrium between the high P_o, low P_o, and inactivated modes. This dynamic equilibrium generates the well-known bell-shaped steady-state Ca²⁺ dependence of the RyR channel (Laver et al. 1995). As described above, small, fast Ca²⁺ elevations from a low Ca²⁺ concentration will upset the existing dynamic equilibrium momentarily in favor of the high P_o mode. Consequently, the P_o rises to a level above that predicted by steady-state measurements before activity spontaneously decays as the three modes reequilibrate at the new higher Ca²⁺ concentration. Such suprasteady-state P_o followed by a spontaneous decay has been experimentally observed previously (Györke and Fill 1993; Valdivia et al. 1995; Laver and Curtis 1996; Laver and Lamb 1998). Application of a second incremental Ca²⁺ elevation will induce another transient modal gating shift and a second transient of channel activity like that reported by Györke and Fill 1993. The magnitude of the transient modal gating shift (i.e., adaptation) will depend on Ca²⁺ stimulus speed and magnitude. Slow and large Ca²⁺ stimuli will be less effective at generating adaptation. Slow Ca²⁺ stimuli are less effective because mode reequilibration is time dependent. Large Ca²⁺ stimuli are less effective because the channel begins to spend time in the inactivated mode. Thus, a relatively large slow Ca²⁺ stimulus will induce inactivation, not adaptation. This is consistent with the experimental results of Sitsapesan et al. 1995 and Schiefer et al. 1995. If refractory behavior was a characteristic of the inactivated mode, then this modal gating scheme would predict refractory behavior only at high Ca²⁺ levels. Interestingly, Schiefer et al. 1995 reported clear refractory behavior at 1 mM (following a 72% spontaneous decay), but found no evidence of refractory behavior at 10 μM (after an ∼30% spontaneous decay). In cells, the RyR channel is subjected to very brief (<1 ms) large (>10 μM) Ca²⁺ stimuli (Stern 1992). The modal gating scheme predicts that such large, fast Ca²⁺ stimuli will trigger one or two brief opening events followed by fast deactivation. These predictions are also quite consistent with the experimental record (Zahradníková et al. 1999b).

Thus, modal gating reconciles a large body of apparently contradictory experimental results and, thus, provides a useful comprehensive theoretical context for understanding RyR Ca²⁺ regulation. In this context, RyR inactivation and adaptation should not be viewed as mutually exclusive, but rather two different manifestations of the same underlying mechanism (i.e., modal gating). However, this modal gating scheme is still deficient because the potential impact of certain physiologically important ligands (e.g., luminal Ca, cytosolic Mg, and ATP) is not considered. This deficit, and others, will have to be addressed to correlate single RyR channel data with local Ca²⁺ release events in cells.

The Fast Ca²⁺ Spike Concern

Here, the possibility that the fast Ca²⁺ spike drives the adaptation phenomenon is discussed. It is known that flash photolysis of certain caged Ca²⁺ compounds (e.g., DM-nitrophen and NP-EGTA) can generate a very fast Ca²⁺ overshoot (i.e., the Ca²⁺ spike) at the leading edge of a sustained Ca²⁺ elevation. Lamb et al. 1994 suggested that the adaptation phenomenon might reflect slow RyR deactivation following a fast Ca²⁺ spike. The suggestion was that the Ca²⁺ activation sites on the RyR channel are rapidly occupied during the brief Ca²⁺ spike (lasting ∼1 ms), resulting in fast RyR activation to a high P_o level. As the Ca²⁺ concentration falls to a substantially lower level after the brief Ca²⁺ spike, the RyR channel may simply “turn off” (i.e., deactivate) very slowly as occupancy of Ca²⁺ activation sites falls. This concern was clearly legitimate considering the vacuum of knowledge that existed in 1994.

Lamb et al. 1994 estimated the properties of the fast Ca²⁺ spike using the available published properties of the Ca²⁺ cage complex. Györke and Fill 1994 began to experimentally evaluate the potential impact of the Ca²⁺ spike on the adaptation phenomenon. They reported no compelling evidence to support the theoretical contentions of Lamb et al. 1994. Subsequently, it became clear that the previous estimates of Ca²⁺ spike properties were wrong. The experiments of Escobar et al. 1997 revealed that the Ca²⁺ spike was considerably faster and smaller than previously thought. This supported the intuitive assumption of Györke and Fill 1994 that it was very unlikely that such a brief Ca²⁺ signal (lasting <0.2 ms) could drive the slow adaptation phenomenon (lasting >1,000 ms). Another interesting insight gained from the Escobar et al. 1997 study was that the fast Ca²⁺ spike is actually a reasonable representation of the fast Ca²⁺ signals that may occur in the dyadic cleft during openings of single dihydropyridine receptor (DHPR) channels (Stern 1992). This latter insight prompted Zahradníková et al. 1999b to further explore the potential impact of the fast Ca²⁺ spikes on single RyR channel activity. They improved the experimental recording conditions (i.e., increasing bandwidth, minimizing flash artifacts, etc.), so that they could define the impact of a Ca²⁺ spike alone (with little or no sustained Ca²⁺ elevation) during the first few milliseconds following its application. The rationale was that bandwidth and flash artifacts may have masked the impact of the Ca²⁺ spike in previous studies (Györke and Fill 1993; Györke et al. 1994; Valdivia et al. 1995). They showed that a fast Ca²⁺ spike alone, albeit slightly smaller than those applied previously, induced one or two brief opening events during the first few milliseconds after the flash. When Zahradníková et al. 1999b duplicated the Györke and Fill 1993 stimuli (i.e., spike plus sustained Ca²⁺ elevation), the classical adaptation phenomenon was observed. Thus, the RyR channel's response to a Ca²⁺ spike alone is dramatically different than its response to af Ca²⁺ spike followed by a sustained Ca²⁺ elevation. Zahradníková et al. 1999b concluded that Ca²⁺ spikes are simply too brief to drive the very slow adaptation phenomenon.

Lamb et al. 2000 have a different interpretation of the Zahradníková et al. 1999b data with adaptation again being driven by the Ca²⁺ spike and not by the sustained Ca²⁺ elevation. This interpretation is based, in part, on the fact that the Zahradníková et al. 1999b Ca²⁺ spikes were somewhat smaller (≤30 μM peak or estimated Ca²⁺ time integrals of 2–7 μMms) than those applied by Györke and Fill 1993(30–60 μM peaks or estimated Ca²⁺ time integrals of 8–30 μMms). The Lamb group suggests that the Zahradníková et al. 1999b data simply show that there is some sort of critical threshold for the Ca²⁺ spike to induce the adaptation phenomenon. In other words, the RyR channel distinguishes a Ca²⁺ spike peaking at 40 μM (with a Ca²⁺ time integral of 8 μMms) from one peaking at 30 μM (with a Ca²⁺ time integral of 6 μMms) and its response to each is different (slow or fast deactivation, respectively). They speculate that the action of large Ca²⁺ spikes is mediated by some hypothetical very low affinity Ca²⁺ binding sites that are preferentially occupied only during large Ca²⁺ spikes. However, this new hypothesis is inconsistent with common kinetic principles of receptor–ligand interaction and directly contradicts existing experimental evidence regarding RyR behavior.

Common kinetic principles dictate that very low affinity Ca²⁺ binding sites typically have fast kinetics (conversely high affinity sites typically have slow kinetics). It is difficult to understand how the hypothetical low affinity sites could mediate a very slow phenomenon like adaptation. In numerical terms, the low affinity sites would have a K _d near 50 μM and an off-rate of 1 s⁻¹ (i.e., the published time constant of RyR adaptation). Consequently, the probability of that site being occupied during a fast 50-μM Ca²⁺ spike lasting <1 ms will be <0.001; thus, the spike is unlikely to have a dramatic impact on such a site (Escobar et al. 1997). Additionally, the probability of a state of being occupied in any kinetic reaction is typically described by a probability distribution and not by a particular triggering level. Lamb et al. 2000(this issue) acknowledge the difficulty of explaining their new hypothesis in specific kinetic terms, and offer no specific kinetic scheme to support their point of view. Instead, they simply suggest that large Ca²⁺ spikes must drive the RyR channel into some unusual configuration and/or induce some unknown mechanisms. On the other hand, we have forwarded a specific and relatively simple Markovian gating scheme (Fig. 1) that describes adaptive behavior arising from Ca²⁺-dependent modal gating changes driven by the sustained component of the photolytic Ca²⁺ stimuli.

As described earlier, the Lamb et al. 2000 predicts that adaptation of a single RyR channel occurs when some critical Ca²⁺ spike threshold is exceeded (i.e., ≥30 μM peak or Ca²⁺ time integral ≥8 μMms). However, there is experimental evidence that suggest otherwise. Györke and Fill 1993 and Valdivia et al. 1995 used the same method but different caged-Ca²⁺ compounds, DM-nitrophen and NP-EGTA, respectively. Consequently, the applied Ca²⁺ stimuli had a similar sustained Ca²⁺ elevation, but fast Ca²⁺ spikes of dramatically different amplitude (and time integral). The similarity of RyR adaptation in both works suggested that adaptation is not highly dependent on subtle features of the fast Ca²⁺ spike. More recently, our group (Zahradníková, A., and S. Györke, unpublished results) has also explored the impact of large Ca²⁺ spikes on single RyR channel function. In this work, large Ca²⁺ spikes (80–150 μM peak, Ca²⁺ time integrals of up to 15 μMms) were generated by photolysis of NP-EGTA (3 mM). The large Ca²⁺ spikes triggered only solitary RyR openings, not the slow adaptation phenomenon. The openings were reminiscent of the spike-activated events previously reported by Zahradníková et al. 1999b. Thus, it does not appear that adaptation depends on the amplitude or Ca-time integral of the fast Ca²⁺ spike.

The premise that the RyR channel undergoes slow deactivation (lasting seconds) after the fast Ca²⁺ spike is also inconsistent with existing experimental evidence. The rate of RyR deactivation in response to a fast Ca²⁺ reduction has been measured (Schiefer et al. 1995; Vélez et al. 1997; Zahradníková et al. 1999b). These experimental data show that RyR deactivation from high Ca²⁺ concentrations is fast (τ's <10 ms), not slow (lasting seconds). Thus, the slow adaptation process is not likely due to very slow RyR deactivation.

What then is the impact of the Ca²⁺ spike on RyR channel function? The fast Ca²⁺ spike essentially supercharged the Ca²⁺ stimulus in the flash photolysis studies (Györke and Fill 1993). Its impact is best illustrated using the RyR scheme presented above. Simulated RyR channel response to a fast Ca²⁺ elevation with and without a fast Ca²⁺ spike at its leading edge is shown in Fig. 1E and Fig. D, respectively. The sustained component of the Ca²⁺ stimulus elevated Ca²⁺ from 0.1 to 1.0 μM. The fast Ca²⁺ spike peaked at ∼50 μM and lasted 0.2 ms. The rate and extent of the slow spontaneous decay (i.e., adaptation) is identical in the presence or absence of the fast Ca²⁺ spike. The presence of the fast Ca²⁺ spike, however, introduces a brief peak in channel activity that rapidly decays (i.e., deactivates). This brief peak is generated by the spike-activated events as described experimentally by Zahradníková et al. 1999b. In essence, the impact of the fast Ca²⁺ spike is limited to accelerating the closed to open transition of the channel. It does not impact the rate or extent of the much slower adaptation phenomenon. This is consistent with the original assumption of Györke and Fill 1993 that the fast Ca²⁺ spike is simply too fast to impact the adaptation phenomenon.

Mechanical Solution Change Studies

Several studies have explored the complex dynamics of single RyR channel Ca²⁺ regulation using the flash photolysis methodology (Györke and Fill 1993; Györke et al. 1994; Valdivia et al. 1995; Vélez et al. 1997; Zahradníková et al. 1999b). The data are quite consistent between studies, and are generally interpreted in terms of adaptation, not inactivation. Other studies have explored the dynamics of RyR Ca²⁺ regulation using Ca²⁺ stimuli generated by different mechanical solution change methodologies (Schiefer et al. 1995; Sitsapesan et al. 1995; Laver and Curtis 1996). These studies report RyR activation followed by either a slow spontaneous decay or no decay at all. When RyR channel activity spontaneously decayed, the decay was interpreted as inactivation, not adaptation. This interpretation and the absence of fast Ca²⁺ spikes in these latter studies have been construed as evidence against the adaptation phenomenon.

The following questions are addressed below. First, are the mechanical solution change data internally consistent enough to dismiss data collected using a different methodology? Second, are the stimuli in the mechanical solution change studies “true” [Ca²⁺] steps and the only ones suitable for defining the nonstationary behavior of RyR? Finally, is conventional Ca²⁺-dependent inactivation the only mechanism consistent with the mechanical solution change data? We believe the answer to each of these questions is no.

Three different mechanical solution change strategies have been applied to study single RyR channel function in planar bilayers (Schiefer et al. 1995; Sitsapesan et al. 1995; Laver and Curtis 1996; Laver and Lamb 1998). Schiefer et al. 1995 used a piezo-based method and achieved complete solution exchange over a 1-ms period. Sitsapesan et al. 1995 used a solenoid-based method that exchanged solutions over a period of 10 ms. Laver and Curtis 1996 and Laver and Lamb 1998 used a “puffing” method that exchanged solutions over a period ranging from 20 to 110 ms. Each of these mechanical solution change studies also applied different size Ca²⁺ stimuli. Some applied small Ca²⁺ stimuli (<10 μM; Schiefer et al. 1995, Laver and Curtis 1996). All applied very large Ca²⁺ stimuli (≥100 μM; Schiefer et al. 1995; Sitsapesan et al. 1995; Laver and Curtis 1996; Laver and Lamb 1998). The reported rates of Ca²⁺ activation varied from 0.2 to 20 ms, whereas the reported rates of inactivation varied from 200 to 15,000 ms. Inactivation was highly voltage-dependent in one study (Sitsapesan et al. 1995), but was voltage-independent in another (Schiefer et al. 1995). Two of the studies report inactivation only at Ca²⁺ concentrations (≥100 μM) known to inactivate channels under steady-state conditions (Schiefer et al. 1995; Sitsapesan et al. 1995). Two other studies report inactivation at Ca²⁺ concentrations (1 μM) that do not inactivate channels under steady-state conditions (Laver and Curtis 1996; Laver and Lamb 1998). The variability in results between the different solution exchange studies probably reflects the different methodologies used and ultimately the types of Ca²⁺ stimuli applied (see below). Another potential contributing factor may be a limited sample size in some cases (Schiefer et al. 1995; Laver and Lamb 1998). We suggest that the data presented in the solution exchange studies is important, but is not internally consistent enough to categorically dismiss results collected using a different methodology.

Recently, studies of RyR Ca²⁺ dynamics performed with improved time resolution show that RyR Ca²⁺ activation is very fast (activation time constant 0.1 ms; Zahradníková et al. 1999b). Such a rapid response time is consistent with the local control theory (Stern 1992). In vivo, the RyR channel may be activated by very fast, brief local Ca²⁺ changes associated with single openings of a DHPR channel. Considering the fast kinetics of RyR channel Ca²⁺ activation, the Ca²⁺ stimuli applied by the mechanical solution change studies described above cannot be regarded as true instantaneous Ca²⁺ steps. The possible exception is the Schiefer et al. 1995 study. However, the other studies applied relatively slow Ca²⁺ changes that required 10–110 ms to complete due to considering the large unstirred layers that exist immediately adjacent to the bilayer (Laver and Curtis 1996). Consequently, the Ca²⁺ stimuli applied in all but one of the mechanical solution change studies can be more accurately described as Ca²⁺ ramps instead of steps. The point is that the same critical scrutiny that was applied to the photolytic Ca²⁺ stimuli has not yet been applied to the mechanical Ca²⁺ stimuli.

The dynamics of RyR channel behavior in response to a very fast Ca²⁺ step or a relatively slow Ca²⁺ ramp are likely to be different. The potential impact of Ca²⁺ stimulus speed on single RyR channel gating can be seen in simulated channel data presented in Fig. 1. Not surprisingly, RyR behavior to a fast Ca²⁺ step (rise time ≤100 μs) or a ramp-like Ca²⁺ stimulus (rise time 100 ms; Laver and Curtis 1996) was quite different. Changes in Ca²⁺ stimulus speed impacted both Ca²⁺ activation and spontaneous decay (Fig. 1, D–F). The point is that Ca²⁺ stimuli with such slow rise times (10 to 100 ms) can have rather dramatic impact on RyR channel function. This may explain the tight parallel between the dynamic and stationary behavior of single RyR channels in certain mechanical solution change studies (Sitsapesan et al. 1995). The high sensitivity to Ca²⁺ stimulus speed (Zahradníková et al. 1999b) and the very fast Ca²⁺ stimuli thought to occur in vivo (Stern 1992) suggest that the relatively slow Ca²⁺ stimuli available in most mechanical solution change studies may not be appropriate to study the dynamics of RyR regulation especially in the physiologically relevant range of Ca²⁺ stimuli rates (<1 ms).

We also believe that the mechanical solution change results provide evidence for both conventional inactivation and adaptation. Schiefer et al. 1995 and Sitsapesan et al. 1995 report a spontaneous decay in RyR activity at Ca²⁺ concentrations (i.e., ≥100 μM) where inactivation is observed under steady-state conditions. Thus, we agree that it is appropriate to conclude that the spontaneous decay was due to inactivation. In other cases, it is more difficult to justify the inactivation interpretation. For example, Laver and Curtis 1996(see their figure 3B) report that RyR activity decays following a Ca²⁺ elevation to 1 μM Ca, a Ca²⁺ concentration where there is no evidence of inactivation under steady-state conditions. Laver and Curtis also report that the peak P_o reached was well above that expected under steady-state conditions (see Figure 4 in Laver and Curtis 1996). This unusual behavior is difficult to understand if the decay was due to conventional inactivation. More recently, Laver and Lamb 1998 applied a 1-μM Ca²⁺ “puff” to induce a burst of RyR channel activity that decayed over time. They applied a second sustained Ca²⁺ elevation to 100 μM after the spontaneous decay in channel activity was complete. The single RyR channel did not reactivate in the presence of 100 μM Ca. Laver and Lamb 1998 interprets these results as evidence that the RyR channel becomes refractory in response to the 1-μM Ca²⁺ stimulus, and suggests that conventional Ca²⁺ inactivation regulates single RyR channels at such low Ca²⁺ concentrations. However, this interpretation is inconsistent with the classical steady-state Ca²⁺ dependence of the RyR channel. First, there is no evidence of conventional inactivation at 1 μM Ca²⁺ under steady-state conditions. Second, there is substantial spontaneous RyR channel activity at 100 μM Ca²⁺ and, thus, the channel should have reactivated at some point during their second sustained Ca²⁺ stimulus. It is difficult to understand how the spontaneous decay at 1 μM Ca²⁺ could be due to conventional inactivation. Instead, we suggest that a spontaneous shift to a low (or zero) P_o mode may have been mistaken for conventional absorbing inactivation.

Schiefer et al. 1995 report a nonrefractory decrease in P_o after 500 ms steps to 1–100 μM Ca. There was no or only a barely detectable decrease of P_o (<10%) for steps to 0.3–3 μM Ca. However, several of their observations are consistent with the RyR adaptation hypothesis. First, they reported a K _d for Ca²⁺ activation of 0.7 μM. This is closer to the 0.3-μM K _d reported for the adaptation response (Györke and Fill 1993) than the 1.5–4-μM K _d reported under steady-state conditions (Györke and Fill 1993; Györke et al. 1994; Zahradníková and Zahradník 1995; Laver et al. 1995). Second, Schiefer et al. 1995 observed only a single open time component with a time constant of 3 ms. This is similar to that reported for H-mode openings (Zahradníková and Zahradník 1995; Zahradníková et al. 1999a), openings during the first phase of adaptation (Zahradníková et al. 1999a), as well as solitary spike-activated openings (Zahradníková et al. 1999b). Under steady-state conditions, the RyR channel displays at least two distinct open times (Laver et al. 1995; Zahradníková and Zahradník 1995; Armisén et al. 1996; Laver and Lamb 1998). Third, Schiefer et al. 1995 estimated a P_o of 0.2 at 0.3 μM Ca. This is considerably higher than the P_o (<0.05) reported under steady-state conditions (Györke and Fill 1993; Laver et al. 1995), but quite close to the peak P_o (∼0.3) after Ca²⁺ elevation to 0.5 μM Ca²⁺ (Zahradníková et al. 1999a). Lack of refractory behavior at low Ca, the K _d for Ca²⁺ activation, the single open time constant, and the high P_o can all be easily explained evoking the adaptation hypothesis.

In summary, the mechanical solution change studies present clear evidence supporting the existence of inactivation at high Ca²⁺ concentrations (i.e., ≥100 μM). However, these same studies also present data that are consistent with adaptation at low Ca²⁺ concentrations (<10 μM). We believe that the mechanical solution change studies show evidence that inactivation and adaptation coexist. In any event, the dynamics of RyR Ca²⁺ regulation are complex and simple conventional interpretations are likely to be insufficient.

Correlating Single RyR Behavior to Ca²⁺ Release Phenomena in Cells

The identity of the negative control mechanism(s) that counters the inherent positive feedback of CICR in heart has been debated over the last 15 years. Two candidate mechanisms are conventional Ca²⁺-dependent inactivation and adaptation. However, it appears that neither of these mechanisms alone is sufficient to explain the properties of CICR in cells. It is clear that a more comprehensive understanding of the mechanisms that govern intracellular Ca²⁺ release is required.

Fabiato 1985 was the first to propose that Ca²⁺-dependent inactivation is the negative control mechanism that regulates CICR in the heart. This proposal was controversial because early patch-clamp studies found no evidence of inactivation of cell-averaged (global) Ca²⁺ release in experiments using a conventional two-pulse protocol. Subsequent patch-clamp studies, using a sustained trigger Ca²⁺ stimulus, showed that SR Ca²⁺ release does, indeed, “turn-off” (Yasui et al. 1994). Interestingly, the “turned-off” Ca²⁺ release could be reactivated by a further increase in the trigger Ca²⁺ stimulus. Other groups have reported such paradoxical behavior in variety of preparations (e.g., Pizarro et al. 1997) and found it to be analogous to quantal or incremental Ca²⁺ release observed from IP₃-sensitive Ca²⁺ stores. This is interesting because the RyR and IP₃-receptor are homologous intracellular Ca²⁺ release channels. Each IP₃ increment of an incremental IP₃ stimulus induces a small transient Ca²⁺ release. The mechanism that turns-off Ca²⁺ release after an incremental IP₃ stimulus is not desensitization because a second incremental IP₃ stimulus could reactivate Ca²⁺ release. This property of IP₃-sensitive Ca²⁺ stores is interesting here for the following two reasons: (1) it is reminiscent of the RyR adaptation phenomenon; and (2) it could be related to the apparent quantal or incremental Ca²⁺ release observed from ryanodine sensitive Ca²⁺ stores (Yasui et al. 1994; Pizarro et al. 1997). The IP₃ literature has focused on two potential explanations of quantal Ca²⁺ release. First, quantal release phenomenon could be generated by Ca²⁺ stores with heterogeneous IP₃ sensitivity, so that each stimulus increment recruits a new segment of the Ca²⁺ store population. Second, a homogenous Ca²⁺ store population could generate quantal release if each release was governed by an adaptation-like phenomenon. The RyR-IP₃R homology, the homogeneity of IP₃ binding affinity, and the existence of RyR adaptation supports the second hypothesis. Therefore, it is possible that much of the complexity of global Ca²⁺ signaling in cells may be attributable to properties of individual Ca²⁺ release channels.

Is this the case for RyR channels in heart cells? One caveat here is that the conditions that produce RyR adaptation in vitro may not exist in vivo. In the heart, the RyR channels operate in local Ca²⁺ microdomains, where even small Ca²⁺ stimuli are thought to elevate local Ca²⁺ concentrations to high levels (Stern 1992). Additionally, RyR channels in vivo operate in essentially all-or-none clusters (Stern 1992), where activation of one activates all. Thus, the small incremental Ca²⁺ stimuli, known to induce RyR adaptation in vitro, may not occur in the local control environment of the cell. A second caveat is that termination of local Ca²⁺ release events in cells is ∼10 times faster than both RyR adaptation (Györke and Fill 1993) and inactivation (Schiefer et al. 1995; Sitsapesan et al. 1995), as defined in bilayers (Györke and Fill 1993; Valdivia et al. 1995). Thus, the impact of RyR adaptation and/or inactivation in the heart is not yet clear.

Recently, Sham et al. 1998 extended the findings of Yasui et al. 1994 to the local Ca²⁺ release level. Not surprisingly, considering the caveats described above, they found only weak evidence for quantal/adaptive behavior of local Ca²⁺ release units. They activated a subset of local Ca²⁺ release units and applied a second incremental Ca²⁺ stimulus. The second incremental Ca²⁺ stimulus preferentially activated release units that had not been activated by the first stimulus. Their interpretation was that local Ca²⁺ release is terminated by an inactivation-like mechanism, not an adaptation-like process. However, there is one interesting problem here. Intuitively, the initial small, but sustained, Ca²⁺ stimulus should have continued to recruit (i.e., activate/inactivate) additional release units throughout its duration. In contrast, Sham et al. 1998 showed that the sustained Ca²⁺ stimulus activated/inactivated a subset of release units only at the beginning of the Ca²⁺ stimulus. This rather paradoxical behavior was unexplained. It appears as if local release units were sensitive to the rate of Ca²⁺ change during the stimulus and not necessarily stimulus amplitude. Such rate-sensing behavior has been considered a hallmark of quantal Ca²⁺ release behavior (Pizarro et al. 1997). The point is that unconventional behavior is difficult to reconcile with conventional mechanisms. Consequently, the Sham et al. 1998 data clearly illustrate the complexity of local SR Ca²⁺ release regulation more than they identify the mechanism(s) that may underlie it. Interestingly, Callamaras and Parker 2000 recently showed that such rate sensing, or quantal behavior of local Ca²⁺ release events may occur during IP₃-dependent Ca²⁺ signaling in nonmuscle cells.

At this point, there is an insufficient understanding of the mechanisms that regulate local Ca²⁺ signaling in heart. It is becoming clear that none of the candidate negative control mechanisms by themselves is sufficient. In efforts to define the mechanisms that underlie complex Ca²⁺ signaling phenomena in cells, two general themes are developing. The first evolves around defining the extent to which single Ca²⁺ release channel gating mechanisms govern the complexity of local Ca²⁺ release events. We believe that defining RyR modal gating dynamics under relatively simple ionic conditions (i.e., no Mg²⁺ and ATP) is an important first step in this direction. The second evolves around defining how interactions between Ca²⁺ release channels contribute to the complexity of local Ca²⁺ signaling in cells. Recently, Stern et al. 1997 has forwarded a local control model of RyR-mediated Ca²⁺ release that predicts quantal behavior as a collective phenomenon of stochastically interacting RyR channels. This model describes Ca²⁺ release in the well defined spatial RyR geometry in skeletal muscle and, thus, may not fully apply to other less ordered systems. However, it shows that groups of interacting RyR channels can indeed exhibit collective phenomena (i.e., “group dynamics”) that are qualitatively different from those predicted solely from the properties of individual RyR channels.

Concluding Remarks

In this perspective, we attempt to forward the concept that there will be no simple answers to the complex questions concerning RyR-mediated Ca²⁺ signaling in the heart. An emphasis on reconciling and/or unifying apparently contradictory data sets is clearly the path that will advance knowledge. In this context, we believe there has been substantial progress. We suggest that Ca²⁺-dependent modal gating may be the mechanism that underlies the complex dynamics of single RyR channel Ca²⁺ regulation, and we have presented a specific kinetic modal gating scheme that reconciles a large body of apparently contradictory results. This scheme suggests that RyR adaptation and inactivation are two distinct manifestations of the same underlying mechanism (i.e., modal gating).

Table 1.

Modal Gating Scheme Rate Constants

Transition	Value	Units	Transition	Value	Units
C1-C2	0.5	mM−1ms−1	C2-C1	1	ms−1
C2-C3	0.8	mM−1ms−1	C3-C2	0.525	ms−1
C3-C4	0.8	mM−1ms−1	C4-C3	0.2	ms−1
C4-O1	0.8	mM−1ms−1	O1-C4	0.25	ms−1
O1-C5	0.0025	ms−1	C5-O1	0.01	μM−1ms−1
C5-C6	0.5	ms−1	C6-C5	0.01	ms−1
C5-O2	1	ms−1	O2-C5	2	ms−1
O2-C4	0.001	ms−1	C4-O2	0.001	ms−1
O1-I	0.00001	μM−1ms−1	I-O1	0.001	ms−1