Interaction between Quaternary Ammonium Ions in the Pore of Potassium Channels

Abstract

We have examined the interaction between internal and external ions in the pore of potassium channels. We found that external tetraethylammonium was able to antagonize block of Shaker channels by internal TEA when the external and internal solutions contained K⁺ ions. This antagonism was absent in solutions with Rb⁺ as the only permeant ion. An externally applied trivalent TEA analogue, gallamine, was less effective than the monovalent TEA in inhibiting block by internal TEA. In addition, block by external TEA was little affected by changes in the concentration of internal K⁺ ions, but was increased by the presence of internal Na⁺ ions in the pore. These results demonstrate that external and internal TEA ions, likely located at opposite ends of the pore selectivity filter, do not experience a mutual electrostatic repulsion. We found that these results can be simulated by a simple 4-barrier-3-site permeation model in which ions compete for available binding sites without long-range electrostatic interactions.

INTRODUCTION

Ion channels have a variety of physiological roles that depend critically on their ability to allow only certain types of ions to rapidly pass through the pore in these proteins. High selectivity implies an intimate interaction between the ion and the pore and may have an adverse effect on ion flux.

It is often considered that electrostatic ion repulsion in multi-ion channel pores is a key element for overcoming the tight binding implied by high selectivity. First proposed for Ca channels (Almers and McClesky 1984; Hess and Tsien 1984), this idea has recently been brought into sharp focus by the 3.2-Å resolution crystal structure of a bacterial K channel (KcsA; Doyle et al. 1998). A Rb⁺ Fourier difference map indicates occupancy of the pore in this channel by three ions. Two of these are within ∼7.5 Å of each other, at the ends of the selectivity filter formed by the highly conserved amino acid sequence in the channel P region. Even though Rb⁺, not K⁺, ions were located, K⁺ ions may occupy similar sites since Rb⁺ and K⁺ share much physical similarity and have generally similar permeation properties. Doyle et al. 1998 conclude: “two K⁺ ions at close proximity in the selectivity filter repel each other. The repulsion overcomes the otherwise strong interaction between ion and protein and allows rapid conduction in the setting of high selectivity.”

The current view of a through-space interaction in K channels comes, in part, from experiments in which K⁺ ions on one side of the membrane antagonize positively charged blocking molecules applied to the other. These blocking molecules include (among others) the cations tetraethylammonium (Armstrong 1971), Ba²⁺ (Neyton and Miller 1988a,Neyton and Miller 1988b), and the scorpion toxin charybdotoxin (MacKinnon and Miller 1988; Park and Miller 1992). The ability of K⁺ ions to enhance the off rate of some blocking ions (e.g., Yellen 1984b; Neyton and Miller 1988b) appears to be especially compelling evidence for a repulsive interactions between these two ions.

While these results are consistent with a through-space electrostatic interaction between a K⁺ ion at one site and the blocking ion at another, they do not establish this mechanism. In these types of experiments, the permeant K⁺ ion could entirely cross the pore and bind at (or extremely close to) the blocking site. In fact, in many cases only permeant ions can antagonize blocking molecules (e.g., Yellen 1984b; MacKinnon and Miller 1988; Neyton and Miller 1988b). Thus, experiments showing internal permeant ion inhibition of block by external ions, while quite valuable for other reasons, do not demonstrate a through-space electrostatic repulsion across any reasonable distance in the pore.

The interaction between impermeant ions may represent a better test for direct electrostatic repulsion. Newland et al. 1992 found that TEA applied to one side of a K channel inhibited block by TEA applied to the other. Since TEA cannot pass all the way through the pore, this result shows that the antagonism cannot be by mutually exclusive binding to the same site. Modification of residues near the inner end of the selectivity filter (e.g., M440 and T441 in Shaker channels) strongly affect internal TEA block (Yellen et al. 1991; Choi et al. 1993) and modifications of residues just outside the selectivity filter (e.g., Shaker T449) affect external TEA block (MacKinnon and Yellen 1990; Kavanaugh et al. 1991; Heginbotham and MacKinnon 1992). Thus, if the antagonism between external and internal TEA ions, likely located close to each end of the selectivity filter, experience an electrostatic repulsion, then K⁺ ions at opposite ends of the selectivity filter would also be mutually repulsive.

There are several possible tests of the through-space electrostatic repulsion mechanism for the antagonism between internal and external TEA ions. (a) The antagonism would be quantitatively mutual. That is, internal TEA would antagonize external TEA block by the same amount that external TEA antagonizes block by internal TEA. (b) If the antagonism between TEA ions is electrostatic in nature, it cannot depend on the identity of the permeant ion. And (c) a multivalent TEA analogue should produce larger antagonism than monovalent TEA.

The study of Newland et al. 1992 included the data for the first test listed above. They found that while the antagonism between internal and external TEA was qualitatively mutual, external TEA was more effective at inhibiting block by internal TEA than internal TEA was in antagonizing block by external TEA. An electrostatic mechanism for the antagonism between these blocking ions is not consistent with this result.

We have further examined the issue of antagonism between TEA ions in K channels. We made two experimental tests of the electrostatic mechanism. We found that the antagonism between external and internal TEA ions, present in K⁺-containing solutions, was absent when the K⁺ ions were replaced by Rb⁺. We found that an externally applied trivalent TEA analogue, gallamine, was less, not more, effective at inhibiting block by internal TEA. In addition, we found, in contrast to the report by Newland et al. 1992, that internal K⁺ ions did not inhibit block by external TEA. In an effort to resolve this discrepancy, we found that occupancy of the pore by internal Na⁺ ions increased block by external TEA—a result opposite to the expectation of the electrostatic mechanism.

Our results support the notion that the apparent interaction between external and internal TEA ions is not electrostatic in nature, but depends on the ionic conditions. We tested the possibility that the apparent antagonism between TEA might result from competition for occupancy of a limited number of sites in the pore. A very simple form of a 4-barrier-3-site permeation model was able to reproduce our results. Thus, we conclude that the apparent antagonism between internal and external TEA ions observed in K⁺ but not Rb⁺ solutions is not electrostatic in nature and is consistent with a competition between ions for sites in the pore.

METHODS

K Channel Constructs

Most of the experiments reported here were done on the inactivation-deletion version of Shaker B, ShB Δ6-46 (Hoshi et al. 1990). Some data were also obtained with the T449Y mutation that increases external TEA affinity (MacKinnon and Yellen 1990).

Oocyte Isolation and Microinjection

Frogs, Xenopus laevis, were maintained as described by Goldin 1992. Isolated ovarian lobes were rinsed with Ca-free OR-2 solution (82.5 mM NaCl, 2.5 mM KCl, 1 mM MgCl, and 5 mM HEPES, pH 7.6 with NaOH), and then defolliculated by incubation for 60–90 min with 2 mg/ml collagenase Type IA (Sigma-Aldrich). Cleaned oocytes were transferred and maintained for 2 h in ND-96 solution (96 mM NaCl, 2 mM KCl, 1.8 mM CaCl, 1 mM MgCl, 5 mM HEPES, and 2.5 mM Na-pyruvate, pH 7.6 with NaOH) before injection of RNA coding for the channel of interest. Injected oocytes were transferred to multi-well tissue culture plates and incubated at 18°C in ND-96 solution supplemented with 100 U/ml penicillin and 100 μg/ml streptomycin.

Electrophysiological Recordings

Potassium channel currents were assayed electrophysiologically 1–5 d after RNA injection. Electrophysiological recordings were done at room temperature (20–22°C) with excised inside/out or outside/out macropatches using an Axopatch 1-D amplifier (Axon Instruments, Inc.). Three types of glass were used in these experiments. Most of the data were obtained with Corning 7052 glass (Garner Glass Co.) with tip diameters of ∼2–4 μm. Some data were obtained with GC-150F glass (Warner Instrument Corp.), also with 2–4-μm openings. We also used fused quartz (Garner Glass Co.) fabricated with a laser puller (P-2000; Sutter Instrument Co.) to tip diameters of 1–3 μm. The measured junction potentials for the solutions used were all within 4 mV of one another, and so no correction for these was applied. The holding potential was −70 mV. Data acquisition was performed using a 12-bit analogue/digital converter controlled by a personal computer. Current records were usually filtered at 5 kHz.

The standard external solution contained (mM): 5 KCl, 135 NMDG-Cl, 2 CaCl₂, 2 MgCl₂, 10 mM HEPES, pH 7.2 (with NMDG). Gallamine triethiode (Sigma-Aldrich) up to 5 mM was added to this solution. TEA was included in this solution by equimolar replacement of NMDG. The standard internal solution consisted of (mM): 110 KCl, 25 KOH, 10 EGTA, 10 HEPES, pH 7.2 with HCl. We also used similar solutions but with K⁺ replaced by Rb⁺. TEA, up to 5 mM, was added to the internal solution as required. Na⁺-free internal solutions of different K⁺ concentrations were made by an equimolar replacement of K⁺ by NMDG in the standard internal solution. Solutions with different Na⁺ concentrations were made from a solution of 20 mM K⁺ and 115 NMDG by equimolar replacement of NMDG. We also used a solution with nominally zero external K⁺ concentration: flame photometry analysis showed that this solution contained <5 μM potassium.

Data Analysis

As described in results, several different equations were fit to the data. These were done using the Simplex algorithm (Caceci and Cacheris 1984), either in our own implementation or that incorporated in the Origin software package (version 5.0; Microcal Software Inc.). When given, error limits for the fitted parameters are the estimated errors from the fitting routines.

Permeation Model Simulations

We used a 4-barrier-3-site permeation model to simulate our results. In this model, the ions are considered to move from site to site by overcoming an intervening energy barrier. We used a three-site model since there are at least this number of ions in the pore (Doyle et al. 1998; Stampe et al. 1998). Eyring 1935 described the rate for an ion crossing a permeation barrier as:

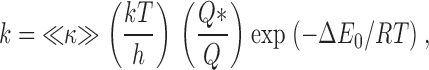where k, T, and h are Boltzmann's constant, the absolute temperature, and Planck's constant, respectively. Q and Q* are the partition functions for the ion at the energy minimum and near the peak of the energy barrier, respectively. The parameter ≪κ≫has been described as “an ad hoc fudge factor (transmission coefficient)” (Hanggi et al. 1990); it is the average likelihood for the ion to successfully cross the energy barrier.

Considerable effort has gone into computing the pre-exponential component of this equation appropriate for ion permeation through membrane ion channels. This computation is quite complex, especially in aqueous solutions. Moreover, the KscA structure shows that the prefactor may be different for different steps in the permeation processes. For example, the ion is at least partially hydrated in the external solution just outside the narrow selectivity filter and in the relatively large “cavity” at the inner side of the selectivity filter. Thus, these steps will likely require a prefactor appropriate for aqueous solutions that will include the ion translocation and dehydration processes. In contrast to bulk aqueous solutions, there are very few water molecules associated with the ions in the selectivity filter and the ions are likely interacting strongly with the pore lining, and so permeation steps in the selectivity may require a different prefactor.

There are several derivations of the form that the prefactor may take. The simplest of these is just kT/h (Glasstone et al. 1941), which has the value 5.8 × 10¹² s⁻¹. As discussed in Nonner et al. 1999, Kramers 1940 showed that the prefactor for a monovalent ion crossing a large, parabolic barrier of length l is given by:

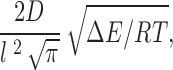where D is the diffusion coefficient for the ion which is 2 × 10⁻⁵ cm²/s for K⁺ ions. Ions in solution have a mean free path on the order of 0.1 Å. However, the “jump,” for example, from the external aqueous solution to the first site in the selectivity filter will not be the same as for the translocation of the ion in aqueous solution as the former certainly requires considerable dehydration. If this occurs over a distance of, say, 1 Å, for a 10-RT barrier, then the Kramer prefactor would be ∼7 × 10¹¹ s⁻¹.

Hill 1975 also grappled with computing the prefactor in aqueous solutions and determined it should have the form:

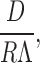where D is the diffusion coefficient and R represents a “capture distance.” Λ is the thermal de Broglie wavelength given by:

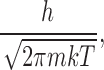where m is the mass of the ion. For K⁺ ions and an arbitrary (but reasonable) capture distance of 2.5 Å, the Hill prefactor is ∼5 × 10¹¹ s⁻¹.

Andersen 1989 provides another derivation of a prefactor that may be appropriate for aqueous conditions:

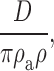where ρ_a and ρ define the shape of parabolic energy minimum and maximum: the distance over which the energy level changes by 1 RT. If these distances are each 0.5 Å, then the Andersen prefactor is near 2.5 × 10¹¹ s⁻¹.

The latter three calculations produced quite similar prefactor values of 2.5–7 × 10¹¹ s⁻¹, about an order of magnitude smaller than the 5.8 × 10¹² s⁻¹ value of kT/h. We used the permeation model to simulate block by external and internal TEA ions, a computation that requires only ratios of the simulated currents. Thus, our simulations (see Fig. 11) are independent of the precise value of the prefactor. Nevertheless, we used a prefactor value of 3 × 10¹¹ s⁻¹, which, according to the calculations above, is a reasonable value for permeation steps from aqueous solutions into the pore selectivity filter. For simplicity, we used this same prefactor for all rate constants in our simulations of the three-site permeation model.

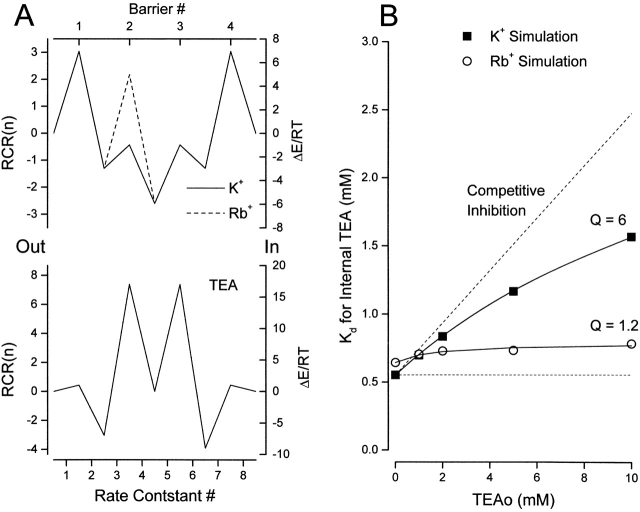
Figure 11.

Simulation of apparent antagonism between external and internal TEA. (A, left ordinate) Rate constant representation (RCR, see methods) for (top) K⁺ (solid line) and Rb⁺ (dashed line) permeation of the model pore and for TEA block of the pore (bottom). (Right ordinate) Transition energies for the model using a frequency factor of 3 × 10¹¹ s⁻¹. The barrier heights would be three RT larger if the Eyring frequency factor (5.8 × 10¹²) were used. See text for details. The external solution is on the left side of the energy profiles. (B) Simulation of the apparent K _d for block by internal TEA as a function of the external TEA concentration with the K⁺ and Rb⁺ rate constants from A. Solid lines are fits of with the indicated values of Q for simulations with K⁺ (▪) and Rb⁺ (○) rate constants. In these simulations, external and internal ion concentrations were 10 and 150 mM, respectively. The size of the simulated current at 0 mV with the K⁺ ion rate constants was near 1 pA.

Andersen 1999 proposed that the properties of these types of models be expressed graphically with a reduced rate constant representation (RCR):

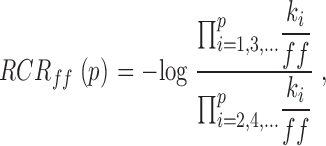where p is the total number of rate constants in the model, k_iis the rate constant for the i ^th step (forward rate constants are odd numbers, reverse rate constants are even), and ff is the prefactor used. We used this formalism for presentation of the model parameters in Fig. 11.

Mathematical details for a two-site version of this model can be found in Begenisich and Cahalan 1980 and some of the general properties of the three-site version are described in Begenisich and Smith 1984. Most of the calculations were done with our own implementation of the model, but ion occupancy probabilities were obtained from software written by Thieu Dang, provided by Edwin McCleskey (Vollum Institute, Oregon Health Sciences University).

RESULTS

TEA Antagonism in Shaker K Channels

The most extensive analysis of the antagonism between internal and external TEA was done with RBK1 (rKv1.1) channels (Newland et al. 1992). However, Newland et al. 1992 also demonstrated an antagonism between TEA in Shaker channels. An example of this type of experiment is illustrated in Fig. 1.

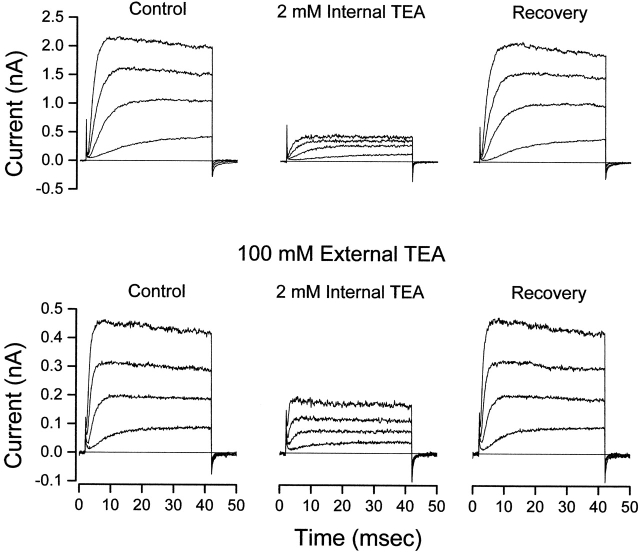
Figure 1.

Internal TEA is less effective in the presence of external TEA. (Top) Shaker channel currents at several voltages before, during, and after recovery from application of 2 mM internal TEA with no TEA in the external solution. (Bottom) Currents from another patch before, during, and after recovery from application of 2 mM internal TEA with 100 mM TEA in the external solution. Currents elicited with 40-ms steps to voltages of −30, −10, +10, and +30 mV.

Fig. 1 (top) contains Shaker channel currents at several potentials before, during, and after application of 2 mM internal TEA. In the absence of external TEA, internal TEA substantially blocked the channel. Fig. 1 (bottom) shows that this concentration of internal TEA was much less effective if applied in the presence of 100 mM external TEA.

Fig. 2 summarizes the results of many similar experiments. Shown is the fraction of current at a membrane potential of 0 mV that was blocked by the indicated concentration of internal TEA in the absence (▪) and presence (○) of 100 mM external TEA. The data are consistent with the binding of a single TEA ion to the channel that results in block of the channel:

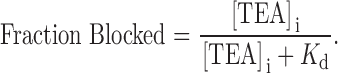1

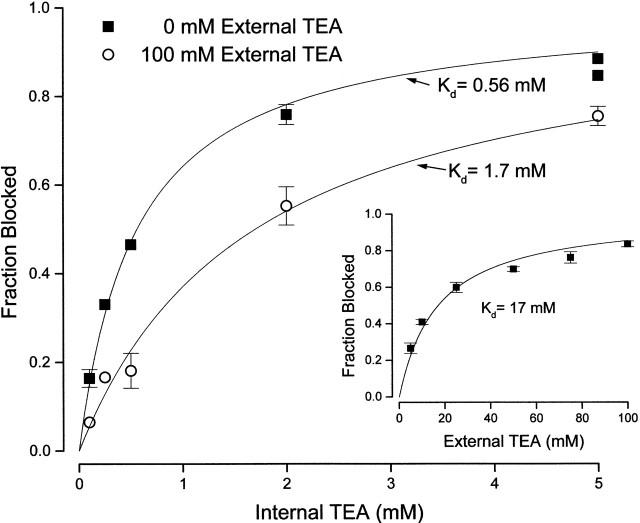
Figure 2.

Channel block by internal TEA in the absence and presence of external TEA. Fraction block of Shaker channel current at the indicated internal TEA concentrations in the absence (▪) and presence (○) of 100 mM external TEA. Currents measured at 0 mV. (Solid lines) Fits of to the data with the indicated dissociation constants. Mean values of three measurements except at 5 mM TEA_i in the absence of TEA_o (two observations) and single measurements at 0.1 and 0.25 mM TEA_i at 100 mM TEA_o. For remaining data, standard error bars are omitted if smaller than symbol. (Inset) Channel block by external TEA. Block of Shaker current at a potential of 0 mV at the indicated concentrations of external TEA. Mean values from four to five measurements with SEM limits. (Line) Best fit of to the data with the indicated dissociation constant.

The lines in Fig. 2 are best fits of to the data. In the absence of external TEA, internal TEA blocked the channels with a K _d value of 0.56 mM, similar to the value of 0.7 mM of Yellen et al. 1991. In the presence of 100 mM external TEA, internal TEA still blocked the channels as described by , but with a reduced affinity indicated by the larger K _d value of 1.7 mM. That is, the presence of external TEA apparently reduced the affinity of the channel for internal TEA.

With both external and internal TEA present, there are four possible states of the channel: unblocked channels, channels blocked by internal TEA, channels blocked by external TEA, and channels occupied by both external and internal TEA. To quantitatively evaluate the interaction between the TEA ions, consider the following:

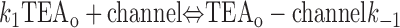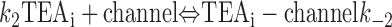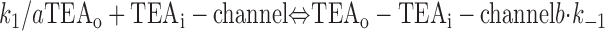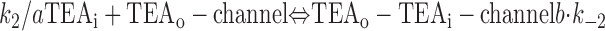The first two lines represent the interaction of external and internal TEA, respectively, in the absence of any TEA on the opposite side of the channel. In the third line, external TEA binds to a channel with internal TEA already occupying the internal binding site. With internal TEA present, the on rate for external TEA (k ₁) is reduced by a factor a and the off rate (k ₋₁) increased by a factor b. For electrostatic repulsion between the TEA ions, these two factors would be the same but, in general, need not be. The interaction of internal TEA with a channel already occupied by external TEA is likewise modified, as shown in the last line.

With this scheme, the apparent binding constant for internal TEA will be a function of the concentration of external TEA:

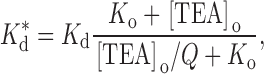2

where K _d is the binding constant in the absence of external TEA and K _o (= k ₋₁/k ₁) is the affinity of external TEA for its binding site (in the absence of internal TEA). With Q = a · b, this is the form of the equations used by Newland et al. 1992. The parameter Q, then, is a measure of the magnitude of the interaction between internal and external TEA. A value of one represents no interaction; an infinite value yields the well-known expression for mutually exclusive competitive inhibitors:

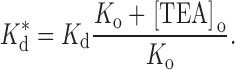3

Thus, the parameter Q in can be used to provide a quantitative measure of the ability of external TEA to reduce the effectiveness of internal TEA in blocking the channel. To extract this parameter, the binding affinity of external TEA (K _o) is required. This is obtained from the concentration dependence of block of the channels by external TEA, as illustrated in Fig. 2, inset. The data are well described by with a binding affinity of 17 mM.

The apparent dissociation constants for internal TEA block at 0 and 100 mM external TEA obtained from the data in Fig. 2 are shown in Fig. 3 with additional values obtained at 25 and 50 mM external TEA. The data are well described by (with K _o = 17 mM) with an interaction parameter Q of 4.6. This is similar to the value of 5.3 that Newland et al. 1992 obtained for RBK1 channels, which are almost 100-fold more sensitive to external TEA than are Shaker channels.

Figure 3.

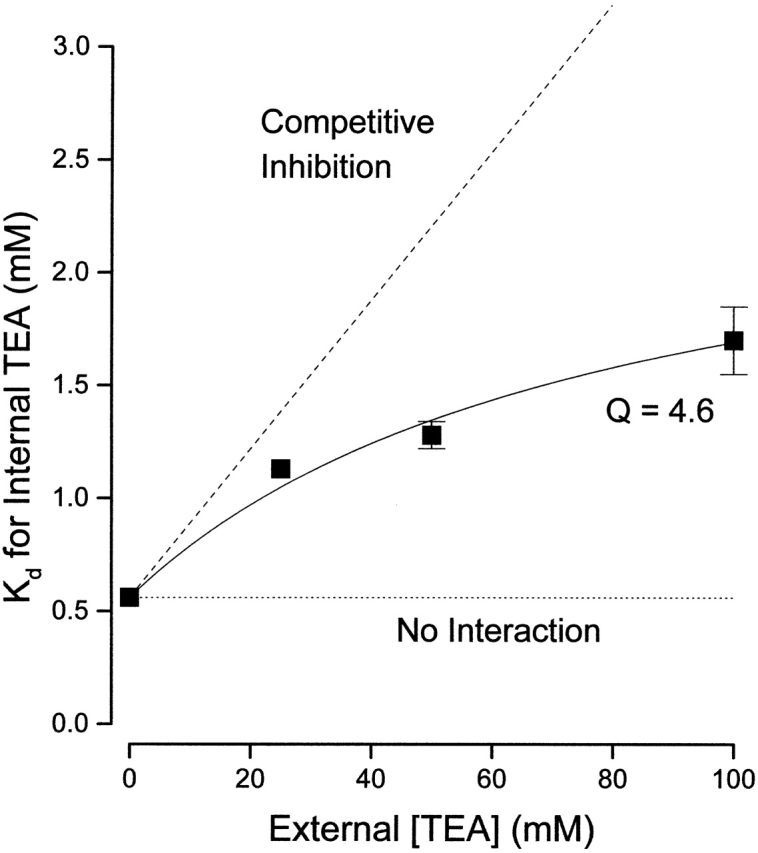
Interaction between external and internal TEA. Ordinate is the apparent dissociation constant for block by internal TEA at the indicated concentrations of external TEA. Error limits illustrated (when larger than symbol) are the estimated errors from the fitting routine (see methods). The dotted line is the expectation for no interaction between internal and external TEA. The dashed line is the expectation for competitive inhibition (). Solid line is the best fit of to the data with a value of Q of 4.6.

We also tested the antagonism between external and internal TEA ions with the wild-type threonine at position 449 replaced with a tyrosine, the amino acid in native RBK1 channels, that produces a high affinity TEA receptor in Shaker channels. We found that 2 mM internal TEA (in the absence of external TEA) blocked 77 ± 0.4% (n = 4) of the current. This is equivalent to an apparent K _d value of 0.62 mM, quite similar to the value for wild-type channels (Fig. 2). In the presence of 1 mM external TEA, this concentration of internal TEA only blocked 64 ± 7% (n = 3) of the current, equivalent to a K _d value of 1.4 mM. We determined that the K _d value of the T449Y channels for external TEA was ∼0.43 mM (data not shown), very similar to the 0.59 mM value reported by MacKinnon and Yellen 1990. An analysis of these data in terms of revealed a value of Q of 5.2 for T449Y Shaker channels, similar to the value (4.6) for wild-type channels (Fig. 3), and nearly identical to the value of 5.3 for RBK1 channels (Newland et al. 1992). Thus, the apparent interaction between TEA ions appears independent of the affinity of the channel for external TEA.

TEA Antagonism in Shaker K Channels in Rb⁺ Solutions

If the ability of external TEA to antagonize the effectiveness of internal TEA is due to a through-space electrostatic repulsion between these ions, then the antagonism should be independent of which permeant ion is used to carry current. However, as illustrated in Fig. 4, the antagonism between external and internal TEA present with K⁺-containing solutions was absent in solutions in which Rb⁺ replaced K⁺.

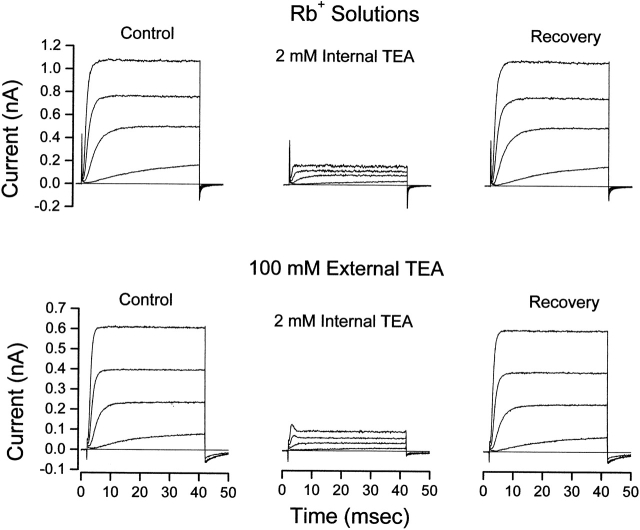
Figure 4.

Lack of interaction between internal and external TEA in the presence of Rb⁺ ions. (Top) Shaker channel currents at several voltages before, during, and after recovery from application of 2 mM internal TEA with no TEA in the external solution. (Bottom) Currents from another patch before, during, and after recovery from application of 2 mM internal TEA with 100 mM TEA in the external solution. Currents elicited with 40-ms steps to voltages of −30, −10, +10, and +30 mV. Currents measured in K⁺-free, Rb⁺ solutions as described in methods.

Shown in Fig. 4 (top) are channel currents in Rb⁺ solutions at several potentials before, during, and after recovery from application of 2 mM internal TEA. As with solutions containing K⁺ as the permeant ion, this concentration of internal TEA inhibited a substantial amount of channel current. Fig. 4 (bottom) shows that, in contrast to the results with K⁺ as the permeant ion, external TEA did not protect from block by internal TEA with Rb⁺ as the permeant ion.

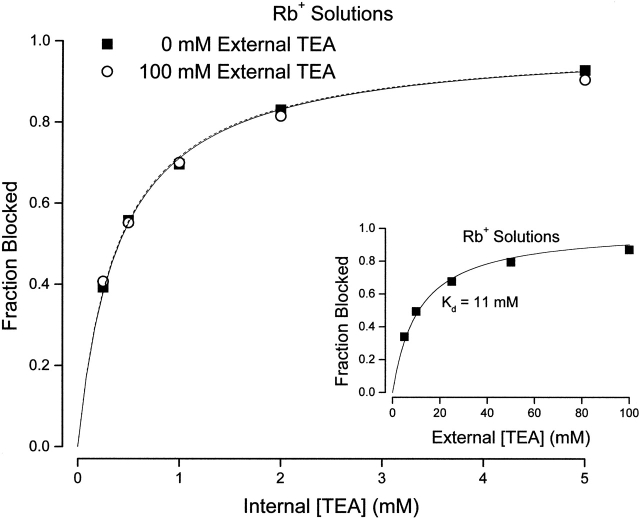
Fig. 5 summarizes the results of many similar experiments. Shown is the fraction of current at a membrane potential of 0 mV that was blocked by the indicated concentration of internal TEA in the absence (▪) and presence (○) of 100 mM external TEA. Both sets of data are well described by (lines) with apparent K _d values of 0.4 and 0.41 in the absence and presence of 100 mM TEA, respectively. That is, with Rb⁺ as the permeant ion, external TEA was entirely ineffective in protecting the channels from block by internal TEA.

Figure 5.

Channel block by internal TEA in the absence and presence of external TEA in Rb⁺ solutions. Fraction block of Shaker channel current by the indicated internal TEA concentrations in the absence (▪) and presence (○) of 100 mM external TEA. Currents measured at 0 mV. (Dotted line) Fit of to the data in the absence of external TEA with a K _d value of 0.4 mM. (Solid line) Fit of to the data in the presence of 100 mM external TEA with a K _d value of 0.41 mM. Mean values of three to four measurements. All standard error limits were smaller than the symbols. (Inset) Channel block by external TEA in the presence of Rb⁺ ions. Block of Shaker current at a potential of 0 mV at the indicated concentrations of external TEA. Mean values from three to four measurements. All standard error limits were smaller than the symbols. (Line) Best fit of to the data with the indicated dissociation constant.

The inability of external TEA to protect the channels from internal TEA block in the presence of Rb⁺ could occur if external TEA did not bind to the channel. The data in Fig. 5 (inset), however, show that, if anything, external TEA had a greater affinity for the channel in Rb⁺ solutions. The data are best fit by , with a K _d value of 11 mM that is somewhat smaller than the value of 17 mM obtained in the presence of K⁺ ions (Fig. 2).

Apparent K _d values, obtained in Rb⁺ solutions, for block by internal TEA as a function of external TEA are illustrated in Fig. 6 (○), along with the comparable data in K⁺ solutions from Fig. 3 (▪). In contrast to the results in K⁺ solution, with Rb as the permeant ion, block of Shaker channels by internal TEA was independent of external TEA. The data in Rb⁺ solutions are consistent with a constant K _d value of 0.4 mM (and a value of Q = 1). Thus, the apparent interaction between external and internal TEA depends on the identity of the permeant ion and so is not likely to be mediated by a through-space electrostatic repulsion mechanism.

Figure 6.

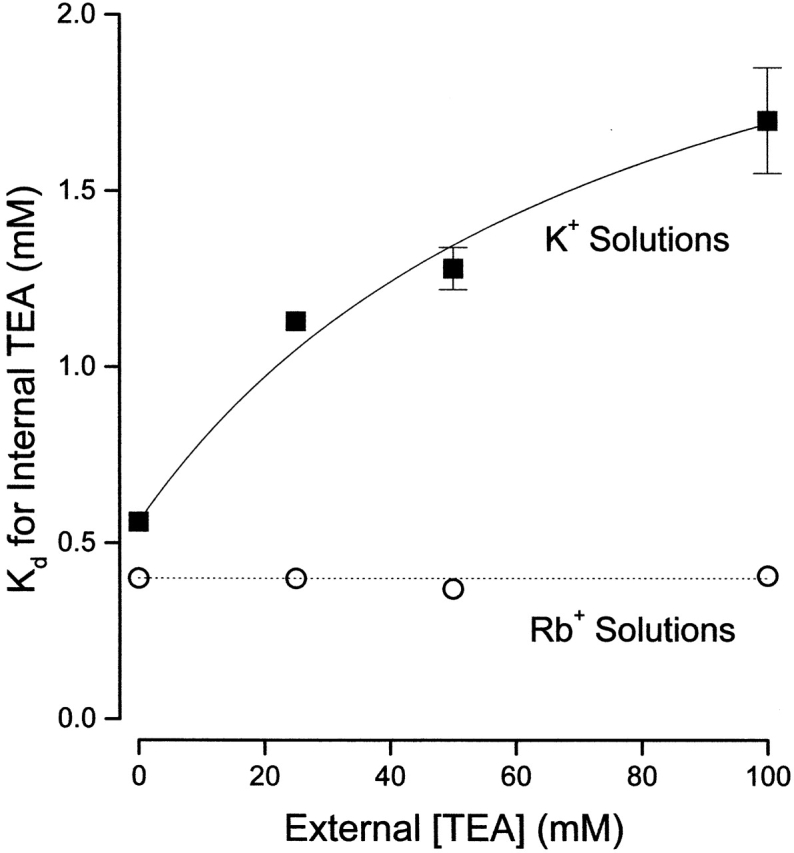
Lack of interaction between external and internal TEA in the presence of Rb⁺ ions. Ordinate is the apparent dissociation constant for block by internal TEA at the indicated concentrations of external TEA in K⁺ (▪, from Fig. 3) and Rb⁺ (○) solutions. Error limits illustrated (when larger than symbol) are the estimated errors from the fitting routine (see methods). Solid line from Fig. 3. Dotted line represents a constant apparent K _d value of 0.4 mM.

Antagonism between Multivalent TEA Ions

We made another test of the electrostatic mechanism for the interaction between TEA ions in K⁺ solutions. If the antagonism between these ions is electrostatic in nature, it will be much stronger between internal TEA and an external multivalent TEA analogue. It is possible to quantitatively predict the magnitude of this increased interaction by determining the expected value of the interaction parameter, Q. The value of Q for interaction of an external TEA analogue of valence z Q _z compared with the value of monovalent TEA (Q ₁) is given by (see ) Q _z = Q ^z ₁.

Since, from Fig. 3, Q ₁ is 4.6, the value of Q for the electrostatic interaction between internal TEA and external divalent and trivalent TEA analogues is expected to be 4.6² (21) and 4.6³ (97), respectively.

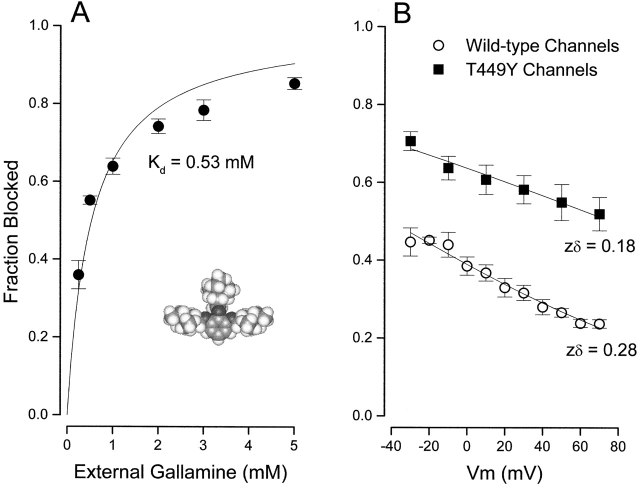
The neuromuscular blocking agent, gallamine, (Fig. 7 A, inset) contains three tetraethylammonium groups connected by ether oxygen linkages to a benzene ring. The data in Fig. 7 A shows that this compound blocked Shaker K channels with an affinity (0.53 mM) substantially higher than that of TEA (17 mM, Fig. 2). We determined the voltage dependence of block of wild-type channels by 0.25 mM external gallamine (Fig. 7 B, ○). Such data are often analyzed with the Woodhull 1972 equation:

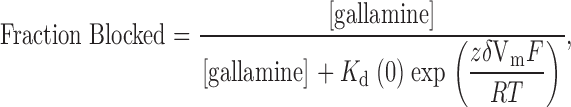4

where K _d(0) represents the affinity of the channel for gallamine at zero membrane voltage, z is the valence (+3), and δ is the location (fraction of the membrane field) where gallamine blocks the channel. There are difficulties in applying this equation to data from multi-ion pores (e.g., Begenisich 1992), but monovalent TEA ions appear to block wild-type Shaker channels with a value of δ near 0.15 (Heginbotham and MacKinnon 1992; Newland et al. 1992). Shaker channels with the T449Y mutation exhibit a much higher affinity for TEA and a smaller “electrical distance” of 0.04 (Heginbotham and MacKinnon 1992).

Figure 7.

External gallamine block of Shaker K channels. (A) Block of Shaker channels (at 0 mV) by the indicated external gallamine concentration. (Solid line) Fit of to the data with the indicated value of the dissociation constant. Mean and SEM limits from three to five measurements, except as indicated. (Inset) Space-filling model of gallamine. (B) Voltage dependence of channel block by external gallamine. Block of wild-type (○) and T449Y (▪) channels by 0.25 mM external gallamine at the indicated membrane voltages. Lines are fits of to these data with the indicated values of zδ.

The analysis of the data in Fig. 7 B shows that gallamine blocked wild-type Shaker channels with an apparent value of zδ of 0.28, equivalent to two of the three charges located at the same electrical distance as monovalent TEA. This same concentration of gallamine was considerably more effective in blocking T449Y channels (▪) and with a reduced voltage sensitivity. Thus, it is likely that gallamine binds at, or very close to, the same external location as TEA, with an effective valence at least twice that of TEA.

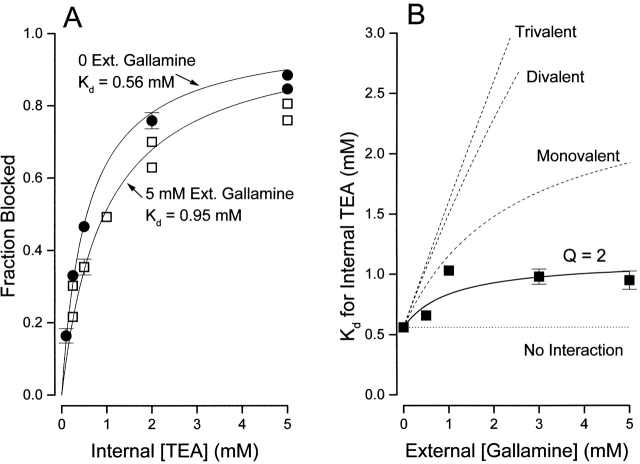
Consequently, gallamine may be considered a suitable multivalent TEA analogue for the test of the electrostatic interaction mechanism. We determined internal TEA block of the channels in the presence of various concentrations of external gallamine. Fig. 8 A shows that 5 mM external gallamine slightly decreased block by internal TEA. The apparent dissociation constant for internal TEA increased from 0.56 mM in the absence to 0.95 mM in the presence of 5 mM external gallamine.

Figure 8.

Interaction between external gallamine and internal TEA. (A) Block of Shaker channels (at 0 mV) by the indicated internal TEA concentrations in the absence (•) and presence (□) of 5 mM external gallamine. Lines are fits of to the data with the indicated K _d values. n = 2–5; duplicate values plotted individually, mean values (n = 3–5) with SEM limits only if larger than symbols. (B) Ordinate is the apparent dissociation constant for block by internal TEA at the indicated concentrations of external gallamine. Error limits illustrated (when larger than symbol) are the estimated errors from the fitting routine (see methods). Solid line is the best fit of to the data with a Q value of 2.0. The dashed lines illustrate the predicted effects of an external trivalent, divalent, and monovalent antagonist (see text for details).

We determined the K _d value for internal TEA block at several concentrations of external gallamine and these are illustrated in Fig. 8 B. The data are best fit by with a value of the interaction parameter, Q, of 2. Gallamine blocked the channels as if two of its three charges were at the external TEA site. Thus, an electrostatic interaction would predict a value of Q of 21 (see above). Shown in Fig. 8 B are the predictions (dashed lines) for internal TEA interactions with trivalent (Q = 97), divalent (Q = 21), and monovalent (Q = 4.6) charges. Thus, external gallamine interacted with internal TEA much less than predicted for a divalent interaction and even less than monovalent external TEA. This result and the lack of interaction of TEA ions in the presence of Rb⁺ argue against a through-space, electrostatic repulsion between quaternary ammonium ions in the pore of the Shaker K channel.

Interaction between Internal Ions and External TEA

As noted in the introduction, the observed reduction in RBK1 channel block by external TEA with elevated internal K⁺ ions (Newland et al. 1992) is consistent with an electrostatic repulsion between these two ions. We have examined external TEA block of Shaker channels with different concentrations of internal K⁺ and some of these results are illustrated in Fig. 9.

Figure 9.

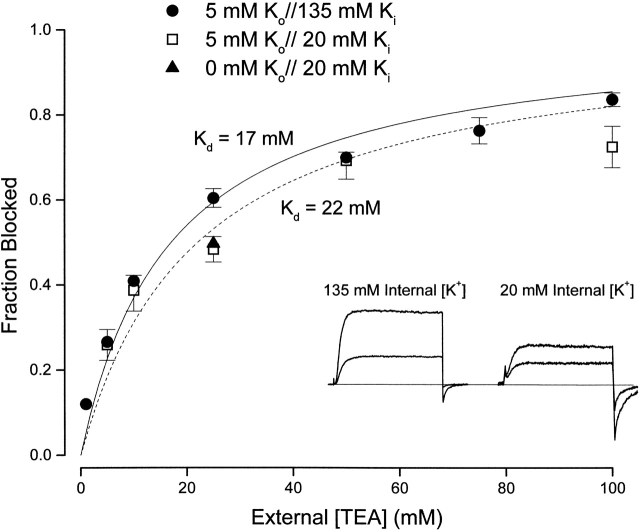
Interaction between external TEA and internal K⁺ ions. (Inset) Currents (at 0 mV) recorded with 135 mM (left) and 20 mM (right) internal K⁺ in the absence (larger current) and presence of 25 mM external TEA. (Main figure) Channel block (at 0 mV) at the indicated concentrations of external TEA in 135 mM (•) and 20 mM (□) internal K⁺. Block by 25 mM TEA was measured (▴) with 20 mM internal K⁺ and a nominally 0 K⁺ external solution (see methods).

Fig. 9 (inset) contains Shaker channel currents recorded in 135 (left) and 20 (right) mM internal K⁺. Currents in the absence (larger) and presence of 25 mM external TEA are illustrated. In contrast to the results of Newland et al. 1992, block by external TEA appears, if anything, to be larger with elevated internal K⁺. This view is supported by data in Fig. 9 showing channel block as a function of external TEA concentration with 135 (•) and 20 (□) mM internal K⁺. The apparent K _d value for external TEA block in 135 and 20 mM internal K⁺ was 17 ± 1 and 22 ± 2.8 mM, respectively. From additional, similar data (not shown), we determined that channel block with 50 mM internal K⁺ was consistent with an apparent K _d value of 17.6 ± 2.7 mM. Removal of external K⁺ (see methods) with 20 mM internal K⁺ had little or no effect on block by 25 mM external TEA (Fig. 9, ▴).

Thus, an almost sevenfold change in internal K⁺ and removal of external K had little effect on block of Shaker channels by external TEA. If anything, we found slightly more block in solutions with elevated internal K⁺. This result is in contrast to that of Newland et al. 1992; however, the two experimental conditions differed. In their experiments, Newland et al. 1992 used Na⁺ as a K⁺ replacement, while we used NMDG. Thus, in their low K⁺ solutions, there would be a considerable amount of Na⁺. Therefore, one possible explanation for the different results is that internal Na⁺ ions increase the effectiveness of external TEA. We tested this hypothesis as illustrated in Fig. 10.

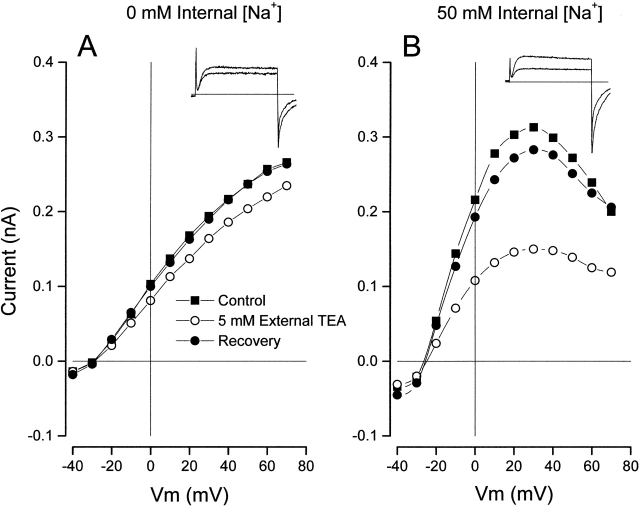
Figure 10.

Internal Na⁺ ions and block by external TEA. (Left) Inset shows Shaker currents (at 0 mV) recorded in the absence (larger) and presence of 5 mM external TEA with an internal solution without Na⁺ ions. The main figure shows the Shaker channel current–voltage relation recorded before (▪), during (○), and after (•) recovery from application of 5 mM external TEA. Internal solution with 20 mM K⁺ and NMDG (see methods). (Right) Same as left, but data was recorded in the presence of 50 mM internal Na⁺ ions (and 20 mM K⁺).

Fig. 10 A contains data obtained with 20 mM internal K⁺ in the absence of Na⁺, and B contains data obtained with 20 mM K⁺ and 50 mM Na⁺. The insets show currents measured in the absence (larger) and presence of 5 mM external TEA. With no internal Na⁺, this concentration of TEA produces only a small block of the current, consistent with the results shown in Fig. 9. This same concentration of TEA, however, blocked a substantial amount of current with 50 mM internal Na⁺. The current–voltage relations in these conditions are also illustrated before (▪), during (○), and after recovery from (•) application of 5 mM TEA. The decline of current at large positive potentials in the presence of Na⁺ is due to a voltage-dependent channel block by this ion, a behavior common to many types of K channels (e.g., Bergman 1970; Bezanilla and Armstrong 1972; French and Wells 1977; Yellen 1984a).

From other experiments like those illustrated in Fig. 10, we determined that external TEA blocked Shaker channels with an apparent K _d value of 7.5 ± 0.85 mM in 20 mM internal K⁺ and 50 mM Na⁺ (three measurements each at three external TEA concentrations). This is considerably smaller than the value of 22 mM (see above and Fig. 9) obtained in the absence of internal Na⁺ ions. From additional experiments with 115 mM internal Na⁺, we obtained an apparent K _d value for block by external TEA of 7.6 ± 1.2 mM (three measurements each at five internal TEA concentrations), not significantly different from the value with 50 mM internal Na⁺. Thus, the presence of an internal blocking ion (Na⁺) increased the ability of external TEA to block the channels. This is in the opposite direction expected for an electrostatic repulsion between an internal blocking ion (Na⁺) and external TEA. It is also opposite to the action of internal TEA, which inhibits block by external TEA (Newland et al. 1992). The effect of internal Na⁺ is another example, like the lack of TEA antagonism in Rb⁺ solutions, of how the actions of TEA depend on the ionic conditions.

DISCUSSION

The objective of the study described here was to critically examine the evidence supporting through-space electrostatic repulsion between TEA ions in the pore of K channels. Certainly, ions of like charge repel each other, but in the context of multi-ion pores the relevant questions are: (a) Over what distance and over which structures does this occur? (b) How strong is the repulsion? and (c) Does repulsion play an important role in ion selectivity and permeation?

Under some conditions, there appears to be mutual antagonism between internal and external TEA ions (Newland et al. 1992; Immke et al. 1999). Since TEA is an impermeant blocking ion that likely occupies sites at either end of the channel selectivity filter, it was reasonable to suggest that the antagonism is mediated by electrostatic repulsion (Newland et al. 1992). If this is the underlying mechanism, then the antagonism between internal and external TEA should be independent of the identity of the permeant ion. We made this test in Shaker K channels and found that the antagonism, present with K⁺-containing solutions, was entirely absent in solutions with Rb⁺ as the permeant ion.

If the mutual antagonism between internal and external TEA (in K⁺ solutions) is due to electrostatic repulsion between these ions, then multivalent ions should demonstrate a considerably stronger antagonism. We made this test with an external multivalent TEA analogue. Not only was the antagonism with internal TEA not nearly as strong as predicted, it was actually weaker than that produced by monovalent TEA.

This latter result is the opposite expected of an electrostatic mechanism and also argues against another possibility. Perhaps there is electrostatic repulsion between external and internal TEA ions in K⁺ solutions, but this is balanced by some other stabilization energy when K⁺ ions are replaced by Rb⁺. If so, then the threefold stronger repulsion between external gallamine and internal TEA in K⁺ solutions would still be expected to result in an increased antagonism that was not observed.

The apparent antagonism between internal K⁺ ions and external TEA has also been cited as evidence in favor of electrostatic repulsion in the pore of K channels. We found that reducing the concentration of internal K⁺ ions did not allow increased channel block by external TEA unless Na⁺ ions were used as K⁺ replacements. The ability of an internal blocking ion like Na⁺ to increase block by external TEA cannot be explained by an electrostatic repulsion mechanism.

Taken together, our results suggest that internal and external TEA ions in the pore of Shaker K channels do not experience a mutual electrostatic repulsion. If the antagonism observed between external and internal TEA ions in K⁺ solutions is not mediated by electrostatic repulsion, then how does this occur? Spassova and Lu 1999 found that block of ROMK1 channels by intracellular TEA is different in K⁺ and in Rb⁺ solutions, similar to our findings. They suggest that an ion binding at the inner end of the selectivity filter may induce a conformational change and alter ion binding to a more external site. Immke et al. 1999 have recently investigated TEA block of Kv2.1 channels. They found that block of K⁺ currents by external TEA was reduced in the presence of internal TEA, an antagonism between TEA ions in the pore of this channel. Currents through these channels carried by Na⁺ ions (in the absence of K⁺ ions) are very insensitive to block by external or internal TEA. Sensitivity to TEA block is recovered in solutions with small (30–100 μM) concentrations of K⁺. These authors suggest that occupancy of the channel by K⁺ ions alters the pore conformation and so can modulate TEA block.

The common theme in our results and those of Spassova and Lu 1999 and Immke et al. 1999 is that TEA effects are sensitive to the ionic composition of the experimental solutions. In particular, we showed that the TEA antagonism was absent in Rb⁺ solutions and that occupancy of the inner pore by Na⁺ ions increased block by external TEA. Certainly, conformational changes induced by ion binding could alter TEA affinity. However, there is another class of models in which TEA block could be dependent on the ionic conditions. It seems possible that if TEA and other blocking ions (like Na⁺) and permeant ions compete for occupancy of a few available binding sites, then the effects of TEA might depend on the presence of other ions. Therefore, we investigated whether such models could account for our observation of an apparent antagonism between external and internal TEA ions in K⁺ but not Rb⁺ solutions.

Permeation Model Simulations

We used the 4-barrier-3-site model described in methods. We used a profile for K ions with high lateral and low internal barriers, known to be able to simulate all known multi-ion permeation properties (Hille and Schwarz 1978). The middle energy minimum was more negative than the lateral values: a condition known to allow both high affinity for the permeant ion and high flux rates (Dang and McCleskey 1998; Kiss et al. 1998). This pattern also provides high flux ratio values (Stampe et al. 1998).

Our results (and those of Immke et al. 1999; Spassova and Lu 1999) demonstrate that TEA block is sensitive to the ionic conditions. This suggests the possibility that these effects may result from a competition for the availability of limited sites in the pore. For example, TEA occupancy of its external binding site might cause a redistribution of the occupancy of sites in the pore by permeant ions. If internally applied TEA competed for some internal site in the pore, such a redistribution of permeant ions would affect block by internal TEA.

To determine whether this proposition was at all reasonable, we attempted to simulate our results with a permeation model based on Eyring rate theory (Eyring et al. 1949). This model includes competition for available sites and contains a central, high-affinity binding site for K⁺ ions. Such models can reproduce many of the properties of multi-ion pores (Hille and Schwarz 1978; Kiss et al. 1998; Stampe et al. 1998), including high flux rates in the face of high permeant ion affinity (Dang and McCleskey 1998). We found that this type of model could simulate an apparent antagonism between TEA ions that depends on the properties of the permeant ion.

Fig. 11 illustrates the simulation of the interaction between external and internal TEA with K⁺ and Rb⁺ as permeant ions. Details of the modeling are described in methods. The left ordinate of Fig. 11 A is the RCR (Andersen 1999) of the model for a frequency factor of 3 × 10¹¹ s⁻¹ (see methods). The ordinate on the right provides the energy levels in RT units for this same frequency factor. The solid line represents the model energy profile for K⁺ ions. The characteristics of high lateral and low internal barriers allow the expression of many multi-ion pore properties (Hille and Schwarz 1978; Kiss et al. 1998; Stampe et al. 1998). The stepwise increase in local minima allows high flux rates in the face of high affinity between the ion and the model pore (Dang and McCleskey 1998). TEA block was simulated by allowing this ion to bind at external and internal sites but without the ability to cross the pore (high internal barriers). The RCR reflects how the energy barrier profile affects the rate constants (abscissa in Fig. 11 A), but does not include the contribution from membrane potential. In our simulations, the energy minima and maxima were symmetrical and the minima placed at 0.1, 0.5, and 0.9 of the electric field (from outside to inside).

We used the model rate constants for K⁺ and TEA ions and simulated dose-dependent block by internal TEA in the absence and at various concentrations of external TEA. These data allowed computation of the apparent K _d for internal TEA block as a function of external TEA as shown in Fig. 11 B. We made no attempt to quantitatively simulate the interaction between external and internal TEA. The K⁺ ion profile used was symmetric, simple and the same as one used previously to simulate our flux-ratio results (Stampe et al. 1998). Nevertheless, as illustrated in Fig. 11 B (▪), this simple model not only simulated our experimental findings, but the value of Q obtained by fitting to the simulations was quite similar to the experimental data with K⁺ as the permeant ion (Newland et al. 1992; Fig. 3).

Even in this simple model with symmetrical barrier shapes, there are 10 adjustable parameters that describe the permeant ion properties: four energy maxima, three energy minima, and three positions for the minima. To simulate the antagonism between TEA ions in Rb⁺ solutions, any or all of these could be adjusted. Instead, we took as simple an approach as possible and chose to give Rb⁺ ions all the same properties of K ions except one: a larger second energy maximum (Fig. 11 A, dotted line). With this profile for the permeant ions, there was very little antagonism between external and internal TEA (Fig. 11 B, ○).

Thus, this simple version of a three-site permeation model was able to simulate the antagonism between external and internal TEA ions in K⁺ solutions without invoking electrostatic repulsion or a conformational change. The model also predicted that this antagonism depends on the nature of the permeant ion. Only a small change in the properties of the permeant ion predicted an elimination of the TEA antagonism, as we observed with Rb⁺ as the permeant ion.

As described in methods, we computed the probabilities for occupancy of various states in the model. We tested whether the addition of TEA to the external side of the model pore would cause a redistribution of occupancy of the permeant ions. We found that, like the antagonism between TEA ions, redistribution depends on the properties of the permeant ion. For example, with the model parameters for K ions, the probability of occupancy of all three sites by the permeant ion was ∼0.37. When 5 mM TEA was added to the model, this value was increased to 0.52 for those channels not blocked by TEA. With the Rb⁺ ion model profile, addition of TEA caused little or no redistribution of permeant ion occupancy. The largest change was in the state with the middle and inner sites occupied, where TEA increased the probability only slightly from 0.49 to 0.52. Thus, our observation that the antagonism between external and internal TEA ions depended on the permeant ion is consistent with a competition between blocking and permeant ions for the availability of limited sites in the pore. According to the model simulation, this can arise if TEA occupancy of its external binding site causes a redistribution of the occupancy of permeant ions in the pore.

Possible Implications

Our results suggest that the antagonism between external and internal TEA ions in the pore of the Shaker K channels is not due to mutual electrostatic repulsion. These blocking ions likely occupy sites at opposite ends of the narrow selectivity filter (MacKinnon and Yellen 1990; Kavanaugh et al. 1991; Heginbotham and MacKinnon 1992; Yellen et al. 1991; Choi et al. 1993). These monovalent blocking ions experience little or no electrostatic repulsion over the distance of the structure. Thus, any electrostatic interactions within this structure may be only short range in nature. A similar conclusion was reached by Vergara et al. 1999. These authors found that there was very little interaction between an external TEA ion and a K⁺ ion likely at the outermost position in the selectivity filter. They further suggest the ring of conserved aspartates (Shaker position 447) may provide electrostatic shielding in this part of the pore structure.

Thus, we suggest that long-range electrostatic repulsion between permeant ions may not be the mechanism that overcomes the high ion affinity and allows high flux rates. While an appealing and intuitive concept, there is no direct evidence supporting long-range electrostatic repulsion between permeant ions in any channel. Moreover, repulsion between ions in pores is not the only mechanism for assuring high selectivity and high flux rates. Dang and McCleskey 1998 demonstrated that these two contradictory requirements are met by model multi-ion channels in which permeant ions have “stepwise changes in binding affinity.” We found that similar permeation models can also account for the difference in TEA ion antagonism in K⁺ and Rb⁺ solutions.

Thus, while not directly addressing repulsion between permeant ions within the pore selectivity filter, our results are a reminder that the presence of electrostatic interactions between permeant ions located at opposite ends of this structure has not been established. Likewise, it has been shown only that permeation based on stepwise changes in binding affinity can simulate experimental data. Clearly, considerable additional data are required to determine the mechanism by which K channels provide both high affinity and high flux rates.

If the antagonism between these ions is electrostatic in nature, it will be much stronger between internal TEA and an external multivalent TEA analogue. It is possible to quantitatively predict the magnitude of this increased interaction by determining the expected value of the interaction parameter, Q.

The equilibrium binding constant for a reaction is exponentially related to the free energy change, ΔG ⁰ of the reaction: K _eq = exp(−ΔG ⁰/RT), which can be divided into entropic (ΔS) and enthalpic (ΔH) components: ΔG ⁰ = ΔH − TΔS.

One component of the change in enthalpy will arise from the electrostatic energy between the interacting ions: ΔG ⁰ = ΔH _e + ΔH _r − TΔS, where ΔH _e represents the electrostatic component and ΔH _r the rest of the change in enthalpy. Thus, the equilibrium constant can be written as: K _eq = exp(−ΔH _e/RT) · exp[(−ΔH _r + TΔS)/RT] or K _eq = exp(−ΔH _e/RT) · K _eq ⁰, where K _eq ⁰ is the equilibrium constant in the absence of electrostatic interaction. The relation to the interaction parameter, Q, of can be seen by considering the binding of internal TEA to a channel occupied by external TEA. The equilibrium constant for this reaction is: K*_i = a · b · k ₋₂/k ₂ = Q · K _i, where K _i is the binding constant without the electrostatic presence of external TEA. Comparing the last two equations allows an assignment for Q = exp(−ΔH _e/RT).

Even with a known channel structure and precise location of the interacting ions, an exact calculation of the electrostatic energy, ΔH _e, is challenging. However, this quantity certainly is proportional to the product of the valences of the interacting ions. Therefore, the value for the interaction between internal TEA and an external ion of valence z will be: Q _z = exp(−zΔH ₁/RT) and Q_z = Q ^z ₁.