Intracellular Mg²⁺ Enhances the Function of Bk-Type Ca²⁺-Activated K⁺ Channels

Abstract

BK channels modulate neurotransmitter release due to their activation by voltage and Ca²⁺. Intracellular Mg²⁺ also modulates BK channels in multiple ways with opposite effects on channel function. Previous single-channel studies have shown that Mg²⁺ blocks the pore of BK channels in a voltage-dependent manner. We have confirmed this result by studying macroscopic currents of the mslo1 channel. We find that Mg²⁺ activates mslo1 BK channels independently of Ca²⁺ and voltage by preferentially binding to their open conformation. The mslo3 channel, which lacks Ca²⁺ binding sites in the tail, is not activated by Mg²⁺. However, coexpression of the mslo1 core and mslo3 tail produces channels with Mg²⁺ sensitivity similar to mslo1 channels, indicating that Mg²⁺ sites differ from Ca²⁺ sites. We discovered that Mg²⁺ also binds to Ca²⁺ sites and competitively inhibits Ca²⁺-dependent activation. Quantitative computation of these effects reveals that the overall effect of Mg²⁺ under physiological conditions is to enhance BK channel function.

INTRODUCTION

Intracellular free Mg²⁺ concentration has been measured to be between 0.4 and 3 mM under normal physiological conditions (Flatman 1984; Gupta et al. 1984; Corkey et al. 1986; Flatman 1991). At such concentrations, Mg²⁺ modulates a variety of Ca²⁺ and K⁺ channels to affect the excitability or excitation-contraction coupling in neurons, cardiac myocytes, and smooth muscle cells (Altura et al. 1987; Matsuda et al. 1987; Vandenberg 1987; White and Hartzell 1988; Altura and Gupta 1992; Chuang et al. 1997; Romani et al. 2000). After central nervous system injury, [Mg²⁺]_i is significantly reduced, contributing to a number of factors including increased neurotransmitter release and oxidative stress that initiate an autodestructive cascade of biochemical and pathophysiological changes, known as secondary injury, that ultimately results in irreversible tissue damage (Vink and Cernak 2000). Pharmacological studies have shown that Mg²⁺ may be an effective therapeutic agent after neurotrauma to improve survival and motor outcome and to alleviate cognitive deficits (Vink and Cernak 2000). Magnesium supplements are also important in the prevention and management of cardiovascular diseases that predispose to hypertension or congestive heart failure (Laurant and Touyz 2000; Seelig 2000).

The activation of large conductance Ca²⁺ activated K⁺ channels (BK channels) depends on both voltage and intracellular calcium (Marty 1981; Pallotta et al. 1981). Because of this property, BK channels are uniquely suited to play a role in biological processes that involve both calcium signaling and voltage changes. These include neurotransmitter release (Robitaille et al. 1993; Yazejian et al. 1997), electric tuning of cochlear hair cells (Hudspeth and Lewis 1988a,Hudspeth and Lewis 1988b; Wu et al. 1995), and vascular smooth muscle contraction (Nelson et al. 1995; Brenner et al. 2000; Pluger et al. 2000). The function of BK channels is further modulated by intracellular Mg²⁺, resulting in a reduced single-channel conductance (Ferguson 1991; Zhang et al. 1995; Morales et al. 1996; Wachter and Turnheim 1996), an increased open probability at certain [Ca²⁺]_i (Squire and Petersen 1987; Zamoyski et al. 1989; McLarnon and Sawyer 1993; Zhang et al. 1995; Bringmann et al. 1997), and an increased apparent cooperativity of Ca²⁺ in activating the channel (Golowasch et al. 1986; Oberhauser et al. 1988; Trieschmann and Isenberg 1989). These Mg²⁺ effects on BK channel function may contribute significantly to its physiological and pathophysiological roles.

A series of previous studies have focused on the Mg²⁺ block of BK channels. These studies have suggested that Mg²⁺ reduces the single-channel conductance by binding to a site inside the pore with fast kinetics and blocking the channel (Ferguson 1991; Laver 1992; Zhang et al. 1995; Morales et al. 1996). However, the mechanism by which Mg²⁺ increases the channel open probability and the cooperativity of Ca²⁺-dependent activation is not clear. In particular, how voltage, Ca²⁺, and Mg²⁺ interact during channel activation is not elucidated. The increased cooperativity of Ca²⁺-dependent activation by Mg²⁺ was taken to suggest that Mg²⁺ exposed Ca²⁺ binding sites that had been buried in BK channels before Mg²⁺ was added, bringing the total Ca²⁺ binding sites to be more than six (Golowasch et al. 1986). However, the extent to which Mg²⁺ affects BK channel activation seemed to depend on [Ca²⁺]_i. At certain [Ca²⁺]_i Mg²⁺ activated the channel, whereas at other [Ca²⁺]_i Mg²⁺ had little effect or even reduced channel activation (Zhang et al. 1995; Komatsu et al. 1996; Kazachenko and Chemeris 1998). These results have not been explained with a single molecular mechanism. Such lack of understanding in the molecular mechanism combined with the complexity derived from the opposing Mg²⁺ actions of channel block and channel activation make it difficult to assess the physiological consequence of Mg²⁺ effects on BK channels.

Recent studies on cloned slo family of BK channels have revealed that voltage and Ca²⁺ activate BK channels through distinct mechanisms (Cox et al. 1997a; Cui et al. 1997; Horrigan et al. 1999; Cui and Aldrich 2000). Similar to voltage-gated K⁺ channels, BK channels contain the S4 domain that may function as an intrinsic voltage sensor (Atkinson et al. 1991; Adelman et al. 1992; Butler et al. 1993; Aggarwal and MacKinnon 1996; Mannuzzu et al. 1996; Seoh et al. 1996; Diaz et al. 1998; Cui and Aldrich 2000). In response to membrane depolarization, BK channels can be activated in the absence of Ca²⁺ binding (Pallotta 1985; Meera et al. 1996; Cui et al. 1997; Horrigan et al. 1999). Ca²⁺ binds to the channel at sites located in the intracellular carboxyl terminus of the α subunit (Moss et al. 1996; Schreiber et al. 1999; Bian et al. 2001) with a high affinity (K _d = ∼1–10 μM; McManus and Magleby 1991; Cox et al. 1997a). It modulates the responses of the channel to voltage by shifting the voltage dependence of the steady-state open probability (P_o) and the activation kinetics to a more negative voltage range (Marty 1981; Pallotta et al. 1981; McManus and Magleby 1991; Adelman et al. 1992; Cox et al. 1997a; Cui et al. 1997). Both voltage- and Ca²⁺-dependent activation of the channel involve allosteric mechanisms (Cox et al. 1997a; Cui et al. 1997; Horrigan et al. 1999) that are individually well described by Monod-Wyman-Changeux (MWC; Monod et al. 1965)–type models for allosteric proteins (McManus and Magleby 1991; Cox et al. 1997a; Horrigan and Aldrich 1999; Horrigan et al. 1999). It has been demonstrated that although voltage sensor movements and Ca²⁺ binding both activate the channel, they do not affect each other directly. The voltage- and Ca²⁺-dependent mechanism activate the channel through separate pathways, and then converge to affect the final transition between the open and closed conformation (Cui and Aldrich 2000). In this study, we investigate whether Mg²⁺ activates the channel by affecting the separate voltage or Ca²⁺-dependent activation, or by affecting the final transition between the open and closed conformation. Our results demonstrate that Mg²⁺-dependent activation does not directly depend on voltage or Ca²⁺ but the binding of Mg²⁺ will affect the close-open transition. We have also discovered that in addition to activation of the channel, Mg²⁺ also binds to the high affinity Ca²⁺ sites and competitively inhibits Ca²⁺-dependent activation. The combination of Mg²⁺-dependent activation and competitive inhibition increases the apparent cooperativity of the response of mslo1 to Ca²⁺. The quantitative description of each individual Mg²⁺ effect enabled us to estimate the overall effect of intracellular Mg²⁺ on BK channel function under physiological conditions.

An abstract of this work has been presented in the 45th Annual Meeting of Biophysical Society.

MATERIALS AND METHODS

Clones and Channel Expression

The mbr5 clone of mslo1 (Butler et al. 1993), the cDNA of mslo3 (Schreiber et al. 1998), and mslo3 tail (Schreiber et al. 1999) were provided to us by Dr. Larry Salkoff (Washington University School of Medicine, St. Louis, MO). The cDNA of mslo1 core, including nucleotides 1–2,025 of the coding region (Met 1–Lys 648) subcloned into PSD64TF, was provided to us by Dr. Yasushi Okamura (National Institute of Advanced Industrial Science and Technology, Tsukuba, Japan). cRNA was transcribed in vitro using the “mMessage mMachine” kit with T3 or SP6 polymerase (Ambion Inc.). 0.05–0.5 ng of cRNA were injected into Xenopus laevis oocytes 2–6 d before recording.

Electrophysiology

Macroscopic currents were recorded from inside-out patches formed with borosilicate pipettes of 1∼2 megohm resistance. Data were acquired using an Axopatch 200-B patch-clamp amplifier (Axon Instruments, Inc.) and Pulse acquisition software (HEKA Electronik). Records were digitized at 20-μs intervals and low-pass filtered at 10 kHz with the 4-pole Bessel filter (Axon Instruments, Inc.). The pipette solution contained the following (in mM): 140 potassium methanesulfonic acid, 20 HEPES, 2 KCl, and 2 MgCl₂, pH 7.20. The basal internal solution contained the following (in mM): 140 potassium methanesulfonic acid, 20 HEPES, 2 KCl, and 1 EGTA, pH 7.20. Methanesulfonic acid was purchased from Sigma-Aldrich. The “0 [Ca²⁺]_i” solution was the same as the basal internal solution except that it contained 5 mM EGTA, having a free [Ca²⁺]_i of ∼0.5 nM that was too low to affect mslo1 channel activation (Cui et al. 1997). MgCl₂ was added to these internal solutions to give the appropriate free [Mg²⁺]_i. CaCl₂ was added to the basal internal solutions with amounts calculated using a program similar to published (Fabiato and Fabiato 1979) to give rise various free [Ca²⁺]_i. The free [Ca²⁺]_i was then measured with a calcium-sensitive electrode (Orion Research Inc.) with the same procedure as previously described (Cox et al. 1997b). Although theoretically only [Ca²⁺]_i ≥10 μM can be accurately measured by the calcium-sensitive electrode, we find that the response of the electrode (mV) to log([Ca²⁺]_i) between ∼1 and 10 μM by calculation follows well the same straight line as at [Ca²⁺]_i ≥10 μM. The calcium-sensitive electrode was always calibrated right before measurements, and then recalibrated immediately after measurements. The results of calibration and recalibration were the same, indicating that the electrode was stable during measurements. The presence of Mg²⁺ in the solution had negligible effects on the accuracy of such measurements. The response of mslo1 channels was also compared with previous results to ensure that each time the [Ca²⁺]_i was measured correctly. Since the activity of mslo3 channels is pH-dependent (Schreiber et al. 1998) in the recording of mslo3 channels, the pH of internal solutions was adjusted to be 8.0. Mg²⁺ effects on mslo1 channels were not affected by pH. A sewer pipe flow system (model DAD12; Adams and List Assoc. Ltd.) was used to supply and exchange the internal solution to the cytoplasmic face of the patch. Experiments were conducted at room temperature (23°C).

RESULTS

Separating the Activation and Block of mslo1 Channels by Intracellular Mg²⁺

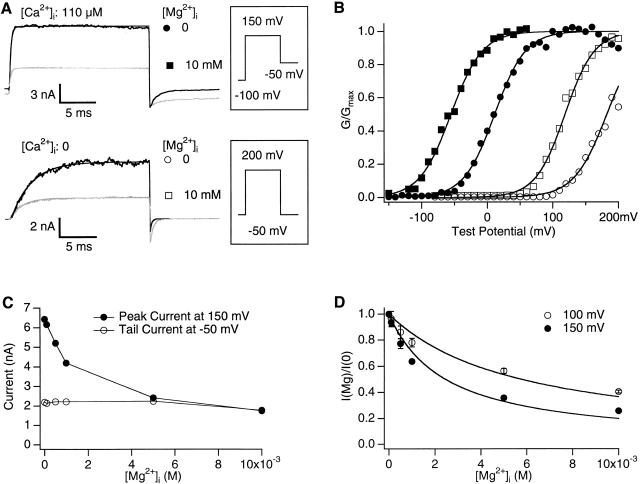
Fig. 1 shows that intracellular Mg²⁺ both reduces the current amplitude at positive voltages and shifts the conductance-voltage (G-V) relations of the mslo1 channel. In Fig. 1 A mslo1 currents were recorded from an inside-out patch with a symmetric 140 mM intra- and extracellular [K⁺] at 110 μM and 0 [Ca²⁺]_i. At positive voltages, 10 mM [Mg²⁺]_i reduces the outward current at both [Ca²⁺]_i's. Fig. 1 B shows the G-V relations of the mslo1 channel in the absence or presence of 10 mM [Mg²⁺]_i at 0 and 110 μM [Ca²⁺]_i, respectively. At both [Ca²⁺]_i's, the G-V relation is shifted to the left on the voltage axis by ∼65 mV. Thus, at any given voltages within the range of G-V relations, the mslo1 channel is activated more in the presence of 10 mM [Mg²⁺]_i.

Figure 1.

Intracellular Mg²⁺ blocks and activates mslo1 channels. (A) mslo1 currents recorded from an inside-out patch with 0 (dark traces) or 10 mM (light traces) [Mg²⁺]_i at [Ca²⁺]_i of 0 (bottom) and 110 μM (top). The voltage protocols are schematically displayed next to the current traces. At 110 μM [Ca²⁺]_i, the holding, test, and repolarizing potentials were −100, 150, and −50 mV, respectively. At 0 [Ca²⁺]_i, they were −50, 200, and −50 mV, respectively. Smooth lines are exponential fits to current traces. The time constant is 0.23 ms at 0 [Mg²⁺]_i, 0.26 ms at 10 mM [Mg²⁺]_i with 110 μM [Ca²⁺],_i and 2.84 ms at 0 [Mg²⁺]_i, 1.72 ms at 10 mM [Mg²⁺]_i with 0 [Ca²⁺]_i. (B) G-V relations of mslo1 channels with 0 (circles) or 10 mM (squares) [Mg²⁺]_i at [Ca²⁺]_i of 0 (open symbols) and 110 μM (closed symbols). Corresponding symbols are also shown in A. The smooth lines are fits with the Boltzmann function, G/G_max = 1/(1 + exp(−ze(V − V_1/2)/kT)), where G is conductance, z is the valence of equivalent charge, e is the elementary charge, V_1/2 is the voltage where conductance is half-maximum, k is Boltzmann's constant, and T is the absolute temperature. At 110 μM [Ca²⁺]_i, z = 1.08 and V_1/2 = 11.4 mV with 0 [Mg²⁺]_i, and z = 0.92, V_1/2 = −52.4 mV with 10 mM [Mg²⁺]_i. At 0 [Ca²⁺]_i, z = 1.01 and V_1/2 = 182.6 mV with 0 [Mg²⁺]_i, and z = 1.20, V_1/2 = 117.0 mV with 10 mM [Mg²⁺]_i. (C) The response to [Mg²⁺]_i of the peak current at the test potential of 150 mV and the instantaneous tail current at the repolarizing potential of −50 mV. [Ca²⁺]_i was 1 μM. Data points are connected by thin straight lines. (D) Mg²⁺ block of the peak current at test potentials of 100 and 150 mV. The ratio of the current with internal Mg²⁺ to that without internal Mg²⁺, I(Mg)/I(0), from three (at 150 mV) or five (at 100 mV) patches were averaged and plotted versus [Mg²⁺]_i. Error bars in all figures represent the SEM. Smooth lines are fits of the Woodhull model (Woodhull 1973) I(Mg)/I(0) = 1/(1 + [Mg²⁺]_i /K _D(0)exp(−2δeV/kT)), where K _D(0) = 31.5 mM is the dissociation constant at 0 mV and δ = 0.22 is the fraction of the voltage across the membrane that influences Mg²⁺ at its binding site, as measured from the intracellular surface.

Previous single-channel studies have demonstrated a fast voltage-dependent block of BK channels by intracellular Mg²⁺, resulting in a reduction of single-channel conductance at positive voltages (Ferguson 1991; Laver 1992). Our results indicate that the same block causes the reduction of the current amplitude at the macroscopic current level. First, the Mg²⁺ block is voltage-dependent: 10 mM [Mg²⁺]_i blocks the outward current at 150 mV, but the instantaneous tail current at the repolarizing potential of −50 mV is similar in size with or without Mg²⁺ (Fig. 1 A, 110 μM [Ca²⁺]_i). In both cases, the mslo1 channel is fully activated at 150 mV and 110 μM [Ca²⁺]_i (Fig. 1 B) so that the similar instantaneous tail current indicates that the single-channel conductance is the same at the repolarizing potential of −50 mV with or without Mg²⁺. Thus, the negative voltage of −50 mV relieves the Mg²⁺ block of the channel at the preceding 150 mV. Similarly shown in Fig. 1 C, the block of the peak current at 150 mV increases with increasing [Mg²⁺]_i, whereas the instantaneous tail current at −50 mV is not blocked and remains the same for the entire range of [Mg²⁺]_i. Fig. 1 D plots the averaged dose–response of the block at 100 and 150 mV, showing that Mg²⁺ induced block is more pronounced at higher voltages. The curves are fit by the Woodhull model (Woodhull 1973; Fig. 1 D, legend) with K _D of 31.5 mM at 0 mV and electric distance of 0.22 from the inside of the membrane. These results are similar to those obtained previously from studies at the single-channel level (Ferguson 1991; Laver 1992). Second, the relief of the Mg²⁺ block is very fast, at least faster than the time resolution of our macroscopic current recording (≪0.1 ms) so that all the blockade has been relieved at the beginning of tail current measurements. Similarly, the block at positive voltages is also fast. The activation time course of mslo1 channels can be fit with a single-exponential function in the absence as well as in the presence of intracellular Mg²⁺ with similar time constants (Fig. 1 A; Cui et al. 1997; Horrigan et al. 1999). Therefore, the time course of Mg²⁺ block is much faster than the time course of channel activation at 150 mV and 110 μM [Ca²⁺]_i (∼0.25 ms, Fig. 1 A).

The characteristics of the Mg²⁺ block allowed us to construct G-V relations by measuring the tail current amplitude at a fixed negative voltage of −50 mV after each test potential (Fig. 1) and separate the gating properties from the block. The tail current at −50 mV is not affected significantly by the Mg²⁺ block at [Mg²⁺]_i up to 10 mM (Fig. 1A and Fig. C). At higher [Mg²⁺]_i such as 100 mM, a fraction of the tail current would be blocked even at −50 mV (unpublished data). However, since the block and unblock were very fast the single-channel conductance at the repolarization to −50 mV after each test pulse would reach the same value instantly. Therefore, the macroscopic tail current only reflected the differences in the amount of open channels at the end of different test pulses and G-V relations would still represent the gating properties only. A fast block of mslo1 channels by intracellular Ca²⁺ similar to the Mg²⁺ block was shown previously to be separable from the gating properties with the same treatment (Cox et al. 1997b).

Mg²⁺ Affects Gating and Permeation through Distinct Binding Sites

In the experiment shown in Fig. 1 A, at 110 μM [Ca²⁺]_i, the holding potential was −100 mV and the repolarizing potential was −50 mV. At both these negative voltages, there was little Mg²⁺ block, as suggested by the results of Fig. 1 C. On the other hand, a steady-state inward current was observed in the presence of 10 mM [Mg²⁺]_i, but not in the absence of Mg²⁺, suggesting that Mg²⁺ activated mslo1 channels at these negative voltages even though the block was largely relieved. Unlike the Mg²⁺ block, the activation of mslo1 channels by Mg²⁺ seems to be insensitive to voltage, resulting in a parallel shift of G-V relations on the voltage axis without affecting the slope (Fig. 1 B). Such insensitivity to voltage in the change of G-V relations is more prominent when we compare the results at 0 and 110 μM [Ca²⁺]_i. The voltage of half-maximum activation (V_1/2) at 0 [Ca²⁺]_i is ∼170 mV more positive than at 110 μM [Ca²⁺]_i (Fig. 1 B). Nevertheless, 10 mM Mg²⁺ shifts the G-V relation to the left on the voltage axis with a similar amount at both [Ca²⁺]_i's (Fig. 1 B and 2 C). This result indicates that the binding of Mg²⁺ that activates the channel is not sensitive to membrane potential, obviously in contrast to the voltage dependence of Mg²⁺ binding in channel block. Therefore, the Mg²⁺ ion that activates the channel cannot be the Mg²⁺ ion that blocks it. Results in later sections also support the conclusion that Mg²⁺ affects the gating and permeation through distinct binding sites and mechanisms. In the following, we will primarily focus on the effects of Mg²⁺ on voltage- and Ca²⁺-dependent activation of the channel without considering the Mg²⁺ block.

The Activation by Mg²⁺ Is Not Directly Affected by Voltage or Ca²⁺

Mg²⁺ activates mslo1 channels by shifting G-V relations to the left on the voltage axis (Fig. 1 B and Fig. 2), which is similar to the Ca²⁺-dependent activation of mslo1 channels (Marty 1981; McManus and Magleby 1991; Pallotta et al. 1981; Adelman et al. 1992; Cui et al. 1997). It has been demonstrated that each of the four mslo1 channel subunits contains a high affinity Ca²⁺ binding site in the tail domain, which includes the Ca²⁺ bowl that contains repetitive negatively charged amino acids (Shen et al. 1994; Moss et al. 1996; Schreiber et al. 1999; Bian et al. 2001). The dissociation constant of Ca²⁺ binding is estimated to be ∼1 or 10 μM when the channel is open or closed, respectively (Cox et al. 1997a). Ca²⁺ activates the channel by preferentially binding to and stabilizing the open states, which can be described by allosteric mechanisms such as the MWC model (Monod et al. 1965; McManus and Magleby 1991; Cox et al. 1997a; Horrigan et al. 1999). Then, what is the mechanism of activation of the mslo1 channel by Mg²⁺? To answer this question, we first investigated whether Mg²⁺ activates the channel by affecting the Ca²⁺-dependent activation.

Figure 2.

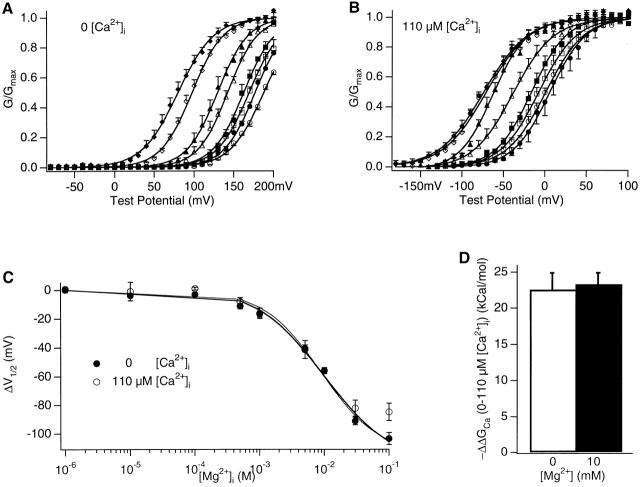
G-V relations in the presence of 0∼100 mM [Mg²⁺]_i at 0 (A) or 110 μM [Ca²⁺]_i (B). The symbols represent [Mg²⁺]_i at (in mM) 0 (open circle), 0.1 (closed circle), 0.5 (open square), 1 (closed square), 5 (open triangle), 10 (closed triangle), 30 (open diamond), and 100 (closed diamond). G-V relations from a number (n) of patches at each [Mg²⁺]_i are averaged and plotted. Smooth curves are Boltzmann fits to averaged G-V relations. At 0 [Ca²⁺]_i (A), z and V_1/2 at various [Mg²⁺]_i (mM) are as follows for 0, 1.17, 186.4 mV (n = 12); for 0.1, 1.30, 177.0 mV (n = 4); for 0.5, 1.26, 169.5 mV (n = 4); for 1, 1.30, 162.7 (n = 4); for 5, 1.36, 142.4 mV (n = 4); for 10, 1.32, 129.6 mV (n = 4); for 30, 1.30, 97.76 mV (n = 7); and for 100, 1.13, 80.1 mV (n = 8), respectively. At 110 μM [Ca²⁺]_i (B), z and V_1/2 at various [Mg²⁺]_i (mM) are as follows: for 0, 1.10, 1.2 mV (n = 10); for 0.1, 1.17, 5.8 mV (n = 5); for 0.5, 1.12, −7.6 mV (n = 6); for 1: 1.20, -16.0 (n = 6); for 5, 1.06, −38.2 mV (n = 5); for 10, 1.26, −62.5 mV (n = 4); for 30, 0.97,−70.4 mV (n = 4); and for 100, 0.95, −73.4 mV (n = 4), respectively. (C) Left shifts of G-V relations on the voltage axis caused by various [Mg²⁺]_i at 0 and 110 μM [Ca²⁺]_i. ΔV_1/2 = (V_1/2 at each [Mg²⁺]_i − V_1/2 at 0 [Mg²⁺]_i) obtained from n = 4 patches at 0 [Ca²⁺]_i and n = 6 patches at 110 μM [Ca²⁺]_i are averaged and then plotted. The smooth curves are fits of to data at 0 [Ca²⁺]_i with z = 1.30. For the thick curve, m is fixed at 4, K_C = 15.0 mM, K_O = 3.6 mM. For the thin curve, m is let free in the fit and is 1.94, K_C = 45.7 mM, K_O = 2.12 mM. (D) Changes in the activation energy provided by Ca²⁺ binding as the result of an increased [Ca²⁺]_i from 0 to 110 μM in the absence or presence of 10 mM [Mg²⁺]_i. −ΔΔG_Ca = (zV_1/2 at 0 [Ca²⁺]_i − zV_1/2 at 110 μM [Ca²⁺]_i)eN, where e is elementary charge and N is Avogadro's number. Averaged from n = 4 patches.

Mg²⁺ might activate the mslo1 channel by affecting the Ca²⁺-dependent activation in two ways: (1) by binding to the same high affinity Ca²⁺ binding sites to activate the channel, or (2) by binding to other separate sites to increase Ca²⁺ affinity or efficacy. In either case, Ca²⁺ should also affect the Mg²⁺-dependent activation reciprocally (Colquhoun 1998). Contrary to this prediction, Fig. 1 B shows that either in the absence of (at 0 [Ca²⁺]_i; materials and methods) or nearly saturated Ca²⁺ binding (at 110 μM [Ca²⁺]_i; Cox et al. 1997a) 10 mM [Mg²⁺]_i shifted the G-V relation on the voltage axis by a similar amount. The activation of the channel at other [Mg²⁺]_i's is also not affected whether the high affinity Ca²⁺ binding sites are empty (at 0 [Ca²⁺]_i) or saturated with Ca²⁺ (at 110 μM [Ca²⁺]_i) (Fig. 2). Fig. 2 (A and B) shows that at both [Ca²⁺]_i's, increasing [Mg²⁺]_i from 0.1 to 100 mM gradually shifts the G-V relation to the left on the voltage axis without affecting the slope. The averaged amounts of G-V shift (ΔV_1/2) at both [Ca²⁺]_i's are plotted versus [Mg²⁺]_i in Fig. 2 C. Clearly, despite the large differences in [Ca²⁺]_i and in the voltage range of G-V curves at the two [Ca²⁺]_i's (Fig. 2A and Fig. B), ΔV_1/2 is similar at various [Mg²⁺]_i from 1 μM up to 30 mM (Fig. 2 C).

The above results demonstrate that Ca²⁺ does not affect Mg²⁺-dependent activation of mslo1 channels. Conversely, it can be also directly demonstrated that Mg²⁺ does not affect the Ca²⁺-dependent activation. Recently, it has been shown that the free energy contributions to mslo1 channel activation provided by voltage (ΔG_V) and by Ca²⁺ binding (ΔG_Ca) are simply additive (Cui and Aldrich 2000). This property dictates that, in response to an increase in [Ca²⁺]_i, the shift of G-V relations on the voltage axis is simply determined by the change in the contribution of Ca²⁺ binding to the free energy of channel opening, ΔΔG_Ca (ΔΔG_Ca = ΔG_Ca at the high [Ca²⁺]_i − ΔG_Ca at the low [Ca²⁺]_i). As a consequence, ΔΔG_Ca can be directly measured from the properties of the G-V relation: ΔΔG_Ca = Δ(zV_1/2), where Δ(zV_1/2) = zV_1/2 at the high [Ca²⁺]_i − zV_1/2 at the low [Ca²⁺]_i (Cui and Aldrich 2000). The parameters z and V_1/2 are obtained from the Boltzmann fit to G-V relations (Fig. 1, legend). With this method, we have compared the contribution of Ca²⁺ binding to the free energy of mslo1 channel opening in the presence or absence of 10 mM [Mg²⁺]_i (Fig. 2 D). When [Ca²⁺]_i increases from 0 μM to the near-saturating 110 μM in the absence of intracellular Mg²⁺, the G-V relation shifts ∼170 mV to the left on the voltage axis (Fig. 1 B). From such results, it is calculated that, at near-saturating [Ca²⁺]_i, Ca²⁺ binding contributes −22.6 ± 2.2 kcal/mol to the free energy of mslo1 channel opening (Fig. 2 D). Likewise, in the presence of 10 mM [Mg²⁺]_i, the G-V relation shifts a similar amount on voltage axis with the same [Ca²⁺]_i increases without significantly changing the slope (Fig. 1 B and 2 B), and the free energy of Ca²⁺ binding contributed to channel opening is −23.3 ± 1.8 kcal/mol, similar to that in the absence of Mg²⁺ (Fig. 2 D). This result indicates that Mg²⁺ does not affect the contribution of Ca²⁺ binding to the free energy of mslo1 channel opening. In other words, neither the affinity of Ca²⁺ binding nor the efficacy of Ca²⁺-dependent activation is affected by Mg²⁺.

The Mg²⁺ Binding Site Is Located in the Core Domain

Since Mg²⁺ activates the channel without affecting Ca²⁺-dependent activation, the Mg²⁺ binding sites must be distinct from the high affinity Ca²⁺ binding sites located in the tail domain (Moss et al. 1996; Schreiber et al. 1999; Bian et al. 2001). Recordings of the mslo3 channel and the channel resulting from the coexpression of the mslo1 core and mslo3 tail (Fig. 3) confirm this conclusion. The tail domain of mslo3 lacks the Ca²⁺ bowl and is not sensitive to Ca²⁺ (Fig. 3 A; Schreiber et al. 1998). Similar to mslo1 channels, the mslo3 channel was blocked by 10 mM [Mg²⁺]_i (Fig. 3 B), and the block was voltage-dependent (the ratio I_{[Mg2+]i = 0}/I_{[Mg2+]i = 10 mM} for the peak current at 130 mV was 3.3, but for the tail current at −50 mV was 1.0). However, Mg²⁺ did not affect its activation (Fig. 3 C), suggesting that mslo3 lacks the Mg²⁺ binding sites for activation, although Mg²⁺ can block the channel. To test whether the Mg²⁺ binding sites for activation are located in the tail or the core domain, we recorded currents from channels expressed from a RNA mixture of the mslo1 core domain and the mslo3 tail domain (Fig. 3 D; Wei et al. 1994; Schreiber et al. 1999). This channel is not sensitive to the [Ca²⁺]_i change from 0 to 110 μM due to the lack of high affinity Ca²⁺ binding sites (Schreiber et al. 1999). If the Mg²⁺ binding sites for activation are also located in the tail domain, then this channel should not be activated by Mg²⁺ since its tail is derived from the Mg²⁺-insensitive mslo3 and apparently should lack the binding sites. However, 10 mM [Mg²⁺]_i activated this channel, shifting the G-V relation to the left on the voltage axis by ∼56 mV (Fig. 3 F), similar to that in the activation of mslo1 (Fig. 1 and Fig. 2). This result indicates that the core domain of mslo1 confers Mg²⁺ sensitivity to the chimeric channel. Therefore, the Mg²⁺ binding sites for activation are most likely located in the mslo1 core, which are distinct from the high affinity Ca²⁺ binding sites.

Figure 3.

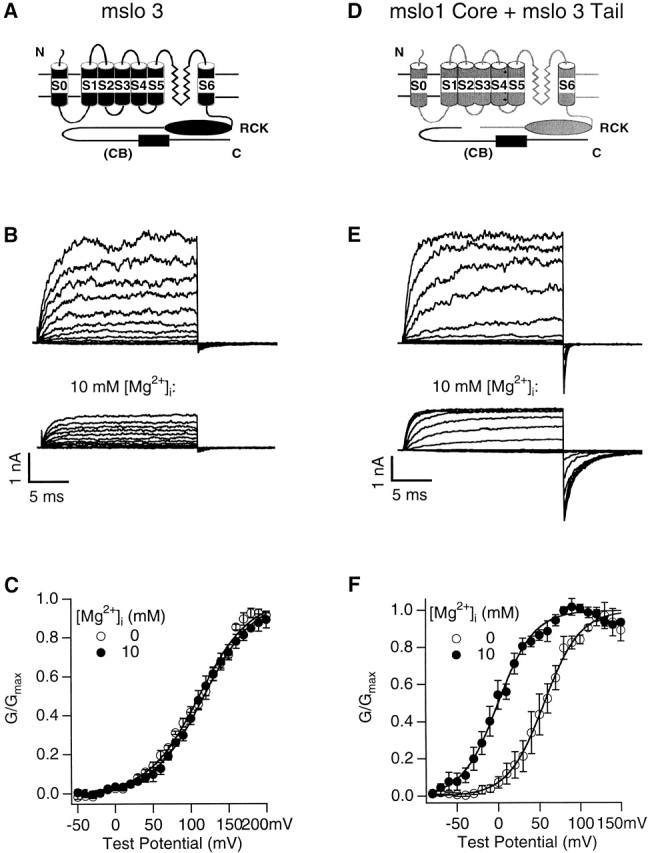
Mg²⁺ effects on mslo3 channels or the channels from coexpression of the mslo1 core and mslo3 tail. (A and D) Schematic representation of mslo3 (A) and the mslo1 core (light) and the mslo3 tail (dark) (D). S0–S6 are transmembrane segments, RCK indicates the RCK domain (Jiang et al. 2001), and CB signifies the lack of calcium bowl. (B) mslo3 currents from an inside-out patch in the absence (top) or presence (bottom) of 10 mM [Mg²⁺]_i. The holding and repolarizing potentials are −50 mV. The test potentials are from −80 to 200 mV with 20-mV increment. [Ca²⁺]_i = 0. (C) G-V relations of mslo3 channels in the absence or presence of 10 mM [Mg²⁺]_i. [Ca²⁺]_i = 0. G-V curves are averaged from n = 6 patches, and then fitted with the Boltzmann equation (smooth lines) with z = 0.76 and V_1/2 = 111.3 mV at 0 [Mg²⁺]_i and z = 0.76 and V_1/2 = 117.6 mV at 10 mM [Mg²⁺]_i, respectively. (E) Currents from an inside-out patch that coexpresses the mslo1 core and mslo3 tail in the absence (top) or presence (bottom) of 10 mM [Mg²⁺]_i. The voltage protocol is the same as in B except that the test potential stops at 140 mV. [Ca²⁺]_i = 1.1 μM. (F) G-V relations of channels from the coexpression of the mslo1 core and mslo3 tail in the absence or presence of 10 mM [Mg²⁺]_i. [Ca²⁺]_i = 1.1 μM. Smooth lines are fits of the Boltzmann equation with z = 1.14 and V_1/2 = 55.9 mV at 0 [Mg²⁺]_i and z = 1.16 and V_1/2 = 0.2 mV at 10 mM [Mg²⁺]_i, respectively. n = 4 patches.

The Allosteric Mechanism of Mg²⁺-dependent Activation

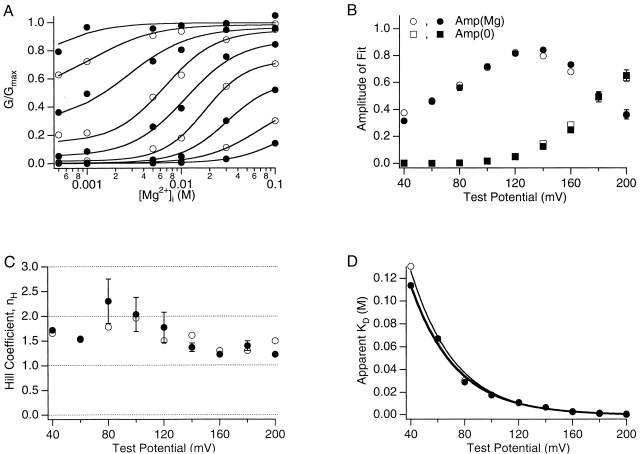
Fig. 4 A shows the Mg²⁺ dose–response curves of the steady-state open probability (G/G_max) at 0 [Ca²⁺]_i and various voltages. At all voltages, the open probability increases with [Mg²⁺]_i. The Mg²⁺-dependent component of the open probability, G(Mg), is fitted with the Hill equation. Fig. 4 C plots the Hill coefficient from the fits. At most voltages, the Hill coefficient is between 1 and 2. Since Hill coefficient indicates the lower limit for the number of positively cooperating binding sites (Stryer 1995), it is clear that the mslo1 channel has at least two Mg²⁺ binding sites for activation. The Hill coefficient in Fig. 4 C shows a weak voltage dependence that peaks at ∼80–120 mV. The maximum Hill coefficient of Mg²⁺ dependence is obviously smaller than that of Ca²⁺ dependence (see Fig. 6E), which arises from the binding of Ca²⁺ to four high affinity Ca²⁺ sites that progressively promotes channel opening (Cox et al. 1997a; Cui et al. 1997). The smaller Hill coefficient of Mg²⁺-dependent activation indicates either of the following possibilities. First, the channel has fewer Mg²⁺ binding sites, possibly two, considering the symmetry of the tetrameric channel (Jiang et al. 2001; Zagotta 2001). Second, as for Ca²⁺ binding, the channel has four Mg²⁺ sites, one on each subunit (Shen et al. 1994), but the binding of each Mg²⁺ promotes channel opening less than the binding of each Ca²⁺ to the high affinity Ca²⁺ site.

Figure 4.

Mg²⁺ dependence of mslo1 currents. (A) Average normalized G-V relations at 0 [Ca²⁺]_i and the following [Mg²⁺]_i: 0, 0.1, 0.5, 1, 5, 10, 30, and 100 mM were transformed to dose–response curves as displayed (data at 0 and 0.1 mM [Mg²⁺]_i is not shown on the logarithm scale). Alternating closed and open circles represent the dose–response curves (ascending right to left) at different voltages between 40 and 200 mV in 20-mV increments. Smooth curves represent fits to the Hill equation (G/G_max = Amp(Mg)/(1 + (K _d/[Mg²⁺]_i)^nH) + Amp(0)), where n_H is Hill coefficient, K _d is the apparent Mg²⁺ dissociation constant, Amp(0) = G/G_max at 0 [Mg²⁺]_i, and Amp(Mg) is the Mg²⁺-dependent component of G/G_max. (B–D) The amplitudes, Hill coefficient, and apparent dissociation constant determined from fits to the Hill equation are plotted versus voltage. Open symbols represent parameters determined from the fits in A. Closed symbols represent the mean values from four experiments. In D, solid lines are fits with the function K _d(V) = K _d(0)exp(zeV/kT). The thin line fits the results determined in A, K _d(0) = 378.8 mM and z = 0.77. The thick line fits the mean results from four experiments, K _d(0) = 242.3 mM and z = 0.77.

Figure 6.

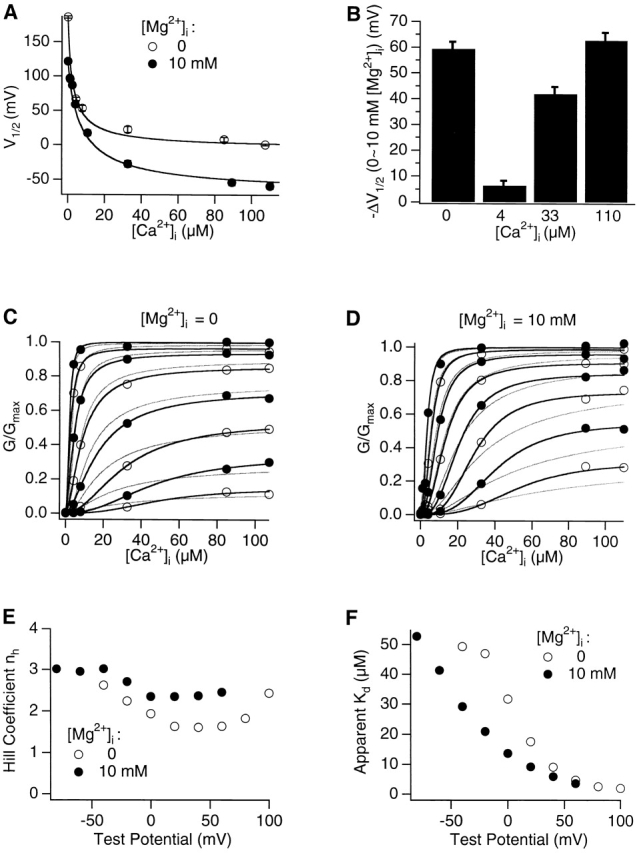
Effects of intracellular Mg²⁺ on Ca²⁺-dependent activation. (A) V_1/2 of G-V relations at various [Ca²⁺]_i in the presence or absence of 10 mM [Mg²⁺]_i. The smooth lines are fits of to data. Each data point is averaged from n = ∼4–8 patches. (B) The difference in V_1/2 in the presence or absence of 10 mM [Mg²⁺]_i. At each [Ca²⁺]_i, ΔV_1/2 = (V_1/2 at 10 mM [Mg²⁺]_i − V_1/2 at 0 [Mg²⁺]_i), averaged from n = 4–6 patches. (C) and D) [Ca²⁺]_i dependence of normalized conductance in the absence (C) or presence (D) of 10 mM [Mg²⁺]_i. Each data point is averaged from n = 4–8 patches. Alternating open and closed circles represent the curves (ascending right to left) at different voltages between −40 and 100 mV (C) or between −80 and 60 mV (D) in 20-mV increments. Dark or light smooth curves represent fits to the Hill equation or to (Fig. 2), respectively. (E and F) Hill coefficient (E) and apparent K_d (F) obtained from fits of data in the presence or absence of 10 mM [Mg²⁺]_i to the Hill equation.

The apparent K _d from the Hill equation fits clearly shows a voltage dependence (Fig. 4 D). At 0 mV, the apparent K _d is 242.3 mM, whereas at 180 mV, it is 1.6 mM. Such apparent voltage dependence appears to be in contrast to the results in Fig. 1 B and Fig. 2 that the shifts of G-V relations caused by Mg²⁺ are insensitive to voltage. In other words, the results in Fig. 1 B and Fig. 2 indicate that the binding of Mg²⁺ is not directly dependent on voltage, whereas the apparent K _d in Fig. 4 indicates that it is influenced by voltage. These results can be reconciled by concluding that the binding of Mg²⁺ must be dependent on the conformation of the channel but not on voltage per se. The Mg²⁺ affinity is higher at the open conformation than at the closed. At more positive voltages, more channels are open, therefore, the apparent K _d decreases with voltage. This mechanism of cooperative Mg²⁺ binding is described by the model for allosteric transitions (Fig. 1), which is similar to the mechanism of Ca²⁺-dependent activation of the channel (Cox et al. 1997a; Cui et al. 1997).

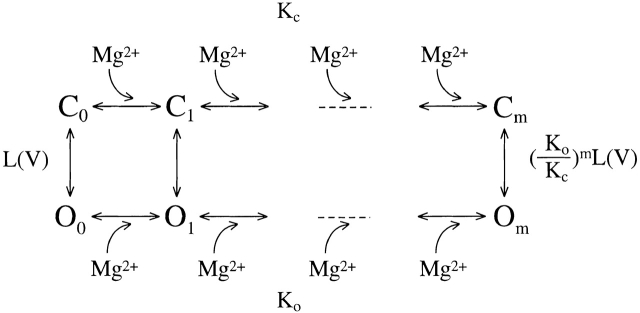
Scheme S1.

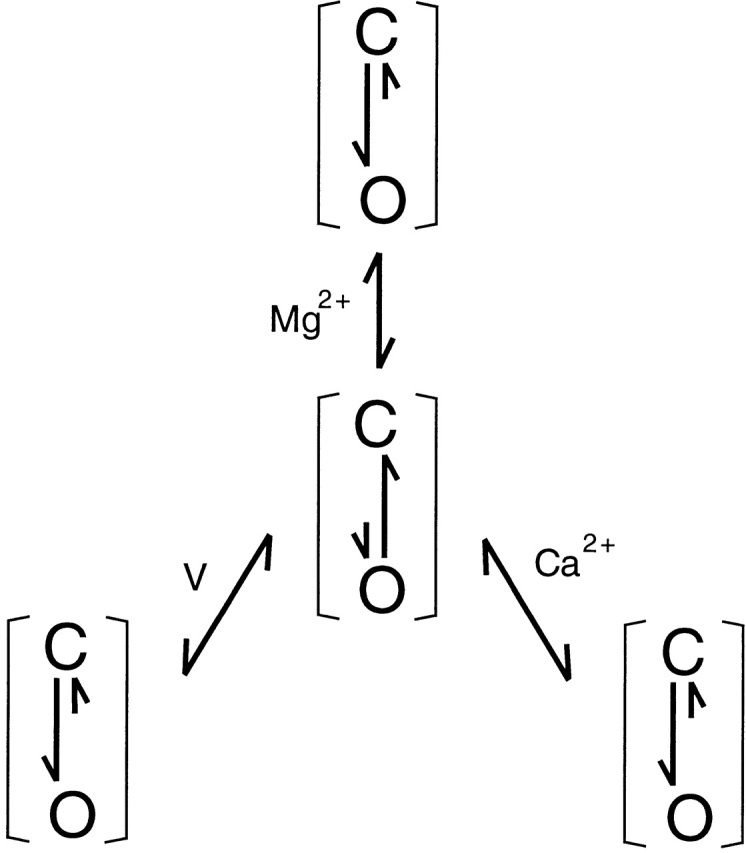
In Fig. 1, each channel has m Mg²⁺ binding sites. K_C and K_O are the microscopic dissociation constants of Mg²⁺ at closed (C) and open (O) conformation, respectively. L(V) is the equilibrium constant between C₀ and O₀, the closed and open conformation with no Mg²⁺ bound. In Fig. 2 C, the shift of G-V relations versus [Mg²⁺]_i at 0 [Ca²⁺]_i is fitted with derived from Fig. 1 (Cui and Aldrich 2000),

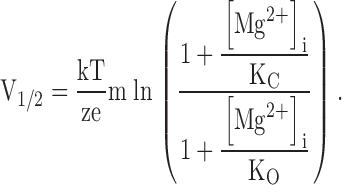1

The fit results in a number of Mg²⁺ binding sites m = 2 when it is let free, K_C and K_O being 45.7 and 2.12 mM, respectively. The model fits the data equally well (Fig. 2 C) if the number of Mg²⁺ binding sites is assumed to be four, resulting in a K_C and K_O of 15.0 mM and 3.6 mM, respectively.

Ca²⁺ Also Binds to the Low Affinity Mg²⁺ Sites of Activation

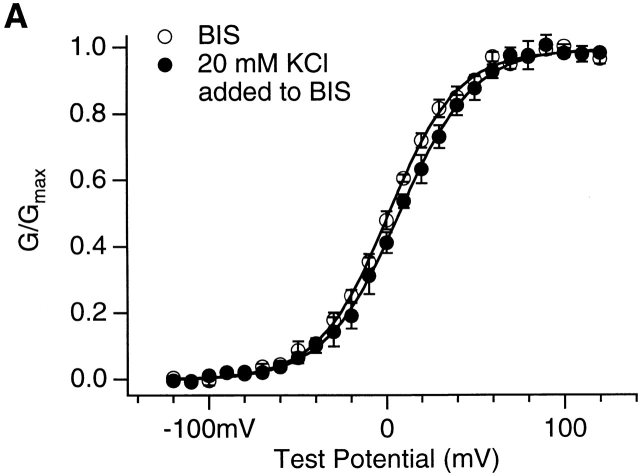
In the above experiments, we added MgCl₂ to the basal internal solution to vary [Mg²⁺]_i (materials and methods). With such a method, besides the change of [Mg²⁺]_i, [Cl⁻]_i and the osmolarity of intracellular solution were also changed. To examine if increased intracellular Cl⁻ or osmolarity contribute to our observed mslo1 channel activation, we compared the G-V relations in the basal internal solution with or without the addition of 20 mM KCl. Fig. 5 A shows that the addition of 20 mM KCl caused 6-mV shift of the G-V relation to a more positive voltage range. Such change is much smaller and to an opposite direction as compared with the changes caused by addition of 10 mM MgCl₂ (Fig. 1 B). In fact, such a small change in G-V relations is within the variability of mslo1 channels, and is often observed among experiments even under identical conditions. This result indicates that the increase of intracellular [K⁺]_i (from 142 to 162 mM), [Cl⁻]_i (from 2 to 22 mM), or osmolarity had little effect on the activation of mslo1 channels under our experimental condition.

Figure 5.

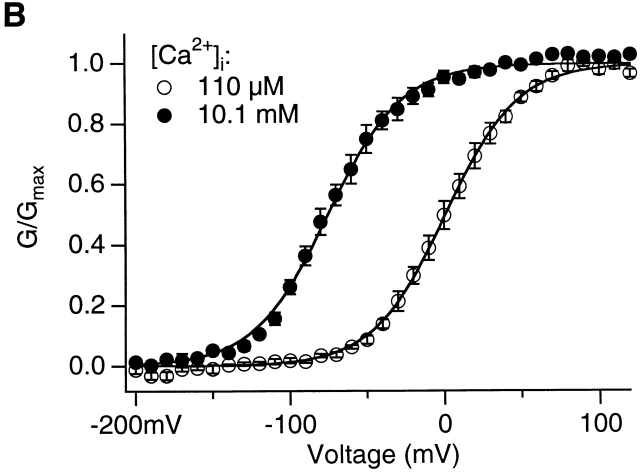
The effects of [KCl]_i and high [Ca²⁺]_i on the activation of mslo1 channels. (A) G-V relations of mslo1 channels with or without 20 mM KCl added to the basal internal solution (BIS; materials and methods). The total [Cl⁻]_i is 22 mM and 2 mM, respectively. The total [K⁺]_i is 162 and 142 mM, respectively. [Ca²⁺]_i = 110 μM. The data was averaged from the results of n = 4 patches. Smooth lines are Boltzmann fits to data. With BIS, z = 1.29 and V_1/2 = 1.1 mV. With 20 mM [KCl]_i added to BIS, z = 1.21 and V_1/2 = 7.2 mV. (B) G-V relations of mslo1 channels at 110 μM or 10.1 mM [Ca²⁺]_i. Smooth lines are Boltzmann fits to data. At 110 μM [Ca²⁺]_i, z = 1.09 and V_1/2 = 1.0 mV. At 10.1 mM [Ca²⁺]_i, z = 1.06 and V_1/2 = −75.1 mV.

Then, are these sites only selective to Mg²⁺, or does Ca²⁺ also bind to them? It has been well- known that the activation of mslo1 channels is not saturated at [Ca²⁺]_i, even above 1 mM (Wei et al. 1994; Cui et al. 1997) although the dissociation constants of the high affinity Ca²⁺ binding sites are estimated to be 1 and 10 μM at open and closed conformations, respectively (Cox et al. 1997a). The continued activation of mslo1 channels at [Ca²⁺]_i above 110 μM was suggested to derive from a binding site nonspecific for divalent cations (Wei et al. 1994). It was also reported that Ca²⁺ sensitivity persisted in mslo1 channels when the Ca²⁺ bowl was substituted with sequences from the mslo3 tail, suggesting that a second class of Ca²⁺ binding sites might exist (Schreiber et al. 1999). As shown in Fig. 5 B, adding 10 mM [Ca²⁺]_i to the internal solution that contained 110 μM [Ca²⁺]_i shifted the G-V relation to more negative voltages by ∼75 mV. This effect is similar to that of 10 mM [Mg²⁺]_i at 110 μM [Ca²⁺]_i (Fig. 1 B), suggesting that Ca²⁺ may bind to the Mg²⁺ binding sites and activate mslo1 channels to the same extent. 10 mM [Ca²⁺]_i also activates the chimera channel expressed from the mix of mslo1 core and mslo3 tail, shifting the G-V relation by −70 mV (unpublished data). This chimera channel lacked the Ca²⁺ sensitivity when [Ca²⁺]_i was lower than 110 μM because of the absence of the high affinity Ca²⁺ sites (Schreiber et al. 1999). Therefore, its activation by 10 mM [Ca²⁺]_i is most likely through the low affinity Mg²⁺/Ca²⁺ binding sites. Based on extensive analysis of mslo1 channel activation in the presence of high [Ca²+] (1–100 mM), Zhang et al. 2001 also concluded that Ca²⁺ at high concentrations activates the channel through the low affinity Mg²⁺/Ca²⁺ binding sites. It is worth pointing out that these results do not exclude the possibility that Ca²⁺ at 10 mM concentration may activate the channel by binding to yet another class of low affinity Ca²⁺ sites that differ from both the high affinity Ca²⁺ sites and the Mg²⁺ sites. However, we consider it a less likely mechanism.

Mg²⁺ Competitively Antagonizes Ca²⁺-dependent Activation

When the high affinity Ca²⁺ binding sites in mslo1 channels are either empty of ([Ca²⁺]_i = 0) or nearly saturated by Ca²⁺ ([Ca²⁺]_i = 110 μM), 10 mM [Mg²⁺]_i shifts the G-V by about −65 mV (Fig. 1 and Fig. 2). These results indicate that the binding of Mg²⁺ to the low affinity Mg²⁺/Ca²⁺ sites has no effect on Ca²⁺-dependent activation via the high affinity Ca²⁺ sites. However, when [Ca²⁺]_i was between 0 μM and the saturating 110

μM, 10 mM [Mg²⁺]_i shifted the G-V to less extents (Fig. 6A and Fig. B). The amount of G-V shift caused by 10 mM [Mg²⁺]_i dropped to <5 mV at 4 μM [Ca²⁺]_i, and then increases at higher [Ca²⁺]_i (Fig. 6 B). Such a Ca²⁺ dependence of the Mg²⁺ induced G-V shift indicates that, besides activating the channel by binding to the low affinity Mg²⁺/Ca²⁺ sites, Mg²⁺ also interferes with Ca²⁺ binding at the high affinity Ca²⁺ sites. Such interference is consistent with the mechanism that Mg²⁺ competitively binds to the high affinity Ca²⁺ sites and antagonizes Ca²⁺-dependent activation. Thus, Mg²⁺ may affect channel activation by two separate mechanisms. Mg²⁺ binds to the low affinity Mg²⁺/Ca²⁺ sites and activates the channel, shifting the G-V to the left on voltage axis. Meanwhile, Mg²⁺ also binds to the high affinity Ca²⁺ site and prevents Ca²⁺ from binding to the same site. Unlike Ca²⁺, Mg²⁺ may bind to the high affinity Ca²⁺ sites with an affinity that does not depend on the conformation of the channel and, thus, unable to activate the channel. Therefore, in the absence of Ca²⁺ ([Ca²⁺]_i = 0) the binding of Mg²⁺ to the high affinity Ca²⁺ sites has no effect on channel activation. The net effect of Mg²⁺ on channel activation may derive only from its binding to the low affinity Mg²⁺/Ca²⁺ sites. At low [Ca²⁺]_i, due to the competition from Mg²⁺, Ca²⁺ activates the channel to a lesser extent than it would have in the absence of Mg²⁺. The net effect on the G-V by adding Mg²⁺ to the low [Ca²⁺]_i solution would be the left shift derived from the binding of Mg²⁺ to low affinity Mg²⁺/Ca²⁺ sites minus the lost Ca²⁺-dependent activation due to the competitive binding of Mg²⁺ to high affinity Ca²⁺ sites. This net leftward shift is less than the Mg²⁺ induced G-V shift at 0 [Ca²⁺]_i. As [Ca²⁺]_i increases, Mg²⁺ is less competitive in binding high affinity Ca²⁺ sites, and this results in reduced losses of Ca²⁺-dependent activation. The loss of Ca²⁺-dependent activation becomes zero at the saturating [Ca²⁺]_i, where the Mg²⁺ competition is negligible. Thus, the net left-ward shift of G-V increases with [Ca²⁺]_i, and at saturating [Ca²⁺]_i it becomes the same as at 0 [Ca²⁺]_i.

If the above mechanism is correct, the competitive inhibition of Ca²⁺-dependent activation by Mg²⁺ should depend on the ratio of [Mg²⁺]_i/[Ca²⁺]_i. At 10 mM [Mg²⁺]_i the competitive inhibition becomes negligible when [Ca²⁺]_i is increased to 110 μM. However, at the same [Ca²⁺]_i of 110 μM the competitive inhibition should become evident again if [Mg²⁺]_i is increased. This prediction is confirmed by the results shown in Fig. 2. The G-V shift caused by [Mg²⁺]_i up to 10 mM is the same at 0 and 110 μM [Ca²⁺]_i. However, at 30 mM [Mg²⁺]_i, the G-V shifts less at 110 μM [Ca²⁺]_i than at 0 [Ca²⁺]_i (Fig. 2 C). At these two [Ca²⁺]_i's, the difference in G-V shift caused by 100 mM [Mg²⁺]_i is even larger (Fig. 2 C), indicating the loss of Ca²⁺-dependent activation caused by the competitive inhibition. The above mechanism is also supported by the result that the Mg²⁺ induced G-V shift of the channel from the coexpression of mslo1 core and mslo3 tail is not affected whether [Ca²⁺]_i is 0 or 1.1 μM (Fig. 3).

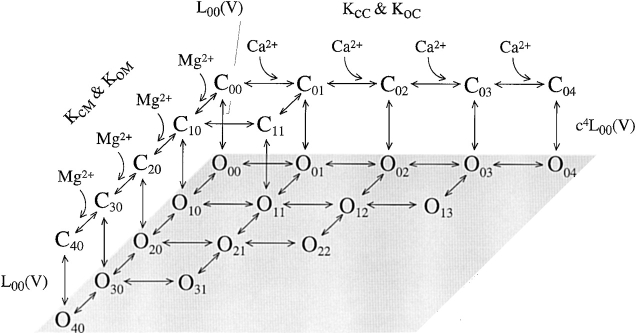
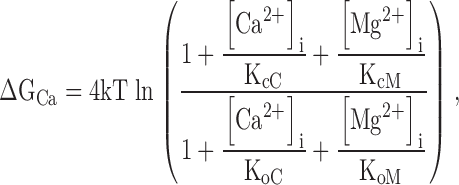
Fig. 2 shows a kinetic model of such competitive inhibition. In this scheme, Ca²⁺-dependent activation of the mslo1 channel follows the MWC model (Cox et al. 1997a). The four high affinity Ca²⁺ binding sites can be occupied by either Mg²⁺ or Ca²⁺. The affinity for Ca²⁺ is higher at open states (dissociation constant: K_oC) than at closed states (K_cC), thus, the binding of Ca²⁺ activates the channel. On the other hand, the binding of Mg²⁺ does not affect channel gating because the affinity for Mg²⁺ is the same at both open and closed states (K_oM = K_cM). The occupancy of Mg²⁺ on a site prevents the binding of Ca²⁺ to the same site, thereby Mg²⁺ competitively inhibits Ca²⁺-dependent activation. Taken together, Fig. 2 describes voltage and Ca²⁺-dependent activation and the competitive inhibition by Mg²⁺, whereas Fig. 1 describes voltage and Mg²⁺-dependent activation of the mslo1 channel. Since Mg²⁺-dependent activation is not directly affected by voltage or Ca²⁺ but linked to voltage and Ca²⁺-dependent activation through the transition between closed and open conformations, the energy provided by Mg²⁺ and Ca²⁺ binding and voltage are additive in activating the channel (Cui and Aldrich 2000). The open probability of mslo1 channels, therefore, is described by:

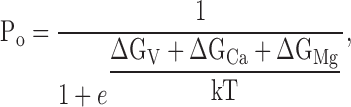2

where

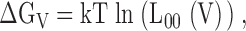3

4

and

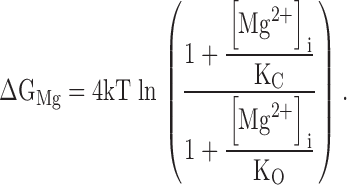5

Scheme S2.

The position of the G-V relation on voltage axis in the presence of both intracellular Ca²⁺ and Mg²⁺ is determined by:

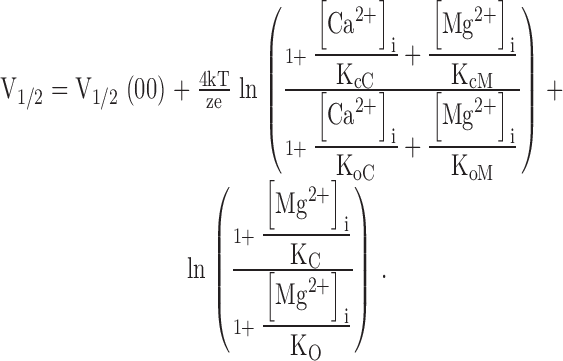6

where V_1/2(00) is the V_1/2 at 0 [Ca²⁺]_i and [Mg²⁺]_i. Such combination of Fig. 1 and Fig. 2 can account for our experimental data at various [Ca²⁺]_i, [Mg²⁺]_i, and voltages (Fig. 6, A–D) with the same parameters (Fig. 2, legend, and Fig. 2 footnote).

The above results demonstrate that intracellular Mg²⁺ has two opposing effects on the activation of the mslo1 channel: activating the channel by binding to the low affinity Mg²⁺/Ca²⁺ sites, and inhibiting Ca²⁺-dependent activation by competitively binding to the high affinity Ca²⁺ sites. Neither effect of Mg²⁺ changes the dissociation constants of Ca²⁺ binding to the channel at the open or closed conformation. In other words, Mg²⁺ does not affect the intrinsic Ca²⁺ affinity for the channel or the efficacy of Ca²⁺ in activating the channel. However, the combination of these two effects of Mg²⁺ changes the Ca²⁺ dose-response of channel activation as shown in Fig. 6. The [Ca²⁺]_i dependence of the steady-state open probability (G/G_max) at 0 (Fig. 6 C) or 10 mM [Mg²⁺]_i (Fig. 6 D) are shown with voltages at −40–100 mV and −80–60 mV, respectively. Since at low [Ca²⁺]_i both the activation and inhibition effects of Mg²⁺ are manifested, whereas at high [Ca²⁺]_i the inhibition effect is diminished, the curve in the presence of 10 mM [Mg²⁺]_i is more sigmoidal than that in the absence of Mg²⁺ at a certain voltage. This difference is reflected in Fig. 6 E where the Hill coefficient in the presence of 10 mM [Mg²⁺]_i is larger than that in the absence of Mg²⁺ at all voltages. Fig. 6 F shows that at all voltages the apparent K _d from Hill fits is smaller in the presence of 10 mM [Mg²⁺]_i. These results demonstrate that the effect of Mg²⁺ on the channel activation is to increase the apparent Ca²⁺ sensitivity of channel activation.

DISCUSSION

We have investigated three effects of intracellular Mg²⁺ on the mslo1 BK type Ca²⁺-activated K⁺ channel: (1) the block of the channel pore, (2) the allosteric activation of the channel, and (3) the competitive inhibition of Ca²⁺-dependent activation. Our results suggest that these effects are underlined by three distinct classes of Mg²⁺ binding sites and separate molecular mechanisms. Mg²⁺ binds to a site that may be in the inner mouth of the pore with rapid binding/unbinding kinetics and blocks the ion permeation. By binding to a class of low affinity Mg²⁺/Ca²⁺ sites Mg²⁺ activates the channel. Mg²⁺ also binds to the high affinity Ca²⁺ sites and inhibits Ca²⁺-dependent activation by preventing Ca²⁺ from binding to the same site.

Previous studies have shown that intracellular Mg²⁺ blocks BK channels and changes channel activation. Single-channel studies have revealed that the voltage-dependent block of Mg²⁺ (K _d ∼30 mM at 0 mV) results in a reduced single-channel conductance at positive voltages due to the rapid binding kinetics (Ferguson 1991; Laver 1992; Morales et al. 1996; Wachter and Turnheim 1996). Our results from the study of macroscopic currents are consistent with this mechanism. The mechanisms of Mg²⁺ effects on channel activation, on the other hand, were not clear. Golowasch et al. 1986 discovered that intracellular Mg²⁺ (at concentrations 1–10 mM) changed the Ca²⁺ dependence of BK channel open probabilities, increasing the Hill coefficient from 2 to as high as 5.8. Under their experimental conditions, Mg²⁺ did not activate the channel in the absence of Ca²⁺. These results led to their conclusion that Mg²⁺, as a modulator of Ca²⁺-dependent activation, revealed Ca²⁺ sites already present in the channel protein in the absence of Mg²⁺. By studying the effects of divalent cations Oberhauser et al. 1988 further supported this mechanism. Other subsequent studies also found similar results that Mg²⁺ was unable to open the channel by itself and its effect on channel activation was dependent on [Ca²⁺]_i (Squire and Petersen 1987; Trieschmann and Isenberg 1989; Zamoyski et al. 1989; McLarnon and Sawyer 1993; Zhang et al. 1995; Bringmann et al. 1997). However, the mechanism proposed by Golowasch et al. 1986 cannot account for the observation that the open probability of some BK channels increased at high [Ca²⁺]_i but decreased at low [Ca²⁺]_i (≤10 μM) after adding Mg²⁺ (at concentrations 2–5 mM; Komatsu et al. 1996; Kazachenko and Chemeris 1998). A recent study of the mslo1 homologue from Drosophila, dslo, suggested that dslo might contain as many as eight Ca²⁺ binding sites since the Hill coefficient of the channel's response to [Ca²⁺]_i was larger than four. Nevertheless, such a high Hill coefficient was obtained in the absence of intracellular Mg²⁺, which did not address the role of Mg²⁺ in the function of Ca²⁺-dependent activation (Bian et al. 2001). In the studies presented here, we recorded macroscopic currents that enabled us to observe the channel activation at much wider range of voltages than previous single-channel studies. Our results demonstrate that Mg²⁺ activates BK channels independently of Ca²⁺. On the other hand, Mg²⁺ may competitively inhibit Ca²⁺-dependent activation. Neither effect changes the intrinsic Ca²⁺ affinity for its binding site or the efficacy of Ca²⁺ in activating the channel upon binding. However, these two opposing effects result in the change of the Ca²⁺ dose-response of channel activation and an enhanced Hill coefficient. It is important to note that the Hill coefficient in our results is no larger than four, even in the presence of 10 mM [Mg²⁺]_i (Fig. 6 E), which is consistent with our conclusion that no additional high affinity Ca²⁺ sites in the mslo1 channel are exposed by Mg²⁺. This result is qualitatively different from the result of Golowasch et al. 1986 and the reason for such discrepancy needs to be further investigated.

Three Distinct Classes of Binding Sites for Intracellular Divalent Cations

The sites for Mg²⁺-dependent activation are distinct from the site for Mg²⁺ block in mslo1 channels. Three lines of evidence lead to this conclusion: first, Mg²⁺-dependent activation has different voltage dependence from Mg²⁺ block (Fig. 1). Second, Mg²⁺ that blocks the BK channel binds to a site in the channel pore with a bimolecular interaction (Fig. 1; Ferguson 1991; Laver 1992). On the other hand, there are at least two cooperative binding sites for Mg²⁺ in the activation of a mslo1 channel (Fig. 2 and Fig. 4). Third, Mg²⁺ does not activate the mslo3 channel, but blocks it similarly as to mslo1 (Fig. 3 B). This conclusion is also consistent with previous results that the potency of various cations in blocking BK channels follows a different sequence than the effectiveness of divalent cations in activating the channel (Oberhauser et al. 1988). Different voltage dependence of Mg²⁺-dependent activation and Mg²⁺ block was also observed in smooth muscle BK channels (Zhang et al. 1995).

The sites for Mg²⁺-dependent activation do not seem to discriminate between Mg²⁺ and Ca²⁺ as far as the effect on channel activation is concerned (Fig. 1 B and 5 B; see Zhang et al. 2001, in this issue). Mg²⁺ (or Ca²⁺) activates the channel because the affinity of these sites is higher at the open conformations than at the closed. It is interesting that both Mg²⁺ and Ca²⁺ activate the channel with similar effectiveness through the low affinity sites although the ionic radius of Mg²⁺ (0.7 Å) differs from Ca²⁺ (1.2 Å) quite significantly. It suggests that these sites may not be sensitive to the size of divalent cations at either open or closed conformations. On the contrary, the effectiveness of divalent cations in activating the channel through the high affinity Ca²⁺ sites seems to be based on their radii. Only cations with radii >0.72 Å (Co²⁺) or <1.13 Å (Sr²⁺) are able to activate the channel and the effectiveness increases with larger radii within this range (Oberhauser et al. 1988). Consistent with the findings by Oberhauser et al. 1988, our results show that Mg²⁺ is too small to activate the mslo1 channel through the high affinity Ca²⁺ sites. However, we find that Mg²⁺ can bind to these sites and effectively compete with Ca²⁺ although the affinity of Mg²⁺ for these sites is much lower. These results suggest that the conformational change at these sites during channel activation may be just large enough to affect the affinity for large cations with radii >0.72 Å (Co²⁺) but not enough for small cations like Mg²⁺.

Extracellular Mg²⁺ has been shown to screen negative charges on the external surface of BK channels, resulting in a shift of the voltage activation curve (MacKinnon et al. 1989). This screen effect was nonselective among cations because external Na⁺ and K⁺ also resulted in similar shifts of the voltage activation curve (MacKinnon et al. 1989). This shift could be well fitted with the Gouy-Chapman model that quantitatively describes the effects of surface potential on the activation of various ion channels (Hille et al. 1975; McLaughlin 1977; MacKinnon et al. 1989). Unlike these results with external cations, the [Mg²⁺]_i dependence of the G-V shift is much steeper than the [Mg²⁺]_o-dependent shifts, with about −50 mV change of ΔV_1/2 between [Mg²⁺]_i of 1 and 10 mM (Fig. 2 C). Such a steep [Mg²⁺]_i dependence cannot be accounted for by the screen effect because the Gouy-Chapman model has a maximum possible slope of only 29.3 mV per 10- fold change in [Mg²⁺]_i at our experimental temperature (Hille et al. 1975).

The Allosteric Linkage among Mg²⁺, Ca²⁺, and Voltage-dependent Activation

Previous results have demonstrated that Ca²⁺ and voltage do not directly interact in activating the mslo1 channel, but are energetically linked through the transition between closed and open conformations of the channel (Cui and Aldrich 2000). The results in Fig. 2 D further support this conclusion because Ca²⁺ binding at 110 μM [Ca²⁺]_i contributes the same energy of 23 kcal/mol to channel activation at 0 or 10 mM [Mg²⁺]_i, although the voltage range of channel activation is 65 mV apart. Similarly, Mg²⁺-dependent activation of the mslo1 channel derives from the difference of its affinity for the channel at open or closed conformations (Fig. 4). It does not directly depend on Ca²⁺ or voltage (Fig. 1 and Fig. 2), but it is influenced by voltage and Ca²⁺ because they affect conformational changes during channel activation. It is striking that three separate pathways affect the transition between closed and open conformations of the mslo1 channel with a similar allosteric mechanism (Cox et al. 1997a; Horrigan et al. 1999; Cui and Aldrich 2000):

Mg²⁺, Ca²⁺, and depolarization all shift the C-O transition towards open conformations and promote the activation of the channel. However, they do not directly interact with each other during activation. In this study, we found that Mg²⁺ activated the mslo1 channel by shifting the G-V relation to more negative voltage ranges. The G-V relation at all [Mg²⁺]_i could be well fitted with the Boltzmann equation with a similar slope (Fig. 2A and Fig. B). These characteristics are similar to those of Ca²⁺-dependent activation (Fig. 6; Cui et al. 1997). Therefore, the voltage dependence of the channel in Fig. 1 II is simplified as a one-step transition between open and closed conformations (Cox et al. 1997a; Horrigan et al. 1999; Cui and Aldrich 2000).

The pathways of channel activation start with the voltage sensor and ionic binding sites. Similar to other voltage-dependent channels, the S4 transmembrane segment is likely to be part of the voltage sensor in mslo1 channels (Yang and Horn 1995; Aggarwal and MacKinnon 1996; Mannuzzu et al. 1996; Seoh et al. 1996; Yang et al. 1996; Diaz et al. 1998; Cui and Aldrich 2000). The high affinity Ca²⁺ sites are located in the tail domain of mslo1 subunits, including the Ca²⁺ bowl that contains repeated aspartate and glutamate residues (Moss et al. 1996; Schreiber and Salkoff 1997; Schreiber et al. 1999; Bian et al. 2001). The structural identity of the low affinity Mg²⁺/Ca²⁺ sites is not clear, but our results indicate that they are located in the core domain (Fig. 3). Recently, the X-ray crystal structure of the RCK domain (a structural domain for regulating the conductance of K⁺ channels) of the E. coli K⁺ channel has been solved (Jiang et al. 2001). The core of the RCK domain forms a Rossmann fold that usually contains a binding site for a metal ion. The core of slo channels also contains a RCK domain (Fig. 3A and Fig. D) with a similar structure (Jiang et al. 2001). Therefore, it is likely that the low affinity Mg²⁺/Ca²⁺ site resides in the RCK domain. The primary sequence of the RCK domain in slo channels is flanked by the S6 transmembrane domain, which may be part of the activation gate (Yellen 1998), on one side and the tail domain that contains the Ca²⁺ bowl (Schreiber et al. 1999) on the other. This position and other mutation experiments suggest the RCK to be important in the function of BK channels, possibly involved in Ca²⁺ and voltage-dependent gating (Jiang et al. 2001). The prospect that the low affinity Mg²⁺/Ca²⁺ site is also located in the RCK domain is intriguing because it suggests that all three pathways that activate the BK channel might converge at the RCK domain.

Intracellular Mg²⁺ Enhances BK Channel Function at Physiological Conditions

The three effects of Mg²⁺ on mslo1 channels are opposite in changing the K⁺ current across membrane, each with a specific dependence on voltage, [Ca²⁺]_i, and [Mg²⁺]_i. Therefore, their contribution to cell physiology is complex. By combining the quantitative description of all three individual effects we are able to simulate the overall effect of Mg²⁺ on the whole cell BK channel conductance (Fig. 7). It is clear that, at voltages below 0 mV, [Mg²⁺]_i of ∼1–5 mM enhances BK channel function over the entire range of [Ca²⁺]_i. Even at [Ca²⁺]_i of ∼10–100 μM, where the channel has a substantial open probability (≥0.1; Fig. 6), BK channel conductance is increased by ∼30–100%. Such an increase enhances the polarization of membrane potential by BK channels and can lead to significant consequences in neurotransmitter release, electric tuning in cochlear hair cells, and smooth muscle contraction. In these physiological processes, BK channels are co-localized with voltage-dependent Ca²⁺ channels (Roberts et al. 1990; Robitaille et al. 1993; Yazejian et al. 1997; Marrion and Tavalin 1998; Yazejian et al. 2000) or RYR (Jaggar et al. 2000) and functionally coupled to them by sensing the Ca²⁺ entering cytosol through these channels. Due to the spacial proximity between BK channels and voltage-dependent Ca²⁺ channels or ryanodine receptors the local [Ca²⁺]_i surrounding these BK channels is >10 μM (Roberts 1994; Neher 1998; Jaggar et al. 2000; Yazejian et al. 2000).

Figure 7.

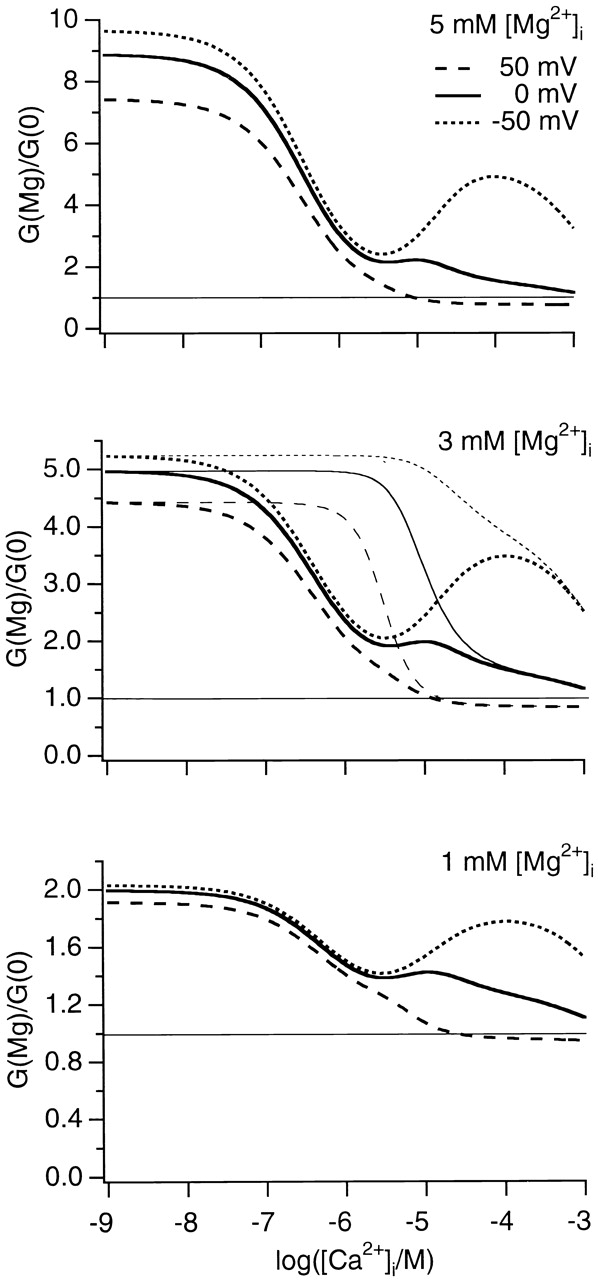
The ratio of conductance with or without intracellular Mg²⁺. The conductance, G = γP_o, in the presence of 5, 3, or 1 mM [Mg²⁺]_i versus that in the absence of Mg²⁺ are plotted against [Ca²⁺]_i (top to bottom), where γ is the single-channel conductance. Results at three physiological voltages (50, 0, and −50 mV) are displayed. The horizontal straight line indicates the ratio of 1. P_o is computed from ∼5 with parameters described in Fig. 2 legends and Fig. 2 footnote. γ is computed from the Woodhull model and the parameters described in Fig. 1 legend. We assume that Ca²⁺ is equivalent to Mg²⁺ in blocking the channel (Cox et al. 1997b) and in activating the channel by binding to the low affinity Mg²⁺/Ca²⁺ sites (Fig. 5). Therefore, even in the absence of Mg²⁺, the low affinity Mg²⁺/Ca²⁺ sites are occupied by Ca²⁺ and contribute to activation; similarly, the channel is blocked by Ca²⁺. At 3 mM [Mg²⁺]_i (middle) we also computed the ratio of conductance without considering the competition of Mg²⁺ at the high affinity Ca²⁺ sites (thin curves).

The contribution of each Mg²⁺ effect on BK channel conductance is particularly prominent at specific voltage and [Ca²⁺]_i ranges. For example, since the open probability of mslo1 channels is close to 1 at 50 mV and [Ca²⁺]_i ≥10 μM Mg²⁺ can no longer increase it. The only observable effect of Mg²⁺ is to block the channel. Therefore, the whole cell BK channel conductance is reduced by Mg²⁺ under this condition (Fig. 7). The combined Mg²⁺ block and Mg²⁺-dependent activation, but not the competitive inhibition of Ca²⁺-dependent activation, is also plotted in Fig. 7 at 3 mM [Mg²⁺]_i (middle, thin curves). The comparison of this result with the ones that include the competitive inhibition (Fig. 7, thick curves) demonstrates that the competitive inhibition of Ca²⁺-dependent activation by Mg²⁺ results in a significant reduction of the Mg²⁺-dependent activation at [Ca²⁺]_i of ∼0.1–100 μM.

Scheme S3.