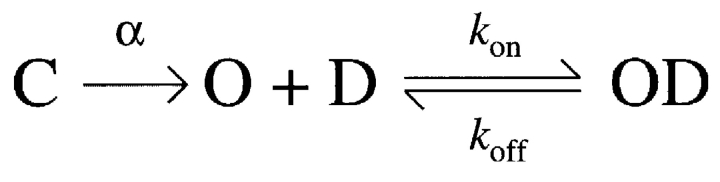Mechanism of Block of hEag1 K⁺ Channels by Imipramine and Astemizole

Abstract

Ether à go-go (Eag; K_V10.1) voltage-gated K⁺ channels have been detected in cancer cell lines of diverse origin and shown to influence their rate of proliferation. The tricyclic antidepressant imipramine and the antihistamine astemizole inhibit the current through Eag1 channels and reduce the proliferation of cancer cells. Here we describe the mechanism by which both drugs block human Eag1 (hEag1) channels. Even if both drugs differ in their affinity for hEag1 channels (IC₅₀s are ∼2 μM for imipramine and ∼200 nM for astemizole) and in their blocking kinetics, both drugs permeate the membrane and inhibit the hEag1 current by selectively binding to open channels. Furthermore, both drugs are weak bases and the IC₅₀s depend on both internal an external pH, suggesting that both substances cross the membrane in their uncharged form and act from inside the cell in their charged forms. Accordingly, the block by imipramine is voltage dependent and antagonized by intracellular TEA, consistent with imipramine binding in its charged form to a site located close to the inner end of the selectivity filter. Using inside- and outside-out patch recordings, we found that a permanently charged, quaternary derivative of imipramine (N-methyl-imipramine) only blocks channels from the intracellular side of the membrane. In contrast, the block by astemizole is voltage independent. However, as astemizole competes with imipramine and intracellular TEA for binding to the channel, it is proposed to interact with an overlapping intracellular binding site. The significance of these findings, in the context of structure–function of channels of the eag family is discussed.

INTRODUCTION

Ether à go-go 1 (Eag1) channels (K_V10.1; Catterall et al., 2002) are transmembrane proteins belonging to the family of voltage-gated K⁺ channels (Warmke et al., 1991; Brüggemann et al., 1993; Ludwig et al., 1994; Warmke and Ganetzky, 1994). In adult mammals, the expression of Eag1 channels is restricted to the nervous system (Ludwig et al., 1994; Occhiodoro et al., 1998; Shi et al., 1998; Pardo et al., 1999; Ludwig et al., 2000; Saganich et al., 2001). However, Eag1 channels are also ectopically expressed in many cancer cell lines and are thought to be important for tumor growth (Meyer and Heinemann, 1998; Meyer et al., 1999; Pardo et al., 1999; Ouadid-Ahidouch et al., 2001; Gavrilova-Ruch et al., 2002).

In particular, transfection of Eag1 into mammalian cells confers a transformed phenotype and favors tumor progression in vivo, while inhibition of Eag1 expression inhibits cell proliferation (Pardo et al., 1999). The molecular mechanisms responsible for this phenomenon are unknown. Interestingly, it has recently been published that, when present in the growth medium of Eag1-expressing tumor cells, both the tricyclic antidepressant imipramine (Gavrilova-Ruch et al., 2002) and the antihistamine astemizole (Ouadid-Ahidouch et al., 2001) slow cell proliferation. This effect was proposed to result from the selective blockade of Eag1 channels by both drugs. Therefore, knowledge about the mechanism of block of Eag1 channels by these substances should facilitate the analysis of the role these channels play in cell cycle regulation. Experimental evidence is presented here that gives insight into a common mode of action for these drugs, and the significance of these findings, in the context of structure–function of channels of the eag family, is discussed.

MATERIALS AND METHODS

Human ether à go-go 1 channels (hEag1; Occhiodoro et al., 1998; Pardo et al., 1999) cloned into pTracer-CMV (Invitrogen) were stably expressed in HEK-293 cells (human embryonic kidney; DSMZ). Cells were grown in DMEM/nutrient mixture F-12 with glutamax-I (GIBCO BRL) supplemented with 10% fetal calf serum and Zeocin (300 μg/ml).

For electrophysiological experiments, cells were grown for 24–72 h on poly-l-lysine–coated glass coverslips. All electrophysiological experiments were performed at room temperature. Macroscopic currents were recorded in the whole-cell, inside-out, or outside-out configurations of the patch-clamp technique (Hamill et al., 1981) using an EPC-9 amplifier (HEKA). Patch pipettes with a tip resistance of 0.9–1.5 MΩ were made from Corning #0010 capillary glass (WPI). Series resistance was compensated by >60%. The control internal solution contained (in mM) 100 KCl, 45 NMDG, 10 1,2-bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid tetrapotassium salt (BAPTA·K₄), 10 HEPES/HCl, pH 7.35. In experiments where the pH of the internal solution was set to 6.4 or 8.4 (Figs. 8 and 9), HEPES was replaced with an equivalent concentration of MES or CHES, respectively. The control external recording solution contained (in mM) 160 NaCl, 2.5 KCl, 2 CaCl₂, 1 MgCl₂, 8 glucose, 10 HEPES/NaOH, pH 7.4. In experiments where the pH of the external solution was set to 6.4 or 8.4 (Figs. 8 and 9), HEPES was replaced with an equivalent concentration of BIS-TRIS propane. In experiments using high external [K⁺], [Na⁺] was lowered so that the sum of [K⁺] and [Na⁺] remained constant. Cell-attached patches (Fig. 4) were recorded using 140 mM external K⁺ and a pipette solution containing control external recording solution without glucose. Inside-out patches (Figs. 9 and 10) were recorded using a pipette solution containing (in mM) 145 NaCl, 5 KCl, 3 CaCl₂, 1 MgCl₂, 10 HEPES/NaOH, pH 7.4, and a bath solution containing (in mM) 160 KCl, 0.5 MgCl₂, 10 EGTA, 10 BIS-TRIS propane/KOH, pH 6.0–8.4.

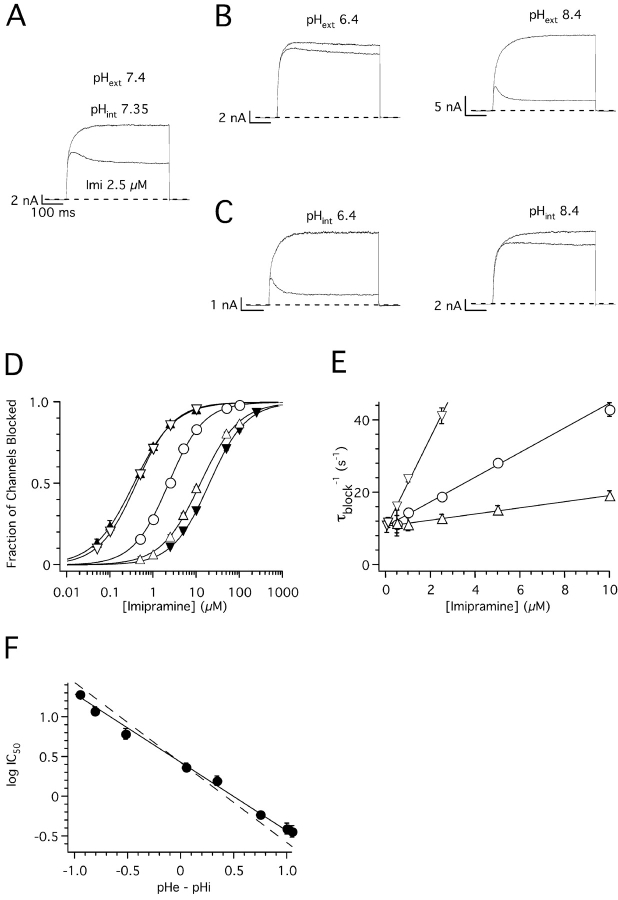
Figure 8.

pH dependence of imipramine block of hEag1 channels. (A–C) Superimposed whole-cell current traces recorded during 1-s depolarizations to 80 mV from a holding potential of −70 mV in the absence (top) and presence (bottom) of 2.5 μM imipramine. Currents were recorded in control external and internal solutions (A), or in conditions where either the pH of the external (pH_ext; B) or internal solutions (pH_int; C) was varied to the indicated values. (D) Dose–response plots for imipramine at pH_ext//pH_int relations of 7.4//7.35 (open circles), 6.4//7.35 (closed inverted triangles), 8.4//7.35 (closed triangles), 7.4//6.4 (open inverted triangles), and 7.4//8.4 (open upright triangles). The steady-state fraction of channels blocked was calculated as in Fig. 1 B. The data were fitted using the Hill equation (solid lines, see text for average IC₅₀). (E) Rate of current block (τ_block ⁻¹) as a function of nonsaturating imipramine concentrations recorded at pH_ext 7.4, and pH_int 6.4 (open inverted triangles), 7.35 (closed circles), or 8.4 (open triangles). Straight lines through τ_block ⁻¹ data represent fits to the data with linear functions with slopes of 12.6, 3.4, and 0.9 s⁻¹μM⁻¹, and y intercepts of 10.4, 10.7, and 10.7 μM to data recorded at pH_int 6.4, 7.4, and 8.4, respectively. Symbols and associated error bars in D and E represent means ± SEM for three (control) and five cells (rest of the conditions). (F) logIC₅₀ plotted as a function of the difference between pH_ext and pH_int. Closed circles and associated error bars represent means ± SD of individual fits to cells shown in D, plus four cells tested at pH_ext//pH_int 7.1//7.7, five cells at 7.1//6.8, three cells at 7.6//6.8, and five cells at 7.1//8. Straight line through symbols represents the best fit of a linear function with slope −0.86, and y intercept 0.43, to the data. The dotted line has the same y intercept, but a slope of −1.

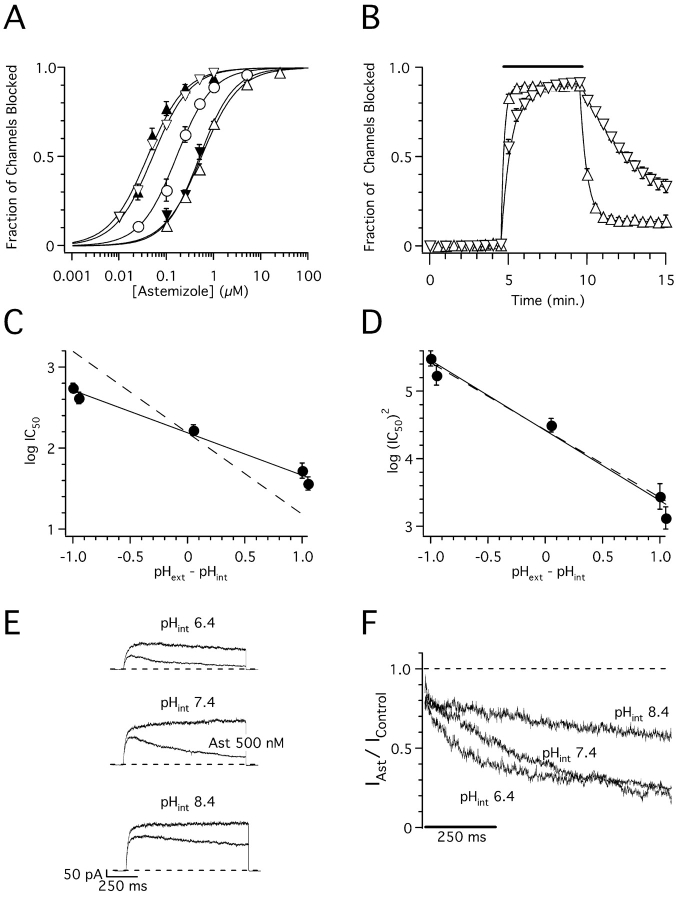
Figure 9.

pH dependence of astemizole block of hEag1 channels. (A) Dose–response plots for astemizole at pH_ext//pH_int relations of 7.4//7.35 (open circles), 6.4//7.35 (closed inverted triangles), 8.4//7.35 (closed upright triangles), 7.4//6.4 (open inverted triangles), and 7.4//8.4 (open upright triangles). The steady-state fraction of channels blocked was calculated as in Fig. 1 D. The data were fitted using the Hill equation (solid lines, see text for average IC₅₀). Symbols and associated error bars represent means ± SEM for three (control and pH_ext 8.4), five (pH_ext 6.4 and pH_int 8.4), and ten cells (pH_int 6.4). (B) Time course of block onset and washout in cells recorded with pH_ext 7.4 and pH_int 6.4 (open inverted triangles) or 8.4 (open triangles). The recording protocol consisted of a 1-s test pulse to 80 mV applied every 30 s. The fraction of channels blocked was calculated from the mean current recorded during the last 20 ms of the test pulse. During the time indicated by the solid line, cells were exposed to 250 nM (pH_int 6.4) or 5 μM astemizole (pH_int 8.4). Solid lines through symbols represent the best fit of single exponential functions (see text for time constants) to the experimental data during drug application and washout. Symbols and associated error bars represent means ± SEM for three cells tested in each condition. (C and D) logIC₅₀ (C) and log(IC₅₀)² (D) plotted as a function of the pH difference between pH_ext and pH_int. Closed circles and associated error bars represent means ± SD of individual fits of cells shown in A. Straight line through symbols represents the best fit of linear functions with slopes and y intercepts given in the text to the data. The dotted lines have the same y intercepts, but slopes of −1. (E) Superimposed hEag1 current recorded in the same inside-out patch during 1-s depolarizations to 80 mV from a holding potential of −70 mV in the absence (top) or presence (bottom) of a 500 nM astemizole concentration at the indicated bath pHs. Each current trace presented is the average of three recordings at each condition. (F) Inside-out current traces in the presence of astemizole were normalized dividing them point by point by the respective preapplication traces. Traces shown represent the average current ratios from five patches recorded as in E.

Figure 4.

Membrane permeability of imipramine and astemizole. Superimposed hEag1 current traces recorded during 1-s depolarizations to 60 mV from a holding potential of −70 mV in the absence, presence, and after washout of the indicated bath concentrations of imipramine (A) or astemizole (B) in cell-attached patches.

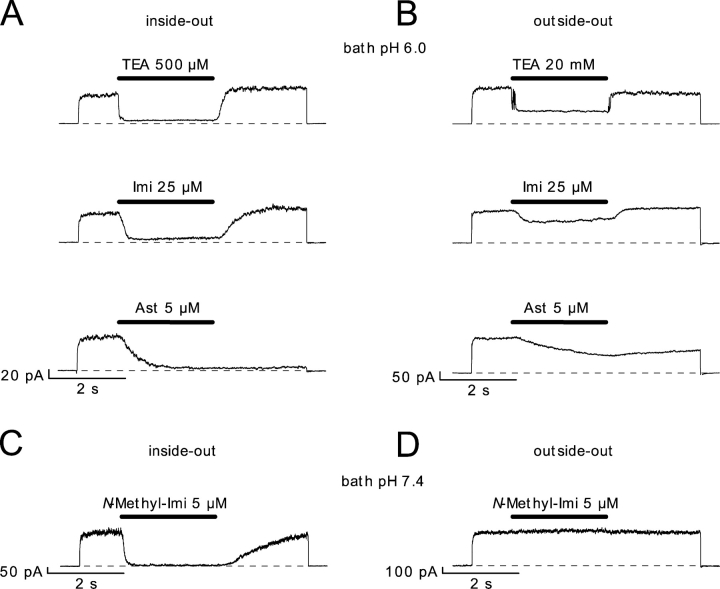
Figure 10.

Block of hEag1 channels by imipramine, N-methyl-imipramine, and astemizole in cell-free patches. (A and B) Successive 6-s recordings at 80 mV in the same inside-out (A) or outside-out patches (B), respectively. At the time indicated by the solid line, the substances where applied during 2.5 s at the indicated concentrations. The bath solution had, in both cases, a pH of 6.0, while the pipette solution had a pH of 7.4. (C and D) Effect of application of N-methyl-imipramine on representative inside-out (C) and outside-out (D) patches, at both external and internal pH of 7.4.

N-methyl-imipramine (Fig. 10) was synthesized from imipramine as follows. 10 ml of a 1.26 M NaOH solution was slowly added to 20 ml of a 394 mM imipramine hydrochloride solution cooled to 0°C. The resulting mixture was stirred for 30 min at this temperature. Then, saturated aqueous solutions of NaCl (50 ml) and CH₂Cl₂ (50 ml) were added and the aqueous layer was extracted with CH₂Cl₂ (3 × 50 ml). The combined organic layers were dried (MgSO₄) and evaporated to dryness to provide a yellow oil. The oil was dissolved in acetone (10 ml), and 540 μl of CH₃I (2.28 g/ml) was added dropwise under an atmosphere of argon. After stirring for 2 h at room temperature, the solvent was removed in vacuo, and the resulting crude product was washed with acetone. Drying under vacuum provided N-methyl-imipramine iodide as a white powder (2.95 g, 89%), which was subjected to NMR spectroscopy. The obtained spectra matched the simulated spectra of N-methyl-imipramine iodide (Shayman and Barcelon, 1990).

Astemizole and N-methyl-imipramine were diluted from a DMSO stock solution. The final concentration of DMSO was always 0.1%, a concentration that showed no discernible effects on hEag1 currents (n = 4). Imipramine was used from stocks in distilled water. Both drugs were purchased from Sigma-Aldrich.

Data processing and curve fitting were performed with Igor Pro (WaveMetrics). Where used, statistical significance of the difference between two groups of data was analyzed with Excel using Student's t test for a two-tailed distribution of samples with unequal variance. All quantitative data in the text are expressed as mean ± SD.

RESULTS

Dose-dependent Inhibition of hEag1 Currents by Imipramine and Astemizole

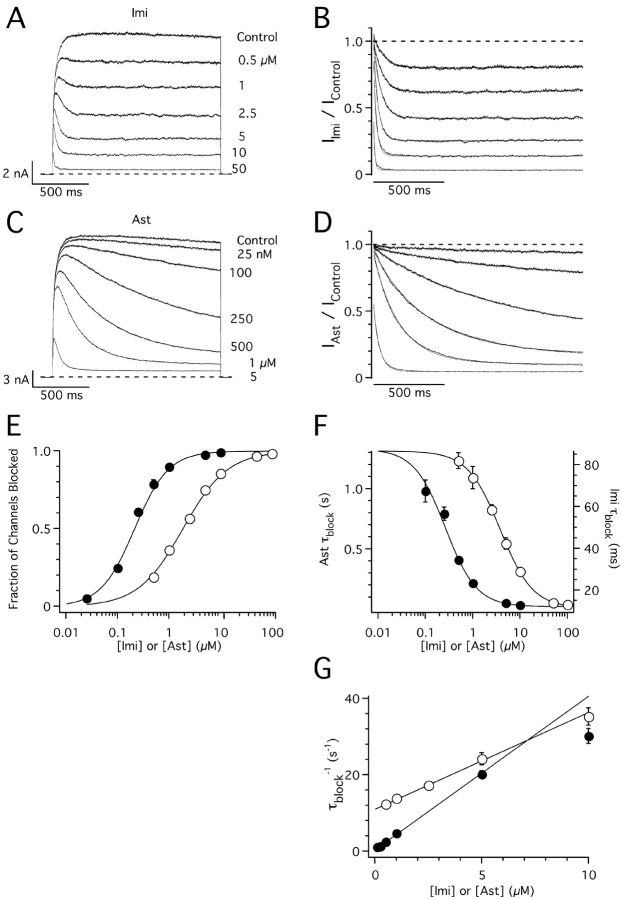
hEag1 channels do not inactivate during sustained depolarizations to potentials that activate most of the channels (Fig. 1 A, control trace). However, in the presence of imipramine (Fig. 1 A) or astemizole (Fig. 1 C), a clear time- and dose-dependent decay of hEag1 currents was observed. This suggests that both drugs block open hEag1 channels (Armstrong, 1969). After both drugs attained the equilibrium concentration near their active site, consecutive current traces recorded at 30-s intervals were identical (unpublished data). Thus, there is no trapping of imipramine and astemizole by closure of hEag1 channels (Armstrong, 1971; Choquet and Korn, 1992; Mitcheson et al., 2000a).

Figure 1.

Concentration dependence of hEag1 block by imipramine and astemizole. (A and C) Superimposed hEag1 current traces recorded during 1.5 s test depolarizations to 80 mV from a holding potential of −70 mV in the absence and presence of the indicated concentrations of imipramine (Imi, A) or astemizole (Ast, C). Test potential was chosen to achieve the maximal open probability of hEag1, whose activation curve saturates above 60 mV (not depicted). The effects of drug application were monitored with test pulses applied every 30 s until a steady-state block was reached. (B and D) Current traces in the presence of imipramine or astemizole were normalized dividing them point by point by the respective preapplication traces. Solid lines indicate the best fit to a single exponential function. (E) Dose–response plots for imipramine (open circles) and astemizole (closed circles). The steady-state fraction of channels blocked was calculated from the asymptotic values of single exponential fits to current ratios as shown in B and D. Solid lines represent fits to the data using the Hill equation, with IC₅₀ values and Hill coefficients of 1.87 μM and 1.04 for imipramine, and 0.21 μM and 1.32 for astemizole, respectively. (D) Time constant of block (τ_block) for imipramine (open circles) and astemizole (closed circles) derived from the least-squares fits of single exponential functions used in E. Solid lines represent fits to the data using the Hill equations, with maximum, minimum, IC₅₀, and Hill coefficients of 86.7 ms, 11.6 ms, 3.75 μM, and 1.27 for imipramine, and 1.33 s, 0.024 s, 0.26 μM, and 1.32 for astemizole, respectively. (G) The rate of current block is represented (τ_block ⁻¹) as a linear function of nonsaturating imipramine (open circles) or astemizole (closed circles) concentrations. Solid lines represent fits to the data with a linear function, with slope and y intercept of 2.5 s⁻¹μM⁻¹ and 11.1 μM for imipramine, and 4 s⁻¹μM⁻¹ and 0.4 μM for astemizole, respectively. The range of drug concentrations used to fit τ_block ⁻¹ data to the linear function was between 0.5 and 10 μM for imipramine and between 25 nM and 5 μM for astemizole. Symbols and associated error bars in E–G represent means ± SEM for six and seven cells for imipramine and astemizole, respectively.

The time course of the block induced by both drugs (I_Drug/I_Control) followed a single exponential function at all concentrations tested (Fig. 1, B and D). The respective I_Drug/I_Control traces start at values close to one for nonsaturating drug concentrations, indicating that channel block proceeds after channel opening. Dose–response curves constructed from the asymptotic values of mono-exponential fits to I_Drug/I_Control traces gave IC₅₀ values of 1.8 ± 0.2 μM (n = 6) for imipramine, and 196 ± 36 nM (n = 7) for astemizole (Fig. 1 E). At these concentrations, the time constant of current decay (τ_block) was ∼50 ms for imipramine and ∼500 ms for astemizole (Fig. 1 F).

The linear relationship between the rate of channel block (τ_block ⁻¹) and nonsaturating drug concentrations (Fig. 1 G) suggests the following bimolecular reaction:

where D represents drug molecules and C, O, and OD denote the closed, open, and blocked states of the channels, respectively. When k _on[D] < α, drug binding is rate limiting the overall reaction. In such cases,

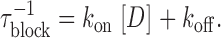(1)

The association (k _on) and dissociation (k _off) constants, obtained from the linear regions in Fig. 1 G, are 2.5 μM⁻¹s⁻¹ and 11.1 s⁻¹ for imipramine, and 4.0 μM⁻¹s⁻¹ and 0.4 s⁻¹ for astemizole. These rate constants give K _D values (k _off/k _on) of 4.7 μM for imipramine and 109 nM for astemizole, in good agreement with IC₅₀ values calculated from dose–response curves. Thus, the main difference between both drugs is the long half-life of astemizole at its binding site in hEag1 channels.

Channel activation becomes rate limiting for the overall reaction in Scheme I at saturating drug concentrations, where k _on[D] ≥ α (French and Shoukimas, 1981; Kuo, 1998). Consequently, at these drug concentrations, I_Drug/I_Control traces start at values well below one (Fig. 1, B and D), and the experimental data points for the observed macroscopic binding rate fall below the respective regression lines in Fig. 1 G.

(SCHEME 1).

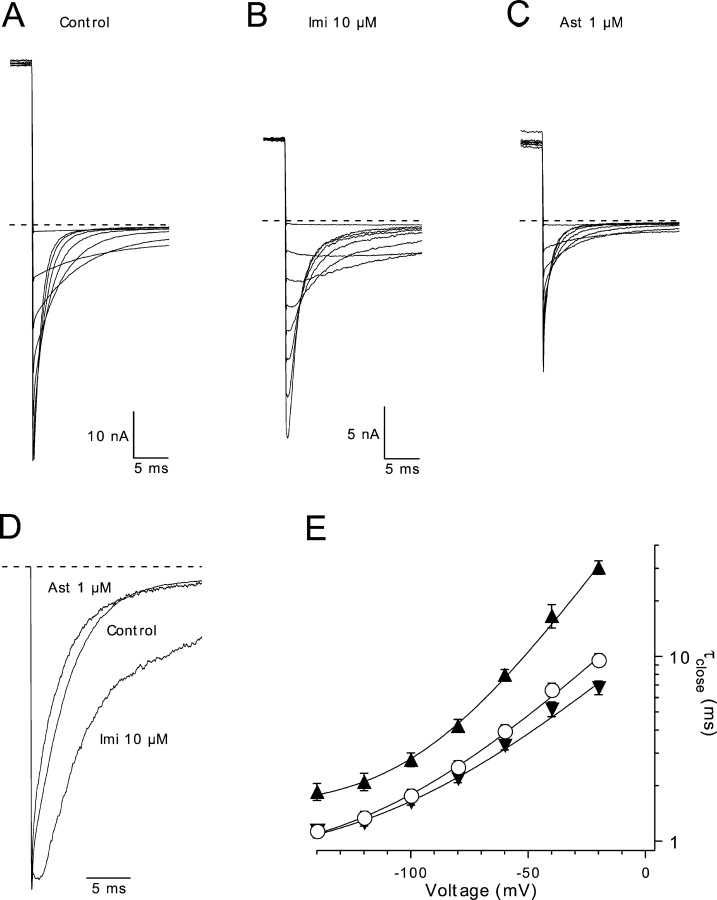
Effects of Imipramine and Astemizole on hEag1 Closing Kinetics

Scheme I implies that imipramine and astemizole need to unbind before hEag1 channels can close. The analysis of tail currents recorded in high external [K⁺] supports this hypothesis for imipramine. hEag1 currents deactivate through a mono-exponential time course in control conditions (Fig. 2 A). However, in the presence of imipramine, tail currents showed a transient increase before deactivating (Fig. 2, B and D). This indicates that imipramine unbinding is faster than channel closing (Armstrong, 1969). Deactivation was slowed in the presence of imipramine (Fig. 2 E), suggesting that its binding interferes with the channels' closing gate, a phenomenon that has been termed “foot-in-the-door” effect (Yeh and Armstrong, 1978).

Figure 2.

Deactivation kinetics in the presence of imipramine and astemizole. (A–C) Superimposed tail current traces recorded at potentials between −140 and 0 mV after 330-ms depolarizations to 80 mV from a holding potential of −60 mV in the absence of drugs (A), and in the presence of 10 μM imipramine (B) and 1 μM astemizole (C). All traces were recorded consecutively from the same cell. (D) Scaled tail current traces from A–C recorded at −60 mV. (E) Average time constant of a single exponential fit to the decay phase of the tail current (τ_close) recorded in control conditions (open circles), 10 μM imipramine (closed triangles), and 1 μM astemizole (inverted closed triangles). Solid lines represent fits to the data with an arbitrary exponential function: τ_close(V) = τ_∞ + τ(0) e^−kV, with τ_∞ , τ(0), and k values of 0.75 ms, 15.87 ms, and −0.027 (control); 1.52 ms, 65.13 ms, and −0.039 (imipramine); and 0.75 ms, 10.75 ms, and −0.025 (astemizole), respectively. Symbols and associated error bars represent means ± SEM for five cells.

In contrast, tail currents recorded in the presence of astemizole were a scaled-down version of the control trace (Fig. 2, C and D), indicating that only unblocked channels contribute to macroscopic tail currents. At saturating astemizole concentrations, tail currents were completely absent (unpublished data). This can be accounted for by the small k _off derived in Fig. 1 G for the astemizole–hEag1 interaction.

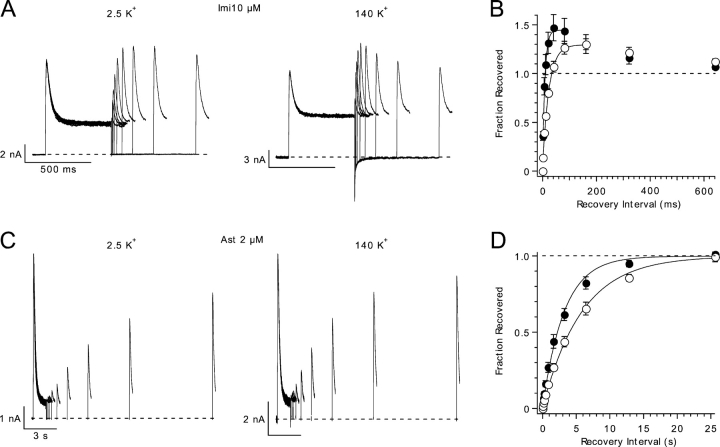
Time Course of the Recovery from Block

To further analyze the unbinding of imipramine and astemizole from hEag1 channels, and to assess the effect of K⁺ on this process, we used a double-pulse protocol in which two identical test pulses were separated by an interval of variable duration. In these conditions, hEag1 channels recovered from imipramine (Fig. 3 A) and astemizole block (Fig. 3 C) following a mono-exponential time course. Drug trapping by channel closing was not observed even at a recovery potential of −120 mV (unpublished data). The time constant of recovery at −70 mV was 24 ± 1 ms (n = 5) for imipramine and 6.14 ± 1.57 s (n = 6) for astemizole.

Figure 3.

Influence of high extracellular K⁺ on the recovery from imipramine and astemizole block. (A) Recovery of hEag1 at −70 mV from block by 10 μM imipramine with 2.5 (left) or 140 mM external K⁺ (right) is demonstrated using two depolarizations to 100 mV from a holding potential of −70 mV separated by an interval of variable duration. The first depolarization is 500 ms long, and the first 100 ms from the second depolarization is shown. (B) Time course of recovery from imipramine block in low (open circles) and high extracellular [K⁺] (closed circles). The fraction of channels that have recovered by the time of the second depolarization (Fraction Recovered) is calculated as: Fraction Recovered = (I₂ − I_SS)/(I₁ − I_SS), where I₁ and I₂ represent peak current during the first and second pulse, respectively, and I_SS represents the sustained current at the end of the first pulse. The solid lines are single exponential fits with time constants and asymptotic values of 8.7 ms and 1.45, and 23.7 ms and 1.3 for 2.5 and 140 mM external K⁺, respectively. (C) Recovery of hEag1 at −70 mV from block by 2 μM astemizole in low (left) or high (right) concentrations of external K⁺. Two depolarizations to 80 mV from a holding potential of −70 mV were applied separated by a variable interval. The first depolarization is 1 s long, and the first 250 ms from the second depolarization is shown. (D) Time course of recovery from astemizole block in low (open circles) and high extracellular K⁺ (closed circles). Fraction of channels recovered was calculated as in B. The solid lines are single exponential fits with time constants of 5.8 and 3.2 s, for 2.5 and 140 mM external K⁺, respectively.

k _off depends on the driving force for K⁺ ions for blockers that occlude the permeation pathway (Armstrong, 1966). A 56-fold increase in the extracellular [K⁺] did not result in any obvious alteration in the rate of current block at depolarized potentials (unpublished data). However, high external [K⁺] accelerated the recovery of hEag1 channels from imipramine block by 63.1 ± 3.1% (n = 5), and by 43.9 ± 8.0% (n = 6) from that by astemizole (Fig. 3, B and D). The time constant of recovery at −70 mV recorded in the presence of 140 mM external K⁺ was 8.8 ± 0.5 ms (n = 5) for imipramine and 3.52 ± 1.27 s (n = 6) for astemizole. The simplest interpretation for this effect is that the influx of K⁺ ions during repolarization is relieving occlusion by internal blockers (Armstrong, 1966, 1971; Demo and Yellen, 1991; Choi et al., 1993; DeCoursey, 1995). This suggests that both drugs are binding to the permeation pathway of hEag1 channels entering from its intracellular side. This requires them to permeate through the membrane, given that both drugs were applied to the bath.

During recovery from imipramine block, the peak current elicited by the second pulse transiently surpassed that elicited by the first pulse (Fig. 3, A and B). This “overshoot” seems to result from the faster activation of the current during the second pulse, which causes more channels to accumulate in the open state before they are blocked. The current activates faster because, first, imipramine slows current deactivation (Fig. 2), and thus some channels are still open at short intervals after the first pulse. Second, the activation kinetics of Eag1 channels depends on the prepulse potential (Terlau et al., 1996). Thus, the activation kinetics of the first test pulse current are slow due to the negative holding potential (−70 mV), while that of the second are accelerated by the previous depolarization. Accordingly, the overshoot was reduced for depolarized holding potentials (−50 mV) and augmented for more hyperpolarized holding potentials (−90 mV; unpublished data).

Imipramine and Astemizole are Membrane Permeant

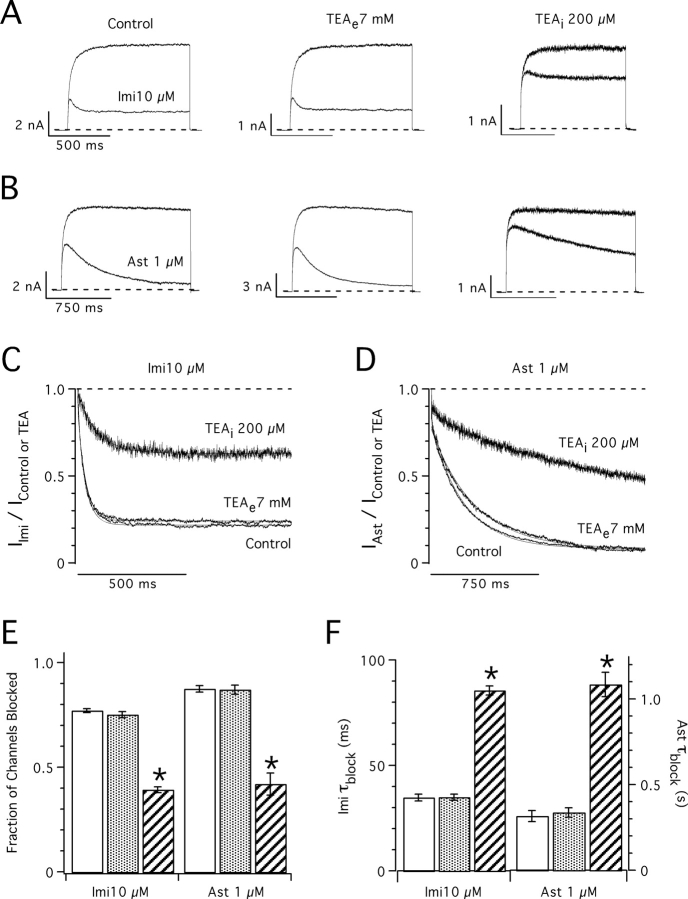
The ability of imipramine and astemizole to permeate the membrane was investigated using cell-attached patches (Fig. 4). In this configuration, drugs can only access the channels contained in the patch by passing through the membrane. hEag1 channels recorded in these conditions were blocked by bath applications of imipramine (Fig. 4 A) and astemizole (Fig. 4 B). This experiment, however, does not exclude an extracellular site of action for imipramine and/or astemizole (Brock et al., 2001). To determine the sidedness of the block by these drugs, we tested for competition with TEA. This cation is an open-pore blocker of voltage-gated K⁺ channels (Armstrong, 1966, 1969, 1971). K⁺ channels have two binding sites for TEA located at the intra- and extracellular ends of the selectivity filter (MacKinnon and Yellen, 1990; Yellen et al., 1991). Since it is permanently charged, TEA is virtually membrane impermeant and can be confined to either side of the membrane by inclusion in the bath or pipette solutions (for review see Stanfield, 1983).

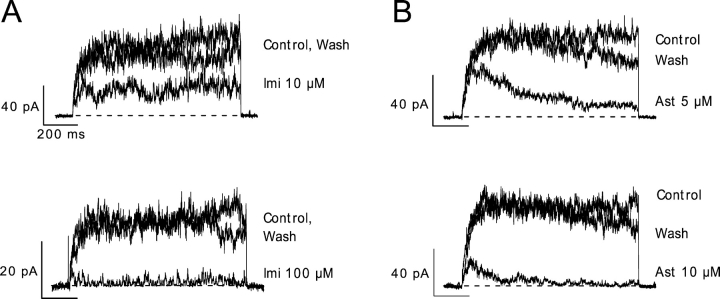
TEA blocks ∼50% of the hEag1 current at 80 mV when present at 7 mM in the external solution or 200 μM in the internal solution (unpublished data). While 7 mM external TEA did not affect the block by imipramine or astemizole (Fig. 5, A–F), both drugs showed a ∼50% reduced potency in the presence of 200 μM internal TEA (Fig. 5, A and B). While 10 μM imipramine blocked 77 ± 2% (n = 5) of the control current, it only blocked 39 ± 3% (n = 5; P < 10⁻⁷) of the current in the presence of internal TEA (Fig. 5 E). On the other hand, 1 μM astemizole blocked 87 ± 3% of the control current (n = 5) and only 42 ± 12% of the current recorded in the presence of internal TEA (n = 5; P < 10⁻⁵). The time course of block by both drugs was approximately two times slower with internal TEA than in the control (Fig. 5 F). τ_block for imipramine was increased from 35 ± 4 ms in the control to 86 ± 5 ms with internal TEA (P < 10⁻⁶), and that for astemizole was increased from 317 ± 73 ms to 1084 ± 158 ms (P < 0.005) in the same conditions. The simplest interpretation of these results is that imipramine and astemizole compete with internal TEA for overlapping binding sites (Choi et al., 1991). This strongly suggests that the binding sites for imipramine and astemizole are located in the intracellular portion of the permeation pathway of hEag1 channels.

Figure 5.

Competition of imipramine and astemizole with internal TEA. (A and B) Superimposed hEag1 current traces recorded during 1-s (A) or 1.5-s (B) depolarizations to 80 mV from a holding potential of −70 mV. The indicated concentrations of imipramine (A) or astemizole (B) were applied in control conditions (left), in the presence of 7 mM TEA in the external solution (TEA_e; middle), or in the presence of 200 μM TEA in the internal solution (TEA_i; right). Both external and internal concentrations of TEA⁺ were chosen to achieve ∼50% of current block by this cation. (C and D) Current traces in the presence of imipramine (A) or astemizole (B) were normalized dividing them point by point by the respective preapplication traces. Solid traces through the points indicate the best fit to a single exponential function. (E) Steady-state fraction of channels blocked was calculated from the asymptotic values of single exponential functions fit to current ratios as shown in C and D. (F) Time constant of block (τ_block) derived from the least-squares fits of single exponentials used in E. Columns and associated error bars in E and F represent means ± SEM for five cells recorded in control conditions (open columns), and in the presence of external TEA (closed columns), and five cells recorded in the presence of internal TEA (hatched columns).

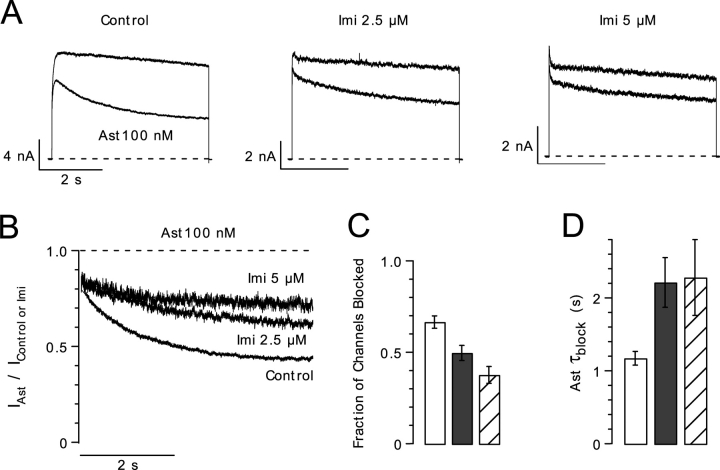
The fact that both drugs compete for binding with internal TEA suggests that both drug binding sites overlap. We tested for competition between imipramine and astemizole (Fig. 6). While 100 nM astemizole blocked 66 ± 3% (n = 5) of the control current, this concentration of the drug blocked 38 ± 5% (n = 5; P < 0.002) of the current in the presence of 5 μM imipramine (Fig. 6 C). As in the case of internal TEA, the simplest interpretation of this result is that both drugs compete for overlapping binding sites in hEag1 channels.

Figure 6.

Competition of imipramine and astemizole for overlapping binding sites. (A) Superimposed hEag1 current traces recorded during 5-s depolarizations to 60 mV from a holding potential of −70 mV in the absence (top) and presence (bottom) of 100 nM astemizole, in control external solution (left) or in external solutions containing 2.5 (center) or 5 μM (right) imipramine. (B) Current traces in the presence of astemizole from A were normalized by a point-wise division by the respective preapplication control trace. (C) The steady-state fraction of channels blocked was calculated from the asymptotic values of single exponential functions fit to the respective current ratios, as shown in B. (D) Single time constant (τ_block) of exponential fits used in C. Columns and associated error bars in C and D represent the means ± SEM for five cells tested in control conditions (open columns), and in the presence of 2.5 (closed columns) or 5 μM imipramine (hatched columns).

Voltage Dependence of Imipramine– and Astemizole–hEag1 Interactions

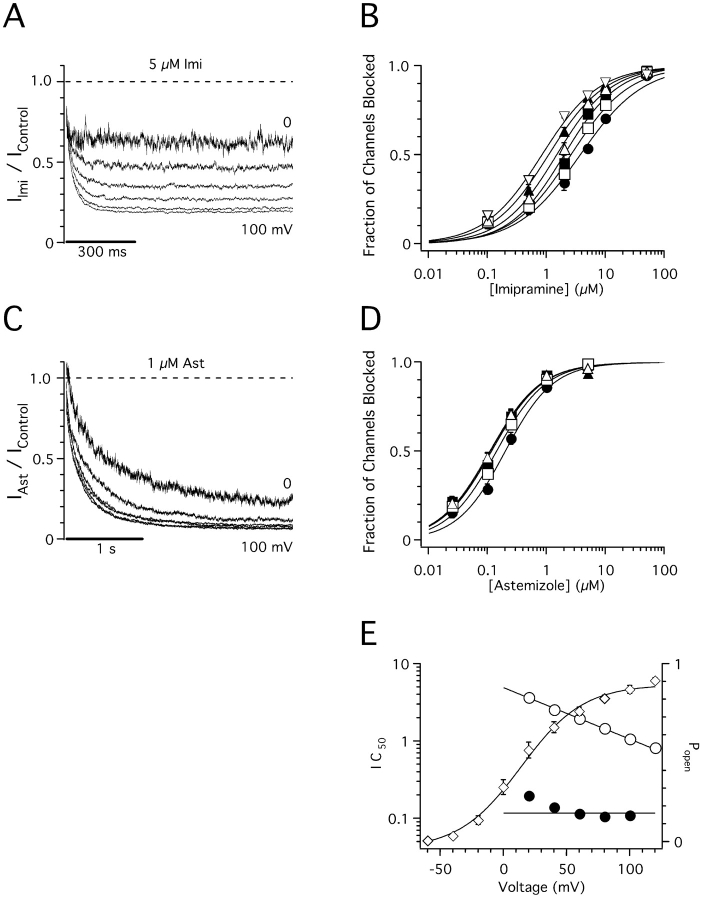
Imipramine and astemizole are both weak bases predicted to be protonated most of the time (99 and 93%, respectively) in our standard, pH 7.4 recording solution. If they bind to hEag1 channels in their charged form, and their binding sites lie deep in the membrane, their binding would be affected by a fraction of the potential difference across the membrane (Woodhull, 1973). Thus, to further characterize the binding site of both drugs, we investigated if their binding affinity is affected by membrane potential.

The fraction of blocked current by a constant concentration of imipramine increases with increasing depolarization of the membrane potential (Fig. 7 A). In particular, the IC₅₀ decreased as an exponential function of test pulse potential (Fig. 7 E). This variation can be well described with the single exponential function

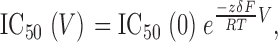(2)

where z represents the valence of the blocker, and δ reflects the fraction of the electric field across the membrane that is sensed by the blocker (Woodhull, 1973). Given that imipramine has a single protonation site (z = 1), it is estimated from these results to sense 39% of the membrane electric field at its binding site (Fig. 7 E).

Figure 7.

Voltage dependence of imipramine and astemizole block of hEag1 channels. (A and C) Current traces recorded during 1-s (A) or 3-s (C) depolarizations to potentials between 0 and 100 mV in the presence of 5 μM imipramine (A) or 1 μM astemizole (C) were normalized dividing them point by point by the respective preapplication control traces at each potential. (B and D) Dose–response plots for imipramine (B) and astemizole (D) at membrane potentials of 20 (filled circles), 40 (open squares), 60 (filled squares), 80 (open upright triangles), 100 (filled upright triangles), and 120 mV (open inverted triangles). The steady-state fraction of channels blocked was calculated from the asymptotic values of single exponential fits to current ratios, as shown in A and C using test depolarizations of 1 and 1.5 s for imipramine and astemizole, respectively. The data were fitted using the Hill equation (solid lines). IC₅₀ values are plotted in E as a function of test potential. Symbols and associated error bars in B and D represent mean ± SEM for three (0.1, 2, 5, and 50 μM) and five (0.5 and 5 μM) cells for imipramine, and six (0.1, 1, and 5 μM) and nine (0.025 and 0.25 μM) cells for astemizole. (E, left axis) IC₅₀ values derived from A (open circles) or B (closed circles) plotted as a function of the test potential. Solid line through imipramine data represents the fit to the data to Eq. 2, with IC₅₀(0), and zδ values of 4.92 μM and −0.39 e₀, respectively. Solid line through astemizole data represents the equation IC₅₀(V) = 0.12 μM. (E, right axis) Open probability of hEag1 channels at the different test potentials (P_open; open diamonds). P_open was defined as the fractional tail current recorded after a given test pulse to that recorded after a test pulse to 160 mV. Isochronal tail currents were measured at −80 mV, 500 μs after the end of the 50-ms test pulse in an external solution containing 50 mM K⁺ and no Mg²⁺. Symbols and associated error bars represent mean ± SEM for six cells. Solid line through P_open data represents the best fit to a Boltzmann equation with half activation at 13.8 mV.

In contrast to imipramine, the block induced by a constant concentration of astemizole is insensitive to membrane potential at voltages >60 mV (Fig. 7 C), where hEag1 open probability is >60% (Fig. 7 E). This finding suggests either (a) that astemizole blocks hEag1 channels by binding in its uncharged form or (b) that the binding site lies out of the major drop of transmembrane potential.

Imipramine and Astemizole Block hEag1 Channels in their Charged Form

The binding affinity of a base that blocks in its charged form should increase with increasing acidity of the solution surrounding the binding site, and the opposite should happen if the active form is uncharged (Albert, 1952). Thus, to confirm that the blocking moiety of imipramine is the charged one, and to determine the active form of astemizole, we assessed the effect of pH variations on the binding affinity of both drugs.

Variations in both intra- and extracellular pH (pH_int, pH_ext) influence hEag1 behavior. Exposure of inside-out patches to pH_int 6.4 resulted in an ∼63% reduction (compared with the values at pH_int 7.4) of the current recorded at 100 mV, while pH_int 8.4 increased current amplitude by 32% (see Fig. 9 E). These changes seem to result from the block of hEag1 channels by protons (Starkus et al., 2003), since no obvious changes in the activation threshold of the current could be detected. Whole-cell currents recorded at pH_int 6.4 started to activate at the same potentials as control (∼−40 mV), but showed current rectification at potentials positive to 80 mV (unpublished data). In contrast, changes in pH_ext shifted the voltage dependence of hEag1 currents (Terlau et al., 1996). Compared with the values at pH_ext 7.4, pH_ext 6.4 shifted the activation ∼15 mV in the depolarizing direction, while pH_ext 8.4 slightly shifted the activation by −3 to −5 mV. In consequence, currents recorded at 80 mV were ∼22% reduced at pH_ext 6.4, and ∼2% increased at pH_ext 8.4, compared with control pH_ext (unpublished data). Similar changes induced by pH_ext variations have been explained in terms of changes in the transmembrane potential sensed by the channels due to titration by protons of negative charges at the membrane surface (for review see McLaughlin, 1989).

Whole-cell currents were more inhibited by bath applications of imipramine as pH_ext was made more alkaline (Fig. 8 B) or pH_int was made more acidic (Fig. 8 C). Similar IC₅₀ values are recorded at pH_ext//pH_int 8.4//7.35 (364 ± 62 nM) and 7.4//6.4 (395 ± 61 nM), or when this relation is 6.4//7.35 (19.2 ± 1.4 μM) and 7.4//8.4 (9.8 ± 0.6 μM; Fig. 8 D). Therefore, the effectiveness of imipramine does not depend primarily on either pH_ext or pH_int but rather on their algebraic difference. Changes in the rate of current block by imipramine at different pH_int can be fully accounted for by changes in k _on[D] (Eq. 1), without any detectable change in k _off (Fig. 8 E). Thus, variations in the apparent potency of imipramine reflect a change in the concentration of the active compound close to the binding site, and not a change in the affinity of the binding site for the drug.

As imipramine was bath applied, only the concentration of charged imipramine inside the cell ([imi⁺]_int) is expected to change with variation in pH_ext//pH_int (for review see Ariëns and Simonis, 1963; Ritchie and Greengard, 1966). In our experimental conditions, [imi⁺]_int is given by

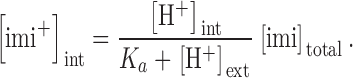(3)

Given that measurements of Fig. 8 were made at pH << pK_a, and assuming that a constant effect is produced at a constant [imi⁺]_int, Eq. 3 can be rewritten as (Choquet and Korn, 1992)

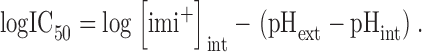(4)

Fig. 8 F plots (log IC₅₀) as a function of the difference between pH_ext and pH_int. The best linear fit to the experimental values gives a slope of −0.86, in close agreement with the theoretical value of −1 implied in Eq. 4 (drawn as a dotted line in Fig. 8 F). The calculated [imi⁺]_int required to induce a 50% reduction in the hEag1 current by this fit is 2.7 μM. Therefore, the observed experimental variations in IC₅₀ can be accounted for by changes in [imi⁺]_int at the different pH_ext//pH_int combinations employed.

In cases where pH_int < pH_ext, [imi⁺]_int > [imi]_tot (Ariëns and Simonis, 1963; Ritchie and Greengard, 1966). Trapping of charged imipramine in the interior of the cell can explain that the block washout time course at constant pH_ext is slowed as pH_int is made more acidic. A single exponential fit to the fraction of original current recovered at pH_ext 7.4 after ∼90% inhibition gave time constants of 6 ± 1, 19 ± 6, and 46 ± 8 s at pH_int of 8.4, 7.4, and 6.4, respectively, in our recording conditions (n = 4, 3, 5).

Assuming that the uncharged form of astemizole is membrane permeant (Fischer et al., 1998), its concentration inside the cell at steady state when applied externally is expected to remain constant at constant pH_ext (Ariëns and Simonis, 1963). However, the block of hEag1 channels by astemizole was affected by changes in the pH_ext//pH_int relation. IC₅₀ shifted to the left for pH_ext > pH_int, and to the right for pH_ext < pH_int (Fig. 9 A). Similar IC₅₀ values were obtained when pH_ext//pH_int were 8.4//7.35 (37 ± 7 nM) and 7.4//6.4 (54 ± 12 nM), or when this relation was 6.4//7.35 (419 ± 68 nM) and 7.4//8.4 (556 ± 69 nM; Fig. 9 A). Fig. 9 C shows the variation in (logIC₅₀) as a function of the difference between pH_ext and pH_int. The best linear fit to the experimental values gave a slope of −0.53. This suggests the following empirical relation

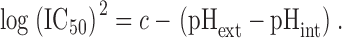(5)

Fig. 9 D shows the variation in log(IC₅₀)² as a function of the difference between pH_ext and pH_int. The best linear fit to the experimental values gives a slope of −1.04, in accord with the theoretical value of −1 implied in Eq. 5 (drawn as a dotted line in Fig. 9 D). The fact that IC₅₀ varies linearly as function of the pH_ext//pH_int relation shows that it does not depend primarily on a certain value of each of them. Therefore, the affinity of the binding site for astemizole in hEag1 channels can be assumed as constant in the pH 6.4–8.4 range. Equal effects at different pH_int should therefore reflect an equal amount of the active compound close to the binding site.

Astemizole is a very lipophilic weak base with two protonation sites (pK _a1 5.6 and pK _a2 8.5; Fischer et al., 1997, 1998). Table I shows the calculated percentages of the un-, mono-, and diprotonated forms of astemizole at each of the evaluated pHs. Fig. 9 B shows that after removal of astemizole from the bath, the hEag1 currents recover much slower at acidic pH_int. This washout had an average time constant of 25 s at pH_int 8.4, and of 235 s at pH_int 6.4 in our recording conditions. This is consistent with the protonated forms of astemizole being charged and membrane impermeable, and the unprotonated form being uncharged and membrane permeable (Fischer et al., 1997). The time course of block onset in Fig. 9 B was also slower at pH 6.4 (60 s) than at 8.4 (20 s). This can be accounted for by the time required to concentrate protonated astemizole inside the cell.

TABLE I.

Percentile Contribution of the Different Forms of Astemizole (pK_a1 = 5.6 and pK_a2 = 8.5) at Different pH

	pH
	6.4	7.4	8.4
	%	%	%
Unprotonateda	0.7	7.3	44.2
Monoprotonatedb	85.7	91.3	55.7
Diprotonatedc	13.6	1.4	0.1

^a=100 × [H⁺]² ÷ den.

^b=100 × [H⁺] × K_a1 ÷ den.

^c=100 × K_a1 × K_a2 ÷ den, where den = [H⁺]² + [H⁺] × K_a1 + K_a1 × K_a2 (Netter, 1969).

These results suggest that the charged forms of astemizole are more potent inhibitors of hEag1 channels than the neutral form. To avoid the complications resulting from the change in total concentration of internal astemizole by changes in the pH_ext//pH_int relation in whole-cell experiments, we directly applied astemizole to the intracellular side of inside-out patches. A constant total astemizole concentration (500 nM) blocked more current at pH_int of 6.4–7.4 than at 8.4 (Fig. 9 E). There was a positive correlation between the change in the fraction of protonated drug (mono- plus diprotonated), and the variation in the fractional, isochronal block observed at the end of the pulse. A 40% decrease in total protonated astemizole from pH_int 7.4 to 6.4 (Table I) correlates with a 44 ± 13% (n = 5) decrease in the observed potency of block. On the other hand, a 7% increase in total protonated astemizole from pH_int 7.4 to 6.4 (Table I) correlates with a 5 ± 4% increase in block (n = 5).

The idea that both protonated forms of astemizole are involved in the block of hEag1 channels is further supported by the observation that the rate of block at pH_int 6.4 (6.7 ± 2 s⁻¹), is larger than at 7.4 (2.8 ± 0.2 s⁻¹; n = 5; Fig. 2 F). At this pH_int range, the predicted monoprotonated concentration is expected to change little (a decrease of 6%), but the diprotonated concentration should increase almost 10-fold (Table I). Thus, an interesting possibility is that the increase in the rate of current block at pH_int 6.4 reflects the increased participation of the diprotonated form, with an increased affinity for the binding site. The ideal situation would have been to compare the degree of block at pH_int = pK_a1 and pH_int = pK_a2. Unfortunately, the inside-out currents during a 100-mV depolarization were reduced to ∼15% of their value at pH_int 5.7, and complete but reversibly disappeared with time in this solution (unpublished data). We also analyzed whether a hypothetical increase in the proportion of double-charged astemizole could introduce voltage sensitivity to the block by astemizole. However, in two cells without any apparent run-down, analyzed at pH_int 6.4 up to 160 mV and at two concentrations of astemizole around the IC₅₀, no sign of voltage dependence of the effect could be found (unpublished data).

Taken together, all results are consistent with the idea that both imipramine and astemizole bind to hEag1 channels in their charged forms from the intracellular side. Fig. 10 A shows that the direct application of a saturating dose of imipramine (25 μM) at pH 6.0 (99.97% protonated) causes a complete current suppression in inside-out patches, while it is less effective in outside-out patches. Current inhibition in outside-out patches (∼30%) can be accounted for by the ∼1 μM [imi⁺] inside the pipette (pH 7.4) predicted by Eq. 3. It should be noted that the permeation of imipramine is an extremely fast process. The predicted concentration of neutral imipramine in the bath, in Fig. 10 B, is 7.5 nM neutral imipramine. This concentration of neutral drug equilibrates with the pipette solution surrounding the intracellular face of the channels with a time constant (182 ms) nearly indistinguishable from the time constant of direct block in inside-out patches (155 ms). At external pH 7.4, the actions of imipramine in inside-out and outside-out patches were kinetically indistinguishable in our recording conditions (unpublished data). This extremely fast rate of membrane permeation of imipramine can account for the fact that no evident reduction in the whole-cell current upon addition of 100 μM imipramine to an intracellular, pH 6.4 solution was observed (unpublished data).

To further characterize the sidedness of block by imipramine, we synthesized the permanently charged, quaternary derivative N-methyl-imipramine. When 5 μM N-methyl-imipramine was applied to the cytoplasmic side of inside-out patches, a rapid and completely reversible inhibition of the current was observed (Fig. 10 C). However, the same concentration of this drug had virtually no effect when applied to the extracellular side in outside-out patches (Fig. 10 D). Assuming that imipramine and N-methyl-imipramine share a common site of action, these observations are incompatible with the idea that imipramine acts from the extracellular side (Kuo, 1998).

While the block induced by imipramine was fully reversed after 2-s washout during the depolarization to 100 mV in Fig. 10 A, hEag1 current did not recover from astemizole block during the same period (Fig. 10 A, bottom). Full recovery did occur, however, in a 30-s interval at the holding potential between identical pulses (unpublished data). The time constant for the astemizole block in inside-out patches was 387 ms, 2.5 times that of imipramine. The 10 nM predicted concentration of neutral astemizole in Fig. 10 B equilibrated with a time constant of 1.7 s. Therefore, the rate of open channel block in the case of astemizole is not rate limiting, and the 0.6 s⁻¹ rate represents an estimate of the equilibration process across the membrane. The slow membrane permeation of astemizole made it possible to induce a substantial block of whole-cell currents when 25 μM astemizole was added to a pH 6.4 intracellular solution (unpublished data).

DISCUSSION

We present here evidence that the charged forms of imipramine and astemizole block the current through hEag1 K⁺ channels by binding to sites in the intracellular portion of the permeation pathway only accessible when the channels are open. This mechanism of block can be described using the model developed by Armstrong (1966)(1969, 1971) to explain the action of internal quaternary ammonium (QA) ions on the K⁺ conductance of squid giant axon, which has been subsequently applied to explain the effects of a number of QA ions and protonated tertiary amines on different K⁺ channels (French and Shoukimas, 1981; Swenson, 1981; Choi et al., 1993; DeCoursey, 1995; Snyders and Yeola, 1995; Horrigan and Gilly, 1996).

Even if their mechanism of block is similar, imipramine and astemizole strongly differ in the affinity, kinetics, and voltage dependence of their interaction with hEag1 channels. Comparing the state-dependent interaction of both compounds with hEag1 renders information about the closed and open conformation of these channels, as well as some unexpected pharmacokinetic characteristics of both drugs. Some differences between imipramine and astemizole in binding to hEag1 are reminiscent of the difference between TEA and QA compounds with longer alkyl side chains, which show an increasing affinity and decreasing dissociation rate with increasing length of the alkyl side chain (Choi et al., 1993). Thus, a first conclusion is that like the delayed rectifier K⁺ channel of squid axon and Shaker K⁺ channels, hEag1 channels seem to have an auxiliary hydrophobic binding site in the intracellular vestibule of the channel that accommodates the bulky chain of astemizole. In the following paragraphs we will consider the interaction of both compounds with hEag1 separately.

Imipramine Binding to hEag1

Imipramine blocks several cardiac (Delpon et al., 1992; Valenzuela et al., 1994) and neuronal (Ogata et al., 1989; Wooltorton and Mathie, 1993, 1995; Kuo, 1998; Cuellar-Quintero et al., 2001) voltage-gated and Ca²⁺-activated K⁺ channels (Dreixler et al., 2000; Terstappen et al., 2001; Gavrilova-Ruch et al., 2002) as well as EGL-2 channels (Weinshenker et al., 1999), hERG channels (Teschemacher et al., 1999), neuronal (Ogata et al., 1989; Yang and Kuo, 2002) and cardiac (Ogata and Narahashi, 1989; Habuchi et al., 1991) Na⁺ channels, and Ca²⁺ channels (Ogata et al., 1989). There are some differences in the affinity with which imipramine inhibits these different ion channels, but in all cases the reported IC₅₀ values are in the μM range (1 to 30 μM). Moreover, in all cases, the dose–response curves are well fitted with a Hill coefficient close to 1. The IC₅₀ value we report here for hEag1 (1.9 μM at 80 mV) is in good agreement with those published for the native Eag currents in IGR1 melanoma cells (3.4 μM at 50 mV; Gavrilova-Ruch et al., 2002) and for cloned hERG channels (3.4 μM at 20 mV; Teschemacher et al., 1999).

The fact that different ion channels show comparable affinities for imipramine suggests structural conservation at the binding site across these very diverse ion channel targets, and indicates that a similar mode of action of imipramine could account for the inhibition of all these channels (Wooltorton and Mathie, 1993). Unfortunately, only in few cases has the detailed mechanism of action of imipramine been analyzed. Within the K⁺ channel family there is strong evidence that imipramine blocks native A-type channels in atrial myocytes (Delpon et al., 1992; Casis and Sanchez-Chapula, 1998) and hippocampal neurons (Kuo, 1998) by an open-channel block mechanism similar to that described here for hEag1 channels. However, contrary to our conclusions, Kuo (1998) suggests that imipramine blocks channels in its uncharged form, and that the binding site is located at the extracellular side of the channels. Wooltorton and Mathie (1993)(1995), who analyzed the effects of several tricyclic compounds on the K⁺ current of rat sympathetic neurons, also proposed the existence of an external binding site with a high affinity for the uncharged form of these compounds.

Although our conclusions differ, there is no conflict between the data shown in those studies and the data presented here. Also we observe that (a) apparent affinity for tricyclic compounds (all weak bases with pK_as between 8.9 and 10; Wooltorton and Mathie, 1995) increases with alkalinization of pH_ext and that (b) these compounds do not show any obvious effect on the whole-cell current when included in the pipette. However, we interpret (a) to result from an indirect increase in the concentration of charged imipramine inside the cell, and (b) from the extremely high speed of membrane permeation of this compound. This interpretation is based on a number of accompanying experimental observations that are incompatible with an uncharged blocker and an extracellular binding site, and on measurements of a very fast rate of membrane permeation for imipramine. In particular, we find that the block of imipramine is strongly voltage dependent and estimate that imipramine passes 39% of the electric field across the membrane before reaching its binding site for which it competes with intra- but not extracellular TEA. Moreover, increasing the amount of protonated imipramine on the intracellular side of the channels by variations of pH_ext and pH_int in whole-cell and inside-out patch recordings increases the block of hEag1 currents by the precise amount predicted for imipramine acting in its charged form. Finally, we synthesized a quaternary derivative, permanently charged form of imipramine, N-methyl-imipramine, and we show that it blocks hEag1 channels in inside-out but not outside-out patches.

Interestingly, all but one of the published previous experimental observations can be explained assuming that the binding site is intracellular and the charged form is the active compound. Wooltorton and Mathie (1995) reported that N-methyl-amitriptyline, a permanently charged derivative of amitriptyline, does not inhibit the whole-cell K⁺ current when included in the patch pipette during whole-cell recordings. However, it should be noted that permanently charged, quaternary derivatives of open pore blockers can be as much as 100 times less potent than tertiary forms even if they share the same site and mechanism of action (Kirsch and Narahashi, 1983). Thus, taking into consideration that 50 μM amitriptyline blocked ∼90% of the current (Wooltorton and Mathie, 1995), the single concentration of 50 μM N-methylamitriptyline used by Wooltorton and Mathie (1995) does not provide conclusive evidence against an intracellular site of action. While we cannot exclude that imipramine and other tricyclic compounds block different ion channels by different mechanisms, we propose that this class of drugs blocks hEag1 and likely other K⁺ channels by an open-pore block acting from inside the cell.

What can we learn about hEag1 channels from their interaction with imipramine? The voltage dependence of imipramine binding and its competition with internal TEA argue that it binds close to the inner end of the selectivity filter that is known to accommodate the binding site for internal TEA of related K_V channels (Yellen et al., 1991; Choi et al., 1993). Interestingly the fraction of the electric field sensed by imipramine (39%) is similar to that reported for Na⁺ ions, which also block Eag1 channels by an open-channel block mechanism (45%; Pardo et al., 1998). Given that Na⁺ exclusion of the permeation pathway occurs directly at the selectivity filter (Zhou et al., 2001), this suggests that the protonation site in imipramine (a tertiary nitrogen) penetrates as far as this position. The access of imipramine to this site requires hEag1 channels to open. Thus opening of Eag channels must create a widening of its intracellular entryway that allows a compound as large as imipramine to reach the inner end of the selectivity filter. The reverse process constricts the intracellular permeation pathway, making it too narrow for imipramine, which has to unbind before the channel can close. Accordingly, no trapping of imipramine in closed channels was observed. Eag channels are structurally related to both K_V and cyclic nucleotide gated channels (Warmke et al., 1991; Warmke and Ganetzky, 1994) that differ in the putative position of their activation gate. While for K_V channels it is supposed to coincide with a bend in the distal part of the S6 segment (Del Camino et al., 2000), cyclic nucleotide gated channels have been suggested to switch to their conducting state by a movement of the selectivity filter itself (Flynn et al., 2001). The data presented here argue for a major rearrangement of the intracellular opening of the channel during activation. Whether this gate for imipramine also gates the access of the much smaller K⁺ ions remains to be investigated.

Amino acid residues located at the base of the pore helix and along the S6 segment are determinants for the binding of different compounds that block open K⁺ channels (for review see Decher et al., 2004). While residues in S6 vary substantially between different K⁺ channels, the COOH-terminal end of the pore helices just before the selectivity filter is highly conserved (Mitcheson et al., 2000b). The first of two positions are occupied by a polar residue (either Ser or Thr) and the next position is either Val or Ile (Mitcheson et al., 2000b). It remains to be tested whether these residues are important for the binding of tricyclic compounds.

Astemizole Binding Site

In contrast to imipramine, the actions of astemizole on K⁺ channels seem restricted to some members of the eag family. For example, concentrations up to 10 μM astemizole have no significant effects on the cardiac I_sK currents, IRK1 inward rectifier K⁺ channels, and the voltage-gated K⁺ channels Kv1.1 (Suessbrich et al., 1996), Kv2.1, and Kv4.2 (unpublished data). Some marginal effects of astemizole at high concentrations have been reported for the outward currents of ventricular cardiomyocytes (Berul and Morad, 1995). However, concentrations <10 μM had no effects on these currents. The Eag-like channels 2 (hELK₂) are also not sensitive to astemizole (Becchetti et al., 2002).

In contrast, HERG channels are highly sensitive to astemizole (Suessbrich et al., 1996; Zhou et al., 1999). This suggests structural conservation in the architecture of HERG and hEag1 that supports the selective inhibition by this drug. A common feature of these channels is the lack of the Pro-X-Pro motif that is believed to induce a sharp bend in the pore-lining S6 helices of other voltage-gated K⁺ channels (Del Camino et al., 2000). This is supposed to confer a larger volume to the inner cavity of HERG and hEag channels, as to accommodate large molecules like astemizole (Mitcheson et al., 2000b). Instead of the Pro-X-Pro motif described before, the corresponding sequence of HERG and hEag channels reads Ile-Phe-Glu. The Phe at this position (656 of HERG and 495 of hEag) has been shown to be a major determinant for the particular sensitivity of HERG channels to a large number of open pore blockers (Mitcheson et al., 2000b; Chen et al., 2002; Fernandez et al., 2004). Ficker et al. (2002) report that mutation of Phe 656 to Cys dramatically reduces the affinity of HERG channels to astemizole. It is tempting to speculate that this conserved aromatic residue might also be involved in the block of hEag1 channels by astemizole, which we have shown here to bind in its charged form. The binding of a charged blocker to an aromatic residue could occur through cation–π interactions, which have been proposed to be a major source of high affinity drug–receptor interactions (for review see Zacharias and Dougherty, 2002). Proximity of the protonations sites in astemizole to Phe 656 of hEag1 channels could also account for the lack of voltage sensitivity of the block by this drug. Note in Fig. 3 of Del Camino et al. (2000) that the sharp bend site in K_V channels is located at considerable distance from the selectivity filter, where the major drop of electric potential across the membrane takes place (MacKinnon and Yellen, 1990; Yellen et al., 1991).

While the open states of both HERG and hEag channels are similar in allowing the binding of relatively large molecules in the permeation pathway, their closed states seem to differ in this respect. Thus MK-499, a charged organic compound of similar size and structure as astemizole, is trapped in closed HERG channels (Mitcheson et al. 2000a). In contrast to this, we report here that both astemizole and the smaller imipramine have to dissociate from hEag1 channels before they can close. This argues that the permeation pathway, in particular the inner cavity that is supposed to be the trapping site, is of smaller diameter in closed hEag1 than in HERG channels. In conclusion, while the open states of these related channels share pharmacological and therefore presumably structural features, their closed states seem to differ substantially.

The reported IC₅₀ for astemizole in cloned HERG is 0.9 nM (Zhou et al., 1999; but note that native rERG currents in GH3 cells showed IC₅₀ values in the range of 50 nM; Barros et al., 1997), while that for hEag1 is 196 nM (Fig. 1) when both channels are expressed in HEK-293 (human embryonic kidney) cells. Therefore, some of the structural differences with HERG must explain the lower affinity for the drug by hEag1. Gessner et al. (2004) have shown that specific residue differences between hEag1 and hEag2 channels are critical for the stabilization of various drugs in the pore of Eag channels. However, these residues do not seem to be involved in the block we describe here because hEag2 channels expressed in Xenopus oocytes were blocked indistinguishable from hEag1 channels by astemizole (IC₅₀ for both ∼1.5 μM; unpublished data). A major difference between HERG and hEag1 kinetics is the strong voltage-dependent inactivation of the first ones. Although it is still a matter of debate, inactivation has been proposed to increase the sensitivity of HERG channels to some substances (Suessbrich et al., 1997; Zhang et al., 1999; Lees-Miller et al., 2000; Ficker et al., 2001; but see Kiehn et al., 1996; Snyders and Chaudhary, 1996; Thomas et al., 2002). In fact, it has been proposed that aromates in the S6 segment reposition during activation/inactivation gating by means of allosteric changes that take place during the process of inactivation (Chen et al., 2002). This might account for the higher affinity of HERG channels for astemizole.

Possible Implications

The investigation of the physiological function of Eag1 channels has been largely precluded by the lack of selective blockers (Bauer and Schwarz, 2001). Based on the modulation of Eag activation kinetics by the resting membrane potential and divalent cations (Terlau et al., 1996), currents through endogenous Eag channels have been identified in a number of preparations (Meyer and Heinemann, 1998; Occhiodoro et al., 1998; Meyer et al., 1999; Pardo et al., 1999; Ouadid-Ahidouch et al., 2001; Gavrilova-Ruch et al., 2002). However, in both the central and peripheral nervous system, it is impossible to isolate currents through Eag channels based solely on these properties, due to the overwhelming presence of other K⁺ currents. To elucidate the function of these channels in the nervous system, astemizole might be a useful tool, as it appears to be specific for channels of the Eag family. HERG channels, which are also blocked by this compound, can easily be distinguished by their higher affinity for the drug and their distinctive biophysical properties.

In addition, Eag channels have been suggested to promote the proliferation of cancer cells (Pardo et al., 1999). It has recently been published that the exposure of breast cancer cells to astemizole (Ouadid-Ahidouch et al., 2001) and of melanoma cells to imipramine (Gavrilova-Ruch et al., 2002) causes a significant reduction in their proliferation rate. These effects have been ascribed to an interaction of both drugs with Eag channels. Our observation that both imipramine and astemizole block Eag channels by occlusion of the permeation pathway, which most likely entails no major allosteric changes, argues that ion permeation through the channels is affecting cell cycle. Given the role of Eag channels in cancer, the development of further specific inhibitors of Eag channels as well as the investigation of those described here might have considerable clinical relevance (Catterall et al., 2002).