Altered Inactivation of Ca²⁺ Current and Ca²⁺ Release in Mouse Muscle Fibers Deficient in the DHP receptor γ₁ subunit

Abstract

Functional impacts of the skeletal muscle-specific Ca²⁺ channel subunit γ₁ have previously been studied using coexpression with the cardiac α_1C polypeptide in nonmuscle cells and primary-cultured myotubes of γ₁-deficient mice. Data from single adult muscle fibers of γ−/− mice are not yet available. In the present study, we performed voltage clamp experiments on enzymatically isolated mature muscle fibers of the m. interosseus obtained from γ+/+ and γ−/− mice. We measured L-type Ca²⁺ inward currents and intracellular Ca²⁺ transients during 100-ms step depolarizations from a holding potential of −80 mV. Ratiometric Ca²⁺ transients were analyzed with a removal model fit approach to calculate the flux of Ca²⁺ from the sarcoplasmic reticulum. Ca²⁺ current density, Ca²⁺ release flux, and the voltage dependence of activation of both Ca²⁺ current and Ca²⁺ release were not significantly different. By varying the holding potential and recording Ca²⁺ current and Ca²⁺ release flux induced by 100-ms test depolarizations to +20 mV, we studied quasi-steady-state properties of slow voltage–dependent inactivation. For the Ca²⁺ current, these experiments showed a right-shifted voltage dependence of inactivation. Importantly, we could demonstrate that a very similar shift occurred also in the inactivation curve of Ca²⁺ release. Voltages of half maximal inactivation were altered by 16 (current) and 14 mV (release), respectively. Muscle fiber bundles, activated by elevated potassium concentration (120 mM), developed about threefold larger contracture force in γ−/− compared with γ+/+. This difference was independent of the presence of extracellular Ca²⁺ and likely results from the lower sensitivity to voltage-dependent inactivation of Ca²⁺ release. These results demonstrate a specific alteration of voltage-dependent inactivation of both Ca²⁺ entry and Ca²⁺ release by the γ₁ subunit of the dihydropyridine receptor in mature muscle fibers of the mouse.

INTRODUCTION

Voltage-dependent Ca²⁺ channels are important mediators between cell membrane excitation and cellular functions. In striated muscle, L-type Ca²⁺ channels (dihydropyridine receptors [DHPRs]) play crucial roles in shaping the intracellular Ca²⁺ signal that activates contraction. The process involves the interaction between DHPRs and Ca²⁺ release channels (ryanodine receptors [RyRs]) of the sarcoplasmic reticulum (SR). In heart muscle, Ca²⁺ ions entering the cell via the voltage-activated DHPRs trigger Ca²⁺ release via RyRs in a process termed calcium-induced Ca²⁺ release (Bers, 2001). In contrast, skeletal muscle exhibits a direct conformational coupling between the DHPR and the RyR (Dirksen, 2002). The main functional roles of the DHPR (voltage sensing, pore formation, and coupling to RyR) have been traced to the α₁ subunit, but tightly associated polypeptides (auxiliary subunits) perform functions that are still incompletely resolved (for reviews see Walker and De Waard, 1998; Arikkath and Campbell, 2003).

The dihydropyridine-sensitive α_1S polypeptide of skeletal muscle is stably associated with four auxiliary subunits that are also found in the purified channel complex, β₁, γ₁, δ, and α₂. The latter two originate from the same gene and are postranslationally cleaved, but remain linked by disulfide bridges (Arikkath and Campbell, 2003). γ₁ is most specific for skeletal muscle (Biel et al., 1991). It is a polypeptide of 32 kD molecular weight, consisting of 222 amino acid residues, that is encoded by a gene with four translated exons residing as a single copy in the haploid mouse genome (Powers et al., 1993; Wissenbach et al., 1998). It exhibits four putative membrane-spanning α helices (Bosse et al., 1990; Jay et al., 1990) and both NH₂ and COOH termini are located on the cytoplasmic side.

Because it proved difficult to express the skeletal muscle α_1S subunit in heterologous expression systems, functional coexpression studies of the γ₁ subunit have been performed together with the cardiac α_1C pore-forming subunit (Singer et al., 1991; Wei et al., 1991; Lerche et al., 1996; Eberst et al., 1997; Sipos et al., 2000). These investigations indicated alterations in steady-state inactivation caused by γ₁ (shift to more negative potentials) and enhanced activation and inactivation kinetics. The experiments could, however, only provide indirect clues as to possible functions of γ₁ in skeletal muscle. Neither could one be sure that α_1S resembles α_1C regarding interaction with γ₁ nor did these experiments provide information on a possible modulation of Ca²⁺ release.

Two laboratories have independently generated mice lacking expression of the γ₁ subunit (Ahern et al., 2001; Freise et al., 2000). Unlike α_1S−/− and β₁−/− mice that die at birth because of complete failure of EC coupling, γ−/− mice showed no obvious deviation from the normal phenotype. Nevertheless, in myotubes derived from the γ-knockout mice, several functional differences have been described in comparison to myotubes of control animals (Freise et al., 2000; Ahern et al., 2001; Ursu et al., 2001). Changes in Ca²⁺ inward current densities were reported using neonatal or embryonic mice as the source of myoblasts for myotube cultures (Freise et al., 2000; Ahern et al., 2001; Held et al., 2002). The experiments indicated a partial suppression of L-type current by the γ subunit. In contrast, myotubes of older γ−/− mice (4 wk and more) showed no significant deviations from controls in the L-type current densities, and a difference in sensitivity to 8-Br-cAMP observed in myotubes of young mice was not found either (Ursu et al., 2001; Held et al., 2002). This points to a γ₁-controlled cAMP modulation of the channel restricted to an early period of development. In addition, compatible with the coexpression studies in nonmuscle cells, a shift to more positive potentials of the curve that describes steady-state inactivation of the Ca²⁺ channels as a function of voltage was found in myotubes (Freise et al., 2000; Ahern et al., 2001). This effect was independent of cAMP and of the age of the mice (Held et al., 2002).

Because the primary function of the DHPR protein in skeletal muscle is voltage sensing to control Ca²⁺ release from the SR (Melzer et al., 1995), excitation–contraction coupling events were investigated by Ursu et al. (2001) and Ahern et al. (2001) in γ₁−/− myotubes and by Ursu et al. (2001) in isolated fast and slow twitch muscles. The flux of Ca²⁺ underlying the depolarization-induced Ca²⁺ transients was found to be slightly larger in γ−/− myotubes (Ursu et al., 2001) but voltage sensor charge movements were not statistically different (Ahern et al., 2001). Neither were contractile properties of extensor digitorum longus (EDL) and soleus, investigated by single twitches and tetani both under normal and fatiguing conditions, found to be different (Ursu et al., 2001). Yet, voltage clamp studies of Ca²⁺ currents and EC coupling events in mature fibers of γ₁ knockout mice have not yet been performed. Therefore, the purpose of the present investigation was to study functional effects of eliminating the γ₁ subunit on Ca²⁺ inward currents and Ca²⁺ release under voltage clamp conditions in enzymatically isolated adult skeletal muscle fibers of γ₁-deficient mice. The results show that of the different effects attributed to the γ₁ subunit, the alteration of voltage-dependent inactivation prevails in mature muscle. In particular, we demonstrate that γ₁ enhances inactivation of SR Ca²⁺ release in a voltage-dependent manner.

MATERIALS AND METHODS

Muscle Preparation

As described by Freise et al. (2000), pairs of heterozygous inbred mice (γ+/−) with the 129 SVJ background were mated in the animal facility of the University of Homburg to give rise to either wild-type (γ+/+) or homozygous γ₁-deficient (γ−/−) offspring. γ+/+ and γ−/− pairs were shipped to the Animal Research Center of the University of Ulm for further separate breeding. Homozygous offspring of the parent animals were used for experiments. The age of the animals used for the experiments varied between 111 and 294 d (γ+/+) and between 91 and 292 d (γ−/−). Animals were killed in agreement with regulations of the local Animal Care Committee (lethal exposure to CO₂ followed by cervical dislocation). For force recordings, EDL muscles were dissected from the hindlimbs of the mice in Krebs-Ringer solution bubbled with carbogen (95% O₂ + 5% CO₂). They were trimmed down to a flat fiber bundle to facilitate diffusional exchange. For voltage clamp experiments, interosseus muscles were dissected in Krebs-Ringer solution and single fibers were isolated by enzymatic treatment in dissociation solution at 37°C as described by Jacquemond (1997).

Solutions

Solutions used for the experiments had the following compositions (concentrations in mM): Krebs-Ringer solution for muscle dissection, fiber storage, and contraction experiments, 118 NaCl, 3.4 KCl, 0.8 MgSO₄, 1.2 KH₂PO₄, 11.1 glucose, 25 NaHCO₃, 2.5 CaCl₂, pH 7.4; contracture solution, 2 TES, 1 MgSO₄, 11 glucose, 2.5 CaSO₄, 4.8 KCl, 57.6 K₂SO₄, 40 Na₂SO₄, pH 7.4; Ca²⁺-free contracture solution, 2 TES, 11 glucose, 3.5 MgSO₄, 4.8 KCl, 57.6 K₂SO₄, 40 Na₂SO₄, pH 7.4; dissociation solution for muscle fiber isolation, Krebs-Ringer solution containing 2 mg/ml collagenase; external (bathing) solution for voltage clamp experiments, 135 TEA-OH, 135 HCH₃SO₃, 2 MgCl₂, 10 CaCl₂, 5 4-aminopyridine (4-AP), 10 HEPES, 0.001 TTX, 5 glucose, 0.05 N-benzyl-p-toluene sulphonamide (BTS), pH 7.4; internal (pipette) solution for intracellular perfusion, 145 CsOH, 135 aspartic acid, 0.75 Na₂ATP, 4.25 MgATP (5.16 mM total Mg²⁺, resulting in 1 mM free Mg²⁺), 1.5 CaCl₂ (resulting in 20 nM free Ca²⁺), 10 HEPES, 15 EGTA, 0.2 fura-2, 5 Na₂creatinePO₄, pH 7.2.

Contractions

Force recordings were performed at 25°C as described previously (Ursu et al., 2001). Extracellular electrical field stimulation was performed by applying supramaximal shocks of 1 ms duration. The experiments started in normal Krebs-Ringer solution by eliciting a twitch and a tetanus (500 ms, 125 Hz) that was used for contracture force normalization. To permanently depolarize the muscle fibers, the volume of the recording chamber (40 ml) was replaced with contracture solution containing 120 mM [K⁺] (at constant [K⁺]x[Cl⁻]) immediately after the test tetanus. As the result, a contracture developed, followed by a slow spontaneous relaxation caused by inactivation. After 5 min, the high [K⁺] solution was washed out with normal Krebs-Ringer solution.

Voltage Clamp and Data Acquisition

Single cell experiments were performed at room temperature (20–23°C) in external solution containing 50 μM of the myosin II ATPase inhibitor BTS to suppress contractions (Cheung et al., 2002; Shaw et al., 2003). Fibers were voltage clamped with two microelectrodes using an Axoclamp 2B amplifier (Axon Instruments, Inc.). Micropipettes were fabricated from borosilicate glass (GB150TF-10; Science Products). The voltage recording electrodes were filled with 3 M KCl and had a mean resistance of 6.76 ± 0.51 MΩ (n = 20) when measured in extracellular solution.

The current passing electrodes were filled with artificial internal solution containing 15 mM EGTA and 0.2 mM fura-2 and had a mean resistance of 2.79 ± 0.09 MΩ (n = 20). After inserting the voltage-recording electrode, the control voltage was set to −80 mV with the voltage clamp circuit at minimum gain (30). Then the current-passing electrode was gently sealed to the membrane and the previously applied positive pressure was released, which usually led to establishing the contact to the cytoplasm. The amplifier gain was then increased to the final value of 800 used in all experiments.

The progress of diffusion of intracellular solution into the fiber was observed by measuring the increase in the resting fluorescence of fura-2 at 360 nm excitation (see also Schuhmeier et al., 2003). To study voltage-dependent activation of slow Ca²⁺ inward current and Ca²⁺ release, fibers were stimulated with 100-ms depolarizing pulses of increasing amplitude separated by intervals of 60 s (activation protocol). Voltage activation was started after 30 min of loading. [Ca²⁺]-dependent fura-2 fluorescence changes were recorded at 380 nm excitation and the ratio R (=F ₃₈₀/F ₃₆₀) calculated. For the fura-2 concentration at the time when voltage activation was performed, we used a mean estimate of 83 μM, obtained with a method described by Klein et al. (1988). The estimate resulted from F ₃₆₀ recordings in fibers that were compared with equivalent measurements in quartz microcapillaries of two different inner diameters (50 and 100 μm) containing 50, 100, and 200 μM of dye in internal solution. Assuming comparable diffusion rates for EGTA and fura-2, the concentration of the chelator in the fibers corresponding to the dye concentration is 6 mM, which we used for the calculations.

Current, voltage, and fluorescence were recorded simultaneously at 2 kHz sampling frequency using a CED 1401+ interface (Cambridge Electronic Design) connected to an AMD K6-2 computer. For data acquisition and analysis, we used own software written in Delphi (Borland International).

Ca²⁺ Current Analysis

Current–voltage relations were least-squares fitted using

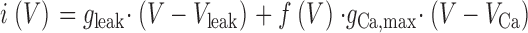(1)

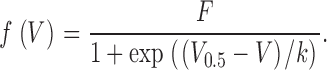(2)

Here, g_leak and V _leak are conductance and reversal potential of a linear leak component and g _Ca,max and V _Ca are maximal conductance and reversal potential of the Ca²⁺ current. g _leak and g _Ca,max are normalized by the linear capacitance. The gating function f(V) is defined by Eq. 2. V _0.5, k, and F are the voltage of half-maximal activation, the voltage sensitivity, and the maximal value, respectively. F was unity for f(V) to describe fractional activation of conductance.

Ca²⁺ Input and Entry Flux Analysis

Free Ca²⁺ was calculated from voltage-activated changes of R (see above) using Eq. 3 after background and bleaching corrections (Klein et al., 1988; Schuhmeier et al., 2003).

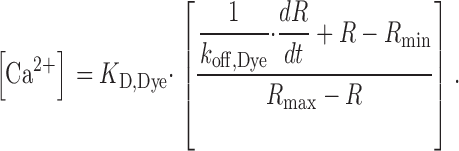(3)

Ca²⁺ input flux, i.e., the total flux of Ca²⁺ into the myoplasm, was derived as described by Schuhmeier and Melzer (2004). In brief, a kinetic model describing the removal of released Ca²⁺ to different compartments (see Melzer et al., 1986) was fitted to the repolarization intervals of four consecutive depolarizing voltage pulses (50 ms, 0 mV, intervals 150 ms) usually applied 2 min after the last pulse of the activation protocol. The model consisted of the indicator dye described by R _min, R _max (3.52 and 0.41, respectively, determined for this setup), rate constants k _on,Dye, k _off,Dye and concentration [Dye]_total, of a saturating buffer (parameters k _on,S, k _off,S, and [S]_total), and an uptake mechanism (rate constant k _uptake). K _Dye = k _off,Dye/k _on,Dye was set to 0.276 μM determined in vitro (Schuhmeier et al., 2003). The best fit values of kinetic constants (k _off,Dye, k _on,S, k _off,S, and k _uptake) in the removal model were used to calculate the depolarization-induced Ca²⁺ flux into the myoplasm from other voltage-activated fluorescence records in the experiment.

Ca²⁺ entry flux was calculated from the measured Ca²⁺ current as described by Schuhmeier and Melzer (2004) assuming a fractional fiber volume for Ca²⁺ distribution of f_V = 0.71 (see Baylor et al., 1983) and a volume capacitance ratio V_C = 0.32 liter F⁻¹ (mean value obtained from simultaneous volume and capacitance measurements).

Depletion Correction and Conversion of Release Flux to Permeability

We subjected the calculated Ca²⁺ input flux records to an analysis procedure that corrects for the effect of store depletion caused by the release to derive the time course of SR Ca²⁺ permeability during a depolarizing voltage step (Gonzalez and Ríos, 1993; Schneider et al., 1987). Permeability was calculated as flux divided by the time-dependent Ca²⁺ content in the SR, both referred to the myoplasmic water volume. The Ca²⁺ content is the difference between an initial Ca²⁺ content and the released amount. The procedure assumes that permeability is constant during the plateau phase of the flux trace and determines the initial Ca²⁺ concentration in the SR that leads to zero slope in the plateau phase of the calculated permeability traces (see Schuhmeier and Melzer, 2004).

Statistics

Unless otherwise stated, averaged data are presented and plotted as means ± SEM (n = number of experiments). Student's two-sided t test was used to test for significant differences of mean values (assuming two independent populations; P = 0.05).

RESULTS

Activation of Ca²⁺ Current and Fluorescence Signal

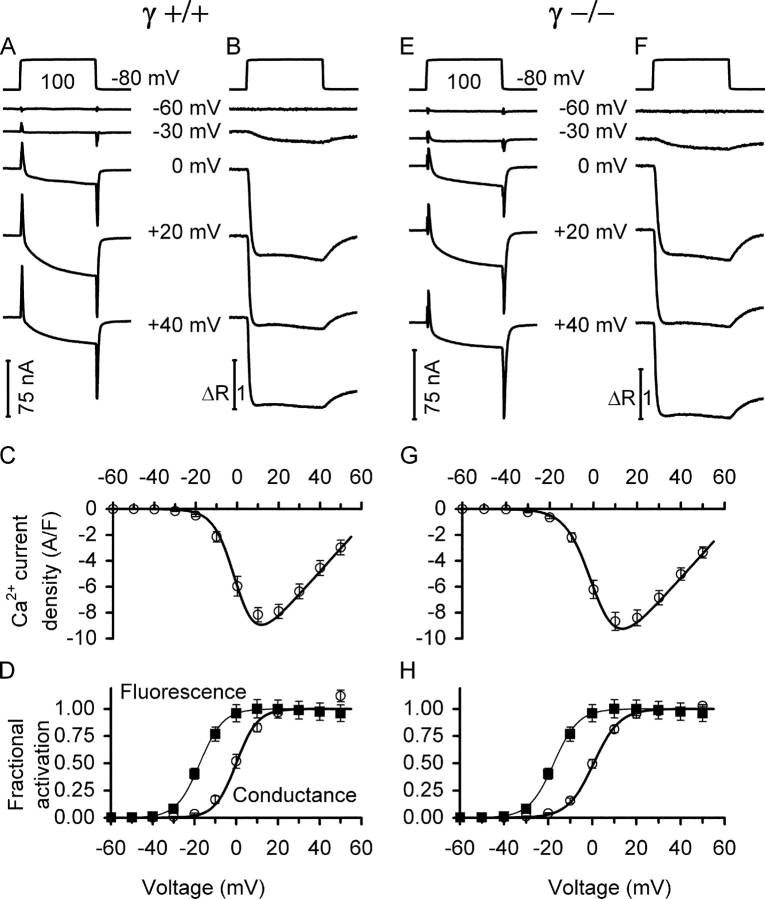
Fig. 1 shows traces of analogue leak-compensated inward currents (A and E) and simultaneously measured fura-2 fluorescence ratios (B and F) for various voltage steps from the holding potential of −80 mV. The figure shows results from individual muscle fibers of γ+/+ (A and B) and γ−/− mice (E and F) and averaged data obtained from several fibers (C, D and G, H, respectively). Fig. 1 (C and G) presents the voltage dependence of activation of the inward currents (normalized by the linear membrane capacitance) for a number of γ+/+ and γ−/− fibers, respectively. Fig. 1 (D and H) shows the voltage dependence of fractional activation of both Ca²⁺ conductance and Ca²⁺-dependent fluorescence signals. Continuous lines represent curves drawn by using Eqs. 1 and 2.

Figure 1.

Voltage-activated slow Ca²⁺ inward current and myoplasmic Ca²⁺ signals. Comparison of L-type Ca²⁺ currents (A and E) and fura-2 fluorescence ratio signals (B and F) at five different pulse voltages for a γ+/+ and a γ−/− muscle fiber, respectively. The top traces show representative recordings of the applied voltage steps. C and G show leak-corrected current–voltage relations for several fibers, including measurements at more voltages. D and H show the voltage dependence of normalized activation of the Ca²⁺ signals (squares) and conductance (circles, derived from C and G, respectively) for the same set of measurements. Continuous lines are least squares fits of Eqs. 1 and 2 to the data points. Fit parameters for the Ca²⁺ signals were V _0.5 = −20.86 ± 1.56 mV and k = 5.79 ± 0.21 mV in γ+/+, and V _0.5 = −18.90 ± 1.46 mV and k = 5.22 ± 0.29 mV in γ−/−, exhibiting no significant difference. For other values see Table I. Values were determined as the average of the measurement points in the last 8 ms of the 100-ms depolarization. Data of 16 γ+/+ and 19 γ−/− muscle fibers, respectively.

The mean values of the parameters that were obtained from least squares fits to the individual datasets were used for the plots (for values regarding fluorescence see Fig. 1 legend, for other values see Table I). A comparison of the averaged data and best fit parameter values showed no significant difference between the two types of fibers at P = 0.05, except for the k value of the current that was marginally larger in γ−/− (P = 0.047). Passive electrical properties of the two types of fibers were measured at the resting potential using depolarizing and hyperpolarizing pulses of 10 mV amplitude (50 ms duration). Both resting conductance and capacitance in γ+/+ fibers were slightly larger than in γ−/−. The difference in conductance (340.48 ± 26.59, n = 19, and 283.32 ± 17.84 nS, n = 16, respectively) was not significant (P = 0.076), while the difference in capacitance was (5.35 ± 0.24 and 4.22 ± 0.21 nF, respectively, P = 0.0013). Whether these relatively small deviations have a structural basis is unclear. Volume was not systematically determined for each fiber. A comparison of volume in a subset of the fibers showed no significant difference.

TABLE I.

Comparison of Parameters Describing Voltage-dependent Activation of Ca²⁺ Current, Ca²⁺ Input Flux, and Permeability in γ+/+ (n = 16) and γ−/− (n = 19) Fibers

	Ca2+ current			Input flux peak		Input fluxend level			Permeability peak		Permeabilityend level
	γ+/+	γ−/−		γ+/+	γ−/−	γ+/+	γ−/−		γ+/+	γ−/−	γ+/+	γ−/−
V 0.5 (mV)	0.00 ± 1.51	0.61 ± 1.06	V 0.5 (mV)	−13.16 ± 1.25	−13.63 ± 1.02	−16.69 ± 1.50	−16.92 ± 1.11	V 0.5 (mV)	−14.76 ± 1.43	−15.11 ± 1.00	−13.49 ± 1.65	−13.93 ± 1.05
k (mV)	5.08 ± 0.22	5.87 ± 0.30a	k (mV)	7.13 ± 0.24	6.79 ± 0.21	6.05 ± 0.23	5.55 ± 0.19	k (mV)	6.82 ± 0.30	6.35 ± 0.21	5.90 ± 0.35	5.48 ± 0.22
g Ca,max (S/F)	95.02 ± 6.18	78.88 ± 7.32	a (μM·ms−1)	121.8 ± 13.43	86.99 ± 11.89	21.21 ± 1.55	16.37 ± 1.84	a (%·ms−1)	3.69 ± 0.31	3.59 ± 0.49	1.21 ± 0.06	1.26 ± 0.11
V Ca (mV)	67.05 ± 3.41	68.43 ± 2.35	b (μM·ms−1V−1)	482.6 ± 153.2	497.1 ± 155.1	−87.58 ± 9.78	−58.23 ± 9.68a	b (%·ms−1V−1)	30.85 ± 4.51	29.10 ± 4.86	0.012 ± 0.77	0.052 ± 0.40
Cm (nF)	5.35 ± 0.24	4.22 ± 0.21a						CaSR,50 (mM)	2.87 ± 0.24	2.34 ± 0.27	0.81 ± 0.08	0.72 ± 0.12
i Ca,10 (A/F)	−8.16 ± 0.56	−8.67 ± 0.70	F 50 (μM·ms−1)	144.03 ± 17.08	108.83 ± 17.81	17.00 ± 1.36	13.55 ± 1.56	P 50 (%·ms−1)	5.19 ± 0.43	4.94 ± 0.68	1.22 ± 0.06	1.26 ± 0.10

Voltage dependence was described by the product of a Boltzmann function (see Eq. 2) with voltage of half-maximal activation V _0.5 and voltage sensitivity k and a linear function. For flux and permeability, a and b describe the linear part (i.e., F = a + bV) of the activation curve at large voltages. a is the extrapolated value of this part at V = 0 mV. In the case of the Ca²⁺ current, the linear function corresponds to the open channel current–voltage relation. g _Ca,max is the maximal Ca²⁺ conductance (normalized by linear capacitance C_m) and V _Ca is the apparent reversal potential (see Eq. 1). i _Ca,10 is the maximal inward current density (at +10 mV), F ₅₀ the Ca²⁺ input flux at +50 mV, and P ₅₀ the permeability at +50 mV. Ca_SR,50 is the estimated Ca²⁺ content of the SR determined in the depletion analysis for the permeability calculation using depolarizing pulses to +50 mV. It was split up into the initial value (listed under column “permeability peak”) and the value at the end of the 100-ms pulse (listed under column “permeability end level”). Errors are SEM.

^aP values were 0.047, 0.042, and 0.0013 for the three parameters k, b, and C_m that showed significant differences.

Ca²⁺ Input Flux

In myotubes derived from satellite cells of adult mice, a small but significant increase in the amplitude of the peak Ca²⁺ release flux determined fluorimetrically had been observed in the absence of the γ subunit (Ursu et al., 2001). Therefore, our next goal was to quantify Ca²⁺ release from the SR in the two types of muscle fibers. For this purpose, we analyzed the fura-2 calcium transients (i.e., the fluorescence ratio signals, Fig. 1) and derived the underlying Ca²⁺ input flux (see materials and methods).

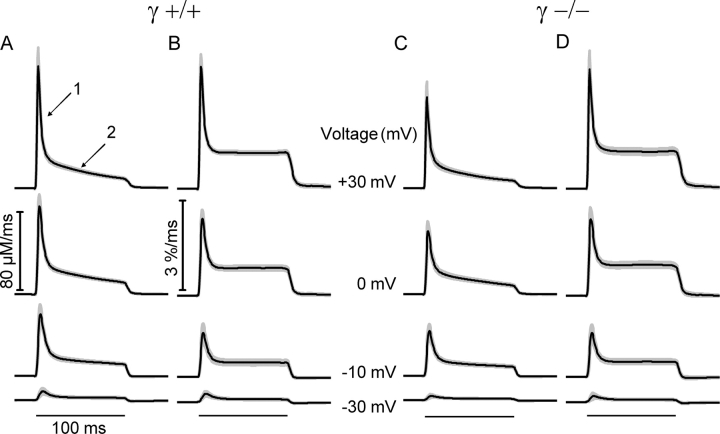
Fig. 2 shows averaged records and their point-by-point SEM of the calculated fluxes at several different test voltages for the 16 experiments on γ+/+ and the 19 experiments on γ−/− cells. In both groups of cells, the time course of the calculated Ca²⁺ input flux shows a fast (arrow 1 in A) and a slow decay component (arrow 2 in A) after the initial peak as has been reported in many previous publications for other muscle preparations (e.g., Schneider et al., 1987; Gonzalez and Ríos, 1993; Csernoch et al., 1999b; Schuhmeier and Melzer, 2004). Comparing the averaged traces at each voltage showed no significant differences in time course and scale of the flux responses.

Figure 2.

Time course of the flux of Ca²⁺ mobilization. (A and C) Mean flux of Ca²⁺ mobilization (Ca²⁺ input flux) at four different voltages. Ca²⁺ input flux was calculated using the result of fitting traces generated by a model to the relaxation phases of fluorescence at the end of depolarizing pulses (removal model fit) as described by Schuhmeier and Melzer (2004). Best fit values of the free model parameters k _off,Dye, k _on,S, k _off,S, and k _Uptake (for definitions see Schuhmeier and Melzer, 2004) were 31.98 ± 2.14 s⁻¹, 18.11 ± 3.98 μM⁻¹s⁻¹, 4.81 ± 0.49 s⁻¹, and 5.91 ± 1.05 × 10³ s⁻¹, for γ+/+, and 33.11 ± 1.61 s⁻¹, 14.60 ± 1.84 μM⁻¹s⁻¹, 4.41 ± 0.49 s⁻¹, and 5.40 ± 0.69 × 10³ s⁻¹ for γ−/−, respectively. (B and D) Same sets of records but corrected for SR depletion and normalized for the initial SR content as described in the text. Fat lines show mean values and shaded areas indicate point by point determined SEM. The horizontal lines at the bottom show the timing of the depolarization. Data are from the same experiments as shown in Fig. 1.

Correction for SR Depletion

The most likely cause for the slow decay of Ca²⁺ input flux visible during the plateau phase that became more prominent at larger flux amplitudes (arrow 2 in Fig. 2 A) is progressive depletion of the SR of its stored Ca²⁺, thus reducing the driving force for Ca²⁺ efflux from the SR. Using procedures described in previous studies (Schneider et al., 1987; Gonzalez and Ríos, 1993; Schuhmeier and Melzer, 2004), we calculated a depletion-corrected permeability change from the flux records under the assumptions that the slow decline results exclusively from depletion and that during the plateau phase permeability is constant.

The mean result of this calculation, performed for each individual experiment is presented in Fig. 2 in comparison to the uncorrected Ca²⁺ input fluxes (B versus A for γ+/+ and D versus C for γ−/−). The result shows a very similar time course in both types of fibers, consistent with Ca²⁺ permeability reaching a maximum early during the voltage pulse and then decaying to a lower value due to rapid partial inactivation as has been described for other muscle preparations (Schneider et al., 1987; Gonzalez and Ríos, 1993; Csernoch et al., 1999b; Schuhmeier and Melzer, 2004).

Fig. 3 compares the voltage dependence of peak and end level both for Ca²⁺ input flux (A and B) and for permeability (C and D). Fig. 3 (A and B) is normalized to the maximal value at +50 mV in the controls (γ+/+). Absolute amplitudes of the release flux estimates depend on the assumed fractional loading of the cell with the EGTA in the pipette solution (see Schuhmeier and Melzer, 2004). The estimation of intracellular fura-2 concentration at the time of the measurements (see materials and methods) indicated a mean fractional loading of 41%. With this value, the peak amplitudes of Ca²⁺ input flux at +50 mV were 144.03 ± 17.08 μM/ms and 108.83 ± 17.81 μM/ms for γ+/+ and γ−/−, respectively. The calculated peak permeabilities at +50 mV were very similar, showing values of 5.19 ± 0.43%/ms and 4.94 ± 0.68%/ms, respectively. For comparison, using the procedure described in materials and methods, we estimated the size of the maximal flux of Ca²⁺ entry (at +10 mV) from the data of Fig. 1 (C and G). The values were 0.18 ± 0.01 μM·ms⁻¹ and 0.19 ± 0.01 μM·ms⁻¹ for γ+/+ and γ−/−, respectively. Thus, the Ca²⁺ input flux is essentially identical to the Ca²⁺ release flux in both preparations and has only a small contribution from Ca²⁺ entry. The peak release flux values were larger than reported previously for voltage-clamped rat fibers (e.g., Garcia and Schneider, 1993; Shirokova et al., 1996; Csernoch et al., 1999a,b) but similar to flux amplitudes reported for action potential–stimulated mouse fibers (e.g., Baylor and Hollingworth, 2003). Because the rat experiments were performed on cut segments of muscle fibers, the long depolarization during dissection may have contributed to a lower release activity in these experiments.

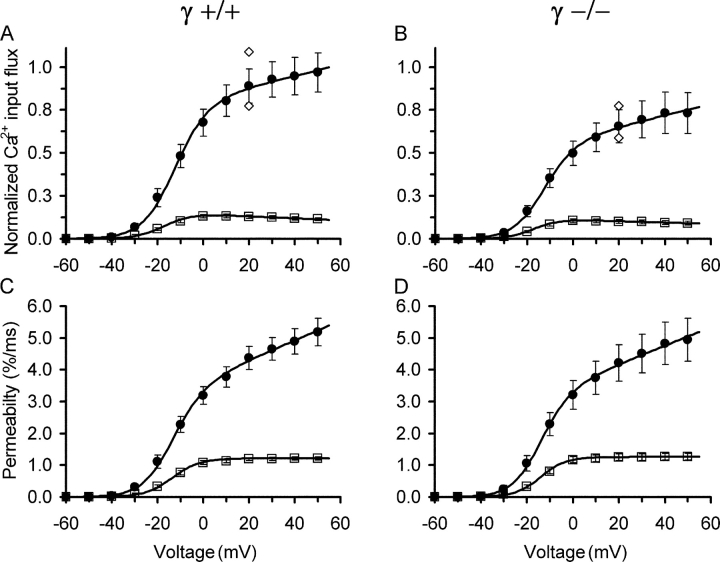
Figure 3.

Voltage dependence of the flux of Ca²⁺ mobilization (A) Mean values of peak (filled circles) and end levels (average of last 8 ms of pulse, open squares) of the calculated Ca²⁺ input flux records in γ+/+ fibers plotted versus pulse voltage. Values are normalized to the mean peak at +50 mV. (B) Corresponding flux values in γ−/− fibers using the scale of A. The mean peak values at +50 mV were 144.03 ± 17.08 μM·ms⁻¹ in A and 108.83 ± 17.81 μM·ms⁻¹ in B. Open diamonds represent the peak flux values determined with +20-mV pulses that were applied 1 min before the first and 1 min after (smaller value) the last pulse of the activation protocol, respectively. The decrease indicates a mild rundown. (C and D) Same measurements after correction for SR depletion. The continuous lines are drawn according to Eq. 2 with F representing a sloping linear function of the form a + bV using the mean values of the best fit parameters. For best fit parameters see Table I. Same set of experiments as in Fig. 1.

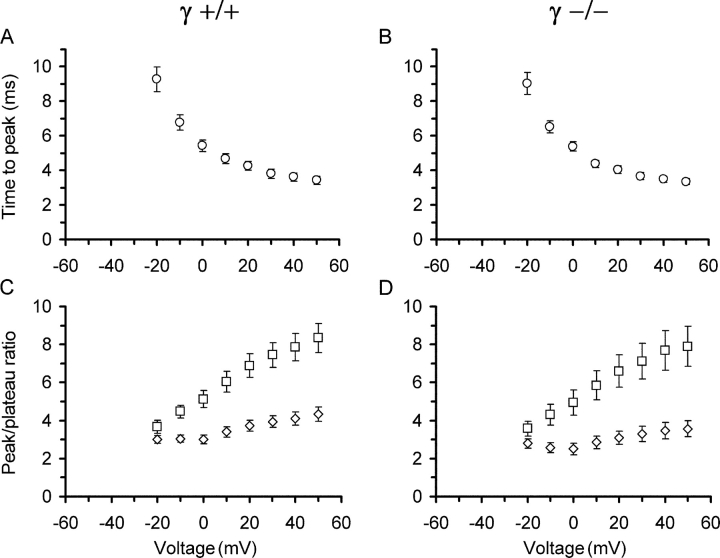
Fig. 4 (A and B) shows the time to peak of the estimated input flux records as a function of voltage. The time decreases with depolarization in a very similar way in γ+/+ and γ−/− cells reaching minimal values at +50 mV of 3.43 ± 0.24 ms and 3.35 ± 0.17 ms, respectively. Finally, in Fig. 4 (C and D), the ratios of peak to end level (both measured from the baseline) are plotted versus voltage for flux and permeability. Differences in these functions might indicate alterations in the relative contribution of calcium-induced calcium release to the total Ca²⁺ input flux. However, again the values are very similar and not significantly different at any voltage.

Figure 4.

Kinetic characteristics of voltage-activated Ca²⁺ input flux. (A and B) Time to peak Ca²⁺ input flux as a function of voltage in γ+/+ and γ−/− muscle fibers, respectively. A time delay of 2.7 ms caused by analogue Bessel-filtering of command pulse and fluorescence signal has been taken into account and is not included in the values. (C and D) Ratios of peak to plateau values (squares, uncorrected flux; diamonds, after correction for SR depletion) for the same measurements and voltages. Data derived from results in Fig. 3.

Table I summarizes the parameters that characterize the voltage dependence of both Ca²⁺ current and Ca²⁺ input (i.e., release). The comparison showed that none except two of the parameters were significantly different from the control data in the γ−/− cells. The exceptions were k of the current and the parameter b of the release flux end level. Because P values of these two parameters were borderline (0.047 and 0.042) we do not think that this indicates a physiologically relevant effect.

In conclusion, the experimental data described so far provide little indication that properties of the voltage-dependent input flux of Ca²⁺ activated within a 100-ms step of depolarization are changed. Thus, neither entry from the extracellular space nor release from the SR seem to be affected by elimination of the DHPR γ₁ subunit in adult muscle fibers.

Ca²⁺ Current Inactivation

A consistent finding in several functional investigations of the γ₁ subunit coexpressed with the (cardiac) α₁ subunit in nonmuscle cells and performed on myotubes of knockout mice (both neonatal and adult) was a change in the “steady-state” voltage dependence of inactivation of Ca²⁺ conductance (see introduction). We therefore investigated whether this functional difference was preserved in the fully differentiated state of the muscle fiber or whether it disappeared with maturation like the modulatory effect on Ca²⁺ current density.

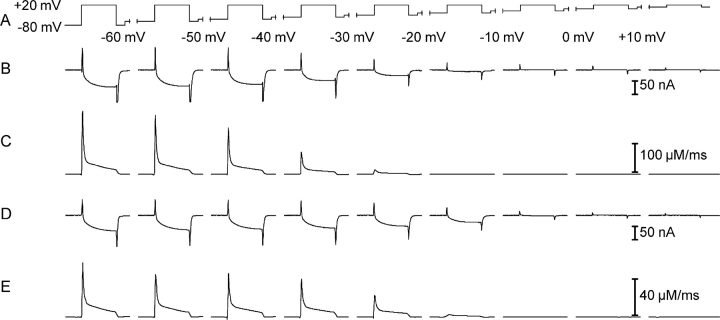
To study the process of slow voltage–dependent inactivation, we used a pulse paradigm in which increasingly depolarizing steady voltage levels were applied. Each new depolarization interval lasted 30 s and was ended with a short (100 ms) test depolarization to a fixed voltage of +20 mV (Fig. 5 A). This cumulative inactivation procedure was chosen to avoid repeated long depolarizations of increasing amplitude that would have led to repeated strong and long-lasting activation of Ca²⁺ release with a high risk of prematurely destroying the muscle fibers.

Figure 5.

Analysis of slow voltage–dependent inactivation. (A) Pulse paradigm to study inactivation. Test steps to +20 mV (100 ms duration) were applied from increasingly depolarized holding potential levels (maintained for 30 s). (B and D) Slow Ca²⁺ inward currents elicited by the test steps at different holding potentials measured in a representative γ+/+ and a γ−/− muscle fiber, respectively. (C and E) Calculated Ca²⁺ input fluxes for the same experiments and holding potentials.

Fig. 5 (B and C) shows Ca²⁺ inward current and calculated Ca²⁺ input flux induced by the test pulses at the different holding potentials in a γ+/+ muscle fiber. The progressively smaller amplitudes of the test pulse responses show the transition to the inactivated state of the DHPR.

Fig. 5 (D and E) shows the results from the same type of experiment performed in a muscle fiber of a γ−/− mouse. When comparing the traces, it becomes evident that small activation by the +20 mV pulse of both Ca²⁺ current and Ca²⁺ release is still possible at a holding potential of −20 mV in the γ−/− fiber. At the same potential, the γ+/+ fiber shows no trace of response. Therefore, membrane depolarization appears to be less efficient in inactivating DHPR in the γ−/− fiber.

The qualitative impression obtained from Fig. 5 is confirmed quantitatively when comparing mean values of the fractional inactivation at different voltages from several fibers. The experimental results of Fig. 6 were obtained from eight γ+/+ and 11 γ−/− fibers using the experimental protocol of Fig. 5 A.

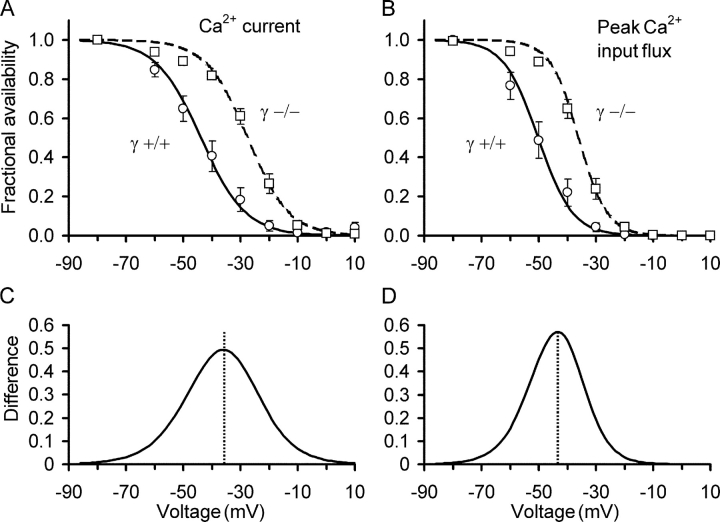
Figure 6.

Voltage dependence of steady-state inactivation of Ca²⁺ entry and Ca²⁺ input flux. (A) Fractional availability of slow Ca²⁺ inward current as a function of steady voltage presented as the mean of 8 γ+/+ (circles, continuous line) and 11 γ−/− experiments (squares, dashed line). (B) Voltage dependence of the fractional availability of peak Ca²⁺ input flux for the same experiments as in A. Lines are least squares fits by Eq. 2 with F = 1. The mean values of the best fit parameters found for each individual fiber were used for calculating the curves. (C and D) Difference of best fit curves for γ+/+ and γ−/− shown in A and B, respectively. Experimental protocol as demonstrated in Fig. 5.

Fig. 6 A shows the L-type Ca²⁺ current amplitude determined at the end (average of last 8 ms) of the test pulses as a function of the inactivating voltage. The lines are Boltzmann functions calculated by using Eq. 2 (for parameters see Table II). The results of the two groups of experiments differed significantly in their voltage V _0.5 of half-maximal inactivation (−27.55 ± 1.31 mV in γ−/− versus −43.83 ± 2.82 mV in γ+/+) but not in the steepness of the inactivation curves (sensitivity parameter k = 7.24 ± 0.40 mV in γ−/− versus k = 7.81 ± 0.34 mV in γ+/+).

TABLE II.

Comparison of Parameters Describing Voltage-dependent Inactivation of Ca²⁺ Current and Ca²⁺ Input Flux in γ+/+ (n = 8) γ−/− (n = 11) Fibers

	Ca2+ current			Input flux peak		Input flux end level
	γ+/+	γ−/−		γ+/+	γ−/−	γ+/+	γ−/−
V 0.5 (mV)	−43.83 ± 2.82	−27.55 ± 1.31a	V 0.5 (mV)	−50.21 ± 2.79	−39.09 ± 1.36a	−48.89 ± 2.67	−33.56 ± 1.53a
k (mV)	7.81 ± 0.34	7.24 ± 0.40	k (mV)	5.98 ± 0.29	4.96 ± 0.30a	6.47 ± 0.27	5.17 ± 0.41a

Voltage dependence was described by a Boltzmann function (see Eq. 2) with voltage of half-maximal activation V _0.5, voltage sensitivity k, and F = 1. Errors are SEM. All V _0.5 mean values of γ−/− were highly significantly different from the corresponding means of γ+/+ (P values from left to right of 2.5 × 10⁻⁵, 1.1 × 10⁻⁶, and 5.7 × 10⁻⁵, respectively). The differences in the steepness of the inactivation curves for peak and end level of the flux, represented by the k values were of lower significance (P = 0.029 and P = 0.028, respectively).

^aSignificant difference.

Thus, as observed in myotubes (Freise et al., 2000; Ahern et al., 2001), inactivation of the L-type Ca²⁺ current was less pronounced in γ−/− fibers compared with γ+/+ fibers at the different voltages tested; or put in another way, γ₁ appears to favor slow voltage–dependent inactivation of Ca²⁺ conductance.

Inactivation of Ca²⁺ Flux

Because inactivation of the DHPR-mediated Ca²⁺ current (slow L-type current) was affected by γ₁ knockout and because the DHPR voltage sensor also controls Ca²⁺ release from the SR, it was important to determine whether the Ca²⁺ input flux derived from the fura-2 ratio signals was changed by the knockout in a similar way. The example of Fig. 5 indicates that this is indeed the case and the statistical evaluation of the same γ+/+ and γ−/− fibers that were used for Fig. 6 A confirmed this notion. In Fig. 6 B, we plotted the mean peak values of the Ca²⁺ input flux traces versus conditioning voltage. Again, the results of the two groups showed significant differences. V _0.5 exhibited a mean value of −36.09 ± 1.36 mV in γ−/− versus −50.21 ± 2.79 mV in γ+/+ and the sensitivity parameter k was 4.96 ± 0.30 mV in γ−/− versus 5.98 ± 0.329 mV in γ+/+. For the input flux end level, alterations were similar.

Thus, as for the Ca²⁺ current, the Ca²⁺ input flux exhibited a shift in its voltage dependence of inactivation to more positive membrane potentials in γ−/− fibers. To demonstrate the range in which the test pulse signals are altered more clearly, Fig. 6 (C and D) shows the difference between the inactivation curves of γ+/+ and γ−/− at the various conditioning voltages. The details of the results obtained with the inactivation protocol are summarized in Table II. In summary, the experiments reported here provide first results on voltage-dependent inactivation of Ca²⁺ release in mammalian muscle and demonstrate that this inactivation is altered in a very similar way as L-type current inactivation in adult muscle fibers of the DHPR γ-knockout mouse.

K⁺ Contractures in EDL Fiber Bundles

Previous measurements in adult γ-knockout muscle using single twitches or short tetani did not indicate any difference in force responses (Ursu et al., 2001). However, if the steady-state voltage dependence of inactivation is altered whereas the voltage dependence of activation is unchanged, one might expect differences in the amplitude of the free Ca²⁺ transient and of the force transient during long depolarizations.

To investigate the effect of long depolarizations well above the activation threshold on force development in intact adult muscle under normal intracellular conditions, we measured the isometric tension of isolated fiber bundles of the EDL stimulated by a strong increase in the extracellular bath concentration of potassium.

The bundles were dissected from γ−/− and control mice of comparable size and were trimmed to similar diameter. The force induced by potassium stimulation was normalized by the tetanic force obtained before the potassium contracture.

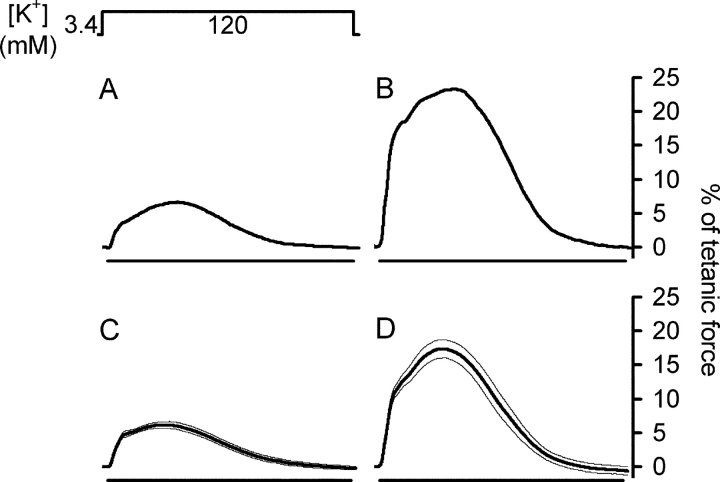
Fig. 7 shows typical K⁺ contractures in a γ+/+ (A) and a γ−/− preparation (B) displayed in percent of tetanic force. The bath solution (Krebs-Ringer solution) in the recording chamber containing 3.4 mM potassium was replaced (within ∼15 s) by a solution containing 120 mM potassium. The amplitudes of the slow force transients relative to tetanus force in γ−/− muscle were consistently larger than in γ+/+ muscle as shown in this example. Fig. 7 (C and D) presents the averaged responses from 11 γ+/+ and 11 γ−/− bundles, respectively. The normalized force amplitude was 18.50 ± 1.41% of tetanic force in γ−/− muscle compared with 6.37 ± 0.43% in γ+/+ muscle.

Figure 7.

Force production induced by long lasting potassium depolarization. (A and B) Potassium-stimulated contractures in a representative fiber bundle of a γ+/+ and a γ−/− mouse, respectively. Contracture amplitudes are presented as normalized to tetanic force before the potassium concentration increase. (C and D) Averaged normalized contracture data from 11 γ+/+ and 11 γ−/− preparations, respectively. Horizontal bars indicate the time (5 min) during which the bath potassium concentration was increased from 3.4 to 120 mM. Fat lines are mean values, thin lines indicate SEM.

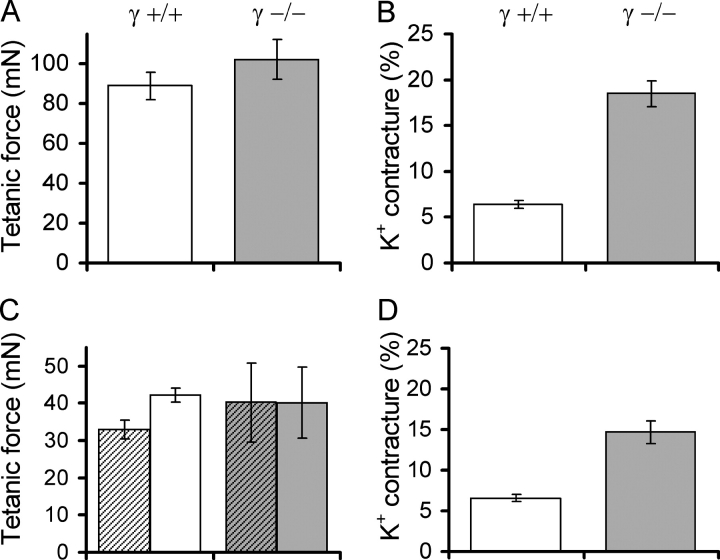
Thus, long-lasting K⁺-induced depolarization caused a strong (2.9-fold) increase in relative force in γ−/− EDL muscle compared with controls (Fig. 8 B). Because the tetanic force measured before applying the potassium depolarization showed no significant difference (Fig. 8 A), the absolute amplitude of the contracture force was similarly increased in γ−/−.

Figure 8.

Force production during potassium stimulation in Ca²⁺-free solution. (A) Mean tetanic force before potassium stimulation of 11 γ+/+ (left) and 11 γ−/− fibers (right). All solutions contained 2.5 mM Ca²⁺. (B) Fractional peak force of the potassium contractures (i.e., normalized to tetanic force) in the same sets of preparations, respectively. (C) Mean tetanic force in nominally Ca²⁺-free solution (10 min equilibration) in four γ+/+ and three γ−/− preparations. Tetanic force before removing Ca²⁺ (i.e., with 2.5 mM Ca²⁺) is indicated by hatched columns. (D) Fractional force of potassium contractures in the same sets of fibers, respectively.

K⁺ Contractures in Ca²⁺-free Solution

Because inactivation was changed for both Ca²⁺ inward current and Ca²⁺ input flux, it seemed necessary to investigate whether the increase in fractional contracture force was possibly related to an effect of Ca²⁺ entry. Therefore, we tested whether the difference could be altered by removing extracellular Ca²⁺ to suppress the Ca²⁺ inward current. The 2.5 mM Ca²⁺ in the external bathing solution was replaced by an equal amount of Mg²⁺. As tested by applying repeated tetani of 500 ms duration, contractions were only marginally influenced by this change in the divalent ion constitution of the solution. After 10 min of equilibration in the Ca²⁺-free solution, the preparation was subjected to a high K⁺ solution in which Ca²⁺ was likewise replaced by Mg²⁺. The contracture response was normal in time course and amplitude. Fig. 8 (C and D) compares tetanic force and contracture force in γ−/− fiber bundles under Ca²⁺-free conditions. The behavior and normalized amplitudes were quite similar as shown in Fig. 8 (A and B) for Ca²⁺-containing solutions. Again, the K⁺ contracture was larger in the γ−/− preparation compared with γ+/+ both in absolute terms and in relative terms (i.e., normalized to the preceding last tetanus: factor 2.3). Thus the difference observed between γ+/+ and γ−/− muscle regarding K⁺ contracture force does not seem to depend on the external Ca²⁺ concentration and Ca²⁺ entry.

DISCUSSION

In the present study, we investigated skeletal muscle Ca²⁺ signaling in mice lacking the DHPR auxiliary subunit γ₁. In contrast to the heterologous expression approach, gene-targeted knockout offers the chance to identify functional roles of a protein in its normal environment. In the case of the β subunit, disruption of the coding gene led to nonviable homozygous offspring (Strube et al., 1996) and permitted physiological tests only on cultured myotubes. These experiments indicated a complete block of EC coupling as in α_1S-deficient mice. Eliminating the γ₁ subunit showed more subtle effects when studied in myotubes (Freise et al., 2000; Ahern et al., 2001; Ursu et al., 2001). Accordingly, adult, homozygous γ₁-knockout mice are viable and therefore allow, as we showed here, the functional investigation in terminally differentiated muscle fibers.

Because of the established bifunctional role of the skeletal muscle DHPR as a voltage-dependent Ca²⁺ channel and as a voltage sensor for the activation of RyR we combined the recording of Ca²⁺ inward currents with measurements of intracellular Ca²⁺ transients. Using the Ca²⁺ transients, we quantified the flux of Ca²⁺ from its sources (SR and extracellular space) in the muscle fiber, which is commonly termed “Ca²⁺ input flux”. Since Ca²⁺ input flux was about two orders of magnitude larger than the flux of Ca²⁺ entry from the extracellular space and showed an utterly different time course, it likely consists of almost pure Ca²⁺ release flux from the SR.

In the comparative approach presented here, experimental conditions and analysis procedures were identical for both γ+/+ and γ−/−. Therefore, possible systematic errors in the quantification are of minor impact. The focus was on differences in the behavior of the two types of cells. In our experimental strategy, we included, in addition to protocols previously applied to myotubes (Ursu et al., 2001), a new approach to study the effects of long-lasting depolarization on Ca²⁺ release, which has hitherto not been possible in mammalian muscle preparations.

Activation of Ca²⁺ Current and Ca²⁺ Release by Short Depolarizations

Experiments on primary cultured myotubes obtained from myoblasts of neonatal mice indicated an amplitude modulation of the Ca²⁺ inward current by the γ₁ subunit. The mean maximal current density was ∼30% larger in γ−/− myotubes (Freise et al., 2000; Held et al., 2002). Even though small, this difference has potential physiological relevance because it was shown to be modulated by cAMP. Myotubes derived from satellite cells of older animals (1–4 mo), on the other hand, showed no significant difference in size of the Ca²⁺ current densities (Ursu et al., 2001; Held et al., 2002). Similarly, in the present experiments, current density and voltage dependence of activation were not different in adult muscle fibers of γ−/− mice as compared with WT.

Investigating EC coupling in γ−/− myotubes (from adult animals) with short step depolarizations indicated ∼30% higher flux of Ca²⁺ input than for WT (Ursu et al., 2001), pointing to a certain degree of suppression of voltage-dependent activation of Ca²⁺ release by the γ subunit. This result seemed at first consistent with the increase in force amplitude observed in the present study in potassium contractures. However, in the isolated adult muscle fibers, voltage clamp activation by short depolarizations (100 ms as applied in myotubes) indicated no comparable difference in Ca²⁺ signals and in the calculated Ca²⁺ release flux at any voltage (Fig. 3). Thus, the data indicate that the force increase obtained with long-lasting potassium depolarizations in γ−/− fibers is not the consequence of altered voltage sensor activation. Differences regarding the amplitude of Ca²⁺ currents and Ca²⁺ release flux activated by short depolarizations in the fully reprimed state seem to be confined to developmental stages of muscle and to be lost after terminal differentiation. Held et al. (2002) suggested two independent mechanisms linked to the γ₁ subunit that affect amplitude and steady-state inactivation, respectively. A bifunctional role has also been attributed to the neuronal γ₂ subunit (stargazin) that affects the targeting of AMPA receptors in addition to steady-state inactivation (Chen et al., 2000). For γ_1, only the mechanism related to inactivation seems to be retained in adult muscle.

Inactivation of Ca²⁺ Current and Ca²⁺ Release

Both heterologous expression studies (Singer et al., 1991; Lerche et al., 1996; Eberst et al., 1997; Sipos et al., 2000) and subsequent experiments on γ−/− myotubes (Freise et al., 2000; Ahern et al., 2001) indicated alterations of steady-state inactivation of the L-type Ca²⁺ current by the γ subunit. In cells lacking expression of the subunit, stronger conditioning depolarizations had to be applied than in cells expressing γ₁ to reach the same degree of inactivation. These findings could be confirmed for adult muscle fibers in the present study. On average, the voltage of half-maximal current inactivation was 16 mV more positive in γ−/− fibers than in controls. This is quite similar to the shifts reported for myotubes (Freise et al., 2000; Ahern et al., 2001; Held et al., 2002).

However, the main function of the skeletal muscle DHPR is the control of Ca²⁺ release from the SR. In contrast to Ca²⁺ inward current, Ca²⁺ release exhibits two distinct types of inactivation during step depolarization, a fast one operating within tens of milliseconds (Melzer et al., 1984, 1987; Simon et al., 1991) and a slow one that takes many seconds for completion (Brum et al., 1988; Pizarro et al., 1988; Melzer et al., 1995). While fast inactivation of Ca²⁺ release flux appears to be a Ca²⁺-dependent property of the release channels (Schneider and Simon, 1988; Jong et al., 1993), slow inactivation is known to reside in the DHPR and is voltage dependent (Ríos and Pizarro, 1991; Melzer et al., 1995).

Slow voltage–dependent inactivation of Ca²⁺ release has been studied in voltage-clamped adult muscle fibers of the frog both by force measurements and by Ca²⁺ measurements (e.g., Caputo and Fernandez, 1979; Caputo and Bolanos, 1987; Pizarro et al., 1988; Schnier et al., 1993). In adult mammalian muscle, properties of inactivation have been indirectly assessed by K⁺ depolarization and force measurements (Chua and Dulhunty, 1988, 1989; Dulhunty, 1991), but data on Ca²⁺ release flux inactivation in mammalian muscle have not been available until now. The higher sensitivity to long-lasting depolarization and the lower robustness of Ca²⁺ release had also precluded the investigation of Ca²⁺ release inactivation in myotubes. In the present study, we succeeded to study the properties of Ca²⁺ release inactivation due to conditioning depolarization and we could demonstrate that this process is affected in a very similar way as is Ca²⁺ current inactivation by the elimination of the γ subunit. Slow inactivation is likely controlled by the same voltage-dependent mechanism that causes L-type current inactivation. The present results are consistent with this hypothesis, even though the strict identity of the DHPRs that generate Ca²⁺ inward current and those that control Ca²⁺ release remains to be demonstrated (Lamb, 1992).

K⁺ Contractures

Considering the voltage clamp results on interosseus fibers, it seems likely that the observed difference in potassium contracture force in EDL muscle can be attributed to the altered inactivation properties of the DHPR during long depolarization rather than to an alteration in activation. A direct or indirect effect of a Ca²⁺ inward current showing weaker inactivation can be ruled out because the difference in force responses remained unchanged when extracellular Ca²⁺ was removed. Ca²⁺ current as the cause of the increased contracture force seemed also unlikely because of the small estimated size of Ca²⁺ entry compared with the total amount of Ca²⁺ mobilization. This leaves as the likely cause for the force difference the lower sensitivity to depolarization of SR Ca²⁺ release inactivation in the γ−/− muscle.

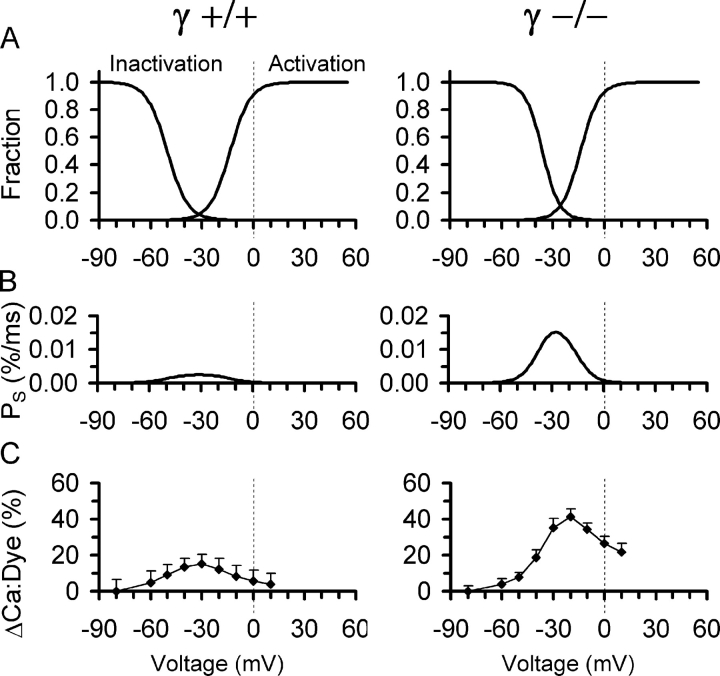
Fig. 9 summarizes the results on voltage-dependent Ca²⁺ release obtained from the single cell experiments and provides a tentative explanation of the force results obtained with the multicellular muscle preparation. The curves on the right in each panel of Fig. 9 A show the voltage dependence of fractional activation of plateau permeability (obtained from Fig. 3, C and D, squares). This provides an estimate of the steady-state permeability as a function of voltage in the absence of slow inactivation. The curves on the left of each panel show the fractional inactivation of Ca²⁺ input flux derived from the data in Fig. 6 B. The expected voltage dependence of release permeability in the steady state in the presence of slow inactivation can be calculated as the product of plateau permeability and fractional inactivation. Fig. 9 B compares the result of this calculation for γ+/+ (left panel) and γ−/− (right panel), respectively. Because of the selective shift of the inactivation curve caused by the elimination of γ₁, a “window” of noninactivatable permeability appears with a maximum at −30 mV (Fig. 9 B, right). Thus, a steady depolarization in the voltage range of about −50 to −10 mV can be expected to cause a steady release flux that should lead to a measurable elevation of Ca²⁺ in the myoplasm. In the inactivation experiments, steady elevations of Ca²⁺ and a difference between γ+/+ and γ−/− consistent with the predicted voltage dependence of Fig. 9 B were in fact indicated by the fluorescence recordings. Fig. 9 C shows the mean values of the increase above resting levels (measured at −80 mV) of the indicator's fractional occupancy by Ca²⁺. The values were obtained from the baselines immediately before each test pulse at the end of the preceding conditioning period of the inactivation experiments described in conjunction with Figs. 5 and 6. The maximal change was 2.75-fold larger in γ−/− (Fig. 9 C, right).

Figure 9.

Altered steady-state Ca²⁺ release flux in γ-deficient muscle fibers. (A) Voltage dependence of activation and inactivation of SR Ca²⁺ release. Activation, normalized least squares fits of permeability during the plateau phase of 100 ms activation, obtained from Fig. 3 (C and D). Inactivation, mean least squares fits of peak Ca²⁺ flux during test pulses as function of conditioning potential, obtained from Fig. 6 B. (B) Steady-state Ca²⁺ release permeability P_S calculated as the product of plateau permeability and fractional inactivation predicting a larger “window flux” in γ−/−. (D) Measurements of steady-state increase in the fraction of Ca²⁺-bound indicator as a function of conditioning voltage (experiments of Fig. 6 and Table II) indicating the presence of noninactivating (steady-state) Ca²⁺ release fluxes in a window of voltages.

The strong change in window release flux evidenced by Fig. 9 (B and C) marks the voltage region in which the shift of the inactivation curve by γ elimination causes a particularly pronounced effect. According to microelectrode measurements (Chua and Dulhunty, 1988), increasing the potassium concentration from 3.4 to 120 mM will lower the membrane potential to about −17 mV. Taking into account diffusional delays, it is therefore likely that during the application of the high-K⁺ solution, the membrane potential of many cells in the preparation will be in the critical voltage window, meaning that functional differences between γ+/+ and γ−/− will be expressed particularly strong. A slowing of inactivation, which has been reported for Ca²⁺ currents in γ−/− (and γ+/−) myotubes (Freise et al., 2000; Ahern et al., 2001) but could also be present in Ca²⁺ release, may add to the effect. We, therefore, believe that the alteration in inactivation is the cause of the observed difference in K⁺ contracture force.

Conclusions

In summary, the results of the present investigation suggest that the slow voltage–dependent inactivation of Ca²⁺ current and Ca²⁺ release is the main target of functional alteration by the γ₁ subunit in adult muscle fibers. Short term activation of Ca²⁺ current and Ca²⁺ release that had been implicated in γ₁ effects based on experiments in nonmuscle cells and myotubes were not found to be changed by the elimination of this auxiliary subunit in mature fibers. The finding that inactivation of SR Ca²⁺ release is affected is important because the SR is the predominant source of Ca²⁺ during voltage activation of skeletal muscle fibers.

The γ₁ subunit bears the potential for a modulatory role in EC coupling. By affecting steady-state inactivation, it can control the availability of DHPRs for voltage-dependent activation of Ca²⁺ release and may change the force response on the single fiber level. Whether γ₁-mediated modulation is actually used under physiological circumstances remains equally unclear at present as the molecular mechanism of slow inactivation in general. Alterations of the voltage dependence of slow inactivation of K⁺ contractures have been reported for rat EDL, for instance as a result of chronic administration of tri-iodothyronine (rightward shift; Chua and Dulhunty, 1989) and of exercise training (leftward shift; Joumaa and Leoty, 2002).

The shift of the inactivation curve to more negative potentials caused by γ₁ is reminiscent of the effect of Ca²⁺-antagonistic drugs on the voltage sensor for EC coupling (Berwe et al., 1987; Ríos and Brum, 1987; Pizarro et al., 1988; Erdmann and Lüttgau, 1989; Neuhaus et al., 1990), which has in part been attributed to selective binding of the drugs to the inactivated conformation of the DHPR (Ríos and Pizarro, 1991). γ₁ has been shown to interact directly with α_1S, probably via the first two transmembrane domains (Arikkath and Campbell, 2003). This interaction might stabilize the inactivated state in analogy to some Ca²⁺ antagonists and extracellular metal ion substitutions (e.g., Pizarro et al., 1988; Erdmann and Lüttgau, 1989; Feldmeyer et al., 1990; Ríos and Pizarro, 1991; Schnier et al., 1993; Melzer et al., 1995) and may even influence the force of action potential–induced twitches or tetani under certain conditions. It seems, therefore, worthwhile to search for possible conditions that increase the strength of the γ₁–α_1S interaction beyond the normal level, thus provoking a true Ca²⁺-antagonistic effect.