Developmental regulation of calcium-dependent feedback in Xenopus rods

Abstract

The kinetics of activation and inactivation in the phototransduction pathway of developing Xenopus rods were studied. The gain of the activation steps in transduction (amplification) increased and photoresponses became more rapid as the rods matured from the larval to the adult stage. The time to peak was significantly shorter in adults (1.3 s) than tadpoles (2 s). Moreover, adult rods recovered twice as fast from saturating flashes than did larval rods without changes of the dominant time constant (2.5 s). Guanylate cyclase (GC) activity, determined using IBMX steps, increased in adult rods from ∼1.1 s⁻¹ to 3.7 s⁻¹ 5 s after a saturating flash delivering 6,000 photoisomerizations. In larval rods, it increased from 1.8 s⁻¹ to 4.0 s⁻¹ 9 s after an equivalent flash. However, the ratio of amplification to the measured dark phosphodiesterase activity was constant. Guanylate cyclase–activating protein (GCAP1) levels and normalized Na⁺/Ca²⁺, K⁺ exchanger currents were increased in adults compared with tadpoles. Together, these results are consistent with the acceleration of the recovery phase in adult rods via developmental regulation of calcium homeostasis. Despite these large changes, the single photon response amplitude was ∼0.6 pA throughout development. Reduction of calcium feedback with BAPTA increased adult single photon response amplitudes threefold and reduced its cutoff frequency to that observed with tadpole rods. Linear mathematical modeling suggests that calcium-dependent feedback can account for the observed differences in the power spectra of larval and adult rods. We conclude that larval Xenopus maximize sensitivity at the expense of slower response kinetics while adults maximize response kinetics at the expense of sensitivity.

INTRODUCTION

Mature rod photoreceptors can operate in near darkness. This exquisite sensitivity is made possible by the large collecting area provided by specialized outer segments filled with rhodopsin, the high quantum efficiency of rhodopsin, and the great amplification of the phototransduction cascade (Pugh and Lamb, 1993). However, these cells must operate over a range of light intensities (Normann and Werblin, 1974), and thus they adapt by appropriately shaping the response recoveries through calcium-dependent (Koutalos and Yau, 1996) and calcium-independent (Nikonov et al., 2000) mechanisms. It is very likely that similar feedback mechanisms dominate phototransduction in cones to prevent saturation in the presence of background illumination and dramatically extend their response range (Pugh et al., 1999; Arshavsky et al., 2002).

Surprisingly, little is known about how rod physiological properties develop. Rod differentiation and elaboration of the mature outer segment is one of the final steps in retinal development and occurs over an extended period. In mice, rods reach their final position at approximately postnatal day 10, and at that point, outer segments begin to elongate. However, they reach their mature length only after postnatal day 21 (LaVail, 1973). In humans, rods in the parafoveal and peripheral regions mature at different rates, but both take many weeks to achieve their final size (Hendrickson, 1994). In lower vertebrates that develop more rapidly, such as Xenopus or zebrafish, the rod outer segments still require an extended period to reach maturity, many weeks after hatching. During this extended period of rod maturation, the animals exhibit electroretinogram (ERG) responses (Nilsson and Crescitelli, 1969; Witkovsky et al., 1976; Brockerhoff et al., 1995) and visually directed behavior (Brockerhoff et al., 1995; Solessio et al., 2004). Transcription of phototransduction genes appears to be coordinated and precedes outer segment formation (Bowes et al., 1988). Thereafter, outer segment growth is gradual (Kinney and Fisher, 1978b; Galbavy and Olson, 1979), and mature length is reached when the rates of disk synthesis and removal are equal (LaVail, 1973). Membrane and rhodopsin molecules synthesized in the inner segment are incorporated at the basal end of the outer segment (Horst et al., 1990). It is believed that elements of the phototransduction pathway are transported along with membranes to the outer segment, although certain molecules (e.g., arrestin or transducin) may be under a separate regulatory mechanism (Whelan and McGinnis, 1988; Mendez et al., 2003).

Outer segment length, opsin, and other phototransduction protein content appear to exhibit logistic growth (Fulton et al., 1995). One model hypothesizes that the magnitude of the photoresponses in immature rods will scale with outer segment length, and experiments support this view (Matthews, 1984). However, ERG recordings suggest that the immature rod-mediated responses are less sensitive than expected from a simple scaling model (Fulton et al., 1995). Electrophysiological recordings in neonatal rat (Ratto et al., 1991) and Xenopus tadpole rods (Xiong and Yau, 2002) show lower sensitivity than expected, and furthermore suggest that a low availability of 11-cis retinal may contribute to this reduced sensitivity. In addition, little is known about the development of the mechanisms that govern the inactivation of rod photoresponses (Fulton and Hansen, 2003). Using suction electrode recordings, we characterized the development of the photoresponse in larval and adult Xenopus rods under conditions where vitamin A is not limiting. We applied ensemble variance analysis to determine the amplitude of responses to single photon absorption (Baylor et al., 1979a) and the Pugh and Lamb phototransduction model (Pugh and Lamb, 1993) to evaluate the kinetics of activation. We find that as the animal matures, the amplification of the response increases and the GCAP–GC feedback loop strengthens. As a result, the overall kinetics become more rapid, permitting faster response shutoff in adult rods. In all, growing rods trade sensitivity for faster response kinetics. A linear model applied to small responses was used to quantify the changes in feedback (Nikonov et al., 1998).

MATERIALS AND METHODS

Husbandry and Staging

Adult Xenopus (Xenopus Express) were housed in tanks containing 2–4 liters of 0.1X MMR per frog, and supplemented with 1 g/L of seasalt (Instant Ocean). 1X MMR consists of 100 mM NaCl, 2 mM KCl, 1 mM MgCl₂, 2 mM CaCl₂, 5 mM HEPES, pH 7.5. Animals were fed three times a week with newly purchased salmon pellets (Xenopus Express) and kept at 20–22°C in 12 h L/D cycles. Tadpoles were generated by in vitro fertilization (Sive et al., 2000) in order to have developmentally synchronized embryos and raised in 2–5 liter tanks in 0.5 g/L seasalt (Instant Ocean) + 4 mM NaHPO₄, and fed a diet consisting of both nettle powder (Wundlich-Deitz) and tadpole powder (Xenopus Express). Tadpoles were kept under natural lighting conditions. Room temperature was 22°C. All procedures were approved by the SUNY Upstate Medical University IACUC and were conducted in accordance with the Guide for the Care and Use of Laboratory Animals (1996, National Academy of Sciences). The developmental stage of each animal was determined according to standardized morphological characteristics (Nieuwkoop and Faber, 1994). Animals of two different ages were used in this study. For the purpose of this investigation, we define young tadpole as larval animals of developmental stage 48–50; their outstanding morphological features included absence of barbels and any extending limbbuds. We grouped all post-metamorphic juveniles with fully reabsorbed tails and body sizes at least 2.5 cm in length as froglets. Additional recordings were performed on rods of stage 54 tadpoles to confirm the linearity in the relationship between saturating currents and length of the rod outer segments.

Cell Preparation

Xenopus were dark adapted for at least 12 h. Under dim, red light the animals were cooled in ice, decapitated, and pithed. Next, using infrared illumination and intensifiers, the eyes were enucleated and the retinas gently separated from the pigment epithelium. The retinas were placed in a Xenopus Ringer's solution: (in mM) NaCl 110, KCl 2.5, MgCl₂ 1.6, CaCl₂ 1, HEPES 3, glucose 10, NaHCO₃ 0.5, Na₂HPO₄ 1, pH 7.6. For cell dissociation, small pieces of tissue were cut out from the central region of the froglet retina, transferred to the recording chamber, and minced gently with a pair of forceps. In the case of young tadpoles the entire retinas were used. After mechanical dissociation we generally obtained 50 or more isolated cells, including those with broken rod outer segments (ROS), intact rods, rods with truncated inner segments, and small clusters of photoreceptors. Saturating currents in rods with truncated inner segments were generally smaller in magnitude, ∼50% of that observed in rods with intact inner segments. On the other hand, photocurrents did not differ significantly in intact rods found in isolation or as members of a small cluster of photoreceptors. Therefore, recordings were performed exclusively from rods with intact inner segments, whether in isolation or in small clusters. Recordings from young tadpole and froglet rods were performed from cells with ROS diameters of ∼6-7 μm or larger.

The recording chamber containing the cells had a volume of 0.25 ml, with glass bottom and top to allow visualization of the rods. Sides of the chamber were left open to insert the recording and microperfusion pipettes. The chamber was clamped on the stage of an inverted microscope (Nikon) and superfused continuously using a gravity-fed system flowing at a rate of 0.3 ml/min. All recordings were performed at room temperature (20°C). Under these conditions, the photoresponses of cells in the recording chamber were consistent for at least 2–3 h. Cells were viewed using an infrared illumination system and a CCD camera (Cohu). Measurements of ROS length and diameter were taken directly from the video monitor using a calibrated scale.

Electrophysiological Recordings

Circulating currents of isolated rods were recorded using the suction electrode technique (Baylor et al., 1979a). Glass pipettes were pulled with a horizontal electrode puller (Sutter Instruments) to a tip diameter of ∼25 μm and fire polished to a final diameter of 6–7 μm. The electrodes were filled with Xenopus Ringer's solution. Rods were identified by their characteristic morphology and their outer or inner segments gently drawn into the recording pipette. The resistance of the seal made by the rod in the pipette ranged between 6 and 8 MΩ.

A collimated beam from a 120-W tungsten lamp passed through a narrowband 520-nm filter and was attenuated in 0.5 log increments with neutral density filters. The beam was focused on the bottom of the perfusion chamber clamped to the stage of the inverted microscope. For 20-ms flashes, maximal beam intensity (indicated by log I = 0) at 520 nm is 5,600 photons μm⁻². Changes in circulating current elicited by 20-ms flashes were recorded with an Axopatch 1D amplifier (Axon Instruments). Currents were low-pass filtered at 20 Hz and sampled at 100 Hz. Data were collected with a PClamp7 acquisition system (Axon Instruments) running on a personal computer. Unless specified otherwise, responses were averaged four to eight times, and sufficient time was allowed between stimuli to avoid light adaptation (10–20 s with dim flashes and 1–3 min with saturating flashes). Analysis and plotting of data was performed with Clampfit (Axon Instruments), SigmaPlot, and SigmaStat (SPSS, Inc.). Statistical differences between groups were determined using the t-distribution and a significance level of 5% (α = 0.05). Error bars in graphs indicate the SEM. Sample size (n) is indicated in the text.

Ensemble Variance Analysis

This approach is based on the assumption that Poisson statistics govern the distribution of the photoresponse amplitudes (Baylor et al., 1979b) and can be used to estimate both the collecting area as well as the amplitude of the single events. Dark-adapted rods were exposed to dim flashes eliciting response amplitudes <5% the level of the saturating current. The square of the average of 16 or more responses was compared with the excess ensemble variance elicited by the same flashes. The number of photoisomerizations was estimated from the scaling factor needed to make the onset of the waveforms overlap (Fig. 2 B). On average, an estimated 1–2 photons/flash were elicited per flash in each rod (Table I).

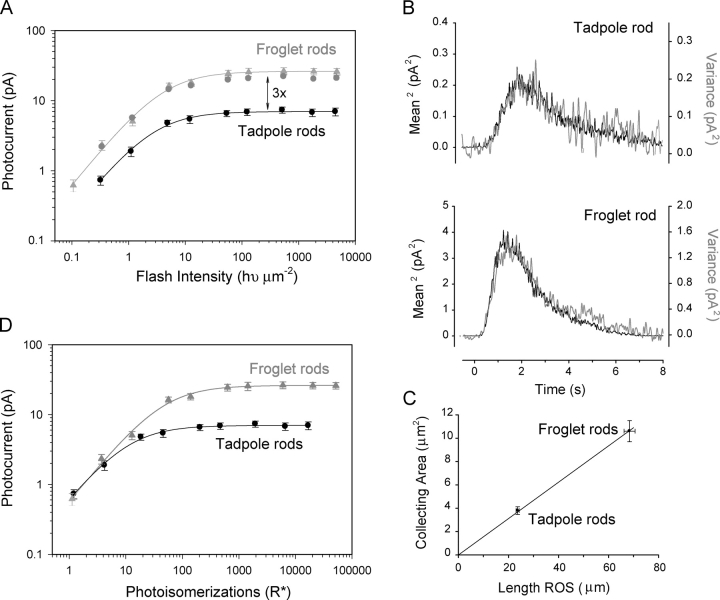
Figure 2.

Intensity–response curves of larval and adult Xenopus rod photoreceptors. (A) Responses are plotted as a function of flash intensity for tadpoles (black circles, n = 6) and froglets (gray triangles, n = 8). The amplitude of the responses of froglet rods were three times larger than the responses of tadpole rods, similar to the saturating currents. The gray circles represent the scaled (i.e., multiplied by three) responses of tadpole rods. (B) The squared value of the mean responses (black) was compared with the ensemble variance (gray) for young tadpole and froglet rods (16–25 flash repetitions). Flash intensity was 0.32 hυ/μm². Applying Poisson statistics to these examples, the estimated mean number of photoisomerizations per flash (R*) was 1.1 for the tadpole rod, and 2.5 for the froglet rod. The estimated values of the collecting areas were 3.8 and 8.6 μm² for the tadpole and froglet rods, respectively. (C) Tadpole and froglet rod collecting areas plotted as a function of ROS length. On average, the collecting areas grew in proportion to ROS length and triple in value, indicating that the optical density per unit of ROS length (pigment density) does not vary with stage of development. (D) Peak responses from A plotted as a function of photoisomerizations per flash (R*). On average, the response of both tadpole and froglet rods to single photoisomerizations (arrow) did not differ (∼0.6 pA). At low light intensities (0–10 R*), the responses from tadpole and froglet rods were the same.

TABLE I.

Parameters of Tadpole and Froglet Responses Under Control Conditions and After Loading the Cells with BAPTA-AM

	Le	TP	SC	Kd	Niso	S PhA	CoA	ExA	ExN	ExT	Var
	μm	s	pA	ph/μm2		pA	μm2	pA		s	pA2
Tadpoles
mean	23.7	2.0	7.3	2.4	1.2	0.6	3.8	0.5	0.06	1.2	0.022
SEM	0.6	0.12	0.5	0.2	0.13	0.08	0.33	0.07	0.01	0.2	0.006
n	14	14	15	8	9	9	9	7	7	7	7
Froglets
mean	68.4	1.3	25.4	3.2	2.6	0.6	10.6	1.7	0.06	0.56	0.07
SEM	2.2	0.06	2.4	0.5	0.5	0.1	0.9	0.1	0.01	0.04	0.012
n	13	13	14	8	12	12	12	6	6	6	6
Froglets-BAPTA
mean	68.7	2.9	20.7	0.9	1.2	1.7	11.6	2.2	0.08	3.1	0.9
SEM	2.45	0.35	2.0	0.2	0.3	0.3	1.3	0.45	0.01	1.0	0.16
n	8	6	13	8	13	6	13	5	5	4	8
Tadpoles-BAPTA
mean	24.6	2.9	5.2	1.8	1.1	0.86	3.5	0.3	0.06	2.9	0.03
SEM	0.8	0.15	0.26	0.14	0.13	0.04	0.4	0.1	0.02	0.5	0.003
n	14	10	14	7	4	6	4	4	4	7	5

Le, ROS length; TP, time to peak; SC, saturating current; Kd, intensity–response functions were fit with Michaelis-Menton functions and Kd is the flash intensity required to reach 50% of the maximal response; Niso, number of isomerizations/flash computed using the ensemble variance analysis; S PhA, amplitude of responses to single photons; CoA, collecting area; ExA, exchanger current; ExN, exchanger current relative to saturating current (ExA/SC); ExT, time constant of exponential function fitting the exchanger current; Var, noise variance under dark-adapted conditions.

Amplification Constant

To calculate the amplification constant (A), the population averaged dim responses were normalized to their respective saturating currents. The early phase of the responses were fit with the Lamb-Pugh model (Pugh and Lamb, 1993) using

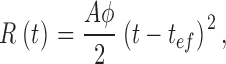(1)

where R(t) is the onset phase of the response, A is the amplification constant, φ is the number of photoisomerizations per flash, and t_ef is the combined delay of all the stages in the transduction cascade (and filters in the recording setup). In response to single photoisomerizations (φ = 1), the onset of the responses is sufficiently slow such that t_ef (in the order of 20 ms) was considered negligible.

Fourier Analysis

We estimated power density spectra to obtain frequency representations of single photon responses. The FFT of the average single photon response was calculated (pClamp9.0 software; Axon Instruments). Window lengths were 10.24 or 20.48 s long, which for sampling frequencies of 100 Hz, yield a total of 1,024 or 2,048 samples per episode. No weighting window was applied to reduce edge effects. Spectra obtained from multiple rods were averaged and a running average window was applied to smooth the spectra at frequencies >0.3 Hz.

Noise Variance Measurements

The variance of membrane current was measured under dark- and light-adapted conditions. Total duration of the records for each rod was 160 s. Transduction noise was determined by subtracting variances obtained from the same rod under the light- and the dark-adapted conditions.

IBMX Treatments

To estimate α', the normalized catalytic activity of the GC, we used the phosphodiesterase (PDE) jump approach (Hodgkin and Nunn, 1988; Cornwall et al., 2000). In brief, the inner segment of an isolated rod was drawn into the recording pipette and stimulated with saturating flashes. Pulses of 0.5 mM 3-isobutyl-1-methylxanthine (IBMX) (Sigma-Aldrich), 2 s in duration, were applied via a microsuperfusion system (Adams and List) at the indicated times after the flash. Using pClamp software, we calculated F(t), the normalized currents relative to the saturating current, and determined α' from the maximum value obtained in the time derivative of F(t)^{1/ nH}, where n_H is the Hill coefficient of the cGMP channels, to which we assigned a value of 2 (Nikonov et al., 1998).

To complete these experiments, a single rod was repeatedly exposed to saturating flashes so that the IBMX pulse could be applied at incrementing times after the flash. Despite long recovery times between flashes (2–3 min), the 50% recovery times measured throughout these series of experiments were shorter than those described in the experiments run to determine the value of the dominant time constant (Fig. 4). We believe that this may be due to light adaptation caused by the repeated presentation of light flashes necessary to complete these measurements.

Figure 4.

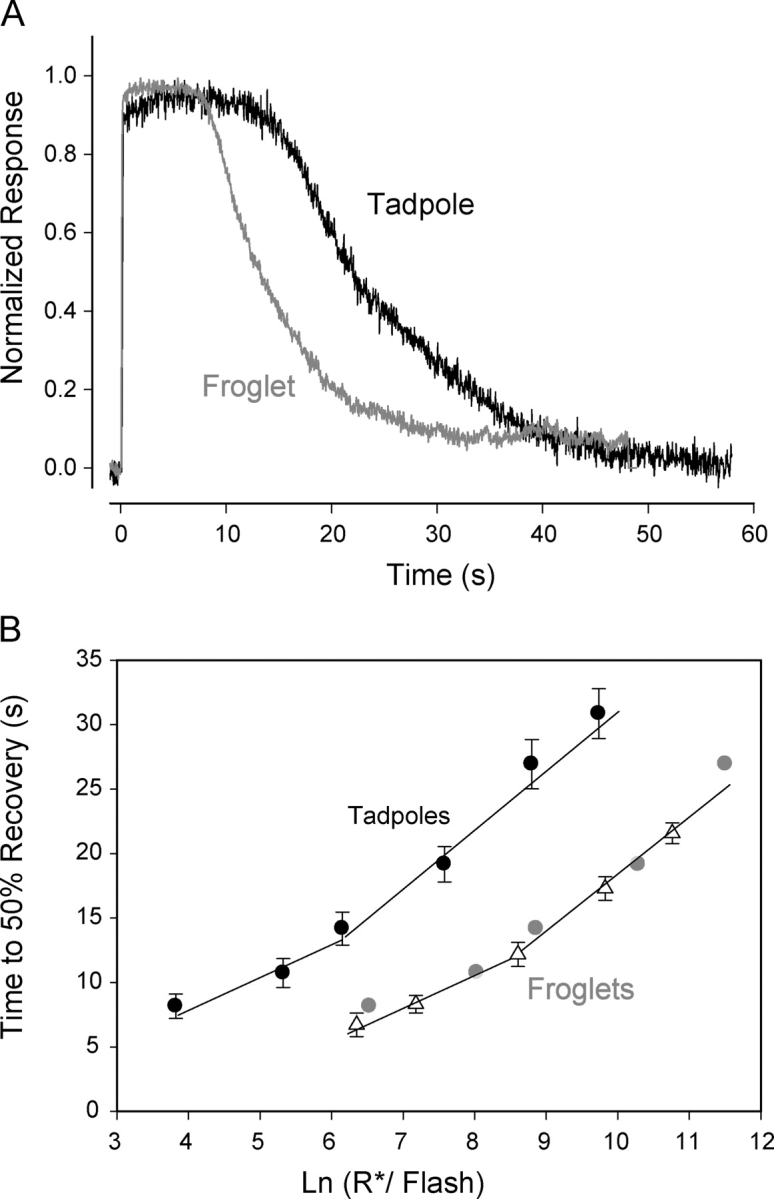
Responses of Xenopus rods to saturating flashes. (A) Responses of tadpole (black) and froglet (gray) rods to saturating flashes producing ∼6 × 10³ photoisomerizations were recorded. Responses of froglet rods recovered faster from saturation than tadpole rods. Responses were normalized relative to their respective saturating currents. (B) Time to 50% recovery from saturation as a function of the number of photoisomerizations (R*) elicited by a saturating flash was measured. The recovery time of tadpole rods (black circles, n = 9) increased with flash intensity. Two linear segments were used to fit the data. The dominant time constant value of 2.5 s was estimated from the slope of the shallow segment. In response to flashes producing the same number of photoisomerizations, froglet rods (triangles, n = 8) recovered approximately twice as fast as tadpole rods. Recovery time of froglet rods increased with intensity at the same rate as that of tadpole rods but more intense flashes (15×) were required to produce similar recovery times. Displacement of the tadpole data by 2.7 ln units brought the two curves to a close match (gray circles). However, only a 0.5 ln units shift along the abscissa can be accounted for by the 1.6-fold increase in amplification in the tadpole rods. Therefore, the remaining ∼10-fold difference must result from a stronger shutoff mechanism present in froglet rods.

BAPTA Treatments

Pieces of retina were incubated for 5 min in Xenopus Ringer's solution containing 1 μM (froglets) or 0.1 μM (tadpoles) 1,2-bis (2-aminophenoxy) ethane-N,N,N′,N′-tetraacetic acid tetrakis (acetoxymethyl ester) (BAPTA-AM) (Sigma-Aldrich). The tissue was placed into the recording chamber, rinsed in Ringer's solution, and gently triturated to isolate the rods. Collecting area and amplification of rods loaded with BAPTA-AM did not differ from control; however a systematic 20–25% drop in saturating currents was observed (see Table I). When rods were treated with higher BAPTA-AM concentrations (10-fold increase) the onset phase of the responses slowed down as well, and the value of the amplification constants decreased relative to control values (not depicted). We cannot explain the concentration-dependent action of BAPTA-AM on the amplification constant, although it may result from toxicity following the hydrolysis of BAPTA-AM. Therefore, all results in this study are from rods treated with low concentrations of BAPTA-AM.

GCAP1 Immunohistochemistry

Stage 48 tadpoles and juvenile froglets were dark adapted overnight under conditions identical to those used for the physiology experiments. Stage 48 tadpoles or enucleated froglet eyes were fixed by immersion in 4% PFA in 0.1 M phosphate buffer (pH 7.4) for 1–2 h. The fixed tissue was processed by serial immersions through 5, 15, and 30% sucrose in 0.1 M phosphate buffer. The tissue was transferred to O.C.T. embedding medium (Sakura Finetek), frozen, and cryosectioned at 14–16 μm. Sections of tadpole and froglet retinas were laid in close proximity on the same slide and processed simultaneously for antibody staining by permeabilizing in PBS containing 0.1% Triton X-100 (PBST). Nonspecific antibody reaction was blocked by preincubation with PBST containing 5% normal goat serum. Anti-GCAP1 rabbit polyclonal antibody (UW101; a gift of K. Palczewski, University of Washington, Seattle, WA) was used at 1:100, 1:250, or 1:500 dilutions to determine optimal antibody staining concentrations. Primary antibody was incubated for 8 h at 4°C. Cy3-conjugated goat α-rabbit antibody (Jackson ImmunoResearch Laboratories) was used at a dilution of 1:750 and incubated at room temperature (18–20°C) for 1 h. The sections were washed in 1X PBST with 0.1% Triton X-100, coverslipped, and mounted. Additional controls such as Cy3-conjugated secondary antibody alone or no antibody (to measure background autofluorescence) were included in the experiment and processed simultaneously as described above. No detectable background staining was observed under these conditions. Confocal images were obtained using a Carl Zeiss MicroImaging, Inc. LSM 510 confocal laser scanning microscope using a 25X objective using the same detector gain and laser power for tadpole and froglet sections of the retina. Images were collected at 0.18-μm steps through the entire thickness of the tissue. Projections were made from slices of identical thickness.

RESULTS

Photoresponse and Collecting Area Increase with ROS Length

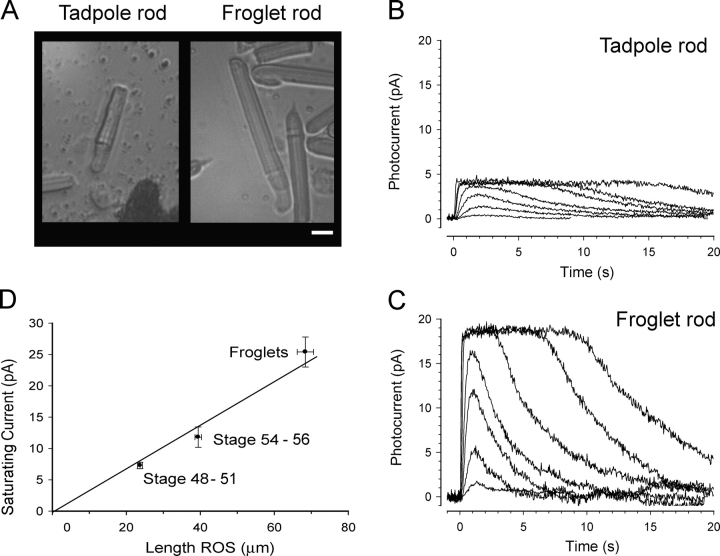
To investigate the properties of the rod light responses in developing Xenopus, we used rods isolated from stage 48–50 tadpoles (young tadpoles). This was the earliest stage at which we could reliably record responses using the suction electrode technique. For comparison, we characterized the photoresponses of post-metamorphic sexually immature frogs (froglets), in which rods have reached their maximal length (Kinney and Fisher, 1978a). Fig. 1 A shows that the length of froglet ROS was three times longer than those in young tadpoles. In parallel, the amplitude of the light responses was also greater in the froglet rods. Figs. 1 (B and C) shows typical responses of young tadpole and froglet rods exposed to a sequence of 20-ms flashes of increasing intensity. The saturating currents of the light responses (which we take to measure the circulating dark current) tripled in magnitude and grew in direct proportion to the ROS length (Fig. 1 D), indicating that the current density does not change with changes in ROS length. Using linear interpolation, we estimated that the current density value of both young tadpoles and froglet rods is 0.3 pA/μm ROS, in line with values reported previously for Xenopus rods (Xiong and Yau, 2002) and approximately half the value measured in Bufo rods (Baylor et al., 1979a).

Figure 1.

Light responses of larval and adult Xenopus rod photoreceptors. (A) Isolated rod photoreceptors from a stage 48 tadpole (left) and froglet (right) in the recording chamber following retinal dissociation. Typically rod outer segments (ROS) of froglet rods were three times the length of ROS in young tadpole rods. ROS diameters of both young tadpole and froglet rods used for this study had reached mature dimensions of 6–7 μm. Bar, 10 μm. (B) Photocurrents recorded from a tadpole rod using the suction electrode technique. Photocurrents were elicited by a series of 520-nm flashes, 20 ms in duration of the intensities 0.32, 1.1, 4.9, 12.0, 54.0, 123.7, 514.3 hυ/μm². Recordings of dim flashes are averages of eight responses, recordings of saturating flashes are averages of two responses. (C) Photocurrents recorded from a froglet rod stimulated as in B. Relative to tadpole rods, the saturating current tripled in magnitude and the responses were faster at onset and recovery. (D) Dependence of saturating current on rod length. The plot shows averaged values grouped according to stage of development: young tadpoles corresponding to stages 48–50, limbbud tadpoles corresponding to stages 54–56, and froglets. Double error bars indicate SEM. On average, froglet ROS were three times as long as ROS of young tadpoles. The saturating currents grew in the same proportion, suggesting that the density of the currents (0.3 pA/μm) does not change with development. Current density was estimated from the slope of the line interpolating the data and passing through the origin (R² > 0.99).

Similar to the changes in ROS length and saturating current magnitude, the amplitude of the maximal responses of froglet rods increased by a factor of three compared with young tadpoles (Fig. 2 A). Both young tadpoles and froglets had similar intensity response curves, however the froglet responses were displaced vertically by a factor of three when plotted as function of light intensity. This demonstrates that, like the saturating currents, the response amplitude grew in proportion to the ROS length. In contrast, the light intensity required to elicit the half-maximal response (Kd) did not differ significantly with developmental stage (Table I). There are several possible ways to reconcile these two observations. For example, the collecting area increased with ROS length without a corresponding change in the amplitude of the single-photon response. Alternatively, the collecting area did not change but the amplitude of the single event increased with ROS length.

To distinguish between these two alternatives, we determined the collecting area of young tadpole and froglet rods by applying ensemble variance analysis (see materials and methods). Fig. 2 B shows that when scaled, the square of the mean responses to dim flashes and the ensemble variance have similar time courses. From that scaling factor, we derived the collecting areas for young tadpoles and froglets (Table I) and found that, analogous to the dark currents, the collecting area grew in proportion to the length of the ROS (Fig. 2 C). The ROS diameters of young tadpole and froglet rods analyzed in these experiments were the same. Therefore, these results demonstrate that the absorption properties, i.e., concentrations of visual pigment, per unit length of ROS do not vary throughout development.

Single Photon Response Amplitude Remains Constant During Development

We estimated the sensitivity (defined as the mean amplitude of the response per photoisomerization) of young tadpole and froglet rods using ensemble variance analysis. The single photon response amplitude of rods from both stages was ∼0.6 pA (Table I). The single photon amplitude can also be obtained from the intensity–response curves, once the collecting area is known, by replotting the amplitude as a function of photoisomerizations per flash (R*) (Fig. 2 D). At intensity levels of one R*, the mean amplitude of the responses in both young tadpole and froglet rod is close to 0.6 pA. This amplitude is in close agreement with that obtained using ensemble variance (Table I). Moreover, the data overlap closely for rods from both stages at intensity levels <5–10 R*. This overlap is consistent with linear addition of single photon events by rods in response to dim flashes, regardless of developmental stage and length of ROS. With higher intensities, the responses of the young tadpole rods diverged from the froglet rods at ∼10 R* and saturate to the saturating current limits (∼7.5 pA; Table I). Responses of froglet rods continue to grow and saturate at ∼25 pA (Table I). The intensity required to elicit the half-maximal responses (Kd), obtained from regression fits of the Michaelis-Menton equation, was 10 R* for young tadpole rods and 33 R* for froglet rods (R² > 0.99). In summary, these results suggest that the response of a single frog rod is equivalent to that of three young tadpole ROS joined together. However, this view does not explain the dissimilarities in the time course of the photoresponses of young tadpoles and froglet rods (Fig. 1, B and C, and Fig. 2 B).

Developmental Changes of Single Photon Response Kinetics

The time course of the single photon response was estimated by scaling dim responses by the number of R*. Fig. 3 A shows the population mean responses of young tadpole and froglet rods, which averaged ∼0.6–0.7 pA. The response of the froglet rods grew at a faster pace than that of tadpoles and peaked at 1.3 s, significantly earlier than young tadpoles that peaked at 2 s (Table I). The froglet rods recovered faster than the responses of young tadpoles. The altered kinetics could arise from changes in the amplification of the transduction cascade and/or in the mechanisms that govern the recovery phase of the response (Nikonov et al., 1998).

Figure 3.

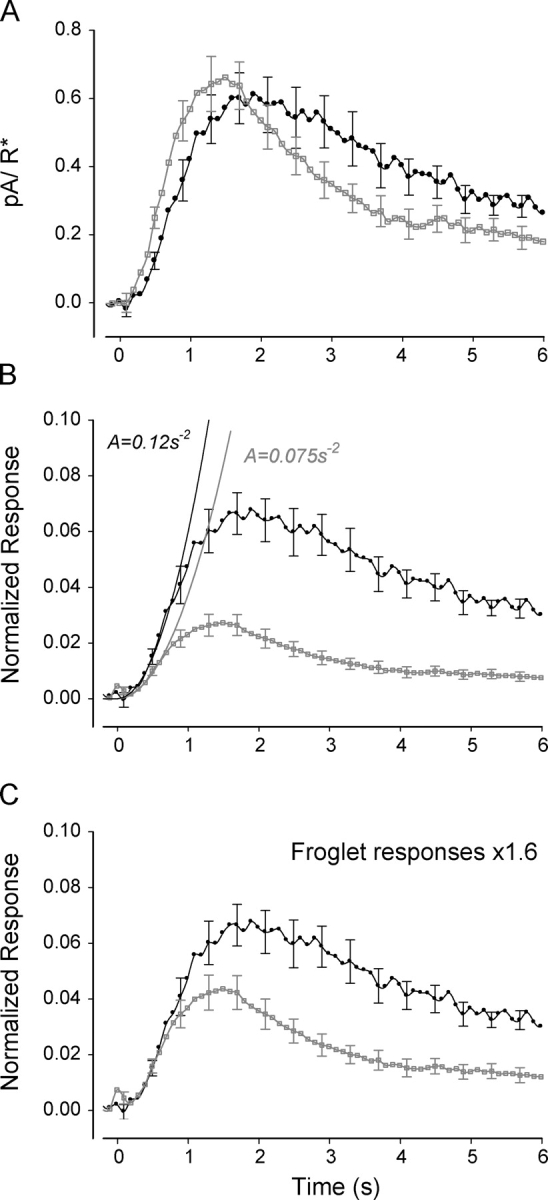
Time course of Xenopus rod responses to single photoisomerizations. (A) Averages of single photon responses from nine tadpole rods (black circles) and eight froglet rods (gray squares). On average, the population responses had the same amplitude of ∼0.6 pA, however the time-to-peak in tadpole rods (2 s) was considerably longer than that of froglet rods (1.3 s). In addition, the responses of froglet rods recover at a faster rate than those of tadpole rods. Error bars represent SEM and are shown every fourth data point for clarity. (B) Average single-photon responses normalized relative to the saturating currents. The normalized responses of tadpole rods (black circles) grew at a faster rate and reached higher amplitudes than those of froglet rods (gray squares). The solid black lines represent the fits of the activation theory of Pugh and Lamb (1993) to the rising phase of the normalized responses. The amplification of the tadpole rods was 1.6 times greater than in froglet rods, a difference that cannot be explained in terms of their respective ROS volumes. (C) Responses of froglet rods (gray squares) were scaled ×1.6 to match the amplification of the tadpole rods (black circles). The recovery of the froglet rod responses was significantly faster than that of the tadpole rod, suggesting that the shutoff mechanisms strengthen as the rod develops.

The amplification constant of the photoresponse embodies the gain of the processes that relate the activation of rhodopsin to the subsequent change in membrane current (Pugh and Lamb, 1993). It applies primarily to the initial phase of the response (300–400 ms in amphibia), when inactivation mechanisms can be neglected. To estimate the amplification constant, currents were first normalized relative to the saturating currents (Fig. 3 B). After normalization, the responses of froglet rods were significantly smaller than those of young tadpoles. The estimated amplification factor for froglet rods (Eq. 1) was 0.075 s⁻² and the corresponding prediction from the model is shown in Fig. 3 B. This value is comparable to the amplification value of other amphibian rods (Pugh and Lamb, 1993). On the other hand, the amplification of the young tadpole rods was slightly larger, 0.12 s⁻², a 1.6-fold increase relative to the froglets. If we assume that all elements in the activation cascade of tadpole and froglet rods remain equal, and that ROS cytosolic volume increases threefold in the three-times-longer froglet rods, then amplification in tadpoles is expected to be three times larger than in froglets (Pugh and Lamb, 1993). However, they only differ by a factor of 1.6 (see discussion). This difference suggests that a doubling in the gain of the activation stages takes place as the rods mature.

To compare the time course of recoveries, the transduction pathways of both froglet and tadpole rods must be equally activated. However, as shown above, single photoisomerizations activate the transduction cascades of tadpole and froglet rods unequally. To compensate for these differences, and assuming that linearity applies to small responses, we scaled the responses of froglet rods by a factor of 1.6. This manipulation brought the onset of tadpole and froglet rod responses to match closely (Fig. 3 C), consistent with equal activation. However, in the later phases, the time course of the responses differed significantly, consistent with differences in recovery. The response of the froglet rod begins the recovery process earlier than the tadpole rod and thus reaches lower amplitude. The acceleration in the temporal properties of recovery is an indication that the mechanisms involved in the shutoff of the transduction cascade strengthen during development.

Developmental Control of Recovery to Saturating Flashes

The recovery phase of a photoresponse is driven by a number of molecular mechanisms working at different levels along the transduction pathway (Fain et al., 2001; Arshavsky et al., 2002). Which aspects of the recovery mechanisms are under developmental control? We first examined recovery from saturating flashes, to determine whether there were developmental changes in the dominant and/or nondominant time constants. Fig. 4 A shows the normalized responses of both young tadpole and froglet rods to saturating flashes eliciting ∼6,000 R*. The froglet rod recovered from saturation 10–12 s earlier than the young tadpole rod. To quantify the differences in recovery, we measured the times to achieve 50% recovery (T_50%) for a series of saturating flashes of different intensities. The T_50% of both young tadpole and froglet rods increased with flash intensity (Fig. 4 B). For equal stimulus intensities, the time to recovery of froglet rods was approximately half that of young tadpole rods. The T_50% versus ln(R*) curves for young tadpole and froglet were parallel and could be brought to overlap following a translation (∼2.7 ln units) along the abscissa (gray circles). From this, it is clear that, to produce equal saturation times, flashes applied to froglet rods must be 15 times as intense as those applied to young tadpole rods.

We computed the dominant time constant (a measure of the slowest step in the shutoff of the transduction cascade) from the T_50% recovery versus ln(R*) relationship. This is a nonlinear function, so piecewise linear fits were used (Pepperberg et al., 1992; Nikonov et al., 1998). The lower range (<∼10,000 R*) is the region where “response time invariance” was demonstrated in salamander rods (Nikonov et al., 1998) and in theory, the region where the slope of the relation is a measure of the dominant time constant. If we assume that the same range applies to Xenopus rod responses, then for both young tadpole and froglet rods, the dominant time constant is 2.5 s (R² > 0.95), and similar to other amphibian rods (Pepperberg et al., 1992). However, as we show below, guanylate cyclase activity does not reach maximal levels during the saturating response to flashes producing <6,000 R*, and as a result, the feedback mechanisms are not fully activated. Therefore, it is likely that brighter flashes are required to reach the region of “linear time invariance” in Xenopus rod responses. Consideration of the region with steeper slope (Murnick and Lamb, 1996) results in a doubling of the estimated value of the dominant time constant of both tadpole and froglet rods. These results show that the processes that contribute to the dominant time constant remain the same through development. The magnitude of the apparent changes in nondominant time constants estimated from shifting the tadpole dataset along the intensity axis to overlie the froglet data will depend on the value assigned to the dominant time constant (Nikonov et al., 1998).

Rate of Activation of the Guanylate Cyclase Increases During Development

In rods, calcium-dependent feedback mechanisms control the time of saturation without altering the dominant time constant (Murnick and Lamb, 1996; Nikonov et al., 1998; Burns et al., 2002). Therefore, we examined whether developmental changes in the feedback modulation of guanylate cyclase (GC) activity could underlie our observed differences in recovery times. To measure GC activity, we used the IBMX jump method (Hodgkin and Nunn, 1988) on young tadpole and froglet rods during their response to saturating flashes producing ∼6,000 R*. In this method, the GC activity (α') was estimated using the rate of change of the circulating current during rapid exposure to IBMX at varying times after the flash (materials and methods; Fig. 5 A). In froglet rods, the value of α'_dark was ∼1.1 s⁻¹, and quickly rose to a peak value (α'_peak) of 3.7 s⁻¹ 5 s after the flash (Fig. 5, B and C), although it is possible that α'_peak may reach even higher values at intermediate times we did not sample. In young tadpole rods, the resting value of α'_dark was 1.8 s⁻¹, ∼1.6-fold larger than in froglet rods, although as indicated by the error bars in the graph, the measurements of α' were more variable. In response to the flash, α' of young tadpole rods increased at a slower rate than that of froglet rods, requiring 9 s to reach α'_peak of 4.0 s⁻¹ (Fig. 5, B and D). The values of α'_peak were the same in tadpole and froglet rods, but the strength of the feedback, quantified by the ratio α'_peak/α'_dark, was 2.2 and 3.3, respectively (Fig. 5 D), amounting to a 1.5-fold difference in the range of GC activity.

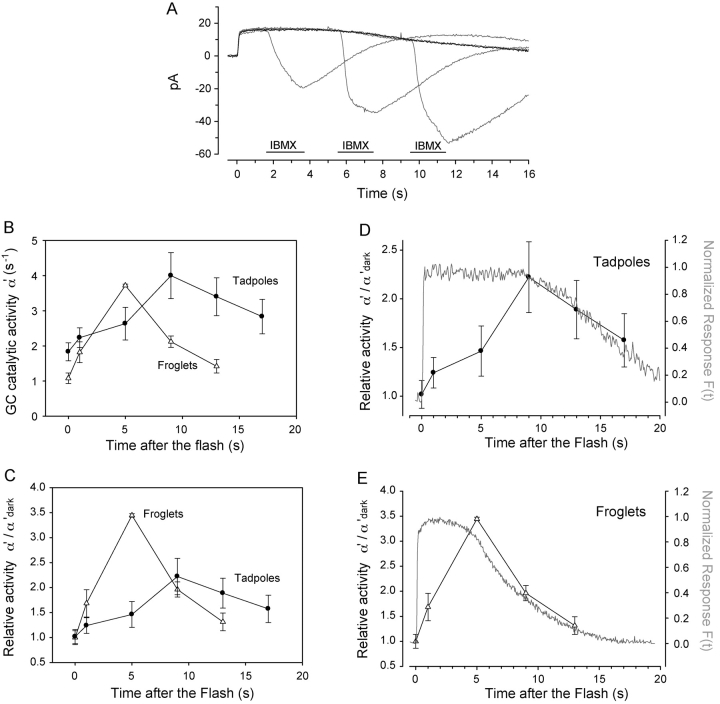
Figure 5.

Guanylate cyclase activity in developing Xenopus rods. (A) Overlay shows currents recorded from a froglet rod in response to brief applications of IBMX at various instances (periods) after stimulation with a saturating flash. Black trace is the control response to 6,000 photoisomerizations. The gray traces are a succession of responses with IBMX applied 1, 5, and 9 s after the flash. Pulse application of IBMX lasted 2 s, concentration was 0.5 mM. (B) Guanylate cyclase activity during the response to a saturating flash was estimated. In froglet rods (triangles, n = 5), resting GC activity (α'_dark) was ∼1.1 s⁻¹ and rose rapidly to reach a peak value of 3.8 s⁻¹, 5 s after the flash. In tadpole rods (circles, n = 6), α'_dark was 1.6× as active (1.8 s⁻¹), and increased gradually in response to the flash, requiring 9 s to reach its peak activity of ∼4 s⁻¹. (C) Relative guanylate cyclase activity (α'/α'_dark) of froglet rods (triangles) increased 3.5-fold in 5 s. α'/α'_dark in tadpole rods (circles) grew at a slower rate, increasing only 1.4-fold 5 s after the flash and reaching a peak 2.2-fold increase 9 s after the flash. In that same time (9 s after the flash), α'/α'_dark in the froglet rods had already recovered halfway to its resting value. (D and E) The time course of the recovery phase of α'/ α'_dark matched closely the recovery of the photocurrents in both tadpole and froglet rods. The shorter time to onset of recovery of the froglet rod response correlates with the fast increase in α'/α'_dark activity, while the slower onset of recovery in tadpole rods corresponds to a comparatively sluggish change in α'/α'_dark activity. These results suggest that feedback activity mediated by GC strengthens during development to speed up the recovery phase of the responses.

We compared the time courses of the photoresponse, and the relative GC activity using double-axis plots, scaled to respective maximal values (Fig. 5, E and F). For both tadpoles and froglets at these flash intensities, the time required to reach peak GC activity matched the time the response remained in saturation. Correspondingly, the rate of change of GC activation per unit time (i.e., the slope of the curve) is lower in tadpoles than in froglets (Fig. 5 B; compare D with E). The relative GC activity (α'/α'_dark) reached its peak level when the responses began to recover from saturation, i.e., when channels begin to reopen and intracellular calcium flows back into the rod outer segment, causing the cyclase activity to decline. Therefore, it is most likely that we did not determine the maximal GC activity in these experiments since we would expect it to remain saturated for some time during the response (Hodgkin and Nunn, 1988). Moreover, the dynamic range of GC is ∼10-fold in other amphibians (Hodgkin and Nunn, 1988; Calvert et al., 1998), while we have only stimulated the activity ∼4-fold. Nonetheless, the rate of GC activation is clearly slower in tadpoles than froglets and may in part explain the longer response saturation times for young tadpoles compared with froglets.

We derived the dark activity of the PDE by applying the steady-state relationship, β_dark = α'_dark (Hodgkin and Nunn, 1988). Froglet rods had a β_dark of ∼1.1 s⁻¹, well within the range of values previously reported for other amphibians (Hodgkin and Nunn, 1988; Koutalos et al., 1995; Nikonov et al., 2000). However, in young tadpole rods, the value of β_dark, 1.8 s⁻¹, was higher. Both background illumination as well as pigment bleaches increase PDE activity and result in a faster response recovery (Fain et al., 2001), but we find that the faster froglet rod actually has a lower PDE activity. This indicates that the developmental changes that alter temporal characteristics in the growing rod are not explained simply by an increased PDE activity driven, for example, by a substoichiometric ratio of 11-cis retinal to opsin, as has been suggested to account for developmental changes in other studies (Ratto et al., 1991; Xiong and Yau, 2002).

Developmental Control of GC by GCAP

What developmental change(s) can explain the faster activation of GC observed in froglet rods? Three possible mechanisms might shape the relative GC activity: GC concentration, GCAP concentration, and calcium dynamics. We cannot rule out differences in GC concentration and α'_max based on our experimental results. However, the concentration of GCAPs (Palczewski et al., 1994; Subbaraya et al., 1994), the calcium-binding proteins that regulate GC activity, may differ with stage of development, mediating faster activation of GC in froglet rods. In addition, any developmental changes in the mechanisms that regulate the dynamics of intracellular calcium, via calcium buffering and/or extrusion (Yau and Nakatani, 1984; Lagnado et al., 1992; Gray-Keller and Detwiler, 1994) could alter the kinetics of activation of GCAPs and, correspondingly, of the GC.

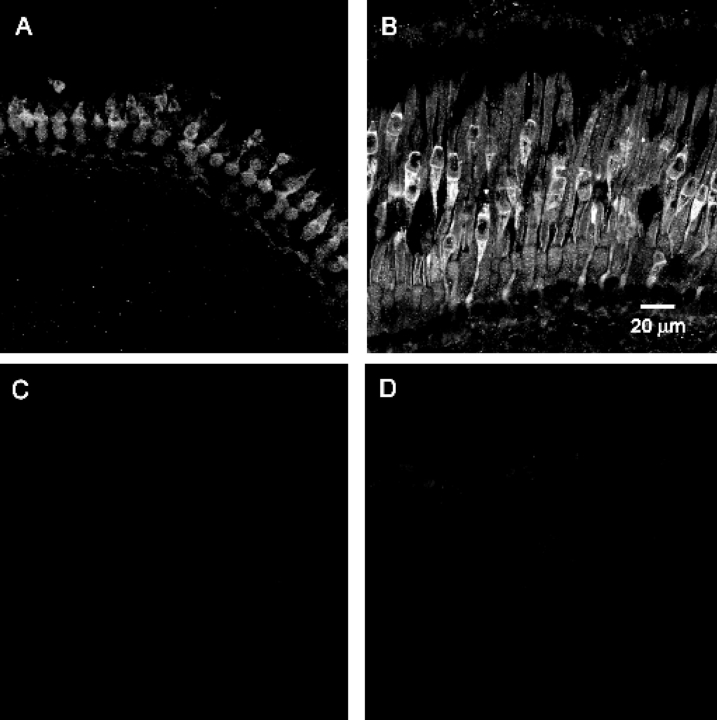
GCAP proteins have been found in the retinas of many vertebrate species, including mammals and frogs (Palczewski et al., 1994, 2004). In addition, GCAP-related proteins have been described in Rana pipiens (Li et al., 1998). We examined fixed cryosections of Xenopus retina using antibodies to mouse GCAP1 and GCAP-2, and Rana GCIP. Only anti–mGCAP1 gave a detectable signal. In both young tadpoles and froglets, we observed significant staining of the cones (Fig. 6) and cells in the inner plexiform layer (not depicted). Froglet cones labeled more intensely than tadpole cones. In froglet rods, there was visible staining in the rod outer segments, although the staining was not as intense as in cones (Fig. 6 B). In contrast, there was no detectable staining in young tadpole rods. These results suggest differences in the GCAP concentration of developing photoreceptors and are consistent with the faster rate of GC activation measured during the light response of froglet rods (Fig. 5). It is worth noting that while GCAP1 has been found in rods of lower vertebrates (Palczewski et al., 2004), in mammalian retinas, anti–GCAP1 antibody labeling is preferentially restricted to cones while GCAP2 immunostaining labels both rods and cones (Kachi et al., 1999).

Figure 6.

GCAP1 immunolabeling in dark-adapted Xenopus retina. (A) In larval retinas (stage 48), anti-GCAP1 labeling was found mainly in cone photoreceptors with very weak labeling of rod outer segments. (B) In froglet retinas, anti-GCAP1 labeling was found in both cone and rod photoreceptors, although labeling was significantly stronger in cones than in rods. Note that GCAP1 staining in cones also increased as the retinas matured. In (C) control tadpole and (D) froglet retinas probed with secondary antibody, fluorescence levels can be hardly detected. All confocal images were processed identically.

Developmental Control of GC: Calcium Dynamics

To assess the changes in intracellular free calcium levels during the light response, we measured the Na⁺/Ca²⁺,K⁺ exchanger currents in response to saturating flashes (Yau and Nakatani, 1984). The exchanger currents are electrogenic in nature and are detectable primarily during the early phase of a saturating response as a slowly decaying current, a reflection of the clearance of calcium by action of the exchanger following closure of the cGMP-gated channels by the intense flash. Typically, the exchanger currents consist of two components that are well described by exponential decay functions (Gray-Keller and Detwiler, 1994). The first component has fast kinetics, the time constant is ∼0.5–1 s and has an amplitude of ∼70% of the total current, while the second component has slower kinetics and a time constant in the order of 5 s (Gray-Keller and Detwiler, 1994; Calvert et al., 2002). To carefully characterize the latter component, circulating currents must be suppressed 15 s or more. Given that we were interested in the calcium changes that occur during the initial seconds after the flash, we focused primarily on the fast component and, as a first approximation, fit the exchanger currents of young tadpole and froglet rods with single, decaying, exponential functions. The relative magnitudes of the exchanger currents were the same in both tadpole and froglet rods, amounting on average to 6% of the saturating currents (Table I). However, the time course of the exchanger current decay, as determined by the time constant, in froglet rods decayed twice as fast as those of young tadpoles (Table I and visible in the saturating responses shown in Fig. 4 A). Assuming that the exchanger current reflects intracellular free calcium levels (Gray-Keller and Detwiler, 1994; Neher, 1998), this result indicates that calcium kinetics are faster in froglet compared with young tadpole rods. This in turn would tend to increase the rate of GC activation by GCAP, thus accelerating the recovery phase of the photoresponse. The origin of the changes in calcium kinetics could arise from developmental modifications targeting the exchanger's pumping efficacy, its expression levels, or the calcium buffering capacity of the rod.

Developmental Control of GC: Calcium Buffers

We manipulated the calcium buffering capacity of rods using BAPTA (see materials and methods), which increases the buffering capacity of the cells, slowing down changes in intracellular calcium and subsequent activation of calcium-dependent feedback mechanisms during responses to dim flashes (Torre et al., 1986). Application of BAPTA to young tadpole rods produced only a minor increase in photocurrent relative to the control responses (Fig. 7 A and Table I), suggesting that calcium-dependent feedback does not play a dominant role in regulating their dim responses. We found slower kinetics of the Na⁺/Ca²⁺,K⁺ exchanger currents, confirming that BAPTA had been incorporated into the cytosol of young tadpole rods (Table I). Application of BAPTA to froglet rods dramatically prolonged the dim responses (Fig. 7 B). The early phases of the responses were comparable to those obtained under control conditions, indicating that amplification remained unaltered. However, BAPTA extended the rising phase of the response, leading to almost a tripling in amplitude as well as a delay in the time to reach the maximal response (Table I), presumably by delaying the calcium-dependent inhibitory action of the feedback loop(s). The biphasic nature of the response can be attributed to the delayed activation of the feedback loop (Torre et al., 1986; Rieke and Baylor, 1998). As a result of the increase in the amplitude of the responses, the intensity required to elicit the half-maximal responses (Kd) decreased threefold relative to controls (Table I). Altogether, these observations are consistent with the notion that in froglet rods, calcium-dependent feedback acts quickly enough to shorten the responses to dim flashes. In young tadpole rods, the dim responses in BAPTA grew slightly relative to control, however not to the degree observed with froglet rods (Fig. 7 B). This suggests that calcium feedback in tadpole rods is sluggish and does not respond quickly enough to play a crucial role in the shaping of the responses to dim flashes. The insensitivity of young tadpole responses to alteration of calcium dynamics is consistent with lower concentrations of GCAP1 and slower GC activation as well as with a higher calcium buffering capacity in the outer segment of tadpole rods. Given that single photon response amplitudes grow in proportion to the saturating current (or ROS length) when feedback is minimized, we conclude that as the ROS develops, calcium-dependent mechanisms strengthen to modify the amplitude and kinetics of the responses.

Figure 7.

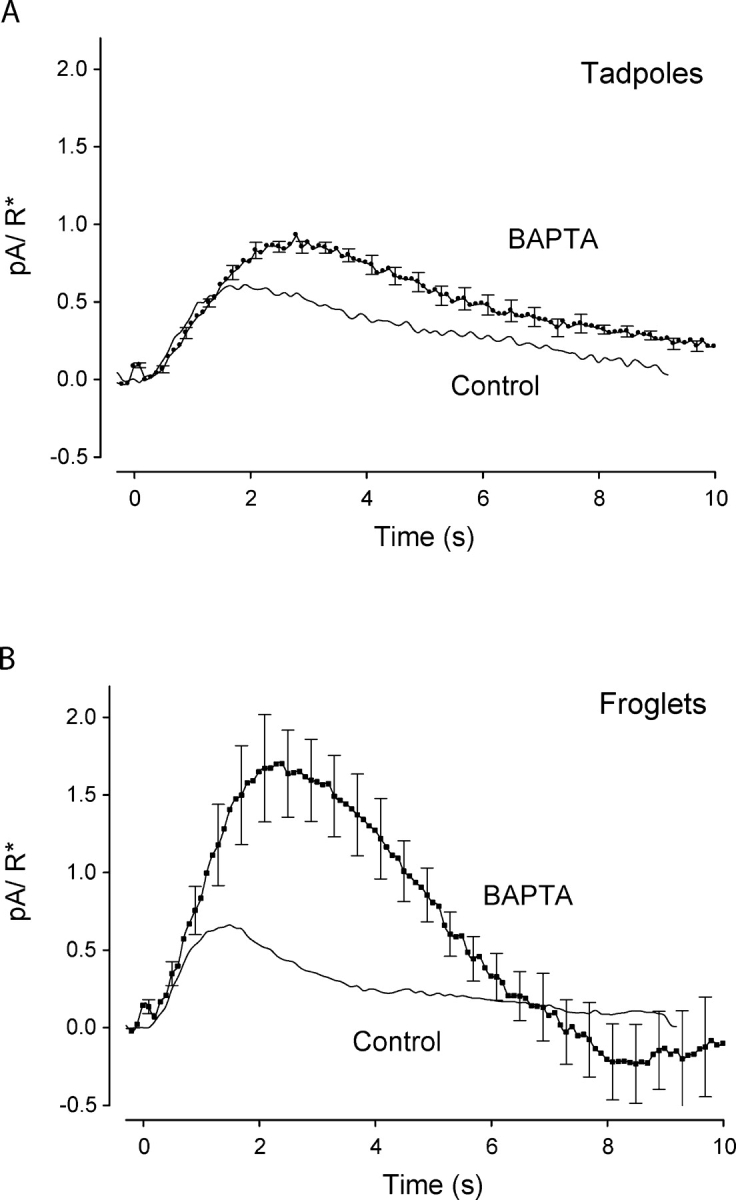
Calcium buffering in developing Xenopus rods. Population average single-photon responses from young tadpole rods (n = 6) and froglet rods (n = 6) loaded with BAPTA-AM were compared with control responses without BAPTA-AM. (A) The recovery of the single-photon response of tadpole rods with BAPTA-AM slowed down relative to tadpole control response. The single-photon response amplitude increased 1.6-fold with BAPTA-AM. (B) The single-photon response of froglet rods was greatly altered by BAPTA-AM. The onset of the response with BAPTA was coincident with the control response; however, the peak amplitude of the responses with BAPTA in the rods increased by almost threefold over the control amplitude. The recovery phase overshoots the baseline, the product of delayed activation of GC.

Developmental Changes on the Power Spectra

The faster kinetics of froglet photoresponses indicates that the rods operate over a wider frequency bandwidth than young tadpole rods. Fig. 8 A compares the power spectra of the single photon response of froglet and tadpole rods. The spectra overlap in the low frequency range and have the characteristic low-pass shape (Baylor et al., 1979b); however, the power spectrum of froglet rods extends to higher frequencies. Application of BAPTA did not significantly alter the spectrum of tadpole rods, but it had a strong influence in the spectrum of froglet rods, particularly in the low frequency range where power density increased 10-fold (Fig. 8 A). For frequencies >∼0.3 Hz, the asymptotic decay of the spectrum remained unaltered. Thus, the spectrum can be explained in terms of a low frequency, relatively planar region that is dependent on the amount of calcium buffering, and a high frequency region, characterized by asymptotic decay and low sensitivity to extrinsic calcium buffers (piecewise-linear fits in Fig. 8 A). The point where the two regions intersect slides along the high frequency asymptote as a function of extrinsic calcium buffers. If we define, as a first approximation, the frequency of the intersection point as the cutoff frequency of the spectrum, then, by strengthening calcium-dependent feedback mechanisms, froglet rods trade power in the low frequency region of the spectrum for increased response bandwidth.

Figure 8.

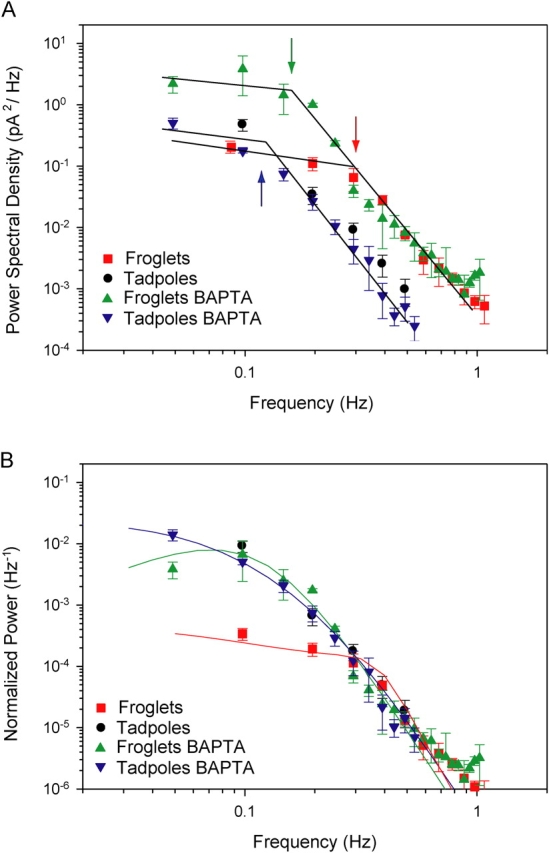
Power spectral density of Xenopus rod single-photon responses in control conditions and when intracellular Ca²⁺ changes were buffered with BAPTA-AM. (A) Population average power spectra were computed from single-photon responses of froglet (squares) and tadpole (circles) rods in control solution and froglet (upward triangle) and tadpole (downward triangle) rods loaded with BAPTA-AM. Data were fit with piecewise-linear approximations. Arrows indicate approximate cutoff frequencies. Under both conditions, the tadpole rod spectra overlap closely over the entire frequency range. Above 0.3 Hz, the froglet rod spectra obtained in control and BAPTA-containing conditions also overlap one another. However, <0.3 Hz the spectrum of the BAPTA-loaded rods continues to gain power, while the control froglet spectrum diverges to superimpose on the low frequency power density of the froglet responses <∼0.15 Hz. (B) Population average power spectra of single photon responses were normalized relative to the square of their respective saturating current values. Spectra of tadpole rods (control and BAPTA) and froglet rod responses with BAPTA overlap closely. The spectrum of control froglet rod responses has lower power levels at frequencies <0.15 Hz. Data fit with model predictions (see appendix ).

To compare the transduction mechanisms of tadpole and froglet rods, we scaled the single photon responses relative to their saturating currents (Fig. 3 B). In the frequency domain, this is equivalent to normalizing the power spectral density relative to the square of their respective saturating currents (Fig. 8 B). Following this procedure, the spectra of the tadpole and froglet rods overlap in the high frequency end of the spectrum, sharing the same asymptotic roll-off. The normalized spectra of the tadpole rods (control and BAPTA) and froglet rods with BAPTA agree closely, consistent with the notion that under these conditions, their transduction mechanisms do not differ greatly. On the other hand, when calcium is allowed to vary naturally in froglet rods, the spectrum exchanges power in the low frequency range of the spectrum for a higher cutoff frequency, which is consistent with the action of negative feedback loops (see appendix ).

DISCUSSION

Phototransduction Changes During Development of Xenopus Rods

Linear growth of the rod outer segments increases collecting area and proportionally increases the magnitude of the saturating current. This suggests that rods become more sensitive as they grow to adult dimensions. However, the results presented here show that additional developmental changes to the phototransduction cascade affect both the activation and recovery phases of the photoresponse. The overall result is a more rapid response to light in adult rods. Thus, rods do not merely grow by adding identical “phototransduction” units; a mature rod is just not a tadpole rod with a longer outer segment.

We traced changes in feedback to calcium-dependent mechanisms that determine both the duration for which the response remains in saturation following a bright flash, as well as the time course of recovery in response to dim flashes. As rods develop, the concentration of GCAPs in the outer segments increases (Fig. 6), and the kinetics of the Na⁺/Ca²⁺,K⁺ exchanger currents accelerate (Table I). The role of GCAP in shaping photoresponses has been established (Burns et al., 2002), but the changes in kinetics of the Na⁺/Ca²⁺,K⁺ exchanger require further consideration. Faster exchanger currents are a measure of faster changes in free Ca²⁺ concentration that may lead to faster activation of GC by way of the calcium-dependent GCAPs (Palczewski et al., 1994). Faster calcium kinetics may arise from developmental adjustments in the exchanger or in the cytosolic capacity to buffer calcium (Torre et al., 1986; Gray-Keller and Detwiler, 1994; Neher, 1998). Within the limitations of the model, our analysis indicates that either option is possible (Fig. 9). However, the relative amplitude of the exchanger currents was the same in tadpole and froglet rods, arguing against the idea that a developmental increase in relative expression of the exchanger underlies the acceleration of the photoresponse.

Figure 9.

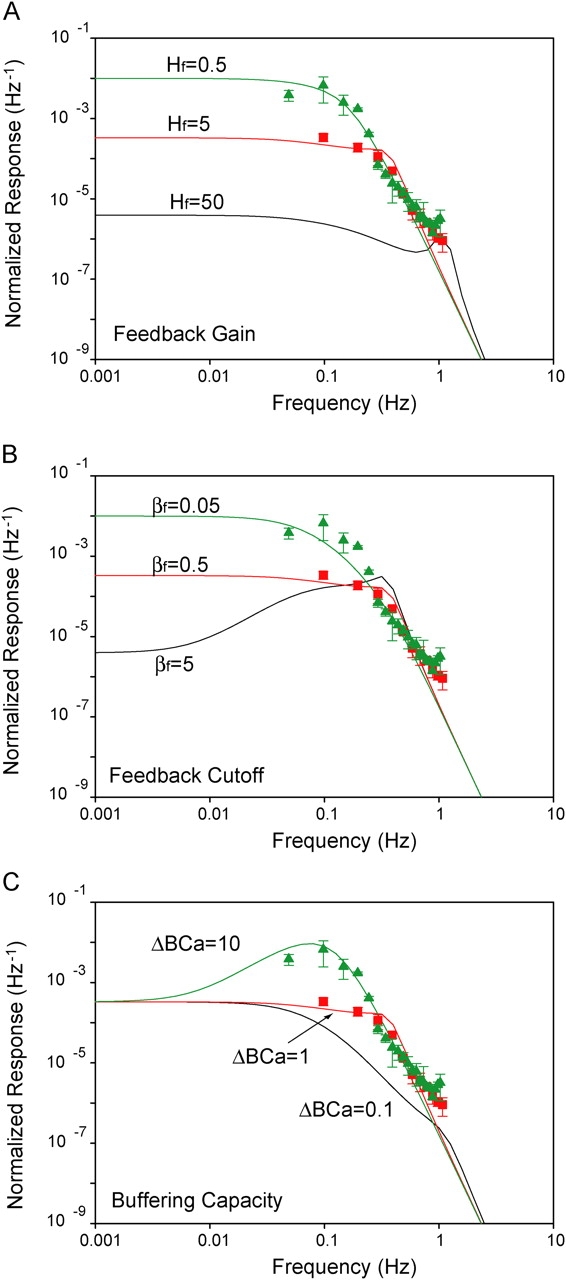
Measured and predicted power spectral densities of Xenopus rod single-photon responses. Power spectra of froglet rod responses with BAPTA (triangles) and under control conditions (squares) are compared with predictions from a linear model. Three parameters in the feedback stage of the model were varied independently to determine their influence on the shape of the spectrum. (A) the gain (H_f); (B) the cutoff frequency (β_f); and (C) the buffering capacity (ΔB_Ca), which is inversely related to both gain and cutoff frequency of the feedback loop (Eqs. A3–A5). Values assigned to the model parameters are indicated along with the respective functions.

The rate of activation of the GC increases as the ROS grows to adulthood. We demonstrated a close correspondence between the duration of saturating responses and the rate of increase in GC activity (Fig. 5). The higher rate of GC activation in froglet rods could be attributed to differences in GC concentration, GCAP concentrations, and/or calcium kinetics. While we cannot rule out developmental differences in GC concentration, the GCAP immunohistochemistry experiments (Fig. 6), the dynamics of the Na⁺/Ca²⁺,K⁺ exchanger currents (Table I), the BAPTA experiments (Fig. 7), and the power analysis (Fig. 8) all indicate that calcium feedback is not nearly as effective in tadpole rods relative to juvenile rods.

The value of dark activity of the PDE in froglets (1.1 s⁻¹) is comparable to that of salamander rods (Hodgkin and Nunn, 1988; Koutalos et al., 1995; Nikonov et al., 2000) but smaller than that of tadpole rods (1.8 s⁻¹). Therefore, the faster response kinetics we observed as rods mature cannot be explained in terms of a substoichiometric ratio of 11-cis retinal to opsin. Nikonov et al., (1998) postulated that whenever calcium-dependent feedback can be neglected, the cGMP synthesis/hydrolysis equilibrium acts as a low-pass filter with a cutoff frequency proportional to the dark PDE activity. Since the responses of tadpole rods to dim flashes are only marginally dependent on calcium (Fig. 7), the higher value of β_dark may be a strategy used by tadpole rods to accelerate the responses in view of the weak feedback loop. ERG recordings in rat indicate that the recovery of rod responses does not change with development (Fulton and Hansen, 2003). A possible interpretation is that in infant rat, the substoichiometric ratio of 11-cis retinal to opsin (Ratto et al., 1991) activates the transduction cascade, producing faster recovery to saturating stimuli.

We also note that the responses we recorded from stage 48–51 tadpole rods were 5–20 times more sensitive and ∼4 times slower to peak than those reported by Xiong and Yau (2002). Because both studies used virtually identical methods, it appears that these differences may be a result of different husbandry conditions. Specifically, we have found that photosensitivity, response kinetics, and rhodopsin content depend critically on the diet (unpublished data). Xiong and Yau (2002) showed that young tadpoles in their study were chromophore deficient and clearly had less chromophore than those in the present study. In older animals (stages >52), results showed closer correspondence in sensitivity but not in time to peak. It is not clear that the dependence on husbandry that we observed reflects an inherent limitation in the capacity to regenerate the chromophore in developing Xenopus tadpoles retinas.

In addition to our findings on developmental control of the recovery mechanisms, we also found developmental differences in the forward stages of the transduction pathway. The onset of the response to single photons was faster in froglet than in tadpole rods (Fig. 3 A). When the feedback mechanisms mediating the recovery were attenuated with BAPTA, the responses of froglet rods continued to grow, and peaked with amplitudes that were ∼1.6-fold larger than those of tadpole rods (Fig. 7 and Table I). That is, the gain of the forward transduction pathway was increased in froglet rods. The same conclusion can be obtained in terms of the amplification factor often used to characterize the properties of the activation phase of the response (Fig. 3 B). According to Pugh and Lamb (1993)(Eqs. 12 and 21) the amplification factor is inversely proportional to the cytosolic volume of the ROS. Assuming that the volume of ROS in froglet grows in proportion to length (Fig. 1), we expect the amplification in tadpole rods to be three times greater than in froglet rods. However, the amplification increased by a factor of only 1.6 (Fig. 3 B). These results imply compensatory developmental changes in other factors contributing to the response amplification, adjusting to the volume change. The possible changes are decreases in the rate of Rh* activation of transducin, the coupling of activated transducin to PDE, PDE catalytic activity, or Hill coefficient for the cGMP channel (Pugh and Lamb, 1993). Further experiments will be necessary to resolve this point.

Remarkably, direct measurements suggest that the amplification factor (A) and the dark activity of PDE (β_dark) decrease by the same ratio (1.6×) as rods mature. Put in other terms, the ratio of A to β_dark (∼0.072 s⁻¹) must hold constant through development. The same conclusion can be inferred by comparing the power spectra of larval and froglet rod responses to single photoisomerizations in the presence of BAPTA-AM. Under these conditions, the normalized spectra of larval and froglet rods are almost overlapping (Fig. 8 B) and, as described in appendix , the power spectra can be well fit by Eq. A1. Given that K_E and (we assumed) K_R do not change during development, inspection of Eq. A1 suggests that the ratio of A to β_dark must be equal in larval and adult Xenopus rods for the spectra to overlap in the low frequency range. Similar values in the ratio of A to β_dark in salamander rods (0.08 s⁻¹) (Nikonov et al., 2000) and salamander red cones (0.1 s⁻¹) (Pugh and Lamb, 1993; Cornwall et al., 1995) suggest a connection between the values that photoreceptors (at least in lower vertebrates) adopt for A and β_dark.

Single Photon Response

Despite developmental changes in both the activation and recovery phases of the photoresponse, the amplitude of single photon responses (and thereby sensitivity) remained unchanged at ∼0.6 pA. A similar correspondence has been observed in Rana (Matthews, 1984). Behavioral studies with Xenopus tadpoles (Solessio et al., 2004) and mature Bufo (Aho et al., 1988) demonstrate that rods in lower vertebrates have the capacity to signal single photoisomerizations. This is remarkable given that noise variance (continuous noise and discrete events) in Xenopus increases linearly with length of the developing rods (Table I). Thus, the amplitude (0.6 pA) of the response to a single photon is large enough that it does not need to adjust to changes in noise level. Perhaps the amplitude of ∼0.6 pA is critical for visual function throughout development in Xenopus.

The power spectra of the responses to single photons provide important insights that may explain how the developing rods balance amplification and feedback, and yet maintain the single photon response amplitude of 0.6 pA. Fig. 8 A shows that responses from tadpole and froglet rods share similar power levels in the low frequency range, but the bandwidth of the froglet rods exhibits a higher cutoff frequency. Thus, it appears that developing rods balance the strength of activation and feedback to extend their frequency range as long as they keep power in the low frequency range at ∼0.3 pA² Hz⁻¹. It may be that information in the low frequency range is critical for the transmission of single photon signals to bipolar cells, while the higher frequency components are important for improved time resolution and adaptation.

APPENDIX

Mathematical Model

To explore quantitatively the role of feedback in shaping the power spectrum, we derived an expression for the power spectrum using a “small signal response model” adapted from Nikonov et al. (1998). Linearity is generally applicable under these conditions. In conditions that minimize calcium feedback, e.g., with BAPTA in the rods, the power spectrum was predicted using a model that consists of a cascade of three first order reactions (Nikonov et al., 1998, Eq. 19). An expression can be derived for the power spectrum:

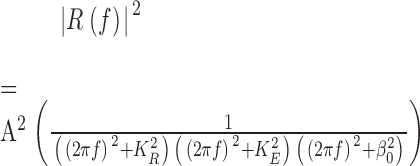(A1)

The model requires that one knows the amplification factor A, the rate constant for the first-order inactivation of rhodopsin K_R, the rate constant for the inactivation of PDE K_E, and β₀ = β_dark, the phosphodiesterase activity in the dark (see Table II). We determined the values of these parameters from our experiments by deriving K_E from the value of the dominant time constant (Nikonov et al., 1998) and assigning β₀ the value of GC catalytic activity in the dark (α'_dark) (Hodgkin and Nunn, 1988). K _R is the inverse of T_R, the time constant characterizing the inactivation of the catalytic activity of rhodopsin. This is the only variable in Eq. A1 that we could not directly measure. Instead, we estimated its value indirectly, by varying its value systematically in Eq. A1 until the model best fit the tadpole experimental spectrum, where we have shown that there is little feedback at work. By assigning T_R = 0.8 s (it is 0.4 in salamander rods), the model spectrum (Fig. 8 B, continuous line) fit the data of the tadpole rods quite well. The values of the parameters used in the model are summarized in Table II.

TABLE II.

Parameters Used in the Linear Model

		Tadpoles		Froglets
Parameters	Units	Control	BAPTA	Control	BAPTA
A	s−2	0.12	0.12	0.08	0.08
KR	s−1	1.25	1.25	1.25	1.25
KE	s−1	0.4	0.4	0.4	0.4
β0	s−1	1.8	1.8	1.1	1.1
Hf0	s−2	–	–	5.0	5.0
βf0	s−1	–	–	0.5	0.5
ΔBCa	–	–	–	1	10

A, amplification factor; K_R, rate constant of inactivation of rhodopsin; K_E, rate constant of inactivation of PDE; β₀, phosphodiesterase activity in the dark; H_f0, gain of feedback stage; β_f0, rate constant of feedback stage; ΔB_Ca, fractional change in buffering capacity.

To fit the spectra of the froglet rod responses, the model included the cGMP feedback loop acting across the final stage. The expression for the power spectrum was modified according to Nikonov et al. (1998), their equation A6.6:

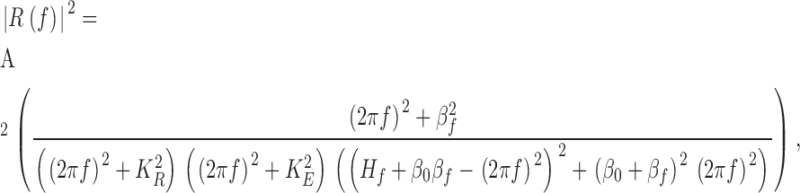(A2)

where the calcium-dependent feedback acting by way of GC is described in terms of a first order reaction. H_f is the gain of the feedback stage,

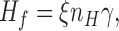(A3)

and β_f the rate constant of the feedback stage,

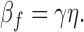(A4)

ξ is the proportionality factor relating changes in GC activity to changes in free calcium (Nikonov et al., 1998, Eq. A6.3), n_H is the Hill coefficient for the cGMP-gated channels, γ is the factor converting calcium currents into concentration changes, and η is the fraction of unused exchange current at rest (Nikonov et al., 1998, Eq. 15). The parameter γ is inversely proportional to the rod's capacity to buffer calcium changes and may therefore be expressed as

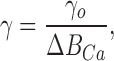(A5)

where ΔB_Ca is the fractional change in buffering capacity. That is, both H_f and β_f are inversely proportional to ΔB_Ca:

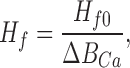(A6)

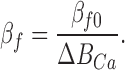(A7)

Therefore, when ΔB_Ca increases sufficiently, to the point that H_f and β_f can be considered negligible, Eq. A2 is approximately equal to Eq. A1.

We explored the role of the independent variables H_f and β_f, the gain and the rate constant of the feedback stage, in shaping the power spectrum (Fig. 9, A and B). A family of parametric low-pass filter curves resulted when systematically varying H_f in Eq. A2. The scale of the ordinates is extended to show that all spectra are limited by the same high frequency asymptote. With negligible feedback gain (H_f → 0), the spectra fit the BAPTA data well. As gain increased, the cutoff frequency increased and the region of constant power shifted down along the asymptote. The model fits the data reasonably when H_f = 5 (and β_f was constant at 0.5 s⁻¹). Similarly, a family of curves is obtained when β_f is the independent variable and H_f remains constant (H_f = 5) (Fig. 9 B). As the feedback rate constant increases, the power in the low frequency range decreases and the bandwidth increases. The spectrum takes a band-pass profile for extremely fast feedback (β_f = 5).

Given that both H_f and β_f are inversely proportional to the rod's capacity to buffer calcium changes (Eqs. A6 and A7), we analyzed a third situation where buffering capacity is the independent variable (Fig. 9 C). This case resembles the effects of manipulating BAPTA levels. Similar to the cases described above, the spectra share a common asymptote in the high frequency range; however, the situation differs with low frequencies, as the spectra converge to a common level. With high buffering levels (ΔB_Ca = 10), the spectra take a band-pass profile that closely resembles the spectrum of the froglet rods loaded with BAPTA. The model also approximates the tadpole data reasonably well, suggesting that slower kinetics of the feedback system also explains the tadpole responses (unpublished data). By lowering buffering 10-fold (ΔB_Ca = 1), resonance is lost and the model behaves as a low-pass filter that describes well the spectrum of the froglet rods under control conditions (continuous lines in Fig. 8 B). Despite differences in the low frequency range, all three cases studied capture the essentials observed in the data, that is, a tradeoff of power in the low frequency range for bandwidth.