Unique elastic properties of the spectrin tetramer as revealed by multiscale coarse-grained modeling

Abstract

The force-extension profile of tetrameric spectrin is determined by using multiscale computer simulation. Fluctuation results of atomistic simulations of double spectrin repeat units (DSRU) are used to systematically build a coarse-grained (CG) model for the tetrameric form of spectrin. It is found that the spectrin tetramer can be modeled as a soft polymer with a unique flat force-extension profile over the range of biologically important lengths. It is also concluded that in the cytoskeletal network of the red blood cell the tetramer is in an “overcompressed” state. These findings are in contrast to the commonly used models of spectrin tetramer elasticity, namely the “entropic spring” polymer models. From these results, it is concluded that stable intact helical linker regions are needed to maintain the soft elasticity of the spectrin tetramer.

Understanding both the resting shape and the associated large reversible deformations of the red blood cell has long been a common goal for both cell biologists and physicists (1–3). It has been found that the red blood cell's unique shape and elastic properties are related to the structure of its underlying cytoskeleton. Although the specific proteins that comprise the cytoskeleton have long been identified (1), the exact mechanism by which the red blood cell deforms and maintains its shape is still a topic of debate. The cytoskeleton of the red blood cell is a mesh network of spectrin tetramers, where the tetramers form the vertices that contain a bond to an actin-band 4.1 complex. The elasticity of the cell is thought to originate from the spectrin tetramer's ability to deform easily.

Experimentally, rotary shadowing studies on isolated spectrin tetramer units in low ionic strength solvents have shown that the spectrin tetramer can extend into a linear flexible polymer with an average extension of 194 nm (4). Also, the contour length of the spectrin tetramer is estimated to be ≈200 nm. However, the number of spectrin molecules per area of membrane suggest that, in the erythrocyte, the end-to-end distance of the tetramer is ≈70 nm (5). Furthermore, AFM experiments on erythrocytes under physiological conditions show the spectrin tetramer to be in a compressed state in the network, with an average length between 35 and 100 nm (6, 7). These findings indicate that in the resting state of the red blood cell the average extension of the tetramer is only a fraction of its contour length. Also, mechanical measurements of the shear modulus of the erythrocyte suggest that the spectrin tetramer is easily expandable (8). The common explanation for the small extension of the tetramer in the cell and its accompanying soft elasticity has commonly been that the helical linkers which connect the modular repeat units of spectrin can unfold in the cell upon overstretching and result in the tetramer behaving as an effective entropic polymer (with free hinges between repeat units) that prefers to assume compressed conformations to minimize its entropy. This model of tetramer elasticity has been supported by in vitro experiments that demonstrate forced unfolding of multiple domains of spectrin with AFM tips (9–11), along with accompanying atomistic nonequilibrium molecular dynamics simulations demonstrating the unfolding events at a molecular level (12–15).

However, there have also been a number of experiments that contradict the simple entropic elasticity models. One of these is the finding that the shear modulus of the red blood cell network can decrease with increasing temperature, which is at odds with the prediction that the shear modulus of an entropic network should be proportional to the temperature (16). Other experiments have found that the fluctuations of the spectrin tetramer can increase in regions of greater deformation in the cell, again in contradiction to an entropic polymer stiffening upon extension (17).

In this work, the elasticity of the spectrin tetramer is directly determined by using coarse-grained (CG) molecular dynamics (MD) simulations. Importantly, atomistic equilibrium MD has been used to elucidate the conformational flexibility of individual spectrin repeat units and the bending flexibility between consecutive repeat units (18). Here, information obtained from these atomistic MD simulations of consecutive spectrin repeat units is used to parametrize a CG model of the spectrin tetramer in a multiscale fashion, so that that the much larger length scale structure of the spectrin tetramer can be accurately simulated using the resulting CG model. The thermodynamic force-extension relationship for the resulting CG tetramer model is consequently determined.

From the CG simulations, two defining trends of the tetramer elasticity emerge. First, the force-extension profile is found to be flat over an extension range of 120 nm, before starting to stiffen upon high extensions. Second, in the extension ranges found in the red blood cell cytoskeleton, the tetrmaer is found to be in a slightly “overcompressed” state. The present results indicate that the tetramer can have a force constant close to zero over a long range of extensions, and that no domain unfolding is required to achieve a soft elasticity. We do not exclude the possibility that domain unfolding can still occur at very large extensions approaching the contour length of the tetramer, but that these unfolding events can actually be deterrents to the reversible flexibility of the spectrin tetramer and that a stable linker region is vital to conferring the high elasticity of the spectrin tetramer.

Results

Values of Coarse-Grained Parameters.

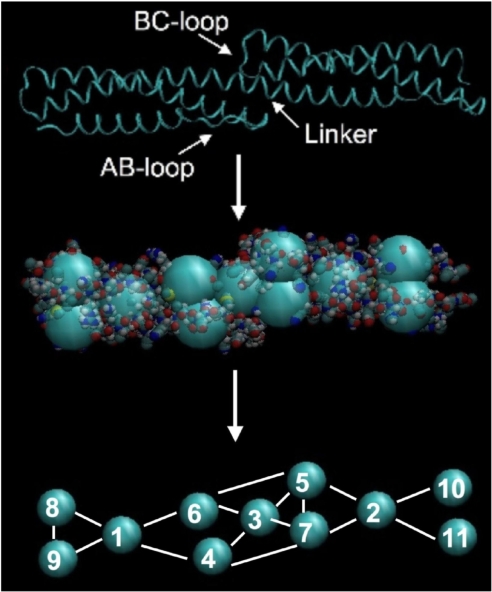
The CG representation of the double spectrin repeat units (DSRU) is shown Fig. 1. The internal coordinates (ICs) used in building the CG model of the DSRU include harmonic bonds, harmonic angles and dihedral angles. The average values for all of the ICs were derived from the CG representation of the trajectory produced from atomistic simulations (CG-A) of the DSRU. The force constants for all of the ICs were determined as a self-consistent solution to the fluctuations derived from the same CG-A trajectory. Once the solution for all of the IC was determined, the average values and force constants of equivalent IC from the two repeat units of the DSRU were assigned the mean value of their solutions (see Methods). The final IC force constants of the resulting CG model for a single DSRU are provided in supporting information (SI) Text.

Fig. 1.

A ribbon representation of the HEβ89 double spectrin repeat unit (DSRU) crystal structure (Top) with the AB-loop of the first spectrin repeat unit, the BC-loop of the second spectrin repeat unit and the connecting linker region marked accordingly. A pictorial representation of the systematic coarse-graining of the HEβ89 DSRU (Middle), along with the numbering scheme of the resulting coarse-grained (CG) sites (Bottom). The bonding internal coordinates (ICs) are also shown.

In coarse graining the spectrin DSRU, the aim is not only to match the local IC fluctuations to those found in atomistic simulations, but also to match the vital global fluctuations of the CG model to the corresponding collective fluctuations of the atomistic simulation. In the spectrin DSRU, the global fluctuation that is important in building a representative description of the tetramer is the collective bending fluctuation between the first repeat unit of the DSRU with respect to the second repeat unit. The collective bending fluctuation between consecutive repeat units of the DSRU were determined here in a similar way to that in our previous work (18). In the present case, the positions of CG site 1 and CG site 3 (see Fig. 1) are aligned along the z axis, and the position of the CG site 2 in the xy-plane is determined for each frame of the trajectory. A plot of the x and y coordinates of CG site 2 from the atomistic simulation and a constant temperature simulation of the parametrized CG DSRU system is shown in SI Fig. 5. The distributions of CG site 2 from the atomistic and CG simulation (SI Fig. 5) show similar size and shape, indicating that the ICs used in the coarse-graining procedure are able to capture the collective fluctuations between consecutive spectrin repeat units. The collective bending fluctuation is important in determining the overall elasticity of the CG tetramer because it is the strongest determinant of the persistence length of the tetramer. In particular, the force constants of the IC which involve interactions of CG sites belonging to both repeat units were found to have the most effect in determining the collective bending fluctuations. All of the ICs are presented in detail in Methods.

Force-Extension Profile of the CG Tetramer Model.

Two spectrin tetramer models were studied. The interactions within and between the CG consecutive spectrin repeat units were represented by the force constants of the specific ICs between CG sites that were determined from the fluctuation-matching scheme, as presented in Methods. The details of how a CG-tetramer is built from the CG-DSRU is also presented in Methods. This tetramer model, which includes all parametrized interactions, is referred to as the CG-bend model. For comparative purposes an altered version of this model was also studied. In this alternate model the interaction between CG sites belonging to two different repeat units are ignored and only the parametrized interactions within the individual repeat units are included. Specifically, a force constant of k = 0 is used for the bond IC between CG sites 6–5 (see Fig. 1), the bond IC between CG sites 7–4, the angle IC between CG sites 7–3-4, the angle IC between CG sites 1–3-2 and the dihedral IC between CG sites 6–5-4–7 (see SI Tables 1–3 for a complete list of the parametrized ICs and their force constants). This model, which contains no interactions between CG sites of consecutive repeat units, is referred to as the free angle model and represents a scenario of the spectrin tetramer in which the linker regions between all consecutive triple coiled-coil repeat units have unfolded from an alpha-helical conformation to a loop conformation.

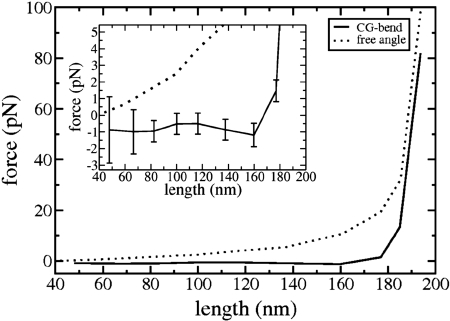
The force extension results of both the fully parametrized CG-bend tetramer model and the free angle model are presented in Fig. 2. At very large extensions (>180 nm), the two models show a similar behavior. Namely, they display a sharp increase in the force with a small increase in the extension. At the high extensions, the force exerted on both the CG-bend and free angle tetramer models is positive, meaning that the systems want to contract to lower extensions. For both systems, upon decreasing the extension of the tetramer from the highly extended state the force exerted on the system decreases.

Fig. 2.

Force vs. extension length profile of the parametrized CG-bend tetramer model (solid line) as well as the free angle model (dotted line). (Inset) A zoomed image of the graph at smaller force values, along with the error associated with the determination of the average thermodynamic force for the CG-bend tetramer model at each extension.

For the free angle model, the force exerted on the tetramer decreases with decreasing extension, through the entire extension range sampled, and the slope of this change is greater at large extensions. In this model, at longer extensions, the tetramer is more geometrically restricted than at shorter extensions. At shorter extensions, the geometric confinement of the system is relaxed in two ways. One way is that the two strands of the tetramer are able to sample distances further away from each other. The second way in which geometric confinements are relaxed at shorter extensions is that the system as a whole can assume many large collective bent configurations. Both of these effects contribute to the system being able to sample more configurations at lower extensions, resulting in the dominant entropic contribution to the elastic behavior of the free angle model seen in Fig. 2. This entropic change in the force extension profile of the free angle model has the same characteristic trend as found in other entropic polymer models such as the entropic worm-like chain model (19). In particular, the entropic free angle tetramer prefers to be in a compressed state and it stiffens upon expansion.

The fully parametrized CG-bend model, which is used to represent the spectrin tetramer with no unfolded structural domains, yields a force-extension profile very distinct from the entropic behavior of the free angel model. In the CG-bend tetramer model the force exerted on the system is invariant with extension up to a length of 160 nm. Hence, the CG-bend model effectively has a force constant of effectively zero over a large extension range, particularly from 48 nm to 160 nm (see Fig. 2 Inset). Once the system is expanded beyond 160 nm, the force-extension profile of the CG-bend model starts to rise with a higher gradient than its free-angle counterpart, and the two curves approach each other at large extensions.

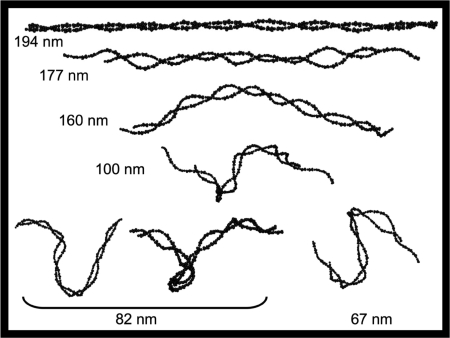
To help develop a physical understanding of the force-extension profile of the CG-bend tetramer model, sample structures from the simulation of the tetramer at different lengths are shown in Fig. 3. The tetramer structure at 194 nm shows the system in a highly extended state of low entropy and high internal energy, in which its angle and dihedral (as well as bonding) internal coordinates are being stretched beyond their equilibrium values. At the lower extension of 177 nm, the internal energy of the tetramer has decreased, the entropy has increased and thermodynamic force being sampled is close to the free energy minimum of the system. This is indicated by the fact that the average value of the force sampled at this extension is still positive but approaching zero (Fig. 2 Inset). Upon further decreasing the extension of the tetramer to 160 nm, the force exerted on the system actually decreases to a negative value. This sign reversal indicates that the tetramer has “overcompressed” and prefers to expand from this extension. The snapshot of the tetramer at an extension length of 160 nm in Fig. 3 reveals that the tetramer assumes a collectively bent conformation in its over-compressed state. Upon further decreasing, the extension length of the tetramer, the system responds by forming more bent conformations, as shown in Fig. 3 for extension lengths of 100, 82, and 67 nm. By forming these large-scale bent structures, the system is able to find a balance between trying to maximize the number of conformations and at the same time wanting to minimize its internal energy from bending. Below the zero force length, the combination of the entropy change and energy change with length are able to maintain a delicate balance upon decreasing length, so as to maintain a unique relatively “flat” thermodynamic force profile. The zero force length predicted by the CG-bend model is between 160 and 180 nm (see Fig. 2). This finding is consistent with the finding from rotary shadowing studies of the tetramer that determine an equilibrium length of 194 nm, close to the contour length of the spectrin tetramer (4).

Fig. 3.

Snapshots from the equilibrium simulations of the CG-bend tetramer model at various extension lengths. All lengths are shown in nanometers.

Discussion

Various causes of hereditary elliptocytosis have been tied to pathogenic mutations of residues in the linker region connecting consecutive spectrin repeat units (20). Many of these mutations are proline, and subsequent experiments and MD simulation have shown that this proline mutation leads to the unfolding of the helical structure of the spectrin linker region and subsequent unfolding of adjacent triple coiled-coil repeat units (21). Our results suggest that a stable helical linker region is vital to conferring the high elasticity of the spectrin tetramer. Our earlier atomistic MD simulations have shown that the helical linker and its interactions with the AB-loop and BC-loop residues of the repeat units determine the collective bending fluctuations of the consecutive repeat units (18). The present CG simulation studies of the CG-bend tetramer, which has been parameterized directly from the above mentioned atomistic simulations, reveals that these bending fluctuations are vital to having a soft elastic tetramer that slightly favors expansion over a wide range of its length.

The “flat” and negative force-extension profile calculated for the CG-bend model of the tetramer in Fig. 2 is similar to the isometric force-extension profiles predicted for semiflexible polymers which have persistence lengths that are comparable to their contour lengths (19, 22). For such polymers, the resulting force-extension can depend on which variable (force or length) is allowed to fluctuate. In the real cell, both the extension length of spectrin and the force along that length are under fluctuations, hence the exact length at which the force of the tetramer reaches zero and then becomes negative may be shifted from the value that is predicted in the isometric studies here. Future detailed studies of nonequilibrium simulations of the CG-bend tetramer model may be insightful.

The elastic behavior of the spectrin tetramer presented here is a very different description of the elastic spectrin tetramer tether of the red blood cell cytoskeletal network from other elasticity models previously considered for this system. These results warrant revisiting the interpretation of some of the elasticity experiments conducted on red blood cells, as they may help to explain some of the conflicting conclusions on the elasticity behavior of the tetramer. Ultimately, a direct experiment measure of the mechanical force of the tetramer as a function of its extension by experiments similar to those done for single strands of multiple spectrin domains would be very valuable.

Methods

The multiscale procedure for developing the coarse-grained model for the spectrin tetramer is described. The method for calculating the force-extension profile for the CG spectrin tetramer is also presented.

The CG Model.

The CG model in Fig. 1 has 11 sites for a DSRU. Each site corresponds to a particular structural domain of the DSRU. CG site 3 (CG3) is constructed from the center of mass of the helical linker region of the DSRU. CG sites 1 (CG1) and 2 (CG2) incorporate the triple helical cores of the two repeat units. The BC-loop of the second repeat unit are incorporated into CG site 5 (CG5) and the AB-loop of the first repeat unit is incorporated into CG site 4 (CG4). CG site 6 (CG6) and CG site 7 (CG7) represent the helical regions directly preceding and following the helical linker region of the DSRU, respectively. CG site 9 (CG9) and CG site 8 (CG8) in the first repeat unit are the equivalent of CG7 and CG5 in the second repeat. Also CG6 and CG4 in the first repeat unit are equivalent to CG site 10 (CG10) and CG site 11 (CG11) in the second repeat unit.

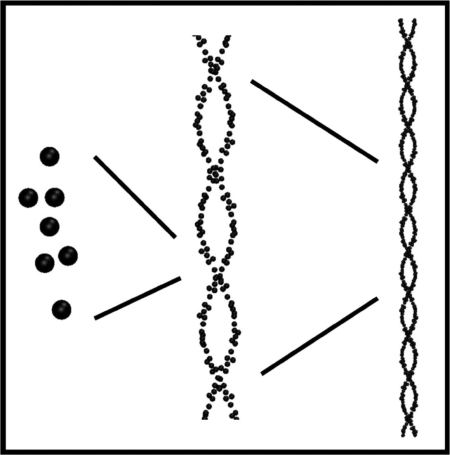
Because four of the 11 CG sites are duplicates, as stated above, each strand of the CG spectrin tetramer is constructed by translating CG site 1 through CG site 7 along a five-pitch helix 37 times, with each translation corresponding to the creating of another spectrin repeat unit, as shown in Fig. 4. At each translation step the position of CG3 is determined along the contour of a five-pitch helix representing the length of a single strand of the tetramer. The position of CG2 is then placed along the vector connecting the positions of CG3 from the first repeat unit and CG3 of the next repeat unit. The positions of CG5 and CG7 are then determined by RMS best fitting to the average structure of the DSRU using the positions of CG1 to CG7 determined from atomistic simulations (Fig. 1 Bottom). The final best-fitted internal coordinates of the CG repeat units are presented SI Tables 1–3. Two antiparallel interwound helices of five pitches are constructed in this way and linked to their images in the periodic boundaries.

Fig. 4.

Schematic diagram showing the CG spectrin tetramer built from the CG representation of two consecutive repeat units.

The CG potential for the tetramer is a sum of pair-wise additive harmonic bonding interactions, harmonic angle interactions, CHARMM dihedral interactions (23), and nonbonding Weeks–Chandler–Anderson interactions (24) between various CG sites, such that

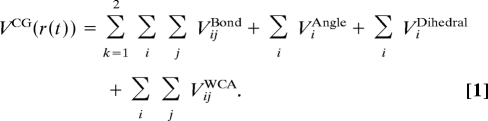The details of how the force constants for the first three terms (bonding interaction) of the CG potential were determined from atomistic MD simulations is discussed in the following section. Here the actual internal coordinates used are presented.

The harmonic bond interaction between any two CG sites in the tetramer (and a CG DSRU) is given by

where r_ij is the distance between CG site i and CG site j. Fig. 1 explicitly shows the bonding interactions between various CG sites that are included within individual repeat units and between two repeat units (with 37 individual repeat units in each single strand of the tetramer). The bonds CG4–CG3 and CG6–CG3 are between CG sites of the first repeat unit and the CG site representing the connecting linker region between the two repeat units (CG3). Likewise the bonds CG5-CG3 and CG7-CG3 are between CG sites of the second repeat unit and the CG site representing linker region (CG3). There are two bonds between CG sites of the first repeat unit and the CG sites of the second repeat unit, namely CG5–CG6 and CG7–CG4. The values for the all of the force constants of the bonding potentials of the coarse-grained HEβ89 spectrin DSRU are given in SI Table 1.

The harmonic angle interaction between any designated three CG sites in the tetramer (and a CG DSRU) is given by

where θ_i is the bending angle between three CG sites defining the ith bending internal coordinate. There are various bending interaction included between CG sites within an individual repeat unit that are explicitly listed in SI Table 2. There are also two bending interaction involving CG sites of both repeat units. These are the interactions of the bending angles defined by CG7–CG3–CG4 (see Fig. 1) and the bending angle defined by CG1–CG3–CG2 (see Fig. 1). The values for the force constants of the bending potentials of the coarse-grained HEβ89 spectrin DSRU are given in SI Table 2.

The single well CHARMM dihedral interaction between any four CG sites in the tetramer (and a CG DSRU) is given by

where φ_i is the dihedral angle between four CG sites defining the ith dihedral internal coordinate and Δ is the phase input parameter (Δ = φ_i⁰ − 180). Two of the five dihedral interactions in the DSRU considered are defined by CG2–CG5–CG7–CG3 of the second repeat unit (see Fig. 1) and CG1–CG4–CG6–CG3 of the first repeat unit (see Fig. 1). There are two identical dihedral interactions, one in the first repeat unit defined by CG8–CG9–CG6–CG4 (see Fig. 1) and one in the second repeat unit defined by CG5–CG7–CG10–CG11 (see Fig. 1). There is one additional dihedral interaction which involves CG sites of both repeat units and is defined by CG6–CG5–CG4–CG7 (see Fig. 1). The values for the force constants of the dihedral potentials of the coarse-grained HEβ89 spectrin DSRU are given in SI Table 3.

The self-avoidance between the two strands of the tetramer and the effective excluded volume arise from the Weeks–Chandler–Anderson interaction,

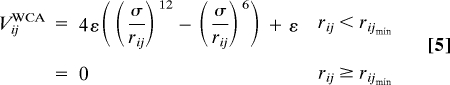between two CG sites belonging to different strands. The parameter σ is chosen in such a way as to make r_ijmin equal to the cross-sectional area diameter of a single spectrin repeat unit, through the relation r_ijmin = 2^1/6σ. The parameters used are r_ijmin = 11 Å and ε = 2 kcal/mol.

Determining the CG Parameters.

Internal coordinates of the CG representation of the DSRU are used to build an effective CG model based on atomistic MD simulations of double spectrin repeat units. The details of the atomistic MD simulations of the DSRU containing the eighth and ninth repeat units of the beta polypeptide of the human erythroid spectrin (HEβ89) are given in ref. 18. The center-of-mass of the subdomains of the HEβ89 DSRU were obtained from the last 45 ns of the all-atom trajectory. The CG representation of the atomistic trajectory (CG-A) then provides the target data for developing the coarse-grained models of the spectrin DSRU. The equilibrium values of the internal coordinates were obtained from the corresponding averages determined from the coarse-grained atomistic trajectory. The fluctuations for each internal coordinate were also calculated from the coarse-grained atomistic trajectory and used to determine the effective force constants of the CG model (25, 26). Because the fluctuations of the internal coordinates of the CG model can be calculated by normal mode analysis (NMA) (27), the effective force constants in the CG model are determined by matching the fluctuations computed from the NMA to that observed from the coarse-grained atomistic trajectory. Because the fluctuation of a given IC depends on its force constant as well as the force constants of all of the other internal coordinates, an iterative relationship is used to determine a self-consistent solution for all of the force constants of the CG model. Particularly the relation

is used, where k_j is the force constant of the jth IC in the CG model, δIC_j is the corresponding fluctuation of the jth IC as computed with the NMA, and δIC_j^CG–A is the fluctuation of the jth IC determined from the atomistic MD trajectory. The self-consistent approach to determining the set of CG parameters described above is based on the parameterization scheme previously used to construct CG models of F-actin filaments (26). It is important to note here that the effective force constants calculated by using the fluctuation matching approach described above implicitly incorporate the effects of viscous behavior of the underlying atomistic system, particularly due to electrostatic interactions.

Determination of Force–Extension Profile.

The goal of the CG simulations is to map out the elasticity of the tetrameric spectrin, by establishing its thermodynamic force-extension relationship under isothermal (constant temperature) conditions. By thermodynamic force it is meant that

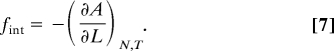Here, A is the Helmholtz free energy, L is the extension length, f_int is the force exerted by the tetramer, and the subscript “N, T” denote that isothermal conditions are maintained. To evaluate the thermodynamic force at each extension length, the free energy derivative is calculated with respect to L. From a statistical mechanical perspective this is the derivative of the natural logarithm of the canonical partition function Q(N, L, T),

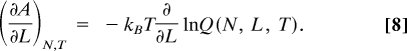With the length L taken to be in the z-direction, the evaluation of this derivative yields an expression for the thermodynamic force,

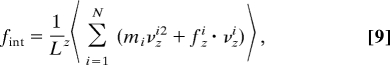which can be evaluated from the CG molecular dynamics simulations. Equilibrium isothermal simulations were carried out at different periodic box lengths and the instantaneous value of the force was calculated from the positions, velocities and forces of each particle in the system via Eq. 9. The CG MD simulations were carried out using the CHARMM simulation package (28). A Nosé–Hoover thermostat was used to maintain a constant temperature of 310 K (29). At each length an initial structure of the tetramer was equilibrated for 20 ns, following sampling of the thermodynamic force for at least 100 ns. The results presented earlier report the force exerted on the polymer system, where force = −f_int.