Evolutionary tradeoffs can select against nitrogen fixation and thereby maintain nitrogen limitation

Abstract

Symbiotic nitrogen (N) fixing trees are absent from old-growth temperate and boreal ecosystems, even though many of these are N-limited. To explore mechanisms that could select against N fixation in N-limited, old-growth ecosystems, we developed a simple resource-based evolutionary model of N fixation. When there are no costs of N fixation, increasing amounts of N fixation will be selected for until N no longer limits production. However, tradeoffs between N fixation and plant mortality or turnover, plant uptake of available soil N, or N use efficiency (NUE) can select against N fixation in N-limited ecosystems and can thereby maintain N limitation indefinitely (provided that there are losses of plant-unavailable N). Three key traits influence the threshold that determines how large these tradeoffs must be to select against N fixation. A low NUE, high mortality (or turnover) rate and low losses of plant-unavailable N all increase the likelihood that N fixation will be selected against, and a preliminary examination of published data on these parameters shows that these mechanisms, particularly the tradeoff with NUE, are quite feasible in some systems. Although these results are promising, a better characterization of these parameters in multiple ecosystems is necessary to determine whether these mechanisms explain the lack of symbiotic N fixers—and thus the maintenance of N limitation—in old-growth forests.

Biological nitrogen (N) fixation—the conversion of atmospheric N₂ gas to biologically useful N—lies at the heart of one of the most intriguing patterns in terrestrial ecosystem ecology: N is thought to limit net primary production (NPP) in many old-growth temperate and boreal forests, despite the existence of numerous N-fixing bacteria in these biomes. Intuition holds that symbiotic N fixers (a symbiosis between a plant and N-fixing bacteria, hereafter “N fixers”) should have a competitive advantage when N limits NPP and thus should invade and out-compete nonfixing plants (hereafter “nonfixers”) in N-limited ecosystems. Newly fixed N from their activity would increase N supply, rendering N limitation a transient phenomenon. Yet N limitation is common in old-growth temperate and boreal forests, where no N fixers exist as canopy trees (1, 2). This paradox suggests two fundamental questions about temperate and boreal forests: (i) Why do N fixers not persist beyond early succession? (ii) Why have no old-growth dominant species evolved N-fixing symbioses?

The first of these questions addresses a well documented successional pattern: In temperate and boreal ecosystems, N fixers dominate early primary succession but are replaced during the course of succession by nonfixers, even when N may still limit NPP (3–6). Some recent modeling studies have investigated this question (7–10), as outlined below. The second question has received little attention in the literature (but see ref. 11) but is equally important to explaining the paradox of N limitation. Unlike the successional question, this is inherently a question about an old-growth plant-nutrient ecosystem that tends toward equilibrium: Given a forest at or near biogeochemical steady state, why have no late-successional N fixers evolved?

There are two potential answers to this second question, neither of which exclude the other: (i) there are phylogenetic constraints to the evolution of late-successional N fixers (in the sense of ref. 11) and (ii) there are traits inherent to N fixation that lead to selection against N fixers when they appear in old-growth systems. Given that N-fixing bacteria are ubiquitous in natural ecosystems (1), phylogenetically diverse (12), and that they form symbioses with hundreds of plant species from nine plant families (6), many of which are temperate and boreal trees, phylogenetic constraints might not explain the absence of old-growth N fixers. In this article, we therefore explore the second hypothesis, using a simple evolutionary model to investigate factors that can select against N fixers in an old-growth N-limited environment.

Before focusing on the evolutionary question, we briefly review recent models that have investigated the ecological question of successional dynamics. Vitousek and Field (7) developed a simulation model of N fixer versus nonfixer competitive dynamics, assuming that fixation of atmospheric N is energetically more costly than soil N uptake when soil N is plentiful, and that N fixers take all N from fixation. In their model, N fixation cannot be suppressed unless there are additional restrictions, such as limitation of N fixation by another resource [phosphorus (P) or light, specifically] or selective herbivory on N fixers. Jenerette and Wu (9) analyzed a similar but spatially explicit model and found that N limitation can be maintained on local scales because of self-organized spatial heterogeneity (and without any additional constraints), although it cannot be maintained at the landscape scale. Rastetter et al. (8) investigated the conditions under which N fixation is physiologically optimal within aggregate vegetation, allowing N acquisition from soil N uptake and/or N fixation and assuming colimitation by N and carbon (C). They found that optimal allocation favors N fixation only when the C cost of soil N uptake relative to N fixation is too high. Wang et al. (10) added a P cycle to the model in Rastetter et al., emphasizing the importance of P in allowing N fixers to become established early in succession and the role of N-rich phosphatases in liberating P.

These models identify potential mechanisms to exclude N fixers and maintain N limitation during succession, and, in part, our work builds on these previous models. Because the topic of succession is inherently one of transient dynamics, simulations are an appropriate approach (as in refs. 7–10). Simulations have the advantage of highlighting particular resources [e.g., light (7, 8, 10), P (7, 10), or C (8, 10)] that can produce a given pattern in a given system, but because of computational limitations it is impossible to explore the entirety of parameter space. The equilibrium pattern we consider is analytically simpler, allowing us to generalize the above-mentioned mechanisms to other resources/systems and to derive critical threshold values for these mechanisms. Unlike previous models, however, our focus is on impediments to the evolution of N fixation in old-growth species, an issue that is also central to explaining persistent N limitation.

Here, we present and analyze a simple resource-based evolutionary model to explore ecological and physiological mechanisms that can select against N fixation despite N limitation. Although individual plants and NPP are often limited by multiple resources (13–15), our model assumes that N alone limits NPP. By assuming N limitation, we can show that colimitation with another resource (as in ref. 8) is not necessary to exclude N fixers and maintain N limitation. As in refs. 8 and 10, plants in our model can acquire N from N fixation and/or the soil (available soil N is modeled explicitly), which is more biologically realistic than fixation being the only N source (as in refs. 7 and 9). N fixation is known to be physiologically costly in terms of energy, C, and other resources (e.g., Mo, V, Fe, and P) (1, 16). We initially present the model with no explicit cost of N fixation, but we add costs later as tradeoffs between N fixation and other plant processes. These costs could result from energetic or C costs (as in ref. 8), but they are not limited to or dependent on these specific mechanisms.

In our model analysis, we introduce mutants with different N fixation rates and physiological/ecological tradeoffs, determine their success, and ultimately determine which N fixation strategies are evolutionarily stable. This approach concurrently reveals which tradeoffs can maintain the ecosystem-level pattern of N limitation. Throughout this article, we assume that plants (not their bacterial symbionts) control N fixation. In some symbioses, plants can prevent the initiation of nodulation (17) and punish nonfixing symbionts with sanctions (18), although this is not known to be general for N fixing symbioses. Absent any restrictions, this model suggests that evolution will select for N fixation, thus eliminating N limitation. However, tradeoffs with N fixation, if they are severe enough, can prevent N fixation from evolving despite N limitation of NPP, thereby maintaining N limitation.

Model and Analytical Approach.

Our model includes a plant population B with units [mass C area⁻¹] and a plant-available nitrogen pool A (nitrate, ammonium, and available organic N) with units [mass N area⁻¹]. We do not include an organic N pool in the soil for simplicity, although the qualitative results are identical if we do [supporting information (SI) Appendix 1]. The equations describing our basic model are

Here, ω is the N use efficiency (NUE) [equivalent to litter C:N (19)], ν is the uptake rate of available N, μ is the biomass turnover rate, I is the abiotic N input flux, k is the soil leaching rate of plant-available N, and δ is the proportion of the N in litterfall that is lost from the system in plant-unavailable forms [e.g., dissolved organic nitrogen (DON); in the sense of refs. 20 and 21]. All parameters are assumed to be positive; in particular, δ must be positive for sustained N limitation to be possible. We employ linear soil N uptake kinetics (νA) for simplicity, although the results of our model are qualitatively identical if we use any function that increases with A (SI Appendix 1). The strategy of interest is the N fixation rate F, which is in units of [mass N·mass C⁻¹·time⁻¹].

This is a “green slime” model, without individuals, spatial heterogeneity, or differentiation between plant tissue types. This has advantages in terms of analytical tractability and generality, but it renders some interpretations difficult. For instance, μ is the average biomass turnover rate, corresponding in real ecosystems to a combination of mortality, litterfall, root turnover, leakage out of plant tissues, or any other turnover mechanism, which is not frequently quantified for terrestrial plants. We will use the terms “turnover” and “mortality” interchangeably.

Starting from equilibrium, we allow the N fixation trait to evolve and determine the evolutionarily stable (ESS) (cannot be invaded once established) and convergence stable (will be approached from any starting point) fixation strategies (e.g., see refs. 22–24). Unless otherwise stated, we refer to evolution in phenotypic terms—i.e., the evolutionary effect on the trait of N fixation—hence a “large mutation” means an evolutionary change that produces a large change in the N fixation rate. This approach traditionally assumes that the ecological dynamics (competitive exclusion) happen much faster than the evolutionary time scale, that there are no genetic barriers to evolution of the trait of interest, and that only small mutations occur (23). In the case of N fixation, large mutations seem genetically plausible (e.g., switching to another symbiotic strain or turning N fixation off), so we relax the last assumption, considering both large and small mutations. The N fixation trait F is drawn from a continuous strategy space with lower bound 0 and an upper bound set by the environment or plant physiology (the latter if there is an upper limit to the N fixation rate). We call this upper bound F*, recognizing that it may vary across environments and/or plant species.

Although we focus our analysis and discussion on the evolution of N fixation, our model can also apply to ecological invasions of N fixers into old-growth ecosystems as long as immigration events similarly are sufficiently rare relative to the other key parameters in the system. A key difference between the immigration and mutation scenarios is the steepness of the tradeoff curves. Newly evolved symbioses would likely have less efficient N fixation (owing to the smaller amount of evolutionary time to work out the symbiotic arrangement), so we would expect steeper tradeoff curves for evolutionary invasions than ecological invasions. Furthermore, although we focus on invasions of old-growth systems, our model is consistent with the well documented pattern of the dominance of N fixers in primary succession (3–6, 25): when the soil available N pool, A, is small, nonfixers (F = 0) die out but N fixers (F > 0) can grow (see Eq. 1 when A is small).

Results

Equilibria and Stability.

The system described by Eqs. 1 and 2 has a locally stable, feasible equilibrium when the plant population can survive and when plant-unavailable N losses are greater than N fixation inputs (SI Appendix 1). We make the weak assumption that the environment can support plants, so the first condition is always true. The second condition is that

When N fixation inputs (BF) match or exceed plant-unavailable N losses ($B\frac{\mu \delta }{\omega }$), plants grow indefinitely, so sustained N limitation becomes impossible and some other resource must limit NPP at steady state. Thus, $F^{*}=\frac{\mu \delta }{\omega }$, the upper limit of F* in this model, yields sole limitation by another resource. Below this singular point, $F^{*}<\frac{\mu \delta }{\omega }$ yields colimitation (where both resources are necessary for further growth) or N limitation (if the physiologically maximum N fixation rate cannot overcome N limitation) at equilibrium. Hereafter, we refer to F* as the colimitation strategy, even though it can yield sole limitation in special cases.

Basic Evolutionary Analysis.

Initially, we determine the conditions that allow a rare mutant (F_m) to invade an established “resident” (F_r) population, which is when the mutant's initial growth rate in the environment set by the resident,

is positive (i.e., when F_m > F_r). This matches our intuition: an N-limited mutant will invade an N-limited resident if the mutant fixes more N, if all other factors are equal. Because this is a single resource, mean-field model, a successful invader will always exclude the resident (26). As more productive N fixers appear, they will continue to invade until the N fixation rate reaches F*, at which point N is no longer the sole limiting resource. If there is a net cost to N fixation beyond this point (when the population is no longer N-limited), the strategy F* is a continuously stable strategy (CSS) (which is both convergence stable and an ESS), meaning that it will evolve and remain (24). Conversely, a net benefit to N fixation beyond F* would select for increasing amounts of N fixation. For the remainder of this article we assume there is no net benefit to N fixation when the population is no longer N-limited, so non-N-limited N fixers do not invade or out compete F*. Regardless of the evolutionary stability of the colimitation strategy, it is clear that without any constraints, N fixers will invade and outcompete nonfixers and ultimately overcome N limitation, which is exactly the opposite of what happens in temperate and boreal forests.

Constrained Evolution.

We now put evolutionary tradeoffs in the model. In the basic model we let N fixation evolve without being linked to other plant traits, but in reality there are likely to be tradeoffs. Here, we present three candidates that can produce the paradoxical pattern of persistent N limitation: tradeoffs between N fixation and (i) mortality, (ii) soil N uptake, and (iii) NUE. These tradeoffs may be functions of a C cost [as in (8) for soil N uptake] or any other specific mechanism, but we implement them as effects of N fixation on these two other plant processes, leaving the underlying mechanisms unspecified for generality. As will become clear, from the perspective of whether N fixation can evolve (and thus whether N limitation can be maintained), the specific mechanisms causing the tradeoffs do not matter. Although the first two tradeoffs are not new ideas (1, 7, 8, 27), here we treat them generally and derive, to our knowledge for the first time, the conditions necessary to prevent the evolution of N fixation and thereby maintain N limitation over evolutionary as well as ecological time.

A number of researchers have proposed that N fixers suffer more herbivory than nonfixers by virtue of having higher N (protein) content (1, 7, 27–29). The one terrestrial model that has included this mechanism (7) concluded that the activity of N fixers could be ecologically suppressed if herbivory rates were five times higher on fixers than on nonfixers (corresponding to a 36% higher turnover), given the other parameters in the model. Here, we consider a similar tradeoff, but we treat herbivory as a special case of mortality and consider mortality more generally. Furthermore, we extend the tradeoff from an ecological to an evolutionary framework and show that substantially smaller differences in mortality can exclude N fixers altogether in some situations. We assume that the mortality rate increases with N fixation, which could result from preferential herbivore damage, an increased pathogen infection rate (the process of forming root nodules may incur an increased probability of such infection), a higher rate of litterfall or root shedding, lower shade tolerance, or any other cause of mortality or turnover. Specifically, we let μ be positive and increase with F.

In the basic model, we assumed that N fixation varied independently of soil N uptake; but, in reality, there is an inherent tradeoff between these two processes. For example, root tissue can be allocated to construct either fine roots or root nodules, and photosynthate can be fed either to N fixing bacteria or to mycorrhizal fungi/decomposers in the rhizosphere to acquire N. Other models have used an explicit C or energetic cost of N fixation (e.g., ref. 8), using biochemical information about the relative costs of fixing N₂ versus taking up various forms of inorganic N from the soil (16). These costs are potential examples of the type of tradeoff we employ, but, because the plant-level cost may differ from the biochemical cost (due to N availability, biomass allocation costs, bacterial efficiency, or other physiological or ecosystem-level issues), we implement the cost more generally. To incorporate this tradeoff, we assume that the soil N uptake rate ν decreases with F but remains positive.

Compared with nonfixers, N fixers have more N in their leaves (29–32). It has been argued that N fixers have evolved to live an N-rich lifestyle and that a high N content allows them to sustain high growth rates and defensive capabilities (30). However, a high N content in leaf litter, which would occur in N-rich plants if they did not retranslocate more N than N-poor plants, may also be typical of N fixers (32). Because high litter N is synonymous with a low NUE (19), the N-rich lifestyle espoused by N fixers requires more N acquisition per unit growth. To incorporate a tradeoff between N fixation and NUE, we let ω decrease with F but stay positive.

When the mortality rate, N uptake rate, and NUE depend on N fixation, the mutant's growth rate changes from that given by Eq. 4 to

where μ_i, ν_i, and ω_i [the mortality rate, N uptake rate, and NUE of type i (mutant or resident)] are functions of the fixation rate of type i, F_i. A mutant will invade when the equilibrium available soil N pool set by the mutant, (μ_m − ω_mF_m)/(ω_mν_m), is less than that of the resident, (μ_r − ω_rF_r)/(ω_rν_r) (see SI Appendix 1 for equilibrium expressions). This means that selection will minimize the equilibrium available soil N pool [Ā, in the sense of R* (26)], so the N fixation ESSs are the local maxima of 1/Ā,

Evolutionary Possibilities.

To evaluate the evolutionary consequences of the fitness function, Eq. 6, it is essential to understand its shape as a function of varying amounts of N fixation. Local fitness maxima of Eq. 6 (ESSs) may be either bounds of F (0 or F*) or hilltops within the N fixation strategy space, but we focus on four qualitatively different evolutionary landscapes: monotonically decreasing fitness (Fig. 1a), an overall decrease in fitness with a local maximum at F* (Fig. 1b), an overall increase in fitness with a valley of decreased fitness (Fig. 1c), and monotonically increasing fitness (Fig. 1d). The costs of N fixation are present in each panel, but they decrease from the left (Fig. 1a) to the right (Fig. 1d); correspondingly, N fixation evolves more easily from left to right.

Fig. 1.

Possible evolutionary outcomes allowed by this model. The N fixation strategy (the units of which are equivalent to kilograms of N per hectare per y, given a 1,000 kilograms of C per hectare stand of this type) is plotted on the horizontal axis, and the fitness function (Eq. 6, where μ, ν, and ω are functions of F) is on the vertical axis (normalized so nonfixers are at 0). Eq. 6 is equivalent to 1/Ā, the reciprocal of the equilibrium soil available N pool. Evolution will maximize Eq. 6, locally if mutations are small or globally if they are large. (a) Nonfixation is the CSS (indicated by a closed circle) (7 is true, 8 is false). (b) Both nonfixation and F* are ESSs (open circles) but nonfixation wins (7 is true, 8 is false). (c) Both are ESSs, but F* wins (7 and 8 are true). (d) F* is the CSS (7 is false, 8 is true). These show a progression of decreasing N fixation costs from a–d. To plot Eq. 6, we used saturating functions with positive intercepts for μ(F), ν(F), and ω(F).

First, if Eq. 6 is monotonically decreasing between F = 0 and F*, as in Fig. 1a, nonfixation is the CSS. In this case any N-limited N fixer that appears in a population of nonfixers will die out because its total costs (decreased soil N acquisition, decreased growth, and/or increased mortality) are too high relative to the benefit of fixed N. Thus, in the case illustrated in Fig. 1a, N fixation will not evolve or persist.

The second case, illustrated in Fig. 1b, occurs when Eq. 6 is decreasing, but not monotonically. Similar to the first case, N fixation cannot evolve from nonfixation because the costs of fixing N exceed the benefits for any level of N fixation. Unlike the first case, however, a population of N fixers at F* can theoretically be maintained (assuming small mutations), because the fitness at F* exceeds the fitness at slightly less than F*. The stability of the colimited ESS (and thus the prevention of N limitation) in Fig. 1b is biologically tenuous, however, because a nonfixer beats any N fixer; any mutation that turns off N fixation would win.

The third case (Fig. 1c) differs from the second in that fitness is higher at F* than at F = 0, although there is still a fitness valley between the two. Nonfixers still cannot be invaded locally, but mutants that fix near or at F* can evolve and would not be replaced by nonfixers. This function shape could be caused by the existence of startup costs of N fixation—such as building nodules, weeding out ineffective symbiotic strains, or preferential herbivory on fixers but no herbivore preference for one type of fixer over another—that can only be overcome by fixing a lot of N. Thus, the evolution of N fixation from a nonfixing resident population in Fig. 1c depends on mutations being large enough.

Finally, when Eq. 6 increases monotonically, as in Fig. 1d, our model resembles the basic model without tradeoffs because the costs of N fixation are always outweighed by the benefits: N-limited N fixers will always invade nonfixers, and N fixers fixing more N will continue to invade until N no longer limits them, leaving a single CSS at F*.

As stated above, although local maxima between nonfixation and F* are theoretically possible, we do not consider them here for two reasons. First, evolutionary hilltops between the boundaries could only arise if the tradeoffs with N fixation themselves increase as a function of N fixation (i.e., ∂²μ(F)/∂F² > 0, ∂²ν(F)/∂F² < 0, and/or ∂²ω(F)/∂F² < 0), which we find less likely than linear or saturating functions because of the above-mentioned startup costs. Second, and more importantly, because N limitation can occur at F* (if the physiological N fixation rate has reached its maximum), these other cases would not add qualitatively different evolutionary possibilities to those in Fig. 1.

Critical Conditions.

These four distinct evolutionary possibilities highlight the importance of two key conditions: (i) whether nonfixation is an ESS (as in Fig. 1 a–c) and (ii) whether a colimited N fixer beats a nonfixer even if nonfixation is an ESS (as in Fig. 1c).

Nonfixation is an ESS when the startup costs of N fixation render small amounts of N fixation a net detriment. This is true when the fitness function, Eq. 6, decreases at F = 0 (as in Fig. 1 a–c). This occurs when ∂/∂F(μ/νω)|_F=0 > 1/ν₀, or equivalently, when

where 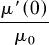, , and 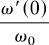are the proportional changes in the derivatives of μ, ν, and ω with respect to F, evaluated at F = 0; and μ₀, ν₀, and ω₀ are the mortality rate, soil N uptake rate, and NUE, respectively, of nonfixers. Because μ′ > 0, ν′ < 0, and ω′ < 0, Eq. 7 says that nonfixation is an ESS if the proportional startup costs of N fixation in terms of changes in mortality (μ′(0)), soil N uptake (ν′(0)), and/or NUE (ω′(0)) are great enough relative to a threshold determined by the ratio of two key plant traits: ω₀ and μ₀. The higher the ratio of the NUE to the tissue turnover rate of the average nonfixer, the easier it is for N fixation to evolve.

Both NUE and tissue turnover are relatively easy to constrain, as there are large global datasets on main components that comprise them. Reasonable ranges are 34.5–64.5 grams of C per gram of N for NUE and 0.05–2 y⁻¹ for the turnover rate, with central estimates of 45.5 gram of C per gram of N and 0.5 y⁻¹ (see SI Appendix 2 for a justification of the parameter ranges). With an initial N fixation rate of 1 mg of N per gram of C per y (equivalent to 1 kilogram of N per hectare per y, given a 1,000 kilogram of C per hectare stand of this type), and approximately linear tradeoffs with N fixation when F is small, the threshold that determines whether nonfixation is an ESS ranges from 1.7% to 129% with a central estimate of 9.1%. Using the central estimate, any combination of changes in the mortality rate, N uptake rate, or NUE that exceed 9.1% are sufficient to render nonfixation an ESS. For example, if the initial mutation that allows N fixation is accompanied by 4% decreases in the N uptake rate and NUE and a 2% increase in the mortality rate, this mutant will be selected against, despite being N-limited and capable of N fixation.

When nonfixation is an ESS, a colimited N fixer can still outcompete a nonfixer if the benefits of fixing a relatively large amount of N outweigh the startup costs of N fixation. The colimited N fixer's fitness is higher (equivalently, it drives the equilibrium soil N pool, Ā, lower) if

where μ_F*, ν_F*, and ω_F* are the mortality rate, N uptake rate, and NUE, respectively, at F*. The first term is always <1, but a sufficiently large middle term can allow an N fixer to win. As with the ESS threshold, Eq. 8 says that a higher ratio of NUE to mortality rate favors the N fixer, but here it is the NUE and the mortality rate of the N fixer that matters. Furthermore, Eq. 8 indicates that a higher F*, and thus a greater N deficit, favors the N fixer.

As described above, F* could be determined by a number of factors, such as the relative availability of other resources. This model does not include other resources explicitly, but because Eq. 3 must be true for N limitation to be possible, it gives the upper bound of F*. If we let F* = μ_F*δ/ω_F*, Eq. 8 becomes

The parameter δ is the fraction of N in litter lost from the system (e.g., leached DON; in the sense of ref. 20). If F* is at its maximum, a higher δ (and thus greater losses of unavailable N) makes it easier for an N fixing population to remain. Although δ is not as well studied as ω and μ, a reasonable (although less constrained) range of (1 − δ) (and thus the proportional change required for a nonfixer to win) is 0.3–0.997, with a central estimate of 0.9 (see SI Appendix 2). Given this central estimate, any multiplicative combination of proportional changes in the mortality rate, N uptake rate, or NUE that exceeds 10% is sufficient to select against N fixers. For example, if the N fixer at F* has a 4% lower N uptake rate and NUE and a 3% higher mortality rate, the N fixer will be outcompeted by a nonfixer and N limitation will prevail. At the lower end of the range of δ, a 0.3% difference in any of the plant traits alone is sufficient to select against N fixers.

Discussion

In an ecosystem at equilibrium, N limitation is only possible when losses of plant-unavailable N exceed inputs by N fixation (Eq. 3). One interpretation of this result is that unavailable N losses open a niche for N fixers in old-growth ecosystems, the size of which corresponds to the size of the unavailable N loss flux. Our evolutionary analysis investigates the conditions under which this niche can be filled.

Without any tradeoffs, and assuming no genetic barriers to N fixation, our model cannot select against N fixers, and thus does not allow persistent N limitation. However, tradeoffs between N fixation and mortality, soil N uptake, or NUE, if they are sufficiently large, can select against N fixation as a strategy and thereby maintain N limitation indefinitely (as long as there are losses of plant-unavailable N). Importantly, the thresholds for how harsh the tradeoffs need to be are determined by three key traits: the ratio of the (i) NUE and (ii) mortality rate of the plant population and (iii) the proportion of litter lost as unavailable N. It is interesting to note that the purely environmental parameters in the model, the abiotic N input flux I and the available N leaching constant k, have no influence on the evolution of N fixation.

As can be seen in Eqs. 7 and 8, a low NUE (ω) makes it harder for N fixers to evolve. This happens because plants with a low NUE receive a low biomass gain per unit N fixation, but pay the same cost in terms of increased mortality, decreased soil N uptake, or decreased NUE. Although this seems sensible, it is intriguing given that existing N fixers tend to have lower foliar (29–32) and litter (32) C:N ratios (and thus NUEs) than nonfixers. McKey (30) suggested that this N-rich lifestyle is adaptive for N fixers because of higher growth rates and defensive capabilities, but they still have to pay for this N fixation, and a lower return on investment (ω) means an even higher cost for the same amount of growth. Moreover, N-rich litter acts to fertilize N-limited competitors. Therefore, we suggest that N fixers' low C:N ratios reinforce their role as early successional specialists: they grow quickly and reproduce before the competitors they facilitate exclude them, but cannot become established in old-growth forests precisely because of the costs of maintaining high N content.

A high mortality or turnover rate also makes it harder for N fixers to evolve (Eqs. 7 and 8). Plants with high turnover rates lose more N and therefore need to take up more N to maintain or increase their biomass. As they take up more N, they pay the same cost per unit N fixation in terms of the tradeoffs with mortality, N uptake, or NUE, making the N fixation strategy less beneficial.

Scaling up from individual parameters, the fitness function plotted in Fig. 1 is the reciprocal of the equilibrium soil available N pool (Ā) that would be set by any given N fixation strategy. Fitness is determined by the NUE, mortality rate, and soil N uptake rate (as functions of the N fixation rate), but it is the combination that is critical. A higher Ā makes it harder for N fixers to evolve, and the fitness function indicates that N fixers can evolve in N-limited systems only if they take up more soil N, leaving less for their competitors [in the sense of R* (26)]. Consistent with low C:N ratios, data from early successional forests dominated by N fixers show high N mineralization rates (25) and available N losses (33) (likely because of the presence of N fixers), indicating a high Ā. This evidence further suggests that existing N fixers are fit for early succession but not for old-growth forests.

The proportion of N in litter lost as unavailable N is the third and final trait that can influence selection against N fixation but does so only when the fixation rate is at its maximum (as in Eq. 9): high losses of unavailable N favor N fixers. Although it makes sense that greater losses of unavailable N augment the niche for N fixation, it is again at odds with high N mineralization rates under N fixers (25), which suggest less recalcitrant litter and thus lower organic N losses; this would again select against N fixers as succession proceeds.

A low NUE, high turnover rate, high Ā, and low losses of unavailable N all help to select against N fixers in steady state environments. Interestingly, at least three of these—NUE, leaf lifespan, and leaf mass per unit area (a good measure of litter recalcitrance)—seem to be correlated across terrestrial plants worldwide (31) (assuming that litter and foliar C:N are positively correlated). The end of the spectrum typically associated with old-growth temperate and boreal forests—high NUE, low turnover rate, and high litter recalcitrance—is exactly where it should be easiest for N fixers to evolve.

This highlights a picture of two contrasting empirical patterns. First, existing N fixers exhibit characteristics that fare poorest in old-growth systems, with low NUE, high turnover rates, high Ā, and low litter recalcitrance. Second, existing old-growth temperate and boreal forests of nonfixers are at the opposite end of the plant trait spectrum, where it should be easiest for N fixation to evolve. A satisfying explanation to this juxtaposition would be that, at any location along this plant trait axis (including the point where current old-growth systems reside), the tradeoffs between N fixation and other traits are too severe for N fixation to evolve in old-growth systems. Therefore, with no chance of surviving in old-growth systems, existing N fixers have evolved traits to succeed in early successional environments. Given that unavailable N loss fluxes—and thus the open niche for N fixers—are generally small relative to annual N turnover within a forest, the startup costs of N fixation may be enough of a cost to select against N fixation. To evaluate this explanation, however, it is necessary to look at data for the critical tradeoff thresholds and the actual threshold strengths.

Our central parameter estimates show that modest tradeoffs with N fixation—10% changes in either the mortality rate, soil N uptake rate, or NUE, or a combination of changes in each that sums to 10%—could be sufficient to select against N fixation. The plant traits that determine these thresholds vary substantially in nature, however, and our parameter ranges indicate that the needed tradeoffs could be exceedingly small (so small, in fact, that they would be nearly impossible to detect against background noise) or quite substantial. To determine the critical tradeoff strengths for a given system, it would be necessary to gather all of the parameters from the same ecosystem. There are only three parameters to measure, all of which are relatively straightforward.

Our model predicts how large the tradeoffs need to be to select against N fixation; along with published data on the parameters that feed into this prediction, we have some sense for the threshold tradeoff strengths. The other piece of the puzzle is the magnitude of the actual tradeoffs. Three studies in grasslands and oak savannas have detected increased herbivory on legumes (27–29) (although they do not report how much N these individual plants are fixing), implying the effects were large enough to be detected. We are not aware of data that explicitly compare the N uptake rate of N fixers versus nonfixers, but a back of the envelope calculation of the structural costs of building nodules [excluding the metabolic costs of N fixation itself, which are likely to be more expensive (16); see SI Appendix 3] yields a possible effect of at least 0.2–5.1%, suggesting that just part of the tradeoff between N fixation and soil N uptake alone could potentially be sufficient to select against N fixation. Perhaps most convincing, a comparison of litter N content from N fixing to nonfixing angiosperms along a successional sequence in New Zealand gives a 3.1–38% change in NUE (32), with the 38% coming from the sites nearest each other in space and time. This tradeoff alone would be sufficient to select against N fixation in many environments. Moreover, all of these data were taken from established symbioses, and we would expect tradeoffs for newly evolved symbioses to be more severe.

In contrast to temperate and boreal forests, tropical forests are often dominated by putative N fixers (leguminous trees) and limited by resources other than N (2). Our model may suggest ways to reconcile these fundamental differences between temperate and tropical forests. For example, we incorporate a positive relationship between N fixation and mortality, arguing that higher foliar N increases protein and thus herbivory. Although there is evidence to support this tradeoff (27–29), it is also possible that N fixation decreases mortality. Many defensive secondary compounds are N-rich, so N fixers may have increased herbivore defenses (7), ultimately decreasing their mortality relative to nonfixers. If herbivory is a stronger selective force in tropical forests than in temperate forests (34), there could be both a negative relationship between N fixation and mortality in tropical forests (increasing the chances of a situation like Fig. 1 d) and a positive relationship in temperate and boreal forests (like Fig. 1 a–c). At present, this is speculation, and it leaves many intriguing questions unanswered (such as why there would be coexistence between N fixers and nonfixers).

In the absence of disturbance, sustained N limitation in an ecosystem requires losses of plant-unavailable N and the exclusion of symbiotic N fixers from the N-limited ecosystem. Our model provides three mechanisms to explain the exclusion of N fixers from N-limited ecosystems: tradeoffs between N fixation and (i) mortality, (ii) soil N uptake, and (iii) NUE. Furthermore, it states explicitly the conditions necessary for the exclusion of N fixers, which could be quite mild, and which traits influence the exclusion conditions. Specifically, low NUE, high plant turnover, high equilibrium available N pools, and low losses of unavailable N tend to select against N fixation. Although complete datasets on these parameters are sparse, the ranges we found suggest that the three mechanisms, and particularly the tradeoff with NUE, are quite feasible. Targeted data in well characterized systems may yet unravel this paradox in ecosystem ecology.