Abstract
The nuclear spin polarization of 129Xe can be enhanced by several orders of magnitude by using optical pumping techniques. The increased sensitivity of xenon NMR has allowed imaging of lungs as well as other in vivo applications. The most critical parameter for efficient delivery of laser-polarized xenon to blood and tissues is the spin-lattice relaxation time (T1) of xenon in blood. In this work, the relaxation of laser-polarized xenon in human blood is measured in vitro as a function of blood oxygenation. Interactions with dissolved oxygen and with deoxyhemoglobin are found to contribute to the spin-lattice relaxation time of 129Xe in blood, the latter interaction having greater effect. Consequently, relaxation times of 129Xe in deoxygenated blood are shorter than in oxygenated blood. In samples with oxygenation equivalent to arterial and venous blood, the 129Xe T1s at 37°C and a magnetic field of 1.5 T were 6.4 s ± 0.5 s and 4.0 s ± 0.4 s, respectively. The 129Xe spin-lattice relaxation time in blood decreases at lower temperatures, but the ratio of T1 in oxygenated blood to that in deoxygenated blood is the same at 37°C and 25°C. A competing ligand has been used to show that xenon binding to albumin contributes to the 129Xe spin-lattice relaxation in blood plasma. This technique is promising for the study of xenon interactions with macromolecules.
Optical pumping of rubidium vapor with circularly polarized laser light and spin exchange with 129Xe or 3He nuclei enhances the nuclear spin polarization by several orders of magnitude (1, 2) and allows NMR detection of xenon or helium in very low concentration (3). The laser-polarized gas, often referred to as hyperpolarized gas, can be imaged directly in the airways of the lungs after introduction into the respiratory system. This technique has been applied successfully in lung ventilation studies (4, 5). Furthermore, the high solubility of xenon in blood and lipids and the wide range of chemical shifts of xenon in different solvents (6) suggests a variety of in vivo MR applications, including functional imaging, investigation of blood flow, and studies of perfusion, blood volume, and permeability.
One of the major challenges for MR applications of hyperpolarized xenon is the efficient delivery of gas to blood and organs of interest while maintaining a large nonequilibrium polarization. The simplest administration route is via the respiratory system. Preliminary 129Xe MR images of xenon in brain have been obtained with this technique in an animal model (7). Compartmental models have been used to predict the concentration of hyperpolarized xenon in human tissues (8, 9) after administration to the lungs. Many parameters that determine xenon dynamics in lungs, circulatory system, and tissues have been well characterized in radioactive nuclear imaging studies (for a review see ref. 9). In contrast, some critical NMR parameters, such as 129Xe relaxation times in blood, lungs, and tissues, are still under investigation. The spin-lattice relaxation time (T1) for xenon mixed with oxygen in the lungs (typically 80% xenon and 20% oxygen) is in the range of 10–30 s (10, 11). The spin-lattice relaxation time of 129Xe in blood determines the loss of polarization during transit from the lungs to the tissue of interest. Therefore, the signal from xenon in tissue depends critically on 129Xe T1 in the blood (9). A difference in the relaxation times of xenon in oxygenated and deoxygenated blood could be used as a contrast mechanism in functional MRI, where blood would act as an endogenous contrast agent. The 129Xe spin-lattice relaxation time in blood and its dependence on the blood oxygenation level, however, are still matter of contention (12–16).
Albert et al. (12) measured the 129Xe spin-lattice relaxation time in blood at 2.35 T by using thermally polarized xenon. Values of 4.5 s and 9.6 s for xenon dissolved in the red blood cells and in plasma were reported. The blood oxygenation level in these experiments was approximately 20%. The long measurement times (12) caused the blood samples to separate out, which may explain the different relaxation times found in the two compartments. Experiments performed by Bifone et al. (13) with hyperpolarized xenon have shown that the rapid exchange time between red blood cells and plasma (12 ms) yields a single T1 for 129Xe in both compartments. Those authors report a T1 of 5 s at a field of 9.4 T. In these experiments, the hyperpolarized gas was introduced by injecting a small amount of saline equilibrated with xenon into the blood sample in an open tube placed in the NMR coil. Exchange of gas at the sample surface might have affected the relaxation time measurement. No attempt was made to measure the dependence of the relaxation time on the oxygenation state of the blood.
Albert et al. (14) performed experiments at a field strength of 1.5 T showing a dependence of the xenon relaxation time on blood oxygenation. Those authors found a significantly longer 129Xe T1 in oxygenated blood. This result indicates interaction with paramagnetic deoxyhemoglobin (17, 18) as the dominant relaxation mechanism for 129Xe in blood. In these experiments, the hyperpolarized gas was introduced by bubbling xenon into blood samples that had been substantially diluted with saline. Albert et al. report that a strong signal from gaseous 129Xe could be detected, suggesting that gas exchange may have perturbed the relaxation time measurement. Because of the dilution of the samples, only the signal of xenon in saline and plasma could be detected, whereas the signal from xenon in the blood cells dropped below the level of noise. Therefore, the relaxation times had to be determined solely from the decay of the saline/plasma signal, and relaxation times in oxygenated and deoxygenated blood were extrapolated from measurements at different dilutions. Furthermore, gas exchange from bubbling xenon through the sample might have altered the blood oxygenation level during the experiment.
Tseng et al. (15) measured T1 of hyperpolarized 129Xe in blood foam at 4.7 T. These experiments have shown the opposite dependence of the xenon relaxation time on blood oxygenation compared with ref. 14. Values of 21 s and over 40 s were reported for oxygenated and deoxygenated blood, implying that interaction with paramagnetic oxygen in solution is the main cause of 129Xe relaxation. The foam presents a large exchange surface between the gas compartment and the blood. Oxygen, as well as xenon, exchanges very efficiently with the dissolved phase, and the contribution of oxygen on the 129Xe spin-lattice relaxation time may have been overestimated.
In this paper we present measurements of the spin-lattice relaxation time of hyperpolarized 129Xe in human blood at a clinically relevant field of 1.5 T. Xenon dissolved in a small amount of saline was injected in a closed system containing blood equilibrated with different mixtures of gases. To ensure that the hematocrit was similar to typical in vivo values, a small amount of plasma was removed from the blood samples. After the injection, the sample tube was filled completely. No signal from gaseous xenon was observed in our experiments, which confirms that we have successfully prevented xenon exchange with the gas phase. We have determined the contribution of dissolved oxygen to the 129Xe spin-lattice relaxation time by comparison of blood samples equilibrated with carbon monoxide and pure oxygen. The effect of paramagnetic deoxyhemoglobin was investigated by comparing samples equilibrated with different mixtures of oxygen and nitrogen. We found a temperature dependence of the relaxation times from measurements at 37°C and 25°C. We also have studied the xenon relaxation time in plasma and its dependence on dissolved oxygen and on the presence of ligands that bind to albumin.
MATERIALS AND METHODS
Optical Pumping.
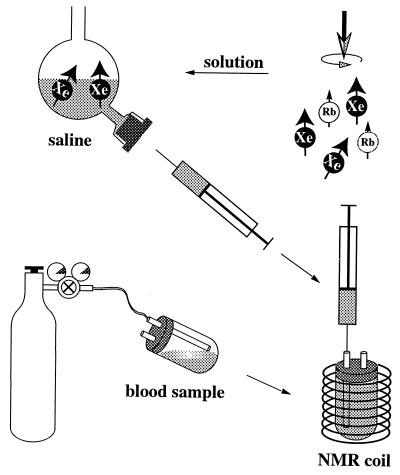
Optical pumping was performed by using equipment built in-house. Cylindrical glass cells of 60 cm3 containing a visible amount of rubidium metal were filled with a mixture of 180 torr of isotopically enriched xenon (82% 129Xe; Urenco, Almelo, The Netherlands) and 100 torr N2 (BOC, Redhill, U.K.) and pressurized with approximately 10 bar of helium (BOC). The cell was placed in the 130 Gauss field of a Helmholtz magnet and heated to 125°C. Hyperpolarization was achieved by optical pumping of the D1 electron transition of the Rb vapor with circularly polarized light from a 90-W diode laser array (Opto Power, Tucson, AZ) and spin exchange to the 129Xe nuclei. After 10–15 min of optical pumping, the cell was cooled to 80°C, and the xenon was collected in a distillator immersed in liquid nitrogen. During transport to the MR magnet, the frozen xenon was placed near one pole of a small horseshoe magnet to prevent rapid relaxation in zero magnetic field. The xenon was brought back to the gas phase in the bore of the MR magnet and admitted to the degassed saline, following the procedure described in detail in ref. 13. The gas was dissolved by vigorous shaking. The saline then was extracted, by using syringe and needle, through a self-sealing rubber septum, and injected into the blood sample in the NMR coil (see Fig. 1). The resulting 129Xe gas polarization was typically between 5% and 10% in the MR magnet after freezing, transport, and thawing.
Figure 1.
Schematics of sample preparation: blood samples are equilibrated with gas from a cylinder, then the sample tube is placed in the NMR coil. Hyperpolarized xenon is dissolved in saline in custom-made glassware. A known amount of saline then is drawn into a syringe and injected into the blood sample, thereby filling the tube completely.
NMR Spectroscopy.
All NMR experiments were performed by using a Siemens (Erlangen, Germany) Magnetom Vision 1.5 T clinical MR system. A home-built solenoid (129Xe)/saddle (1H/19F) double-resonance coil was used. 129Xe chemical shifts are expressed relative to gaseous 129Xe (0 ppm).
For measuring 129Xe, T1, a variable flip angle NMR sequence was used. As the large nonequilibrium polarization is nonrenewable, each rf pulse irreversibly destroys a fraction of the magnetization. By increasing the flip angles of multipulse sequences, this loss can be compensated for, and no correction to the data is necessary to calculate the signal decay induced by T1 processes (19, 20). We used a sequence of eight pulses with an inter-pulse delay of 1 s for measuring 129Xe T1 in blood and sequences of 12 pulses with inter-pulse delays between 1 and 4 s for the measurements in plasma and the protein solutions. The flip angles θn were calculated according to (sin2θN−n)−1 = N − n + 1, with N being the total number of pulses applied (see ref. 20). Rectangular pulses of 50 μs were used throughout, and the pulse amplitudes were varied to achieve the different flip angles.
Sample Preparation.
Freshly drawn blood was left for about 1 hr in heparinized sample tubes at 4°C for the red blood cells to settle. Subsequently, part of the plasma was removed. To achieve different oxygenation levels, the samples were equilibrated with different gases in sample tubes sealed with a rubber septum with two thin glass capillaries for administering the gas (see Fig. 1). Gas was flushed through the tube for approximately 30 min. The sample was shaken gently to increase gas exchange while flushing. Vigorous bubbling of gas through the blood was avoided to prevent formation of highly paramagnetic methemoglobin, as methemoglobin can severely affect relaxation time measurements (the 129Xe T1 in metmyoglobin solution, for instance, has been reported to be as short as 5.2 ms in ref. 21). The content of methemoglobin was measured by spectrophotometry after the treatment, and its concentration was below the detection level. Immediately after the flushing procedure, the capillaries were closed to prevent gas exchange with air, and the sample was placed in the NMR coil. For the spin-lattice relaxation measurements, 1–1.5 ml of saline, equilibrated with one atmosphere of hyperpolarized xenon, was injected through one of the capillaries into the sample tube containing 3.6–4 ml of blood, filling the sample tube completely. No residual gas pockets were observed, nor was any signal detected from gaseous xenon. As part of the plasma had been removed, the hematocrit values of the samples were comparable to those of undiluted blood (see Table 1). Most importantly, introduction of the laser-polarized xenon in solution ensures that no macroscopic xenon gas compartment is present, and the xenon relaxation time is measured in a closed system. The sample preparation procedure is shown schematically in Fig. 1.
Table 1.
Summary of all sample parameters obtained from blood gas meter measurements
| Sample | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Gas | O2 | CO | N2 | Air | N2 | Mix* | Air |
| Temp (°C) | 25 | 25 | 25 | 25 | 37 | 37 | 37 |
| Hematocrit (%) | 38 | 36 | 39 | 38 | 38 | 45 | 34 |
| pH | 7.66 | 7.58 | 7.94 | 7.63 | 7.72 | 7.41 | 7.43 |
| pH corr.** | 7.86 | 7.77 | 7.94 | 7.63 | 7.72 | 7.41 | 7.43 |
| pCO2 (kPa) | 1.48 | 1.94 | 1.05 | 3.07 | 1.15 | 4.45 | 3.06 |
| pCO2 corr.** (kPa) | 0.83 | 1.09 | 0.59 | 1.72 | 1.15 | 4.45 | 3.06 |
| pO2 (kPa) | 71.0 | – | 1.95 | 5.88 | 3.15 | 6.84 | 10.84 |
| pO2 corr.** (kPa) | 70.7 | – | 0.95 | 5.06 | 3.15 | 6.84 | 10.84 |
| sO2 (%) | 100 | – | 39.8 | 83.1 | 67.2 | 86.2 | 96.3 |
| sO2 (%) corr.** | 100 | – | 64.4 | 98.1 | 67.2 | 86.2 | 96.3 |
, mixture of 90% N2, 5% O2, and 5% CO2. ∗∗, blood gas analysis was performed at a sample temperature of 37°C throughout, whereas NMR measurements were performed at 25°C for samples 1–4. The corrections of pH, pCO2, pO2, and sO2 for these samples were calculated by using standard hemoglobin saturation curves versus temperature to obtain the corresponding values at 25°C (Materials and Methods).
Immediately after the NMR experiments, the oxygenation level, sO2, and the partial pressures of oxygen, pO2, and carbon dioxide, pCO2, were measured by using a blood gas analysis instrument (ABL 505, Radiometer, Copenhagen). These values are measured at a sample temperature of 37°C. Therefore, for samples measured at 25°C the values for pO2, pCO2, and sO2 had to be corrected. This correction was done by using a numerical method accounting for the shift of the standard oxygen dissociation curve in blood with a 50% blood oxygenation level at a partial oxygen pressure of 3.578 kPa at 37°C (see ABL 505 manual, chapter 3, and refs. 22 and 23 cited therein).
The plasma samples were prepared by centrifuging freshly drawn blood at a temperature of 4°C at 2,000 rpm for 10 min. Subsequently, the plasma was frozen at −18°C. We performed two sets of experiments: for three samples we used the same preparation method as for the blood samples by equilibrating them with different gases and injecting a small amount of saline containing hyperpolarized xenon. One of these samples contained flucloxacillin sodium British Pharmacopia (BP) (Floxapen; Beecham Research, Hertfordshire, U.K.) in 100 mM concentration, which was chosen to investigate the effect of ligand binding to albumin on the xenon spin-lattice relaxation time in plasma. Two plasma samples, one with and one without flucloxacillin, were prepared in custom-made glassware in which the hyperpolarized xenon could be admitted directly to the plasma, and the gas was dissolved by shaking. We performed these measurements to investigate the effect of the small amount of saline on the 129Xe relaxation time. Before introduction of the hyperpolarized gas, oxygen was removed from these samples by equilibrating the sample (1.5 ml) with 100 ml of helium for 20 min repeatedly. The same glassware and degassing procedure were used for measurements in albumin solution, which we performed to confirm whether flucloxacillin affects xenon binding to albumin. We used BSA powder (Sigma) and deuterated water with low paramagnetic impurity content (Aldrich). Flucloxacillin sodium BP was added in various concentrations to BSA/D2O samples of 3 ml each.
RESULTS AND DISCUSSION
Blood samples with different oxygenation state were prepared as outlined in Materials and Methods. Oxygenation parameters for the blood samples are shown in Table 1. In addition to varying the oxygenation state of the blood and thereby changing the ratio of oxy- and deoxyhemoglobin, we investigated blood that was equilibrated with carbon monoxide (CO). The 125Xe spin-lattice relaxation times for all samples are summarized in Table 2.
Table 2.
Hyperpolarized 129Xe spin-lattice relaxation times for all blood samples
| Sample | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Gas | O2 | CO | N2 | Air | N2 | Mix* | Air |
| Temp (°C) | 25 | 25 | 25 | 25 | 37 | 37 | 37 |
| T1,rbc (s) | 6.01 ± 0.26 | 7.72 ± 0.38 | 2.95 ± 0.24 | 5.11 ± 0.66 | 3.85 ± 0.15 | 4.00 ± 0.32 | 6.27 ± 0.33 |
| T1,plasma(s) | 5.40 ± 0.27 | 7.97 ± 0.32 | 2.81 ± 0.16 | 5.26 ± 0.70 | 3.57 ± 0.18 | 3.90 ± 0.28 | 6.58 ± 0.42 |
| T1,average(s) | 5.71 ± 0.35 | 7.84 ± 0.47 | 2.88 ± 0.27 | 5.19 ± 0.91 | 3.71 ± 0.22 | 3.95 ± 0.40 | 6.42 ± 0.50 |
The decay of the signal from xenon in plasma/saline and from xenon in the red blood cells were determined independently for both peaks. ∗, mixture of 90% N2, 5% O2, and 5% CO2.
A typical hyperpolarized 129Xe NMR spectrum of xenon in blood is shown in Fig. 2. The signal at a chemical shift of 197 ppm is caused by xenon in the saline/plasma mixture, whereas the signal at a chemical shift of 220 ppm corresponds to xenon in the red blood cells. The spectrum in Fig. 2 was obtained after a 21° rf pulse. The position of the signal of xenon in the red blood cells is shifted by 2–3 ppm downfield in samples equilibrated with pure oxygen and with CO, whereas the position of the saline/plasma signal is only shifted by a fraction of a ppm. The shift of the signal corresponding to xenon in the red blood cells may reflect the different susceptibilities in red blood cells containing oxygenated and deoxygenated hemoglobin, respectively.
Figure 2.
Typical single-shot hyperpolarized 129Xe NMR spectrum of xenon in blood. The flip angle applied was 21°. The signal at a chemical shift of 197 ppm is caused by xenon in the saline/plasma mixture, whereas the signal at a chemical shift of 222 ppm corresponds to xenon in the red blood cells.
The two peaks corresponding to xenon in the red blood cells and to xenon in plasma/saline were integrated to calculate the 129Xe spin-lattice relaxation times in both environments. Because of the fast exchange of xenon between plasma and red blood cells (13), these two longitudinal relaxation times are identical within the experimental errors.
The contributions of dissolved oxygen and paramagnetic hemoglobin to the 129Xe longitudinal relaxation time can be discriminated by comparing the measurements from different samples.
CO binds much more strongly than oxygen to hemoglobin, and full saturation with CO is achieved when equilibrating a blood sample with carbon monoxide. No effect on 129Xe relaxation is expected from deoxyhemoglobin in either sample 1, which is equilibrated with pure O2, or in sample 2, which is equilibrated with CO. As shown in Table 1, full saturation of hemoglobin with oxygen is achieved in sample 1. In addition, this sample contains 70.7 kPa of dissolved oxygen. Therefore, the difference in longitudinal 129Xe relaxation times for samples 1 and 2 should directly reflect the contribution of oxygen in solution. The 129Xe T1 is reduced from 7.84 s ± 0.47 s, in the sample equilibrated with CO, to 5.71 s ± 0.35 s, in the sample equilibrated with pure oxygen. The amount of dissolved oxygen in sample 1, however, is much larger than typical values for arterial blood (10–15 kPa). For the small difference in dissolved oxygen between arterial and venous blood, which is of the order of 5 kPa, this contribution to the 129Xe T1 in blood is smaller than that of deoxyhemoglobin, as discussed below.
Samples 5, 6, and 7 are equilibrated with pure N2, with a mixture of 90% N2, 5% O2, and 5% CO2, and with air, respectively. They provide information about the contribution of deoxyhemoglobin to the 129Xe relaxation time. We have measured shorter 129Xe T1 for samples with higher concentrations of deoxyhemoglobin. In sample 7, hemoglobin is oxygenated to 96.3%, and the 129Xe T1 is 6.42 ± 0.50 s, compared with only 3.71 s ± 0.22 s in sample 5 with 67.2% hemoglobin oxygenation. We conclude that relaxation caused by deoxyhemoglobin is a very significant relaxation mechanism.
The same trend is observed when comparing samples 1, 3, and 4. Although sample 1 contains 70.7 kPa of dissolved oxygen (as opposed to only 0.95 kPa oxygen in sample 3), the corresponding 129Xe T1 of 5.71 s ± 0.35 s is almost twice as long as the 129Xe relaxation time in sample 3, 2.88 s ± 0.27 s, which contains 64.4% oxyhemoglobin.
Decreasing the oxygenation of blood reduces the concentration of dissolved paramagnetic oxygen and increases the concentration of deoxyhemoglobin. The two relaxation mechanisms partially compensate each other. However, comparison of the results for samples 1, 3, and 4 shows that interaction of xenon with deoxyhemoglobin is by far the more efficient mechanism. In this context, the hematocrit of the sample is very important, as the contribution of deoxyhemoglobin depends strongly on concentration (14). The hematocrit values of our samples are all within the range of typical in vivo values (Table 1).
Both oxy- and carboxyhemoglobin are paramagnetic, whereas deoxyhemoglobin is paramagnetic (17). Xenon binding sites in horse hemoglobin have been identified by x-ray crystallography. These results indicate that the xenon binding sites on hemoglobin are located close to the G-H and A-B helix corner regions, respectively (24). Interaction with the paramagnetic metal ion is likely to be responsible for relaxation of 129Xe in deoxyhemoglobin. Moreover, configurational changes induced by oxygen and carbon monoxide also could affect xenon binding to hemoglobin and contribute to the different relaxivities of oxy-, carboxy-, and deoxyhemoglobin.
Results for samples measured at temperatures of 37°C and 25°C show temperature dependence of the 129Xe spin-lattice relaxation times. We observe shorter 129Xe T1s at lower temperature: the 129Xe T1 drops from 3.71 s ± 0.22 s at 37°C to 2.88 s ± 0.27 s at 25°C for the samples equilibrated with nitrogen (samples 5 and 3), and from 6.42 s ± 0.50 s at 37°C to 5.19 s ± 0.91 s at 25°C for the samples equilibrated with air (samples 7 and 4). The ratio of the relaxation times of oxygenated blood to those of deoxygenated blood, however, is the same at both temperatures within our experimental error.
From our results, we conclude that the 129Xe T1 in venous blood is shorter than that in arterial blood. As discussed, interaction with paramagnetic deoxyhemoglobin is more efficient than interaction with dissolved oxygen and determines the dependence of the xenon spin-lattice relaxation time on the oxygen saturation level. Samples 6 and 7 were measured at 37°C, and the blood oxygenation levels in these samples are very similar to physiological values (Table 1). Longitudinal 129Xe relaxation times are 6.42 s ± 0.50 s for arterial blood and 3.95 s ± 0.40 s for venous blood.
The 129Xe longitudinal relaxation time in plasma is longer than in full blood. We found a 129Xe T1 of 13.18 s ± 0.12 s in plasma equilibrated with air (sample P1). We also measured the longitudinal relaxation times of xenon in two plasma samples that were equilibrated with nitrogen. One of them contained 100 mM flucloxacillin. The results are summarized in Table 3. 129Xe T1 increases to 14.34 s ± 0.10 s when dissolved oxygen is removed (sample P2), and even further to 15.44 s ± 0.27 s upon introduction of flucloxacillin (sample P3). In samples P4 and P5, hyperpolarized xenon was introduced directly without using saline (as explained in Materials and Methods). The 129Xe T1 increases from 13.32 s ± 0.10 s in sample P4 to 16.17 s ± 0.19 s in sample P5, which contains flucloxacillin in 100 mM concentration. The position of the 129Xe signal was shifted by 1 ppm downfield in the samples that contained flucloxacillin, compared with the samples without flucloxacillin.
Table 3.
Hyperpolarized 129Xe spin-lattice relaxation times in all plasma samples
| Sample | Preparation | T1 (s) |
|---|---|---|
| P1 | Equilibrated with air | 13.18 ± 0.12 |
| P2 | Equilibrated with N2 | 14.34 ± 0.10 |
| P3 | 100 mM flucloxacillin, equilibrated with N2 | 15.44 ± 0.27 |
| P4 | Equilibrated with He | 13.32 ± 0.10 |
| P5 | 100 mM flucloxacillin, equilibrated with He | 16.17 ± 0.19 |
Samples P1–P3 were measured by adding a small amount of saline equilibrated with hyperpolarized xenon, whereas samples P4 and P5 were measured after admitting gaseous hyperpolarized xenon to the plasma.
From comparison of samples P4 and P5 with samples P2 and P3, we conclude that the introduction of a small amount of saline increases the xenon relaxation time by less than 10%. As the 129Xe T1 in full blood is determined mainly by mechanisms that are intracellular in origin, and as the hematocrit of our samples is comparable to in vivo conditions, our method of introducing the hyperpolarized xenon in solution into the blood represents only a very small perturbation. We notice, however, that the increase of the xenon spin-lattice relaxation time upon adding flucloxacillin is more pronounced in pure plasma (as can be seen from comparison of samples P4 and P5) than in the case of plasma that contains saline (samples P2 and P3, respectively). The fact that the xenon relaxation time increases in the presence of flucloxacillin suggests that flucloxacillin acts as a competing ligand that is able to prevent xenon from binding to proteins in plasma. To verify this hypothesis, we performed experiments in 5% (wt/vol) BSA solution.
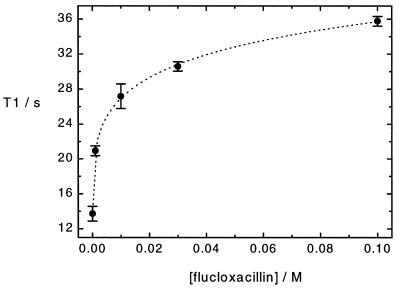
Plasma contains approximately 5% (wt/vol) albumin (see, for instance, ref. 25). To assess the contribution of protein binding to xenon relaxation in plasma, we conducted a series of measurements in a solution of 5% (wt/vol) BSA in fully deuterated water (D2O) and various concentrations of flucloxacillin up to 100 mM. By using a fully deuterated solvent, we excluded cross-relaxation from xenon to water protons. Flucloxacillin, a fluorinated drug, displaces 5-fluorouracil from BSA, as shown from 19F NMR spin-lattice relaxation time measurements (A.S.K. Dzik-Jurasz, personal communication; the use of 19F NMR as a tool for studying ligand binding to macromolecules is reviewed in ref. 26). We measured hyperpolarized 129Xe spin-lattice relaxation times in samples of different flucloxacillin concentration. Our results are displayed in Fig. 3. The xenon relaxation time is increased from 13.71 s ± 0.84 s in the pure 5% (wt/vol) BSA in D2O solution to 35.77 s ± 0.55 s in 5% (wt/vol) BSA in D2O and 100 mM flucloxacillin. The position of the 129Xe signal was shifted by 2 ppm downfield in the sample containing 100 mM concentration of flucloxacillin compared with the 5% (wt/vol) BSA in D2O solution sample.
Figure 3.
Hyperpolarized 129Xe T1 in 5% (wt/vol) BSA in D2O and different concentrations of flucloxacillin. Dotted line is a guide for the eye.
Control experiments on a 100 mM flucloxacillin/D2O solution and on pure D2O show that xenon association with flucloxacillin does not significantly contribute to 129Xe T1. The dependence of solution viscosity on flucloxacillin concentration was measured by capillary viscometry. No significant effects were observed for flucloxacillin concentrations up to 100 mM. These findings suggest that xenon and flucloxacillin compete for one or more binding sites on BSA and that the presence of flucloxacillin affects xenon binding to the protein. Therefore, dipolar interaction between xenon and protons of the protein is reduced, which results in the longer spin-lattice relaxation time. Thus, we conclude that binding to albumin contributes to the longitudinal xenon relaxation time in plasma. However, as seen from comparison of samples P4 and P5, introduction of flucloxacillin changes the 129Xe T1 by only about 20%, and removal of dissolved oxygen changes the xenon relaxation time in plasma by less than 10%. This result indicates that other mechanisms, such as interaction with paramagnetic ions and other proteins (25), and cross-relaxation to the solvent contribute to xenon relaxation in plasma.
CONCLUSIONS
We have investigated the 129Xe nuclear magnetic spin-lattice relaxation time in human blood in vitro. We have shown that interactions with dissolved oxygen and with paramagnetic deoxyhemoglobin both contribute to 129Xe relaxation in blood. As the contribution from deoxyhemoglobin is larger than that of oxygen in solution, the xenon spin-lattice relaxation time in deoxygenated blood is shorter than in oxygenated blood. For similar oxygenation level, the 129Xe T1 is longer at 37°C than at 25°C. The ratio of the relaxation times of oxygenated to deoxygenated blood is the same at both temperatures.
At a temperature of 37°C and at a magnetic field of 1.5 T, we measured a 129Xe spin-lattice relaxation time of 6.4 s ± 0.5 s in arterial blood, and a T1 of 4.0 s ± 0.4 s in venous blood. These values are comparable to typical blood transit times from the lungs to tissues such as the brain (27). Therefore, delivery of laser-polarized xenon to tissues is limited by loss of polarization during vascular transport. Intravenous injection of laser-polarized xenon in a suitable solution characterized by much longer 129Xe T1 and higher xenon solubility (13, 28, 29) might increase the hyperpolarized 129Xe NMR signal from the target tissue. However, the difference of the xenon spin-lattice relaxation times in oxygenated and deoxygenated blood could be exploited as a potential contrast mechanism for hyperpolarized 129Xe functional MRI.
By introducing flucloxacillin, we have demonstrated that xenon binding to albumin affects the xenon spin-lattice relaxation time in plasma. We believe that using competitive binding is a promising technique for studying the specificity of xenon-protein interactions, as we have demonstrated in our measurements in BSA solution. This method could be applied, for instance, to investigate the general anesthetic properties of xenon (21) and their origins in more detail.
Acknowledgments
We thank J. Iqbal and M. Booth for their help with sample characterization. Financial support from the Institute of Cancer Research and from the Cancer Research Campaign (CRC Grant SP/1780/0103) is gratefully acknowledged.
References
- 1.Happer W, Miron E, Schaefer S, Schreiber D, van Wijngaarden W A, Zeng X. Phys Rev A. 1984;29:3092–3110. [Google Scholar]
- 2.Walker T G, Happer W. Rev Mod Phys. 1997;69:629–642. [Google Scholar]
- 3.Raftery D, Long H, Meersmann T, Grandinetti P J, Reven L, Pines A. Phys Rev Lett. 1991;66:584–587. doi: 10.1103/PhysRevLett.66.584. [DOI] [PubMed] [Google Scholar]
- 4.Albert M S, Cates G D, Driehuys B, Happer W, Saam B, Springer C S, Jr, Wishnia A. Nature (London) 1994;370:199–201. doi: 10.1038/370199a0. [DOI] [PubMed] [Google Scholar]
- 5.Wagshul M E, Button T M, Li H F, Liang Z, Springer C S, Zhong K, Wishnia A. Magn Reson Med. 1996;36:183–191. doi: 10.1002/mrm.1910360203. [DOI] [PubMed] [Google Scholar]
- 6.Miller K W, Reo N V, Schoot Uiterkamp A J M, Stengle D P, Stengle T R, Williamson K L. Proc Natl Acad Sci USA. 1981;78:4946–4949. doi: 10.1073/pnas.78.8.4946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Swanson S D, Rosen M S, Agranoff B W, Coulter K P, Welsh R C, Chupp T E. Magn Reson Med. 1997;38:695–698. doi: 10.1002/mrm.1910380503. [DOI] [PubMed] [Google Scholar]
- 8.Peled S, Jolesz F A, Tseng C-H, Nascimben L, Albert M S, Walsworth R L. Magn Reson Med. 1996;36:340–344. doi: 10.1002/mrm.1910360303. [DOI] [PubMed] [Google Scholar]
- 9.Martin C C, Williams R F, Gao J-H, Nickerson L D H, Xiong J, Fox P T. J Magn Reson Imaging. 1997;7:848–854. doi: 10.1002/jmri.1880070512. [DOI] [PubMed] [Google Scholar]
- 10.Mugler J P, III, Driehuys B, Brookeman J R, Cates G D, Berr S S, Bryant R G, Daniel T M, de Lange E E, Downs J H, III, Erickson C J, et al. Magn Reson Med. 1997;37:809–815. doi: 10.1002/mrm.1910370602. [DOI] [PubMed] [Google Scholar]
- 11.Jameson C J, Jameson A K, Hwang J K. J Chem Phys. 1988;89:4074–4081. [Google Scholar]
- 12.Albert M S, Schepkin V D, Budinger T F. J Comput Assist Tomogr. 1995;19:975–978. doi: 10.1097/00004728-199511000-00025. [DOI] [PubMed] [Google Scholar]
- 13.Bifone A, Song Y-Q, Seydoux R, Taylor R E, Goodson B M, Pietrass T, Budinger T F, Navon G, Pines A. Proc Natl Acad Sci USA. 1996;93:12932–12936. doi: 10.1073/pnas.93.23.12932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Albert M S, Balamore D, Sakai K, Kacher D, Walsworth R L, Oteiza E, Jolesz F A. International Society for Magnetic Resonance in Medicine (ISMRM) Fourth Meeting Proceedings. Berkeley, CA: ISMRM; 1996. p. 1357. [Google Scholar]
- 15.Tseng C H, Peled S, Nascimben L, Oteiza E, Walsworth R L, Jolesz F A. J Magn Reson. 1997;126:79–86. doi: 10.1006/jmre.1997.1145. [DOI] [PubMed] [Google Scholar]
- 16.Kacher D F, Balamore D, Jolesz F A, Albert M S. International Society for Magnetic Resonance in Medicine (ISMRM) Fifth Meeting Proceedings. Berkeley, CA: ISMRM; 1997. p. 1403. [Google Scholar]
- 17.Pauling L, Coryell C D. Proc Natl Acad Sci USA. 1936;22:159–163. doi: 10.1073/pnas.22.3.159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tilton R F, Kuntz I D. Biochemistry. 1982;21:6850–6857. doi: 10.1021/bi00269a035. [DOI] [PubMed] [Google Scholar]
- 19.Zhao L, Mulkern R, Tseng C-H, Williamson D, Patz S, Kraft R, Walsworth R L, Jolesz F A, Albert M S. J Magn Reson B. 1996;113:179–183. [PubMed] [Google Scholar]
- 20.Patyal B R, Gao J-H, Williams R F, Roby J, Saam B, Rockwell B A, Thomas R J, Stolarski D J, Fox P T. J Magn Reson. 1997;126:58–65. doi: 10.1006/jmre.1997.1159. [DOI] [PubMed] [Google Scholar]
- 21.Albert M S, Springer C S, Murphy R, Wishnia A. Proceedings of the Society of Magnetic Resonance in Medicine (SMRM) 11th Annual Meeting. Berkeley, CA: SMRM; 1992. p. 2104. [Google Scholar]
- 22.Siggaard-Andersen O, Wimberley P D, Gothgen I H, Siggaard-Andersen M. Clin Chem. 1984;30:1646–1651. [PubMed] [Google Scholar]
- 23.Siggaard-Andersen O, Wimberley P D, Gothgen I H, Fogh-Andersen N, Rasmussen J P. Scand J Clin Lab Invest. 1988;48:85–88. [Google Scholar]
- 24.Schoenborn B P. Nature (London) 1965;208:760–762. doi: 10.1038/208760a0. [DOI] [PubMed] [Google Scholar]
- 25.Tortora G J, Anagnostakos N P. Principles of Anatomy and Physiology. New York: Harper & Row; 1987. [Google Scholar]
- 26.Jenkins B G. Life Sci. 1991;48:1227–1240. doi: 10.1016/0024-3205(91)90517-f. [DOI] [PubMed] [Google Scholar]
- 27.West J B. Respiratory Physiology—The Essentials. Baltimore: Williams & Wilkins; 1995. [Google Scholar]
- 28.Goodson B M, Song Y-Q, Taylor R E, Schepkin V D, Brennan K M, Chingas G C, Budinger T F, Navon G, Pines A. Proc Natl Acad Sci USA. 1997;94:14725–14729. doi: 10.1073/pnas.94.26.14725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wolber, J., Rowland, I. J., Leach, M. O. & Bifone, A. (1999) Magn. Reson. Med., in press. [DOI] [PubMed]