Comparing in vitro, in situ, and in vivo experimental data in a three-dimensional model of mammalian cochlear mechanics

Abstract

Normal mammalian hearing is refined by amplification of the motion of the cochlear partition. This partition, comprising the organ of Corti sandwiched between the basilar and tectorial membranes, contains the outer hair cells that are thought to drive this amplification process. Force generation by outer hair cells has been studied extensively in vitro and in situ, but, to understand cochlear amplification fully, it is necessary to characterize the role played by each of the components of the cochlear partition in vivo. Observations of cochlear partition motion in vivo are severely restricted by its inaccessibility and sensitivity to surgical trauma, so, for the present study, a computer model has been used to simulate the operation of the cochlea under different experimental conditions. In this model, which uniquely retains much of the three-dimensional complexity of the real cochlea, the motions of the basilar and tectorial membranes are fundamentally different during in situ- and in vivo-like conditions. Furthermore, enhanced outer hair cell force generation in vitro leads paradoxically to a decrease in the gain of the cochlear amplifier during sound stimulation to the model in vivo. These results suggest that it is not possible to extrapolate directly from experimental observations made in vitro and in situ to the normal operation of the intact organ in vivo.

The mammalian auditory system exhibits remarkable sensitivity and frequency selectivity to incoming sound stimuli, properties that are established by the mechanical motion of a flexible partition within the cochlea (1–6). Sound stimulation to the cochlea leads to a wave of transverse motion on the partition that propagates from base to apex (Fig. 1a). This motion peaks at a position that depends on stimulus frequency. When the cochlea is functioning normally, and during low-intensity stimulation, the motion near the peak is boosted by several tens of decibels by forces exerted on it by the so-called cochlear amplifier (7).

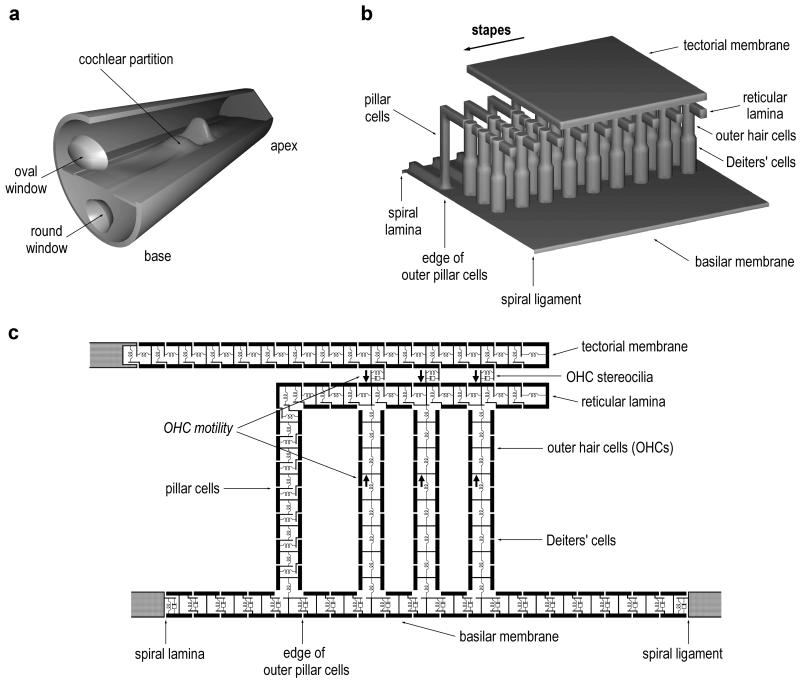
Figure 1.

(a) Schematic of the mammalian cochlea, shown unrolled and not to scale. The cochlea is a liquid-filled duct that is divided lengthwise into two chambers by the flexible cochlear partition. Sound stimulation is provided by the piston-like motion of the stapes bone in the oval window. This produces a wave of transverse motion on the partition that propagates from base to apex. (b) A short longitudinal segment of the cochlear partition, showing the organ of Corti sitting on top of the BM. The BM is composed of flexible protein fibers that span the cochlear duct from spiral lamina to spiral ligament. The overlying TM has been partially removed to reveal the tops of the OHCs and the reticular lamina. The pillars of Corti comprise two cells (outer and inner) in a triangular arrangement (shown here schematically). The foot of the inner pillar cell sits on the spiral lamina edge of the BM. The pillar cells couple vertical motion of the BM to radial shearing motion between the reticular lamina and the TM. (c) A single cross-section of the 3-DOC model, illustrating how the solid structures of the cochlear partition are each divided into several discrete (mass) elements, coupled (visco-)elastically to each other. The mass elements are 10 μm square. In addition to its axial stiffness, each model OHC produces a force acting in antiphase between its bottom and top that is controlled by the bending of its stereociliary bundle. All of the mass elements are surrounded by an inviscid, linear, and incompressible fluid; except for the TM, the density of the mass elements is the same as that of the fluid.

The cochlear partition has three main components (Fig. 1b): the basilar membrane (BM), tectorial membrane (TM), and the organ of Corti. The organ of Corti contains two types of sensory hair cell: outer and inner. Both cell types perform mechanical-to-electrical transduction, converting motion of the BM into changes in cell membrane voltage, with the inner hair cells being primarily responsible for providing the higher auditory centers with information about BM motion. Outer hair cells (OHCs) possess the additional property of electrical-to-mechanical transduction, whereby the length of the cell is controlled by the voltage across its lateral membrane. This process, which has been observed in vitro in OHCs isolated from the cochlea (8, 9) and in situ in cochleae isolated from the animal (10, 11), is thought to provide the driving force for cochlear amplification in vivo. Although much is now known about the properties of this voltage-to-length interaction in vitro (12–14), the OHC is but one component of the cochlear amplifier. To understand how the motion of the BM is boosted in vivo, it is necessary to characterize the role played by each of the structures of the cochlear partition while taking into account loading by the fluids that surround them.

The aim of the work described in this paper was to compare the operation of the cochlear amplifier and its components in vitro, in situ, and in vivo by observing responses in a three-dimensional model of cochlear mechanics under different simulated experimental conditions. Two main investigations were performed on the model: (i) The effects of acetylcholine on OHCs in vitro were compared with those on the cochlear amplifier in vivo, and (ii) the motion of the organ of Corti that occurs during localized stimulation by the OHCs in situ was compared with that produced by normal stimulation via the stapes in vivo.

METHODS

The model used here, referred to throughout as the three-dimensional organ of Corti (3-DOC) model, is unique in two ways: (i) the organ of Corti (with overlying TM) is included in the simulations as a three-dimensional structure sitting on top of the BM, and (ii) this structure is embedded within the cochlear fluids. A complete description of the 3-DOC model, including details of its formulation, is available elsewhere (15). In brief, the model is built by using a three-dimensional finite difference formulation of discretized physical equations that describe the cochlea when it is divided into 10-μm sections along its length and 10-μm sections vertically and radially within the organ of Corti.

Within a single cross-section of the 3-DOC model, the solid structures of the cochlear partition are each divided into several discrete elements (Fig. 1c). These elements are connected together by either visco-elastic or elastic coupling, in either one or two dimensions. The two-dimensional coupling in the pillars of Corti, reticular lamina, and TM allows for the axial and transverse mechanical properties of these structures. The coupling in the pillars of Corti simulates realistically the rotation of the inner and outer pillars of Corti about the spiral lamina, with the radial motion at the top of the pillars relative to the BM vertical motion being determined by the ratio of pillar height to pillar width. All of the solid structures are surrounded by an inviscid, linear, and incompressible fluid, and fluid coupling along the length of the cochlea is included over the entire cross-section. The model is linear because it is intended to simulate the operation of the real cochlea near auditory threshold only: that is, where the effects of cochlear amplification are greatest. Furthermore, all stimuli to the model are sinusoidal, so that the formulation and analysis of the model matrix (rank ≈10⁶) is performed in the frequency domain. Stimulation is provided either by motion of the stapes or by localized excitation of a single row of OHCs situated some distance from the stapes.

The 3-DOC model is 30 mm long, 1 mm wide, and 0.5 mm high. The density of the fluids is 10³ kg/m³, and, with the exception of the TM, that of the solid structures is 1.3 × 10³ kg/m³; the height of the TM [40 μm (18)] is included by increasing the density of the TM mass elements by a factor of 4 (because the discretization is 10 μm). Except where stated otherwise, the structural parameters are the same for all of the responses shown here, and the values quoted are those for a 10-μm cross-section at the base of the model. The values for the cellular components are directly comparable with values of driving-point impedances measured experimentally because the cells are typically 10 μm in diameter. The values for the BM and TM correspond to experimentally measured values normalized to a deflection space constant of 10 μm. Appropriate adjustments are made to experimental data that are available only from parts of the cochlea distant from the base.

The BM stiffness halves every 2.5 mm away from the base; the stiffness of the other structures of the cochlear partition halves every 7.5 mm from the base. The BM point stiffness is 5 N/m (19), measured in the center of the BM, and its resistance is 1.4 × 10⁻⁶ Ns/m (to give the correct response in the absence of OHC motility). The TM is isotropic, with axial and transverse stiffness values of 0.05 N/m (18). The Deiters’ cell axial stiffness is 25 N/m (20), and that of the OHC is 0.01 N/m (14). The bending stiffness of the OHC stereociliary bundle is 0.1 N/m (21).

In addition to its axial stiffness, a real OHC produces a force acting in antiphase between its bottom and top (OHC “motility”) that is controlled by the membrane potential of the cell (8, 9). This potential is influenced by changes to the cell’s electrical conductance and by changes in the extracellular potentials surrounding the cell (16, 17); both are related directly to the displacement of the stereociliary bundle during relative motion between the reticular lamina and TM in the radial direction. The magnitude of normal motility of each model OHC (axial force vs. deflection of the bundle) is 330 pN/nm. This is somewhat higher than the maximum value measured in vitro (14, 22), but it may be that OHCs are adversely affected by the isolation process. The phase of OHC motility, expressed as the lag between a downward force on the Deiters’ cells relative to deflection of the OHC bundle in the inhibitory direction, is 135°. This is approximately equivalent to assuming that changes in OHC apical conductance—allowing for the 90° phase lag associated with the charging of the cell membrane capacitance—and extracellular potential modulate the cell membrane potential equally.

Fluid viscosity may affect behavior throughout the real cochlea, but it is most likely to be significant between structures having a small separation and the largest probability of opposing motion. For this reason, resistance is added to each stereociliary bundle to simulate fluid viscosity between the reticular lamina and TM. The value used (6 × 10⁻⁸ Ns/m) corresponds to a 5-μm separation between these structures. Because the pillars of Corti represent the triangular arrangement of the inner and outer pillar cells in the real cochlea, they are given axial and transverse stiffnesses equal to the axial stiffness of an individual pillar cell: 100 N/m (23). The axial stiffness of the model reticular lamina is also 100 N/m, equivalent to assuming that the cross-sectional area of microtubules in this structure—which is formed from projections from the outer pillar and Deiters’ cells—is similar to that of the pillar cells. The transverse stiffness of the model reticular lamina is large enough to ensure that the combined pillar cells/reticular lamina structure rotates as a single unit about the spiral lamina.

RESULTS

Response of the 3-DOC Model During Sound Stimulation to the Stapes.

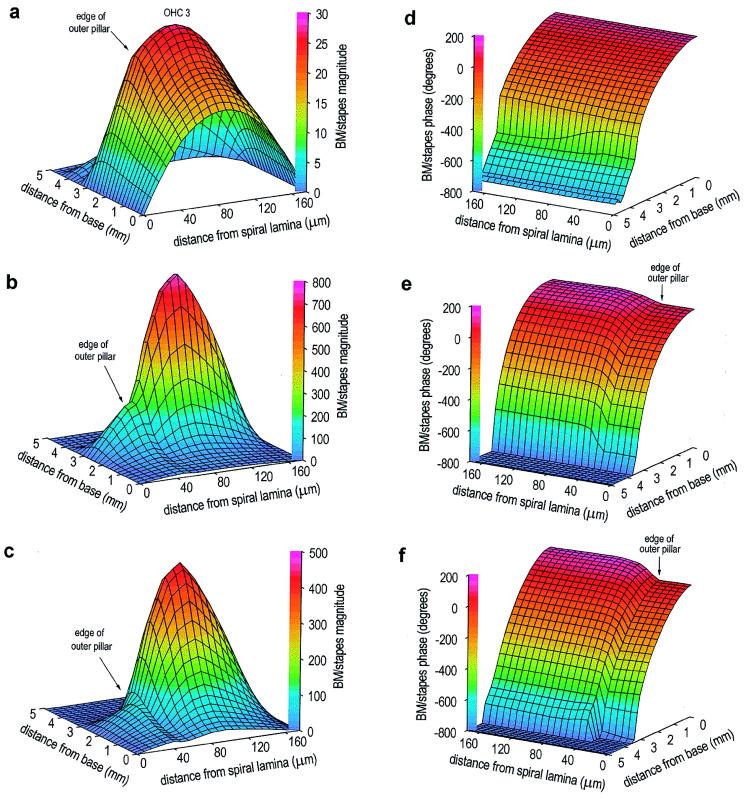
Fig. 2 shows the motion of the BM in the 3-DOC model during sound stimulation to the stapes (30 kHz) for three values of OHC motility: zero, normal (330 pN/nm), and enhanced (560 pN/nm). The presence of normal motility boosts the motion of the BM by up to 30 dB (Fig. 2b): maximally near the position of the motion peak obtained with no motility (Fig. 2a), and little change in motion near the base. This place-dependent increase in motion of the BM, driven by OHC motility, is the characteristic of the cochlear amplifier that serves to increase both the sensitivity and frequency selectivity of the mammalian auditory system; however, in the 3-DOC model, the changes induced by cochlear amplification (Fig. 2b vs. Fig. 2a) are slightly less pronounced than those seen in the best experimental preparations. In the presence of normal OHC motility in the model, the motion near the center of the BM (beneath the third row of OHCs) is four times greater than that beneath the edge of the outer pillar cells, producing a pronounced inflexion point in the radial profile (Fig. 2b). Beneath the pillar cells, the phase is constant at each position from the base (Fig. 2e), but the motion here differs from that beneath the OHCs by ≈90° (at the peak).

Figure 2.

Response of the model BM during sound stimulation to the stapes (30 kHz), for three values of OHC motility. All panels show BM motion vs. stapes motion, on a linear scale. (a) Magnitude, no OHC motility. Motion peak occurs 2.5 mm from the base of the cochlea; there is also a smaller, secondary peak 3.9 mm from the base. The rotation of the pillar cells as a single unit about the spiral lamina is indicated by the linear increase in motion to the edge of the outer pillar cells (40 μm from spiral lamina). (b) Magnitude, normal OHC motility (330 pN/nm). Motion peak occurs 3.0 mm from the base, and the secondary peak is no longer present. Motion at the center of the membrane at the peak is ≈30 dB greater than that with no OHC motility. Motion near the base is unchanged. At each position from the base, motion across the BM width is now asymmetric. (c) Magnitude, enhanced OHC motility (560 pN/nm). Motion peak occurs 2.6 mm from the base. BM motion is less than that observed with normal OHC motility. The largest change occurs beneath the pillar cells, producing an exaggerated inflexion point at the edge of the outer pillar cells. (d) Phase, no OHC motility. Monotonic accumulation of phase with distance from the base exceeds 360°, which indicates the presence of a travelling wave. (e) Phase, normal OHC motility. There is now a difference in BM phase across its width. (f) Phase, enhanced OHC motility. There is a slightly enhanced phase variation across the width of the BM.

The Effects of Acetylcholine.

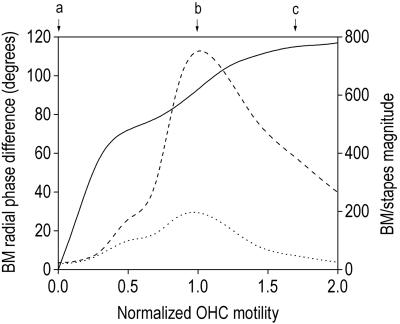
Tests of the cochlear efferent system performed in vivo, involving mass stimulation of the crossed olivo-cochlear bundle (the pathway providing efferent innervation to the OHCs) or total perfusion of the cochlea with acetylcholine (the putative efferent neurotransmitter), cause inhibition of the cochlear amplifier (24). Paradoxically, stimulation of the OHCs with acetylcholine in vitro (i.e., when the cells are isolated from the cochlea) enhances OHC motility (25). However, the behavior of the 3-DOC model is consistent with these observations: Increasing the motility by 70% (mirroring the in vitro measurements) reduces the gain of the cochlear amplifier significantly (Fig. 2c vs. Fig. 2b; Fig. 3). This unexpected result may be attributable to the forces associated with OHC motility acting in antiphase between the reticular lamina (and hence the BM beneath the pillar cells) and the BM beneath the OHCs. As OHC motility increases from zero in the 3-DOC model, the phase difference that develops between the motion in the two regions of the BM also increases (Fig. 2f vs. Fig. 2e; Fig. 3). When this phase difference—which influences the phase of the OHC feedback loop—exceeds 90°, the OHC forces exerted directly on the reticular lamina act to effectively reduce the stimulus to OHC motility, producing a reduction in the amplification of motion across the entire BM, but with a greater reduction beneath the pillar cells (Fig. 3). Note that this aspect of the behavior of the model is fundamentally different from a reduction in cochlear amplifier gain caused by saturation of OHC motility (which in any case would not be consistent with the excitatory effect of acetylcholine in vitro).

Figure 3.

Motion of the model BM at the position of the peak during sound stimulation to the stapes (30 kHz), as a function of OHC motility (normalized relative to the optimum value of 330 pN/nm). The solid line shows the phase difference between motion at the edge of the outer pillar cells and beneath row three of the OHCs. The magnitude of the motion at these two positions—relative to that of the stapes—is shown by the dotted and dashed lines, respectively. Letters at the top of graph indicate the motility values used for Fig. 2 a–c.

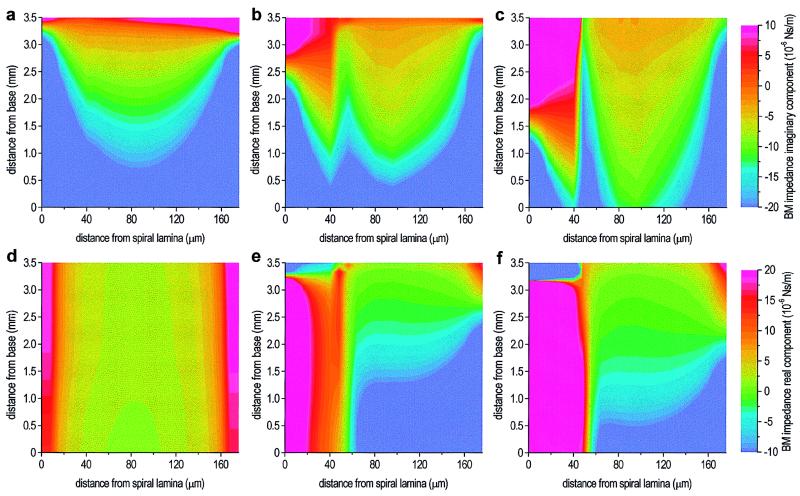
To investigate further the decrease in cochlear amplifier gain with enhanced OHC motility, it is helpful to study the effects of OHC motility on the effective impedance of the BM (Fig. 4). This impedance is calculated as the fluid pressure difference across the BM divided by the velocity of the BM. It reflects the inherent mechanical properties of the BM plus the forces acting on it by the solid structures of the organ of Corti and the TM and by fluid loading. The experimental determination of the effective BM impedance in vivo would require localized measurements of the liquid pressure differential and the BM velocity; the former is currently impossible within the organ of Corti.

Figure 4.

The real and imaginary components of the effective model BM impedance during sound stimulation to the stapes (30 kHz), for three values of OHC motility. (a) Imaginary component, no OHC motility. In basal regions, the imaginary component is stiffness-dominated (negative value), becoming mass-dominated (positive value) apical to the peak, indicating that true resonance occurs apical to the peak (because of the relatively large resistance). At each position from the base, the BM stiffness increases symmetrically to either side of a central minimum, consistent with simple stretching of the BM fibers because of a uniform hydrodynamic load. (b) Imaginary component, normal OHC motility. Small reduction in stiffness basal to the peak, and significant radial asymmetry. (c) Imaginary component, enhanced OHC motility. Further reduction in stiffness beneath the OHCs and pillar cells. Beneath the pillar cells, the position of resonance has moved significantly toward the base. (d) Real component, no OHC motility. The (positive) resistance value is approximately constant along the length of the model. (e) Real component, normal OHC motility. Dramatic changes in value basal to the peak, with a large increase beneath the pillar cells and negative values beneath the OHCs. (f) Real component, enhanced OHC motility. There is a further increase in resistance beneath the pillar cells, and the negative values beneath the OHCs are now smaller than those with normal motility.

The presence of normal OHC motility produces a small reduction in BM stiffness beneath the OHCs and pillar cells (Fig. 4b vs. Fig. 4a). However, the largest effect is on the effective BM resistance (Fig. 4e vs. Fig. 4d): The negative value beneath the OHCs basal to the peak is indicative of the addition of mechanical energy, and it is this that is responsible for the large increase in BM motion (Fig. 2b vs. Fig. 2a). The increase in the (positive) value of the real component beneath the pillar cells suppresses slightly the increase in motion here, resulting in the inflexion point that is evident in Fig. 2b. Enhanced motility causes further reductions in BM stiffness (Fig. 4c vs. Fig. 4b), and the region of negative resistance beneath the OHCs is reduced in size (Fig. 4f vs. Fig. 4e). This, combined with a further increase in resistance beneath the pillar cells, explains the reduction in the cochlear amplifier gain.

The effective BM impedance is consistent with the hypothesis that the paradoxical effects of acetylcholine are the result of antiphase coupling of OHC forces to the reticular lamina and the BM (via Deiters’ cells). This results in the addition of mechanical energy beneath the OHCs and an increase in resistance beneath the pillar cells. The relative importance of these effects changes with the amount of OHC motility, leading to the nonmonotonic relationship that exists between motility and cochlear amplifier gain.

Response of the 3-DOC Model During Localized Stimulation to Individual OHCs.

In experimental preparations that involve isolation of the cochlea from the animal, direct electrical stimulation of OHC motility results in forces that are sufficient to move the organ of Corti (10, 11). However, as in any mechanical system, the prevailing mechanics of the organ of Corti in such an in situ preparation will control the motion observed. It would therefore be helpful to know the extent to which the mechanics of the organ of Corti in situ reflect the mechanics of the intact cochlea in vivo.

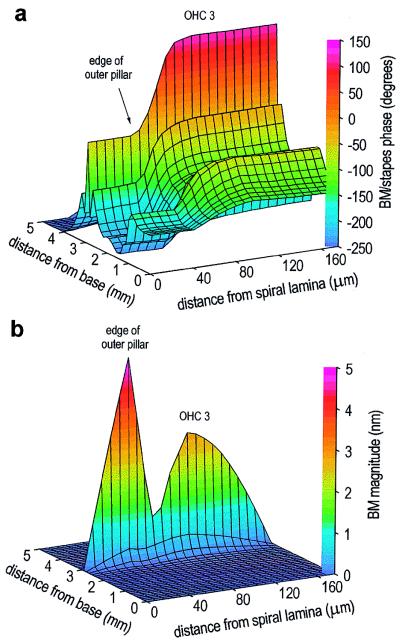
This is investigated in the 3-DOC model by locally stimulating (40 kHz, 50 pN) motility in the three OHCs located 3.0 mm from the base, in the absence of sound stimulation to the stapes (Fig. 5). Localized stimulation produces a phase difference of 180° between the motion of the BM beneath the pillar cells and that beneath the OHCs (Fig. 5a). This phase difference is associated with a minimum in the magnitude of BM motion between the outer pillar cells and the OHCs (Fig. 5b). The motion beneath the outer pillar cells is significantly greater than that beneath the third row of OHCs. The motion at the outer edge of the reticular lamina (and hence the TM), determined by the motion of the BM at the edge of the outer pillar cells transformed by the geometry of the organ of Corti, is more than three times greater than that at the center of the BM. These features of the response of the 3-DOC model during localized stimulation are all consistent with observations made during in situ experimental preparations. Comparison with the behavior of the model during normal sound stimulation to the stapes (Table 1) suggests that the mechanics of the organ of Corti are fundamentally different in situ and in vivo.

Figure 5.

Response of the model BM during localized stimulation (40 kHz, 50 pN) of motility in OHCs located 3.0 mm from the base (corresponding to the position of the motion peak during sound stimulation at 30 kHz; see Fig. 2b). Forward transduction in the OHCs throughout the model is switched on. (a) Phase. At the position of stimulation, the BM motions beneath the pillar cells and beneath the OHCs are in antiphase (i.e., a phase difference of 180°). (b) Magnitude. As during sound stimulation to the stapes, the pillar cells rotate as a rigid structural unit, but now the motion beneath the edge of the outer pillar cells is larger than at the center of BM, with a minimum occurring between these two regions.

Table 1.

Comparison of the behaviour of the 3-DOC model during localized and stapes stimulation

	Localized stimulation	Stapes stimulation
Relative magnitude of TM and BM motions	TM > BM	TM < BM
Relative phase of TM and BM motions	180°	90°
Effect of acetylcholine	Excitatory	Inhibitory

DISCUSSION

Previous models of cochlear mechanics have included multidimensional representations of the fluids that surround the cochlear partition (26). However, in these models, the micromechanical structure of the partition is simplified dramatically in the model’s formulation, usually by reducing the organ of Corti from a two-dimensional structure in each cross-section to either a line structure (in three-dimensional models) or a point structure (in one- and two-dimensional models). The modeller achieves this simplification by deducing the degrees of freedom and prescribing modes of vibration. However, a fundamental difficulty in cochlear mechanics is conceptualizing the dominant mechanics of the structurally complex three-dimensional cochlear partition; the lack of experimental data about motion within the organ of Corti makes it difficult to test the accuracy of the assumptions implicit in these simple models. Fig. 1c shows that, in each cross-section of the 3-DOC model, there are several dozen degrees of motional freedom. It is very unlikely that motion in the real cochlea would be truly independent in each of these positions, so that many of the model elements must be redundant. However, it is only after analysis of the model that it is possible to determine which they are. The preservation of a large number of potential degrees of freedom for motion within the 3-DOC organ bypasses the difficult procedure of surmising the dominant modes of vibration a priori.

The behavior of the 3-DOC model is remarkably insensitive to changes in the parameter values, an attractive attribute for any realistic model of a biological system and one that contrasts with many other cochlear models. In particular, the nonmonotonic effect of OHC motility on the total response demonstrates the attractive feature of natural selection for optimum gain. Basal to and at the peak, the radial motions of the TM and reticular lamina are approximately in antiphase because of the largely inertial load provided by the TM, which results from the low TM stiffness relative to that of the stereociliary bundles. Basal to the peak, the magnitude of TM radial motion is significantly smaller than that of the reticular lamina, so this phase relationship has little effect on the stimulus to the OHCs. However, very near the peak, the TM actually moves more than the reticular lamina. This motion of the TM reveals itself at the level of the BM as a secondary maximum just apical to the peak (Fig. 2a) and is consistent with the hypothesis that the TM contributes mass- rather than stiffness-loading to the cochlear partition (27–29). The 3-DOC model appears to confirm two other aspects of this hypothesis: The secondary maximum is most noticeable in the absence of OHC motility, and viscous damping in the subtectorial space is not sufficient to suppress this secondary maximum.

Preliminary investigations suggest that the parameters that most influence the overall response of the 3-DOC model are the stiffness of the stereociliary bundle and the properties of the TM. It is tempting to suggest that changes to these components explain the vulnerability of the real cochlear amplifier to surgical trauma. However, in its present form, the 3-DOC model is unlikely to provide the definitive description of the cochlear amplifier; the model will undoubtedly need refinement and modification as more data on both the structural parameters and motion within the organ of Corti become available. Nevertheless, the model does provide explanations for apparently paradoxical experimental observations, which suggests that the sort of complex approach adopted here can reveal effects that are not covered by, and hence would never be detected in, simpler representations of the real cochlea.

ABBREVIATIONS

BM

basilar membrane

TM

tectorial membrane, OHC, outer hair cell

3-DOC

three-dimensional organ of Corti