Current-dependent Block of Rabbit Sino-Atrial Node I_f Channels by Ivabradine

Abstract

“Funny” (f-) channels have a key role in generation of spontaneous activity of pacemaker cells and mediate autonomic control of cardiac rate; f-channels and the related neuronal h-channels are composed of hyperpolarization-activated, cyclic nucleotide–gated (HCN) channel subunits. We have investigated the block of f-channels of rabbit cardiac sino-atrial node cells by ivabradine, a novel heart rate-reducing agent. Ivabradine is an open-channel blocker; however, block is exerted preferentially when channels deactivate on depolarization, and is relieved by long hyperpolarizing steps. These features give rise to use-dependent behavior. In this, the action of ivabradine on f-channels is similar to that reported of other rate-reducing agents such as UL-FS49 and ZD7288. However, other features of ivabradine-induced block are peculiar and do not comply with the hypothesis that the voltage-dependence of block is entirely attributable to either the sensitivity of ivabradine-charged molecules to the electrical field in the channel pore, or to differential affinity to different channel states, as has been proposed for UL-FS49 (DiFrancesco, D. 1994. Pflugers Arch. 427:64–70) and ZD7288 (Shin, S.K., B.S. Rotheberg, and G. Yellen. 2001. J. Gen. Physiol. 117:91–101), respectively. Experiments where current flows through channels is modified without changing membrane voltage reveal that the ivabradine block depends on the current driving force, rather than voltage alone, a feature typical of block induced in inwardly rectifying K⁺ channels by intracellular cations. Bound drug molecules do not detach from the binding site in the absence of inward current through channels, even if channels are open and the drug is therefore not “trapped” by closed gates. Our data suggest that permeation through f-channel pores occurs according to a multiion, single-file mechanism, and that block/unblock by ivabradine is coupled to ionic flow. The use-dependence resulting from specific features of I_f block by ivabradine amplifies its rate-reducing ability at high spontaneous rates and may be useful to clinical applications.

INTRODUCTION

The “funny” current, or “pacemaker” (I_f) current, was first described in cardiac pacemaker cells of the mammalian sino-atrial node (SAN)* as a current slowly activating on hyperpolarization at voltages in the diastolic depolarization range, and contributing essentially to generation of cardiac rhythmic activity and its control by sympathetic innervation (Brown et al., 1979; Brown and DiFrancesco, 1980; Yanagihara and Irisawa, 1980). A pacemaker current had been described previously in another cardiac preparation able to pace spontaneously, the Purkinje fiber, where it had been erroneously interpreted as a pure K⁺ current (current I_K2: Noble and Tsien, 1968). Soon after the discovery of I_f, a reinterpretation of the nature of I_K2 led to the demonstration that in this preparation, too, the pacemaker current was the same as in the SAN (DiFrancesco, 1981a,b). I_f-type hyperpolarization-activated currents were subsequently described in other cardiac regions and in a variety of neuronal cells (for reviews see DiFrancesco, 1993; Pape, 1996).

Further investigation in SAN and other types of cells revealed the specific properties of I_f. I_f is a current carried by both Na⁺ and K⁺, inward in the pacemaker range of voltages, activated on hyperpolarization from a threshold of about −40/−50 mV and fully activated at about −100/−110 mV (DiFrancesco, 1981b; DiFrancesco et al., 1986). f-channels are modulated by intracellular cAMP by an action involving direct cAMP binding to channel proteins and not mediated by a phosphorylation mechanism (DiFrancesco and Tortora, 1991), although phosphorylation-dependent processes may also be operating to modulate I_f at a different site (Chang et al., 1991; Accili et al., 1997).

In heart, neurotransmitter-induced control of cardiac rhythm is mediated by I_f through its second-messenger cAMP, whose synthesis is stimulated and inhibited by β-agonists and muscarinic agonists, respectively (DiFrancesco et al., 1986; DiFrancesco and Tromba, 1988a,b). Moderate vagal activity, such as the one present during basal vagal tone, controls cardiac rate by modulation of I_f, rather than by the opening of ACh-activated K⁺ channels (DiFrancesco et al., 1989).

Ionic, kinetic, and modulatory properties of the I_h current (the neuronal equivalent of the cardiac I_f) are similar to those of I_f (Pape, 1996). The physiological function of I_h depends on the cell type where the current is expressed and is based on its ability to generate a depolarization following an appropriate stimulus: a neurotransmitter-mediated input able to modify the intracellular cAMP content, or membrane hyperpolarization.

The neuronal I_h current contributes to controlling the resting potential, and hence modulating excitability, of several types of neurons, such as CA1 hippocampal neurons, DRG neurons, and cerebellar neurons (Maccaferri et al., 1993; Magee, 1998; Cardenas et al., 1999; Southan et al., 2000). In neurons where repetitive activity is present, I_h can contribute, like I_f does in cardiac pacemaker, to the firing discharge (McCormick and Pape, 1990; Kamondi and Reiner, 1991; Golowasch and Marder, 1992; Maccaferri and McBain, 1996; Thoby-Brisson et al., 2000). Several types of sensory neurons express h-channels, which may be involved either in the direct perception of external stimuli, or in modulating the transduction of sensory stimuli into electrical signals (Demontis et al., 1999; Vargas and Lucero, 1999; Stevens et al., 2001). Recently, h-channels have been involved in neuronal plasticity by their action at presynaptic membranes (Beaumont and Zucker, 2000; Mellor et al., 2002).

A significant advancement in the study of the molecular properties of pacemaker channels has been obtained with the cloning of a new family of channels (hyperpolarization-activated, cyclic nucleotide gated [HCN] family: Gauss et al., 1998; Ludwig et al., 1998; Santoro et al., 1998; Vaccari et al., 1999). HCN channels have a structure similar to that of K⁺ voltage–dependent (Kv) and cyclic nucleotide–gated (CNG) channels: six transmembrane domains with an S4 segment rich in positively charged residues, which in analogy to Kv channels may act as a voltage-sensitive element, a “pore” region between S5 and S6, and a consensus sequence for binding of cyclic nucleotides at the COOH terminus. The electrophysiological properties of HCN channels expressed heterologously clearly indicate that they are the molecular determinants of native pacemaker channels in the heart and nervous system (Gauss et al., 1998; Ludwig et al., 1998, 1999; Santoro et al., 1998; Ishii et al., 1999; Vaccari et al., 1999; Moroni et al., 2000).

The relevance of I_f in the control of heart rate makes it an important pharmacological target. Several f-channel blocker molecules have been developed, such as UL-FS49 (Goethals et al., 1993; DiFrancesco, 1994), ZD7288 (BoSmith et al., 1993; Gasparini and DiFrancesco, 1997; Shin et al., 2001), and ivabradine (Thollon et al., 1994; Bois et al., 1996). These molecules have been shown to induce heart rate slowing with limited inotropic side effects, and have therefore a potential for therapeutic application in those cases where it is useful to slow heart rate without altering other cardiovascular functions. A typical example is the treatment of angina pectoris or other clinical forms of myocardial ischemia, where cardiac rate slowing is beneficial since it decreases the oxygen requirement by cardiac muscle and thus reduces the risk of ischemic insult, but other modes of employment are possible. This underlines the significance of developing new drugs specifically interacting with pacemaker channels.

In this paper we have investigated the action of ivabradine on native f-channels in rabbit SAN cells. A previous study has shown that ivabradine acts with a high degree of specificity on f-channels from the intracellular side of the membrane (Bois et al., 1996). We find that ivabradine blocks f-channels when they are open, and its block is strongly use-dependent. The block is exerted preferentially when the current deactivates on depolarization, and is relieved when it activates on hyperpolarization.

Experiments where the current flow across f-channels is varied at a constant voltage (by use of Cs⁺, an extracellular I_f blocker, or of a low-Na⁺ extracellular solution) reveal that block depends on the current driving force, rather than simply on voltage. The block by ivabradine is similar to that exerted by intracellular cations on inwardly-rectifying K⁺ channels, and reveals that permeation across f-channels occurs as in multiion, single-file pores.

MATERIALS AND METHODS

The experiments performed in this work conformed with the guidelines of the care and use of laboratory animals established by Italian State (D.L. 116/1992) and European directives (86/609/CEE).

A description of the methods used to obtain and voltage-clamp isolated SAN cells has been published elsewhere (DiFrancesco et al., 1986; Accili et al., 1997). Briefly, New Zealand female rabbits (0.8–1.2 Kg) were anesthetized by intramuscular injection of 4.6 mg Kg⁻¹ xylazine and 60 mg Kg⁻¹ ketamine and killed by cervical dislocation. After full exanguination the heart was quickly removed and placed in prewarmed (37°C) Tyrode solution (in mM: NaCl, 140; KCl, 5.4; CaCl₂, 1.8; MgCl₂, 1; D-glucose, 5.5; HEPES-NaOH, 5; pH 7.4) containing 1,000 U heparin. SAN tissue was then surgically isolated and cut into 5–6 stripes, and the enzymatic cell dissociation procedure was performed. Collagenase (224 U ml⁻¹, Worthington), Elastase (1.9 U ml⁻¹, Sigma-Aldrich), and Protease (0.6 U ml⁻¹, Sigma-Aldrich) were used to degrade intercellular matrix and loosen cell-to-cell adhesion in order to ease the mechanical cell dispersion procedure. Isolated single cells were maintained at 4°C in Tyrode solution for the day of the experiment. Cells under study were allowed to settle into plastic Petri dishes on the stage of an inverted microscope, and were perfused with Tyrode solution to which BaCl₂ (1 mM), MnCl₂ (2 mM), and, when required, 4-aminopiridine (5 mM) were added to ameliorate I_f dissection over other ionic components. Control and test solutions were delivered by a fast-perfusion temperature-controlled device allowing rapid solution changes.

Whole-cell pipettes were filled with an intracellular-like solution containing (in mM): K-Aspartate, 130; NaCl, 10; EGTA-KOH, 5; CaCl₂, 2; MgCl₂, 2; ATP (Na-salt), 2; creatine phosphate, 5; GTP (Na-salt), 0.1; pH 7.2. In low (35 mM) Na⁺ solution, Na⁺ was replaced by an equimolar amount of choline chloride. Ivabradine (3-(3-{[((7S)-3,4-dimethoxybicyclo [4,2,0] octa-1,3,5-trien7-yl) methyl] methylamino} propyl)-1,3,4,5-tetrahydro-7,8-dimethoxy-2H-3-benzazepin-2-one hydrochloride; Fig. 1 A) was added to the extracellular solution by dissolving a stock solution (0.1–10 mM) to the final concentration desired. The drug was provided by the Institut de Recherches Internationales Servier, France. All experiments were performed at the controlled temperature of 32 ± 0.5°C. Currents were recorded and on-line filtered at a corner frequency of 1 KHz with an Axopatch 200B amplifier, and acquired using the pClamp 7.0 software (Axon Instruments, Inc.).

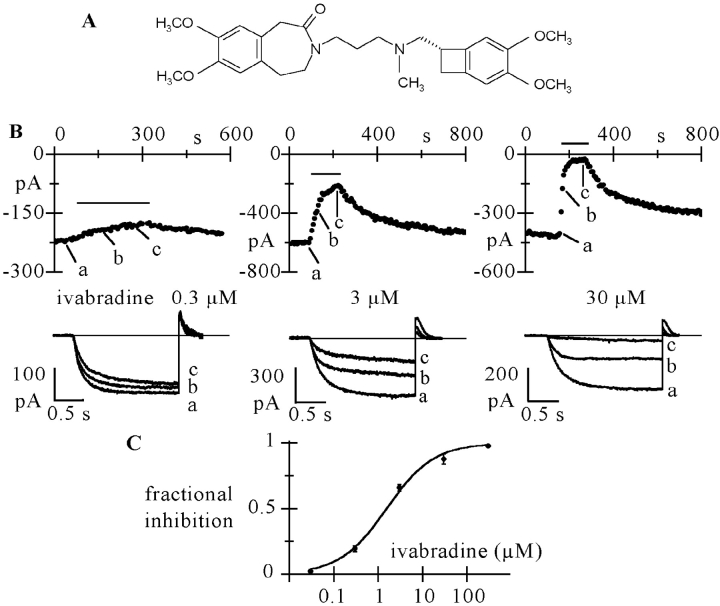
Figure 1.

Ivabradine blocks I_f. (A) Structure of ivabradine. (B) Activating/deactivating steps (−100 mV*1.8 s/+5 mV*0.45 s) were applied every 6 s from a holding potential of −35 mV, and a given concentration of ivabradine perfused until full block developed. The time-course of I_f amplitude at −100 mV during block onset and removal is shown for three cells challenged with 0.3 (left), 3 (middle) and 30 μM ivabradine (right). Lower panels show current traces recorded just before and during block development (a to c). Zero current level drawn as a full line. C: dose–response relationship of I_f block by ivabradine from a total of n = 32 cells (mean ± SEM). Each cell was exposed to one drug dose only. Mean data points were fitted to the Hill equation y = 1/(1 + (IC₅₀/x)^h) where x is drug concentration, IC₅₀ the half-block concentration and h the Hill factor (full line: best fitting values in text).

RESULTS

Superfusion of SAN cells with ivabradine caused a reduction of whole-cell I_f current which accumulated in a concentration-dependent way during repetitive trains of activating/deactivating voltage steps (−100/+5 mV), until steady-state block was reached. Typical time courses of block onset and recovery and sample traces are shown for three different concentrations (0.3, 3, and 30 μM) in Fig. 1 B.

We obtained a mean steady-state current block of 19.5 ± 2.2% (n = 3), 65.9 ± 2.4% (n = 19), 87.8 ± 4.0% (n = 4); a time constant of block development (τ_on) of 90.2 ± 2.2 s (n = 3), 61.5 ± 2.7 s (n = 21), and 13.2 ± 0.7 s (n = 4); and a time constant of block recovery (τ_off) of 159.4 ± 17.9 s (n = 3), 136.2 ± 16.2 s (n = 6), and 178.5 ± 39.8 s (n = 3) for 0.3, 3, and 30 μM ivabradine, respectively. Full current recovery following wash-off of the drug was apparently not achieved in the experiments shown in Fig. 1. However, due to its slow time course, recovery could be underestimated by the possible presence of current run-down, which occurs on a similar time scale (DiFrancesco et al., 1986).

A dose–response relation of the current block was obtained using the same voltage protocol for a wider range of drug concentrations (Fig. 1 C). Fitting the dose–response curve with the Hill equation yielded a half-block concentration of 1.5 μM and a slope coefficient of 0.8. The concentration dependence of I_f block was similar to that reported previously by Bois et al. (1996).

Experiments such as those in Fig. 1 indicate the presence of accumulation of inhibition during repetitive steps, a property that could reflect either relatively slow kinetics of drug-channel interaction, or that the f-channel block by ivabradine is use-dependent. To further investigate this aspect, in Fig. 2 we tried to establish whether the drug binds to f-channel closed and open configurations with different affinities. An I_f activation/deactivation protocol (same as in Fig. 1) was first applied; when perfusion with ivabradine started, the repetitive protocol was interrupted and the membrane voltage held for 100 s at −35 mV, where f-channels are closed.

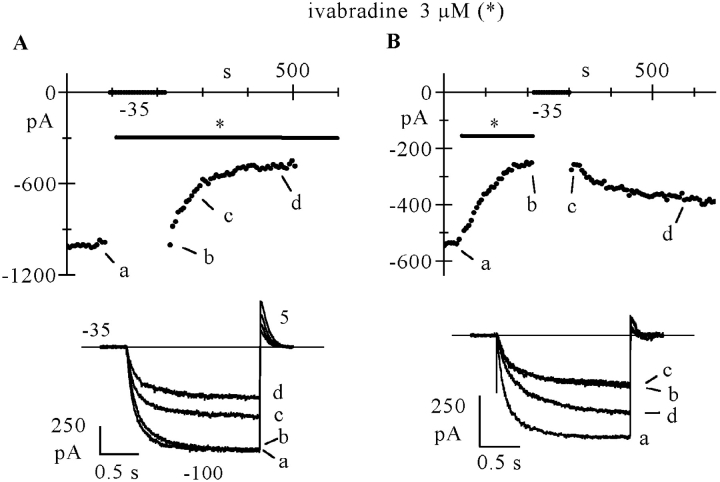
Figure 2.

I_f block by ivabradine and block removal require open channels. (A) Time-course of I_f amplitude at −100 mV during an activation/deactivation protocol (−100/+5 mV, 1/6 Hz) from a holding potential of −35 mV. At the beginning of the perfusion with ivabradine (3 μM), the protocol was interrupted for 100 s while the cell was held at the holding potential. During this time no current reduction was observed. (B) In another cell, the same protocol was applied in the presence of the drug (3 μM) until full block developed. The protocol was interrupted and the cell held at −35 mV for 90 s while simultaneously removing the drug from the perfusing solution. During this time, no reversal of current inhibition occurred. Sample traces shown in the bottom panels were recorded at various times as indicated.

Fig. 2 A, top, shows the time course of the I_f amplitude at −100 mV; sample current traces recorded at various times (a–d, as indicated) are plotted in the lower panel. Ivabradine (3 μM) did not show appreciable affinity for the closed conformation of f-channels since the current amplitude at −100 mV just after resuming the pulsing protocol was not decreased by the long exposure to the drug at −35 mV. As expected, reapplication of activating/deactivating steps in the presence of the drug caused the current to decrease with a time course similar to that in Fig. 1 (τ_on = 51.9 s; fractional steady-state block = 0.513). Similar results were obtained in n = 4 cells, where the current size during the first step to −100 mV after the rest period at –35 mV (for 66–120 s) was 99.2 ± 1.3% of the control size. These data indicate that channel opening is a necessary requirement for ivabradine-induced block to occur.

Further, we checked if channel unblocking takes place when f-channels are in the closed configuration (Fig. 2 B). Following full block elicited by a standard activation/deactivation protocol, the membrane was held at −35 mV while the drug was washed off. After 90 s at −35 mV, the repetitive protocol was resumed and, as apparent from Fig. 2 B, the current amplitude was the same as at the end of the blocking protocol, indicating that no block reduction had occurred while clamping at −35 mV. Removal of block then proceeded normally (τ_off = 94.8 s). Similar data were obtained in n = 3 cells, where the current size during the first step following the rest period (84 to 144 s) was 101.2 ± 3.0% of the control size.

The results of Fig. 2 argue in favor of the hypothesis that binding/unbinding reactions are limited to the open state. This can be interpreted by assuming that the drug can only access the blocking site while the channel is open. It is noteworthy that a “trapping” mechanism has been proposed for HCN channel block by another molecule (ZD7288), on the basis of experiments suggesting the existence of a wide intracellular channel vestibule which is normally inaccessible when the channel is closed and able to confine the drug molecule upon closing (Shin et al., 2001).

As well as a dependence on the open/closed state of f-channels, block due to molecules such as UL-FS49 and ZD7288 also displays a voltage dependence, with hyperpolarization favoring the unblocking process (DiFrancesco, 1994; Shin et al., 2001).

To study the voltage dependence of the action of ivabradine on I_f, in view of the requirement of open channels for block to occur, we first investigated steady-state block at voltages negative to the activation threshold, where f-channels are open at least part of the time, by applying long activating steps. We found that the block exerted by the drug using this protocol was much smaller than that observed with activating/deactivating protocols (as in Figs. 1 and 2) with the same hyperpolarizing step. A comparison between the two different protocols is shown in Fig. 3. On the left (Fig. 3 A), 3 μM ivabradine applied during activation/deactivation protocols (−70/+5 mV, upper; −100/+5 mV, lower) caused a current reduction of 78.3% at −70 mV and 63.9% at −100 mV (compare control records with full-block records labeled by asterisks). These data are in accordance with the results in Fig. 1. Panels on the right (Fig. 3 B), on the other hand, refer to experiments where steps of several tens of seconds were applied to −70 (upper) and −100 mV (lower), and the drug applied after the current had reached steady-state activation. The current decrease with the latter protocol was much smaller (14.0% at −70 mV and 6.0% at −100 mV). The mean I_f block was 12.4 ± 1.9% at −70 mV (n = 4) and 6.4 ± 1.6% at −100 mV (n = 5) with the long-step protocols, as compared with the values of 77.4 ± 5.7% at −70 mV (n = 4) and 65.9 ± 2.4% at −100 mV (n = 19, as reported above) resulting from activating/deactivating protocols.

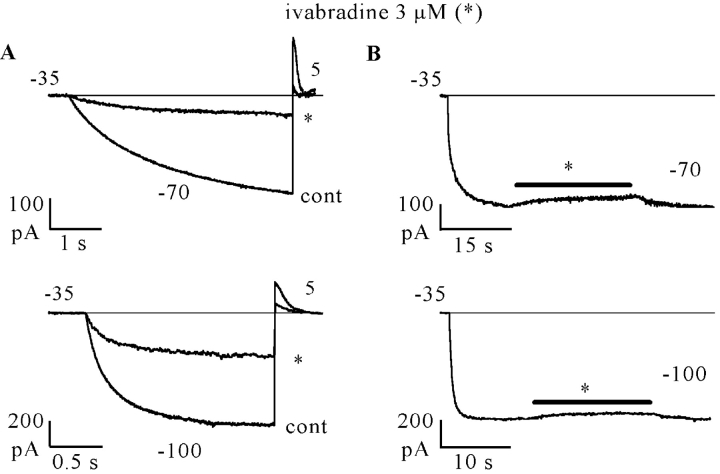
Figure 3.

I_f block by ivabradine depends on the voltage protocol used to activate the current. (A) I_f in control (cont) and after full block by ivabradine (3 μM, asterisks) induced by activation/deactivation protocols at −70 mV (top) and −100 mV (bottom) in two cells. (B) Action of the same drug concentration when applied during steady-state I_f activation at −70 mV (top) or −100 mV (bottom) in two cells.

These large differences indicate that the binding reaction is strongly affected by voltage, and by the actual voltage protocol used. The use of long-step protocols shows that the steady-state blocking action of the drug at hyperpolarized voltages is modest, and suggests that most of the drug action observed with activating/deactivating protocols as in Figs. 1, 2, and 3 A is not exerted during the hyperpolarizing step, but during the decay tail at 5 mV, when the channels are open and the membrane depolarized. According to this hypothesis, while on the one hand the channels need to be open for block to occur, on the other the block occurs mostly during current deactivation and is relieved during current activation.

To verify the presence of hyperpolarization-induced block relief, we used the analysis shown in Fig. 4. A standard activation/deactivation protocol was first applied and the drug (3 μM) was perfused until steady-state block developed. On the left side of Fig. 4 A the control trace and traces recorded after 30, 60, and 174 s (corresponding to steady-state block) of drug perfusion are plotted in sequence. Once steady-state block was achieved, while still in the presence of the drug, a long (40 s) step to –100 mV was applied, during which the current underwent a gradual, slow increase with time toward levels approaching that in control conditions. A double exponential fit of the current during the 40-s long step (Fig. 4 B) clearly revealed the presence of two kinetically distinct processes. Although the early part of current activation developed with a time constant of 235 ms, a value similar to that in control conditions (259 ms), the late one increased with a much slower time constant of 7.5 s; this second process did not therefore reflect normal activation kinetics, but rather removal of block possibly associated with unbinding of the drug. Resuming the activation/deactivation protocol reestablished the previous current block, as apparent from the set of current traces recorded every 30 s after the long step to −100 mV (right side of Fig. 4 A).

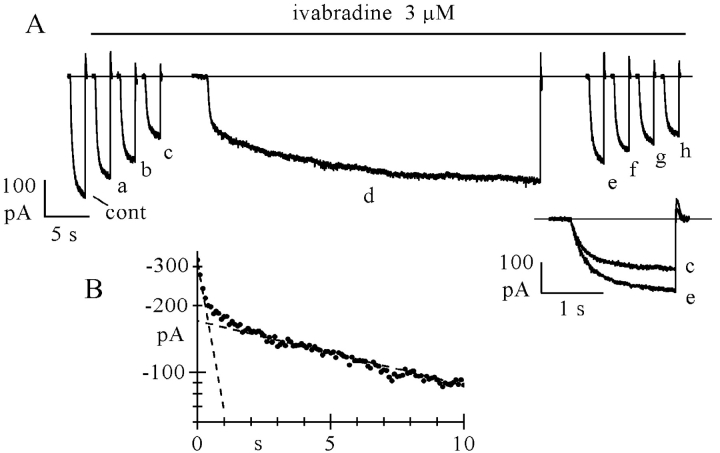
Figure 4.

Hyperpolarization favors removal of block. A long (40 s) hyperpolarizing step to −100 mV was preceded and followed by a repetitive activation/deactivation protocol (−100/+5 mV) during perfusion with ivabradine (3 μM). (A) Left to right: current traces recorded in control (cont) and 30 (a), 60 (b), and 174 s (c) after switching on of drug perfusion; current record during the 40 s step (d); current traces recorded just after termination of the 40 s step (e) and 30 (f), 60 (g), and 90 s later (h). Note that I_f increased slowly during the long −100 mV step; the inset shows a superimposition of traces c and e. (B) Semilog plot of the first 10 s of the long step record; fitting with the sum of two exponentials (broken lines) yielded a fast and a slow component (time constant values in text).

In n = 6 cells, the mean time constants of current activation at −100 mV in control, in the early fraction of >25-s long steps to –100 mV during drug perfusion (3 μM), and on return from the long-step protocol were: 215 ± 15, 237 ± 28, and 213 ± 14 ms, respectively, whereas the slow increase at −100 mV had a time constant of 7.0 ± 0.5 s. These data indicate that ivabradine, as has been proposed for UL-FS49 and ZD7288 (Goethals et al., 1993; DiFrancesco, 1994; Shin et al., 2001), binds to the channel blocking site less favorably at hyperpolarized than at depolarized voltages.

We next proceeded to quantify the degree of block in a fuller range of activation/deactivation voltages by measuring the current decrease caused by 3 μM ivabradine at steady-state in the range −110 to 20 mV. At voltages below threshold (more negative than −40 mV), we applied long steps to the test voltage to activate the current at steady-state and then applied the drug until block developed fully, as in Fig. 3 B; in Fig. 5, mean fractional block values thus obtained are plotted as open circles.

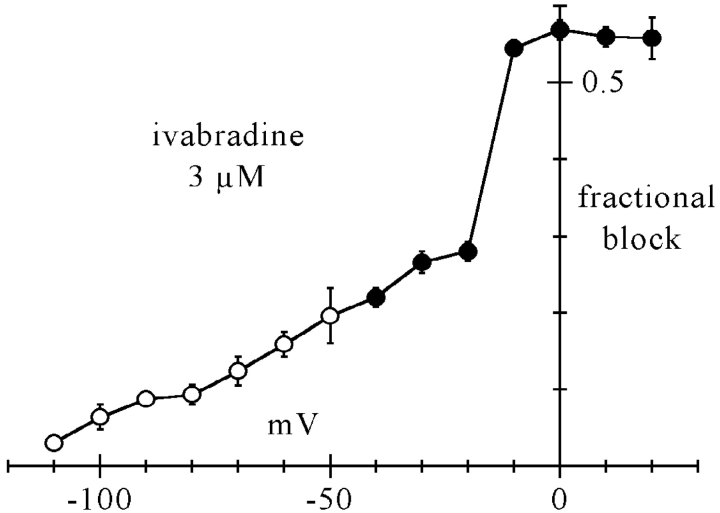
Figure 5.

Voltage dependence of steady-state f-channel block by 3 μM ivabradine. Measurements were made by two protocols. At voltages more negative than −40 mV (open circles) I_f was activated by long steps to test potentials and the drug perfused after steady-state activation had been reached; fractional block was measured as the ratio between blocked and control current amplitude. At voltages equal or more positive than −40 mV (filled circles), the membrane was held at the test voltage and a fixed activating voltage step (−100 mV*1.2 s) was applied repetitively (1/6 Hz); the drug was perfused during this protocol and fractional block measured for each test voltage as the ratio between blocked and control current at −100 mV at steady-state. Each point represents the mean ± SEM from 3–5 cells.

In agreement with the observation in Fig. 4 that hyperpolarization removes block, the fraction of blocked current decreased at more negative voltages; at −100 mV the blocked fraction was small (6.4 ± 1.6%). We took advantage of these features to measure the fractional block at voltages above threshold. We held the membrane at a variable test potential (−40 to 20 mV) and applied repetitive (1/6 Hz) steps to −100 mV for 1.2 s; since at −100 mV little block occurs, and block removal requires relatively long times (mean time constant of 7.0 s, see above), we can assume that the block obtained with this protocol develops essentially entirely during deactivation at the test voltage. The mean fractional current block values measured by these protocols are also plotted in Fig. 5 as filled circles.

Like ivabradine, other I_f-blocking molecules such as UL-FS49 and ZD7288 have been reported to cause a voltage-dependent block whose efficiency increases at more positive potentials (DiFrancesco, 1994; Shin et al., 2001). However, the action of ivabradine is peculiar in that a relatively sharp change of fractional block appears when going from voltages where the current is just inward (i.e., −20 mV) to voltages where the current is just outward (i.e., −10 mV); the block at deactivating voltages then seems to level up to a constant value of ∼0.56. This behavior differs from that of a purely voltage-dependent block mechanism, such as those attributable to charged molecules entering the pore for a fraction of the membrane voltage drop (Hille, 2000), according to which the current inhibition would be expected to increase smoothly at more depolarized potentials up to full block. The observation of a steep change in the degree of block across the expected current reversal potential led us to hypothesize that the direction of current flow could be a determinant of block.

To test this hypothesis, we searched for conditions able to discriminate between the efficiency of ivabradine blocking action in the presence and absence of current flow. One way to obtain this was to use Cs⁺, which is a known extracellular blocker of I_f. Cs⁺ ions block f-channels in a voltage-dependent way, by entering channels from outside for a fraction (∼71%) of the membrane electric field on hyperpolarization (DiFrancesco, 1982). Although Cs⁺ blocks the current flow, it does not affect channel opening/closing, as shown for example by envelope tests used to verify the time course of channel opening (by application of hyperpolarizing steps of variable duration and a fixed depolarizing step where tail currents are measured) in the presence of Cs⁺ (DiFrancesco, 1982). Thus, in the presence of Cs⁺, channels enter their open state normally on hyperpolarization, but no (or little) current is carried across the membrane.

In Fig. 6, we applied a protocol similar to that in Fig. 4, but added 5 mM Cs⁺ to the perfusate during the prolonged (45 s) hyperpolarization to −100 mV, following steady-state block by 3 μM ivabradine achieved by a standard activation/deactivation protocol (−100/+5 mV: sample traces representing control [cont], mid [a], and full block [b] are shown on the left side). As expected, during perfusion with Cs⁺ the current was strongly reduced. At the end of the long hyperpolarizing step, Cs⁺ was washed out and the repetitive –100/+5 mV protocol resumed in the continuous presence of the drug. As apparent from the traces on the right side of Fig. 6, the current elicited by the first step to −100 mV following Cs⁺ perfusion had not recovered toward the control amplitude, but had kept the amplitude after full ivabradine block (compare trace d with trace b in the inset).

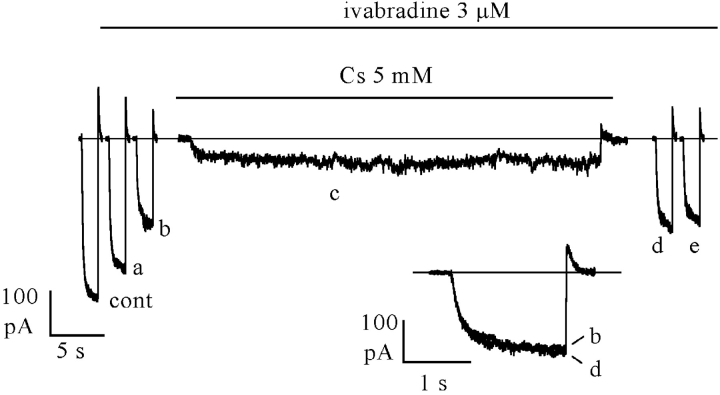
Figure 6.

Inward current is required to relieve channel block by ivabradine. I_f block by 3 μM ivabradine was induced by a standard activation/deactivation protocol (−100/+5 mV); sample traces are shown on the left (cont, control; a, 30 s; and b, 120 s after drug perfusion; the latter corresponding to steady-state block). In the continuous presence of the drug, a prolonged (45 s) step to −100 mV was then applied while simultaneously adding 5 mM Cs⁺ (c); Cs⁺ was washed off at the end of the long step and the repetitive pulsing protocol resumed (traces d, 6 s and e, 36 s after Cs⁺ wash-out). Note that no block removal occurred during the prolonged hyperpolarization (compare records b and d in the inset).

The protocol was repeated in the same cell in the absence of Cs⁺, under which conditions block removal was normally observed during the prolonged step to −100 mV, as in Fig. 4 (unpublished data). In n = 5 cells where the protocol of Fig. 6 was applied, the size of the current recorded after steady-state block by ivabradine (3 μM) and after a long step in the presence of Cs⁺ (trace d) was essentially identical (101.4 ± 2.9%) to that preceding Cs⁺ perfusion (trace c). In n = 10 cells, the current increased up to 137.9 ± 3.7% of the control value with the same protocol in the absence of Cs⁺ (see Fig. 4). These data illustrate a remarkable difference between the actions of ivabradine and of another I_f blocker, UL-FS49 (DiFrancesco, 1994), and suggest that voltage hyperpolarization alone is not sufficient to remove block of open f-channels by ivabradine.

The most economical interpretation of the Cs⁺ result is that relief of ivabradine block involves a current-dependent “kick-off” mechanism, similar to that operating in channels with multiion, single-file pores when a blocking ion is present (Hille, 2000). However, since the possibility could not be excluded that Cs⁺-bound f-channels, although open, have a modified affinity for ivabradine, we investigated the action on ivabradine block of changes in the current flow caused by changes in the chemical gradient, rather than in membrane voltage.

In Fig. 7, the fractional block curve measured in the control Tyrode solution, as replotted from Fig. 5 (filled circles), is compared with that obtained with similar protocols in a low (35 mM) Na⁺ solution (open circles). The low Na⁺ curve still displays a region of steep slope and has an overall voltage-dependence similar to the curve in Tyrode, but is shifted to more negative voltages. The shift is such as to determine a large difference of blocking degrees between the two curves at intermediate voltages. For example, at −30 mV, the fractional block was 0.266 ± 0.014 in normal Na⁺, and 0.607 ± 0.016 in the low Na⁺ solution (see inset current traces).

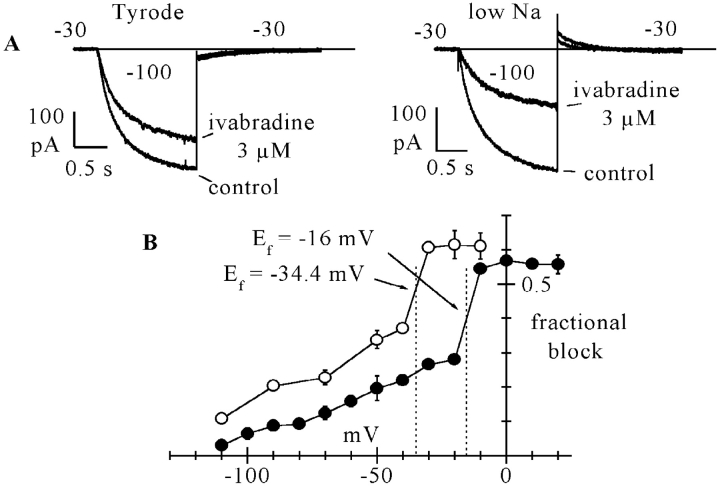
Figure 7.

Dependence of the ivabradine-induced I_f block by the current driving force. (A) Sample I_f traces from two cells showing the different degrees of steady-state block induced by 3 μM ivabradine at the same test potential of −30 mV with normal (140 mM, left) and reduced (35 mM, right) external Na⁺ concentration, as measured by activation/deactivation protocols (−100/−30 mV). Fractional block was ∼24% in normal and 54% in reduced Na⁺ concentration. Notice that at −30 mV, as expected, the deactivating I_f tail was inward in normal Na⁺, and outward in reduced Na⁺ conditions. (B) Comparison between mean fractional block curve in normal Tyrode solution (filled circles, as from Fig. 5) and in lowered Na⁺ (open circles). Each point of the curve in low Na⁺ represents the mean ± SEM from 3–6 cells. Vertical dotted lines correspond to the I_f reversal potentials measured from mean fully activated I/V relations from n = 7 cells in the two conditions (E_f = −16.0 mV in normal Tyrode and E_f = −34.4 mV in 35 mM Na⁺ as indicated). Arrows show the intercepts of the block curves with corresponding E_f values.

An interesting feature in Fig. 7 is that in both curves, the region of steepest slope was located across the expected I_f reversal potential (E_f). In n = 7 cells, we measured fully activated I/V relations in normal and reduced external Na⁺ according to standard protocols (DiFrancesco et al., 1986); E_f obtained from linear fitting of mean I/V curves (see Fig. 8) was −16.0 mV in normal Tyrode solution and −34.4 mV in low Na⁺ solution, with a shift of 18.4 mV. These values are indicated by dotted lines in Fig. 7 B, and clearly intercept the I/V curves in their regions of steepest slope.

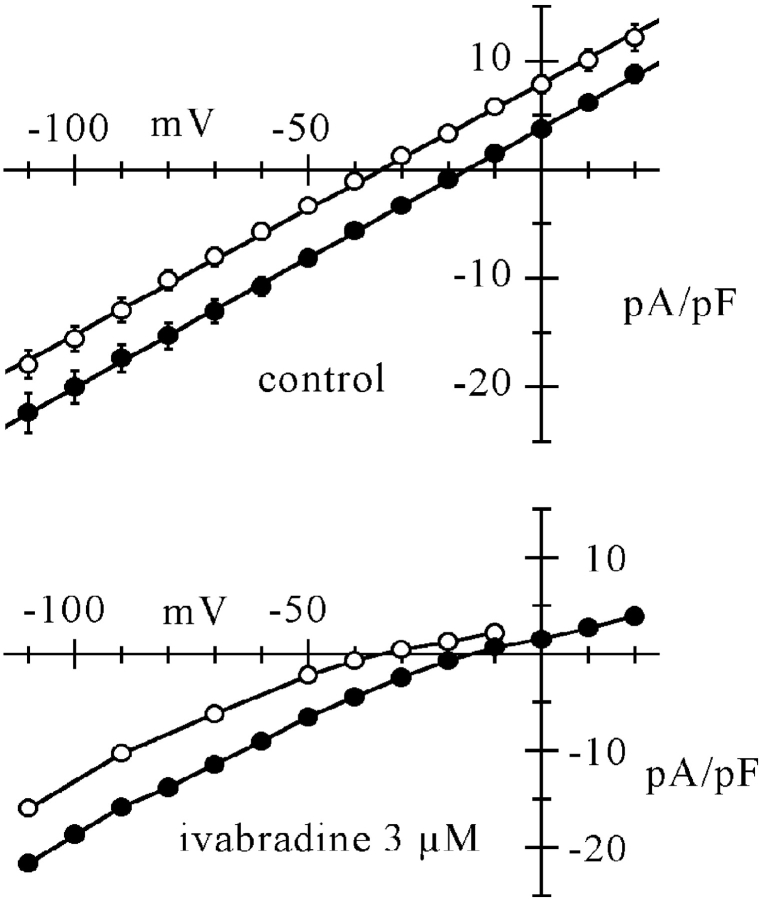
Figure 8.

Ivabradine causes inward rectification of I_f, which depends on E − E_f. Top: mean fully activated I/V relations measured from n = 7 cells exposed to both normal Tyrode solution (filled circles) and reduced (35 mM) Na⁺ concentration (open circles). I/V relations were measured as described previously (DiFrancesco et al., 1986), by applying pairs of steps, one to fully activate (1 s to −125 mV) and one to fully deactivate I_f (1 s to 15 mV), each followed by a step to the same test voltage, where the amplitude of the different current was measured. Mean ± SEM values are plotted. Linear fitting (straight lines) yielded reversal potentials (E_f) of −16.0 and −34.4 mV for normal and reduced Na⁺ concentration, respectively. Bottom: same curves, multiplied by fractional block values in normal and low Na⁺ solution as deduced from data in Fig. 7 at corresponding voltage and Na⁺ concentration. Strong rectification is apparent in the outward part of both curves, independently of the reversal potential. Lines through points.

These data agree with the results of Fig. 6 to indicate that the direction of ionic flow is a main determinant of the degree of block by ivabradine, i.e., block appears to be current-dependent rather than voltage-dependent, a feature typical of intracellular cation block of inward rectifiers.

To illustrate the inwardly rectifying action of ivabradine, in Fig. 8 mean fully activated I/V relations from n = 7 cells exposed to normal and reduced external Na⁺ concentration are shown in control conditions (top) and under conditions of steady-state block by 3 μM ivabradine (bottom). The latter curves were simply obtained by multiplying control curves of the top panel of Fig. 8 by the corresponding fractional block from Fig. 7. It is apparent that the drug induces inwardly rectifying behavior in both I/V relations, with the reduction of current becoming substantial at voltages E>E_f, independently of the E_f value.

DISCUSSION

Previous work (Bois et al., 1996) has indicated that ivabradine, a recently developed drug able to specifically slow cardiac rate in the absence of significant side effects on cardiac inotropism (Thollon et al., 1994; Peréz et al., 1995) acts in SAN cells by selectively blocking I_f channels from the intracellular side.

Other drugs have been synthesized on the basis of their ability to slow heart rate, such as UL-FS49 and ZD7288, and are known to exert their action by blocking the cardiac I_f current or the related neuronal I_h current (BoSmith et al., 1993; Goethals et al., 1993; DiFrancesco, 1994; Pape, 1994; Gasparini and DiFrancesco, 1997). The correlation between the inhibitory action on I_f and the bradycardic effect is a direct consequence of the relevance of I_f to the generation and control of pacemaker activity in mammalian heart (DiFrancesco, 1993). The aim of the present study was to provide a more detailed characterization of the blocking effect of ivabradine on f-channels in SAN cells.

Ivabradine Blocks Open f-channels, Leading to Use-dependent Blocking Action

When tested by an activation/deactivation protocol, ivabradine blocked I_f in a dose-dependent manner (Fig. 1) with a half-block concentration of 1.5 μM, a value similar to that obtained by Bois et al., 1996 (2.18 μM). Peréz et al. (1995) report an half inhibitory concentration of 8.5 μM for the effect of ivabradine on pacing rate in isolated guinea-pig right atria. These data agree with the view that the I_f block is the physiological target of the rate-reducing activity of the drug.

Use-dependent block is a mode of action shared by several ion channel blockers and arises from a preferential affinity of the drug for a specific conformational state of the channel (Hille, 2000). The experiments in Fig. 2 revealed that ivabradine binding/unbinding reactions are restricted to open f-channels only. The simplest interpretation of this finding is that the drug needs to enter a fraction of the channel pore before binding to the blocking site. According to this view, ivabradine molecules are able to access their binding site, located within the pore, and block ion flow only when the channel gate is open; when bound, drug molecules are confined from the intracellular environment by the channel gate. This idea agrees with the notion that native f/h- and HCN channels have a wide inner hydrophilic vestibule guarded by an intracellular gate (Shin et al. 2001). The structural analysis of HCN channels (Chen et al., 2001; Shin et al., 2001; Viscomi et al., 2001; Wainger et al., 2001; Wang et al., 2001) points to the involvement of the COOH terminus and the S6 segments as physical domains involved in channel gating. Thus, trapping of the drug could be associated with physical occlusion of a large intracellular channel vestibule by the interaction between these and possibly other channel domains. A recent investigation using cystein mutagenesis has confirmed the hypothesis that blocking molecules can be trapped inside HCN channels by an intracellular structure controlling voltage-dependent gating (Rothberg et al., 2002).

Ivabradine Causes a Current-dependent Block of f-channels

A block mechanism exclusively based on restricted access to the drug binding site, i.e., where drug-channel interactions are entirely controlled by the balance between open and closed states, should be expected to produce a voltage dependence of block similar to that of channel gating. However, binding can itself be voltage-dependent, in which case the occurrence of block is a more complex function of channel state and drug binding conditions. Several agents block hyperpolarization-activated channels in a voltage-dependent way. Block of I_f in SAN cells by extracellular Cs⁺ ions is markedly voltage-dependent and increases at negative voltages (DiFrancesco, 1982). In contrast to heart rate–reducing agents, Cs⁺ blocks I_f from outside, and its action can be explained by the simple assumption that Cs⁺ ions enter the channel pore for a fraction of the electrical distance (∼71% from outside) before binding to the blocking site (DiFrancesco, 1982), according to a model developed originally to explain Na⁺ channel block by hydrogen ions (Woodhull, 1973; see Hille, 2000). The block exerted on I_f by UL-FS49, a rate-reducing agent, is also voltage-dependent, but exerted this time from the intracellular side of the channel and decreasing at more negative potentials; Woodhull block model applied to UL-FS49 yields a blocking site located within the pore at some 61% of the electrical distance from outside (DiFrancesco, 1994).

Another rate-reducing molecule, ZD7288, has also been reported to exert a voltage-dependent block on hyperpolarization-activated channels (Shin et al., 2001). ZD7288, UL-FS49, and ivabradine (structures in Lillie and Kobinger, 1986; Harris and Constanti, 1995; Fig. 1), are all permanently charged cations at physiological pH and therefore require an aqueous pathway to reach the blocking site within the channel pore. This agrees with the idea that a wide aqueous vestibule exists in the pore of I_f channels (Shin et al., 2001), and that rate-reducing agents block I_f by interacting with channels within the pore vestibule.

In a detailed investigation of the action of ZD7288, Shin et al. (2001) interpreted the combined open-channel block and hyperpolarization-induced block relief properties of this molecule in terms of kinetic models where drug-channel interactions only occur when channels are open, but at the same time the drug affinity changes with the channel state. In one model, affinity is higher for bound-closed than for bound-open states, whereas in a second model two open states with different binding affinities and no binding to closed states are hypothesized. According to this interpretation, bound drug molecules remain “trapped” by channel gates and cannot be released from the binding site when channels are in the closed (or in a secondary open) state. In both models, smooth fractional block curves increasing with hyperpolarization are generated as experimentally observed, and the voltage dependence of block directly reflects that of the rate constants of drug binding to the different states of the channel.

Despite the similarities between ivabradine and ZD7288 in their actions, such as the open-channel block and block relief by hyperpolarization, the effect of ivabradine reported here does not appear to conform to models where block is governed by voltage-dependent drug binding.

First, in the presence of external Cs⁺, hyperpolarization does not relieve a previously induced block (Fig.6). Early experimentation on I_f in Purkinje fibers (DiFrancesco, 1982) and in the SAN (DiFrancesco et al., 1986) has shown, by use of envelope tests, that in the presence of Cs⁺, current activation during hyperpolarization proceeds normally, even if channels are blocked. The activation time-course was reported to be either moderately accelerated (DiFrancesco, 1982) or unchanged by Cs⁺ (DiFrancesco et al., 1986). Since therefore Cs⁺ blocks inward current without impairing channel activation gating, Cs⁺-induced I_f inhibition should not prevent a hyperpolarization-driven removal of ivabradine molecules from their binding sites if this simply depended on gates being open. The Cs⁺ result discriminates between a current-dependent and a voltage-dependent block relief mechanism, and rules in favor of the former. Although the requirement of restricted drug interaction with open channels typical of “open channel blockers” remains (i.e., ivabradine has a preferential affinity to open channels), the results with Cs⁺ (Fig. 6) imply that on hyperpolarization, even when channels are open, the drug remains associated with the blocking site unless inward current is flowing.

Second, experiments where the driving force is changed by varying chemical gradients, rather than voltage (Fig. 7), strengthen the evidence that block is indeed a function of the driving force, and not of voltage alone. The block curve in normal Tyrode solution (Fig. 5) did not have a smooth voltage dependence, as expected for a pure voltage-dependent process, but showed a steep slope just across the I_f reversal potential, suggesting the possibility that block could be affected by changes in the direction of current flow. This was confirmed by the use of low Na⁺ solutions, which produced a block curve which was shifted relative to the curve in Tyrode by approximately the same shift in reversal potential (−22.5 mV, see Fig. 7). Also in low Na⁺, a steep slope in the block curve was measured across the new reversal.

A voltage-dependent binding within the channel pore of a blocking molecule not competing with permeable ions would yield a simple Boltzmann distribution function for the fractional block b (b = ratio between blocked channels and channels in control), as follows:

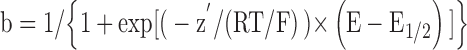(1)

where z′ is the equivalent valence of the blocking charge (i.e., z′ = z δ is the valence z of the blocking molecule multiplied by the fraction δ of electrical field crossed to reach the binding site) and E_1/2 is the voltage at which half block occurs. For example, this type of treatment and the above equation (with a negative value of z′ since block is in this case exerted from outside and increasing on hyperpolarization), apply to the I_f block by external Cs⁺ ions (DiFrancesco, 1982). Obviously, in this model, z′ cannot be higher than z, the valence of the blocking drug.

On the other hand, multiion single-file models where the blocking molecules compete with permeable ions for the same binding sites, generate a voltage dependence of block that can be steeper than is justifiable by the above Boltzmann distribution (Hille and Schwarz, 1978; Hille, 2000). The steepness of the conductance-voltage relation during block is therefore used as a means to identify channels behaving as multiion, single-file pores (Hille, 2000).

Although the block curves in Fig. 7 do not display a Boltzmann-type of voltage-dependence, clearly their maximal slope is not compatible with a simply voltage-dependent block. The derivative of the block function against voltage at E = E_1/2 is calculated from Eq. 1 as z′/(4RT/F); since at physiological pH ivabradine has a net valence of ∼1 (Delpon et al., 1996), the slope expected in this case should be 0.0097 mV⁻¹ for both curves. However, the slopes in Fig. 7, as measured in the steepest region (across reversal potentials), are 0.0265 and 0.0236 mV⁻¹ for control and low Na⁺ (requiring z′ = 2.7 and 2.4), respectively.

As well as a steep change of block degree, the fractional block of I_f by ivabradine undergoes a change in the mode of voltage dependence when the direction of current flow reverses (Fig. 7); whereas a shallow voltage-dependent decrease of block on hyperpolarization appears at E < E_f (inward current), the curve flattens up to a constant block (∼60%) at E > E_f (outward current). The reason for this behavior is unclear, but it suggests that the blocking mechanism may be more complex than that arising from antagonism between drug and permeable ions for binding sites within the pore, and may involve changes in the drug–channel interactions which depend on the direction of current flow. It is also possible, however, that the block is underestimated at the most depolarized voltages, since the time for drug–channel interaction becomes shorter with higher depolarization due to shortening of the deactivation time constant (DiFrancesco, 1999).

A possible dependence of HCN channel block by ZD7288 on the direction of current flow was not directly investigated by Shin et al. (2001). However, even in the hypothesis that this type of block could accommodate the very steep voltage-dependence reported for the ZD7288 block curve (z δ = 4.2), the latter curve differs importantly from the one described here; in fact, the voltage region of steepest slope is far more negative that the current reversal potential (see Shin et al., 2001, Fig. 3). This property cannot be easily reconciled with a current-dependent block. The I_f block by UL-FS49 also does not appear to be current-dependent, since Cs⁺ does not impair block relief by hyperpolarization (DiFrancesco, 1994). This indicates that even if I_f blockers have similar properties, different types of block may indeed be operating.

Ivabradine Induces f-channel Inward Rectification which Depends on E-E_f

The dependence upon driving force, rather than voltage, is a property of inwardly rectifying K⁺ channels (Kir). Typically, rectification in these channels depends on E − E_K rather than E, i.e., a strong current reduction is observed only at voltages more positive than the K⁺ equilibrium potential, E_K.

Rectification in Kir channels is attributable to channel block by internal cations, and its dependence on the ion-driving force, rather than voltage alone, is explained by the assumption that Kir channels are multiion, single-file pores (Hille and Schwarz, 1978; see Hille, 2000). In multiion, single-file pores, ions move in an ordered fashion along a set of binding sites extending across the full length of the channel, and several ions can simultaneously occupy available binding sites. Under these conditions, blocking ions (i.e., ions which cannot overcome one of the energy barriers along the pore path) are driven in and out of the blocking site along with the flow of ions, which therefore determines the extent of block.

Multiion single-file pores can in fact explain several other properties of K⁺ channels (Hille and Schwarz, 1978). Direct confirmation of single-file arrangement in Kcsa K⁺ channels has been provided recently by X-ray crystallographic analysis by MacKinnon and collaborators (Morais-Cabral et al., 2001; Zhou et al., 2001).

Hyperpolarization-activated channels are structurally similar to voltage-dependent K⁺ (Kv) channels (Santoro and Tibbs, 1999), and have in particular the same GYG selectivity filter motif, which is at the basis of the multiion permeation properties of K⁺ channels (Morais-Cabral et al., 2001; Zhou et al., 2001). In view of the conservation of ion conduction pores among K⁺ channels (Lu et al., 2001), they too are therefore likely to have a pore with multiion, single-file conduction properties. Indeed, some of the permeability properties of pacemaker channels (in rods: h-channels) require multiple ion binding sites (Wollmuth, 1995).

In conclusion, we find that the I_f block by ivabradine has unusual properties when compared with the block exerted on I_f by other rate-reducing agents (such as UL-FS49 and ZD7288). These properties are summarized by the dependence of block on the current driving force (E-E_f) rather than on voltage alone. Ivabradine block of I_f is therefore similar to the one exerted by blocking cations on Kir channels and responsible for inward rectification. Our data agree with the notion that f-channels have multiion, single-file pores, and that ivabradine blocks current flow by entering the pore from the intracellular side and competing with permeating ions for a binding site along the permeation pathway. Ivabradine molecules bind preferentially to open channels and cannot reach or leave their binding site when the channel gates are closed; block relief on hyperpolarization, however, requires not only that drug molecules are freed from trapping, but also that an active “pushing” mechanism operates during inward current flow to displace drug molecules and drive them out of the pore.

Finally, the use-dependence of drug action resulting from the specific features of I_f block by ivabradine and the high affinity of interaction with I_f channels (Bois et al., 1996) make this substance particularly suitable for possible use in a clinical setting, since they amplify the rate-reducing ability at high frequencies, i.e., when it is most needed, and reduce possible side effects due to interaction of the molecule with other ion channels, respectively.