Techniques for extracting single-trial activity patterns from large-scale neural recordings

Summary

Large, chronically-implanted arrays of microelectrodes are an increasingly common tool for recording from primate cortex, and can provide extracellular recordings from many (order of 100) neurons. While the desire for cortically-based motor prostheses has helped drive their development, such arrays also offer great potential to advance basic neuroscience research. Here we discuss the utility of array recording for the study of neural dynamics. Neural activity often has dynamics beyond that driven directly by the stimulus. While governed by those dynamics, neural responses may nevertheless unfold differently for nominally identical trials, rendering many traditional analysis methods ineffective. We review recent studies – some employing simultaneous recording, some not – indicating that such variability is indeed present both during movement generation, and during the preceding premotor computations. In such cases, large-scale simultaneous recordings have the potential to provide an unprecedented view of neural dynamics at the level of single trials. However, this enterprise will depend not only on techniques for simultaneous recording, but also on the use and further development of analysis techniques that can appropriately reduce the dimensionality of the data, and allow visualization of single-trial neural behavior.

Introduction

A large literature is based on the recording of single neurons, one at a time. This approach typically depends on being able to collect repeated views of the same neural process. For example, on repeated ‘trials’, the same stimulus may be shown to an animal trained to behave consistently. The trial-averaged responses of sequentially-recorded neurons can then be combined to estimate what would have been observed had it been possible to record simultaneously. Still, evoking exactly the same response from the brain across repeated trials is rarely possible. In such cases, the trial-averaged response may not be representative of what occurred on individual trials. Certainly it cannot tell us how the responses of different neurons covaried across trials. There are thus a variety of motivations for large-scale simultaneous recordings using arrays of electrodes [1–4]. Many of these motivations have been reviewed extensively, especially in the contexts of neural coding [5–7], and motor prosthetics [8–11]. We therefore survey these topics briefly, and focus on motivations related to the study of neural dynamics, especially in the context of motor control. We review recent studies illustrating two key facts. First, and unsurprisingly, interesting temporal dynamics can be observed in neural recordings in a variety of contexts. Second, and perhaps more surprisingly, those dynamics can unfold differently on different trials. This latter fact provides strong motivation not only for simultaneous recordings, but also for analysis methods that can reduce the high-dimensionality of the recorded data in a revealing way. We therefore end by reviewing recent progress in the development and application of dimensionality reduction techniques appropriate for simultaneously-recorded extracellular responses.

General motivations for implanted-array recording

A straightforward advantage of implanted electrode arrays (Fig. 1A,B) is that a large dataset can be recorded in a single day, allowing rapid iteration of analysis and experimental design. Furthermore, isolations are typically stable for hours, in some cases days. Thus, the desire to collect a good deal of data quickly from stable isolations can provide sufficient motivation [e.g., 12], particularly if neural plasticity is the topic of study [e.g., 13,14]. Still, the strongest motivations relate to the simultaneous nature of array recordings, and the need to know how the activity of different neurons varies together across not-quite-identical trials [15]. For example, measuring covariance on a fine timescale is one of the few ways to assess functional connectivity in vivo [e.g., 16]. Covariance measurements are also important when examining how sensory information is represented. This is true both when relative spike timing is hypothesized to convey information [e.g., 17], and in the more traditional case of rate coding, where correlations may affect the accuracy of the representation [18–21]. Although many of the above issues can be addressed via recordings from multiple conventional electrodes [e.g., 22], implanted-arrays have an advantage both in isolation stability and in scale (the number of comparable pairs scales as the square of the number of recorded neurons). Most importantly from the standpoint of this review, the study of neural dynamics benefits from recording as much data as possible on single trials. As discussed further below, this is especially true in the context of motor and premotor processes.

Figure 1.

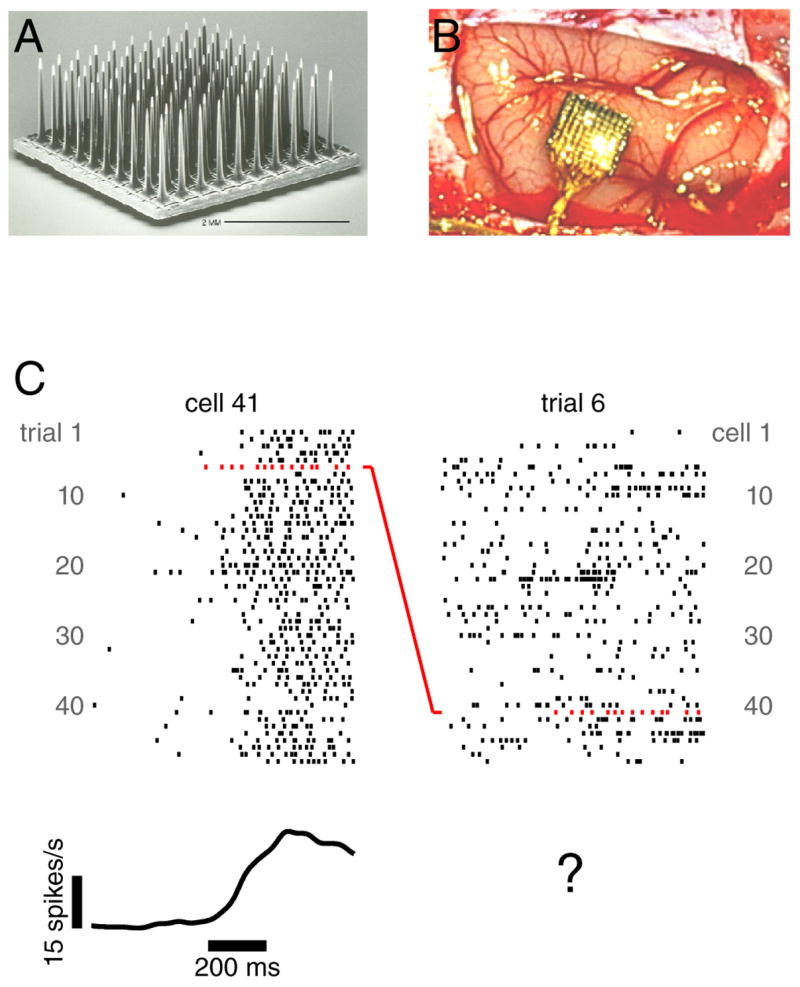
Illustration of array recordings. A. A silicon 100-electrode array (image courtesy of Cyberkinetics Neurotechnology Inc.). B. A similar array immediately following implantation in dorsal premotor cortex. C. Example data recorded from that array during a delayed-reach task. Ticks indicate the occurrence of action potentials. Each row plots the response of one neuron on one trial. Left: the response of one neuron across many rightward reaches to a 6 cm distant target. The trace at bottom plots the mean after convolving with a 25 ms Gaussian. All data are aligned to the onset of the target (left side of scale bar). Right: the response of many neurons for a single reach. All neurons were judged to have tuned delay-period activity (although for most neurons this trial did not employ the preferred target). Note that one spike train appears in both the left and right plots: that of neuron 41 for trial 6 (red rasters).

Array recordings and neural dynamics during motor control

In the study of motor control, many of the advantages of implanted arrays simply parallel those for sensory systems. Additional information may be ‘coded’ by spike synchrony and/or rate covariance [23–26], and abnormal synchrony may signal dysfunction [27,28]. And as with sensory systems, uncovering functional connectivity may be central to understanding how motor circuits function [29]. But perhaps the greatest advantage of array recordings is their potential to address a limitation inherent to the study of motor control: a given movement is rarely repeated perfectly across repeated trials [26,30–35], and the neural events preceding the movement may be very different across trials [36,37]. Under such circumstances, a neuron’s trial-averaged firing rate may not reveal its true behavior. Of course, even sensory systems can exhibit considerable trial-to-trial variability, [e.g., 38]. Still, such concerns are typically greater for the motor system; a consequence of it being harder to train a repeatable movement than to design a repeatable stimulus.

Array recordings have the potential to overcome the obstacles posed by across-trial variability: one may hope to gain statistical power across neurons instead. Trial-to-trial variability might then become an asset, providing different views of the same dynamic process. Unfortunately, gaining statistical power across neurons (Figure 1C, right column) is not as trivial as gaining statistical power by averaging across trials (Figure 1C, left column). It requires analysis methods capable of productively reducing the high dimensionality of the recorded responses [7,39,40]. Before committing to that path, it is reasonable to ask whether trial-by-trial variability is, in practice, large enough to pose a problem. If not, across-trial averaging may be all that is needed. We therefore review recent results indicating that trial-to-trial variability is indeed a concern both during movement generation, and during the internal neural events – planning, decision-making – that precede it. We then return to the issue of analysis methods that can tackle such variability.

Trial-by-trial variability during movement generation

The relationship between cortical activity and movement is a contentious issue [12,41–46]. Issues of dynamics are central to that debate. How do the temporal patterns of neural activity relate to quantities such as hand velocity and muscle activity? What are the network dynamics generating those patterns? In addressing such questions, a neuron’s time-evolving firing rate is often estimated by averaging across trials. For example, in figure 2, the mean rate (gray trace) is statistically reliable (the SE is modest), and is hoped to indicate the ‘true’ rate underlying the 51 spike-trains above. The corresponding 51 reaches (not shown) were very similar, but not identical to one another. In particular, peak hand velocity had a SD (±19 cm/s) that was substantial relative to the mean (60 cm/s). Such variability is endemic to reaching (e.g., in [47] mean movement duration was 545±242 ms). However, in this case variability was under partial experimental control. Red and green targets instructed different reach speeds, and a segregated analysis reveals different neural responses (red and green traces). The mean across all trials (gray) is a mixture of these two patterns, and is probably something that never occurred on any given trial. And of course, even the segregated averages contain some remaining variability, and may not be entirely representative.

Figure 2.

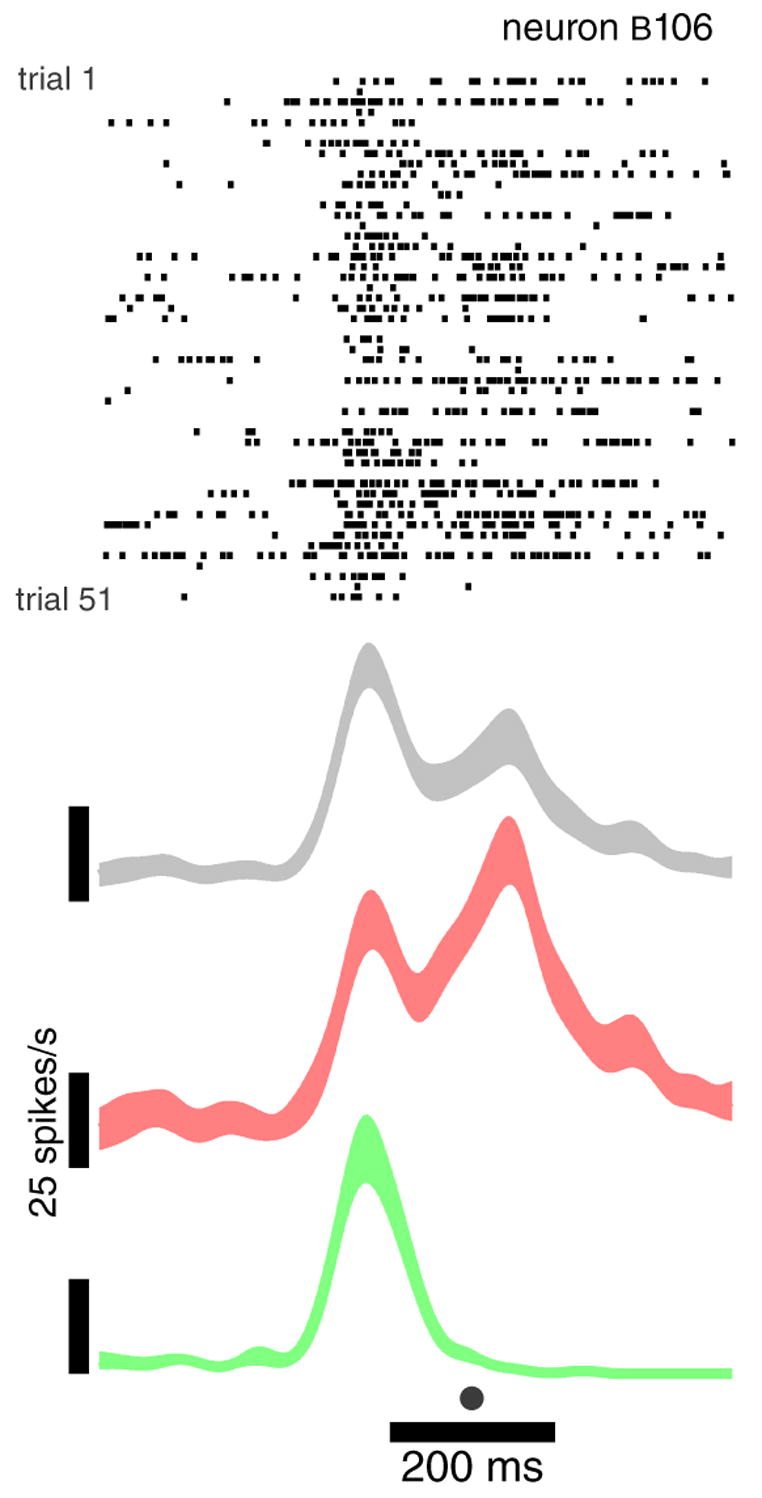
Example recording from a neuron in motor cortex, using a single electrode. Data are for 51 reaches to a 6-cm-distant rightwards target (one row per trial, ticks mark spike times). Data are aligned at the time of peak hand velocity (dot at bottom). Movement duration varied between 150–250 ms. Traces plot the mean firing rate ±SE (trace width), after convolving with a 25 ms Gaussian. The mean is shown separately for all trials (grey), instructed-fast trials (red), and instructed-slow trials (green).

In freely-moving rodents, the above problem is often magnified - a rat may explore a maze differently each time - and that field has gravitated strongly to simultaneous recordings [e.g., 48]. Still, for primates, careful behavioral control can produce similar movements, and detailed behavioral measurements can allow restriction of analysis to the most similar [26]. For these reasons, trial-to-trial variability poses the greatest concern not for the study of movement per se, but for the study of the internal processes – decision making, motor planning – that precede movement. It is in these cases that simultaneous recordings – and accompanying analysis methods – are most needed.

Challenges arising from uncontrolled variability during internal processing

Neural dynamics are of obvious relevance to motor control (where a temporally-patterned output is the goal; e.g., [49] ) but are presumably also central to many forms of cognitive and sensory processing [e.g., 50,51, for recent review see 52]. In such cases, the relevant dynamics may be largely internal: they may not be relatable on a moment-by-moment basis to any externally measurable quantity. An example from the sensory domain is illustrated in figure 3A. Presentation of an odor initiates an evolving pattern of neural activity that outlasts the stimulus, and takes time to return to its starting state [53, also see 54,55,56]. In that study, not all neurons were recorded simultaneously, and some trial-averaging was performed to combat noise (each trajectory averages three trials). This is acceptable, as the ‘neural trajectories’ appear quite repeatable for a given odor concentration. But in other cases – especially cases of premotor processing – a stimulus may initiate a process that unfolds differently on different trials. Horowitz et al. [57] found that neurons in the superior colliculus exhibited ‘streaky’ behavior during a discrimination task, as if the system vascillated between the two choices. Because neurons were recorded sequentially, further examination of such dynamics was not possible. More recently, Briggman et al [58] studied choice behavior in the leech, and monitored many neurons simultaneously using optical imaging. Principal components analysis (PCA) allowed a low-dimensional view of dynamics on single trials (fig. 3B). A similar plot could likely have been created using sequential recordings, after sorting trials according to choice. Yet that approach would have missed a rather interesting feature: the network sometimes vacillated before settling on a choice (green trace).

Figure 3.

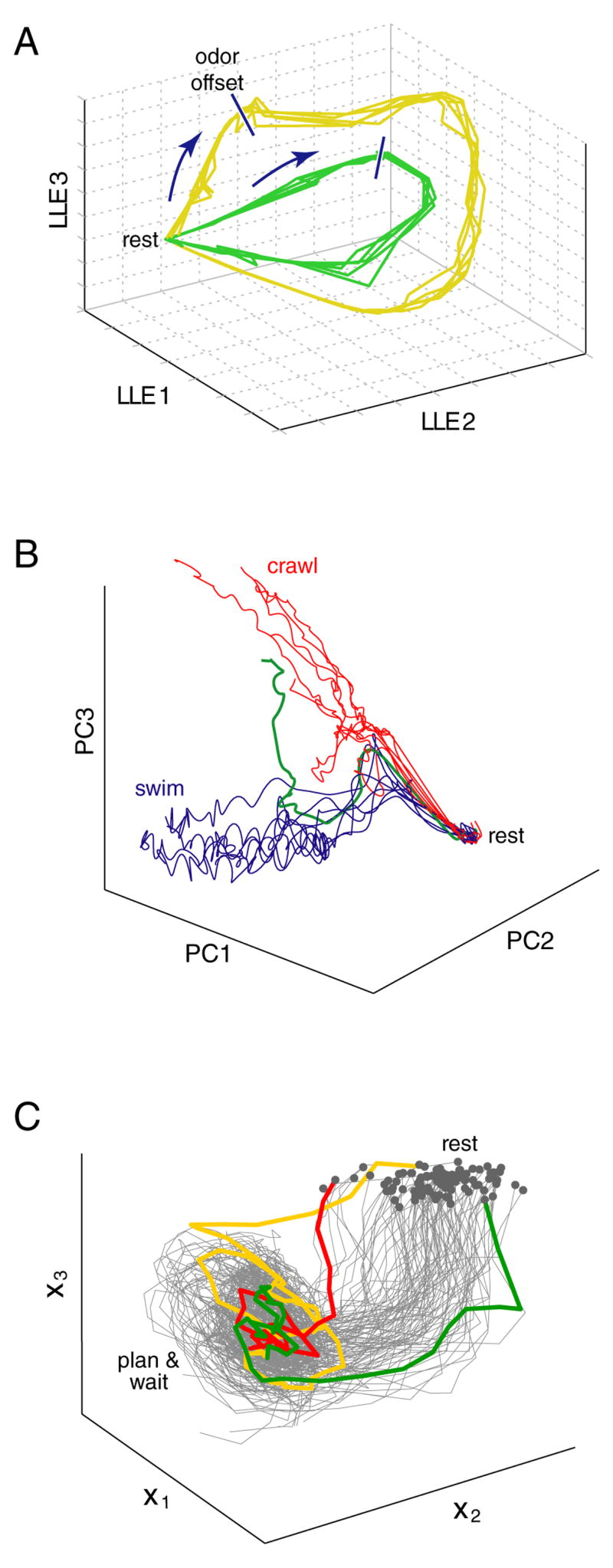
Reduced-dimensionality views of neural trajectories in three systems. A. Three-dimensional projection of the extracellularly-recorded spiking activity of 110 locust antennal-lobe neurons, using local linear embedding (LLE). Odor presentation drives the neural state in the direction indicated by the arrows. The state continues to evolve following odor offset, and returns to rest after ~6 seconds. The size of the looping trajectory is concentration dependent (yellow > green). Each of the 10 traces is an average of three trials. Reprinted in modified form from [53]. B. Three-dimensional projection, using PCA, of the activity of 143 neurons from one of the leech midbody ganglia, recorded using voltage-sensitive dye imaging. An electrical stimulus induced the network to ‘choose’ between crawling (red trials) or swimming (blue trials) motor patterns. Reprinted in modified form from [58]. C. Three-dimensional projection of the spiking activity of 75 units (14 single-neuron and 61 multi-neuron extracellular recordings) recorded from premotor cortex of a monkey planning a reach. Trajectories were extracted using a dynamical systems approach, in which the state of the dynamical model had three dimensions (x₁,x₂,x₃). All data are from the ‘planning’ (pre-movement) period, starting with target onset, and ending at the time of the go cue. Reprinted in modified form from [40].

Even in the absence of a choice, across-trial variability is a prevalent feature of premotor processing. Most obviously, reaction time typically varies across trials, and the latency of premotor responses may vary with it [59,60]. Churchland et al. [37], recording in monkey premotor cortex, found that response variability declines dramatically during movement planning (Figure 4, black trace). It appears that the mean is rather un-representative of individual-trial behavior early on, but becomes representative with time. Their interpretation was that the neural state converges to an appropriate movement plan over time; i.e., that the neural circuit exhibits attractor dynamics. Yet as with Horowitz [57], no attempt was made to visualize the neural trajectory on individual trials. This was in part because most recordings were sequential, but also because it is non-trivial to extract meaningful structure from noisy, high-dimensional neural data. For example, ‘raw’ plots of single-trial responses (e.g., Figure 1C, right column) were not terribly revealing even when data were recorded simultaneously.

Figure 4.

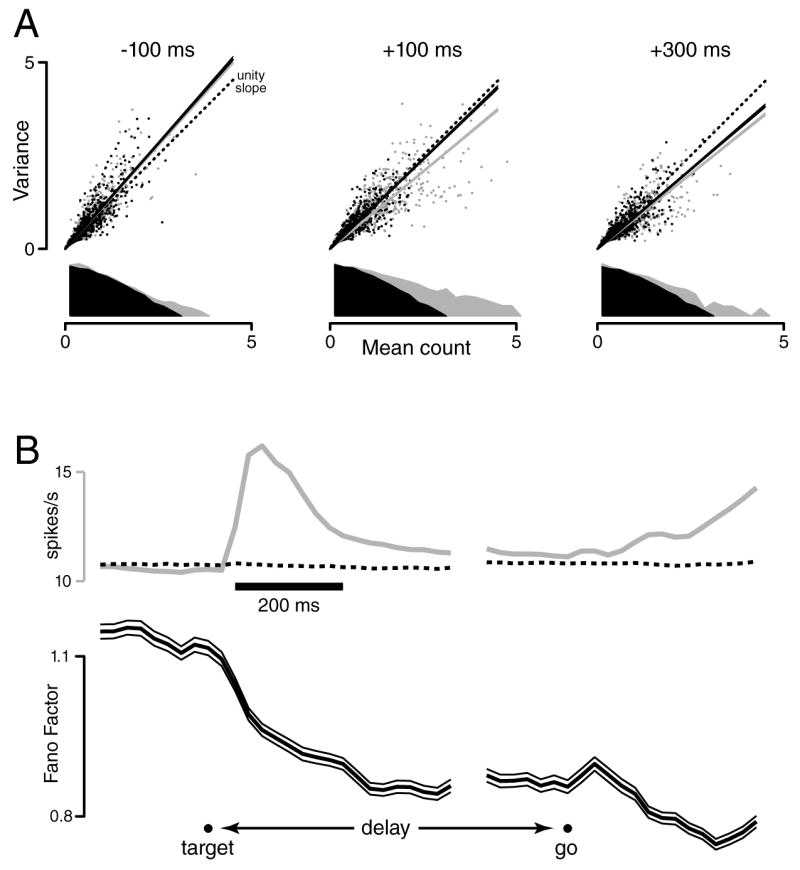
Across-trial neural variability during a delayed-reach task. A. Scatterplots of spike-count variance versus mean, using a 50 ms sliding window (one dot per neuron/target-location). For clarity, only 25% of the 4264 points are plotted). The grey marginal distribution plots, on a log vertical scale, the distribution of mean counts. Three plots are shown, with the window centered 100 ms before, 100 ms after, and 300 ms after target onset. The slope of the variance/mean relationship (grey line) is reduced following target onset. That reduction is still present (black line) when distributions of mean counts are down-selected to match across times (black dots/distributions). B. Mean firing rate (grey, across all neurons/condition) and the Fano Factor (black, with flanking 95% CIs,) as a function of time. The Fano factor is the slope of the linear regression (black lines in A), after matching the distribution of rates across times. The dotted trace plots the mean firing rate after that matching, which by construction changes very little. Even for the unrestricted mean (grey), the overall firing rate changes only modestly, as it is computed across both preferred and non-preferred conditions, and across responses of both signs. Analysis was performed with data locked to target onset (left) and the go cue (right). A break appears in the plot due to the variable delay period.

None of the studies reviewed above depended on implanted arrays (although Briggman et al. depended on simultaneous imaging, see also [38,61]). Still, they illustrate a rising interest in neural dynamics during ‘internal processing’, and a rising appreciation of the challenges posed by across-trial variability. Those challenges are typically greater for internal processing than for movement generation, for three reasons. First, training can reduce variability in the movement trajectory, but may not reduce variability in the preceding ‘neural trajectory’. In [37], monkeys had extended (~10⁶ trials) training, yet neural events were still inconsistent across trials. Second, while behavioral measurements can be used to segregate movement-related recordings prior to analysis (e.g., into reaches of similar trajectories), the behavioral measurements most relevant to internal processing (choice, reaction time) are less rich, and available only after the neural events have unfolded. Finally, in the case of movement generation, one can make millisecond-by-millisecond comparisons between noisy neural signals and high-fidelity behavioral recordings. But for internal processing, if one wishes to relate neural activity to another time-varying physiological signal, there are few choices other than the activity of other neurons. This necessitates simultaneous recordings, and analysis methods capable of contending with the noisiness of neural responses.

Statistical methods for overcoming/exploiting trial-to-trial variability

Simultaneous recordings, on their own, simply increase the number of noisy spike trains to be analyzed (e.g. Figure 1C, right column). The high dimensionality of the data (one dimension per neuron) makes it difficult to directly view the ‘neural trajectory’, or to extract concise descriptions of its structure. To truly exploit the simultaneity of the recordings, methods that reduce the dimensionality of the data are typically needed.

An implicit form of dimensionality reduction is often performed in the context of neural prosthetic systems, when the trajectory of the arm is ‘decoded’ from simultaneously-recorded neurons [62–64]. High (~100) dimensional neural data is collapsed into a low (e.g., 3) dimensional arm trajectory estimate. The decoded trajectory is thus a concise ‘explanation’ or summary of the high-dimensional neural data. Decoding techniques include linear filters [63,64], the population vector [62,65,66], and recursive Bayesian decoding using state-space models [67–69]. Most of these approaches attempt to infer something that can be directly observed/inferred on most trials (e.g., actual or expected arm trajectory), yet in some ways this is an advantage, as it allows evaluation of the performance of different decoding techniques.

Yet while a variety of ‘decoders’ have been shown to perform well in a prosthetics context, their suitability as general dimensionality reduction techniques bears two caveats. First, such decoders assume that the critical dimensions present in the neural data can be expressed in external co-ordinates, such as hand velocity. In general, the critical dimensions may have no direct relationship with quantities expressed in external co-ordinates; they may be related more closely with the internal dynamics of the neural system from which the data were recorded. Furthermore, when decoding into external quantities, most decoders assume a ‘tuning’ model. Yet the degree to which neurons in the motor cortices obey these tuning models is a matter of debate [12,41–46]. The second caveat is that, when studying internal processing, there is no ongoing behavior to which the trial-to-trial neural variability can be compared. This comparison is usually necessary not only to test, but also to construct the decoder. In this case, unsupervised techniques are needed that can identify low-dimensional statistical regularities in the high-dimensional neural data, without relation to externally measurable quantities. Instead of an arm trajectory, the goal is to extract a low-dimensional neural trajectory that provides a summary of the high-dimensional neural data. One’s confidence that this can be achieved is certainly increased by the success of the related decoding methods in the prosthetics context. However, in the case of internal dynamics, verification will depend not on direct comparison with ongoing behavior, but on whether the neural trajectory can be used to predict some future behavioral quantity, such as reaction time, choice, or accuracy.

Unsupervised dimensionality reduction techniques that have been productively applied to neural data include PCA [55,58] and Local Linear Embedding (LLE) [53,56,70]. As was illustrated in figure 3A,B, these techniques can reveal low-dimensional neural trajectories that would not have been readily apparent looking at the high-dimensional data directly. PCA has also recently been used to view neural trajectories during fictive hunting in the marine mollusk Clione [71]. Importantly – and underscoring the need for simultaneous recordings – those trajectories were different across trials. However, a possible drawback of ‘static’ dimensionality techniques (including PCA, LLE, and the population vector) is that they do not exploit a key property of the data: the temporal relationship between the datapoints. Such information could both help identify the important dimensions in the data, and allow for the identification of a low-dimensional hidden dynamical system that can summarize and explain the simultaneously-recorded spike trains. To illustrate this idea, consider multiple noisy video sequences of a bouncing ball, where the ball's trajectory may not be identical in each sequence. A static method would first apply a dimensionality reduction technique, and then simply connect the resulting low-dimensional points in time. Alternately, the time labels can be exploited for dimensionality reduction by attempting to directly identify a hidden dynamical system underlying the sequence of noisy video frames, thereby uncovering the various laws of physics governing the motion of the ball.

The central idea of this dynamical systems approach [36,40,72–77] is that the responses of different neurons reflect different views of a common dynamical process, whose effective dimensionality is much smaller than the number of neurons involved. While the neural trajectory might evolve differently on different trials, the commonalities among trajectories provide clues about properties that do not vary from trial-to-trial. Such properties include the rules governing the time-evolution of the neural trajectories (the dynamics), as well as how the activity of each neuron relates to the underlying trajectory.

The dynamical systems approach has been previously applied to simultaneous spike trains in cat [73] and monkey [72] visual cortex. In those studies, the neural responses were driven on a moment-by-moment basis by visual stimuli. The dynamical systems approach, however, is particularly well-suited for cognitive tasks in which the neural responses are not purely stimulus-driven, and may evolve differently on different trials. For example, work using hidden dynamical models indicates that neurons in monkey frontal cortex transition between discrete states during an instructed delay period [36,74,75] (Fig. 5A). Because the state transitions occurred at different times on different trials, the dynamical model was often able to make predictions that were more accurate than those of a static model [36]. We have recently explored dynamical models with a continuum of states in the context of motor preparation [40]. Trajectories extracted from simultaneous recordings in monkey premotor cortex indicate that motor planning proceeds along different paths on different trials (Fig 3C). The dynamical systems approach has also been fruitfully applied to detecting singing-like and awake-like states in sleeping songbirds [77], stimulus onset and saccadic eye-movement times in monkeys performing free-viewing tasks [76], and the instructed state in a delayed-reach task [78] (see Fig. 5B).

Figure 5.

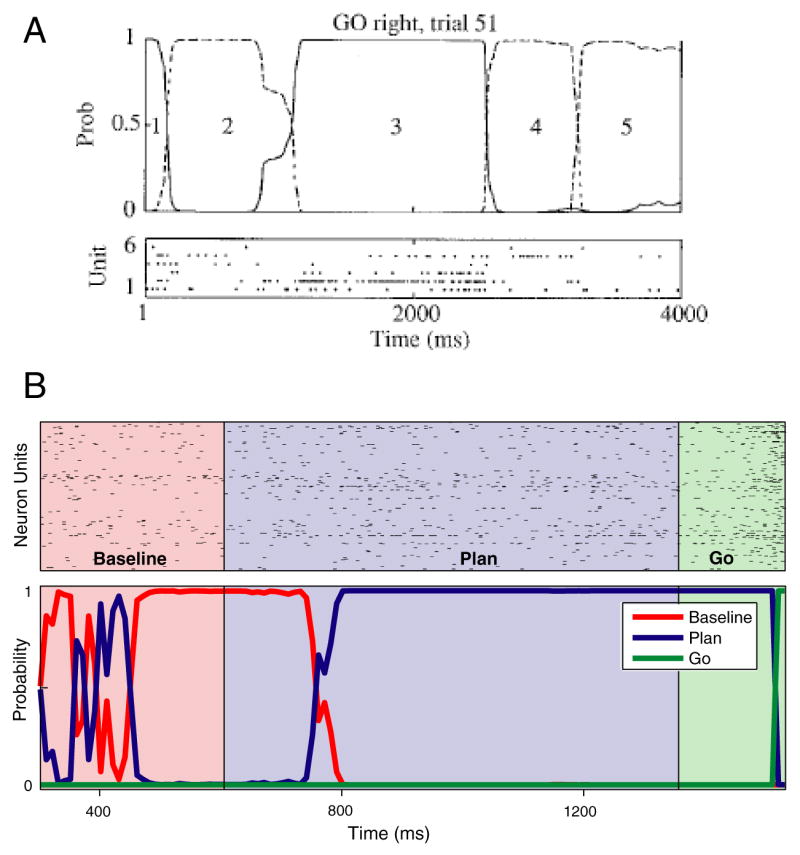
Inferring underlying internal state from noisy neural data. A. Inferring internal state in a monkey performing a GO/NO-GO task. Rasters at bottom show the activity of 6 neurons, recorded on the same trial from frontal cortex. Neural activity was assumed to depend on the state of a hidden Markov model. Traces at top plot the inferred probability of the states of that model, based on the spiking data below. The most likely underlying state progresses in order, from 1 though 5, although different states are visited for different lengths of time. On other trials, the states progressed in different orders. Reprinted in modified form from [36] B. Inferring internal state during a delayed-reach task. Neural data from many simultaneously-recorded neurons (top) was assumed to be generated by an underlying 3-state model. Those states corresponded to the instructions during the task: ‘baseline’ – before target information is known, ‘plan’ – after the target is presented, and ‘go’ – around the time of execution. Colored traces at bottom plot the probability of each state versus time. Unlike in [36], the focus of this study was on prosthetics, and the internal state being inferred is already largely known (it presumably follows the instruction with a modest lag). This provides an opportunity to directly assess the accuracy of the method. Reprinted in modified form from [78].

The use of a dynamical systems approach requires some assumptions about the nature of the dynamics underlying the data being analyzed. For example, does the system evolve continuously, or by jumping from state to state? Such questions can often be answered by first visualizing the data in a low-dimensional space using static techniques. Indeed, static techniques alone may be sufficient if one desires only to obtain the trajectories without learning the rules governing their time-evolution. Still, in all cases, it is critical that the data be collected simultaneously if we wish to investigate the system dynamics.

Conclusions

Implantable electrode arrays are a necessity for the development of cortically-based motor prosthetics, due to the single-trial statistical power they provide. The same single-trial power may also prove critical when addressing many basic science questions. This is particularly likely to be true for the study of premotor processes, including movement choice and planning. It may also be true for ‘internal processing’ in more cognitive and perceptual domains. To succeed, this approach will require the use and development of analysis methods that appropriately reduce the dimensionality of the data, and extract the dynamic commonalities that underlie different single-trial responses.